Abstract
Natural modes and frequencies of three-dimensional (3D) deformation of the human brain were identified from in vivo tagged magnetic resonance images (MRI) acquired dynamically during transient mild acceleration of the head. Twenty 3D strain fields, estimated from tagged MRI image volumes in 19 adult subjects, were analyzed using dynamic mode decomposition (DMD). These strain fields represented dynamic, 3D brain deformations during constrained head accelerations, either involving rotation about the vertical axis of the neck or neck extension. DMD results reveal fundamental oscillatory modes of deformation at damped frequencies near 7 Hz (in neck rotation) and 11 Hz (in neck extension). Modes at these frequencies were found consistently among all subjects. These characteristic features of 3D human brain deformation are important for understanding the response of the brain in head impacts and provide valuable quantitative criteria for the evaluation and use of computer models of brain mechanics.
1. Introduction
Traumatic brain injury (TBI) is a serious public health issue. TBI affects 40% of American adults over their lifetimes (Gardner et al., 2018); 2.8 million Americans seek medical treatment for TBI every year (Gardner et al., 2018). TBI is particularly serious for geriatric patients (Gardner et al., 2018) but TBI also affects 3 million children every year worldwide (Dewan et al., 2016). TBI increases the chances of developing anxiety and depressive disorders (Scholten et al., 2016). Even sub-concussive head impacts, if repeated, can cause chronic traumatic encephalopathy (CTE), a neurodegenerative disorder affecting memory, cognition, and emotion. Mild TBI and CTE are associated with diffuse injury caused by rapid brain deformation from high skull accelerations that arise in accidents, assaults, or contact sports.
Better understanding of brain mechanics is needed to develop rational approaches to prevention and treatment of acceleration-induced TBI (Fahlstedt et al., 2016; McAllister et al., 2012; Patton et al., 2015; Wu et al., 2020). Frequency content offers a powerful and simple measure of the accuracy of a computer model. If a model accurately captures the material properties and interfacial attachments of the brain, it may be expected to accurately predict its natural frequencies. Modal frequencies may also reflect differences between individuals or changes in individual brain behavior over time. A mechanical system is deformed more easily by loading near its natural frequency, which may make the brain vulnerable to certain impacts.
It is challenging, but feasible, to measure motion of the intact, living human brain at sub-injury levels using magnetic resonance imaging (MRI). Magnetic resonance elastography (MRE) of the brain (Atay et al., 2008; Clayton et al., 2012; Guertler et al., 2018; Johnson et al., 2013; Kruse et al., 2008; Sack et al., 2009) relies on phase-contrast MRI to visualize low-amplitude shear waves in brain tissue excited by harmonic skull excitation. MRE studies suggest that low frequency modes or low frequency shear waves are potentially more damaging to the human brain than high frequency shear waves since they appear to penetrate deeper into the brain and cause more deformation (Okamoto et al., 2019).
Deformation of the brain due to mild (sub-injury), transient skull acceleration in human volunteers has been measured using tagged MRI, both in two-dimensional (2D) slices (Bayly et al., 2005; Sabet et al., 2008) and in 3D volumes (Chan et al., 2018; Gomez et al., 2019). In tagged MRI, variations in longitudinal magnetization are induced in tissue by a combination of radiofrequency pulses and magnetic field gradients. These variations in magnetization induce differences in image intensity (Figure 1) associated with material elements, which can be tracked and analyzed to estimate tissue displacement vector fields, as well as strain tensor fields in 2D or 3D. Such MRI-derived strain fields have been compared to predictions of computational models of brain biomechanics under sub-injury loading to evaluate these models (Zhao and Ji, 2020). Measurement of brain motion during injury-level impact in cadaveric specimens has been done at higher temporal resolution, but lower spatial resolution, by Hardy et al. (2007) and Alshareef et al. (2018), including estimates of natural frequency (Alshareef et al., 2018).
Figure 1.
Tagged MRI at different times relative to mild, impact-induced, rotational deceleration. Row (a): Gel phantom. Row (b): Brain of a human subject imaged in vivo. Scale bar: 5 cm.
Dynamic deformation of elastic or viscoelastic solids can be described in terms of oscillatory spatial modes. The brain might be particularly vulnerable to motion at frequencies corresponding to such modes (Wu et al., 2020). Previous research on identifying specific natural modes of 3D brain deformation has largely relied on analysis of simulated brain motion (Laksari et al. (2018), e.g.) rather than actual brain behavior. Laksari et al. (2018) used dynamic mode decomposition (DMD) to analyze the transient behavior of a finite element computer model of brain motion (Giordano et al., 2014), which exhibited dominant natural frequencies around 30 Hz. Wu et al. (2020) used computer modeling to estimate natural frequencies in the brain of 40–70 Hz from parameters that maximized first principal strain (Wu et al., 2020).
DMD, previously used by Laksari et al. (2018) and Schmid (2010) to identify dominant frequencies and modes from simulations, can also be applied to experimental data. DMD requires only short time series of full-field data, overcoming limitations of traditional Fourier analysis. DMD decomposes the data into the contributions of specific mode shapes, each multiplied by a time-varying coefficient. Typical modal behavior is a decaying oscillation with characteristic damped natural frequency and damping ratio. Laksari et al. (2015) used a related approach to analyze previously-published 2D tagged MRI data (Feng et al., 2010) of mild frontal impact (“yes” nodding). They estimated natural frequencies near 15 Hz for a rigid-body component of brain motion in the sagittal plane (Laksari et al., 2015). Such experimental observations of natural frequency could be used to evaluate computer models.
The objective of the current study is to identify and characterize oscillatory modes of 3D deformation in the human brain by applying DMD to full-field, 3D strain tensor fields from tagged MRI acquired during transient skull accelerations (Knutsen et al., 2020). The data were acquired during two motions of the head: rotation about the long axis of the neck (turning “no”) and extension of the neck (nodding “yes”). Specific targets include the mode shapes, damped natural frequencies, and damping ratios of the dominant modes of 3D brain deformation.
2. Methods
Data consisting of twenty 3D displacement and strain fields due to mild head acceleration (neck rotation or neck extension) were previously obtained from 19 human volunteers (11 M, 8 F, 21–42 years (mean 31 ± 6)) (Knutsen et al., 2020). DMD (Laksari et al., 2018; Schmid, 2010; Tu et al., 2014) was used to extract the fundamental mode of oscillation (“mode 1”) from strain fields in both cases. To validate and illustrate our implementation, DMD was also applied to (i) data from simulations of a finite element computer model and (ii) data from tagged MRI experiments using a gelatin (“gel”) cylinder phantom (Figure 1).
2.1. Tagged MRI Experiments
2.1.1. Tagged MRI in human volunteers
Experimental methods, image acquisition, and estimation of displacement and strain fields are described in detail in Knutsen et al. (2020) and summarized briefly here for convenience. Subjects were scanned in the Clinical Center at the National Institutes of Health (NIH) under a protocol approved by the NIH CNS Institutional Review Board. MR images were acquired on a Siemens 3 T mMR Biograph scanner (Siemens, Munich, Germany) during constrained head accelerations of neck rotation and neck extension. In neck rotation (rotation within the axial plane), the subject’s head was placed in a “cradle” device that, when voluntarily activated by the subject, would rotate the head 32° toward the left shoulder. An elastomeric bumper arrested the rotation of the cradle, creating mild angular deceleration at impact (peak α = ~150–250 rad/s2; ~50 ms duration) and measurable brain deformation. Pre-impact angular velocity in neck rotation was in the range ω = ~2.5–4.0 rad/s. Neck extension (rotation within the sagittal plane) was performed similarly, except the subject’s head was supported by a cradle which was raised slightly and then voluntarily released by a latch. The cradle was allowed to drop onto a soft pad causing mild angular deceleration (peak α = ~200–350 rad/s2; ~50 ms duration) with pre-impact angular velocity ω = ~1.5–2.0 rad/s. The angular acceleration pulse contained frequency content up to > 80 Hz (See Supplementary Material Figures S.2–S.5).
Initiation of motion was detected by an optical sensor, triggering a “spatial modulation of magnetization” (SPAMM) tagging sequence, generating images with a spatial pattern that deforms with tissue. Tagged images were acquired by a 2D segmented cine gradient-echo sequence (TR/TE = 3.01/1.67 ms, tag spacing = 8 mm, FOV = 240×240 mm, slice thickness = 8 mm, gap between slices = 2 mm, temporal resolution Δt = 18 ms, number of image frames = 10–12). For neck rotation, image acquisition was triggered by an optical encoder (MR338, MICRONOR, USA) at 28.5° rotation (3.5° before impact). The encoder provided angular position, velocity, and acceleration data with 0.85 ms temporal resolution; impact time and duration were determined from the start and width of the acceleration pulse.
Tagged MR images (Fig. 1) were used to estimate 3D displacement vector and Lagrangian strain tensor fields (Gomez et al., 2019; Knutsen et al., 2020; Knutsen et al., 2014). The 3D strain tensor was used in DMD analysis, since it completely characterizes deformation without the contribution of rigid-body motion. In addition to analyzing the 3D strain tensor fields, we analyzed 2D strain tensor fields from tagged MRI during neck rotation, obtained previously (Knutsen et al., 2014), to test if there was an effect of temporal sampling rate. Four 2D strain data sets (all from the same subject) were obtained using 6 ms/frame, 12 ms/frame, 18 ms/frame, and 24 ms/frame. More details can be found in references (Knutsen et al., 2014), (Knutsen et al., 2020) and (Gomez et al., 2019).
2.1.2. Tagged MRI of gel phantom
For validation, strain tensor fields from tagged MRI of a cylindrical gel phantom were also analyzed. Because the gel phantom has a simple geometry with known material properties, results can be compared readily to theoretical estimates. The phantom consisted of a soft gel (103.7 g Knox gelatin in 1.8 L water) in a rigid acrylic cylindrical case with an inner diameter of 11.4 cm and length of 18 cm (Knutsen et al., 2014). The shear modulus of this gel (1710 Pa) (Bayly et al., 2008) falls within the range reported for brain tissue (Budday et al., 2017b; Chatelin et al., 2010; Franceschini et al., 2006; Johnson et al., 2013). Tagged MRI data were obtained with the phantom held in the same cradle used for human neck rotation. Upon release, the phantom rotated 32°, driven by the gravitational force of an offset weight, until motion of the case was arrested by a soft bumper. The resulting angular deceleration induced visible dynamic deformation in the gel phantom (Figure 1).
2.2. Finite element simulation
2.2.1. Geometry, boundary conditions, material properties, and discretization
The ability of DMD analysis to identify modes of oscillation was verified by applying it to data from a finite element (FE) simulation of the cylindrical gel phantom subjected to angular acceleration. The FE model, representing a rigid container of soft viscoelastic, isotropic material, was implemented using COMSOL Multiphysics (v. 5.4, Burlington, MA). The model domain consisted of a 2D circular region, assuming plane strain deformation. The 2D cylinder geometry had an inner diameter of 11.4 cm replicating the gel phantom of Knutsen et al. (2014). Material properties were consistent with experimental measurements (Bayly et al., 2008): density of , bulk modulus of 106 Pa, shear modulus of 1710 Pa and shear viscosity of 1 Pa∙s. The system was discretized using a free-triangular mesh with 940 quadratic Lagrange elements (convergence was checked – Supplementary Material Table S1).
Three types of simulation (Figure 2) were performed in COMSOL: (i) an eigenvalue modal response (Figure 2a); (ii) a frequency response (Figure 2b); (iii) a transient response (Figure 2c/2d) to be analyzed by DMD. All three approaches can identify dominant modes of oscillation.
Figure 2.
Summary and comparison of the three methods used to analyze the finite element model of the gel phantom. Each column depicts a different method used to identify and characterize modes and natural frequencies of the model. (a) Eigenvalue analysis of system matrices; (b) response to harmonic excitation at a range of frequencies (frequency sweep); (c-d) DMD of the response to transient acceleration of the case; The first three mode shapes are depicted below for each method. Red = positive strain; blue = negative strain. These “bow-tie” patterns in Cartesian strain component εxy correspond to axisymmetric patterns in the radial-circumferential shear (εrθ) component of strain in polar coordinates, as shown for the modes obtained by DMD of the transient response. Mode shapes are of arbitrary amplitude; the mode shape can be multiplied by an arbitrary scalar and still satisfy the eigenvalue problem. Corresponding estimates of natural frequencies are summarized in Table 1.
2.2.2. Eigenvalue analysis
In an eigenvalue analysis, the modes of oscillation and natural frequencies are obtained directly from the eigenvalues and eigenvectors of the discretized system matrix equation (Craig et al., 2006). To isolate the modes that would be excited by rotation of the cylindrical case, we compute the boundary integral of the circumferential displacement (Eq. 1).
| (1) |
The mode with displacement field um is excited by angular rotation of the case if cm ≠ 0 (Figure 2a). Natural frequencies were found from the imaginary parts of the eigenvalues corresponding to these rotational modes.
2.2.3. Frequency response
Frequency response analysis was performed by modeling harmonic, tangential motion of the outer boundary of the cylinder at frequencies ranging from 0 Hz to 75 Hz in steps of 0.25 Hz. We estimated the natural frequencies of the system by plotting the total elastic strain energy of the system vs. frequency and identifying the frequencies at the resonant peaks (Figure 2b). The corresponding mode shape (in terms of displacement or strain) was obtained from the deformed shape of the system at these resonant frequencies; the maximum deformation occurs π/2 radians out-of-phase with the excitation at resonance.
2.2.3. Transient response
To simulate the transient response, the outer boundary of the cylinder model experienced a small tangential displacement applied as a half-sine pulse of 0.025 seconds duration and 0.01 radian amplitude (Figure 2c). Strain values were collected at a grid of points, analogous to voxels in the gel phantom experiment, and the data were analyzed using DMD, as described below, to identity the modes of oscillation, natural frequencies, and modal coefficients of the system. Results were confirmed with varying number of mesh elements, impact duration, and rotation amplitude (see Supplementary Material Table S.1).
2.3. Data analysis: dynamic mode decomposition (DMD)
DMD was implemented in Matlab (v. 2019a, The Mathworks, Natick, MA) and used to extract dominant modes of oscillation from measured and simulated strain fields (Schmid, 2010; Tu et al., 2014). The first steps follow directly the implementation of Schmid (2010). Large data matrices consisting of strain estimates from tagged MRI were created. The strain data were rearranged into column “snapshots” {wn}, where {wn} = [εxx(x, y, z, tn), εxy(x, y, z, tn) …, εzz(x, y, z, tn)]T (6P × 1, where P is the total number of data voxels). Each column represents an array of strain values at a specific time. We applied the method of Tu et al. (2014), combining two strain snapshots in a combined column array, , to eliminate problems due to standing waves. These columns were organized into a matrix , where (12P × N, where N is the total number of combined snapshots). Two new matrices (12P × N − 1) are created from described by Eq. (2).
| (2) |
A dynamic model is obtained by first performing the singular value decomposition, , then obtaining the reduced-order matrix . The matrix (M × M, where M < N ≪ P) is the estimated dynamic transition matrix of a low-dimensional, discrete representation of the system. The [M] eigenvalues μm and eigenvectors {ym} of are used to find natural frequencies and mode shapes, [Ψm] [Eq. 4]. A damping ratio can be estimated from . Mode shapes were estimated using Eq. (3) (Eq. 2.10 in reference (Schmid, 2010)).
| (3) |
Each strain snapshot can be reconstructed from the modes.
| (4) |
Modes obtained by DMD can be sorted by frequency, but also by their contribution to the overall variance. The modal coefficient amn (the coefficient of the mth mode at the nth time point) can be estimated 189 using Eq. (5).
| (5) |
The standard deviation of the mth row of the A matrix, denoted as am, describes the variance of that modal coefficient, and was used to sort the contributions of the modes. Note that for oscillatory modes, both the coefficient and the mode shape are complex, so that contributions of both complex conjugate 194 components were included.
To visualize modal dynamics, a column array, a0, of initial values of modal coefficients was estimated using Eq. (6), where is the first column of the matrix .
| (6) |
Subsequent estimates of reconstructed modal coefficient arrays, an, were obtained using Eq. (7), where [Μ] is the M × M matrix of eigenvalues.
| (7) |
Modal coefficients, mode shapes, natural frequencies, and damping ratios were obtained for each data set (neck rotation or neck extension in a given subject). Oscillatory motion involves complex eigenvalues and eigenvectors; both real and imaginary components of modal coefficients and mode shapes are presented. Mode shapes are illustrated using Cartesian components of shear strain: εxy in neck rotation, εyz in neck extension. These are typically the largest strain components, though each mode contains all strain components and any component could be chosen for illustration. By multiplying each mode shape by the corresponding modal coefficient, the behavior of each mode of can be animated in 2D or 3D (see supplementary movies).
3. Results
3.1. Simulation: modes of oscillation from eigenvalue analysis, frequency response and DMD of transient response
Figure 2 depicts the first three mode shapes resulting from each type of simulation (eigenvalue analysis, frequency response, transient response analyzed by DMD, and a characteristic response of the simulation results in polar coordinates). Table 1 summarizes the natural frequencies of these modes.
Table 1.
Natural frequencies for each of the three modes of oscillation of the FE model, identified by different analysis approaches: eigenvalue analysis, frequency sweep, and DMD of the time-domain impulse response.
| Mode Number | Eigenvalue Analysis [Hz] | Frequency Sweep [Hz] | DMD Analysis [Hz] |
|---|---|---|---|
| 1 | 14.00 | 14.00 | 13.83 |
| 2 | 25.75 | 25.63 | 24.80 |
| 3 | 37.40 | 37.21 | 34.89 |
3.2. Experiment: modes of oscillation in the gel phantom
Two-dimensional strain fields from tagged MRI of the gel phantom in rotation (Knutsen et al., 2014) were analyzed by DMD. Estimates of fundamental frequency were insensitive to sampling rate between Δt =6 ms/frame and Δt =18 ms/frame; these results are summarized in Table 2.
Table 2.
Damped natural frequency, f1, of the first mode of 2D deformation, estimated by DMD of 2D strain fields from tagged MRI of the experimental gel phantom and human brain in neck rotation, with varying temporal resolution, Δt (ms/frame).
| Damped Natural Frequency (Phantom) | Damped Natural Frequency (Brain Rotation) | ||||||||
| Δt (ms) | 6 | 9 | 12 | 18 | Δt (ms) | 6 | 12 | 18 | 24 |
| f1 (Hz) | 14.43 | 14.53 | 14.46 | 14.32 | f1 (Hz) | 7.32 | 7.54 | 7.40 | 7.39 |
Figure 3 illustrates results of the DMD analysis of gel phantom tagged MRI data. Also shown for comparison are results from DMD of the transient response of the 2D cylinder simulation. Figure 3 includes the times series of the complex (real and imaginary) modal coefficients, and the corresponding (complex) mode shapes. The frequencies and mode shapes from DMD agree closely between simulation and experiment, as well as with predictions from eigenvalue analysis and frequency response of the FE model.
Figure 3.
Example modal coefficients and mode shapes (real and imaginary parts, arbitrary magnitude) for the first mode of oscillation in gel phantom experiments and simulation. [a-c] DMD of strain data from tagged MRI of experimental gel phantom (Δt = 6 ms/frame). [d-f] DMD of separate strain data obtained by tagged MRI of the experimental gel phantom at a lower sampling rate (Δt = 12 ms/frame). [g-i] DMD of transient response from FE simulation (Δt = 10 ms/frame). The frequency estimate for simulation is within 3% of those for the experimental phantom. The normalized correlation coefficient (0 < C < 1) between simulated and experimental mode shapes is 0.98. Scale bar: 5 cm.
3.3. Experiment: modes of oscillation in the human brain due to neck rotation and neck extension
DMD of 2D strain fields in the human brain acquired at different sampling rates (Knutsen et al., 2014) showed that the estimated frequency of the first mode was insensitive to sampling rate in the range used (Table 2). This is expected because the lowest sampling frequency (41.7 Hz for Δt =0.024 sec) is well above the minimum (Nyquist) frequency to characterize these oscillations.
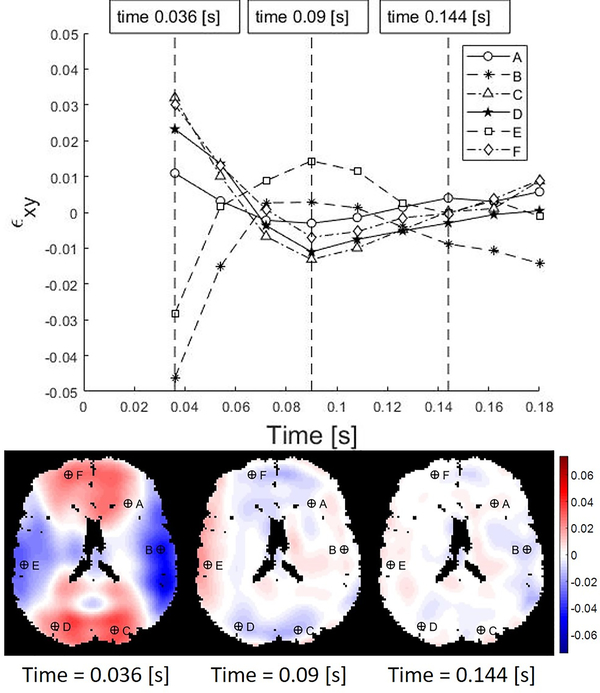
Full 3D strain fields were estimated at each voxel throughout the brain from MRI data (Knutsen et al., 2020). Example strain data, consisting of (i) time series of the strain component, εxy, at six representative voxels randomly selected from left/right anterior, middle, and posterior regions, and (ii) 2D maps of εxy at three times, are shown in Figure 4 (times are relative to the initiation of impact). These strain data suggest that decaying oscillations of spatially coherent modes play an important role in the response to skull acceleration.
Figure 4.
Shear strain values in the human brain resulting from angular acceleration in neck rotation. The labeled markers indicate locations at which the strain time series are extracted. In this and subsequent figures, times are relative to start of image acquisition, and data from the free response after impact are shown. Temporal resolution Δt = 18 ms.
Figures 5 and 6 show example results of DMD applied to 3D strain fields from human subjects in neck rotation and neck extension. Figure 5 depicts the responses of the first modes of 3D deformation due to neck rotation and neck extension in a single subject (shear in the axial plane for neck rotation and shear in the sagittal plane for neck extension). Figure 6 illustrate the first modes of 3D deformation due to neck rotation and neck extension, respectively, each in two different subjects. For each type of motion (rotation or extension), both the qualitative features of each mode shape and the frequencies of oscillation are similar between subjects. In neck rotation, the Cartesian shear strain in the axial plane, εxy, exhibits symmetric regions on the right and left sides, opposite in sign to shear strains in central-anterior/posterior regions. In neck extension, common features include relatively high shear strains εyz at the inferior and superior surfaces, where the brain is tethered to the skull.
Figure 5.
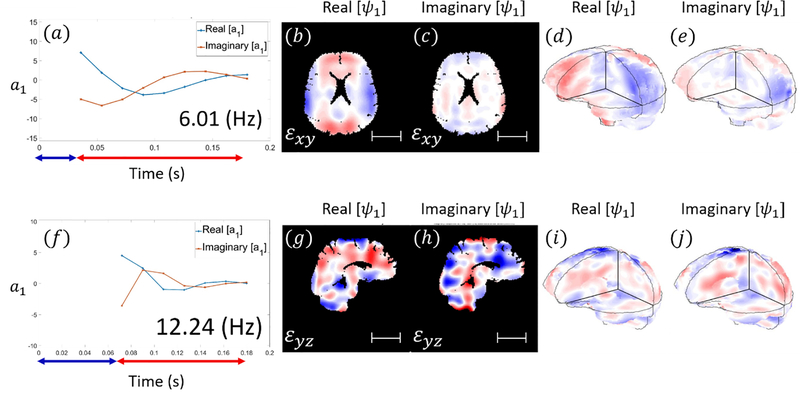
Modal coefficients and mode shapes (real and imaginary parts; arbitrary magnitude) for the first mode of 3D deformation obtained by DMD in a single subject. [a-e] neck rotation. [f-j] neck extension (Subject M, 31 yrs.). Blue arrows indicate the time period before and during impact while red arrows indicate time interval after impact. Scale bar: 5 cm.
Figure 6.
Modal coefficients and mode shapes (real and imaginary parts of complex values; arbitrary magnitude) for the first mode of 3D brain deformation in neck rotation (a-j) and neck extension (k-t), obtained by DMD for two additional different subjects ([a-e] F, 31 yrs.) ([f-j] F, 34 yrs.) ([k-o] F, 23 yrs.) ([p-t] M, 34 yrs.). Blue arrows on the time axis indicate the time period before and during impact while red arrows indicate time interval after impact. Scale bar: 5 cm.
Values for natural frequency and damping ratio are summarized in Figure 7 and Table 3. The average damped natural frequency of the first mode of 3D deformation in neck rotation across 10 subjects was 6.66 ± 0.86 Hz (mean ± std. deviation). The damped natural frequency of the second mode in neck rotation was 14.41 ± 0.70 Hz. The damped natural frequency of the first oscillatory mode in neck extension was 11.19 ± 1.18 Hz. The first (fundamental) natural frequencies are significantly different between rotation and extension (p < 10−4, Student’s t-test, unpaired, two-tailed).
Figure 7.
(a) Damped natural frequencies (f1) and (b) damping ratios (ζ1) of modes of human brain deformation in neck rotation and neck extension. Boxes show 25th/75th percentile values, and whiskers show 5th/95th percentile values for each mode number and excitation type. The difference in natural frequency between rotation and extension is statistically significant with p<0.0001. Symbols: Red line: median; red +: outlier; green *: mean.
Table 3.
Estimates of damped natural frequencies (f1) and damping ratios (ζ1) from DMD for the first mode of brain deformation due to neck rotation and neck extension in all subjects.
| Neck Rotation | ||||||||||
| Subject 1 | Subject 2 | Subject 3 | Subject 4 | Subject 5 | Subject 6 | Subject 7 | Subject 8 | Subject 9 | Subject 10 | |
| f1 (Hz) | 6.06 | 8.26 | 6.93 | 6.48 | 6.87 | 5.50 | 5.89 | 6.01 | 6.88 | 7.73 |
| ζ1 | 0.70 | 0.54 | 0.32 | 0.43 | 0.27 | 0.51 | 0.56 | 0.32 | 0.13 | 0.21 |
| Neck Extension | ||||||||||
| Subject 8 | Subject 11 | Subject 12 | Subject 13 | Subject 14 | Subject 15 | Subject 16 | Subject 17 | Subject 18 | Subject 19 | |
| f1 (Hz) | 12.24 | 11.70 | 12.58 | 9.72 | 12.24 | 10.53 | 9.54 | 10.39 | 10.50 | 12.46 |
| ζ1 | 0.37 | 0.38 | 0.28 | 0.40 | 0.28 | 0.49 | 0.37 | 0.32 | 0.39 | 0.28 |
Each of these modes exhibited a damping ratio ς < 1, consistent with damped oscillatory motion. A larger range of estimated damping ratio was found for the first mode of oscillation in neck rotation; this may reflect the challenge of quantifying damping from data with fewer oscillations, or true variability.
4. Discussion and conclusion
Oscillatory modes of 3D deformation in the intact, living, human brain were identified using strain fields estimated from tagged MRI during mild head acceleration. Oscillatory modes of deformation of a gel phantom subjected to angular acceleration were also characterized by DMD of strain fields from tagged MRI. DMD was also performed on strains from a corresponding simulation of the gel phantom. The natural frequency and shape of each mode characterize its temporal and spatial behavior, respectively. Importantly, the modes of oscillation identified from tagged MRI of the experimental gel phantom agreed closely, both quantitatively and qualitatively, with theoretical predictions.
Consistent damped natural frequencies were found for modes of oscillation in the human brain, for each type of head motion. The brain typically exhibited a lower natural frequency (~7 Hz) in neck rotation than in neck extension (~11 Hz). Brain anatomy (Wu et al., 2020) and connection to the skull (i.e., by falx and vasculature) will influence natural frequencies and could explain the dependence of frequency on direction. In contrast, differences in loading amplitude and duration are small and not predictive of frequency (see Supplementary Material, Figure S.6), and unlikely to explain frequency differences in neck rotation vs extension.
Observed frequencies are lower than those previously estimated from simulations (Laksari et al., 2018; Wu et al., 2020), and have significant implications for the design of head protection, because reducing high-frequency components of impact is unlikely to be effective in reducing deformation in low-frequency modes. Differences between observations in experiment and computer simulations could reflect inaccurate assumptions or approximations in the computer models with respect to material properties or interfaces. In the modeling study of Wu et al. (2020) natural frequencies (40–70 Hz) were estimated from model parameters that maximized local first principal strain; these might be frequencies of higher-order modes (Wu et al., 2020).
Current estimates of natural frequency (7–11 Hz) in the living human brain at sub-injury amplitudes, are slightly lower than estimates in the cadaver brain (12–20 Hz) at injury-level amplitudes (Alshareef et al., 2018). These frequency differences may arise from post-mortem changes in material properties (Weickenmeier et al., 2018) or boundary conditions, or possibly differences in amplitude of loading. Since tagged MRI data were obtained from human volunteers (Knutsen et al., 2020), measurements were limited to small deformations in the brain, comparable to those experienced during normal activity. The type and range of head motions that can be recorded during scans is also constrained by the MRI head coil. Thus, we were not able to directly investigate the effect of loading amplitude in this study. In parametric studies of the gel phantom simulation, modal frequency is insensitive to loading (Supplementary Material Table S.1) even though the material exhibited mild nonlinearity (strain-stiffening). The nonlinear, viscoelastic behavior of brain tissue remains an area of active research (Budday et al., 2017a; Budday et al., 2017b; Chatelin et al., 2010). Future studies directly investigating the effect of loading amplitude on frequency are warranted, potentially in an animal model with a gyrencephalic brain, such as the pig.
Results from DMD analysis of data from tagged MRI of a gel phantom during angular acceleration agreed closely with results from DMD analysis of data from a corresponding FE simulation. Furthermore, the mode shapes and frequencies from DMD agree with those from frequency response and eigenanalysis of the FE model. The ability to predict natural frequencies and mode shapes under specific loading conditions might be a valuable validation criterion for computer models of brain biomechanics.
Inherent limitations exist in tagged MRI studies. In order to acquire full 3D displacement fields throughout the brain, temporal resolution was limited to 18 ms, and rotation/extension motion must be repeated multiple times to acquire images. Analysis of 2D strain data acquired at varying temporal sampling rates confirmed that temporal resolution does not affect the key conclusions. Variations between repeated motions likely degraded image quality, contributing to noise in strain estimates. Typically, fewer than two cycles of oscillation were acquired, limiting precision of frequency and damping estimates. Numbers of subjects in each group are too small to investigate effects of age or gender; this is a future objective.
DMD of tagged MRI has provided quantitative estimates of natural frequencies of the human brain due to mild angular accelerations in neck rotation and neck extension. The accuracy of these estimates is supported by analyses simulations and experiments involving a simple gel phantom. This quantitative information on oscillatory modes of brain motion could inform the design of helmets and other protective measures, and guide the development and evaluation of computational models of brain mechanics.
Supplementary Material
5. Movie: Mode 1 of brain of human subject in neck extension – view 2
4. Movie: Mode 1 of brain of human subject in neck extension (with cut-out) – view 1
2. Movie: Mode 1 of brain of human subject in neck rotation (with cut-out) – view 1
3. Movie: Mode 1 of brain of human subject in neck rotation – view 2
1. Supplementary Table: Effect of Material, Impact, and Simulation Parameters on Estimated Frequency
Acknowledgements
We acknowledge support from NIH grants R01/R56 NS055951 and U01 NS112120 and the Department of Defense in the Center for Neuroscience and Regenerative Medicine.
Footnotes
Conflict of interest statement
We have no conflicts of interest to report.
References
- Alshareef A, Giudice JS, Forman J, Salzar RS, Panzer MB, 2018. A Novel Method for Quantifying Human In Situ Whole Brain Deformation under Rotational Loading Using Sonomicrometry. J Neurotrauma 35, 780–789. [DOI] [PubMed] [Google Scholar]
- Atay SM, Kroenke CD, Sabet A, Bayly PV, 2008. Measurement of the dynamic shear modulus of mouse brain tissue in vivo by magnetic resonance elastography. J Biomech Eng 130, 021013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayly PV, Cohen TS, Leister EP, Ajo D, Leuthardt EC, Genin GM, 2005. Deformation of the human brain induced by mild acceleration. J Neurotrauma 22, 845–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayly PV, Massouros PG, Christoforou E, Sabet A, Genin GM, 2008. Magnetic Resonance Measurement of Transient Shear Wave Propagation in a Viscoelastic Gel Cylinder. J Mech Phys Solids 56, 2036–2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budday S, Sommer G, Birkl C, Langkammer C, Haybaeck J, Kohnert J, Bauer M, Paulsen F, Steinmann P, Kuhl E, Holzapfel GA, 2017a. Mechanical characterization of human brain tissue. Acta Biomaterialia 48, 319–340. [DOI] [PubMed] [Google Scholar]
- Budday S, Sommer G, Holzapfel GA, Steinmann P, Kuhl E, 2017b. Viscoelastic parameter identification of human brain tissue. J Mech Behav Biomed Mater 74, 463–476. [DOI] [PubMed] [Google Scholar]
- Chan DD, Knutsen AK, Lu YC, Yang SH, Magrath E, Wang WT, Bayly PV, Butman JA, Pham DL, 2018. Statistical Characterization of Human Brain Deformation During Mild Angular Acceleration Measured In Vivo by Tagged Magnetic Resonance Imaging. J Biomech Eng 140, 1010051–10100513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatelin S, Constantinesco A, Willinger R, 2010. Fifty years of brain tissue mechanical testing: from in vitro to in vivo investigations. Biorheology 47, 255–276. [DOI] [PubMed] [Google Scholar]
- Clayton EH, Genin GM, Bayly PV, 2012. Transmission, attenuation and reflection of shear waves in the human brain. J R Soc Interface 9, 2899–2910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig RR, Kurdila A, Craig RR, 2006. Fundamentals of structural dynamics, 2nd ed. John Wiley, Hoboken, N.J. [Google Scholar]
- Dewan MC, Mummareddy N, Wellons JC 3rd, Bonfield CM, 2016. Epidemiology of Global Pediatric Traumatic Brain Injury: Qualitative Review. World Neurosurg 91, 497–509 e491. [DOI] [PubMed] [Google Scholar]
- Fahlstedt M, Halldin P, Kleiven S, 2016. The protective effect of a helmet in three bicycle accidents--A finite element study. Accid Anal Prev 91, 135–143. [DOI] [PubMed] [Google Scholar]
- Feng Y, Abney TM, Okamoto RJ, Pless RB, Genin GM, Bayly PV, 2010. Relative brain displacement and deformation during constrained mild frontal head impact. J R Soc Interface 7, 1677–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franceschini G, Bigoni D, Regitnig P, Holzapfel GA, 2006. Brain tissue deforms similarly to filled elastomers and follows consolidation theory. Journal of the Mechanics and Physics of Solids 54, 2592–2620. [Google Scholar]
- Gardner RC, Dams-O’Connor K, Morrissey MR, Manley GT, 2018. Geriatric Traumatic Brain Injury: Epidemiology, Outcomes, Knowledge Gaps, and Future Directions. J Neurotrauma 35, 889–906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giordano C, Cloots RJ, van Dommelen JA, Kleiven S, 2014. The influence of anisotropy on brain injury prediction. J Biomech 47, 1052–1059. [DOI] [PubMed] [Google Scholar]
- Gomez AD, Knutsen AK, Xing F, Lu YC, Chan D, Pham DL, Bayly P, Prince JL, 2019. 3-D Measurements of Acceleration-Induced Brain Deformation via Harmonic Phase Analysis and Finite-Element Models. IEEE Trans Biomed Eng 66, 1456–1467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guertler CA, Okamoto RJ, Schmidt JL, Badachhape AA, Johnson CL, Bayly PV, 2018. Mechanical properties of porcine brain tissue in vivo and ex vivo estimated by MR elastography. J Biomech 69, 10–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardy WN, Mason MJ, Foster CD, Shah CS, Kopacz JM, Yang KH, King AI, Bishop J, Bey M, Anderst W, Tashman S, 2007. A study of the response of the human cadaver head to impact. Stapp Car Crash J 51, 17–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson CL, McGarry MD, Van Houten EE, Weaver JB, Paulsen KD, Sutton BP, Georgiadis JG, 2013. Magnetic resonance elastography of the brain using multishot spiral readouts with self-navigated motion correction. Magn Reson Med 70, 404–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knutsen AK, Gomez AD, Gangolli M, Wang WT, Chan D, Lu YC, Christoforou E, Prince JL, Bayly PV, Butman JA, Pham DL, 2020. In vivo estimates of axonal stretch and 3D brain deformation during mild head impact. Brain Multiphysics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knutsen AK, Magrath E, McEntee JE, Xing F, Prince JL, Bayly PV, Butman JA, Pham DL, 2014. Improved measurement of brain deformation during mild head acceleration using a novel tagged MRI sequence. J Biomech 47, 3475–3481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruse SA, Rose GH, Glaser KJ, Manduca A, Felmlee JP, Jack CR Jr., Ehman RL, 2008. Magnetic resonance elastography of the brain. NeuroImage 39, 231–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laksari K, Kurt M, Babaee H, Kleiven S, Camarillo D, 2018. Mechanistic Insights into Human Brain Impact Dynamics through Modal Analysis. Phys Rev Lett 120, 138101. [DOI] [PubMed] [Google Scholar]
- Laksari K, Wu LC, Kurt M, Kuo C, Camarillo DC, 2015. Resonance of human brain under head acceleration. J R Soc Interface 12, 20150331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAllister TW, Ford JC, Ji S, Beckwith JG, Flashman LA, Paulsen K, Greenwald RM, 2012. Maximum principal strain and strain rate associated with concussion diagnosis correlates with changes in corpus callosum white matter indices. Ann Biomed Eng 40, 127–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okamoto RJ, Romano AJ, Johnson CL, Bayly PV, 2019. Insights Into Traumatic Brain Injury From MRI of Harmonic Brain Motion. J Exp Neurosci 13, 1179069519840444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patton DA, McIntosh AS, Kleiven S, 2015. The Biomechanical Determinants of Concussion: Finite Element Simulations to Investigate Tissue-Level Predictors of Injury During Sporting Impacts to the Unprotected Head. J Appl Biomech 31, 264–268. [DOI] [PubMed] [Google Scholar]
- Sabet AA, Christoforou E, Zatlin B, Genin GM, Bayly PV, 2008. Deformation of the human brain induced by mild angular head acceleration. J Biomech 41, 307–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sack I, Beierbach B, Wuerfel J, Klatt D, Hamhaber U, Papazoglou S, Martus P, Braun J, 2009. The impact of aging and gender on brain viscoelasticity. Neuroimage 46, 652–657. [DOI] [PubMed] [Google Scholar]
- Schmid PJ, 2010. Dynamic mode decomposition of numerical and experimental data. Journal of Fluid Mechanics 656, 5–28. [Google Scholar]
- Scholten AC, Haagsma JA, Cnossen MC, Olff M, van Beeck EF, Polinder S, 2016. Prevalence of and Risk Factors for Anxiety and Depressive Disorders after Traumatic Brain Injury: A Systematic Review. J Neurotrauma 33, 1969–1994. [DOI] [PubMed] [Google Scholar]
- Tu JH, Rowley CW, Luchtenburg DM, Brunton SL, Kutz JN, 2014. On dynamic mode decomposition: Theory and applications. Journal of Computational Dynamics 1, 391–421. [Google Scholar]
- Weickenmeier J, Kurt M, Ozkaya E, de Rooij R, Ovaert TC, Ehman RL, Butts Pauly K, Kuhl E, 2018. Brain stiffens post mortem. J Mech Behav Biomed Mater 84, 88–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu T, Antona-Makoshi J, Alshareef A, Giudice JS, Panzer MB, 2020. Investigation of Cross-Species Scaling Methods for Traumatic Brain Injury Using Finite Element Analysis. Journal of Neurotrauma 37, 410–422. [DOI] [PubMed] [Google Scholar]
- Zhao W, Ji S, 2020. Displacement- and Strain-Based Discrimination of Head Injury Models across a Wide Range of Blunt Conditions. Annals of Biomedical Engineering 48, 1661–1677. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
5. Movie: Mode 1 of brain of human subject in neck extension – view 2
4. Movie: Mode 1 of brain of human subject in neck extension (with cut-out) – view 1
2. Movie: Mode 1 of brain of human subject in neck rotation (with cut-out) – view 1
3. Movie: Mode 1 of brain of human subject in neck rotation – view 2
1. Supplementary Table: Effect of Material, Impact, and Simulation Parameters on Estimated Frequency