Scalable machine learning-assisted model exploration and inference using Sciope

Abstract

Summary

Discrete stochastic models of gene regulatory networks are fundamental tools for in silico study of stochastic gene regulatory networks. Likelihood-free inference and model exploration are critical applications to study a system using such models. However, the massive computational cost of complex, high-dimensional and stochastic modelling currently limits systematic investigation to relatively simple systems. Recently, machine-learning-assisted methods have shown great promise to handle larger, more complex models. To support both ease-of-use of this new class of methods, as well as their further development, we have developed the scalable inference, optimization and parameter exploration (Sciope) toolbox. Sciope is designed to support new algorithms for machine-learning-assisted model exploration and likelihood-free inference. Moreover, it is built ground up to easily leverage distributed and heterogeneous computational resources for convenient parallelism across platforms from workstations to clouds.

Availability and implementation

The Sciope Python3 toolbox is freely available on https://github.com/Sciope/Sciope, and has been tested on Linux, Windows and macOS platforms.

Supplementary information

Supplementary information is available at Bioinformatics online.

1 Introduction

Stochastic models of biochemical reaction networks are an integral part of the systems biologist’s toolbox. By formulating discrete models from known or hypothesized molecular interactions, in silico analysis of complex biochemical processes is made possible. A key challenge encountered in modelling is characterized by very large uncertainties associated with model parameters. Given an efficient simulation method, two related applications can be discerned. In model parameter space exploration, the modeller’s objective is to use the simulator to screen for different qualitative behaviours displayed by the model under large variations in parameters. Model exploration is often the first step in understanding a system, and applies also when no experimental data are available. In model inference, the task is to fit model parameters to observed experimental data. A popular approach for parameter inference in systems biology is Approximate Bayesian Computation (ABC) (Marin et al., 2012). ABC inference requires substantial hyperparameter tuning (such as choosing the prior, tuning acceptance thresholds and distance metrics). ABC can become prohibitively slow for high-dimensional problems and it is of utmost importance to select informative summary statistics. Several open and capable software packages for ABC inference are available, such as PyABC (Klinger et al., 2018). However, traditional methods struggle with high-dimensional problems and stochastic descriptions.

Machine-learning-assisted methods have been proposed to tackle this problem with a data-driven approach to both exploration and likelihood-free inference. Recently, we presented a human-in-the-loop workflow based on semi-supervised and active learning to aid model exploration (Wrede and Hellander, 2019). For likelihood-free parameter inference, regression approaches using Random Forests (Raynal et al., 2019) and deep artificial neural networks (Jiang et al., 2018; Wiqvist et al., 2019), as well as classification (Gutmann et al., 2018), have been introduced in conjunction with ABC. We saw the need for a software toolbox that (i) focuses on making such ML-assisted methods easy-to-use for practical modelling projects, (ii) supports rapid development of new ML-assisted tools for exploration and inference and (iii) incorporates specific support for stochastic simulations of biochemical reaction networks. We here introduce the SCalable Inference, Optimization and Parameter Exploration (Sciope) toolbox. Sciope provides an integrated environment to generate initial parameter designs, to generate training data (by black-box simulation), to do massive feature generation and dimension reduction, and to build different types of surrogate models such as Gaussian Process models and Convolutional Neural Networks and use them for inference tasks. Sciope is also the main implementation of the human-in-the loop workflow presented in (Wrede and Hellander, 2019). Sciope supports basic ABC routines for completeness, but is not intended to be a complete environment for the many flavours of ABC. However, it supports implementations of novel summary statistic learning via artificial neural networks. It can thus be a good complement for scalable pre-processing for other tools that specializes on ABC, such as PyABC. An overview of Sciope’s core features and contributions is listed in the Supplementary Material.

The sheer computational cost associated with simulation and feature extraction for complex high-dimensional and stochastic models becomes a bottle-neck both for end-users and method developers. For this reason, Sciope is built with a Dask (Matthew 2015) backend to support massive parallelism on platforms from laptops to clouds. Sciope is realized as a Python3 toolbox and will form the backend in the next generation of the StochSS software-as-a a service (Drawert et al., 2016).

2 Overview

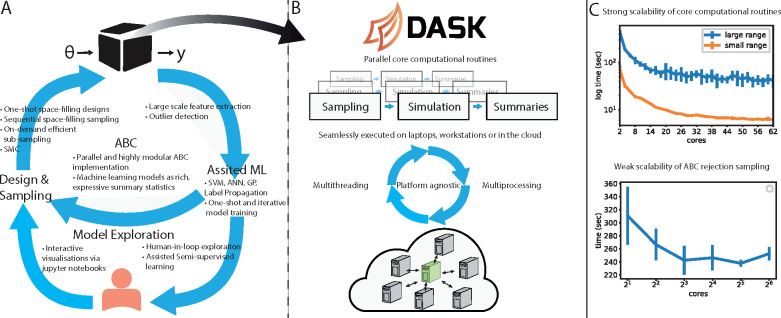
The only requirement to use Sciope is a user-provided black-box simulator that emits time series data in the supported format. Sciope includes wrappers for GillesPy2, a popular package to simulate discrete models of gene regulatory networks. Users in the systems biology application area thus only need to define their model using the Python API or using SBML. Figure 1A summarizes the unique features of Sciope. They include model exploration based on semi-supervised learning (Wrede and Hellander, 2019), surrogate modelling, summary statistics selection and state-of-the-art deep neural network architectures to summarize data for ABC inference (Åkesson et al., 2020). Continued development will focus on enabling additional ML-assisted technologies for inference and exploration.

Fig. 1.

(A) Sciope is a high-level Python toolbox for scalable, ML-assisted inference and model parameter exploration with a large pool of features and utilities. The user is only required to provide a black-box simulator to be able to use Sciope. To use the distributed mode, the user also needs to setup a Dask cluster. The main supported features of each module, post-processing, assisted machine leaning, model exploration and design and sampling are presented in the figure. Examples are provided under https://github.com/Sciope/Sciope/examples and in the Supplementary Material. (B) From a computational point of view, parameter inference and model exploration workflows share multiple elements, such as repeated simulation of the model with different parameters, and the evaluation of a large number of summary statistics/features for each simulated time series. Both these steps are embarrassingly parallel. Sciope provides a scalable and unified solution for flexible parallel execution across different platforms via a high-level API built around Dask. The complexity of Dask’s low-level task interface is effectively hidden from the users. (C) Strong scalability test for the core computational routines (top) for two different parameter bounds (see Supplementary Information for scalability efficiency and more details). Weak scalability test for ABC inference with rejection sampling where the number of trials are proportional to the number of cores (bottom)

A key feature is the easy setup of parallel computational experiments where the complexity is hidden from the user. Inference and model exploration tasks share many computationally expensive core routines, as illustrated in Figure 1B. Sciope parallelizes these stages using the Dask task backend, which provides the flexibility to scale out computations in modern cloud environments.

3 Results

The Supplementary Material contains several examples of the toolbox workflow on example models from systems biology. They serve to demonstrate the machine learning-enabled exploration and inference capabilities highlighted in Figure 1A. Here, we demonstrate the performance of the library when used in distributed mode using cloud resources. We ran an exploration workflow and an ABC inference task for a well-known GRN model of a genetic oscillator (Vilar et al., 2002) (involving 15 kinetic parameters, see Supplementary Table S1 for parameter bounds).

Supporting near real-time model exploration workflows. In machine-learning-assisted model exploration, interactivity is of key importance since a human-in-the-loop guides the workflow and drives the next steps. Both of the visualization tools supported in Sciope, and the human interaction, function optimally with a maximum number of parameter points—a batch—observed in one exploration cycle. However, the wall time to do sampling, simulation and summary statistics extraction for a batch can be considerable for an expensive model. Sciope’s goal concerning model exploration is to converge to a near real-time experience by transiently scaling out the computations to a cloud or cluster.

As can be seen in Figure 1C (top), the runtime for generating a batch of 1000 trial points converges to the runtime of the longest running individual simulation tasks, as illustrated by two different sizes of parameter ranges. The task granularity is one invocation of the simulator and a wide parameter range leads to a larger spread in simulation runtime, see Supplementary Figure S1 for a detailed explanation.

High-throughput likelihood-free inference. In comparison with model exploration, ABC inference typically requires a very large number of trials but does not involve a human-in-the loop. Hence, latency is less of a concern. Instead, it is important to support high-throughput of trials for traditional ABC and generation of training data for ML approaches. Figure 1C (bottom) illustrates weak scaling during ABC inference. In this experiment, the number of desired accepted samples increases proportionally to the number of cores so that the workload per core stays constant. As can be observed, the runtime decreases only marginally with increased number of accepted samples. As we scale out, we are able to more efficiently handle the computations of longer simulation runtimes, and hence, we observe a slight decrease in the total runtime and variability.

Funding

The work was funded by the NIH [NIH/2R01EB014877-04A1], the eSSENCE strategic collaboration on eScience and the Göran Gustafsson foundation.

Conflict of Interest: none declared.