New insights about electronic mechanism of electrocyclic reactions: theoretical study about stereoselectivity in cyclobutenes

Abstract

This work presents the study of a series of electrocyclic reactions with the main aim of obtaining new insights into the reaction process along IRCs. The energy variation of the different reaction paths as well as the different transition states have been calculated. These trends are according to the experimental data. The natural bond orbitals have been obtained and the second order perturbational theory analysis has been carried out to determine the main charge transfers due to delocalization. Bond reactivity indexes have been used to describe the reactivity mechanism in a local way. These reactivity indexes are also based on NBOs and this has made it possible to connect the results of the indexes with the previous analysis. To determine quantitatively the bond structure, we used the quantum theory of atoms in molecules and we have hereby completed the information obtained from the NBO analysis. Finally, we used the Hirshfeld population analysis as an approximation to understand how the load density changes in the different reaction pathways, and we have connected these variations with the information obtained from the bond structure.

The results has found that the reaction path with the lowest energy barrier Transition State Inward Conrotatory (TSIC) or Transition State Outward Conrotatory (TSOC) is determined by two magnitudes: the charge donations by delocalisation of the substituents (which we obtained from the Second Order Perturbational Theory Analysis of the NBOs) and in the case that these donations were very similar, the non-covalent interactions dominated (which we studied by means of the interaction energies of the Hirshfeld charges). Additionality, the most important factor influencing the lower energy reaction path was the interaction of lone pairs of the substituents with the σ∗(C–C) bond that is broken at the opening of the cycle. The alignment of these lone pairs with the C–C bond favours charge donation between them and, as can be seen in the discussion, this alignment varies depending on whether the structure is TSIC and TSOC.

Stereoselectivity, electrocyclic reactions, bond reactivity indices, QTAIM, NBO analysis, density functional theory (DFT).

1. Introduction

The electronic control of the stereoselectivities of the electrocyclic reactions of cyclobutenes has been studied by organic chemists for over forty years [1, 2, 3, 4, 5, 6]. Some theories have been used to explain phenomena such as torquoselectivity. Torquoselectivity is a special kind of stereoselectivity observed in electrocyclic reactions defined as "the preference for inward or outward rotation of substituents in conrotatory or disrotatory electrocyclic reactions." [7, 8, 9] This property determines the reaction product and is dependent on the feasibility of the substituent group and their electronic and steric effects, among others [10]. In this regard, it is a key factor in the reaction mechanic and for this reason in this paper a systematic study is postulated to deal with torquoselectivity in a series of reactions studied by Houk and co-workers [1] using the orbital symmetry.

This orbital symmetry theory was used by Woodward-Hoffmann (WH) in the so-called Woodward-Hoffmann rules. However, these insights obtained about the electrocyclic reactions postulate electronic reorganization as a pericyclic process. In many cases this pericyclic reorganization cannot explain the behaviour of competitive electrocyclic reactions or reaction yields. Therefore, new considerations beyond orbital symmetry are necessary. More recent studies of the diverse phases at atomic level of the reactants and the initial components exploring bond structures have shown that to understand the reaction mechanic it is important to take into account the physicochemical atomic scale [10, 11, 12, 13, 14, 15, 16, 17, 18, 19].

The nature of chemical bonds was studied by Silvi and collaborators using the bond progression theory as an extension of Bader's work and the scalar field related to the electron localization function (ELF) [20, 21, 22, 23, 24, 25]. The use of such research led to the proposal of electronic rearrangements via pseudoradicals rather than the pericyclic rearrangement suggested by Woodward-Hoffmann. (WH) [26, 27] and showed the electrocyclic reactions as pseudodiradical ring opening reactions {2n + 2π} [28, 29]. In addition, we use the analysis of natural bond orbitals (NBO), the quantum theory of atoms in molecules (QTAM), and the electronic structure principles such as minimum polarisability, minimum electrophilicity and maximum hardness, to find new insights into the process of electronic rearrangement in accordance with experimental data [30, 31, 32, 33].

Table 1 shows the reaction set (21 reactions) analyzed in this study (see Figure 1). There is molecular variety in the reaction set analyzed from reactions with only Z stereochemistry Z, only E stereochemistry and competitive reactions with E, Z stereochemistry. The main aim is to build a systematic study to understand the nature of the chemical bond, electronic reorganization and stereochemistry prediction according to the experimental data. The main idea is that these considerations can be applied both to electrocyclic reactions with orbital symmetry and to unusual reactions that have not been understood under the WH rules [32].

Table 1.

Thermal ring opening reaction of cyclobutenes, reaction set (21 reactions) analyzed in this study.

Reaction	Substituents	Stereochemistry of products	Ref.
1	none		[34]
2	1-Cl		[35]
3	1-Br		[35]
4	1-CN		[36]
5	3-Cl	E	[37]
6	cis-3,4-di-Cl	E,Z	[37]
7	trans-3,4-di-Cl	E,E	[37]
8	3-OEt	E	[37]
9	3-OAc	E	[37]
10	cis-3,4-di-OMe	E,Z	[37]
11	cis-3,4-di-OEt	E,Z	[37]
12	cis-3-Cl-4-Me	E,Z	[37]
13	cis-3-Cl-4-OMe	E,E	[37]
14	cis-3-OMe-4-Me	E,Z	[37]
15	3,3-di-OMe		[38]
16	3-CH2CH2OAc	E	[39]
17	3-F	E	[40]
18	3,3-di-F		[40]
19	3-CF3	E (95%)	[40]
20	3-CF3	Z (5%)	[40]
21	3-CHO	Z	[41]

Figure 1.

Ring opening reaction of Cyclobutenes studied.

2. Computational details

All the structures included in this study were optimized at the B3LYP/6-31+G(d,p) [42, 43] in conjunction with the triple zeta quality plus polarization functions TZP-DKH basis set were used to calculate the atomic charges and valence orbital population level using the Gaussian09 package [44]. UCA-FUKUI software [45] (http://www2.uca.es/dept/quimica_fisica/software/UCA-FUKUI_v2.exe) was used to calculate the bond reactivity indices (see below). A detailed description of the methodology implemented in this version of the program has been included in reference [46] in terms of various examples. Molecular orbital images (NBOs and NHOs) were obtained with GaussView software [46] and second order energy analysis was performed with the NBO code [47]. The software AIMALL (http://aim.tkgristmill.com/index.html) was used to calculate molecular descriptors related to the Quantum Theory of Atoms in Molecules (QTAIM) methodology. All the Transition State Inward Conrotatory (TSIC) or Transition State Outward Conrotatory (TSOC) in the reactions were determined by one and only one imaginary frequency.

In the following sections, different models and methodologies are explained that are used to determine and analyze the mechanism of the reactions under study. First, we use the bond reactivity index $\Delta {\omega }_i^{\left(NBO\right)}$ to describe the reactivity [48] of the sample of molecules and provide a basic idea of the electronic mechanism.

Natural bond orbitals (NBOs) describe the electron Lewis structure [49]. NBOs are localized molecular orbitals whose that provides an accurate description of Lewis-like electron density. The donor-acceptor interactions [49] have been analysed via a second order perturbation theory. The delocalization energy E⁽²⁾ related with donor NBO (i) → acceptor NBO (j) was estimated with Eq. (1),

$$E^{\left(2\right)}=\Delta E_{ij}=q_i\frac{F{\left(i,j\right)}^2}{{\epsilon }_j-{\epsilon }_i}$$ (1)

where ε_i and ε_j are the orbital energies (of i and j), q_i the partial occupancies, and F(i,j) the Fock matrix element. These interactions could be considered corrections of the ideal Lewis structure.

Bond structure of the NBO analysis supplies qualitative information that is simple to be interpreted and facilitates comparisons between transition states. To obtain a quantitative description of the molecular bond structure, we used QTAIM analysis [50, 51, 52] and especially the ellipticity ε (computed in the BCPs), which is the most appropriate indicator in this framework. A diagonalization of the stress-tensor $\sigma \left(\mathbf{r}\right)$, returns the principal electronic stresses. The stress tensor stiffness S_σ, has been found to be a good descriptor of the ‘resistance’ of the bond-path to the applied distortion since it follows the same trend as the ellipticity.

The variations of the atomic populations can give an idea of how the charge density varies along the IRC. We have chosen the Hirshfeld populations analysis [53, 54, 55] (instead of Mulliken, for example) because these populations are quite independent of the basis set used and this feature is very desirable for this type of calculations. We also calculated the interaction energies between atomic charges using this population analysis to study atomic repulsions and steric effects.

3. Results

3.1. Opening of the four-carbons cycle of the structure 3-CH₂CH₂OAc

Figure 2 shows that the activation energies obtained for the reaction paths of 3-CH₂CH₂OAc are E_a(Reagent-TSOC) = 32.92 kcal/mol and E_a(Reagent-TSIC) = 38.23 kcal/mol. From this, we can conclude that the E_a of the TSOC is a little lower. This is a global view of the reaction, so you can see a local study of the most important stages of the reaction (reagents, TSs and products) and for this we have used several theoretical methodologies to determine the bond structure of these geometries. Figures S1-S3 in the Supporting Information show the IRC-Energies (both paths TSIC and TSOC) for the reactions: 1-Br; 1-Cl; 1-CN; 3,3-di-F; 3,3-di-OMe; 3-CF₃; 3-CHO; 3-Cl; 3-F; 3-OAc; 3-OEt; cis-3,4-di_Cl; cis-3,4-di_OEt; cis-3,4_di-OMe; cis-3-Cl-4_Me; cis-3OMe-4-Me; NONE; OCH₃-t-Bu; trans-3,4-di-Cl.

Figure 2.

IRC-Energy for both paths (TSIC and TSOC trajectories) for 3-CH₂CH₂OAc.

3.1.1. Reagent that leads to the TSs (TSIC and TSOC)

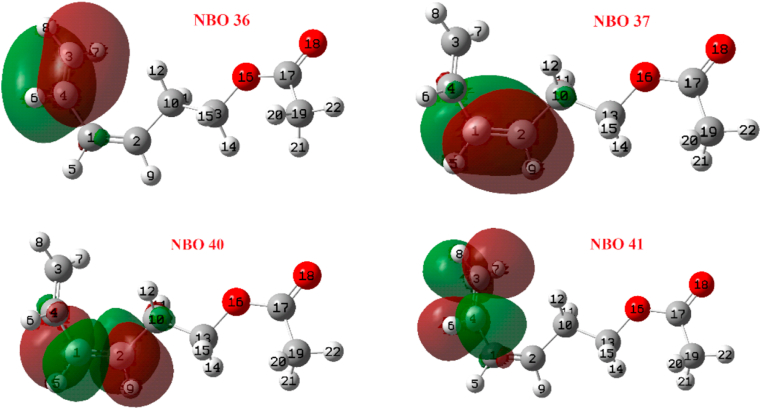
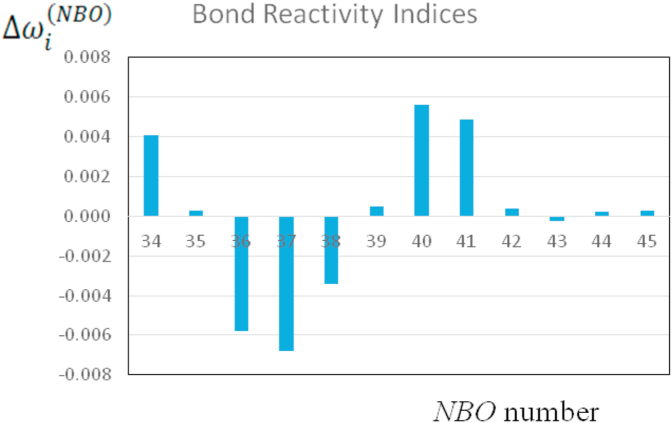
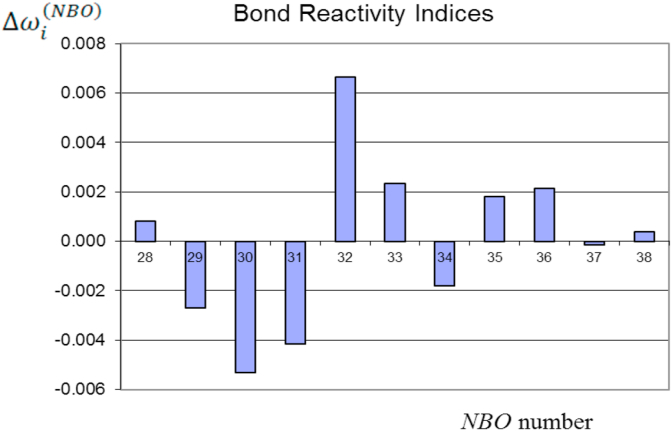
Table 2 includes the reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$, the partial occupations and the orbital energies of the NBOs while Figure 3 shows the $\Delta {\omega }_i^{\left(NBO\right)}$ values from Table 2. NBO 37 shows the highest nucleophilic character (most negative) while NBO 40 has the highest electrophilic character (see Figure 4). That is, NBO 37 → NBO 40 charge transfer is favoured predicting a weakening and breaking of the bond C1 = C4 (π-bonding).

Table 2.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs of the reagent leading to the TSs (TSIC and TSOC). Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$(a.u.)	Type
35	20	1.9909	-0.3678	0.0041	BD C17–O18
36	36	1.8035	-0.3126	0.0003	LP O16
37	3	1.9461	-0.2640	-0.0082	BD C1–C4
38	38	1.8460	-0.2411	-0.0043	LP O18
39	206	0.2062	0.0214	0.0020	BD C17–O18
40	189	0.0416	0.0503	0.0055	BD C1–C4
41	203	0.0269	0.2694	0.0001	BD C13–O16
42	191	0.0086	0.3346	0.0000	BD C2–C3
43	207	0.0628	0.3706	-0.0002	BD C17–C19
44	204	0.1065	0.3711	-0.0006	BD O16–C17
45	200	0.0147	0.3882	0.0000	BD C10–C13
46	187	0.0129	0.3906	0.0008	BD C1–C2
47	193	0.0232	0.3943	-0.0003	BD C2–C10
48	194	0.0041	0.3984	0.0007	BD C3–C4

Figure 3.

Reactivity indices $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs of the reagent leading to the TSs (TSIC and TSOC).

Figure 4.

Selected NBOs from Figure 3.

To quantitatively estimate how the bonds of the molecule change, we have calculated the ellipticities (ε) by applying the QTAIM methodology. Table 3 shows that the most remarkable ellipticity value is for BCP 5, which corresponds to the path C1–C4 (see Figure S4 in the supporting information). The value obtained (ε = 0.395) corresponds to a double bond, which is consistent with the NBO 37 π-bonding C1 = C4.

Table 3.

Ellipticities corresponding to the bonds of the reagent leading to the TSs (TSIC and TSOC). The highlighted values are the most remarkable.

BCP	Atoms	Ellipticity	BCP	Atoms	Ellipticity
1	C1–C2	0.039	12	C10–H11	0.002
2	C3–C4	0.040	13	C10–H12	0.002
3	C2–C10	0.002	14	C13–H14	0.043
4	C2–C3	0.011	15	C13–H15	0.043
5	C1–C4	0.395	16	C13–O16	0.002
6	C1–H5	0.016	17	C17–C19	0.057
7	C4–H6	0.014	18	O16–C17	0.001
8	C3–H7	0.003	19	C17–O18	0.138
9	C3–H8	0.002	20	C19–H21	0.007
10	C2–H9	0.002	21	C19–H20	0.007
11	C10–C13	0.041	22	C19–H22	0.006

3.1.2. Comparison of transition states (TSIC and TSOC)

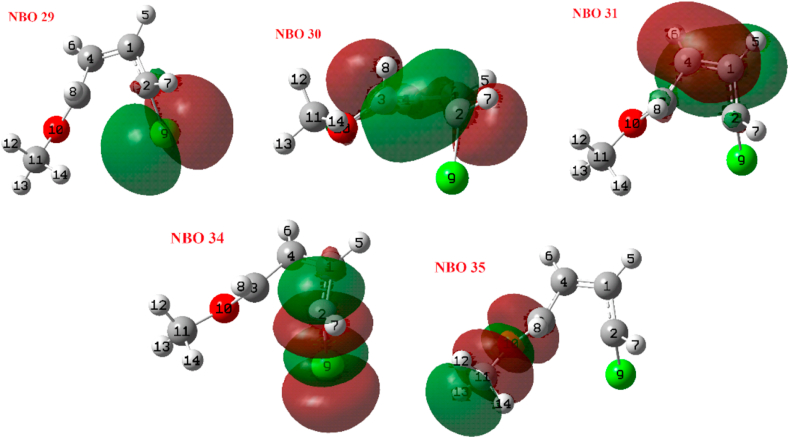
The results of the TSIC and TSOC transition states are shown below. Table 4 shows the reactivity descriptors $\Delta {\omega }_i^{\left(NBO\right)}$ of the main NBOs of the TSIC. Partial occupations and orbital energies have also been included. In Figure 5 shows a graph with the $\Delta {\omega }_i^{\left(NBO\right)}$ from Table 4. Figures 5 and 6 show that NBO 38 (σ-bonding orbital C2–C3) is by far the most nucleophilic and NBO 39 (σ-antibonding orbital C2–C3) is the most electrophilic. This means that the charge transfer of NBO 38 → NBO 39 and the breakage of the corresponding bond is favoured. In the case of the TSOC we found similar results for NBOs 36 and 39 (Table 5 and Figures 7 and 8), the difference that can be remarked in this case is that NBO 36 (σ-bonding orbital C2–C3) is much more stable than the corresponding NBO 38 of the TSIC, this probably resulting in the activation energy of the TSOC being smaller. Tables S1-S22 in the Supporting Information show the orbital energies and partial occupations of NBOs in the TSIC and TSOC for the set of reactions that have been studied. They show that the most characteristic orbitals are the σ-bonding and anti-binding NBOs of the C2–C3 and the π-bonding and anti-bonding NBOs of the C1–C4. The energy and occupation values vary according to the substitutes in a very complex way and general conclusions cannot be obtained so there would be no other choice than to analyze them case by case.

Table 4.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs corresponding to the TSIC. Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.)	Type
34	20	1.9909	-0.3675	0.0034	BD C17–O18
35	36	1.8035	-0.3122	0.0001	LP O16
36	3	1.7752	-0.2436	0.0002	BD C1–C4
37	38	1.8454	-0.2409	-0.0033	LP O18
38	5	1.7204	-0.2359	-0.0104	BD C2–C3
39	191	0.2000	-0.0257	0.0106	BD C2–C3
40	206	0.2062	0.0217	0.0000	BD C17–O18
41	189	0.2545	0.0301	-0.0007	BD C1–C4
42	203	0.0276	0.2711	0.0003	BD C13–O16
43	204	0.1068	0.3712	-0.0003	BD O16–C17
44	207	0.0627	0.3712	-0.0001	BD C17–C19
45	200	0.0248	0.3787	-0.0005	BD C10–C13
46	193	0.0185	0.3966	0.0008	BD C2–C10

Figure 5.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs corresponding to the TSIC.

Figure 6.

Selected NBOs from Figure 5.

Table 5.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs corresponding to the TSOC. Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.)	Type
34	20	1.9908	-0.3705	0.0031	BD C17–O18
35	36	1.8045	-0.3159	0.0001	LP O16
36	5	1.7450	-0.2466	-0.0083	BD C2–C3
37	38	1.8455	-0.2437	-0.0032	LP O18
38	3	1.7954	-0.2400	-0.0006	BD C1–C4
39	191	0.1931	-0.0067	0.0080	BD C2–C3
40	206	0.2045	0.0190	0.0013	BD C17–O18
41	189	0.2465	0.0372	-0.0001	BD C1–C4
42	203	0.0258	0.2681	0.0000	BD C13–O16
43	204	0.1074	0.3663	-0.0004	BD O16–C17
44	207	0.0625	0.3687	-0.0002	BD C17–C19
45	200	0.0145	0.3834	-0.0001	BD C10–C13
46	196	0.0246	0.4173	0.0004	BD C3–C10

Figure 7.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs corresponding to the TSOC.

Figure 8.

Selected NBOs from Figure 7.

We have also applied the second order perturbational theory analysis (SOPTA) to the NBOs of the transition state structure (TSIC), finding two important interactions by delocalization. The first is a donation from NBO 36 (π bonding) corresponding to the double bond C1 = C4 to the NBO 39 (σ anti-antibonding) corresponding to the single bond C2–C3 (see Figure 6). The second order energy value E⁽²⁾ is 27.75 kcal/mol, the partial occupation of NBO 36 is 1.745 (relatively low) and the occupation of NBO 39 is 0.193 (relatively high). The second important interaction is the donation of NBO 38 (σ bonding) corresponding to the simple bond C2–C3 to NBO 41 (π anti-bonding) corresponding to the double link C1 = C4. The second order energy value E⁽²⁾ is 35.23 kcal/mol, the partial occupation of NBO 38 is 1.795 (relatively low) and the occupation of NBO 41 is 0.246 (relatively high). These charge donations are consistent with the results of the reactivity descriptors, NBO 38 tending to decrease its charge density while NBO 39 (anti-bonding) tends to increase its partial occupancy. SOPTA determined that NBOs 36 and 41 also participate in this process. Note that the two bonds corresponding to these four NBOs are the ones that disappear when the cycle is broken and the products are formed.

Table 6 shows the ellipticities corresponding to the TSIC BCPs (Figure S5 in the Supporting Information). The values corresponding to BCPs 1 and 5 (ε = 0.198 and 0.206) show that the double bonds (π) C1 = C2 and C3 = C4 are formed in a synchronized way. The bond C1–C4 has changed from an ellipticity of 0.395 (for the reagent) to 0.279 in the transition state structure, which indicates that this bond is also being broken at the same time as the double bonds C1 = C2 and C3 = C4 are formed. Tables S23-S56 (Supporting Information) show the ellipticities of BCPs for the rest of the sample (see also Figures S15-S52).The values for the bonds C1 = C2 and C3 = C4 make it possible to determine when the rupture of these bonds is synchronized and when it is not. For example, for the reagents 1-CN and 3-CHO the rupture is very synchronized while for the rest it is less so. Reagent 3-OAc is remarkable because in the TSIC a very synchronized rupture is produced, while in the TSOC it is not.

Table 6.

Ellipticities corresponding to the BCP in the TSIC. The highlighted values are the most remarkable.

BCP	Atoms	Ellipticity	BCP	Atoms	Ellipticity
1	C1–C2	0.198	12	C10–H12	0.008
2	C2–C10	0.038	13	C10–H11	0.008
3	C2–C3	0.322	14	C13–H14	0.044
4	C1–C4	0.279	15	C13–H15	0.043
5	C3–C4	0.206	16	C13–O16	0.004
6	C1–H5	0.029	17	C17–C19	0.058
7	C4–H6	0.020	18	O16–C17	0.001
8	C3–H7	0.037	19	C17–O18	0.138
9	C3–H8	0.017	20	C19–H21	0.007
10	C2–H9	0.013	21	C19–H20	0.007
11	C10–C13	0.049	22	C19–H22	0.006

The ellipticity shown by the σ C2–C3 bond (ε = 0.322) might seem to correspond to a π bond but, in this case, it is due to the deformation of the electron density between these atoms due to the "intermediate" geometry of the transition state structure. This can be seen in the deformed shape of NBO 36 (Figure 8), which is due to the decrease in the overlap of the natural hybrid orbitals (NHO) that make up the NBO, which are partially rotated with regard to the initial structure of the reagent. Table 7 and Figure S6 (Supporting Information) show completely analogous results for TSOC.

Table 7.

Ellipticities corresponding to the BCP in the TSOC. The bold values are the most remarkable.

BCP	Atoms	Ellipticities	BCP	Atoms	Ellipticities
1	C1–C2	0.1998	12	C10–H11	0.0119
2	C3–C10	0.0379	13	C10–H12	0.0083
3	C2–C3	0.2115	14	C13–H14	0.0424
4	C1–C4	0.2893	15	C13–H15	0.0426
5	C1–H5	0.0225	16	C13–O16	0.0051
6	C3–C4	0.2039	17	O16–C17	0.0023
7	C4–H6	0.0262	18	C17–C19	0.0575
8	C2–H7	0.0160	19	C17–O18	0.1387
9	C2–H8	0.0377	20	C19–H20	0.0068
10	C3–H9	0.0382	21	C19–H21	0.0069
11	C10–C13	0.0437	22	C19–H22	0.0059

In Table 8, the variations of the atomic populations for the processes Reagent → TSIC and TSIC →Product can be seen. These charge variations can give a qualitative idea of how the charge density changes along the IRC. We have chosen the Hirshfeld population analysis because these populations are quite independent of the basis set used and this characteristic is important in this type of calculation.

Table 8.

Atomic population variations (Hirshfeld), Reagent → TSIC and TSIC →Product. The bold values are the most remarkable.

Atoms	Reagent → TSIC	TSIC → Product	Atoms	Reagent → TSIC	TSIC → Product
1	-0.0064	0.0142	12	-0.0002	0.0024
2	0.0143	-0.0365	13	-0.0029	0.0042
3	0.0069	-0.0339	14	-0.0018	0.0021
4	-0.0049	0.0104	15	-0.0008	0.0026
5	-0.0024	0.0011	16	0.0000	0.0003
6	-0.0022	-0.0019	17	0.0001	0.0004
7	0.0050	0.0041	18	0.0001	0.0010
8	0.0002	0.0089	19	0.0000	0.0003
9	-0.0020	0.0093	20	0.0003	0.0005
10	-0.0023	0.0040	21	0.0000	0.0001
11	-0.0010	0.0061	22	-0.0001	0.0004

Figure 9 shows the same charge variations using the following colour code: the redder the more negative the charge variation and the greener the more positive. The black colour indicates zero charge variation. The figure on the left (Reagent → TSIC) shows that atoms 1 and 4 have the most negative charge variations; that is, there is an increase in electron density in these atoms due to the beginning of the formation of the π-bonds C1–C2 and C3–C4. In contrast, atoms 2 and 3 show a significant decrease in electron density. This is because the σ-bond C2–C3 is about to break and the electron density between C2 and C3 is decreasing.

Figure 9.

Atomic population variations (Hirshfeld), Reagent → TSIC (left) and TSIC→Product (right).

The right of Figure 9 shows the atomic charge variations for the TSIC →Product transformation. In this case, the C2 and C3 atoms have the greatest increase in net charge due to the formation of the π-bonds C1–C2 and C3–C4. On the contrary, the C1 and C4 atoms present a great decrease in electron density due to the breaking of the π-bond C1–C4. Table 9 and Figure 10 show equivalent results for the Reagent → TSOC and TSOC → Product processes. Tables S57-S90 and Figures S53-S86 (in the Supporting Information) show the variations in the net atomic charge for the rest of the cases. As can be seen, the charge transfer largely dependent on the substituents of the cycle and it seems difficult to draw general conclusions.

Table 9.

Atomic population variations (Hirshfeld), Reagent → TSOC and TSOC → Product. The highlighted values are the most remarkable.

Atoms	Reagent → TSOC	TSOC → Product	Atoms	Reagent → TSOC	TSOC → Product
1	-0.0108	0.0159	12	0.0068	-0.0008
2	-0.0014	-0.0268	13	0.0002	0.0010
3	0.0090	-0.0295	14	0.0014	-0.0007
4	-0.0152	0.0187	15	0.0016	0.0002
5	-0.0041	0.0004	16	-0.0001	-0.0003
6	-0.0059	0.0003	17	0.0007	-0.0003
7	-0.0012	0.0125	18	0.0016	-0.0004
8	0.0046	0.0036	19	0.0004	-0.0001
9	0.0047	0.0042	20	0.0006	0.0004
10	-0.0007	0.0050	21	0.0002	-0.0002
11	0.0069	-0.0032	22	0.0006	-0.0002

Figure 10.

Atomic population variations (Hirshfeld), Reagent → TSOC (left) and TSOC→Product (right).

3.1.3. Stabilization of the electron density in the electrostatic potential surface created by the molecule

The stabilization of the electronic density in the electrostatic potential surface (ESP) generated by the molecule can be estimated by the integral (2).

$$I=\int V^{ESP}\left(r\right)\cdot \rho \left(r\right)dv$$ (2)

where $V^{ESP}\left(r\right)$ is the electrostatic potential and $\rho \left(r\right)$ is the electronic density. This can be used as an estimation of the repulsions and attractions between the components of the molecule (electrons and nucleus) and gives us an idea of the steric effect in the molecule (and that we will apply to the TS). We will use the expansion (3) of the density in terms of NBOs,

$$\rho \left(r\right)={\sum _i{C}_i\left|{\varphi }_i^{NBO}\left(r\right)\right|}^2$$ (3)

where the $C_i$ coefficients are the partial occupations of the NBOs, which allows us to rewrite the integral (2) as Eq. (4).

$$I=\int V^{ESP}\left(r\right)\cdot \left[{\sum _i{C}_i\left|{\varphi }_i^{NBO}\left(r\right)\right|}^2\right]dv$$ (4)

Finally, reordering the integral I we obtain Eq. (5).

$$I=\sum _i{C}_i\int V^{ESP}\left(r\right)\cdot {\left|{\varphi }_i^{NBO}\left(r\right)\right|}^{2}dv=\sum _i{I}_i$$ (5)

This allows a local view of the steric effect to be obtained. At the same time, as the NBOs of the TSIC and TSOC states are comparable, the corresponding integrals are also comparable. When calculating the stabilization integrals of these two states (TSIC and TSOC) we found, as expected, that the lesser stabilization integrals correspond to the C–H σ-bonding NBOs. In the case of the TSIC, the integrals corresponding to NBO 26 (C3–H8) and NBO 30 (C2–H9) show relatively low stabilization values (0.815 and 0.838, respectively) compared to the NBOs of the TSOC, NBO 31(C2–H8) and NBO 29 (C3–H9), which have relatively higher values (0.867 and 0.865, respectively). This is probably because, as can be seen in Figure 11, in the case of the TSIC the H8 is in an eclipsed position with the H6, and also the H9 with the H5, which generates greater repulsion than in the case of the TSOC where this does not happen. We believe that this is one of the main reasons why the TSIC presents higher activation energy than the TSOC.

Figure 11.

Representation of the structure of the TSIC. The atoms H8 and H9 are in an eclipsed position with regard to H6 and H5 respectively.

We have also calculated the interaction energies between the net charges of these hydrogens. The interaction energy between H6 and H8 is 0.000327 a.u. and 0.000237 a.u. in the case of the interaction between H5 and H9. In both cases the interaction is very repulsive and is in agreement with the result of the stabilization integrals $I_i$. As an example, in the text of Figures S60-S65, S58-S73 and S79-S86 (in the Supporting Information), the most important interaction energies between hydrogens of the 4C cycle have been included, showing they do not seem to have a decisive effect in general. Electrostatic interactions depend on each particular case. For example, in the case of trans-3,4-di-Cl the most important interaction is that of the chlorines (0.001549 a.u for the TSIC versus 0.001252 a.u for the TSOC), in which case the highest activation energy is that of the TSIC which agrees with the repulsive energy value.

3.1.4. Comparison of products obtained from TSIC and TSOC

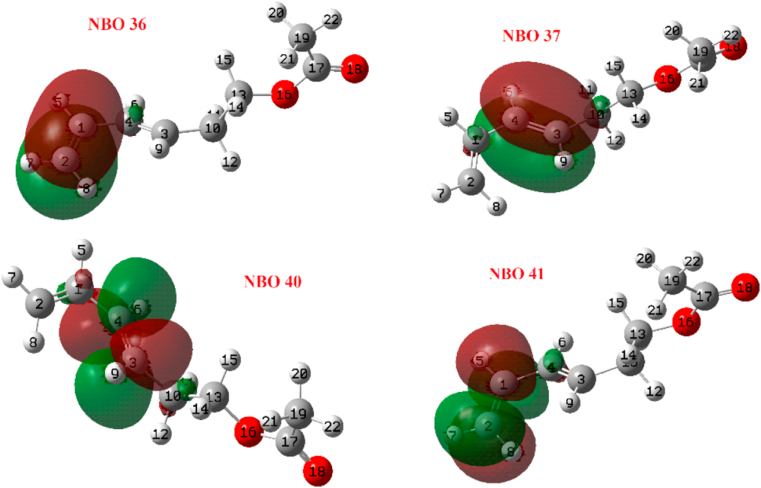
Table 10 includes the reactivity indices $\Delta {\omega }_i^{\left(NBO\right)}$, the partial occupations of the NBOs and their orbital energies while Figure 12 shows the $\Delta {\omega }_i^{\left(NBO\right)}$ values from Table 10. NBOs 36 and 37 have the highest nucleophile character (most negative) while NBOs 40 and 41 have the highest electrophilic character (see Figure 13). That is, the transfer of charge between these four orbitals is favoured, which predicts the weakening and breaking of the π-bonds C1 = C2 and C3 = C4 in the event that the reaction is in the opposite direction. In the case of the reagent that leads to the TSOC, we find completely equivalent results in Table 11 and Figure 14. The most reactive NBOs can be seen in Figure 15.

Table 10.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs of the product obtained through the TSIC. Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.)	Type
34	20	1.9908	-0.3692	0.0037	BD C17–O18
35	36	1.8042	-0.3144	0.0002	LP O16
36	8	1.9409	-0.2785	-0.0053	BD C3–C4
37	2	1.9270	-0.2734	-0.0066	BD C1–C2
38	38	1.8456	-0.2425	-0.0033	LP O18
39	206	0.2051	0.0202	0.0007	BD C17–O18
40	188	0.0819	0.0597	0.0052	BD C1–C2
41	194	0.0574	0.0608	0.0046	BD C3–C4
42	203	0.0264	0.2694	0.0003	BD C13–O16
43	204	0.1070	0.3683	-0.0003	BD O16–C17
44	207	0.0625	0.3698	0.0002	BD C17–C19
45	200	0.0169	0.3799	0.0003	BD C10–C13

Figure 12.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs of the product obtained through the TSIC.

Figure 13.

Selected NBOs from Figure 12.

Table 11.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs of the product obtained through the TSOC. Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.)	Type
34	20	1.9909	-0.3698	0.0041	BD C17–O18
35	36	1.8047	-0.3150	0.0003	LP O16
36	2	1.9428	-0.2762	-0.0058	BD C1–C2
37	8	1.9216	-0.2720	-0.0068	BD C3–C4
38	38	1.8453	-0.2430	-0.0034	LP O18
39	206	0.2050	0.0197	0.0005	BD C17–O18
40	194	0.0803	0.0545	0.0056	BD C3–C4
41	188	0.0591	0.0576	0.0049	BD C1–C2
42	203	0.0277	0.2684	0.0004	BD C13–O16
43	204	0.1072	0.3675	-0.0003	BD O16–C17
44	207	0.0625	0.3695	0.0002	BD C17–C19
45	200	0.0189	0.3742	0.0003	BD C10–C13

Figure 14.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs of the product obtained through the TSOC.

Figure 15.

Selected NBOs from Figure 14.

Table 12 shows that the most remarkable ellipticity values are BCP 1, corresponding to path C1–C2, and BCP 3, corresponding to path C3–C4 (see Figure S7 in the Supporting Information). The values obtained (ε = 0.376 and 0.365 respectively) correspond to double bonds, which are coherent with the NBO 37 π-bonding C1 = C2 and NBO 36 π-bonding C3 = C4 respectively. In the case of the reagent that leads to TSOC the results are completely equivalent, as can be seen in Table 13 and Figure S8 (Supporting Information).

Table 12.

Ellipticities corresponding to the BCP of the product obtained through the TSIC. The bold values are the most remarkable.

BCP	Atoms	Ellipticities	BCP	Atoms	Ellipticities
1	C1–C2	0.3760	12	C2–C10	0.0391
2	C1–C4	0.0834	13	C10–H11	0.0053
3	C3–C4	0.3655	14	C13–H14	0.0430
4	C1–H5	0.0220	15	C13–H15	0.0417
5	C4–H6	0.0169	16	C13–O16	0.0051
6	C10–H12	0.0063	17	O16–C17	0.0021
7	C3–H7	0.0192	18	C17–C19	0.0576
8	C3–H12	1.0594	19	C17–O18	0.1385
9	C3–H8	0.0198	20	C19–H21	0.0071
10	C2–H9	0.0212	21	C19–H20	0.0067
11	C10–C13	0.0461	22	C19–H22	0.0059

Table 13.

Ellipticities corresponding to the BCP of the product obtained through the TSOC.

BCP	Atoms	Ellipticities	BCP	Atoms	Ellipticities
1	C1–C2	0.3669	11	C10–H11	0.0038
2	C3–C4	0.3690	12	C10–H12	0.0021
3	C1–C4	0.0864	13	C13–H14	0.0427
4	C1–H5	0.0166	14	C13–H15	0.0424
5	C4–H6	0.0190	15	C13–O16	0.0061
6	C2–H7	0.0212	16	O16–C17	0.0023
7	C3–H9	0.0185	17	C17–C19	0.0576
8	C2–H8	0.0197	18	C17–O18	0.1384
9	C3–C10	0.0388	19	C19–H21	0.0071
10	C10–C13	0.0465	20	C19–H20	0.0068
11	C10–H11	0.0038	21	C19–H22	0.0059

3.1.5. Evolution of natural hybrid orbitals (NHOs) throughout the reaction

It has been seen that in some cases the NBOs obtained for TSs show deformations (with regard to their usual shape). These NBOs are composed of linear combinations of natural hybrid orbitals (NHOs) that make their partial occupation maximum. For this reason, we have carried out an analysis of how these NHOs evolve during the reaction.

Figure 16 shows NHOs 5, 6, 9 and 10 that make up NBOs 37 (π-bonding C1 = C4), 40 (π-bonding C1 = C4), 24 (π-bonding C2–C3) and 42 (π-bonding C2–C3) of the reagent. In Figure 17 the same NHOs can be seen in the TSs, in which case the overlap between the NHOs that form NBO 24 (π-bonding C2–C3) is smaller due to the change of geometry of the molecule that forces these NHOs to spin during the IRC. It also shows the evolution of the NHO, which, in the case of NBO 24, is composed of approximately 23% of natural atomic orbital (NAO) type "s" and 77% of NAO type "p". In the structure of the TS, the composition is approximately 4% type "s" and 96% type "p". Finally, in the reaction product (Figure 18) these NHOs form NBOs 36 π-bonding C3 = C4 and NBO 37 π-bonding C1 = C2. The composition of the NHOs is approximately 99.5% type "p". The conclusion that can be obtained is that the NHOs of the σ-bonds lose the contribution of the NAOs type "s" until they form bonds type π where this contribution is zero.

Figure 16.

NHOs that constitute NBOs 24, 37, 40 and 42 of the reagent.

Figure 17.

NHOs that constitute NBOs 36 and 37 in the TSIC (left) and the NBOs 36 and 38 in the TSOC (right).

Figure 18.

NHOs that constitute NBOs 36 and 37 in the product of the TSIC (left) and the TSOC (right).

3.2. Opening of the four-carbons cycle of the structure cis-3-Cl-4-OMe

Figure 19 shows that the activation energies obtained for the reaction paths of cis-3-Cl-4-OMe are E_a(Reagent-TSOC) = 35.18 kcal/mol and E_a(Reagent-TSIC) = 30.09 kcal/mol. In this case, the E_a of the TSIC is a little lower. This is a global view of the reaction. Below we can see a local study of the most characteristic structures of the reaction (reagents, TSs and products) and for this we have used several theoretical methodologies to determine the bonding structure of these geometries.

Figure 19.

IRC-Energy for both paths (TSIC and TSOC trajectories) for the cis-3-Cl-4-OMe.

3.2.1. Comparison of reagents that lead to TSIC and TSOC structures

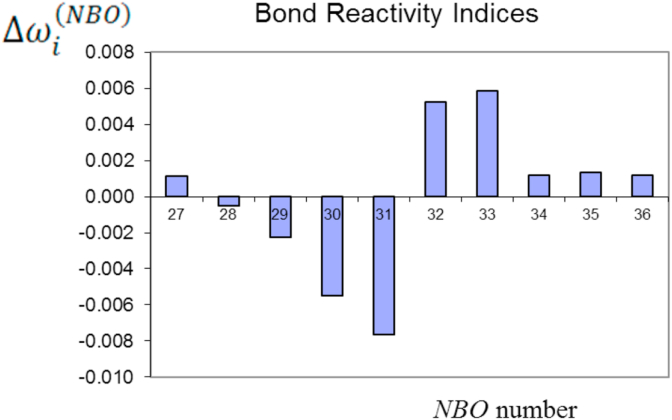
Table 14 includes the reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ in addition to the partial occupations of the NBOs and their orbital energies. Figure 20 shows the $\Delta {\omega }_i^{\left(NBO\right)}$ values of Table 15, NBOs 30 and 31 showing the highest nucleophilic character ($\Delta {\omega }_i^{\left(NBO\right)}$ most negative) and NBO 32 the highest electrophilic character (see Figure 21). In this case, load transfer NBO 31→ NBO 32 is favoured, which predicts a weakening and breaking of the bond (π) C1 = C4. In the case of the reagent that leads to TSOC, we find completely equivalent results in Table 15 and Figure 22 (the most reactive NBOs can be seen in Figure 23).

Table 14.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs of the reagent leading to the TSIC. Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$(a.u.)	Type
28	28	1.9783	-0.3188	0.0008	LP Cl9
29	29	1.9628	-0.2998	-0.0027	LP Cl9
30	31	1.9039	-0.2887	-0.0053	LP O10
31	3	1.8978	-0.2854	-0.0042	BD C1–C4
32	132	0.0290	0.0529	0.0066	BD C1–C4
33	136	0.0574	0.1085	0.0023	BD C2–Cl9
34	134	0.0646	0.2865	-0.0018	BD C2–C3
35	141	0.0086	0.3047	0.0018	BD O10–C11
36	139	0.0394	0.3307	0.0021	BD C3–O10
37	130	0.0197	0.3870	-0.0001	BD C1–C2
38	137	0.0182	0.3915	0.0004	BD C3–C4

Figure 20.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs of the reagent leading to the TSIC.

Table 15.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs of the reagent leading to the TSOC. Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.)	Type
28	28	1.9778	-0.3128	-0.0035	LP Cl9
29	29	1.9622	-0.2938	0.0007	LP Cl9
30	31	1.9120	-0.2913	-0.0046	LP O10
31	3	1.9005	-0.2874	-0.0047	BD C1–C4
32	132	0.0308	0.0538	0.0084	BD C1–C4
33	139	0.0557	0.1145	0.0017	BD C3–Cl9
34	141	0.0069	0.3085	0.0022	BD O10–C11
35	134	0.0413	0.3088	-0.0005	BD C2–C3
36	136	0.0404	0.3258	0.0027	BD C2–O10
37	130	0.0344	0.3705	-0.0016	BD C1–C2
38	137	0.0211	0.3858	-0.0007	BD C3–C4

Figure 21.

Selected NBOs from Figure 20.

Figure 22.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs of the reagent leading to the TSOC.

Figure 23.

Selected NBOs from Figure 22.

To estimate quantitatively how the bonds of the molecule change we have calculated the ellipticities (ε) by applying the QTAIM methodology. Table 16 shows that the most remarkable ellipticity value is that of BCP 3, which corresponds to path C1–C4 (see Figure S9 in the Supporting Information). The value obtained (ε = 0.3795) corresponds to a double bond which is consistent with NBO 31 π-bond C1 = C4. In the case of the reagent that leads to TSOC, the results are completely equivalent, as can be seen in Table 17 and Figure S10 (in the Supporting Information).

Table 16.

Ellipticities corresponding to the reagent that leads to the TSIC. The bold values are the most remarkable.

BCP	Atoms	Ellipticities	BCP	Atoms	Ellipticities
1	C1–C2	0.0345	8	C3–H8	0.0303
2	C2–C3	0.0577	9	C2–Cl9	0.0093
3	C1–C4	0.3795	10	C3–O10	0.0386
4	C3–C4	0.0363	11	Cl9–H14	1.0214
5	C1–H5	0.0121	12	O10–C11	0.0175
6	C4–H6	0.0099	13	C11–H12	0.0446
7	C2–H7	0.0244	14	C11–H13	0.0426
8	C3–H8	0.0303	15	C11–H14	0.0429

Table 17.

Ellipticities corresponding to the reagent that leads to the TSOC. bold values are the most remarkable.

BCP	Atoms	Ellipticities	BCP	Atoms	Ellipticities
1	C1–C2	0.0191	8	C2–H8	0.0298
2	C2–C3	0.0515	9	C3–Cl9	0.0062
3	C1–C4	0.3751	10	C2–O10	0.0538
4	C3–C4	0.0392	11	O10–C11	0.0149
5	C1–H5	0.0088	12	C11–H14	0.0444
6	C3–H6	0.0215	13	C11–H12	0.0415
7	C4–H7	0.0119	14	C11–H13	0.0436

3.2.2. Comparison of transition states (TSIC and TSOC)

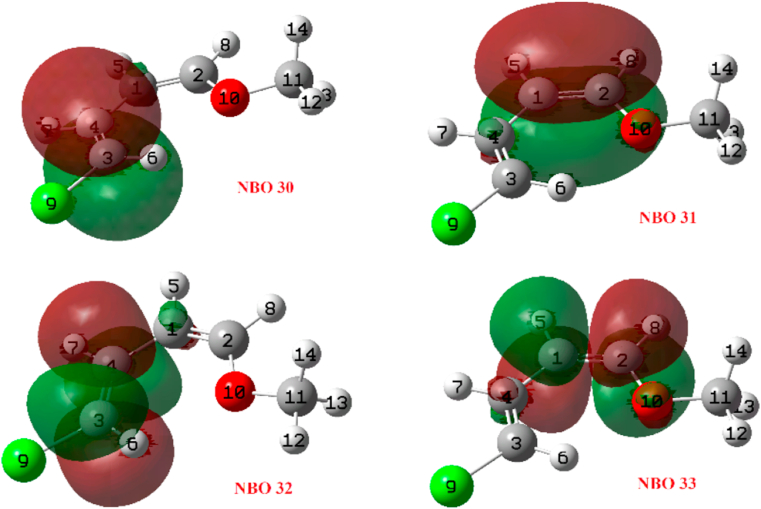
We now present the results of the TSIC and TSOC transition states. Table 18 shows the reactivity descriptors $\Delta {\omega }_i^{\left(NBO\right)}$ of the main NBOs in the TSIC. Partial occupations and orbital energies have also been included. Figure 24 shows a graph with the $\Delta {\omega }_i^{\left(NBO\right)}$ from Table 18. Figures 24 and 25 show that NBOs 29 and 30 (lone pairs of Cl9 and orbital σ-bonding C2–C3, respectively) are the most nucleophilic and NBOs 31, 34 and 35 (orbital π-bonding C1 = C4, σ-bonding C2–Cl9 and π-antibonding O10 = C11 binder, respectively) are the most electrophilic. This means that the charge transfer from NBO 30 to the neighbouring orbitals and the rupture of the corresponding bond are favoured.

Table 18.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs of the TSIC. Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.)	Type
27	28	1.9779	-0.3201	0.00012	LP Cl9
28	31	1.7877	-0.3155	0.00005	LP O10
29	29	1.9580	-0.3064	-0.00039	LP Cl9
30	5	1.7427	-0.2580	-0.00041	BD C2–C3
31	3	1.7829	-0.2441	0.00024	BD C1–C4
32	134	0.3459	-0.0406	0.00008	BD C2–C3
33	132	0.2531	0.0318	-0.00013	BD C1–C4
34	136	0.0425	0.1327	0.00026	BD C2–Cl9
35	141	0.0106	0.2684	0.00022	BD O10–C11
36	139	0.0381	0.3821	-0.00005	BD C3–O10

Figure 24.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs of the TSIC.

Figure 25.

Selected NBOs from Figure 24.

In the case of TSOC, different results are obtained (Table 19 and Figures 26 and 27). In this case NBO 30 (σ-bonding C2–C3) has a high electrophilic character, which indicates that the bond has less tendency to break than in the previous case and that the reaction is not as favoured as in the TSIC case, which is consistent with the activation energy values.

Table 19.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs of the TSOC. Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.)	Type
27	28	1.9779	-0.3201	-0.0025	LP Cl9
28	31	1.7877	-0.3155	-0.0002	LP O10
29	29	1.9580	-0.3064	-0.0020	LP Cl9
30	5	1.7427	-0.2580	0.0157	BD C2–C3
31	3	1.7829	-0.2441	0.0082	BD C1–C4
32	134	0.3459	-0.0406	-0.0044	BD C2–C3
33	132	0.2531	0.0318	-0.0050	BD C1–C4
34	136	0.0425	0.1327	-0.0052	BD C2–Cl9
35	141	0.0106	0.2684	-0.0004	BD O10–C11
36	139	0.0381	0.3821	-0.0044	BD C3–O10

Figure 26.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs corresponding to the TSOC.

Figure 27.

Selected NBOs from Figure 26.

In this case, we have also applied the second order perturbational theory analysis (SOPTA) to the NBOs of the TSIC and found three important interactions by delocalisation. The first is a donation from NBO 31 (π-bonding) corresponding to the double bond C1 = C4 to NBO 32 (σ-antibonding) corresponding to the single bond C2–C3 (see Figure 25). The second order energy value E⁽²⁾ is 27.37 kcal/mol, the partial occupation of NBO 31 is 1,783 (relatively low) and the occupation of NBO 32 is 0.346 (relatively high). The second important interaction is the donation of NBO 30 (σ-bonding) corresponding to the single bond C2–C3 to NBO 33 (π-antibonding) corresponding to the double bond C1 = C4. The second order energy value E⁽²⁾ is 33.29 kcal/mol, the partial occupation of NBO 30 is 1,743 (relatively low) and the occupation of NBO 3 is 0.253 (relatively high). The third major interaction is the donation of NBO 28 (lone pair) corresponding to O10 to NBO 32 (σ-antibonding) corresponding to the C2–C3 bond. The second order energy value E⁽²⁾ is 45.23 kcal/mol, and the partial occupation of NBO 28 is 1,788 (relatively low). This charge delocalization from the breaking NBOs 30 and 31 to the corresponding antibonding NBOs 32 and 33 is closely related to the formation of the new π-bonds in the reaction product (see below).

Table 20 shows the ellipticities corresponding to the BCPs of the TSIC. The values of BCPs 2 and 4 (ε = 0.208 and 0.209, see Figure S11 in the Supporting Information) show that the double bonds C1 = C2 and C3 = C4 are starting to form in a synchronized way. The C1–C4 bond has gone from an ellipticity of 0.380 for the reagent to 0.294, indicating that this PI bond is also being broken at the same time as the double bonds C1 = C2 and C3 = C4 are being formed. The ellipticity shown by the σ bond C2–C3 (ε = 0.386) might seem to correspond to a π bond, but in this case, it is due to the deformation of the electron density between these atoms caused by the "intermediate" geometry of the transition state structure. Table 21 and Figure S12 (Supporting Information) show completely analogous results for TSOC.

Table 20.

Ellipticities corresponding to the BCP of the TSIC. The bold values are the most remarkable.

BCP	Atoms	Ellipticities	BCP	Atoms	Ellipticities
1	C2–C3	0.3860	8	C3–H8	0.0609
2	C1–C2	0.2083	9	C2–Cl9	0.0742
3	C1–C4	0.2938	10	C3–O10	0.0477
4	C3–C4	0.2095	11	O10–C11	0.0155
5	C1–H5	0.0240	12	C11–H12	0.0455
6	C4–H6	0.0247	13	C11–H13	0.0448
7	C2–H7	0.0422	14	C11–H14	0.0443

Table 21.

Ellipticities corresponding to the BCP of the TSOC. The bold values are the most remarkable.

BCP	Atoms	Ellipticities	BCP	Atoms	Ellipticities
1	C1–C2	0.2119	8	C2–H8	0.0333
2	C2–C3	0.3655	9	C3–Cl9	0.0539
3	C1–C4	0.2775	10	C2–O10	0.0479
4	C3–C4	0.2115	11	O10–C11	0.0207
5	C1–H5	0.0288	12	C11–H13	0.0434
6	C3–H6	0.0626	13	C11–H12	0.0415
7	C4–H7	0.0188	14	C11–H14	0.0428

Table 22 shows the net atomic charge variations for the processes Reagent→ TSIC and TSIC→ Product. Figure 28 shows the same charge variations using a colour code. Figure 28 (left, Reagent →TSIC) shows that atoms 1, 2 and 4 have the most negative charge variations; that is, there is an increase in electron density in these atoms, which may be due to the beginning of the appearance of the π-bonds C1–C2 and C3–C4. In contrast, atom 3 shows a significant decrease in electron density. This may be due to the fact that the σ-bond C2–C3 is about to break and the electron density between C2 and C3 is decreasing and, in addition, the substituent that is donating most of the charge is bound to this carbon. The right of Figure 28 shows the atomic charge variations for the TSIC→ Product transformation, in which case the atoms of the cycle have the highest net charge increase, which is due to the formation of the π-bonds C1 = C2 and C3 = C4. Similar results can be seen in Table 23 and Figure 29 for the Reactive→TSOC and TSOC→ Product processes, the main difference being the order in which the substitutes donate load to the cycle.

Table 22.

Hirshfeld charge variations: Reagent → TSIC and TSIC →Product. The bold values are the most remarkable.

Atoms	Reagent →TSIC	TSIC →Product	Atoms	Reagent →TSIC	TSIC →Product
1	-0.0202	0.0070	8	0.0149	-0.0056
2	-0.0381	-0.0110	9	-0.0079	0.0571
3	0.0129	-0.0219	10	0.0468	-0.0111
4	-0.0304	-0.0238	11	0.0154	-0.0016
5	-0.0129	0.0063	12	0.0122	0.0001
6	-0.0078	-0.0068	13	0.0074	-0.0026
7	-0.0087	0.0181	14	0.0163	-0.0042

Figure 28.

Hirshfeld charge variations: Reagent → TSIC (left) and TSIC→Product (right).

Table 23.

Hirshfeld charge variations: Reagent → TSOC and TSOC → Product. The bold values are the most remarkable.

Atoms	Reagent →TSOC	TSOC → Product	Atoms	Reagent →TSOC	TSOC → Product
1	-0.0207	-0.0186	8	0.0008	0.0173
2	0.0050	-0.0243	9	0.0289	0.0047
3	-0.0131	-0.0300	10	0.0046	0.0427
4	-0.0050	-0.0127	11	0.0003	0.0110
5	-0.0086	0.0000	12	0.0006	0.0043
6	0.0064	-0.0052	13	0.0022	0.0092
7	-0.0030	-0.0076	14	0.0016	0.0092

Figure 29.

Hirshfeld charge variations: Reagent → TSOC (left) and TSOC→Product (right).

3.2.3. Comparison of products obtained from TSIC and TSOC

Table 24 includes the reactivity bond indexes $\Delta {\omega }_i^{\left(NBO\right)}$, the partial occupations of the NBOs and their orbital energies. Figure 30 shows the values of Table 23, NBOs 30 and 31 showing the highest ($\Delta {\omega }_i^{\left(NBO\right)}$ most negative) nucleophilic character, while NBOs 32 and 33 have the highest electrophilic character (see Figure 31). In other words, the transfer of charge between these four orbitals is favoured, which predicts a weakening and rupture of the π-bonds C1 = C2 and C3 = C4 in the case of a reaction in the opposite direction. In the case of the reagent that leads to TSOC, we find completely equivalent results in Table 25 and Figure 32. In this case, the most reactive NBOs can be seen in Figure 33.

Table 24.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs of the product obtained through the TSIC. Partial occupations and orbital energies have also been included. The bold bonds are the most remarkable.

Level	NBO	Occupancy	Energy (a.u.)	$\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.)	Type
27	28	1.96976	-0.3164	0.0011	LP Cl9
28	29	1.9245	-0.3131	-0.0005	LP Cl9
29	31	1.82259	-0.3095	-0.0022	LP O10
30	2	1.94809	-0.28	-0.0055	BD C1–C2
31	8	1.89254	-0.267	-0.0076	BD C3–C4
32	131	0.18722	0.0356	0.0052	BD C1–C2
33	137	0.1819	0.0428	0.0059	BD C3–C4
34	135	0.03066	0.1541	0.0012	BD C2–Cl9
35	141	0.00587	0.2804	0.0014	BD O10–C11
36	139	0.02064	0.3833	0.0012	BD C3–O10

Figure 30.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs of the product obtained through the TSIC.

Figure 31.

Selected NBOs from Figure 30.

Table 25.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$(a.u.) of the NBOs of the product obtained through the TSOC. Partial occupations and orbital energies have also been included. The bold values are the most remarkable.

Level	NBO	Occupancy	Energy	$\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.)	Type
27	31	1.8303	-0.3161	-0.0017	LP O10
28	28	1.9770	-0.3056	0.0014	LP Cl9
29	29	1.9251	-0.3037	-0.0013	LP Cl9
30	8	1.9367	-0.2737	-0.0053	BD C3–C4
31	2	1.9158	-0.2724	-0.0070	BD C1–C2
32	137	0.1600	0.0401	0.0050	BD C3–C4
33	131	0.1898	0.0412	0.0052	BD C1–C2
34	139	0.0216	0.1656	0.0014	BD C3–Cl9
35	141	0.0066	0.2752	0.0012	BD O10–C11
36	135	0.0241	0.3739	0.0010	BD C2–O10

Figure 32.

Reactivity indexes $\Delta {\omega }_i^{\left(NBO\right)}$ (a.u.) of the NBOs of the product obtained through the TSOC.

Figure 33.

Selected NBOs from Figure 32.

Table 26 shows that the most remarkable ellipticity values are those of BCP 1, corresponding to path C1–C2 and BCP 3 corresponding to path C3–C4 (see Figure S13 in the Supporting Information). The values obtained (ε = 0.407 and 0.404 respectively) correspond to double bonds, which is coherent with NBO 31 π-bonding C1 = C2 and NBO 30 π-bonding C3 = C4, respectively. In the case of the reagent that leads to TSOC, the results are completely equivalent, as can be seen in Table 27 and Figure S14 (Supporting Information).

Table 26.

Ellipticities corresponding to the BCPs of the product obtained through the TSIC. The bold values are the most remarkable.

BCP	Atoms	Ellipticities	BCP	Atoms	Ellipticities
1	C1–C2	0.4066	8	C2–Cl9	0.0708
2	C1–C4	0.1308	9	H8–Cl9	0.0241
3	C3–C4	0.4036	10	C3–O10	0.0142
4	C1–H5	0.0203	11	O10–C11	0.0160
5	C4–H6	0.0356	12	C11–H13	0.0453
6	C2–H7	0.0589	13	C11–H12	0.0456
7	C3–H8	0.0430	14	C11–H14	0.0456

Table 27.

Ellipticities corresponding to the BCPs of the product obtained through the TSOC. The bold values are the most remarkable.

BCP	Atoms	Ellipticities	BCP	Atoms	Ellipticities
1	C1–C2	0.4244	8	C2–O10	0.0460
2	C1–C4	0.1240	9	C3–Cl9	0.0615
3	C3–C4	0.3990	10	H6–O10	0.0486
4	C1–H5	0.0379	11	O10–C11	0.0156
5	C3–H6	0.0454	12	C11–H12	0.0452
6	C4–H7	0.0210	13	C11–H13	0.0459
7	C2–H8	0.0555	14	C11–H14	0.0459

4. Discussion

The previous section presents the general results obtained from the calculation methodologies used in this work. In this section we discuss the calculated data in relation to the stereochemistry, mainly commenting on the connection between the global point of view (energy barrier) and the local view of the different calculation methodologies employed (NBO, local reactivity indices, QTAIM and Hirshfeld population analysis). The results obtained are then discussed on a case-by-case analysis.

For cis-3-Cl-4-OMe the TSIC shows a lower energy barrier. In this case the delocalisation charge donations are responsible for the higher stabilisation of TSIC, mainly in the case of the LP donation from the O10 to the σ∗ (C2–C3) bond, which is E⁽²⁾ = 45.23 kcal/mol in TSIC and only 6.54 kcal/mol in TSOC.

In the 3-CH2CH2OAc case, the TSOC shows a lower energy barrier. The NBO analysis of the charge donations shows no significant differences between TSIC and TSOC, but the interaction energies between the net charges of H6 and H8 and H5 and H9 in TSOC are 0.000235 a.u. and 0.000236 a.u. respectively. In the case of the TSIC the interactions are 0.000327 a.u. and 0.000237 a.u. In both cases the interactions are very repulsive but are lower in the case of TSOC which justifies a lower energy barrier.

For the 3,3-di-OMe system the TSOC shows a lower energy barrier. The second order perturbational theory analysis performed on the TSOC gives two important donations, the first one from the LP (O8) to the σ (C2–C3) bond with a value E⁽²⁾ = 39.00 kcal/mol and a second donation LP (O13) to the σ (C2–C3) bond with a value E⁽²⁾ = 29.38 kcal/mol. In the case of TSIC the LP donation (O13) to the σ (C2–C3) bond has a value E⁽²⁾ = 35.81 kcal/mol, however, the LP donation (O8) to the σ (C2–C3) bond is negligible (E⁽²⁾ = 0.88 kcal/mol), this is the reason why TSIC is less stable than TSOC and the corresponding energy barrier.

The 3-F molecule leads to a lower energy barrier for TSOC. In this case, the NBO analysis shows that for TSIC LP (F10) → σ(C2–C3) with an E⁽²⁾ = 13.76 kcal/mol is obtained, while for TSOC LP (F10) → σ(C2–C3) with an E⁽²⁾ = 24.03 kcal/mol. This justifies the lower energy barrier in the TSOC case. On the other hand, the interaction energies of the Hirshfeld charges have been obtained, for TSIC a repulsion energy between the atoms C3 and F10 of 0.00165 a.u. has been obtained, while in the case of TSOC the equivalent interaction is C2–F10 with an energy value of 0.00138 a.u., which is considerably lower. The higher repulsion of TSIC also justifies a higher energy barrier.

In 3-OAc, a lower energy barrier is obtained for TSOC. In this case, the NBO analysis shows that in the TSIC case a charge donation LP (O10) → σ∗(C2–C3) with a value E⁽²⁾ = 14.66 kcal/mol is obtained, while for TSOC a LP (O10) → σ∗(C2–C3) with a value E⁽²⁾ = 31.11 kcal/mol is obtained. This may justify the lower energy barrier in the TSOC case.

In the case of 3-OEt the TSOC shows a lower energy barrier. The TSIC shows the charge donation by delocalisation LP (O10) → σ∗(C2–C3) with a value E⁽²⁾ = 0.70 kcal/mol, while for TSOC the donation LP (O10) → σ∗(C2–C3) with a value E⁽²⁾ = 35.56 kcal/mol is obtained. This justifies the lower energy barrier in the TSOC case.

For cis-3-Cl-4-Me the TSOC leads to a lower energy barrier. The TSIC shows a charge donation by delocalisation LP (Cl9) → σ∗(C2–C3) with a value E⁽²⁾ = 6.14 kcal/mol, whereas for TSOC the LP (Cl9) → σ∗(C2–C3) donation has a value E⁽²⁾ = 14.95 kcal/mol. This justifies the lower energy barrier in the TSOC case.

The cis-3-OMe-4-Me molecule leads to a lower energy barrier for TSOC. The NBO analysis in the TSIC case shows a charge donation by delocalisation LP (O9) → σ∗(C2–C3) with a value E⁽²⁾ = 4.15 kcal/mol, while for TSOC LP (O9) → σ∗(C2–C3) with a value E⁽²⁾ = 34.92 kcal/mol. This may justify the lower energy barrier in the TSOC case.

For the OCH3-t-Bu system the TSOC shows a lower energy barrier. In the TSIC case a charge donation by delocalisation LP (O22) → σ∗(C2–C3) with a value E⁽²⁾ = 30.26 kcal/mol is obtained, while for TSOC a donation LP (O22) → σ∗(C2–C3) with a value E⁽²⁾ = 36.86 kcal/mol is obtained. This may justifies the lower energy barrier in the TSOC case.

In the case of the trans-3,4-di-Cl compound, TSOC provides a lower energy barrier. In the case of TSIC, the delocalisation charge donations LP (Cl9) → σ∗(C2–C3) with an E⁽²⁾ = 9.43 kcal/mol and LP (Cl10) → σ∗(C2–C3) with a value E⁽²⁾ = 9.43 kcal/mol are obtained, while for TSOC LP (Cl9) → σ∗(C2–C3) with an E⁽²⁾ = 16. 22 kcal/mol and LP (Cl10) → σ∗(C2–C3) with a value E⁽²⁾ = 16.22 kcal/mol. This could justify the lower energy barrier in the TSOC case.

The cases 1-Br, 1Cl, 1-CN, 3-Cl, 3,3-di-F, Cis-3,4,di-OMe have symmetrically equivalent TSIC and TSOC transition states. In the cases 3-CF3, 3-CHO, cis-3,4-di-Cl and cis-3,4-di-OEt the differences between the energy barriers are not large enough to obtain a conclusion at this level of calculation. The QTAIM analysis shows an interesting result when studying the C–C bond of the four-carbon cycle which is directly bonded to the substituent originating the charge donations by delocalisation. A high degree of consistency can be observed between the QTAIM results and the conclusions obtained from the NBO analysisis. Table 28 shows the stress tensor shiffness values and ellipticities of this C–C bond for the relevant cases of the study. As a general result, it can be considered that the C–C bond presented in the table has a certain double bond character and that the effect of charge donation by delocalisation near this double bond advances the formation of the double bond and favours this reaction path. This can be verified by comparing delocalisation energy with ellipticity values which measure the double bond character of the same bond in the two transition states (TSIC and TSOC), in the same way the stress tensor shiftness values can also be analysed, which, logically, shows that the double bond character is proportional to its stiffness. The only exceptional case is the 3,3-di-OMe case because there are two lone pairs of two different substituents and the situation is not comparable to the rest, all the other cases show a great coherence between the donations by delocalisation and the double character of this bond.

Table 28.

Stress tensor shiffness and ellipticity of the C–C bond of the four-carbon cycle that is directly bonded to the substituent that gives rise to the most important charge donations by delocalisation.

Case	Transition State	Stress tensor shiffness	Ellipticity
3-CH2CH2OAc	TSIC	3.0078	0.1985
	TSOC	3.0000	0.2039
cis-3-Cl_4_OMe	TSIC	3.1894	0.2095
	TSOC	3.0977	0.2119
3,3-di-OMe	TSIC	3.2000	0.2152
	TSOC	3.1693	0.1732
3-F	TSIC	3.2966	0.2108
	TSOC	3.4050	0.2401
3-OAc	TSIC	3.1765	0.1949
	TSOC	3.2490	0.2223
3-OEt	TSIC	3.0900	0.2094
	TSOC	3.1640	0.2161
cis-3-Cl-4-Me	TSIC	3.1833	0.2100
	TSOC	3.3365	0.2244
cis-3_OMe-4-Me	TSIC	3.0995	0.2142
	TSOC	3.2374	0.2259
OCH3-t-Bu	TSIC	2.8752	0.1601
	TSOC	3.0338	0.2041
trans-3,4-di-Cl	TSIC	3.2124	0.2059
	TSOC	3.2727	0.2155

5. Conclusions

The stereoselectivity of electrocyclic reactions for a representative and large sample of cyclobutenes has been studied. The energy variation along the different reaction paths has been calculated from a global perspective. From a local point of view, several theoretical methodologies have been used to obtain a detailed molecular description and to determine the differences between the different reaction pathways. Natural bond orbitals have been obtained and a second order perturbational theory analysis has been performed to determine the main charge transfers due to delocalization. Bond reactivity indexes have been used to describe the reactivity mechanism in a local way. These reactivity indexes are also based on NBOs, making it possible to connect the results of the indexes with the previous analysis. To determine quantitatively the bond structure we used the quantum theory of atoms in molecules and we have thereby completed the information obtained from the NBO analysis. Finally, we have used the Hirshfeld population analysis as an approximation to understand how the load density changes in the different reaction pathways, and we have connected these variations with the information obtained from the bond structure.

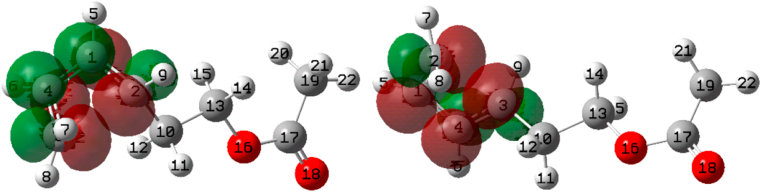
It has been found that the reaction path with the lowest energy barrier (TSIC or TSOC) is determined by two magnitudes: the charge donations by delocalisation of the substituents (which we obtained from the Second Order Perturbational Theory Analysis of the NBOs) and in the case that these donations were very similar, the non-covalent interactions dominated (which we studied by means of the interaction energies of the Hirshfeld charges). The most important factor influencing the lower energy reaction path was the interaction of lone pairs of the substituents with the σ∗(C–C) bond that is broken at the opening of the cycle. The alignment of these lone pairs with the C–C bond favours charge donation between them and, as can be seen in the discussion, this alignment varies depending on whether the structure is TSIC and TSOC, Figure 34 shows as a representative example an image of the cis-3-OMe-4-Me case.

Figure 34.

Left) TSIC (unfavourable case). Right) TSOC (favourable case). The two figures correspond to the cis-3-OMe-4-Me system.

Finally, with respect to the inconclusive cases, in the 3-CF3 and 3-CHO cases the atoms with unshared pairs are relatively far from the breaking sigma bond, and in the cis-3,4-di-Cl and Cis-3,4-di-OEt cases the positions of the substituents make two situations TSIC and TSOC very analogous from the point of view of the lone pairs.

Declarations

Author contribution statement

Alejandro Morales-Bayuelo, Jesús Sánchez-Márquez: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by Universidad del Sinú, Seccional Cartagena (MEDBS-PD/2021–03) and Ministerio de Ciencia, Innovación y Universidades del Gobierno de España (No. ENE2014-58085-R).

Data availability statement

No data was used for the research described in the article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

Appendix A. Supplementary data

The following is the supplementary data related to this article: