Genome-wide association study-based deep learning for survival prediction

Abstract

Informative and accurate survival prediction with individualized dynamic risk profiles over time is critical for personalized disease prevention and clinical management. The massive genetic data, such as SNPs from genome-wide association studies (GWAS), together with well-characterized time-to-event phenotypes provide unprecedented opportunities for developing effective survival prediction models. Recent advances in deep learning have made extraordinary achievements in establishing powerful prediction models in the biomedical field. However, the applications of deep learning approaches in survival prediction are limited, especially with utilizing the wealthy GWAS data. Motivated by developing powerful prediction models for the progression of an eye disease, age-related macular degeneration (AMD), we develop and implement a multilayer deep neural network (DNN) survival model to effectively extract features and make accurate and interpretable predictions. Various simulation studies are performed to compare the prediction performance of the DNN survival model with several other machine learning-based survival models. Finally, using the GWAS data from two large-scale randomized clinical trials in AMD with over 7800 observations, we show that the DNN survival model not only outperforms several existing survival prediction models in terms of prediction accuracy (eg, c-index =0.76), but also successfully detects clinically meaningful risk subgroups by effectively learning the complex structures among genetic variants. Moreover, we obtain a subject-specific importance measure for each predictor from the DNN survival model, which provides valuable insights into the personalized early prevention and clinical management for this disease.

1 |. INTRODUCTION

Accurate “time-to-event” data based survival prediction is fundamental to effective clinical management and precision medicine of human diseases.^1,2 It relies on a survival model to predict the dynamic risk profile of a future event over time (eg, disease onset, recurrence, progression, or death) based on the individual’s current status, such as clinical characteristics, genetic information, and medical images. Most importantly, such a prediction addresses the patient’s key concern regarding the disease progression pattern in the future and shapes the physician’s decision making for the treatment or clinical management strategy. Note that the survival prediction is fundamentally different from typical prediction models that predict a future event (whether occurs or not) by fixing the time of interest through a binary classification.^3,4 Despite its essential role in precision medicine, the survival prediction remains a challenging task,^5–7 largely due to the complex nature of diseases and the heterogeneity between patients. Therefore, there is an urgent need for developing accurate and personalized survival prediction models with improved capacity in learning the complex structures and interplays among predictors. Recent advances in high-throughput technologies have generated large volumes of molecular profiling data for each patient, which provides unprecedented opportunities in identifying potential biomarkers and further establishing accurate survival prediction models.^8–10 In particular, several national-wide large-scale longitudinal studies, such as the trans-omics for precision medicine and All of Us, are underway using whole-genome sequencing and other omics technologies, with the ultimate goal of accelerating precision medicine. However, how to effectively utilize the wealthy amount of data is challenging. The first challenge comes from how to connect high-dimensional predictors with the outcome of interest. This problem is particularly difficult in survival prediction because the events of interest are sometimes censored due to either a short study period or loss of follow-up during the study. The second challenge is how to model the complex structure among numerous biomarkers, where the specific structure is largely unknown. The third challenge is that given the heterogeneity of patients, how to interpret the importance of each predictor for each patient and further how to identify patient subgroups to provide personalized prevention or treatment strategy.

The recent advances in multilayer deep neural network (DNN) models have made extraordinary achievements in providing new effective risk prediction models from complex and high-dimensional biomedical data, such as omics and biomedical imaging.^11–14 However, the application of deep learning in survival prediction is still limited. Faraggi and Simon¹⁵ proposed a single-layer neural network based on the Cox proportional hazards (PH) model. However, its performance did not exceed the regular Cox model in a prostate cancer survival dataset with 475 patents and only four clinical predictors. More recently, multiple efforts have been devoted to evaluating Cox-based neural network survival models using larger datasets with omic biomarkers. For example, Katzman et al¹⁶ demonstrated that a single hidden layer neural network survival model performed marginally better than the Cox model and random survival forest (RSF) model in a breast cancer survival dataset with 1980 patients and nine predictors. In another study, Ching et al¹⁷ applied a single hidden layer neural network survival model to 10 TCGA cancer survival datasets (sample sizes range from 302 to 1077) with high-throughput gene expression biomarkers, from which the neural network survival models resulted in comparable or better performance than the Cox model, the penalized Cox models such as Cox-LASSO and the RSF model. In another study¹⁸ that also used TCGA cancer survival datasets (sample sizes range from 194 to 1092 with up to 17 000 gene expression biomarkers), the neural network survival models yielded comparable performance to the penalized Cox model and better performance than the RSF model. Hao et al¹⁹ developed a pathway-based neural network survival model and applied it to a TCGA cancer dataset (sample size 522 with 860 pathways and 5567 genes). However, all these studies have limited sample sizes, particular in the presence of tens of thousands of predictors, and thus may lead to severe model over-fitting problem. Moreover, the patient-specific predictor importance was not considered in those studies. The scenario of tied events, which is commonly seen in practice, especially when the sample size is large, was not carefully considered in these studies.

In this article, we propose and evaluate a multi-hidden-layer Cox-based DNN survival model to predict the progression of a progressive eye disease, namely, age-related macular degeneration (AMD). The genome-wide association study (GWAS) of AMD is the first and most successful GWAS research, where the massive GWAS data provide unprecedented opportunities to study disease risk and progression. Although some attempts have been tried to predict AMD progression risks using genetic information such as SNPs, most statistical models focus on the structured regression framework, which typically only accounts for (generalized) linear effects of the SNPs and thus have considerable limitations. To the best of our knowledge, there has no existing work on survival prediction using deep learning to effectively extract features from the GWAS data. Therefore, we develop and apply the DNN survival model to build an accurate and interpretable prediction model for the AMD progression.

The rest of the article is organized as follows. Section 2 describes the deep learning survival methods and prediction evaluation procedures. We assess the performance of three machine/deep learning survival prediction models (DNN, LASSO, RSF) through extensive simulation studies in Section 3 and apply them to the GWAS data from two large-scale clinical studies of AMD in Section 4. Discussion and conclusion are presented in Section 5.

2 |. METHODS

First, we define notation for survival observations. For each subject i ∈ {1, …, n}, the observations are {Y_i, δ_i ,Z_i}, where Y_i = min (T_i, C_i) is the minimum of survival time T_i and censoring time C_i; δ_i = I(T_i ≤ C_i) is the (right-)censoring indicator; Z_i is the vector of covariates.

2.1 |. Cox-based DNN survival model

The Cox PH model is the most popular regression model for censored survival data. It assumes that the hazard function of survival time T takes the form $h\left(t\mid Z_i\right)=h_0(t)\text{exp}\left(Z_i^T\theta \right)$, where h₀(t) is the unspecified baseline hazard function at time t and θ is a vector of covariate effects. The term $Z_i^T\theta$ is called the linear predictor or prognostic index. On the other hand, the DNN model is well known for its capacity in learning complex covariate structures (ie, nonlinearity, interactions).²⁰ By the universal approximation theorem,^21,22 for any continuous function g(Z; θ), it is guaranteed to exist a neural network that approximates this function. Moreover, this theorem holds even if we restrict the neural networks to have just one single hidden layer. Therefore, even very simple neural network architecture can be extremely powerful. The synergy of the powerful DNN and the popular Cox model leads us to build the Cox-based DNN survival model and apply it to AMD progression prediction.

2.1.1 |. Assumption and loss function of DNN survival model

The DNN survival model we consider here can be written as $h\left(t\mid Z_i\right)=h_0(t)e^{g\left(Z_i;\theta \right)}$. The major difference between this DNN model and the regular Cox model is that DNN takes the prognostic index g(Z_i; θ) as an unknown function with parameters θ, instead of assuming a simple linear relationship. In this way, the DNN model can approximate various nonlinear covariate structures by estimating g(Z_i; θ). We will employ a feedforward DNN with multiple hidden layers to estimate the unspecified g(Z; θ), as shown in Sections 2.1.2 and 2.1.3. In fact, one can regard the regular Cox model as a special case of DNN when $g\left(Z_i;\theta \right)=Z_i^T\theta$.

In large-scale clinical and observational studies, it is quite common that more than one observations develop events at the same time. Such events are called tied events. To handle this scenario, we approximate the partial likelihood via Efron’s approach.²³ Moreover, to deal with high-dimensional covariates, we introduce the L₁ penalty to the DNN loss function −l(θ; Z) + λ‖θ‖₁, where l(θ; Z) is the Efron approximation of log partial likelihood:

$$l(\theta ;Z)=\frac{1}{N_D}\sum _{j\in D}\left\{\sum _{i\in H_j}g\left(Z_i;\theta \right)-\sum _{l=0}^{m_j-1}\text{log}\left(\sum _{i\in R_j}{e}^{g\left(Z_i;\theta \right)}-\frac{l}{m_j}\sum _{i\in H_j}{e}^{g\left(Z_i\theta \right)}\right)\right\},$$ (1)

where D is the set of all events with size N_D and {t_j} is the set of unique event times; H_j is the set of subjects {i} such that Y_i = t_j and δ_i = 1 and m_j is the size of H_j; and R_j is the risk set satisfying Y_i ≥ t_j.

2.1.2 |. DNN architecture

First, we introduce the general form of an L-hidden-layer feedforward DNN, which is composed of one input layer, L hidden layers and one output layer (with one node in our case). For each subject, DNN inputs the vector of covariates Z into its input layer and output a scalar prognostic index g(Z; θ). For each hidden layer l ∈ {1, …, L} with n_l number of nodes, it takes the input n_l−1-dimensional a^(l−1) from the (l − 1)th layer and outputs n_l-dimensional a^(l) through a n_l-dimensional activation function f^l. Mathematically, the lth hidden layer model can be written as a^(l) = f^(l)(W₀^(l) + W^(l)a^(l−1)), where W₀^(l) is the bias vector with length n_l; W^(l) is an n_l × n_l−1 weight matrix. f^(l)(⋅) is a vector of activation functions f^(l)(⋅). Often a common f^(l)(⋅) function is assumed for all the nodes in the lth hidden layer and it is usually a nonlinear function, such as the sigmoid²² $f(x)=\frac{1}{1+e^{-x}}$, the tangent $f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$, the rectified linear unit (ReLU)²⁴ f(x) = max(0, x), and the scaled exponential linear units (SeLU)²⁵ f(x) = λ × ReLU(x) + λI(x < 0)α(e^x − 1), where λ and α are constants. The final or output layer also has weights and an output function f ^out, which is an identity function.

Take a simple one-hidden layer neural network, for example. We have p-dimensional input covariates z_i from the ith subject, n₁ number of hidden nodes with k = 1, …, n₁ and one single output node. For the kth hidden node, we have $a_k^{(1)}=f_k^{(1)}\left(w_{k0}^{(1)}+{\sum }_{j=1}^p{w}_{kj}^{(1)}{z}_{ij}\right)$. Similarly, the output node is $o_i=f^{\text{out}}\left(w_0^{(2)}+{\sum }_{k=1}^{n_1}{w}_k^{(2)}{a}_k^{(1)}\right)=w_0^{(2)}+{\sum }_{k=1}^{n_1}{w}_k^{(2)}{a}_k^{(1)}$ by assuming f^out is an identity function. Typically we have o_i = g(z_i; θ). The full parameter set θ is composed of $\left\{w_{k0}^{(1)},k=1,\dots ,n_1\right\}$, $\left\{w_{kj}^{(1)},k=1,\dots ,n_1,j=1,\dots ,p\right\}$, $w_0^{(2)}$, and $\left\{w_k^{(2)},k=1,\dots ,n_1\right\}$.

2.1.3 |. DNN optimization and survival prediction

Tosolve for $\widehat{\theta }$, we use the mini-batch stochastic gradient descent algorithm²⁶ to minimize the loss function in Equation (1). Comparing with the standard stochastic gradient descent that uses all samples for each iteration, the mini-batch algorithm is much faster. Specifically, we randomly divide all observations into mini-batches with size N_B and update $\widehat{\theta }$ by adding the gradient contributed by each mini-batch. In particular, the loss function for the rth batch is

$$-l^r(\theta ;Z)+\lambda \Vert \theta {\Vert }_1=-\frac{1}{N_D^r}\sum _{j\in D^r}\left\{\sum _{i\in H_j^r}g\left(Z_i;\theta \right)-\sum _{l=0}^{m_j^r-1}\text{log}\left(\sum _{i\in R_j^r}{e}^{g\left(Z_i;\theta \right)}-\frac{l}{m_j^r}\sum _{i\in H_j^r}{e}^{g\left(Z_i;\theta \right)}\right)\right\}+\lambda \Vert \theta {\Vert }_1,$$

where $N_D^r$, D^r, $H_j^r$, $m_j^r$, and $R_j^r$ are the corresponding terms for the rth batch similar to those defined in Equation (1). Then we update θ by adding the gradient contributed by the rth batch through:

$${\Delta }_r=-{\nabla }_{\theta }{l}^r(\theta ;Z)+\lambda {\nabla }_{\theta }\Vert \theta {\Vert }_1$$

$$\theta \leftarrow \theta -\gamma {\Delta }_r,$$

where γ is the learning rate (also called step size). This process will be repeated for N_E times (also called epochs) before convergence. We employ the Glorot uniform initializer²⁷ to randomly select initial values. Once we get $\widehat{g}\left(Z_i;\widehat{\theta }\right)$, we can obtain the predicted survival probability for subject i at time t through $\widehat{S}\left(t\mid Z_i\right)=\text{exp}\left\{-{\widehat{H}}_0(t)e^{\widehat{g}\left(Z_i,\widehat{\theta }\right)}\right\}$.

2.1.4 |. DNN hyperparameters

To perform the survival prediction based on the DNN survival model, we need to select the DNN hyperparameters. The main hyperparameters include the number of hidden layers, number of nodes per hidden layer, choice of activation function, the L₁ penalty parameter, batch size, epoch size, and learning rate. Based on our limited experience, we found that selecting hyperparameters in a sequential manner helps to understand how each parameter influences the model prediction performance. We select hyperparameters in the following ordering: number of hidden layers, number of nodes per layer, activation function, learning rate, L₁ penalty, epoch size, and batch size. In this work, we perform cross-validations in the training data and select the combination of hyperparameters that lead to the most optimal prediction performance on the validation data. Specific hyperparameter choices are presented in Section 3 for simulation studies and in Section 4 for real data analysis.

2.1.5 |. DNN interpretation

It is important to understand and interpret the fitted neural network prediction model. One way is to export feature (ie, predictor) importance measures that decide the top important features in a prediction model. The local interpretable model-agnostic explanation (LIME) method²⁸ provides prediction importance of each predictor for each subject in the model by perturbing the feature values and evaluating how the prediction results change. To perform LIME, we first perturb the value of one feature of one individual sample by adding some random noise (to get a new data point), and then obtain a new prognostic index $\widehat{g}$ from the DNN model. We repeat this perturbation (eg, for 1000 times). Next, we fit a simpler model (ie, a linear regression) between the 1000 pairs of perturbed feature values and their corresponding estimated prognostic index $\widehat{g}\left(Z;\widehat{\theta }\right)$ values, and obtain the regression coefficient. We do this for all features across all samples. Finally, the most important features will be identified by the rank of absolute coefficient values. Therefore, the magnitude of the individualized feature importance reflects the estimated effect size on the prognostic index by increasing one unit value in this feature for each individual sample. LIME has been widely applied to neural network models with continuous or categorical outcomes, but not with censored survival outcomes yet. In this article, we apply the LIME method to the neural network survival model and produce subject-specific predictor importance measures with meaningful interpretations.

2.2 |. Evaluation metrics for survival prediction performance

We calculate the Harrell’s concordance index (c-index)²⁹ to measure the proportion of concordance pairs (ie, the predicted and observed outcomes are concordant) among all comparable pairs (ie, the true progression statuses can be ordered for two observations within one pair). Pairs are not comparable if both are censored, or one is censored at time c₁ and the other event occurs at time t₂ with t₂ > c₁. The c-index is between 0 and 1 with a larger value indicating a better prediction model, which can be estimated by $\widehat{C}=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{\delta }_{i}I\left(Y_i<Y_j\right)I\left(\widehat{g}\left(Z_i;\widehat{\theta }\right)>\widehat{g}\left(Z_j;\widehat{\theta }\right)\right)+0.5*I\left(\widehat{g}\left(Z_i,\widehat{\theta }\right)=\widehat{g}\left(Z_j,\widehat{\theta }\right)\right)}{{\sum }_{i=1}^n{\sum }_{j=1}^n{\delta }_{i}I\left(Y_i<Y_j\right)+I\left(\widehat{g}\left(Z_i;\widehat{\theta }\right)=\widehat{g}\left(Z_j;\widehat{\theta }\right)\right)}$.

We also obtain the time-dependent Brier score.^30,31 At a specific time point t, the Brier score measures the mean squared error between the observed progression status at time t (ie, Y_i(t) = I(Y_i ≥ t)) and the predicted survival probability (ie, $\widehat{S}\left(t\mid Z_i\right)$). A lower Brier score indicates a better prediction model. A Brier score of 33% corresponds to predicting the risk by a random number drawn from Uniform [0, 1] and 25% corresponds to predicting 50 % risk for every observation. The estimated Brier score is expressed as $\widehat{BS}(t,\widehat{S})=\frac{1}{M}{\sum }_{i\in D_M}{\widehat{W}}_i(t){\left\{Y_i(t)-\widehat{S}\left(t\mid Z_i\right)\right\}}^2$, where D_M is the test dataset with size M, $\widehat{S}\left(t\mid Z_i\right)$ is estimated using the training data, and ${\widehat{W}}_i(t)=\frac{\left(1-Y_i(t)\right){\delta }_i}{\widehat{G}\left(Y_i-\right)}+\frac{Y_i(t)}{\widehat{G}(t)}$ is the inverse probability of censoring weights with $\widehat{G}(t)=\widehat{P}(C>t)$.³¹

We also obtain the time-dependent ROC curve and its associated area under the curve (AUC).³² The AUC measures the discrimination capability of $\widehat{g}(Z;\widehat{\theta })$. It ranges between 0 and 1, with higher AUC indicating better discrimination ability. Specifically, we first derive the time-dependent sensitivity and specificity

$$\text{sensitivity}(c,t)=P\{\widehat{g}(Z;\widehat{\theta })>c\mid T\le t\},$$

$$\text{specificity}(c,t)=P\{\widehat{g}(Z;\widehat{\theta })\le c\mid T>t\},$$

where c is some arbitrary cut-off. For a given t, sensitivity(c, t), and specificity(c, t) determine the ROC curve profile and its associated AUC at time t.

2.3 |. K-fold cross-validations

Overfitting is a common issue for all machine learning models. One way to alleviate the issue is to perform K-fold cross-validation. Specifically, the original data D_N are split into K subsets D_k, k = 1, …, K, accounting for the censoring proportions. For the kth cross-validation, models are trained in the samples D_N \ D_k (original data without the kth subset) and then validated in the test samples D_k. Finally, the K-fold cross-validation estimates (ie, c-index and Brier score) are calculated by averaging over the test data results, as shown below

$$\widehat{\mathit{\text{CvBS}}}(t,\widehat{S})=\frac{1}{K}\sum _{k=1}^K\frac{1}{M_k}\sum _{i\in D_k}{\widehat{W}}_i(t){\left\{Y_i(t)-{\widehat{S}}_k\left(t\mid Z_i\right)\right\}}^2,$$

$$\widehat{CvC}=\frac{1}{K}\sum _{k=1}^K\frac{1}{M_K}\frac{{\sum }_{i\in D_k}{\sum }_{j\in D_k}{\delta }_{i}I\left(Y_i<Y_j\right)I\left({\widehat{g}}_k\left(Z_i;{\widehat{\theta }}_k\right)>{\widehat{g}}_k\left(Z_j;{\widehat{\theta }}_k\right)\right)+0.5I\left({\widehat{g}}_k\left(Z_i;{\widehat{\theta }}_k\right)={\widehat{g}}_k\left(Z_j;{\widehat{\theta }}_k\right)\right)}{{\sum }_{i\in D_k}{\sum }_{j\in D_k}{\delta }_{i}I\left(Y_i<Y_j\right)+I\left({\widehat{g}}_k\left(Z_i;{\widehat{\theta }}_k\right)={\widehat{g}}_k\left(Z_j;{\widehat{\theta }}_k\right)\right)},$$

where M_k is the sample size of the kth subset.

2.4 |. Implementation

Our DNN survival model is built with Keras³³ and Tensorflow³⁴ to ensure computational stability and efficiency. Keras is a deep learning framework that provides a convenient way to define and train deep learning models. It provides high-level building blocks for deep learning models.³⁵ For example, one can define a neural network model with a few lines of codes in Keras. We use Tensorflow for low-level operations such as differentiation, which serves as the backend engine of Keras. Via Keras and Tensorflow, our DNN survival model is compatible with both GPUs and CPUs.

3 |. SIMULATION STUDIES

We use simulations to evaluate the prediction performance of DNN and compare it with Cox-LASSO (abbreviated as LASSO)³⁶ and RSF.^37,38 Two main simulation settings are considered. In the first setting, data are generated with sparse signals (ie, only a few predictors with nonzero effects on the survival outcome). In the second setting, all predictors have nonzero but weak signals, which is common in settings with genetics or genomics predictors. Within each simulation setting, we generate multiple scenarios with different structures in predictors’ effects. For each scenario, we train the models in a training dataset, and then test them in an independent test dataset and summarize the results across 200 replications. The sample sizes for both training and test datasets are 1000.

All three models involve the selection of tuning parameters. For LASSO, we use fivefold cross-validation to select the tuning parameter in the L₁ penalty using the training data. After the tuning parameter is determined, we then train the LASSO model using the entire training data and finally validate the model in the test data. For RSF, we train the model by utilizing the default setting of 1000 trees and $\sqrt{p}$ number of randomly selected predictors at each split. In the case of DNN, it is widely known for its exhaustive process in selecting optimal tuning parameters since there are many tuning parameters to consider. The tuning process is even more time consuming given that we have multiple simulation scenarios. Therefore, for all simulation scenarios, we use the sequential tuning strategy as described in Section 2.1.4 and choose one common set of hyperparameters as follows: two hidden layers, 30 nodes per hidden layer, activation function SeLU, L₁ penalty =0.1, batch size N_B =50, epoch size N_E =1000, and learning rate γ = 0.01 (for sparse signals) or γ = 0.0001 (for weak signals).

3.1 |. Simulation I: Survival data with sparse signals

We consider five scenarios of predictor effects following Mi et al,³⁹ which includes linear effects only (scenario 1) and linear effects together with nonlinear effects (scenario 2) or with interactions (scenario 3) or with both nonlinear and interaction effects (scenario 4) or with nonlinear, interaction and threshold effects (scenario 5). The total number of predictors is set at p = 10, 50, 100, 500, respectively. The true models for these five scenarios are illustrated as follows:

$$\text{Scenario }1:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^5{Z}_{ij}\right),$$

$$\text{Scenario }2:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^5{Z}_{ij}+Z_{i6}^2+Z_{i7}^2\right),$$

$$\text{Scenario }3:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^5{Z}_{ij}+Z_{i6}+Z_{i7}+5Z_{i6}{Z}_{i7}\right),$$

$$\text{Scenario }4:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^5{Z}_{ij}+Z_{i6}+Z_{i7}+5Z_{i6}{Z}_{i7}+Z_{i8}^2+Z_{i9}^2\right),$$

$$\text{Scenario }5:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^5{Z}_{ij}+Z_{i6}+Z_{i7}+5Z_{i6}{Z}_{i7}+I\left(Z_{i8}<-0.5\cup Z_{i9}<-0.5\right)-I\left(Z_{i8}\ge -0.5\cap Z_{i9}\ge -0.5\right)\right),$$

where h₀(t) = kλ^kt^k−1 is the baseline Weibull hazard function with λ = 0.1, k = 2. For Z_i = (Z_i1, …, Z_ip), we first generate Z_i from MVN(0, Σ) with Σ = {σ_jj′ = e^{−|j−j′|},1 ≤ j,j′ ≤ p} and then transform Z_i4 into a binary predictor through I(Z_i4 >0) and Z_i5 into a multinomial predictor through I(Z_i5 > −0.5)+I(Z_i5 >0.5). The right censoring rates are set at 50%.

In Table 1, we compare the prediction accuracy of the DNN, RSF, LASSO under the five simulation scenarios in terms of c-index. We also present the c-index from fitting the true model as the bench mark. LASSO performs the best in scenario 1 where all predictor effects are linear, but its performance declines in all the other four scenarios. RSF generally has higher c-index than LASSO in nonlinear scenarios. For our proposed method, its performance is worse than LASSO as expected in scenario 1 but is better than RSF, while it outperforms both LASSO and RSF in all nonlinear scenarios. Moreover, it can be seen that when p is small, DNN produces c-index values that are very close to the truth for all five scenarios. In this sparse simulation setting, all three methods’ performance (in terms of c-index) declines as p increases. LASSO is most robust to the increase of p among all three methods. The performance of DNN seems to be mostly affected when p increases. However, it still achieves the highest c-index for the complex nonlinear scenarios (3, 4, and 5) compared with the other two methods across all p’s.

TABLE 1.

The c-index values, mean and standard deviation (SD) (range from 0 to 100) from 200 replications for the DNN, RSF, LASSO, and True models with sparse signals under five scenarios: linear effects (scenario 1) and linear effects together with nonlinear effects (scenario 2) or with interactions (scenario 3) or with nonlinear and interaction effects (scenario 4) or with interaction and indicator effects (scenario 5)

	p	DNN	RSF	LASSO	True
Scenario 1	10	88.0 (0.7)	82.9 (1.0)	88.2 (0.6)	87.4 (0.6)
	50	85.7 (1.0)	82.8 (1.0)	88.2 (0.6)
	100	83.2 (1.0)	82.4 (1.2)	88.2 (0.6)
	500	82.2 (1.0)	81.1 (1.1)	88.0 (0.7)
Scenario 2	10	88.7 (0.9)	80.9 (1.2)	80.0 (1.0)	89.8 (0.5)
	50	84.2 (1.6)	80.2 (1.1)	80.0 (1.0)
	100	80.6 (2.0)	79.5 (1.1)	79.9 (0.9)
	500	74.3 (3.1)	77.9 (1.0)	79.9 (1.0)
Scenario 3	10	93.1 (0.6)	79.7 (1.8)	74.0 (1.4)	94.0 (0.4)
	50	91.4 (0.7)	75.6 (1.5)	73.9 (1.5)
	100	89.8 (0.8)	74.4 (1.6)	73.9 (1.4)
	500	81.6 (1.8)	72.0 (1.5)	73.7 (1.4)
Scenario 4	10	92.1 (0.8)	80.1 (1.8)	71.4 (1.3)	94.4 (0.4)
	50	88.9 (1.5)	75.6 (1.5)	71.3 (1.4)
	100	84.5 (2.0)	74.2 (1.6)	71.4 (1.3)
	500	76.3 (1.8)	71.4 (1.4)	71.1 (1.4)
Scenario 5	10	92.4 (0.6)	79.4 (1.7)	73.3 (1.3)	94.0 (0.4)
	50	90.4 (0.8)	75.2 (1.6)	73.1 (1.4)
	100	88.6 (0.8)	74.0 (1.4)	73.0 (1.4)
	500	80.4 (2.0)	71.4 (1.5)	72.7 (1.3)

Note: The number of predictors is set at p = 10, 50, 100, 500.

Abbreviations: DNN, deep neural network; RSF, random survival forest.

3.2 |. Simulation II: Survival data with weak signals

In genetics and genomics data, we often observe that many predictors have (nonzero) weak effects due to correlations among SNPs or genes. Moreover, there are various types of omics predictors, such as gene expressions (ie, continuous), mutations (ie, binary), and SNPs (ie, multinomial). Therefore, we generate data that include various types of predictors with weak effects. The total number of predictors is set as p = 20, 50, 100, 500 and we consider the following five scenarios:

$$\text{Scenario }1:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^p{\beta }_j{Z}_{ij}\right),$$

$$\text{Scenario }2:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^p{\beta }_j{Z}_{ij}+Z_{i1}^2+Z_{i2}^2\right),$$

$$\text{Scenario }3:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^p{\beta }_j{Z}_{ij}+Z_{i3}{Z}_{i4}\right),$$

$$\text{Scenario }4:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^p{\beta }_j{Z}_{ij}+Z_{i1}^2+Z_{i2}^2+Z_{i3}{Z}_{i4}\right),$$

$$\text{Scenario }5:h\left(t\mid Z_i\right)=h_0(t)\text{ exp }\left(\sum _{j=1}^p{\beta }_j{Z}_{ij}+I\left(Z_{i1}<-0.5\cup Z_{i2}<-0.5\right)-I\left(Z_{i1}\ge -0.5\cap Z_{i2}\ge -0.5\right)+Z_{i3}{Z}_{i4}\right),$$

where h₀(t) is the baseline Weibull hazard function with λ = 0.01,k = 10. Similarly to the first simulation setting, we first generate Z_i from a multivariate normal distribution MVN(0, Σ) with Σ = {σ_jj′ = e^{−|j−j′|},1 ≤ j,j′ ≤ p}. Then the first 20% Z_ij remain continuous, the second 20% Z_ij are transformed into binary predictors through I(Z_ij >0) and the rest 60% Z_ij are transformed into multinomial predictors through I(Z_ij >−0.5)+I(Z_ij >0.5). For predictor effects, we set β_j = 0.2 for continuous and binary predictors. For multinomial predictors, we mimic the linkage disequilibrium effect in SNP data by generating β_j from MVN(0.2, 0.01 × Σ) with the same Σ. The right censoring rates are 50%.

Table 2 summarizes the prediction performance results (in terms of c-index) under the five simulation scenarios. As the size of p increases, our proposal method improves in all scenarios. In particular, when p is large (eg, p = 500), our proposed method outperforms the other two models significantly in all simulation settings. The c-index of LASSO also increases as p gets larger, but remains unchanged or even slightly decreases when p increases from 100 to 500. RSF also improves with larger p but its performance is generally lower than the other two methods.

TABLE 2.

The c-index values, mean and SD (range from 0 to 100) from 200 replications for the DNN, RSF, and LASSO models with weak signals under five scenarios: linear effects (scenario 1) and linear effects together with nonlinear effects (scenario 2) or with interactions (scenario 3) or with nonlinear and interaction effects (scenario 4) or with interaction and indicator effects (scenario 5)

	p	DNN	RSF	LASSO
Scenario 1	20	66.8 (1.3)	55.5 (5.8)	67.0 (1.4)
	50	73.7 (1.3)	58.2 (7.6)	74.0 (1.2)
	100	78.2 (1.2)	60.8 (7.6)	78.6 (1.1)
	500	82.1 (1.4)	62.9 (4.8)	75.9 (1.5)
Scenario 2	20	64.6 (1.6)	53.7 (4.9)	63.2 (1.4)
	50	71.3 (1.3)	57.1 (7.3)	71.8 (1.2)
	100	76.6 (1.2)	60.1 (7.3)	76.9 (1.1)
	500	81.5 (1.3)	62.5 (5.0)	75.9 (1.5)
Scenario 3	20	67.4 (1.3)	55.2 (5.9)	67.5 (1.3)
	50	73.2 (1.2)	56.6 (7.7)	73.6 (1.2)
	100	77.7 (1.2)	60.0 (7.8)	78.2 (1.1)
	500	81.8 (1.4)	62.7 (5.0)	75.6 (1.5)
Scenario 4	20	65.5 (1.5)	53.5 (5.1)	63.9 (1.4)
	50	71.0 (1.3)	56.3 (7.5)	71.4 (1.2)
	100	76.0 (1.2)	59.3 (8.0)	76.5 (1.2)
	500	81.3 (1.4)	62.4 (5.1)	75.6 (1.5)
Scenario 5	20	64.8 (1.3)	54.3 (4.8)	64.8 (1.4)
	50	72.0 (1.2)	56.5 (7.6)	72.4 (1.2)
	100	77.1 (1.2)	59.6 (7.9)	77.6 (1.2)
	500	81.8 (1.4)	62.7 (5.1)	75.1 (1.5)

Note: The number of predictors is set at p = 20, 50, 100, 500.

Abbreviations: DNN, deep neural network; RSF, random survival forest.

3.3 |. Simulation III: Sample size effect on prediction performance

We also evaluate the effect of sample sizes on the prediction performance of the DNN survival model in the presence of large-dimensional predictors, given that is usually when DNN models show advantages. We choose the scenarios 4 and 5 with p = 100 or 500 under the sparse signal setting from Section 3.1. Table 3 presents the c-index values for each scenario. Overall, for both scenarios, the c-index increases as the sample size increases, and the increment is more dramatic between smaller sample sizes such as from n = 200 to 500 or n = 500 to 1000. This demonstrates that the DNN survival model requires a moderately large sample size (ie, n = 1000 at least) to achieve reasonable prediction performance when the number of predictors is relatively large (p = 100 or more).

TABLE 3.

Effect of sample sizes n on DNN’s performance in terms of c-index (mean and SD from 200 replications) in the presence of high-dimensional predictors

		n
	p	200	500	1000	1500	2000
Scenario 4	100	65.4 (4.3)	78.9 (2.0)	84.5 (2.0)	87.8 (1.7)	89.0 (1.6)
	500	57.2 (3.2)	62.3 (3.0)	76.3 (1.8)	79.9 (1.7)	82.4 (1.1)
Scenario 5	100	66.7 (4.7)	82.8 (1.8)	88.6 (0.8)	89.6 (0.6)	90.5 (0.5)
	500	58.2 (3.3)	63.2 (3.4)	80.4 (2.0)	86.0 (2.4)	87.8 (1.0)

Note: Both scenarios (4 and 5) are from the sparse signal setting. The number of predictors is set at p = 100 or 500.

Abbreviation: DNN, deep neural network.

4 |. APPLICATION TO AREDS DATA

4.1 |. Study population

We apply the three machine learning models for predicting AMD progression using genetic and clinical variables. Data are from the age-related eye disease studies (AREDS), which is composed of the first study AREDS⁴⁰ and the subsequent study AREDS2⁴¹ (with independent participants), designed to assess risk factors and effects of various supplements on AMD development and progression. Both studies collected DNA samples of consenting participants.⁴² The two studies are combined for the following model development and analysis.

4.2 |. Survival outcome and baseline predictors

To measure the disease progression, a severity score, scaled from 1 to 12 (with larger value indicating more severe AMD), is determined for each eye at every examination during study follow-up. In this article, our outcome of interest is time-to-late-AMD, where “late-AMD” is defined as the stage with severity score ≥9. There are 30% of subjects progressed to late-AMD before the study ends. We develop prediction models on the individual eye level. There are a total of 7803 eyes free of late-AMD at baseline. We include a list of potential predictors, including age at baseline, smoking status (never, former, or current smoker), education status (≤ or > high school), and top common SNPs (MAF >5%) that have been reported to be associated with AMD progression (identified from the GWAS study of AMD progression in Yan et al⁴³ with various p-value cut-offs). Table 4 summarizes the baseline characteristics of the study samples. We also preprocess the continuous predictors, for example, dividing age by 100 to scale it within (0, 1) and dividing SNP data (originally coded between [0, 2]) by 2 to make them within [0, 1], as we find such a scaling procedure enhances the prediction performance in survival machine learning models.

TABLE 4.

Baseline characteristics of study samples in the AREDS and AREDS2 data

N = 7803	n	Mean (SD) or %
Age		69.5 (6.2)
Gender
Female	4466	57%
Male	3337	43%
Education
≤ high	2369	30%
> high	5434	70%
Smoke
Never	3623	46%
Former	3752	48%
Current	428	6%
Baseline severity score		4.2 (2.5)

4.3 |. Model development and evaluation

We perform 10-fold cross-validation in the combined AREDS and AREDS2 data. The splitting is stratified based on the censoring status and study cohort. For LASSO and RSF, we use the same tuning procedure as in the simulations. For DNN, we first perform a grid search for tuning parameters and select the set of hyperparameters that gives the best average prediction performance (ie, c-index) across the 10 test validations. The final choice of DNN hyperparameters is given as follows: two hidden layers, 300 nodes per hidden layer, activation function SeLU, L₁ penalty =0.01, batch size N_B = 50, epoch size N_E = 1000, and learning rate γ = 0.00001. We also include Ridge (a Cox PH model with L₂ penalty) and a benchmark genetic risk score (GRS) model, which is a regular Cox PH model using age, smoking status, education status, and an AMD GRS from Ding et al⁴⁴ for comparisons.

We first examine the prediction performance, measured by c-index (×100), employing various numbers of top genetic variants across different models. Specifically, we choose four different p-value cut-offs from the first AMD progression GWAS article⁴³ (ie, p < 10⁻⁷, 10⁻⁶, 10⁻⁵, 10⁻⁴) to obtain different numbers of top variants, as shown in Table 5. The prediction performance becomes relatively stable for all methods when the p-value cut-off reaches 10⁻⁵, which corresponds to 663 SNPs (and three nongenetic predictors). We also include in the last column of Table 5 the DNN model computing time for fitting the entire data once. It can be seen that the computing time increases only moderately (slower than the linear trend) as the number of predictors increases. On average, it takes about 1 hour in the presence of 8000 observations and 1000 predictors.

TABLE 5.

The 10-fold cross-validation c-index (×100) from five survival models (GRS, LASSO, Ridge, RSF, DNN) using different p-value cut-offs in the AREDS and AREDS2 data

	Number of predictors	GRSa	LASSO	Ridge	RSF	DNN	Time (minutes)
p <10−7	92	73.2 (1.6)	72.4 (1.7)	72.3 (1.7)	68.5 (1.4)	72.2 (1.8)	49
p <10−6	165	73.2 (1.6)	72.6 (1.5)	72.6 (1.5)	68.2 (1.3)	72.6 (1.6)	47
p <10−5	666	73.2 (1.6)	74.4 (1.3)	74.3 (1.3)	70.1 (1.8)	76.1 (1.2)	62
p <10−4	1500	73.2 (1.6)	75.2 (1.1)	74.8 (1.0)	71.1 (1.7)	76.5 (1.4)	77

Note: The last column shows the DNN’s computing time for running on the entire dataset once.

Abbreviations: AREDS, age-related eye disease studies; DNN, deep neural network; GRS, genetic risk score; RSF, random survival forest.

^aGRS is invariant to the choice of p-value cut-offs as it does not use individual SNPs but rather a composite score.

Then, we choose the result from p = 666 as our main result and report in Table 6 the c-index, 10-year AUC, and 10-year Brier score (a predictive error measurement) from all four models. DNN achieves higher c-index (76.1) and AUC (81.8) as well as lower Brier score (0.136) than all the other models including LASSO, Ridge, RSF, and the benchmark GRS model. The LASSO and Ridge produce very similar performance results in terms of all metrics.

TABLE 6.

The 10-fold cross-validation c-index (×100), 10-year AUC (×100), and 10-year Brier score from five survival models (GRS, LASSO, Ridge, RSF, DNN) in the AREDS and AREDS2 data

	GRS	LASSO	Ridge	RSF	DNN
c-index (SD)	73.2 (1.6)	74.4 (1.3)	74.3 (1.9)	70.1 (1.8)	76.1 (1.2)
10-year-AUC (SD)	78.2 (2.1)	79.5 (1.6)	78.7 (1.5)	74.3 (2.1)	81.8 (2.1)
10-year-BrS (SD)	0.151 (0.005)	0.146 (0.006)	0.147 (0.005)	0.170 (0.008)	0.136 (0.011)

Abbreviations: AREDS, age-related eye disease studies; AUC, area under the curve; DNN, deep neural network; GRS, genetic risk score; RSF, random survival forest.

Figure 1 presents the time-dependent Brier scores for the test data (all 10 CV test datasets combined) under each prediction model. The Brier score profile from our DNN survival model is consistently lower than all the other models across most time points, demonstrating its better performance than the other models. Similarly, Figure 2 presents the time-dependent AUC values for the test data (all 10 CV test datasets combined) under each model, as an additional matric to evaluate the model prediction performance. Similar to the time-dependent Brier scores, the AUC profile from our DNN survival model is consistently higher than all the other models across all time points.

FIGURE 1.

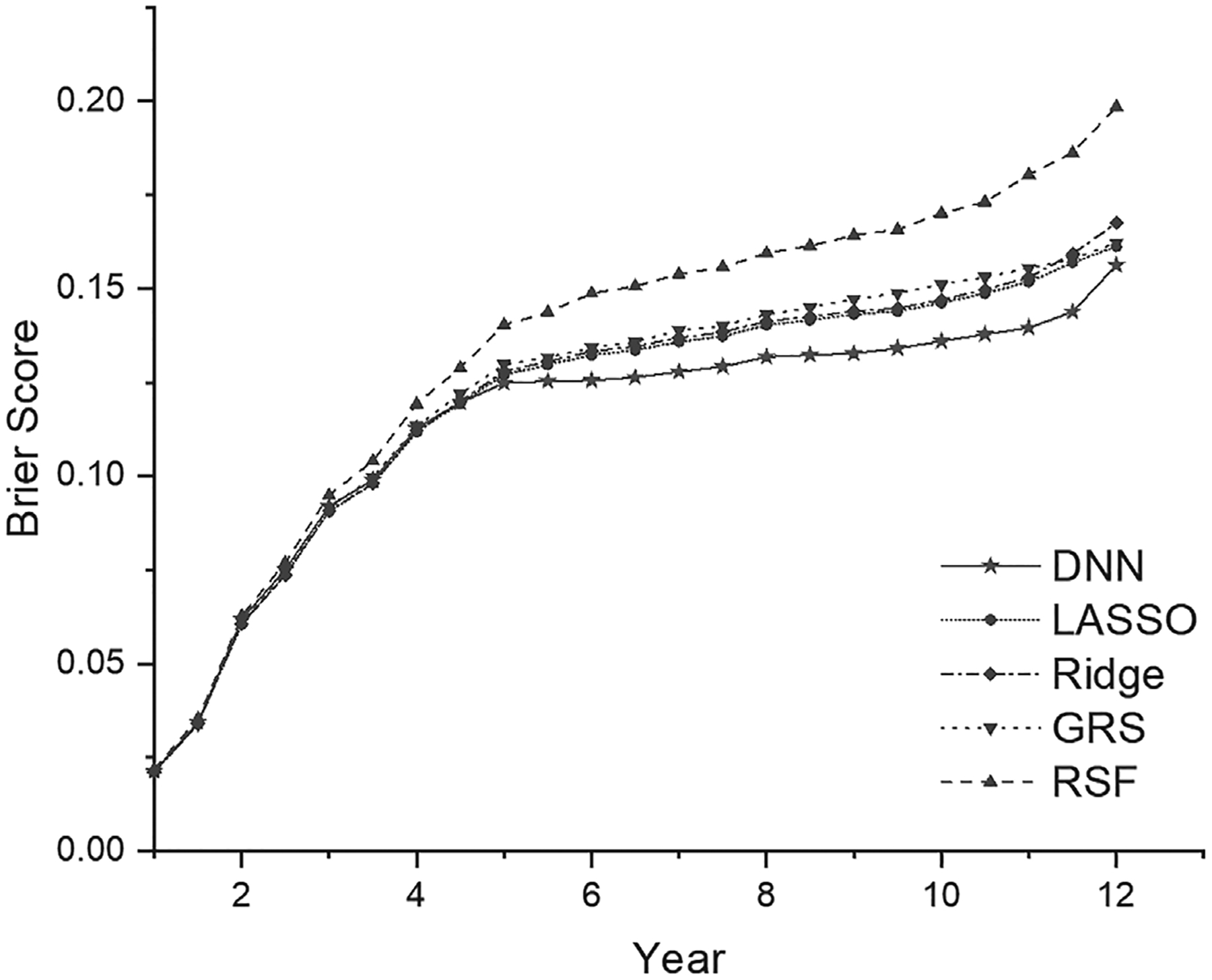
The time-dependent Brier score (predictive error) in the test data from five survival prediction models (GRS, LASSO, Ridge, RSF, DNN). DNN, deep neural network; GRS, genetic risk score; RSF, random survival forest

FIGURE 2.

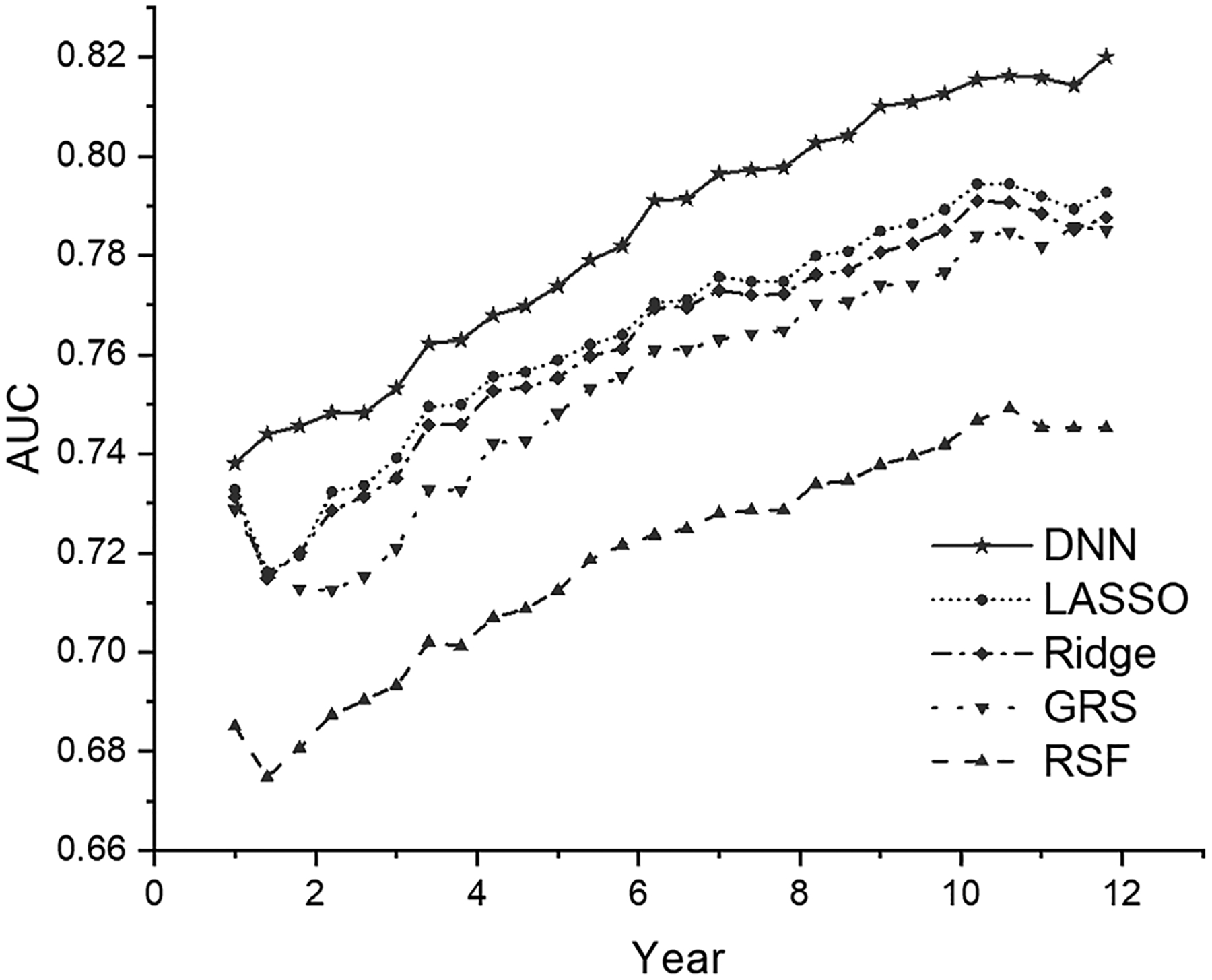
The time-dependent AUC value in the test data from five survival models (GRS, LASSO, Ridge, RSF, DNN). AUC, area under the curve; DNN, deep neural network; GRS, genetic risk score; RSF, random survival forest

4.4 |. DNN interpretation and subgroup identification

To interpret the DNN-based prediction, we obtain the prediction importance measure for the test data samples using the LIME method under our DNN survival model. We use ninefolds data to train a DNN model and then interpret the model in the rest onefold test data. One big advantage of the LIME method is that it provides a subject-specific interpretation of the predictor importance. Figure 3 illustrates the top clinical and genetic predictors (named by their corresponding gene names). Among the top predictors, (older) age and smoking are harmful (colored in red) to AMD progression, whereas genetic variants (carrying minor alleles) can be either harmful (red) or protective (green). For example, the minor allele of locus rs10922098 in the CFH gene region shows a protective effect for AMD progression; while the minor allele of locus rs12987936 in the CROCC2 gene region shows a harmful effect for AMD progression. Moreover, we notice that one predictor could be important for some subjects but may not be crucial for others (visualized by different vertical color bands within each predictor), which suggests there are possible heterogeneous subgroups in this population.

FIGURE 3.

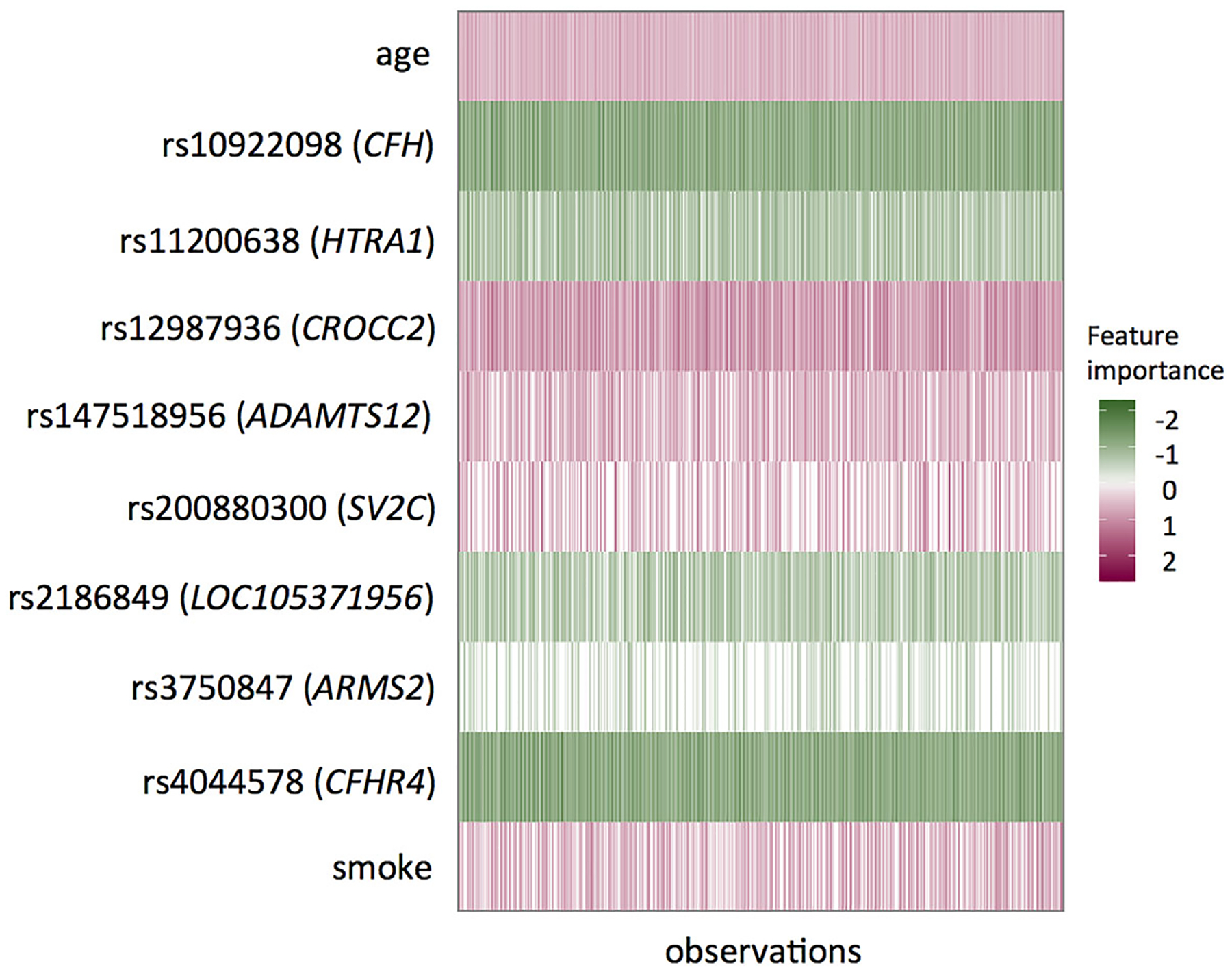
The representation of individualized importance measures for the top predictors in one split of the test dataset from the LIME method. Each row represents one predictor and each vertical column represents one sample. The unit of age is 10-year. LIME, local interpretable model-agnostic explanation

Motivated by the heterogeneity across subjects shown in Figure 3, we further identify two distinct subgroups of AMD patients by performing the Gaussian mixture model on the predicted prognostic risk factors $\widehat{g}$ (output from the DNN model), as illustrated in the histogram of Figure 4. The corresponding Kaplan-Meier plot on progression-free probability indicates significantly different progression profiles between the two subgroups (namely, the low-risk and high-risk subgroups), with a very significant log-rank test result (p = 4.1×10⁻¹⁶⁶). Furthermore, we find significant differences between the two subgroups in terms of age, smoking status, education level, and most top genetic variants in Figure 3. The comparison results are summarized in Table 7. On average, the high-risk individuals are older, with more smokers and lower education level compared with the low-risk individuals. The high-risk individuals also carry more AMD risk alleles compared with the low-risk individuals (eg, GRS is 1.07 vs 0.94). Moreover, as shown in Figure 5, the separate LIME plots for the two subgroups also demonstrate that the individual predictors’ importance measures are different between the two subgroups. In particular, the harmful predictors generally have stronger impacts (darker in red) on the high-risk subgroup than in the low-risk subgroup; whereas the protective predictors show stronger impacts (darker in green) on the low-risk subgroup than the high-risk subgroup. These results provide potentially useful insights for the early prevention and tailored clinical management for the AMD patients.

FIGURE 4.

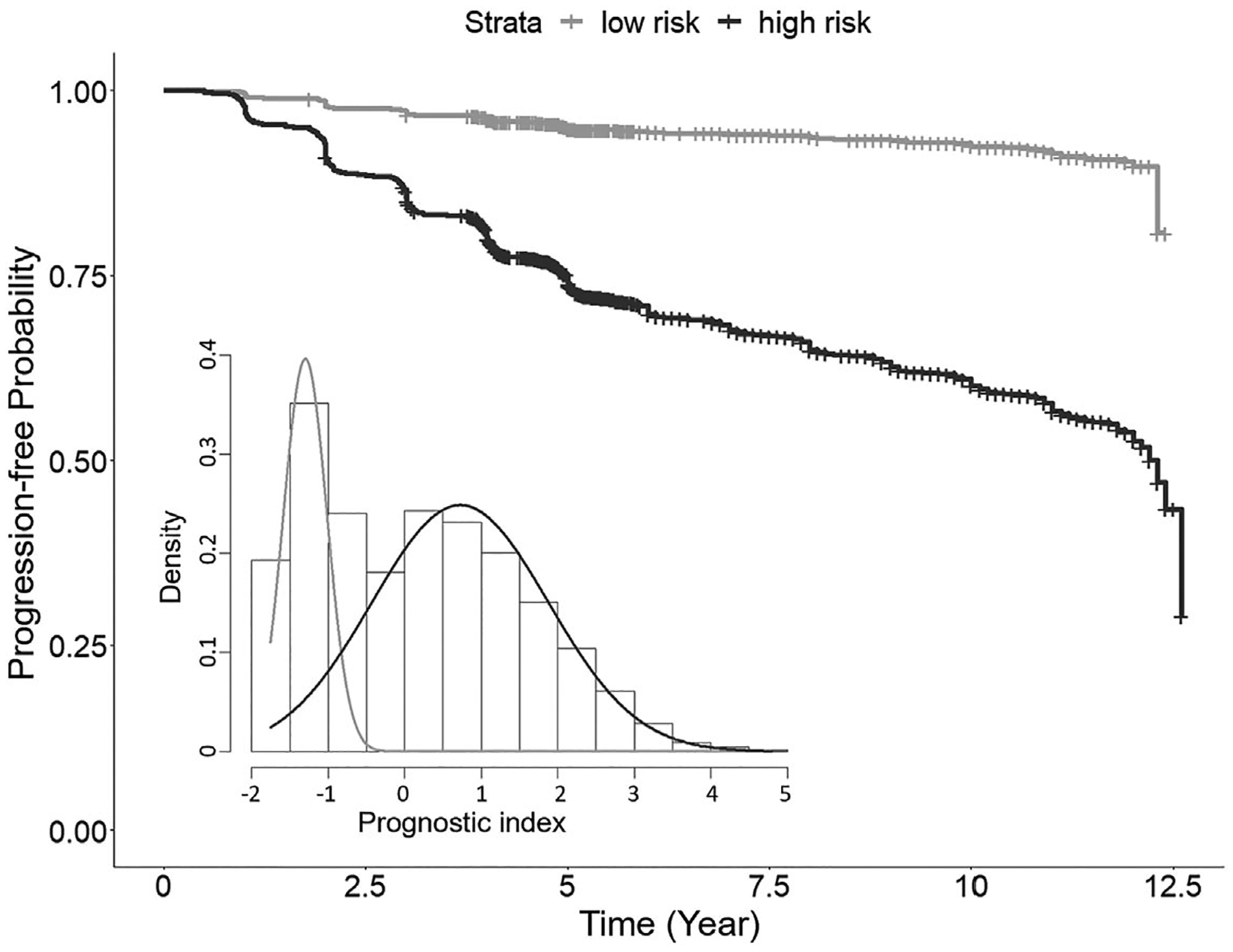
The Kaplan-Meier estimated progression-free profiles for the two identified risk subgroups in the AREDS and AREDS2 test data. The gray curve represents the low-risk subgroup and the black curve represents the high-risk subgroup. The histogram shows the predicted diagnostic index values of all cross-validation results, with two subgroups identified by the Gaussian mixture model. AREDS, age-related eye disease studies

TABLE 7.

Comparison between the low-risk (n = 2516) and high-risk (n = 5287) subgroups in AREDS and AREDS2 data

	Low-risk subgroup Mean (SD) or n (%) or risk allele frequency	High-risk subgroup Mean (SD) or n (%) or risk allele frequency	p-values
Top predictors
Age	66.1 (5.4)	71.1 (5.9)	<2.2 × 10−16
Smoke			<2.2 × 10−16
Never	1343 (53%)	2280 (43%)
Former	1088 (43%)	2664 (50%)
Current	85 (3%)	343 (6%)
Education
≤ high school	625 (25%)	1744 (33%)	3.2 × 10−13
> high school	1891 (75%)	3543 (67%)
rs10922098 (CFH)	0.34	0.61	<2.2 × 10−16
rs11200638 (HTRA1)	0.17	0.39	<2.2 × 10−16
rs12987936 (CROCC2)	0.18	0.18	0.35
rs147518956 (ADAMTS12)	0.27	0.32	1.8 × 10−13
rs200880300 (SV2C)	0.04	0.06	1.0 × 10−3
rs2186849 (LOC105371956)	0.47	0.50	1.0 × 10−3
rs3750847 (ARMS2)	0.17	0.40	<2.2 × 10−16
rs4044578 (CFHR4)	0.33	0.62	<2.2 × 10−16
Other characteristics
GRS	0.94 (0.13)	1.07 (0.13)	<2.2 × 10−16
Gender
Female	1439 (57)	3027 (57)	0.98
Male	1077 (43)	2260 (43)
Baseline severity	3.0 (2.3)	4.7 (2.4)	<2.2 × 10−16

Abbreviations: AREDS, age-related eye disease studies; GRS, genetic risk score.

FIGURE 5.

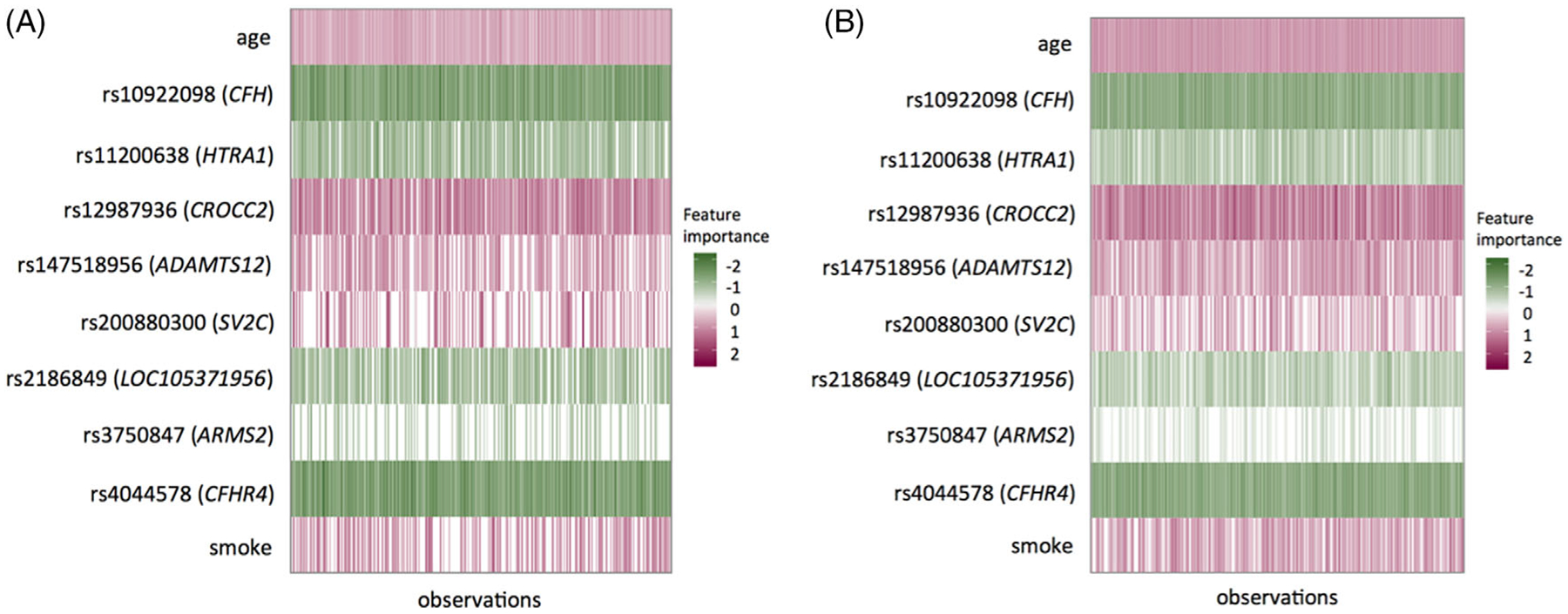
The representation of individualized importance measures for the top predictors in the low-risk, A and high-risk, B, subgroups, respectively. Each row represents one predictor and each vertical column represents one sample. The unit of age is 10-year

5 |. DISCUSSION AND CONCLUSION

In this work, we develop a multilayer DNN survival model and successfully apply it on a real study with both large n and large p to examine and evaluate its effectiveness in making accurate dynamic survival predictions and detecting clinically meaningful subgroups. To open up the “black-box” of DNN, a novel LIME method is implemented to calculate the individualized importance measure of each predictor. Moreover, our work demonstrates the power of DNN in the presence of various types of complex nonlinear structures in the predictors through extensive simulation studies. As we did not perform hyperparameter tuning separately for each scenario, further enhanced performance of DNN would be expected if separate tuning was performed. Some existing tools that are compatible with Keras and Tensorflow to facilitate such a hyperparameter searching process may be considered, for example, the Auto-Keras.⁴⁵ Our work presents the first deep-learning-based survival prediction model for AMD progression and the model framework can be readily applied to other progressive disorders where large GWAS or omics data are collected.

We evaluate survival models based on the pooled dataset of AREDS and AREDS2, whereas Ding et al⁴⁴ used AREDS as the training data and AREDS2 as the test data. However, as noted by Ding et al,⁴⁴ AREDS and AREDS2 populations are different in multiple aspects such as disease severity and age (at enrollment). As a result, the top significant SNPs identified by GWAS are largely nonoverlapping between the two studies.⁴³ As expected, in Ding et al,⁴⁴ the GRS-based Cox model trained in AREDS achieves a c-index of 0.75 in AREDS but drops to 0.63 in AREDS2. To establish a prediction model that is generalizable to a broader AMD population, we pooled them together. Unsurprisingly, the benchmark GRS model performance in the pooled data improves to 0.73 in terms of a 10-fold CV-based c-index, as shown in Table 6.

One potential limitation of our DNN survival model is that it involves tuning of multiple hyperparameters, which is usually computationally expensive. According to our real data analysis and simulations, we could heuristically start from a two-hidden-layer DNN and perform a grid search for the other tuning parameters such as the optimal node size. In general, the DNN model size should be moderate to avoid overfitting. Moreover, the utilization of GPUs could significantly boost the computing speed of our DNN survival model. To further improve the DNN survival model, there are multiple future directions. For example, one may first obtain low-dimensional signals by performing unsupervised feature extraction such as autoencoder⁴⁶ and then use the extracted signals as predictors. In this way, the noises in the original data can be reduced. Another possible extension is to build a DNN survival model based on the Bayesian approach,⁴⁷ which could perform variable selection to identify relevant predictors under the high-dimensional nonlinear setting. Finally, we predict disease progression on the eye level by assuming that the two eyes are independent of each other in one individual. Ideally one should take the correlation into account when constructing the prediction model. One possible extension includes using a copula model to account for the dependence between the two eyes from the same subject^48,49 and predicting the joint progression profiles of the two eyes through a DNN. We are investigating some of these extensions.

Abbreviation:

AREDS

age-related eye disease studies