Abstract
Brain-predicted age difference (brainPAD) has been used in schizophrenia to assess individual-level deviation in the biological age of the patients’ brain (i.e., brain-age) from normative reference brain structural datasets. There is marked inter-study variation in brainPAD in schizophrenia which is commonly attributed to sample heterogeneity. However, the potential contribution of the different machine learning algorithms used for brain-age estimation has not been systematically evaluated. Here, we aimed to assess variation in brain-age estimated by six commonly used algorithms [ordinary least squares regression, ridge regression, least absolute shrinkage and selection operator regression, elastic-net regression, linear support vector regression, and relevance vector regression] when applied to the same brain structural features from the same sample. To assess reproducibility we used data from two publically available samples of healthy individuals (n=1092 and n=492) and two further samples, from the Icahn School of Medicine at Mount Sinai (ISMMS) and the Center of Biomedical Research Excellence (COBRE), comprising both patients with schizophrenia (n=90 and n=76) and healthy individuals (n=200 and n=87). Performance similarity across algorithms was compared within each sample using correlation analyses and hierarchical clustering. Across all samples ordinary least squares regression, the only algorithm without a penalty term, performed markedly worse. All other algorithms showed comparable performance but they still yielded variable brain-age estimates despite being applied to the same data. Although brainPAD was consistently higher in patients with schizophrenia, it varied by algorithm from 3.8 to 5.2 years in the ISMMS sample and from to 4.5 to 11.7 years in the COBRE sample. Algorithm choice introduces variations in brain-age and may confound inter-study comparisons when assessing brainPAD in schizophrenia.
Keywords: brain age prediction, schizophrenia, structural MRI, machine learning, regression
1. Introduction
Schizophrenia is a severe mental illness that presents with positive and negative symptoms [APA, 2013] and brain structural alterations [Haijma et al. 2013; Radua et al. 2012; Steen et al. 2006; van Erp et al. 2016, 2018; Vita et al. 2006]. Lower intracranial volume is a consistent finding that reflects early developmental vulnerability [Bois et al. 2015; Fusar-Poli et al. 2014]. Moreover, cortical thickness and subcortical volumes [Haijma et al. 2013; Radua et al. 2012; Steen et al. 2006; van Erp et al. 2016, 2018; Vita et al. 2006] generally show a steeper age-related decline in patients than that observed in healthy individuals [Haijma et al. 2013; van Haren et al. 2008, 2011, 2016; Olabi et al. 2011]. Collectively, these findings suggest that schizophrenia is associated with lifelong deviation from normative neuroanatomical trajectories.
Application of machine learning algorithms to neuroimaging data offers a new lens for the examination of brain structural deviation in schizophrenia. Using these algorithms, it is possible to generate estimates of the biological age of an individual’s brain (i.e., brain-age) by comparing their neuroimaging data against a normative population dataset of the same neuroimaging features [Franke et al. 2010; Franke and Gaser, 2019]. In each individual, subtracting their chronological age from their brain-age generates a metric that quantifies the degree of deviation; this is referred to here as “brain-predicted age difference” (brainPAD) although the term brain-age-gap-estimation has also been used to denote the same metric; a positive brainPAD indicates that the biological age of an individual’s brain is “older” than their actual age, and a negative brainPAD reflects the inverse.
A recent study using brain structural magnetic resonance imaging (sMRI) data from 35,474 healthy individuals and 1,110 patients with schizophrenia found a moderate increase in brainPAD (Cohen’s d effect size = 0.51) in patients [Kaufmann et al. 2019]. Five further studies have estimated brainPAD in schizophrenia using various machine learning algorithms applied to sMRI data [Koutsouleris et al. 2014; Schnack et al. 2016; Nenadic et al. 2017; Hajek et al. 2019; Shahab et al. 2019], Koutsouleris and colleagues [2014] used a support vector regression (SVR) algorithm trained on data from 800 healthy individuals, and found that patients with schizophrenia (n=141) had a mean brainPAD of 5.5 years. Schnack and colleagues [2016] using a SVR algorithm trained on healthy individuals (n=386) reported that patients with schizophrenia from two independent samples (n=341 and n=60) had mean brainPAD of 3.8 years and 5.6 years. Using relevance vector regression (RVR), Nenadic and colleagues [2017] reported that patients with schizophrenia (n=45) had a mean brainPAD of 2.6 years compared to 70 healthy individuals. A similar mean brainPAD of 2.6 years in patients with schizophrenia (n=43) was reported by Hajek and colleagues [2019] using RVR trained on data from 504 healthy individuals. Shahab and colleagues [2019] used random forest regression trained on data from 50 healthy individuals, and showed that patients with schizophrenia (n=81) had a mean brainPAD of 7.8 years. Inter-study variability has been typically considered in terms of sample characteristics while brainPAD estimation can also be influenced by the algorithm used and the choice of neuroimaging features entered into the model. At present, the influence of these various algorithms on brain-age estimation remains unclear as their comparative performance has not been systematically evaluated.
In response, the current study evaluated six algorithms, namely ordinary least squares (OLS) regression [Rudolph et al. 2017], least absolute shrinkage and selection operator (Lasso) regression [Bagarinao et al. 2018; Cole, 2020], ridge regression [Guggenmos et al. 2017; Zhao et al. 2019], elastic-net regression [Khundrakpam et al. 2015], SVR, and RVR, which are commonly used because they are interpretable and resilient to over-fitting. The six algorithms were applied to the same morphological features from each of four independent samples. Two samples comprised healthy individuals participating either in the Human Connectome Project (HCP) [van Essen et al. 2013] or the Cambridge Centre for Ageing and Neuroscience project (Cam-CAN) [Shafto et al. 2014]. Two further samples, from the Icahn School of Medicine at Mount Sinai (ISMMS) and the Center of Biomedical Research Excellence (COBRE) [Aine et al. 2017], comprised both patients with schizophrenia and healthy individuals. Using four datasets enabled testing the robustness of the results to sample composition. The sMRI data of all samples were processed using identical pipelines to extract FreeSurfer-derived regional morphometric measures. We chose these measures as they are amongst the most widely used features in brain imaging studies of schizophrenia [van Erp et al. 2016, 2018], are cost-efficient alternatives to using more fine-grained parcellations for brain-age estimation [Valizadeh et al. 2017] and have been employed to study brain-age in recent large scale studies in neuropsychiatric disorders [Han et al. 2000; Kaufmann et al. 2019].
2. Materials and Methods
2.1. Samples
Human Connectome Project:
The HCP (www.humanconnectome.org) acquired sMRI data from 1113 adults living in the USA. Following exclusion of participants with medical problems, we used data from 1092 individuals aged 22–37 years [mean age=28.8 years, standard deviation (SD)=3.7 years; 507 males] (details in Supplementary Methods).
Cambridge Centre for Ageing and Neuroscience Project.
The Cam-CAN Project (www.mrc-cbu.cam.ac.uk) acquired sMRI data from 652 adults living in the UK. Following exclusion of participants with medical morbidity and/or poor image quality, we used data from 492 individuals aged 18–87 years (mean age=54.4 years, SD=18.3 years; 248 males) (details in Supplementary Methods).
Ethical approval enabling sharing de-identified data from the HCP and Cam-CAN was obtained by the respective coordinating study centres.
ISMMS Sample:
This sample was recruited and assessed at the Icahn School of Medicine at Mount Sinai (ISMMS) (details in Supplementary Methods). It comprised 90 outpatients (mean age=27.4 years, SD=7.5 years; 69 males) fulfilling diagnostic criteria of schizophrenia according to the Diagnostic and Statistical Manual of Mental disorders, 5th Edition (DSM-5) [APA, 2013] and 200 healthy individuals without a personal or family history of major psychiatric disorders (mean age=37 years, SD=12.4 years; 110 males). The study was approved by the Institutional Review Board of the Icahn School of Medicine at Mount Sinai and all participants gave written informed consent.
COBRE Sample:
This sample was recruited by Center of Biomedical Research Excellence (COBRE) (http://cobre.mrn.org & http://coins.mrn.org) (details in Supplementary Methods). It comprised 76 outpatients (mean age=37.9 years, SD=14.2 years; 62 males) fulfilling DSM-IV criteria for schizophrenia [APA, 2000] and 87 healthy individuals (mean age=38.2 years, SD=11.8 years; 62 males) without a personal or family history of major psychiatric disorders. The study was approved by the Institutional Review Board of the University of New Mexico and all participants gave written informed consent.
All participants in the ISMMS and in the COBRE samples were screened to exclude those with IQ<70, a history of neurological disorders, severe head trauma, substance abuse or dependence within the last 12 months and MRI contra-indications.
Neuroimaging Acquisition, Processing and Feature Extraction
T1-weighted images for all samples were acquired on 3T Siemens scanners (Siemens Medical Systems, Erlangen, Germany). The acquisition parameters are described in the Supplementary Material. The initial studies on sMRI-based brain-age prediction used voxel-based analyses [Franke et al. 2010; Franker and Gaser, 2019]. The T1-weighted MRI images of the four study samples were processed using identical pipelines to extract morphometric measures using FreeSurfer 6.0 (http://surfer.nmr.mgh.harvard.edu) (Supplementary Material). Cortical reconstruction was based on the Desikan-Killiany atlas [Desikan et al. 2006] and subcortical segmentation was performed using the probabilistic atlas in FreeSurfer [Fischl et al. 2002]. In each participant’s dataset, this procedure generated measures of total intracranial volume and regional measures of cortical thickness (n=68), cortical surface area (n=68) and subcortical volumes (n=16) (Supplementary Table S2).
Machine learning algorithms for brain-age prediction
The linear models examined can be generally formalized as follows:
where yi is the age of the ith individual, p is the number of features, xi,j is the value of jth feature of the ith subject, and βj is the regression coefficient.
We evaluated the following six algorithms:
(1). Ordinary least squares (OLS) regression:
OLS regression algorithm fits a linear model by minimizing the residual sum of squares between the observed yi in the training dataset (i=1,..,N, the sample size) and the values f(xi) predicted by the linear model. The object function is as follows:
where yi is the actual value of the chronological age. The least squares solution was computed using the singular value decomposition (SVD).
(2). Ridge regression:
Ridge regression is a regularized linear model that minimizes the sum of the squared prediction error in the training data and a L2-norm regularization, i.e., the sum of the squares of regression coefficients [Hoerl and Kennard, 1970]. The object function is as follows:
The tuning parameter λ controls the model’s complexity. If λ = 0, ridge regression becomes a traditional linear regression model. The optimal choice of λ parameter in this study was based on 10-fold cross-validation (see below).
(3). Least absolute shrinkage and selection operator (Lasso) regression:
Lasso is another form of regularized linear regression using an L1-norm penalty, aiming to minimize the sum of the absolute value of the regression coefficients [Tibshirani, 1996]. The objective function is as follows:
The L1-norm regularization tends to set most coefficients to zero and retains one random feature among the correlated ones, thus resulting in a sparse predictive model that facilitates optimization of the predictors and reduces the model complexity.
(4). Elastic-net regression:
This linear regression model combines both L1-norm (i.e., Lasso regression) and L2-norm (i.e., ridge regression) regularizations in the OLS loss function [Zhou and Hastie, 2005]. The object function is as follows:
This allows the number of selected features to be larger than the sample size while achieving a sparse model. A hyperparameter α (between 0 and 1) is used to control the relative weighting of the L1-norm and L2-norm contributions. The optimal choice of the α parameter in this study was based on 10-fold cross-validation (see below).
(5). Linear support vector regression (SVR):
Linear SVR aims to find a function f(xi) whose predictive value deviates by no more than a required accuracy ε from the actual yi for all the training data while maximizing the flatness of the function [Smola and Scholkopf, 2004]. Flatness maximization is implemented using the L2-norm regularization by minimizing the squared sum of the regression coefficients. The object function is as follows:
where l is the quantity of ‘support vectors’, which are the samples that deviate by more than ε from the actual yi used to fit the model. A parameter C regulates the smoothness of functionf(xi). The optimal choice of C parameter in this study was based on 10-fold cross-validation (see below).
(6). Relevance vector regression (RVR):
RVR is a Bayesian sparse learning model and has an identical functional form to SVR [Tipping, 2001]. The function is as follows:
where β = (β0…,βp) is a vector of weights and Φi(x) = K(x,xi) is a linear kernel function defining the basis function. The sparsity of RVR is induced by the hyper-priors on model parameters in a Bayesian framework with the maximum a posteriori (MAP) principle. RVR determines the relationship between the target output and the covariates by enforcing sparsity. The L1-norm-like regularization used in RVR encourages the sum of absolute values to be small, which often drives many parameters to zero and provides significantly few basic functions. Notably, RVR has no algorithm-specific parameter.
The scikit-learn library (version 0.23.1) was used to implement OLS regression, ridge regression, Lasso regression, and elastic-net regression (http://scikit-learn.org/) [Pedregosa et al. 2011], the LIBSVM function in MATLAB (Mathworks, Natick, MA) was used to implement SVR (https://www.csie.ntu.edu.tw/~cjlin/libsvm/) [Chang and Lin, 2011], and the PRoNTo toolbox (http://www.mlnl.cs.ucl.ac.uk/pronto/) was used to implement RVR [Schrouff et al. 2013].
Brain-age prediction framework
The six algorithms were applied separately to each sample (HCP, Cam-CAN, ISMMS and COBRE) using identical procedures involving the following steps: (i) prior to modeling, each neuroimaging measure was linearly scaled so that all values in the feature set ranged between 0 and 1; (ii) a nested 10-fold cross-validation (10F-CV) was applied to the dataset of healthy individuals which was randomly split into 10 equal-sized subsets. For each cross-validation, one subset was left out as the test subset while the remaining nine subsets were used together as the training set for estimating the model parameters. These parameters were then applied to the left-out subset. Specifically, for ridge regression, Lasso regression, elastic-net regression, and SVR, cross-validation procedure was applied with an outer 10F-CV to evaluate model generalizability and an inner 10F-CV to determine the optimal parameters (λ, α, or C) for these algorithms; (iii) the performance of each algorithm was quantified by the mean absolute error (MAE), averaged across all cross-validation folds; (iv) for each algorithm, the regression weights for each brain region were used for the comparative evaluation of the algorithms; the absolute value of these weights represents the importance of the corresponding features in the brain-age prediction of the model [Haufe et al. 2014].
For the ISMMS and COBRE samples, each of the 6 models was estimated in the healthy participants of each sample and then the regional regression weights were applied to the brain structural data of the respective patient group; brainPAD was then calculated for each algorithm by subtracting the chronological age of each individual from their brain-age as predicted from that algorithm.
Statistical analysis
Comparative evaluation of the algorithms was conducted within each dataset separately (i.e., HCP, Cam-CAN, ISMMS, COBRE) based on the within-sample similarity in predicted brain-age and brain regional regression weights as assessed using correlation analyses and hierarchical clustering with Ward’s minimum variance method for Euclidian distances implemented in MATLAB (Mathworks, Natick, MA) (Supplementary Material). In the ISMMS and COBRE samples only, case-control differences in brainPAD were examined using the t-statistic and effect sizes were expressed in terms of Cohen’s d. Significance was set at PFDR<0.05 with the false-discovery-rate (FDR) correction [Benjamini and Hochberg, 1995].
Results
Comparative Performance of the algorithms in the HCP and Cam-CAN samples
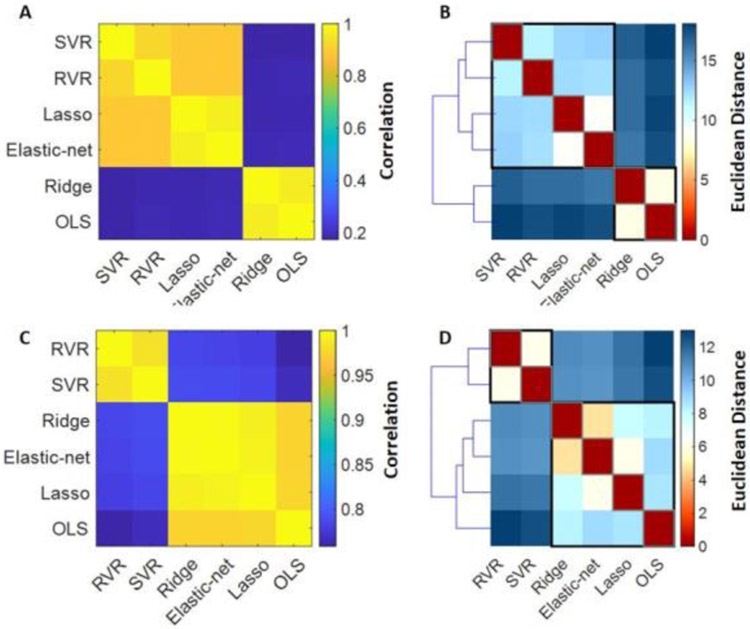
The MAE and R values for each algorithm in the HCP and Cam-CAN samples are shown in Supplementary Table S3 and Supplementary Figure S1. In the HCP sample, MAE values for all algorithms ranged between 2.6-2.7 and pairwise correlations in individual predicted brain-ages between-algorithms ranged from 0.17-0.97 (Figure 1A). Hierarchical clustering of the individual predicted brain-ages identified three clusters; elastic-net regression and Lasso formed one cluster, SVR and RVR formed another and OLS and ridge regressions formed a third cluster (Figure 1B). In the Cam-CAN sample, MAE values for all algorithms ranged between 7.2-7.7 and correlations in individual predicted brain-ages between-algorithms ranged from 0.76-0.99 (Figure 1C). Hierarchical clustering of the individual predicted brain-ages in the Cam-CAN sample showed that elastic-net regression, Lasso and ridge regression together formed one cluster, SVR and RVR formed another cluster while OLS regression showed the lowest similarity with all the other algorithms (Figure 1D).
Figure 1. Similarity in predicted brain age in healthy individuals in the HCP and Cam-CAN samples across algorithms.
(A) HCP: Similarity matrix representing between-algorithm correlations of individual predicted brain-ages in healthy individuals; (B) HCP: Distance matrix and dendrogram resulting from hierarchical clustering of the individual brain-age results of the six algorithms; (C) Cam-CAN: Similarity matrix representing between-algorithm correlations of individual predicted brain-ages in healthy individuals; (D) Cam-CAN: Distance matrix and dendrogram resulting from hierarchical clustering of the individual brain-age results of the six algorithms. OLS: Ordinary least squares regression; Lasso: Least absolute shrinkage and selection operator; SVR: Support vector regression; RVR: Relevance vector regression; HCP: Human Connectome Project; Cam-CAN: Cambridge Centre for Ageing and Neuroscience Project.
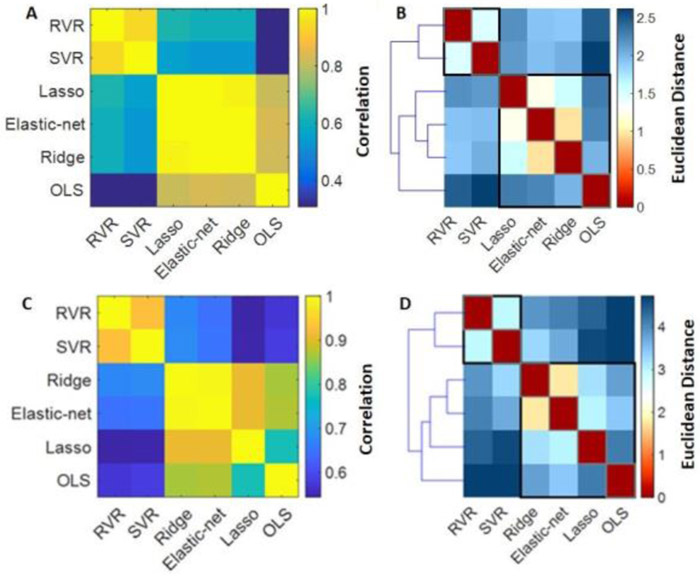
Comparative Performance of the algorithms in the healthy individuals from the ISMMS and COBRE samples
The MAE and R values for each algorithm in the ISMMS and COBRE samples are shown in Supplementary Table S4 and Supplementary Figure S2. In the ISMMS sample, correlations in individual predicted brain-ages between-algorithm ranged from 0.61-0.99 (Figure 2A). Hierarchical clustering of the individual predicted brain-ages in the ISMMS sample identified three clusters; the OLS regression model showed a very low degree of similarity with all the other algorithms while the elastic-net regression, Lasso and ridge regression clustered together as did the SVR and RVR (Figure 2B). The regional regression weights of each algorithm are shown in Supplementary Table S5 and Supplementary Figures S3-S5. In the COBRE sample, individual predicted brain-ages showed moderate to high between-algorithm correlations (R range=0.55-0.99) (Figure 2C). Hierarchical clustering of the individual predicted brain-ages showed that elastic-net and ridge regression together formed one cluster, and SVR and RVR formed another cluster; and OLS and Lasso regression formed a third (Figure 2D).
Figure 2. Similarity in predicted brain age in healthy individuals in the ISMMS and COBRE samples across algorithms.
(A) ISMMS: Similarity matrix representing between-algorithm correlations of individual predicted brain-ages in healthy individuals; (B) ISMMS: Distance matrix and dendrogram resulting from hierarchical clustering of the individual brain-age results of the six algorithms in healthy individuals; (C) COBRE: Similarity matrix representing between-algorithm correlations of individual predicted brain-ages in healthy individuals; (D) COBRE: Distance matrix and dendrogram resulting from hierarchical clustering of the individual brain-age results of the six algorithms in healthy individuals;. OLS: Ordinary least squares regression; Lasso: Least absolute shrinkage and selection operator; SVR: Support vector regression; RVR: Relevance vector regression. COBRE: Center of Biomedical Research Excellence; ISMMS: Icahn School of Medicine at Mount Sinai.
BrainPAD in Schizophrenia
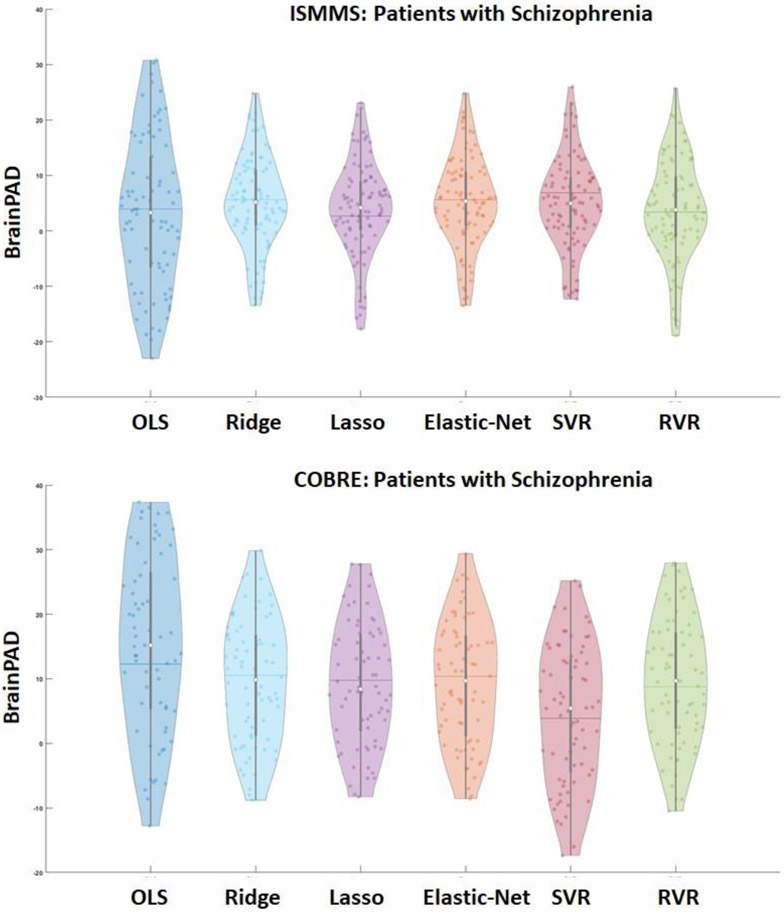
In the ISMMS sample, with the exception of OLS regression, the mean brainPAD values obtained by all algorithms were statistically higher in patients with schizophrenia compared to healthy individuals (all PFDR<0.001), with a range of 3.8 to 5.2 years (Supplementary Table S6; Figure 3A). The effect size of case-control differences was moderate (d range: 0.23-0.66) (Supplementary Table S6). No sex differences in brainPAD were observed in patients with schizophrenia (PFDR>0.05). Similarly in the COBRE sample, the mean brainPAD values obtained by all algorithms were higher in patients with schizophrenia compared to healthy individuals (PFDR<0.001), with a range of 4.5 to 11.7 years (Supplementary Table S7; Figure 3). The effect size of case-control differences was large (d range=0.69-1.14) (Supplementary Table S7). No sex differences in brainPAD were observed in patients with schizophrenia (PFDR>0.05).
Figure 3. Brain-predicted age difference the ISMMS and COBRE samples.
Violin plots showing the distribution of individual brain-predicted age difference (brainPAD) scores in patients with schizophrenia in the ISMMS sample (top panel) and the COBRE sample (lower panel). Horizontal line within each violin plot represents the mean and the white circle the median values. OLS: Ordinary least squares regression; Lasso: Least absolute shrinkage and selection operator; SVR: Support vector regression; RVR: Relevance vector regression. COBRE: Center of Biomedical Research Excellence; ISMMS: Icahn School of Medicine at Mount Sinai.
Discussion
In this study, we compared the performance of six commonly used linear machine learning algorithms in brain-age prediction in healthy individuals and patients with schizophrenia. Regardless of algorithm, brainPAD was consistently higher in patients with schizophrenia than in healthy individuals although the mean brainPAD values differed by algorithm.
Evaluation of the six algorithms in two sizable samples of healthy individuals from the HCP and Cam-CAN yielded reproducible results with regards to the similarity between Lasso regression and elastic-net regression, and between the SVR and RVR that consistently clustered together. This pattern was also repeated in the smaller case-control samples suggesting that it is largely independent of sample size or composition. OLS regression underperformed in all samples. OLS regression is widely used in the neuroscience research as it is relatively easy to implement even when the number of predictor variables is large. However, the presence of collinearity among the predictor variables may be a particular vulnerability of OLS regression when applied to brain structural data due to the lack of regularization (or penalty) term in the OLS model. By contrast, ridge regression and SVR apply L2-norm regularization, Lasso regression includes L1-norm regularization, elastic-net regression includes both L1-norm and L2-norm regularization, and RVR applies regularization through a Gaussian prior. Regularized algorithms tended to shrink many regional weights to zero, so the brain-age prediction was based on relatively few brain regions. It is worth noting that, across models, these regional feature weights are selected based on statistical properties and, they do not necessarily convey information about neurobiological processes [Haufe et al. 2014].
BrainPAD in patients with schizophrenia was higher than those of healthy individuals across all six algorithms. The mean brainPAD in patients ranged from 3.4 to 5.2 years in the ISMMS sample and from 4.3 to 9.4 years in the COBRE sample. In general, these findings are aligned with the range of the brainPAD values reported in previous studies in schizophrenia (range=2.6-8 years) [Koutsouleris et al. 2014; Schnack et al. 2016; Nenadic et al. 2017; Hajek et al. 2019; Shahab et al. 2019]. The current study demonstrates that the choice of algorithm has significant implications for brainPAD estimation given the variation observed when different algorithms were applied to the same dataset.
We acknowledge several limitations that could be addressed in future studies. The focus of this study was on the methodological aspects of computing brain-age in schizophrenia and not on the biological meaning of increased brainPAD in patients. The mechanisms underlying increased brainPAD in schizophrenia remain unclear. Schnack et al. [2016] have previously shown that the greater deviance in brainPAD is likely to occur within the first five years from disease onset thus implicating mechanisms that may be relevant or more active at the early stages of schizophrenia. All models used FreeSurfer-derived morphometric features and it is possible that the results may differ if finer morphometric parcellations are used. Schizophrenia is associated with abnormalities in other structural phenotypes, such as gyrification [Palaniyappan and Liddle, 2012] as well as in patterns of brain activation and functional connectivity [Karbasforoushan and Woodward, 2012] which were not examined here. Only linear regression models were evaluated while future work could assess nonlinear regression models such as Gaussian process regression [Jiang et al. 2019], random forest regression, and deep learning models [Bashyam et al. 2020; Cole et al. 2017; Jiang et al. 2019] but at the cost of interpretability and model complexity.
In summary, we provide evidence that linear machine learning algorithms, with the exception of OLS regression, provided similar performance for brain-age prediction on the basis of a combination of cortical and subcortical structural measures. There was variation in the mean brainPAD across algorithms even through they were applied to the same datasets. Therefore algorithm choice could be an important source of inter-study variability. Further studies are needed to address variations in brain-age prediction in schizophrenia attributable to other parameters and in other neuroimaging phenotypes.
Supplementary Material
Highlights.
Different machine learning algorithms have been used to compute brain-predicted-age-difference (brainPAD) in schizophrenia
Inter-study BrainPAD variability is typically attributed to schizophrenia-related heterogeneity rather than the algorithms used
Comparison of 6 different algorithms in 4 independent samples yielded consistent differences in their performance
BrainPAD estimates in the same sample of patients with schizophrenia differed by up to 10 years depending on the algorithm used
Acknowledgments
Funding
This work was supported by the Kyung Hee University under grant KHU 20202302 and by the National Institute of Mental Health under grant R01MH113619.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest: The authors have declared that there are no conflicts of interest in relation to the subject of this study.
References
- Aine CJ, Bockholt HJ, Bustillo JR, Cañive JM, Caprihan A, Gasparovic C, Hanlon FM, Houck JM, Jung RE, Lauriello J, Liu J, Mayer AR, Perrone-Bizzozero NI, Posse S, Stephen JM, Turner JA, Clark VP, Calhoun VD. Multimodal Neuroimaging in Schizophrenia: Description and Dissemination. Neuroinformatics. 2017;15(4):343–364. doi: 10.1007/s12021-017-9338-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- American Psychiatric Association. Diagnostic and statistical manual of mental disorders (5th edition). American Psychiatric Publishing, Washington, DC; 2013. [Google Scholar]
- American Psychiatric Association. Diagnostic and statistical manual of mental disorders (4th edition). American Psychiatric Publishing, Washington, DC; 2000. [Google Scholar]
- Bagarinao E, Watanabe H, Maesawa S, Mori D, Hara K, Kawabata K, Yoneyama N, Ohdake R, Imai K, Masuda M, Yokoi T, Ogura A, Wakabayashi T, Kuzuya M, Ozaki N, Hoshiyama M, Isoda H, Naganawa S, Sobue G. An unbiased data-driven age-related structural brain parcellation for the identification of intrinsic brain volume changes over the adult lifespan. Neuroimage. 2018;169:134–144. doi: 10.1016/j.neuroimage.2017.12.014. [DOI] [PubMed] [Google Scholar]
- Bashyam VM, Erus G, Doshi J, Habes M, Nasralah I, Truelove-Hill M, Srinivasan D, Mamourian L, Pomponio R, Fan Y, Launer LJ, Masters CL, Maruff P, Zhuo C, Völzke H, Johnson SC, Fripp J, Koutsouleris N, Satterthwaite TD, Wolf D, Gur RE, Gur RC, Morris J, Albert MS, Grabe HJ, Resnick S, Bryan RN, Wolk DA, Shou H, Davatzikos C. MRI signatures of brain age and disease over the lifespan based on a deep brain network and 14 468 individuals worldwide. Brain. 2020;143(7):2312–2324. doi: 10.1093/brain/awaa160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate - a practical and powerful approach to multiple testing. J Roy Stat Soc B Met. 1995;57(1):289–300. http://www.jstor.org/stable/2346101. [Google Scholar]
- Bois C, Whalley HC, McIntosh AM, Lawrie SM. Structural magnetic resonance imaging markers of susceptibility and transition to schizophrenia: a review of familial and clinical high risk population studies. J Psychopharmacol. 2015;29(2):144–154. doi: 10.1177/0269881114541015. [DOI] [PubMed] [Google Scholar]
- Cole JH, Poudel RPK, Tsagkrasoulis D, Caan MWA, Steves C, Spector TD, Montana G. Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. Neuroimage. 2017;163:115–124. doi: 10.1016/j.neuroimage.2017.07.059. [DOI] [PubMed] [Google Scholar]
- Cole JH. Multimodality neuroimaging brain-age in UK biobank: relationship to biomedical, lifestyle, and cognitive factors. Neurobiol Aging. 2020;92:34–42. doi: 10.1016/j.neurobiolaging.2020.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang CC, Lin CJ. LIBSVM: A Library for Support Vector Machines. Acm T Intel Syst Tec 2011;2(3). https://dl.acm.org/doi/10.1145/1961189.1961199. [Google Scholar]
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31(3):968–980.doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33(3):341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Franke K, Ziegler G, Klöppel S, Gaser C; Alzheimer's Disease Neuroimaging Initiative. Estimating the age of healthy subjects from T1-weighted MRI scans using kernel methods: exploring the influence of various parameters. Neuroimage. 2010;50(3):883–892. doi: 10.1016/j.neuroimage.2010.01.005. [DOI] [PubMed] [Google Scholar]
- Franke K, Gaser C. Ten Years of BrainAGE as a Neuroimaging Biomarker of Brain Aging: What Insights Have We Gained? Front Neurol. 2019;10:789. doi: 10.3389/fneur.2019.00789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fusar-Poli P, Smieskova R, Serafini G, Politi P, Borgwardt S. Neuroanatomical markers of genetic liability to psychosis and first episode psychosis: a voxelwise meta-analytical comparison. World J Biol Psychiatry. 2014;15(3):219–228. doi: 10.3109/15622975.2011.630408. [DOI] [PubMed] [Google Scholar]
- Guggenmos M, Schmack K, Sekutowicz M, Garbusow M, Sebold M, Sommer C, Smolka MN, Wittchen HU, Zimmermann US, Heinz A, Sterzer P. Quantitative neurobiological evidence for accelerated brain aging in alcohol dependence. Transl Psychiatry. 2017;7(12):1279. doi: 10.1038/s41398-017-0037-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haijma SV, Van Haren N, Cahn W, Koolschijn PC, Hulshoff Pol HE, Kahn RS. Brain volumes in schizophrenia: a meta-analysis in over 18 000 subjects. Schizophr Bull. 2013;39(5):1129–38. doi: 10.1093/schbul/sbs118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hajek T, Franke K, Kolenic M, Capkova J, Matejka M, Propper L, Uher R, Stopkova P, Novak T, Paus T, Kopecek M, Spaniel F, Alda M. Brain Age in Early Stages of Bipolar Disorders or Schizophrenia. Schizophr Bull. 2019;45(1):190–198. doi: 10.1093/schbul/sbx172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han LKM, Dinga R, Hahn T, Ching CRK, Eyler LT, Aftanas L, Aghajani M, Aleman A, Baune BT, Berger K, Brak I, Filho GB, Carballedo A, Connolly CG, Couvy-Duchesne B, Cullen KR, Dannlowski U, Davey CG, Dima D, Duran FLS, Enneking V, Filimonova E, Frenzel S, Frodl T, Fu CHY, Godlewska BR, Gotlib IH, Grabe HJ, Groenewold NA, Grotegerd D, Gruber O, Hall GB, Harrison BJ, Hatton SN, Hermesdorf M, Hickie IB, Ho TC, Hosten N, Jansen A, Kähler C, Kircher T, Klimes-Dougan B, Krämer B, Krug A, Lagopoulos J, Leenings R, MacMaster FP, MacQueen G, McIntosh A, McLellan Q, McMahon KL, Medland SE, Mueller BA, Mwangi B, Osipov E, Portella MJ, Pozzi E, Reneman L, Repple J, Rosa PGP, Sacchet MD, Sämann PG, Schnell K, Schrantee A, Simulionyte E, Soares JC, Sommer J, Stein DJ, Steinsträter O, Strike LT, Thomopoulos SI, van Tol MJ, Veer IM, Vermeiren RRJM, Walter H, van der Wee NJA, van der Werff SJA, Whalley H, Winter NR, Wittfeld K, Wright MJ, Wu MJ, Völzke H, Yang TT, Zannias V, de Zubicaray GI, Zunta-Soares GB, Abé C, Alda M, Andreassen OA, Bøen E, Bonnin CM, Canales-Rodriguez EJ, Cannon D, Caseras X, Chaim-Avancini TM, Elvsåshagen T, Favre P, Foley SF, Fullerton JM, Goikolea JM, Haarman BCM, Hajek T, Henry C, Houenou J, Howells FM, Ingvar M, Kuplicki R, Lafer B, Landén M, Machado-Vieira R, Malt UF, McDonald C, Mitchell PB, Nabulsi L, Otaduy MCG, Overs BJ, Polosan M, Pomarol-Clotet E, Radua J, Rive MM, Roberts G, Ruhe HG, Salvador R, Sarró S, Satterthwaite TD, Savitz J, Schene AH, Schofield PR, Serpa MH, Sim K, Soeiro-de-Souza MG, Sutherland AN, Temmingh HS, Timmons GM, Uhlmann A, Vieta E, Wolf DH, Zanetti MV, Jahanshad N, Thompson PM, Veltman DJ, Penninx BWJH, Marquand AF, Cole JH, Schmaal L. Brain aging in major depressive disorder: results from the ENIGMA Major Depressive Disorder working group. Mol Psychiatry. 2020; doi: 10.1038/s41380-020-0754-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haufe S, Meinecke F, Gorgen K, Dahne S, Haynes JD, Blankertz B, Biessmann F. On the interpretation of weight vectors of linear models in multivariate neuroimaging. Neuroimage. 2014;87:96–110. doi: 10.1016/j.neuroimage.2013.10.067. [DOI] [PubMed] [Google Scholar]
- Hoerl AE, Kennard RW. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics. 2000;42(1):80–86. doi: 10.2307/1271436. [DOI] [Google Scholar]
- Jiang H, Lu N, Chen K, Yao L, Li K, Zhang J, Guo X. Predicting Brain Age of Healthy Adults Based on Structural MRI Parcellation Using Convolutional Neural Networks. Front Neurol 2019;10:1346. doi: 10.3389/fneur.2019.01346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karbasforoushan H, Woodward ND. Resting-state networks in schizophrenia. Curr Top Med Chem. 2012;12(21):2404–24014. doi: 10.2174/156802612805289863. [DOI] [PubMed] [Google Scholar]
- Kaufmann T, van der Meer D, Doan NT, Schwarz E, Lund MJ, Agartz I, Alnæs D, Barch DM, Baur-Streubel R, Bertolino A, Bettella F, Beyer MK, Bøen E, Borgwardt S, Brandt CL, Buitelaar J, Celius EG, Cervenka S, Conzelmann A, Córdova-Palomera A, Dale AM, de Quervain DJF, Di Carlo P, Djurovic S, Dørum ES, Eisenacher S, Elvsåshagen T, Espeseth T, Fatouros-Bergman H, Flyckt L, Franke B, Frei O, Haatveit B, Håberg AK, Harbo HF, Hartman CA, Heslenfeld D, Hoekstra PJ, Høgestøl EA, Jernigan TL, Jonassen R, Jönsson EG, Karolinska Schizophrenia Project (KaSP), Kirsch P, Kłoszewska I, Kolskår KK, Landrø Nl, Le Hellard S, Lesch KP, Lovestone S, Lundervold A, Lundervold AJ, Maglanoc LA, Malt UF, Mecocci P, Me lie I, Meyer-Lindenberg A, Moberget T, Norbom LB, Nordvik JE, Nyberg L, Oosterlaan J, Papalino M, Papassotiropoulos A, Pauli P, Pergola G, Persson K, Richard G, Rokicki J, Sasnders AM, Selbæk G, Shadrin AA, Smeland OB, Soininen H, Sowa P, Steen VM, Tsolaki M, Ulrichsen KM, Vellas B, Wang L, Westman E, Ziegler GC, Zink M, Andreassen OA, Westlye LT. Common brain disorders are associated with heritable patterns of apparent aging of the brain. Nat Neurosci. 2019;22(10):1617–1623. doi: 10.1038/s41593-019-0471-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khundrakpam BS, Tohka J, Evans AC; Brain Development Cooperative Group. Prediction of brain maturity based on cortical thickness at different spatial resolutions. Neuroimage. 2015;111:350–359. doi: 10.1016/j.neuroimage.2015.02.046. [DOI] [PubMed] [Google Scholar]
- Koutsouleris N, Davatzikos C, Borgwardt S, Gaser C, Bottlender R, Frodl T, Falkai P, Riecher-Rössler A, Möller HJ, Reiser M, Pantelis C, Meisenzahl E. Accelerated brain aging in schizophrenia and beyond: a neuroanatomical marker of psychiatric disorders. Schizophr Bull. 2014;40(5):1140–1153. doi: 10.1093/schbul/sbt142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nenadić I, Dietzek M, Langbein K, Sauer H, Gaser C.BrainAGE score indicates accelerated brain aging in schizophrenia, but not bipolar disorder. Psychiatry Res Neuroimaging. 2017;266:86–89. doi: 10.1016/j.pscychresns.2017.05.006. [DOI] [PubMed] [Google Scholar]
- Olabi B, Ellison-Wright I, McIntosh AM, Wood SJ, Bullmore E, Lawrie SM. Are there progressive brain changes in schizophrenia? A meta-analysis of structural magnetic resonance imaging studies. Biol Psychiatry. 2011;70(1):88–96. doi: 10.1016/j.biopsych.2011.01.032. [DOI] [PubMed] [Google Scholar]
- Palaniyappan L, Liddle PF. Aberrant cortical gyrification in schizophrenia: a surface-based morphometry study. J Psychiatry Neurosci. 2012;37(6):399–406. doi: 10.1503/jpn.110119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E.. Scikit-learn: Machine Learning in Python. J Mach Learn Res. 2011;12:2825–2830. https://dl.acm.org/doi/10.5555/1953048.2078195. [Google Scholar]
- Radua J, Borgwardt S, Crescini A, Mataix-Cols D, Meyer-Lindenberg A, McGuire PK, Fusar-Poli P. Multimodal meta-analysis of structural and functional brain changes in first episode psychosis and the effects of antipsychotic medication. Neurosci Biobehav Rev. 2012;36(10):2325–2333. doi: 10.1016/j.neubiorev.2012.07.012. [DOI] [PubMed] [Google Scholar]
- Rudolph MD, Miranda-Domínguez O, Cohen AO, Breiner K, Steinberg L, Bonnie RJ, Scott ES, Taylor-Thompson K, Chein J, Fettich KC, Richeson JA, Dellarco DV, Galván A, Casey BJ, Fair DA. At risk of being risky: The relationship between "brain age" under emotional states and risk preference. Dev Cogn Neurosci. 2017;24:93–106. doi: 10.1016/j.dcn.2017.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnack HG, van Haren NE, Nieuwenhuis M, Hulshoff Pol HE, Cahn W, Kahn RS. Accelerated Brain Aging in Schizophrenia: A Longitudinal Pattern Recognition Study. Am J Psychiatry. 2016;173(6):607–616. doi: 10.1176/appi.ajp.2015.15070922. [DOI] [PubMed] [Google Scholar]
- Schrouff J, Rosa MJ, Rondina JM, Marquand AF, Chu C, Ashburner J, Phillips C, Richiardi J, Mourão-Miranda J. PRoNTo: pattern recognition for neuroimaging toolbox. Neuroinformatics. 2013;11(3):319–337. doi: 10.1007/s12021-013-9178-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahab S, Mulsant BH, Levesque ML, Calarco N, Nazeri A, Wheeler AL, Foussias G, Rajji TK, Voineskos AN. Brain structure, cognition, and brain age in schizophrenia, bipolar disorder, and healthy controls. Neuropsychopharmacology. 2019;44(5):898–906. doi: 10.1038/s41386-018-0298-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shafto MA, Tyler LK, Dixon M, Taylor JR, Rowe JB, Cusack R, Calder AJ, Marslen-Wilson WD, Duncan J, Dalgleish T, Henson RN, Brayne C, Matthews FE, Cam-CAN. The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) study protocol: a cross-sectional, lifespan, multidisciplinary examination of healthy cognitive ageing. BMC Neurol. 2014;14:204. doi: 10.1186/s12883-014-0204-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smola AJ, Schölkopf B. A tutorial on support vector regression. Stat Comput. 2004;14:199–222. 10.1023/B:STCO.0000035301.49549.88. [DOI] [Google Scholar]
- Steen RG, Mull C, McClure R, Hamer RM, Lieberman JA. Brain volume in first-episode schizophrenia: systematic review and meta-analysis of magnetic resonance imaging studies. Br J Psychiatry. 2006;188:510–8. doi: 10.1192/bjp.188.6.510. [DOI] [PubMed] [Google Scholar]
- Tibshirani R Regression Shrinkage and Selection via the Lasso. J Roy Stat Soc B Met 1996;58(1):267–288. http://www.jstor.org/stable/2346178. [Google Scholar]
- Tipping ME. Sparse Bayesian learning and the relevance vector machine. J Mach Learn Res Sum. 2001;1(3):211–244. 10.1162/15324430152748236. [DOI] [Google Scholar]
- Valizadeh SA, Hänggi J, Mérillat S, Jäncke L. Age prediction on the basis of brain anatomical measures. Hum Brain Mapp. 2017;38(2):997–1008. doi: 10.1002/hbm.23434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Erp TG, Hibar DP, Rasmussen JM, Glahn DC, Pearlson GD, Andreassen OA, Agartz I, Westlye LT, Haukvik UK, Dale AM, Melle I, Hartberg CB, Gruber O, Kraemer B, Zilles D, Donohoe G, Kelly S, McDonald C, Morris DW, Cannon DM, Corvin A, Machielsen MW, Koenders L, de Haan L, Veltman DJ, Satterthwaite TD, Wolf DH, Gur RC, Gur RE, Potkin SG, Mathalon DH, Mueller BA, Preda A, Macciardi F, Ehrlich S, Walton E, Hass J, Calhoun VD, Bockholt HJ, Sponheim SR, Shoemaker JM, van Haren NE, Hulshoff Pol HE, Ophoff RA, Kahn RS, Roiz-Santiañez R, Crespo-Facorro B, Wang L, Alpert KI, Jönsson EG, Dimitrova R, Bois C, Whalley HC, McIntosh AM, Lawrie SM, Hashimoto R, Thompson PM, Turner JA. Subcortical brain volume abnormalities in 2028 individuals with schizophrenia and 2540 healthy controls via the ENIGMA consortium. Mol Psychiatry. 2016;21(4):547–553. doi: 10.1038/mp.2015.63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Erp TGM, Walton E, Hibar DP, Schmaal L, Jiang W, Glahn DC, Pearlson GD, Yao N, Fukunaga M, Hashimoto R, Okada N, Yamamori H, Bustillo JR, Clark VP, Agartz I, Mueller BA, Cahn W, de Zwarte SMC, Hulshoff Pol HE, Kahn RS, Ophoff RA, van Haren NEM, Andreassen OA, Dale AM, Doan NT, Gurholt TP, Hartberg CB, Haukvik UK, Jørgensen KN, Lagerberg TV, Melle I, Westlye LT, Gruber O, Kraemer B, Richter A, Zilles D, Calhoun VD, Crespo-Facorro B, Roiz-Santiañez R, Tordesillas-Gutiérrez D, Loughland C, Carr VJ, Catts S, Cropley VL, Fullerton JM, Green MJ, Henskens FA, Jablensky A, Lenroot RK, Mowry BJ, Michie PT, Pantelis C, Quidé Y, Schall U, Scott RJ, Cairns MJ, Seal M, Tooney PA, Rasser PE, Cooper G, Shannon Weickert C, Weickert TW, Morris DW, Hong E, Kochunov P, Beard LM, Gur RE, Gur RC, Satterthwaite TD, Wolf DH, Belger A, Brown GG, Ford JM, Macciardi F, Mathalon DH, O'Leary DS, Potkin SG, Preda A, Voyvodic J, Lim KO, McEwen S, Yang F, Tan Y, Tan S, Wang Z, Fan F, Chen J, Xiang H, Tang S, Guo H, Wan P, Wei D, Bockholt HJ, Ehrlich S, Wolthusen RPF, King MD, Shoemaker JM, Sponheim SR, De Haan L, Koenders L, Machielsen MW, van Amelsvoort T, Veltman DJ, Assogna F, Banaj N, de Rossi P, Iorio M, Piras F, Spalletta G, McKenna PJ, Pomarol-Clotet E, Salvador R, Corvin A, Donohoe G, Kelly S, Whelan CD, Dickie EW, Rotenberg D, Voineskos AN, Ciufolini S, Radua J, Dazzan P, Murray R, Reis Marques T, Simmons A, Borgwardt S, Egloff L, Harrisberger F, Riecher-Rössler A, Smieskova R, Alpert KI, Wang L, Jönsson EG, Koops S, Sommer IEC, Bertolino A, Bonvino A, Di Giorgio A, Neilson E, Mayer AR, Stephen JM, Kwon JS, Yun JY, Cannon DM, McDonald C, Lebedeva I, Tomyshev AS, Akhadov T, Kaleda V, Fatouros-Bergman H, Flyckt L, Karolinska Schizophrenia Project, Busatto GF, Rosa PGP, Serpa MH, Zanetti MV, Hoschl C, Skoch A, Spaniel F, Tomecek D, Hagenaars SP, McIntosh AM, Whalley HC, Lawrie SM, Knöchel C, Oertel-Knöchel V, Stäblein M, Howells FM, Stein DJ, Temmingh HS, Uhlmann A, Lopez-Jaramillo C, Dima D, McMahon A, Faskowitz JI, Gutman BA, Jahanshad N, Thompson PM, Turner JA. Cortical Brain Abnormalities in 4474 Individuals With Schizophrenia and 5098 Control Subjects via the Enhancing Neuro Imaging Genetics Through Meta Analysis (ENIGMA) Consortium. Biol Psychiatry. 2018;84(9):644–654. doi: 10.1016/j.biopsych.2018.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K; WU-Minn HCP Consortium. The WU-Minn Human Connectome Project: an overview. Neuroimage. 2013;80:62–79. doi: 10.1016/j.neuroimage.2013.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Haren NE, Hulshoff Pol HE, Schnack HG, Cahn W, Brans R, Carati I, Rais M, Kahn RS. Progressive brain volume loss in schizophrenia over the course of the illness: evidence of maturational abnormalities in early adulthood. Biol Psychiatry. 2008;63(1):106–113. doi: 10.1016/j.biopsych.2007.01.004. [DOI] [PubMed] [Google Scholar]
- van Haren NE, Schnack HG, Cahn W, van den Heuvel MP, Lepage C, Collins L, Evans AC, Hulshoff Pol HE, Kahn RS. Changes in cortical thickness during the course of illness in schizophrenia. Arch Gen Psychiatry. 2011;68(9):871–880. doi: 10.1001/archgenpsychiatry.2011.88. [DOI] [PubMed] [Google Scholar]
- van Haren NEM, Schnack HG, Koevoets MGJC, Cahn W, Hulshoff Pol HE, Kahn RS. Trajectories of subcortical volume change in schizophrenia: A 5-year follow-up. Schizophr Res. 2016;173(3):140–145. doi: 10.1016/j.schres.2015.09.027. [DOI] [PubMed] [Google Scholar]
- Vita A, De Peri L, Silenzi C, Dieci M. Brain morphology in first-episode schizophrenia: a meta-analysis of quantitative magnetic resonance imaging studies. Schizophr Res. 2006;82(1):75–88. doi: 10.1016/j.schres.2005.11.004. [DOI] [PubMed] [Google Scholar]
- Zhao Y, Klein A, Castellanos FX, Milham MP. Brain age prediction: Cortical and subcortical shape covariation in the developing human brain. Neuroimage. 2019;202:116149. doi: 10.1016/j.neuroimage.2019.116149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H, Hastie T. Regularization and Variable Selection via the Elastic Net. J R Stat Soc Ser B Methodol. 2005;67(2):301–320. http://www.jstor.org/stable/3647580. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.