Graphical abstract
Keywords: COVID-19, Spatially stratified heterogeneity, SEIR model for a stratum, Space-time R0, Latent and infection ratio, Mainland China
Abstract
Objectives
The novel coronavirus (COVID-19) epidemic is reaching its final phase in China. The epidemic data are available for a complete assessment of epidemiological parameters in all regions and time periods.
Methods
This study aims to present a spatiotemporal epidemic model based on spatially stratified heterogeneity (SSH) to simulate the epidemic spread. A susceptible-exposed/latent-infected-removed (SEIR) model was constructed for each SSH-identified stratum (each administrative city) to estimate the spatiotemporal epidemiological parameters of the outbreak.
Results
We estimated that the mean latent and removed periods were 5.40 and 2.13 days, respectively. There was an average of 1.72 latent or infected persons per 10,000 Wuhan travelers to other locations until January 20th, 2020. The space-time basic reproduction number (R0) estimates indicate an initial value between 2 and 3.5 in most cities on this date. The mean period for R0 estimates to decrease to 80%, and 50% of initial values in cities were an average of 14.73 and 19.62 days, respectively.
Conclusions
Our model estimates the complete spatiotemporal epidemiological characteristics of the outbreak in a space-time domain. These findings will help enhance a comprehensive understanding of the outbreak and inform the strategies of prevention and control in other countries worldwide.
Introduction
As of this writing, the novel coronavirus (COVID-19) outbreak is considered to be almost over in China after an intensive spread lasting over two months. The complete data of the COVID-19 epidemic in China enables us to make a complete and accurate estimation of the epidemiological parameters in the country. Early confirmed cases were mainly linked to a seafood wholesale market in Wuhan, Hubei province, China, starting from late November 2019 (Li et al., 2020, Zhu et al., 2020). The epidemic transmission in the early phase was associated with the movement of populations from the seafood market and away from Wuhan. Massive human movements via railways and airlines from Wuhan due to the annual Chinese (Lunar) New Year holiday migration enabled the virus to spread nationwide and worldwide (Peeri et al., 2020). Travel restrictions and quarantine measures in Wuhan were effective in delaying the overall epidemic progression in mainland China and reduced the exportation of cases to international locations (Chinazzi et al., 2020). Strict control strategies activated by governments and individuals (e.g., transportation restrictions, holiday extensions, and self-isolation measures) were effective in weakening the outbreak trend in China (Lin et al., 2020).
Previous studies of the epidemiological characteristics of COVID-19 focused on clinical and descriptive statistics (Chan et al., 2020, Guan et al., 2020, Huang et al., 2020, Li et al., 2020, Sun et al., 2020, Zhu et al., 2020). Modeling studies of COVID-19 transmission patterns include forecasting future spreads (Al-qaness et al., 2020, Alsayed et al., 2020, Wu et al., 2020), exploring characteristics and determinants (Li et al., 2020, Liu et al., 2020, Xiong et al., 2020), risk assessment (Boldog et al., 2020, Jung et al., 2020, Tang et al., 2020), control/restriction measure effects (Chinazzi et al., 2020, Tang et al., 2020), estimation of epidemiological parameters (e.g., basic reproduction number, R 0) (Chen et al., 2020, Mollalo et al., 2020, Wang et al., 2020, Zhang et al., 2020, Zhao et al., 2020a) and others. Epidemiological and modeling studies indicate that the COVID-19 epidemic has an R 0 value of 2–3 (Li et al., 2020, Wu et al., 2020, Zhang et al., 2020, Zhao et al., 2020a), which is lower than that of the 2003 severe acute respiratory syndrome (SARS) outbreak (Lipsitch, 2003, Riley et al., 2003). However, the COVID-19 epidemic spread in China produced various regional outbreaks with diversified epidemiological characteristics, which varied by region and human movements from the epidemic center. Moreover, epidemiological parameters/indicators (e.g., R 0, infective rate, and removed rate) generally varied by region and time during the epidemic period because of the various control strategies activated by multiple governments and other entities.
A variety of epidemics indicate the region-varying and time-varying parameter characteristics (McCallum and Partridge, 2010), and a global model is inappropriate for all regions in such a large-scale area (e.g., mainland China). Control strategies (e.g., transportation control programs and 2-week self-isolation measures) in various regions might cause heterogeneous interactions between subpopulations in the region to varying degrees. A global model would be confounded if the population exhibits spatially stratified heterogeneity (SSH) (Buttle et al., 2016, Wang et al., 2016, Xu et al., 2011). Traditional mathematical models of infectious diseases, such as susceptible-infected-removed (SIR) and susceptible-exposed/latent-infected-removed (SEIR) models, are appropriate and applicable under the mass interaction assumption (i.e., subpopulations mix fully and homogeneously, and have identical interactions with one another) (Kermack and Mckendrick, 1991). Control strategies for the restriction of human migration between regions may cause a disagreement with a global model due to this assumption. Moreover, epidemic outbreaks strongly associated with human movement from the epidemic source (e.g., the COVID-19 epidemic in China) generally indicate a spatiotemporal heterogeneity typical of human movements. Therefore, to better estimate the spatiotemporal epidemiological characteristics of an outbreak, SSH-based models can identify similar characteristics within strata (e.g., region groups) and different characteristics between strata (Wang et al., 2010b).
Given the above considerations, here we provide an SEIR model with a time-varying infective rate for each SSH-identified stratum to simulate the spatiotemporal epidemic spread of the COVID-19 outbreak in geographical strata of mainland China, based on the SSHs (Wang et al., 2016, Wang et al., 2010b) of the epidemic spread and human movements from infection sources. This study estimates the spatiotemporal epidemiological characteristics of the outbreak (e.g., space-time varying R 0) all over the country, the spatial distribution of the imported latent and infected populations from the epidemic source, and several other indicators (e.g., latent and removed periods) in strata (administrative cities in mainland China).
Materials and methods
SSH q statistic
The SSH refers to ubiquitous phenomena (those within strata are more similar than those between strata), implies potential distinct mechanisms by stratum, and enforces the applicability of statistical inferences (Wang et al., 2016). The geographical detector (GeoDetector) q statistic is generally applied to quantitatively evaluate the SSH of an explained variable (Wang et al., 2016, Wang et al., 2010b) and assess the determinant power of explanatory variables and their interactions without linear assumptions (Yin et al., 2019). The fundamental formula of the q statistic is given by:
| (1) |
where q, with a value ranging from 0 to 1, is the SSH measure of an explained variable or the determinant power of a factor to the objective. N is the number of explained variable observations, and σ 2 indicates the variance of all the observations. The explained variable is stratified into L strata, denoted by h = 1, 2, …, L, which are determined by prior knowledge, the determinant factor, or a classification algorithm. Nh is the number of observations, and is the corresponding variance within stratum h.
There must be at least two subregions in each stratum for the variance calculation within strata if the explained variable distributes spatially (Wang et al., 2010b). However, a stratum containing only one subregion is allowable, when the explained variable observations are constructed in a space-time domain. There might be one or more subregions in a specific stratum under a given geographical stratification. The variance is calculated according to the spatiotemporal data in a specific stratum with multiple subregions and temporal observations. Specifically, if a stratum has only one subregion, its variance can be calculated based on temporal observations. Multiple geographical stratification solutions in a large-scale area can be comparatively analyzed to identify an appropriate one to indicate the significant SSH of the epidemic spread and human movements from an infection source. Various epidemic models in strata can be combined to introduce a model of a complete spatiotemporal spread of the epidemic.
The GeoDetector software is accessible at http://geodetector.cn/, and the q statistics in this study were performed with the use of the R software package (R Foundation for Statistical Computing).
SEIR model for a stratum
After determining a specific geographical stratification solution, the study area is stratified into L strata denoted by h = 1, 2, …, L. The epidemic SEIR model is separately calibrated in each of the various strata. The population in stratum h is divided into four subpopulations: the susceptible (Sh), the exposed/latent (Eh), the infected (Ih), and the removed/isolated/recovered/dead (Rh). The numbers of four subpopulations in stratum h are denoted by Sh(t), Eh(t), Ih(t), and Rh(t), respectively, at time t. And the population amount in stratum h is assumed to be constant and can be denoted by Nh = Sh(t) + Eh(t) + Ih(t) + Rh(t). In the current stratified model, SEIR models in various strata have a set of similar differential equations as follows:
| (2) |
| (3) |
| (4) |
| (5) |
where λh is the latent rate at which exposed individuals become infectious in stratum h (1/λh indicates the estimated latent period, Tl,h), and γh is the removed rate at which infectious individuals are removed (1/γh denotes the estimated removed period, Tr,h). The infective rate in stratum h denoted by βh indicates the average infection number per infectious individual per timestep (e.g., one day), and is due to the temporal change of the effects of control programs and other factors; therefore, it is considered to depend on time:
| (6) |
where ah, bh, ch and dh are the coefficients of an inverse logistic function to describe the temporal βh(t) in stratum h. Control measures have no explicitly representative parameters included in the model. However, they are reflected in the observed data, and thus, are adopted in the parameters in the modeling.
The SEIR model with time-varying infective rates is constructed stratum by stratum according to a specific stratification solution. The SEIR model for each SSH-identified stratum can describe the spatiotemporal variation of the epidemic spread and can be used to estimate the epidemiological characteristics in a space-time domain.
In each stratum, the SEIR model has a total of eight parameters to be estimated, including four coefficients of the βh(t) function (ah, bh, ch, dh), γh, λh, Eh(1) and Ih(1). The latter two are the estimated numbers of the latent and infected subpopulations in stratum h, respectively, which are imported from the infection source at time t = 1 (the initial time of the simulation). The initial removed subpopulation is assumed to be zero and the susceptible subpopulation is calculated by Sh(t) = Nh − Ih(t) − Eh(t) − Rh(t).
Using spatiotemporal data of the COVID-19 epidemic in China, we can fit the proposed SEIR model, estimate the model parameters in all the strata, and then estimate the spatiotemporal epidemiological characteristics. The mean latent and removed periods, respectively, can be estimated as follows:
| (7) |
| (8) |
where L is the number of strata, is the estimated latent rate, and is the estimated removed rate in stratum h.
During the modeling process, the latent and infected subpopulations imported from the infection source (Wuhan for the COVID-19 epidemic) are estimated at the initial time in all strata. Following this, we can then calculate the latent and infected ratio (L&I ratio) imported from Wuhan at t = 1 in stratum h as follows:
| (9) |
where RLI,h is the L&I ratio at t = 1 in stratum h, and are the estimated imported latent and infected subpopulations, respectively, and nh(1) denotes the cumulative number of Wuhan travelers to stratum h from January 1st, 2020 at t = 1. Note that the former is the date when the seafood market was closed, and human movements from Wuhan to elsewhere in the country contributed to the regional variation of the initial epidemic status by stratum.
Finally, the space-time R 0 in all the strata during the period of the simulation can be estimated by:
| (10) |
where R 0, h(t) is the R 0 estimate at time t in stratum h, and , , and are the parameter estimates of the infective rate function. The estimated R 0 function depends on time, varies by stratum, and describes the complete spatiotemporal characteristics of the COVID-19 epidemic spread in mainland China.
Data and stratification
We collected the spatiotemporal data of daily new COVID-19 confirmed cases in administrative cities of mainland China from the daily bulletins of the National Health Commission of the People’s Republic of China (NHC) and various Provincial/Municipal Health Commissions. The final epidemic dataset was comparatively verified through the public platform of the 2019-nCoV-infected pneumonia epidemic from the Chinese Center for Disease Control and Prevention (China CDC) (China CDC, 2020). Additionally, demographic data were collected from the 2019 China Statistical Yearbook to identify the populations in the strata.
The Huanan seafood wholesale market and Wuhan were considered to be the primary and secondary epidemic centers. Human movements of populations from these two sources were associated with the spatiotemporal epidemic spread. We used the data of location-based service (LBS) requests of mobile devices to indicate human migrations from the sources to elsewhere. The datasets of LBS requests, which cover over 80% of mobile devices supported by the three telecommunication operators in China, were provided by Wayz Inc., Shanghai, China, and applied to identify the generations of the COVID-19 epidemic spreads in mainland China during the early phase (Hu et al., 2020). The LBS-requesting statistics are implemented every two hours with high-resolution location information, and private individual information was deleted from the raw data of the mobile devices.
Based on these above-mentioned data sources, we evaluated the SSHs of the spatiotemporal data of COVID-19 confirmed cases and the LBS-requesting data of mobile devices from two epidemic sources. Three stratification solutions were carried out for comparative analysis. First, considering the distance from the epidemic source, the study area (mainland China) was stratified into four subareas of increasing distance (strata): Wuhan, Hubei province excluding Wuhan, provinces adjacent to Hubei, and the rest of the country (Solution 1). Second, provinces, municipalities, and autonomous regions were considered as the strata (Solution 2). Third, all administrative cities were considered as strata (Solution 3).
In each stratum, the spatiotemporal observations of an explained variable were used to calculate the corresponding variance. That is to say, the variance in calculating the SSH q value is about the number of confirmed cases or device traces. Note that the variances in Solution 3 were calculated based on temporal observations since each stratum has only one subregion (city). The variances of the spatiotemporal observations within all strata were compared with the variance of all observations; according to Eq. (1), the SSH q value of the explained variable can be calculated under a specific stratification solution. There were three stratification solutions for the evaluations of the SSHs of the explained variables. The SSH q values of each variable can be compared under different solutions. As shown in Table 1 , spatiotemporal COVID-19 cases and two categories of device traces from the market and Wuhan had significantly weak SSH in the strata of Solution 2 (q statistics < 0.1). However, they had strong SSH in the strata of both Solution 1 and Solution 3. The q statistics of device traces from Wuhan and the seafood market (after January 1st, 2020) were higher than 0.86 and 0.95, respectively. The spatiotemporal COVID-19 cases had q statistic values over 0.26. It is thus apparently inappropriate to construct the SEIR model for strata by provinces. The q statistics in strata of cities were generally higher than those in the four strata separated by increasing distance from the epidemic source. In addition, more strata reveal more details of the epidemic in the space-time domain. We, therefore, selected Solution 3 to implement the stratification, i.e., the proposed SEIR model of simulating the spatiotemporal COVID-19 epidemic spread was constructed in strata of administrative cities in mainland China.
Table 1.
q statistic values of COVID-19 cases and device traces with various stratification solutions.1
| Stratification | Cases2 | Market devices3 | Wuhan devices | |
|---|---|---|---|---|
| Before Jan. 1st | After Jan. 1st | |||
| Solution 1 | 0.2682 | 0.7155 | 0.9524 | 0.8630 |
| Solution 2 | 0.0677 | 0.0598 | 0.0865 | 0.0632 |
| Solution 3 | 0.2742 | 0.7158 | 0.9530 | 0.8650 |
For all the q statistic values, p < 0.001.
The COVID-19 cases were cumulatively summed until February 29th, 2020.
Mobile device data from the seafood market was divided into two subsets separated by the date of January 1st, 2020, for the q statistic calculations.
Experimental setups
Each administrative city in mainland China was considered as one single stratum, and the SEIR model for a stratum was correspondingly constructed to simulate the epidemic spread. The experimental period was set from January 20th to February 29th, 2020, with a time step of one day (t = 1, 2, …, 41). The population amount in stratum h at the end of 2018 was assigned to Nh, which was set as a constant during the modeling process. The infected subpopulation, Ih, had an initial value of the cumulative confirmed cases in the city at t = 1 (January 20th) and was assumed not to exceed Nh. The latent subpopulation, Eh, was assumed to have a value ranging from zero to the cumulative number of Wuhan travelers to the city at t = 1 and had an initial importation ratio of 1/1000. Note that the initial values of these two variables were also set as the model parameters and would be re-estimated during the modeling process. The removed subpopulation, Rh, had an initial value of zero at t = 1, and the susceptible subpopulation, Sh, can be simply calculated. The latent rate, λh, and the removed rate, γh, were assumed to have bounds of 1/14–1/3 (day−1) and 1/9–1 (day−1), respectively. That is to say, the latent and removed periods were estimated, respectively, from three to fourteen days and from one day to nine days, which covered the corresponding values considered in most previous studies (e.g., Guan et al., 2020, Lin et al., 2020, Wu et al., 2020).
Based on the control of the spatiotemporal COVID-19 epidemic data, the proposed SEIR model can be solved according to Eqs. (2), (3), (4), (5), (6), and the parameter estimates of the SEIR models in strata were obtained afterward. Furthermore, the spatiotemporal epidemiological parameters of the COVID-19 outbreak in mainland China could be calculated according to Eqs. (7), (8), (9), (10). The root mean square error (RMSE), coefficient of determination (R 2), and adjusted R 2 were selected to evaluate the model performance (goodness-of-fit, see Appendix A). The calculation was implemented by comparing the observed and estimated (modeled) numbers of the cumulative cases. The calculations of the proposed SEIR model were implemented using MATLAB programming (MathWorks). Thematic mapping to display the geographical distributions of epidemiological parameters was implemented in the ArcGIS platform (ESRI).
Results
Model performance
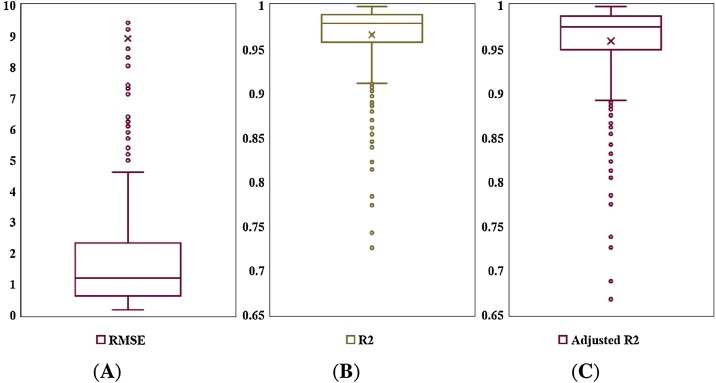
The SEIR model for a stratum was constructed amongst a total of 315 applicable administrative cities in mainland China. The observations of the cumulative confirmed cases were applied to be compared with the modeled values for the evaluation of model performance. Table 2 shows the details of the model performance. Regarding the modeling accuracy, the mean values of R 2 and adjusted R 2 of the presented model were 0.9663 and 0.9592, respectively, and the corresponding values of one standard deviation (1-StdDev) were 0.0396 and 0.0480, respectively. Although several cities had slightly low-value R 2 and adjusted R 2 (lower than 0.7), over 75% of cities had adjusted R 2 values over 0.9. The proposed SEIR model indicated a satisfactory overall performance in reducing the estimation errors and improving accuracy. Several cities with extremely high numbers of confirmed cases (e.g., Wuhan and several cities in Hubei) expanded the range of the RMSE value range (maximum value reached 1423.55 persons). However, the mean RMSE value was 8.9190 persons (1-StdDev = 81.15 persons), and the RMSE “box” was located around the low values from one to two persons (Figure 1) indicating an overall point-by-point accuracy of the model in most cities.
Table 2.
Performance of the SEIR model for a stratum.
| Indicator | Mean | Min. | Max. | StdDev |
|---|---|---|---|---|
| RMSE | 8.9190 | 0.1659 | 1423.55 | 81.15 |
| R2 | 0.9663 | 0.7256 | 0.9985 | 0.0396 |
| Adjusted R2 | 0.9592 | 0.6674 | 0.9982 | 0.0480 |
Figure 1.
Boxplots of the accuracy indicators found from modeling the COVID-19 spread in administrative cities from January 20th to February 29th, 2020: (A) RMSE; (B) R2; (C) adjusted R2. Note that several very large scatters in the RMSE boxplot are not shown for conciseness.
Furthermore, as shown in Figure 1, under the condition of consistent coordinate-axis ranges, the “box” of adjusted R 2 values was slightly wider than R 2 and exhibited a slight sinking which brings the “box” nearer to the horizontal axis. The adjusted R 2, however, still had a median value of 0.9751 with only a few lower outliers. The proposed SEIR model was further confirmed to have very good accuracy in modeling the COVID-19 outbreak in mainland China.
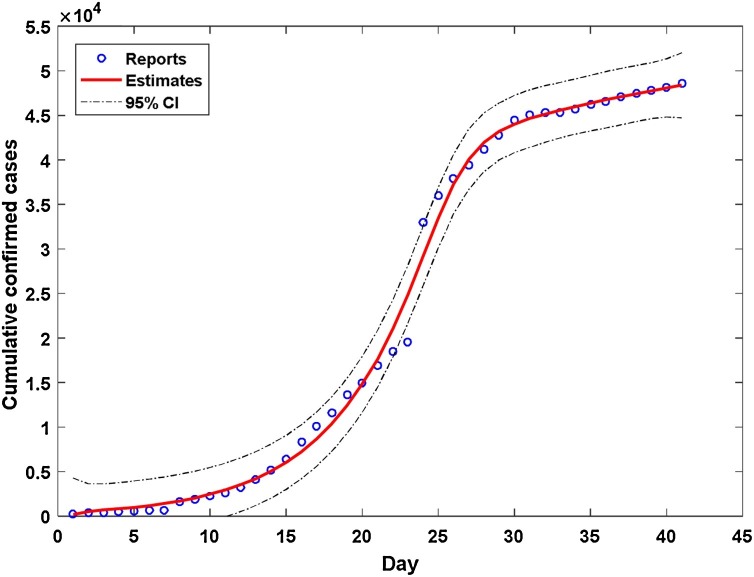
For the detailed modeling information in strata (cities), the temporal estimates of the cumulative cases can be plotted by stratum. Figure 2 demonstrates the information of the temporal estimates in Wuhan (the most severely affected city of the COVID-19 epidemic). Blue circles correspond to the cumulative cases, the solid red line denotes the estimated curve, and the dashed lines depict the 95% confidence intervals (CIs). Note that clinically diagnosed cases were reported as confirmed ones on February 12th, 2020, leading to a very rapid increase in the numbers. The presented model was able to deal with such a sudden shift condition and still reached an overall satisfactory performance (see Figures S1 and S2 for more modeling results in severe cities inside/outside Hubei province). Note that another sudden shift condition (a community transmission in prison caused a rapid increase of the number of cases) occurred in Jining, Shandong province, on February 20th, 2020. The model received a less-satisfactory modeling performance to match the reported numbers in this city but can still in part reflect temporal epidemiological characteristics.
Figure 2.
Estimates of the temporal cumulative cases in Wuhan. Day 1 is January 20th, 2020.
Epidemiological parameter estimates
Table 3 shows the statistics of the epidemiological parameter estimates in strata (cities). The mean latent and removed periods, Tl and Tr, of the COVID-19 epidemic in China, were estimated to be 5.40 days (1-StdDev = 1.29, 95% CI: 5.26–5.54) and 2.13 days (1-StdDev = 0.31, 95% CI: 2.10–2.17), respectively. Most cities exhibited a clustering trend, with low 1-StdDev values of Tl and Tr estimates, as well as the latent and removed rates, λ and γ. When considering the importations from Wuhan to other cities, the imported latent and infected subpopulations in strata at t = 1 (January 20th, 2020) were also estimated, and the mean values of and were 32.18 persons (1-StdDev = 157.75, 95% CI: 14.69–49.67) and 0.88 persons (1-StdDev = 12.11, 95% CI: 0.00–2.22), respectively. Based on the cumulative number of Wuhan travelers to various cities until t = 1, we further estimated the L&I ratios in strata at t = 1. The mean RLI,h value was 1.72 × 10−4 (1-StdDev = 2.12 × 10−4, 95% CI: 1.49 × 10−4–1.96 × 10−4). In other words, until January 20th, there was an average of 1.72 latent or infected persons per 10,000 Wuhan travelers to elsewhere.
Table 3.
Estimates of the epidemiological parameters of the SEIR model for a stratum.
| Indicator | Mean | Min. | Max. | StdDev | 95% CIs |
|---|---|---|---|---|---|
| λ (day−1) | 0.19 | 0.07 | 0.30 | 0.03 | [0.1887, 0.1959] |
| Tl (days) | 5.40 | 3.32 | 14.00 | 1.29 | [5.26, 5.54] |
| γ (day−1) | 0.48 | 0.19 | 0.71 | 0.05 | [0.4703, 0.4820] |
| Tr (days) | 2.13 | 1.40 | 5.32 | 0.31 | [2.10, 2.17] |
| (persons) | 32.18 | 0.00 | 2452.56 | 157.75 | [14.69, 49.67] |
| (persons) | 0.88 | 0.00 | 214.14 | 12.11 | [0.00, 2.22] |
| RLI,h (×10−4) | 1.72 | 0.03 | 20.34 | 2.12 | [1.49, 1.96] |
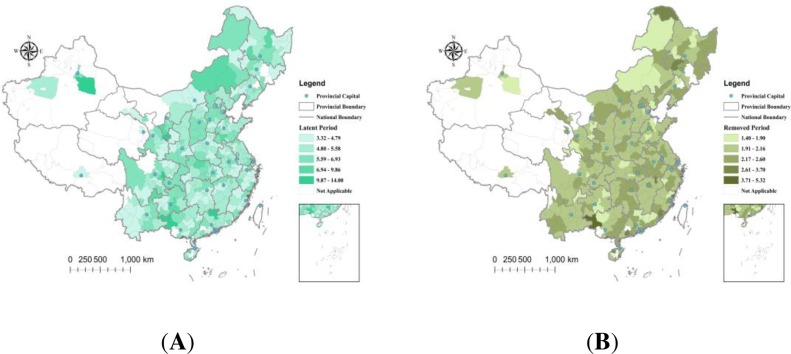
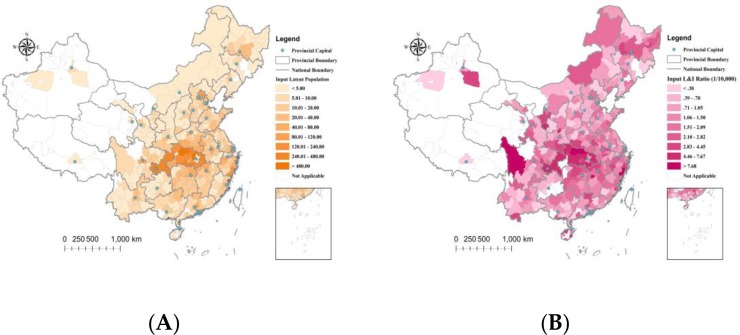
As shown in Figure 3 , the geographical distributions of the latent and removed periods in strata indicated a spatial homogeneity of the virus characteristics. We detected no obvious clustering trends of the latent and removed rates distributed in cities. However, the COVID-19 epidemic spread was strongly linked to human movements from the infection center, and the geographical distributions of the latent populations and L&I ratios from Wuhan at t = 1 indicated a strong spatial heterogeneity. The latent populations and L&I ratios generally decreased by the distance from the epidemic source (Figure 4 ). Several outliers that appeared in the geographical distribution of the L&I ratios might be caused by the low-value cumulative number of Wuhan travelers in these cities.
Figure 3.
Geographical distributions of the epidemiological period estimates: (A) latent periods (days); (B) removed periods (days).
Figure 4.
Geographical distributions of the estimates of the imported (A) latent subpopulations (persons) and (B) L&I ratios (1/10,000) from Wuhan at t = 1 (January 20th, 2020).
Space-time R0 estimates
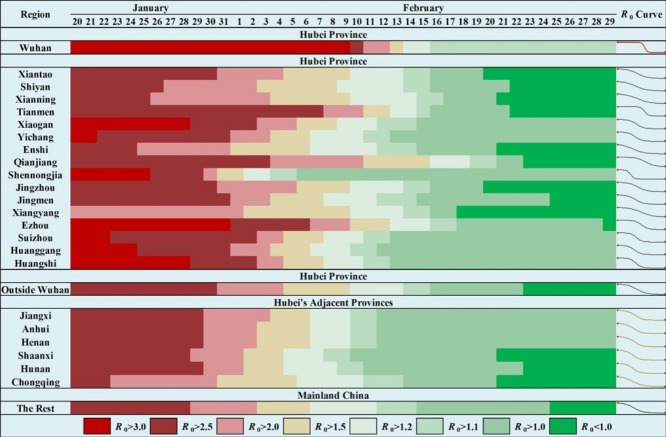
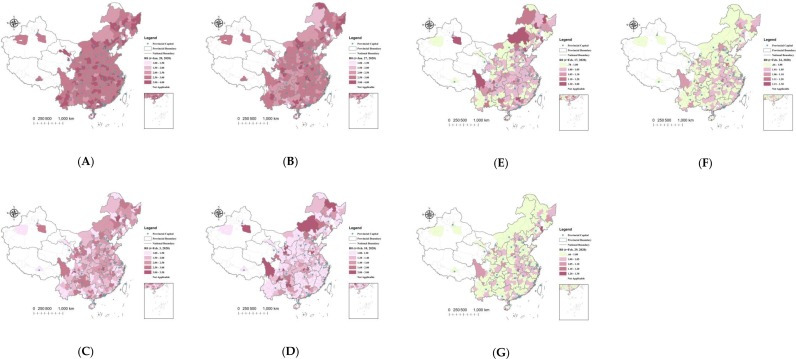
Figure 5 depicts the geographical distributions of the R 0 estimates at t = 1 (January 20th, 2020), t = 8 (January 27th), t = 15 (February 3rd), t = 22 (February 10th), t = 29 (February 17th), t = 36 (February 24th), and t = 41 (February 29th, the experimental end date), respectively. The experimental start date was set as January 20th (the next day after the first case was reported outside Hubei). Most cities had an initial R 0 value between 2 and 3.5 at t = 1. After two weeks of the outbreak (t = 15), the R 0 values in over 50% of cities had decreased to lower than 2, approximately 20% of the cities had R 0 values lower than 1.5, and the R 0 values in other severely affected cities ranged from 2 to 3. After three weeks of the outbreak (t = 22), 21 out of 315 cities had R 0 estimates lower than 1, and only a few severely affected cities maintained R 0 values larger than 2. The number of cities with estimates of R 0 < 1 after four weeks of the outbreak (t = 29) was 87, and the R 0 values in most cities decreased to lower than 1.5. At t = 36 (February 24th), over 50% (184 out of 315) of the cities had estimates of R 0 < 1, and this number was 196 (over 60%) at t = 41 (February 29th).
Figure 5.
Geographical distribution of R0 estimates in the administrative cities of mainland China, at: (A) t = 1 (January 20th, 2020); (B) t = 8 (January 27th, 2020); (C) t = 15 (February 3rd); (D) t = 22 (February 10th, 2020); (E) t = 29 (February 17th); (F) t = 36 (February 24th, 2020); (G) t = 41 (February 29th, the end of the experimental time period).
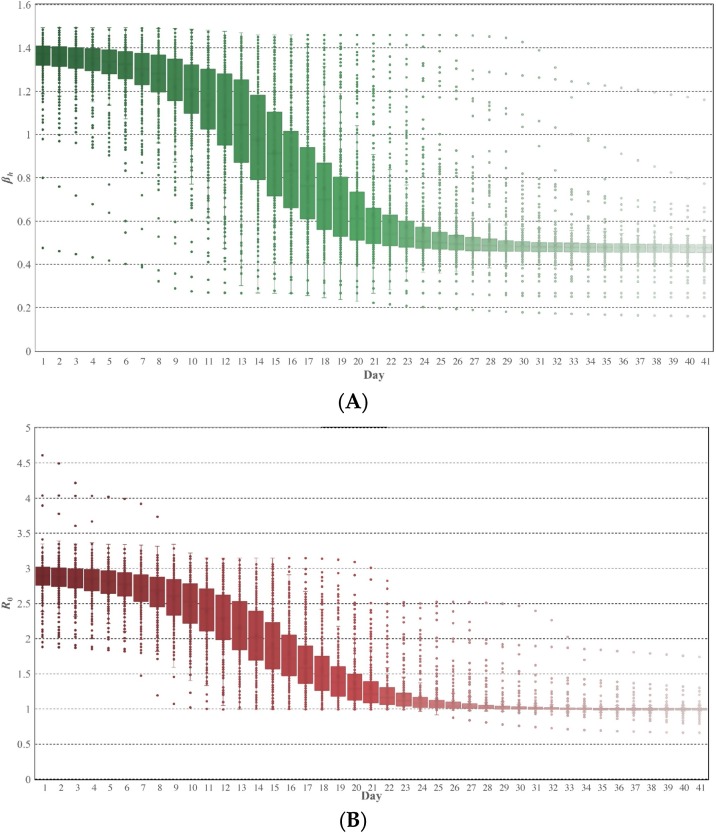
Temporal boxplots of infective rate (βh) and R 0 estimates in the administrative cities of mainland China are demonstrated in Figure 6 . They both indicated a mirrored “S” characteristic. The βh estimates started with an initial value of about 1.4 (i.e., an average of 1.4 infections per day per infectious individual), showed an obvious descending trend after one week of the outbreak, and after a descending period of two weeks, maintained a relatively stable value of about 0.5. The spatial heterogeneity of the βh estimates in strata was more significant during the descending period (“boxes” are obviously narrower in stable periods). Similar spatial heterogeneity appeared as well in the R 0 estimates in strata.
Figure 6.
Temporal boxplots of the epidemiological characteristics: (A) βh estimates; (B) R0 estimates. Day 1 is January 20th, 2020.
Additionally, a clear descending trend appeared in temporal R 0 estimates, starting after one week of the outbreak and lasting two weeks to maintain a relatively stable value. The mean periods of R 0 estimates decreasing to 80% and 50% of the initial values in strata were 14.73 and 19.62 days, respectively. At the end of the experiment (February 29th), nearly all cities had R 0 estimates lower than 30% of the initial values.
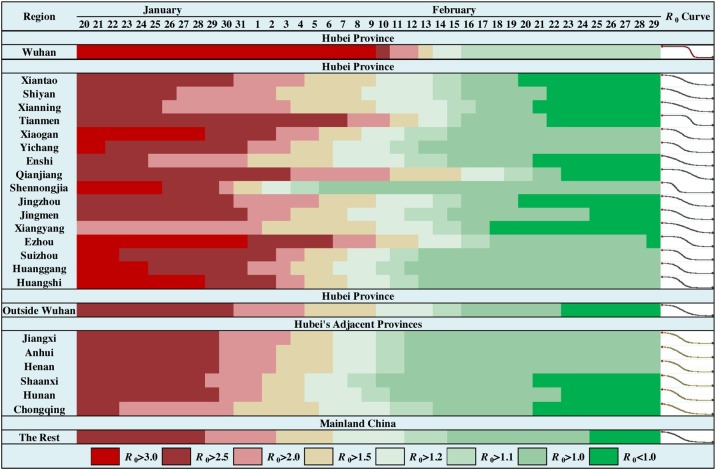
As shown in Figure 7 , the time evolution of the R 0 estimates in Hubei’s cities indicated several features (see Figure S3 for details). The initial R 0 values were between 2.6 and 3.2 (except Xiangyang). The descending trend’s start date varied by city; in many cities, this began about one week into the outbreak, but the date could also be delayed by three weeks (e.g., Wuhan and Tianmen). The descending periods also varied by city, and most cities maintained a descending trend for about two weeks (Figures 7 and S3). However, the descending period could be shortened to about one week (e.g., Wuhan and Shennongjia) or expanded to about four weeks (e.g., Qianjiang). Figure S4 depicts the temporal curves of R 0 estimates in the nine most severely affected cities outside Hubei. The curves indicate a general consistency around the start date and consistency in the descending trend. The epidemic spread had a substantial spatial heterogeneity in Hubei, and the heterogeneity decreased outside Hubei (Figure 7). An exception should be noted about the temporal curve of R 0 estimates in Jining, Shandong province. The specific community transmission in a prison on February 20th, 2020, caused high-value R 0 estimates before that date. However, after the reports of the community outbreak, the R 0 estimates were corrected by the modeling.
Figure 7.
Time evolution of R0 estimates in Wuhan, Hubei excluding Wuhan, provinces adjacent to Hubei and the rest of mainland China.
Discussion
Epidemiological parameters usually exhibit stratified heterogeneity in regions and in time for various reasons, e.g., the various temporal characteristics of the influenza-A 2009 pandemics in temperate zones, tropical zones, and Pacific islands (McCallum and Partridge, 2010). A global model is inappropriate when epidemiological parameters vary in regions and by time. SSH can account for the universal features of phenomena (Wang et al., 2016) and is adequate to evaluate the local heterogeneity (non-homogeneity) in strata. Effective stratifications (e.g., zoning and discretization) can reduce the errors and improve the accuracy of modeling and estimation (Cao et al., 2013, Wang et al., 2010a, Wang et al., 2009). The COVID-19 outbreak in mainland China was obviously influenced by human movements from infection sources and presents a significant SSH in regions and by distance (in part caused by the much more significant SSHs of human movements from Wuhan to elsewhere). Therefore, based on the SSHs of the COVID-19 epidemic spread and human movements, modeling in strata is more appropriate for improving the modeling of the spread of the epidemic in mainland China. Moreover, a comprehensive understanding of the epidemic in China will help inform the measures and strategies of prevention and control in other countries worldwide, many of which are currently experiencing concurrent outbreaks.
This study presented an SEIR model for each SSH-identified stratum to simulate a complete spread of the COVID-19 epidemic and accurately estimate the spatial and spatiotemporal epidemiological parameters in mainland China. The model had an overall satisfactory performance with a median adjusted R 2 value of 0.9751, and the estimations were consistent with most previous studies. We estimated that the mean latent and removed periods were 5.40 and 2.13 days, respectively, which are very close to the previous estimates (Guan et al., 2020, Li et al., 2020, Linton et al., 2020, Sun et al., 2020). Furthermore, an added value of this study is the estimations of the imported latent and infected subpopulations in strata from Wuhan on the initial experimental date (January 20th, 2020). The results showed the average imported latent and infected subpopulations from Wuhan to other cities were 32.18 and 0.88 persons, respectively, due to the annual Chinese New Year holiday migrations. Additional estimation of the imported L&I ratios indicated that there was an average of 1.72 latent or infected persons per 10,000 Wuhan travelers to other locations, until January 20th.
Another main contribution of the current study is the estimation of the space-time characteristics of R 0 during the COVID-19 epidemic spread in mainland China. To our knowledge, this is the first study to construct simultaneously time-varying and region-varying R 0 estimates of epidemic spreads. The results indicated that the initial R 0 values were between 2 and 3.5 in most cities on January 20th, 2020, which are very close to previous estimates (Chen et al., 2020, Jung et al., 2020, Li et al., 2020, Wang et al., 2020, Wu et al., 2020, Zhang et al., 2020, Zhao et al., 2020b, Zhao et al., 2020a). The R 0 values in over 50% of cities decreased to lower than 2 after two weeks of the outbreak, and only a few severely affected cities maintained R 0 values larger than 2 after three weeks of the outbreak. There were 87 cities with estimates of R 0 < 1 after four weeks of the outbreak (February 17th), and on February 29th, the number of cities was 196 (over 60% of all cities considered). The mean periods of R 0 estimates to decrease to 80% and 50% of the initial values in strata were 14.73 and 19.62 days, respectively. The temporal curves of R 0 estimates indicated stronger spatial heterogeneity in Hubei than the rest of mainland China. In most cities, a prominent descending tread in temporal R 0 estimates started one week into the outbreak and lasted two weeks to maintain a relatively stable value. The start date of the prominent descending trend of R 0 estimates in Hubei could be delayed about 2–3 weeks, and the descending period could be shortened to about one week or expanded to about four weeks.
To evaluate the SSHs of the COVID-19 epidemic spread and human movements from the infection sources, we comparatively analyzed three stratification solutions of mainland China (four distance-dependent subareas, provinces, and administrative cities). Stratifications with higher q statistic values and interpretably practical implications are considered better solutions to construct the stratified models. Therefore, we selected a relatively better stratification solution in this study instead of the strictly “best” one (e.g., the one with the highest q statistic value). This might be a limitation of the current study but remains a flexible extension of the proposed SEIR model and its applications for modeling the spread of other infectious diseases. A general and comprehensive solution to identify the stratification with higher q statistic value and practical implications is one of our main future studies. The SEIR model for each SSH-identified stratum was verified to have a good regression accuracy with much smaller residuals in modeling the COVID-19 outbreak in mainland China. The localization of the SEIR model identified by SSH can bring out better modeling performance. The epidemic spreads in most cities had a relatively consistent trend with various spatiotemporal epidemiological characteristics, especially in the early-phase outbreak lasting two months.
Further prospective applications request cross-validations for the proposed model. Moreover, during the modeling process, the modeling results are sensitive to the initial parameter values and their bounds. In this study, the initials and bounds of the parameter values were set up according to observations as well as previous studies. It is important to implement a further analysis of the corresponding parameter sensitivities in the future. Another future study direction is the further validation of the model's universality to the COVID-19 epidemic in other large-scale areas (e.g., globally) and to other infectious diseases. We also intend to apply the proposed SEIR model in countries outside China to enhance understanding of the COVID-19 epidemic worldwide.
Conclusions
This paper introduces an SEIR model for each SSH-identified stratum based on the SSHs of the COVID-19 epidemic spread and human movements from infection sources. The proposed model estimates the spatial and spatiotemporal epidemiological parameters of the COVID-19 outbreak in the space-time domain, such as the geographical distribution of L&I ratios and the space-time R 0 estimates. The following conclusions were achieved:
-
(1)
The mean latent and removed periods of the COVID-19 epidemic were 5.40 days (95% CI: 5.26–5.54) and 2.13 days (95% CI: 2.10–2.17), respectively. The geographical distributions of these two epidemiological parameters indicated a spatial homogeneity amongst cities in mainland China.
-
(2)
Due to the annual Chinese New Year holiday migrations, on January 20th, 2020 (the next day after the first case was reported outside Hubei), the average imported latent and infected subpopulations traveling from Wuhan were estimated as 32.18 (95% CI: 14.69–49.67) and 0.88 (95% CI: 0.00–2.22) persons, respectively.
-
(3)
There was an average of 1.72 (95% CI: 1.49–1.96) latent and infected persons per 10,000 Wuhan travelers to other locations until January 20th. The geographical distributions of the imported latent and infected subpopulations amongst cities from Wuhan indicated a spatial heterogeneity decreasing by distance.
-
(4)
The space-time R 0 estimates indicated an initial value between 2 and 3.5 in most cities on January 20th. There were 87 cities that had an estimate of R 0 < 1 on February 17th (four weeks after the large-scale outbreak), increasing to 196 cities by February 29th. The mean period for R 0 estimates to decrease to 80% and 50% of the initial values in cities were an average of 14.73 and 19.62 days, respectively.
-
(5)
A noticeable descending trend in temporal R 0 estimates in most cities started one week after the outbreak and lasted two weeks, maintaining a relatively stable value. In the outbreak center (Hubei province, China), however, the start date could be delayed 2–3 weeks, and the lasting period could be shortened to one week or expanded to four weeks.
In short, the findings will improve a comprehensive understanding of the epidemic spread in China and inform the strategies of prevention and control of the epidemic for policymakers. The proposed SEIR model can describe the complete spatiotemporal spread of the COVID-19 epidemic in China, conclude the space-time epidemiological characteristics and parameters, and easily model applications in other countries worldwide.
Ethics approval and consent to participate
No individual data were collected, and ethical approval or individual consent was not applicable.
Availability of data and materials
The LBS-requesting mobile device data were provided by Wayz Inc., Shanghai, China, and are not available for distribution due to the constraint in the consent. The dataset of the COVID-19 cases is available from multiple public sources. The MATLAB codes that support the proposed SEIR model computing in this study are available from the corresponding authors on reasonable request.
Funding
This work was supported by the National Natural Science Foundation of China (42061075 and 41531179), the National Science and Technology Major Project (2016YFC1302504), and the Science and Technology Major Project of Jiangxi Province, China (2020YBBGW0007).
Disclaimer
The funders had no role in study design and conduct; data collection, management, analysis, and interpretation; manuscript preparation, writing, and review; the decision to submit the manuscript for publication.
Authors’ contributions
Conceptualization: Hui Lin, Jinfeng Wang, and Bisong Hu; Resources and Data curation: Vincent Tao, Jingyu Qiu, and Hui Lin; Formal analysis: Bisong Hu, Pan Ning, Adam Thomas Devlin, and Haiying Chen; Methodology: Bisong Hu and Jinfeng Wang; Software: Jinfeng Wang; Visualization: Bisong Hu, Pan Ning, Adam Thomas Devlin, and Haiying Chen; Validation, Bisong Hu and Jinfeng Wang; Writing—original draft: Bisong Hu; Writing—review and editing: Bisong Hu, Jinfeng Wang, and Hui Lin; all the other authors contributed to the writing. All authors have read and agreed to the published version of the manuscript and have final responsibility for the decision to submit it for publication.
Conflict of interests
We declare no competing interests.
Acknowledgments
We would like to acknowledge the support for the data collection from Wayz Inc., Shanghai, China. The authors would like to appreciate the relevant government departments in China and multiple public sources for providing the open COVID-19 datasets, the socioeconomic statistical data, and the geographical datasets. The authors are very grateful to the editors and reviewers for their valuable comments.
Footnotes
Supplementary data associated with this article can be found, in the online version, at https://doi.org/10.1016/j.ijid.2021.04.021.
Appendix A. Model performance indicators
Three indicators were selected to evaluate the performance of the proposed SEIR model in this study, including the root mean square error (RMSE), the coefficient of determination (R 2), and the adjusted R 2. In stratum h, the performance of the specific SEIR model was assessed by
| (A1) |
| (A2) |
| (A3) |
where y h,t, and are the observed and estimated (modeled) numbers of the COVID-19 cumulative cases, respectively, in stratum h and at time t, and is the mean of all the observed values. T is the total number of considered timesteps (T = 41 in this study). denotes the adjusted R 2 in stratum h. k is the number of the independent regressors (estimated parameters) in the SEIR model. These measures can be separately calculated by stratum and combined together to evaluate the overall performance of the proposed SEIR model.
Appendix A. Supplementary data
The following are Supplementary data to this article:
References
- Al-qaness M.A.A., Ewees A.A., Fan H., Abd El Aziz M.A.E. Optimization method for forecasting confirmed cases of COVID-19 in China. J Clin Med. 2020;9:674. doi: 10.3390/jcm9030674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alsayed A., Sadir H., Kamil R., Sari H. Prediction of epidemic peak and infected cases for COVID-19 disease in Malaysia, 2020. Int J Environ Res Public Health. 2020;17 doi: 10.3390/ijerph17114076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boldog P., Tekeli T., Vizi Z., Dénes A., Bartha F.A., Röst G. Risk assessment of novel coronavirus COVID-19 outbreaks outside China. J Clin Med. 2020;9:571. doi: 10.3390/jcm9020571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buttle J.M., Allen D.M., Caissie D., Davison B., Hayashi M., Peters D.L., et al. Flood processes in Canada: regional and special aspects. Can Water Resour J Rev Can Ressour Hydr. 2016;41:7–30. doi: 10.1080/07011784.2015.1131629. [DOI] [Google Scholar]
- Cao F., Ge Y., Wang J. Optimal discretization for geographical detectors-based risk assessment. GIScience Remote Sens. 2013;50:78–92. doi: 10.1080/15481603.2013.778562. [DOI] [Google Scholar]
- Chan J.F.-W., Yuan S., Kok K.-H., To K.K.-W., Chu H., Yang J., et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet. 2020;395:514–523. doi: 10.1016/S0140-6736(20)30154-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen T.-M., Rui J., Wang Q.-P., Zhao Z.-Y., Cui J.-A., Yin L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect Dis Poverty. 2020;9:24. doi: 10.1186/s40249-020-00640-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- China CDC . 2020. Public platform of the 2019-nCov-infected pneumonia epidemic (in Chinese)http://2019ncov.chinacdc.cn/2019-nCoV/ [Google Scholar]
- Chinazzi M., Davis J.T., Ajelli M., Gioannini C., Litvinova M., Merler S., et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020 doi: 10.1126/science.aba9757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan W., Ni Z., Hu Yu, Liang W., Ou C., He J., et al. Clinical characteristics of coronavirus disease 2019 in China. N Engl J Med. 2020;382:1708–1720. doi: 10.1056/NEJMoa2002032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu B., Qiu J., Chen H., Tao V., Wang J., Lin H. First, second and potential third-generation spreads of the COVID-19 epidemic in mainland China: an early exploratory study incorporating location-based service data of mobile devices. Int J Infect Dis. 2020;96:489–495. doi: 10.1016/j.ijid.2020.05.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y., et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020;395:497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung S., Akhmetzhanov A.R., Hayashi K., Linton N.M., Yang Y., Yuan B., et al. Real-time estimation of the risk of death from novel coronavirus (COVID-19) infection: inference using exported cases. J Clin Med. 2020;9:523. doi: 10.3390/jcm9020523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kermack W., Mckendrick A. Contributions to the mathematical theory of epidemics—I. Bull Math Biol. 1991;53:33–55. doi: 10.1016/S0092-8240(05)80040-0. [DOI] [PubMed] [Google Scholar]
- Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N Engl J Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Q., Zhao S., Gao D., Lou Y., Yang S., Musa S.S., et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int J Infect Dis. 2020;93:211–216. doi: 10.1016/j.ijid.2020.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linton N.M., Kobayashi T., Yang Y., Hayashi K., Akhmetzhanov A.R., Jung S., et al. Incubation period and other epidemiological characteristics of 2019 novel coronavirus infections with right truncation: a statistical analysis of publicly available case data. J Clin Med. 2020;9:538. doi: 10.3390/jcm9020538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipsitch M. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300:1966–1970. doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S., Qin Y., Xie Z., Zhang J. The spatio-temporal characteristics and influencing factors of Covid-19 spread in Shenzhen, China—an analysis based on 417 cases. Int J Environ Res Public Health. 2020;17:7450. doi: 10.3390/ijerph17207450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCallum L., Partridge J. Epidemiological characteristics of influenza A(H1N1) 2009 pandemic in the Western Pacific Region. West Pac Surveill Response J. 2010;1:5–11. doi: 10.5365/wpsar.2010.1.1.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollalo A., Rivera K.M., Vahedi B. Artificial neural network modeling of novel coronavirus (COVID-19) incidence rates across the continental United States. Int J Environ Res Public Health. 2020;17:4204. doi: 10.3390/ijerph17124204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peeri N.C., Shrestha N., Rahman M.S., Zaki R., Tan Z., Bibi S., et al. The SARS, MERS and novel coronavirus (COVID-19) epidemics, the newest and biggest global health threats: what lessons have we learned? Int J Epidemiol. 2020;49:717–726. doi: 10.1093/ije/dyaa033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riley S., Fraser C., Donnelly C.A., Ghani A.C., Abu-Raddad L.J., Hedley A.J., et al. Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Science. 2003;300:1961–1966. doi: 10.1126/science.1086478. [DOI] [PubMed] [Google Scholar]
- Sun K., Chen J., Viboud C. Early epidemiological analysis of the coronavirus disease 2019 outbreak based on crowdsourced data: a population-level observational study. Lancet Digit Health. 2020;2:e201–e208. doi: 10.1016/S2589-7500(20)30026-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang B., Wang X., Li Q., Bragazzi N.L., Tang S., Xiao Y., et al. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. J Clin Med. 2020;9:462. doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H., Wang Z., Dong Y., Chang R., Xu C., Yu X., et al. Phase-adjusted estimation of the number of coronavirus disease 2019 cases in Wuhan, China. Cell Discov. 2020;6:10. doi: 10.1038/s41421-020-0148-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Christakos G., Hu M. Modeling spatial means of surfaces with stratified nonhomogeneity. IEEE Trans Geosci Remote Sens. 2009;47:4167–4174. doi: 10.1109/TGRS.2009.2023326. [DOI] [Google Scholar]
- Wang J., Haining R., Cao Z. Sample surveying to estimate the mean of a heterogeneous surface: reducing the error variance through zoning. Int J Geogr Inf Sci. 2010;24:523–543. doi: 10.1080/13658810902873512. [DOI] [Google Scholar]
- Wang J.-F., Li X.-H., Christakos G., Liao Y.-L., Zhang T., Gu X., et al. Geographical detectors‐based health risk assessment and its application in the neural tube defects study of the Heshun Region, China. Int J Geogr Inf Sci. 2010;24:107–127. doi: 10.1080/13658810802443457. [DOI] [Google Scholar]
- Wang J.-F., Zhang T.-L., Fu B.-J. A measure of spatial stratified heterogeneity. Ecol Indic. 2016;67:250–256. doi: 10.1016/j.ecolind.2016.02.052. [DOI] [Google Scholar]
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong Y., Wang Y., Chen F., Zhu M. Spatial statistics and influencing factors of the COVID-19 epidemic at both prefecture and county levels in Hubei Province, China. Int J Environ Res Public Health. 2020;17:3903. doi: 10.3390/ijerph17113903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu L., Liu Q., Stige L.C., Ben Ari T., Fang X., Chan K.-S., et al. Nonlinear effect of climate on plague during the third pandemic in China. Proc Natl Acad Sci. 2011;108:10214–10219. doi: 10.1073/pnas.1019486108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin Q., Wang J., Ren Z., Li J., Guo Y. Mapping the increased minimum mortality temperatures in the context of global climate change. Nat Commun. 2019;10:1–8. doi: 10.1038/s41467-019-12663-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S., Diao M., Yu W., Pei L., Lin Z., Chen D. Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: a data-driven analysis. Int J Infect Dis. 2020;93:201–204. doi: 10.1016/j.ijid.2020.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S., Lin Q., Ran J., Musa S.S., Yang G., Wang W., et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak. Int J Infect Dis. 2020;92:214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S., Musa S.S., Lin Q., Ran J., Yang G., Wang W., et al. Estimating the unreported number of novel coronavirus (2019-nCoV) cases in China in the first half of January 2020: a data-driven modelling analysis of the early outbreak. J Clin Med. 2020;9:388. doi: 10.3390/jcm9020388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu N., Zhang D., Wang W., Li X., Yang B., Song J., et al. A novel coronavirus from patients with pneumonia in China, 2019. N Engl J Med. 2020;382:727–733. doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The LBS-requesting mobile device data were provided by Wayz Inc., Shanghai, China, and are not available for distribution due to the constraint in the consent. The dataset of the COVID-19 cases is available from multiple public sources. The MATLAB codes that support the proposed SEIR model computing in this study are available from the corresponding authors on reasonable request.