Abstract
The novel corona-virus disease (COVID-19) pandemic has caused a major outbreak in more than 200 countries around the world, leading to a severe impact on the health and life of many people globally. By October 2020, more than 44 million people were infected, and more than 1,000,000 deaths were reported. Computed Tomography (CT) images can be used as an alternative to the time-consuming RT-PCR test, to detect COVID-19. In this work we propose a segmentation framework to detect chest regions in CT images, which are infected by COVID-19. An architecture similar to a Unet model was employed to detect ground glass regions on a voxel level. As the infected regions tend to form connected components (rather than randomly distributed voxels), a suitable regularization term based on 2D-anisotropic total-variation was developed and added to the loss function. The proposed model is therefore called ”TV-Unet”. Experimental results obtained on a relatively large-scale CT segmentation dataset of around 900 images, incorporating this new regularization term leads to a 2% gain on overall segmentation performance compared to the Unet trained from scratch. Our experimental analysis, ranging from visual evaluation of the predicted segmentation results to quantitative assessment of segmentation performance (precision, recall, Dice score, and mIoU) demonstrated great ability to identify COVID-19 associated regions of the lungs, achieving a mIoU rate of over 99%, and a Dice score of around 86%.
Keywords: Deep learning, Computed tomography, COVID-19, Image segmentation, Convolutional encoder decoder, Total variation
1. Introduction
Since December 2019, a novel corona-virus (SARS-CoV-2) has spread from Wuhan to the whole China, and then to many other countries. At the end of January 2020, the World Health Organization (WHO) declared COVID-19 a Public Health Emergency of International Concern [1]. By October 2020, more than 44 million confirmed cases, and more than 1,000,000 deaths were reportedd across the world [2]. While infection rates are decreasing in some countries, numbers of new infections continue quickly growing in many other countries, signaling the continuing and global threat of COVID-19 [3], [4], [5].
Up to this point, no effective treatment has yet been proven for COVID-19. Therefore for prompt prevention of COVID-19 spread, accurate and rapid testing is extremely pivotal. The reverse transcription polymerase chain reaction (RT-PCR) has been considered the gold standard in diagnosing COVID-19. However, the shortage of available tests and testing equipment in many areas of the world limits rapid and accurate screening of suspected subjects. Even under best circumstances, obtaining RT-PCR test results takes more than 6 hours and the routinely achieved sensitivity of RT-PCR is insufficient [6]. On the other hand, the radiological imaging techniques like chest X-rays and computed tomography (CT) followed by automated image analysis [7] may successfully complement RT-PCR testing. CT screening provides three-dimensional view of the lung and is therefore more sensitive (although less widely available) compared to chest X-ray radiography.
In a systematic review [8] the authors indicated that CT images are sensitive in detection of COVID-19 before observation of some clinical symptoms. Typical signs of COVID-19 in CT images consist of unilateral, multifocal and peripherally based ground glass opacities (GGO), interlobular septal thickening, thickening of the adjacent pleura, presence of pulmonary nodules, round cystic changes, bronchiectasis, pleural effusion, and lymphadenopathy [9], [10]. Accurate and rapid detection and localization of these pathological tissue changes is critical for early diagnosis and reliable severity assessment of COVID-19 infection. As the number of affected patients is high, manual annotation by well-trained expert radiologists is time consuming, subject to inter- and intra-observer variability, and slows down the CT analysis. The urgent need for automatic segmentation of typical COVID-19 CT signatures is widely appreciated and deep learning methods can offer a unique solution for identifying COVID-19 signs of infection in clinical-quality images frequently suffering from variations in CT acquisition parameters and protocols [11].
In this work, we present a deep learning based framework for automatic segmentation of pathologic COVID-19-associated tissue areas from clinical CT images available from publicly available COVID-19 segmentation datasets. Our solution is based on adapting and enhancing a popular deep learning medical image segmentation architecture Unet for COVID-19 segmentation task. As COVID-19 tissue regions tend to form connected regions identifiable in individual CT slices, a “connectivity promoting regularization” term was added to the specifically designed training loss function to encourage the model to prefer sufficiently large connected segmentation regions of desirable properties.
The main contributions of our work can be summarized as follows:
-
•
Development of a novel connectivity-promoting regularization loss function for an image segmentation framework detecting pathologic COVID-19 regions in pulmonary CT images,
-
•
Quantitative validation showing improved performance attributable to our new TV-Unet approach compared to published state-of-the-art segmentation approaches
-
•
Public sharing the developed software code facilitating research and medical community use(https://github.com/narges-sa/COVID-CT-Segmentation)
This paper is therefore a novel contribution in the rapidly advancing effort to develop techniques and approaches for reliable detection and quantification of COVID-19 disease in human lungs affected by the disease. Our work brings additional advances attributable to the new TV-Unet approach and demonstrates the performance improvement of our approach compared to recently reported approaches.
2. Related works
COVID-19 segmentation from CT images has recently received focused attention of the medical imaging community. There has been a huge progress in the performance of image segmentation models using various deep learning frameworks in recent years [12], [13], [14], [15], [16], [17]. In [18], Fan et al. proposed Inf-Net, to identify infected regions from chest CT slices. In their proposed model, a parallel partial decoder is used to aggregate high-level features and generate a global map. Then, the implicit reverse attention and explicit edge-attention are utilized to model the boundaries and enhance the representations. Unfortunately, this model used a very small dataset of CT-labeled images for segmentation, which consisted of only 100 CT slices, making it hard to generalize and compare their result. In order to have a fair comparison, results from TV-Unet and other methods which were implemented in the Inf-Net, namely Semi-Inf-Net, and Semi-Inf-Net+FCN8s [18], Unet++ [19], DeepLab-v3 [20], and FCN8s [21] are provided in the Discussion. In [22], Elharrouss et al. proposed an encoder-decoder based model for lung infection segmentation using CT-scan images. The proposed model initially considers the image structure and texture to extract the ROI of infected area, and then uses the ROI along with the image structure to predict the infected regions. Elharrouss et al. also trained this model on a small dataset of CT images, and achieved reasonable performance. In [23], Ma et al. prepared a new benchmark of 3D CT data with 20 cases that contained 1800+ annotated slices and provided several pre-trained baseline models that facilitated for out-of-the-box 3D segmentation. In [24], a novel COVID-19 diagnosis system was reported, utilizing a joint approach to deep image classification and segmentation (JCS). In their work, a large-scale COVID-19 dataset is used for classification and segmentation purposes (COVID-CS dataset) which contains 144,167 chest CT images of 400 COVID-19 subjects and 350 uninfected cases. They reached Dice score of 78.5% on the segmentation test set.
3. The proposed framework
Despite a large number of patients suffering from COVID-19, despite a growing number of COVID-19 volumetric CT scans, the availability of labeled CT images that can be used for training of deep learning methods is still limited. Therefore, our strategy relies heavily on the use of transfer learning, initiating the training from a model previously developed for medical image segmentation (segmentation of neuronal structures in electron microscopic stacks), and adapt it toward this task. To better suit the segmentation task at hand, we employed an architecture similar to the Unet, one of the most successful deep learning medical image segmentation approaches, and modified its loss function to prefer COVID-19 specific foreground mask connectivity.
3.1. Unet architecture
Unet is one of the popular segmentation models which is based on encoder-decoder neural architecture and use of skip connections, and was originally proposed by Ronneberger et al. [17]. The network architecture of Unet is illustrated in Fig. 1 . In the encoder part, model gets an image as input and applies multiple layers of convolution, max-pooling and ReLU activation, and compresses the data into a latent space. In the decoder part, the network attempts to decode the information from the latent space using transposed convolution operation (deconvolution) and produce the segmentation mask of the image. The rest of the operations are similar to the aforementioned ones in the encoder part. One difference between Unet and plain encoder-decoder model is the use of skip-connections to send the information from the corresponding high-resolution layers of the encoder to the decoder, which can help the network to better capture small details that are present in high-resolution. Fig. 1 illustrates the general architecture of a Unet model.
Fig. 1.
The architecture of Unet model
Similar to other neural segmentation models, Unet uses the loss function in Eq. (1) during training.
| (1) |
Where : {1, ..., K} considering that and K denotes the total number of classes. When using the binary cross-entropy, K=2. Moreover, the soft-max is defined as = where represents the activation in feature channel K [17].
Additionally, in a network that contains many convolutional layers, the initial weights greatly affect the performance. In this regard, approximately unit-variances of the initial weights of network feature maps performed best. In the network with convolutional and ReLU layers such as Unet, using a Gaussian distribution with a standard deviation of is an effective solution. In this method, N represents the number of incoming nodes of one neuron [25].
3.2. Connectivity regularization
The segmentation maps usually consist of a number of connected components, and single-pixel regions are rare. To encourage our segmentation model to generate segmentation maps with connected components of desirable sizes, we found that incorporating an explicit regularization term in the training loss function can greatly improve connectivity requirements for the predicted segmentation regions. It is worth noting that Unet trained from scratch can also implicitly learn such behavior from training data to some extent, assuming sufficient data sizes are available, which is not quite the case in our situation. Several strategies were developed and considered to impose desired connectivity requirements within images such as adding group-sparsity or incorporate total variation terms [26], [27], [28]. Based on achieved experience, we decided to use total variation (TV) as its gradient update is computationally attractive during the backward pass stage.
TV penalizes the generated images with large variations among neighboring pixels, leading to more connected and smoother solutions [27]. Total variation of a differentiable function defined on an interval has the following expression if is Riemann-integrable:
| (2) |
Total variation of 1D discrete signals () is straightforward, and can be defined as:
| (3) |
where is a matrix as below:
For 2D signals (), we can use isotropic or anisotropic versions of 2D total variation [26]. To simplify our optimization problem, we have used the anisotropic version of TV, which is defined as the sum of horizontal and vertical gradients at each pixel:
| (4) |
In our case we can add the total variation of the predicted binary mask for COVID-19 pixels to the loss function. Adding this 2D-TV regularization term to our framework will promote the connectivity of the produced segmentation regions. The new loss function for our model would then be defined as:
| (5) |
where is the binary cross-entropy loss, M(x) is a COVID-19 probability mask generated in the last layer of the network, and is a constant that needs to be tuned. In this paper, based on the model performance on the validation and test set, was set as 1/(255*number of pixels) to provide the model with balance weights.
4. COVID CT segmentation dataset
We have combined all available data from the COVID-19 CT segmentation dataset [29], consisting of 929 CT slices from 49 patients. Out of these, 473 CT-image slices are labeled as including COVID-19 pathologies with Ground-Glass pathology regions identified by expert tracing. The remaining 456 CT image slices are labeled as COVID-19 pathology-free. CT-slice sizes were either 512512 or 630630. While a small subset of the 929 CT images also have regions of additional pathologies identified and labeled as Consolidation and/or Pleural Effusion, these pathologies were not consistently available for all the data. After consulting with a board-certified radiologist (GS) who confirmed that Ground-Glass pathology is most relevant for detecting COVID-19, this work focuses on the Ground Glass mask, and does not consider the Consolidation and Pleural Effusion masks due to their small numbers and lack of consistency across the dataset.
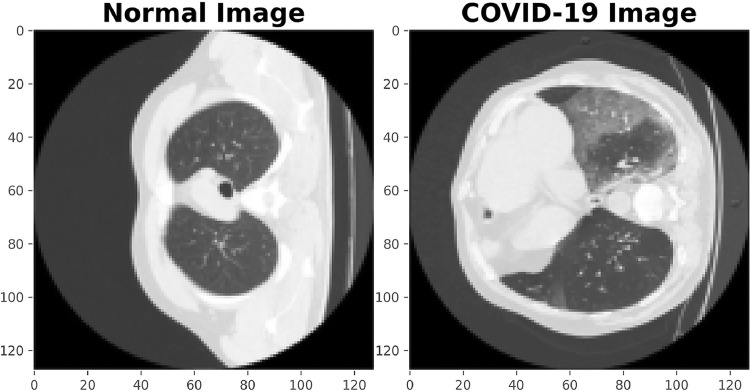
Some sample images from the used dataset are shown in Figs. 2 and 3 . Fig. 2 demonstrates the difference between normal and COVID-19 images. The images in Fig. 3 denote the original images, and their corresponding COVID-19 Ground-Glass masks. The red boundary contours in the second row are drawn to better show the parts containing COVID-19, and are not a part of the original image.
Fig. 2.
The difference between normal and COVID-19 images.
Fig. 3.
Sample images from the COVID-19 CT segmentation dataset. The first row shows two COVID-19 images. The red boundary contours in the second row denote regions of COVID-19 Ground-Glass pathology and are not a part of the original image data.The third row shows Ground-Glass masks.
4.1. Training, validation, and testing sets
To evaluate the effect of radically different training/testing set composition and to demonstrate the robustness of the obtained results, two different splits of training, validation, and testing sets are selected from this dataset (Table 1 ).
Table 1.
Training/Validation/Testing splits prior to data augmentation.
| Data | Number of Images in Split 1 |
Number of Images in Split 2 |
|---|---|---|
| Training | 654 | 590 |
| Validation | 75 | 64 |
| Test | 200 | 275 |
| Total | 929 | 929 |
In Split 1, data from a relatively large number of 46 training/validation-set patients and a small number of only 3 testing-set patients were used. 729 CT image slices formed the training and validation sets, and 200 images the testing set. In Split 2, a more balanced distribution of patient numbers was used with 654 CT image slices from 35 patients included in the training and validation sets, and 275 images from 14 patients formed the testing set.
5. Experimental results
In this section we provide a detailed experimental analysis of the proposed segmentation framework, by presenting both qualitative and quantitative results as well as comparing our results with a baseline approach.
5.1. Evaluation metrics
There are several metrics that are used by the research community to measure the performance of segmentation models, including precision, recall, Dice coefficient and mean Intersection over Union (mIoU). These metrics are also widely used in medical domain, and are defined as below.
Precision is calculated as the ratio of pixels correctly predicted as COVID divided by total pixels predicted as COVID-19
| (6) |
where TP refers to the true positive (the number of correctly labeled COVID-19 pixels) and FP refers to the false positive (the number of incorrectly labeled COVID-19 pixels).
Recall is the ratio of pixels correctly labeled as COVID-19 divided by total number of actual COVID-19 pixels and is defined as:
| (7) |
where TP is the number of false positives, and FN refers to the false negatives and is the number of pixels mistakenly labeled as non-COVID.
Precision-Recall (PR) curve is a popular way to holistically look at the model performance as a plot of the precision (y-axis) versus the recall (x-axis) rates for different thresholds.
Dice coefficient (also known as Dice score or DSC) is another popular metric especially for the multi-class image segmentation:
| (8) |
where A and B denote the predicted and ground-truth masks.
Intersection over union (also known as the Jaccard index) is used to evaluate the similarity between ground truth and predicted segmentation masks. It is defined as the size of the intersection divided by the size of the union of the target mask and predicted segmentation map
| (9) |
where A and B are the predicted and ground-truth masks. Mean-IoU is the average IoU value over all classes. If A and B are both empty, IoU(A,B) is defined as 1. IoU ranges between 0 and 1.
It is worth mentioning that Dice coefficient and IoU are positively correlated.
5.2. Model hyper-parameters
Model hyper-parameters govern the machine learning processes and as such are crucial for achieving good performance, especially in the case of deep neural networks. Hyper-parameter tuning can be done in two different ways, automatically and manually. In this work, we manually evaluated different combinations of hyper-parameters and selected the best combination. To simplify the tuning process, we fixed the number of epochs to 100, and the batch-size to 32. We designed and compared different loss functions (such as binary cross-entropy (BCE) [30], Dice coefficient loss [31], and BCE plus total variation regularization), different optimizers (such as ADAM [32], Adagrad [33], Adadelta [34] and stochastic gradient descent (SGD)[35]), and different learning rates On First Split. We used adaptive learning rate scheduling and early stopping [36] criteria as below, which achieved good performance on the validation set:
-
•
Learning rate is decayed whenever the validation loss does not improve for 5 continuous epochs.
-
•
Early stopping is applied whenever the validation loss does not improve for 10 continues epochs.
Table 2 shows the impact of the loss function design on First Split on the model performance with binary cross-entropy and the proposed connectivity regularized loss function achieving the best performance.
Table 2.
Overall performance with different Loss Functions employed, the best cut-off threshold of 0.3 used. Best performance shown in bold font.
| Loss | Optimizer | Learning Rate | mIOU | DSC | Average Precision |
|---|---|---|---|---|---|
| BCE | ADAM | 0.001 | 0.993 | 0.839 | 0.92 |
| DSC | 0.990 | 0.764 | 0.90 | ||
| BCE+DSC | 0.993 | 0.843 | 0.91 | ||
| BCE+DSC+TV | 0.988 | 0.645 | 0.91 | ||
| BCE+TV | 0.995 | 0.864 | 0.94 |
The impact of the optimizer on the model performance is shown in Table 3 . As we can see, ADAM achieves the highest performance in terms of all metrics.
Table 3.
Overall performance for different Optimizer selection, using the best cut-off threshold of 0.3. Best performance shown in bold font.
| Loss | Optimizer | Learning Rate | mIOU | DSC | Average Precision |
|---|---|---|---|---|---|
| BCE+TV | ADAM | 0.001 | 0.995 | 0.864 | 0.94 |
| SGD | 0.985 | 0.573 | 0.8 | ||
| Adadelta | 0.991 | 0.780 | 0.9 | ||
| Adagrad | 0.992 | 0.784 | 0.9 |
Table 4 provides the analysis of model performance for two different learning rate values when using (the best performing) ADAM optimization.
Table 4.
Overall model performance for different Learning Rates, again for the best cut-off threshold of 0.3. Best performance shown in bold font.
| Loss | Optimizer | Learning Rate | mIOU | DSC | Average Precision |
|---|---|---|---|---|---|
| BCE+TV | ADAM | 0.001 | 0.995 | 0.864 | 0.94 |
| 0.0001 | 0.993 | 0.838 | 0.92 |
Table 5 demonstrates the impact of varying the value of on the final result when using (the best performing) ADAM optimization with the learning rate of 0.001.
Table 5.
Overall model performance for different using the best cut-off threshold of 0.3. Best performance shown in bold font.
| Loss | lamda | mIOU | DSC | Average Precision |
|---|---|---|---|---|
| BCE+TV | 1 | 0.991 | 0.770 | 0.86 |
| 1/number of pixels | 0.992 | 0.824 | 0.90 | |
| 1/(256*number of pixels) | 0.995 | 0.864 | 0.94 |
Note that the model predicts a probability for each pixel, showing its likelihood of belonging to the pathologic COVID-19 region (zero denotes Non-COVID pixels and one denotes COVID-19 pathology). These probabilities are thresholded, different thresholds yield certain sensitivity/specificity rates. Threshold value of 0.3 achieved the best performance on the validation set and was therefore used to report the results of the proposed model. The impact of modifying the threshold values on the model accuracy is given in Section 5.4.
5.3. Predicted masks
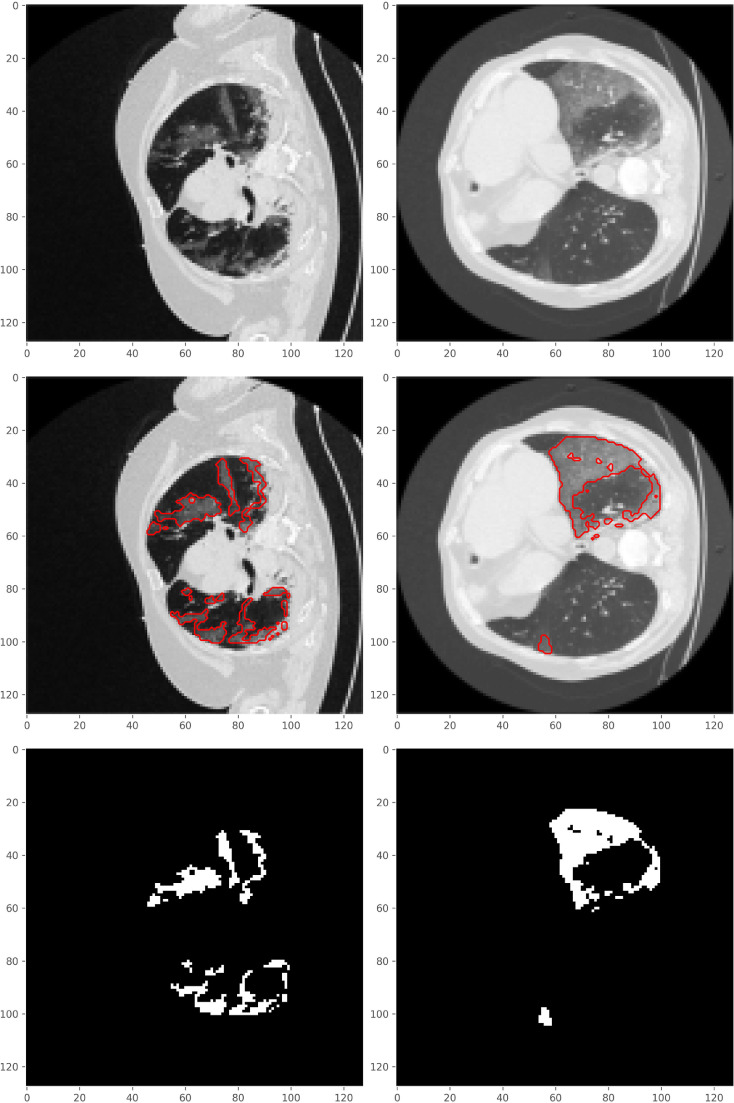
Qualitative result showing how close our predicted masks are to the ground-truth masks are given in Fig. 4 for 5 sample images from the test set. As can be seen when the desired region is very tiny, the Unet trained from scratch cannot distinguish the segmentation region and background very well, while the proposed TV-Unet model performs notably better. If, however, the GT-mask consists of only a few isolated points (e.g., the second row in Fig. 4), our model sometimes fails detecting such points. Clearly, such isolated points do not provide a strong-enough supporting information for local detection of COVID-19 infection.
Fig. 4.
Predicted segmentation masks by Unet trained from scratch and the proposed TV-Unet for a typical sample images from the testing set.
5.4. Cut-off threshold impact on model performance
As discussed previously, our model predicts a probability score for each pixel, showing the likelihood of its being in a COVID-19 pathology region. Different cut-off thresholds can be used on those probabilities to decide COVID-19 labeling. By increasing the cut-off threshold, less and less pixels would be labeled as COVID-19 pathology. Tables 6 and 7 show the model performance (in terms of precision, recall, and mIoU) for eight different values of cut-off thresholds for the Split-1 and Split-2 datasets. The cut-off threshold of 0.3 results in the highest Dice score, and mIoU metric, and therefore was employed to compare our model with other baseline models.
Table 6.
Precision, recall, Dice score, and mIoU rates of TV-Unet model for different threshold values for Split 1. Confidence intervals provided for recall metric. Best performance shown in bold font.
| Threshold | Recall | Precision | mIoU | DSC |
|---|---|---|---|---|
| 0.1 | 0.955 0.028 | 0.736 | 0.992 | 0.831 |
| 0.2 | 0.913 0.039 | 0. 811 | 0.994 | 0.859 |
| 0.3 | 0.867 0.047 | 0. 859 | 0.994 | 0.863 |
| 0.4 | 0.813 0.054 | 0. 900 | 0.994 | 0.854 |
| 0.5 | 0.746 0.060 | 0. 933 | 0.993 | 0.829 |
| 0.6 | 0.662 0.065 | 0. 959 | 0.992 | 0.783 |
| 0.7 | 0.547 0.089 | 0. 978 | 0.990 | 0.702 |
| 0.8 | 0.362 0.066 | 0. 990 | 0.986 | 0.531 |
Table 7.
Precision, recall, Dice score, and mIoU rates of TV-Unet model for different threshold values for Split 2. Best performance shown in bold font.
| Threshold | Recall | Precision | mIoU | DSC |
|---|---|---|---|---|
| 0.1 | 0.892 | 0.626 | 0.987 | 0.7363 |
| 0.2 | 0.833 | 0.700 | 0.989 | 0.7609 |
| 0.3 | 0.781 | 0.750 | 0.990 | 0.7643 |
| 0.4 | 0.730 | 0.789 | 0.990 | 0.7582 |
| 0.5 | 0.674 | 0.825 | 0.990 | 0.7413 |
| 0.6 | 0.610 | 0.859 | 0.990 | 0.7139 |
| 0.7 | 0.535 | 0.890 | 0.989 | 0.6692 |
| 0.8 | 0.422 | 0.926 | 0.987 | 0.5801 |
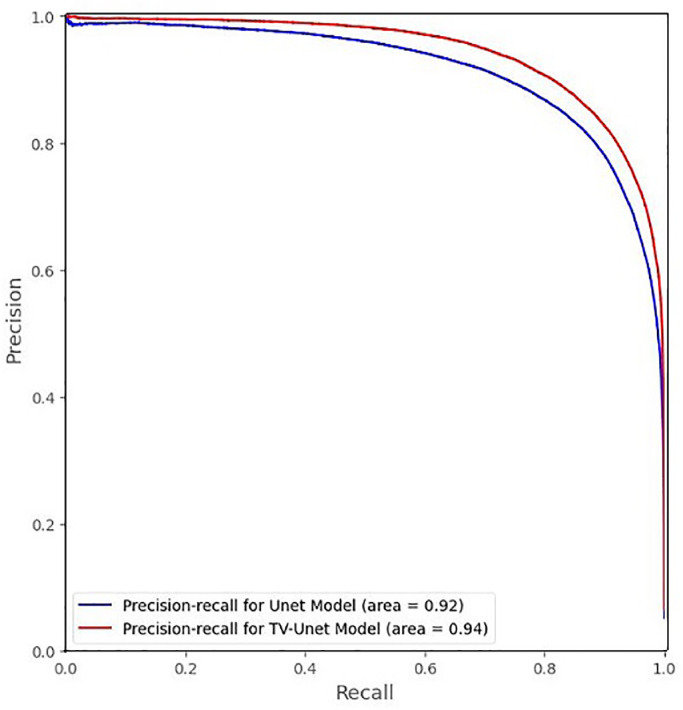
To see the holistic view of the proposed model performance on all possible threshold values, Figs. 5 and 6 provide the precision-recall curves on the test sets in Split 1 and Split 2, respectively. Fig. 5 shows average precision of 0.92 for the Unet trained from scratch and 0.94 for our TV-Unet for Split 1 dataset (an improvement of around 0.02 in terms of average-precision). Fig. 6 shows average precision of 0.67 for the Unet trained from scratch and 0.88 for our TV-Unet for Split 2, a relative improvement of 31%.
Fig. 5.
Precision-Recall curve for Split-1.
Fig. 6.
Precision-Recall curve for Split-2.
5.5. Model performance comparison with Unet trained from scratch
For a fair comparison between the proposed TV-Unet model and the Unet trained from scratch, corresponding cut-off thresholds were identified for similar recall rates for each model and compared in terms of other performance metrics. Tables 8 and 9 provide the comparison between these two models for four different recall rates. Consistency, with which our TV-Unet model outperforms that of the Unet trained from scratch when considering all metrics, shows the added value of the connectivity-promoting regularization. We have an average improvement of around 2% in terms of Dice score in Split 1 and 10.9% in Split 2 studies.
Table 8.
Comparison of Unet trained from scratch and the proposed TV-Unet model performance in terms of precision, mIOU and DSC for Split 1. Best performance for each method shown in bold font.
| Model | Recall | Precision | mIOU | DSC |
|---|---|---|---|---|
| Unet | 0.975 | 0.575 | 0.985 | 0.727 |
| 0.945 | 0.688 | 0.990 | 0.798 | |
| 0.91 | 0.765 | 0.992 | 0.832 | |
| 0.85 | 0.834 | 0.993 | 0.841 | |
| TV-Unet | 0.975 | 0.675 | 0.990 | 0.798 |
| 0.945 | 0.760 | 0.993 | 0.842 | |
| 0.91 | 0.812 | 0. 994 | 0.860 | |
| 0.85 | 0.871 | 0.995 | 0.864 |
Table 9.
Comparison of the Unet trained from scratch and TV-Unet model performance in terms of precision, mIOU and DSC for Split 2. Best performance for each method shown in bold font.
| Model | Recall | Precision | mIOU | DSC |
| Unet | 0.810 | 0.594 | 0.983 | 0.655 |
| 0.643 | 0.621 | 0.985 | 0.633 | |
| 0.535 | 0.655 | 0.985 | 0.595 | |
| 0.422 | 0.693 | 0.984 | 0.527 | |
| TV-Unet | 0.810 | 0.727 | 0.990 | 0.764 |
| 0.643 | 0.842 | 0.990 | 0.729 | |
| 0.535 | 0.890 | 0.989 | 0.670 | |
| 0.422 | 0.926 | 0.987 | 0.580 | |
5.6. Training convergence analysis
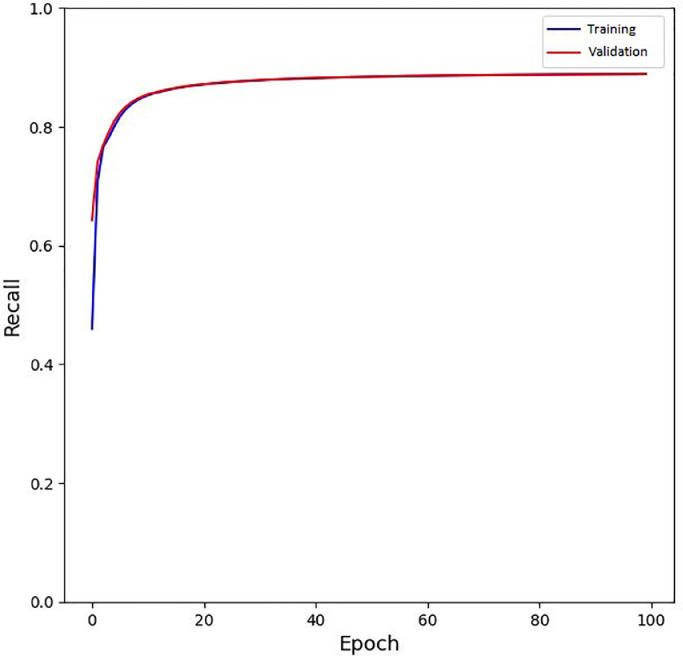
To see the model convergence during training, we provide the loss function, recall, and precision rates of the model on different epochs, in Fig. 7, Fig. 8, Fig. 9 . It is worth to mention that for precision and recall, the default threshold value of 0.3 is used in these figures.
Fig. 7.
The training and validation loss of the model during training.
Fig. 8.
The training and validation recall of the model during training.
Fig. 9.
The training and validation precision of the model during training.
6. Discussion
The general lack of available pulmonary CT datasets and especially a lack of expert-annotated CT data can be seen in so-far available publications for COVID-19 pathology detection in CT images. This lack of data also forces researchers to develop 2D CT-slice-based methods rather than volumetric 3D data analyses. The entire medical imaging community is anxiously awaiting the arrival of large annotated 3D CT datasets the analysis of which will however greatly benefit from the experience gained on current 2D CT data.
One of important accomplishments to date is a number of new approaches and publicly available albeit small COVID-19 CT datasets that can be used for method comparisons. One such dataset with semi-supervised COVID-19 segmentations (COVID-SemiSeg) was recently reported in [37]. The COVID-SemiSeg dataset consists of two sets. The first one contains 1600 pseudo labels generated by Semi-Inf-Net model and 50 labels by expert physicians. The second set includes 50 multi-class labels. Overall, there are 48 images that can be used for performance-comparison assessment and these CT data were used to compare our TV-Unet approach with other methods.
Our TV-Unet model reported above was therefore compared with the Inf-Net [18] and with other promising image segmentation models trained on COVID-SemiSeg dataset, including Unet++, Semi-Inf-Net, DeepLab-v3, FCN8s, and Semi-Inf-Net+FCN8s.
Consistently using the SemiSeg dataset, Table 10, Table 11, Table 12 provide performance comparisons of individual methods in terms of recall and Dice coefficient. As can be seen from these tables, the proposed TV-Unet model outperformed all other models in all three tested experiments, which focused on a) identifying COVID-19-specific pathologic regions, Ground-Glass regions, and COVID-19 Consolidation regions.
Table 10.
Comparison of the TV-Unet model performance with other recent methods in terms of Sensitivity, Specificity and DSC for pathologic regions on COVID-SemiSeg dataset. Best performance is shown in bold font.
| Model | Sensitivity | Specificity | Dice Score |
|---|---|---|---|
| Unet+ | 0.672 | 0.902 | 0.518 |
| Inf-Net | 0.692 | 0.943 | 0.682 |
| Semi-Inf-Net | 0.725 | 0.960 | 0.739 |
| TV-Unet | 0.808 | 0.960 | 0.801 |
Table 11.
Comparison of the TV-Unet model performance with other methods in terms of Sensitivity, Specificity and DSC for the Ground-Glass mask on COVID-SemiSeg dataset. Best performance shown in bold font.
| Model | Sensitivity | Specificity | Dice Score |
|---|---|---|---|
| DeepLab-v3+ (stride=8) | 0.478 | 0.863 | 0.375 |
| DeepLab-v3+ (stride=16) | 0.713 | 0.823 | 0.443 |
| FCN8s | 0.537 | 0.905 | 0.471 |
| Semi-Inf-Net+FCN8s | 0.720 | 0.941 | 0.646 |
| TV-Unet | 0.762 | 0.979 | 0.655 |
Table 12.
Comparison of the TV-Unet model performance with several other methods in terms of Sensitivity, Specificity and DSC for the Consolidation mask on COVID-SemiSeg dataset. Best performance shown in bold font.
| Model | Sensitivity | Specificity | Dice Score |
|---|---|---|---|
| DeepLab-v3+ (stride=8) | 0.120 | 0.584 | 0.117 |
| DeepLab-v3+ (stride=16) | 0.245 | 0.560 | 0.188 |
| FCN8s | 0.212 | 0.567 | 0.221 |
| Semi-Inf-Net+FCN8s | 0.186 | 0.639 | 0.238 |
| TV-Unet | 0.558 | 0.988 | 0.537 |
7. Conclusion
A novel deep learning framework for COVID-19 segmentation from CT images was reported. We used the popular Unet architecture as the main framework, and improved its performance by an added connectivity promoting regularization term to encourage the model to generate larger contiguous connected segmentation maps. We showed that our trained model achieved a high accuracy rate for detecting of pathologic COVID-19 regions. We report the model performance under various hyper-parameter settings, which can be helpful for future research by the community to know the impact of different parameters on the final results. Last but not least, we demonstrated that our TV-Unet approach outperformed other reported methods. We will further extend this work to semi-supervised setting, in which a combination of labeled and unlabeled data will be used for training the model. Such an approach will undoubtedly be extremely useful as collecting accurate segmentation labels for COVID-19 remains very challenging.
Acknowledgment
The authors would like to thank radiologist, Dr. Ghazaleh Soufi, for her advice on the important signals in chest CT images for detecting COVID-19. We would also like to thank the providers of the publicly available pulmonary CT datasets. M. Sonka’s research effort supported, in part, by NIH grant R01-EB004640.
References
- 1.W. H. O., Coronavirus disease (COVID-19) pandemic, 2020, http://www.who.int/emergencies/diseases/novel-coronavirus-2019.
- 2.https://www.worldometers.info/coronavirus/.
- 3.Paules C.I., Marston H.D., Anthony S.F. Coronavirus infections more than just the common cold. Jama. 2020;323.8:707–708. doi: 10.1001/jama.2020.0757. [DOI] [PubMed] [Google Scholar]
- 4.Remuzzi A., Giuseppe R. COVID-19 and Italy: what next? The lancet. 2020;395.10231:1225–1228. doi: 10.1016/S0140-6736(20)30627-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kafieh, Rahele, Arian R., Saeedizadeh N., Minaee S., Yadav S.K., Vaezi A., Rezaei N., Haghjooy S., Javanmard COVID-19 in Iran: a deeper look into the future. medRxiv. 2020 [Google Scholar]
- 6.Y. Fang, H. Zhang, J. Xie, M. Lin, L. Ying, P. Pang, W. Ji, Sensitivity of chest CT for COVID-19: comparison to RT-PCR, Radiology 0(0) (????) 200432. 32073353. [Online].Available: 10.1148/radiol.2020200432. [DOI] [PMC free article] [PubMed]
- 7.Minaee, Shervin, Kafieh R., Sonka M., Yazdani S., Soufi G.J. Deep-COVID: predicting COVID-19 from chest x-ray images using deep transfer learning. Med. Image Anal. 2020 doi: 10.1016/j.media.2020.101794. [DOI] [PMC free article] [PubMed] [Google Scholar]; Pre-pub ahead of print
- 8.Salehi S., Abedi A., Balakrishnan S., Gholamrezanezhad A. Coronavirus disease 2019 (COVID-19): a systematic review of imaging findings in 919 patients. Am. J. Roentgenol. 2020:1–7. doi: 10.2214/AJR.20.23034. [DOI] [PubMed] [Google Scholar]
- 9.Ding X., Xu J., Zhou J., Long Q. Chest CT findings of COVID-19 pneumonia by duration of symptoms. Eur. J. Radiol. 2020;127 doi: 10.1016/j.ejrad.2020.109009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Meng H., et al. CT imaging and clinical course of asymptomatic cases with COVID-19 pneumonia at admission in Wuhan, China. J. Infect. 2020 doi: 10.1016/j.jinf.2020.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.F. Shan, Y. Gao, J. Wang, W. Shi, N. Shi, M. Han, Z. Xue, D. Shen, Y. Shi, Lung infection quantification of COVID-19 in CT images with deep learning, 2020, ArXiv preprint arXiv:2003.04655.
- 12.Badrinarayanan, Vijay, Kendall A., Cipolla R. SegNet: a deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017;39.12:2481–2495. doi: 10.1109/TPAMI.2016.2644615. [DOI] [PubMed] [Google Scholar]
- 13.Chen, Liang-Chieh, Zhu Y., Papandreou G., Schroff F., Adam H. Proceedings of the European Conference on Computer Vision (ECCV) 2018. Encoder-decoder with atrous separable convolution for semantic image segmentation; pp. 801–818. [Google Scholar]
- 14.Huang, Zilong, Wang X., Huang L., Huang C., Wei Y., Liu W. Proceedings of the IEEE International Conference on Computer Vision. 2019. Ccnet: criss-cross attention for semantic segmentation; pp. 603–612. [Google Scholar]
- 15.Minaee, Shervin, Boykov Y., Porikli F., Plaza A., Kehtarnavaz N., Terzopoulos D. Image segmentation using deep learning: A survey. arXiv preprint arXiv:2001.05566. 2020 doi: 10.1109/TPAMI.2021.3059968. [DOI] [PubMed] [Google Scholar]
- 16.Minaee, Shervin, Abdolrashidi A., Su H., Bennamoun M., Zhang D. Biometric recognition using deep learning: A survey. arXiv preprint arXiv:1912.00271. 2019 [Google Scholar]
- 17.Ronneberger, Olaf, Fischer P., Brox T. International Conference on Medical image computing and computer-assisted intervention. Springer, Cham; 2015. U-net: Convolutional networks for biomedical image segmentation. [Google Scholar]
- 18.Fan, Deng-Ping, Zhou T., Ji G.-P., Zhou Y., Chen G., Fu H., Shen J., Shao L. Inf-net: Automatic COVID-19 lung infection segmentation from CT images. IEEE Transactions on Medical Imaging. 2020 doi: 10.1109/TMI.2020.2996645. [DOI] [PubMed] [Google Scholar]
- 19.Zhou, Zongwei, Siddiquee M.M.R., Tajbakhsh N., Liang J. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, 3-11. Springer, Cham; 2018. Unet++: A nested u-net architecture for medical image segmentation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chen, Liang-Chieh, Zhu Y., Papandreou G., Schroff F., Adam H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European conference on computer vision (ECCV) 2018:801–818. [Google Scholar]
- 21.Long, Jonathan, Shelhamer E., Darrell T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition. 2015:3431–3440. [Google Scholar]
- 22.Elharrouss, Omar, Subramanian N., Al-Maadeed S. An encoder-decoder-based method for COVID-19 lung infection segmentation. arXiv preprint arXiv:2007.00861. 2020 doi: 10.1007/s42979-021-00874-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ma, Jun, Wang Y., An X., Ge C., Yu Z., Chen J., Zhu Q., et al. Towards efficient COVID-19 CT annotation: A benchmark for lung and infection segmentation. arXiv preprint arXiv:2004.12537. 2020 [Google Scholar]
- 24.Wu Y.-H., Gao S.-H., Mei J., Xu J., Fan D.-P., Zhang R.-G., Cheng M.-M. JCS: An explainable COVID-19 diagnosis system by joint classification and segmentation. arXiv preprint arXiv: 2004.07054. 2020 doi: 10.1109/TIP.2021.3058783. [DOI] [PubMed] [Google Scholar]
- 25.He K., Zhang X., Ren S., Sun J. Delving deep into rectifiers: Surpassing humanlevel performance on imagenet classification. arXiv:1502.01852. 2015 [Google Scholar]
- 26.Chambolle A. An algorithm for total variation minimization and applications. Journal of Mathematical imaging and vision. 2004;20.1-2:89–97. [Google Scholar]
- 27.Minaee, Shervin, Yao W. An ADMM approach to masked signal decomposition using subspace representation. IEEE Transactions on Image Processing. 2019;28.7:3192–3204. doi: 10.1109/TIP.2019.2894966. [DOI] [PubMed] [Google Scholar]
- 28.Zhang, Jian, Zhao D., Gao W. Group-based sparse representation for image restoration. IEEE Transactions on Image Processing. 2014;23.8:3336–3351. doi: 10.1109/TIP.2014.2323127. [DOI] [PubMed] [Google Scholar]
- 29.http://medicalsegmentation.com/covid19/.
- 30.Yi-de M., Qing L., Zhi-Bai Q. Automated image segmentation using improved pcnn model based on cross-entropy, in proceedings of 2004 international symposium on intelligent multimedia. Video and Speech Processing, 2004,IEEE. 2004:743–746. [Google Scholar]
- 31.Sudre C.H., Li W., Vercauteren T., Ourselin S., Cardoso M.J. Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations. In Deep learning in medical image analysis and multimodal learning for clinical decision support, Springer. 2017:240–248. doi: 10.1007/978-3-319-67558-9_28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kingma D.P., Ba J. Adam: A method for stochastic optimization (cite arxiv:1412.6980comment: Published as a conference paper at the 3rd international conference for learning representations. San Diego,2015. 2014 [Google Scholar]
- 33.Duchi J.C., Hazan E., Singer Y. Adaptive subgradient methods for online learning and stochastic optimization, J. Mach. Learn. Res. 2011;12:2121–2159. [Google Scholar]
- 34.Zeiler M.D. ADADELTA: An adaptive learning rate method, ArXiv, abs/1212.5701. 2012 [Google Scholar]
- 35.Rumelhart D.E., McClelland J.L. Learning internal representations by error propagation, in Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations, MIT Press. 1987:318–362. [Google Scholar]
- 36.Prechelt L., Müller K. Early stopping - but when, orr g. b. Neural Networks: Tricks of the Trade. Lecture Notes in Computer Science. 1998;1524 [Google Scholar]
- 37.https://github.com/DengPingFan/Inf-Net.