Impact of intervention on the spread of COVID-19 in India: A model based study

Abstract

The outbreak of coronavirus disease 2019 (COVID-19), caused by the virus severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has already created emergency situations in almost every country of the world. The disease spreads all over the world within a very short period of time after its first identification in Wuhan, China in December, 2019. In India, the outbreak, starts on $2^{\mathit{nd}}$ March, 2020 and after that the cases are increasing exponentially. Very high population density, the unavailability of specific medicines or vaccines, insufficient evidences regarding the transmission mechanism of the disease also make it more difficult to fight against the disease properly in India. Mathematical models have been used to predict the disease dynamics and also to assess the efficiency of the intervention strategies in reducing the disease burden. In this work, we propose a mathematical model to describe the disease transmission mechanism between the individuals. Our proposed model is fitted to the daily new reported cases in India during the period $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020. We estimate the basic reproduction number, effective reproduction number and epidemic doubling time from the incidence data for the above-mentioned period. We further assess the effect of implementing preventive measures in reducing the new cases. Our model projects the daily new COVID-19 cases in India during ${13}^{\mathit{th}}$ November, 2020 to ${25}^{\mathit{th}}$ February, 2021 for a range of intervention strength. We also investigate that higher intervention effort is required to control the disease outbreak within a shorter period of time in India. Moreover, our analysis reveals that the strength of the intervention should be increased over the time to eradicate the disease effectively.

1. Introduction

Coronaviruses, related to the family Coronaviridae are single-stranded, positive-sense RNA viruses (Chen et al., 2020). In the year 1960, the human coronaviruses were first classified and scientists used the term ‘corona’ due to its crown-like visibility on the surface area (Kahn and McIntosh, 2005). Three major outbreaks occurred because of coronaviruses in the years $2003,2012$ and 2015. The outbreak occurred in China in the year 2003 was named as ‘Severe Acute Respiratory Syndrome’ (SARS) outbreak. Saudi Arabia in 2012 (Killerby et al., 2020) and South Korea in 2015 (Willman et al., 2019) were affected by ‘Middle East Respiratory Syndrome’ (MERS) outbreak.

Recently, in December, 2019, a newly invaded coronavirus, first identified in Wuhan, the capital city of the Hubei province of China caused an outbreak (Cohen and Normile, 2020). This is considered as the fourth coronavirus outbreak. It has been reported that due to viral pneumonia, 27 people were infected which includes 7 critically ill cases (Tang et al., 2020), and this outbreak has grabbed substantial attentions all over the globe. The Chinese officials declared on $7^{\mathit{th}}$ January, 2020 that this infectious disease is transmitted through a biological pathogen, named novel coronavirus and on ${10}^{\mathit{th}}$ January, 2020, the World Health Organization (WHO) referred the novel coronavirus as ‘2019-nCoV’. Finally, on ${11}^{\mathit{th}}$ February, 2020, WHO declared the official name of the disease and the causing virus as coronavirus disease 2019 (COVID-19) and severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) respectively (WHO, 2020a). WHO also published preliminary guidelines for all the countries to deal with this outbreak. The guidelines are mainly based on how to provide health care support to the infected patient and build awareness among the ordinary people about this new disease (WHO, 2020b).

Plenty of research works indicate that COVID-19 possibly spread from animal to human (zoonotic) (Linton et al., 2020, Rothan and Byrareddy, 2020). Moreover, a rapid number of new occurrences of COVID-19 reveals the key fact that the secondary transmission can occur through human to human (Li et al., 2020) via direct communication or through droplets spread by coughing or sneezing from an infected person (Hui et al., 2020). This human to human transmission is considerably growing almost everywhere in the world by means of the international movement (European Centre for Disease Prevention et al., 2020) and as soon as an area of a specific country is affected then COVID-19 rapidly grows through local transmission. Person infected with SARS-CoV-2 virus shows symptoms like fever, cough, and shortness of breath, muscle ache, confusion, headache, sore throat, rhinorrhea, chest pain, haemoptysis, diarrhoea, dyspnoea and nausea and vomiting (Chen et al., 2020, Hui et al., 2020, Rothan and Byrareddy, 2020). WHO situation report (WHO, 2019a) reveals that the COVID-19 pandemic spread on the Western Pacific, European, South-east Asia, Eastern Mediterranean, America and African Region with their respective territories, causing a huge number of infected cases. At the initial phase of the pandemic, new cases were quickly increased in various countries like USA, Spain, Germany, France, Italy, UK, Iran, Switzerland, India, Netherlands, Austria, etc. (WHO, 2019a).

In India, the first confirmed case of COVID-19 was reported on ${30}^{\mathit{th}}$ January, 2020 (WHO, 2019b). Government of India declared a countrywide lock-down for 21 days as a preventive measure for the COVID-19 outbreak on ${24}^{\mathit{th}}$ March, 2020 (Pulla, 2020). Besides the lock-down, the Ministry of Health and Family Welfare (MOHFW) of India, suggested various individual hygiene measures e.g. frequent hand washing, social distancing, use of mask, avoiding touching eyes, nose, or mouth, etc. (MOHFW, 2020, Khanna and Honavar, 2020). The government also continuously using various media and social networking websites to aware the citizen. However, the factors like very high population density, the unavailability of specific medicines or vaccines, insufficient evidences regarding the transmission mechanism of the disease also make it difficult to fight against the disease properly in India.

Mathematical models have been used to predict the disease dynamics and also to assess the efficiency of the intervention strategies in reducing the disease burden. In the context of COVID-19, several studies have been done using real incidence data of the affected countries and examined different characteristics of the outbreak as well as evaluated the effect of intervention strategies implemented to curb the outbreak in the respective countries (Ferretti et al., 2020, Kucharski et al., 2020, Mandal et al., 2020, Tang et al., 2020, Wang et al., 2020, Zhao et al., 2019, Zhao et al., 2020). Several mathematical models have also been proposed to understand the transmission dynamics of COVID-19 in India. Most of these studies have considered Susceptible-Exposed-Infected-Recovered (SEIR) as the base model and extended it by incorporating various new compartments such as asymptomatic (Mahajan et al., 2020), isolated (Bajiya et al., 2020), quarantined (Khajanchi and Sarkar, 2020, Sarkar et al., 2020), protected (Gupta et al., 2021), death (Tiwari et al., 2020, Mahajan et al., 2020, Gupta et al., 2021), lock-down (Sardar et al., 2020), etc. In these studies, the proposed models are fitted to the COVID-19 cases and deaths data of India and the effect of different control measures have been examined for different control scenarios (Rafiq et al., 2020, Khajanchi and Sarkar, 2020, Sarkar et al., 2020, Bajiya et al., 2020). Among the control strategies lock-down gained special attention. A bunch of studies has analysed the impact of lock-down in reducing the peak of the epidemic (Tiwari et al., 2020), projection of cases in the presence of lock-down (Sardar et al., 2020, Gupta et al., 2021, Mahajan et al., 2020), suitable duration of effective lock-down (Ray et al., 2020). A different aspect of the transmission dynamics of COVID-19 in India i.e the temporal growth pattern of COVID-19 infection and death counts in various states of India has also been studied (Asad et al., 2020, Verma et al., 2020).

In this work, we propose a deterministic compartmental model to describe the disease transmission mechanism between the individuals. We consider the outbreak situation of India during the period from $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020 and our model is fitted to the daily new reported cases. In this study, we explore several important aspects of the disease dynamics. First, we provide realistic estimates of some key quantities like the basic reproduction number, time-varying effective reproduction number and epidemic doubling time from the incidence data with the help of proposed model for the above-mentioned period. We divide the whole outbreak period into several phases and in each phase, we estimate the strength of intervention strategy. In other words, we measure the success rate of different preventive strategies implemented in India during the COVID-19 outbreak. The effectiveness of preventive measures in reducing the disease burden is investigated and the projection of cases is provided for different levels of intervention strength. Moreover, depending on the intensity of the intervention strength, the possibility of different scenarios like the second wave of infection, eradication of disease are also explored.

The rest of the paper is organized as follows. In Section 2, we briefly describe our proposed model. Section 3 is devoted in describing the procedure of model fitting. The estimation of basic reproduction number, effective reproduction number and epidemic doubling time from actual incidence data is described in Section 4. In Section 5, the efficiency of the intervention is studied. Finally we discuss the findings obtained from our study in Section 6.

2. Description of the model

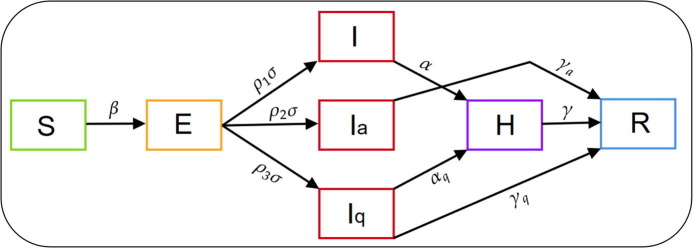
We adopt deterministic compartmental modelling approach to describe the disease transmission mechanism. Depending on the health status, the total human population is categorized into seven compartments: susceptible (S), exposed (E), symptomatic (I), asymptomatic ($I_a$), quarantined ($I_q$), hospitalized (H) and recovered (R). Susceptible population becomes exposed with the disease after experiencing close contacts with the symptomatic as well as asymptomatic individuals. We assume that the rate of disease transmission from asymptomatic individuals to susceptible individuals is less than that of from symptomatic individuals. The rate of new infection is given by $\frac{\beta S(I+\eta I_a)}{N}$, where $\beta$ denotes the transmission rate of the disease and $\eta (<1)$ is the modification parameter that accounts the reduction in the transmission rate from the asymptomatic individuals. At any instant of time, the total population is given by $N=S+E+I+I_a+I_q+H+R$. Since we consider the outbreak situation which usually persists for a shorter period of time, we do not incorporate any demographic factors (i.e birth, death, etc.) into the model. We assume that after the incubation period (${\sigma }^{-1}$), ${\rho }_1$ fraction of the exposed individuals move to symptomatic compartment, ${\rho }_2$ fraction move to the asymptomatic compartment and the remaining fraction, $({\rho }_3=1-{\rho }_1-{\rho }_2)$ move to the quarantined compartment. The individuals in the symptomatic compartment (I) show severe symptoms of the disease and after ${\alpha }^{-1}$ period of time they are hospitalized. On the other hand, the asymptomatic individuals who do not show any symptom of the disease get natural recovery at a rate ${\gamma }_a$ and move to the recovered class $(R)$. The individuals in the quarantined compartment ($I_q$) are those individuals who exhibit mild symptoms and are advised to be quarantined. From quarantined class ($I_q$), individuals move to the hospitalized class (H) at a rate ${\alpha }_q$. They can also get natural recovery and move to the recovered class (R) at a rate ${\gamma }_q$. Individuals admitted in the hospitals move to recovered class at a rate $\gamma$. We also consider that the hospitalized individuals die due to the disease at a rate $\delta$. The recovered population increases due to the recovery of asymptomatic, quarantined and hospitalized individuals at the rates ${\gamma }_a,{\gamma }_q$ and $\gamma$ respectively. We incorporate different intervention strategies in the model. The intervention strategies includes the preventive measures such as lock-down, spreading awareness program through media, proper hand sanitization, social distancing, wearing mask, etc. which results in slowing down the disease transmission process. In terms of model parameter, the implementation of intervention implies that there would be a reduction in the disease transmission rate. This reduction in the transmission rate is considered as the strength of the intervention, k, where $0⩽k⩽1$. In the presence of intervention, the parameter $\beta$ is modified as $(1-k)\beta$ throughout the period of implementation. In this study, we consider the COVID-19 outbreak situation in India during the period $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020 and divide the whole outbreak period into four phases. For the initial phase (i.e $2^{\mathit{nd}}$ March, 2020 to ${24}^{\mathit{th}}$ March, 2020), we choose $k=0$, because no such nationwide preventive measures were implemented by the Government of India during that period. For the remaining three phases, we estimate the intervention strength (k) separately for each of the phases by fitting our model to the daily new reported COVID-19 cases in India (detailed description is provided in Section 3). The following set of ordinary differential equations represents the transmission dynamics of the disease:

$$\begin{array}{c}\frac{\mathit{dS}}{\mathit{dt}}=-(1-k)\beta \frac{S(I+\eta I_a)}{N},\hfill \\ \frac{\mathit{dE}}{\mathit{dt}}=(1-k)\beta \frac{S(I+\eta I_a)}{N}-\sigma E,\hfill \\ \frac{\mathit{dI}}{\mathit{dt}}={\rho }_1\sigma E-\alpha I,\hfill \\ \frac{{\mathit{dI}}_a}{\mathit{dt}}={\rho }_2\sigma E-{\gamma }_a{I}_a,\hfill \\ \frac{{\mathit{dI}}_q}{\mathit{dt}}={\rho }_3\sigma E-({\alpha }_q+{\gamma }_q)I_q,\hfill \\ \frac{\mathit{dH}}{\mathit{dt}}=\alpha I+{\alpha }_q{I}_q-(\gamma +\delta )H,\hfill \\ \frac{\mathit{dR}}{\mathit{dt}}={\gamma }_a{I}_a+{\gamma }_q{I}_q+\gamma H\text{.}\hfill \end{array}$$ (1)

The schematic diagram and the description of the parameters used in the model (1) is presented in Fig. 1 and Table 1 respectively.

Fig. 1.

Schematic diagram of the model (1).

Table 1.

Description of parameters used in the model (1).

Parameters	Description	Value	Reference
$\beta$	Rate of disease transmission	$1.7399$	Estimated
$\eta$	Modification parameter	$0.1002$	Estimated
$\sigma$	Rate of transition from exposed to infected class	$0.1923{\mathit{day}}^{-1}$	(Li et al., 2020)
${\rho }_1,{\rho }_2,{\rho }_3$	Fractions of population move from the compartment E to the compartments $I,I_a$ and $I_q$ respectively	$0.3362,0.4204,0.2434$	Estimated
$\alpha$	Rate of transition from symptomatic to hospitalized class	$0.2174{\mathit{day}}^{-1}$	(Li et al., 2020)
${\alpha }_q$	Rate of transition from quarantined to hospitalized class	$0.1429{\mathit{day}}^{-1}$	Assumed
$\gamma$	Recovery rate of the individuals in hospitalized compartment	$0.0701{\mathit{day}}^{-1}$	(Covid19India, 2020)
${\gamma }_a$	Recovery rate of asymptomatic population	$0.13978{\mathit{day}}^{-1}$	(Tang et al., 2020)
${\gamma }_q$	Recovery rate of quarantined population	$0.11624d{\mathit{ay}}^{-1}$	(Tang et al., 2020)
$\delta$	Rate of disease induced death	$0.0175{\mathit{day}}^{-1}$	(Covid19India, 2020)
k	Strength of intervention	$0,0.5042,0.6544,0.7282$	Estimated for different outbreak phases

3. Model fitting

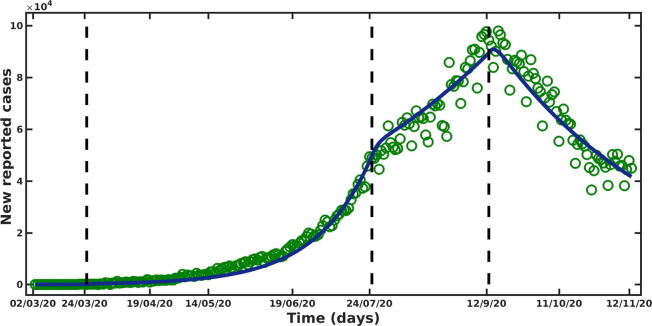
Though the first confirmed case of COVID-19 was reported on ${30}^{\mathit{th}}$ January, 2020 (WHO, 2019b), from $2^{\mathit{nd}}$ March, 2020 onwards, the new cases are being reported continuously. Therefore, we choose $2^{\mathit{nd}}$ March, 2020 as the starting date of the outbreak in India. We consider the outbreak period from $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020 and our model is fitted to the daily reported new cases data for the above-mentioned period (Johns Hopkins University and Medicine, 2020). We estimate five unknown model parameters: $(i.)$ the transmission rate ($\beta$), $(\mathit{ii}.)$ modification parameter ($\eta$), $(\mathit{iii}.)$ fraction of population move to symptomatic class from exposed class (${\rho }_1$), $(\mathit{iv}.)$ fraction of population move to asymptomatic class from exposed class (${\rho }_2$) and $(v.)$ strength of the intervention $(k)$, by fitting the model to the daily reported cases data. It is to be noted that, Government of India declared a countrywide lock-down from ${25}^{\mathit{th}}$ March, 2020 for 21 days (Pulla, 2020). Therefore, we assume that during initial phase of outbreak, i.e from $2^{\mathit{nd}}$ March, 2020 to ${24}^{\mathit{th}}$ March, 2020, no such preventive measures was taken by the Government of India and we consider the strength of intervention, $k=0$ during this period. After that countrywide lock-down started and various precautionary measures have been implemented by the government with varying intensity over the time. It is noteworthy that strictness of the intervention strategy essentially can change the slope of the epidemic curve. We choose the time points at which the rate of change in the new infection is changed substantially. From the time series of daily COVID-19 cases data (see green circles in Fig. 2 ), it is clearly visible that the epidemic curve starts to change its behaviour around the last week of July and the second week of September. More specifically, during the period ${25}^{\mathit{th}}$ March, 2020 to the last week of July, 2020, the new COVID-19 cases grow exponentially. In the subsequent time, the rate of increase in the new cases is reduced and the peak is achieved in the middle of September. After that, a clear change in the slope (i.e from positive to negative) of the epidemic curve is observed. Based on these observations, we consider the following three outbreak phases: $(i.)$ ${25}^{\mathit{th}}$ March, 2020 to ${24}^{\mathit{th}}$ July, 2020,$(\mathit{ii}.)$ ${25}^{\mathit{th}}$ July, 2020 to ${12}^{\mathit{th}}$ September, 2020, $(\mathit{iii}.)$ ${13}^{\mathit{th}}$ September, 2020 to ${12}^{\mathit{th}}$ November, 2020 and estimate the value of intervention strength k separately for each phase.

Fig. 2.

Model fitting to daily new COVID-19 reported cases for the time period $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020. The blue solid line represents the model solution and green circles are the discrete data points. The vertical lines represent the starting point of different outbreak phases.

The daily new reported cases from the model is given by

$$N^m(t,\mathrm{\Theta })={\int }_{t-1}^t(\alpha I(\tau )+{\alpha }_q{I}_q(\tau ))d\tau ,$$ (2)

where $\mathrm{\Theta }=\{\beta ,\eta ,{\rho }_1,{\rho }_2,k\}$.

We perform our model fitting by using in-built function lsqnonlin in MATLAB (Mathworks, R2014a) to minimize the sum of square function. In our case, the sum of square function $\mathit{SS}(\mathrm{\Theta })$ is given by,

$$\mathit{SS}(\mathrm{\Theta })={\displaystyle \sum _{i=1}^n}{\left(N^d(t_i)-N^m(t_i,\mathrm{\Theta })\right)}^2,$$ (3)

where, $N^d(t_i)$ is the actual data at $t_i^{\mathit{th}}$ day and n is the number of data points. The model fitting to the daily new reported cases is displayed in Fig. 2. The values of the estimated parameters are given in Table 1.

4. Basic reproduction number

Basic reproduction number is a key quantity in epidemiology which quantifies the average number of secondary cases generated from a single primary cases during this infectious period. However, since intervention is incorporated in our model, in a similar way we can define the control reproduction number, ${\mathcal{R}}_c$. The control reproduction number ${\mathcal{R}}_c$ measures the average number of secondary cases generated from a single primary cases in a situation where some interventions are implemented. This quantity can be calculated from a mathematical model by following next generation matrix approach. Following (Driessche et al., 2002), the new infection matrix F and the transmission matrix V are given by,

$$F=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill (1-k)\beta \hfill & \hfill \eta (1-k)\beta \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),V=\left(\begin{array}{cccc}\hfill \sigma \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\rho }_1\sigma \hfill & \hfill \alpha \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\rho }_2\sigma \hfill & \hfill 0\hfill & \hfill {\gamma }_a\hfill & \hfill 0\hfill \\ \hfill -{\rho }_3\sigma \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha }_q+{\gamma }_q\hfill \end{array}\right)\text{.}$$

The control reproduction number, ${\mathcal{R}}_c$ is defined as the spectral radius of the matrix ${\mathit{FV}}^{-1}$,

$${\mathcal{R}}_c=\frac{{\rho }_1(1-k)\beta }{\alpha }+\frac{\eta {\rho }_2(1-k)\beta }{{\gamma }_a}\text{.}$$ (4)

It is to be noted that, the first term is the number of new infection caused by symptomatic individual (I) whereas the second term is the number new infection due to the infection by asymptomatic individual ($I_a$) in the presence of intervention. Using the estimated parameter (see Table 1) we calculate the control reproduction number ${\mathcal{R}}_c$ for different outbreak phases. For the first phase (i.e from $2^{\mathit{nd}}$ March to ${25}^{\mathit{th}}$ March, 2020) when there is no intervention strategy, ${\mathcal{R}}_c$ turns out to be $3.22$. During the next two outbreak phases (from ${25}^{\mathit{th}}$ March to ${24}^{\mathit{th}}$ July, 2020 and from ${25}^{\mathit{th}}$ July to ${12}^{\mathit{th}}$ September, 2020 respectively), the value of the control reproduction number becomes $1.59$ and $1.11$ respectively. Finally, in the last phase (i.e from ${13}^{\mathit{th}}$ September to ${12}^{\mathit{th}}$ November, 2020) the control reproduction number decreases to $0.87$.

4.1. Estimation of basic reproduction number from actual epidemics

The basic reproduction number $({\mathcal{R}}_0)$ for communicable diseases can be estimated through the actual epidemic data by using various statistical as well as mathematical methods (Massad et al., 2010). In this study, we estimate ${\mathcal{R}}_0$ from the initial growth phase of the epidemics (Massad et al., 2001, Sardar et al., 2015, Pinho et al., 2010). At the early stage of the epidemic, there is a non-linear relationship between the cumulative number of cases $C(t)$ and the force of infection $\mathrm{\Lambda }$ which can be mathematically written as $C(t)\propto \exp (\mathrm{\Lambda }t)$. Therefore, the number of exposed, symptomatic and asymptomatic population progress in the following form,

$$\begin{array}{ccc}E\hfill & \propto \hfill & E_0\exp (\mathrm{\Lambda }t),\hfill \\ I\hfill & \propto \hfill & I_0\exp (\mathrm{\Lambda }t),\hfill \\ I_a\hfill & \propto \hfill & I_{a0}\exp (\mathrm{\Lambda }t)\text{.}\hfill \end{array}$$ (5)

where $E_0,I_0$ and $I_{a0}$ are constants. Further, the number of non-susceptible population can be assumed negligible i.e. $S(t)=N$. Substituting the Eq. (5) into the model (1), we have

$$\begin{array}{c}{E}_0(\mathrm{\Lambda }+\sigma )=\beta (I_0+\eta I_{a0}),\hfill \\ I_0(\mathrm{\Lambda }+\alpha )={\rho }_1\sigma E_0,\hfill \\ I_{a0}(\mathrm{\Lambda }+{\gamma }_a)={\rho }_2\sigma E_0\text{.}\hfill \end{array}$$ (6)

Using the expression of ${\mathcal{R}}_0$ from Eq. (4) and applying the above Eqs. (6) we have determined relation between the ${\mathcal{R}}_0$ and the force of infection $\mathrm{\Lambda }$ as follows:

$$\begin{array}{ccc}{\mathcal{R}}_0& =& \left(\frac{{\rho }_1}{\alpha }+\frac{{\rho }_2\eta }{{\gamma }_a}\right)\left[\frac{\mathrm{\Lambda }+\sigma }{\frac{{\rho }_1\sigma }{\mathrm{\Lambda }+\alpha }+\frac{\eta {\rho }_2\sigma }{\mathrm{\Lambda }+{\gamma }_a}}\right]\text{.}\end{array}$$ (7)

Here we first estimate the force of infection $\mathrm{\Lambda }$ and then estimate ${\mathcal{R}}_0$ by using Eq. (7). Following Favier et al., 2006, Pinho et al., 2010, the relation between the number of new cases per day and the cumulative number of cases per day $C(t)$ as: number of new cases $~$ $\mathrm{\Lambda }C(t)$.

The force of infection ($\mathrm{\Lambda }$) can be calculated from the COVID-19 incidence data in the following ways (Sardar et al., 2015):

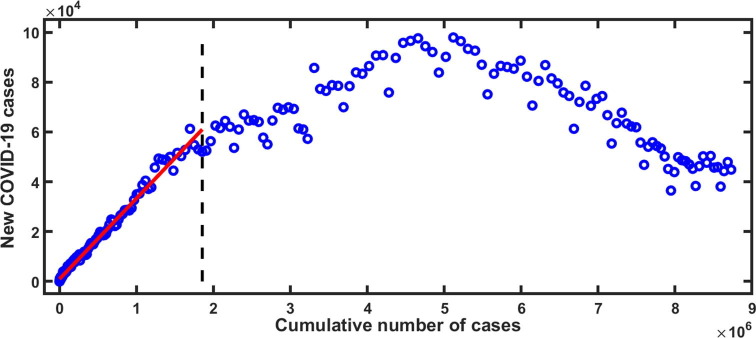
• Step 1. We plot the number of new COVID-19 cases (per day) in $x-\mathit{axis}$ versus the cumulative number of COVID-19 cases (per day) in $y-\mathit{axis}$.

• Step 2. In the scatter plot, we point out the threshold of cumulative cases up to which new cases show the exponential growth.

• Step 3. Then we fit a linear regression model using the least square technique to this exponential growth data.

• Step 4. The slope of the fitted line is considered as the force of infection ($\mathrm{\Lambda }$).

We obtain $\mathrm{\Lambda }=0.0324\pm 0.00028{\mathit{day}}^{-1}$ based on the slope of the estimated line shown in Fig. 3 . Using the Eq. (7) along with the parameter values form Table 1, we obtain the estimate of ${\mathcal{R}}_0=1.3575$ with upper and lower bounds $1.3608$ and $1.3542$ respectively. This estimate of ${\mathcal{R}}_0$ indicates that the initial transmissibility of COVID-19 is pretty much higher than 1, which in turns implies that it is essential to control the disease at the initial phase.

Fig. 3.

The daily number of new COVID-19 cases against the cumulative number of COVID-19 cases in India, from $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020. The box indicates the growing linear parts of the plots corresponding to the initial growth of the epidemics. The least squares linear fit of the linear phase corresponding to data in dot box gives $\mathrm{\Lambda }=0.0324\pm 0.00028$ with correlation coefficient $R\approx 0.9941$.

4.1.1. Epidemic doubling time

The doubling time of an epidemic is a measure of the rate of spread of a disease. It is the required time to double the number of cases in the epidemic. There is an inverse relationship between epidemic strength and the doubling time i.e. if an epidemic declines, the doubling time increases and vice versa. Following (Ferretti et al., 2020), we obtain the epidemic doubling time for our study is $T_2=\frac{\ln (2)}{\mathrm{\Lambda }}\approx 21.4$ days. Although the time duration is modest but there is a risk of huge number people becoming infected within that time. Therefore, it is necessary to apply some preventive measures, else there will be a large outbreak in the above mentioned period.

4.2. Effective reproduction number $R(t)$

Study regarding the time span of an epidemic is very crucial and can be achieved to a certain extent through the estimation of $R(t)$, the effective reproduction number. It is defined as the actual average number of secondary cases from a typical primary case at time t (Nishiura and Chowell, 2009). The value of $R(t)$ provides information about the severity of the disease over different time points and alert epidemiologists to suggest about the control measures (Sardar et al., 2015). Some recent studies focused on estimating the effective reproduction number using epidemic data (Wallinga and Teunis, 2004, Thompson et al., 2019, White et al., 2020). We estimate $R(t)$ from the daily new infection curve of the infected COVID-19 cases data by using the following equation derived from the renewal equation of a birth process:

$$\begin{array}{ccc}R\left(t\right)& =& \frac{b\left(t\right)}{{\int }_{a=0}^{\infty }b(t-a)g\left(a\right)\mathrm{d}a},\\ & & \end{array}$$ (8)

where, the term $b(t)$ corresponds to the number of new cases in the day t and the term $g\left(\right)$ is the generation interval distribution for a disease (Pinho et al., 2010).

We derive the expression of the generation interval distribution $g(t)$ from the model (1) by applying the method discussed in Pinho et al., 2010, Wallinga and Lipsitch, 2007. The rates of leaving the exposed and infectious compartments are indicated by $b_1,b_2$ and $b_3$. These quantities are constant and extracted from the model (1) as $b_1=\sigma ,b_2=\alpha$ and $b_3={\gamma }_a$. Moreover, the generation interval distribution is the convolution of three exponential distributions with a mean $T_c=1/b_1+1/b_2+1/b_3$. Following Pinho et al., 2010, Akkouchi, 2008, we have the following explicit expression for the convolution:

$$g(t)={\displaystyle \sum _{i=1}^3}\frac{b_1{b}_2{b}_3\exp (-b_{i}t)}{{\displaystyle \prod _{j=1,j\ne i}^3}(b_j-b_i)},$$ (9)

with $t⩾0$. The validity of the above relation (9) holds for a minimum threshold value of the force of infection $\mathrm{\Lambda }$, defined as $\mathrm{\Lambda }>\min (-b_1,-b_2,-b_3)$ (Wallinga and Lipsitch, 2007).

Using the daily COVID-19 incidence data and applying the expression of $g(t)$ in Eq. (9), we estimate $R(t)$ from Eq. (8). Fig. 4 shows the time evolution of the effective reproductive number $R(t)$ to the COVID-19 outbreak in India, from $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020. The result is shown here for $t>3$, since, the method used here to derive the expression of $R(t)$ is not applicable for lower values of t. Here the value of $R(t)$ lies near the value 2 most of the times though it was pretty high at the initial stage. However, from the last week of September, the value of $R(t)$ is observed to be lower than unity which essentially describes the decreasing trend in new COVID-19 cases in India.

Fig. 4.

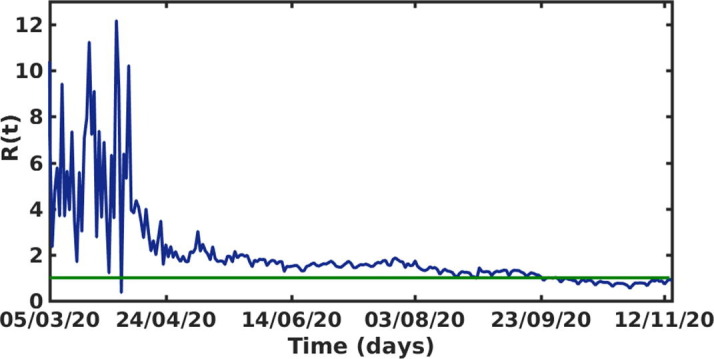
The effective reproductive number $R(t)$ versus time t (days) of the COVID-19 outbreak in India during $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020. The parameter values are taken from Table 1.

5. Effect of intervention

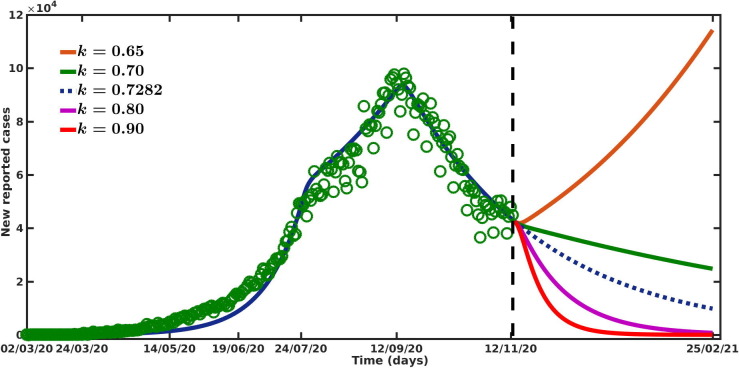
In this section, we study the effect of intervention strategies (e.g. lock-down, spreading awareness program through media, proper hand sanitization, social distancing, wearing mask, etc.) in reducing the new COVID-19 cases through our model. Implementation of interventions implies that there would be a reduction in the disease transmission rate $\beta$. This reduction in the transmission rate is considered as the strength of the intervention k and it has the functional expression $(1-k)\beta$. We have calibrated our model to the daily new COVID-19 cases during the period $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020 and estimated the strength of intervention k (see Table 1) for four different outbreak phases. Now we project the daily new COVID-19 cases for a range of values of k, during the period ${13}^{\mathit{th}}$ November, 2020 to ${25}^{\mathit{th}}$ February, 2021. The estimated value of k during the last outbreak phase (i.e from ${13}^{\mathit{th}}$ September, 2020 to ${12}^{\mathit{th}}$ November, 2020) is considered as the baseline value of k. We now investigate the possible scenarios by changing the intervention strength (k) from its baseline value.

We first keep the value of k at its baseline value, i.e $k=0.7282$ and simulate the model (1) for the time period ${13}^{\mathit{th}}$ November, 2020 to ${25}^{\mathit{th}}$ February, 2021. We see from Fig. 5 that in such a situation, the new COVID-19 cases gradually decreases. It is to be noted that, if the strength of intervention ($k=0.7282$) is maintained for the subsequent time (i.e from ${13}^{\mathit{th}}$ November, 2020 to ${25}^{\mathit{th}}$ February, 2021), a total number of $3.0642$ million new cases may occur during this time period (see Table 2 ). Now, if the strength of intervention is slightly increased (i.e for $k=0.8$), then significant reduction in the cases is observed (see Fig. 5). It is also to be noted from Fig. 5 that further increment in the intervention strength (for $k=0.9$) effectively eradicate the disease within the above-said time period. Our model projects total $1.6214$ million and $1.1183$ million cases for the intervention strength $k=0.8$ and $k=0.9$ during ${13}^{\mathit{th}}$ November, 2020 to ${25}^{\mathit{th}}$ February, 2021 (see Table 2). We also observe that if the intervention strength is reduced from its baseline value, say for $k=0.7$, the total number of new cases during the projection period rises to $3.875$ million. However, further reduction in intervention strength may end up with second wave of infection. For $k=0.65$, we see that the number of new cases starts to grow exponentially (see Fig. 5). In such a scenario, the total new cases at the end of ${25}^{\mathit{th}}$ February, 2021 is projected to be $8.0140$ million (see Table 2). .

Fig. 5.

Projection of new COVID-19 reported cases for the time period ${13}^{\mathit{th}}$ November, 2020 to ${25}^{\mathit{th}}$ February, 2021 for different values of intervention strength k. The green circles are the real data for the period $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020.

Table 2.

Projected number of final cumulative cases and relative change in final cumulative case $(\%)$ for different values of k. The $\uparrow$ implies there is increase and the $\downarrow$ implies there is decrease in the final cumulative case.

Strength of the intervention (k)	Final cumulative cases	Relative change in final cumulative case (%)
$0.65(\downarrow 10.73\%)$	$8.0140$ million	$65\%\left(\uparrow \right)$
$0.70(\downarrow 3.87\%)$	$3.875$ million	$27\%\left(\uparrow \right)$
$0.7282\left(\mathit{Estimated}\right)$	$3.0642$ million	$0\%$
$0.80(\uparrow 9.86\%)$	$1.6214$ million	$43\%\left(\downarrow \right)$
$0.90(\uparrow 23.59\%)$	$1.1183$ million	$60\%\left(\downarrow \right)$

The final cumulative new cases with respect to intervention strength (k) is shown in Fig. 6 . We observe that a rapid change occurred for $k\in [0.6,0.7]$. We see that, the final number of cumulative new cases gradually decreases if the strength of the intervention is increased. However, for higher values of k (i.e for $k\in [0.7,0.95]$), the final cumulative cases are reduced significantly.

Fig. 6.

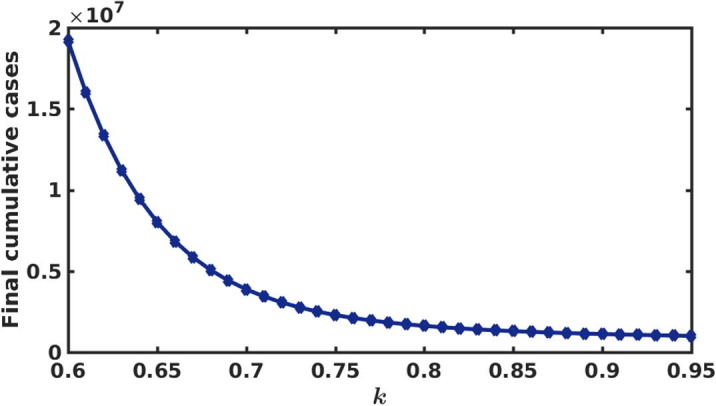
Final cumulative new cases during the period ${13}^{\mathit{th}}$ November, 2020 to ${25}^{\mathit{th}}$ February, 2021 for different values of strength of intervention (k).

The percentage of relative change in the final cumulative new cases for different k is presented in Fig. 7 . This quantifies what would be the percentage of relative change (reduction or increment) in final cumulative new cases if we change the intensity of intervention strength k from its baseline value (i.e $k=0.7282$). For $k\in [0.6,0.7282)$, we see from Fig. 7 that the relative change in final cumulative case is negative. This implies that even a small reduction in the intervention strength from its base value leads to large increment in the new COVID-19 cases. For instance, only $3.87\%$ reduction in k (i.e for $k=0.70$) results in $27\%$ increase in the final cumulative cases (see Table 2). Also if we reduce the intervention strength by $10.73\%$ (i.e for $k=0.65$) from its baseline value, the final cumulative new cases is increased by $65\%$ (see Table 2). For $k\in (0.7282,0.95]$, we see that up to $60\%$ reduction in the final cumulative cases can be achieved. More specifically, $9.86\%$ (i.e for $k=0.80$) and $23.59\%$ (i.e for $k=0.90$) increment in k, leads to $43\%$ and $60\%$ reduction in the cumulative cases respectively (see Table 2). This analysis indicates that intensity of the intervention should be strengthened over the time to control the disease spread effectively.

Fig. 7.

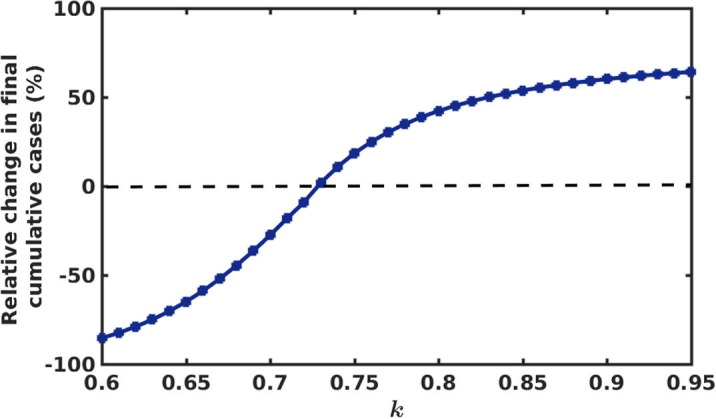
Percentage of relative change in the final cumulative new cases for different values of strength of intervention (k).

6. Discussion and conclusion

The COVID-19 outbreak in India is a potential threat to the country due to its rapid spread. Mathematical models are very effective tool to predict the time span and pattern of the outbreak. Moreover, mathematical models can also provide useful insights regarding the impact of intervention in lowering the disease incidence.

In this study, we proposed a deterministic compartmental model to describe the disease transmission mechanism among the population. We considered the COVID-19 outbreak in India and fitted our proposed model to the daily new reported cases during the period $2^{\mathit{nd}}$ March, 2020 to ${12}^{\mathit{th}}$ November, 2020. It is to be noted that, during this period the epidemic curve behaves in a non-monotonic fashion. Therefore we divided the whole time interval into some sub-intervals and in each phase we estimated the intervention strength separately. Consideration of such a large duration of the ongoing outbreak period enabled us to quantify the magnitude of the strictness of the intervention strategies taken by the government at different times. However, it was not well explored by the previous model based studies in the context of India (Bajiya et al., 2020, Khajanchi and Sarkar, 2020, Rafiq et al., 2020, Sarkar et al., 2020). Some other model parameters are also estimated by fitting our model to the daily new reported cases. By looking at the estimated parameters, it is observed that the rate of disease transmission is quite high which basically implies the high infectiousness of the disease. The percentage of the symptomatic individuals coming from exposed individuals is estimated to be more than $33\%$, whereas the percentage of the asymptomatic and quarantined individuals are estimated as more than $42\%$ and $24\%$ respectively. This indicates that the contribution of the asymptomatic population to COVID-19 cases in India is pretty high.

Based on the estimated parameters and actual COVID-19 incidence data, we estimated basic reproduction number, effective reproduction number and epidemic doubling time to get an overview of the outbreak. We obtained the estimate of basic reproduction number ${\mathcal{R}}_0$ as $1.3575$ with upper and lower bounds are $1.3608$ and $1.3542$ respectively. The estimated value of ${\mathcal{R}}_0$ is in accordance with the previous studies (Marimuthu et al., 2020, Hilton and Keeling, 2020). The effective reproduction number ($R(t)$) provides information about the severity of COVID-19 over different time points. In our study, the values of $R(t)$ lie around 2 most of the time. However, at the initial period of the epidemic it has high values which confirms the high transmissibility of the disease at the initial stage of the epidemic and from the last week of September its value lies very close to 1 or even below 1, which in turns captures the decreasing trend in new cases quite nicely. The epidemic doubling time is also estimated to be approximately $21.4$ days. This suggests that the rate of disease transmission need to be controlled otherwise a large proportion will be affected within a very short period of time.

We studied the impact of intervention in reducing the disease burden. We basically considered the preventive measures such as lock-down, spreading of awareness program through media, proper hand sanitization, social distancing, wearing mask, etc. which essentially slow down the disease transmissibility. We have estimated the strength of the intervention for different phases of the outbreak separately and considered the value of intervention strength estimated in the last phase as our baseline value. We then examined the sensitivity of the intervention strength in terms of the relative change in the projected final cumulative cases by varying its intensity from the baseline estimate. This investigation may provide a deeper insight to the policy maker to take the decision whether the strictness of an ongoing intervention strategy should be maintained or it could be relaxed. Our study revealed that higher intervention effort is required to control the disease outbreak within a shorter period of time. Further, our analysis showed that the strength of the intervention should not be relaxed over the time rather the intervention should be strengthened to eradicate the disease effectively. A second wave of infection may happen in India if there is an approximately $10\%$ relaxation on the baseline intervention strength. Designing the efficient intervention strategy is one of the crucial factor to curb the disease spread in an outbreak situation. In this regard, our study suggests that strict intervention should be implemented by the Government in the subsequent period of this outbreak. We believe that the findings obtained from this study can provide fruitful insights in framing policies regarding the control of COVID-19 in India. Lastly, an important point is to be noted that the implementation of preventive measures essentially reduce the effective contacts between susceptible and infected individuals which helps to reduce the peak of the infection as well as delays the occurrence of the peak. However, the implementation of the preventive measures like strict lock-down, social distancing, etc. may not be considered for longer period due to its adverse effects on social and financial sustainability. The assessment of the combined effect of preventive measures with some other possible intervention strategies like contact-tracing, implementation of rigorous testing, isolation of COVID-19 positive patients, etc. in reducing disease burden might be an interesting problem to study in the future. It is noteworthy that India has already started its national COVID-19 vaccination programme (Bagcchi, 2021). Therefore, in the presence of existing intervention strategies how vaccination can help to reduce the severity of the future outbreak of this disease would also be an important aspect for future research. However, though our present study did not incorporate the above-said intervention strategies, our model can be modified or extended accordingly to study the combined effect of these control strategies. For example, to study the impact of vaccination strategy, our model can be extended by introducing a new compartment, e.g. vaccinated compartment which keeps tracking the number of vaccinated individuals at each time. Naturally, a proportion (depends on the vaccination rate) of susceptible individuals move to the vaccinated compartment and depending on the efficacy of the vaccine, a proportion of vaccinated individuals move to the infected compartment. We leave these extensions and modifications for future study.

CRediT authorship contribution statement

Abhishek Senapati: Conceptualization, Methodology, Formal analysis, Software, Writing - original draft, Writing - review & editing. Sourav Rana: Conceptualization, Methodology, Visualization, Software, Formal analysis, Writing - review & editing. Tamalendu Das: Formal analysis, Writing - review & editing. Joydev Chattopadhyay: Supervision, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.