Abstract
Since the beginning of COVID-19 (corona virus disease 2019), the Indian government implemented several policies and restrictions to curtail its spread. The timely decisions taken by the government helped in decelerating the spread of COVID-19 to a large extent. Despite these decisions, the pandemic continues to spread. Future predictions about the spread can be helpful for future policy-making, i.e., to plan and control the COVID-19 spread. Further, it is observed throughout the world that asymptomatic corona cases play a major role in the spread of the disease. This motivated us to include such cases for accurate trend prediction. India was chosen for the study as the population and population density is very high for India, resulting in the spread of the disease at high speed. In this paper, the modified SEIRD (susceptible–exposed–infected–recovered–deceased) model is proposed for predicting the trend and peak of COVID-19 in India and its four worst-affected states. The modified SEIRD model is based on the SEIRD model, which also uses an asymptomatic exposed population that is asymptomatic but infectious for the predictions. Further, a deep learning-based long short-term memory (LSTM) model is also used for trend prediction in this paper. Predictions of LSTM are compared with the predictions obtained from the proposed modified SEIRD model for the next 30 days. The epidemiological data up to 6th September 2020 have been used for carrying out predictions in this paper. Different lockdowns imposed by the Indian government have also been used in modeling and analyzing the proposed modified SEIRD model.
Keywords: COVID-19, Coronavirus, Pandemic, Modified SEIRD (susceptible–exposed–infected–recovered–deceased), Long short-term memory (LSTM), Lockdown
Introduction
The world witnessed the COVID-19 (corona virus disease 2019) pandemic that affected the lives of many people across the globe. The spread of this virus has taken an exponential speed. Therefore, on 11th March 2020, the World Health Organization (WHO) announced COVID-19 as a “global pandemic” [21, 22]. Due to the outbreak of COVID-19, an unavoidable situation was created, whereby the authorities of various countries and continents had to put restrictions on the movement of people and non-essential activities. Some of these restrictions included imposing lockdowns, maintaining social distancing, work from home in academics, and business continuity plans. Thus, the spread of COVID-19 has left a significant impact on the environment as well as on the lifestyle of human beings [1, 36]. Almost all educational institutions were closed, sports leagues were canceled, and people were advised to work from home and perform contactless financial transactions using various digital platforms.
COVID-19 was first reported in the Wuhan city of China on 17th November 2019, and from there, it spread to the whole world [21, 22, 24]. Since this disease spread through human-to-human contact, therefore, a large number of cases have been reported worldwide [16]. Recent studies have found that a healthy person can be infected by coming in contact with an infected person or with the surface touched by an infected person to which the Coronavirus got transferred. In addition, the symptoms of Coronavirus in an infected person are visible after a specific period. During this period, the infected person is a carrier of Coronavirus and can infect other healthy persons. As of 6th September 2020, more than 27 million people have been infected, and more than 0.8 million people have died from COVID-19 across the globe (Worldometer, COVID-19 CORONAVIRUS PANDEMIC, 2020). Therefore, COVID-19 has become a big threat to people and the environment [33].
To tackle this difficult situation, the first step is to take precautionary measures to prevent the infection and the second step is that infected people must quarantine themselves and get medical help. Taking precautions on an individual level is also required, such as the use of sanitizer, use of face masks, and maintaining social distancing [14]. These resources, namely sanitizers and face masks, are the need of time [44]. However, it is equally important to properly dispose-off the used masks to protect the environment. Governments have also taken many steps to arrange the necessary resources to provide better medical services to infected people. An estimate of these resources is created so that all the needs of people can be met in time. Researchers are using different methods to estimate resources.
For a country like India, having a large population of around 1.38 billion, it is a challenging task to handle this pandemic efficiently [45, 46]. In India, the first COVID-19-positive case was reported in the Thrissur district of Kerala on 30th January 2020, of a student who returned from Wuhan University, China. During the initial period, there was not a substantial increase in the number of cases in India, and by 15th March, the number of cases barely crossed the figure of 100. As of 6th September 2020, COVID-19 has spread to 215 countries with more than 7 million active infected cases globally. In India, the number of COVID-19 cases has crossed 4.2 million with more than 0.8 million active infected cases, 3.3 million recovered cases, and 72,816 as the total number of deaths, which makes India the worst-affected country in Asia. The variation in the total number of infected cases is evident in India, with the highest reported cases from Maharashtra and the lowest from Mizoram [12]. Furthermore, the research of Covid-19 trend prediction for India was limited. In addition, India is a dense country in terms of population and culture. Therefore, it is very important to perform the trend prediction for India to efficiently control the pandemic and take timely measures to stop the spread of the same.
The number of cases globally as well as in India is increasing at a very rapid rate. As is evident from the data, Maharashtra is the worst-affected state in terms of total cases, which accounts for about 21% of the cases in India. The next three worst-affected states/union territories are Andhra Pradesh, Tamil Nadu, and Karnataka having approximately 32% of the total cases, and the rest of Indian states/ union territories having another 47% cases. North-eastern states of India are much better, like Mizoram and Sikkim, each having less than 2000 cases so far. To understand the future spread of the pandemic and to devise management strategies, various models have been designed, which provide information regarding the time of attainment of infection peak, the number of infected cases, and the requirement of medical infrastructure to manage the spread [10, 38, 39].
Further, it is observed that asymptomatic cases lead to a high spread of the disease. Due to the absence of symptoms, these people do not follow the proper guidelines as laid by the government. This causes exponential growth of infection spread in a community and provides the motivation to include such cases for precise trend prediction. In this paper, a modified SEIRD (susceptible–exposed–infected–recovered–deceased) model has been proposed for predicting the trend of COVID-19 in India and its four worst-affected states. It uses a parameter, epsilon for COVID-19 predictions, which takes into account the proportion of the exposed population that is asymptomatic but infectious and is unknowingly spreading the infection. The proposed model utilizes the reported data of infections, recoveries, and deaths caused by COVID-19 to make predictions. We have used the data of India and its four states having the highest number of total cases to make predictions using the modified SEIRD model. Considering the data up to 6th September 2020, Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka are the four states with the highest number of reported cases. This paper predicts the number of cases in infected, exposed, recovered, and deceased compartments. The effect of different lockdowns imposed by the Indian government has also been utilized in modeling using the proposed modified SEIRD model. Although the study is done for India and its states in this paper, the proposed SEIRD model can be used for any country and its states using the reported data of that country.
Furthermore, this paper utilizes deep learning (DL) based long short-term memory (LSTM) model to perform short-term predictions for the next 30 days, i.e., from 7th September 2020 to 6th October 2020. The results obtained by the LSTM model have been compared with the results of the modified SEIRD model. The epidemiological data up to 6th September 2020 has been used to obtain predictions in this paper. Student t test has been used in this paper to compare the predictions obtained from the proposed modified SEIRD model and the LSTM model [3]. The t test is useful when the sample size is petite as compared to the large population size. Since the data available is limited, the t test becomes an appropriate choice to find the confidence intervals for COVID-19 predictions.
The rest of the paper is organized as follows: the next section, “Review of Literature”, presents the review of literature. In “Models Used for Predictions”, both the proposed modified SEIRD model and the LSTM model have been explained. “Experimental Setup and Results” presents the experimental setup and results, followed by the “Conclusion and Future Work” at the end.
Review of Literature
COVID-19 is a communicable disease that has been declared as a pandemic by the WHO. Moreover, there is no medicine or vaccine available to cure this infection as of now. Hence, the only way to protect oneself from this pandemic is to get protected from the contact of an infected person. With the ongoing pandemic threat, researchers started to study the future of COVID-19. These research groups are mainly divided into two categories, where one tries to find the vaccine and the other group tries to predict the damage that can be caused by this disease. Based on the predictions, resources can be prepared to treat people and minimize fatalities. This paper predicts the future trend of COVID-19 by modeling the effect of different lockdowns imposed by the Indian government and contributed to the later research in the area.
Since the beginning of COVID-19, various researchers have predicted its spreading trend for different countries and their states [7, 11, 41]. Ahmed [2] has studied the effect of patient age, and their gender, their geographical location on the infection spread. In his work, the population of India that has arrived from different regions is taken into consideration. These people were divided into six groups to study the regional effect of Corona on a patient. Clustering and multiple linear regression are two techniques that have been used for this study. Clustering has been used to find the similarity between different groups. Multiple linear regression has been used to predict the source of infection by assigning the new patient case into one of the above-defined groups. In every group, different age distributions have been studied, and their recovery rates [6] were calculated.
Ceylan [9] utilized auto-regressive integrated moving average (ARIMA) models to predict the future trend of the coronavirus disease in the three worst-affected countries of Europe, namely Italy, Spain, and France. The author formulated several ARIMA models using different parameter values. The best models were then used for estimating the spread of the disease in each of the three countries. Patrikar et al. [30] have used the modified SEIR method in their work to predict the curve of COVID-19 for India. In this modified SEIR, the effect of social distancing has been studied on the COVID-19, and different graphs have been obtained. In the paper, the authors performed a short-term forecast of COVID-19 for different states of India in the worst-case scenario.
SEIR model was also used to study the effect of temperature on COVID-19 outbreak in China [37]. In the paper, the authors incorporated climatic factors in the original SEIR model to analyze their impact on the spread of COVID-19. Due to the dynamic nature of the Coronavirus spread, many researchers have performed short-term forecasting of the future spread of this deadly virus. Roosa et al. [32] performed 5- and 10-day forecasts of the total confirmed cases for Guangdong and Zhejiang provinces of China. The authors used the logistic growth model, Richards growth model, and a sub-epidemic wave model to generate predictions. A bootstrap approach was adopted in the paper to compute the uncertainty bounds for predicting cumulative cases shortly.
Arora et al. [4] made use of different variations of Long Short-Term Memory models for short-term prediction of COVID-19 cases in India. Deep LSTM, Bi-directional LSTM (Bi-LSTM), and Convolutional LSTM (Conv-LSTM) were used to calculate one-week predictions for different states and union territories of India. Tomar and Gupta [42] also used LSTM along with power-law curve fitting to predict the trend of COVID-19 in India. The authors forecasted the total number of confirmed, recovered, and deceased cases for a short period of the next 30 days. In addition, the paper analyzed the effect of different values of transmission rate on the number of predicted infected cases. Santosh [35] discussed the use of active learning with the help of Multimodal data to combat the Coronavirus outbreak. Fong et al. [13] presented a case study using CMC that was improved by deep learning network and fuzzy rule induction for gaining better stochastic insights about the epidemic development experiments.
Xie et al. [47] also used a deep learning method to estimate the parameters of the SEIR model. This model was further used to predict the short-term trend prediction of the COVID-19 pandemic in the Shaanxi province of China. Pal et al. [28] combined the COVID-19 data with the weather statistics of different countries to predict active cases using a shallow LSTM model. The authors used Bayesian optimization together with fuzzy rules to predict the future risk of Coronavirus in their work.
Chakraborty and Ghosh [10] proposed a hybrid approach to generate ten-day predictions for the United Kingdom, France, India, Canada, and South Korea. The model combined the Wavelet model and ARIMA models for computing predictions for the next ten days. The researchers have recently conducted various studies and the dynamics of this pandemic for different regions across the globe [1, 21–23, 25, 26, 48]. The forecast of COVID-19 in the Indian context also has been investigated by many researchers using mathematical and epidemiological models, but limited contribution exists for its states [7, 8, 20, 30].
The surge of the pandemic was seen later in India than in other countries like China, United States, Italy, Russia, Spain, and France. Therefore, the focus of the past study was limited to developed countries, and the research for India is minimal. In addition, India holds second place in terms of the population across the globe. Further, the majority of the people in India are living in slums. Therefore, it is important to predict the trend of COVID-19 for India and its states to efficiently control the spread by taking timely measures. In the literature, including [4, 37], short-term predictions have been performed for India, but the asymptomatic infectious cases were not considered in any of the above-mentioned literature. Therefore, to fill this research gap, we have proposed an epidemiology model for India and its worst-affected four states by considering both lockdowns as well as asymptomatic infectious cases. The model works with the reported data and hence takes care of the increase in cases due to any festival or gathering during that period.
In this paper, a compartmental epidemiological model, named modified SEIRD (susceptible–exposed–infected–recovered–deceased) model, has been proposed for the prediction of COVID-19 peak in India and its four states with the highest number of total cases. Further, short-term predictions for the next 30 days have also been computed using the LSTM model, and the results are compared with the predictions of the proposed model. Both the proposed model and the LSTM model were statistically analyzed using a t test. In addition, long-term predictions were computed using the proposed model for India and its four worst-affected states. The predictions are as good as the quality of data available, and therefore, the future spread of the virus may also affect the results. The next section presents the proposed modified SEIRD model and the LSTM model used for predictions in this paper.
Models Used for Predictions
This section describes the proposed modified SEIRD model based on SEIR and SEIRD epidemiology models, and the long short-term memory model (LSTM) model, that has been used in this paper for predictions the trend of COVID-19 in India and its four states having the highest number of total cases.
Proposed Modified SEIRD Model
The proposed SEIRD model for COVID-19 is based on the SEIRD epidemiology model, which is a widely used model to predict the trend of an epidemic. The SEIRD model is not able to represent the COVID-19 scenario efficiently as the exposed compartment is only considering that infection is spreading through symptomatic people. Whereas, in COVID-19, it was found that asymptomatic cases are also contributing to the spread of infection. Thus, there is a need to add asymptomatic cases for the study. In this paper, the existing SEIRD model is modified by including a parameter epsilon in the exposed compartment representing asymptomatic infectious cases. The SEIRD model has its roots in the SEIR model that was developed based on the basic SIR model.
To model the trend of any epidemic, researchers have used various epidemiology models in the past [5, 8, 20, 34, 40, 43]. The most popular category of the epidemiological model is compartment model. The main property of the compartmental model is the whole population is assigned to different compartments. The evolution of the compartment model started with SIR [27, 29] model in which three basic compartments were introduced.
S(t): The number of individuals who are susceptible to the disease, i.e., who are not (yet) infected on day t.
I(t): The number of infected individuals on day t, assumed to be infectious and can transmit the infection to others.
-
R(t): The number of individuals who were infected, but they have recovered on day t and developed an immunity. This also includes the people who have died [49]. Some authors name this compartment as a Removed compartment.
It is a mathematical modeling technique that uses ordinary differential equations to show the movement of individuals from one compartment to another in the corresponding epidemic. Over time the derivatives of SIR have been developed to capture the different epidemic situations. SEIR [48, 50] and SEIRD [19, 31] are such examples in which two other compartments have been introduced; exposed E(t) and deceased D(t).
E(t): The number of individuals who have been in contact with the infected people and are exposed to the disease on day t, but disease symptoms are not yet visible in them. Such individuals are called asymptomatic.
D(t): The number of causalities due to the spread of infectious disease on day t.
SEIRD model assumes that the exposed population is non-infectious, whereas it has been seen in COVID-19 cases that asymptomatic individuals are tested positive and are also responsible for spreading the disease. Hence, we have modified the SEIRD model to include infectivity in the exposed population. The SEIRD model has been modified with the introduction of parameter ‘ε’ (epsilon), which accounts for the part of the exposed population that is asymptomatic but infectious, and hence infecting others [8]. The proposed model is named as modified SEIRD model and is shown in Fig. 1.
Fig. 1.
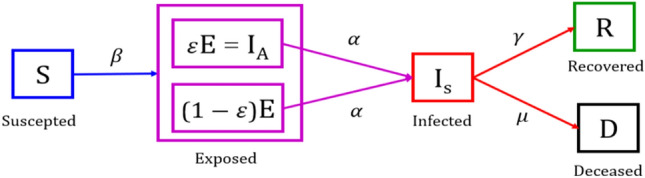
Modified SEIRD model
The following differential equations govern the modified SEIRD model:
1 2 3 4 5
Here, N = S + E + I + R + D, is the total population. Each person belongs to one of the four compartments, namely suspected, exposed, infected, recovered, and deceased. A person can shift from one compartment to another. The parameters used in Eqs. (1)–(5) regulate the shift of people among different compartments. These parameters are discussed below:
Beta (β): This parameter represents the transmission rate per capita. It denotes the number of persons who come in contact with an infected person per day.
Epsilon : This parameter denotes the proportion of exposed people that are infectious and unknowingly infecting other susceptible people.
Alpha : It represents the onset rate where is the average latent period.
Gamma : It represents the recovery rate where is the mean infectious period.
Mu : This parameter denotes the rate at which infected people become deceased.
To study the growth of the infection, researchers have used the basic reproduction number, Ʀ0, and effective reproduction number, Ʀe, as evaluation metrics in their work [25, 26]. Basic reproduction number Ʀ0 is defined as the average number of secondary infections generated when one infected person is introduced into a host population where everybody is susceptible. Ʀ0 is calculated by the following equation:
| 6 |
Effective reproduction number, Ʀe, is the average number of new infections generated by an infectious individual on day t, in the partially susceptible population S. It is calculated by the following equation:
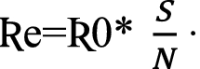 |
7 |
Equations (6) and (7) clearly show the increase by a factor in the value of Ʀ0 and the corresponding increase in Ʀe by the exposed infectious population. Hence, the parameter , representing the proportion of the infectious exposed population, contributes to the growth of COVID-19. A high value of this parameter indicates that there are more infectious exposed persons, and contact tracing should be done so that these persons can be isolated to reduce the spread of the disease.
Long Short-Term Memory (LSTM) Model
Deep learning (DL) is a branch of machine learning which is inspired by the working of the human brain. Some of the popular DL techniques are deep neural network (DNN), convolutional neural network (CNN), recurrent neural network (RNN), etc. RNNs are an extension of DNNs that consist of feedback links along with feed-forward connections [17]. Unlike a DNN, RNNs use the previous output to compute the next output. Therefore, they can efficiently process natural language, recognize speech, and perform image captioning compared to other DL techniques [15].
RNN suffers from the problem of vanishing and exploding gradient [18]. To solve these problems, LSTM networks are used. LSTM is an extension of RNN, which allows the network to learn long-term dependencies in the input data. It processes and predicts time-series data very efficiently. Each LSTM cell comprises of three gates: Input Gate, Forget Gate, and Output Gate. Figure 2 depicts these three gates present in each LSTM cell.
Fig. 2.
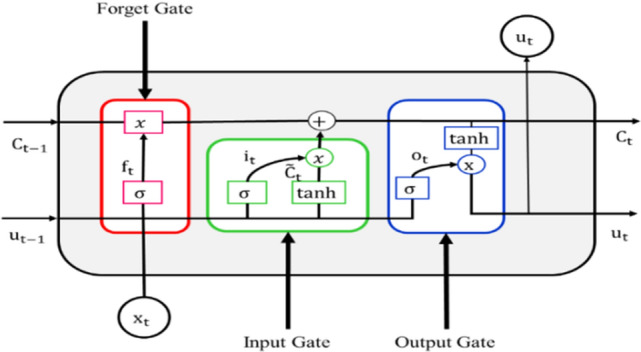
LSTM cell
The following equations are used in LSTM cells. and are the weights and biases, respectively:
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
In each LSTM cell, activation function is used, which distributes the gradients computed in the backpropagation algorithm while training the LSTM network [15]. Hence, it solves the vanishing and exploding gradient problem of RNN.
As the data of COVID-19 are time-series data and LSTM models time-series data very well, so LSTM has been used for prediction in our work.
Experimental Setup and Results
In this section, the experimental setup and results are discussed in detail.
Experimental Setup
In this paper, the experimentation was performed in Python using Jupyter Notebook and PyCharm Integrated Development Environment. COVID-19 data were collected for India as well as its four states having the highest number of total cases. The epidemiological data till 6th September 2020 were taken from the covid19india.org website [12]. For India, the data for confirmed, recovered, and deceased cases are available since 30th January 2020. For the states, the data are available from 14th March 2020. In the case of India, data are available for daily confirmed, total confirmed, daily recovered, total recovered, daily deceased, and total deceased cases. Therefore, no pre-processing was required for the data of India. However, in the case of states, only daily confirmed, daily deceased, and daily recovered cases were available. Therefore, pre-processing was performed on these data to obtain total confirmed, total deceased, and total recovered cases for all states. These have been calculated by taking the cumulative sum of daily confirmed cases, daily deceased cases, and daily recovered cases, respectively.
For experimentation, the proposed modified SEIRD, an epidemiological model, and LSTM, a deep learning-based model, have been used to make predictions. Further, both models have been statistically analyzed using a t test. The experimental setup for both of these models has been described in the upcoming sub-sections.
Experimental Setup for the Proposed Modified SEIRD Model
For experimentation, the proposed modified SEIRD model uses various parameters mentioned in “Proposed Modified SEIRD Model”. The values of these parameters, β, ε, α, γ, and , have been estimated in this paper using different functions of Python’s lmfit library. The minimize function has obtained the optimized values of these parameters. This function uses the least square method for obtaining an optimal solution. The initial value of infected, I0, is taken as 1 based on the assumption that the infection started from one person. The initial value of each of exposed, E0, recovered, R0, and deceased, D0, is initialized to 0. The value of S0 is calculated by the following equation:
| 14 |
Using the data of a Lockdown period, the value of β and other parameters have been calculated. There are four lockdown and four unlock periods in India to date. Hence, the data are divided into nine time periods: Before Lockdown [30th January–24th March], Lockdown 1.0 [25th March–14th April], Lockdown 2.0 [15th April–3rd May], Lockdown 3.0 [4th May–17th May], Lockdown 4.0 [18th May–31st May], Unlock 1.0 [1st June–30th June], Unlock 2.0 [1st July–31st July], Unlock 3.0 [1st August–31st August] and Unlock 4.0 [1st September onwards].
To obtain the optimal values of the parameters, the proposed modified SEIRD model takes an initial value, lower bound and upper bound, as input for each parameter. For India, the initial value of β was taken as 0.5 with bounds [0.001, 1]. The parameter ε was initialized to 0.1 with bounds [0.0001, 1]. For α, the initial value taken was 1/5, and its bounds were [1/6, 1]. For parameter γ, the initial value was 1/10 with [1/14, 1] as bounds. For parameter , 0.001 was the initial value, and [0.001, 1] were the selected bounds. For the four states, the same initial values and bounds have been taken except for the lower bound of which was taken as 0.005. The optimal parameter values for curve fitting obtained for a particular Lockdown/Unlock period are used for obtaining the predictions in the next lockdown/unlock period. Figure 3 shows the object flow diagram for the proposed modified SEIRD model.
Fig. 3.
Object flow diagram for the modified SEIRD model
The next subsection describes the experimental setup required by the LSTM model for predicting the COVID-19 trend.
Experimental Setup for LSTM Model
The six different time-series of daily confirmed, daily recovered, daily deceased, total confirmed, total recovered, and total deceased for India and its states obtained after pre-processing have been used for creating one LSTM for each of these series. These models have been created using the Keras API. Since LSTM is very sensitive to the range of data provided to it as input; therefore, pre-processing was required to normalize the input data to [0, 1]. Normalization was done using the following equation through the MinMaxScaler function of the sklearn library:
| 15 |
After normalization, the input data were split into 80:20 ratios as training and testing datasets, respectively. Further, these datasets were divided into the feature set and the output value set. The dimensionality of the feature set and output value set depends on the hyper-parameter named number_of_previous_days. Its value signifies the number of previous days’ output used to predict the output for the current day. Length of the training set is taken as and value of number_of_previous_days as . The dimensionality of the feature set and output value set is taken as ) and respectively.
The LSTM models designed for confirmed and recovered time-series have four different LSTM layers, and each layer has 100 LSTM cells. On the other hand, the LSTM model designed for Deceased time-series also has four LSTM layers with 150 LSTM cells per layer. After LSTM layers, one fully connected layer was added with 100 neurons in the Confirmed and Recovered model and 150 neurons in the Deceased model with a linear activation function. After this, a fully connected layer was added with one neuron as the output layer and linear activation function.
The LSTM model uses the Adam optimizer and mean squared error (MSE) loss with batch size 16 and 100 epochs in this paper. To avoid overfitting of the model, dropout and early stopping was taken into account. In this paper, the probability of dropout is taken as 0.4 and the patience value for early stopping as 5, i.e., if the testing loss has not improved in consecutive five epochs, the training will stop.
Finally, these models were fine-tuned against the hyper-parameter, number_of_previous_days, for the data of India and its four states having the highest number of total cases. The value of this hyper-parameter ranges between 1 and 90. The value of number_of_previous_days was selected with minimum testing loss. The optimal values of this hyper-parameter for India and its four states having the highest number of total cases have been tabulated in Table 1. For the final predictions, the best performing LSTM model is taken as the optimal LSTM model. Figure 4 depicts the object flow diagram for the LSTM model.
Table 1.
The optimal values of number_of_previous_days hyper-parameter
| State/country | Optimal value of number_of_previous_days hyper-parameter | |||||
|---|---|---|---|---|---|---|
| Daily confirmed | Daily recovered | Daily deceased | Total confirmed | Total recovered | Total deceased | |
| India | 10 | 5 | 60 | 5 | 90 | 10 |
| Maharashtra | 10 | 5 | 80 | 5 | 5 | 5 |
| Andhra Pradesh | 60 | 5 | 5 | 5 | 5 | 60 |
| Tamil Nadu | 80 | 5 | 5 | 5 | 5 | 20 |
| Karnataka | 80 | 15 | 64 | 10 | 5 | 60 |
Fig. 4.
Object flow diagram for LSTM model
The results obtained by both the proposed modified SEIRD model and LSTM model are presented in the next subsection.
Results
This section discusses the predictions obtained by both the proposed modified SEIRD model and LSTM model for India and its four worst-affected states. The proposed modified SEIRD model performs both short-term and long-term predictions, whereas LSTM performs only short-term predictions. Further, the predictions obtained by both models have been statistically analyzed using a t test. The corresponding results are discussed in detail below.
Short-Term Predictions Obtained Using the Proposed Modified SEIRD and LSTM Models
This section discusses the short-term predictions performed using the proposed modified SEIRD model as well as the LSTM model for India and its four worst-affected states for the next 30 days, i.e., from 7th September 2020 till 6th October 2020. The predictions for six time-series, namely, daily confirmed, daily recovered, daily deceased, total confirmed, total recovered, and total deceased, have been obtained using both the models. Case fatality rate, recovery rate, and mean absolute percentage error (MAPE) defined mathematically using the following equations have also been computed to analyze the results:
| 16 |
| 17 |
| 18 |
The recovery rate and case fatality rate on 7th September 2020 and on 6th October 2020 (30 days from now) for both the models have been given in Tables 2 and 3, respectively.
Table 2.
Recovery and case fatality rate for India and its four worst-affected states on 7th September 2020
| Country/state | Actual recovery rate (%) | SEIRD recovery rate (%) | LSTM recovery rate (%) | Actual case fatality rate (%) | SEIRD case fatality rate (%) | LSTM case fatality rate (%) |
|---|---|---|---|---|---|---|
| India | 77.27 | 77.36 | 77.03 | 1.69 | 1.70 | 1.71 |
| Maharashtra | 71.03 | 71.35 | 71.57 | 2.93 | 2.94 | 2.96 |
| Andhra Pradesh | 79.10 | 79.06 | 81.17 | 0.89 | 0.91 | 0.92 |
| Tamil Nadu | 87.21 | 87.22 | 87.02 | 1.69 | 1.70 | 1.68 |
| Karnataka | 73.48 | 73.23 | 74.74 | 1.46 | 1.55 | 1.52 |
Table 3.
Predicted recovery and case fatality rate for India and its four worst-affected states on 6th October 2020
| Country/state | SEIRD recovery rate (%) | LSTM recovery rate (%) | SEIRD case fatality rate (%) | LSTM case fatality rate (%) |
|---|---|---|---|---|
| India | 79.49 | 85.14 | 1.47 | 1.77 |
| Maharashtra | 62.79 | 73.53 | 2.22 | 3.07 |
| Andhra Pradesh | 93.70 | 92.73 | 0.89 | 0.96 |
| Tamil Nadu | 92.11 | 88.73 | 1.76 | 1.60 |
| Karnataka | 79.13 | 70.88 | 1.01 | 1.25 |
It can be observed from Table 2 that the values of recovery rate calculated by both the models are very close to the actual recovery rate values on 7th September 2020. Similarly, the case fatality rates computed by both the models for India and its four states in consideration closely resemble the actual case fatality rates. Moreover, the recovery rates and case fatality rates achieved by the proposed model are similar to the values obtained by LSTM as well. This indicates that the proposed modified SEIRD model can accurately predict the trend of COVID-19 in India and its states by modeling all the essential parameters correctly.
The short-term predictions performed by the proposed modified SEIRD model show that by 6th October 2020, the recovery rate for India may increase by more than 2%, and the case fatality rate may decrease by less than 0.23%. For the state of Maharashtra, the proposed model shows a drop of around 8% in the recovery rate and a drop of about 0.7% in the case fatality rate. Surprisingly, LSTM shows a drastic reduction in the value of the recovery rate for this state. In Tamil Nadu, the proposed model predicts a positive change in the Recovery Rate, but the LSTM model predicts a reduction in this value. However, both the models agree on a gradual decline in the value of the case fatality rate for Tamil Nadu.
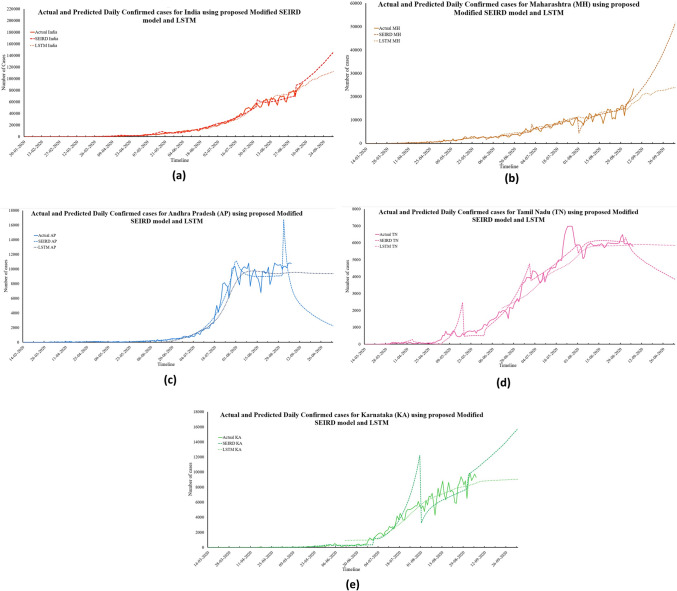
For the remaining three states, the proposed modified SEIRD model and the LSTM have similar predictions for the recovery rate of COVID-19 disease in the upcoming 30 days. Regardless, an opposite trend in the values of case fatality rates can be observed for Andhra Pradesh and Karnataka, where one model predicts a hike, but the other indicates a decline in the value. Figure 5a–e presents the predictions made by both the models for daily confirmed cases in India and its four worst-affected states.
Fig. 5.
a–e Actual and predicted daily confirmed cases for India and its four worst-affected states
Based on the predictions of the proposed modified SEIRD model, by October, the number of daily confirmed in India, Maharashtra, and Tamil Nadu will be 161,255; 56,421, and 3744, respectively. For Andhra Pradesh, Karnataka, this number is expected to be 2045 and 16,334, respectively. Similarly, using the LSTM model, the estimated number of Daily Confirmed cases is 115,693; 24,140; 9393; 5849; and 9056 for India, Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka, respectively.
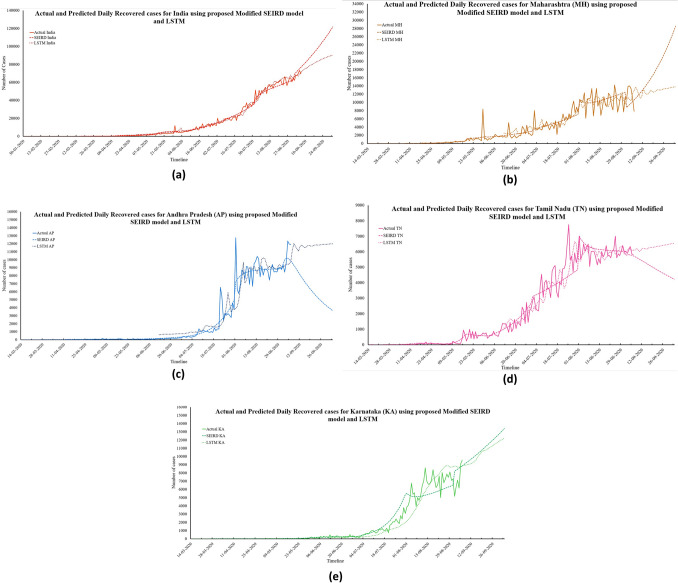
As it is evident from Fig. 5, that the predictions made by both the models were found to be significantly similar to each other. This claim is also verified by the values of mean absolute percentage error (MAPE) for both models. For the proposed modified SEIRD model, these values were 0.14, 0.12, 0.08, 0.15, and 0.26 for India and its four states, respectively. In the case of the LSTM model, MAPE values were 0.09, 0.15, 0.10, 0.22, and 0.51 for India, Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka, respectively. Figure 6a–e presents the predictions made by both the models for daily recovered cases in India and its four worst-affected states.
Fig. 6.
Actual and predicted daily recovered cases for India and its four worst-affected states
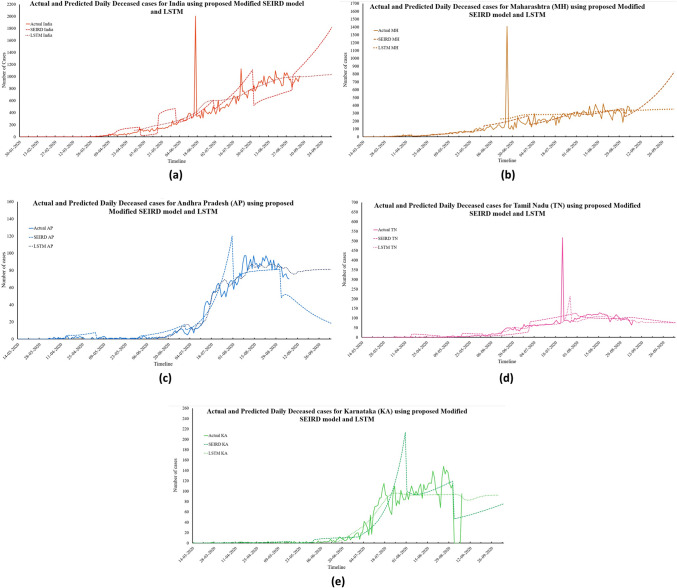
The graphs in Fig. 6 show a rising trend in the number of daily recovered cases. According to the proposed modified SEIRD model, there will 132,096; 31,322; 3302; 4094; and 13,949 daily recovered cases in India, Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka by 6th October 2020, respectively. However, based on the predictions obtained by the LSTM model, India and its four states will have 92,217; 14,015; 12,029; 6587; and 12,392 daily recovered cases. The proposed model was able to perform accurate predictions for this Daily Recovered time-series data. The MAPE values obtained from the proposed model were 0.20, 0.23, 0.16, 0.29, and 0.31 for India, Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka, respectively. Further, it was observed that during the celebration of Ganesh Puja, there was a sharp increase in the cases. Figure 7a–e presents the predictions made by both the models for daily deceased cases in India and its four worst-affected states.
Fig. 7.
Actual and predicted daily deceased cases for India and its four worst-affected states
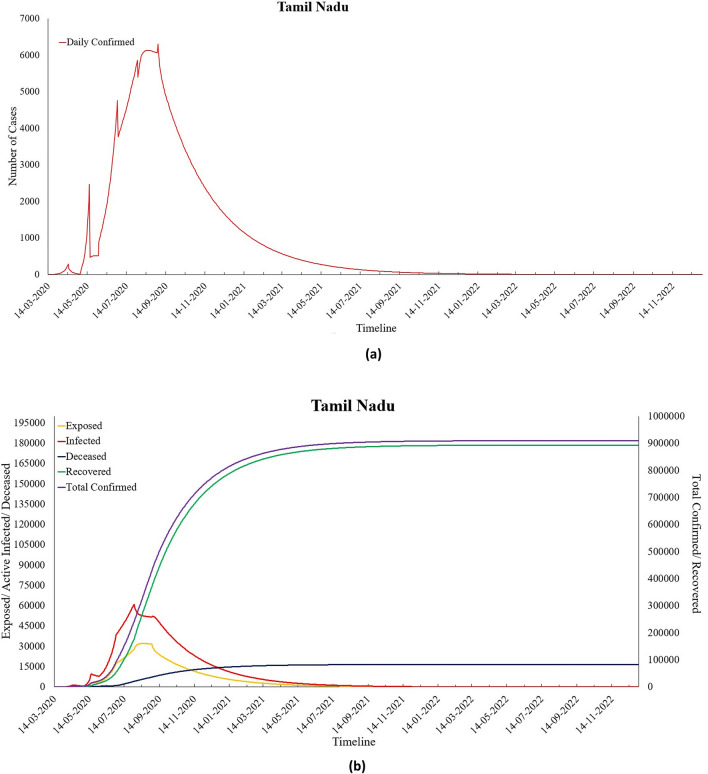
To lessen the impact of any pandemic, it is necessary to control the number of deceased patients. The trend of daily deceased individuals for the next 30 days can be observed in Fig. 13a–f. The proposed modified SEIRD model and the LSTM model predict 881 and 1254 Daily Deceased for India on 6th October 2020. For the four Indian states in consideration, this value will remain below 400, with 903, 17, 73, and 79 daily death cases estimated by the proposed model; and 355, 81, 75, and 92 daily deceased cases as per the LSTM model. Using the daily deceased cases, the proposed modified SEIRD model was able to obtain extremely accurate predictions. The MAPE values corresponding to both the models were found to be below 0.50 for India and its four states in consideration. Figure 8a–e presents the predictions made by both the models for total confirmed cases in India and its four worst-affected states, along with their confidence intervals obtained through t test.
Fig. 13.
a Predicted daily confirmed cases for Tamil Nadu and b predictions for Tamil Nadu
Fig. 8.
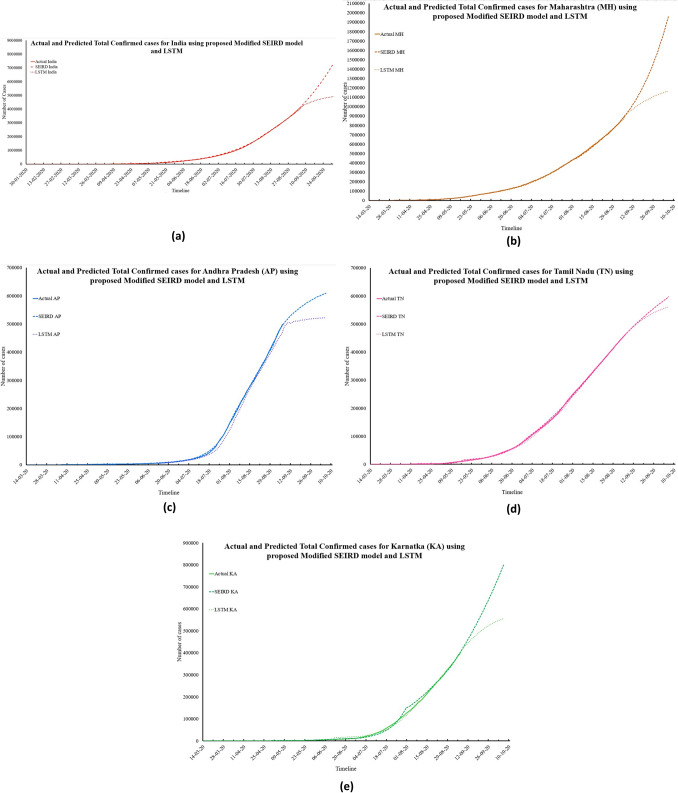
Actual and predicted total confirmed cases for India and its four worst-affected states
The predictions obtained by the proposed modified SEIRD model show that the number of total confirmed cases in India, Maharashtra, and Tamil Nadu will be 7,978,139, 1,958,813, and 597,125, respectively. For Andhra Pradesh and Karnataka, this number is expected to be 609,271 and 7,995,014, respectively. Similarly, using the LSTM model, the estimated numbers of total confirmed cases are 4,963,588; 1,165,173; 522,265; 561,403; and 555,945 for India, Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka, respectively. For the same time-series, the MAPE values for the proposed model were found to be 0.07, 0.01, 0.02, 0.06, and 0.09, corresponding to India and its four states, respectively. For the LSTM model, the corresponding MAPE values were 0.03, 0.02, 0.02, 0.08, and 0.23. These low error values indicate the effectiveness of the proposed modified SEIRD model in performing predictions. Figure 9a–e presents the predictions made by both the models for total recovered cases in India and its four worst-affected states, along with their confidence intervals obtained through t test.
Fig. 9.
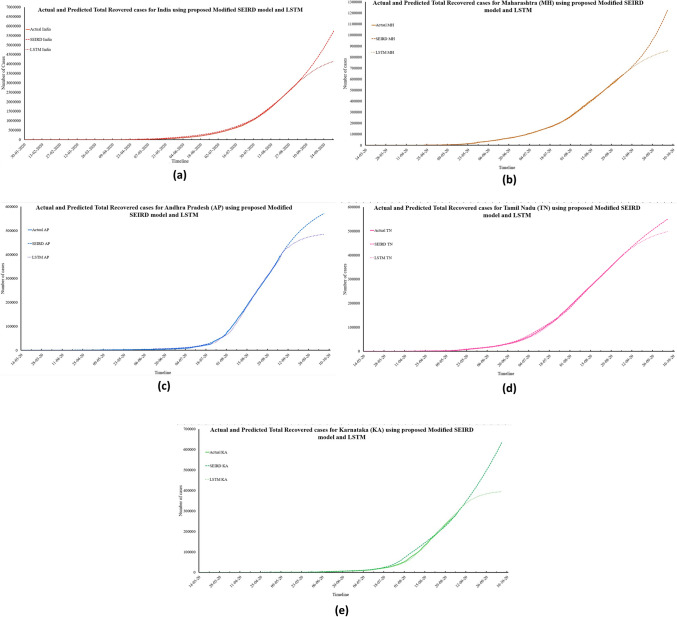
Actual and predicted total recovered cases for India and its four worst-affected states
Figure 9 depicts an increasing number of total recovered cases in the upcoming 30 days. According to the predictions made by the proposed modified SEIRD model, there will be 6,341,556; 1,230,034; 570,892; 550,029; and 632,678 total recovered cases in India, Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka by 6th October 2020, respectively. However, based on the predictions obtained from the LSTM model, India and its four states will have 4,225,898; 856,769; 484,299; 498,192; and 394,032 total recovered cases. Based on the above values, the MAPE for India was found to be 0.30 and 0.11 for the proposed modified SEIRD model and LSTM model, respectively. For Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka, the proposed model achieved MAPE of 0.01, 0.05, 0.2, and 0.1 respectively, whereas the LSTM model had MAPE values of 0.02, 0.04, 0.21, and 0.05, respectively. Figure 10a–e presents the predictions made by both the models for total deceased cases in India and its four worst-affected states, along with their confidence intervals obtained through t test.
Fig. 10.
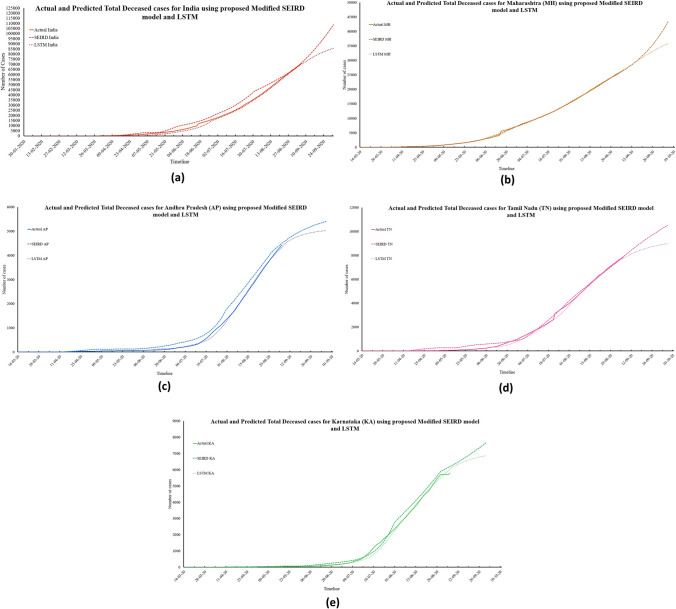
Actual and predicted total deceased cases for India and its four worst-affected states
The proposed modified SEIRD model and the LSTM model predict 117,380 and 87,711 cases for total deceased in India on 6th October 2020. For the four Indian states Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka in consideration, this count will be 43,415; 5402; 10,498; and 8108 for total death cases estimated by the proposed model; and 35,819; 5026; 8983; and 6933 for total deceased cases as per the LSTM model. For this time-series data, it was found that the predictions of the proposed model were highly synced with the predictions made by LSTM. This can be verified from the fact that for India, the proposed model and LSTM achieved low MAPE values of 0.11 and 0.03, respectively. Furthermore, the MAPE value for the proposed modified SEIRD model was found to be below 0.55 for all the four states in consideration. It was also observed that the states which have celebrated festivals (Ganesh Chaturthi in Maharashtra and Onam in Kerala) had seen a significant increase in COVID-19 cases and deaths as people moved out for the celebrations. Maharashtra celebrated Ganesh Chaturthi on 22 August, and according to a research report published by the State Bank of India, Maharashtra registered 3.7 lakh COVID-19 cases after the festival, which accounted for 46 percent of the total cases reported by the state. Similar was the case with Kerala, as Onam is celebrated for 10 days. This year it starts on August 22 and ends on August 31. According to the same report, there was an addition of 1.38 lakh cases after Onam, which is nearly 65% of all its cases. Both of these states show a sharp increase in cases in the first week of September itself.
Further, to verify the results obtained by both the models, statistical hypothesis testing using Student t test distribution has been performed. The actual and predicted values of total and daily cases of confirmed, recovered, and deceased for India and its four worst-affected states have been used for performing t test. The t test is used to perform a hypothesis test of the null hypothesis that both the models are performing equally well for short-term predictions. In this paper, a paired t test using two samples for means assuming unequal variance has been used. The null hypothesis and the alternate hypothesis are defined as follows:
| 19 |
| 20 |
where is the mean of the proposed modified SEIRD model and is the mean of the LSTM model in consideration.
A t test is used to estimate whether the observed data belongs to the null hypothesis or not. If the observed test statistic differs significantly from the hypothesized values, then the null hypothesis is rejected, and we claim the desired performance of the proposed algorithm by accepting the alternate hypothesis. For the experimentation, we have selected two values of α: 0.01 and 0.05, respectively. In statistical hypothesis testing using t test, probability p is calculated. If the value of p is less than 0.01, then the null hypothesis is rejected, and the alternate hypothesis is accepted with 99% confidence. Otherwise, p is rechecked with another value of α. If the p-value is less value than that of 0.05, the null hypothesis is rejected, and the alternate hypothesis is accepted with 95% confidence.
For daily confirmed cases, the p values obtained for India and its four states were less than 0.01 except for the state of Tamil Nadu. In the case of daily recovered predictions, all the p values were below the 0.01 significance level. Therefore, in both these cases, the null hypothesis is rejected, and the alternate hypothesis is accepted with 99% confidence. However, for the time-series data for daily deceased cases, the p values are greater than the significance level 0.01. However, these values are smaller than the second significance level, 0.05, selected for the experimentation. Therefore, the null hypothesis is rejected, and the alternate hypothesis is accepted at a 95% confidence level. Similarly, p values obtained for total confirmed, total recovered, and total deceased cases were less than 0.01, resulting in the acceptance of alternate hypothesis with 99% confidence.
The results mentioned above show that the predictions of the proposed modified SEIRD model closely correspond with the predictions obtained from the LSTM model. Since the LSTM model is only suitable for performing short-term predictions; therefore, the proposed model is used to calculate the long-term predictions of COVID-19 in India and its states into consideration. The results for the same are presented in the next section.
Long-Term Predictions Obtained Using the Proposed Modified SEIRD Model
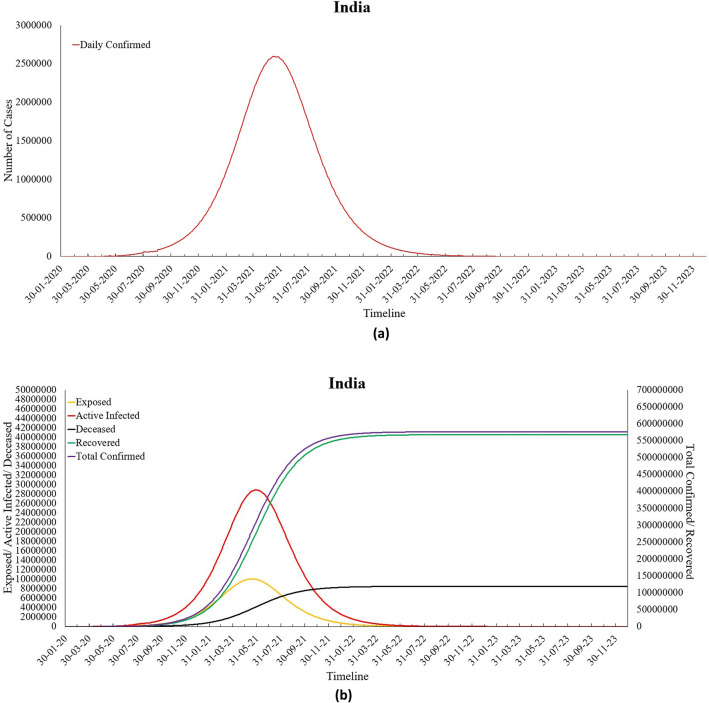
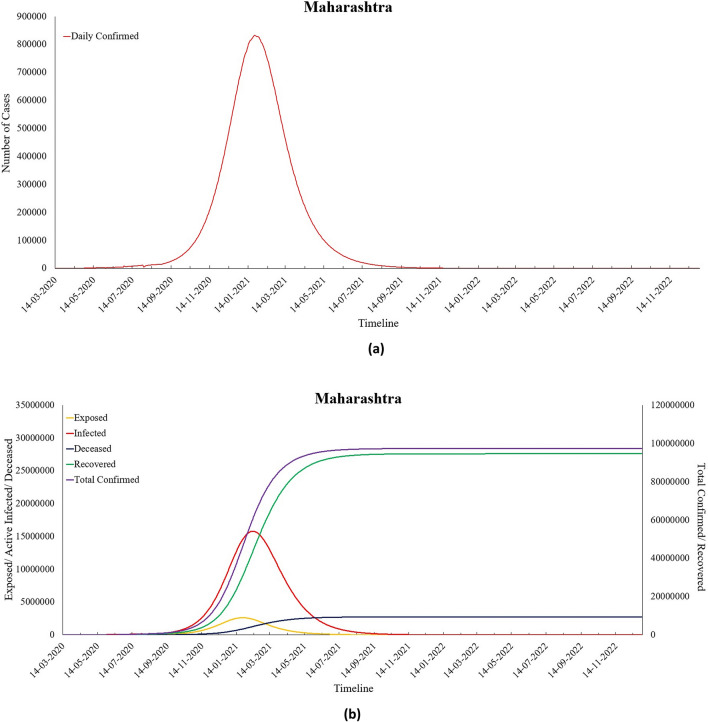
India is a geographically diverse nation, consisting of 36 states and union territories. Owing to India’s large population and high population density, the Indian government implemented various nationwide lockdowns to curb the spread of Coronavirus. Though the COVID-19 pandemic did not leave any state/union territory unaffected, some states have been far more affected by this deadly disease as compared to others. As of 6th September 2020, the top four Indian states with the highest number of total confirmed cases are Maharashtra, Andhra Pradesh, Tamil Nadu, and Karnataka. The estimates for the COVID-19 peak in India and its four worst-affected states have been provided in Table 4. It can be observed from this table that India will witness its peak by the end of May 2021. The number of Daily cases at the peak in India will be 2,575,464 with 28,851,377 number of active cases and 307,485,213 number of total confirmed cases. Similar results have also been tabulated below for the four worst-affected states of India. The curve for daily confirmed cases for India has been shown in Fig. 11a, while Fig. 11b presents the curves for exposed, active infected, recovered, deceased, and total confirmed cases for India. Table 5 shows the parameter values obtained for India by the proposed modified SEIRD model.
Table 4.
Estimates for the peak of COVID-19 pandemic in India and its four worst-affected states
| Country/state | Time of peak | Daily cases at peak | Active cases at peak | Total confirmed cases at peak |
|---|---|---|---|---|
| India | 28th May 2021 | 2,575,464 | 28,851,377 | 307,485,213 |
| Maharashtra | 11th February 2021 | 762,463 | 15,786,451 | 60,196,367 |
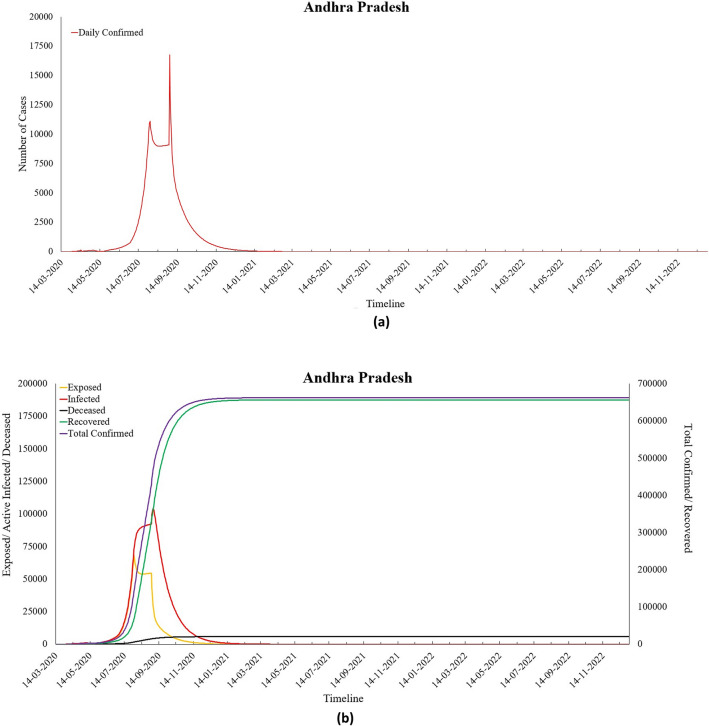
| Andhra Pradesh | 3rd September 2020 | 11,169 | 103,929 | 469,389 |
| Tamil Nadu | 31st July 2020 | 5863 | 61,022 | 241,205 |
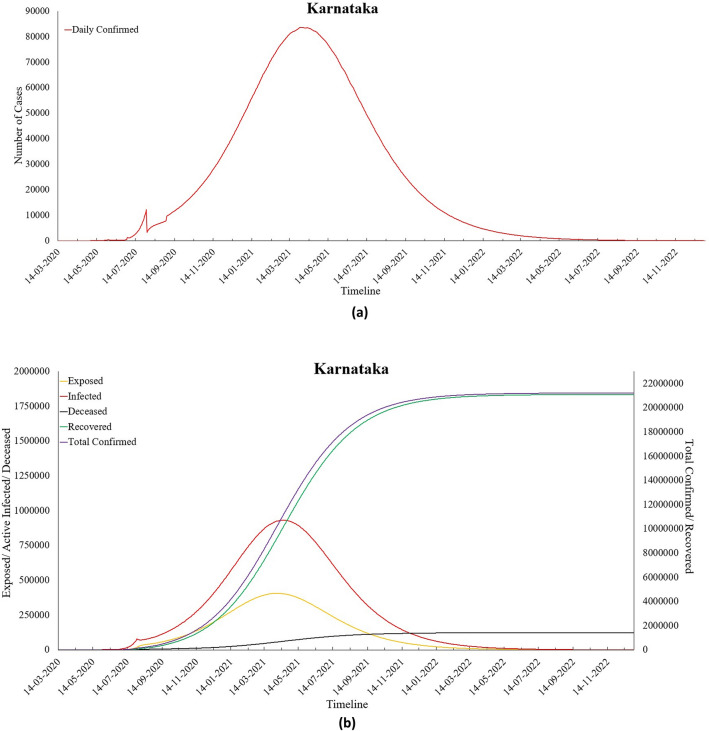
| Karnataka | 17th April 2021 | 82,922 | 931,483 | 1,1154,532 |
Fig. 11.
a Predicted daily confirmed cases for India and b predictions for India
Table 5.
Parameter values obtained for India
| India | Before lockdown | Lockdown 1.0 | Lockdown 2.0 | Lockdown 3.0 | Lockdown 4.0 | Unlock 1.0 | Unlock 2.0 | Unlock 3.0 | Unlock 4.0 |
|---|---|---|---|---|---|---|---|---|---|
| β | 0.162 | 0.306 | 0.095 | 0.239 | 0.084 | 0.082 | 0.119 | 0.066 | 0.115 |
| ε | 0.999 | 0.384 | 0.0001 | 0.0001 | 0.0001 | 0.999 | 0.0001 | 0.999 | 0.0001 |
| α | 0.166 | 0.166 | 0.166 | 0.185 | 0.166 | 0.166 | 0.166 | 0.206 | 0.258 |
| γ | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.081 | 0.087 |
| μ | 0.007 | 0.007 | 0.008 | 0.001 | 0.006 | 0.003 | 0.002 | 0.001 | 0.001 |
The results obtained for India witness a peak of COVID-19 cases for India on 28th May 2021 with 2,575,464 daily cases, and the disease may die out towards the end of the year 2023. These results are based on the current situation; however, these may vary depending on various decisions taken by the Indian government and the precaution measures taken by people from time to time. It can be seen from Table 2 that the value of β that represents the infection transmission rate per capita increased during Lockdown 1.0. This resonates with the decision of the Central government to extend the lockdown. The effect of lockdowns was also observed on the parameter , whose value reduced as lockdowns were extended, and people became aware of the importance of precautionary measures. However, during Unlock 1.0, the value of increased, thus, causing a rise in the number of exposed people. It was observed that both the parameters and decreased over time, except during Unlock1.0 when the government gave many relaxations, more people were exposed, and the value of suddenly increased. The increase in the value of signifies a reduction in the average latent period, and an increased depicts a reduction in the time to recover , resulting in an increase in recovery rate among the Indian population. There has also been a reduction in the value of the reproduction number for India, and it has reduced from Ʀ0 = 3.028 to Re = 1.124 as of 6th September 2020. This indicates that there has been a reduction in the number of secondary infections produced by an infected person. This positive change in parameter values can be attributed to the restrictions imposed by the Indian authorities. Next, Table 6 presents the parameter values obtained for the Maharashtra state, while its predictions have been shown in Fig. 12a, b.
Table 6.
Parameter values obtained for Maharashtra
| MH | Before lockdown | Lockdown 1.0 | Lockdown 2.0 | Lockdown 3.0 | Lockdown 4.0 | Unlock 1.0 | Unlock 2.0 | Unlock 3.0 | Unlock 4.0 |
|---|---|---|---|---|---|---|---|---|---|
| β | 0.297 | 0.239 | 0.092 | 0.075 | 0.071 | 0.062 | 0.067 | 0.066 | 0.094 |
| ε | 0.001 | 0.001 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.0001 |
| α | 0.999 | 0.434 | 0.397 | 0.515 | 0.999 | 0.499 | 0.977 | 0.286 | 0.318 |
| γ | 0.010 | 0.019 | 0.018 | 0.023 | 0.043 | 0.041 | 0.045 | 0.068 | 0.047 |
| μ | 0.004 | 0.013 | 0.003 | 0.003 | 0.002 | 0.004 | 0.002 | 0.002 | 0.001 |
Fig. 12.
a Predicted daily confirmed cases for Maharashtra and b predictions for Maharashtra
The Maharashtra state has witnessed the highest number of Coronavirus cases since the advent of the pandemic in India. The main reason behind this can be Maharashtra’s high population density and the presence of Asia’s largest slum named Dharavi. Due to this, Maharashtra had a very high Ʀ0 in the initial days of the pandemic. However, by mid-August 2020, Ʀe has reduced below 1.2 as computed by the proposed model. The proposed modified SEIRD model indicates that on 24th January 2021, Maharashtra will record 832,135 daily confirmed cases, which would be the highest for this state. The number of Total Confirmed cases would have crossed 45 million by that time, out of which 30 million would have recovered from this disease. For Maharashtra, the death rate has always remained higher than most of the other Indian states, and the recovery rate has been lower than the national average. Due to the severity of the infection, the Maharashtra government decided to extend the duration of restrictions imposed on its residents. However, several relaxations were offered during Unlock 3.0 and Unlock 4.0; the impact of this has been captured by the β parameter of the proposed model. Its value sees a decreasing trend until Unlock 2.0, but an increase in this value can be seen during Unlock 3.0 and Unlock 4.0. Surprisingly, a downfall in the proportion of exposed population is observed at the same time. However, under the prevailing circumstances, the proposed model predicts more than 2.7 million COVID-19 deaths in the state by the end of the year 2022. Table 7 shows the parameter values obtained for Tamil Nadu, while its predictions for Tamil Nadu have been shown in Fig. 13a, b.
Table 7.
Parameter values obtained for Tamil Nadu
| TN | Before lockdown | Lockdown 1.0 | Lockdown 2.0 | Lockdown 3.0 | Lockdown 4.0 | Unlock 1.0 | Unlock 2.0 | Unlock 3.0 | Unlock 4.0 |
|---|---|---|---|---|---|---|---|---|---|
| β | 0.451 | 0.207 | 0.001 | 0.339 | 0.045 | 0.152 | 0.104 | 0.073 | 0.096 |
| ε | 0.999 | 0.999 | 0.0001 | 0.0001 | 0.999 | 0.0001 | 0.0002 | 0.999 | 0.0001 |
| α | 0.166 | 0.293 | 0.166 | 0.999 | 0.166 | 0.278 | 0.213 | 0.191 | 0.203 |
| γ | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.080 | 0.116 | 0.111 |
| μ | 0.016 | 0.002 | 0.012 | 0.0005 | 0.002 | 0.0008 | 0.002 | 0.002 | 0.002 |
As of 6th September 2020, Tamil Nadu had the third-highest number of COVID-19 cases in India and has crossed 0.4 million total confirmed cases. The values of Ʀ0 and Ʀe for this state were found to be 7.86 and 0.98 (as of 6th September 2020), respectively, as calculated by the proposed model. Out of these, almost 87% of people have recovered, and 1.7% of people have succumbed to this deadly disease. This southern state of India witnessed a sharp spike in the number of COVID-19 cases since June 2020, and based on the predictions of the proposed modified SEIRD model, Tamil Nadu will have seen the peak already on 31st July 2020. By the end of the year 2022, it is projected that 1.1% of the state’s current population would have been infected from the virus and around 0.0002% of people would lose their battle against this pandemic. As shown in Table 7, the parameter values computed from the model indicate a hike in the recovery rate () as well as the death rate () in the state. Next, Table 8 presents the parametric values obtained by the proposed model for Andhra Pradesh, while Fig. 14a, b represents its predictions.
Table 8.
Parameter values obtained for Andhra Pradesh
| AP | Before lockdown | Lockdown 1.0 | Lockdown 2.0 | Lockdown 3.0 | Lockdown 4.0 | Unlock 1.0 | Unlock 2.0 | Unlock 3.0 | Unlock 4.0 |
|---|---|---|---|---|---|---|---|---|---|
| β | 0.322 | 0.240 | 0.095 | 0.001 | 0.120 | 0.167 | 0.122 | 0.100 | 0.055 |
| ε | 0.947 | 0.999 | 0.999 | 0.0001 | 0.999 | 0.0001 | 0.999 | 0.0001 | 0.0001 |
| α | 0.468 | 0.999 | 0.166 | 0.166 | 0.166 | 0.166 | 0.166 | 0.166 | 0.346 |
| γ | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.096 | 0.098 |
| μ | 0.0008 | 0.003 | 0.009 | 0.0005 | 0.0005 | 0.003 | 0.0017 | 0.0008 | 0.0005 |
Fig. 14.
a Predicted daily confirmed cases for Andhra Pradesh and b predictions for Andhra Pradesh
For Andhra Pradesh, it can be seen that the per capita transmission rate of the disease, represented by β, significantly increased during the fourth lockdown and the first unlock period. However, at the time of writing this paper, Andhra Pradesh, along with Tamil Nadu, has surpassed its COVID-19 peak. The state observed its peak on the 3rd September 2020 with the maximum recorded daily confirmed cases of 16,778. It can also be verified in Fig. 8a. There is a significant difference in the shape of the curve obtained for Andhra Pradesh and Tamil Nadu. The main reason behind this is that both these states saw a steep rise in the number of COVID-19 cases around the second half of the year 2020. This scenario can also be seen by observing the trend of their parameter values. The infection curve for Andhra Pradesh has started seeing a downward trend, which is also reflected by the increasing value of the recovery rate. In addition, the value of the reproduction number for Andhra Pradesh has gone below the value of 1, which indicates that the decline of this deadly disease in the state. Next, Table 9 presents the parameter values for the state of Karnataka, while Fig. 15a, b presents the predictions for the same.
Table 9.
Parameter values obtained for Karnataka
| KA | Before lockdown | Lockdown 1.0 | Lockdown 2.0 | Lockdown 3.0 | Lockdown 4.0 | Unlock 1.0 | Unlock 2.0 | Unlock 3.0 | Unlock 4.0 |
|---|---|---|---|---|---|---|---|---|---|
| β | 0.606 | 0.153 | 0.121 | 0.093 | 0.302 | 0.093 | 0.149 | 0.077 | 0.075 |
| ε | 0.217 | 0.0001 | 0.0001 | 0.999 | 0.0001 | 0.0001 | 0.999 | 0.391 | 0.999 |
| α | 0.166 | 0.166 | 0.166 | 0.166 | 0.166 | 0.166 | 0.721 | 0.166 | 0.206 |
| γ | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.071 | 0.089 |
| μ | 0.012 | 0.006 | 0.004 | 0.006 | 0.0005 | 0.003 | 0.003 | 0.001 | 0.0005 |
Fig. 15.
a Predicted daily confirmed cases for Karnataka and b predictions for Karnataka
The results obtained for Karnataka show that there will be a peak of COVID-19 cases on 17th April 2021 with 82,921 Daily infections, and the disease will die out towards the end of the year 2022. The values of Ʀ0 and Ʀe for Karnataka were found to be 8.05 and 1.20 (as of 6th September 2020), respectively, as calculated by the proposed model. Overall, β has reduced over time, which depicts a reduction in the transmission rate per capita in this state except lockdown 4.0 and Unlock 2.0. It was seen that during Unlock 1.0, ε, also reduced.
However, Unlock 2.0 witnessed a surge in its value, thereby indicating an increase in the number of exposed individuals as more relaxations were offered to the public. On average, it was found that γ, the recovery rate has increased in the state, leading to a higher number of recovered individuals. It can be seen from the results that the value of μ that denotes the rate of deceased population has decreased over time.
Conclusion and Future Work
With the exponential growth in the number of Corona Virus Disease 2019 (COVID-19) cases worldwide, countries need to prepare themselves with appropriate measures to tackle this epidemic. This can be achieved through proper predictions that can help the governments to take decisions accordingly and create more infrastructures if required. This prediction is particularly essential for a country like India, which ranks second in population size with high population density in several states. In this paper, a modified SEIRD (susceptible–exposed–infected–recovered–deceased) model was proposed and presented to perform COVID-19 predictions for India and its four states having the highest number of total cases. This model also considered asymptomatic infectious population for computing the predictions and the peak for the infection. Further, long short-term memory (LSTM) model was used in this paper to perform short-term predictions. Both models used the past reported data, hence the increased cases due to different festivals such as Ganesh Chaturthi, and Onam were considered eventually. To predict the trend of the pandemic, data up to 6th September 2020 was utilized for experimentation purposes. The results obtained by the proposed modified SEIRD model and LSTM model were compared for the next 30 days. The results were also statistically analyzed using a t test for short-term predictions. The effect of different lockdowns imposed in India was also analyzed and modeled in the proposed model. We obtained good results using the models presented in the paper for predictions, but the results can be improved further by considering and analyzing the age and comorbidity of the population.
Acknowledgements
The authors would like to acknowledge Prof. Daman Saluja and Ms. Apoorva Uboveja (B.R. Ambedkar Centre for Biomedical Research); Dr. Anita Mangla and Dr. Neeru Dhamija (Daulat Ram College), and Dr. Uma Chaudhary (Bhakaracharya College of Applied Sciences) of University of Delhi for the valuable discussion at an initial level that created our interest in carrying out this research.
Declarations
Conflict of Interest
The authors have no conflict of interest.
Footnotes
This article is part of the topical collection “Computer Aided Methods to Combat COVID-19 Pandemic” guest edited by David Clifton, Matthew Brown, Yuan-Ting Zhang and Tapabrata Chakraborty”.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Punam Bedi, Email: pbedi@cs.du.ac.in.
Shivani Dhiman, Email: shivani.mcs17.du@gmail.com.
Pushkar Gole, Email: pgole@cs.du.ac.in.
Neha Gupta, Email: neha.phd.2018@gmail.com.
Vinita Jindal, Email: vjindal@keshav.du.ac.in.
References
- 1.Acuña-Zegarra MA, Santana-Cibrian M, Velasco-Hernandez JX. Modeling behavioral change and COVID-19 containment in Mexico: a trade-off between lockdown and compliance. Math Biosci. 2020;325:108370. doi: 10.1016/j.mbs.2020.108370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ahmed S. Potential of age distribution profiles for the prediction of COVID-19 infection origin in a patient group. Inform Med Unlocked. 2020;20:100364. doi: 10.1016/j.imu.2020.100364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Anastassopoulou C, Russo L, Tsakris A, Siettos C. Data-based analysis, modelling and forecasting of the COVID-19 outbreak. PLoS ONE. 2020;15(3):e0230405. doi: 10.1371/journal.pone.0230405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Arora P, Kumar H, Panigrahi BK. Prediction and analysis of COVID-19 positive cases using deep learning models: a descriptive case study of India. Chaos Solitons Fractals. 2020;139:1–9. doi: 10.1016/j.chaos.2020.110017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Batista B, Dickenson D, Gurski K, Kebe M, Rankin N. Minimizing disease spread on a quarantined cruise ship: a model of COVID-19 with asymptomatic infections. Math Biosci. 2020;329:108442. doi: 10.1016/j.mbs.2020.108442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bhapkar HR, Mahalle PN, Dey N, Santosh KC. Revisited COVID-19 mortality and recovery rates: are we missing recovery time period? J Med Syst. 2020;44(12):1–5. doi: 10.1007/s10916-020-01668-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bhatia R, Abraham P. Lessons learnt during the first 100 days of COVID-19 pandemic in India. Indian J Med Res. 2020;151(5):387–391. doi: 10.4103/ijmr.IJMR_1925_20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brauer F, Driessche PV, Wu J. Lecture notes in mathematical epidemiology. Berlin: Springer; 2008. [Google Scholar]
- 9.Ceylan Z. Estimation of COVID-19 prevalence in Italy, Spain, and France. Sci Total Environ. 2020;729(2020):138817. doi: 10.1016/j.scitotenv.2020.138817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chakraborty T, Ghosh I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: a data-driven analysis. Chaos Solitons Fractals. 2020;135:1–10. doi: 10.1016/j.chaos.2020.109850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chatterjee K, Chatterjee K, Kumar A, Shankar S. Healthcare impact of COVID-19 epidemic in India: a stochastic mathematical model. Med J Armed Forces India. 2020;76(2):147–155. doi: 10.1016/j.mjafi.2020.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.COVID-19. From COVID19 India. 2020. https://www.covid19india.org/. Retrieved 2 June 2020.
- 13.Fong SJ, Li G, Dey N, Crespo RG, Herrera-Viedma E. Composite Monte Carlo decision making under high uncertainty of novel coronavirus epidemic using hybridized deep learning and fuzzy rule induction. Appl Soft Comput. 2020;93:106282. doi: 10.1016/j.asoc.2020.106282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Garba SM, Lubuma JM-S, Tsanou B. Modeling the transmission dynamics of the COVID-19 Pandemic in South Africa. Math Biosci. 2020;328:108441. doi: 10.1016/j.mbs.2020.108441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Goodfellow I, Bengio Y, Courville A. Deep learning. Cambridge: The MIT Press; 2016. [Google Scholar]
- 16.Hamzah FB, Lau CH, Nazri H, Ligot DV, Lee G, Tan CL, et al. CoronaTracker: worldwide COVID-19 outbreak data analysis and prediction. Bull World Health Organ. 2020;1:32. [Google Scholar]
- 17.Haykin S. Neural networks: a comprehensive foundation. 2. Upper Saddle River: Prentice Hall PTR; 1998. [Google Scholar]
- 18.Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. 1997;9:1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 19.Korolev I. Identification and estimation of the SEIRD epidemic model for COVID-19. J Econ. 2020 doi: 10.1016/j.jeconom.2020.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kumar A, Roy R. Application of mathematical modeling in public health decision making pertaining to control of COVID-19 pandemic in India. Spec Issue SARS-CoV-2 (COVID-19) Epidemiol Int (E-ISSN: 2455-7048). 2020;5(2):23–36.
- 21.Li L, Yang Z, Dang Z, Meng C, Huang J, Meng H, et al. Propagation analysis and prediction of the COVID-19. Infect Dis Model. 2020;5(7):282–292. doi: 10.1016/j.idm.2020.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li Y, Wang B, Peng R, Zhou C, Zhan Y, Liu Z, et al. Mathematical modeling and epidemic prediction of COVID-19 and its significance to epidemic prevention and control measures. Ann Infect Dis Epidemiol. 2020;5(1):1–9. [Google Scholar]
- 23.Luo J. When will COVID-19 end? Data-Driven Prediction. 2020. https://www.people.sutd.edu.sg/jianxi_luo/public_html/COVID19PredictionPaper.pdf.
- 24.Ma, J. Coronavirus: China’s first confirmed Covid-19 case traced back to November 17. China. 2020. https://www.scmp.com/news/china/society/article/3074991/coronavirus-chinas-first-confirmed-covid-19-case-traced-back. Retrieved 15 Aug 2020.
- 25.Mandal M, Jana S, Nandi SK, Khatua A, Adak S, Kar TK. A model based study on the dynamics of COVID-19: prediction and control. Chaos Solitons Fractals. 2020;136:109889. doi: 10.1016/j.chaos.2020.109889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mandal S, Bhatnagar T, Arinaminpathy N, Agarwal A, Chowdhury A, Murhekar M, et al. Prudent public health intervention strategies to control the coronavirus disease 2019 transmission in India: a mathematical model-based approach. Indian J Med Res. 2020;151(2–3):190. doi: 10.4103/ijmr.IJMR_504_20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Osman MA. A simple SEIR mathematical model of malaria transmission. Asian Res J Math. 2017;7(3):01–22. doi: 10.9734/ARJOM/2017/37471. [DOI] [Google Scholar]
- 28.Pal R, Sekh AA, Kar S, Prasad DK. Neural network based country wise risk prediction of COVID-19. Appl Sci. 2020;10:6448. doi: 10.3390/app10186448. [DOI] [Google Scholar]
- 29.Pan A, Liu L, Wang C, Guo H, Hao X, Wang Q, et al. Association of public health interventions with the epidemiology of the COVID-19 outbreak in Wuhan, China. JAMA. 2020;323(19):1915–1923. doi: 10.1001/jama.2020.6130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Patrikar S, Poojary D, Basannar DR, Kunte R. Projections for novel coronavirus (COVID-19) and evaluation of epidemic response strategies for India. Med J Armed Forces India. 2020;76(3):268–275. doi: 10.1016/j.mjafi.2020.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rajagopal K, Hasanzadeh N, Parastesh F, Hamarash II, Jafari S. A fractional-order model for the novel coronavirus (COVID-19) outbreak. Nonlinear Dyn. 2020;101(2020):711–718. doi: 10.1007/s11071-020-05757-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Roosa K, Lee Y, Luo R, Kirpich A, Rothenberg R, Hyman JM, et al. Short-term forecasts of the COVID-19 epidemic in Guangdong and Zhejiang, China: February 13–23, 2020. J Clin Med. 2020;9(2):1–9. doi: 10.3390/jcm9020596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sahoo BK, Sapra BK. A data driven epidemic model to analyse the lockdown effect and predict the course of COVID-19 progress in India. Chaos Solitons Fractals. 2020;139:110034. doi: 10.1016/j.chaos.2020.110034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Santosh K. COVID-19 prediction models and unexploited data. J Med Syst. 2020;44(9):1–4. doi: 10.1007/s10916-020-01645-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Santosh KC. AI-driven tools for coronavirus outbreak: need of active learning and cross-population train/test models on multitudinal/multimodal data. J Med Syst. 2020;44:93. doi: 10.1007/s10916-020-01562-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Shakil MH, Munim ZH, Tasnia M, Sarowar S. COVID-19 and the environment: a critical review and research agenda. Sci Total Environ. 2020;745(2020):141022. doi: 10.1016/j.scitotenv.2020.141022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Shi P, Dong Y, Yan H, Zhao C, Li X, Liu W, et al. Impact of temperature on the dynamics of the COVID-19 outbreak in China. Sci Total Environ. 2020;728(2020):138890. doi: 10.1016/j.scitotenv.2020.138890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shinde GR, Kalamkar AB, Mahalle PN, Dey N, Chaki J, Hassanien AE. Forecasting models for coronavirus disease (COVID-19): a survey of the state-of-the-art. SN Comput Sci. 2020;1(197):1–15. doi: 10.1007/s42979-020-00209-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Srikusan R, Karunamoorthy M. Implementing early detection system for Covid-19 using anomaly detection. In: Santosh KC, Joshi A, editors. COVID-19: prediction, decision-making, and its impacts, book series in lecture notes on data engineering and communications technologies. Barcelona: Springer Nature; 2020. pp. 1–141. [Google Scholar]
- 40.Sun J, Chen X, Zhang Z, Lai S, Zhao B, Liu H, et al. Forecasting the long-term trend of COVID-19 epidemic using a dynamic model. Res Sq. 2020 doi: 10.21203/rs.3.rs-31770/v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Taboe HB, Salako KV, Tison JM, Ngonghala CN, Kakaï RG. Predicting COVID-19 spread in the face of control measures in West Africa. Math Biosci. 2020;328:108431. doi: 10.1016/j.mbs.2020.108431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tomar A, Gupta N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures. Sci Total Environ. 2020;728:1–6. doi: 10.1016/j.scitotenv.2020.138762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wang S, Pan Y, Wang Q, Miao H, Brown AN, Rong L. Modeling the viral dynamics of SARS-CoV-2 infection. Math Biosci. 2020;328:108438. doi: 10.1016/j.mbs.2020.108438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.World Health Organization. Coronavirus disease (COVID-19). 2020. https://www.who.int/. Retrieved 13 Aug 2020.
- 45.Worldometer. COVID-19 coronavirus pandemic. 2020. https://www.worldometers.info/coronavirus/?. Retrieved 2 June 2020.
- 46.Worldometer. India population. 2020. Worldometer: https://www.worldometers.info/world-population/india-population/#:~:text=The%20current%20population%20of%20India,of%20the%20total%20world%20population. Retrieved 15 Aug 2020.
- 47.Xie J, Wang M, Liu R. Deep learning-based COVID-19 diagnosis and trend predictions. In: Joshi A, Dey N, Santosh K, editors. Intelligent systems and methods to combat Covid-19. Warsaw: Springer briefs in computational intelligence; 2020. pp. 57–66. [Google Scholar]
- 48.Yang Z, Zeng Z, Wang K, Wong S-S, Liang W, Zanin M, et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J Thorac Dis. 2020;12(3):165–174. doi: 10.21037/jtd.2020.02.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yi N, Zhang Q, Mao K, Yang D, Li Q. Analysis and control of an SEIR epidemic system with nonlinear transmission rate. Math Comput Model. 2009;50(9–10):1498–1513. doi: 10.1016/j.mcm.2009.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhao Z, Li X, Liu F, Zhu G, Ma C, Wang L. Prediction of the COVID-19 spread in African countries and implications for prevention and control: a case study in South Africa, Egypt, Algeria, Nigeria, Senegal and Kenya. Sci Total Environ. 2020;729(2020):138959. doi: 10.1016/j.scitotenv.2020.138959. [DOI] [PMC free article] [PubMed] [Google Scholar]