Abstract
Purpose:
To enable generation of high-quality deep learning segmentation models from severely limited contoured cases (e.g. ~10 cases).
Methods:
Thirty head-and-neck CT scans with well-defined contours were deformably registered to 200 CT scans of the same anatomic site without contours. Acquired deformation vector fields were used to train a principal component analysis (PCA) model for each of the 30 contoured CT scans by capturing the mean deformation and most prominent variations. Each PCA model can produce an infinite number of synthetic CT scans and corresponding contours by applying random deformations. We used 300, 600, 1000, and 2000 synthetic CT scans and contours generated from one PCA model to train V-Net, a 3D convolutional neural network architecture, to segment parotid and submandibular glands. We repeated the training using same numbers of training cases generated from 7, 10, 20, and 30 PCA models, with the data distributed evenly between each PCA model. Performance of the segmentation models was evaluated with Dice similarity coefficients between auto-generated contours and physician-drawn contours on 162 test CT scans for parotid glands and another 21 test CT scans for submandibular glands.
Results:
Dice values varied with the number of synthetic CT scans and the number of PCA models used to train the network. By using 2000 synthetic CT scans generated from 10 PCA models, we achieved Dice values of 82.8%±6.8% for right parotid, 82.0%±6.9% for left parotid, and 74.2%±6.8% for submandibular glands. These results are comparable with those obtained from state-of-the-art auto-contouring approaches, including a deep-learning network trained from more than 1000 contoured patients and a multi-atlas algorithm from 12 well-contoured atlases. Improvement was marginal when >10 PCA models or >2000 synthetic CT scans were used.
Conclusions:
We demonstrated an effective data augmentation approach to train high-quality deep learning segmentation models from a limited number of well-contoured patient cases.
Keywords: Data augmentation, principal component analysis, autosegmentation, convolutional neural networks, deep learning
1. INTRODUCTION
Precise image segmentation is crucial for accurate disease diagnosis and efficient radiation treatment planning.1 Deep learning has emerged recently as an effective tool for medical image segmentation with reduced human effort and variability.2-5 Modern deep learning segmentation models, such as convolutional neural networks (CNNs), have millions of trainable parameters and thus typically require an extensive set of data for training. The amount of well-curated data available for training is critically important for constructing a robust model for auto-segmentation.6 However, obtaining manual contours for training deep learning models is a time-consuming task and requires considerable expertise.7,8 In many clinical applications, the availability of well-curated training data is very limited. The sparsity of data is worsened by variation in image quality from differences in image acquisition procedures used across protocols, machines, and institutions. The accumulation of consistent and high-quality data remains a bottleneck to improving the segmentation performance of deep learning models.
Varied data augmentation approaches have been introduced to overcome this challenge by artificially increasing the amount of training data.9 Traditional data augmentation functions such as flipping or random rotation,10,11 random nonlinear deformation,12 or image cropping are used to synthesize new samples from original training data.13,14 These functions have proven to be effective in improving the performance of trained deep learning model. However, the augmented data are unable to represent actual patient population variations,15 and the data variation relies strongly on the manual choice of the applied transformations.16 To eliminate the bias resulting from the manual choice, Hauberg et al.17 developed an approach to learn digit-specific spatial transformations from learning data to create new samples. Ratner et al.18 proposed to combine domain-specific transformations by using a generative sequence model. Cubuk et al.19 constructed a search algorithm that could find the optimal augmentation policies to improve the classification accuracy. However, these transformations are simple and insufficient to capture many of the subtle variations in medical images. In most recent years, many deep learning methods have been developed for data augmentation. Zhao et al.20 used a deep learning model to learn appearance and spatial transformations to create new labeled magnetic resonance imaging (MRI) scans. Further, the image-to-image generative adversarial networks (GANs) technique has been widely used for synthesizing images for many medical imaging applications.21-24 For example, Frid-Adar et al.25 applied the GAN framework as data augmentation for liver lesion classification. However, the training of GANs typically requires a substantial amount of data,9,25,26 making it impractical when the availability of initial well-curated data is severely limited.
In this study, we proposed a simple but effective data augmentation approach by synthesizing labeled images with principal component analysis (PCA).27.This approach was developed based on creating synthetic images with known deformation.28 Instead of applying arbitrary deformations, we used a PCA-driven machine learning approach to capture actual anatomy variations in unlabeled patient populations.29,30 The learned anatomy changes were modeled to generate random deformations that can sample realistic variations in anatomy. Then, new synthetic images with the appearance of real patient anatomy were generated via applying the PCA-informed random deformations. These synthetic CT scans were used to train a CNN for auto-segmentation. We assessed the effectiveness of our data augmentation method for auto-segmenting parotid glands and submandibular glands on CT scans.
2. MATERIALS AND METHODS
2.1. Patient data
CT scans acquired during radiotherapy simulation and the corresponding clinical contours of 30 head and neck patients who received external photon beam radiation treatment at The University of Texas MD Anderson Cancer Center were used as templates to synthesize new training data. These contours were reviewed and approved by radiation oncologists sub-specializing in head and neck cancer. Another 200 CT scans without contours were used to sample anatomic differences in other patients with head-and-neck cancer. All 230 CT scans had the same voxel size of 1 mm × 1 mm × 2.5 mm. In this proof-of-principle study, we investigated the segmentation of parotid glands (two structures, left and right parotids) and submandibular glands (as a single structure). These structures were chosen because they are important organs at risk that must be spared during radiation treatment, but manually contouring them is not straightforward.
2.2. Learning anatomy variations
To perform data augmentation, we evaluated the application of a known deformation, representing realistic anatomy variations, to a well-contoured CT scan. This deformation was learned by capturing the most prominent variations between the CT scans with contours and those without contours through PCA.27 This learning process was developed from the active shape model.31,32 We first chose the 30 well-contoured CT scans as reference images, and then registered each of them to the other 200 CT scans without contours, using a dual-force demons deformable image registration algorithm.33 Before registration, we performed histogram equalization to match the contrast of the two images, using a number of 256 bins of the histogram. The histogram equalization was performed locally by separating the images into small blocks with a size of 20 x 20 voxels. A 6-level multiresolution scheme was used to accelerate the registration and improve the robustness. In demons registration, we used an upper bound of step size as 1.25, and the Gaussian variance of 1.5 for regularization of deformation vector fields. Refer to Wang et al.33 for details about this deformable registration algorithm.
The resulting deformation vector field (DVF) maps characterize the distribution of anatomic differences between the reference image and other images. Mathematically, the DVF maps can be represented by:
| #(1) |
where dx (., i), dy (., i) and dz (., i) are the displacement field matrices from image i, i = 1, 2, …, N, to the reference image along the left-right, anterior-posterior, and superior-inferior directions, respectively, and stands for the voxel position.
To create the active shape model, we vectorized the DVF for image i to be . For each reference image, we let be the matrix consisting of all the DVFs resulting from registration. We defined the sample covariance matrix of G as E:
| #(2) |
where denotes the mean deformation over N images, and T represents the transpose.
We calculated the eigenvalues and eigenvectors of the covariance matrix E to represent anatomy variations in the training dataset. Let λ and be the set of eigenvalues and eigenvectors of the covariance matrix E, respectively. They can be calculated by:
| #(3) |
According to the theory of PCA,27 a combination of a small number of eigenvectors corresponding to the large eigenvalues can capture the most prominent variations of the deformation. These eigenvectors consist a subset of and are known as principal modes. Assuming λ(1) ≥ λ(2) ≥ ⋯ ≥ λ(N), the first Mth eigenvectors are able to represent at least α percent of the total variations that deviate from the mean deformation. The first Mth eigenvectors should satisfy:
| #(4) |
where α stands for a value between 0 and 100. The principal modes, , , … , , and the mean deformation, , constituted the active shape model. For this study, we set the parameter α to 90, which means the active shape model represented at least 90% of the total variations in that patient population.
2.3. Synthesizing new samples
The acquired active shape model, named the PCA model, enables us to sample the most variations and generate a new random deformation, denoted by d, by using the equation:
| #(5) |
where βj is a random coefficient that quantifies the new deformation contributed by the jth eigenvector. To ensure that the new deformation is realistic, we set a maximum value, Dmax, for the randomly generated parameter (βj) based on the following equation:
| #(6) |
In our implementation, βj was generated using a uniform distribution in the range of . The Dmax was carefully chosen by manually reviewing the generated deformations with certain Dmax value. In this study, Dmax was set to 6 to ensure that the new deformations are reasonable and include a considerably large proportion of possible deformations.
Let the pair (x, lx) represent the reference CT scan and its corresponding contours, respectively, and let τk be the newly generated transformation representing the process of applying the generated random deformations (d). The synthetic CT scans were created by applying the transformations to the original well-contoured CT scans:
| #(7) |
| #(8) |
where represent the synthetic CT scan and corresponding contours, generated by transformation τ. Theoretically, an infinite number of synthetic CT scans can be created as the deformations can be generated randomly.
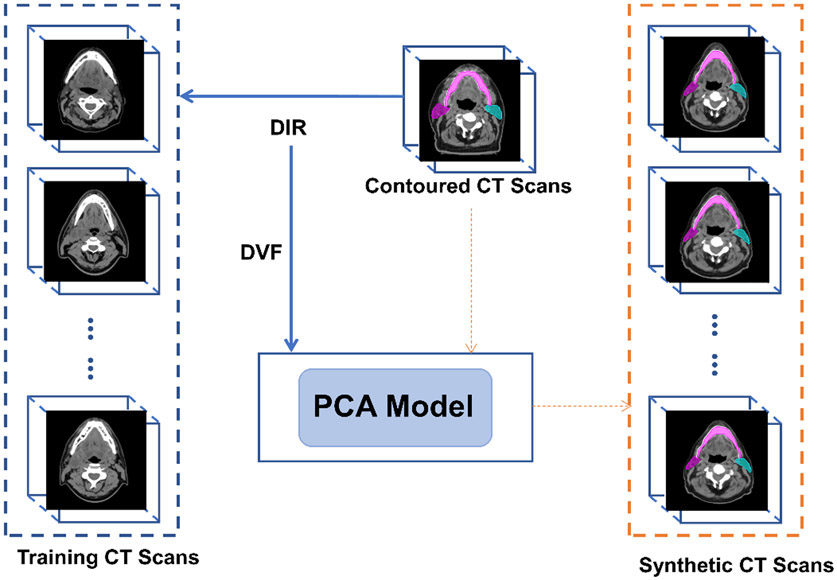
In brief, we first captured anatomic variations in the patient population by training an active shape model (PCA model). The synthetic CT scans and the corresponding contours were then created by applying random deformations to the reference CT scans. When creating the synthetic CT scans, DVFs in both directions are needed: the DVF from contoured CT scan to the random CT scan to generate contours on synthetic CT; and the DVF from the random CT scan to the contoured CT scan for backward image resampling to create random CT scan. The former DVF was the random deformation (d); and the latter DVF was created by inversing the former DVF using an iterative approach, similar to the one described by Yan et al.34 This process is summarized in Figure 1.
Fig. 1.
General workflow of the principal component analysis (PCA) approach to generate synthetic CT scans. Deformation vector fields (DVF) from deformable image registration (DIR) between a well-contoured image and other CT scans are used to create the PCA model. Then, the PCA model can simulate random deformations applied to the contoured CT scan, to create infinite number of synthetic CT scans with contours.
2.4. Training data
The aforementioned process was used to create 30 PCA models by using the 30 well-contoured CT scans as the PCA model template. Each PCA model can generate a random synthetic patient within a space of patient anatomy variations represented by the 200 CT scans without contours, and each individual model can produce an infinite number of synthetic CT scans and corresponding contours.
We used 300, 600, 1000, and 2000 synthetic CT scans and contours generated from a single PCA model to train a CNN-based model described in the next section for auto-segmentation of parotid and submandibular glands. Of the synthetic CT scans, 80% were used for training and 20% were used for cross validation. We repeated this process by using the same numbers of synthetic CT scans generated from 7, 10, 20, and 30 PCA models, with the scans distributed evenly between each PCA model. Scans generated from rough 80% of the total number of PCA models (e.g. 6 out of 7 PCA models) were used for training, and the scans generated from the rest of the PCA models were used for cross validation.
In addition, the CNN-based model was trained on subsets of 200, 300, 600, 1000, 1500, 2000, 5000, and 10,000 synthetic CT scans and contours generated from 10 PCA models to investigate the impact of training data quantity on the segmentation performance.
2.5. Segmentation model
In this study, we used V-Net,35 a three-dimensional CNN-based model, for autosegmentation. We modified the original V-Net architecture by adding batch renormalization layers to the end of each convolutional and up-sampling layer. During the network training, the parotid glands and submandibular glands were trained separately, and the patch size of the data for both training sets was set to 512 × 512 × 50. A previous study showed that the dimension of the parotid glands is typically 46.3 ± 7.7 mm along the longitudinal axis,36 and thus the patch size is sufficient to include the parotid glands in the longitudinal direction. The submandibular glands are smaller along the longitudinal direction (14.3 ± 5.7 mm).
In addition, the CT numbers were capped between–1000 HU to 3000 HU during training. We used the Dice similarity coefficient37 as the loss function in our implementation, and the Adam optimizer38 was chosen as the optimization algorithm with a learning rate of 5 × 10−4.
2.6. Evaluation
We evaluated the performance of the trained segmentation models for parotid glands by calculating the Dice coefficients between the auto-generated contours and the physician-drawn contours on 162 independent test CT scans from patients with head-and-neck cancer who received proton radiation treatment at MD Anderson Cancer Center. Among the 162 test scans, 156 contained the left parotid contours and 147 contained the right parotid contours. This test dataset is a subset of the test dataset used in Rhee et al.39 Other 21 CT scans with manual contours of submandibular glands were used as the test dataset for segmentation of submandibular glands.
For the comparison, we also used a paired non-parametric Wilcoxon signed-rank test at a significance level of 0.05 (defined by a p < 0.05) to evaluate whether a statistically significant difference exists between different models.
3. RESULTS
3.1. Synthesized CT scans
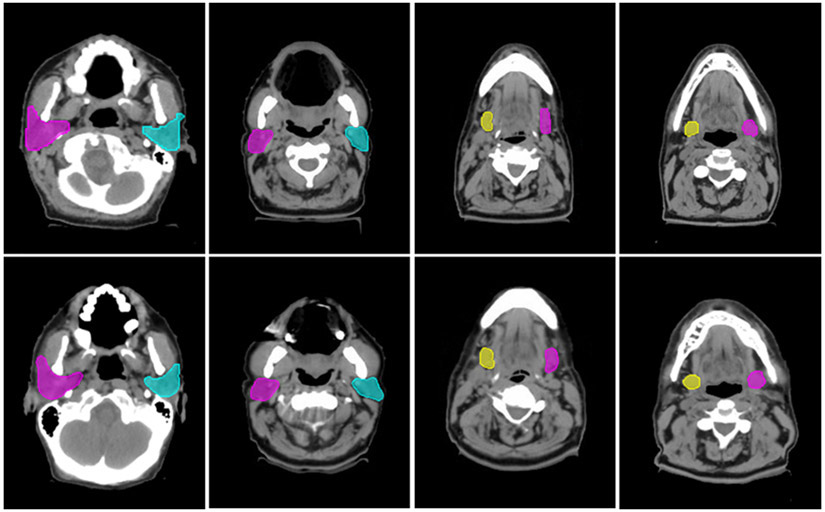
Our proposed data augmentation method enables the generation of synthetic CT scans to simulate realistic patients. Figure 2 shows some examples of the synthetic CT scans and the corresponding contours, depicting variations in the synthetic CT scans that emulate the real patient anatomy.
Fig. 2.
Comparisons between original and synthetic CT scans with contours. The top row are the original CT scans, and the bottom row are the corresponding synthetic CT scans.
3.2. Segmentation accuracy
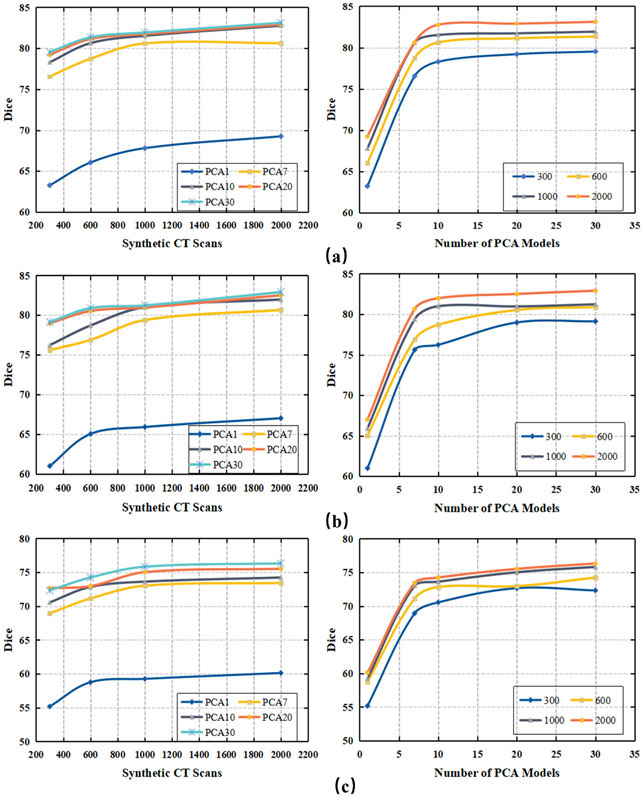
We investigated the extent of change in segmentation accuracy with the number of PCA models used to create the synthetic CT scans for training, and the number of synthetic CT scans used to train the segmentation model. In Figure 3, the segmentation performance was plotted varying with the number of synthetic CT scans used for training the results, and the number of PCA models used to create the synthetic CT scans. For left and right parotids, the Dice values were calculated based on the average results from 162 testing patients; for the submandibular glands, the results were calculated from the average of 21 testing patients. In general, use of more PCA models and more synthetic CT scans for the model training led to more accurate segmentation. In our particular evaluation, we achieved the best segmentation accuracy as Dice coefficients of 83.1%±6.1% (left parotid), 82.9%±6.7% (right parotid), and 76.3%±7.7% (submandibular glands) when 30 PCA models and 2000 synthetic CT scans generated from these PCA models were used to train the V-net model.
Fig. 3.
Dice values vary with the number of synthetic CT scans (shown in the left column) and the number of PCA models used to generate the synthetic CT scans (shown in the right column) for training the V-net. Different numbers of PCA models were used to generate the synthetic CT scans (e.g., PCA1 represents one PCA model). Numbers of synthetic CT scans were evenly distributed between the PCA models. (a) Left parotid; (b) right parotid; (c) submandibular gland.
3.3. Impact of the number of PCA models
The number of PCA models represent the number of well-contoured patients used for the data training. The goal is to use as few well-contoured patients as possible to train a high-performance deep learning segmentation model. In our study, using 1 PCA model led to Dice coefficient values of only 68.3% ± 11.1% for the left parotid, 66.5% ± 10.5% for the right parotid, and 60.1% ±8.5% for the submandibular glands. These findings indicate that using 1 patient as the PCA template cannot capture enough variations to train a good segmentation model. As we increased the number of PCA models from 1 to 10, the segmentation performance increased significantly for all 3 structures. The segmentation performance did not show obvious improvement (p > 0.05) when the PCA model number was increased from 10 to 30 when a sufficient number of synthetic CT scans (e.g., 2000) were generated for training the segmentation model. This observation showed that our data augmentation approach could train a high-quality segmentation model from as few as 10 well-contoured patients.
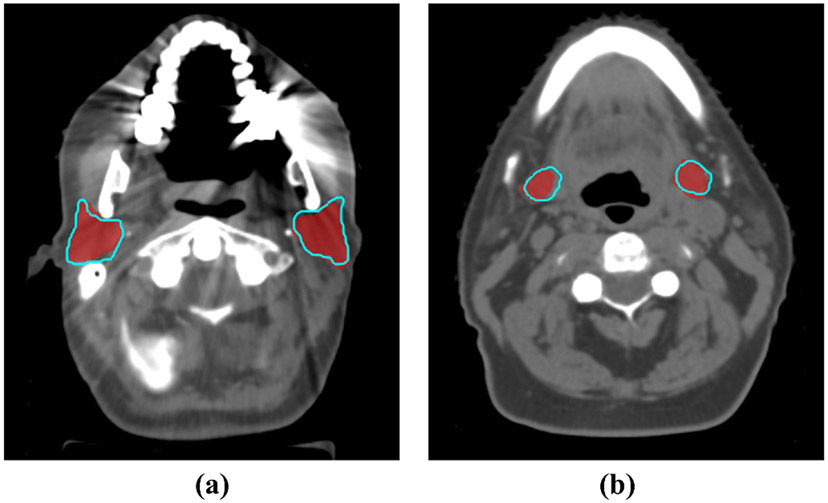
Figure 4 shows two examples of the segmentation results from the V-Net model trained from synthetic generated CT scans with 10 PCA models, compared with the physician-drawn contours. The auto-segmented contours are quite consistent with the manually delineated contours.
Fig. 4.
Physician-drawn contours (red colorwash) were compared with the auto-segmentation results (blue contours) by our networks trained on 2000 synthetic CT scans generated by 10 PCA models. (a) Parotid glands (Dice=86.9%). (b) Submandibular glands (Dice=82.0%).
3.4. Impact of the number of synthetically generated CT scans
The number of synthetic CT scans used for training affects the segmentation performance. We wished to determine a range of numbers of synthetic CT scans, with the goal of balancing the time needed for generating synthetic CT scans from PCA models and the accuracy of the segmentation. Figure 3 shows that segmentation accuracy increased considerably when the number of synthetic CT scans was increased from 300 to 1000. However, when more than 1000 synthetic CT scans were generated for training, the increase in segmentation performance slowed, with the curves becoming flat. In terms of segmentation accuracy, no statistically significant difference was found between using 1000 and 2000 synthetic CT scans for training (p > 0.05).
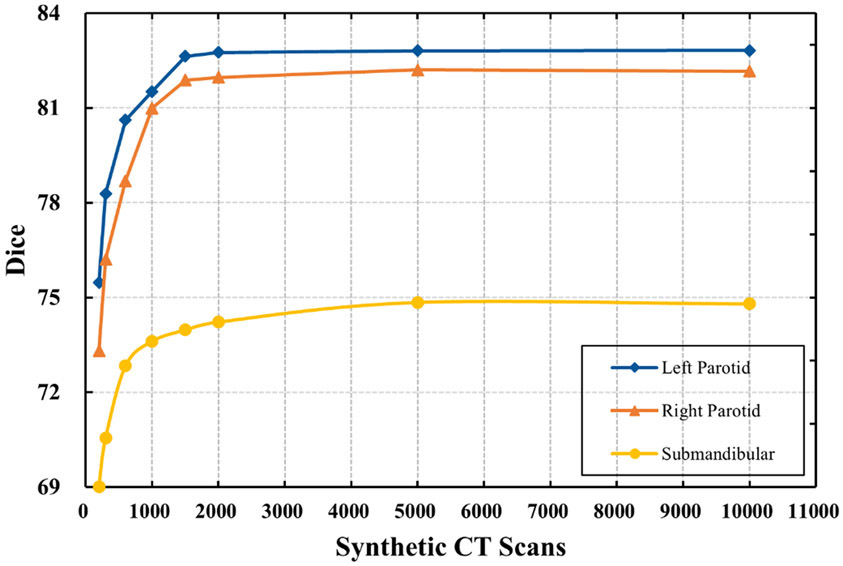
Although the difference between the models trained on 1000 and 2000 training cases was not significant (p > 0.05), the average Dice coefficient still increased. To validate this observation, we further evaluated the segmentation accuracy by training the V-Net model with 10,000 synthetic CT scans generated from 10 PCA models (Fig. 5). The results showed that the improvement in segmentation performance was still negligible when the number of synthetic CT scans was increased from 2000 to 10,000. Our study showed that using 2000 synthetic CT scans may be sufficient to obtain good segmentation of the structures under consideration.
Fig. 5.
Dice values varied with the number of synthetic CT scans used to train the V-net. Synthetic CT scans were generated from 10 PCA models, with the number of synthetic CT scans evenly distributed between the PCA models.
3.5. Comparison with the state of the art
To further evaluate our approach, we compared our segmentation performance with one of the state-of-the-art deep learning segmentation methods39 and a multi-atlas segmentation method, multi-atlas contouring service (MACS),37,40 used routinely in our clinic. The CNN-based segmentation model developed by Rhee et al39 was trained from more than 1000 well-contoured patients to segment the parotid glands. In this model, a two-dimensional (2D) CNN-based architecture, FCN-8s,41 was modified with additional batch renormalization layers added to the end of every layer. The MACS used 12 well-contoured atlases, which are a subset of our PCA model templates, to perform multi-atlas segmentation. The same test dataset was used to evaluate the segmentation performance of parotid glands for the 3 approaches. The comparison is summarized in Table 1. This comparison showed that by training from 10 well-contoured patients, we could achieve segmentation accuracy comparable to that of the state-of-the-art CNN-based segmentation model39 (p > 0.05). Compared with the MACS, our segmentation method showed comparable segmentation results when using more than 20 well-contoured patients, and the differences were not significant (p > 0.05).
Table 1.
Performance comparison between our models and state-of-the-art autocontouring tools.
| Segmentation Method | Dataset | Right Parotid | Left Parotid | Submandibular |
|---|---|---|---|---|
| Dice±SD | Dice±SD | Dice±SD | ||
| CNN (Rhee et al.39) | ~1000 (real) | 82.3±6.5 | 82.4±4.8 | NA |
| V-Net | ~1000 (real) | 81.4±5.9 | 81.3±5.5 | NA |
| MACS (Yang et al37)/MACS-AS (Yang et al42) | 12 (real)/20 (real) | 84.5±9.2 | 84.1±7.9 | 74.0±7.6 |
| PCA 10 | 2000 (synthetic) | 82.8±6.8 | 82.0±6.9 | 74.2±6.8 |
| PCA 20 | 2000 (synthetic) | 82.9±7.1 | 82.5±7.2 | 75.5±6.3 |
| PCA 30 | 2000 (synthetic) | 83.1±6.1 | 82.9±6.7 | 76.3±7.7 |
The best Dice results of PCA 10, 20, and 30 were chosen for comparison. MACS, multi-atlas contouring service; MACS-AS multi-atlas contouring service with atlas selection; V-Net means our V-Net model trained with the same training dataset of Rhee et al39. PCA, principal component analysis. PCA 10 means that 10 PCA models were used to create synthetic CT scans; SD: standard deviation.
However, the CNN-based segmentation by Rhee et al39 was developed based on a modified FCN-8s41 architecture, which is different from the V-Net architecture used in our approach. For a comparison, we used the same training dataset of Rhee et al39 (more than 1000 well-contoured patients) to train our V-Net model for parotid segmentation. Using the same test dataset, the average Dice coefficient was 81.4% ± 5.9% for the right parotid, and 81.3% ± 5.5% for the left parotid. This confirmed that our proposed data augmentation approach with more than 20 well-contoured patients could achieve better performance than a CNN model trained from more than 1000 well-contoured patients (p < 0.05).
The CNN-based segmentation39 was not trained to segment the submandibular glands. For comparison, we used the same test dataset (21 patients) to compare the results from multi-atlas segmentation with atlas selection (MACS-AS).42 The segmentation of MACS-AS was obtained by using the leave-one-out test. Among the 21 patient scans, when 1 scan was set as testing, MACS-AS chose 12 or less most similar patients as atlases to perform a multi-atlas segmentation. This comparison is also shown in Table 1. When we used 10 PCA models, we achieved performance similar to that of the MACS-AS, with a Dice value of 74.2%±6.8%. When we used 30 PCA models for training, our approach outperformed the MACS-AS.
4. DISCUSSION
We proposed an effective data augmentation method using the PCA method, which can create synthetic CT scans to train deep learning segmentation models. This approach was able to learn the anatomy variations in a patient population through the simple PCA method. We tested our approach on the segmentation of parotid and submandibular glands with great success. The segmentation accuracy was comparable with that of state-of-the-art deep learning segmentation approaches. Essentially, our approach enabled deep learning model training from a severely limited dataset (only 10 well-contoured patients), making the deep learning segmentation widely applicable in varied clinical situations with limited contoured datasets, one example being newly emerging technology for which patient data are limited, such as MR-Linac patient treatment.43 On the other hand, using our approach can also greatly reduce the effort in curating the training data for deep learning models, making deep learning more practical for clinical use. One need only curate 20 or fewer well-contoured head-and-neck patients instead of 1000 patients to train a high-performance deep learning model for most normal tissue auto-contouring. In this study, we used V-Net to demonstrate the effectiveness of our data augmentation approach. However, this approach can be used with any other supervised deep learning segmentation networks.
All of the PCA model-training and synthetic CT scan-generating were implemented in C++ and were performed on a PC (Intel i5-8500 CPU, 32 GB RAM). Each PCA model took about 26 hours to create, and each synthetic CT scan took about 6 minutes to generate. For this study, we used a high-performance computing cluster with four GPU nodes at MD Anderson, for which each node contains four V100 GPUs. We used only two of the GPUs to train our deep-learning segmentation models because of resource sharing. Training took about 4 hours when using 300 synthetic CT scans, 9 hours when using 600 scans, 19 hours when using 1000 scans, and 36 hours when using 2000 scans. The segmentation took about 30 seconds for each patient, making the model quite practical for clinical implementation.
There is a clear trend of improvement in segmentation performance when using more PCA models or more training cases, as shown in Figure 3. However, we noticed that the Dice value decreased from 80.99% ± 7.2% to 80.96% ± 6.8% when increasing the number of PCA models from 10 to 20 with 1000 synthetic CT scans for right Parotid segmentation. This decrease is not significant though. A possible explanation might the limited anatomic variations of the PCA models. With 1000 random synthetic CT scans, it might not be enough to capture necessary variations with more PCA models. Using more synthetic CT scans (e.g., 2000 scans) to train the CNN model can overcome this issue, which has been demonstrated in our results. In addition, using more CT scans to create PCA models could potentially address this issue also.
The performance comparison between our approach and other state-of-the-art auto-segmentation tools in Table 1 shows that our approach is comparable to or even outperform some state-of-the-art auto-segmentation approaches. Although our approach did not outperform MACS in terms of segmentation accuracy in this validation, our approach was about 20 times faster in performing a segmentation task than MACS, which normally took about 10 minutes to segment one patient. Also, Rhee et al39 has shown that the CNN-based segmentation was more robust than MACS in some extreme cases, such as irregular patient positioning or abnormally large tumors.
We used the parotid and submandibular glands to demonstrate our approach. These two organs were selected because contouring them, either manually by clinicians or automatically by segmentation algorithms, is often challenging. Their contrast with surrounding tissues is low on CT scans, and their shape and appearance vary significantly from patient to patient. Also, dental artifacts can often affect parotid contouring. Given our success in using this approach to auto-segment the parotid and submandibular glands, we are confident that this approach can be extended to other structures in head and neck, and even other anatomic sites. Moreover, because we previously showed that the PCA model can be used to create synthetic MR images for validating deformable registration algorithms,44,45 we are confident that we can extend this approach for MRI-based auto-segmentation as well.
The dual-force demons registration algorithm33 was used to capture the anatomical variations between difference patients to create PCA models. The accuracy of the registration algorithm has been validated in clinical settings both quantitatively and qualitatively for head and neck cancer radiotherapy28,46-49 However, it is worth mentioning that the registration accuracy is not an important concern in our study. In the PCA models, only prominent anatomical variations were kept to represent inter-patient variations. Detailed patient-to-patient registration could be left out from the model if the variation it represents is not typical in the patient population. Rather than registration accuracy, our approach only needs to capture meaningful and realistic anatomical variations so that the synthetic CT created from the PCA models could be close to real patient anatomy. This could be visually verified from the synthetic CT images illustrated in Figure 2.
Training the PCA model and generating synthetic CT scans using the PCA model were straightforward. Our validation demonstrated the effectiveness of the PCA model in capturing anatomic variations among the patient population, and the application of this for deep learning model training. Thus, the PCA model is an attractive tool for the preparation of training data. The PCA model can use a small number of principal components to simulate a large variation space by learning the variations from a group of patients. However, there are limits to the learning capability of any PCA model, so the number of PCA models could affect the segmentation accuracy, because one PCA model may not capture enough variations. The CT images used to train the PCA model could affect the segmentation performance as well. All CT images used to train the PCA model, and the test data, were from our institution. If the trained V-Net model is used to segment CT scans obtained outside our institution, the performance might be impacted.
Recent years, many deep learning-based data augmentation methods have been proposed to overcome the data sparsity in medical imaging.20,25,9,50 Particularly, GANs received increased attention for data augmentation due to its performance. However, some researchers have reported that the synthetic image quality from GANs might not be good enough. As in a visual Turing test reported by Frid-Adar et al.25, two experts could identify 62.5% and 58.6% of the GAN-synthesized liver lesion images. Although GANs have been improved with current cutting-edge architectures, they still could not produce a synthetic image with good fidelity.50 In our approach, image quality of the synthetic CT scans is not an issue since they were deformed from actual CT images. Moreover, training a high-quality GAN requires a substantial amount of training data.9 Therefore, GANs might not be a practical data augmentation approach if the initial dataset is extremely limited.
Notably, our PCA model captures variations in anatomic shape only. However, the image appearance or intensity difference could also affect the segmentation results. In our future work, we will develop an appearance model51 based on the PCA to capture inter-scan intensity difference. By combining the shape and appearance models, we expect to include more variations in the training data, and potentially to improve the model segmentation performance. Considering the MRI scans, in which the intensity values are not calibrated like those for CT scans, the appearance model may be more useful for MR-based auto-segmentation.
5. CONCLUSIONS
We presented a simple yet effective approach to create synthetic CT scans with contours for training deep learning segmentation models and demonstrated its efficiency by developing auto-segmentation models for the parotids and submandibular glands. Our approach enables the training of high-quality deep learning segmentation models from a severely limited number of well-contoured data (as less as the number of atlases used in most multi-atlas segmentation approaches). Our approach could equal or even surpass the performance of some state-of-the-art deep learning-based auto-segmentation approaches. Our work not only makes deep learning-based auto-segmentation applicable to more clinical situations with limited available data but also greatly reduces the effort needed for data curation for deep learning training.
Acknowledgments:
Funded in part by Cancer Center Support (Core) Grant P30 CA016672 from the National Cancer Institute, National Institutes of Health, to The University of Texas MD Anderson Cancer Center.
Footnotes
Meeting presentations: Presented in part at the 62nd American Association of Physicists in Medicine meeting in July 2020.
REFERENCES
- 1.lin D, Vasilakos AV, Tang Y, Yao Y. Neural networks for computer-aided diagnosis in medicine: A review. Neurocomputing. 2016;216:700–708. doi: 10.1016/j.neucom.2016.08.039 [DOI] [Google Scholar]
- 2.Cardenas CE, McCarroll RE, Court LE, et al. Deep Learning Algorithm for Auto-Delineation of High-Risk Oropharyngeal Clinical Target Volumes With Built-In Dice Similarity Coefficient Parameter Optimization Function. Int J Radiat Oncol. 2018;101(2):468–478. doi: 10.1016/j.ijrobp.2018.01.114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nikolov S, Blackwell S, Mendes R, et al. Deep learning to achieve clinically applicable segmentation of head and neck anatomy for radiotherapy. ArXiv180904430 Phys Stat. Published online September 12, 2018. Accessed June 25, 2020. http://arxiv.org/abs/1809.04430 [Google Scholar]
- 4.Ibragimov B, Xing L. Segmentation of organs-at-risks in head and neck CT images using convolutional neural networks. Med Phys. 2017;44(2):547–557. doi: 10.1002/mp.12045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cardenas CE, Yang J, Anderson BM, Court LE, Brock KB. Advances in Auto-Segmentation. Semin Radiat Oncol. 2019;29(3):185–197. doi: 10.1016/j.semradonc.2019.02.001 [DOI] [PubMed] [Google Scholar]
- 6.Halevy A, Norvig P, Pereira F. The Unreasonable Effectiveness of Data. IEEE Intell Syst. 2009;24(2):8–12. doi: 10.1109/MIS.2009.36 [DOI] [Google Scholar]
- 7.Teguh DN, Levendag PC, Voet PWJ, et al. Clinical Validation of Atlas-Based Auto-Segmentation of Multiple Target Volumes and Normal Tissue (Swallowing/Mastication) Structures in the Head and Neck. Int J Radiat Oncol. 2011;81(4):950–957. doi: 10.1016/j.ijrobp.2010.07.009 [DOI] [PubMed] [Google Scholar]
- 8.Hong TS, Tomé WA, Harari PM. Heterogeneity in head and neck IMRT target design and clinical practice. Radiother Oncol. 2012;103(1):92–98. doi: 10.1016/j.radonc.2012.02.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shorten C, Khoshgoftaar TM. A survey on Image Data Augmentation for Deep Learning. J Big Data. 2019;6(1):60. doi: 10.1186/s40537-019-0197-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Krizhevsky A, Sutskever I, Hinton GE. ImageNet Classification with Deep Convolutional Neural Networks. In: Pereira F, Burges CJC, Bottou L, Weinberger KQ, eds. Advances in Neural Information Processing Systems 25. Curran Associates, Inc.; 2012:1097–1105. http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf [Google Scholar]
- 11.Pereira S, Pinto A, Alves V, Silva CA. Brain Tumor Segmentation Using Convolutional Neural Networks in MRI Images. IEEE Trans Med Imaging. 2016;35(5):1240–1251. doi: 10.1109/TMI.2016.2538465 [DOI] [PubMed] [Google Scholar]
- 12.Oliveira A, Pereira S, Silva CA. Augmenting data when training a CNN for retinal vessel segmentation: How to warp? In: 2017 IEEE 5th Portuguese Meeting on Bioengineering (ENBENG). IEEE; 2017:1–4. doi: 10.1109/ENBENG.2017.7889443 [DOI] [Google Scholar]
- 13.Shijie J, Ping W, Peiyi J, Siping H. Research on data augmentation for image classification based on convolution neural networks. In: 2017 Chinese Automation Congress (CAC). IEEE; 2017:4165–4170. doi: 10.1109/CAC.2017.8243510 [DOI] [Google Scholar]
- 14.Taylor L, Nitschke G. Improving Deep Learning using Generic Data Augmentation. ArXiv170806020 Cs Stat. Published online August 20, 2017. Accessed June 25, 2020. http://arxiv.org/abs/1708.06020 [Google Scholar]
- 15.Eaton-Rosen Z, Bragman F, Ourselin S, Cardoso MJ. Improving Data Augmentation for Medical Image Segmentation. Published online April 11, 2018. Accessed June 25, 2020. https://openreview.net/forum?id=rkBBChjiG [Google Scholar]
- 16.Dosovitskiy A, Fischer P, Springenberg JT, Riedmiller M, Brox T. Discriminative Unsupervised Feature Learning with Exemplar Convolutional Neural Networks. IEEE Trans Pattern Anal Mach Intell. 2016;38(9):1734–1747. doi: 10.1109/TPAMI.2015.2496141 [DOI] [PubMed] [Google Scholar]
- 17.Hauberg S, Freifeld O, Larsen ABL, Fisher III JW, Hansen LK. Dreaming More Data: Class-dependent Distributions over Diffeomorphisms for Learned Data Augmentation. ArXiv151002795 Cs. Published online June 30, 2016. Accessed June 3, 2020. http://arxiv.org/abs/1510.02795 [Google Scholar]
- 18.Ratner AJ, Ehrenberg HR, Hussain Z, Dunnmon J, Ré C. Learning to Compose Domain-Specific Transformations for Data Augmentation. ArXiv170901643 Cs Stat. Published online September 30, 2017. Accessed June 3, 2020. http://arxiv.org/abs/1709.01643 [PMC free article] [PubMed] [Google Scholar]
- 19.Cubuk ED, Zoph B, Mane D, Vasudevan V, Le QV. AutoAugment: Learning Augmentation Strategies From Data. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE; 2019:113–123. doi: 10.1109/CVPR.2019.00020 [DOI] [Google Scholar]
- 20.Zhao A, Balakrishnan G, Durand F, Guttag JV, Dalca AV. Data augmentation using learned transformations for one-shot medical image segmentation. ArXiv190209383 Cs. Published online April 6, 2019. Accessed May 21, 2020. http://arxiv.org/abs/1902.09383 [Google Scholar]
- 21.Yi X, Walia E, Babyn P. Generative adversarial network in medical imaging: A review. Med Image Anal. 2019;58:101552. doi: 10.1016/j.media.2019.101552 [DOI] [PubMed] [Google Scholar]
- 22.Chuquicusma MJM, Hussein S, Burt J, Bagci U. How to fool radiologists with generative adversarial networks? A visual turing test for lung cancer diagnosis. In: 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018). IEEE; 2018:240–244. doi: 10.1109/ISBI.2018.8363564 [DOI] [Google Scholar]
- 23.Moradi M, Madani A, Karargyris A, Syeda-Mahmood TF. Chest x-ray generation and data augmentation for cardiovascular abnormality classification. In: Angelini ED, Landman BA, eds. Medical Imaging 2018: Image Processing. SPIE; 2018:57. doi: 10.1117/12.2293971 [DOI] [Google Scholar]
- 24.Calimeri F, Marzullo A, Stamile C, Terracina G. Biomedical Data Augmentation Using Generative Adversarial Neural Networks. In: Lintas A, Rovetta S, Verschure PFMJ, Villa AEP, eds. Artificial Neural Networks and Machine Learning – ICANN 2017. Vol 10614. Lecture Notes in Computer Science. Springer International Publishing; 2017:626–634. doi: 10.1007/978-3-319-68612-7_71 [DOI] [Google Scholar]
- 25.Frid-Adar M, Diamant I, Klang E, Amitai M, Goldberger J, Greenspan H. GAN-based Synthetic Medical Image Augmentation for increased CNN Performance in Liver Lesion Classification. Neurocomputing. 2018;321:321–331. doi: 10.1016/j.neucom.2018.09.013 [DOI] [Google Scholar]
- 26.Salimans T, Goodfellow I, Zaremba W, et al. Improved Techniques for Training GANs. In: Lee DD, Sugiyama M, Luxburg UV, Guyon I, Garnett R, eds. Advances in Neural Information Processing Systems 29. Curran Associates, Inc.; 2016:2234–2242. http://papers.nips.cc/paper/6125-improved-techniques-for-training-gans.pdf [Google Scholar]
- 27.Wold S, Esbensen K, Geladi P. Principal component analysis. Chemom Intell Lab Syst. 1987;2(1-3):37–52. doi: 10.1016/0169-7439(87)80084-9 [DOI] [Google Scholar]
- 28.Yu ZH, Kudchadker R, Dong L, et al. Learning anatomy changes from patient populations to create artificial CT images for voxel-level validation of deformable image registration. J Appl Clin Med Phys. 2016;17(1):246–258. doi: 10.1120/jacmp.v17i1.5888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Söhn M, Birkner M, Yan D, Alber M. Modelling individual geometric variation based on dominant eigenmodes of organ deformation: implementation and evaluation. Phys Med Biol. 2005;50(24):5893–5908. doi: 10.1088/0031-9155/50/24/009 [DOI] [PubMed] [Google Scholar]
- 30.Badawi AM, Weiss E, Sleeman WC, Yan C, Hugo GD. Optimizing principal component models for representing interfraction variation in lung cancer radiotherapy: Optimizing interfraction lung models. Med Phys. 2010;37(9):5080–5091. doi: 10.1118/1.3481506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cootes TF, Taylor CJ, Cooper DH, Graham J. Active Shape Models-Their Training and Application. Comput Vis Image Underst. 1995;61(1):38–59. doi: 10.1006/cviu.1995.1004 [DOI] [Google Scholar]
- 32.Cootes T, Hill A, Taylor C, Haslam J. Use of active shape models for locating structures in medical images. Image Vis Comput. 1994;12(6):355–365. doi: 10.1016/0262-8856(94)90060-4 [DOI] [Google Scholar]
- 33.Wang H, Dong L, Lii MF, et al. Implementation and validation of a three-dimensional deformable registration algorithm for targeted prostate cancer radiotherapy. Int J Radiat Oncol. 2005;61(3):725–735. doi: 10.1016/j.ijrobp.2004.07.677 [DOI] [PubMed] [Google Scholar]
- 34.Yan C, Zhong H, Murphy M, Weiss E, Siebers JV. A pseudoinverse deformation vector field generator and its applications. Med Phys. 2010;37(3):1117–1128. doi: 10.1118/1.3301594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Milletari F, Navab N, Ahmadi S-A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. ArXiv160604797 Cs. Published online June 15, 2016. Accessed June 25, 2020. http://arxiv.org/abs/1606.04797 [Google Scholar]
- 36.Dost P Ultrasonographic biometry in normal salivary glands. Eur Arch Otorhinolaryngol. 1997;254(S1):S18–S19. doi: 10.1007/BF02439713 [DOI] [PubMed] [Google Scholar]
- 37.Yang J, Amini A, Williamson R, et al. Automatic contouring of brachial plexus using a multi-atlas approach for lung cancer radiation therapy. Pract Radiat Oncol. 2013;3(4):e139–e147. doi: 10.1016/j.prro.2013.01.002 [DOI] [PubMed] [Google Scholar]
- 38.Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. ArXiv14126980 Cs. Published online January 29, 2017. Accessed June 25, 2020. http://arxiv.org/abs/1412.6980 [Google Scholar]
- 39.Rhee DJ, Cardenas CE, Elhalawani H, et al. Automatic detection of contouring errors using convolutional neural networks. Med Phys. 2019;46(11):5086–5097. doi: 10.1002/mp.13814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhou R, Liao Z, Pan T, et al. Cardiac atlas development and validation for automatic segmentation of cardiac substructures. Radiother Oncol. 2017;122(1):66–71. doi: 10.1016/j.radonc.2016.11.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shelhamer E, Long J, Darrell T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans Pattern Anal Mach Intell. 2017;39(4):640–651. doi: 10.1109/TPAMI.2016.2572683 [DOI] [PubMed] [Google Scholar]
- 42.Yang J, Haas B, Fang R, et al. Atlas ranking and selection for automatic segmentation of the esophagus from CT scans. Phys Med Biol. 2017;62(23):9140–9158. doi: 10.1088/1361-6560/aa94ba [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Winkel D, Bol GH, Kroon PS, et al. Adaptive radiotherapy: The Elekta Unity MR-linac concept. Clin Transl Radiat Oncol. 2019;18:54–59. doi: 10.1016/j.ctro.2019.04.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ger RB, Yang J, Ding Y, et al. Accuracy of deformable image registration on magnetic resonance images in digital and physical phantoms. Med Phys. 2017;44(10):5153–5161. doi: 10.1002/mp.12406 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ger RB, Yang J, Ding Y, et al. Synthetic head and neck and phantom images for determining deformable image registration accuracy in magnetic resonance imaging. Med Phys. 2018;45(9):4315–4321. doi: 10.1002/mp.13090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yang J, Beadle BM, Garden AS, et al. Auto-segmentation of low-risk clinical target volume for head and neck radiation therapy. Pract Radiat Oncol. 2014;4(1):e31–e37. doi: 10.1016/j.prro.2013.03.003 [DOI] [PubMed] [Google Scholar]
- 47.Yang J, Zhang Y, Zhang L, Dong L. Automatic Segmentation of Parotids from CT Scans Using Multiple Atlases. Med Image Anal Clin Gd Chall. Published online January 1, 2010. [Google Scholar]
- 48.Wang H, Garden AS, Zhang L, et al. Performance Evaluation of Automatic Anatomy Segmentation Algorithm on Repeat or Four-Dimensional Computed Tomography Images Using Deformable Image Registration Method. Int J Radiat Oncol. 2008;72(1):210–219. doi: 10.1016/j.ijrobp.2008.05.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.McCarroll RE, Beadle BM, Balter PA, et al. Retrospective Validation and Clinical Implementation of Automated Contouring of Organs at Risk in the Head and Neck: A Step Toward Automated Radiation Treatment Planning for Low- and Middle-Income Countries. J Glob Oncol. 2018;(4):1–11. doi: 10.1200/JGO.18.00055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bowles C, Chen L, Guerrero R, et al. GAN Augmentation: Augmenting Training Data using Generative Adversarial Networks. ArXiv181010863 Cs. Published online October 25, 2018. Accessed November 11, 2020. http://arxiv.org/abs/1810.10863 [Google Scholar]
- 51.Cootes TF, Edwards GJ, Taylor CJ. Active appearance models. IEEE Trans Pattern Anal Mach Intell. 2001;23(6):681–685. doi: 10.1109/34.927467 [DOI] [Google Scholar]