Analysis of biological noise in the flagellar length control system

Summary

Any proposed mechanism for organelle size control should be able to account not only for average size but also for the variation in size. We analyzed cell-to-cell variation and within-cell variation of length for the two flagella in Chlamydomonas, finding that cell-to-cell variation is dominated by cell size, whereas within-cell variation results from dynamic fluctuations. Fluctuation analysis suggests tubulin assembly is not directly coupled with intraflagellar transport (IFT) and that the observed length fluctuations reflect tubulin assembly and disassembly events involving large numbers of tubulin dimers. Length variation is increased in long-flagella mutants, an effect consistent with theoretical models for flagellar length regulation. Cells with unequal flagellar lengths show impaired swimming but improved gliding, raising the possibility that cells have evolved mechanisms to tune biological noise in flagellar length. Analysis of noise at the level of organelle size provides a way to probe the mechanisms determining cell geometry.

Graphical abstract

Highlights

• •Chlamydomonas flagella show dynamic length fluctuations
• •Length variation involves processes inside the cell body and in the flagella
• •Long-flagella mutants have increased length variability
• •Flagellar length variation leads to variation in cell motility

Biological Sciences; Molecular Biology; Cell Biology; Biophysics; Mathematical Biosciences

Introduction

The mechanisms by which cells control the size of their organelles remain incompletely understood. Indeed, what it means for organelle size to be “controlled” is not entirely clear. In some cases, limited availability of molecular precursors can limit organelle size (Goehring and Hyman, 2012), but such a limiting precursor condition is unlike what we normally think of as “control,” where active systems monitor a quantity and adjust it back to a pre-defined set point. One way that a control system can manifest itself is by constraining variation. In the case of organelles, this viewpoint suggests that the function of a size control system could be explored by examining the variation in organelle size within or among cells. Analysis of biological fluctuations (noise) has been extensively employed in neurobiology to probe mechanisms regulating single-channel opening and closing (Neher and Stevens, 1977) as well as in the study of gene expression (Elowitz et al., 2002; Raser and O'Shea, 2004; Kaern et al., 2005; Perkins and Swain. 2009). An important contribution of gene expression noise studies was to draw attention to the difference between “intrinsic” noise, caused by fluctuations within the machinery of a promoter at each individual gene, for example due to stochastic binding of transcription factors to promoter DNA, and “extrinsic” noise, caused by variation in the rest of the cell that affect all genes, for example variation in the number of RNA polymerase molecules. Much as measurement of noise in gene expression has provided information about the mechanism of transcription, measurement of noise can provide a lens with which to view other cellular processes such as organelle dynamics and cellular structure. Cell-to-cell variation in organelle size and number has been observed in genetically identical cells (Marshall, 2007; Mukherji and O'Shea, 2014; Chang and Marshall, 2017, 2019). For example, analysis of variation in the copy number of various organelles, as well as joint variation in organelle number and size, has been used to gain insight into the mechanisms of organelle fission, fusion, and inheritance (Mukherji and O'Shea, 2014; Amiri et al., 2020).

Here we analyze variations in the size of eukaryotic flagella as a way to gain information about flagellar length control different from what can be obtained by analyzing average length alone. Flagella are used as a model organelle because their simple geometry allows size to be defined by a single number, the length. Cilia and flagella are interchangeable terms for microtubule-based organelles that project from the surface of most eukaryotic cells (Pazour and Rosenbaum, 2002) and perform motile and sensory functions (Scholey and Anderson, 2006). Our studies employ the flagella of the unicellular green alga Chlamydomonas reinhardtii. This organism has long been used in studies of flagellar length control because its flagella are easy to measure and because mutants exist in which flagellar length is altered (Randall, 1969; Wemmer and Marshall, 2007). Flagella are dynamic structures in which the flagellar microtubules that determine length undergo continuous turnover (Marshall and Rosenbaum 2001). The continuous assembly of tubulin at the tip requires an active transport known as intraflagellar transport (IFT). IFT is mediated by the kinesin-driven movement of protein complexes called IFT particles that bind to and transport tubulin and other flagellar building blocks out to the flagellar tip, where they assemble into the growing structure (Qin et al., 2004; Hao et al., 2011; Bhogaraju et al., 2013; Ishikawa and Marshall, 2017a, 2017b). The lengths of cilia and flagella are known to vary from cell to cell in a variety of organisms (Randall, 1969; Wheatley and Bowser, 2000; Adams et al., 1985), suggesting these organelles can be used to analyze biological noise at the level of cellular structure. In wild-type Chlamydomonas cells, the average flagellar length is generally 10–12 microns and the standard deviation in length approximately 2–3 microns. The length distribution of flagella in wild type is approximately Gaussian, but among mutants that alter flagellar length, mutants having similar average lengths can be distinguished on the basis of differences in the shape of the length distribution (Kannegaard et al., 2014), supporting the idea that length variation is an important aspect of the length phenotype.

Theoretical models for flagellar length regulation make distinct predictions concerning the nature of flagellar length fluctuation and variation (Bressloff 2006; Hendel et al., 2018; Fai et al., 2019; Banerjee and Banerjee, 2020; Patra et al., 2020); hence a measurement of length fluctuation has the potential to test existing models and inform future modeling efforts.

Here, we take advantage of the fact that each Chlamydomonas cell contains two identical flagella, to measure two components of flagellar length variation: a correlated component that reflects cell-to-cell variation in length and an uncorrelated component that reflects within-cell variation in length between the two flagella. We demonstrate that these types of variation stem from a combination of dynamic fluctuations and cell-body-related variation. The existence of an active length-control system is indicated by a constraint on fluctuations in individual flagella over time. We leveraged Chlamydomonas genetics to explore molecular pathways that might contribute to noise, showing that mutations that increase length lead to an increase in the uncorrelated component of variation, reflected by an increase in the magnitude and timescale of length fluctuations. We show that this result is consistent with predictions of prior length control models but that different models make different predictions about which length-altering parameter changes can explain the increase in uncorrelated variation. Finally, we show that differences in flagellar length have an effect on biological fitness in terms of cell motility and suggest that the biological noise seen in wild-type vegetative cells may represent a balance between the requirements of two different types of motility, swimming, and gliding.

Results

Measuring biological noise in the flagellar length control system

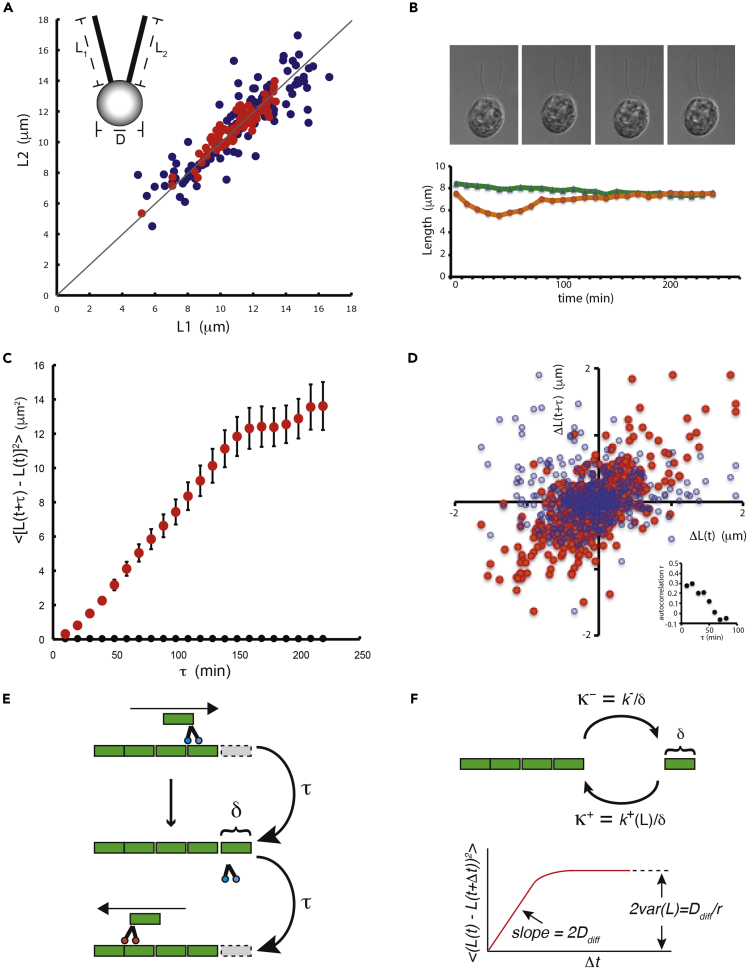
Each Chlamydomonas cell has two identical flagella whose lengths we denote L1 and L2 (Figure 1A inset), where L1 is the left-most of the two flagella relative to the field of view of the microscope. Our quantitative analysis of noise in flagellar length is based on approaches previously developed for analyzing noise in gene expression. By comparing two measurements per cell (in our case, the lengths of the two flagella in a single Chlamydomonas cell), it is possible to decompose the total variation into a correlated component of variation, defined as follows:

η²_ext = {<L₁L₂> − < L₁><L₂>}/<L₁><L₂> (Equation 1)

Figure 1.

Measuring correlated and uncorrelated noise in flagellar length control system

(A) Correlated and uncorrelated components of variation can be visualized in measurements of flagellar length in fixed Chlamydomonas cells with two equivalent flagella. The lengths of the two flagella in a cell are denoted L1 and L2 as illustrated in the diagram, where L1 is whichever flagellum happens to be to the left of the other in the field of view of the microscope. Graph plots length of one flagellum versus length of the other flagellum. Correlated variation is reflected by scatter along the diagonal L₁ = L₂ (gray line). Uncorrelated variation is reflected by scatter perpendicular to this axis. (Blue) Wild-type asynchronous culture; (red) wild-type gametes. (Inset) Diagram of a Chlamydomonas cell showing the three measurements reported in this paper.

(B) Dynamic changes in flagellar length. Image shows four successive time points, taken 10 min apart, of a 3D time series of a single living cell embedded in agarose and imaged with DIC microscopy. Graph below plots sample traces showing the length of two flagella within one cell versus time.

(C) Quantifying fluctuations in length observed in living cells. (Red) Mean-squared change in length plotted versus time, showing constrained diffusion-like behavior. Error bars signify standard error of the mean. (Black) Mean-squared change in length in glutaraldehyde-fixed cells as an indicator of measurement error.

(D) Correlation between length changes in successive 10-min intervals (red markers, r = 0.28) compared with length changes during 10-min intervals separated by 60 min (blue markers, r = 0.015). Inset gives autocorrelation of length changes (specified by the Pearson coefficient r, which is unitless) versus time lag.

(E) IFT-coupled model for length fluctuations. Tubulin subunits (green) are brought to the end of the flagellum by anterograde IFT particles (blue) and deposited onto the tip, elongating the flagellum. Tubulin subunits disassembling from the tip are immediately brought back to the cell body by retrograde IFT particles (orange), shortening the flagellum. At steady state, elongation and shortening events occur at the same average rate, but stochastic differences in the quantity of tubulin added or removed results in a net change in length of δ at a rate comparable to the frequency 1/τ of IFT trains arriving at or departing from the tip.

(F) IFT-uncoupled model for length fluctuations. IFT maintains a pool of tubulin monomers near the tip, which undergo association or dissociation events at rates Κ⁺ and Κ⁻, respectively. Assembly rate Κ⁺ is length dependent, creating an effective restoring force. The resulting Ornstein-Uhlenbeck process, which describes diffusion of flagellar length constrained by the presence of a restoring force, defines the slope and asymptote of the mean-squared length change versus time plot, as indicated by the diagram. This theoretical prediction can be directly compared with Figure 1C.

and an uncorrelated component of variation, defined as follows:

η²_int = < (L₁ − L₂)² > / 2<L₁><L₂> (Equation 2)

These expressions are taken directly from those used in the study of correlated and uncorrelated variation in gene expression (Elowitz et al., 2002). The correlated component measures how much the two flagellar lengths vary together, from cell to cell, in the cell population, whereas the uncorrelated component measures how much the two flagella in one cell vary in length relative to one another. This decomposition is useful because it highlights two types of variation that are expected to have distinct biological impacts and may reflect different sources of biological variation. For example, uncorrelated variation may represent, at least in part, fluctuations within the length-control machinery associated with each flagellum, whereas correlated variation may represent, at least in part, fluctuations in cell-wide features such as precursor availability.

In order to measure correlated and uncorrelated noise in the case of flagellar length, we measured the lengths of both flagella (L1, L2) in a population of cells and plotted them one against the other (see Figure 1A). It can be seen that the lengths are correlated (r = 0.87) but that there is also scatter off the diagonal indicating differences in length within a cell.

As shown in Figure 1A and summarized in Table 1, flagellar lengths in wild-type cells demonstrated measurable levels of both correlated (variation in L1 + L2) and uncorrelated noise (variation in L1 − L2). We found (Table 1) that the correlated noise is greater in magnitude than the uncorrelated noise. The uncorrelated noise is, however, significantly greater than the estimated measurement error (see methods), thus we can conclude that both types of variation affect flagellar length.

Table 1.

Summary of noise measurements

Strain	<L>	<Diam>	R	η2int (x10−2)	η2ext (x10−2)	n
Asynchronous cultures
wt	11.1 ± 2.7	6.8 ± 0.9	0.61	0.73 (0.54–0.95)	5.0 (4.0–6.1)	105
lf1	13.8 ± 6.9	6.1 ± 1.2	0.27	13.5 (9.1–18.7)	10.8 (6.9–15.0)	141
lf4	17.8 ± 7.4	6.2 ± 1.2	0.22	1.5 (0.92–2.08)	15.6 (11.4–20.0)	88
Cell-cycle arrested
wt (dark)	9.9 ± 0.9	6.2 ± 1.0	0.75	0.32 (0.25–0.41)	0.57 (0.38–0.78)	70
wt (gamete)	10.9 ± 1.4	5.2 ± 0.7	0.07	0.12 (0.09–0.15)	1.6 (1.0–2.3)	92
lf1 (gamete)	13.9 ± 5.7	4.5 ± 0.9	0.36	2.2 (1.1–4.2)	12.2 (5.8–18.3)	18
lf4 (gamete)	23.5 ± 8.4	5.2 ± 0.7	0.06	1.8 (0.57–3.7)	10.8 (3.6–20.9)	22

<L> denotes average flagellar length in μm, with standard deviation listed. <Diam> is the average cell diameter in μm. r is the correlation coefficient between flagellar length and cell diameter. η²_int and η²_ext denote the uncorrelated and correlated components of variation, respectively. Noise measures η² listed are the actual measurements multiplied by 100. n is the number of cells measured. 95% confidence intervals for noise measures are given in parentheses.

Constrained fluctuation in flagellar length reveals a length control system

To ask whether flagellar length variation is fixed or dynamic, we embedded cells in agarose and acquired time-lapse 3D movies using DIC microscopy, allowing us to measure length fluctuations as a function of time (Figure 1B). A plot of the mean-squared change in flagellar length as a function of time interval (Figure 1C; plot shows calculated mean-squared changes for both individual flagella averaged in multiple cells as described in methods) shows that flagellar lengths appear to undergo random-walk dynamics at time scales ranging from 10 to 150 min, such that the mean-squared length change is linearly proportional to the time interval. At longer timescales, the mean-squared length change reaches a plateau, suggesting that the magnitude of the length variation is constrained. This constraint on length variation presumably reflects the existence of a flagellar length control system. This live-cell analysis demonstrates that flagellar length variation is not simply locked in from the time of initial assembly but rather reflects length fluctuations in time due to fluctuations in the assembly and disassembly processes.

At very short time intervals, the mean-squared change in length curve shows a slight upward arc, which would be consistent with processive or ballistic motion rather than a random walk. To confirm this, we plotted the change in length for successive 10-min time intervals (Figure 1D, red markers), which indicates a correlation between successive changes in length (r = 0.28). In contrast, when we compare the change in length during 10-min time intervals separated by 60 min (Figure 1D, blue markers), the correlation vanishes (r = 0.015). Thus, successive changes in length are partially correlated at short timescales but uncorrelated at longer timescales (Figure 1D, inset), consistent with a persistent random walk.

Magnitude of fluctuations versus potential mechanisms of length dynamics

We next asked whether the observed magnitude and timescale of these fluctuations are consistent with current models for flagellar dynamics. In this analysis, we make the assumption that changes in flagellar length directly reflect the addition or removal of tubulin from the flagellar outer doublets.

Existing models of flagellar length dynamics fall into two classes depending on how they treat the role of IFT. In tightly IFT-coupled models, it is assumed that tubulin is transported to the end of the flagellum by anterograde IFT particles, where it assembles onto the tip, elongating the flagellum. At the same time, tubulin subunits disassemble from the tip, bind to retrograde IFT particles, and are trafficked back to the cell body. At steady state, assembly and disassembly rates balance, but random variation in assembly or disassembly rates, for example due to variation in IFT injection (Ludington et al., 2013), could lead to stochastic changes of flagellar length in steps corresponding to IFT arrivals. We denote the step size δ with an average time between steps of τ, the reciprocal of IFT arrival frequency (Figure 1E).

In full-length flagella at steady state, the average frequency of IFT injection and arrival at the tip is approximately 1.25 trains per second (Engel et al., 2009). The slope of the mean-squared change in length versus time plot (Figure 1C) is 0.0014 μm²/s. Considering random steps of size δ at a frequency of 1.25 steps per second (τ = 0.8 s), we find, using the relation slope = δ²/τ (Berg 1983), that the size of the random step per IFT train must be approximately 0.033 μm. Given 233 protofilaments per cross-section and 8 nm per dimer, each IFT train would thus need to carry approximately 960 tubulin dimers. At steady-state lengths, each IFT train contains on average 16 IFT particles (Pigino et al., 2009; Vannuccini et al., 2016). Thus, if random IFT train arrivals were driving the observed length fluctuations, it would be necessary for each IFT particle to carry on the order of 60 tubulins. This greatly exceeds the value of tubulins usually thought to associate with IFT particles (4 tubulins per particle; Bhogaraju et al., 2014), suggesting that statistical fluctuations in the rate of IFT are unlikely to explain the observed flagellar length fluctuations.

An alternative to the IFT-coupled model is an uncoupled model, in which IFT maintains a pool of tubulin monomers near the tip, but the addition or removal of tubulin at the tip takes place independently of the arrival or departure of IFT trains. This type of model has been used to represent the dynamics of tubulin assembly in flagella (Banerjee and Banerjee, 2020; Patra et al., 2020). We represent tubulin monomers undergoing association or dissociation by rates Κ⁺ and Κ⁻, respectively. We assume that assembly is length dependent, taking place at a rate k⁺(L) in units of microns per second, but disassembly is length independent occurring at a rate k⁻ microns per second. Given an effective monomer size δ, Κ⁺ = k⁺/δ and Κ⁻ = k⁻/δ, respectively. At steady state, Κ⁺ = Κ⁻ = Κ_ss. In this representation, the association and dissociation events lead to a random walk with a diffusion constant D_diff = Κ_ssδ ², and the length dependence of k⁺ leads to an effective restoring force given by the derivative of the rate of change in length with respect to the length, r = d(k⁺(L)-k⁻)/dL, evaluated at L = L_ss. Given prior experimental measurements that assembly rate, k⁺, is proportional to 1/L with a proportionality constant A (Marshall et al., 2005), then r = A/L_ss² = k⁺(L_ss)/L_ss = K_ssδ/L_ss. Length fluctuations are thus governed by a random walk process constrained by a linear restoring term. For such a process, the plot of mean-squared length change versus time (Figure 1C) takes a well-defined form, diagrammed in Figure 1F, in which the mean-squared length change increases linearly with time lag (for small time lag), with slope 2D_diff, and then plateaus at twice the variance in length (2 var(L) = 2 D_diff/r). Figure 1C shows an initial slope of 0.0014 μm²/s and a plateau at 2var(L) = 14 μm². Hence var(L) ∼ 7 μm². We can relate observables var(L) and L_ss to obtain the effective monomer size δ of the random process as follows:

$$var\left(L\right)=\frac{D_{diff}}{r}=\frac{K_{ss}{\text{δ}}^2}{\raisebox{1ex}{$K_{ss}\delta $}\!\left/ \!\raisebox{-1ex}{$L_{ss}$}\right.}=L_{ss}\delta$$ (Equation 3)

Using var(L) ∼ 7 μm² and an average flagellar length at steady state L_ss = 10 μm, we estimate the effective monomer size δ = 0.7 μm. Considering, as above, the number of protofilaments in the flagellum, the effective monomer size for a fluctuation of 0.7 μm would correspond to approximately 20,000 tubulin dimers. Such large steps cannot correspond to individual tubulin dimer assembly or dissociation events, but rather to “bursts” of assembly or disassembly, as have been described in studies of transcriptional noise (Sanchez and Golding, 2013) and invoked in models of organelle biogenesis (Amiri et al., 2020). One possibility is that the random walk is driven by microtubule dynamic instability, in which periods of processive growth alternate with periods of processive shrinkage. Such a dynamic instability model would potentially explain the correlation of fluctuations between successive time points over short timescales (Figure 1D).

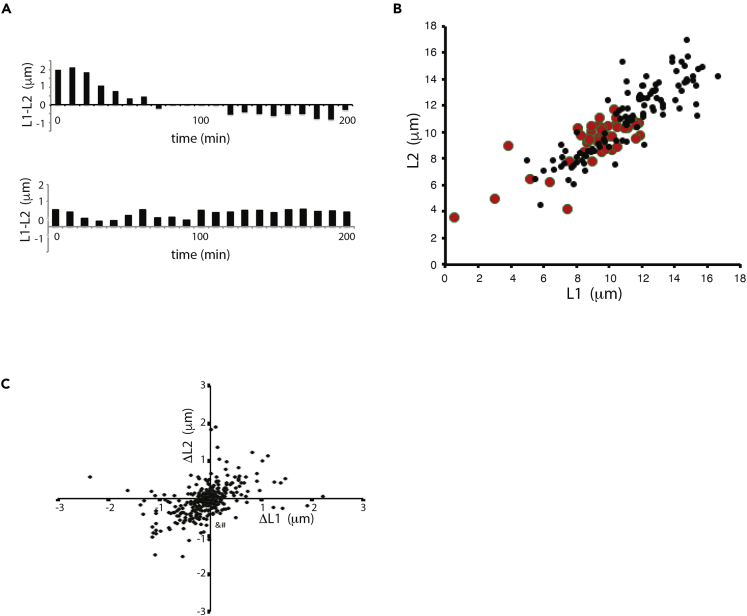
Dynamic fluctuation versus locked-in variation

Figures 1B–1D demonstrate that flagellar lengths undergo dynamic variation, indicating that at least some of the variation seen in Figure 1A must be due to dynamic fluctuations. Because the two flagella in a cell are nucleated by basal bodies of different age (one mother basal body, one daughter basal body), it is also possible that some of the variation between flagella in a cell (“uncorrelated variation”) might reflect a stable difference between the two flagella, such that one would persistently tend to be longer than the other. In order to test this possibility, we analyzed the signed difference in length between the two flagella (examples are shown in Figure 2A). Out of sixteen live cells analyzed, eleven show at least one sign change in the difference between the flagellar lengths during the course of observation, such that the initially longer flagellum becomes shorter at some point. This result argues that neither flagellum is stably designated to be longer than the other. Furthermore, in ptx1 mutant cells, which lack the known biochemical and functional differences between the two flagella (Kamiya and Witman 1984; Horst and Witman, 1993), the uncorrelated variation was not reduced relative to wild-type cells (Figure 2B).

Figure 2.

Locked-in versus dynamic length variation

(A) Sign change test for locked-in flagellar length differences. Each plot shows the length difference between two flagella in one cell, plotted for successive time points. Top example is of a cell showing signal reversal, indicating that neither flagellum is consistently longer than the other.

(B) Genetic test for locked-in flagellar differences using ptx1 mutant that eliminates functional asymmetry between flagella. (Red) ptx1 mutant cells (black); wild type. Average length in ptx1 mutants is reduced compared with wild type, but uncorrelated variation is larger than in wild type (η²_int = 0.013 [95% confidence interval 0.007–0.02] for ptx1 versus η²_int = 0.007 [95% confidence interval 0.005–0.01] for wt), indicating the PTX1-dependent biochemical asymmetry in the two flagella is not a substantial source of uncorrelated variation.

(C) Correlated variation has a dynamic component. Scatterplot shows fluctuations in the lengths of both flagella in a cell during a 10-min time-step. Each point represents data from one cell at one time interval. ΔL1 and ΔL2 indicate the change in length of the two flagella in a cell during a single 10-min time interval, plotted one against the other.

In order to ask whether the correlated variation in flagellar length has a dynamic component, we compared length fluctuations in the two flagella of single cells (Figure 2C). Individual fluctuations show a small but statistically significant correlation (r = 0.32; n = 327; P < 0.00001), indicating that the correlated variation in length contains a contribution from dynamic fluctuations. This plot includes data from experiments performed on three different occasions. Each dataset individually also showed the positive correlation. This positive correlation is the opposite of what we had expected to observe based on the fact that the two flagella are competing for a shared pool of tubulin, which would suggest anticorrelated length fluctuations. Instead, the positive correlation may reflect a fluctuating process in the cell body that affects both flagella equally.

Contribution of cell body to flagellar length variation

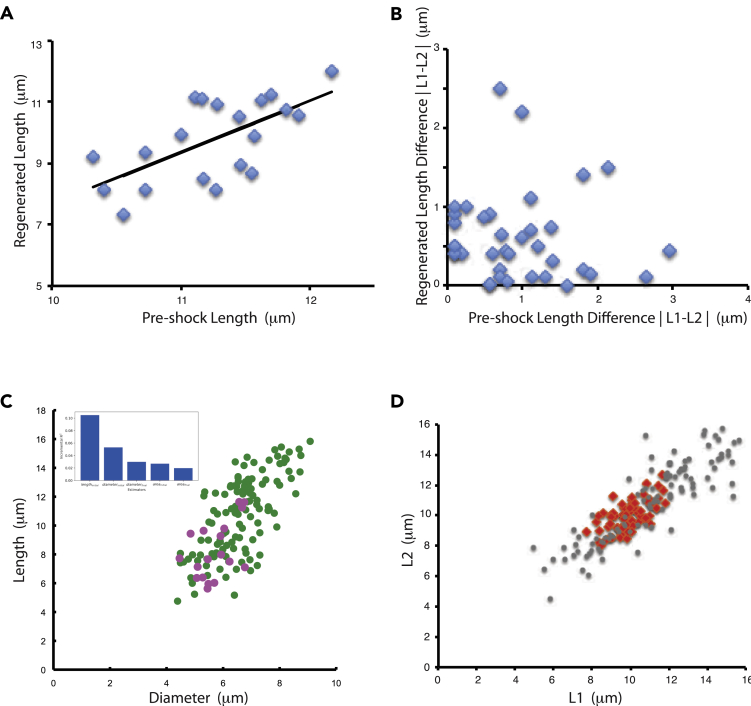
We next asked whether some of the correlated variation between cells could be driven by variation in the cell body. Flagella are easily detached from Chlamydomonas cells by a transient pH shock (Quarmby and Hartzell, 1994), after which they regenerate. We used two microfluidic device, one commercial and one custom-built, to trap individual Chlamydomonas cells and hold them in position while media is exchanged (see Figures S1A and S1C). Using these systems, we imaged flagella in single cells before, during, and after flagellar regeneration, allowing us to ask whether cells with long versus short flagella would regenerate correspondingly long or short flagella. Because flagella are completely removed during this experiment and regrown, any correlation in length before and after regeneration would have to reflect a property of the cell body itself. As shown in Figures 3A, S1B, and S1E, there is a significant correlation between average flagellar length before deflagellation and after regeneration (r = 0.65; P = 0.0011 for data in Figure 3A). We note, in these experiments, that flagella are shorter after regeneration compared with their pre-pH shock length, consistent with previous studies of flagellar regrowth (Rosenbaum et al., 1969). This result indicates that part of the cell-to-cell difference in flagellar lengths is due to some difference in the cell body. In contrast, the differences in length between the two flagella within one cell are completely uncorrelated in cells before and after regeneration (Figure 3B).

Figure 3.

Contribution of cell body to length variation

(A) Testing for cell-body-specific differences in flagellar length. Plot shows flagellar length before and after regeneration induced by pH shock on cells trapped in a microfluidic device. Each marker is one flagellum. Line indicates best fit to data.

(B) Testing for cell-body retention of flagellar length differences. Plot shows the difference in length between the two flagella of a cell before and after regeneration induced by pH shock.

(C) Contribution to correlated length variation from cell size variation measured by correlation between average length of the two flagella with the cell diameter in asynchronous cultures. (Green) Wild-type cells. (Pink) mat3 mutant cells having smaller average size than wild type (Umen and Goodenough, 2001). Correlation coefficients were 0.61 for wild-type cells alone and 0.70 for the combination of wild-type cells plus mat3 cells. Inset gives result of dominance analysis of flagellar length after regeneration (based on data in Figure S1E in terms of length prior to regeneration and different measures of cell size). Plot shows the incremental r² contribution of each predictor in the model.

(D) Flagellar length variation is reduced in cells arrested in the cell cycle by growth in the dark. (Red) Growth-arrested cells. (Gray) Vegetatively growing cells.

What is it about the cell body that differs from cell to cell and is able to create correlated variations in flagellar length? We found that the correlated component of flagellar length variation between cells, as quantified by the average of the lengths of the two flagella in a given cell, was itself strongly correlated with cell size (Figure 3C). In contrast to our expectation that length would be proportional to cell volume, based on the assumption that ribosome number and hence precursor quantity should be proportional to cell volume, we observed linear scaling with cell diameter rather than with cell volume. We do not currently have any hypothesis for why flagellar length would be proportional to diameter. Dominance analysis of flagellar length before and after regeneration in our pH shock experiments (inset Figure 3C) indicates that cell size is one predictor of flagellar length after regeneration, but that length prior to regeneration is a stronger predictor, indicating that other features of cell state must affect length besides just cell size.

The other obvious candidate for a cell property that varies from cell to cell is cell-cycle state. To address this possibility, we measured flagellar length variation in cells arrested in G1 by growth in the dark in minimal media (Figure 3D), as well as to gamete cultures that are arrested in a G0-like state in preparation for mating (Figure 1A). Correlated variation was significantly reduced by both types of cell-cycle arrest (Table 1), suggesting that cell-to-cell differences in cell-cycle state normally contribute to correlated variation in the asynchronous cultures.

Do cell size and cell-cycle state both affect flagellar length variation? As shown in Table 1, the correlation between cell size and flagellar length is stronger in G1-arrested cells (r = 0.75) than in asynchronous cultures (r = 0.61), suggesting that when variation due to cell-cycle progression is eliminated, the remaining correlated variation is more closely determined by cell size variation. Other factors external to the flagella, such as cell age or extracellular environmental conditions, may account for the residual variation that is not explained by cell size and cell-cycle state.

Identifying genes that regulate noise in flagellar length control system

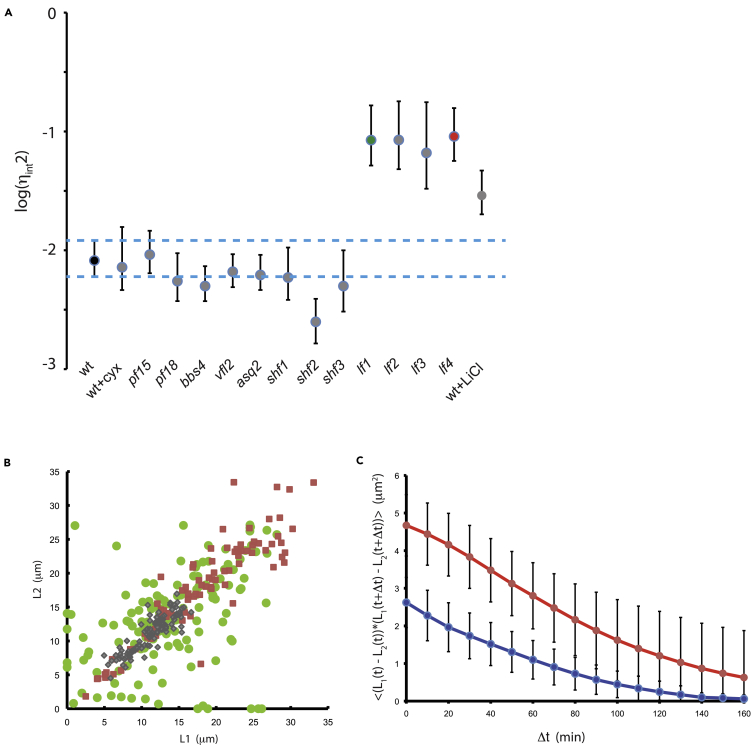
Mutations that increase uncorrelated variation could potentially reveal genes involved in constraining flagellar length variation or coordinating lengths of the two flagella within a cell. We therefore tested a panel of mutants and pharmacological treatments affecting a range of cellular processes for possible roles in noise suppression (Figure 4A).

Figure 4.

Identification of genes that affect flagellar length noise

(A) Analysis of candidate genes for effect on noise. Points represent median calculated value of uncorrelated variation. Error bars are 95% confidence intervals for each strain. Dotted blue lines show the 95% confidence interval for uncorrelated variation in wild-type cells. Green and red data markers indicate lf1 and lf4 mutants. All measurements were made using 2D image data to allow a large number of different strains to be measured more rapidly. The uncorrelated variation plotted on the Y axis is a unit-less quantity.

(B) Increased correlated and uncorrelated variation in long flagella mutants. (Green circles) lf1, (red squares) lf4, (gray diamonds) wild type. All data shown are from 3D measurements of flagellar length in cells from asynchronous cultures.

(C) Autocovariance of lf1 (red) and wild type (blue) based on measurements of length fluctuations in living cells, showing higher mean-squared fluctuations (judged by the autocovariance at zero lag) and slower decay for lf mutants. Error bars signify standard error of the mean.

Treatment with cycloheximide had no effect on uncorrelated noise, indicating that variation in gene expression is unlikely to play a role in regulating flagellar length on a dynamic basis.

We next considered possible mechanisms for communication between flagella that might play a role in constraining uncorrelated variation. One way that flagella could communicate with each other is via hydrodynamic coupling between the two beating flagella (Brumley et al., 2014); however, two mutations that paralyze flagellar motility (pf15 and pf18) showed no increase in uncorrelated variation.

A second way that flagella communicate is via protein fibers connecting their basal bodies, which are known to play a role in synchronization of flagellar beating (Wan and Goldstein, 2016). We therefore analyzed asq2 mutant cells, which we have previously shown to be defective in the physical connections between mother and daughter basal bodies (Feldman et al., 2007; Feldman and Marshall, 2009), and vfl2 mutants, which lack fibers that normally connect the basal bodies to the nucleus (Wright et al., 1985). Neither mutation had an effect on uncorrelated variation.

We next examined mutants with altered flagellar length. Mutations in the SHF1, SHF2, and SHF3 genes have been reported to cause cells to form short flagella, roughly half wild-type length. Noise measurements in these mutants did not show any increase in uncorrelated variation. In contrast, we saw a dramatic increase in uncorrelated variation in lf1, lf2, lf3, and lf4 mutants, all of which have abnormally long flagella (McVittie, 1972; Barsel et al., 1988; Berman et al., 2003; Nguyen et al., 2005; Tam et al., 2007; Wemmer et al., 2019). This suggested that increased length might somehow lead to increased uncorrelated variation. To confirm this hypothesis, we measured noise in wild-type cells treated with lithium, which increases flagellar length (Nakamura et al., 1987) due to an increase in IFT activity (Ludington et al., 2013). As with the lf mutants, we found that lithium-treated cells also showed increased uncorrelated length variation.

To further examine the role that LF genes play in noise regulation, we examined individual mutants in more detail. Figure 4B plots the distribution of flagellar length pairs in lf1 and lf4 mutants. It was previously reported that the lf1 mutation leads to increased variance in length (McVittie, 1972), but that analysis did not distinguish between correlated variation from cell to cell and uncorrelated variation between the two flagella. As indicated in Figure 4B, we found that both mutations lead to increased noise, but in different ways: although the correlated variation is similar between the two mutants, the uncorrelated variation is 9-fold higher in lf1 versus lf4 (Table 1). One obvious difference is that lf1 mutants are more likely to be uniflagellar, which is one of the reasons that the uncorrelated variation is higher in lf1 than lf4, but even ignoring such cells, it is clear from Figure 4B that lf1 mutants show greater differences between the lengths of their two flagella than lf4 mutants. This suggests the two genes act in fundamentally different ways within the length control system.

Given that correlated variation appears to result at least in part from variation in cell size (Figure 3C), one possible explanation for increased correlated variation in lf4 mutants could be that lf4 mutants have a wider variation in cell size. Because the scaling of flagellar length with cell diameter is apparently linear (Figure 3C), variation in cell diameter should produce a proportional correlated variation in length. Based on our measurements, the standard deviation in cell diameter in lf4 is larger than wild-type cells by a ratio of 1.3. However, this 1.3-fold increase in cell size variability is far less than the doubling of standard deviation in flagellar lengths as well as in correlated variation (Table 1), suggesting that increased cell size variability is unlikely to be the sole explanation for the increased correlated variation in lf4.

Long flagella mutants were also found to differ from wild-type cells in terms of the timescale of their length fluctuations (Figure 4C). The longer autocorrelation time for the lf1 mutant (101 min for wild type and 183 min for lf1) suggests that perturbations to flagellar length will persist for longer in the mutant, consistent with the idea that whatever the length control system is, its influence is weaker in the mutant cells.

We conclude from this limited candidate screen that LF1 and LF4 genes act to reduce biological noise in flagellar length. In fact, both genes seem to have a larger effect on noise than they do on the average flagellar length: uncorrelated variation increases 18-fold in LF1 and 2-fold in LF4, but average length only increases 24% in lf1 and 60% in lf4 (Table 1). Thus, although the lf mutants are usually described as having a “long flagella” phenotype, our measurements suggest that the primary phenotype is increased variation.

Noise analysis of flagellar length control models

The noise measurements reported here provide a way to test hypothetical flagellar length control system models, because any model for such a system must be able to account for not only the average steady-state behavior of the system but also the fluctuations that occur within the system. For example, any model that claims to explain flagellar length control must be able to account for the results of Figure 4 that mutations leading to increased average length also lead to increased uncorrelated variation.

We previously described a model, outlined in Figures 5A and 5B, for flagellar length control (Marshall and Rosenbaum, 2001; Marshall et al., 2005), based on the length dependence of IFT. Our IFT-based length control model contains three parameters, A, D, and P, which represent the efficiency of IFT for binding tubulin, the rate of disassembly at the tip, and the quantity of flagellar structural protein synthesized by the cell, respectively. As previously derived (Marshall and Rosenbaum, 2001) and explained further in methods, the steady-state average flagellar length for this model is:

$$L_{ss}=\frac{P}{2+\frac{D}{A}}$$ (Equation 4)

Figure 5.

Model predictions for noise versus length

(A) Schematic of balance-point mode for flagellar length control. Flagellar microtubules undergo constant disassembly (red arrow) at a length-independent rate D. This disassembly is balanced by assembly, which occurs at a rate limited by the rate of IFT (blue arrow). The rate of IFT entry is proportional to 1/L based on experimental measurements (Engel et al., 2009). Precursor protein from the cytoplasm binds with first-order binding. The available free precursor pool is the total pool P minus the quantity of precursor already incorporated into the two flagella. Hence the net assembly rate is given by A(P-2L)/L.

(B) Steady-state length is determined by the balance point between length-independent disassembly (red line) and length-dependent assembly (blue line). Mutations can increase flagellar length either by increasing assembly (blue dotted line) or by decreasing disassembly (red dotted line).

(C) Simulation results for the balance point model in which a Gaussian perturbation is added to the net rate of assembly (see methods). The resulting plot of mean-squared change in length versus time interval has a similar form to experimental observations. Inset shows a typical simulation trace of length versus time.

(D) Results of applying fluctuations to the disassembly rate D. Graph shows three curves, each representing a parameter change that increases the average length. For each curve, one parameter (A, D, or P) was varied, the average length determined, and then the uncorrelated variation computed by stochastic simulations in which a Gaussian perturbation was applied to the assembly parameter D. The Y axis of the graph plots the uncorrelated length variation (here denoted η²) normalized by the uncorrelated variation denoted obtained in simulations using the wild-type values of the three parameters (denoted η₀²). This normalized noise is unitless. Parameter values for the wild-type case are those previously derived from experimental measurements (Marshall and Rosenbaum, 2001). (Blue circles—length increased by decreasing D; red squares—length increase by increasing A; green diamonds—length increase by increasing P).

(E) Results of applying fluctuations to the assembly coefficient A. Again the three curves show the normalized uncorrelated variation as a function of flagellar length as each of the three parameters is changed so as to cause an increased length. (Blue—length increased by decreasing D; red—length increase by increasing A; green—length increase by increasing P).

(F) Results of stochastic simulation of the balance point model in which the three parameters A, D, and P are held constant, but noise is applied to the net rate of assembly obtained from the balance point model at each time point. As with panels D and E, the three model parameters were changed to increase average length and the normalized uncorrelated variation plotted. (Blue—length increased by decreasing D; red—length increase by increasing A; green—length increase by increasing P). The black line included in this plot shows the analytical prediction of a small signal noise analysis assuming an intrinsic noise source acting within one flagellum, given in the text as Equation 5.

(G) A length control model based on diffusive return of IFT kinesin (Hendel et al., 2018).

(H) Stochastic simulation of the diffusion-based model showing that the diffusion model recapitulates a mean-squared change in length versus time lag curve that resembles a constrained random walk-like behavior. Inset shows sample traces of two flagella simulated in a cell.

(I) Uncorrelated variation as a function of average length in the diffusion model. As with panels D–F, uncorrelated variation is normalized by the value seen with parameters giving wild-type length. (Blue) Variation of the build-size parameter reflecting the length increment per arrival of cargo. (Red) variation of the disassembly rate parameter reflecting the steady-state rate of tubulin removal from the tip.

Clearly, average length can be increased by increasing A, increasing P, or decreasing D. But would any of these parameter changes be able to explain the increase in noise seen in long flagella mutants? Stochastic simulations based on the model of Equation 4 predict fluctuations that have a form consistent with experimental observations (Figure 5C). Using such simulations, we ask how length-increasing parameter changes affect noise.

First, we consider the case in which the source of biological noise in length is fluctuation in one of the three parameters, A, P, or D, of Equation 4. Because variation in P will affect both flagella to the same extent, such variation could contribute to correlated variation but not to uncorrelated variation. We next consider the effect of random fluctuations in the disassembly rate D (Figure 5D). We varied each of the three parameters (A, P, and average value of D) so as to increase length and then simulated length dynamics in which D is allowed to fluctuate (see methods for stochastic simulation details). The result plotted in Figure 5D clearly shows that for noise generated by fluctuations in D, any parameter change that increases length will actually lead to decreased uncorrelated variation, not increased variation as was seen in the lf mutants. Similarly, we consider the effect of random fluctuation in the assembly rate constant A (Figure 5E). Once again, we vary each of the three parameters so as to increase average length and found that no matter which parameter was varied, the uncorrelated variation decreases as length increases. We conclude that in our model, random fluctuations in any of the three parameters cannot explain the increase of uncorrelated variation with increasing length that our experimental results with long flagella mutants have shown.

As an alternative to fluctuations of the model parameters A, D, or P, we consider a noise process in which random fluctuations are applied, not to the parameters of the model, but to the net assembly rate dL/dt. This type of noise is what one would expect if noise was created by stochastic variation in assembly processes at the flagellar tip, such as the on and off rate of tubulin. We varied the three model parameters A, D, and P and asked how these parameter changes would affect the uncorrelated variation due to fluctuations in the net assembly rate (Figure 5F). Although variation in A or P predicted a decrease in uncorrelated variation with increasing length, we found that variation in D predicted an increase.

A small-signal linear noise analysis as derived in methods predicts that the variability of length differences between the two flagella in one cell will depend on model parameters as follows:

$${\eta }_{int}^2=\frac{1}{DP}+\frac{1}{2AP}$$ (Equation 5)

It is clear from inspection that of the parameter changes leading to increased length (increased A, increased P, or decreased D), only decreased D will lead to increased uncorrelated variation. Equation 5 is plotted in Figure 5F superimposed on the results of the previously described stochastic simulation.

The model presented in Figures 5A and 5B is highly simplified, and, in particular, it relies on the assumption that the IFT injection rate is proportional to 1/L without specifying the mechanistic origin of this dependence. This assumption is based on experimental observations (Ludington et al., 2013) and is compatible with several different models (Ludington et al., 2015). Predictions based on this model cannot, therefore, discriminate among these particular models that all yield the same type of overall behavior. Moreover, predictions based on this model rely on adding arbitrary “noise sources” to the differential equations of the model, which is itself inherently deterministic.

We therefore considered a less abstract model in which the length dependence of IFT injection arises from the need for the IFT kinesin motor to return back to the cell body from the flagellar tip by diffusion (Figure 5G). Diffusive return of kinesin has been experimentally observed (Chien et al., 2017). We have previously shown (Hendel et al., 2018; Ma et al., 2020) that this diffusive return leads to a length dependence of IFT injection that can in principle explain flagellar length control. Because diffusion is itself an inherently stochastic process, this model includes its own noise source. We therefore asked whether the diffusion-based length control model could predict increased uncorrelated variation with increasing length. Simulations of the model were seen to generate a mean-squared change in length versus lag plot that shows the same features as experimental data—linear increase for short time lags followed by a plateau for large time lags (Figure 5H). The parameters describing this model are discussed in detail elsewhere (Hendel et al., 2018); here we consider two key parameters that correspond to the parameters A and D in our original balance-point model. The build size parameter δ is a proportionality constant that determines the increase in flagellar length due to arrival of an IFT particle as a function of the quantity of cargo bound to the particle. The decay parameter D corresponds exactly to the disassembly parameter D in Equation 4 and represents the rate of removal of tubulin from the tip. When these model parameters were changed so as to increase average flagellar length (Figure 5I), we found that increasing the build size led to increased uncorrelated variation in longer flagella, whereas decrease in the disassembly rate led to a decrease in uncorrelated variation.

Comparing the predictions of the two types of models shows that they can both explain increased uncorrelated variation in long flagella, but they make entirely different predictions about which parameters should be capable of creating this change. In one model, changing the disassembly rate led to increased noise in longer flagella, whereas in the other model, it led to a decrease.

Biological relevance of flagellar length variation

In order to investigate the biological significance of noise in flagellar length control, we asked whether uncorrelated noise (i.e., inequality in flagellar lengths) or correlated noise (i.e., cell-to-cell variation in the lengths of both flagella) affects flagella-driven motility. Chlamydomonas cells bend their two flagella in opposite directions in order to swim forward in a breast-stroke-like motion. Inequality in lengths, as measured by uncorrelated noise, might thus be expected to prevent a cell from swimming forward effectively in a straight line. To test this prediction, we observed Chlamydomonas cells swimming using a high-speed camera (Video S1) and measured the lengths of both flagella as well as swimming speed. To measure a range of different flagellar lengths, we analyzed motion of both wild-type and mutant cells with altered flagellar length but normal motile machinery, as discussed in methods. As shown in Figure 6A, we found that optimal swimming occurred when both flagella were of approximately equal length and when their lengths were in the range 8–12 microns. Outside of this range, swimming speed decreased dramatically. The defects in swimming were different depending on the type of length variation. When both flagella were too long, the extra length of flagellum appeared to flail ineffectively through the media, presumably impeding forward progress (Video S2). This observation is consistent with an earlier report showing that lf mutants of Chlamydomonas display reduced swimming speed and beat frequency, with a reduction that correlates with the length of the flagella (Khona et al., 2013). On the other hand, if both flagella were too short, they were unable to generate an asymmetrical bending motion. Consequently, the flagella just moved back and forth like flippers (Video S3) but could not create overall forward motion because symmetrical swimming movements cannot be used to propel organisms at low Reynolds number (Purcell 1977). If the two flagella were of sufficiently unequal length, the cells swam in circles (Video S4). These results indicate that to the extent that a length control system may have evolved to ensure effective swimming, it must satisfy two goals: ensure equality of flagellar length within a cell and ensure that the two flagella are in roughly the right average length range. Satisfying these two goals means that both correlated and uncorrelated variation would need to be constrained.

Figure 6.

Noise affects fitness as judged by flagella-driven motility

(A) Contour plot of swimming speed (red fastest, blue slowest) versus the lengths of the two flagella. White dots signify lengths of flagella in wild-type cells superimposed on swimming speed distribution. Cells with the least uncorrelated variation (closest to diagonal) swim fastest in any given length range.

(B) Contour plot of gliding speed (red fastest, blue slowest) versus the lengths of the two flagella. Cells with the most uncorrelated variation (farthest from diagonal) glide fastest in any given length range.

We next compared the actual distribution of flagellar lengths with the range of flagellar lengths that gives optimal swimming efficiency. As indicated by the dots in Figure 6A, wild-type cells have a joint distribution of lengths for their two flagella that correspond to the optimal range of flagellar lengths for fast swimming. Thus, any increase in noise that would lead to variation outside this range would decrease swimming fitness. The joint length distribution in gametes matches the region of optimal swimming even more closely (Figure S2A) due to the lower uncorrelated variation in gametes (see above).

Although flagella are used for swimming when cells are in suspension, they can also generate gliding motility when cells are adhered to a solid substrate (Bloodgood 1981). Gliding is an important type of motion for a soil-dwelling alga and one that is thought to possibly have evolved prior to bending-type flagellar motility required for swimming (Mitchell, 2007). Gliding involves motion of transmembrane proteins in the flagellar membrane adhering to the surface and then being pulled by a kinesin- and dynein-dependent motile process known as intraflagellar transport (IFT) (Shih et al., 2013; Collingridge et al., 2013). Does flagellar length variation affect gliding motility in a similar way to its effects on swimming motility? To answer this question, we imaged live cells during gliding using DIC microscopy and measured their flagellar lengths and gliding speeds, assessed as the distance the cell traveled over a fixed period of time (see methods). The results of this analysis (Figure 6B) were strikingly different from those of the swimming speed analysis. Unlike swimming, which was fastest when the two flagella were of equal length, gliding was fastest when the two flagella were of unequal length (correlation coefficient between length difference and gliding velocity r = 0.52, n = 141, p < 10⁻⁷). Gliding velocity correlated with the difference in the lengths of the two flagella but not with the average of the two flagella (r = −0.014), confirming prior reports that overall flagellar length did not influence gliding speed (Bloodgood, 1981). Gliding thus appears to be sensitive to uncorrelated variation affecting the length of one flagellum versus the other but not correlated variation affecting both flagella.

We noted that in gliding cells with unequal length flagella, cells always moved in the direction of the longer flagellum. We hypothesize that this behavior might reflect the tug-of-war nature of gliding motility (Shih et al., 2013; Collingridge et al., 2013) such that one flagellum can only glide if the other flagellum is not gliding. In cells with equal length flagella, we would therefore expect to see the cell jitter back and forth rather than undergo long periods of directed movement, and indeed this is the case. As shown in Figure S2B, we find that the frequency of reversal of gliding direction is highest in cells that have equal length flagella (r = −0.35 between length difference and reversal frequency, p = 10⁻⁵). Cells in which one flagellum is much longer than the other show a low frequency of directional reversal and tend to move at high speed in the direction of the longer flagellum. A more extreme form of this observation was previously reported by Bloodgood who observed that cells in which one flagellum had been sheared off always glided in the direction of the remaining flagellum and did not undergo any directional reversals (Bloodgood, 1981).

Discussion

Length control versus noise reduction

The results presented here show that the flagellar length control system in Chlamydomonas reinhardtii exhibits both correlated and uncorrelated variation. The overall effect of these noise sources is that in a wild-type cell, the coefficient of variation (standard deviation in flagellar length divided by average flagellar length) is in the range 10%–20%, which is comparable with the measured variability in the length of vertebrate cilia (Wheatley and Bowser, 2000) and bacterial flagellar hooks (Koroyasu et al., 1998). Although it is commonplace to compare cells and cellular structures with man-made machines, such a high level of size variability would not be tolerated in most manufacturing processes. It is therefore interesting to consider whether the level of noise that is observed indicates that cells cannot do any better or alternatively that they do not need to. The close alignment between the distribution of flagellar lengths in wild-type cells and the length range for optimal swimming speed (Figure 6A) strongly suggests that the latter explanation is correct—there is little evolutionary pressure to reduce variability in flagellar length below a level that is tolerable for effective swimming. In fact, quite to the contrary, there may be an advantage to maintain some degree of uncorrelated variation to allow for better gliding motility. Variability in flagellar length may thus benefit a population of cells by giving the population as a whole more flexibility in dealing with changing environmental conditions. Gametes, which need to swim in order to locate cells of the opposite mating type, showed reduced uncorrelated variation, possibly suggesting that they are further optimized for swimming at the expense of gliding. Our results predict that mutations such as lf1 in which the uncorrelated variation in length is high would have better gliding motility compared with wild-type cells.

Using noise to test length control models

An important use of noise analysis is to discriminate among different feedback and control mechanisms for a system (Amir and Balaban, 2018). In some cases, analysis of fluctuations can be used to invalidate a model that otherwise accounts for the average behavior of a system. The present analysis of noise in flagellar length was aimed, in part, at attempting to invalidate our previous models for length control. The balance-point model has been shown to be able to account for the kinetics of flagellar regeneration (Marshall et al., 2005), the dependence of flagellar length on flagellar number (Marshall et al., 2005), and the ability of cells to equalize their flagellar lengths when one is severed (Marshall and Rosenbaum, 2001; Ludington et al., 2012; Hendel et al., 2018). Here we find that our model can, at least qualitatively, account for the observation that long flagella mutants show increased uncorrelated variation (Figure 5F). This is also true for our model based on diffusive return of kinesin (Figure 5I).

Unfortunately, to go beyond testing qualitative predictions and perform direct quantitative comparison, for example between predicted and measured noise power spectra, would require more understanding of the actual noise source within the flagella. Currently, we do not know the source of the noise. As with any chemical reaction, assembly and disassembly of tubulin subunits on the axonemal doublets is an inherently stochastic process and thus constitutes one unavoidable source of noise (Banerjee and Banerjee, 2020; Patra et al., 2020). However, additional sources of variation may include stochastic fluctuations in cargo loading onto the IFT system (Craft et al., 2015); transport of IFT trains through the flagellar pore (Dishinger et al., 2010; Ludington et al., 2013; Hendel et al., 2018; Harris et al., 2020); diffusive return of kinesin-II from the tip (Hendel et al., 2018; Ma et al., 2020); and fluctuation of IFT traffic due to traffic jams, motor pausing, and reversals (Bressloff 2006; Pinkoviezky and Gov, 2014; Mijalkovic et al., 2017; Tang et al., 2019). For example, it has previously been proposed that entry of IFT particles into the flagellum may occur via an avalanche-like process, which naturally leads to a long-tailed distribution of IFT train sizes (Ludington et al., 2013). Fluctuations in active disassembly (Fai et al., 2019) would also contribute to noise.

Several nonlinear stochastic models have recently been proposed for flagellar length dynamics (Fai et al., 2019; Banerjee and Banerjee, 2020; Patra et al., 2020). Two of these studies analyzed models for flagellar length control using master equations to represent the inherently stochastic nature of biochemical reactions, which has the advantage of not requiring an extra “noise source” to be postulated. One study (Banerjee and Banerjee, 2020) analyzed a model closely related to our balance point model, which assumes the 1/L dependence of IFT on length, whereas a second study (Patra et al., 2020) analyzed a more elaborate model in which IFT injection is regulated by a time-of-flight mechanism. A third recent study describes a model for length regulation based on length-dependent transport of disassembly factors (Fai et al., 2019), which is distinct from our current model that assumes length-independent disassembly based on experimental measurement that show flagella shortening at a constant rate when IFT is disabled as well as prior to cell division (Marshall et al., 2005).

Analysis of one stochastic model, in which both IFT entry and the random walk of returning IFT motors are explicitly modeled as random processes, allowed for prediction of fluctuations in length, but the predicted noise, assuming that the source of noise is addition and removal of single tubulins, was much smaller than what we have observed in the present study (Datta et al., 2020). This result is consistent with the calculations reported in Figure 1F, indicating that the magnitude of fluctuations in Figure 1C would require that these fluctuations involve large numbers of tubulins being added or removed during one step.

Here, we have shown that two models, namely the original balance-point model with an assumed 1/L dependence of IFT (Marshall et al., 2005) and a model based on diffusive return of kinesin driving IFT entry (Hendel et al., 2018; Ma et al., 2020), can both account for increased fluctuations in cells with increased average flagellar length but that depending on the model, the specific parameter changes necessary to achieve both conditions (increased length and increased fluctuation) are distinct. Thus, if we can experimentally determine exactly which mechanistic features of the cell are altered in a given long flagella mutation, for example decreased disassembly or increased pool size, it should be possible to rule out some models using fluctuation data.

Finally, we note that length control models have been proposed for other linear structures in the cell (Naoz et al., 2008; Orly et al., 2014; Mohapatra et al., 2017), and we believe that noise analysis such as that reported here could be a productive way to probe these other models as well.

Intrinsic versus extrinsic noise

Two distinct types of noise sources have been described for studies of gene expression: extrinsic noise, which describes variation caused by processes taking place in the cell as a whole cell, such as cell growth or cell-cycle state, and intrinsic noise, which describes variations in transcription rates at an individual promoter (Elowitz et al., 2002; Raser and O'Shea, 2004). These concepts of extrinsic and intrinsic noise sources are based on the distinction between a “system” (such as a promoter) and an “environment” (such as the rest of the cell, not including the promoter). In gene expression studies, the two types of noise are measured using a dual-reporter method (Elowitz et al., 2002), in which two different fluorescent protein reporter constructs are driven by identical promotors, so that variation in expression of both constructs can be measured on a cell-by-cell basis. It is then assumed that the correlated variation reflects extrinsic noise and the uncorrelated variation reflects intrinsic noise. Still, it is important to remember that these mathematical descriptions (Equations 1 and 2) are not definitions of intrinsic or extrinsic noise but are merely statistical descriptors of how the total variation is distributed among a correlated and uncorrelated component.

In applying these concepts to flagellar length control, we consider the “system” to be the flagellum, of which there are two copies, as in a dual-reporter gene construct, and the “environment” to be the cell body along with any factors outside of the cell. We choose this way of defining “system” and “environment” because we are specifically interested in control mechanisms that may exist within flagella to constrain length variation as well as in control mechanisms that may exist within cells to regulate cell-to-cell heterogeneity in flagellar length. Moreover, if it were possible to break the noise sources down into specific contributions associated with the flagella themselves and others associated with the cell body, these two noise measurements could then be used to assess how different molecular pathways may differentially affect flagella-associated or cell-body-associated processes related to flagellar length.

The mathematical decomposition of noise sources into intrinsic and extrinsic, achieved by decomposing total variation from dual-reporter experiments into correlated and uncorrelated components, relies on numerous assumptions that may not hold for a system of interest (Hilfinger and Paulsson, 2011). One assumption of the decomposition is that noise sources are additive, which may not be the case. For example, our simulations of Figures 5D and 5E analyzed multiplicative noise created by fluctuations in model parameters. Of particular relevance to flagellar length control is the fact that the intrinsic/extrinsic decomposition breaks down in the situation where the two systems are competing for a common resource (Stamatakis et al., 2011), which is certainly the case for flagella, which compete for a common cytoplasmic pool of tubulin. Based on such considerations, it is not possible a priori to equate the correlated and uncorrelated components of total variance with extrinsic and intrinsic sources, respectively. We are thus left with the question—does flagellar length entail any contribution that is “intrinsic” in the sense of arising from fluctuations inside the flagella, and does it entail any contribution that is “extrinsic” to the flagella in the sense of arising from variations of a property of the cell body?

Our measurements of flagellar length before and after regeneration suggest that there is a component of the correlated variation coming from the cell body (Figure 3A). How does the cell body affect flagellar length? Size is one clear contributor (Figure 3C). In addition to our results, previous studies have also noted that larger cells sometimes have longer flagella in various mutants (Adams et al., 1985). Why does size affect length? Studies of gene expression have found that cell-to-cell differences in protein abundance for a given gene are often dominated by variation in cell size (Raser and O'Shea, 2004), presumably because larger cells have more ribosomes, thus making more protein per mRNA molecule. Perhaps larger Chlamydomonas cells are able to make a larger pool of flagellar precursor proteins such as tubulin, due to the fact that they have more ribosomes. This idea is consistent with the fact that flagellar length depends on the availability of flagellar precursor proteins (Rosenbaum et al., 1969; Coyne and Rosenbaum 1970). Our results do not, however, explain why length is proportional to cell diameter and not to cell volume.

The observation that average flagellar length is proportional to cell diameter (Figure 3C), together with the fact that correlated variation is reduced in cell-cycle-arrested cells (Figure 3D), all suggest that at least part of the correlated variation is due to features of the cell body, such as size and cell cycle state, that are shared by both flagella, and would thus constitute “extrinsic noise.” What we cannot tell, from our existing data, is whether these shared factors are also responsible for the dynamic component of the correlated variation (Figure 2C). Given the fact that the dynamic fluctuations are taking place on the timescale of tens of minutes (Figures 1C and 1D), it is certainly possible that fluctuations in shared features of the cell body, such as transcription or translation of precursor proteins such as tubulin, could be driving the correlated fluctuations in length. One potential mechanism for such shared fluctuations would be dynamic changes in the polymerization state of cytoplasmic microtubules, which are in competition with flagellar microtubules for a common pool of tubulin (Wang et al., 2013; Kannegaard et al., 2014).

The uncorrelated component of length variation is mainly due to fluctuations in length rather than locked-in variation (see Figures 1C and 2A), but this does not necessarily mean that the source of the fluctuations has to be something inside the flagella. The basal bodies that nucleate the flagella and serve as docking sites for the IFT machinery could undergo fluctuations in state, for example due to variable accumulation of IFT proteins. The fact that length differences are completely uncorrelated in cells before and after flagellar regeneration (Figure 3B) argues against such a model. In any event, the presence of a dynamic uncorrelated component of flagellar length variation strongly suggests the presence of noise sources that are either inside the flagella or that affect flagella-associated structures inside the cell body. Whether the latter type of noise source should count as “intrinsic” or “extrinsic” is not obvious and probably not important.

Limitations of the study

One limitation of this study is that the standard light microscopy being used to monitor changes in flagellar length does not have sufficient resolution to detect individual tubulin assembly or disassembly events. A second limitation is that our analysis of swimming fitness only measured physical swimming speed and does not directly assess how well a cell might survive in the wild as a function of flagellar length.

Resource availability

Lead contact

Wallace Marshall (wallace.marshall@ucsf.edu).

Materials availability

Strains used in this work are available from the Chlamydomonas Resources Center (https://www.chlamycollection.org).

Data and code availability

Data and programs are available upon request.

Methods

All methods can be found in the accompanying transparent methods supplemental file.

Published: April 23, 2021