A predictive coarse-grained model for position-specific effects of post-translational modifications

Abstract

Biomolecules undergo liquid-liquid phase separation (LLPS), resulting in the formation of multicomponent protein-RNA membraneless organelles in cells. However, the physiological and pathological role of post-translational modifications (PTMs) on the biophysics of phase behavior is only beginning to be probed. To study the effect of PTMs on LLPS in silico, we extend our transferable coarse-grained model of intrinsically disordered proteins to include phosphorylated and acetylated amino acids. Using the parameters for modified amino acids available for fixed-charge atomistic force fields, we parameterize the size and atomistic hydropathy of the coarse-grained-modified amino acid beads and, hence, the interactions between the modified and natural amino acids. We then elucidate how the number and position of phosphorylated and acetylated residues alter the protein’s single-chain compactness and its propensity to phase separate. We show that both the number and the position of phosphorylated threonines/serines or acetylated lysines can serve as a molecular on/off switch for phase separation in the well-studied disordered regions of Fused in Sarcoma (FUS) and DDX3X, respectively. We also compare modified residues to their commonly used PTM mimics for their impact on chain properties. Importantly, we show that the model can predict and capture experimentally measured differences in the phase behavior for position-specific modifications, showing that the position of modifications can dictate phase separation. In sum, this model will be useful for studying LLPS of post-translationally modified intrinsically disordered proteins and predicting how modifications control phase behavior with position-specific resolution.

Significance

Post-translational modifications are important regulators of liquid-liquid phase separation, (LLPS) which drives the formation of biomolecular condensates. Theoretical methods can be used to characterize the biophysical properties of intrinsically disordered proteins (IDPs). Our recent framework for molecular simulations using a Cα-centered coarse-grained model can predict the effect of various perturbations such as mutations (Dignon et al. PLoS Comput. Biol., 2018) and temperature (Dignon et al., ACS Cent. Sci., 2019) on LLPS. Here, we expand this framework to incorporate modified residues like phosphothreonine, phosphoserine, and acetyllysine. This model will prove useful for simulating the phase separation of post-translationally modified IDPs and predicting how position-specific modifications can control phase behavior across the large family of proteins known to be phosphorylated and acetylated.

Introduction

Many cellular processes depend on the formation of membraneless nuclear and cytoplasmic assemblies known as membraneless organelles or biomolecular condensates (1, 2, 3). Lacking a phospholipid membrane, these biomolecular condensates (4) can respond rapidly to environmental changes, forming cellular compartments concentrating specific proteins (5) and nucleic acids (6). The formation of many membraneless organelles appears to be driven by interactions between proteins containing intrinsically disordered regions (IDRs) (7). The detailed molecular interactions mediating these membraneless organelles may include cation-π (8), sp²/π (9), hydrogen bonding, salt bridges, and hydrophobic interactions (10, 11, 12). Importantly, recent efforts have demonstrated that IDR liquid-liquid phase separation (LLPS) and, hence, the formation of membranelles organelles can be regulated by a plethora of factors such as salt concentration, pH, RNA (13), ATP (14), temperature (15), and post-translational modifications (PTMs) (16,17).

PTMs enrich the repertoire of the 20 natural amino acids and have been shown to be an important potential means for modulating phase separation (17). Two of the most frequently occurring eukaryotic PTMs (18) are phosphorylation (19) and acetylation (20), which covalently attach a phosphoryl group or an acetyl group, respectively, to select amino acids (21). These modifications can reduce the binding affinity of RNA (22), impair enzyme activity (23), decrease aggregation propensity of fibril-forming segments (24), or trigger the self-assembly of RNA granules (25). Importantly, phosphorylation and acetylation both change the charge of the associated amino acid. Phosphorylated serine and threonine have a net charge between −1 and −2 at neutral pH (the actual value depends on the surrounding environment, though a pK_a of ∼5.9 to ∼6.0 for the −1 to −2 protonation state of phosphoserine/threonine (26) suggests the −2 charge state will be predominant at neutral pH) compared with no net charge for unmodified serine and threonine. Conversely, acetylation neutralizes the +1 charge that lysine has at physiological pH. Because IDRs generally contain many PTM sites that may be simultaneously modified (27), this can dramatically alter the net charge and charge patterning in ways that impact chain properties, phase separation, and aggregation. Hyperphosphorylation and hyperacetylation can lead to large changes in protein charge distribution and, hence, conformation and are associated with aggregation of amyloidogenic proteins in neurodegenerative diseases (20,28,29).

Although in vitro studies have demonstrated the effect of different PTMs on LLPS, studying the effect of each possible combination of PTMs is laborious and difficult. Furthermore, it is challenging to have site-specific control to reproduce modification patterns that are deposited on IDRs in vivo. Therefore, computational studies can be an effective approach to screen a large number of PTM patterns and predict their role on regulating the molecular properties and phase separation of proteins (30,31). All-atom explicit solvent simulations readily incorporate post-translationally modified amino acids (32, 33, 34, 35, 36) and have been used to probe the contacts leading to phase separation (37,38). However, the ability of atomistic force fields to accurately capture the properties of IDRs depends strongly on parameterization (39,40). Additionally, simulations of sufficiently long length and timescales to predict phase-separation behavior (e.g., saturation concentration) are beyond current computational capability for fully atomistic simulations with explicit water. In contrast, coarse-grained (CG) models (41, 42, 43, 44, 45), in particular those in which peptides are represented as chains of single beads and solvation effects are represented implicitly, have been used to efficiently investigate the phase behavior of large macromolecules (46,47). Most current CG modeling approaches capable of studying IDRs are currently parameterized only for the 20 natural amino acids (48), whereas others are suited specifically to probe phosphoregulation of folded domains (49,50). Therefore, there is a need for transferable approach to elucidate the effect of PTMs on the biophysical properties and phase behavior of IDRs associated with the assembly of biomolecular condensates.

Here, we expand our previous amino acid resolution CG hydropathy scale model (HPS) model (48) to incorporate PTMs compatible with the procedure used to obtain the parameters for the 20 natural unmodified amino acids. We use the HPS model as a starting point due to its transferable physics-based philosophy as compared with other commonly available CG paradigms. Many other CG models rely on explicit input from experiment data on a system of interest or a closely related system. Of course, further improvements in the underlying parameters may be needed (51), while preserving its transferable nature, to further enhance its applicability. We refer the readers to recent reviews for extensive discussions on CG models and their applications (41,43,44,47,52). To investigate how the position and the number of modified sites can alter the phase behavior of IDRs, we perform in silico studies of two IDRs: the N-terminal low-complexity (LC) domain of RNA-binding protein Fused in Sarcoma (FUS) LC (which is rich in serine, tyrosine, glutamine, and glycine residues and contains 12 known phosphorylation sites modified by DNA-dependent protein kinase (53)) and the first disordered region (IDR1) of the DEAD box RNA helicase 3, X-linked (DDX3X) with 10 lysine residues known to be acetylated (54). We test how the post-translational state of each molecule modulates IDR compactness and LLPS in a sequence-specific manner. Using CG molecular simulations, we examine the effect of increasing number of modified residues and test the hypothesis that position-specific patterning of PTMs can alter the collapse and phase behavior of IDR sequences. Finally, we test the ability of the model to reveal the origin of experimentally known position-specific effects on phase separation.

Methods

Hydropathy scale model for PTMs

The functional form of the total energy of the system is as follows,

$$\Phi \left(r\right)=\sum _{bonds}{k}_{spring}{\left(r-r_0\right)}^2+\sum _{i<j}\left[{\Phi }_{elec}\left(r_{ij}\right)+{\Phi }_{nb}\left(r_{ij}\right)\right]$$

where ${\Phi }_{bond}$is a standard harmonic spring with $k_{spring}=10\frac{\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{m}\mathrm{o}\mathrm{l}{\mathrm{\AA }}^2}$ and $r_0=$3.8 Å. The screened electrostatic term is represented using a Debye-Hückel type form:

$${\Phi }_{elec}\left(r\right)=\frac{q_i{q}_j}{4\pi Dr}{e}^{\frac{-r}{\kappa }},$$

where $q_i$and $q_j$are the net charges of formally charged amino acids (D,E = −1; K,R = 1; H = 0.5), $D$ is the dielectric constant (which is set to 80 for water), and κ is the screening length, which is set to 10 Å to represent a salt concentration of ∼100 mM. The nonbonded interactions are described by the Ashbaugh-Hatch functional form, which has been previously applied to the study of disordered proteins (55). In this Lennard-Jones-like functional form, the attractiveness of the interactions is scaled by the arithmetic average of hydropathy for the two interacting amino acid types, $\lambda =0.5\left({\lambda }_i+{\lambda }_j\right)$:

$${\Phi }_{LJ}=4{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right],$$

$${\Phi }_{nb}\left(r\right)=\{\begin{array}{l}{\Phi }_{LJ}+\left(1-\lambda \right)\epsilon ,ifr\le 2^{1/6}\sigma \hfill \\ \lambda {\Phi }_{LJ},otherwise\hfill \end{array},$$

where ${\Phi }_{LJ}$ is the standard Lennard-Jones potential and $\sigma$ is the arithmetic average of the vdW radius,

$${\sigma }_{ij}=\frac{\left({\sigma }_i+{\sigma }_j\right)}{2},$$

where $\sigma =2r_{vdW}$ because the atoms are modeled as spheres, and their impenetrable volumes are defined by the vdW radius (56) $r_{vdW}$.

Determining hydropathy values from atomic charges

The original HPS model is based on the hydrophobicity scale put forth by Kapcha and Rossky (57) using the atomic charges from the atomistic optimized potentials or liquid simulations (OPLS) force field for proteins. The hydropathy scale was then scaled to the range of 0–1, with 0 being the least hydrophobic and 1 being the most hydrophobic. We further extend this procedure to obtain hydropathy values for post-translationally modified amino acid residues using partial atomic charges from a set of AMBER forcefield parameters for 32 common PTMs (FF-PTM) (35). Atoms with a partial charge magnitude ranging from 0 to 0.25 are considered nonpolar and are assigned a hydropathy value of −1. In the binary atomic-level hydropathy scale, atoms with a partial charge magnitude greater than 0.25 are considered polar and are assigned a hydropathy value of +1. The residue-level hydropathy values are calculated as a weighted sum of the atomic hydropathy values according to the following rules: hydrophobic (nonpolar) atoms contribute −0.5, hydrophilic (polar) atoms contribute +1, and charged atoms contribute +2. An atom in charged residues is classified as charged if it belongs to the terminal polar group in which the magnitude of the sum of all atomic partial charges in that group is greater than 0.5 (57).

Simulations framework

To obtain the temperature under which a protein chain behaves as an ideal solvent (T_θ), single-chain simulations were conducted for 1 μs at a range of temperatures using replica exchange molecular dynamics (REMD) (58) with a temperature list of 150.0, 170.1, 193.0, 218.9, 248.3, 281.7, 300, 362.4, 411.1, 466.3, 529.0, and 600.0 K to enhance ergodic sampling of the IDR conformational ensemble (59). Simulations were conducted in cubic boxes with periodic boundaries large enough so that a protein chain will not encounter its periodic image, and temperature was maintained using a Langevin thermostat. All single-chain simulations were conducted using LAMMPS (60). To get better sampling for the Rg for proteins in Fig. 1, we simulated DDX3X IDR1, DDX3X IDR1 10acK, FUS LC, FUS LC 12 pS/pT, FUS LC 12 E (−2) using REMD (58) for 5 μs with a temperature list of 150.0, 154.49, 159.11, 163.88, 168.78, 173.84, 179.04, 184.4, 189.92, 195.6, 201.46, 207.49, 213.7, 220.1, 226.69, 233.47, 240.46, 247.66, 255.07, 262.71, 270.57, 278.67, 287.02, 295.61, 304.46, 313.57, 322.96, 332.63, 342.58, 352.84, 363.4, 374.28, 385.48, 397.02, 408.91, 421.15, 433.75, 446.74, 460.11, 473.88, 488.07, 502.68, 517.73, 533.23, 549.19, 565.63, 582.56, and 600.0 K.

Figure 1.

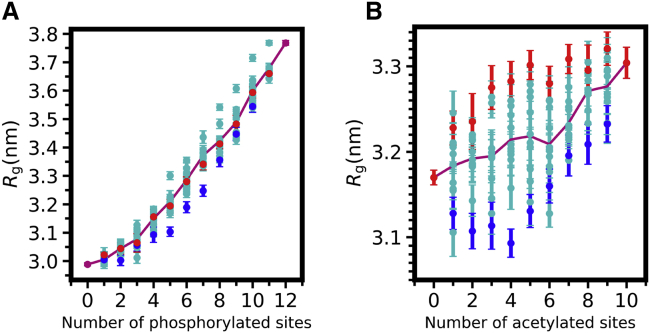
Expanding the HPS model to incorporate phosphorylation and acetylation. (A) Domain representation of FUS LC 12 pS/pT. Negative residues D5 and D46 are highlighted in red. Phosphorylation sites at 7, 11, 19, and 68 (phosphothreonine) and 26, 30, 42, 61, 84, 87, 117, and 131 (phosphoserine) are highlighted in orange. (B) Distribution of radius of gyration of FUS LC (cyan), FUS LC 12 pS/pT (purple), and FUS 12 E (−2) with −2 charge for Glu (blue). (C) Domain representation of DDX3X IDR1. Negative residues are shown in red, positive residues (other than lysine, i.e., arginine) in blue, and lysines in green. (D) Distribution of radius of gyration of DDX3X IDR1 (orange) and DDX3X IDR1 10 acK (purple). In representative snapshots, the unmodified beads are shown in cyan (FUS LC) or orange (DDX3X IDR1), the negatively and positively charged residues in red and blue, respectively, and the modified sites in purple. Dashed lines represent the ensemble average R_g. Error bars represent standard error of the mean (SEM) from 5 equal divisions. To see this figure in color, go online.

Coexistence simulations were conducted using slab geometry (61,62) like in our previous work (15,37,48,63, 64, 65). Simulations were conducted on 100 chains of FUS or DDX3 using the HPS model and the new parameters for PTMs. Simulations were conducted using HOOMD-Blue v2.1.5 (66) for 5 μs each in serial with a Langevin thermostat, during which the first μs was discarded as equilibration.

Single-molecule properties

Using the radius of gyration (R_g) and the polymer-scaling exponent (ν) in different temperatures as descriptors of the phase behavior, we calculate the temperature at which a protein behaves as an ideal polymer: the point where protein-protein interactions and protein-solvent interactions become energetically equally favorable (T_θ) (67). For each temperature, we estimated the polymer-scaling exponent (ν) by fitting to the following equation:

$$R_{ij}=b|i-j{|}^{\nu },$$

where b is the Kuhn length, which is set to 0.55 nm for disordered proteins (68), and $R_{ij}$is the intrachain separation defined as the distance between residue i and residue j. Next, we interpolated the results to find the temperature at which v = 0.5, which is correlated with the critical temperature for phase separation (63).

Sequence-charge decoration

We use the sequence-charge decoration (SCD) parameter, which is a metric first presented in the analytical model of Sawle and Ghosh, to capture the effect of charge patterning on the values of radius of gyration of synthetic polyampholyte sequences (69). They showed that electrostatic interactions are enhanced by local patches of like charges and attenuated when charged residues are more mixed within the sequence. For a sequence with equal number of positive and negative residues (of net charges −1 and +1), highly negative SCD-values correspond to stretches of like charges clustered in the sequence, whereas values near zero result from well-mixed charge residues, with a sequence of strictly alternating positive and negative charges approaching SCD of 0. Positive values of SCD result from sequences that have a large net charge (see Fig. S2 for schematic of SCD). SCD is calculated (67) using the following equation:

$$SCD=\frac{1}{N}\left[\sum _{i=2}^N\sum _{j=1}^{i-1}{q}_i{q}_j{\left(i-j\right)}^{\frac{1}{2}}\right],$$

where i – j is the separation of residues with charges q_i and q_j along a chain of length N.

Phase diagrams

Phase diagrams were extracted from coexistence simulations by measuring the density of protein in the dense phase in the center, and in the low-density phase outside. The critical temperature and critical density were obtained using the top seven highest temperatures for the maximal SCD case and eight for the minimal SCD case in which we observed phase coexistence. We fit the coexistence densities at these temperatures to a fitting function:

$${\rho }_H-{\rho }_L=A{\left(T_c-T\right)}^{\beta },$$

where β is set to 0.325 according to the universality class of the three-dimensional Ising model (66).

Results

Expanding the HPS model to incorporate phosphorylation and acetylation

To extend our primary sequence-specific CG model to study PTMs, we employed the original philosophy of computing CG interaction parameters from the size, net charge, and atomic hydropathy of the post-translationally modified amino acids. Our previous CG representation of the protein represents every natural amino acid by a single bead of unique mass, charge, size, and hydropathy parameter that were computed from a fully atomistic fixed-charge force field parameter for each residue type (35,48,57). Using previously published AMBER force field parameters for modified amino acids (34), we computed CG parameters for serine, threonine, and tyrosine phosphorylation and lysine acetylation (Table S1). We have selected to represent phosphorylated amino acids as bearing a −2 charge, given that at neutral pH the net charge on phosphorylated residues is likely to be close to −2 (see above) (26,70). We note that the proposed framework is not meant to capture dynamic pK_a shifts because of the local environment, which can change the pK_a. To simulate lower pH conditions or if the pK_a is experimentally known or likely to be shifted as may be the case in charge-dense polyelectrolyte chains, it may be useful in these situations to simulate phosphorylated residues with a different net charge (i.e., −1), as previously suggested (71). In principle, these parameterization of CG parameters for modified residues can be applied to any library of noncanonical amino acids with known structure or charge parameters to aid the high-throughput screening of proteins with unknown PTM-regulated phase separation.

To test the effects of these PTMs on CG models of IDRs, we used the HPS-PTM model to characterize the properties of two modified IDRs: phosphorylated FUS LC (FUS LC 12pS/pT) (Fig. 1 A) and acetylated human DDX3X IDR1 protein (DDX3X IDR1 10acK) (Fig. 1 C). Single-chain CG simulations were conducted for 5 μs at a range of temperatures (150–600 K) using REMD to enhance sampling (58). Unmodified FUS LC is nearly uncharged (containing only two charged residues) but can be phosphorylated by DNA-dependent protein kinase at 12 unique sites, displaying either SQ or TQ motif (53). Here, we begin by testing the effect of hyperphosphorylation at all 12 sites (FUS LC 12pS/pT). In the hyperphosphorylated state, FUS LC 12pS/pT is more extended than the unmodified state, having a much larger radius of gyration (R_g) at the reference temperature (295 K) (Fig. 1 B). Hyperphosphorylation also reduces T_θ (Fig. S1, A and C), the temperature at which attractive intramolecular interactions are balanced by repulsive excluded volume interactions (67). Both of these reflect experimental observations that phosphomimetic mutants of FUS are more extended in solution and are less prone to phase separate (24,37).

The observed difference in phase separation is likely caused by the large change in net charge of FUS LC, but phosphoserine and phosphothreonine also differ from the unmodified residues in the other model parameters. In our previous work, we showed that the electrostatic contribution of phosphomimetic mutations was larger than the impact of the change in λ (24). Here, we have explored the contribution of the CG bead size and hydropathy parameters on the chain dimensions. We simulated the FUS LC 12E variant in which a Glu residue has been substituted instead of 12pS/pT residues and has been assigned a charge of −2 to match the charge of pS and pT (instead of its usual −1 charge). This FUS LC 12E (−2) is, indeed, more extended than FUS LC but not to the same extent as FUS LC 12pS/pT. These data indicate that the role of nonelectrostatic interactions is not negligible and, thus, show additional value of the CG model that incorporates explicit modified residues (Fig. 1 B).

Next, we tested the effect of acetylation using single-chain REMD simulations of DDX3X IDR1 and DDX3X IDR1 10acK, which is the acetylated variant of DDX3RX IDR1 by replacing 10 lysines with acetyllysines in positions identified to be acetylated in vivo (54). At the reference 295 K temperature, we found that the modified state is also more expanded than the unmodified state, but the difference is considerably less than that of FUS LC 12pS/pT from unmodified FUS LC (Fig. 1 D). Similarly, T_θ is only slightly decreased (Fig. S1, B and D), consistent with the small change in R_g. This finding is also consistent with experimental results showing that acetylmimetic DDX3X is less prone to phase separate (54).

We suspect that the larger changes in single-chain properties for FUS LC hyperphosphorylation compared with DDX3X IDR1 hyperacetylation may be caused by the nearly uncharged nature of unmodified FUS LC as opposed to the highly charged polyampholytic character of DDX3X IDR1 in which other positively and negatively charged residues are extensively distributed throughout the sequence. Therefore, acetylation of lysine residues across the entire DDX3X IDR1 does not dramatically alter the intramolecular interactions, which we probe further in the following sections. Taken together, these data demonstrate that we can model changes in biophysical properties of IDRs using this CG approach.

Effect of increasing number of PTMs on chain properties of FUS LC and DDX3X IDR1

We next wanted to test the effect of increasing the number of modified sites on the expansion or collapse of the IDRs. The number of possible modification combinations is very large, given by the following equation:

$$\sum _{m=0}^M\frac{M!}{m!\left(M-m\right)!}=2^M,$$

where M is the total number of possible PTM sites, and m is the number of sites that are modified. Although there is only one possible state with 0, or M modifications, there are 924 possible states of FUS with six modified residues, and 252 possible states of DDX3 with five modified residues. We selected a subset of 10 random modification patterns for each number of modifications sites (1 ≤ m ≤ 11 for FUS LC and 1 ≤ m ≤ 9 for DDX3X IDR), and performed simulations on these sequences. Because the position of charged residues can play an important role in chain dimensions (72), we also computed the SCD parameter (69) for all possible sequences (including both the PTMs and the other charged residues in the sequence) to determine the SCD extremes where like-charged residues are clustered together (SCD far from 0) or charged residues are well-mixed (SCD close to 0). See Materials and methods and Fig. S2 for more information on SCD. We included both the SCD minimum and maximum in our simulated sequences to complement our randomly chosen sequences.

For FUS LC, R_g increases with increasing number of phosphorylation sites (Fig. 2 A; Fig. S3, A and B), going from slightly below 3.0 nm for unmodified to 3.8 nm for FUS LC 12pS/pT. This large expansion is consistent with increasing polyelectrolytic character because of phosphorylation, adding increasing numbers of negatively charged sites to FUS LC, which is otherwise nearly uncharged. Interestingly, sequences with the same number of modifications but in different patterns showed a range of R_g, which we explore further (see below).

Figure 2.

Effect of increasing number of PTMs on chain properties of FUS LC and DDX3X IDR1. (A) Random phosphorylation patterns expand FUS LC monotonically. Cyan data points show the ensemble average R_g for each variant of 10 randomly selected phosphorylation patterns for a given number of phosphorylation sites in FUS LC. Violet line represents the mean R_g-value from 10 simulations. Red and blue data points show the R_g of SCD-maximal and SCD-minimal sequences, respectively. (B) Random acetylation patterns in DDX3X yield to a moderate expansion. Cyan data points show the ensemble average R_g for each variant of 10 randomly selected acetylation patterns for a given number of acetylation sites in DDX3X IDR1. Violet line represents the mean R_g-value from 10 simulations. Red and blue data points show the ensemble average R_g of SCD-maximal and SCD-minimal sequences, respectively. Error bars represent standard error of the mean (SEM) from 10 equal divisions of the equilibrated ensembles. To see this figure in color, go online.

We then probed the chain properties of the DDX3X IDR1 as a function of lysine acetylation. To quantify the difference in chain properties as a function of increasing number of acetylation modifications, we performed single-chain simulations selecting 10 random acetylation patterns for each number of acetylated sites, analogous to the procedure we used for FUS LC phosphorylation above. We found that with increasing number of modifications, the chain dimension increases only slightly, from 3.2 to 3.3 nm (Fig. 2 B; Fig. S3, C and D). Importantly, sequences carrying the same number of acetylated lysines but different arrangements of the acetylation sites also exhibit the variation of chain dimensions. As for FUS LC, we further explore the connection between the arrangement of the PTMs and the distribution of R_g below.

Comparing post-translationally modified residues to common modification mimetics

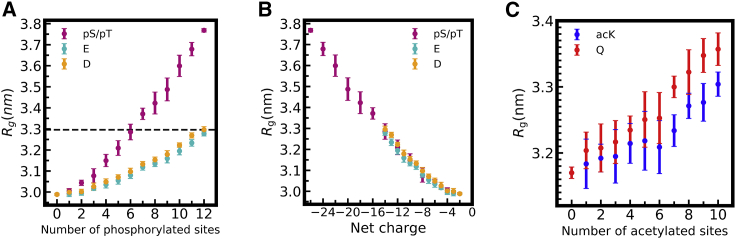
A widely used approach in experimental studies of PTMs is to mimic the change in amino acid character caused by the modification with a natural amino acid substitution. This allows for precise control of the location of modified residues. In the case of phosphorylation, serine and threonine are typically mutated to aspartic acid (73) or glutamic acid (54,74,75), which mimic the negative charge and larger size of the phosphorylated residue. Here, we evaluate aspartic acid or glutamic acid substitutions as phosphomimics using our model. We found that aspartic acid and glutamic acid do not fully recapitulate the chain dimensions observed with phosphorylation (Fig. 3 A), likely because phosphorylated residues are represented as having a −2 charge compared with the −1 charge of the phosphomimics. We tested this hypothesis that the dominant contribution to the difference in chain expansion for phosphorylation versus phosphomimetic mutation is caused by the difference in added charge by replotting R_g as a function of net charge (Fig. 3 B). Indeed, we find that the effect of phosphorylation on FUS LC chain dimensions in the CG model appears to be largely, though not entirely (see Fig. 1 A), driven by the charge of the modifications. Similarly, for the glutamine, which is commonly used to mimic acetylation of lysine (removing the positive charge of the amino acid) (76,77), we find that glutamine substitutions result in similar R_g to lysine acetylation in DDX3X IDR1 (Fig. 3 C). Small differences in the glutamine and acetyllysine chain dimensions again point to the contribution of parameters (i.e., size and hydropathy, Table S1) other than the residue net charge in determining the contacts formed. These observation in turn demonstrate that capturing such effects require the parameterization of CG models in a transferable way, which is an important feature of the approach that we follow in our modeling framework.

Figure 3.

Comparing post-translationally modified residues to common modification mimetics. (A) Effect of FUS LC phosphomimetic substitutions glutamic acid (E, cyan) or aspartic acid (D, orange) on R_g compared with phosphorylation (pS/pT, violet). (B) The same data as in (A) but with the x axis shown as the net charge of FUS LC, demonstrating that the difference between phosphomimetic and phosphorylated R_g can be largely explained by difference in net charge of aspartic acid and glutamine acid (−1) and phosphoserine or phosphothreonine (−2). (C) Effect of DDX3X IDR1 acetylmimetic glutamine (Q, red) substitutions on R_g compared with acetylated lysine (acK, blue). Data represent mean and standard deviation from 10 individual simulations with random phosphorylation or substitution patterns per site except for 0 or n = maximal number of substitutions (for which there is only one pattern: all or none) where the block average and SEM is shown. To see this figure in color, go online.

Different PTM patterns with the same number of modifications have differing effects on LLPS

Although adding more PTMs or mimics resulted on average in a change in the chain dimensions, different patterns of PTMs with the same number of modifications in FUS LC and DDX3X IDR1 show significantly different R_g (Fig. 2). This is an interesting observation for FUS LC and DDX3X IDR1 because it implies that the placement of the PTMs can impact the chain properties. To attempt to explain the variance in R_g, we computed and plotted the SCD for our sequences. Although the impact of charge patterning as measured by SCD is largely predictive of the R_g for FUS LC when looking across all number of modifications simultaneously (Fig. S4 A), the SCD does not fully capture the behavior for DDX3X IDR1 (Fig. S4 C) as is also apparent when examining the SCD only for a given number of modifications (Document S1. Figs. S1–S5 and Tables S1 and S2, Document S2. Article plus supporting material D). These deviations may be cause by contributions from hydropathy patterning (78) as well as inherent limitations in SCD (44). In summary, the impact of other physical parameters on the chain dimensions are not trivial and underscore the potential for CG models to complement theoretical predictions, which only consider charged residue patterning.

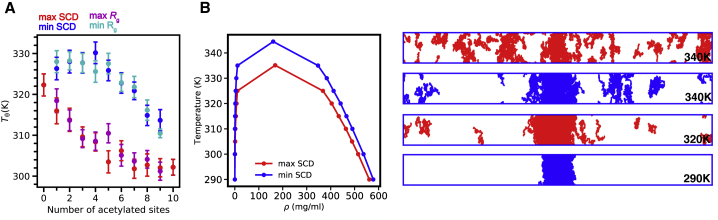
Given that IDR chain dimensions correlate with phase behavior (63,79), we next tested the effect of the placement of PTMs on LLPS. We noted earlier that there may be dramatic differences in the single-chain properties for sequences with the same number of PTMs. To understand the differences between the sequences, we decided to focus on DDX3X IDR1 where, even when the number of modifications is held constant, the arrangement of the acetylation modifications may have a large impact on R_g (Fig. 2 B). For the two sequences with highest or lowest values of R_g and two with extreme values of SCD, we computed T_θ and found that it is significantly different for sequences with the same modification number (and hence same net charge) but different sequence (Fig. 4 A). To demonstrate the position-specific effect of PTMs on the phase diagram of acetylated DDX3X IDR1, we simulated the two sequences with four acetylated lysines that exhibited the greatest difference in single-chain properties (Table S2). We find that positioning four acetylated lysines within the predominantly negatively charged C-terminus of DDX3X IDR1 enhances LLPS compared with the sequence that places the four acetylated lysines in the polyampholytic N-terminal/central region (Fig. 4 B). For reference, we also show the phase diagrams of the acetylmimetic variants in Fig. S5.

Figure 4.

Different PTM patterns with the same number of modifications have differing effects on chain expansion and LLPS. (A) T_θ temperature of R_g-minimal (cyan) and R_g maximal (magenta), SCD minimal (blue), and SCD maximal (red) DDX3X IDR1 sequences acetylated at n = 1 to n = 9 sites. Nonacetylated (0) and fully acetylated (10) variants are shown in red. Error bars calculated based on the posterior uncertainty of the probabilistic surrogate used to fit (T_θ, ν) pairs (see Fig. S1) (B) Phase diagram of SCD minimum and SCD maximum of DDX3X IDR1 acetylated at four lysines are shown along with the simulation snapshots at multiple temperatures. To see this figure in color, go online.

Together, these data demonstrate that the arrangement as well as the quantity of PTMs can have a large impact on the phase separation behavior of IDRs. This also highlights the necessity of methods that allow for control over which PTMs are “activated” to fully characterize a disordered protein and its range of responses to regulation by PTMs.

Predicting effect of different modification patterns on phase separation: comparison with experiment

To test the predictive ability of the model, we decided to further explore the differences in predicted phase behavior for different modification patterns at a set number of modifications. To this end, we examined a series of single-position acetylmimetic (lysine to glutamine substitutions) of DDX3X IDR1 whose phase separation has been previously examined by experiment (54). We again show that in the CG model, single-glutamine mimetics and acetylated lysine residues at the same position yield similar though not identical results (Fig. 5 A). We do notice that the replacement of lysines with acetylated lysines in DDX3X IDR1 has a slightly bigger effect on R_g than substitution of acetylated lysines with glutamines, most prominently near the C-terminus of the sequence (residues 118–162). However, between different single modifications, we observe widely varying effects on chain properties, highlighting the importance of not only the number of PTMs, but the location (Fig. 5 A).

Figure 5.

Predicting effect of different modification patterns on phase separation: comparison with experiment. (A) Lysine acetylation (acK, violet) and lysine-to-glutamine-acetylmimetic mutants (cyan) show a range of R_g-values compared with WT (orange) and all fully acetylated (all K) or fully acetylmimetic (allQ). Error bars represent SEM from 10 equal divisions of the equilibrated ensemble. (B) Correlation of normalized turbidity measured by experiment and R_g predicted by simulations with allQ (10 acetylation-targeted lysines converted to glutamines) (left panel) and without (right panel) to clearly illustrate the behavior of each individual mutant. The values of Spearman (rank order, r_s) and Pearson coefficient (PCC) show strong negative monotonic and linear correlation, respectively. Turbidity values (OD₆₀₀) and corresponding error bars represent mean value and SD from 3 independent experiments (previously published data by Saito et al. (54)). The dashed line is meant to be a guide to the eye and is not intended to support a linear correlation between the two variables. To see this figure in color, go online.

It is worth noting that single-acetylated lysine substitutions in the C-terminus (K118, K130, K138, K162) result in DDX3X IDR1 slight collapse with respect to wild-type (WT), whereas changes in other positions (K35, K50, K55, K64, K66, K81) lead to slight chain expansion. This observation is also consistent with the result in the previous section that four simultaneously acetylated lysines can enhance LLPS or decrease LLPS depending on their location in the C- or N-terminus (because of changes in the SCD), respectively. As discussed throughout the literature (44,78, 79, 80, 81, 82), changes in charge patterning with fixed net charge can be an important parameter, leading to position-specific effects. Based on this, we can say that the observed position dependence in our case mainly comes from the well-known effects in the field. Furthermore, we find that even though SCD can capture changes with an increasing number of PTMs (Fig. S4), it cannot offer precise guidance for a fixed number of PTM sites located in different regions of peptide (Fig. S4, B and D). As we mentioned above, this can either be because of the limitations of SCD in capturing the subtle differences or the role of additional factors related to nonelectrostatic interactions and secondary structures.

Given that R_g is an excellent predictor of IDR phase separation (78), we then quantified the correlation between computationally predicted R_g and previously published data on phase separation measured experimentally by turbidity (Fig. 5 B), where turbidity (optical density at 600 nm (OD₆₀₀)) of the DDX3X IDR1 K to Q mutants are normalized to the OD₆₀₀ of the WT that phase separates avidly generating liquid droplets which scatter light (54). As expected, none of these single-position modifications has as much impact as simultaneous acetylmimetic substitutions at all 10 lysine positions (allQ) (Fig. 5 B). Importantly, R_g is negatively correlated with the extent of phase separation as measured by experimental turbidity values (Fig. 5 B; (54)). As the “allQ” mutant (Fig. 5 B, left panel) significantly differs from the singe-Q variants, we also present the same data zoomed in and the correlation coefficients without this “allQ” variant (Fig. 5 B, right panel). Still, the linear and rank order correlation coefficients show strong correlation between the experimental turbidity and the simulated R_g. It is remarkable that the model can capture site-specific changes in the phase separation of DDX3X mutants so well, highlighting the accuracy of the model with regard to its intended goal of capturing such changes predictively without experimental input.

Discussion

Understanding the role of PTMs on phase separation is a critical element to controlling membraneless organelle formation in cells and engineering LLPS in vitro.

In this study, we found that phosphorylation increases chain dimensions of FUS LC steeply and monotonically but that acetylation of DDX3X IDR1 has only a small average effect on chain expansion. CG single-chain simulations revealed that phosphorylation expands FUS LC more than phosphomimetic mutations largely but not entirely because of the higher net charge of phosphorylation compared with the phosphomimetic substitutions. We found that particular patterns of PTMs with the same number of modified sites result in a large diversity in chain expansion, which is strongly correlated with the propensity to phase separate. Importantly, we show modification patterns with the same number of modified sites can have dramatically different phase separation depending on the position of the modified residues. Furthermore, the model can predict the effect of position-specific modification on experimentally observed DDX3X IDR1 phase separation. Together our data suggest that the CG model can represent how the response of disordered regions to multisite modification depends on the modification patterning. In the future, it will be interesting to probe the effect on phase separation of IDR ensembles containing heterogenous combinations of IDRs with a varied distribution of both number and positions of modifications as may be present in natural systems.

Our findings highlight the importance of combinatorial effects exerted by phosphorylation and acetylation on disordered proteins. Such effects often remain unexplored by in vitro biochemistry approaches because protein modification reactions targeting only certain modification sites are difficult to achieve. However, we have noted that DNA-dependent protein kinase targets FUS LC at 12 SQ or TQ sites for phosphorylation with high specificity, modifying only these 12 out of a total of 52 S/T sites in FUS LC (24). With our CG model we can selectively modify amino acids of disordered regions and predict their effect on single-chain properties and phase behavior. These simulations can then enable future engineering of site-specific phosphorylation by introducing, for example, only SQ/TQ sites (and not other S/T sites) as specific targets for DNA-PK modification. Such computational studies can also aid predictions of phase separation properties of with IDRs with multisite modifications.

It should be noted that threonine/serine phosphorylation and lysine acetylation are not the only PTMs with a known or potential effect on LLPS. Methylation of arginine residues in proteins leads to stimulation (83) or suppression (8,37,84) of phase separation depending on the sequence content and the underlying cellular function. Importantly, methylation of arginine (and lysine) residues does not alter the charge of the residue (unlike lysine acetylation and serine/threonine/tyrosine phosphorylation). Hence, interactions other than charge are likely responsible for the changes to phase behavior by methylation and may be challenging to capture in CG model frameworks. Investigation of the role of methylated arginines and lysines on LLPS using transferable CG models remains important future work.

Author contributions

T.M.P. and J.M. designed and performed the single-chain CG simulations and analyzed the resulting data. N.J. and J.M. designed, performed, and analyzed slab simulations. G.L.D., Y.C.K., and J.M. developed the methodology, provided the software, and supervised the formal analysis. N.L.F. and J.M. contributed to project administration and funding acquisition. T.M.P., N.L.F., and J.M. wrote the manuscript with comments from all authors.