Negative selection on complex traits limits phenotype prediction accuracy between populations

Summary

Phenotype prediction is a key goal for medical genetics. Unfortunately, most genome-wide association studies are done in European populations, which reduces the accuracy of predictions via polygenic scores in non-European populations. Here, we use population genetic models to show that human demographic history and negative selection on complex traits can result in population-specific genetic architectures. For traits where alleles with the largest effect on the trait are under the strongest negative selection, approximately half of the heritability can be accounted for by variants in Europe that are absent from Africa, leading to poor performance in phenotype prediction across these populations. Further, under such a model, individuals in the tails of the genetic risk distribution may not be identified via polygenic scores generated in another population. We empirically test these predictions by building a model to stratify heritability between European-specific and shared variants and applied it to 37 traits and diseases in the UK Biobank. Across these phenotypes, ∼30% of the heritability comes from European-specific variants. We conclude that genetic association studies need to include more diverse populations to enable the utility of phenotype prediction in all populations.

Introduction

The past decade of genome wide association studies (GWASs) has uncovered a plethora of trait-associated loci scattered across the genome.^{1, 2, 3, 4} Geneticists have devoted many resources to turning these associations into phenotype prediction models that aggregate variants across the genome into a polygenic score. Such scores can be used to guide healthcare decisions for a variety of traits and diseases,⁵ and recent work has suggested these polygenic scores may be ready for clinical use.^6,7 While individuals with high polygenic risk for diseases have been found via these scores, for example in atherosclerosis⁸ and breast cancer,⁹ challenges remain in applying these polygenic scores uniformly across populations. Recent analyses have suggested that because many of the largest studies are concentrated on European populations, polygenic scores may be biased and less informative in non-European populations.^{10, 11, 12, 13, 14, 15} There are several reasons why polygenic scores may not transfer well across populations. One possibility is that alleles have different effect sizes in different populations, owing to differences in interactions with the environment.¹⁶ Another possibility is that differences in linkage disequilibrium (LD) between variants across populations means that causal variants may be tagged differently in non-European populations, leading to differences in effect sizes.^11,17 Finally, the original polygenic score performance in Europeans may be inflated because of population stratification.^18,19

Here, we propose that an additional reason for the lack of transferability of polygenic scores is that each population has its own genetic architecture, owing to the evolutionary processes that give rise to traits. Under this reasoning, a population’s demographic history influences the number of causal variants and their frequencies, resulting in some phenotypic variance coming from causal variants that are population specific. For example, work on the genetic architecture of skin color in African populations has uncovered distinct loci affecting the trait in each population, suggesting that populations with independent demographic histories can end up with different genetic architectures and causal variants for the same traits.²⁰ Indeed, modeling work suggests that genetic architecture is an outcome of the evolutionary process rather than a trait-specific property.²¹

Recent exponential growth in human populations has created an excess of new variants that tend to be low frequency and population specific (private variation^{22, 23, 24}). Population genetic models of genetic architecture that include negative selection suggest that, in aggregate, low-frequency variants could contribute substantially to traits.^{25, 26, 27} Application of these models to large-scale genetic datasets has discovered that many traits are under apparent negative selection, ranging from anthropometric traits to molecular phenotypes.^{28, 29, 30, 31, 32, 33} Depending on the interplay between allele frequency and effect size, these variants could make up a large portion of the heritability for many traits, as demonstrated by a recent GWAS on height and BMI using whole-genome sequencing data.^34,35 Because narrow-sense heritability is the proportion of variance explained by additive genetic factors, it is directly related to the accuracy of phenotypic prediction as the variance explained by the polygenic score.³⁶ If these private variants contribute substantially to heritability, it follows that the variants will not be useful for phenotype prediction between populations because they are not present in other populations. The proportion of narrow-sense heritability that private variants explain places an upper bound on the accuracy of polygenic scores between populations.

In this study, we use simulations under demographic scenarios of recent explosive population growth with varying amounts of negative selection as well as analyses of empirical data to test the role of private variants in complex traits.

Material and methods

Population genetic modeling and simulations

We performed forward simulations by using SLiM v.3.³⁷ We simulated a demographic history for a European and an African population according to the demographic model fit by Gravel et al.³⁸ (including migration). The African population size expanded to 14,474 individuals and the European population began at a size of 1,032 individuals after splitting from Africa and grew exponentially at a rate of 0.38% per generation for 920 generations. We simulated a mutational target size of 5 Mb with a mutation rate of 1.2 × 10⁻⁸ per base pair (bp) and a recombination rate of 1 × 10⁻⁸ per bp. To simulate selection across the entire region, we drew selection coefficients for new mutations from a gamma distribution with parameters fit by Kim et al.³⁹ (mean = −0.01026, $\alpha$ = 0.186). We sampled 10,000 haploid genomes from each population. To simulate a quantitative trait, we followed the model described by Eyre-Walker²⁵ and the framework set by Lohmueller²¹ where a SNP’s effect on a trait, $\beta$, is given by

$$\beta =\delta s^{\tau }\left(1+\epsilon \right)C,$$

where $\delta \in \left\{-1,1\right\}$ with equal probability, $\epsilon \sim N\left(0,0.5\right)$, and $s$ is the selection coefficient of a variant segregating in the population at the end of the simulation. $C$ is a scaling factor for effect sizes and controls the heritability for a given mutational target size. In these simulations, $C$ was set to obtain a heritability of ∼0.4 (see Table S1). Finally, $\tau$ reflects the relationship between a SNP’s effect on fitness and the trait. $\tau =0$ indicates no relationship between fitness and the trait, while $\tau >0$ indicates that mutations that are more evolutionarily deleterious are those that have larger effects on the trait. In this model, when $\tau >0$, the trait itself may be under direct selection or it may be correlated with a trait under selection. We call variants private and shared on the basis of their allele frequency in a sample of 10,000 chromosomes from both populations (see below).

To compare our simulation results to the empirical data from the Exome Aggregation Consortium (ExAC), which includes African American individuals, we computed the expected allele frequency for SNP $i$ in simulated admixed African American individuals $\left(p_{AA,i}\right)$ as

$$p_{AA,i}={\alpha }_i{p}_{EUR,i}+\left(1-{\alpha }_i\right)p_{AFR,i}$$

where $p_{EUR,i}$ and $p_{AFR,i}$ denote the allele frequencies in Europe and Africa, respectively. For each SNP, we drew an admixture proportion ${\alpha }_i\sim Beta\left(2,8\right)$ in order to incorporate variance in the admixture proportion along the genome. The parameters of the beta distribution were chosen to match the observed variation in admixture proportion in African American individuals⁴⁰ and result in a mean proportion of African ancestry of 80%.

Defining the proportion of heritability from private variants: h²_private

We begin by describing a model in which an individual, $i,$ in a population, $\phi ,$ has a phenotype, $y_i,$ that is a linear combination of genotypes (${\mathit{x}}_{\mathit{i}}$, $x_{ij}\in \left\{x_{i1},\dots ,x_{iM}\right\}$), effect sizes $\left(\mathit{\beta },{\beta }_j\in \left\{{\beta }_1,\dots ,{\beta }_M\right\}\right)$, and a normally distributed term describing the effect of the environment, $e_i\sim N\left(0,V_E\right)$:

$$y_i={\mathit{x}}_{\mathit{i}}^{\mathit{T}}\mathit{\beta }+e_i.$$

The narrow-sense heritability, $h^2$, of the phenotype, $\mathit{y},$ in the population is given by

$$h^2=\frac{V_A}{Var\left(\mathit{y}\right)}$$

where the variance of the phenotype can be decomposed into additive, dominance, interacting, and environmental terms: $Var\left(\mathit{y}\right)=V_A+V_D+V_I+V_E$. The additive genetic variance is $V_A=2\sum _{j=1}^M{p}_j\left(1-p_j\right){\beta }_j^2$ when there are $M$ variants, where $p_j$ is the allele frequency for variant $j$ and ${\beta }_j$ is the effect size of variant $j$.

We wish to examine the proportion of heritability that comes from a particular class of variants. Consider a sister population, $\psi ,$ that diverged from the population described above $\left(\phi \right)$. Variants in population $\phi$ can be partitioned into those that appear only in $\phi$ (private variants) or those that appear in both populations (shared variants). The total number of variants is the sum of the number of shared and number of private variants, $M=M_p+M_s$. We wish to partition the heritability into these two classes, $h_p^2$ and $h_s^2$, which make up the total heritability: $h^2=h_p^2+h_s^2$. Define $h_{\text{private}}^2$ to be the proportion of the heritability accounted for by the private variants.

The quantity of interest, then, is

$$h_{\text{private}}^2=\frac{h_p^2}{h^2}=\frac{V_{A,p}}{V_A}.$$

The additive genetic variance from private variants is $V_{A,p}=2\sum _{j=1}^M{p}_j\left(1-p_j\right){\beta }_j^2{z}_j$, where $z_j$ is an indicator function that is 1 when the variant $j$ is private (with probability $P\left({\omega }_j\right)$) to the population and 0 otherwise. We describe how $z_j$ is estimated below when analyzing empirical data (see model to identify private variants).

Polygenic score calculation

We compute three sets of polygenic scores on the simulated individuals: (1) using all variants, (2) using variants private to the simulated population of interest, and (3) using variants shared between the simulated European and African populations. For each haploid genome, we sum the effect sizes, $\beta ,$ for each class of variants, resulting in three scores for each genome. We standardize the scores by subtracting the mean of the true polygenic score (class 1) and dividing by the standard deviation of the true polygenic score (class 1). We compute the Pearson correlation between classes 1 and 2 as well as classes 1 and 3 and report the r² value as a percentage.

Model to identify private variants

When analyzing the empirical UK Biobank data, it is challenging to assess whether a particular variant is private or shared. If a variant is seen only in one population, it is possible that it is truly private to that population, or instead, it is shared but at too low a frequency to have been discovered with the number of individuals samples from the other population. To address this issue, we built a probabilistic model to evaluate the probability that a variant is private to a population given the number of copies of the allele in that population (that is, the allele frequency).

We begin with the intuition that rare alleles tend to be private and common alleles tend to be shared between populations, even in the presence of migration. Migration can be thought of as sampling alleles from one population and placing them in the other population. Under this model, rare alleles will tend to stay within a population and not transfer between populations. This suggests that allele frequency is informative in determining whether an allele is private or not.

Wakeley and Hey⁴¹ use coalescent theory to determine the frequency spectrum of private variants. An application of Bayes’ rule allows us to calculate the following probability:

$$P(\omega |i)=\frac{P\left(i|\omega \right)P\left(\omega \right)}{P\left(i\right)},$$

where $i\in \left\{1,\dots ,n\right\}$ is the number of copies of the allele in the sample $\left(n\right)$ and $\omega \in \left\{\mathrm{0,1}\right\}$ is 1 if the allele is private and 0 if not. $P\left(i|\omega =1\right)$ is the site frequency spectrum of private variants, and $P\left(i\right)$ is given by the full site frequency spectrum. For example, in a constant-sized equilibrium population, $P\left(i\right)=\left(\theta /i\right)/\left(\sum _i^n\theta /i\right)$. $P\left(\omega \right)$ is the probability of a variant’s being private to a population.

Wakeley and Hey⁴¹ provide expressions to obtain these quantities in a constant-sized equilibrium population without natural selection. However, here we are concerned with populations that are not in equilibrium and with variants under negative selection, so we obtain these probabilities via simulation under a particular demographic model and distribution of fitness effects.

In the results presented here, we use the demographic model from Gravel et al.³⁸ that relates European and African populations. We use a distribution of fitness effects from Kim et al.,³⁹ assuming that mutations are additive (that is, $h$ = 0.5) and that selection coefficients, $s$, are drawn from a gamma distribution with mean = −0.01026 and shape = 0.186. Using these parameters, we simulate data for 10,000 European chromosomes by using SLiM³⁷ and compute (1) the proportional site frequency spectrum for private variants $\left(P\left(i|\omega \right)\right)$, (2) the proportional site frequency spectrum for all variants $\left(P\left(i\right)\right)$, and (3) the proportion of private variants $\left(P\left(\omega \right)\right)$. We defined private variants in the simulation as those that appear in the simulated European population but not the simulated African population.

Next, we store these quantities in a lookup table and use them to compute the probability that a variant is private given the number of copies of the allele in the empirical data. In the UK Biobank dataset, alleles are present at frequency $1\times {10}^{-6}$ and higher. However, in simulations, the lowest allele frequency is $1\times {10}^{-4}$. For alleles below this frequency, we set the probability equal to the probability for alleles at a frequency of 1 in 10,000.

Testing our probabilistic model to infer private variants

We evaluated the ability of our model to distinguish between private and shared variants by simulating new data and performing binary classification, calling a variant private if the $P\left(\omega |i\right)$ exceeded some threshold, $t$. We varied this threshold and computed the number of true positive (private variants that are truly private), false positives (private variants that are truly shared), false negatives (shared variants that are truly private), and true negatives (shared variants that are truly shared). We summarized this by using receiver operator characteristic and precision recall curves (Figure S1; Tables S2 and S3).

We also validated our model by using data from ExAC.⁴² For each variant in ExAC, we used our model to compute the probability that the variant is private to the non-Finnish European population on the basis of the allele frequency in that population. Then, we checked whether variants were observed in a sample of 10,406 African and African American samples.

Partitioning heritability

We applied our Bayesian model to predict which variants are private to GWAS summary statistics from 37 traits in the UK Biobank released by the Neale lab (see web resources). We computed the additive genetic variance for variants with a high posterior probability of being private to the British cohort and divided that by the total amount of additive genetic variance explained by SNPs to obtain our estimate of h²_private (Note S1). We also performed the inference by using a randomized algorithm to correct for the effects of LD and misestimated effect sizes as well as population stratification (Notes S2, S3, S4, and S5; Figures S3, S4, S5, S6, S7, S8, and S9). Finally, we also independently replicated the results on BMI by using data from the GIANT consortium⁴³ (Note S1). Importantly, this partitioning of the heritability into shared and private components does not make use of the $\tau$-model²⁵ that relates a mutation’s effect on fitness to its effect on the trait.

Results

The distribution of European-specific variants in data and models

We begin by precisely defining private variants in the datasets and models that we consider. Studies of genomic variation point to the out-of-Africa bottleneck and subsequent explosive growth in population size as a key driver of the distribution of genomic variation. We focus on a simplified model of this history (Figure 1A; Gravel et al.³⁸). We define private variants as those that are found in Europe but are absent from Africa and shared variants as those that are found in both populations. Note that by our definition, private variants may be shared between other out-of-Africa populations (e.g., between Europe and East Asia) because of shared recent history.

Figure 1.

Human population history generates population-specific variants

(A) Model for variants that are shared (common to Europe [EUR] and Africa [AFR]) and private (occurring only in EUR and absent from AFR). Bottom, examples of private and shared variants from ExAC.⁴²

(B) The number of non-synonymous variants that are private to European populations and absent from African populations (blue bars) and the number of non-synonymous variants that are shared between the two populations in the 1KG exome dataset and the ExAC dataset (orange bars).

(C) The proportion of non-synonymous alleles above a given frequency that are private to Europe and absent from Africa in the ExAC dataset and in simulations based on human history. Note that because the ExAC dataset contains admixed African American individuals, the proportion of private variants is reduced compared with the original simulation (black dots). Modeling this admixture (red dots) shows a better fit to this dataset. Error bars denote standard deviation across simulation replicates.

One potential concern with this definition of whether a variant is private to Europe is that it may depend on the sample size of the African population used in the comparison. We examined this possibility by computing the probability of not observing an allele present in a sample of African individuals across a range of minor allele frequencies (MAFs) with a sample size of 10,000 chromosomes. This sample size is approximately similar to the sample size of the ExAC dataset (Lek et al.⁴²). We find that variants with a frequency as low as 10⁻³ in the African population have a nearly 100% probability of being sampled in ExAC (Figure S2). Thus, we would correctly classify variants segregating at low frequency in Africa as being shared.

Next, we examined the number of private variants in European populations compared to African populations in two datasets: the 1000 Genomes (1KG) data and the ExAC data. In order to meaningfully compare the two datasets, we focused on variants contained in the exome. For both datasets, there are many more private variants in the European population compared to shared variants (Figure 1B). This is expected under models of human history where many shared alleles were lost during the out-of-Africa bottleneck and new mutations accumulated independently in the out-of-Africa population. Because of the small population size, some of these mutations could drift to a higher frequency than they would have in a larger population.

We next conducted simulations under this model of human evolution, where an ancestral population splits into a group that underwent a genetic bottleneck out of Africa (representing a European population) and a group that stayed within Africa without a bottleneck (representing an African population; Figure 1A ³⁸), coupled with varying levels of negative selection on traits (including no negative selection). We include negative selection by modifying the relationship between a mutation’s effect on the trait and its effect on reproductive fitness by using the model put forth by Eyre-Walker in 2010²⁵ (see material and methods). This model includes a parameter, $\tau$, which ties the selection coefficient of a mutation to its effect on a trait.²⁵ Larger values of $\tau$ imply that more evolutionarily deleterious mutations have larger effects on the trait. Importantly, our model includes exponential growth in the out-of-Africa population, which creates an excess of private variants, as well as low levels of migration between the European and African populations, which can turn some private variants into shared variants. We compared our simulations to data from ExAC and found that our simulations predicted more higher-frequency private alleles than are observed in the data (Figure 1C). However, the ExAC data contains admixed African American individuals. Admixture can introduce variants that are private to Europe into the sample labeled “African.” We simulated this admixture process (see material and methods) and found that the resulting simulation matches the data closely, suggesting that our model is a reasonable approximation of human demography and selection (Figure 1C).

Population genetic models predict population-specific variants account for heritability and impact polygenic scores

We reasoned that since there are many private causal variants in our simulations, they may account for a substantial proportion of the heritability in aggregate. We examined the contribution of private variants to heritability and found that when traits are not tied to fitness $\left(\tau =0\right)$, private variants account for ∼30% of the heritability (Figure 2A). However, when the coupling between trait effects and fitness effects is moderate $\left(\tau =0.25\right)$ or strong $\left(\tau =0.5\right)$, private variants account for over half of the heritability, and there is a maximum of ∼79% under strong coupling (Figures 2B and 2C). These results suggest that many causal variants, which jointly explain much of the heritability, tend to be population specific. This effect is a consequence of how the trait relates to fitness as well as the demographic history of the population.

Figure 2.

The effect of natural selection on the relationship between heritability and allele frequency

(A–C) Cumulative fraction of heritability explained by private and shared variants under (A) no relation between a mutation’s effect on fitness and the trait $\left(\tau =0\right)$, (B) moderate coupling between a mutation’s effect on fitness and the trait $\left(\tau =0.25\right)$, and (C) strong coupling between a mutation’s effect on fitness and the trait$\left(\tau =0.5\right)$. Note that the x axis is on a log scale. As $\tau$ increases, a greater fraction of heritability comes from variation that is found only within Europe.

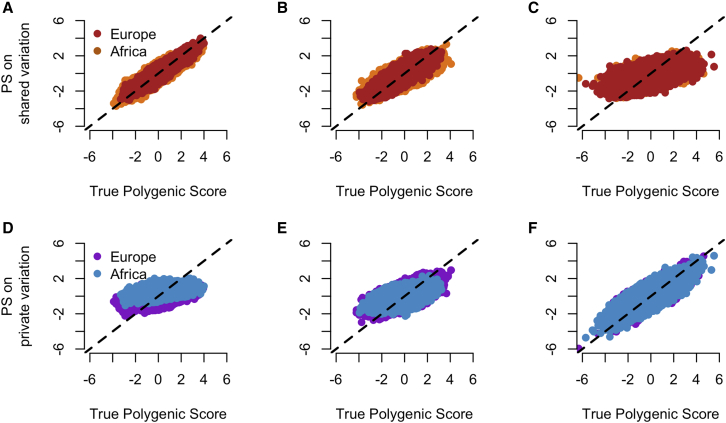
The fact that many of the variants that affect the trait are not shared across populations may limit the applicability of polygenic scores derived from European populations to other populations. This effect would be distinct from imperfect tagging of causal variants due to differences in LD patterns between populations. To test for this effect in simulated data, we calculated true polygenic scores for individuals in the simulated European and African populations and asked how well polygenic scores derived from only private variants and only shared variants correlated with the true polygenic scores. Polygenic scores derived from only shared variants represent the case where a polygenic score can be transferred from Europe to another population. If shared variant effect sizes correlate well between populations, despite not contributing to a majority of additive genetic variance, polygenic scores may still be accurate across populations. We note that these simulations include identification of the true causal SNPs and, as such, are much higher than polygenic score accuracies reported elsewhere.¹³ These simulations represent the best-case scenario for polygenic scores. We found that when traits are independent of fitness, the shared polygenic score has a 91% correlation in Europe and 96% correlation in Africa with the true polygenic score, suggesting that polygenic scores can be applied between populations (Figure 3A). However, we found that when trait effects are tied to fitness effects, the correlation between shared polygenic scores and the true polygenic scores decreases (Figures 3B and 3C) and the correlation between private polygenic scores and true polygenic scores increases (Figures 3D, 3E, and 3F). Note that in the analysis with private polygenic scores, each population uses variants private to that population but not from the other population. That is, the African private polygenic score uses variants private to Africa. This suggests that the reduction in accuracy does not depend on the population’s specific demography, as the same pattern is present in European and African populations. For traits with strong coupling between trait effects and fitness effects ($\tau$ = 0.5), the correlation between the true polygenic scores and the polygenic scores derived from shared variants drops to 62% in Europe and 57% in Africa (Table S4). These findings suggest that polygenic scores based solely on shared variants may be substantially less accurate than polygenic scores using all variants and may not transfer between populations well when the variants with the greatest effects on the trait are those under the most negative selection.

Figure 3.

The relationship between polygenic scores and natural selection

(A–F) Polygenic score accuracy for shared variants only (top row) and private variants only (bottom row) in Europe and Africa on simulated data with different degrees of negative selection. In the bottom row, each score uses private variants from within the population being considered (e.g., for Africa, we use variants private to Africa) but not from the other population. The black line shows the 1:1 line. (A and D) No relationship between a mutation’s effect on fitness and its effect on the trait $\left(\tau =0\right).$ (B and E) Moderate coupling between fitness and trait effects $\left(\tau =0.25\right).\left(\text{C and F}\right)\text{ Strong coupling }\left(\tau =0.5\right)$. As the strength of coupling increases, polygenic scores computed from shared variation become less correlated with the true polygenic score. However, at the same time, polygenic scores computed from private variation become more correlated with the true polygenic scores.

While shared variants do not capture the full distribution of polygenic scores, we asked whether individuals in the tail of the true polygenic score distribution remained in the tail when examining shared variants only. When there is no coupling between fitness and trait effects ($\tau$ = 0), shared variants capture 35% of the tail correctly in Europe and 28% of the tail correctly in Africa (Table 1). However, when there is moderate coupling ($\tau$ = 0.25), this number drops to 11% in Europe and 7% in Africa. When there is strong coupling, the polygenic score based on shared variants identifies none of the individuals in the tails of the distribution. If the trait under consideration is a disease, this analysis suggests that a polygenic score based on shared variation cannot identify individuals at the highest risk for that disease. In contrast, when considering only private variants, the polygenic score correctly identifies 44%–46% of individuals who are at the extremes of the distribution. These results suggest that when using scores derived from European populations, individuals who are truly in the tails of the polygenic score distribution will not be identified via shared variants alone, corresponding to a high false-negative error rate. In addition, the low recall for both of these polygenic scores suggests many individuals that are in the tails of the distribution will be missed.

Table 1.

The effect of natural selection on identifying high-risk individuals

$\tau$	Shared (Europe)	Private (Europe)	Shared (Africa)	Private (Africa)
0	35%	22%	28%	11%
0.25	11%	20%	7%	18%
0.5	0%	46%	0%	44%

Percentage of individuals in the extreme 5% tail of the true polygenic score distribution that are recovered when using only private variants and shared variants in simulated European and African populations. Overall, the percentage of individuals correctly classified is low, suggesting that there will be many false negatives when using polygenic scores to identify individuals in the tails of the risk distribution. Further, as the degree of coupling between fitness effects and trait effects increases, shared variants correctly classify fewer individuals, while private variants classify more individuals correctly.

While our simulations suggest private variants may be an important component of the heritability and may limit phenotype prediction across populations, their precise role depends on the extent of negative selection acting on traits (either directly or through pleiotropy), which remains an open question.^{28, 29, 30,32,33} Thus, we next tested how much of the heritability private variants account for in real GWAS data in European populations, where GWAS data is abundant.

A model for private variation

We built a Bayesian model to classify variants segregating in the UK Biobank as private or shared by using the allele frequency conditional on a demographic model and distribution of fitness effects inferred for a European population (see material and methods). To validate our model, we simulated a new dataset under the same European demographic model and recorded whether each allele was observed in both populations. Then, we calculated the probability of each allele’s being private to the European population. We classified variants as private if the probability $P\left(\omega |i\right)\ge t$, $\omega \in \left\{\mathrm{0,1}\right\}$ is 1 if the allele is private and 0 if not, $i\in \left\{1,\dots ,n\right\}$ is the number of copies of the allele in the sample, and $t$ is some probability cutoff. For each cutoff, we calculated (1) the number of variants that we predict are private and are truly private (true positives), (2) the number of variants that we predict are private and are truly not private (false positives), (3) the number of variants that we predict are not private and are truly private (false negatives), and (4) the number of variants that we predict are not private and are truly not private (true negatives).

We summarize these numbers by using two curves: a precision-recall curve (Figure S1A) and a receiver operator characteristic (ROC) curve (Figure S1B). We find that at a precision of 94%, we have a recall of 99% and that the area under the ROC curve is 0.80, suggesting that our model is able to distinguish between private and shared variants on the basis of allele frequency alone (Table S3). We also tested the model on a simulated dataset including five times more individuals than the 10,000 individuals used in the initial simulation. Importantly, for this comparison, we used the same lookup table, based on 10,000 individuals, as before. This allows us to test how sample size affects our inferences. We find that the precision-recall curve is largely the same, but there is a decrease in the ROC curve (AUROC = 0.70).

In addition, examining $P\left(\omega |i\right)$ versus the allele frequency in the simulated independent dataset (Figure S1C), we find that alleles higher than ∼10% frequency have a negligible probability of being private. This is consistent with the intuition that common alleles are unlikely to be private.

We also examined several posterior probability thresholds in detail ($t\in \left\{0.1,0.23,0.4\right\}$; Table S3). Across these thresholds, we find that the false discovery rate (FDR) from simulations is ∼5%, suggesting that the model is relatively robust to the threshold used.

Next, we empirically validated the performance of our model to infer whether variants are private. Using data from ExAC,⁴² we use our framework described above to calculate the probability that each variant is private by using the allele frequency in the non-Finnish Europeans (NFE). In Figure S1D, we plot this probability for a random subset of 10,000 variants. We see that variants above 10% frequency have a very low probability of being private and that variants below that frequency increase in probability of being private as their frequency decreases.

In addition, we classified variants in ExAC as private to “EUR” by using the simulation-based FDR of 5% $\left(P\left(\omega |i\right)\ge 0.23\right)$ and checked whether those variants were present in the “AFR” subset of samples (Table S2). We see that 83% of the variants we call private are not observed in “AFR” in a sample of 10,406 chromosomes. This suggests that our empirical-based FDR is 17% and is higher than the simulation-based FDR. However, the “AFR” sample in ExAC is a mixture of African American and African samples. Importantly, African American samples are admixed between European and African populations.⁴² This has the effect of introducing European variants into the “AFR” samples, making variants we expect to be private to “EUR” appear shared. Therefore, this estimate of the accuracy is most likely an underestimate.

Nonetheless, these simulations and empirical evaluations suggest that our model is able to distinguish between private and shared variants on the basis of allele frequency alone. Additionally, out of an abundance of caution, we utilize two different empirically based FDRs of 17% in downstream inferences as described below. Importantly, our determination of whether a variant is private or shared is expected to hold regardless of the sample size taken from either population (Table S2).

Inference of heritability accounted for by private variants: h²_private

We used summary statistics for 37 different traits and diseases from the UK Biobank relating to anthropometric and blood-related traits as well as cancer-related and non-cancer related diseases (see web resources) to infer the proportion of the SNP-based heritability attributable to private variants, h²_private. Using these data and our probabilistic method to determine whether a variant is private or not, we find that the average h²_private = 31%, and there is substantial variation across traits (standard deviation: 11%; Figure 4). Examining categories of diseases, we find that cancer-related diseases have h²_private = 12%, while non-cancer-related diseases have h²_private = 32%. Similarly, private variants account for ∼30% of the heritability in blood-related and anthropometric traits. We observe substantial variability across different traits within a category. Two blood pressure-related traits have h²_private of nearly 50%, while other blood-related traits have a lower proportion.

Figure 4.

Estimates of the amount of heritability from private variants

The expected reduction in accuracy when transferring a polygenic score from Europe to Africa (expressed as the percentage of heritability explained by private variants) across 37 traits and diseases in the UK Biobank. We only include SNPs with an MAF > 10⁻³. The mean reduction is 26.7% (SD across traits is 14.7%). “17% FDR correction” refers to randomly setting 17% of the SNPs that we call private to shared. “Max 17% FDR correction” refers to setting the 17% of the SNPs that explain the most heritability from private to shared. Lines indicate standard errors obtained via a 1 Mb block jackknife.

The effect of falsely identified private variants on our inference of h²_private

To ensure that our results from the UK Biobank data described above were not driven by shared SNPs that we mistakenly classified as private, we adjusted for an empirically based FDR. At the threshold used for classifying variants as being private $\left(P\left(\omega |i\right)=0.23\right)$, validation in the empirical data suggest the FDR is ∼17% (see above). In other words, approximately 17% of SNPs that we identify as private may actually be shared. Thus, we adjusted our estimates of h²_private by randomly reclassifying 17% of the private SNPs as shared and re-computed h²_private (“17% FDR correction” in Figure 4). Despite the extremely conservative nature of this correction (because the empirical FDR is based on an admixed sample), we find that a sizeable proportion of the heritability (about 22%) still comes from private variants (Figure 4).

In addition to this conservative correction, we also performed an even more stringent correction where we sorted the SNPs we call private by their heritability and removed 17% of the SNPs that explain the most heritability. As expected, the amount of heritability from private variants goes down, but for most traits, the heritability explained by private variants is still greater than 10% (“Max FDR correction” in Figure 4). This suggests that our central claim, that private variants contribute to heritability, remains true even if our classification method is imperfect.

The effect of population stratification

Recent studies have highlighted the effects of stratification on polygenic scores.^18,19 We considered whether stratification could have an effect on our analyses. To test this, we repeated our analyses by using only those SNPs showing stronger associations with the trait. Specifically, we employed p value cutoffs, using only SNPs with a p value lower than the cutoff (Figure S3). Broadly, for quantitative traits, we observe that as the p value threshold becomes stricter, the proportion of the heritability attributable to private variants decreases. This is due to the power to detect associations for private variants. The power to detect an association will be lower for private variants than shared variants because private variants tend to have lower allele frequencies. Therefore, as the p value cutoff decreases, we expect a lower proportion of heritability to come from private variants. We found that the total variance explained by SNPs for dichotomous traits was much lower than for quantitative traits. This effect produced a statistical artifact where the heritability from private variants tended to be very high for dichotomous traits (Figure S4).

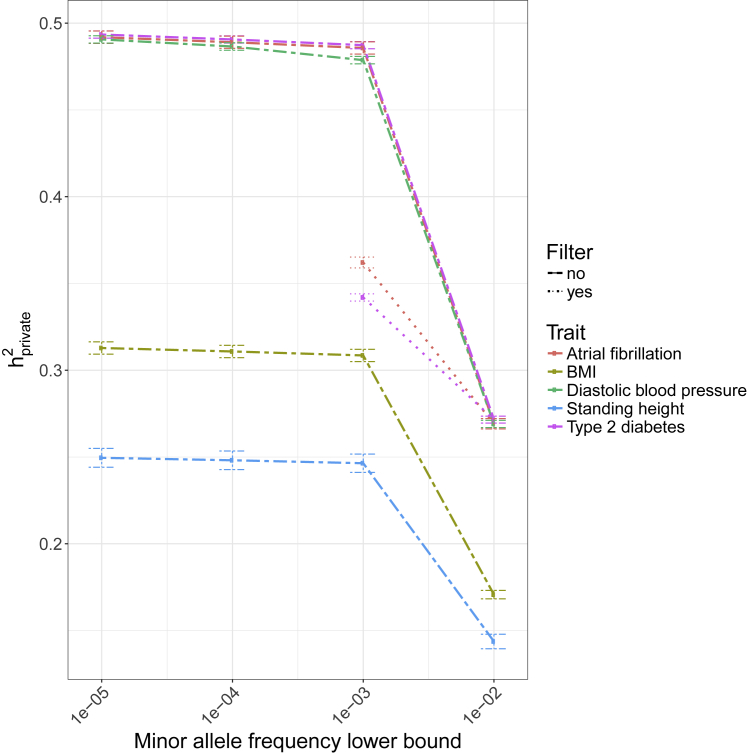
In addition to this analysis, we were also concerned with the effect of differential population structure from rare variants.^35,44 Therefore, we checked the robustness of our results to allele frequency filters. We computed h²_private for atrial fibrillation, BMI, standing height, diastolic blood pressure, and type 2 diabetes with MAF cutoffs from 10⁻⁵, 10⁻⁴, 10⁻³, and 10⁻² (Figure 5). We find that although h²_private decreases, it still remains substantial up to a cutoff of 10⁻². Although this analysis removes both real and spurious signals, it suggests that private variants do indeed explain a non-negligible proportion of heritability.

Figure 5.

The effect of MAF cutoffs on heritability from private variants

“Filter” refers to a quality and allele frequency filter that removes variants with a frequency below 10⁻³, a Hardy Weinberg equilibrium p value < 10⁻¹⁰, or SNP information score < 0.8. We show results for five commonly studied traits. For BMI, diastolic blood pressure, and standing height, the “filter yes” lines are behind the “filter no” lines. This suggests that the variant filter has no effect on the estimated heritability. Lines indicate standard errors obtained via a 1 Mb block jackknife.

Across different p value thresholds, a non-negligible proportion of heritability comes from private variants. However, this analysis does not alleviate all concerns about population stratification, as at a large enough sample size, an association due to stratification can be arbitrarily strong. Similarly, stratification could still occur when using variants at different MAF cutoffs. While these analyses provide evidence that our results are not primarily driven by stratification, they cannot completely rule it out. Further advances in controlling for stratification of rare variants will be crucial to understand the full contribution of private variants to heritability.

The effect of unmodeled LD on our inferences

Our inferences of h²_private make the assumption that the estimated effect sizes for the GWAS SNPs were the true effect sizes of the causal variants. Further, we assumed that the variants were all independent of each other. In truth, these assumptions are violated for a variety of reasons. First, because of LD, SNPs may be correlated with one another. Second, some of the non-zero effect sizes of GWAS SNPs may be due to the fact that the GWAS SNP is tagging (in LD with) an untyped causal variant and is itself not causal. Third, even if the GWAS variants analyzed in our study are the true causal variants, their effect sizes may be misestimated by the effects at nearby SNPs in LD with them. Thus, given these challenges, we carefully considered the effect that unmodeled LD may have on our inferences (see Note S2).

First, we developed an estimator of the SNP-based heritability that downsamples the number of SNPs to be independent of each other. We checked the robustness of our results to this effect by randomly selecting a single SNP in a window and computing the proportion of heritability from private variants by using these randomly selected SNPs. We select only one SNP per window to avoid counting SNPs located nearby each other that are in LD with each other. We randomly selected SNPs to avoid biases due to the fact that more sophisticated methods for fine-mapping SNPs by using LD patterns may have different performance for different allele frequencies. We find similar results via our LD-pruned estimator compared with the full data (Note S3; Figures S5, S6, and S7). We also ensure that our estimates are sensible by estimating the proportion of additive genetic variance from variants we infer to be shared (Figure S8). If the inference procedure works correctly, this number should be $1-\widehat{h_{private}^2}$. In Figure S8, we see that this is indeed the case.

Second, based on first principles, our estimates of h²_private most likely underestimate the true proportion due to LD between tagging and causal variants (see Note S2). Because shared variants tend to be more common, they will tend to be in LD with more (and therefore tag more) variants. Because of this effect, shared variants could have inflated marginal effect sizes compared to private variants. This would lead to overestimating the heritability from shared variants compared to private variants, making our inferences conservative. We tested for this effect in real data by testing the correlation between marginal effect sizes and recombination rate for variants we predict to be private and variants we predict to be shared (Note S4). We found that variants we predict to be private have lower correlation than variants we predict to be shared, consistent with the idea that shared variants tag more variants than private variants (we also note that this reasoning is the motivation for LD score regression⁴⁵). In addition, coalescent simulations show that our estimator of h²_private is indeed slightly downwardly biased (Note S5; Figure S9).

Discussion

In this work, we have shown that recent population growth and negative selection create population-specific genetic architectures for phenotypes, which has the direct effect of reducing the accuracy of polygenic scores when applied between populations. The reduction in accuracy will depend on how differentiated populations are and accuracy decreases as populations become more differentiated. Another case to consider is admixed populations where some causal variants could be introduced and thus become shared variants. In these cases, we expect the utility of polygenic scores to be higher, but this will depend on how recent the admixture was and how many causal variants are transferred between populations, which can vary between individuals.

In our simulation results, we found that when there was no coupling between trait effects and fitness, approximately 30% of the heritability comes from private variants and that this proportion increases as the coupling increases. Although we expect this general pattern to hold, the specific values will depend on the distribution of fitness effect for causal alleles, the mutation target size, and the demographic history of the populations under study. We have used a distribution of fitness effects that was fit to non-synonymous variants³⁹ and note that the estimates of selection on causal alleles could be revised in future studies. In addition, our model with admixture fits the observed data better than a model without admixture (Figure 1C), but we may still be underestimating the number of private alleles, which would cause our estimates to be a lower bound. Nevertheless, our results suggest that a non-negligible proportion of the heritability comes from private alleles.

We find that phenotypes with a majority of heritability explained by private variants are not likely to be predicted well in non-European populations, even if effect sizes are accurately inferred. Our analysis of the UK Biobank data suggests that most traits examined here have at least 20% of the heritability explained by private variants (h²_private > 20%), indicating that cross-population polygenic scores are limited in accuracy and many population-specific causal variants remain to be discovered. We note that our inferences on the empirical data do not make use of the Eyre-Walker $\tau$ model.²⁵ As such, our inferences from empirical data do not make any assumptions about the relationship between a mutation’s effect on fitness and the trait.

At first glance, our result that many traits have a population-specific genetic component seems at odds with recently reported results suggesting that the genetic correlation between traits in European and East Asian populations is very high.^46,47 However, we note that both of these studies examined common variants (MAF > 5%), which are more likely to be shared. Our study explicitly considers a larger range of allele frequencies, which is more likely to include population-specific variants.

Our results have several implications for users of polygenic scores. First, we show that the transferability of polygenic scores depends on the particular trait being examined. For traits with larger values of h²_private (such as diastolic and systolic blood pressure), the transferability would be lower because we find these traits derive more of their heritability from variants that are more likely to be private (h²_private: ≈48% for both). In contrast, we find that traits with lower values of h²_private, such as white blood cell count, can be more easily transferred because the heritability is spread more evenly across the spectrum of MAFs (h²_private: 28%). Although we include standard errors estimated via a jackknife, this procedure may not account for all the uncertainty. Therefore, specific differences across traits should be interpreted cautiously. In addition, our inferences, like those in Lam et al.⁴⁶ and Liu et al.,⁴⁷ focus on the SNP heritability rather than the total heritability of particular traits.

Several recent reviews and commentaries have pointed out the potential for misuse of polygenic scores to justify racism and white supremacy, especially when comparing polygenic scores across populations.^{16,48, 49, 50, 51} Importantly, although our study indicates that population-specific variants play a role in complex traits, it is incorrect to conclude that population-specific variants lead to differences in traits between populations. Previous simulation studies have suggested that the interplay between demography and negative selection will not lead to large differences in trait heritability between populations.^21,27 Instead, these evolutionary forces can change how the heritability is accounted for. For example, as we show here, population growth and negative selection can lead to heritability’s being accounted for by lower-frequency variants that are population specific instead of common variants shared across populations. Further, non-genetic factors most likely play an important role in differences in phenotype between populations.⁵²

We also highlight a crucial issue in identifying individuals in the tails of the phenotype distribution. If polygenic scores are to be used more commonly in the clinic, false-negative rates must be more closely examined across populations and phenotypes. Our work suggests that many causal variants may not be shared between populations, indicating that variants ascertained in European populations may not be informative in other populations. This could occur because, on average, more European-specific variants have been either directly included in GWASs or imputed more often than variants specific to other non-European populations. To ensure equal predictive power of polygenic scores across populations, whole-genome sequencing-based association studies must be undertaken in non-European populations. Such studies would allow for unbiased discovery of private variants accounting for much of the heritability, resulting in improved polygenic prediction in non-European populations. Finally, large imputation panels from the relevant population of interest are necessary to include variation that is not present in Europe.

Declaration of interests

The authors declare no competing interests.

Published: March 9, 2021

Data and code availability

The scripts required to carry out the inference of heritability from private variants can be found at https://github.com/LohmuellerLab/PRS.

Web resources

GWAS summary statistics, http://www.nealelab.is/uk-biobank