SEMI-Automated Optimization of the CHARMM36 Lipid Force Field to Include Explicit Treatment of Long-Range Dispersion

Abstract

The development of the CHARMM lipid force field (FF) can be traced back to the early 1990s with its current version denoted CHARMM36 (C36). The parametrization of C36 utilized high-level quantum mechanical data and free energy calculations of model compounds before parameters were manually adjusted to yield agreement with experimental properties of lipid bilayers. While such manual fine-tuning of FF parameters is based on intuition and trial-and-error, automated methods can identify beneficial modifications of the parameters via their sensitivities and thereby guide the optimization process. This paper introduces a semi-automated approach to reparametrize the CHARMM lipid FF with consistent inclusion of long-range dispersion through the Lennard-Jones particle-mesh Ewald (LJ-PME) approach. The optimization method is based on thermodynamic reweighting with regularization with respect to the C36 set. Two independent optimizations with different topology restrictions are presented. Targets of the optimizations are primarily liquid crystalline phase properties of lipid bilayers and the compression isotherm of monolayers. Pair correlation functions between water and lipid functional groups in aqueous solution are also included to address headgroup hydration. While the physics of the reweighting strategy itself is well understood, applying it to heterogeneous, complex anisotropic systems poses additional challenges. These were overcome through careful selection of target properties and reweighting settings allowing for the successful incorporation of the explicit treatment of long-range dispersion, and we denote the newly optimized lipid force field as C36/LJ-PME. The current implementation of the optimization protocol will facilitate the future development of the CHARMM and related lipid force fields.

1. Introduction

Over the last decade, molecular dynamics (MD) simulations of membranes [1–7] and membrane proteins [8–12] have generated tremendous insight into biomolecular structures and processes. Because of their ability to generate atomistic details of molecular structure and kinetics, simulations have become a standard tool to guide, interpret, and complement experiments. The recent breakthroughs of MD simulations are mostly related with the larger length and time scales now accessible through modern computers, as well as force fields (FFs) that accurately reproduce structural bilayer properties under experimental conditions [13–17]. The CHARMM36 (C36) set has been especially successful. It covers many important lipid types [14, 18–24] and is well-validated for various properties such as bilayer areas, compressibilities, spontaneous curvature, and bending constants [25]. However, monolayer surface tensions from C36 substantially underestimate experiment [14], as expected from the lack of long-range dispersion [26–28]. A solution to this is to include long-range LJ interactions explicitly through the LJ-PME method [27, 29, 30] or the particle-particle particle-mesh (PPPM) method [31]; however, the inclusion of these terms requires additional parametrization of the FF due to substantial degradation in the reproduction of experimental observables.

A major challenge in lipid FF development is the complexity of the physics underlying the parametrization problem, and usually one can only focus on limited aspects of the system of interest under certain conditions (e.g., pressure, temperature, pH, ionic strength). Furthermore, a rigorous description of certain properties may not even be possible with a particular class of FF. For example, additive FFs are deficient in regions where the dielectric response is dominated by electronic polarization so that the permeability of water in bilayers is not well described by C36 [4, 32]. Consequently, FF developers must decide the important scientific targets of their FFs, leading to different parametrization strategies used by different communities. The development of the CHARMM lipid FF has historically utilized quantum mechanical (QM) calculations and experimental data of model compounds before selected parameters are manually adjusted to reproduce experimental properties of lipid bilayers [14, 33]. Such an approach is necessary as building a lipid FF solely based on small molecules that are representative of the various functional groups in a lipid but would neglect the interactions between these groups within a lipid and from neighboring lipids in the condensed phase. As a result, additional efforts are usually required to refine the parameters. For example, developers of the C36 lipid FF tested several methyl acetate (MAS) models before the final set was selected based on the accurate reproduction of bilayer experimental data [14, 34]. This procedure is consistent with the rest of the CHARMM additive FF allowing for application of the FF to complex, heterogeneous systems.

Both the optimization and validation of FFs require significant computational resources. MD simulations of lipid bilayers in the 1990s were restricted to small systems and sub-nanosecond time scales [35–37], which greatly limited the development of reliable lipid FFs. This situation has significantly improved over the last two decades. With the increase of computer power and a variety of MD engines supporting parallel computing and/or graphics processing unit (GPU)-acceleration [38–41], a microsecond all-atom simulation of a thousand lipids is well within capabilities of most computer clusters. However, the atomistic simulation methods still suffer from the fact that the range of time and length scales by which different processes occur in membranes is vast [42]. For a simple calculation of bilayer surface area, the uncertainty from a simulation on the 100 ns timescale is typically less than 1% [25, 43, 44]. This error is acceptable in most circumstances but complicates optimization with noisy parameter sensitivities computed through finite differences [45, 46]. Furthermore, simply obtaining the surface area within the experimental error (which can be larger than 1%) does not assure the accuracy of other properties. Finally, lipid FFs are frequently subjected to adjustments to study new experimental results and utilize simulation approaches, so efficient parametrization methods are essential.

To address these problems, physics-informed methods can be used to identify beneficial modifications of the parameters via reliable sensitivity evaluations and thereby guide the optimization process in a more efficient way [47–50]. This manuscript introduces a semi-automated optimization approach for the CHARMM lipid FF. While both manual and automated FF parametrization have a long history, those two approaches have been developed mostly independently. Several authors have proposed automated strategies to fit force field parameters exclusively with respect to QM target data [51–54]. However, fully automated parametrization with respect to experimental observables was long limited to low-dimensional parameter spaces^{44, 47−49} and has only recently been leveraged to parametrize full FFs in the context of the OpenForceField Initiative [55, 56]. Automated optimization procedures for united-atom lipid FFs have been presented in Refs [57, 58]. Such automated workflows have been developed for a gamut of numerical optimization algorithms, including gradient-based methods [47, 50, 59, 60] as well as global optimization methods based on evolutionary [45] simplex [58, 61], and metamodel-based optimization [45, 49]. However, FF optimization problems are often underdetermined, which can easily lead to unreasonable parameters that are generally not transferrable to simulation setups outside the training set. Therefore, the most used FFs to this day are still based on manual development.

The present work combines automated and manual approaches. While chemical intuition and consistency with the CHARMM FF are encoded in the form of restraints and suitable weights, new iterations of the FF are generated by an automated strategy based on thermodynamic reweighting. This approach allows the incorporation of intricacies specific to the lipid FF. While the primary goal in this paper is to incorporate the Lennard-Jones particle-mesh Ewald (LJ-PME) method [27, 62] into the CHARMM36 lipid FF, the general methodology is transferable to other modifications and other lipid FFs. This paper describes the method and presents the training set, using phosphatidylcholine (PC) lipids as benchmarks. The validation including additional observables and lipid types is presented in the second part of this study “CHARMM36 Lipid Force Field with Explicit Treatment of Long-Range Dispersion: Parametrization and Validation for Phosphatidylethanolamine, Phosphatidylglycerol, and Ether Lipids” by Yu et al. [63] (henceforth denoted Paper II).

2. Methods

2.1. Parameters to Optimize.

Our previous study demonstrated that the C36 lipid FF reproduces experimental observables very well for linear alkanes when the long-range LJ interactions are included [27], so that it is reasonable to maintain the alkane parameters and only modify the head group parameters for the re-parametrization. The next question concerns which part of the head group should be adjusted. To explore the outcomes of different choices, we performed two separate optimizations. In the first, denoted Global, all the nonbonded parameters of the head group along with selected torsions were subject to change. In the other, denoted Linkage, only the nonbonded parameters of the glycerol and ester groups were optimized to maximize consistency with the rest of the CHARMM FF; e.g., the phosphate nonbonded parameters would remain the same for lipids, proteins, and DNA. Supporting Information Table S1 presents the nonbonded parameters explicitly optimized in both the Global and Linkage sets.

2.2. General Optimization Procedure.

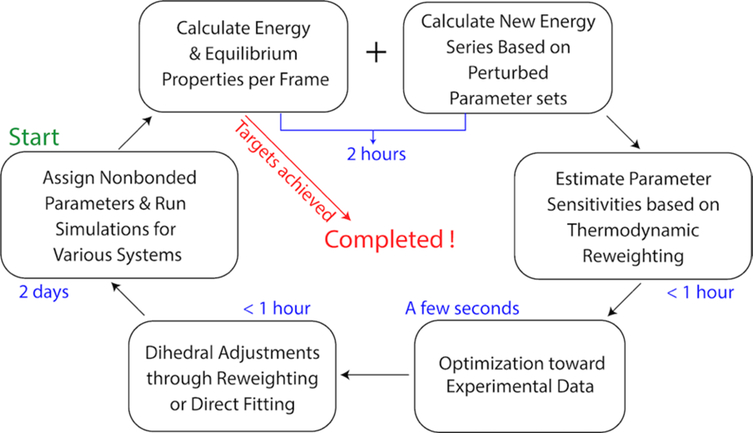
The optimization strategy (Figure 1), FFLiP (Force Field of Lipid Parametrization), was inspired by earlier gradient-based parametrization strategies [59, 60], especially the ForceBalance protocol [47]. Our starting point was the C36 set, which has been parametrized targeting reliable experimental data and high-level QM calculations. Lipid-containing systems were initially simulated with this parameter set. Upon completion of the simulations, equilibrium properties f^sim and potential energies U were calculated for each trajectory frame. The same trajectories were used for potential energy re-calculations in OpenMM 7.4.1 [41] with the perturbed parameter sets. Parameter sensitivities (gradients) of the equilibrium properties were estimated through thermodynamic reweighting [64]

$${\mathbf{S}}_{prop}(\mathbf{\lambda },\mathbf{\delta }\mathbf{\lambda })=\frac{1}{\left|\mathbf{\delta }\mathbf{\lambda }\right|}\left({〈{\mathbf{f}}^{sim}〉}_{\mathbf{\lambda }+\delta \mathbf{\lambda }}-{〈{\mathbf{f}}^{sim}〉}_{\mathbf{\lambda }}\right)=\frac{1}{\left|\mathbf{\delta }\mathbf{\lambda }\right|}\left(\frac{{〈{\mathbf{f}}^{sim}{e}^{-\beta \left(U_{\mathbf{\lambda }+\mathbf{\delta }\mathbf{\lambda }}-U_{\mathbf{\lambda }}\right)}〉}_{\mathbf{\lambda }}}{{〈e^{-\beta \left(U_{\mathbf{\lambda }+\delta \mathbf{\lambda }}-U_{\mathbf{\lambda }}\right)}〉}_{\mathbf{\lambda }}}-{〈{\mathbf{f}}^{sim}〉}_{\mathbf{\lambda }}\right)$$ (1)

where S_prop is the sensitivity matrix of properties, λ is the original parameter set and δλ is the perturbation of that parameter set. ${〈\bullet 〉}_{}$ denotes the average over trajectory, which is also the ensemble average of parameter set λ, approximately. The approximate Jacobian S_prop was calculated in a parallel fashion because the partial derivatives can be computed independently. In the next step, the prediction for the best new set of nonbonded parameters $\mathit{P}=\mathbf{\lambda }+\mathrm{\Delta }\mathit{P}$ is given by solving Eq. (2) in a least-square manner

$$\mathrm{m}\mathrm{i}\mathrm{n}!‖\mathbf{W}(\mathbf{S}\bullet \mathrm{\Delta }\mathbf{P}-\mathbf{F})‖$$ (2)

$$\mathbf{W}=\left(\begin{array}{cc}{\mathbf{W}}_p& 0\\ 0& {\mathbf{W}}_{C36}\end{array}\right)=\left(\begin{array}{cc}\left(\begin{array}{c}{w}_1\\ \ddots \\ w_{N_{prop}}\end{array}\right)& 0\\ 0& \left(\begin{array}{c}{w}_1^{\mathrm{\text{'}}}\\ \ddots \\ w_{N_{param}}^{\mathrm{\text{'}}}\end{array}\right)\end{array}\right)$$

$$\mathbf{S}=\left(\begin{array}{c}{\mathbf{S}}_{prop}\\ {\mathbf{S}}_{param}\end{array}\right)=\left(\begin{array}{c}\left(\begin{array}{ccc}{s}_{\mathrm{1,1}}& \cdots & s_{1,N_{param}}\\ ⋮& \ddots & ⋮\\ s_{N_{prop},1}& \cdots & s_{N_{prop},N_{param}}\end{array}\right)\\ {\mathbf{I}}_{N_{param}}\end{array}\right)$$

$$\mathbf{F}=\left(\begin{array}{c}{\mathbf{F}}_{prop}\\ {\mathbf{F}}_{C36}\end{array}\right)=\left(\begin{array}{c}{\mathbf{f}}^{exp}-{〈{\mathbf{f}}^{sim}〉}_{\mathbf{\lambda }}\\ \begin{array}{c}0\\ ⋮\\ 0\end{array}\end{array}\right)$$

where W is a diagonal weight matrix composed of apparent weights for the target properties (W_p) and weights used for regularization (W_C36; S is the complete sensitivity matrix, which consists of the sensitivity matrix of the target properties and an identity matrix of size N_param (the total number of parameters); F is the target vector, which contains the deviations of simulated results from the experiments and N_param zeros to restrain the parameter set to C36. The least-square problem was solved by the “linalg.lstsq” method in NumPy, which minimizes the Euclidean 2-norm $‖\mathit{W}(\mathit{S}\bullet \mathrm{\Delta }\mathit{P}-\mathit{F})‖$ when the equation is overdetermined [65]. While the number of parameters is not necessarily less than the number of experimental targets (which means underdetermination of the problem in the language of linear algebra), we can avoid this situation by adding parameter restraints (which correspond to F_C36 in the F vector) as additional equations to make sure the number of equations are more than the number of parameters. These additional equations all have the simple form of ΔP_i = 0 (P_i stands for the i^th parameter) and correlate with the W_C36 part in the weight matrix and the identity matrix I_Nparam in the sensitivity matrix. They serve as restraints and ensure that Eq. (2) is overdetermined, and a least-square solution is available. Dihedral parameters associated with the changed nonbonded parameters were adjusted at the end of each optimization cycle through reweighting or direct fitting (see Section 2.4). A new set of simulations was subsequently run to test the new parameters. If the results were satisfactory, the optimization would be terminated. If not, the cycle would continue until optimal parameters were obtained.

Figure 1.

The optimization procedure and approximate time per step.

2.3. Training Set.

The common goal of parametrizing a lipid FF is to find the parameters that reproduce experimentally measured properties. As a result, the quality of a lipid FF is heavily influenced by the availability of experimental data and the quality of the fitting process. For lipids, there are abundant experimental data available including surface area per lipid of single component bilayer, monolayer isotherms, NMR deuterium order parameter, area compressibility, bending constant, NMR relaxation time, and lipid diffusion constant. These experiments provide valuable information regarding the structures, mechanical properties, and dynamics of lipid bilayers and monolayers. The atom-pair-specific radial distribution functions (RDFs) between the phosphate group/ester linkage and water molecules determined recently by McLain et al. [66, 67] provide insights to the hydration of the head groups. However, when choosing the training set, not all of these experiments can be used, especially for dynamic properties, since the reweighting strategy is most efficient when applied to thermodynamic properties that can be computed for individual configurations. In principle, dynamic properties can be added to the training set if the parameter space is sufficiently explored in advance so that a model can be built to predict the results based on the input parameters. The parameter space here is too large to explore and develop such a model, so dynamic properties were excluded from the training set, but were tested in paper II as part of validation. The training targets for the two optimizations are listed in Table 1. The current parametrizations focus on PC lipids, which include DPPC, 1,2-dimyristoyl-sn-glycero-3-phosphorylcholine (DMPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and 1,2-dipropionyl-sn-glycero-3-phosphocholine (C₃-PC). In the Linkage optimization, the RMSD of C₃-PC RDF was used instead of the maximum and minimum used in the Global optimization, partly due to the fixing of the phosphate parameters.

Table 1.

Training target data, along with their scaling factors and weight factors. Properties cover surface area per lipid (A_l), deuterium order parameters (S_CD), overall bilayer thickness (D_B), and radial distribution function (RDF). S_CD (tail) refer to chain order parameters from the 4^th carbon in each tail with available experimental data. The simulation systems used to extract each property are shown in the second column with temperature (the surface tension per leaflet is shown in parenthesis if nonzero), and the hydration number for each system is shown in the third column (N_water/lipid). Scaling and weight factors are defined Section 2.6.

property	system, temperature (K)	Nwater/lipid	target value	scaling factor	weight factor – Global	weight factor – Linkage
Al	DPPC Bilayer, 323.15	30.4	63.1 (Å2) [68]	60 Å2	20	20
SCD (tail)			ref [69, 70]	0.15	0.05 × 11	0.05 × 11
SCD (head group)			ref [71]	0.15	0.5 × 11	0.5 × 11
DB			39.0 (Å) [68]	40 Å	5	5
ΔAl (DMPC-DPPC)	DPPC Bilayer, 323.15	30.4	2.5 (Å2)[68, 72]	2 Å	1	1
	DMPC Bilayer, 303.15	25.7
Al	DMPC Bilayer, 303.15	25.7	60.6 (Å2) [72]	60 Å2	10	10
DB			36.7 (Å) [68]	40 Å	5	10
Al	DPPC Bilayer, 333.15	30.4	65.0 (Å2) [68]	60 Å2	10	10
DB			38.1 (Å) [68]	40 Å	5	5
Al	DMPC Bilayer, 303.15	25.7	60.6 (Å2) [72]	60 Å2	10	10
DB			36.7 (Å) [68]	40 Å	5	10
Al	POPC Bilayer, 303.15	31.1	64.3 (Å2) [68]	60 Å2	5	5
Al	DPPC Monolayer (18 dyn/cm), 321	30.4	54 (Å2) [68]	60 Å2	5	5
Al	DPPC Monolayer (40 dyn/cm), 321	30.4	64 (Å2) [68]	60 Å2	5	5
Al	DPPC Monolayer (55 dyn/cm), 321	30.4	80 (Å2) [68]	60 Å2	5	5
RDF (water atom ~ lipid atom) Maximum	C3-PC in solution, 298.15	250	ref [66]	1	0.75 × 10	0
RDF (water atom ~ lipid atom) Minimum				0.5	0.75 × 6	0
RMSD of RDF from 0.2 to 0.6 nm				1	0	1.5
KA of DPPC Bilayer at 323.15 K	DPPC Bilayer (5 dyn/cm), 323.15	30.4	231 (dyn/cm) [73]	200 dyn/cm	0.75	0.75
	DPPC Bilayer (−5 dyn/cm), 323.15	30.4
DPPC Bilayer Isobaric Expansion	DPPC Bilayer, 323.15	30.4	0.19 (Å2/K) [68]	0.2 Å2/K	1	1
	DPPC Bilayer, 333.15	30.4

2.4. Dihedral Fitting.

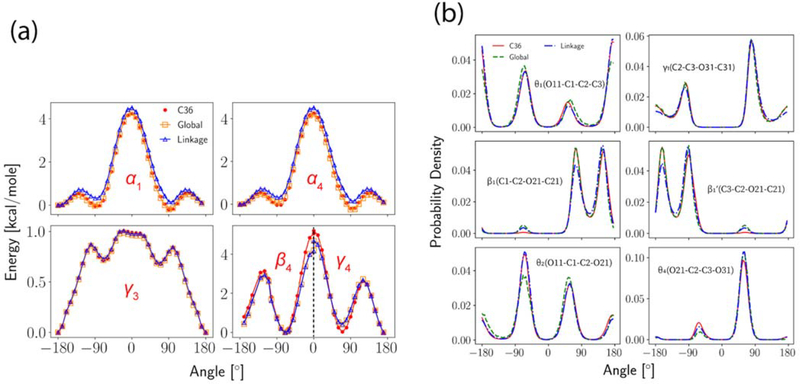
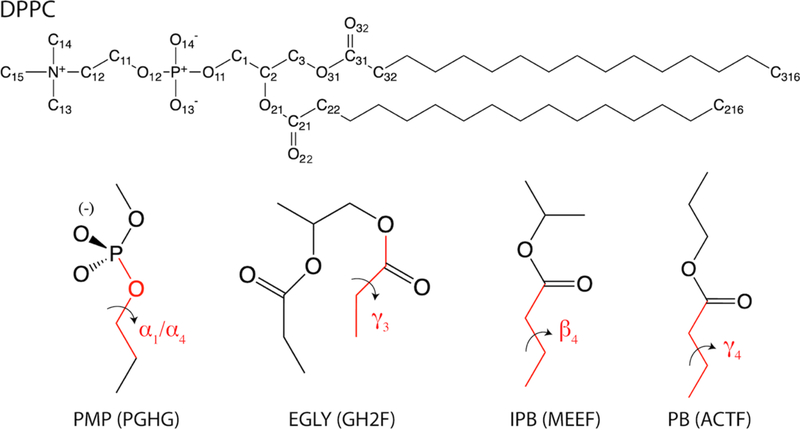
Dihedral parameters play a critical role in bond orientations and dynamics at the atomic level. The C36 lipid FF yields excellent agreement with the experimental deuterium order parameters in the head group region [1, 74], which can be credited to the extensive QM calculations of model compounds representative of the head group and linkage region. Although fitting to the same set of QM data is a reasonable strategy to take for C36/LJ-PME, running the QM calculations has the added difficulty because one needs to find the conformations that are representative of the lipid in a biological environment. In fact, the C36 dihedrals are good targets for two reasons. First, the potential energy scans are relatively easy to obtain and integrate into the workflow. Second, fitting to C36 is expected to reproduce the order parameters which are already in good agreement with experiments. When fitting to C36, two methods were used. The first is fitting to the potential energy scan (PES) of a dihedral using a model compound. The second is fitting through thermodynamic reweighting (Eq. 1). In the first method, all dihedrals but the scanned dihedral were unconstrained, while the scanned dihedral was restrained using a force constant of 10³ kcal/mol during the energy minimization consisting of 200 steepest decent steps and 1000 adopted basis Newton-Raphson steps in CHARMM. In the second method, a 10-ns trajectory block from a DPPC bilayer simulation was used to calculate the torsion angles and the corresponding energy series. In addition, a trajectory sampled by C36 was used to obtain the reference torsion distributions. The dihedral parameters were changed iteratively using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm implemented in scipy [75] until the convergence criteria were met. Table 2 shows the dihedral types fitted in each optimization cycle and the corresponding fitting protocols. The choice of fitting protocol was conditioned on the availability of QM conformational energies from the original publication of C36 [14]. A Monte Carlo simulated annealing approach [76] was used for fitting to the QM/C36 PES. The results for dihedral fittings are discussed in Section 3.

Table 2.

Dihedrals fitted in each optimization cycle and the corresponding fitting protocols. Atom names and model compounds are shown in Figure 2. CHARMM atom types included in parenthesis for each dihedral. Symbols for the dihedrals are consistent with C36 and are used henceforth.

Dihedral	Symbol	Fitting Protocol	Model Compound
O11-C1-C2-C3 (OSLP-CTL2-CTL1-CTL2)	θ1	Reweighting to C36 Torsion Distribution in DPPC Bilayer Simulation	None
C2-C3-O31-C31 (CTL1-CTL2-OSL-CL)	γ1
C1-C2-O21-C21(CTL2-CTL1-OSL-CL)	β1
O11-C1-C2-O21 (OSLP-CTL2-CTL1-OSL)	θ2
O21-C2-C3-O31 (OSL-CTL1-CTL2-OSL)	θ4
P-O12-C11-C12 (PL-OSLP-CTL2-CTL2)	α4	Least Squares Fit to C36 Potential Energy Scan	PMP
P-O11-C1-C2 (PL-OSLP-CTL2-CTL1)	α1		PMP
O31-C31-C32-C33 (OSL-CL-CTL2-CTL2)	γ3		EGLY
C31-C32-C33-C34/C21-C22-C23-C24 (CL-CTL2-CTL2-CTL2)	β4/γ4	Least Squares Fit to QM Potential Energy Scan	IPB/PB

2.5. Parameter Perturbation.

The potential energy in the CHARMM FF is

$$\begin{gathered} V(\widehat{R})=\sum _{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}{K}_b{\left(b-b_0\right)}^2+\sum _{\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}\mathrm{s}}{K}_{\theta }{\left(\theta -{\theta }_0\right)}^2+\sum _{\mathrm{d}\mathrm{i}\mathrm{h}\mathrm{e}\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{s}}\sum _j{K}_{\phi ,j}\left(1+\cos \left(n_j\phi -{\delta }_j\right)\right)+ \\ \sum _{\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{d}\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}i,j}{\epsilon }_{ij}\left[{\left(\frac{R_{\mathrm{m}\mathrm{i}\mathrm{n},ij}}{r_{ij}}\right)}^{12}-{\left(\frac{R_{\mathrm{m}\mathrm{i}\mathrm{n},ij}}{r_{ij}}\right)}^6\right]+\sum _{\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{d}\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}i,j}\frac{q_i{q}_j}{{\epsilon }_D{r}_{ij}} \end{gathered}$$ (3)

where the terms have their usual meanings. The bond and angle terms were left unchanged from C36. As described in Section 2.1, thermodynamic reweighting allows fast evaluations of the parameter sensitivities. However, such evaluations require sufficient conformational overlap between the original and perturbed states for accurate prediction; i.e., the perturbation δλ in eq 1 must be sufficiently small to ensure this criterion is met. A detailed investigation of the magnitude of perturbations is presented in Section 3. Table 3 lists the perturbations used for all parameter types. The perturbations used for partial charges are 10⁻³ e. Percentage perturbations were used for the LJ parameters, since they differ substantially among different atom types. When perturbing the partial charge of an atom, the charge was redistributed to selected neighboring atoms to ensure a fixed net charge. The rules for charge re-distribution are shown in Table S2, which takes the CHARMM definition of integer charge groups into consideration so that the re-distribution was always within a charge group. When there were N equivalent atom sites, for example, O22 and O32, perturbations to them occurred at the same time but the perturbation size for each was scaled by 1/N to limit the conformational change corresponding to these perturbations. In each optimization cycle, all parameters listed in Table S1 were perturbed and subject to potential changes,, thereby providing access to all partial derivatives.

Table 3.

Perturbation sizes used for partial charge, ε and R_min/2 during optimization.

Parameter Type	Perturbation Size
q	10−3 e
ε	0.1% of the parameter in the last optimization step
Rmin/2	0.1% of the parameter in the last optimization step

2.6. Regularization.

As shown in Eq. (2), the optimal parameter set P is given by solving a linear equation which used the sensitivity matrix and a weight matrix. The weight matrix consisted of two parts. The i^th component of the first part, w_i, was set to be the weight factor of property i divided by the scaling factor of property i (see Table 1 for values). Weight factors were determined by considering the uncertainty of experimental data and the correlation between different properties. The weight factors for tail S_CD were significantly lower than the other properties because they are strongly correlated with the surface area. Scaling factors were used to make sure all training targets were at the same order of magnitude. While the user can set the weights for the training targets (properties) according to their significances and the uncertainties from the experimental measurements, the second part of the weight matrix, W_C36, is even more important because it determines how far the parameters can shift from the original C36 set. Such restraints, called regularizations, are usually applied to avoid overshooting of parameters during the fitting process. Incorporating the initial parameters into the target vector is equivalent to adding a harmonic restraint as in the L2 regularization used in ForceBalance [47, 57]. To construct a meaningful W_C36, the relative magnitude of this submatrix (compared to W_p) should be determined to assure that the change of the parameter set in each optimization step is suitably small. Moreover, the relative weights for charges and LJ parameters should be balanced properly, so that all parameters change in a physically meaningful way. The default weight factors for different parameter types in each optimization cycle can be found in Table S3. Apart from these, we used the standard deviations of parameter sensitivity estimated from three independent trajectory blocks to modify the default weight factors in each optimization step.

To justify this modification, consider a property that is determined by only a subset of the system’s coordinates, r₁. Let r denote the full coordinate set, and r₂ those coordinates not belonging to r₁. The potential energy function, U(r), can be decomposed as:

$$U\left(\mathbf{r}\right)=U\left({\mathbf{r}}_1\right)+U\left({\mathbf{r}}_2\right)+U\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=U\left({\mathbf{r}}_1\right)+U^{\mathrm{\text{'}}}$$ (4)

where U(r₁) and U(r₂) are contributions from subset r₁ and r₂, respectively, and U(r₁, r₂) is the contribution from the cross-interactions between the two subsets. With this, an element of the sensitivity matrix in Eq. (1) can be reformatted accordingly as:

$$s(\lambda ,{\delta \lambda )=〈f^{sim}〉}_{\lambda +\delta \lambda }-{〈f^{sim}〉}_{\lambda }=\frac{{〈f^{sim}{e}^{-\beta \left[U_{\lambda +\delta \lambda }\left({\mathbf{r}}_1\right)+U_{\lambda +\delta \lambda }^{\mathrm{\text{'}}}-U_{\lambda }\left({\mathbf{r}}_1\right)-U_{\lambda }^{\mathrm{\text{'}}}\right]}〉}_{\lambda }}{{〈e^{-\beta \left[U_{\lambda +\delta \lambda }\left({\mathbf{r}}_1\right)+U_{\lambda +\delta \lambda }^{\mathrm{\text{'}}}-U_{\lambda }\left({\mathbf{r}}_1\right)-U_{\lambda }^{\mathrm{\text{'}}}\right]}〉}_{\lambda }}-{〈f^{sim}〉}_{\lambda }$$ (5)

Here, we use normal fonts for s, fx^sim and λ instead of bold to indicate that we only focus on one particular property and only one parameter. Suppose that the subset r₁ and r₂ can be chosen in a way such that U(r₁) is strongly coupled with the property f^sim while U' is only weakly coupled or is uncoupled. In such a case, if parameter U(r₁) is substantial, then the property will be dominated by λ as they are strongly coupled with each other through U(r₁). As a result, the gradient of f^sim in the direction of λ estimated by the reweighting would be meaningful. However, if U(r₁) is not substantially influenced by λ, or if a change in λ leads to more change in U' rather than U(r₁), the quality of the reweighting will be impaired since U' will act as a noise to the total potential energy. Although this noise can be reduced by extending the simulation to acquire enough sampling, it is not practical for our membrane systems (which contain more than 10⁴ atoms). An alternative is to set customized weights for parameters according to the standard deviations of the sensitivities estimated from trajectory blocks. Specifically, a candidate w_λ for parameter λ is calculated through

$$w_{\lambda }=S_b\mathrm{*}\frac{\sum _{prop}(w_{prop}\cdot \mathrm{S}\mathrm{T}\mathrm{D}(s_{prop}))}{\sum _{prop}(w_{prop})}$$ (6)

where s_prop is the sensitivity for a particular property, w_prop is the effective weight (weight factor/scaling factor) for the property, which is also used in W_p. STD means standard deviation, and S_b is a scaling factor used to balance W_p and W_C36. The unit of W_λ is 1/e for charges and 1/percentage for ε and R_min/2. During the optimization, w_λ was used if it was greater than the default weight for the parameter type of λ, otherwise the default was kept. Moreover, if the calculated w_λ was larger than a preset upper bound, the parameter would not be allowed to change in the optimization step. Consequently, parameter changes leading to large uncertainties were avoided or at least reduced in a property-dependent manner. Therefore, confidence was increased for the more important properties. The S_b used in each optimization cycle can be found in Table S4, while the upper bounds were determined to be 20/e for charge or 20/percentage for ε and R_min/2. Much higher S_b and default weighting factors (Table S3) were used for the last (third) optimization cycle in the Global optimization, because the simulated properties after the second cycle in that optimization were close to their target values so that harder restraints could be applied.

2.7. Computational Details.

Membrane coordinates were obtained from the CHARMM-GUI [77] Membrane Builder [78, 79] and minimized/equilibrated following the standard six-step procedure offered by CHARMM-GUI. The C₃-PC residue was created by modifying DMPC, removing fatty acid chain C4:C14 and attached H atoms, and converting C3 from methylene to methyl; no new or modified parameters were required. A single molecule was built from the internal coordinates of the residue definition, and then subjected to 80 ns of vacuum Self-Guided Langevin Dynamics (SGLD) [80], with a collision frequency of 1/ps and a dielectric constant of 80 to screen the charges. Nine configurations were randomly selected from the vacuum trajectory and placed on a grid with one molecule at the origin, and the other eight translated to the corners of a 20 Å cube centered on the origin, and randomly rotated. Water coordinates from an equilibrated cube with a 43 Å edge were read, and waters closer than 2.3 Å to any C₃-PC molecule were deleted. The system was relaxed with 50 steps of steepest descent minimization, followed by 1000 steps of the adopted-basis Newton-Raphson minimization. 36 lipids per leaflet (72 in total) are used for all membrane systems and the hydration number for each system is shown in Table 1.

In each optimization cycle, membrane systems were simulated for 200 ns with the exception being the two NPγT simulations of DPPC used to calculate the compressibility modulus, which were simulated for 300 ns. The first 50 ns (for NPT simulations) or 60 ns (for NPγT simulations) were discarded to avoid the unequilibrated part of the trajectory. The block sizes used for the standard deviation calculations of sensitivity were 50 ns and 80 ns, respectively. The C₃-PC system was simulated for 100 ns (first 10 ns discarded) in each optimization cycle and 30 ns blocks were used for the standard deviation calculation. For all systems, the modified TIP3P water model [81, 82] was used to keep consistency with other parts of the force field. All simulations were run in OpenMM 7.4.1 using the Langevin Integrator with a timestep of 2 fs. Pressure was set to be 1 atm, which was maintained by the Monte Carlo Membrane Barostat for membrane systems and by the Monte Carlo Barostat for the C₃-PC system. For the Monte Carlo Membrane Barostat, a semi-isotropic simulation cell was used, where X was constrained to be equal to Y but allowed to vary independently with respect to Z (the bilayer normal direction). The LJ-PME algorithm used in this study is described in reference 27. It uses the Lorentz-Berthelot (LB) combination rules [83] in real space, which are standard for the CHARMM FF. For parametrization, a real-space cutoff (r_cut) of 10 Å was utilized, though simulations using different r_cut were conducted at the end of the parametrization to study its influence.

After the Linkage optimization, 3 replicas of 100 ns CHARMM (LJ-PME) [27] NPT simulations were performed for DPPC bilayer at 323.15 K to check the consistency between OpenMM and CHARMM. The Nosé-Hoover thermostat [84] was used to maintain system temperature, and a modified Andersen-Hoover barostat [85, 86] was used to maintain constant pressure at 1 atm. The initial structure of the DPPC bilayer was taken from the last frame of the OpenMM simulation at the end of the Linkage optimization. The same semi-isotropic simulation cell and r_cut were used to keep consistency with the OpenMM simulations. The last 70 ns from each replica was used for the surface area calculation.

Surface area per lipid (A_l) was calculated as the area of the cross-section perpendicular to the membrane normal divided by the number of lipids in each leaflet. The compressibility modulus of bilayer, K_A, was determined from the isotherm of the surface tension with respect to the total area [25]

$$K_A=A{(\frac{d\gamma }{dA})}_T$$ (7)

where A is the total area, and γ is the total surface tension. The deuterium order parameter (S_CD) was calculated as

$$S_{\mathrm{C}\mathrm{D}}=\left|\frac{1}{2}〈3\mathrm{c}{\mathrm{os}}^2\theta -1〉\right|$$ (8)

where θ is the angle formed by the C-H vector and the bilayer normal, and the average is over the ensemble and time.

To extract the maximum and minimum of C₃-PC~water RDFs, MDTraj [87] was used to calculate the 3 dimensional RDFs from simulation. The experimental data was taken from Foglia et al [66]. Due to the noise in the experimental RDFs, we used the “convolve” function in NumPy [65] to smooth the curve with a window size of 3. The RDFs from simulation were generated with enough sampling so that no smoothing was needed.

3. Results

The long-range dispersion has a significant impact on membrane structure. The C36 lipid FF was parametrized specifically for a Lennard-Jones functional form of the van der Waals interaction with a force-switching function over the range of 8–12 Å [14], and any deviation from this “standard” scheme is expected to cause different structural measurements compared to simulations using this “standard”. For example, changing the switching function to 11–12 Å and simulating in NAMD [88] instead of CHARMM led to a significantly lower A_l (59.1 ± 0.4 Ų compared to 62.9 ± 0.3 Ų) for DPPC bilayer at 323.15 K [14]. While the simulation package and relatively short sampling time of the CHARMM simulation (40 ns) might have also contributed to this difference, the 200 ns simulation at the beginning of the current parametrization also generated a significantly lower A_l (58.9 ± 0.3 Ų) when the long-range dispersion was fully included through LJ-PME. Deuterium order parameters were also in poor agreement with experiment as shown in Figure S2. In this section, we show how this degradation in the reproduction of experimental observables and the inconsistency between monolayer and bilayer were fixed.

3.1. Parameter Sensitivities.

The sensitivity analysis was performed on all training targets associated with the PC headgroup starting from the first optimization cycle. Sensitivities for the surface area of DPPC bilayer at 323.15 K are reported in Figure 3; examples for other training targets can be found in Figure S3. The sensitivities were calculated according to eq 1, and the perturbation sizes δλ were determined by monitoring the effects of the size (see Section 3.2 for more details). A perturbation size of 0.001 elementary charge (e) was chosen for partial charges (about 0.3% the average absolute value of partial charges from head group atoms), and percentage perturbations (0.1%) were used for R_min/2 and ε due to the wide distributions of these two parameters among different atom types.

Figure 3.

Parameter sensitivities for the surface area of DPPC bilayer at 323.15 K. Averages and standard deviation evaluated from three blocks of 50 ns shown for each parameter. The perturbation sizes used are 0.001 e (absolute value) for partial charge and 0.1% of the original parameter for R_min/2 and ε. Note that different scales were used for the plots of initial and final parameter sets.

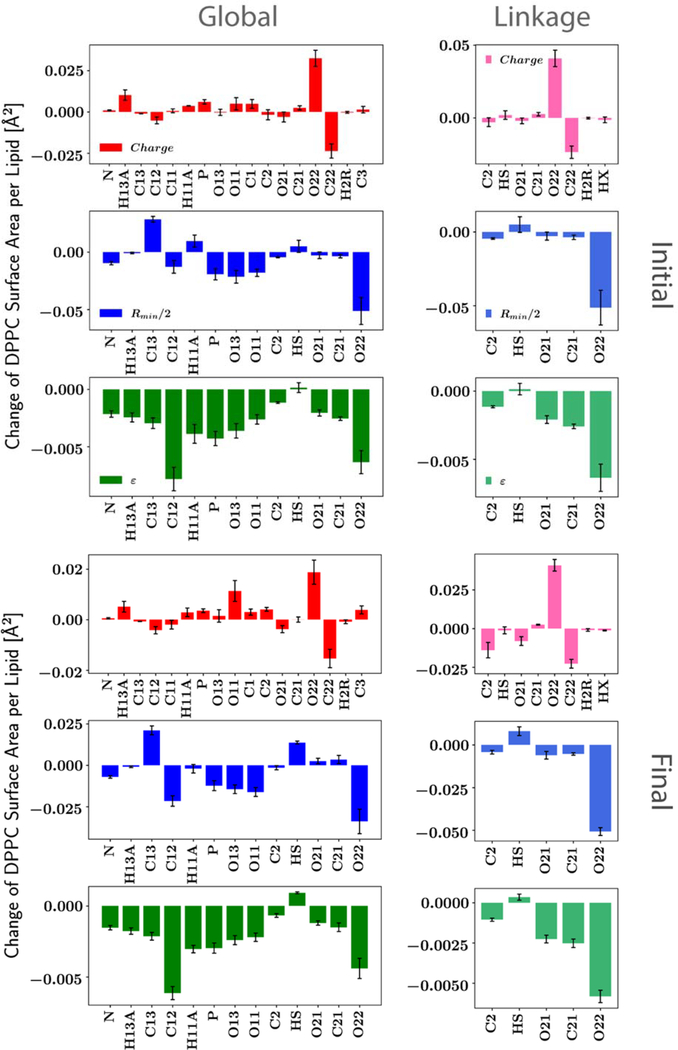
It is evident from Figure 3 that different parameters have different effects on the surface area of DPPC bilayer and its standard deviations. While the perturbations used for the three nonbonded parameter types (charge, R_min/2 and ε) are comparable, ε has much less influence on the surface area compared to the other two, and the sensitivities are generally negative (when increasing the absolute value of ε). This is not surprising since ε does not substantially influence the minimum energy distance between two interacting groups, though the distance distribution for an atom pair is affected by the interplay of all nonbonded parameters (and bonded parameters if linked). The R_min/2 sensitivities do not have a uniform sign, but most are negative. This is counterintuitive as one might expect the volume to increase with larger R_min, hence an increased surface area. However, it is the intersection of the LJ surfaces of the two interacting groups that impact the minimum interaction distances such that the relationship of R_min to interaction distance is not necessarily directly correlated. This result highlights the complexity of interactions in lipid bilayers. For partial charges, the “hot spots” are the two carbonyl groups (C22-O22/C32-O32) at the head-tail linkage region. Moreover, the O22 R_min/2 also has a significant impact on the surface area. Because these atoms are located at the head-tail linkage, two optimizations were performed. As detailed in the Methods, Linkage restricted the changes to the glycerol backbone and the ester groups, while Global also allowed the phosphate and choline groups to vary.

The surface area of DPPC was not the only target for parametrization, and the sensitivity for a single property can only tell us the importance of the parameter for that particular property, but not necessarily others. This is illustrated by Figure S3 and Figure 4. Figure S3 shows additional parameter sensitivities for A_l of DMPC bilayer, overall bilayer thickness (D_B) of a DPPC bilayer, S_CD of carbon C12 in a DPPC bilayer and the first peak of the RDF between the carbonyl oxygen and the water oxygen of the C₃-PC solution. The sensitivities for D_B are inversely related to the sensitivities for A_l, consistent with the compressibility modulus of DPPC bilayers. From the perspective of parametrization, this relationship reveals the essential role hydration plays in the surface area. The sensitivities for A_l of DMPC are very similar to those of DPPC, which means the two areas are highly correlated. For the S_CD of carbon C12, the parameters having substantial influence are not limited to the phosphate-choline link region. Since S_CD is calculated from the C-H bond orientation which is primarily determined by the dihedral parameters once the angle parameters were well-determined, it might not be influenced by the nonbonded parameters directly. However, the nonbonded parameters may influence the interactions within or between lipid molecules (and water). Hence, they can change the overall bilayer structure and the orientation of the head group indirectly.

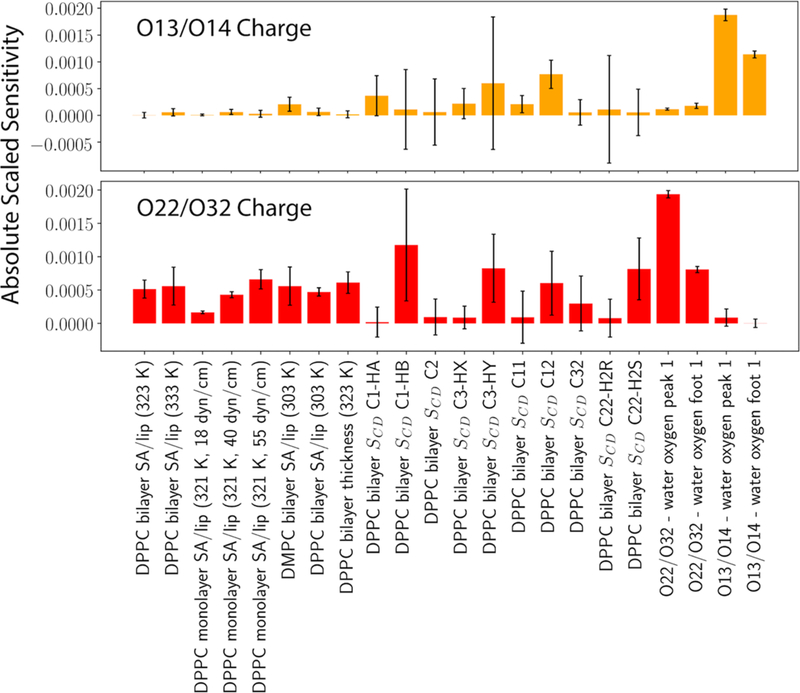
Figure 4.

Absolute scaled parameter sensitivities of O13/O14 and O22/O32 partial charges for various properties.

Figure 4 plots the parameter sensitivities of O13/O14 and O22/O32 charges on a wide range of properties, which are scaled by the scaling factors in Table 1 after taking the absolute values. The parameter perturbations used are the same as those used in Figure 3. It is clear that the standard deviations of the sensitivities for different properties vary significantly. For example, one can be almost certain about O13/O14 charges’ influence on the RDF between O13/O14 and the water oxygen but cannot be so confident with the A_l of DPPC/DMPC bilayers. However, when parametrizing the force field, the influence of the O13/O14 charges on the A_l is nonnegligible, which makes the parametrization challenging.

3.2. Scope of the Linear Prediction.

As noted in the Method Section, one of the major changes from early parametrizations of the CHARMM lipid FF is the application of thermodynamic reweighting. Although this can potentially increase the efficiency of the parametrization, one should be careful about the parameter sensitivities predicted in this way. The reason is simple – to get meaningful sensitivities (gradients), the trajectory sampled by the simulation should represent an equilibrated state. And perhaps more importantly, the gradients calculated at a certain point in the parameter space are only accurate for a specific region around that point, which is hereafter called the linear region.

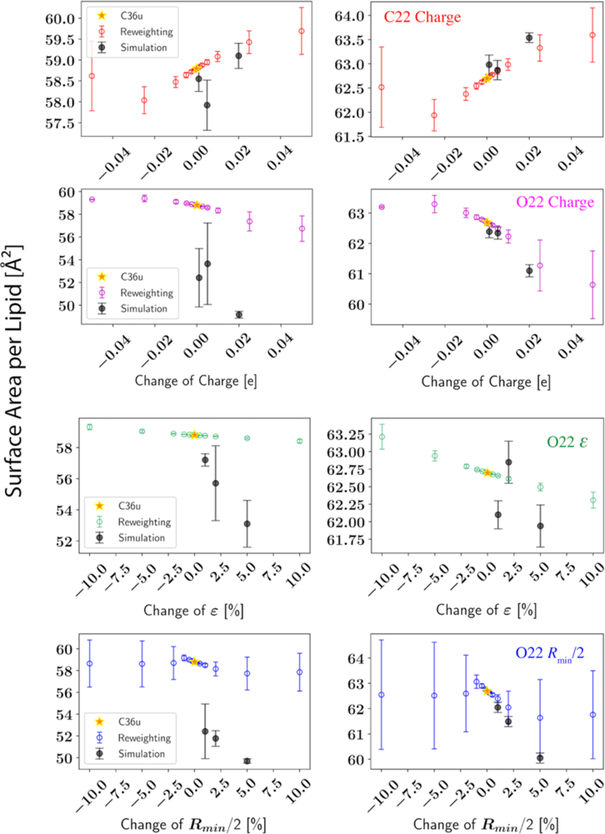
To identify the size of the linear region and to justify our reweighting strategy, we performed reweightings using different perturbation sizes; selected results are shown in Figure 5. For both the starting point (C36) and the end point (examples only shown for the Global parametrization), there are clearly linear regions, but the size of the linear region depends on the parameter. In the view of reweighting, the linear region is typically several hundredths of the elementary charge for partial atomic charges. Interestingly, this region is about 3% for R_min/2 but more than 10% for ε. Moreover, the statistical errors calculated based on 3 trajectory blocks indicate that reweighting for R_min/2 is no longer accurate when the perturbation exceeds 3%. Considering R_min/2 is directly related to the pairwise interaction between two atoms close to each other, changing R_min/2 would lead to a dramatic change in the conformational sampling so that the overlap between the sampled and reweighted states would be greatly reduced, thus leading to large statistical errors. As a result, we set the weight factors for regularization differently for the three parameter types. See Section 3.3 for more details.

Figure 5.

Simulated and reweighted surface area per lipid for DPPC bilayer at 323.15 K. All simulations are performed with LJ-PME. Yellow stars (C36u): simulations using the original C36 parameter set (left) or the final parameter set (right) from the Global optimization; black dots with error bars (Simulation): simulations using perturbed parameters; circles with error bars: predictions by reweighting the yellow-star simulations. The averages and standard deviations shown at error bars of the simulated results are based on 3 independent replicas of 300 ns (last 200 ns used for calculating the A_l), while the averages and standard deviations shown at error bars of the reweighted are from 3 trajectory blocks of 50 ns.

The linear region is harder to detect from direct simulations due to the large statistical errors, while the physics-informed method, reweighting, can greatly reduce the noise in the first derivative. Nevertheless, complications can arise. For example, several simulations near the C36 parameter set condensed to the gel phase leading to huge statistical errors on the mean surface area. Since this only happened to the perturbed set, the microstates representing the gel phase were not captured by the simulation with the C36 set (the one used to reweight). Hence, the formation of a gel phase was not predicted by reweighting. Ideally, one would like to avoid such a scenario where the trajectory used to reweight does not sample some of important regions of the target state. However, the energy landscape of a lipid bilayer is so complex that it is almost certain to be nonergodic. Fortunately, as the optimization went on, the gel phase region of the parameter space was no longer sampled. Therefore, we can have more confidence in the reweighting. This is evident from the bottom row of Figure 5, where the reweightings agree well with the simulations, at least within the linear region.

3.3. Perturbation Sizes and Optimization Weights.

Based on the linear region detected in Section 3.2, the perturbation sizes for the three parameter types can be readily determined. To ensure a well-behaved computation of sensitivities, perturbations were set to be much smaller than the sizes of the linear region (see Table 3). As noted in the Section 2.6, regularization on the parameter change is necessary to avoid overshooting and can be achieved by including the parameter change into the objective function through a user-defined weight factor and a sensitivity of 1. Based on the results of Section 3.2 and a set of tests on different values, the default weight factors were determined to be 4/e for charges, and 6/percentage-change for ε and R_min/2 in the first optimization cycle, because they generated parameter changes within the linear region. Apart from the default values, we computed a candidate weight factor w_λ for parameter λ according to eq 6 and used it instead when larger than the default. Lastly, when w_λ was larger than 20/e for charge or 20/percentage for ε and R_min/2, the weight factor for parameter λ was set to be infinite, since a high w_λ indicates large noise in the reweighting.

3.4. Dihedral Parameter Fitting.

The dihedrals were fitted to either QM or C36. Conformational energies were obtained for α1, α4 and γ3 from C36 by scanning the dihedrals of interest from −180° to 180° in increments of 2°, while other dihedrals were relaxed during the scan to get the minimum energy conformation. QM energies from ref 14 were used for β4 and γ4. The scan of β4 was from −180° to 0° and the scan of γ4 was from 0° to 180°. Since the two dihedrals contain the same four atom types, the fitting was then conducted by giving each dihedral an equal weight. For dihedrals closer to the glycerol region, reweightings were used to match the C36 dihedral distributions based on DPPC bilayer simulations at 323.15 K. In addition to the standard dihedral fittings for each optimization cycle shown in Table 2, additional adjustments were made to N-C12-C12-O12 (α₅) and α₄ at the end of the Linkage optimization to match the experimental order parameters of carbon C11 and C12. The two torsions were selected by checking the correlations between the order parameters and all the head group torsions. Then, the same procedure used for the nonbonded parametrization was used to optimize the torsions (reweighting + least-square fitting) because only small changes were expected. Multiplicities of all dihedrals were kept as they were in C36 for Linkage but allowed to expand for Global. The PES of dihedrals optimized through direct fits are plotted in Figure 6(a), in which the increments for α1, α4 and γ3 are 10° while the increments for β4 and γ4 are those from the original scan. Figure 6(b) illustrates the quality of the reweighting for the last optimization cycle. Overall, the optimized set agrees very well with C36.

Figure 6.

Dihedral fits. (a) Potential energy scans for α1, α4, γ3, β4 and γ4. Reference energy is set to be the lowest energy of the Linkage parametrization; (b) Dihedral angle distributions for θ₁, γ₁, β₁^’ (and β₁), θ₂ and θ₄. The simulation used to reweight is not shown.

3.5. Training Set Evolution.

Table 4 presents the evolution of the level of agreement with the training set during the two optimizations. At the beginning, A_l’s for bilayers were systematically underestimated while the membrane thicknesses were overestimated. Hence, the attractive force brought by the long-range LJ interactions must have a stronger effect in the x-y plane (the membrane normal is z), which can be explained by the heterogeneity of the membrane system. Underestimation of the monolayer surface area was more severe, which was expected since monolayers are not well modeled by the C36 parameter set. The first optimization cycle significantly improved the A_l for both bilayer and monolayer, while the remaining cycle(s) brought the DPPC bilayer properties (A_l, membrane thickness, and S_CD) closer to the experiments, because the weight factors for DPPC bilayer related properties were overall higher than the other properties. In addition to the OpenMM results reported in Table 4, CHARMM simulations of DPPC bilayer at 323.15 K generated an A_l of 62.8 ± 0.2 Ų, which is statistically identical to the OpenMM result. Table 4 also shows that the overall quality of Linkage is comparable to Global, and differences between the two are generally within the statistical errors. To minimize the change to the C36 FF and to maximize the consistency of the FF, the Linkage parametrization is chosen as the LJ-PME version of the CHARMM lipid FF and will be called C36/LJ-PME henceforth.

Table 4.

Training set (percentage) deviations from experimental values. “G-1” can be interpreted as “after the first cycle of the Global parametrization” and “L” stands for the Linkage parametrization. Simulated values using the final parameter sets are also reported with standard errors.

property	expt.	G/L-0	G-1	G-2	G-3	L-1	L-2 (C36/LJ-PME)
Al, DPPC bilayer (323.15 K)	63.1 Å2	−6.7%	−2.1%	1.4%	−0.5% (62.8 ± 0.2 Å2)	−2.9%	−0.63% (62.7 ± 0.2 Å2)
Al, DPPC bilayer (333.15 K)	65.0 Å2	−7.3%	−2.3%	−0.1%	−1.8% (63.8 ± 0.2 Å2)	−4.2%	−2.6% (63.3 ± 0.2 Å2)
Al, DMPC bilayer (303.15 K)	60.6 Å2	−6.4%	2.0%	4.2%	3.3% (62.6 ± 0.4 Å2)	−0.8%	1.8% (61.7 ± 0.2 Å2)
Al, POPC bilayer (303.15 K)	64.4 Å2	−3.9%	2.3%	4.1%	2.2% (65.8 ± 0.4 Å2)	0.4%	1.9% (65.6 ± 0.4 Å2)
chain SCD of DPPC bilayer (averaged)	N/A	26.5%	12.1 %	6.8 %	8.4%	14.9%	13.7%
DB, DPPC bilayer (323.15 K)	39.0 Å	5.6%	1.9%	−1.4%	−0.3% (38.9 ± 0.3 Å)	1.8%	−1.3% (38.5 ± 0.1 Å)
DB, DPPC bilayer (333.15 K)	38.1 Å	6.2%	1.6%	0.2%	0.3% (38.2 ± 0.1 Å)	2.8%	0.5% (38.3 ± 0.1 Å)
DB, DMPC bilayer (303.15 K)	36.7 Å	3.4%	−4.4%	−6.7%	−5.2% (34.9 ± 0.4 Å)	−2.6%	−5.7% (34.6 ± 0.2 Å)
Al, DPPC monolayer (18 dyn/cm)	54.0 Å2	−9.0%	1.9%	4.9%	4.2% (56.3 ± 0.2 Å2)	1.4%	3.1% (55.7 ± 0.2 Å2)
Al, DPPC monolayer (40 dyn/cm)	64.0 Å2	−5.5%	−0.5%	2.3%	0.8% (64.5 ± 0.3 Å2)	−1.5%	0.1% (63.9 ± 0.2 Å2)
Al, DPPC monolayer (55 dyn/cm)	80.0 Å2	−11.4%	−5.4%	−1.9%	−4.1% (76.7 ± 0.3 Å2)	−7.2%	−4.4% (76.5 ± 0.3 Å2)
KA, DPPC bilayer at 323.15 K	0.23 N/m	4 %	34.8%	17.4%	0% (0.23 ± 0.04 N/m)	30.4%	4.3% (0.24 ± 0.02 N/m)

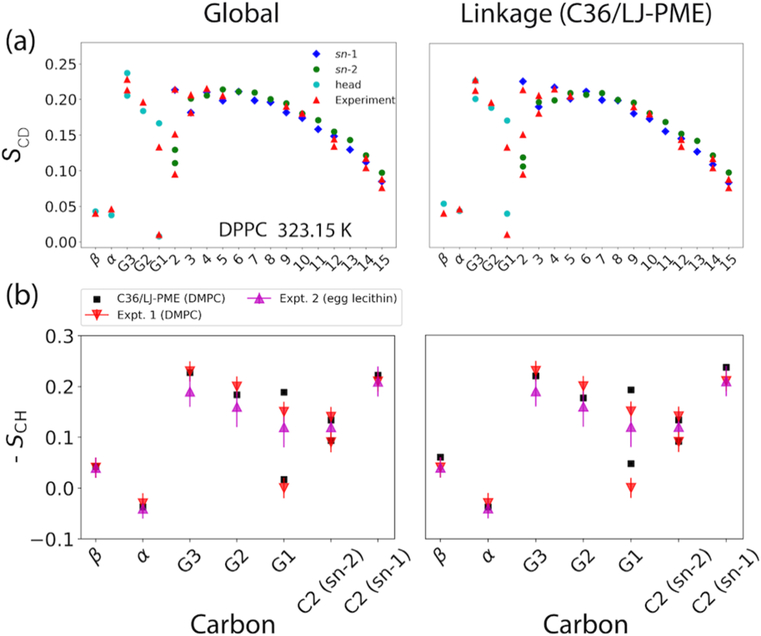
The S_CD profiles of DPPC bilayer are shown in Figure 7(a). The optimized FFs are in excellent agreement with experiment for both head group and tails. While the chain S_CD is strongly correlated with A_l [89], the accurate S_CD of the head group indicates that the reweighting for the dihedral parameters, especially those from the glycerol region, was a success. In addition to the unsigned deuterium order parameter (S_CD), the ¹³C-¹H dipolar order parameter (S_CH) can be measured experimentally [90], which comes with a sign

$$S_{\mathrm{C}\mathrm{H}}=\frac{1}{2}〈3\mathrm{c}{\mathrm{os}}^2\theta -1〉$$ (8)

where θ is the angle formed by the C-H vector and the bilayer normal. Although experiments measuring the sign of this quantity are limited [90], they can provide insightful information regarding the structure of the head group and resolve ambiguity in the sign of the deuterium order parameter. The comparison between simulation and experiment is shown in Figure 7(b). In fact, the optimized FFs correctly obtain the sign for all the head group carbons even though these signs were not considered in the original parametrization of C36. In essence, the high-level QM conformational energies chosen as the starting points for dihedral parametrization of C36 led to the good agreement with experiment.

Figure 7.

(a) Deuterium order parameters (S_CD) of DPPC bilayer at 323.15 K. (b) ¹³C-¹H dipolar order parameters (S_CH) from simulations of DMPC bilayer and two experiments (DMPC [90] and egg yolk lecithin [91]).

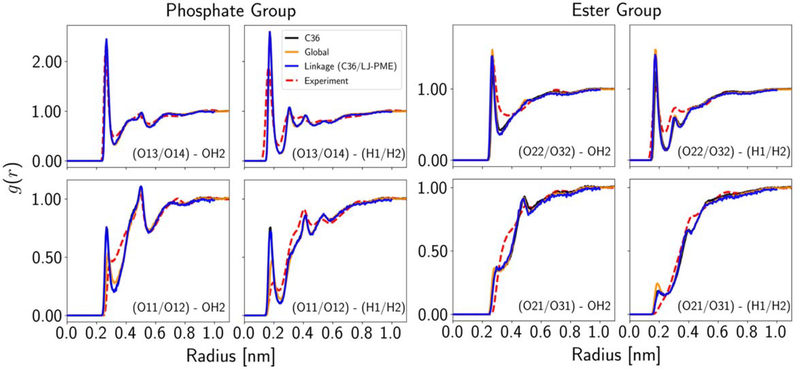
The RDFs between water and C₃-PC molecules are in principle important metrics for binding strength and structure of water molecules around the lipid head. However, the water model (TIP3P) used, the additive formalism of the potential energy, and the uncertainty in the interpretation of the experimental data led us to assign relatively low weights to the RDF. Figure 8 plots the RDFs for the two optimizations, as well as C36. Global improved the RDFs for the phosphate ester oxygens (O11/O12), as their first peaks decreased toward the experiment. This trend was not observed for Linkage (C36/LJ-PME), because nonbonded parameters of the phosphate group were not allowed to change. The ester groups located at the head-tail link region were barely influenced in both optimizations. This is probably a consequence of the competition between the RDF and the surface area (more hydration in the head group region was needed to expand the membrane in the x-y plane). However, there was a shift to the left for the O22/O32 peaks, which was directly due to the decreased van der Waals radius.

Figure 8.

Atom-pair-specific RDFs between water and C₃-PC in solution for each optimization cycle.

3.6. Parameter Evolution.

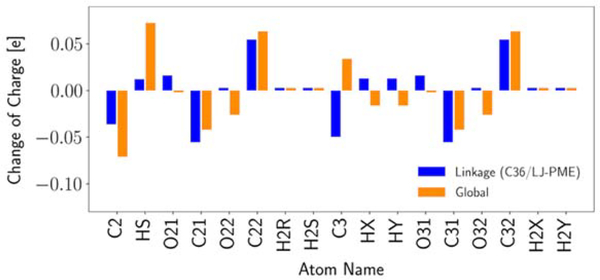
For both optimizations, only nonbonded parameters for the PC head were adjusted. Evolution of these nonbonded parameters are presented in Table S5–S7. All of these parameters were generated by the optimizer directly and not manually adjusted. In Global, changes in the last two optimization cycles are in the same direction as the first cycle but with smaller sizes for most partial atomic charges. For ε, changes are only seen in the first and the second optimization cycles and mostly in the direction of decreasing the well depth. However, no change is observed for the last optimization cycle because of the larger weights and the relatively weak sensitivities. The most interesting part is the oscillation of R_min/2 for O21/O31 and O22/O32, which are the ester and carbonyl oxygens from the ester linkage. Since the O22/O32 R_min/2 has a great influence on the surface area, the oscillation is consistent with the change in the surface area (Table 4). However, the oscillation in O21/O31 R_min/2 is probably more stochastic because of its weak sensitivity. R_min/2 for O13/O14 was modified after cycle 2 according to our interim validation on PG lipids (not published) so that it should be viewed differently. In Linkage, there are more oscillations in the partial charges between the two cycles rather than the consistent trends observed in Global, but the relatively small changes in the second optimization cycle indicate that the final parameter set is very close to the local optimum. In terms of LJ parameters, the biggest changes are for the O22/O32 R_min/2 (decrease) and the O21/O31 R_min/2 (increase), which improve the surface area and the RMSD of RDF, respectively. To compare the partial charges from the two optimizations, Figure 9 plots their changes with respect to C36. Overall, the changes are small. The most evident differences are for HS, C3, O22/O32. While the first two can be explained by the different rules of charge transfer during the optimization (Table S2) and their relatively weak influences on the surface area, the difference in O22/O32 is more likely a consequence of constraining the parametrization to the linkage region and the use of RDF RMSD as the fitting target, which led to more decrease in the O22/O32 R_min/2 in Linkage. Since the decrease in the O22/O32 R_min/2 has a similar effect as the decrease in the O22/O32 charge (in terms of the surface area), less change in the O22/O32 charge is needed in the end.

Figure 9.

Partial charge changes relative to C36. Only parameters from the linkage region are presented.

In principle, the optimization protocol can be set to terminate automatically according to a preset convergence criterion, for example, a threshold for a function using the relative error of the target properties and the change of the parameters as inputs. However, there are many properties involved in this parametrization and, therefore, determining a general meaningful threshold beforehand is not practical. This led us to use human interruptions when the properties are satisfactory according to our experience. However, the program can be easily modified to allow automatic termination if needed.

4. Discussion and Conclusions

In this paper, a semi-automated approach (FFLiP) for optimizing the CHARMM additive lipid FF is presented. The motivation for the optimization is to incorporate long-range Lennard-Jones terms into the FF to obtain consistent surface tensions for lipid bilayers and monolayers, thereby resolving the inconsistency in C36 in the treatment of mono- versus bilayers. The optimization focused on the nonbonded parameters of the PC head group and associated torsions. Unlike the early developments of the CHARMM lipid FF, which started from parametrizations of small model compounds, our method additionally takes advantage of thermodynamic reweighting to estimate the first derivatives of membrane-related properties with respect to parameters of interest and iteratively changes the parameters to generate better predictions for these properties. Compared to the conventional method, which may take months or longer to parametrize a single lipid, the new method only takes a few weeks to find high-quality parameters for several lipids at the same time, and it can be modified easily to include more lipid types as long as experimental data are available.

Due to the large number of parameters, FF parametrizations are often underdetermined. In the current study, we avoid this by using parameter restraints. Since the CHARMM nonbonded parameters were carefully parametrized targeting high-level QM data and condensed phase experimental data to directly address the parameter correlation problem [92], it is expected that these restraints will minimize overfitting. However, the choice of weight factors and the statistical errors from both simulation and experiment can still introduce arbitrariness in a fully automated optimization. Therefore, we adopt a semi-automated approach in which we can monitor the optimization in real time and adjust the weight factors and parameter restraints if needed. Such manual interruptions do not influence the speed of optimization if the workflow is set up properly.

Despite the efficiency of the method, it should be used with care if there is a potential phase change, a concern in lipid bilayer simulations, or a large structural change when parametrizing a macromolecular FF. In such cases, the trajectory sampled by the simulation may not contain enough or any useful information of the target state, so that a meaningful evaluation of the parameter sensitivity is not guaranteed. It should also be noted that most gradient-based optimization algorithms are only capable of finding the local minimum rather than the global minimum. In other words, the user must have an informed initial guess for the parameters to initiate the optimization. However, once having one, the method can be applied to improve the force field in agreement with newly published experimental data or state-of-the-art simulation protocols such as LJ-PME. Here the C36 parameter set was an excellent starting point because it was parametrized carefully to match experimental measurements of various membrane properties and adding LJ-PME to it will does not represent a large change in the energy function, though it does require the parameters to be adjusted to maintain agreement with experimental data. Although not tested, another a potentially good starting point could be a set of user-defined parameters that match high-level QM calculations for the building blocks of lipids with additional parametrization to include intramolecular parameters combining these blocks (a commonly accepted procedure of modern FF development).

When using the method, settings in the reweighting and the optimizer have to be carefully considered. First, because of the non-linear nature of the optimization problem, perturbation size used in the reweighting should be carefully determined by checking the behavior of the property with respect to the parameter changes in order to generate meaningful first derivatives. This can be done at both the reweighting and the simulation level. While additional simulations can provide direct measurements to avoid insufficient conformational overlapping which can cause trouble in the reweighting, they usually come with larger statistical errors so that using them can be a waste of computational resources. When using direct reweighting, the uncertainty of sensitivity can be estimated using trajectory blocks. After obtaining the sensitivity, the optimizer should be set properly to prevent unreasonably large changes of the parameters. This can be achieved by adding restraints to the parameters. The restraints in our protocol are determined by checking the size of the linear region and the standard deviation of the parameter sensitivity, and by enforcing consistency with the CHARMM FF as a whole.

A linear matrix equation is used to predict the iterative refinement of the nonbonded parameter set in this study. For dihedral optimizations, the BFGS algorithm is used, which searches the parameters by estimating the Hessian matrix based on the first derivatives. Considering the fact that the number of nonbonded parameters is larger than the number of observables, the linear equation is underdetermined without extra restraints. However, by adding parameter restraints, it becomes overdetermined so that a least-squares solution can be found. An alternative method to this can be the Levenberg-Marquardt algorithm [47, 57], which applies a damping term to the parameter change when doing a least-squares fit. In our case, the parameters are not expected to change dramatically so that a linear approximation to the first derivative can be used. However, when searching in a larger parameter space or in certain situations where it is hard to get meaningful parameter sensitivities, derivative-free algorithms such as the simplex method should be considered [58].

After two or three optimization cycles, parameters were obtained that allow for the CHARMM lipid FF to be used in conjunction with LJ-PME. This represents an important breakthrough as it eliminates the sensitivity of the FF to the specific treatment of truncation of the LJ terms, including how to treat the long-range dispersion contributions. The resulting parameter set yielded strong agreement with a number of experimental observables. S_CD and S_CH are in good agreement with experiment for both the head group and the tail regions. The optimization also takes the atom-pair-specific RDFs between C₃-PC and water into consideration and improvements are observed. These RDFs mostly measure the short-range interactions between water and lipid atoms, and the inclusion of long-range dispersion is not expected to influence them in a fundamental way without additional parametrization. Most importantly, C36/LJ-PME achieves very good agreement with experimental DPPC monolayer pressure/area isotherm, while the accuracy for bilayer surface area is maintained with respect to the original C36 force field without LJ-PME. This is a significant improvement over C36. Monolayer simulations with C36/LJ-PME can now be compared directly with experiment without adjustment for long-range Lennard-Jones interactions, thereby greatly expanding the kinds of lipid systems that can be examined. Specifically, monolayers are often stable at lipid concentrations, temperatures, pH and ionic strengths that bilayers are not. For example, the molar fraction of the highly charged lipid, phosphatidylinositol 4,5-bisphosphate (PIP₂), is typically less than 5% on average in cell membrane [93], though concentrations in local clusters can be much higher [94]. In experiment, the limit for PIP2 incorporation into bilayer vesicles with PC lipids is approximately 20% [95, 96]. Cholesterol has a stabilizing effect on PIP2 vesicles, but this requires a minimum cholesterol fraction of 20 mol% [96]. In contrast, monolayers can be formed with 100% PIP₂ [97–99]. Another example is phosphatidylethanolamine (PE), for which pure monolayers can be formed [100, 101] but bilayers only exist in a narrow range of hydration [102]. In fact, the large spontaneous curvature of PE promotes the inverse hexagonal (H_II) phase under more physiologically relevant conditions (in this case, full hydration).[102]

It is also important to benchmark the impact of r_cut on the accuracy and the computational cost of the LJ-PME algorithm. Leonard et al. [27] have shown that LJ-PME is relatively insensitive to r_cut and a value as low as 9 Å may be used for pure alkanes. Since alkanes are particularly sensitive chemical species to long-range dispersions, it is expected that any r_cut beyond 9 Å would be suitable for membrane simulations. Table S8 lists the A_l of DPPC bilayer at 323.15 K for different r_cut. It is evident that all r_cut beyond 8 Å produced statistically the same A_l. Considering the consistency of the entire FF, a r_cut of 10 Å is recommended, which yields a simulation speed of 179 ns/day on a single NVIDIA V100 GPU in OpenMM 7.4.1 (2 fs timestep, 15924 atoms). This is 10 ns/day faster than conventional LJ interactions with a force-switching function ranging from 8–12 Å (when other settings remain the same).

The revised force field will be referred to as C36/LJ-PME. To minimize the change with respect to the C36 lipid FF and to maximize the consistency of the CHARMM FF, the Linkage parametrization will be the formal LJ-PME version of the C36 lipid FF and will be available through the program CHARMM, Klauda web site and http://mackerell.umaryland.edu/charmm_ff.shtml. The result from the Global parametrization can be accessed by contacting the authors. While this paper focuses on the optimization problem, Paper II will provide a more extensive validation for the new parameter set.

Figure 2.

Chemical structure of DPPC and model compounds used for dihedral fitting: propylmethyphosphate (PMP), an esterfied glycerol-phosphate analogue (EGLY). isopropylbutyrate (IPB), and propylbutyrate (PB). The CHARMM residue names shown in parenthesis. See Figure S1 for full atom notation including hydrogens.