At the boundaries of syntactic prehistory

Abstract

Can language relatedness be established without cognate words? This question has remained unresolved since the nineteenth century, leaving language prehistory beyond etymologically established families largely undefined. We address this problem through a theory of universal syntactic characters. We show that not only does syntax allow for comparison across distinct traditional language families, but that the probability of deeper historical relatedness between such families can be statistically tested through a dedicated algorithm which implements the concept of ‘possible languages’ suggested by a formal syntactic theory. Controversial clusters such as e.g. Altaic and Uralo-Altaic are significantly supported by our test, while other possible macro-groupings, e.g. Indo-Uralic or Basque-(Northeast) Caucasian, prove to be indistinguishable from a randomly generated distribution of language distances. These results suggest that syntactic diversity, modelled through a generative biolinguistic framework, can be used to provide a proof of historical relationship between different families irrespectively of the presence of a common lexicon from which regular sound correspondences can be determined; therefore, we argue that syntax may expand the time limits imposed by the classical comparative method.

This article is part of the theme issue ‘Reconstructing prehistoric languages’.

1. Introduction

An unresolved problem of historical linguistics is how much similarity is required to demonstrate language relatedness when regular sound correspondences are absent, i.e. when one lacks the standard tool for scientifically grounding lexical etymologies. Even the success of modern quantitative approaches to phylogenetic linguistics ([1] and [2] and all successive work) is in fact based on—and delimited by—this classical tool.

Historical linguists have explicitly stated the need for new methods to address the relatedness issue [3–5], in order to provide classifications deeper than traditional etymological families [6,7]. We propose a way to tackle this long-standing issue by combining the Parametric Comparison Method (PCM, [8–10]) with a theory of possible languages (see [11]) and with dedicated statistical tools.

Within the minimalist biolinguistic program [12–15], a lot of focus has shifted from the ontogeny to the phylogeny and evolution of language, but little has been done to address the problem from the bottom, i.e. starting from comparing historically attested grammars. The PCM compares languages on the basis of non-lexical characters provided by formal biolinguistics and computational theories of mind [16–18]. Since the 1980s [19], formal approaches to grammar have encoded syntactic differences as opposite states of universal binary features, called grammatical parameters, which define the availability (versus the absence) of specific morpho-syntactic properties in each particular language. Such states can be used to set up correspondence sets [20] and as potentially universal taxonomic characters [21]. Since languages can be represented as strings of binary features, they can be compared by means of distance metrics.

In the most up-to-date PCM study [10], phylogenetic experiments have been produced from a parametric dataset of modern languages belonging to 13 traditionally irreducible families. Virtually all taxonomic experiments were able to single out all these families, along with most of their internal articulations, as safely established through etymological methods, proving the existence of a historical signal in parametric syntax.

However, for the prehistoric relations among the deepest established families, there is no independent linguistic standard against which one can assess the signal of the PCM. Therefore, in this article, we formulate purpose-specific statistical tools to complement phylogenetic algorithms and determine the significance of syntactic similarity, represented in the form of numerical distances; this procedure was inspired by the literature on significance testing of language relatedness [3,6,22–25].

Elaborating on Bortolussi et al. [26], we first generate the class of theoretically possible languages predicted by a parameter system; then, we compare random samples of these possible languages with chosen samples of real-world languages. This way, we determine whether the distances drawn from real-world languages can be expected to arise by chance.

We conclude that parametric syntax can provide a methodology to discriminate between significant long-range taxonomic hypotheses and insufficiently substantiated ones.

2. Materials

In the present article, we use a dataset of 94 syntactic parameters, a slightly updated version of that of Ceolin et al. [10], with values assigned in 58 modern languages from 15 traditionally different families of the Old World. Information and references about the languages and the parameter states, along with exploratory analyses and phylogenetic modelling of the data, are shown in the electronic supplementary material.

An important property of this type of data is that many parameter states turn out to be predictable, or completely irrelevant, given the states of other parameters [27–29]; this interdependence structure neutralizes nearly 40% of the taxonomic input (see electronic supplementary material).

3. Methods

(a). Proving the relationship between languages and language families

The statistical procedures traditionally adopted in historical linguistics (e.g. [3,6,22,23,25,30]) aim at providing proofs of relatedness by showing that the similarities observed between two languages cannot be expected to arise by chance. These procedures use meaning lists [31] to calculate the number of sound correspondences [3,22,30] or the amount of phonological similarities [6,23,25] among words which share the same meaning in different languages. In order to estimate the number of correspondences or similarities that one expects to find by chance, these measurements are subsequently applied to lists where words and meanings are re-matched at random, using a Monte Carlo resampling method. If the amount of correspondences or similarities found by re-arranging the word–meaning association is significantly lower than that found in the original lists, then one can prove that two languages are related.

The implicational structure of syntactic parameters drastically reduces the amount of possible combinations of their values: the combinations generated from a set of interdependent parameters are much fewer than the combinations that would be generated if they were not interdependent [26]. Thus, the strategies for statistical testing traditionally adopted on word lists cannot be replicated on parameter systems, because an algorithm that does not take into account parameter implications would also generate impossible languages; rather, we need an algorithm that recombines the parameter values of the languages in the dataset (conventionally expressed as ‘+’ and ‘–’) ensuring that the implicational structure of the parameters is not violated [32]. The implicational constraints operating on the 94 parameters were hard-coded in the algorithm, so that if a combination of parameter values neutralizes other parameters, the latter are assigned a ‘0’, which in the dataset represents neutralized values. At each run, a simulated language is generated by assigning a ‘+’ or a ‘−’ to each parameter, sampling from the probability distribution of ‘+’ and ‘−’ inferred from the real families of the dataset. To remove any bias towards the numerically more represented families, the probability of ‘+’ and ‘−’ for each parameter has been calculated within each of the families; the average of such probabilities is then used to set the parameters in the simulated languages (see electronic supplementary material). Finally, a distance metric is used, as a test statistic, to measure similarity among strings of parametric values.¹ Note that most languages of our sample are from Eurasia: one may object that this could bias our results, due to potential similarities widespread across the same macro-continent (e.g. due to migration bottlenecks and/or successive drifts). Yet, since possible languages are modelled on the diversity found within this very sample, to pass the test, two families will have to exhibit further similarities in addition to specific continent-wide typological patterns. This helps make our test stringent enough to correct for such a bias, and more conservative than others sometimes used to argue for genealogical relationships (e.g. [34]).

(b). Multilateral comparison

While there is a large literature on pairwise significance testing, the question of how to compare ‘groups’ of languages (e.g. ‘multilateral comparison’, in Greenberg's sense [35]) is less obvious. Yet, a proper handling of this issue is very important in view of the reliability of the phylogenetic conclusions [3]. One possibility is to use reconstructed proto-languages, and test whether two language families are related by checking if the two proto-languages pass a pairwise significance test [24]. An alternative is to run many different pairwise tests [36]. A third possibility, proposed by Kessler & Lehtonen [6], is to adapt the test statistic from a pairwise to a multilateral comparison setting: rather than using a measure of similarity between two languages, one can use the average of all pairwise cross-family comparisons between two groups of languages already known to be internally related.²

For the purposes of this article, we adopt Kessler & Lehtonen's test and address the question of whether groups of languages that are suspected to represent a unique family pass a significance test, i.e. yield average internal distances lower than those we see among artificially generated languages. Note that comparing sets of languages (even descending from a single ancestor) rather than single languages, whenever possible, may in principle help lower the risk of chance similarities generated by accidental outliers.

Kessler and Lehtonen's algorithm can be applied recursively. Every time we find that two groups of languages are related, we can consider them as a single family and test if this family is related to other groups of languages. The procedure starts from the two groups in a sample that exhibit the lowest value for the test statistic (the average distance, in our case), subject them to the test and then merge them together in the case they pass the test. Then, one can recalculate all the distances between the groups which are left (including the new group), and test whether the groups exhibiting the smallest distance are related. The procedure stops when none of the group pairs left exhibits a distance that can be considered significant.

In practice, the procedure works like a clustering algorithm of the Neighbor-Joining type [37], with the important difference that whenever the distance exhibited by two nodes cannot be considered significant, the algorithm stops (rather than ‘forcing’ all the taxa into a binary branching tree).

(c). Artificial and observed distances

We calculate the distance between each pair of the real-world languages of our sample (henceforth ‘Observed Distances’) by means of a Jaccard formula (see electronic supplementary material), which is our estimate of the closeness of two languages (i.e. our test statistic).³ Then, we generate a large group of possible languages and we calculate the Jaccard distance of each pair that such a group contains (henceforth ‘Artificial Distances'). This way, we can compare the two sets of distances. We follow Kessler & Lehtonen [6], setting α = 0.05 as our significance threshold for the statistical test.

4. Results

(a). Artificial distances

We have randomly generated 5000 possible languages, a number roughly comparable to that of current human languages, obtaining approximately 12 million distances. The median of the Artificial Distances is 0.476, and the mean is 0.487. The 5th percentile is at 0.3, i.e. 95% of the Artificial Distances have a value higher than 0.3. This means that any pair that falls below this threshold can be associated with p < 0.05, i.e. the likelihood of obtaining such a low distance under the null hypothesis (non-relatedness) would be less than 5%. Any distance below the 0.3 threshold, then, is considered significantly small by our test. In the following sections, we calculate the distances among groups of languages, and assign them a p-value based on their position with respect to the distribution of the Artificial Distances.

(b). Observed distances

Our sample of 58 real languages generates a total of 1653 distances. These distances have a median of 0.444 and a mean of 0.426. As could be expected, both the mean and the median are lower than that of the Artificial Distances.

Henceforth, we apply our test to some empirical subcases. First, we generate a phylogenetic tree using the clustering algorithm UPGMA [39], which is a version of Neighbor-Joining, from our Observed Distances (see electronic supplementary material, figure S2). Then, we take the lower-level groupings represented in the UPGMA tree for granted (i.e. the main subfamilies of Indo-European (IE) and Finno-Ugric, as well as Turkic, Tungusic, Northeast Caucasian, Dravidian, Semitic, Sinitic and the two varieties of Basque), and we subject to our test, in turn: the internal articulation of IE (§4c) and of Finno-Ugric (§4d); the other long-distance groups suggested by our tree (§§4e–g); finally, some other controversial groupings proposed in the literature (§4h).

(c). Indo-European

Our dataset contains 28 IE languages, distributed in six subfamilies (Romance, Greek, Germanic, Celtic, Slavic, Indo-Iranian). For each pair of these subfamilies, we infer an average distance through the following procedure: we take the Jaccard distance between every language of a subfamily and each of those of the other subfamily (thus abstracting away from subfamily internal pairs); then we calculate the average of this set of distances in agreement with Kessler & Lehtonen's [6] procedure described above. Next, we cluster together the subfamilies exhibiting the smallest significant distance, in a recursive way. We obtain the following results:

• Germanic/Slavic, d = 0.205, p = 0.005.

• Germanic-Slavic/Greek, d = 0.244, p = 0.013.

• Greek-Slavic-Germanic/Romance, d = 0.277, p = 0.028.

• Greek-Slavic-Germanic-Romance/Indo-Iranian, d = 0.296, p = 0.043.

• *Greek-Slavic-Germanic-Romance-Indo-Iranian/Celtic, d = 0.324, p = 0.073.

Three out of the five groups obtained exhibit cross-family distances clearly below the significance threshold of 0.3. The average distance between Indo-Iranian and the immediately preceding group falls right below the threshold. On the contrary, the average distance between Celtic and this latter group falls above it. This unexpected result will have to be reconsidered later in the section, after some further data elaboration.

(d). Finno-Ugric

For Finno-Ugric, we sampled six languages, belonging to four recognized groups (Balto-Finnic, Ugric, Volgaic and Permic). The closest groups are Volgaic and Permic (d = 0.048). By using the same hierarchical clustering technique as above, we obtain:

• Volgaic/Permic, d = 0.048, p < 0.001.

• Volgaic-Permic/Balto-Finnic, d = 0.225, p = 0.009.

• Volgaic-Permic-Balto-Finnic/Ugric, d = 0.275, p = 0.028.

All these groups show a distance lower than the significance threshold. The Finno-Ugric unity is thus fully recognized.

(e). Altaic

Our sample contains 11 languages sometimes ascribed to a macro-Altaic (or Trans-Eurasian, see [40]) stock, divided into five well-established groups: Turkic [41], Mongolian [42], Tungusic [43], Korean [44] and Japanese [45]. Whether these groups form less than five separate families, and, if so, how many, is controversial [40,46–54]. Our reference tree acknowledges two relevant clusters from these languages: one comprising Tungusic and Turkic, and then adding Buryat (Mongolian), and a separate one with Japanese and Korean. If we test the groups recursively, as above, we obtain the following results:

• Korean/Japanese, d = 0.182, p = 0.003.

• Tungusic/Turkic, d = 0.158, p = 0.002.

• Tungusic-Turkic/Buryat, d = 0.223, p = 0.009.

These figures show support for a connection between Japanese and Korean [55,56] and for the more classic, though still controversial, ‘micro-Altaic’ including only Tungusic, Turkic and Mongolian, which displays a mean even lower than Finno-Ugric (see [57]).

(f). Uralo-Altaic

The next macro-family our tree points to, Uralo-Altaic, is also far from established, although it has been suggested in the literature [58–61]. By comparing the cross-family distances between ‘micro-Altaic’ and the Finno-Ugric languages, one obtains the following result:

• *Balto-Finnic + Volgaic-Permic-Ugric/Tungusic-Turkic-Buryat, d = 0.307, p = 0.054

At first glance, this result appears to fall above the significance threshold. However, the sampling algorithm originally inferred a plausible distribution of possible languages under the non-committing hypothesis that the five families ascribed to macro-Altaic were five independent data points; now the results of our experiment reduced them to only two (a Japanese/Korean unity and ‘micro-Altaic’). We must then build this information into the algorithm for modelling possible languages and thus Artificial Distances: as a result, the median goes up to 0.5 (with a mean of 0.497), and the significance threshold rises to 0.316, which includes the average distance between the Uralic and Altaic languages of our sample. This new result is due to the fact that the algorithm was over-sampling artificial languages with an Altaic bias (cf. §3a). When we consider Japanese/Korean and ‘micro-Altaic’ as two families (instead of five), then Uralo-Altaic becomes a statistically plausible macro-family too.

In turn, once all Uralic and all three ‘micro-Altaic’ families are considered as a unique family in the algorithm for the generation of possible languages, the significance threshold rises to 0.333. A notable outcome is that this more accurate threshold now suffices to also include Celtic within IE.⁴

Next, we find in the tree a node clustering the whole of Uralo-Altaic with Yukaghir; the distance associated with this node tests above the threshold, even if we consider the updated one:

• *Uralo-Altaic/Yukaghir, d = 0.342, p = 0.103.

(g). The other macro-clusters in our tree

Our tree also proposes some macro-clusters which are not normally considered in the literature. The first we test concerns Northeast (henceforth, NE) Caucasian and Dravidian, which appear consistently together in all the analyses of the distance matrix (see electronic supplementary material). The two families indeed exhibit an interfamily distance well below the significance threshold:

• NE Caucasian/Dravidian, d = 0.263, p = 0.024.

This result needs some attention, of course, and will be briefly discussed below. Although the tree suggests a further connection between this group and IE, this connection does not pass the test:

• *IE-Dravidian-NE Caucasian, d = 0.385, p = 0.195.

Finally, two other groups that emerge from the UPGMA tree are Basque/Japanese-Korean and Wolof/Cantonese-Mandarin. However, both groups clearly test negatively:

• *Basque/Japanese-Korean, d = 0.5, p = 0.619.

• *Wolof/Cantonese-Mandarin, d = 0.4, p = 0.250.

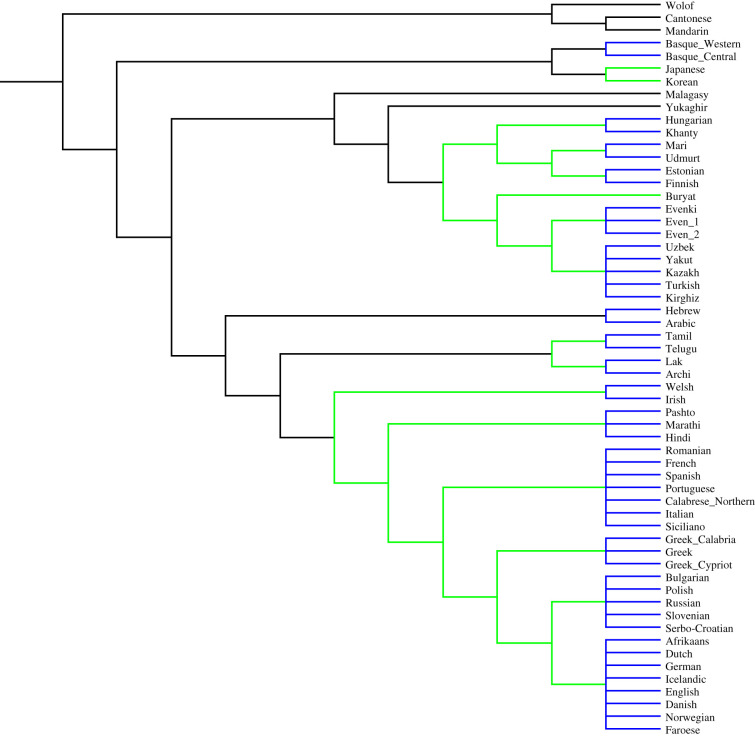
The results of this section are summarized in figure 1.

Figure 1.

A UPGMA tree calculated using our syntactic distances. The groups of languages which have been used as an input for the test (which are then represented under a unique node) are in blue, while the branches which have been shown to be related by the test are in green. The relationships in these green branches can be considered ‘validated’ by both our statistical test and the UPGMA clustering algorithm.

(h). Some macro-families suggested in the literature

There exist other macro-families proposed in the literature, though they do not appear in the clusters recognized by UPGMA. Interestingly, none of them tests positive.

The most salient is, indeed, ‘macro-Altaic’ (above and [10]):

• *Tungusic-Turkic-Buryat/Korean-Japanese, d = 0.606, p = 0.842.

Another hypothesis is that Uralo-Altaic and Dravidian languages, along with Eskimo-Aleut, form a ‘Borean’ macro-family [51]). This hypothesis is also ruled out by the test:

• *Uralo-Altaic/Dravidian, d = 0.411, p = 0.260.

In the macro-comparative literature, Yukaghir has also been proposed to be part of a larger macro-family. In particular, it has at least been hypothetically connected just to Uralic (e.g. [62–69]). Our test, though, fails to hint at this unit:

• *Finno-Ugric/Yukaghir, d = 0.386, p = 0.204.

As for the possible relatives of IE, one of the longest discussed macro-groups is Indo-Uralic, even though most of the attempts to prove it have yielded a negative result [6,70] (but see [71] for a positive test). The test provides a negative result too:

• *Indo-European/Finno-Ugric, d = 0.493, p = 0.510.

Alternatively, IE has also been grouped with Semitic (e.g. [72–80]). This hypothesis also fails the test:

• *Indo-European/Semitic, d = 0.398, p = 0.216.

Other groups more recently and occasionally suggested in the literature [81–88] also test negatively:

• *Basque/Cantonese-Mandarin, d = 0.75, p = 0.972.

• *Basque/NE Caucasian, d = 0.544, p = 0.687.

• *Cantonese-Mandarin/NE Caucasian, d = 0.75, p = 0.972.

If anything, the distances between the two Sinitic languages on the one side and Basque and the NE Caucasian languages on the other are even higher than we would expect from chance (cf. Guardiano & Longobardi's Anti Babelic Principle [89]). This is likely to result from the fact that the number of parameters actually comparable between the groups is very low (eight) due to the high amount of neutralized states, while on average, the other pairwise comparisons involve about 20 non-neutralized parameters. In this respect, the two Sinitic languages represent an outlier of the dataset.

(i). Areal effects

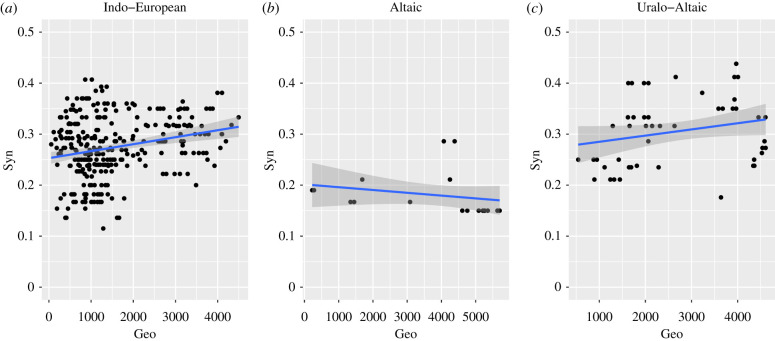
The possible impact of geographical proximity on syntactic similarity was tested through a Mantel correlation test (as in [90]) run on the numerically well-represented groups (IE, Altaic and Uralo-Altaic). The results are summarized in figure 2. First, we correlate syntactic and geographic distances (calculated as Great Circle Distances, GCD) within IE, using, as an approximation, the present-day language positions (cf. electronic supplementary material),⁵ so as to roughly estimate how much horizontal distribution of diversity can arise in a well-established family (also in competition with a strong vertical articulation of subfamilies, witnessed by syntactic experiments as well). We found that in IE the geography-syntax correlation is (weakly) positive: we retrieved τ = 0.133, p < 0.001 according to Kendall's rank correlation, r = 0.241, p < 0.001 with Pearson's linear correlation. We then plotted the Altaic syntactic distances with their corresponding geographic distances to ascertain if the effect of geography is stronger: the result is instead a negative correlation, according to Kendall's correlation (τ = −0.52, p = 0.002), and also according to Pearson's, even though in this case the result is not significant (r = −0.227 and p = 0.297). As for Uralo-Altaic, the correlation with GCD is comparable to that found within IE if we look at Pearson's correlation, and not significant (r = 0.238, p = 0.083), while it is only slightly higher according to Kendall's correlation (τ = 0.204, p = 0.034).

Figure 2.

Syntactic distances (y-axis) and Great Circle Distances (x-axis) for Altaic and Uralo-Altaic. (Online version in colour.)

5. Discussion

(a). Families and macro-families

Our statistical tests confirm that the syntax of languages which are known (IE, Finno-Ugric) or suspected (Altaic) to be related exhibits some similarity that cannot be explained by chance. Moreover, they support a deeper relation between Finno-Ugric and Altaic (so-called Uralo-Altaic), which has been previously proposed in the literature. On the contrary, the tests have returned no support, so far, for Indo-Uralic or for a macro-Altaic unit. Largely unsupported are other long-range hypotheses popular among some macro-comparativists: those connecting Basque to NE Caucasian, and the latter to Sinitic. Thus, our method achieves a result often missed by long-range attempts, i.e. it also provides negative results. Providing such a demarcation tool is very important, since the lack of attention to false positives has raised the most serious objections to the Nostratic framework and, in general, to long-range taxonomic efforts (cf. [3,70]).

A peculiar long-range connection has instead emerged from our experiments which may deserve some future attention: that between NE Caucasian (Nakh-Daghestanian or Caspian) and Dravidian. Diakonoff & Starostin [91] and Nikolayev & Starostin [92] have entertained the hypothesis that NE Caucasian could be related to the extinct Hurro-Urartian family.⁶ Diakonoff [95] classifies Hurro-Urartian and NE Caucasian as part of a family called Alarodian, a quite controversial (see especially [96]) group so baptised by Fritz Hommel in the nineteenth century and meant to also encompass the language of ancient Elam (western Iran), along with some others of the Near-East. Nichols [97, p. 208] states that ‘neither Diakonoff and Starostin, nor Nikolayev and Starostin, take on the burden of proof and discuss whether the incidence of resemblances exceeds chance expectation’, but even she accepts that NE Caucasian must have moved from a prehistoric dwelling south of the Caucasus. In roughly the same broad area, in turn, the hypothesis of a connection between Elamite and the present Dravidian languages has been even recently suggested (Elamo-Dravidian: see [98] and other works). Again, this theory has been criticized on the basis of the absence of classical types of evidence. The results of our method may modestly suggest that the (transitive) connection between (at least part of) the old Alarodian hypothesis and the Elamo-Dravidian one deserves some more investigation, whether there is any genealogical content to it or simply some hint of very strong prehistoric areal contact.

(b). Vertical and horizontal transmission

This point leads us to another issue. Syntactic distances, by themselves, may show that some languages are historically related (for a formal definition see [99], and [100]), without telling if the relation is ancestral or secondary. This problem is common to all non-standard taxonomic methods ([1] and [101]) and on some occasions, when loanwords are ancient or sound laws are few, even to the classical comparative method.

Previous PCM experiments [9,10,102] have found that the disruption of the syntactic phylogenetic signal by well-documented but relatively recent convergence and borrowing (i.e. the past 1000/1500 years) is quite limited (in agreement with [100,103]), even in domains where contact has otherwise strongly shaped other linguistic levels (the Balkans, Southern Italy, the Black Sea area).

Secondary relations normally arise in situations of geographic contact.⁷ This is why we tested the geography–syntax correlation to estimate the plausibility of areal contact as an exhaustive explanation of the Altaic and Uralo-Altaic similarity. The correlations were negative for Altaic, and weakly positive but barely significant, or non-significant, for Uralo-Altaic. In sum, geographical distances and contiguities of the historically documented times are no predictor of syntactic distances among Altaic languages and a very poor one for Finno-Ugric/Altaic pairs. Therefore, from this test, no evidence results that the statistically supported similarity of Altaic and Uralo-Altaic should be attributed to recent horizontal convergence, more than to ancestral unity or prehistoric community.

In any case, a major point achieved here is that the Uralo-Altaic syntactic similarity turns out to be more significant than the Indo-Uralic one. This is true in spite of at least three salient contact situations:

• 1. Between Balto-Finnic and Germanic continuously for at least the past 3000 years.⁸
• 2. Between Hungarian and surrounding IE languages, at least since the arrival of Magyars into Pannonia at the end of the ninth century.⁹
• 3. Between Volgaic and Permic (and reasonably Ob-Ugric) languages and Russian since at least the Russian conquest of Kazan in 1552.

All this was not sufficient for Indo-Uralic, which exhibited a distance of 0.493, to test positive. The distance would not be much lower if we considered Indo-Balto-Finnic instead (i.e. 0.475). Therefore, the syntactic relation between Uralic and Altaic must be more ancient but also deeper (i.e. longer, more intense or qualitatively different, e.g. ancestral) than between IE and Uralic.

Summing up, if convergence were solely responsible for the observed syntactic compactness of Uralo-Altaic, one should anyway conclude that the invoked population contact must have been much closer than retrievable from other types of analysis (phonemic analysis, geography and documentary sources), at that particular time depth. Then, formal syntactic theory, if anything, would capture (and measure) some very ancient contact relations better than the more recent and well-recorded ones, suggesting that they were extremely deep: this is a novel and informative result of its own, contributing to actual growth of historical knowledge.

(c). On the statistical method

Our method has allowed us to make precise hypotheses about the relationship among different language families, and to distinguish between hypotheses of relationships which are plausible and those for which accidental similarity cannot be excluded. This constitutes an important methodological step for the exploration of human prehistory.

In phylogenetic studies, it is common to use bootstrapping scores or posterior probabilities to evaluate the uncertainty of a clade. Therefore, a low score or a low posterior probability is often taken as evidence against the plausibility of a clade. However, phylogenetic algorithms are not typically used to prove language relationship, but to retrieve an internal articulation within an assumption of language relatedness. Moreover, the uncertainty associated with specific nodes is ambiguous: it may point to lack of similarity between two nodes (when the languages grouped together are quite different) but also to lack of distinction (because the languages are quite similar, but they are also similar to languages in other groups). This latter situation is frequent with syntactic parameters, owing to their limited number and binary values, and might often lead to low bootstrapping and posterior scores when they are used to produce phylogenies (see electronic supplementary material).

Nevertheless, one can still prove the relatedness of groups of languages which share distances that cannot be expected to arise by chance, distinguishing them from those that are just the by-product of the binary branching assumption. This is what allows our method to be used to investigate language prehistory. We claim that this enterprise cannot be pursued only by means of classical phylogenetic methods, but also requires realistic and sophisticated theories of language variation and purpose-specific tools for statistical testing.

We are aware that our statistical procedure can and must be strengthened by broadening both the number of parametric characters and the variety of the languages that provide the reference set for the distribution of syntactic diversity. We may also expect that some negative tests might become positive if the number of parameters and the number of languages increased (e.g. Uralo-Altaic/Yukaghir could turn positive, though perhaps just as part of some larger Nostratic or Eurasiatic unity); but, most importantly, it is less likely that the positive tests presented here will conversely be weakened by enlarged empirical coverage.

6. Conclusion

Phylogenetic linguistics and the science of long-term history have made a decisive leap forward in the past three decades thanks to the inauguration of a quantitative paradigm [1–3,6,7,70,108,109]. In this century, a radical qualitative change in the level of characters employed also began to be explored, based on developments in generative syntax and cognitive sciences [8–10]. In this article, we have shown that an interesting step forward in the study of language prehistory may be achieved by combining these two approaches to provide a long-sought solution to a core problem of taxonomic linguistics: working out a computable method for assessing relatedness between families against chance when etymological evidence is missing.

We agree, of course, that a full growth of knowledge in the domain of linguistic prehistory should eventually be pursued through careful attempts at stepwise reconstruction of ancestral features of supposed proto-languages and intermediate stages, and that this is true also of syntactic characters; methods for achieving this goal are being explored. However, a precise method for testing the significance of universally computable syntactic distances is already a breakthrough, because it can direct us towards the most appropriate choice of the long-range hypotheses which are worth further and deeper investigation.

Data accessibility

The code, data and information used to generate the figures and tables in the article can be accessed at https://github.com/AndreaCeolin/Boundaries (doi:10.5281/zenodo.4590104).

Authors' contributions

A.C., C.G., G.L. and M.A.I. wrote the manuscript. C.G. and G.L. conceived the linguistic method. C.G., G.L. and M.A.I. carried out the syntactic analyses. A.C. performed the simulations and the experiments. A.C., L.B. and A.S. conceived the statistical analyses.

Competing interests

The authors declare no competing interests.

Funding

This work was supported by the European Research Council Advanced grant no. 295736 ‘Meeting Darwin's last challenge: toward a global tree of genes and languages' (LANGELIN to GL), by MIUR PRIN 2017K3NHHY ‘Models of language variation and change: new evidence from language contact’ (to CG) and by UniMoRe FAR Impulso 2020 (to MAI).