Evolutionary perspectives on polygenic selection, missing heritability, and GWAS

Abstract

Genome-wide association studies (GWAS) have successfully identified many trait-associated variants, but there is still much we do not know about the genetic basis of complex traits. Here, we review recent theoretical and empirical literature regarding selection on complex traits to argue that “missing heritability” is as much an evolutionary problem as it is a statistical problem. We discuss empirical findings that suggest a role for selection in shaping the effect sizes and allele frequencies of causal variation underlying complex traits, and the limitations of these studies. We then use simulations of selection, realistic genome structure, and complex human demography to illustrate the results of recent theoretical work on polygenic selection, and show that statistical inference of causal loci is sharply affected by evolutionary processes. In particular, when selection acts on causal alleles, it hampers the ability to detect causal loci and constrains the transferability of GWAS results across populations. Lastly, we discuss the implications of these findings for future association studies, and suggest that future statistical methods to infer causal loci for genetic traits will benefit from explicit modeling of the joint distribution of effect sizes and allele frequencies under plausible evolutionary models.

Introduction

The past two decades have seen a remarkable burst of progress in our understanding of the structure of the human genome (Venter et al. 2001; IHGS Consortium 2001) and the mapping of worldwide genetic variation in human populations (International HapMap Consortium, 2003; TGP Consortium, 2012,2015). This progress was met with a great deal of optimism about the potential to discover the genetic basis of heritable, complex diseases. Indeed, the hypothesis known as “common-disease, common-variant” suggested that the genetic variation underlying many complex diseases should be at high frequency in human populations (Reich and Lander, 2001). If the underlying genetic risk variation was not at high frequency, how then to explain the prevalence of common diseases such as asthma and diabetes? The rationale that common variants are likely to drive most heritable variation in complex diseases led to the widespread adoption of Genome-Wide Association Studies (GWAS), which offer improved statistical power relative to linkage scans to discover high-frequency trait-associated variation in the noisy background of the human genome (Risch and Merikangas, 1996).

The GWAS approach has been largely successful from the perspective of discovering intermediate-effect variants at high frequency, each explaining a small proportion of variation in the trait. As of January 2017, 24,000 associated variants were included in the GWAS catalog, which curates robust associations between genetic variants and complex traits (MacArthur et al., 2017). These findings validate the relevance of the GWAS approach, and have improved our understanding of the genetic and molecular bases of complex traits (Manolio, 2010). However, from the perspective of predicting individual risk and population-level trait variance, the GWAS approach has been only moderately successful. While the gap between heritability estimates from genomic data and twin studies may be narrowing (Yang et al., 2015; Wainschtein et al., 2019), robustly associated variants seemingly explain only a small portion of the variance of most complex traits (see for example Nolte et al. 2017). This problem has been dubbed “missing heritability” in reference to the substantial difference between trait variance explained by genome-wide significant variants and estimates of heritability obtained by family-based studies (Manolio et al., 2009). Moreover, the prediction of disease risk from genetic variation (sometimes called polygenic risk prediction) performs fairly well for a small number of traits in well-studied European populations (Bellot et al., 2018), but has much worse performance in under-studied populations (Martin et al., 2017, 2019).

Several hypotheses have been advanced to explain missing heritability, including over-estimation of heritability by family-based studies (Zuk et al., 2012; Ruby et al., 2018), the high polygenicity of complex traits coupled with small effect sizes of most causal variants (limiting our ability to detect these weak effects;Yang et al. 2011), and selection against causal variants of large effect (constraining large effect alleles to low frequency, again hampering detection; Lohmueller 2014b). Most efforts to find missing heritability have focused on the statistical aspects of the problem by proposing new methods that can increase power (e.g., Loh et al. 2015), eliminate confounding by stratification or model-misspecification (e.g., Price et al. 2010b; Young et al. 2018), or detect multiple rare variants within a single locus (e.g.,Wu et al. 2011).

This review takes the perspective that missing heritability can also be viewed as an evolutionary problem. Indeed, each of the aforementioned hypotheses represents a claim about the evolution of complex traits. If heritability has been previously over-estimated, this suggests a deficiency in the additive model assumed in family-based heritabilty estimates, and that trait distributions within populations evolve through interactions between causal alleles or alleles and their environment (or, alternatively, are confounded by covariation with environmental variables; Vilhjálmsson and Nordborg 2012). High polygenicity would suggest that there is a large mutational target of loci in the genome that affect complex traits, suggesting that many variants have weak functional effects (Bulik-Sullivan et al., 2015; Boyle et al., 2017). In contrast, if rare alleles of large effect explain a substantial proportion of trait variance, this suggests that selection must act on causal variation to preferentially constrain the evolution of large effect alleles, inducing a negative correlation between allele frequencies and effect sizes. A growing body of theoretical and empirical work now shows that each of these evolutionary processes can affect the detection of causal variation for complex traits (King et al., 2010; Zuk et al., 2014; Lohmueller, 2014b; Moutsianas et al., 2015; Uricchio et al., 2016; Sanjak et al., 2017a;Simons et al., 2018).

While these evolutionary hypotheses are not mutually exclusive and each may contribute to missing heritability, our focus herein will be on the role of selection in shaping complex trait variation, and its effect on detecting alleles that drive variation in complex traits. Growing interest in this topic has been driven by the suggestion that complex traits are likely to be targets of selection (e.g.. Berg and Coop 2014; Field et al. 2016), and an emerging literature that seeks to infer signals of selection from GWAS summary data has arisen (Guo et al., 2018; Prohaska et al., 2019). Much less attention has been given to the effect of selection on inferred GWAS summary statistics themselves - most studies attempting to infer selection have assumed that GWAS summary statistics are unbiased (e.g., Field et al. 2016; Racimo et al. 2018; Uricchio et al. 2019), but recent work suggests that both demography (Berg et al., 2019; Sohail et al., 2019) and selection (Lohmueller, 2014b) may have substantial effects on both type I and type II errors in association studies, even when efforts are made to correct for stratification. Here, we review evolutionary signatures of selection acting on complex trait variation (including negative selection, stabilizing selection, and polygenic adaptation), which may be detectable in GWAS trait data, and explore the evidence for selection on complex traits provided by empirical studies of complex trait variation. We then consider the implications of existing literature for studies attempting to detect causal variation for traits, and apply a simulation framework that includes genome structure, selection, and recently-inferred human demographic models to illustrate these findings. Lastly, we discuss open questions in the field, especially with regards to the detection of genomic loci harboring rare variants of large effect.

Results & Discussion

What do we (think we) know about selection and complex traits?

Variance induced by causal alleles for additive traits

Complex traits have typically been modeled under an infinitesimal additive model (Barton et al., 2017), in which variance in the trait (V_T) is driven by the sum of environmental (Ve) and genetic (V_G) components,

$$V_T=V_G+V_E.$$ (1)

The number of genes contributing to the additive genetic variance is assumed to be large, such that each allele has a small effect on the phenotype. This framework makes several additional assumptions, including a lack of interactions between the environmental and genetic components or between different genomic loci - these assumptions are unlikely to be universally true (Zuk et al., 2012), but here we focus on additive models. Heritability is then defined as the ratio of the variance due to genetics to the total trait variance, $h^2=\frac{V_G}{V_T}$.

Under this simple model, it is straightforward to compute the genetic variance as a sum over the contributions from individual causal alleles. First, we assume that each derived allele is either non-causal, in which case its effect size is 0, or causal, in which case its effect size β is drawn from some distribution f(β). Hence, individuals who are heterozygous for the causal allele have their phenotype ø modified by β relative to individuals who are homozygous for the ancestral allele, while individuals who are homozygous for the derived allele will have their phenotype modified by 2β. Causal loci are assumed to be in linkage equilibrium with other causal loci. If the causal allele is additionally assumed to be in Hardy-Weinberg equilibrium and to segregate at frequency x in the population, then the variance induced by this allele is

$$V_{\beta }(x)=2x(1-x){\beta }^2+x^2{(2\beta )}^2-{\left[2x(1-x)\beta +x^2(2\beta )\right]}^2=2x(1-x){\beta }^2.$$ (2)

Calculating the total genetic variance requires summing over all frequencies x and the distribution of effect sizes.

$$V_G=2\sum _x\mathbb{E}\left({\beta }^2\mid x\right)\text{Ψ}(x)x(1-x),$$ (3)

Where $\text{Ψ}(x)$ is the number of variants segregating at frequency x and $\mathbb{E}\left({\beta }^2\mid x\right)$ is the expected value of the squared effect sizes of alleles segregating at frequency x (Uricchio et al., 2016). Note that this sum implicitly assumes causal alleles act independently and are not in linkage disequilibrium with other causal alleles (though they may be in linkage disequilibrium with sites that that do not harbor causal alleles). In the absence of any selection (which may act either on the trait itself, or on a trait with a shared genetic basis), the mean-squared-effect size is the same at all values of x, because the probability that any given allele segregates at frequency x is independent of its effect size. Hence, this term can be moved outside of the sum and evaluation of the genetic variance is trivial up to a constant factor corresponding to the distribution of mutant effects.

Models of selection acting on complex traits

A wide range of evolutionary models suggest that selection on causal variation will induce a negative correlation between effect sizes and allele frequencies (Turelli, 1984; Pritchard, 2001; Pritchard and Cox, 2002), meaning that the sum in eqn. 2 may become non-trivial to evaluate. The magnitude of this correlation, and more generally how effect sizes are jointly distributed with allele frequencies, depends on the strength of selection (Eyre-Walker, 2010), the mode of selection (i.e., whether selection is stabilizing (Simons et al., 2018) or purifying (Eyre-Walker, 2010)), and other evolutionary processes such as genetic drift, linkage (Gazal et al., 2017), population demography (Gazave et al., 2013; Lohmueller, 2014b,a), and the degree of pleiotropy with other traits (Simons et al., 2014, 2018). Hence, both $\text{Ψ}(x)\text{ and }\mathbb{E}\left({\beta }^2\mid x\right)$ in eqn. 3 are affected by these evolutionary processes. However, the negative correlation between effect size and selection strength is predicted to some degree by all of these models regardless of these complexities. Notably, most models of trait architecture employed in statistical genetics research have not directly incorporated the effects of these evolutionary processes (Ragsdale et al., 2018).

Models of selection against complex traits have fallen into at least two broad categories, including mechanistic evolutionary models and phenomenological evolutionary models. Mechanistic models propose a specific quantitative relationship between trait values and organismal fitness. The most widely-used mechanistic models derive from the stabilizing selection framework (Robertson, 1956; Barton, 1986), in which it is assumed that a particular trait value confers optimal fitness, while individuals with trait values that are either larger or smaller than the optimum have reduced fitness (Fig. 1A). While any uni-modal function could define the response to selection, most previous work has assumed that the fitness function has a Gaussian shape. Under this model, the population mean tends to be close to the optimal trait value. If the population mean is not located at the optimal trait value, selection will tend to pull the trait distribution back towards to the optimum (Fig. 1A). Stabilizing selection models have several appealing features - first, they offer an intuitive mechanism for explaining the maintenance of variation. Second, stabilizing selection models can naturally accommodate changes in environmental selection pressures resulting in polygenic adaptation (Jain and Stephan, 2017;Stetter et al., 2018). Third, stabilizing selection models can be extended to accommodate selection on multiple traits in a higher-dimensional space (Lande, 1980;Simons et al., 2018). However, there is no general theoretical justification for the commonly-used Gaussian function as the determinant of fitness in response to deviation from the optimal phenotype value.

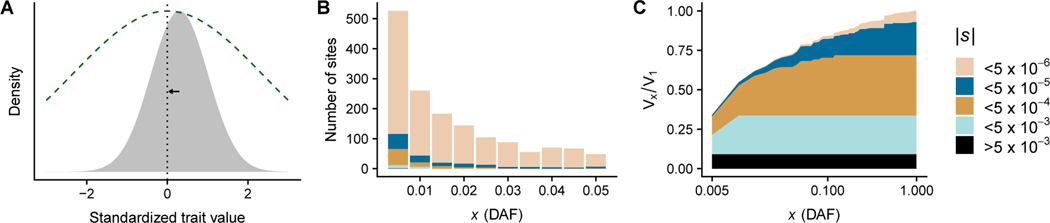
Figure 1:

A) A pictorial representation of a stabilizing selection model. The distribution of phenotypes in the population (gray area) is centered to the right of the current optimal phenotype value (indicated by the peak in the green dashed line). Consequently, individuals with slightly lower than average phenotypes will have the highest fitness, and the distribution will shift to the left over evolutionary time. B) Distribution of selection coefficients as a function of allele frequency in a sample of 200 chromosomes in the stabilizing selection model. We display only the first 10 bins of the frequency spectrum here. Strongly selected alleles are found preferentially at low frequency. Note that s is proportional to β² in a Gaussian stabilizing selection model. C) We plot the cumulative variance explained by alleles at or below frequency x (denoted Vx) due to each category of selection strength in B), relative to the total genetic variance (V₁). We observe that a substantial amount of the genetic variance is due to large effect alleles at very low frequency, despite these alleles being exceedingly rare. Very large effect alleles are not observed at higher frequencies and hence contribute no variance in the more common part of the frequency spectrum. Nearly-neutral alleles make almost no contribution to genetic variance (|s| < 5 × 10⁻⁶), while intermediate effect alleles have a substantial impact both at low frequency and high frequency (5 × 10⁻³ < |s| < 5 × 10⁻⁵). Note that this figure is intended only to illustrate model behaviors – we do not imply that these parameters or calculations conform to any real trait.

Although it is possible to incorporate multiple selected traits into the stabilizing selection framework, it is challenging to derive general results for the response due to selection under these models without employing additional assumptions about how effect sizes for different traits may be related to one another. Phenomenological evolutionary models have been proposed as a way to model the overall response to selection for alleles that may have effects on multiple quantitative traits (note that in the cases when phenomenological models have been employed to model stabilizing selection on genetically related phenotypes, they are sometimes called “apparent” stabilizing selection models - see for example Barton 1990). Phenomenological selection models avoid some of the challenges posed by direct modeling of stabilizing selection by proposing functions that map selection coefficients directly to effect sizes for a focal trait, where the selection coefficient term is supposed to encode the net effect of all selected traits on the causal allele (Keightley and Hill, 1990; Eyre-Walker, 2010). However, there is not generally a theoretical justification provided for the particular mapping functions considered, or the relationship between effect sizes for different traits - rather, these models have attempted to be flexible by allowing the relationship between selection coefficients and effect sizes to be modulated by model parameters. Such models provide a flexible way to capture pleiotropy and the effect of selection against causal variation, but have also been criticized for various theoretical shortcomings, such as sensitivity to the choice of mapping function and unbounded increase in genetic variance as population size grows large (Johnson and Barton, 2005).

Despite critical differences in proposed evolutionary mechanisms for the maintenance of quantitative genetic variance, essentially all evolutionary models of selection against complex trait variation suggest that large effect alleles should be constrained to (or at least preferentially observed at) low frequency. For example, in Fig. 1B we show that large effect alleles (which also have large selection coefficients) are constrained to low frequencies in a model of stabilizing selection. Despite being a small minority of polymorphic variants in the sample, large effect alleles can explain a substantial portion of the variation in the trait (Fig. 1C). In general, calculations of the expectation $\mathbb{E}\left({\beta }^2\mid x\right)$and frequency spectrum $\text{Ψ}(x)$ can be performed analytically under some simple models (e.g., Eyre-Walker 2010), but realistic demographic processes such as population-size changes and migration often make these calculations intractable (but see Živković et al. 2015 for an analytical approach). Therefore, simulations that simultaneously account for selection, non-equilibrium demography, linkage, drift, and mutation have often been applied to evaluate the effect of these processes on genetic variance and the frequency spectrum of causal alleles (Lohmueller, 2014b; Simons et al., 2014).

Empirical evidence for negative selection on complex trait variation

In light of the expectation that selection will constrain large effect alleles to low frequencies, it is natural to ask whether this pattern of correlation between allele frequencies and estimated effect sizes is supported in summary statistics from GWAS data. A complication is that power to detect causal alleles is a function of both allele frequency and effect size (Visscher et al., 2017), and the variance of effect size estimates increases sharply with decreasing allele frequency. Consequently, conditioning on genome-wide significance may induce a negative correlation between effect size (or effect- size-squared) and frequency even if there is no such negative correlation between true effect sizes and allele frequencies. To circumvent this problem, Park et al. (2011) calibrated effect size estimates by statistical power at all allele frequencies, and detected negative correlations between effect sizes and allele frequencies across a range of traits, including height, BMI, diabetes, LDL cholesterol, and cancers. They observed the most striking negative correlation between Type I diabetes effect sizes and frequency - this is consistent with expectation that Type I diabetes would be strongly fitness- decreasing in ancestral humans, since no treatments for this early-onset disease would have been available. Similarly, a recent study found larger per-SNP heritability from young alleles than old alleles over 20 complex traits, a pattern that is also suggestive of negative selection against trait variation (Gazal et al., 2017).

Genomic signals of selection can be inferred from linkage patterns, sequence conservation, or allele frequency differentiation by means that are independent of trait variation - regions predicted to be under selection can then be tested for enrichment in trait-associated variants, which might suggest a role for selection acting on the trait or causal variation for the trait. Several studies found evidence for substantially stronger genomic constraint at GWAS variants (including cardiovascular, developmental, metabolic, and pharmacogenomic traits, as well as cancers), meaning that these associated loci are more conserved across species than random genomic loci (e.g., Gorlov et al. 2008; Maher et al. 2012;Dudley et al. 2012). Moreover, trait-associated SNPs are under stronger background selection (i.e., the effect of linked deleterious alleles on genetic diversity) than matched control SNPs, suggesting that GWAS hits fall in genomic regions undergoing recurrent negative selection (Maher et al., 2012).

Inferring the evolutionary processes shaping complex trait variation

While these studies are suggestive of a role for selection in shaping trait variation, they do not provide insight into the specific evolutionary processes shaping complex traits. More recent work at the interface of statistical genetics and population genetics has sought to characterize the evolutionary mechanisms shaping complex trait variation in human populations. In essence, this work attempts to find evolutionary models that jointly explain the distribution of GWAS summary statistics, allele frequencies, and/or linkage patterns within or between human populations. We note that in discussing these findings, there are important caveats when linking selection signals to complex traits - these caveats have been explored elsewhere (e.g., Novembre and Barton 2018; Rosenberg et al. 2018; Sohail et al. 2019; Berg et al. 2019) and will be covered only briefly here, but we note that essentially all findings linking specific evolutionary models to complex traits should be considered preliminary at this point.

Given the expectation that selection on complex traits will result in larger-effect alleles being constrained to low frequency, several studies have now sought to quantitatively estimate the fraction of heritability that is driven by low-frequency variants and to find evolutionary models that can recapitulate the patterns observed in data. In a study of prostate cancer risk, Mancuso et al. (2016) partitioned the variance explained by causal variants into two bins, one for rare alleles (0.1–1% minor allele frequency) and one for high-frequency alleles (> 1% frequency). They found that 12% of the variance in prostate risk could be attributed to the low-frequency bin, in excess of what might be expected for a neutral model. They simulated trait values using the model of Eyre-Walker 2010, and showed that only a model with a large correlation between effect sizes and deleterious fitness effects against causal alleles generated h² values that were consistent with the 12% value they inferred for the prostate cancer data. This idea has been extended by subsequent studies - for example, Hernandez et al. (2017) developed a new method to partition variance explained into arbitrarily many bins of distinct allele frequency and detected a strong contribution to heritability in gene expression that are globally rare (Hernandez et al., 2017). This suggests that selection has strongly constrained alleles of large effect on gene expression to very low frequencies, and that a substantial portion of genetic variance for expression could not be discovered in traditional GWAS even in very large samples. A key feature of the approach of Hernandez et al. (2017) is that variance due to singleton variants can be directly estimated (i.e., variants that are private to a single sample), providing far greater granularity when inferring the role of selection than approaches that use only higher frequency alleles.

An advantage of approaches that partition heritability into contributions from distinct frequency bins is that they do not require knowledge of the specific alleles that are associated with the trait. However, since selection is likely to affect the distribution of frequencies of associated variants, it may also be possible to infer the evolutionary models affecting complex traits directly from the set of genome-wide-associated variants. Sanjak et al. (2017a) compared the frequency distribution of putatively causal alleles detected through GWAS to several models of complex trait evolution in an effort to determine which models could recapitulate the relatively flat distribution observed in empirical data. They found that a recessive gene-based model in which alleles on each chromosome fail to complement each other (resulting in a deleterious recessive phenotype) generated a similar distribution to the empirical data, whereas several other models (including additive models with alleles of large effect) tended to predict an excess of large-effect, low-frequency GWAS hits. If this non-complementing recessive model is in fact a good description of complex traits, it would imply a substantial non-additive component to missing heritability driven by genetic interactions. However, the authors noted that their data were collected across a range of traits and studies, whereas the models they employed suggested a shared architecture across all traits. Different traits are very likely to be subject to different evolutionary pressures, so it remains unclear if this model is a good fit to individual traits or simply consistent with data pooled across traits. Interestingly, the gene-based recessive model was able to recapitulate the discrepancy in inferred dominance variance between twin studies and SNP-based estimates, while other models were not. In a subsequent project, some of the same authors argued for signatures of Gaussian stabilizing selection across a range of traits measured in the UK Biobank by calculating genetic correlation between lifetime reproductive success (a fitness proxy) to several genetic traits (Sanjak et al., 2017b).

Not all complex phenotypes analyzed to date have been suggestive of a substantial role for rare alleles in driving trait variance or signals of selection. Agarwala et al. 2013 applied an evolutionary framework to GWAS summary data for Type II diabetes and concluded that both strong-selection and weak-selection models were consistent with the data. A subsequent study used summary data from a larger sample to suggest that Type II diabetes evolution was consistent with a nearly-neutral model of trait evolution based on the low rate of discovery of associations at low-frequency alleles. Similarly, Gaugler et al. 2014 argued that common alleles can explain nearly all of the heritability of autism risk, a pattern that suggests nearly-neutral evolution of risk variation for the trait. Studies have also produced some seemingly contradictory results as regards the role of selection on RNA expression in humans. Glassberg et al. 2019 found that only a small portion of variance RNA-expression levels could be attributed to rare alleles in a study of allele-specific expression, in contrast to Hernandez et al. 2017, suggesting that selective constraint on gene-expression is relatively weak. While some of this discrepancy could be attributed to technical differences between the studies (e.g., RNA-expression overall vs allele specific expression and 1MB flanking regions vs 20KB flanking regions), further work will be required to reconcile these studies.

Signals of polygenic adaptation in complex trait variation

Studies of complex trait architecture discussed so far were driven by the expectation that negative selection is likely to constrain causal variation of large effect to low frequency for disease traits. Recently, growing attention has been directed to a polygenic adaptation model in which subtle, coordinated frequency shifts in causal alleles for polygenic traits are indicative of changes in selection pressure. Under polygenic adaptation models, substantial changes in the trait distribution can occur while individual causal alleles change only modestly in frequency. Polygenic adaptation can arise as a natural consequence of stabilizing selection when the phenotype value conferring maximal fitness changes in response to the environment (Jain and Stephan, 2017).

Studies have proposed and applied various signatures of polygenic adaptation to detect these subtle allele frequency shifts. Allele-frequency differentiation between Northern and Southern Europeans at height-associated exceed differentiation at frequency-matched control SNPs, suggesting that height-increasing SNPs have been driven to higher frequencies by selection in Northern Europe (Turchin et al., 2012;Robinson et al., 2015). Berg and Coop formalized this empirical signal of excess frequency differentiation at causal SNPs with a novel statistical test, and suggested that skin pigmentation and height were suggestive of non-neutral signatures (Berg and Coop, 2014), while Field, Boyle, and Telis et al (2016) used a signature of the density of rare variants near causal alleles to suggest recent rapid adaptation in several phenotypes. Researchers have proposed and applied still more methods for inferring polygenic adaptation (e.g.,Sanjak et al. 2017b; Racimo et al. 2018; Edge and Coop 2019; Uricchio et al. 2019), suggesting that several complex traits may harbor signals of recent adaptation to larger or smaller trait values. As recent studies have suggested that signals of polygenic adaptation may have been overestimated in some cases (Novembre and Barton, 2018; Berg et al., 2019; Uricchio et al., 2019; Sohail et al., 2019; Rosenberg et al., 2018), we turn our discussion to potential biases rather than deliberate on the specific selection signals and the associated traits that have been identified (but see also e.g., Prohaska et al. 2019 for more discussion of polygenic adaptation, as well as the section on population stratification herein).

What can selection on complex traits tell us about GWAS?

This growing body of work suggests that selection is likely to act on complex traits. However, most studies completed to date have proceeded by first rejecting simple neutral models of trait evolution, and then proposing a polygenic selection model that could plausibly explain a pattern observed in GWAS summary data (e.g., the proportion of variance explained by rare alleles). Very few studies have taken the next step of formally comparing distinct polygenic selection models (e.g., explicit stabilizing selection models vs. apparent selection - see Johnson and Barton 2005). Consequently, a wide range of selection models have been proposed for a wide variety of traits (including stabilizing selection, negative selection, and polygenic adaptation), and currently it remains unclear to what extent each of these processes is responsible for non-neutral signals observed in GWAS summary data. Moreover, it has become clear that confounding in GWAS summary statistics is a serious concern for polygenic selection detection, and that polygenic selection might affect the statistical inference of causal loci themselves.

Potential biases in selection inference when using GWAS summary statistics

Inferences of selection on complex-trait-associated alleles must be compared to an appropriate null (i.e., neutral) model for trait evolution that includes the influence of possible confounding factors on GWAS summary data. Important (but non-exhaustive) factors that may affect inference include 1) non-equilibrium demography, 2) misspecification of selection models, 3) selection on off-target phenotypes with a shared genetic basis, 4) mis-specification of the drift model, and 5) population stratification.

Non-equilibrium population demography can have a substantial effect on the fraction of variance explained by rare alleles under both neutral and non-neutral evolutionary models. Exponential growth results in an influx of rare alleles (Keinan and Clark, 2012), distorting the frequency spectrum and driving an excess of trait variance due to rare alleles relative to equilibrium demography (Lohmueller, 2014b). In the absence of selection, the overall impact of this effect is generally modest, since the contribution of an allele to genetic variance is weighted by its allele frequency (eqn. 2). However, in the presence of selection, young alleles may have much larger effect sizes than old alleles, resulting in larger contributions from very rare variants to variance in the trait. Note that this is in contrast to deleterious allele load, which has been argued to be largely insensitive to demographic fluctuations experienced by human populations (Simons et al. 2014; Simons and Sella 2016 - see also Lohmueller 2014a; Henn et al. 2016). This implies that methods seeking to infer evolutionary models explaining complex trait variation should incorporate realistic demographic models and/or demographic uncertainty.

The strength of selection against a trait (or variation underlying the trait) and the relationship between effect sizes and selection coefficients has a substantial impact on the proportion of variance that is due to rare alleles. Generally, stronger selection results in a larger proportion of trait variation being carried at low frequency. While studies of human coding regions and conserved non-coding regions have estimated the selection coefficient distributions on these functional elements of the genome (e.g. Eyre-Walker and Keightley 2007; Boyko et al. 2008; Torgerson et al. 2009), it is generally not known how these fitness effects relate to effect sizes for complex traits, or whether the fitness effects that have been estimated for human functional elements are representative of the fitness effects for trait-associated loci. Consequently, mapping evolutionary models to specific traits requires modeling the uncertainty in this relationship between trait effects and fitness effects (Hernandez et al., 2017). Alternatively, if the distribution of selection coefficients is fixed to an arbitrary value, it is likely that model parameters (such as the τ parameter of Eyre-Walker 2010, which was inferred by Mancuso et al. 2016) will not be accurately inferred.

Selection could act directly on a trait of interest, but it could also impact GWAS summary statistics via a relationship between a selected trait and another trait that shares a genetic basis, resulting in a spurious selection signal for a neutral trait. As a trivial example, if the effect sizes of causal alleles for height are correlated with effect sizes for BMI, then we might detect selection on both traits when only one trait is under selection. Although recent studies have proposed new approaches for both modeling and empirically accounting for this confounding (Berg et al., 2017;Simons et al., 2018), a general solution to this problem is not available (Novembre and Barton, 2018).

When detecting polygenic adaptation through allele frequency differentiation, the null model of no adaptation is based on genetic drift that depends on the overall level of differentiation between subpopulations (Edge and Rosenberg, 2015a,b) and the distribution of effect sizes and polygenicity for the trait (Schraiber and Landis, 2015). Hence, it is important to consider any non-adaptive factors that affect the null model, or differentially affect control SNPs and trait-associated SNPs. The rate of genetic drift is a function of both allele frequency and effective population size. Since linked selection is thought to drive systematic variation in effective population size across the human genome as a function of recombination rate and functional density (McVicker et al., 2009), it may be necessary to use control SNPs that are matched for both allele frequency and background selection strength to trait-associated SNPs when making inferences about polygenic adaptation (Berg and Coop 2014 - see also Torres et al. 2018 for evidence that allele frequency differentiation increases as a function of background selection strength). A drift model could also be misspecified through an inaccurate depiction of population history - for example, if the population history is in fact an admixture graph and not a tree (Racimo et al., 2018), or if the branch lengths of the null model are underestimated.

Population stratification is perhaps the most pernicious challenge in estimating selection signals from GWAS summary statistics. If distinct sub-populations have different trait distributions for entirely non-genetic reasons, then mixing individuals from these populations in a GWAS may result in biased effect size estimates at alleles that are differentiated in frequency between the sub-populations. More generally, the stratified individuals need not correspond to categorical sub-populations - differentiation could be continuous along a gradient. While effective methods have been proposed to address this problem under neutral evolutionary scenarios and simple demographic models (Price et al., 2006), recent studies suggest that at least some selection signals detected in GWAS have been susceptible to confounding by population stratification (Berg et al., 2019; Sohail et al., 2019; Uricchio et al., 2019). Stratification confounding is most difficult to resolve when summary statistics from a single continental group are used to infer adaptation within the same continental group (e.g., when Europeans are used for both the GWAS and the selection inference) because the SNPs with the most inflated effect sizes are also the same SNPs that have the largest frequency differences between sub-populations. Applying effect size estimates obtained with one population to estimate selection signals in another population with a distinct pattern of allele frequency drift could partially side-step this problem, because there is no prior expectation that the degree of inflation should correspond to larger than average random drift in the sample used for selection inference. For example, Tucci et al. 2018 used European GWAS summary statistics to compute polygenic scores and perform selection inference in ancient samples from Flores Island. However, this approach needs more careful consideration of when it may or may not be applicable. Generally, most attempts to detect selection from GWAS summary statistics have assumed that the summary statistics are free from cryptic population stratification effects and have been largely applied within Europeans, suggesting that these studies should be taken as preliminary (Novembre and Barton, 2018). In particular, it seems clear that evidence for selection on height within Europeans is much weaker than previously thought, and that the risk of spurious selection inference is very high for methods that pool effect sizes genome-wide for non-significantly associated alleles (Sohail et al., 2019; Berg et al., 2019).

How does selection affect GWAS?

Most of the attention at the interface of complex trait variation and selection has focused on detecting the effect of selection using paired genomic data and GWAS summary statistics. Perhaps equally important to consider is the effect that selection may have on detecting trait-related variation itself. Efforts to understand the effect of selection on GWAS summary statistics have largely focused on models of negative selection against trait variation (e.g., Eyre-Walker 2010).

The power of a single-marker test of association generally depends on the effect size and allele frequency of a causal allele, and LD between the causal allele and alleles in the panel of loci that are being tested for association (Visscher et al., 2017). While selection may alter both the joint distribution of effect sizes and allele frequencies as well as LD patterns, studies have focused mainly on the former relationship to date. Lohmueller showed that both selection and demography have an impact on the rate of discovery of causal loci for complex traits (Lohmueller, 2014b). When fitness effects are highly correlated with effect sizes on a complex trait, relatively few intermediate effect loci are likely to reach genome-wide significance. Recent population growth increases the proportion of variance due to (essentially undetectable) rare alleles, further dampening the power to detect associations at common alleles (Lohmueller, 2014b). Single marker tests of association might also be affected by “synthetic association”, in which rare variants of large effect tag common variants and drive signals of association at the common allele (Dickson et al., 2010), but studies have argued that this effect is not likely to explain associations discovered to date (Wray et al. 2011; see alsoEdge et al. 2013 for further discussion).

To illustrate the effect of selection on GWAS, we simulated phenotypes and genotypes of 5,000 individuals from each of three broad continental groups (West African, European, and East Asian) under a model of human demography, selection, and realistic genome structure at a gene-dense 4.9 MB on chromosome 6 (Fig. 2). We used the phenotype model of Uricchio et al. 2016 to generate the phenotypes, and we assumed that h² = 0.05 for the simulated locus (see Methods for details). Note that we apply this model simply to illustrate the importance of assessing association tests under explicit evolutionary models - it is possible (and even likely) that other evolutionary models will predict different behaviors.

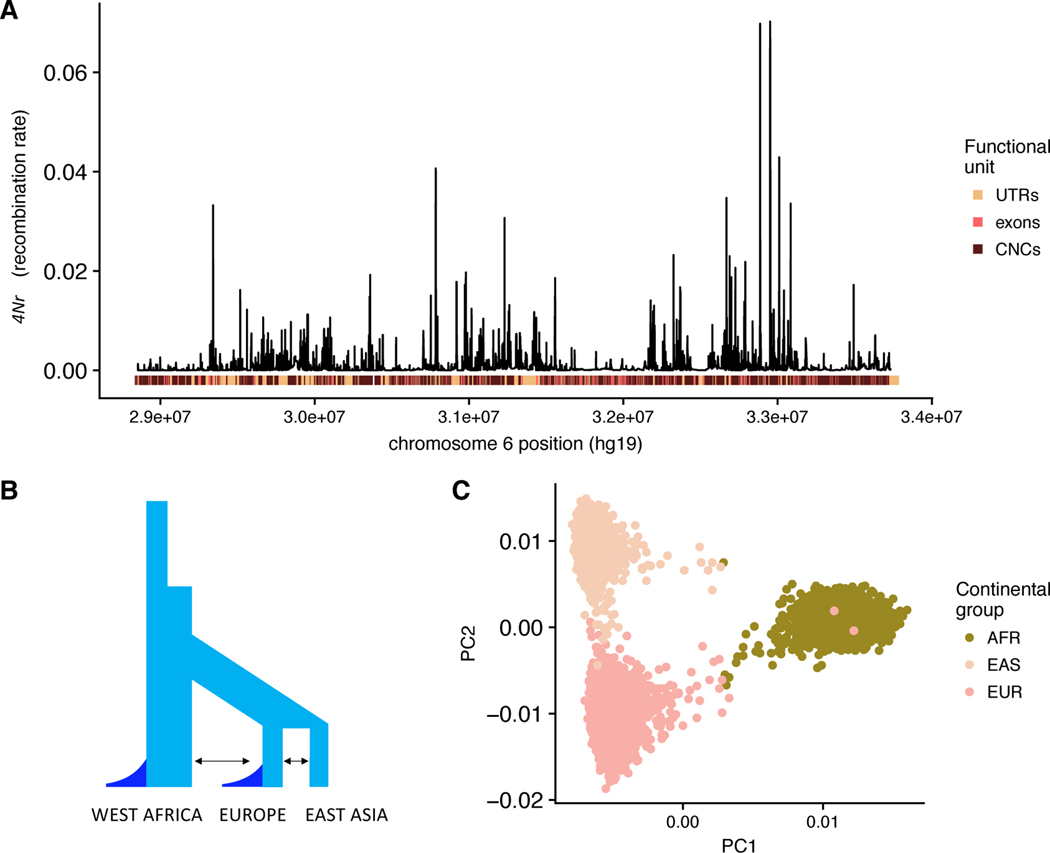
Figure 2:

A) Pictorial representation of the 4.9 MB region on chromosome 6 that we simulate herein. Functional elements are encoded by position along the x-axis, while recombination rate is detailed on the y. The average population scaled recombination rate in the region is 4Nr = 0.0071. B) Simplified pictorial representation of the simulated demographic model. The arrows represent migration. The dark blue represents the exponential growth events in each population. Note that two stages of growth occur in both the West African and European populations. The model is derived from those of Gravel et al. (2011) and Tennessen et al. (2012). C) PCs calculated from the simulated genetic data corresponding to one example simulation. Due to recent migrations, a handful of individuals are intermediate to the clusters corresponding to the continental groups. Abbreviations: UTRs, untranslated regions; CNCs, conserved non-coding regions; AFR, West African continental group; EUR, European continental group; EAS, East Asian continental group.

The model is a hybrid of the models proposed by Simons et al. 2014 and Eyre-Walker 2010, and was motivated by both biological and statistical observations. Biologically, it may be the case that some alleles are modular and affect only a single selected trait (e.g., an allele in a tissue-specific enhancer) while others are pleiotropic and have effects on multiple selected traits (e.g., an allele in an enhancer that is not tissue-specific). Modular alleles are likely to have a direct relationship between selection strength and effect size, while pleiotropic alleles may have selection strength that is determined by a composite of the different selected traits. Statistically, the model is motivated by the observation that the performance of association tests may depend on both the marginal distribution of effect sizes as well as the joint distribution of effect sizes and allele frequencies. A single parameter (ρ) controls the amount of pleiotropy while maintaining the overall marginal distribution of effect sizes. When ρ is close to one, causal alleles for the trait are essentially modular and draw their effect sizes directly from the strength of selection acting on the causal allele. When ρ is close to zero, the causal variation is highly pleiotropic and effect sizes are drawn randomly. Further details of the modeling framework are provided in the Methods section.

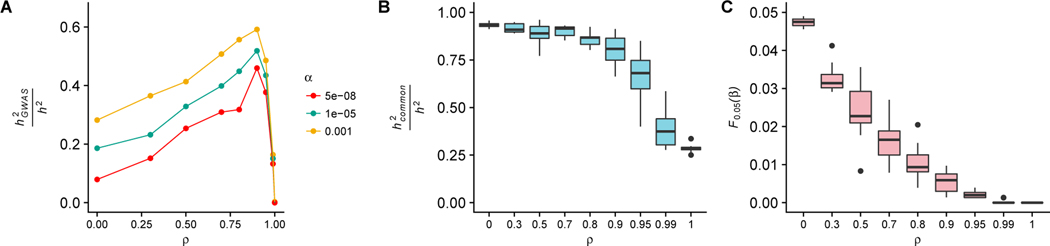
We considered a range of degrees of pleiotropy under the model (captured by the parameter ρ of the model, with ρ = 0 representing high pleiotropy), and fixed τ = 0.48, which was the value inferred in a study of heritibility of prostate cancer risk (Mancuso et al., 2016). The τ parameter controls the scaling relationship between selection coefficients and effect sizes. When ρ = 0, pleiotropy is high and causal alleles are uncorrelated from effect sizes, resulting in the preponderance of genetic variance being driven by common alleles. In contrast, when ρ = 1 causal alleles only affect a single selected trait and their selection effect is directly correlated to the effect on the trait, and a substantial portion of the variance in the trait is driven by rare alleles of large effect (Simons et al., 2014; Uricchio et al., 2016). We might then expect to find that more heritability is captured by single-marker tests when ρ = 0 than when ρ = 1. Indeed, we find that a substantially larger fraction of variance in the trait is captured with single-marker tests when ρ = 0 than when ρ = 1 (Fig. 3A). Interestingly, the amount of heritability captured is non-monotonic between ρ = 0 and ρ = 1, with the greatest values occurring near ρ = 0.9. This effect can be explained by considering how the common-variant-heritability is distributed across causal alleles. While the fraction of h² explained by common causal alleles decreases monotonically as ρ increases (Fig. 3B), so does the number of high-frequency causal alleles of large effect (Fig. 3C). Since the latter quantity falls linearly in ρ while the former decreases much more slowly (Fig. 3B&C), the power to detect individual common alleles initially increases, but ultimately falls sharply when rare alleles dominate the heritability at large values of ρ. In other words, the amount of heritability explained per common causal allele is maximized at intermediate values of pleiotropy. These results suggest that traits with intermediate amounts of pleiotropic selection will have the most large effect common variants discovered by GWAS, at least under this model. Note, however, that the proportion of trait variation explained by significant loci could be substantially lower than the values reported in Fig. 3 if h² is spread diffusely across the genome rather than functionally enriched in relatively small regions.

Figure 3:

A) Fraction of heritability explained by significantly associated loci ($\frac{h_{\text{GWAS }}^2}{h^2}$) at a variety of significance (α) thresholds as a function of the ρ parameter of the Uricchio et al. (2016) phenotype model, with low ρ representing high pleiotropy. Results represent aggregates of all alleles across 10 independent simulations and correspond to samples from the simulated African continental group. B) Fraction of heritability explained by common alleles (minor allele frequency > 1%). C) Fraction of common alleles (minor allele frequency > 0.01) with effect sizes β in the 5% tail of effect sizes (F_0.05(β)) across all causal alleles.

The model considered herein is far from the only way to model pleiotropy. While pleiotropy may be a function of an allele (i.e., a particular allele may affect one or many traits), it could also be a function of a trait (i.e., causal variation for some traits may be highly correlated several other particular traits). Recently,Simons et al. (2018) developed a model of stabilizing selection on multiple quantitative traits, and provided several analytical expressions to capture the variance explained by causal alleles as a function of effect size, selection strength, and allele frequency. A clear advantage of this mechanistic model is that the effect of pleiotropy on the joint distribution of frequencies and effects is not asserted by an ad hoc function - rather, it is learned by analyzing the model itself. In this framework, the authors found that the first loci discovered by GWAS in small samples are likely to be under intermediate or strong selection, while increasing sample size will tend to reveal many loci under weaker selection (which have smaller effect sizes). Fitting their model to GWAS summary data for height and BMI, the authors were able to predict how the discovery rate should increase for GWAS samples in the many hundreds of thousands, finding that more h² will be captured for height.

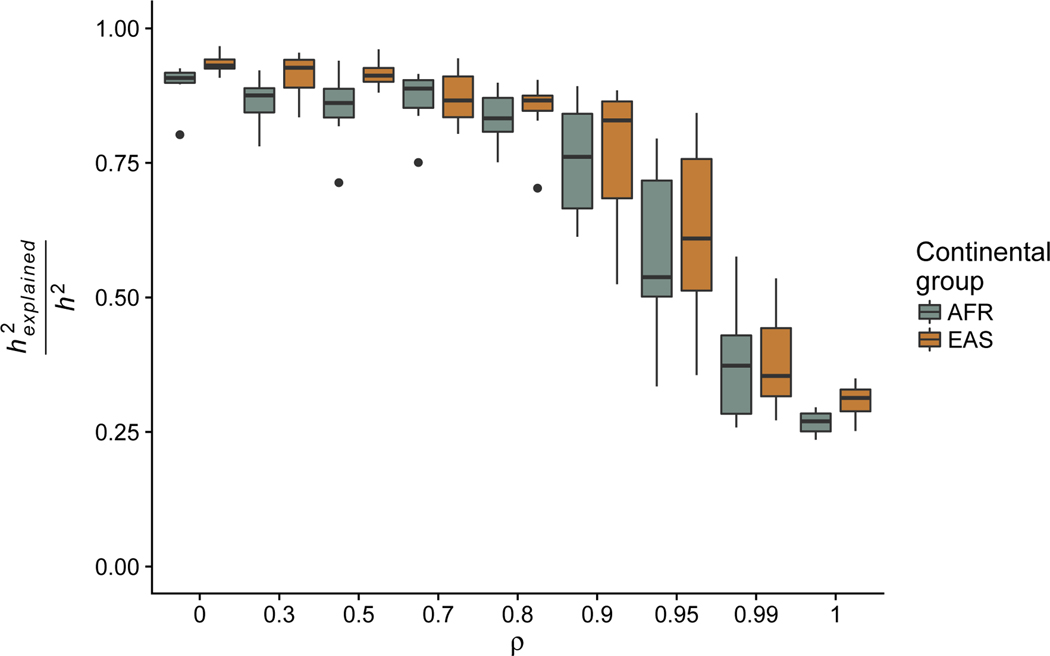
In addition to the role of pleiotropy in affecting the discovery rate of causal alleles, we explored how selection might affect the transferability of GWAS results across populations. The vast majority of GWAS (and other medical studies) have been performed in Europeans (Need and Goldstein, 2009;Rosenberg et al., 2010; Bustamante et al., 2011; Popejoy and Fullerton, 2016). It has been noted that polygenic risk scores perform fairly poorly in under-studied populations - this pattern is consistent with population-specific demographic effects (Martin et al., 2017), but selection could also play a role. In particular, if selection drives rare alleles to be substantial drivers of trait architecture, then such alleles are also likely to be more population-specific and uninformative across populations. We calculated the fraction of h² that would be explained in simulated West African and East Asian continental groups if GWAS had successfully captured all causal variants in Europeans (Fig. 4). While the proportion of h² captured is larger than 90% at low ρ (i.e., high pleiotropy), as the degree of correlation between selection effects and trait effects increases, the proportion of h² that can be explained across populations decreases markedly. The effect is slightly more dramatic in simulated West Africans than East Asians, suggesting an additional role for population demography (although this particular demographic effect may not recapitulated in real data, since the true population demography of East Asian populations likely also includes explosive growth). Note that this calculation provides an overly optimistic upper limit on the fraction of h² that can be captured across populations since we assumed that all h² in Europeans had been discovered in performing the calculations. In contrast, if selection is very weak, the proportion of variation explained by rare alleles might be much lower, and this effect might be attenuated.

Figure 4:

Fraction of heritability explained ($\frac{h_{\text{explained }}^2}{h^2}$) in West African (AFR) and East Asian (EAS) continental groups by all causal loci in Europeans. The ρ parameter is the pleiotropy parameter of the Uricchio et al. (2016) model, with low ρ representing high pleiotropy. Box plots represent the distribution of values across 10 independent simulations.

In response to the possibility that low-frequency variation might explain some proportion of missing heritability, numerous tests of association that pool a set of rare alleles together have now been proposed and widely applied (e.g., Li and Leal 2008; Liu and Leal 2010; Price et al. 2010a; Neale et al. 2011;Wu et al. 2011; Lee et al. 2012). The general idea of these methods is to exploit the potential for multiple rare alleles within a locus to jointly reach significance when power is too low for single causal alleles. These tests have generally been motivated by the idea that selection might drive low-frequency causal alleles to have larger effect sizes than common alleles, but relatively few of the early studies explicitly modeled selection against causal variation (but see Price et al. 2010a; King et al. 2010), tested how evolutionary modeling assumptions would affect the performance of the statistical test, or compared broadly across different tests in a range of plausible evolutionary scenarios (e.g., comparing weak and strong selection or introducing varying levels of pleiotropy). For example,Wu et al. 2011 used a model that maps allele frequencies to effect sizes through an ad hoc function that gradually increases in magnitude as frequency decreases. Although this captures the qualitative effect of selection against causal variation, it is not clear if such a function will be consistent with any plausible evolutionary model of complex traits. Hence it is not clear if estimates of type I and II error from these studies will be robust to unknown features of the evolutionary processes shaping complex trait variation (Uricchio et al., 2016).

Moutsianas et al. (2015) compared a wide variety of rare variant association tests using a range of evolutionary models that included both strong and weak selection in a moderately large samples of 3,000 individuals. The specific evolutionary model controlling the relationship between effect size and allele frequencies had a modest effect on power, with a “moderate” selection model generally having lower power than a “strong” selection model. Uricchio et al. (2016) further explored this phenomenon by fixing the strength of selection against causal variants, but changing the relationship between effect sizes and frequencies across a grid of parameters. They observed that in some scenarios (including the default settings of most of the tests investigated), rare variant tests achieved their greatest statistical power when rare variants made small contributions to the variance. This seemingly counter-intuitive result can be explained by comparing the prior expectation of methods such as SKAT-O (which are optimized to detect intermediate frequency rare variants) and the joint distribution of effect sizes and allele frequencies under evolutionary models (which may result in substantial contributions to genetic variance from much rarer variants, e.g. see Lohmueller 2014b; Sanjak et al. 2017a). Uricchio et al. (2016) further demonstrated that explosive growth exacerbates this problem by shifting even more genetic variance towards very rare alleles.

Various approaches have been proposed to boost power, including shifting more weight onto very rare alleles (Uricchio et al., 2016) or combining signals across semi-independent tests (Moutsianas et al., 2015). Unfortunately, both of these approaches were shown to elevate false-positive rates. In sum, the message of these studies is not that rare variant tests will always be under-powered, or that finding causal rare alleles is hopeless. Rather, these studies suggest that we should cautiously interpret both negative and positive results from rare variant association tests, given the sensitivity of these methods to evolutionary uncertainty and how little we know about the relationship between effect sizes and selection strength. For example, it may be too early to rule out a role for rare variants in complex traits on the basis of power calculations under dubious phenotype models.

While most studies in the realm of detecting individual loci under selection have focused on deleterious variation, it is also plausible that polygenic adaptation will have some effect on detecting causal alleles. In particular, it is now common-place to use a set of principal components as covariates in GWAS to correct for potential population stratification (Price et al., 2006). It has been suggested that this correction could result in under-estimation of effect sizes for traits under polygenic selection, since trait-altering alleles are expected to have larger than average allele frequency differences between sub-populations under polygenic selection models. This effect has been proposed by several studies (e.g., Berg et al. 2019), but to our knowledge it has not been assessed with simulations or observed in real data.

Where do we go from here?

Despite growing sample sizes, novel statistical methods, and deep sequence data, there is still a great deal that we do not know about the genetic basis of complex traits. While there are a number of possible avenues to address this problem, here we rely on a rapidly expanding literature to argue that missing heritability is fundamentally an evolutionary problem. Evolution is the engine that shapes the trajectories of mutations, and mutations confer the heritable portion of trait variance. Hence, an evolutionary view on missing heritability may help clarify the most effective approaches in future association studies. We propose three broad areas in which evolutionary thinking could improve the success rate of GWAS.

First, we echo the views of previous researchers calling for increased diversity in GWAS (Rosenberg et al., 2010; Bustamante et al., 2011; Martin et al., 2017). Diagnostic approaches in personalized medicine will be most effective if polygenic risk prediction can be successfully applied across populations (and even within populations; see Mostafavi et al. 2019). Unfortunately, the continued over-representation of Europeans in GWAS has hampered progress in this area - the potential impact of diagnostic genetics will be severely curtailed if the results cannot be applied to diverse populations (Martin et al., 2019). Perhaps just as critically, the naive transfer of polygenic scores as a predictive tool across populations can lead to erroneous and potentially damaging claims about phenotypic differences between populations (Rosenberg et al., 2018). While several studies of polygenic risk differences across populations have focused on demographic factors, polygenic adaptation, or population-specific effects as explanations for under-performance of polygenic risk prediction, our simulations of complex human demography, selection, and genome structure herein show that negative selection can increase the role of population-specific variation in driving heritability. These population- specific signals could never be applied to genomic prediction across populations because no amount of increased sampling within Europeans would discover this causal variation. Large, ongoing studies with diverse participants such as PAGE (Wojcik et al., 2018) and TOPMed (e.g.,Hu et al. 2018) will help to correct that deficit, but much more work on diverse worldwide populations is needed.

Studies of relatively isolated populations may also provide methodological advantages for the detection of casual alleles that are rare within the worldwide human population but relatively more common locally. Whereas rapid growth increases the relative importance of rare variants in driving genetic variance for complex traits under selection, population bottlenecks have the opposite effect (although the average number of deleterious alleles per chromosome is not strongly affected; see Simons et al. 2014; Lohmueller 2014a). The allele frequency dynamics of recessive and dominant alleles in response to population bottlenecks differ from additive alleles (Balick et al., 2015), suggesting that demography will affect power to detect partially recessive alleles. Taken together, these theoretical results suggest that population isolates can provide increased power for discovery in some contexts. Empirical studies in isolated populations have already demonstrated the success of this approach, including early linkage scans and more recent approaches (e.g., Ober et al. 1998; Holm et al. 2011; Southam et al. 2017; Martin et al. 2018).

Second, we note that there exists a growing recognition that biases in selection detection can be driven by uncorrected population stratification in GWAS (Novembre and Barton, 2018), but we suggest that increased awareness of the effect of selection on the rate of discovery of associated loci is also warranted. We and others have shown that the detection of causal loci is strongly affected by selection strength and demographic history (Lohmueller, 2014b,a; Moutsianas et al., 2015; Uricchio et al., 2016; Sanjak et al., 2017a;Simons et al., 2018) - while the specific quantitative relationship between discovery rate and model parameters are dependent on modeling choices made by each study, all of this work supports a strong impact of selection on GWAS summary statistics and the heritability captured by associated alleles. Since we are only in the very early stages of discovering the evolutionary models that best explain the observed variation in complex traits, we suggest that it may therefore be too early to rule out a substantial role for rare variants in most complex traits.

Third, we suggest that combining the growing knowledge of trait architecture with association methods that robustly account for evolutionary history could improve the rate of detection of rare and low-frequency causal alleles. In particular, most rare variant association methods make prior assumptions about the relationship between effect sizes and frequencies that may not match the empirical data or even the predictions of simple evolutionary models. With the emergence of approaches for determining the relationship between effect sizes, allele frequencies, and genomic features that do not require knowledge of the individual associated alleles (e.g., Mancuso et al. 2016; Hernandez et al. 2017; Palamara et al. 2018; Finucane et al. 2018; Wainschtein et al. 2019), it is possible to apply such methods genome-wide, and to use the genome-wide partitions of heritability as a function of allele frequency as a prior on locus-specific detection of causal alleles. Future studies may benefit from this approach to maximize the efficiency of detecting causal loci.

Methods

Simulations of selection, human demography, and genome structure

We used sfs_coder and sfs_code to simulate a 4.9 megabase region on chromosome 6 (hgl9 coordinates 28850000:33750000) that contains the HLA locus (Uricchio et al., 2015; Hernandez and Uricchio, 2015). The region is functionally dense, with about 12% of basepairs falling into exons, untranslated regions (UTRs), or conserved non-coding regions (CNCs). We chose this locus as an example of a functionally dense locus with complex selection dynamics, but note that sfs_coder can simulate any locus in the human genome. HLA is likely to be the target of balancing selection in addition to negative selection (Hedrick and Thomson, 1983; Tan et al., 2005) – we do not include balancing selection in the current study, although it is plausible that it will have impacts on both the frequency spectrum and effect size distribution of causal alleles for complex traits.

We apply a distribution of selection coefficients that was inferred for coding loci to exons and UTRs (Boyko et al., 2008), and a distribution of selection coefficients that was inferred from conserved non-coding loci for CNCs (Torgerson et al., 2009). We use realistic genome structure that corresponds to the exact coordinates of each functional element (Siepel et al., 2005), and a recombination map that was inferred from human genomes (Harrow et al., 2012).

We apply a demographic model based on those of Tennessen et al. (2012) and Gravel et al. (2011) in our simulations. The Tennessen model is based on the three continental-group model of Gravel, which includes an ancient ancestral expansion in the African ancestral population, a bottleneck event that corresponds to the out-of-Africa event, and subsequent bottlenecks at the founding of Europe and East Asia. The European and East Asian continental-groups undergo exponential growth after these bottlenecks. Tennessen et al. (2012) used a large sample of sequences to infer a second, faster phase of exponential growth in the European and West African continental-groups over the last ≈ 5,000 years, which is appended to the model inferred by Gravel et al. (2011). The lack of an explosive growth phase in the East Asian group does not reflect that no such event occurred - data for this group was not included in the Tennessen et al. (2012) study, so we lack an estimate of more recent explosive growth in East Asians. Migration rates were also inferred between each pair of continental groups, and migration is included in the simulations. A simplified pictorial representation is included in Fig. 2B (inspired by Gutenkunst et al. 2009). We performed 10 replicates of each simulation - plots represent results from simulations that were pooled or averaged as described in the text. We sampled 5,000 individuals from each continental group at the end of each simulation.

Methods to perform the selection, demography, and genomic structure simulations were published previously and described elsewhere (Uricchio et al., 2015). Documentation for the simulations is available online at https://github.com/uricchio/sfs_coder.

We also developed a simple simulator of allele frequency dynamics under a stabilizing selection model with equilibrium demography, implemented in Python. This software was employed because sfs_code does not simulate stabilizing selection. The methods we used were based on previously described software (Uricchio et al., 2019). We used this software to perform the simulations presented in Fig. 1. We supposed that selection coefficients were gamma-distributed (gamma parameters given by α = 0.0415, β = 0.005). These were previously inferred from patterns of variation at human conserved non-coding elements (Torgerson et al., 2009) and suggest a relatively weak mean strength of selection (2Ns ≈ –8), but a long tail of large effects. The heritability of the simulated trait was set to h² = 1.

In a stabilizing selection model, selection does not act directly on each allele per se, but rather at the level of the phenotype (Fig. 1A). Hence, to get the desired distribution of selection coefficients, it is necessary to first map the desired selection coefficients to an appropriate distribution of effect sizes. Following the results of previous work (Robertson, 1956), we set $s=\frac{{\beta }^2}{2\left({\sigma }^2+w^2\right)}$, where w² is the breadth of the fitness function and σ² is the breadth of the phenotype distribution. We suppose that σ² is small compared to w², such that it can be ignored in calculating the distribution over β. In practice, this approximation may be violated in the simulations if the number of polymoprhic loci is large. As such, the values of s reported in Fig. 1 are approximate.

Simulating phenotypes

We used the model of Uricchio et al. (2016) to simulate quantitative phenotypes with h² = 0.05. Briefly, the model is a hybrid of the models previously proposed by Eyre-Walker (2010) and Simons et al. (2014), both of which map selection coefficients in simulated data to effect sizes. The Eyre-Walker model maps selection coefficients to effect sizes β as $\beta =\delta |s{|}^{\tau }$ where s is the selection coefficient and τ is a parameter that controls the shape of the effect size distribution. The δ parameter is a random sign, which allows effect sizes to be either trait-increasing or -decreasing. The original Eyre-Walker model also included a random noise term that allowed effect sizes to vary from the scaling implied by the τ parameter, but this noise term had no effect on the genetic architecture of the trait and is not included here (Eyre-Walker, 2010). In contrast, the model of Simons et al. (2014) is a point mass model with two selection coefficients. Effect sizes are chosen to be either a) exactly equal to the selection coefficient or b) selected randomly from among the two selection coefficients. The amount of randomization can be toggled with a parameter p (Simons et al., 2014). The p parameter qualitatively corresponds to the degree of pleiotropy.

The model of Uricchio et al. (2016) is a hybrid of these two models, which includes the τ and δ parameters of Eyre-Walker and a ρ parameter that corresponds to the ρ of Simons et al. (2014), and additionally generalizes to arbitrary selection coefficient distributions. In our simulations herein, we fix τ = 0.48, which was previously inferred as the best-fitting value of τ for a case-control study of prostate cancer heritability (Mancuso et al., 2016). We additionally suppose that the heritability conferred by the entire 4.9 MB region is 0.05 - the remaining 95% of variation may be driven by environment or other (unmodeled) genomic loci. We then study how association tests might be affected by the pleiotropy through the ρ parameter. When ρ = 1, selection on causal variation is completely modular and effect sizes are proportional to $|s{|}^{\tau }$ whereas ρ = 0 corresponds to a high degree of pleiotropy and effect sizes are drawn randomly with respect to selection coefficients.

Qualitatively, the model of Uricchio et al. (2016) is inspired by a gene-tissue model of disease. If over-expression (or under-expression) of a gene in a particular tissue leads to increased risk of disease, then an allele that affects expression only in that particular tissue (e.g., a tissue-specific enhancer) is likely to be under direct selection, and the selection strength should correspond to the effect size on expression. In contrast, an allele that lies in a promoter that is active in a wide range of tissues (i.e., including tissues that do not increase disease risk) may escape selection, and its effect size may not be directly related to selection strength.

To assign individual effect sizes, each mutation falling within a functional locus inside the 4.9 MB region first randomly draws a selection coefficient from a pre-specified distribution. Within the simulated region, 97,340 base pairs fall in conserved non-coding loci while 501,265 base pairs correspond to genes. For mutations in conserved non-coding loci, we suppose that selection coefficients are drawn from a gamma-distribution as inferred by Torgerson et al. (2009). For mutations falling in coding regions, we suppose that selection coefficients for nonsynonymous alleles are drawn from a different gamma distribution that was inferred specifically from the allele frequency spectrum in genes (Boyko et al., 2008). Effect sizes are then mapped to individual alleles using the ρ and τ parameters of the phenotype model. Detailed methods to simulate traits under these models were previously described (Uricchio et al., 2015, 2016), and documentation is available online at https://github.com/uricchio/sfs_coder.

Simulated association studies

To perform simulated association studies, we regressed phenotypes on genotypes while using PCs as covariates. To perform PCA, we used the software SMARTPCA in the Eigenstrat/Eigensoft package (Patterson et al., 2006; Price et al., 2006) and used the first three PCs in our analyses. To perform the regression, we wrote a custom Python script that uses the LinearRegression method in the sklearn package. We analyzed each continental group independently rather than jointly analyzing all 15,000 samples. Individuals were grouped by sample population rather than based on PC clustering – we note that some of these individuals would likely be excluded in a real GWAS (or clustered with different ancestral groups).

Calculating $h_{\text{GWAS }}^2$ and $h_{\text{explained }}^2$

To calculate the fraction of h² that is explained by trait-associated loci, we used eqn. 3 to sum the heritability due to all causal loci conditional on having association p-values less than a given threshold (α in Fig. 2A) and divided by the total h².

To calculate the fraction of h² that would be explained in West African or East Asian continental groups by European causal loci, we first (optimistically) assumed that all causal loci that confer variation in Europeans are known. We then summed up the total heritability that would be conferred by these loci in West African or East Asian simulated populations (eqn. 3), and calculated $h_{\text{explained }}^2$ as the ratio of the contribution of European causal loci to the total h² in each population. Results of this calculation are shown in Fig. 3.