Cooperative evolution of polar distortion and nonpolar rotation of oxygen octahedra in oxide heterostructures

Oxide interface orientation tunes ferroelectric distortion and antiferrodistortive rotation into competition or cooperation.

Abstract

Polarity discontinuity across LaAlO₃/SrTiO₃ (LAO/STO) heterostructures induces electronic reconstruction involving the formation of two-dimensional electron gas (2DEG) and structural distortions characterized by antiferrodistortive (AFD) rotation and ferroelectric (FE) distortion. We show that AFD and FE modes are cooperatively coupled in LAO/STO (111) heterostructures; they coexist below the critical thickness (t_c) and disappear simultaneously above t_c with the formation of 2DEG. Electron energy-loss spectroscopy and density functional theory (DFT) calculations provide direct evidence of oxygen vacancy (V_O) formation at the LAO (111) surface, which acts as the source of 2DEG. Tracing the AFD rotation and FE distortion of LAO reveals that their evolution is strongly correlated with V_O distribution. The present study demonstrates that AFD and FE modes in oxide heterostructures emerge as a consequence of interplay between misfit strain and polar field, and further that their combination can be tuned to competitive or cooperative coupling by changing the interface orientation.

INTRODUCTION

Quantum confinement of the strongly correlated d-orbital electrons at complex oxide interfaces establishes an intricate orbital hierarchy, which is widely recognized as a source of emergent physics (1, 2). The most prominent example is the 2DEG induced at LAO/STO interfaces, which displays a wide range of quantum phenomena, including metal-insulator transition (3), ferromagnetism, and superconductivity (4, 5). Recent studies have shown that changing the interface orientation can modify the Ti-3d orbital hierarchy, selective occupancy, and spatial confinement of 2DEG (6). The LAO/STO (111) interface, in particular, presents an interesting playground for exploring the emergent physics of 2DEG (6–9), because its buckled honeycomb (111) lattice can induce exotic topological states (10–13) and strong magnetic reconstructions (14–16) owing to a reduced interlayer distance and strong octahedral coupling compared with that of the (001) interface. Because the crystal field adopts trigonal symmetry and the t_2g states are mixed within this symmetry, the three usual orbitals transform into a_1g and e_g′ subbands, each with a balanced contribution from d_xy, d_yz, and d_xz (11, 14, 17).

Another intriguing modification made by changing the interface orientation is the structural distortions of the LAO/STO heterostructure, especially AFD tilts of the AlO₆ octahedron. While STO adopts an undistorted cubic phase (space group, $\mathit{Pm}\overline{3}m$), LAO is stabilized in a rhombohedral phase ($R\overline{3}c$) at room temperature with AFD tilts of the AlO₆ octahedron around the pseudocubic [111] axis ϕ_abc (Fig. 1A), which corresponds to an a⁻a⁻a⁻-type tilt according to the Glazer notation (hereinafter, the Miller indices of LAO are indexed based on the pseudocubic crystal system). In LAO/STO (001) heterostructures, the AFD tilt pattern of LAO is expected to evolve differently from the a⁻a⁻a⁻ pattern owing to the influence of the (tensile) epitaxial strain arising from lattice mismatch and the internal polar field arising from the polarity mismatch with the STO (18). For example, DFT calculation predicts that the tensile misfit strain acting on LAO (e.g., +2.97% in LAO/STO) stabilizes the LAO into a different phase (Imma) instead of $R\overline{3}c$, which is composed of ϕ_ab rotations (a⁻a⁻c⁰) with the rotation axis along the in-plane [110] direction (19) (see Fig. 1B). However, the AFD rotation in LAO/STO heterostructures is governed more strongly by the internal polar field; an uncompensated internal polar field within the LAO film has been shown to suppress the AFD rotation in favor of FE (polar displacement of cation and anion sublattices against one another) distortion that produces a depolarization field that compensates for the polar field (Fig. 1, B and C) (20–22). The AFD rotation evolves in the LAO/STO heterostructure only when the polar field is compensated by the formation of 2DEG above the t_c (18). As such, the structural evolution of LAO/STO (001) heterostructures goes in line with the general notion that the nonpolar AFD rotation and polar FE distortion tend to compete and suppress each other in ABO₃ perovskite oxides (23–26).

Fig. 1. Structural models for FE distortion and AFD rotation of LAO in LAO/STO (001) and (111) interfaces.

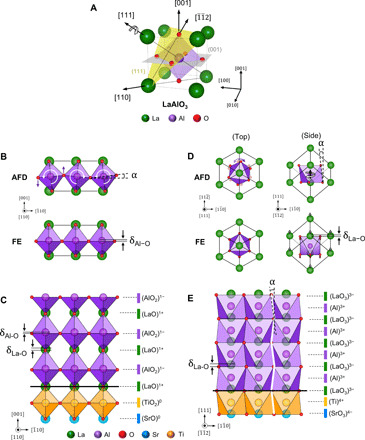
(A) Unit cell of rhombohedral LaAlO₃ (space group $R\overline{3}c$). The (001) and (111) planes are highlighted in gray and yellow, respectively. The AFD tilt of an AlO₆ octahedron around the [111] axis is indicated by an arrow. (B) Structural models illustrating the AFD rotation and FE distortion appearing in the LAO/STO (001) system above and below t_c, respectively. The rotation axis of AFD lies along the [110] direction, and its angle is defined as α. The FE distortion is represented by the displacement (δ_Al-O) of Al from the centrosymmetric position of the AlO₆ octahedron. (C) DFT result showing the structural distortion of a subcritical LAO/STO (001) system. The interface and surface termination are (LaO)⁺/TiO₂ and (AlO₂)⁻, respectively. FE distortion is indicated by δ_Al-O and δ_La-O, and no AFD is observed. (D) Structural models illustrating the AFD rotation and FE distortion appearing in the LAO/STO (111) system simultaneously below t_c (top and side view). The rotation axis of AFD lies along the [111] direction, and its angle is defined as α. The FE distortion is characterized by the amplitude (δ_La-O) of out-of-plane rumpling of oxygen and La atoms. (E) DFT result showing the structural distortion of a subcritical LAO/STO (111) system. The interface and surface termination correspond to (LaO₃)³⁻/Ti⁴⁺ and (LaO₃)³⁻, respectively. Both AFD rotation and FE distortion are observed and indicated by α and δ_La-O, respectively.

The FE distortion and AFD rotation evolve in a different way in the LAO/STO (111) heterostructure compared to those in the (001) counterpart. In the LAO/STO (111) heterostructure, the [111] rotation axis is perpendicular to the strain plane [see Fig. 1 (A and D)]. While the (001) tensile strain favors the Imma phase of LAO (19), the (111) tensile strain prefers to stabilize the out-of-plane [111] rotations and preserve the bulk $R\overline{3}c$ symmetry (27). According to the recent DFT calculations by Gu et al. (28), for perovskite oxides with a large AFD rotation angle and/or small A-site ions, the FE distortion can coexist with the AFD rotation in which A-site ions are pushed out from the strain plane to lower the repulsive interaction with neighboring oxygen ions and induce ionic polarization along the [111] direction (Fig. 1D). Hence, the (111) orientation of the LAO/STO heterostructure can render the cooperative evolution of AFD rotation and FE distortion, as opposed to the competitive evolution in the (001) orientation.

Given that the (competitive or cooperative) evolution of AFD rotation and FE distortion in (001) and (111) LAO/STO heterostructures is strongly influenced by the internal polar field, a question naturally arises on how this structural evolution is influenced by the formation of 2DEG. Among the various formation mechanisms (3, 29–38), the surface V_O (32–34, 38) model has been receiving increasingly positive feedback as it is highly compatible with most of the experimental observations (6, 18, 39, 40). DFT calculations have shown that the formation energy of V_O at the LAO surface decreases with increasing film thickness and becomes zero on reaching the t_c for 2DEG formation (32–34, 37, 38, 41). V_O can form spontaneously above t_c and act as a donor providing electrons to the interface (32–34, 38). Moreover, V_O in ABO₃ perovskites is known to induce local distortion and/or rotations of BO₆ octahedra (42, 43). Therefore, considering the electron donation capability and the local symmetry breaking, surface V_O is expected to relieve the internal polar field and, at the same time, modify the structural evolution of AFD rotation and FE distortion. Thus, it is important to understand whether V_O favorably forms at the LAO (111) surface, acts as the source of 2DEG, and affects AFD-FE coupling.

Here, we demonstrate that the AFD and FE modes are cooperatively coupled in LAO/STO (111) in contrast to the competitive coupling in LAO/STO (001); they coexist below t_c and disappear simultaneously with the formation of surface V_O above t_c. The spatially resolved scanning transmission electron microscopy (STEM) electron energy-loss spectroscopy (EELS) O-K edge combined with DFT calculations provide direct evidence of the presence of V_O at the LAO (111) surface. Tracing the AFD rotation and FE distortion of LAO from the interface to the surface clearly demonstrates that their evolution is strongly correlated with the distribution of V_O near the LAO surface.

RESULTS

Cooperative evolution of FE distortion and AFD rotation in the LAO/STO (111) heterostructures

DFT calculations were conducted for the LAO/STO (001) and the (111) heterostructures to trace the evolution of FE distortion and AFD rotation with the change of LAO thickness across the t_c for 2DEG formation. The t_c of the (001) and the (111) systems for 2DEG formation corresponds to 4 unit cells (u.c.) and 9 bilayers (b.l.), respectively. For the LAO films thicker than the t_c, the formation V_O at the LAO surface was also considered as the formation energy becomes negative (32, 34, 44, 45). For the (001) interface, where the AO and BO₂ layers of the ABO₃ perovskite structure are stacked alternately, LaO⁺/TiO₂ and AlO₂⁻ terminations were chosen for the interface and surface, respectively (Fig. 1C). For the (111) interface, where AO₃ and B layers with opposite charges are stacked alternately, e.g., (LaO₃)³⁻/Al³⁺ for LAO and (SrO₃)⁴⁻/Ti⁴⁺ for STO, (LaO₃)³⁻/Ti⁴⁺ and (LaO₃)³⁻ terminations were chosen for the interface and surface, respectively (Fig. 1E).

To determine the termination state of the LAO/STO (111) interface, atomic-scale imaging (fig. S1), energy-dispersive x-ray spectroscopy (EDS) (6), and EELS profiling (fig. S2) were conducted using aberration-corrected STEM. The EDS elemental maps and line profiles of the constituent cations of STO and LAO clearly showed that STO is terminated by the Ti⁴⁺ layer and LAO is terminated by the (LaO₃)³⁻ layer at the interface (6). The formation of the (LaO₃)³⁻/Ti⁴⁺ interface was also confirmed by intensity profiling of the EELS Sr-L_2,3 and Ti-L_2,3 edges of STO and the La-M_4,5 and Al-K edges of LAO (fig. S2). Given that the LAO/STO (111) interface is terminated into (LaO₃)³⁻/Ti⁴⁺, the surface of LAO, in principle, can be terminated into either Al³⁺ or (LaO₃)³⁻. According to the polar catastrophe model for the LAO/STO (001) interface, an n-type polar field is induced when the interface and surface of LAO are terminated into stoichiometric LaO⁺/TiO₂ and AlO₂⁻ layers with opposite charges, respectively. However, for the LAO/STO (111) system, our DFT simulation showed that the stoichiometric Al³⁺ surface termination results in a p-type polar field for the (LaO₃)³⁻/Ti⁴⁺ interface (fig. S3A), whereas an n-type polar field is induced when symmetric (LaO₃)³⁻ surface termination is chosen (fig. S3B). For this symmetric (LaO₃)³⁻ termination, we found the spontaneous formation of a hole on the surface. To rationalize these findings, we considered the local charge model for the LAO/STO (111) system with (LaO₃)³⁻/Ti⁴⁺ interface termination (fig. S4). The local charge model is constructed to satisfy the charge neutrality inside the LAO (46). We found that, in the presence of a hole on the surface (LaO₃)³⁻ layer, the interface unit cell has a half-positive charge (+0.5e) and the surface unit cell has a half-negative charge (−0.5e), which induces an n-type built-in field across the LAO.

DFT calculations show that the structural distortion in LAO/STO heterostructures evolves in different ways depending on the interface orientation. Here, we focus discussion on the subcritical thickness regime. Below the t_c, polar FE distortion arises in both the LAO (001) and (111) films to compensate the polar field. In the (001) heterostructure, FE distortion is induced in both LaO⁺ and (AlO₂)⁻ layers but relatively larger in the LaO⁺ layer (Fig. 1C). In the (111) heterostructure, FE distortion is measurable only in the (LaO₃)³⁻ layer (Fig. 1E). These FE distortions decrease in proportion with the increase of 2DEG density in both LAO (001) and (111) films when the LAO thickness increases over t_c (see Fig. 2, C and D). In the presence of FE distortion, AFD rotation evolves in different ways depending on the interface orientation. While AFD rotation is suppressed in the (001) heterostructure, the same AFD rotation as in bulk LAO is stabilized in the (111) heterostructure with the rotation axis along the [111] direction (Fig. 1E). The coexistence of AFD rotation and FE distortion in the (111) heterostructure results in a noncentrosymmetric R3c phase of LAO, which is formed by superimposing two different distortions onto the ideal cubic perovskite structure: the FE mode that consists of out-of-plane displacement of mainly La ions and the AFD rotations of AlO₆ octahedra about the [111] direction. When viewed along the $[11\overline{2}]$ in-plane direction, the AFD rotation appears as a ripple pattern and can be characterized by the rotation angle (α) (Fig. 1E). The FE distortion and AFD rotation angle were calculated to be 0.15 Å and ±8.0°, respectively, for the 3-b.l.-thick LAO (111) film.

Fig. 2. Formation of oxygen vacancy (V_O) at LAO surface and its effects on structural distortion in LAO/STO (001) and (111) systems.

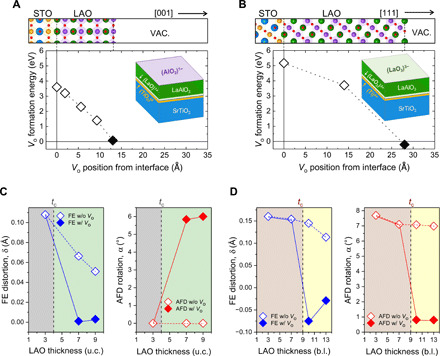
(A and B) V_O formation energy calculated by DFT with V_O at various locations in LAO for (001) and (111) systems, respectively. (C and D) FE displacement (δ) and AFD rotation angle (α) calculated by DFT as a function of LAO (001) and (111) thickness, respectively. For a given set of LAO thickness and interface orientation conditions, two separate calculations were conducted with (closed symbol) and without (open symbol) V_O in LAO. The results indicate competitive and cooperative coupling of FE distortion and AFD rotation in the (001) and (111) systems, respectively.

It is worth discussing the criterion governing the stability of specific AFD rotation mode in the LAO/STO heterostructure with different interface orientation. For ABO₃ perovskite with the Goldschmidt tolerance factor less than unity, like LAO with 0.89, the stable AFD rotation mode is determined as one that reduces the size of A-site dodecahedron, thereby optimizing the A-site coordination and mitigating the size mismatch between A and B cations (27). The polyhedral volume ratio V_A/V_B, the volume of the A-site dodecahedron divided by the volume of the B-site octahedron, can be used as a measure to determine the stable AFD mode. The ratio V_A/V_B is equal to 5.0 for the cubic structure without AFD rotation and deviates (decreases) from 5.0 in proportion with the degree of AFD rotation. According to the DFT calculations on LAO (001) and (111) slab under tensile strain, the phase with the most distorted crystal structure, i.e., the lowest V_A/V_B, has the lowest energy (27). For the LAO (111) under tensile strain, there is a possibility to move oxygen in the tensile-strained (111) plane while optimizing the coordination of La with decreasing V_A/V_B ratio, as illustrated by the purple arrows in Fig. 1D. The situation becomes different for the LAO (001) under tensile strain as the oxygen movements that minimize the V_A/V_B ratio are out of the tensile-strained (001) plane, as illustrated by the purple arrows in Fig. 1B.

Now, we consider compatibility of the AFD rotation predicted for LAO (001) and (111) under tensile strain with the FE distortion required for the compensation of polar field in subcritical LAO/STO heterostructures. For the LAO/STO (001) with FE distortion, the predicted AFD rotation results in the out-of-plane movements of oxygen, which causes antipolar FE displacements of La and Al from oxygen sublattice. Therefore, the AFD mode competes with the FE distortion, so that they are incompatible. In the LAO/STO (111) heterostructure, however, the AFD rotation is structurally compatible with the FE distortion because the atomic displacements induced by the two modes can coexist without interfering with each other. For example, the atomic displacements caused by the rotation of AlO₆ octahedra do not alter the FE distortion occurring along the interface normal because the rotation axis is aligned parallel to the interface normal. In other words, the a⁻a⁻a⁻-type AFD rotation, which is the same as in bulk LAO, is stabilized along the [111] direction, while the internal electric field polarizes the LAO lattice, resulting in phase transition to the noncentrosymmetric R3c phase with FE distortion. Hence, the FE and AFD modes coexist in the LAO/STO (111) heterostructure below t_c. The total energy calculation of the 3-b.l. LAO/STO (111) heterostructure with FE distortion verified that the bulk-like AFD rotation of LAO (a⁻a⁻a⁻ tilt by ~8°) can stabilize the system by lowering the total energy; fig. S5 clearly shows that as the AFD rotation increases, the energy gain associated with the FE distortion becomes larger, reaching around −2 eV per formula unit at the theoretical equilibrium AFD angle of bulk LAO (~8°), demonstrating that AFD rotation and FE distortion are cooperatively coupled in the LAO/STO (111) below t_c. The AFD rotation and FE distortion of LAO propagate into the STO substrate by about three atomic rows due to the strong bond connectivity and geometric constraint (fig. S6), which is consistent with the observation by Jia et al. (47).

We note that the alignment AFD rotation axis parallel to the direction of FE distortion is a sufficient condition but not a necessary condition for AFD-FE cooperative coupling. As shown for the low-temperature quantum paraelectric STO by DFT calculation, even though the FE is along the same axis around which the AFD is, AFD and FE modes compete at small AFD angles (<6°) but cooperate at large angles (>6°) (23–26). For such large AFD angles, there are ABO₃ perovskite oxides, such as LiNbO₃, ZnSnO₃, and LiOsO₃, that exhibit cooperative AFD-FE couplings and undergo a structural phase transition from the paraelectric $R\overline{3}c$ phase to the FE R3c phase (28). The dual nature of AFD-FE coupling found in the aforementioned perovskite oxides has a simple steric origin; for large AFD rotation of BO₆ octahedra (α ~19°), the A-site ion is pushed out-of-plane to lower the repulsive contribution to the energy and induces FE polarization along the [111] direction (28). On the other hand, for a subcritical LAO/STO (111) heterostructure in the present case, the dual nature is driven by the internal polar field even though the AFD rotation angle is as small as ~8°.

Surface oxygen vacancies at LAO/STO (111)

To evaluate whether V_O is energetically favored to form in the LAO/STO (111) heterostructure, we calculated the formation energy of V_O at different (LaO₃)³⁻ layers of 13-b.l.-thick LAO/STO (111), namely, the interface [1st (LaO₃)³⁻], the middle [8th (LaO₃)³⁻], and the surface [14th (LaO₃)³⁻] layers (Fig. 2B). For comparison, the formation energy of V_O was also calculated for the (001) system by considering V_O at different AlO₂⁻ layers, i.e., the interface, the middle (fourth AlO₂⁻), and the surface (Fig. 2A). We found that the formation energy of V_O decreases with increasing the distance from the interface in both systems and becomes zero at the LAO surface, implying spontaneous formation at the LAO surface. We note that the formation of V_O in both LAO/STO systems is assisted by the polar field in the LAO; the gain of electrostatic energy compensates for the energetic cost of V_O formation as V_O cancels the polar field by forming 2DEG at the LAO/STO. Considering the Arrhenius-type dependency of V_O concentration on the formation energy, the position-dependent formation energy predicts that V_O is highly concentrated at the LAO surface (as shown in fig. S7, a small increase of the formation energy from the LAO surface results in orders of magnitude decrease in the V_O concentration). Note that the formation energy of V_O changes less steeply with distance in the (111) interface (approximately −0.19 eV/Å) than that in the (001) interface (approximately −0.26 eV/Å) (Fig. 2, A and B). This is consistent with the smaller increment of polar field per unit length in the (111) system than in the (001) system.

The structural distortion caused by the surface V_O in LAO/STO heterostructures was investigated by DFT calculations across t_c. For the LAO/STO (001) heterostructure, when the thickness of LAO (001) increases over t_c in the absence of surface V_O, the FE distortion decreases in proportion with increasing 2DEG density, but the AFD rotation mode remains suppressed (Fig. 2C). Allowing the spontaneous formation of V_O at the LAO surface, however, enables complete activation of AFD rotation and deactivation of FE distortion. The AFD rotation angle measured for the thick LAO film along the [110] viewing direction is in line with previous DFT calculations that predict that the biaxial tensile strain on LAO (001) stabilizes the ϕ_ab rotations (a⁻a⁻c⁰) with a rotation axis along the in-plane [110] direction (39). These results indicate a thickness-dependent crossover between polar FE and nonpolar AFD lattice distortions across t_c. Note that the AFD rotation and FE distortion value presented in Fig. 2 (C and D) is taken at the central region of LAO. We include the evolution of the AFD rotation and FE distortion as a function of the atomic row for all structure models and provide all the structural information in the Supplementary Materials (figs. S8 and S9 and data files S1 and S2).

It is worth comparing our DFT results with those of Gazquez et al. (18). Regarding the DFT calculations for the subcritical (SrTiO₃)₄/(LaAlO₃)₃ (001) supercell by Gazquez et al. (18), they found no AFD rotation, which is consistent with our observation. However, for the 5- and the 7-u.c.-thick LAO (001) samples without V_O, they claimed that the AFD rotation of AlO₆ octahedral networks is activated in favor of FE distortion, which is inconsistent with our DFT results. In our DFT results, the AFD rotation is always suppressed without V_O at the LAO surface (α ≈ 0°) since a finite internal field still exists in the LAO (001) even for the supercell above t_c. The AFD rotation appeared only when V_O is introduced to the LAO surface since V_O completely cancels the internal field of LAO. Therefore, according to our DFT calculations, even up to 9-u.c. LAO (001) film, the complete evolution of AFD rotation in LAO becomes only possible by the spontaneous formation of V_O. The discrepancy is attributed to the fact that Gazquez et al. (18) artificially neutralized the internal polar field of LAO to activate AFD rotations without need of V_O.

When V_O is introduced to the LAO (111) surface in the DFT calculation, the AFD rotation is disturbed and reduced to α ≈ ±1–3° across the LAO region (Fig. 2D). Simultaneously, the FE distortion is also reduced as the surface V_O cancels the polar field by forming 2DEG at the interface (fig. S10), resulting in the transition of the $R\overline{3}c$ phase of LAO. Hence, in the LAO/STO (111), the FE and AFD modes coexist below t_c but disappear simultaneously with the formation of surface V_O above t_c.

To experimentally probe the formation of V_O at the LAO/STO (111) surface, a series of EELS O-K edges were acquired from the STO substrate to the LAO surface (Fig. 3A). Moving from the LAO/STO interface to the LAO surface, pronounced changes in the spectral features of O-K energy-loss near edge structure (ELNES) (48) were observed: the disappearance of the doublet edge and the chemical shift to lower energy (red shift) of the first peak. Detailed comparisons of two representative EEL spectra extracted from the film surface (red triangle) and the LAO bulk region (blue triangle) are shown in Fig. 3 (B and C, respectively). For the bulk LAO region, the O-K ELNES can be divided into two energy regimes. In the low-energy regime, the first peak around 532 eV, labeled as G, originates from the transition from O 1s to hybridized O 2p and Al 3p states, and the second and third peaks (denoted as A and B) originate from the transition to the hybridized O 2p and La 5d states, which are separated by ~1.7 eV due to the t_2g-e_g crystal field splitting in the dodecahedral coordination (36, 49, 50). The first peak denoted by G is not split into two peaks because the Al 3p states are not affected by crystal field splitting. In the high-energy regime extending from approximately 542 to 548 eV, the first peak labeled C originates from the transition to the hybridized O 2p and La 6p states, and the second peak labeled D originates from the transition to the hybridized O 2p and La 6sp states (50).

Fig. 3. STEM-EELS O-K edge profile, DFT calculation, and local electric field map showing the presence of surface V_O.

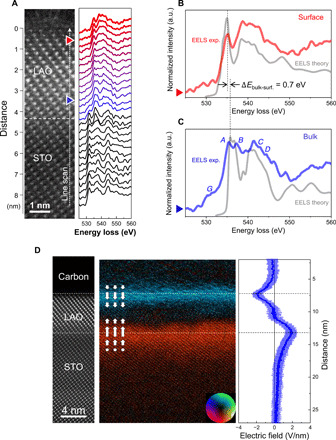
(A) A series of O-K ELNES obtained via a STEM-EELS line scan from the LAO surface to STO substrate with intervals of 2.85 Å. The corresponding STEM annular dark-field (ADF) image of LAO/STO (111) for the EELS experiment is displayed next to the EEL spectra. (B and C) Representative O-K ENLES spectrum extracted from the surface and bulk regions of the LAO film, which are marked by red and blue triangles in (A), respectively. The two extracted O-K ELNES spectra (red from surface and blue from bulk) are compared with the calculated spectra (gray) for the LAO with surface V_O and bulk LAO, respectively. For the calculation, a single-electron core hole was placed in every two oxygen atoms around the surface V_O. The spectral features labeled with uppercase letters (G and A to D) are explained in the main text. The chemical shift of peak A by 0.7 eV is caused by the presence of V_O. (D) Low-magnification atomic electric field map obtained by STEM DPC. The arrows indicate the direction of electric fields along the interface normal. In-plane averaged profile of the electric field along the interface normal are presented on the right. STEM DPC data were calibrated by correcting local variation in sample thickness; the EELS log-ratio method was used to measure local thickness.

To verify whether the observed spectral features of O-K ELNES stem from V_O, DFT calculations were conducted by removing one oxygen from the (LaO₃)³⁻-terminated LAO surface (50 atom-based 2 × 2 × 2 LAO slab), and the results were compared with those of bulk LAO. The major changes caused by the surface V_O are that, as shown in Fig. 3 (B and C, gray line), two peaks (A and B) in the low-energy regime are merged into a single peak, and then the single peak is shifted toward a lower energy by ~0.7 eV (ΔE_bulk-surf.), which is consistent with the experimental measurements. The transition from doublet to singlet suggests that V_O breaks the dodecahedral symmetry by changing the relative distance between the La and O atoms and then modifying the hybridization between the La and O 2p states, resulting in a chemical shift of the O-K edge. This variation was also confirmed by comparing the core-loss EELS simulation and the projected density of states of oxygen atoms (fig. S11). For comparison, we calculated the EELS O-K edge from the (LaO₃)³⁻-terminated LAO (111) surface without V_O (fig. S12). Although the splitting of A and B peaks is not as clear as that of bulk LAO, it is still distinguishable and more obvious than that of the LAO (111) surface with V_O. As a result, the merging of two peaks into a single peak can be used as a spectroscopic fingerprint to verify the presence of V_O on LAO surface. To further investigate the effect of surface V_O concentration on the spectral features of O-K edge, we performed the x-ray absorption near-edge structure (XANES) K-edge simulations for three different surface compositions of LaO₃, LaO_2.25, and LaO₂ using the virtual crystal approximation method (see fig. S13). Similar to the EELS O-K edge results, the most pronounced spectral change made by surface V_O in the XANES O-K edge was the disappearance of A-B peak splitting. As a comparison, the STEM EELS O-K edge obtained from a subcritical LAO/STO (111) film (7-b.l. LAO in thickness) showed that the A peak does not shift toward lower energy and remains well separated from the B peak all the way to the LAO surface, indicating the absence of V_O (fig. S14).

Therefore, the experimentally measured features of O-K ELNES, i.e., the disappearance of peak splitting and chemical shift of the O-K edge by ~0.7 eV, are precisely reproduced by DFT calculations and confirm the presence of V_O at the LAO surface. Furthermore, close examination of the O-K ELNES profiles reveals that the spectral features indicative of V_O extend to ~1.7 nm from the LAO surface (reddish profiles in Fig. 3A and fig. S15), implying the redistribution of surface V_O during the growth. The observed diffusive nature of the V_O profile indicates the dynamic redistribution of V_O during the subsequent growth of LAO over t_c after the spontaneous formation at t_c. While there is the driving force for redistribution of V_O toward the LAO surface during the growth of LAO as V_O can cancel the polar field by existing as bound charges at the surface (because 2DEG is fixed at the interface), the actual distribution is governed by kinetics of V_O diffusion. It is worth noting that the spectral features of O-K ELNES in the near-interface region of STO, where 2DEGs are present, are noticeably distinct from those of bulk STO. The 2DEG occupation distorts electronic structures of the d-orbital hybridization in STO near the interface; thus, the O-K ELNES can be modified from the bulk portion of the STO.

Next, we focus on the STEM differential phase contrast (DPC) to measure the electric field inside the LAO film. The electric field information obtained by STEM DPC indicates the existence of local fields at the LAO/STO interface and LAO surface (more specifically, at the interface with the carbon protection layer) with opposite signs, suggesting the presence of extra space charges therein (Fig. 3D). Evidently, the local field induced at the LAO/STO interface is due to the presence of 2DEG. The electric field with the opposite sign at the LAO film surface indicates the presence of positive charges. Our STEM-EELS data of O-K ELNES strongly indicate that these positive charges are associated with V_O, which donates electrons to the LAO/STO interface. The local field decreases gradually toward the LAO film interior and becomes considerably weak, supporting the compensation of the polar field by V_O and the associated 2DEG formation. While the profiles of the measured electric fields are in good agreement with the DFT calculations, the experimental field strength was lower than the calculated one. This is probably due to the inevitable formation of electrically inactive layers on the surfaces of TEM sample by a high-energy Ga⁺ ion beam during the TEM sample preparation by focused ion beam.

We note that the field-free region in the measured field profile is considerably narrower than that from the DFT calculation, where a distinct zero-field region exists at the center of the LAO film (fig. S10). The observed field profile indicates that the V_O diffuses from the surface into the LAO film interior and that it exists over a relatively wider range of LAO regions, which is consistent with the EELS O-K profile.

FE distortions of LAO/STO (111) heterostructures

The structural changes induced by the formation of V_O in the LAO/STO (111) system can be quantitatively evaluated by tracking the atom positions in STEM annular bright-field (ABF) images (Fig. 4A) (51, 52). From the (111) interplanar spacing (d₁₁₁) measurement, we found no apparent tetragonal compression of LAO, which originates from the Poisson’s effect due to the in-plane tensile strain of LAO to match the STO lattice (Fig. 4B). This behavior is significantly different from that of the (001) system, where the (001) interplanar spacing (d₀₀₁) of LAO is reduced below the bulk value (39). According to Moreau et al. (27), the Poisson’s ratio for LAO (111) under tension is 0.178, whereas it is 0.265 for LAO (001), explaining the observed small tetragonal compression.

Fig. 4. FE distortions of LAO/STO (111) heterostructures measured by STEM and calculated by DFT.

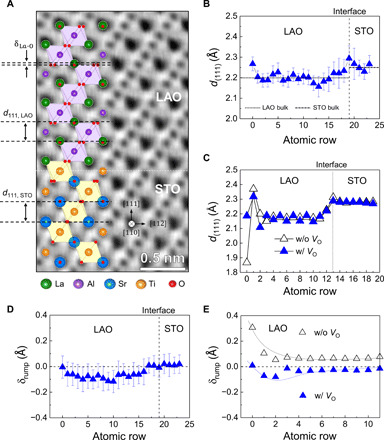
(A) Atomic model of the LAO/STO (111) system overlaid on STEM ABF image. The interplanar spacing of the (111) plane and the FE distortion which was assessed by measuring the amplitude of out-of-plane rumpling of oxygen and La atoms, are indicated by d₁₁₁ and δ_La-O, respectively. (B) Plot of experimentally measured d₁₁₁ from the surface to the interface. (C) Plot of calculated d₁₁₁ from the surface to the interface. The results obtained from the model in the absence of surface V_O and the presence of surface V_O are indicated by open and closed symbols, respectively. (D) Plot of measured δ_La-O. (E) Plot of calculated δ_La-O from the two models with or without V_O. The error bars represent SD.

The LAO/STO (111) system exhibits characteristic structural distortion, particularly where polarity-induced defects exist, i.e., the LAO surface with V_O and the LAO/STO interface with 2DEG. Lattice expansion of STO below the interface (Fig. 4B) has been commonly observed in many experimental and theoretical studies (6, 20, 40, 53). Related literature provides different explanations for this lattice expansion: electrostrictive effect (53), the change in the valence state from Ti⁴⁺ to Ti³⁺ due to the occupancy of 2DEG (30), dilatory distortion resulting from chemical intermixing effects (22), and lattice expansion induced by Sr vacancy (V_Sr) (31). The fact that a similar lattice expansion was observed from the DFT calculation on the defect-free LAO/STO system implies that the most dominant contribution originates from the electrostrictive effect or the change of the valence state of Ti.

A lattice expansion was observed near the LAO surface in the experimental d₁₁₁ plot (Fig. 4B). The LAO (111) surface is a polar surface, rendering it susceptible to structural and chemical reconstruction to compensate for the surface charge. According to DFT calculations, to compensate for the (LaO₃)³⁻ surface charge, the La atoms in the subsurface layer tend to relax outwardly, resulting in the contraction of the first d₁₁₁ and expansion of the second d₁₁₁ (Fig. 4C and fig. S16). Similar surface relaxation has been observed for other perovskite oxide (111) surfaces of SrTiO₃ (54), KTaO₃ (55), and SrRuO₃ (56). The experimental d₁₁₁ plot agrees well with the DFT results, except for the first d₁₁₁. Defining the surface layer for the measurement of the first d₁₁₁ was challenging because the surface is in contact with a carbon protection layer and subject to structural changes due to the Ga⁺ ion beam. When surface V_O is introduced, the effective positive charge of V_O can partly compensate for the surface charges and induce local distortion due to repulsion against neighboring cations. As a consequence, the first d₁₁₁ reverts to the bulk value, while the second d₁₁₁ remains expanded (Fig. 4C). Apparently, for the LAO/STO (111) system with surface V_O, the most pronounced feature of the surface relaxation pattern is the expansion of the second d₁₁₁ (Fig. 4C).

FE distortion in the LAO/STO (111) system can be traced by measuring the amplitude of the out-of-plane rumpling of oxygen and La atoms (δ_rump), as illustrated in Fig. 4A. The δ_rump increases gradually from the surface toward the middle of the LAO film to ~10 pm and decreases back to zero at the interface (Fig. 4D). The δ_rump measured in the 19-b.l. LAO/STO (111), wherein the polar field is canceled by V_O and 2DEG, is significantly different from that typically arising from the depolarization effect in subcritical LAO (111). The sign of the measured δ_rump is negative, which is opposite to the expected depolarization effect. In addition, a large SD (±8.6 pm) exceeding the precision of ±4 pm suggests a large variation in FE distortion on the unit cell scale. The observed FE distortion is attributed to the local distortion caused by V_O, which diffuses inward toward the LAO film from the surface. We found that the profile of experimentally measured FE distortions exhibits a close correlation with the spatial population of V_O in the LAO film, as revealed by the STEM-EELS measurements (fig. S15). Tracing the spectral feature of V_O in the O-K ELNES, the position of the first peak gradually changes from the surface toward the bulk region of LAO and remains almost constant toward the interface, indicating that the V_O concentration increases gradually and then decreases on moving from the surface to the film interior.

To assess how the FE distortion is influenced by V_O in LAO/STO (111), we conducted DFT calculations on cells with and without V_O and measured δ_rump (Fig. 4E). For the model without V_O, a noticeable FE distortion exhibiting a positive δ_rump magnitude less than ~10 pm was observed inside the LAO film. The δ_rump increases toward the LAO surface by a factor of 3. The model with surface V_O shows that the internal FE distortions are diminished to nearly zero throughout the LAO film, except for the negative δ_rump (~10 pm in magnitude) in several subsurface layers. Overall, the FE distortion measured by STEM is consistent with the DFT results obtained from the V_O model. It is presumed that the small negative δ_rump originates from the competition between the extensive (positive) structural relaxation due to the depolarization effect and the local (negative) contribution from the lattice distortion caused by V_O. The electrostatic field difference between the defect-free and V_O structures in our DFT calculations indicates the existence of an additional electrostatic force that drives charge redistribution within several layers near the surface V_O (fig. S17). Considering the LAO/STO (111) sample with a gradient in V_O concentration, the region with the opposite polar state (negative δ_rump) is correlated well with the spatial distribution of V_O. Hence, a small negative δ_rump extending into several subsurface layers is another potential indicator of the presence of V_O inside the LAO (111) film.

AFD rotations of the LAO/STO (111) heterostructure

A two-dimensional map of AFD rotation was obtained by measuring the rotation angle (α) of the ripple pattern observed in the STEM ABF images obtained along the $[11\overline{2}]$ zone axis (Fig. 5). Each pixel in the rotation map is color-coded to represent the sign and magnitude of the measured AFD rotation angle of each AlO₆ octahedron (57). For direct comparison with the DFT models with and without surface V_O, similar AFD rotation maps were obtained from the simulated ABF images of the DFT models.

Fig. 5. AFD rotation of LAO/STO (111) heterostructure–comparison between experimental measurement using STEM ABF and theoretical DFT calculation.

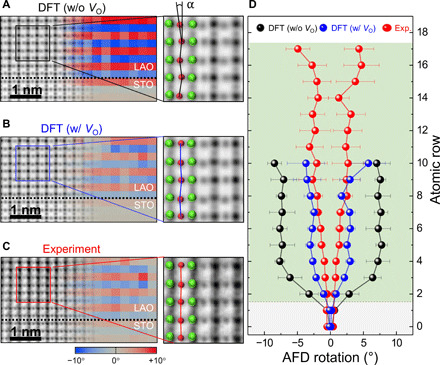
(A and B) AFD rotation maps obtained from the simulated STEM ABF image using the atomic data of DFT model without or with V_O, respectively. Note that the apparent variations in color scale are ascribed to the inherent error of our iterative measurement method for atomic column positions, which is ±1.3° for the present case. The atomic model used for (B) is the same as the one in fig. S4D, i.e., one V_O of four oxygen in the subsurface (LaO₃)³⁻ layer, corresponding to the composition of (LaO_2.25)^1.5−. (C) AFD rotation map obtained from the experimental STEM ABF image. The viewing direction is the $[11\overline{2}]$, which is the same as that for the atomic model in Fig. 1E. The AFD rotation (α) is indicated in the zoomed-in image with the aid of the overlaid atomic model. (D) Plot of measured AFD rotation angles (α) from the results shown in (A) to (C) with the distance from the interface to the surface. Each data point was obtained via in-plane averaging.

For the V_O-free LAO/STO (111) system (Fig. 5A), the alternating characteristic of the AFD rotation is displayed as an alternating stripe pattern in which the measured AFD angle (~±7.5°; SD ±0.42°) is considerably similar to the corresponding value of bulk LAO. In contrast, notable suppression of the AFD rotation angle (~±2.8°; SD ±0.96°) was observed for the LAO/STO (111) with V_O (Fig. 5B), which is in good agreement with the experimental AFD rotation map (Fig. 5C). The line profiles of the AFD rotation angle plotted from the interface to the surface further corroborate that the suppressed AFD rotation measured in the experiment originates from the presence of surface V_O (Fig. 5D). Here, a single surface V_O suppresses the FE distortion and makes the entire LAO film recover the $R\overline{3}c$ phase. The observed suppression of AFD rotation and FE distortion of the LAO/STO (111) heterostructure above the t_c by V_O was highly reproducible as shown by the extra dataset in fig. S18.

DISCUSSION

Regardless of the LAO/STO interface orientation, V_O is energetically favored to form at the LAO surface above t_c, followed by the spontaneous generation of 2DEG at the interface. On the other hand, structural distortions evolve differently depending on the thickness of the LAO and the interface orientation. For the LAO/STO (001) heterostructure, the nonpolar AFD rotation and polar FE distortion tend to compete and suppress each other. The AFD rotations only appear above t_c when the polar field is compensated. Compared with the competitive evolution in LAO/STO (001), we found that the AFD and FE modes are cooperatively coupled in LAO/STO (111); they coexist below t_c and disappear simultaneously with the formation of surface V_O above t_c. Our studies have shown that the LAO/STO heterostructure can serve as a platform to tune AFD-FE coupling by varying the interface orientation and thickness of the LAO film across t_c for 2DEG formation. This AFD-FE tunability offers a previously unidentified pathway for controlling the structural evolution and related physical properties of oxide heterostructures.

MATERIALS AND METHODS

Thin-film growth

LAO/STO heterostructures with the controlled atomic layer were produced using pulsed laser deposition. LAO layers were deposited at their growth temperature of 550°C under an oxygen partial pressure of 10⁻³ mbar. Before deposition, an STO (111) substrate was chemically etched with buffered hydrofluoric (BHF) for 60 s and then annealed at 900°C for 6 hours under oxygen flow to induce single termination of the Ti⁴⁺ surface with controlled step and terrace structures (6). The epitaxial LAO film was grown with a thickness of 20 b.l. on the STO (111) substrate, where the thickness of 1 b.l. is 0.22 nm, assuming a pseudocubic unit cell for LAO. During the growth of the LAO films, reflection high-energy electron diffraction (RHEED) intensity oscillations were obtained in situ with the electron beam aligned parallel to the $[1\overline{1}0]$ orientation of the STO (111) substrate. The periodic RHEED oscillations verified that the growth occurred in a layer-by-layer manner. After deposition, the sample was cooled down to room temperature at the same operating pressure.

Microscopy analyses and simulations

Cross-sectional samples of the (111) LAO/STO heterostructures were prepared via Ga⁺ ion beam milling at an accelerating voltage of 15 kV using a dual-beam focused ion beam system (FIB, Helios 450F1, Thermo Fisher Scientific). Aberration-corrected STEM (JEM-ARM300CF, JEOL) equipped with an EELS (Gatan Quantum ER965) was used to obtain atomic-scale images of the samples in ABF and high-angle annular dark field (HAADF) imaging modes. Detector angle ranges of 7.5 to 17 and 70 to 175 mrad were set for these imaging modes, respectively. The convergence semiangle for forming the focused probe was 23 mrad. The statistical noise floor in all STEM images was removed using Wiener filtering implemented using a commercial software (HRTEM Filter Pro, HREM Research Ltd.). To track the atom positions in STEM images for the measurement of FE distortions and AFD rotations, the center of mass of the column intensity was determined using a commercial software (qHAADF, HREM Research Ltd.). STEM image simulations were performed using the multislice method in the QSTEM software package (58) using the microscope parameters that closely represent the experimental conditions. EELS line scan data across the LAO/STO interface were separately recorded with energy ranges of 400 to 900 eV (for Ti-L_2,3 and O-K edges) and 1500 to 1900 eV (for La-M_4,5 and Al-K edges). The energy dispersion and dwell time per pixel were 0.25 eV and 2.0 s, respectively. The loss energy of the core-loss EELS data was calibrated by tracking the energy drift of the zero-loss peak, which was simultaneously recorded with the core-loss data. The DPC signal was obtained by segmenting all field detector in eight segments (SAAF Octa, JEOL). The beam deflection was measured and converted to an electric field to measure the residual electric field in the LAO film (59, 60). The convergence angle of the electron probe for DPC was 23 mrad. A STEM probe smaller than the length scale of the electric field variation in the region of interest was used to minimize the intensity redistribution in the transmitted disk and observe only a simple shift of the transmitted disk. The angle ranges of the inner and outer detectors were set as 0 to 15 and 15 to 31 mrad, respectively.

Theoretical modeling

For charge carrier distribution and structural evolution, we designed (001)- and (111)-oriented LAO/STO supercells with atomically well-defined interfaces and surfaces. For the case of the LAO/STO (001) interface, we used 2 × 2 in-plane (LAO)_x/(STO)₄, (x = 3, 7, and 9 u.c.) slab geometry with a vacuum thickness of 16 Å. The in-plane lattice constant of the LAO/STO slab was fixed to 2 × 2 a_STO (a_STO= 3.943 Å), obtained with the Perdew-Burke-Ernzerhof (PBE) potential. For the LAO/STO (111) interface, we used symmetric sandwich structures of (LAO)_x/(STO)₄/(LAO)_x (x = 3, 7, 10, and 13 b.l.) supercells separated by a vacuum slab of 16 Å. The interface was terminated with (LaO₃)³⁻/Ti⁴⁺, and the LAO surface was terminated with either stoichiometric Al³⁺- or nonstoichiometric (LaO₃)³⁻. The in-plane lattice constant of the supercells was fixed to $\sqrt{2} a_{\text{STO}}$. First-principles DFT calculations were performed using the generalized gradient approximation–PBE (GGA-PBE) exchange-correlation functionals (61) and projector-augmented wave method (62) with a plane-wave basis, as implemented in the Vienna ab initio simulation package code (63–66). Reliable DFT results for the 2DEG formation in STO/LAO heterostructures have been reported with PBE potential (36, 41, 67–69). For La, Al, O, Sr, and Ti, 5s² 5p⁶ 5d¹ 6s², 3s² 3p¹, 2s² 2p⁴, 4s² 4p⁶ 5s², and 3d³ 4s¹ were considered as valence electrons, respectively. The plane waves were included up to a kinetic energy cutoff of 450 eV. For the Brillouin-zone integration, Г-centered 2 × 2 × 1 and 4 × 4 × 1 k-point meshes were used for the LAO/STO (001) and (111) supercells, respectively. All calculations were converged in energy to 10⁻⁵ eV per cell, and the structures were completely relaxed until the forces were less than 10⁻² eV/Å.

EELS calculation

EELS simulations were performed using the Cambridge serial total energy package (CASTEP) code (70) to achieve EELS ELNES of the O-K edge for LAO. For the bulk LAO, a (111)-oriented LAO u.c. ($\sqrt{2}a\times \sqrt{2}a$ in-plane) composed of 15 atoms was used, and the core hole was considered. To investigate the influence of surface V_O on the EELS ELNES of the O-K edge, one oxygen was removed at the (LaO₃)³⁻ subsurface in a symmetric (LaO₃)³⁻-terminated (111) LAO slab composed of 29 atoms. One core hole was induced on a single oxygen atom to obtain the intensity distribution of EEL spectra within the single-particle approximation, and the single-electron core hole was placed in neighboring oxygen atoms around the surface V_O. The plane-wave basis set and on-the-fly generation ultrasoft pseudopotential were used to describe the exchange-correlation functional within GGA-PBE. We used an energy cutoff of 500 eV and 3 × 3 × 2 and 3 × 3 × 1 Monkhorst-Pack grids of k-points for the bulk and slab, respectively. A Gaussian broadening of 0.2 eV was applied to the calculated EEL spectra for the sake of comparison with the experimental EEL spectra with a limited energy resolution.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/17/eabe9053/DC1