What is the Impact of the Analysis Method Used for Health State Utility Values on QALYs in Oncology? A Simulation Study Comparing Progression-Based and Time-to-Death Approaches

Abstract

Background

Health state utility values (‘utilities’) are an integral part of health technology assessment. Though traditionally categorised by disease status in oncology (i.e. progression), several recent assessments have adopted values calculated according to the time that measures were recorded before death. We conducted a simulation study to understand the limitations of each approach, with a focus on mismatches between the way utilities are generated, and analysed.

Methods

Survival times were simulated based on published literature, with permutations of three utility generation mechanisms (UGMs) and utility analysis methods (UAMs): (1) progression based, (2) time-to-death based, and (3) a ‘combination approach’. For each analysis quality-adjusted life-years (QALYs) were estimated. Goodness of fit was assessed via percentage mean error (%ME) and mean absolute error (%MAE). Scenario analyses were performed varying individual parameters, with complex scenarios mimicking published studies. The statistical code is provided for transparency and to aid future work in the area.

Results

%ME and %MAE were lowest when the correct analysis form was specified (i.e. UGM and UAM aligned). Underestimates were produced when a time-to-death element was present in the UGM but not included in the UAM, while the ‘combined’ UAM produced overestimates irrespective of the UGM. Scenario analysis demonstrated the importance of the volume of available data beyond the initial time period, for example follow-up.

Conclusions

We show that the use of an incorrectly or over-specified UAM can result in substantial bias in the estimation of utilities. We present a flowchart to highlight the issues that may be faced.

Electronic supplementary material

The online version of this article (10.1007/s40258-020-00620-6) contains supplementary material, which is available to authorized users.

Key Points for Decision Makers

A mismatch between the data structure and analysis method results in biased and inaccurate estimates of utility values.

Unexpectedly, analysing utilities as a combination of progression- and TTD-based values performed poorly, even if utilities were generated within a corresponding framework. Over-specification of analyses should therefore be avoided.

The volume of data available has a marked impact on the accuracy of estimates; this especially means the duration of follow-up and number of long-term survivors.

Introduction

Health state utility values are pivotal in cost-utility analysis—the preferred form of cost-effectiveness analysis for health technology assessment (HTA) agencies in the UK, and others internationally. Utility values are used to formally capture changes in patient health-related quality of life (HRQL), which then impact the estimation of quality-adjusted life-years (QALYs), and consequently the incremental cost-effectiveness ratio (ICER). The ‘true’ HRQL of patients (and the pattern this follows through the course of a disease) is not possible to objectively measure, and so preference-based measures such as the EQ-5D may instead be used to capture key determinants of HRQL. These measures capture HRQL through self-reporting of a patient’s current health state, and how this affects their capabilities in different health dimensions (such as self-care and anxiety/depression). Patient responses are then converted into utilities, which are then grouped to produce health state utility values that can populate economic models [1].

The method of grouping utilities by health state in oncology has generally centred around disease progression. In cancer cost-utility analyses, this approach implicitly assumes that progression status is the most important driver of HRQL. Recent literature, however, suggests that progression is not always a good proxy for HRQL [2], an issue magnified with immune-oncology (IO) agents where there can be issues with ‘pseudo-progression’ where the action of the treatment is mistaken for disease progression [3]. The reasons for progression being imperfectly correlated with HRQL may include delays from the effect of cancer growing to the experience of symptoms, and that the impact of disease progression will vary by disease area (for instance, haematological vs. solid tumour cancers). Similarly, there may be differences between tumours growing or spreading to different locations—both of which may be classified as disease progression. Consequently, alternative methods of analysing HRQL data have been proposed, including grouping observations by when the HRQL measure was taken prior to a patient’s death, termed ‘time to death’ (TTD) [4], with other approaches classifying patients by different health states, for instance by response to treatment.

A number of published economic evaluations of IO treatments have used the approach of TTD-based utility values, noting that such an approach avoids a number of issues typically attributed to progression-based analyses [5–7]. A recent review of IO appraisals performed by the National Institute for Health and Care Excellence (NICE) found that of the 21 identified company submissions, 11 defined health states by progression status, seven by TTD, and three by using a model that had aspects of both elements [8]; a per-appraisal summary is presented in the Online Supplementary Materials (OSM).

Under ideal circumstances, the most appropriate health states could be determined by analysis of complete patient-level data from clinical trials—unfortunately this is not always possible due to issues that are common in contemporary studies. These include limited follow-up (many trials include a substantial proportion of survivors who are administratively censored), the absence or limited amount of HRQL data post-progression, the previously highlighted issue of pseudo-progression, the interval between HRQL observations, and the role of missing data. As an example, a previous study considered trial data for seven licensed IO indications, for which overall survival data were available for a mean of 1.95 years after treatment initiation (range 1.38–3.95) with a mean of 40.6% of patients still alive at the end of follow-up (range 9.4–70.0) [8].

Due to such limitations, both progression- and TTD-based methods seek to assign observations in homogenous groups, noting that there may be small differences within the group that may need to be accounted for by covariates (such as treatment assignment). If complete data were available for all patients from treatment initiation until death, the results of each analysis would be identical (as modelled groups would reflect the mean). Even in practice with complete data, results using the two approaches are likely similar as they are correlated; most patients will experience disease progression before their death, with progression being irreversible. There may, however, be important differences in how each of the approaches perform when data are more limited; particularly with regard to the features seen in IO studies—one of which is the presence of long-term survivors, who will represent a substantial amount of censored data and were atypical for studies in end-stage cancer until recently.

To understand the relative performance of progression- and TTD-based methods in analysing HRQL under different study designs (informed by recent IO trials), we conducted a simulation study. The use of such an approach allows us to understand how the application of the different methods varies when the data generation mechanism is known—something that is not possible with ‘real’ data. Based on the findings of this study, we highlight when bias and error may arise with different methods of analysis, and the possible impacts these may have when estimating QALYs in economic models.

Methods

Data Simulation

A simulation study was programmed in the statistical software package R version 3.6.1 [9] following published guidance on simulation studies [10, 11]. In each simulation, survival and utility data were resampled, with 2500 simulations performed for each scenario; at this point results were seen to have converged visually, with Monte Carlo Standard Errors of all outcomes an order of magnitude smaller than the results.

The simulation took approximately 10 days to run (including scenario analyses) on an Intel 8th generation i5 laptop. The statistical code is provided as supplementary material for transparency and to aid future work in the area (see OSM).

Survival Data

Time-to-event data were simulated for a hypothetical IO treatment. In order to mimic published studies, three groups of patients were assumed to exist, with different proportions of each sampled from parametric survival functions. These three groups were those with poor outcomes (in published studies a large number of patients experience only a few months of progression-free survival), those with intermediate outcomes (from several months to several years), and a final group who do not experience disease progression—the ‘plateau’ seen in IO studies of patients with durable survival.

To simulate survival data each patient had a ‘natural’ life expectancy sampled from UK Office for National Statistics Life Tables [12] based on their age and gender; this was then used as the upper limit of their survival. Each patient was then randomized to the poor, intermediate, or long-term survival groups, with a time to progression (TTP) sampled from a corresponding survival distribution. Post-progression survival (PPS) was then sampled for all patients from a further distribution, with overall survival for each patient then given as the minimum of TTP and PPS added together, or alternatively the patient’s natural life expectancy.

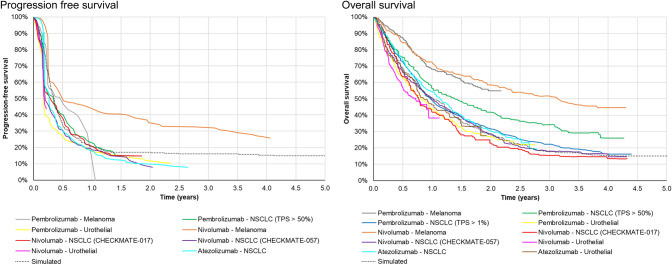
To produce patient characteristics (age and sex) from which to sample life expectancy, similar figures were used to studies previously conducted for IOs in non-small-cell lung cancer, melanoma, and renal cell carcinoma [8]. The values used to generate survival data such as patients sampled to each group, and survival models used to sample survival times are shown in Table 1. The resulting approach mimics well the patterns of survival seen with existing IOs (Fig. 1). Functional R code to demonstrate the approach is presented in the supplementary material.

Table 1.

Setup of the simulation study base case and scenarios

Characteristic	Base-case value	Rationale	Scenario analysis value(s)
Study design settings
Number of patients in study	300	300 patients is approximately what has been seen in immune-oncology studies to date (though this does vary)	150 (scenario 1) 500 (scenario 2)
Cohort age, years	65	The approximate age of patients enrolled in to contemporary immunotherapy studies	55 (scenario 3) 75 (scenario 4)
Male: female ratio	1:1	Although the gender ratio in studies is driven by the prevalence of conditions. In the simulation study, however, this only affects background mortality so is not varied
Utility measurement interval	120 days	Utilities are usually measured at increasing intervals over time, for simplicity a uniform pattern has been imposed	90 days (scenario 5) 180 days (scenario 6)
Administrative censoring for utility values	48 months for all patients	Utilities are generally only collected until the end of the study period. A ‘typical’ data collection period has been used, which is varied in sensitivity analysis to include other observation periods seen in trials	18 months for all patients (scenario 7) 60 months for all patients (scenario 8) Until progression or maximum 60 months (scenario 9) Until 30 days after progression or maximum 60 months (scenario 10)
Missing data	0%	Missing data can be an issue in clinical studies. In the base case this is assumed to be zero, with different mechanisms for missingness explored in sensitivity analysis	10% of observations MCAR (scenario 11) 10% of patients lost to follow up at a random timepoint (all subsequent data censored; permanent MCAR) (scenario 12) Increasing likelihood of censored values as utility decreases (MNAR) (scenario 13) Censoring probability linked to time to death (scenario 14)
Survival simulation
Ratio of patients exhibiting poor/intermediate/background survival	13:7:4	In immune-oncology studies a number of patients have experienced durable survival, this proportion however varies between studies	13:7:0 (scenario 15)—no long-term survivors 13:7:2 (scenario 16)—a lower rate of long-term survivors 13:7:6 (scenario 17)—a higher rate of long-term survivors
Time to progression for patients with poor outcomes (months)	Gamma (shape = 3, scale = 1)	Immuno-oncology studies exhibit a changing hazard over time with a short period on enrollment before many progression and survival events are observed, which decrease in frequency over time, with few being observed beyond 18 months [3]
Time to progression for patients with intermediate outcomes (months)	Weibull (shape = 1.3, scale = 8)
Post-progression survival	Weibull (shape = 1.5, scale = 14)
Percentage of deaths pre-progression	20%
Pseudo-progression	0%	A known issue with immuno-oncology is that the immune response can lead to swelling, which may be (incorrectly) categorized as disease progression. Whilst new measures have been developed to account for this, the impact is explored in sensitivity analysis where a portion of patients are miscategorized for regressions as having PFS as per the intermediate group	10% of long-term survivors incorrectly assumed to have progressed in line with the patterns seen for other groups (scenario 18)
Link between pre- and post-progression survival	Independent distributions	The assumption is made that response to treatment, and post-progression survival are uncorrelated i.e. patient characteristics are not both predictive and prognostic	A scenario analysis (scenario 19) is presented where simulated post-progression survival is multiplied by 1.25 for long-term survivors, and 0.75 for short-term survivors. This implicitly assumes responders to treatment are healthier patients
Utility simulation
Patient utility distribution before progression or being close to death	Beta (α = 80, β = 20) i.e. mean 0.80, quartiles 0.77, 0.80, 0.83	In line with the literature on utilities which show reasonably high levels pre-progression, falling on disease progression [18]
Progressed utility (in progression scenarios) distribution	Beta (α = 60, β = 20) i.e. mean 0.75, quartiles 0.72, 0.75, 0.78
Time at which utility fell before death (in time-to-death scenarios)	Uniform (minimum, 90 days; maximum, 270 days)	Various observations have been reported in the literature, and thus a range is used which varies by scenario
Utility fall before death (distribution)	Normal (mean, 0.5; SD, 0.2)	The absolute fall seen in studies have differed, but all have been substantial

MCAR missing completely at random, MNAR missing not at random, N number of patients, OS overall survival, PFS progression-free survival

Fig. 1.

Example of simulated time to event data compared to published immuno-oncology trials

Utility Data and Generation of Quality-Adjusted Life-Years (QALYs)

Patient utility values were assumed to be correlated at the individual level, using a parameter for simulated underlying health. This underlying health was then used to give three approaches for generating utilities: health decreasing on progression (progression-derived), health decreasing as a patient is approaching death (TTD-derived), and health decreasing on progression and as a patient is approaching death (combination-derived)—the three approaches found in the review of previous NICE appraisals (Supplementary Table 1, OSM).

Using the simulated survival duration and patients’ underlying health status, utility values were then simulated for each day a patient was alive using a beta distribution. This dataset was duplicated for utilities to be produced for the three utility generation mechanisms (UGMs). To each dataset appropriate decrements were applied if: a patient had progressed disease (progression-derived); was in the ‘close-to-death’ window (TTD-derived); was progressed or in the ‘close-to-death’ window (combo-derived). These different approaches are shown stylistically in the OSM Appendix. The utility values for each patient day were then summed across datasets to calculate the QALYs experienced by each cohort.

To ensure the simulation mimics trial data, utility values were sampled according to a measurement interval—120 days in the base case, up to the point at which administrative censoring in the simulated trial was assumed to occur (48 months in the base case). This restricted dataset was then used with each form of analysis to estimate QALYs for the population, which could be compared to the QALYs experienced in the full dataset.

Analytical Approaches

Following the derivation of the full datasets for each of the UGMs, the restricted datasets (with measurement intervals and administrative censoring applied) were then analysed via general estimating equation (GEE) regressions using TTD-based and/or progression-based approaches, for a total of three UGMs, and three utility analysis methods (UAMs). GEE regressions were used as observations would likely be correlated at the patient level (as in real life) due to being reported by the same patient (in our study applied using each patients’ ‘underlying health’) [13].

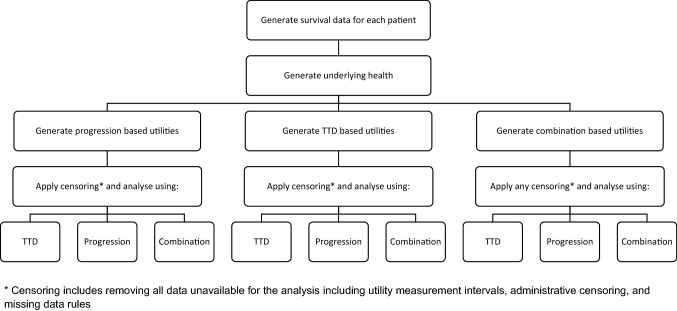
In the simulations, survival was assumed to be known so as to isolate the effect of utility estimation methods (and not conflate this with a survival extrapolation approach). To compare between the three analysis approaches, the estimated utility for each health state from regression models was multiplied by the (known) time spent in each health state, to produce estimated QALYs. For clarity the simulation study design is shown visually in Fig. 2.

Fig. 2.

Visual representation of the generation and analysis of each scenario

Outcomes

The percentage mean error (%ME) and the percentage mean absolute error (%MAE) in estimated versus ‘actual’ QALYs were calculated for each analysis method, using each dataset. The result of these measurements over 2500 simulations were the main outcomes of the study.

These metrics were selected as the %ME gives an estimation of bias, i.e. whether a method is systematically under/over predicting, while the %MAE gives a measure of the absolute error. Percentages were used as the number of QALYs generated in each scenario (and under each UGM) were slightly different, and would also vary between scenarios. As a result the same level of percentage error would result in different levels of absolute error, masking the magnitude of any differences between scenarios.

Scenario Analyses

Scenario analyses were conducted where common features of clinical trials were varied individually to understand the impact on each data generation mechanism and analysis method (Table 1).

Settings relating to trial design and/or patient characteristics included the age and number of patients, interval of utility observation, and duration of time before administrative censoring. The effect of different mechanisms for missing data were also tested (in the base case, data are assumed to be complete)—the mechanisms included data missing completely at random (MCAR) either as individual values censored or patients assumed to be lost to follow-up, missing related to the known event of death date (formally known as missing at random, MAR), and missing linked to lower utility values (formally known as missing not at random, MNAR). Further sensitivity analyses were performed varying survival parameters, including the number of long-term survivors, and the role of pseudo-progression.

A set of more complex scenario analyses were also undertaken, which mimicked the design of IO studies published in the literature. The studies chosen include those of ipilimumab, nivolumab, pembrolizumab and atezolizumab. These scenarios attempted to synthesize multiple issues and understand how each approach would fare when faced with the trial conditions that IO therapies have been studied under (Table 2), given the assumptions inherent in the simulation study.

Table 2.

Setup of ‘real’ scenarios, mimicking previous immunotherapy studies

#	Scenario	Scenario analysis value(s)
A	Ipilimumab in melanoma [19], ipilimumab monotherapy arm	N = 137; utility data available for 54 months for all patients; pseudo-progression present (assumed 25% of long-term survivors) Age = 57; 59% male; survival plateau = 17%
B	Nivolumab in renal cell carcinoma [20], nivolumab monotherapy arm	N = 410; utility data available for 32 months for all patients Age = 62; 77% male; survival plateau = 20%
C	Pembrolizumab in non-small-cell lung cancer [21], pembrolizumab 3 weekly arm	N = 287; utility data available for 27 months for all patients Age = 64; 51% male; survival plateau = 30%
D	Atezolizumab in urothelial carcinoma [22], atezolizumab monotherapy arm	N = 467; utility data available for 23 months for all patients Age = 67; 76% male; survival plateau = 22%

Results

The results of the base-case analysis are shown numerically in Table 3 and visually in the OSM Appendix. In the base case it can be seen that although %MAE is non-zero (due to variability and sampling of utility values), progression and TTD-based UAMs were unbiased and accurate when used appropriately (i.e. when the UGM and UAM matched, ME of 0.0% and − 0.4%, MAE of 0.4% and 0.6%). When there was a mismatch between UGM and UAM (e.g. analysing progression-based utilities as TTD), both methods were less accurate, though not majorly so. The UAM of a combination of progression and TTD (combination-based approach) fared much worse with results showing lower accuracy (MAE 0.7–5.9%) and a degree of bias shown in the ME being non-zero, even when the UGM used this approach (a 5.5% overestimate in QALYs in the base-case scenario). This may be a result of the multicollinearity between progression and TTD, and difficulty in estimating multiple parameters based on a limited number of observations.

Table 3.

Scenario analysis results

Scenario	Utility generation mechanism (UGM)	True QALYs	Utility analysis method (UAM)
			% Mean error (ME)			% Mean absolute error (MAE)
			Prog	TTD	Combo	Prog	TTD	Combo
Base case	Prog-derived	3.4	0	0.2	− 0.7	0.4	0.5	0.7
	TTD-derived	3.3	− 3.5	− 0.4	5.8	3.5	0.6	5.9
	Combo-derived	3.1	− 3.4	− 0.2	5.5	3.4	0.6	5.5
Scenario 1	Prog-derived	3.4	0	0.2	− 0.7	0.4	0.5	0.8
N = 150	TTD-derived	3.3	− 3.4	− 0.4	6	3.5	0.7	6
	Combo-derived	3.1	− 3.4	− 0.3	5.6	3.5	0.7	5.6
Scenario 2	Prog-derived	3.4	0	0.2	− 0.7	0.2	0.3	0.7
N = 300	TTD-derived	3.3	− 3.4	− 0.4	5.8	3.4	0.6	5.9
	Combo-derived	3.1	− 3.4	− 0.3	5.4	3.5	0.5	5.5
Scenario 3	Prog-derived	4.5	0	0.3	− 0.5	0.4	0.5	0.6
Age = 55 years	TTD-derived	4.5	− 3.1	− 0.4	4.3	3.1	0.7	4.3
	Combo-derived	4.2	− 3.1	− 0.3	4	3.1	0.7	4
Scenario 4	Prog-derived	2.4	0	0	− 1	0.4	0.4	1
Age = 75 years	TTD-derived	2.3	− 4.6	− 0.4	8.6	4.7	0.6	8.6
	Combo-derived	2.2	− 4.6	− 0.3	8	4.7	0.6	8.1
Scenario 5	Prog-derived	3.4	0	0.4	− 0.7	0.3	0.5	0.7
Utility interval = 90	TTD-derived	3.4	− 5.6	− 0.4	5.3	5.6	1.1	5.5
	Combo-derived	3.2	− 5.6	− 0.6	4.9	5.6	0.8	5.1
Scenario 6	Prog-derived	3.4	0	0	− 0.7	0.5	0.5	0.8
Utility interval = 180	TTD-derived	3.3	− 1.2	− 0.4	6.1	1.4	0.5	6.1
	Combo-derived	3.1	− 1.2	− 0.1	5.7	1.4	0.6	5.7
Scenario 7	Prog-derived	3.4	0	0.7	− 0.7	0.5	0.8	0.8
Length = 18 months	TTD-derived	3.3	− 7.4	− 0.4	5	7.4	1.8	5.4
	Combo-derived	3.1	− 7.7	− 1	4.6	7.7	1.5	5
Scenario 8	Prog-derived	3.4	0	0.1	− 0.7	0.4	0.4	0.8
Length = 60 months	TTD-derived	3.3	− 2.5	− 0.4	5.9	2.5	0.5	5.9
	Combo-derived	3.2	− 2.4	− 0.2	5.5	2.5	0.6	5.5
Scenario 9	Prog-derived	3.3	0	0.1	− 0.7	0.4	0.4	0.8
Length = 60 months or progression	TTD-derived	3.3	− 2.5	− 0.4	5.9	2.6	0.5	5.9
	Combo-derived	3.1	− 2.5	− 0.2	5.5	2.6	0.6	5.6
Scenario 10	Prog-derived	3.4	0	0.1	− 0.7	0.4	0.4	0.8
Length = 60 months or progression + 30 days	TTD-derived	3.3	− 2.7	− 0.4	5.9	2.7	0.5	5.9
	Combo-derived	3.1	− 2.6	− 0.2	5.6	2.7	0.6	5.6
Scenario 11	Prog-derived	3.4	0	0.1	− 0.7	0.4	0.5	0.8
Missing data = 10% randomly MCAR	TTD-derived	3.3	− 1.8	− 0.4	6	1.9	0.5	6
	Combo-derived	3.1	− 1.8	− 0.1	5.6	1.9	0.6	5.6
Scenario 12	Prog-derived	3.4	0	0.2	− 0.7	0.4	0.5	0.8
Missing data = 10% of patients MCAR	TTD-derived	3.3	− 3.7	− 0.4	5.8	3.7	0.7	5.8
	Combo-derived	3.1	− 3.6	− 0.3	5.4	3.7	0.7	5.4
Scenario 13	Prog-derived	3.4	0.2	0.4	− 0.5	0.5	0.5	0.7
Missing data = proportional to utility (MNAR)	TTD-derived	3.3	− 2.7	− 0.4	5.9	2.7	0.6	5.9
	Combo-derived	3.2	− 2.6	− 0.1	5.7	2.7	0.6	5.7
Scenario 14	Prog-derived	3.4	0	0.2	− 0.7	0.4	0.5	0.8
Missingness increases closer to death	TTD-derived	3.4	− 3	− 0.4	5.8	3	0.6	5.9
	Combo-derived	3.2	− 2.9	− 0.2	5.4	2.9	0.6	5.5
Scenario 15	Prog-derived	1	0	− 0.5	− 2.5	0.4	0.6	2.5
No long-term survivors	TTD-derived	0.8	− 4.5	− 0.4	27.5	4.6	1.1	27.5
	Combo-derived	0.7	− 4.6	− 0.5	25	4.8	1.3	25
Scenario 16	Prog-derived	2.2	0	0.1	− 1.1	0.4	0.5	1.1
Lower rate of long-term survivors	TTD-derived	2.1	− 6.5	− 0.4	8.8	6.5	1	9.1
	Combo-derived	2	− 6.7	− 0.7	8.1	6.7	1	8.5
Scenario 17	Prog-derived	4.3	0	0.2	− 0.6	0.5	0.5	0.7
Higher rate of long-term survivors	TTD-derived	4.3	− 1.4	− 0.4	4.6	1.5	0.5	4.6
	Combo-derived	4.1	− 1.4	− 0.1	4.3	1.5	0.5	4.3
Scenario 18	Prog-derived	3.4	0.1	0.2	− 0.5	0.5	0.5	0.6
10% Pseudo-progression included	TTD-derived	3.3	− 10	− 0.4	5.5	10	0.6	5.7
	Combo-derived	3.2	− 8.1	− 0.2	5.4	8.1	0.6	5.5
Scenario 19	Prog-derived	3.3	0	0.2	− 0.7	0.4	0.5	0.8
Link between pre- and post-progression survival	TTD-derived	3.2	− 4.5	− 0.4	6	4.5	0.7	6.1
	Combo-derived	3	− 4.4	− 0.3	5.7	4.5	0.7	5.7
Scenario A	Prog-derived	4	0.1	0.2	− 0.4	0.2	0.3	0.4
Ipilimumab melanoma	TTD-derived	4	− 14.2	− 0.4	4.3	14.2	0.7	4.5
	Combo-derived	3.7	− 12	− 0.4	4.3	12	0.6	4.4
Scenario B	Prog-derived	3.7	0	0.4	− 0.6	0.2	0.5	0.6
Nivolumab RCC	TTD-derived	3.7	− 4.4	− 0.4	5	4.4	0.9	5.1
	Combo-derived	3.5	− 4.5	− 0.5	4.6	4.5	0.7	4.7
Scenario C	Prog-derived	4.6	0	0.5	− 0.5	0.2	0.5	0.5
Pembrolizumab NSCLC	TTD-derived	4.7	− 3	− 0.4	4.1	3	0.8	4.1
	Combo-derived	4.4	− 2.9	− 0.3	3.8	2.9	0.7	3.8
Scenario D	Prog-derived	3.5	0	0.5	− 0.7	0.3	0.6	0.7
Atezolizumab UCC	TTD-derived	3.4	− 5.3	− 0.4	5.3	5.3	1.1	5.4
	Combo-derived	3.2	− 5.5	− 0.5	4.9	5.5	0.9	5

Scenario analyses demonstrate how different assumptions around study design impacted the results. Varying patient numbers (scenarios 1 and 2) and patient age (scenarios 3 and 4) did not greatly affect results, nor did the frequency at which utility was measured (scenarios 5 and 6). More important, however, was the duration of follow-up data available; having only 18 months of data available (scenario 7) led to exaggerated errors where the UGM and UAM were misaligned (e.g. analysing a TTD UGM within a progression-based UAM increased the ME from − 3.5% in the base case to − 7.4%), although more data did not change the results noticeably from the base case (scenario 8, using a follow-up of 60 months). This pattern of increased error with less information available continued with scenarios 9 and 10, where data were either not collected following the visit where progression was determined, or collected for a limited period; results are more imprecise than when the same length of study is available with all data.

Where data are assumed to be missing, the impact on results depended on the type of missingness. For mechanisms involving data MCAR (whether individual values, scenario 11, or individuals lost to follow-up, scenario 12), this led to increased uncertainty, without necessarily introducing bias (an increase in %MAE, but little change in %ME). This, however, was not the case when values were not missing completely at random—for example, missing data linked to observable outcomes such as death (scenario 13) or unobservable characteristics such as underlying health (scenario 14). In these scenarios, %MAE was increased for all UAMs, but importantly %ME was shown to move further from zero; demonstrating the presence of bias.

Scenarios changing the nature of survival data did have a sizable impact, depending on the changes made. When varying the number of long-term survivors from none (scenario 15), to half the base case (scenario 16),to double the base case (scenario 17), the impact varies by UGM and UAM—despite scenario 15 effectively having no administrative censoring (as nearly all deaths are within the study period), combination-based UAMs continued to perform poorly. This is explained by the limited amount of data available to the model to estimate parameters for patients post progression and close to death (which are highly correlated). As a result, when this UAM was also misspecified (i.e. used to analyse data from a different UGM), the errors were extremely large—over 20% in ME and MAE when analysing a TTD UGM using combination-based UAM with no long-term survivors (scenario 15). Conversely, increasing the number of long-term survivors reduced errors for all UAMs under all UGMs—the larger number of long-term survivors allowed for more data points from patients achieving long-term survival, i.e. in the ‘tail’ of the curve. This meant that even where the UAM was misspecified, the number of data points available ensured the mean values were approximately correct.

Pseudo-progression (scenario 18) was implemented to the study as patients being misclassified as progressed and gaining a group assignment of a short- or medium-term survivor’s PFS, when in reality they were in the long-term survivor group. This misclassified progression led to an overestimate of utility values under UAMs that used progression status (i.e. increasing the mean value for the post-progression group). It may be the case that a TTD approach is more accurate as whether a patient is within the TTD window is known, while progression is no longer a reliable marker of health state (even with only 10% of patients misclassified). To an extent this finding is similar under the assumption of shorter studies (though not as pronounced), where if few progressions have occurred, a TTD approach may have comparable performance to a progression-based UAM (such as in scenario 7) despite ostensibly being the incorrect analysis form. The results, however, did not seem to be impacted by whether post-progression survival and response to treatment were linked (scenario 19), where although the magnitude of results changed, similar patterns to the base case were seen.

Scenarios A–D mimic existing immunotherapy trials (with assumptions around parameters that are not publicly reported or knowable such as utility measurement intervals). It is apparent from these results that the potential for error with an incorrect analysis framework could have a meaningful impact on adoption decisions using contemporary study designs. Using progression and TTD based UAMs under the opposing UGM led to an average MAE of 3.6%, whereas using each UAM in the correct framework had only a 0.6% MAE. In none of the ‘real’ scenarios did the combination-based approach perform well, with generally the largest MAE, and non-zero MEs in all cases, even when matched to the correct UGM.

Discussion

Under ideal conditions, provided the approach used to analyse HRQL matches that of the data-generation mechanism, both progression- or TTD-based utilities are likely to produce good estimates of QALYs. This finding is based on %ME and %MAE, which are anticipated to be low, though not zero (as not all data are observed, and thus estimates produced will never match exactly). An unexpected finding was the poor performance of the combination-based approach to analysis—even where combination-derived utilities were present. This is likely due to the multicollinearity between the values, i.e. it would be expected that the majority of patients progress before dying (with none moving backwards), and limited numbers of patients to estimate coefficients.

As it is not possible to know a priori (and never possible to conclude absolutely) what the main drivers of patient HRQL are, the evidence to support the assumed mechanism of utility generation should be presented, and alternative frameworks explored in any analysis plan. This would be mean in practice fitting both progression- and TTD-based models, then selecting between them for the final analysis based on goodness of fit. This finding is especially strong in the presence of TTD-generated utilities, where this misspecification of progression-based analyses can markedly underestimate the QALYs generated (also shown in the violin plot presented in the OSM Appendix). Although there is no standard threshold for an important level of error in total QALYs estimated, in our simulated example this error can reach 5.4% (scenario 15), which would seem sufficient to impact adoption decisions. It should also be noted that a difference in the mean QALYs would also impact the probability of cost effectiveness at different thresholds, likely in a non-linear fashion. Any utilities generated may also be used in assessments of future products, which would exacerbate the impact of errors in estimation.

The poor performance of the combination-based approach indicates that given the potential for error, a higher bar should be used for justifying such an approach over more simple specifications. Although overspecification of the model is superficially appealing to capture any impacts (even if weak), this has clear negative consequences for accuracy if unjustified. Even if justified, where insufficient data is available to accurately estimate parameters (such as in shorter trials), the potential for error remains high, and it may be preferred to selection either a progression- or TTD-based UAM, depending on which element has the stronger effect.

Although seemingly a self-evident finding, the effects of pseudo-progression and informative missing data should also be considered. In such instances further analysis may be warranted prior to the analysis of utility data—such as reclassifying the progression status of long-term survivors, and multiple imputation for data missingness. In the authors’ experience, though imputation (or at the very least, Last Observation Carried Forward) is common for use within efficacy analysis, this is seldom used with HRQL data when deriving utilities and may be an oversight as approaches for missing data with health outcomes become more standardised [14, 15].

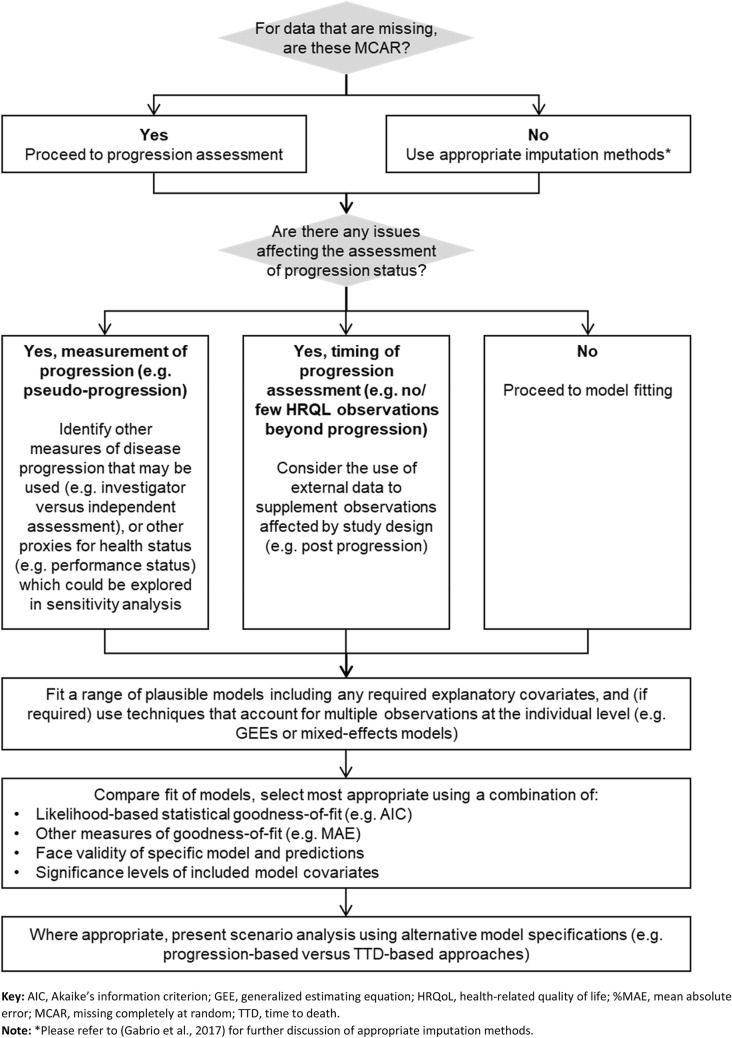
The recommendations that we have derived from our findings are summarised in Fig. 3, and give a suggested approach to analysis of HRQL data in cancer studies (and of IO treatments in particular). This involves first accounting for any issues within the data (such as missing data), before fitting a variety of models. At this stage we would suggest statistical tests and plotting of values may inform the best fitting models and help justify the approach used. We would then also suggest presenting scenario analyses to investigate the impact of structural choices in analysis framework. It should also be noted that the approach we have explored is based on a single dataset with a given intervention; a study with multiple arms (potentially with interventions that have different mechanisms) may need more complex forms of analysis, or indeed analysis by arm.

Fig. 3.

Recommendations for selection of analysis framework for health-related quality of life (HRQL) data

Limitations

There are a number of important limitations with the work presented, the most prevalent of these being the use of simulated data. In having to assume how utility falls when approaching death, or on progression, this does not necessarily represent the way HRQL is reported, or how changes in health are experienced by patients. We have attempted to account for this (for example with variability within patient observations for ‘good’ and ‘bad’ days) though this is unlikely to be perfectly representative. In particular we would highlight that the influence of progression on HRQL is highly uncertain (and likely to vary between cancers). For instance, the timing of HRQL falling related to progression could be when a cancer begins to rapidly grow, whereas tumour imaging would only document this at the next follow-up appointment held between patient and clinician. Alternatively, patients may not experience symptoms until well after radiographic progression has occurred. Understanding when HRQL is impacted around progression would therefore seem relevant for future research in quality of life, as this may not coincide with the timepoint at which progression is measured in practice.

A similar assumption is that survival (in terms of individual survival times) is assumed to be known, whereas in reality many of these would be based on extrapolations. This assumption was imposed to avoid conflating survival modelling questions with those regarding analysis of HRQL data. The shape of these survival curves however is a bigger assumption; for IOs we have assumed background survival for a proportion of patients—should this not be the case (and there be future disease relapse) this may affect our findings, though the durability of survival in IO treated patients is an open question in the medical literature at present, despite encouraging data [16, 17].

A further limitation is in the analysis frameworks used, which are in many ways a ‘straw man’; the timepoint at which HRQL falls prior to death in each analysis is assumed to be known, and be a single decrement. In reality this will likely involve some form of continuous decline over time. To account for this, most published work group periods of time together, (for instance the 30 days before death), though the justification for the groups selected is often arbitrary. Similarly, the combination-based approach was implemented in our simulation regardless of the significance of the coefficients in the analysis, which may be an oversimplification. The development of a standardised strategy and associated algorithm to account for issues such as the appropriate grouping of time to death health states, and model selection would be helpful in establishing best practice for analyses.

Conclusion

The simulation study performed demonstrates that a number of factors can influence accuracy and bias when analysing HRQL data, the most important of which would appear to be the selection of an appropriate analysis framework. Rather than a de facto standard approach of progression or TTD-based utilities, or the inclusion of all possible coefficients (as seen in the combination-based approach), practitioners should investigate the structure of their dataset, and justify the approach taken.

While the simulation study demonstrates the important limitations of different approaches and the importance of adequate data, further work is needed to develop appropriate protocols for analyses and apply these to ‘real’ datasets.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Declarations

Funding

This study was funded by Merck KGaA, Darmstadt, Germany as part of an alliance between Merck KGaA and Pfizer.

Conflict of interest

AJH & AB are employees of Delta Hat Limited, MS is an employee of Merck KGaA, Darmstadt, Germany, and MB is an employee of EMD Serono, Inc., Rockland, MA, USA; a business of Merck KGaA, Darmstadt, Germany.

Ethics approval

N/A—simulated data is used.

Code availability

Full R code is provided as supplementary material.

Consent for publication

Not applicable.

Consent to participate

Not applicable.

Availability of data and materials

N/A—all data is simulated with full parameters given.

Authors contributions

The study was conceptualised and designed by AH, AB, MS and MB. The simulation was performed by AH. Interpretation was provided by AH, AB, MS and MB. The manuscript was drafted by AH, AB, MS and MB.