Abstract
Objective:
Medical electrical impedance tomography is a non-ionizing imaging modality in which low-amplitude, low-frequency currents are applied on electrodes on the body, the resulting voltages are measured, and an inverse problem is solved to determine the conductivity distribution in the region of interest. Due the ill-posedness of the inverse problem, the boundaries of internal organs are typically blurred in the reconstructed image.
Methods:
A deep learning approach is introduced in the D-bar method for reconstructing a 2-D slice of the thorax to recover the boundaries of organs. This is accomplished by training a deep neural network on labeled pairs of scattering transforms and the boundaries of the organs in the data from which the transforms were computed. This allows the network to “learn” the nonlinear mapping between them by minimizing the error between the output of the network and known actual boundaries. Further, a “sparse” reconstruction is computed by fusing the results of the standard D-bar reconstruction with reconstructed organ boundaries from the neural network.
Results:
Results are shown on simulated and experimental data collected on a saline-filled tank with agar targets simulating the conductivity of the heart and lungs.
Conclusions and Significance:
The results demonstrate that deep neural networks can successfully learn the mapping between scattering transforms and the internal boundaries of structures.
Keywords: Electrical impedance tomography, deep learning, neural networks
I. Introduction
Electrical impedance tomography (EIT) is a non-ionizing imaging modality in which low-amplitude, low-frequency currents are applied on electrodes on the body, the resulting voltages are measured, and an inverse problem is solved to determine the conductivity distribution in the region of interest. The most widely studied clinical application for EIT is pulmonary imaging. EIT has been shown to be effective for real-time detection of pneumothorax [1], monitoring mechanical ventilation [2], and detection of atelectasis, pulmonary edema, pleural effusion [3], or pulmonary embolus. Articles surveying pulmonary applications of EIT include [4], [5], and the articles [6]–[9] provide supporting studies. However, the reconstruction problem in EIT is particularly challenging due to the nonlinearity and ill-posed nature of the inverse problem. Algorithms for reconstructing the conductivity distribution generally yield blurred images due to the need for regularization. This motivates the possibility of applying an auxillary algorithm to identify boundaries of inclusions in the images.
In this work a deep learning approach is proposed in tandem with the D-bar method of reconstruction. The D-bar method is a direct (non-iterative) reconstruction algorithm based on concepts in inverse scattering. A type of nonlinear Fourier transform, known as the scattering transform is key to the reconstruction, and is a function of a non-physical complex frequency. The scattering transform can be computed from the measured data and is used to compute complex geometrical optics (CGO) solutions to a related PDE, and the conductivity is then computed directly from the CGO solutions. The details of the method are described further in Section II.
Deep learning is a class of machine learning that utilizes layers of nonlinear processing units to perform tasks such as feature extraction, classification, and prediction. Deep learning specifically makes use of artificial neural networks composed of multiple layers of nonlinear processing units.
Here we wish to extract the boundaries of organs parameterized by 2D curves from the scattering transforms computed from the measured data. This objective follows from the point of view that the computation of the scattering transform is a reliable, albeit ill-posed, step of the reconstruction algorithm that encodes features of the image, but does not yield a correspondence to the resulting image that is discernible by the human eye. The truncation of the scattering transform that is performed in practice to handle the blow-up caused by noise in the data results in smoothing in the subsequent step of the D-bar algorithm, namely the solution of the D-bar equation. The fact that this truncation constitutes a nonlinear regularization strategy was proved in [10]. By replacing the solution of the D-bar equation by a deep learning method, this smoothing step is circumvented. Our goal is to leverage deep learning to reconstruct the boundaries of organs by training an artificial neural network on scattering transform/boundary pairs and then forward feeding a scattering transform through the network to get an approximation of the organ boundaries. This approach is similar in spirit to [11] in which deep learning is applied to reconstructions from limited angle computed tomography (CT) to enhance the portion of the image that cannot be reliably computed from the measured data. We also present a “sparse” reconstruction computed by fusing the results of the standard D-bar reconstruction with reconstructed organ boundaries from the neural network. This results in a cartoonlike reconstruction, which could, after further development, prove useful for identifying pathologies in clinical images.
Previous approaches to compensate for the loss of spatial resolution in EIT images reconstructed by the D-bar method include the use of a priori information in the form of a spatial prior [12]–[15] and post-processing techniques including [16] and the use of a convolutional neural network trained on simulated EIT data to sharpen reconstructions in post-processing of D-bar images [17].
Other applications of deep learning to EIT include the use of a small network with radial basis activation functions to solve the EIT problem, attempting to map boundary voltage measurements to FEM model elements [18], and a similar task, performed by approximating conductivity distributions of simulated data using a 4-layer stacked autoencoder [19]. In [20] an artificial neural network with EIT voltage data was used to detect a single round object against a constant background in the detection of fruit through an industrial process and subsequently applied to test the spatial distribution of moisture inside of bricks and blocks of concrete [21]. Artificial neural networks were applied in a post processing step in a linear solver to improve 2D and 3D reconstructions [22].
The paper is organized as follows. Background information on the mathematical model for EIT is found in subsection I-A of the introduction. The D-bar method and its implementation are described in II. The deep learning method is presented in section III. The sparse reconstruction method is explained in section IV. Results for the reconstructions of organ boundaries for simulated and experimental data with the deep learning method and results from the sparse reconstruction method when applied to the experimental data set are found in section V. Finally, discussion and conclusions are provided in sections VI and VII.
A. Governing equations for EIT
The inverse problem of EIT is modeled by the generalized Laplace equation:
| (1) |
where σ(x, y) is the conductivity, u(x, y) is the electric potential, and Ω is a bounded domain in representing a cross-sectional slice of the chest. Knowledge of the voltages on the boundary is given by the Dirichlet boundary condition
| (2) |
and knowledge of the current density on the boundary is given by the Neumann boundary condition
| (3) |
The continuous, ideal boundary data is represented by the Dirichlet-to-Neumann (DN) map, which takes boundary voltages to boundary current densities:
| (4) |
where ν is the outward normal to the boundary. It was established in [23] through a constructive proof that provided the equations for the D-bar method, that for σ ∈ C2(Ω), the DN map Λσ uniquely determines σ. However, since in practice currents are applied and voltages are measured on the electrodes, the data is the discrete Neumann-to-Dirichlet map, a matrix approximation to the inverse of the operator Λσ.
Let L denote the total number of electrodes applied to the surface. Depending upon the choice of applied current pattern, there are at most L–1 linearly independent vectors of applied currents Jk, where k indicates the kth pattern. We will assume the choice of applied current patterns is an orthonormal set consisting of the maximal L – 1 basis vectors. If the set is not orthonormal, the Gram-Schmidt algorithm can be applied to obtain an orthonormal set of basis vectors. In this case, the voltages measured from the applied currents must be modified through the standard change of basis formula to synthesize voltages that would correspond to the new orthonormal set. The reader is referred to [24], for example, for a detailed discussion of current patterns in EIT. Let jk denote the vector of orthonormal currents and Φ the corresponding L × L – 1 current pattern matrix. Let denote the voltage on the lth electrode corresponding to the kth current pattern jk and adjusted so that . This corresponds to a choice of ground.
Let (u(·),w(·))L denote the discrete inner product defined by
The discrete Dirichlet-to-Neumann map, denoted by Lγ, is approximated by Lγ = Rγ−1, where Rγ denotes the discrete Neumann-to-Dirichlet map. The entries of Rγ are given by
where Aℓ is the area of the ℓth electrode and is the current applied to the lth electrode for the mth current pattern.
II. The D-bar method
The D-bar method applied here is based on the global uniqueness proof [23] for the 2-D inverse conductivity problem and subsequent implementation and development (see [24] and the references therein). It is a direct method based on inverse scattering theory, and consists of several integral equations and intermediate functions to be computed in the inversion process. The method was implemented in real time in [25] and used in clinical studies on patients with cystic fibrosis in [26], [27]. In this section we describe the equations of the D-bar method used to compute the scattering transforms and reconstructions in this work. For a detailed description of the numerical implementation, the reader is referred to [24].
A. Equations of the D-bar method
Functions known as complex geometrical optics (CGO) solutions play a key role in the D-bar method. They are defined by special exponentially growing solutions ψ(z, k) of the Schrödinger equation, where z is the spatial point (x, y) identified with a point in the complex plane z = x + iy, and is a non-physical complex frequency that is introduced as an auxillary parameter.
The following change of variables applied to (1) results in the Schrödinger equation. Let , and
| (5) |
Then (1) becomes
| (6) |
The fact that q is nonzero only in Ω permits the extension of equation (6) to , and the variable is introduced. There exists a unique solution ψ(z, k) to the equation
| (7) |
| (8) |
where the second equation implies ψ has the asymptotic behavior ψ ∼ eikz for large |z| or large |k|.
Equally important to the CGO solution ψ(z, k) is the related function μ(z, k) with asymptotic behavior μ ∼ 1 defined by
| (9) |
because from the change of variables, one can see that σ(z) can be computed directly from μ by
| (10) |
The functions μ are the unique solutions of the Lippmann-Schwinger type equation
| (11) |
satisfying where ∗ denotes convolution. The function gk appearing in (11) is given (in the sense of tempered distributions) by
| (12) |
| (13) |
where is the D-bar operator. The method is known as the D-bar method because a crucial step in the reconstruction algorithm is to solve a D-bar equation in the auxilliary variable k. By differentiating (11) with respect to , the conjugate of k, one can show [23] that μ satisfies the following D-bar equation:
| (14) |
where t(k) denotes the scattering transform, a type of non-linear Fourier transform of q which is defined by
| (15) |
The connection between the CGO solutions, the scattering transform, and the data is through the integral [23], which can be derived using the identity proved in [28],
| (16) |
where Λ1 denotes the DN map corresponding to σ ≡ 1 in Ω. An often-used “short-cut” in the D-bar method is to replace ψ(z, k) in (16) by its asymptotic behavior eikz. This reduces computation time, and is referred to as the “exp” approximation, and the scattering transform is denoted
| (17) |
The integral form of the D-bar equation (14) is the form typically used for numerical solution
| (18) |
The D-bar method with the texp approximation then consists of solving the following equations given the DN map Λσ. For the numerical implementation of each of these steps, the reader is referred to [24].
Step 1: Solve equation (17) to compute the scattering transform texp(k)
Step 2: Solve equation (18) to compute μ(z, k) for each z in the region of interest Ω.
Step 3: Compute the conductivity σ by evaluating (10) at each point z.
B. Implementation of the D-bar method
The D-bar method with the texp approximation was used to assign conductivity values to the organs and backgrounds after the boundaries were obtained from the convolutional neural network. Methods of numerical solution of steps are described in detail in [24]. For the reader’s convenience, we give an outline of the discrete version of the equations in Steps 1 and 2.
From equation (17), we see that it is necessary to express the action of Λσ − Λ1, which we will denote by δΛ, on eikz in terms of the orthonormal basis of current patterns. Let zℓ denote the center of the ℓth electrode and write the expansion
| (19) |
Then since δΛ annihilates the constant function 1, discretizing equation (17) results in
| (20) |
| (21) |
where Aℓ is the area of the ℓth electrode. Note that the domain of computation of texp must be truncated in the k-plane to regularize the ill-posedness. The computations will blow up in the presence of noise for large |k. For simplicity, we truncate to a disk of radius R and will refer to R as the truncation radius, setting texp(k) = 0 for |k| > R, and including the subscript R as a reminder of the truncation, .
Equation (18) then becomes
| (22) |
The method of numerical solution of this equation is too lengthy to include here, and has been described in numerous references, including (give refs). The equation can be solved for each point z in the interior of the domain Ω independently, and the numerical method makes use of the fact that (22) is a convolution integral and therefore can be solved efficiently with FFTs as introduced in [29]. The reader is referred to [24], [30] for further details.
C. Computation of scattering transforms used in network training
The network was trained on scattering transforms computed from the definition, that is, equation (15). Thus, the function ψ(z, k) is required in all of Ω. The solution to equation (7) with asymptotic condition (8) can be expressed as the solution to the the Lippmann-Schwinger equation:
| (23) |
where ∗ denotes convolution in the spatial variable z, Gk(z) is the Faddeev’s Green’s function for the Laplacian [31], [32], satisfying −ΔGk(z) = δ(z), and given by
It is important to note that due to the asymptotic condition on ψ, the Faddeev Green’s function differs from the standard Green’s function for the Laplacian. The function μ(z, k) satisfies
| (24) |
and it is this equation that is solved numerically to obtain ψ from (9) by using a periodization technique enabling the use of FFTs [29]. This was adapted to equation (24) in [30], and the reader is referred again to [24], [30] for details since the method is akin to the solution of equation (22).
To compute the scattering transforms used in the training set, first a piecewise constant σ was constructed with prescribed parameterized organ boundaries (see Section V for the description of the conductivities chosen for training). Next, σ was smoothed by a convolution with a mollifier so that q could be computed from (5). Then equation (24) was solved numerically as described above to obtain ψ(z, k). Finally, t(k) was computed from (15) by numerical quadrature. Figure 1 includes examples of four sets of organ boundaries from the training set, and the corresponding images of the real and imaginary parts of the scattering transforms computed by this method. The conductivity values are not shown in the figure, since the emphasis here is on the organ boundaries.
Fig. 1.
Left: Organ boundaries used in the computation of the scattering transforms at right. Conductivity values of the organs are omitted for simplicity of presentation. Center: Real part of the scattering transform corresponding to the organ boundaries at left with conductivities within the prescribed deviation from the base values. Right: Imaginary part of the scattering transform. Scattering transforms were computed by the discrete version of equation (15) as described in Section II-C.
III. Deep learning
A. Network training
The network is trained by reducing the mean-squared error between the output of the network for a given input and the ground truth. All of the boundaries together were represented by a 128 element vector of concatenated ordered pairs allocated as follows. Each lung was represented by 24 ordered pairs (coordinate points) and the heart was represented by 16 pairs. Denoting the x coordinate of the n-th point on the boundary of the heart by , the y coordinate of the n-th point on the boundary of the heart by and similarly for the left lung (LL) and the right lung (RL), the vector can be written as
and so the output is a vector in . The output does not contain information about the values of the conductivities in each region, only the locations of the boundaries themselves, although the network is trained on scattering transforms corresponding to distributions that are constant in each region. The input to the network is a 2-channel 16 × 16 grayscale image of the real and imaginary parts of the truncated scattering transform. Since the output is a real-valued vector in , the network will learn functions .
The training data for the network consisted of 100,000 thoracic cavity data sets computed by solving equation (7) for simulated heart and lungs in a fixed circular domain with known conductivity values. The two sets of organ boundaries in Figure 2 each served as a base 50% of the time, chosen at random. That is, each simulated distribution varies randomly from one of these two sets of organ boundaries where the area of each organ in the randomly chosen base was scaled by 55 to 105%. This was implemented by maintaining the organ’s shape while stretching or shrinking the coordinates to yield the desired change in area. Additionally, the base distribution was permitted to rotate up to ±30° around the origin. Each organ independently was given a 25% chance of having a simulated injury in which the bottom 20 to 75% of the organ was removed. Conductivity values in the training set were also randomized so that the heart ranged from 1.5 to 2.5 S/m, and each lung (randomized independently) ranged from 0.375 to 0.625 S/m. The conductivity distribution was mollified to satisfy the differentiability required for the change of variables for (7), and the amount of mollification was randomized before equation (7) was solved. The scattering transform for each conductivity distribution in the training set was then computed on a k-grid of size 16 × 16 centered at the origin from the forward solution. The scattering transform truncation radius was chosen at random between 4 and 8.
Fig. 2.
The internal boundaries of the base conductivity distributions. The radius of the domain is 1.
The network was then trained on the 100,000 scattering transforms using Keras with the TensorFlow backend on an Nvidia RTX 2080 GPU for 2000 iterations in batches of 50, which required approximately 2.5 hours. Optimization was performed using AdaDelta, a stochastic gradient descent algorithm featuring a per-parameter learning rate (that is, each weight in the network has its own associated learning rate). Loss, defined to be the mean squared error between the output of the network and the actual, was tracked during training reaching a low of 9.7 ∗ 10−4 on the test/validation set. Loss was lower on the test set since the training set was subjected to dropout layers while the test set was not. Loss for the test set rapidly dropped from 0.02 to 0.0025, but required 700 iterations to reach the order of 10−4.
B. Network architecture
Since the scattering transform is complex-valued, the real and imaginary parts were treated as two separate channels in an image, where each channel is a 16 × 16 image padded with zeros on the outside so that the output of the first convolutional layer is still 16 × 16. The two channels are combined by the first layer of convolutions. More precisely, the first convolutional layer has 32 5 × 5 filters, which are actually 5×5×2 since there are two layers, and the depth of the filters is implicitly defined by the depth of the previous layer (in this case the input layer, which has 2 channels). The first two convolutional layers include a ReLU activation function followed by a 2 × 2 max-pool layer (outputs are 8 × 8 images) and 50% dropout. The third and fourth layers are convolutional layers with 64 3 × 3 filters with a ReLU activation function followed by another 2 × 2 max-pool layer and 50% dropout resulting in 64 4 × 4 blocks. Following the convolutional and max-pool layers is a densely connected 1024 node layer, followed by another 512 densely connected layer. The output layer is also densely connected and has 128 nodes and is the output vector (x1, y1, x2, y2, …, xn, yn) where (xi, yi) represents an approximate point on an internal boundary.
IV. Sparse reconstructions
A sparse, or simplified, reconstruction can be synthesized by fusing the results of the output of the CNN with the reconstruction computed by the D-bar method. The idea is very simple: The organ boundaries computed by the network are superimposed on the D-bar reconstruction, and the average conductivity is computed in each region and assigned to the corresponding region from the CNN. This results in a cartoonlike image with sharp boundaries. The steps are summarized in the flowchart in Figure 5.
Fig. 5.
Flowchart illustrating the steps of the sparse reconstruction algorithm.
V. Results
A. Simulated data
The network was applied to 200 examples of scattering transforms that were not used in training, and the results demonstrated that the network learned the map between scattering transforms and the internal boundaries that produce the transforms. These tests included hearts and lungs of various shapes and sizes, as well as sets with one, two, or three chopped organs (roughly simulated a pathology, such as fluid in the lung, in the case of a chopped lung). The radius of the domain in all cases was 1. Six examples of the network output in the case of multiple simulated injuries are found in Figure 6. Further examples are found in [33]. A comparison of the accuracy of the network output over all 200 examples is found in Table I where three measures of accuracy are applied. The L2 norm of the distance between the actual boundary points and the network outputs was computed from the vector of distances concatenated over the heart, left lung, right lung. Two structural similarity indices (SSIM) were also calculated. The first, denoted by SSIM boundaries only in Table I, compares actual versus network output images of plots of the connected boundaries only. For example, referring to Figure 6 it compares a plot of the red boundaries to a plot of the blue boundaries. The second, denoted by SSIM image in Table I, compares actual versus network output images of plots with the true conductivities assigned to each region to consider the luminance and contrast features of the SSIM. Standard deviations for each measure are provided, and it can be seen that the accuracy is quite consistent for each measure, particularly the SSIM.
Fig. 6.
Results for multiple simulated injuries. The actual boundaries are in blue, with the network predicted boundaries in red.
TABLE I.
Measures of accuracy of network outputs.
| Tissue properties | |||
|---|---|---|---|
| Measure | L2 norm | SSIM boundaries only | SSIM image |
| mean | 0.2991 | 0.9431 | 0.9816 |
| standard deviation | 0.1596 | 0.0138 | 0.0099 |
B. Experimental data
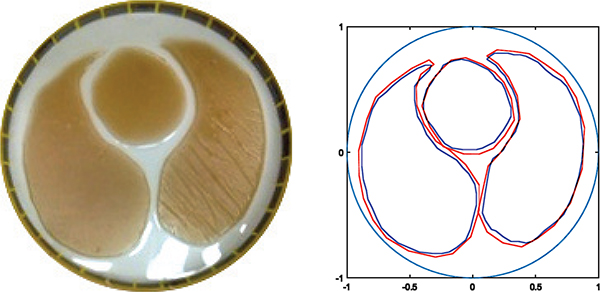
Data was collected on a tank 30 cm in diameter filled with saline, on 32 electrodes, using the ACE1 EIT system at Colorado State University [34], applying adjacent current patterns with current amplitude 3.3 mA at 125 kHz. Agar targets simulating lungs and a heart with conductivities 190 mS/m for the saline, 136 mS/m for the lungs, and 238 mS/m for the heart were placed in the tank. A photo of the experimental tank configuration is found in Figure 7 along with the results of the deep learning algorithm for reconstructing the organ boundaries. Conductivities were assigned to the regions using the method described in Section IV to form a sparse reconstruction. The D-bar reconstruction with the organ boundaries superimposed and the resulting sparse reconstruction is shown in Figure 8. Since the D-bar reconstruction is a difference image, the conductivity values are underestimated, and they are further underestimated in the sparse reconstruction due to the method of assigning the conductivity values. Since the regularized D-bar method results in a smooth reconstruction [10], choosing an average value in the organ boundary region to assign to the sparse reconstruction results in a value that underestimates the true value. Another approach would be to choose the maximum conductivity value in regions of high conductivity and the minimum conductivity value in regions of low conductivity to assign to the sparse reconstruction.
Fig. 7.
Actual vs predicted boundaries on a tank dataset taken with the ACE1 system. Actual boundaries are in blue with the network predicted boundaries in red.
Fig. 8.
D-bar reconstruction with the organ boundaries superimposed. Right: The resulting sparse reconstruction computed by the method in Figure 5. Images are shown on the same color scale and the physical dimensions have been rescaled to a radius of 1.
VI. Discussion
The scattering transforms shown in Figure 1 demonstrate that while the scattering transforms clearly differ for differing organ boundaries, how they encode the shape and size of the boundaries is not visually apparent. However, the results of this work indicate that the complicated relationship between internal organ boundaries and the corresponding scattering transform can be learned by neural networks. This is very promising because organ boundaries in the D-bar reconstructions are blurred by the regularization imposed by truncating the scattering transform, which is necessary to compute reconstructions, but results in loss of exact boundary locations.
Although the case of a missing organ was not considered, very small organs were considered. The three inclusions, two lungs and a heart, were chosen for this study because of the application of interest. In EIT lung difference imaging, there are typically three organs of interest that can be identified in the images: the heart, the left lung, and the right lung, and in our fairly extensive experience with EIT patient data, each of these is a single connected inclusion in the image. This inclusion may change size or shape due to respiration, pathology, or cardiac activity, but these changes are modeled by the examples. While it is conceivable that there may be other inclusions, such as the aorta or a region of air trapping, their presence in a ventilatory image would be quite unusual. For example, the air trapping identified by EIT in [26] was visualized in a ventilation/perfusion ratio map. In summary, the phantom organs included here are representative of ventilatory EIT images, which is sufficient for demonstrating this new method of finding inclusion boundaries.
The approach holds promise for hybrid techniques between the D-bar method and deep learning such as a method in which the organ boundaries computed by deep learning could be used to construct a spatial prior for the D-bar method. The use of a spatial prior in the scattering transform was first proposed in [12], and they have been used with success on experimental tank data in [12], [14] and human subject data in [35], [36].
VII. Conclusion
A novel method of applying deep learning in the D-bar reconstruction algorithm for EIT is presented and examples are shown for simulated and experimental data. The network was trained on randomly generated numerically simulated data using Keras with a Tensorflow backend and was tested on numerically simulated data not used in the training set and the network and experimental data collected on a saline-filled tank with agar targets. The results demonstrate that deep neural networks can successfully learn the mapping between scattering transforms and the internal boundaries of structures. This demonstrates promise for the clinical use of deep neural networks in EIT images in the future.
Fig. 3.
Schematic of one channel in the two-channel network architecture. The real and imaginary parts of the scattering transform are treated as two separate channels and are combined by the first layer of convolutions. Blue boxes represent either a multiply/sum operation with a filter or a max pool on that region, with the output going to the next layer indicated by the red cone. Black arrows represent a densely connected layer.
Fig. 4.
Flowchart of the training method.
Acknowledgments
This manuscript was made possible by Grant Number R21EB024683 from the National Institutes of Health. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.
Contributor Information
Michael Capps, Department of Mathematics, Colorado State University, Fort Collins, CO, 80523 USA. He is now with ClearEdge3D, 12303 Airport Way, Suite 125, Broomfield, CO 80021.
Jennifer L. Mueller, Department of Mathematics, Department of Electrical and Computer Engineering, and School of Biomedical Engineering, Colorado State University, Fort Collins, CO, 80523 USA.
References
- [1].Costa E, Chaves C, Gomes S, Beraldo M, Volpe M, Tucci M, Schettino I, Bohm S, Carvalho C, Tanaka H, R.G. L, and Amato M, “Real-time detection of pneumothorax using electrical impedance tomography,” Crit. Care Med, vol. 36, no. 4, pp. 1230–1238, 2008. [DOI] [PubMed] [Google Scholar]
- [2].Muders T, Luepschen H, and Putensen C, “Impedance tomography as a new monitoring technique,” Curr Opin Crit Care, vol. 16, pp. 269–275, 2010. [DOI] [PubMed] [Google Scholar]
- [3].Arad M, Zlochiver S, Davidson T, Shoenfeld Y, Adunsky A, and Abboud A, “The detection of pleural effusion using a parametric eit technique,” Physiol. Meas, vol. 30, no. 4, pp. 421–8, 2009. [DOI] [PubMed] [Google Scholar]
- [4].Costa E, Gonzalez Lima R, and Amato M, “Electrical impedance tomography,” in Intensive Care Medicine, Vincent J, Ed. Springer, New York, 2009, pp. 394–404. [Google Scholar]
- [5].Nguyen D, Thiagalingam JC, and McEwan AA, “A review on electrical impedance tomography for pulmonary perfusion imaging,” Physiol. Meas, vol. 33, no. 5, pp. 695–706, 2012. [DOI] [PubMed] [Google Scholar]
- [6].Frerichs I, Pulletz S, Elke G, Reifferscheid F, Schädler D, Scholz J, and Weiler N, “Assessment of changes in distribution of lung perfusion by electrical impedance tomography,” Respiration, vol. 77, no. 3, pp. 282–291, 2009. [DOI] [PubMed] [Google Scholar]
- [7].Lowhagen K, Lundin S, and Stenqvist O, “Regional intratidal gas distribution in acute lung injury and acute respiratory distress syndrome - assessed by electric impedance tomography,” Minerva Anestesiologica, vol. 76, no. 12, pp. 1024–1035, 2010. [PubMed] [Google Scholar]
- [8].Reinius H, Borges JB, Freden F, Jideus L, Camargo ED, Amato MB, Hedenstierna G, Larsson A, and Lennmyr F, “Real-time ventilation and perfusion distributions by electrical impedance tomography during one-lung ventilation with capnothorax,” Acta Anaesthesiol Scand, vol. 59, no. 3, pp. 354–368, 2015. [DOI] [PubMed] [Google Scholar]
- [9].Victorino J, Borges J, Okamoto V, Matos G, Tucci M, Caramez M, Tanaka H, Sipmann F, Santos D, Barbas C, Carvalho C, and Amato MP, “Imbalances in regional lung ventilation: a validation study on electrical impedance tomography,” American Journal of Respiratory and Critical Care Medicine, vol. 169, no. 7, pp. 791–800, 2004. [DOI] [PubMed] [Google Scholar]
- [10].Knudsen K, Lassas M, Mueller JL, and Siltanen S, “Regularized D-bar method for the inverse conductivity problem,” Inverse Probl. Imag, vol. 35, no. 4, pp. 599–624, 2009. [Google Scholar]
- [11].Bubba T, Kutyniok G, Lassas M, März M, Samek W, Siltanen S, and Srinivasan V, “Learning the invisible: a hybrid deep learning-shearlet framework for limited angle computed tomography,” Inverse Problems, vol. 39, p. 064002, 2019. [Google Scholar]
- [12].Alsaker M and Mueller J, “A D-bar algorithm with a priori information for 2-dimensional electrical impedance tomography,” SIAM J. Imaging Sci, vol. 9, no. 4, pp. 1619–1654, 2016. [Google Scholar]
- [13].Alsaker M, Hamilton S, and Hauptmann A, “A direct D-bar method for partial boundary data electrical impedance tomography with a priori information,” Inverse Problems and Imaging, vol. 11, no. 3, pp. 427–445, 2017. [Google Scholar]
- [14].Alsaker M and Mueller JL, “Use of an optimized spatial prior in D-bar reconstructions of EIT tank data,” Inverse Problems and Imaging, vol. 12, no. 4, pp. 883–901, 2018. [Google Scholar]
- [15].Hamilton S, Mueller J, and Alsaker M, “Incorporating a spatial prior into nonlinear d-bar eit imaging for complex admittivities,” IEEE T. Med. Imaging, vol. 36, no. 2, pp. 457–466, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Hamilto Sn, Reyes J, Siltanen S, and Zhang X, “A hybrid segmentation and d-bar method for electrical impedance tomography,” SIAM Journal on Imaging Sciences, vol. 9, no. 2, pp. 770–793, 2016. [Google Scholar]
- [17].Hamilton S and Hauptmann A, “Deep d-bar: Real time electrical impedance tomography imaging with deep neural networks,” IEEE Transactions on Medical Imaging, vol. 37, pp. 2367–2377, 2018. [DOI] [PubMed] [Google Scholar]
- [18].Michalikova M, Abed R, Prauzek M, and Koziorek J, “Image reconstruction in electrical impedance tomography using neural network,” Cairo International Biomedical Engineering Conference (CIBEC), 2014. [Google Scholar]
- [19].Li X, Lu Y, Wang J, Dang X, Wang Q, Duan X, and Sun Y, “An image reconstruction framework based on deep neural network for electrical impedance tomography,” in IEEE International Conference on Image Processing (ICIP), 2017. [Google Scholar]
- [20].Kosowski G and Rymarczyk T, “Using neural networks and deep learning algorithms in electrical impedance tomography,” Informatics Control Measurement in Economy and Environment Protection, vol. 7, pp. 99–102, 09 2017. [Google Scholar]
- [21].Rymarczyk T, Kosowski E, and Kosowski G, “Object analysis using machine learning to solve inverse problem in electrical impedance tomography,” IEEE International Conference on Imaging Systems and Techniques, 2018. [Google Scholar]
- [22].Martin S and Choi C, “A novel post-processing scheme for two-dimensional electrical impedance tomography based on artificial neural networks,” PLOS ONE, vol. 12, no. 12, pp. 1–27, 12 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Nachman AI, “Global uniqueness for a two-dimensional inverse boundary value problem,” Ann. Math, vol. 143, no. 1, pp. 71–96, 1996. [Google Scholar]
- [24].Mueller JL and Siltanen S, Linear and Nonlinear Inverse Problems with Practical Applications. Philadelphia, PA: SIAM, 2012. [Google Scholar]
- [25].Dodd M and Mueller J, “A real-time D-bar algorithm for 2-D electrical impedance tomography data,” Inverse Probl. Imag, vol. 8, no. 4, pp. 1013–1031, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Mueller J, Muller P, Mellenthin M, DeBoer E, Murthy R, Capps M, Alsaker M, Deterding R, and Sagel S, “A method of estimating regions of air trapping from electrical impedance tomography data,” Physiological Measurement, vol. 39, no. 5, p. 05NT01, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Muller P, Mueller J, Mellenthin M, Murthy R, Capps M, Wagner B, Alsaker M, Deterding R, Sagel S, and Hoppe J, “Evaluation of surrogate measures of pulmonary function derived from electrical impedance tomography data in children with cystic fibrosis,” Physiological Measurement, vol. 39, no. 4, p. 045008, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Alessandrini G, “Stable determination of conductivity by boundary measurements,” Applicable Analysis, vol. 27, no. 1–3, pp. 153–172, 1988. [Online]. Available: 10.1080/00036818808839730 [DOI] [Google Scholar]
- [29].Vainikko G, “Fast solvers of the Lippmann-Schwinger equation,” in Direct and Inverse Problems of Mathematical Physics, Gilbert R, Kajiwara J, and Xu Y, Eds. Springer US, 2000, pp. 423–440. [Google Scholar]
- [30].Knudsen K, Mueller J, and Siltanen S, “Numerical solution method for the dbar-equation in the plane,” Journal of Computational Physics, vol. 198, no. 2, pp. 500–517, 2004. [Google Scholar]
- [31].Faddeev L, “Increasing solutions of the schroedinger equation,” Soviet Physics Doklady, vol. 10, pp. 1033–1035, 1966. [Google Scholar]
- [32].Siltanen S, “Electrical impedance tomography and Faddeev Green’s functions,” Ph.D. dissertation, Helsinki University of Technology, 1999. [Google Scholar]
- [33].Capps M, “Recovery of organ boundaries in Electrical impedance tomography images using a priori data, optimization, and deep learning,” Ph.D. dissertation, Colorado State University, 2019. [Google Scholar]
- [34].Mellenthin MM, Mueller JL, de Camargo EDLB, de Moura FS, Santos TBR, Lima RG, Hamilton SJ, Muller PA, and Alsaker M, “The ACE1 electrical impedance tomography system for thoracic imaging,” IEEE Transactions on Instrumentation and Measurement, vol. 68, no. 9, pp. 3137–3150, September. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Alsaker M and Mueller J, “EIT images of human inspiration and expiration using a D-bar method with spatial priors,” J. of the Appl. Comp. Electromag. Soc. (ACES), vol. 34, no. 2, pp. 325–330, 2019. [Google Scholar]
- [36].Alsaker M, Mueller J, and Murthy R, “Dynamic optimized priors for D-bar reconstructions of human ventilation using electrical impedance tomography,,” J. Comp. and Appl. Math, vol. 362, pp. 276–294, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]