ClassicalGSG: Prediction of logP Using Classical Molecular Force Fields and Geometric Scattering for Graphs

Abstract

This work examines methods for predicting the partition coefficient (log P) for a dataset of small molecules. Here, we use atomic attributes such as radius and partial charge, which are typically used as force field parameters in classical molecular dynamics simulations. These atomic attributes are transformed into index-invariant molecular features using a recently developed method called Geometric Scattering for Graphs (GSG). We call this approach “ClassicalGSG” and examine its performance under a broad range of conditions and hyperparameters. We train ClassicalGSG log P predictors with neural networks using 10,722 molecules from the OpenChem dataset and apply them to predict the log P values from four independent test sets. The ClassicalGSG method’s performance is compared to a baseline model that employs graph convolutional networks (GCNs). Our results show that the best prediction accuracies are obtained using atomic attributes generated with the CHARMM generalized Force Field (CGenFF) and 2D molecular structures.

Graphical Abstract

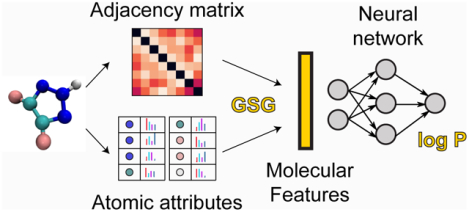
The ClassicalGSG method utilizes neural networks (NNs) to predict the log P values from molecular features generated using a method called Geometric Scattering for Graphs (GSG). The GSG method creates molecular features from the graph representation of the molecule, where each atom has a set of atomic attributes. These atomic attributes are typically used as force field parameters in classical molecular dynamics simulations and include partial charges, Lennard-Jones well depth, Lennard-Jones radius, and atomic type.

1. INTRODUCTION

The partition coefficient (P) measures the relative solubility of a compound between two solvents. It is defined as the ratio of the concentration of an uncharged compound dissolved in an organic solvent (e.g. octanol) in comparison to water. The logarithm of this ratio (log P) is considered to be one of the main factors in determining the drug-likeness of a chemical compound. The log P determines the lipophilicity, which affects bioavailability, solubility, and membrane permeability of a drug compound in the body. Moreover, an orally active drug should have a log P value of less than 5 according to one of the criteria of the famous Lipinski’s Rule of Five.¹ Thus, predicting log P plays an essential role in the drug discovery process and is our main focus in this study. The prediction of log P is also used as a stepping stone to calculate other molecular properties such as the distribution coefficient (log D),² drug solubility (log S),^3,4 and Lipophilic efficiency (LiPE).⁵ All of these properties have been used in drug discovery and design: log D is an effective descriptor for lipophilicity of an ionized compound,⁶ LiPE combines the potency and lipophilicity of a drug compound to estimate its quality, and log S is important to model the solubility of a compound in the human body.

The partition coefficient is widely used in cheminformatics and generally there are diverse experimental methods to measure it.⁷ However, these methods are time-consuming and expensive for large databases of compounds and not feasible for compounds that are not synthesized.⁸ Therefore, a large number of computational methods have been developed to predict accurate values of log P. These methods have a long history and can be classified by both their input features (atomic/fragment, molecular and hybrid) and their models or algorithms (parameteric models vs. machine learning methods) (Table 1).

Table 1:

log P prediction models classifications

		Mathematical models
		Parametric Models	Machine Learning Methods
Features	Atomic/Fragment	XlogP3,9 AlogP,10 ClogP,11 KowWIN,12 JPlogP13	László et al,14 Huuskonen et al15
	Molecular	MlogP,16 iLogP,17,18 Manhold19	AlogPS,20,21 S+logP,22 CSLogP23
	Hybrid	Silicos-IT LogP24	TopP-S,25 OpenChem26

In atomic-based or fragment-based methods^9–15, which is based on atomic or fragment contributions, a set of atomic or fragment based descriptors is used as input to the model, while “molecular” methods use descriptors of the whole molecule, such as topology or molecular fingerprints.^16–23 “Hybrid” models combine atomic and molecular descriptors as input to the model.^24–26 In general, there are challenges with both atomic and molecular descriptors. In Atomic-based or fragment-based methods, the accuracy of the atomic contributions depends on the similarity of the atomic environments of the atoms in the group. Unfortunately, more training data is needed as the number of groups grows larger. Fragment-based methods can struggle with defining the optimal size of fragments that participate in predictions. On the other hand, the accuracy of property-based methods heavily depends on the choice of molecular descriptors. Common descriptors include: 3D molecular structure,²⁵ molecular volume and surface area²⁷, solvation free energies,^17,18,28 number of carbon atoms and heteroatoms.¹⁶ Furthermore, these molecular descriptors can be difficult or computationally costly to generate.

A second way of categorizing log P predictors is by the types of mathematical model used to process the input data. Parameteric models use methods such as least squares estimation or multiple linear regression to fit parameters that govern the relative contributions of the different input features. Machine learning based methods such as Support Vector Machines (SVM),^29–31 Neural Networks (NNs),^25,29,30,32 and Graph convolutional networks (GCN)³³ have been used to predict logP values.

Recently, some methods have been described that create their own custom molecular features from atomic attributes, which go beyond simple additive models. The TopP-S²⁵ predictor was developed by Wu et al and uses the atomic positions to create topological descriptors called Betti barcodes. These Betti barcodes are used as molecular features that are input into deep neural networks, along with atomic attributes such as atom type. Results were shown to further improve upon the addition of 633 “molecular fingerprints” calculated from ChemoPy.³⁴ TopP-S has shown success in predicting log P over other methods like XlogP3, ClogP and KowWIN using a group of independent test sets.

Graph representations of molecules have also shown success in various applications including predicting molecular properties,^33,35–39, virtual screening⁴⁰ and molecular force field calculations.⁴¹ In particular, OpenChem²⁶ uses a graph representation of the molecules. Each atom represents a node in a graph and has a vector of atomic attributes including element type, valence, charge, hybridization, and aromaticity; bonded atoms are connected by an edge in the graph. GCNs are then trained on the graph representations created using these atomic attributes and the 2D structure – or, “graph structure” – of the molecules.

Graph representations are beneficial in that they are invariant to translation, rotation, and reflection symmetries. Another molecular symmetry that should be respected is invariance to the re-indexation of atoms: changing the order in which atoms are input to the model should not affect the computed molecular features. Summation operations respect re-indexation symmetry but it is not straightforward how to capture more detailed information about molecular structure while maintaining re-indexation symmetry. A recently-described method, Geometric Scattering for Graphs (GSG),⁴² provides a solution to this problem. GSG, which is analogous to GCNs, creates molecular features by scattering atomic attributes across a graph using lazy random walks. GSG is fast in creating re-indexation invariant features and also its feature vectors have the same length allowing us to easily measure the similarity of molecules, even those with different numbers of atoms. It has shown promising results in the classification of social network data and predicting Enzyme Commission (EC) numbers.⁴²

Given this abundance of algorithms for creating molecular features, we seek to compare some different methods based on molecular graph representations and their ability to predict log P. Here we use GSG in combination with a set of atomic descriptors that are generated for use with classical molecular dynamics force fields: partial charges, atom type, and Lennard-Jones interaction parameters. We call this method “ClassicalGSG” and examine its performance as a function of different atomic/molecular features. We compare the ClassicalGSG results with GCNs trained on the same data and using a variety of atomic attributes, including those from previous work.³³ We then evaluate the performance of ClassicalGSG on several independent test sets and study the properties of features generated in the pipeline of GSGNN models. In addition, we investigate the properties of molecules with high log P prediction error. We conclude with a discussion about the GSG method generated features, the computational cost of generating atomic attributes with CGenFF and GAFF2, and the relative performance of 2D versus 3D structure in predicting log P values.

2. METHODS

Datasets and generation of atomic attributes

The dataset used in this work is generated by Korshunova et al.²⁶ from the public version of PHYSPROP database.⁴³ This dataset consists of 14176 molecules in SMILES format and their corresponding log P values, which refer to as the OpenChem dataset.

The molecules are converted from SMILES format to mol2 format and their 3D structure is created by OpenBabel (https://github.com/openbabel/openbabel). Then CHARMM General Force Field (CGenFF)^44,45 and General AMBER Force Field 2 (GAFF2)^46,47 parameter files are generated for each molecule. These force field parameter files are either created by CGenFF using the CGenFF tool of the SilcsBio software package (http://silcsbio.com) or by the Antichamber tool implemented in the Ambertools18⁴⁸ package. The process of generating CGenFF parameter files fails for 175 molecules, and GAFF2 for 681 molecules. These 774 molecules are removed from the OpenChem dataset, resulting in a dataset of 13402 molecules. Then 80% of the molecules are used for training and the rest for testing. In addition, we evaluate our trained models on four independent test sets shown in Table 2. Star and NonStar¹⁹ test sets are publicly available on https://ochem.eu/article/17434 and the Husskonen¹⁵ test set can be found on https://ochem.eu/article/164. The FDA dataset contains drug molecules that are approved by the Food and Drug Administration (FDA) of the United Sates and originally prepared by Chen et al.⁹

Table 2:

Independent test sets used for evaluating ClassicalGSG models.

Test set name	Number of molecules
FDA9	406
Huuskonen15	348
Star19	223
NonStar19	43

As mentioned above, we use atomic attributes including partial charges, atom type, and Lennard-Jones interaction parameters. Below, we explain how we generate these atomic attributes.

Atomic partial charges for each atom are extracted from the parameter files generated by either the CGenFF^44,45 or GAFF2^46,47 force field generator tools. To determine atom type classifications, we compared a number of different schemes. In one scheme, we classify atom types in one of five categories as shown in Table 3. This is referred to below as “AC5”. Alternatively, we directly use the atom types as generated by either CGenFF or GAFF2; referred to below as “ACall.” In the third classification scheme, we manually sorted CGenFF atom types into 36 groups (AC36; Table S1) and GAFF2 atom types into 31 groups (AC31; Table S2) based on chemical knowledge. Specifically, efforts were made to make new groups for atom types with different elements and hybridization values and to separately identify atoms that are members of ring structures. Finally, a forth classification scheme simply uses a uniform atom type for all atoms, referred to as “AC1”.

Table 3:

Classifying atoms in 5 categories (AC5).

Atom type	Category number
Hydrogen	1
Oxygen and Nitrogen	2
Carbon with hybridization value < 3	3
Carbon with hybridization value = 3	4
Others	5

The two Lennard-Jones parameters – radius (r) and well-depth (ϵ) – are extracted from either CHARMM or AMBER parameter files for each atom type. In summary the atomic attributes are defined by both the force field generation tool (CGENFF or GAFF2) and the atom classification scheme AC1, AC5, AC36, AC31 or ACall and we generally refer to these as “FF” atomic attributes. The atomic charges and Lennard-Jones parameters are scalar values, but atomic types are represented in one-hot encoding format. For comparison, we also examine a different set of atomic attributes, following previous work for the log P predictor from the OpenChem toolkit (https://github.com/Mariewelt/OpenChem.git).²⁶ These atomic attributes are defined as: atom element type, valence, charge, hybridization, and aromaticity. The 3D structure is generated from SMILES strings by RDkit (https://www.rdkit.org), then again using RDkit the atomic attributes are produced for each molecule and represented in one-hot encoding format as node features in OpenChem. These are referred to below as ”OPENCHEM” atomic attributes.

Log P predictions using GSG

Geometric Scattering for graphs

The Geometric scattering for graphs (GSG) method, which has been introduced in Ref.⁴² is a feature extraction method for graph data types and uses a geometric transform defined on the graph. In the GSG method, molecules are represented by a graph of atoms where each atom has a vector of attributes; a single attribute evaluated at each vertex is also referred to as a “graph signal”. GSG combines the molecular structure (defined using an adjacency matrix) and atomic signal vectors to construct invariant, stable, and informative features as shown in Figure 1.

Figure 1:

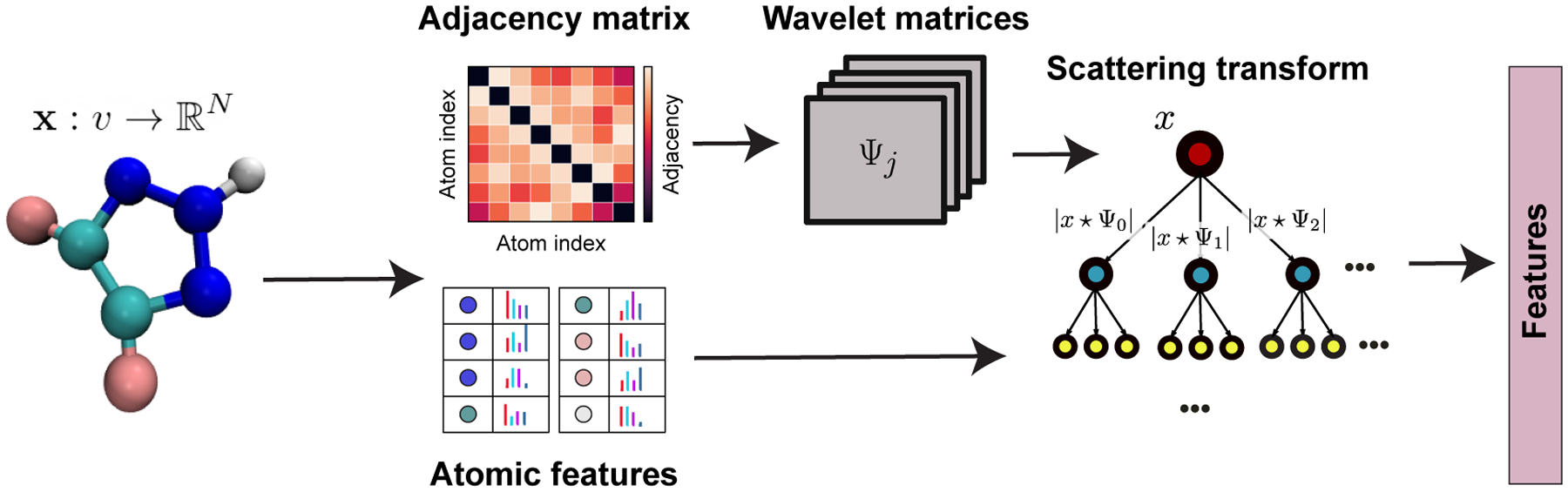
Architecture of the GSG method. The adjacency matrix describes the graph structure of the molecule. Each atom has a set of attributes that are shown as colored bars. Wavelet matrices Ψ are built at different logarithmic scales, j, using the adjacency matrix as described in the text. Finally, the scattering transform is applied to get the graph features using both the wavelet matrices and the signal vectors. Modified from figure made by Feng et al.42

Now we briefly explain the mathematics behind this method. Let G = (V,E,W) be a weighted graph and x(v_l),1 < l <= n be the signal function defined on each node where n is the number of nodes in the graph and v_l represents node l. A graph random walk operator is defined as $P=\frac{1}{2}\left(I+A{D}^{-1}\right)$, where A is the adjacency matrix and D is the degree matrix. P^t describes the probability distribution of a lazy random walk after t steps and hence the term lazy random walk for P. In fact, graph random walks are low-pass filters that act like convolution filters to capture graph features at different scales. Graph wavelet operators – also known as “signal transform operators for graphs” – are defined at the scale 2^j as ${\Psi }_j=P^{2^{j-1}}-P^{2^j}$. Finally, a set of scattering transform operators S₀, S₁ and S₂, are defined using the graph signals and wavelets to compute the molecular-level features. Unique S₀, S₁ and S₂ vectors are created using different moments (q) of x and their wavelet coefficients Ψ, as well as different wavelet scales indexed by j:

$$\begin{gathered} {\left(S_0\right)}_q=\sum _{l=1}^{n}x{\left(v_l\right)}^q,1\le q\le Q \\ {\left(S_1\right)}_{j,q}=\sum _{l=1}^n{\left|{\Psi }_{j}x\left(v_l\right)\right|}^q,1\le j\le J1\le q\le Q \\ {\left(S_2\right)}_{j,j^{\prime },q}=\sum _{l=1}^n{\left|{\Psi }_{j^{\prime }}\left|{\Psi }_{j}x\left(v_l\right)\right|\right|}^q,1\le j<j^{\prime }\le J1\le q\le Q \end{gathered}$$ (1)

The scattering operators are named based on the number of times the wavelets Ψ are used to transform the signal x. For example, S₀ features do not use the wavelet operators, and are simply different moments of the atomic signals. These are called the “Zero order scattering moments.” Accordingly, the S₁ operators with one wavelet transformation are called “First order scattering moments” and S₂ with two wavelet transformations are called the “Second order scattering moments.” Note that these allow mixing between different wavelet scales as j and j^′ are set independently.

We define the set S as the concatenation of all S₀,S₁ and S₂ vectors using all possible values of q, j and j^′ as specified by the ranges in Eq. 1. The set of graph features is generated deterministically from the atomic signals and adjacency matrix. The size of this set of features is equal to QN_s(1 + J(J + 1)/2), where N_s is the number of attributes per vertex, although this is lower if not all zeroth, first and second order features are used.

As mentioned above, one of the inputs to GSG is the adjacency matrix of the graph and we consider two distinct ways to represent it. One is to use the 2D connectivity of the molecule, where A_ij = 1 indicates a bond between atoms i and j, and A_ij = 0 otherwise. Alternatively, the adjacency matrix can be calculated using the 3D structure, where A_ij = f(R_ij), and f(R) is a smooth and differentiable function that is equal to 1 at low R and decreases to 0 as R exceeds some cutoff value R_c⁴⁹:

$$f\left(R_{ij}\right)=\{\begin{array}{ll}0.5\left(\text{cos}\left(\frac{\pi R_{ij}}{R_c}\right)+1\right)\hfill & \text{for }{R}_{ij}\le R_c\hfill \\ 0.0\hfill & \text{for }{R}_{ij}>R_c\hfill \end{array}$$ (2)

where R_c is the radial cutoff and R_ij is the Euclidean distance between atoms i and j. If f(R_ij) is non-zero, nodes i and j are considered connected and disconnected otherwise. The wavelet operators in GSG can be defined using either discrete (2D) or continuous (3D) values in the adjacency matrix.

Neural networks architecture and training

To predict the log P values from the GSG features (S), we develop a feedforward neural network using PyTorch⁵⁰ with a nonlinear activation function such as Rectified Linear Unit (ReLU). To determine the best performing network, we consider three important hyperparamters including the number of hidden layers, the number of neurons in a hidden layer, and the dropout rate whose ranges are shown in Table 4. We perform cross validation using the PyTorch wrapper Skorch https://skorch.readthedocs.io/en/stable/ to tune the hyperparameters. The loss function of our NN model is MSELOSS (Mean Squared Error) and we use the Adam (adaptive momentum estimation)⁵¹ for optimizing the parameters. We use MultiStepLR, which has an adjustable learning rate set to the initial value of 0.005 and dynamically decreases during training every 15 steps by a factor of 0.5. In training our GSGNN models, we used two data regularization methods: L1 norm and standardization using the StandardScaler function from sci-kit learn.⁵² For GSG features with maximum wavelet scales of J = 4, 5 and 6 we mostly benefit from using the standardization method. Other settings can be found in Table 4.

Table 4:

Neural network settings. Square brackets denote possible parameter values used in the grid search method.

Parameter	Values
Number of hidden layers	[2, 3, 4, 5]
Size of hidden layers	[300, 400, 500]
Dropout rate	[0.2, 0.4]
Initial learning rate	0.005
Learning coefficient	0.5
Batch size	256
Max epoch size	400

Log P predictions using GCNs

Graph convolutional neural network

Graph convolutional neural networks (GCNs) extend the application of convolutional neural networks to graph data. The goal of GCNs is to take a graph and generate features according to node attributes and graph structure. The heart of the GCN method is the convolution operator, which aggregates the features of neighboring nodes within the graph. Recently, various implementations of GCNs^38,53–57 have been developed to increase the speed and accuracy of the GCN models. In this paper, we employ the GCN model that was developed in OpenChem²⁶ based on the method introduced by Kipf and Welling.⁵⁶ Similar to the GSG model above, this model takes a graph G = (V,E) as the input where each node has a vector of attributes x. The model processes the graph by passing it through multiple hidden layers performing convolution operations (Figure 2).

Figure 2:

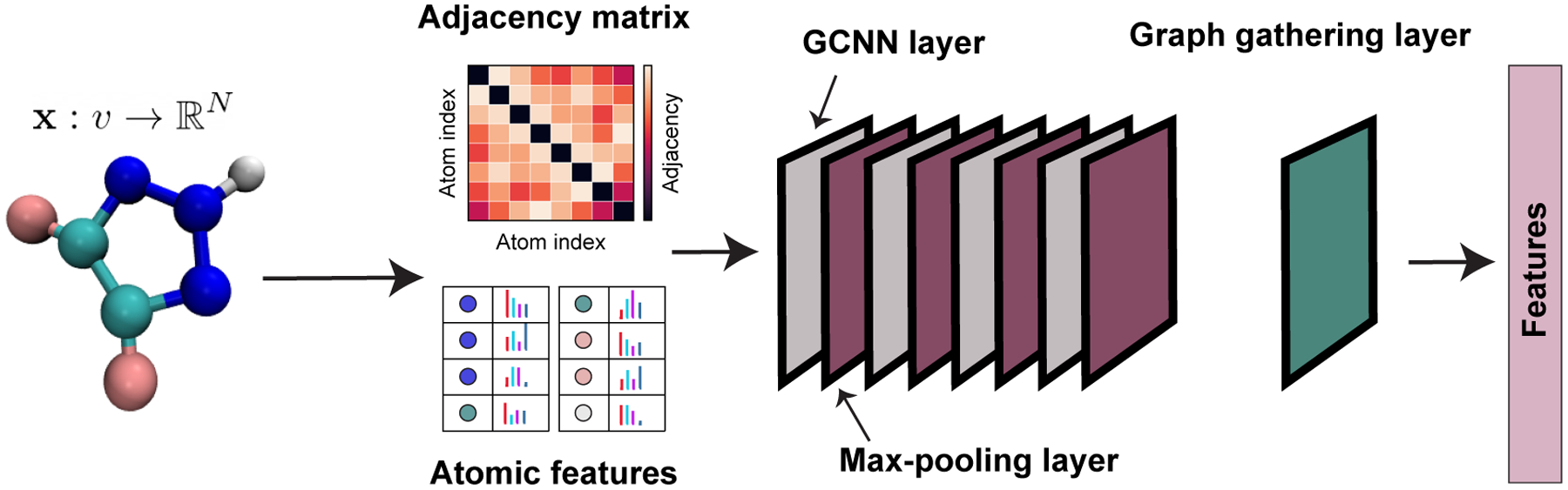
Architecture of the GCN method. The adjacency matrix describes the graph structure of the molecule. Each atom has a set of attributes and are shown as colored bars. GCN layers are shown by gray color and are followed a max-pooling layer which is shown in purple. The graph gathering layer is shown in green color adds features on all nodes to generate the molecular feature vector.

The GCN method works by propagating a feature matrix H – originally set to the value of the attribute vector x for all nodes – through a set of convolution operators as follows:

$$\begin{gathered} H^{(0)}=X \\ {H}^{(l+1)}=\sigma \left(\tilde{A}{H}^{(l)}{W}^{(l)}\right) \end{gathered}$$ (3)

where à = A + I, is the adjacency matrix of the input graph with self-connections, I is the identity matrix, W^(l) is the trainable weight matrix of layer l and σ is a non-linearity function such as ReLU. H^(l) denotes the value of the feature matrix on layer l.

Each convolution layer is followed by a graph max-pooling layer introduced in.⁵⁷ Following these convolution and max-polling operations, the final set of graph features is obtained by a graph gather layer, where the values of each feature are summed over nodes. This last layer gives GCNs their index-invariance property.

GCN architecture and training

We predict log P using GCNs using the model implemented in the OpenChem toolkit https://mariewelt.github.io/OpenChem/html/index.html. This model contains 5 layers of graph convolutions with a hidden layer size of 128. The GCN layers are followed by max-pooling and a graph gather layer. A 2-layer neural network with ReLU as the activation function is added after the graph gather layer. The PyTorch Adam optimizer and the MSELOSS (Mean Squared Error) are used as the parameter optimizer and training loss function, respectively. We use the MultiStepLR learning scheduler, implemented in PyTorch, with an initial value of 0.001, a step size of 15 and a learning coefficient of 0.5 for training the model. Parameters used for the GCN training are summarized in Table 5.

Table 5:

Neural network settings

Parameter	Values
Number of GCN hidden layers	5
Number of NN hidden layers	2
Size of hidden layers	128
Dropout rate	0
Initial learning rate	0.01
Learning coefficient	0.5
Batch size	128
Max epoch size	200

3. RESULTS

Evaluation of molecular representations

For our set of atomic attributes (FF), we use parameters from classical MD force fields: the partial charge σ, and the Lennard-Jones radii and well-depth. We first compare the performance of atomic attributes generated using two different algorithms: GAFF2 and CGenFF. Both algorithms are used to automatically generate force field parameters for small molecule ligands, by matching atomic environments with atoms that are part of existing force fields; GAFF2 uses the Amber⁵⁸ force field, while CGenFF uses the CHARMM^44,45 force field. Here we generate molecular features from atomic attributes using GSG (see Section 2). We examine the four different atom type classification schemes discussed above: AC1, AC5, AC36/AC31 and ACall. The GSG parameters used to construct the molecular features are shown in Table 6.

Table 6:

Parameters for the Geometric Scattering for Graphs algorithm. The square brackets show all of the values examined for each parameter. For “Scattering operators”, ‘z’ represents the zero order operator, ‘f’ is first order, and ‘s’ is second order.

Parameter	Values
Adjacency matrix (A)	[2D, 3D]
Wavelet maximum scale index (J)	[4, 5, 6, 7, 8]
Scattering operators (z, f, s)	Four combinations (z, f), (z, s), (f, s), (z, f, s)
Atom classification	[AC1, AC5, AC36/AC31, ACall]

We trained 160 models for each of the CGenFF and GAFF2 atomic attributes sets, each trained using a 3-fold cross-validation method. After training, we ran tests on subsets of the full database using an 80:20 train:test split. We then calculated evaluation metrics such as the correlation coefficient (r²), Root Mean squared errors (RMSE) and Mean Unsigned Errors (MUE) between the predicted and experimental log P values. In Figure 3, r² and RMSE values are shown for predictions using 2D and 3D molecular structures. Each r² and RMSE is averaged on 20 NN models that are created with all combinations of the 4 geometric scattering operator sets and the 5 wavelet step numbers as shown in Table 6.

Figure 3:

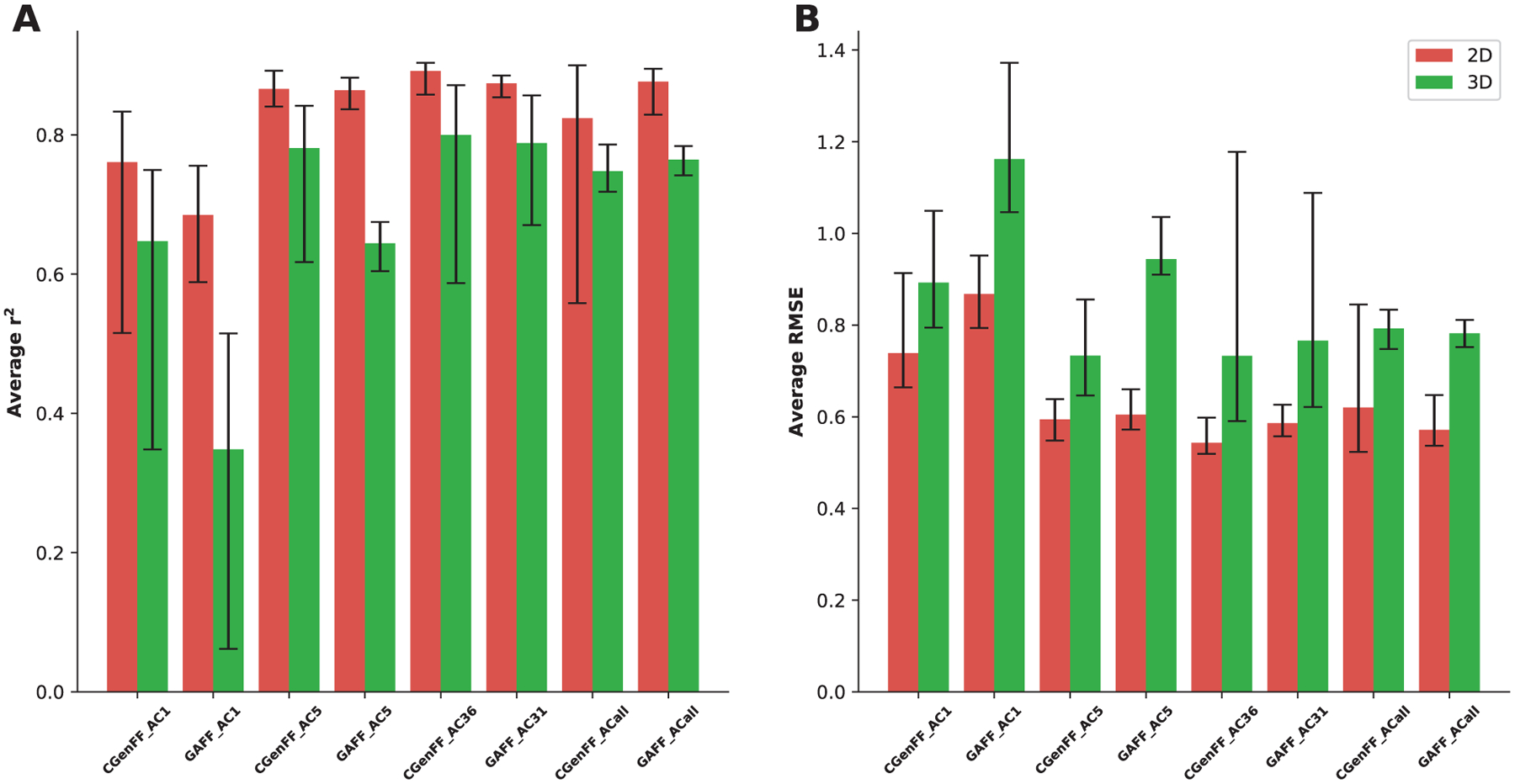
Average r² (A) and RMSE (B) for the OpenChem test set using GSGNN models. Each average is calculated over 20 individual parameter values and the error bars show the best and worst performing models. The atomic attributes are generated with either CGenFF or GAFF2 force fields and using one of three atom type classification schemes (”AC1”, ”AC5”, ”AC36/AC31” or ”ACall”).

We find that models with 2D structure universally have higher accuracy in prediction of log P values. Additionally, it demonstrates that CGENFF atomic attributes on average are more accurate in predicting log P values compared to GAFF2 atomic attributes, although this is not true for ACall. We find that good results on average are obtained by classifying atom types using AC36 categories; the best performing individual models are also found in this category. We thus use CGenFF, 2D structure and AC36 for all models going forward.

We next investigate different scattering moment sets and wavelet scales in Figure 4. We find that for each examined wavelet number (4,5,6,7 and 8) there is at least one model with an r² value of 0.9. The model also performs well for all combinations of scattering moments, making it difficult to determine an optimal set of parameters.

Figure 4:

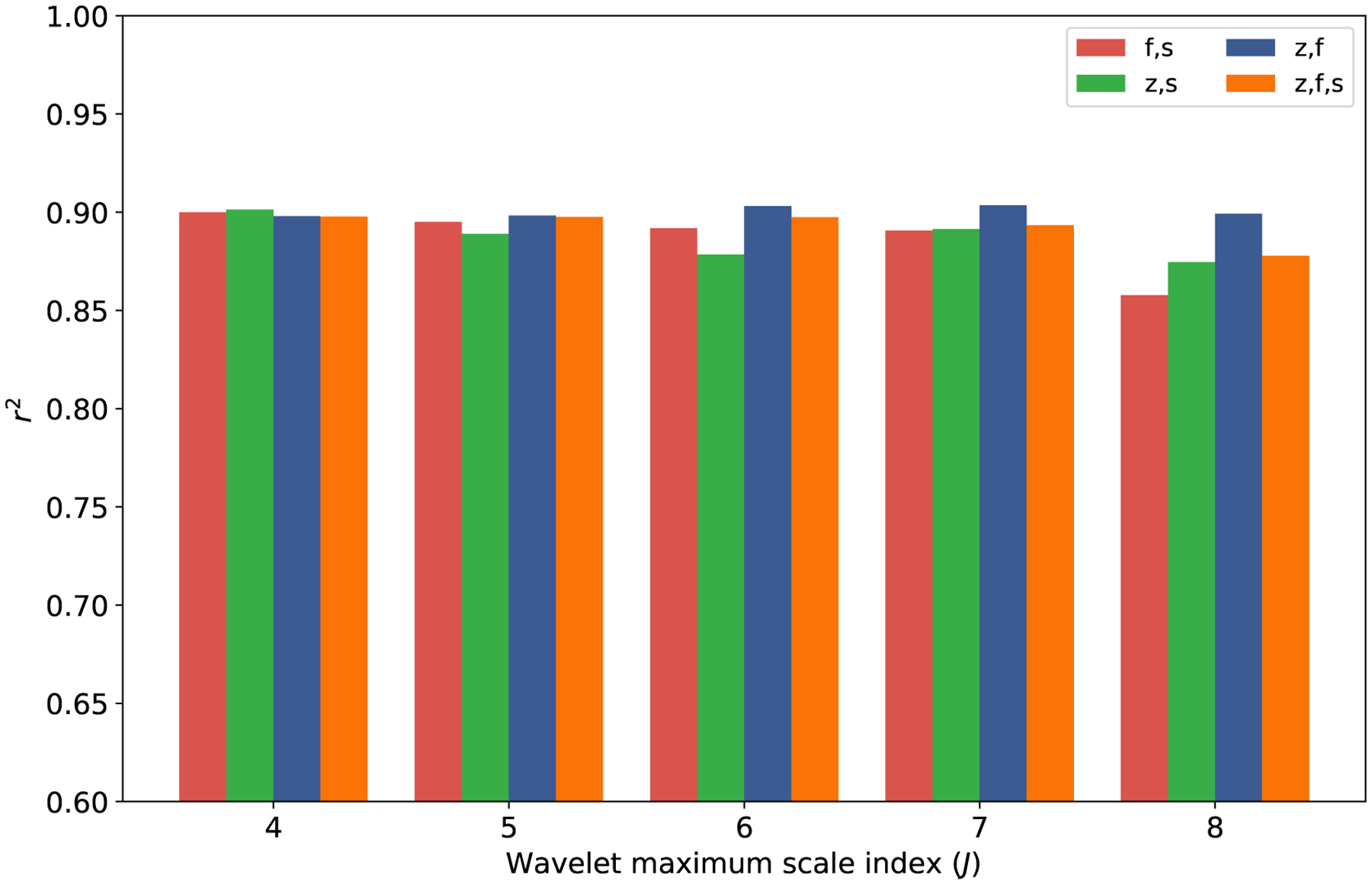
The r² for the OpenChem test set using GSGNN models. The atomic attributes are all generated with CGenFF force fields, AC36 atom type classification scheme, and 2D molecular structure.

To further evaluate the accuracy of our method, we examine four different independent test sets: FDA, Huuskonen, Star and NonStar which are explained in Section 2. To avoid any accidental overlap, we identified shared molecules and removed them from our training dataset. The training dataset contains 10,722 randomly selected molecules from the OpenChem dataset that successfully are processed by CGenFF. The trained models are evaluated using these test sets and the r² between the actual and predicted log P values are calculated. The results are shown in Figure 5. For the Huuskonen and FDA data sets we find that there is at least one GSGNN model with r² = 0.92 and r² = 0.90, respectively. The best performing models for the Star test set is a maximum wavelet scale of J = 4 and zero- and second-order scattering operators, while the best model for NonStar is a maximum wavelet scale of J = 7 and zero-, first- and second-order scattering operators.

Figure 5:

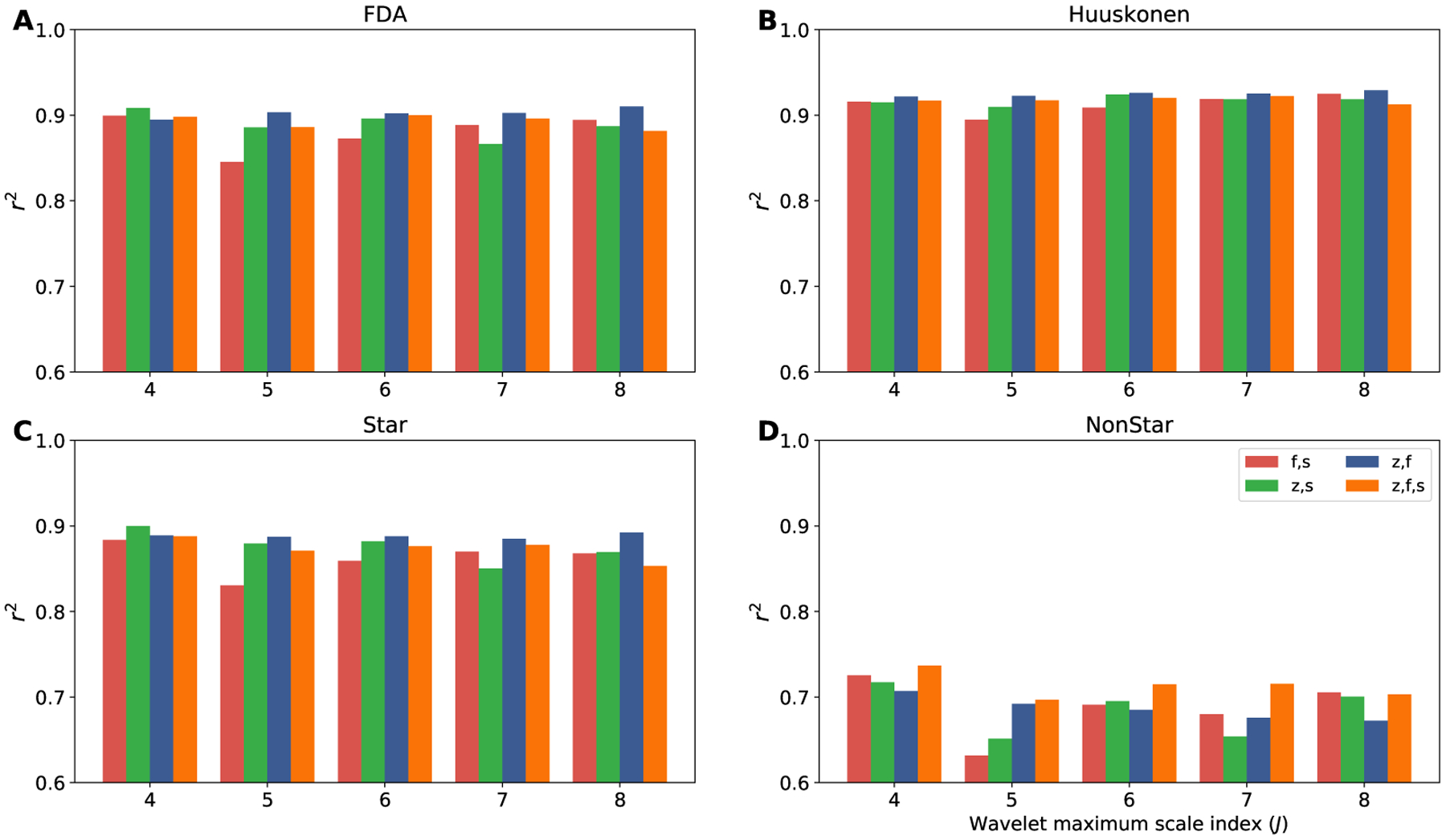
The r² for different test sets using GSGNN models. A) shows r² for the FDA test set. B) represent r² for the Huuskonen test set. C) and D) show r² for the Star and NonStar test sets, respectively. The horizontal axis indicates the maximum wavelet scale J. The atomic attributes are generated with 2D molecular structure, CGenFF force fields and using AC36 atom type classification scheme.

The r², RMSE and MUE of best-performing GSGNN model for each test set are shown in Table 7. In paper²⁵ the log P values for the FDA, Star, NonStar test sets are predicted using their topology-based models (TopP-S) and the different established methods such as ALOGPS, XLOGP3 and KowWIN. We find that our results do not outperform the TopP-S method but we do achieve higher accuracy compared to other known methods such as ALOGPS, KowWIN and XLOGP3 for FDA test set (Table S3), methods like XLOGP3 and ALOGP for Star test set (Table S4) and XLOGP3 method for NonStar test set (Table S5).

Table 7:

The logP prediction performance results for four independent test sets.

Dataset	r2	RMSE	MUE
FDA	0.91	0.56	0.35
Star	0.90	0.49	0.35
NonStar	0.72	1.02	0.81
Huuskonen	0.93	0.37	0.23

Geometric scattering vs graph convolution

To compare the performance of geometric scattering (GSGNN) models to the graph convolution (GCN) models, we trained models using these two methods with two different sets of atomic attributes ”FF” and ”OPENCHEM” as described in Section 2. To rule out the influence of the training/test split, we trained 5 models for each method where the data is randomly divided into training and test sets with 80/20 ratio, respectively. Each of the five GSGNN models is trained using 5-fold cross validation. The RMSE and r² are determined for each model and are shown in Table 8. Note that the atomic attributes for these GSGNN models are generated by 2D molecular structure, CGenFF force fields, and AC36 atom type classification scheme. The GSG parameters that used to generate the molecular features are from one of the best performing models (a wavelet maximum scale of J = 4 and all three of the zero-, first- and second-order scattering operators) from Figure 4. Our results suggest that the ClassicalGSG method, which is a GSGNN model trained on FF atomic attributes, has the most accurate prediction of log P values.

Table 8:

The logP prediction results using different set of features and models

Method name	Atomic attributes	Model	r2 (STD)	RMSE (STD)
ClassicalGSG	FF	GSGNN	0.91 (0.003)	0.52 (0.009)
-	OPENCHEM	GSGNN	0.89 (0.003)	0.57 (0.005)
-	FF	GCN	0.75 (0.091)	0.91 (0.18)
OpenChem	OPENCHEM	GCN	0.79 (0.052)	0.83 (0.122)

Features visualization

To examine the molecular features that are generated in the pipeline of the ClassicalGSG method, we visualize the features generated by the GSG method and the last layer of NN model using t-distributed stochastic neighbor embedding (t-SNE)⁵⁹ plots. The t-SNE plots are intended for projecting high dimensional data into the low dimensional space so it can be visualized readily. Figure 6 shows the GSG and NN features for molecules in the OpenChem test set visualized in a 2D space. Here each point shows a molecule in the OpenChem test set and is colored by its log P value. The initial dimension of GSG features is 1716 while NN features have size of 400. These GSG features are generated from CGenFF atomic charges, 2D molecular structure, AC36 type classification scheme and all three scattering moment operators with wavelet step number of 4.

Figure 6:

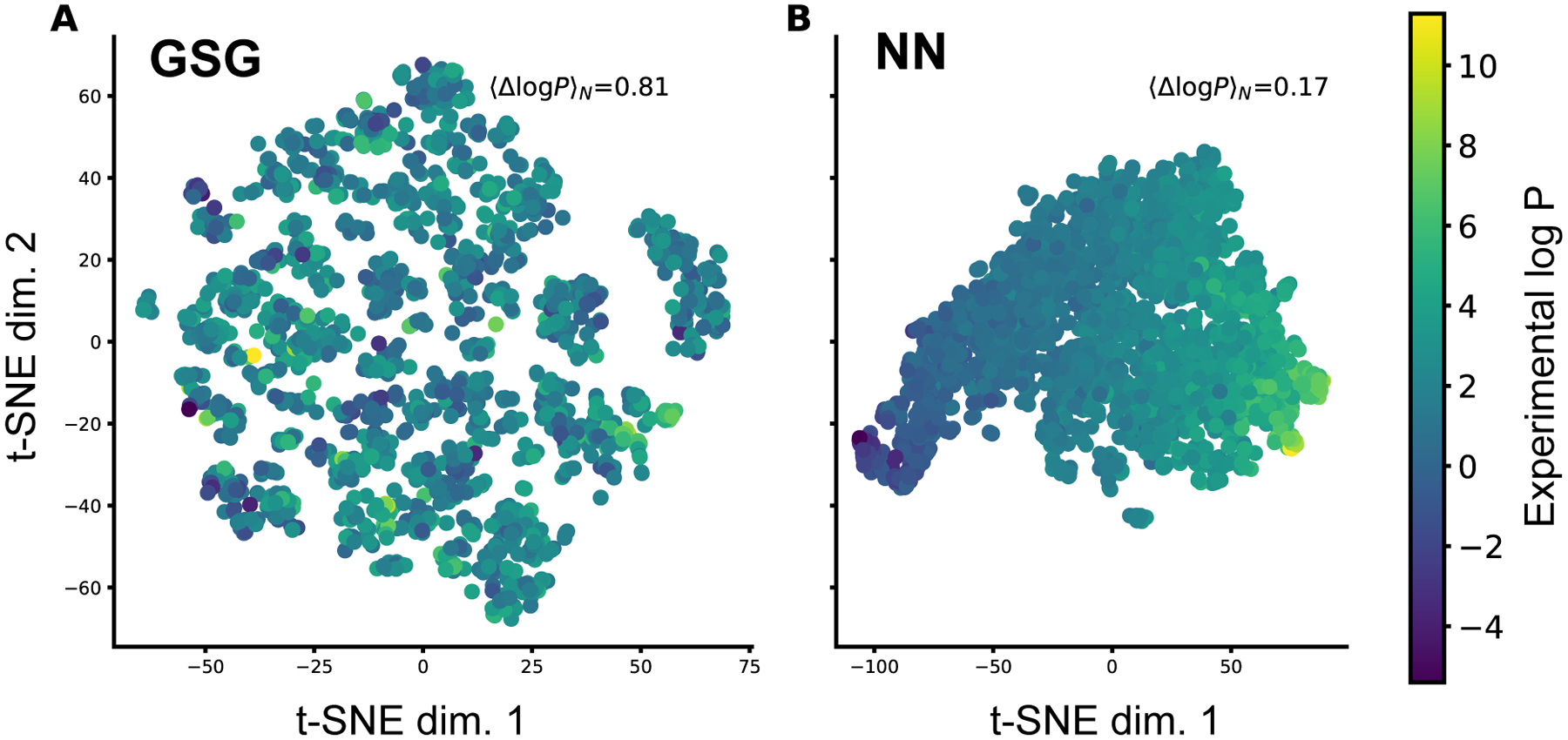
The t-SNE plots with GSG and NN features of the OpenChem test set molecules. Each represents a molecule and is colored by its actual log P value. 〈Δlog P〉_N shows the mean log P difference value calculated over the nearest neighbors in the t-SNE plot. A) The GSG features of size 1716 are projected into 2-dimensional space. B) The NN features from the last hidden layer with size of 400 are projected into 2-dimensional space.

We can observe from Figure 6 that features extracted from NN are more discriminative with respect to log P values. More specifically, in the last layer of the NN model, molecules with similar log P value tend to be near each other and form distinct clusters. In contrast, GSG features are less discriminative where nearby molecules have different log P values. To further verify this, five nearest neighbors are determined for each point in the GSG and NN reduced feature space. Then, the difference between the actual log P value of each point and its five neighbors are calculated and averaged. This value averaged over all the molecules and is shown by 〈Δlog P〉_N inside the figure. The 〈Δlog P〉_N in the reduced GSG features space is 0.81 while this value for the reduced NN features space is only 0.17. The average log P difference between two random points is 2.00. This shows that molecules with similar log P values are closer in the NN features space.

This is noteworthy, as the GSG features are task independent and therefore are not adapted to any particular prediction task, including log P prediction. On the other hand, the NN model, which takes as input the GSG features, is a supervised model that is trained for the specific task of log P prediction. The results in Figure 6, in addition to the results in Tables 7 and 8, illustrate that the GSG features provide not only a translation, rotation, and permutation invariant representation of the molecules, but one that is also sufficiently rich so that, when combined with a downstream supervised NN, the resulting model provides accurate estimates of log P values for molecules.

Features contribution analysis

In order to determine important atomic attributes that contributed to the prediction of log P we performed ablation analysis on the test sets used in Section 3. The molecular features for these models were created by atomic attributes, including atom partial charge, Lennard-Jones radius and epsilon parameters and atomic classification scheme AC36. Feature ablation analysis identifies important features using the change in the model’s prediction upon removal of each feature or group of features. The ablation importance values for 39 atomic attributes are determined using the Captum library,⁶⁰ and are averaged over the 5 models created by 5-fold cross validation in Section 3. The top 10 most important attributes are listed in Table 9. Intuitively, these attributes are associated with polar groups that could have large impacts on molecular hydrophobicity. While none of these atomic types is extremely rare – the least common is N3, which occurs on average 0.33 times per molecule (Table S6) – the most commonly observed atomic types (e.g. non-polar hydrogen, sp3 carbon) are not placed highly in this list. The ablation analysis thus reveals some important information on which features have outsized importance for log P prediction. We also note that the scalar molecular dynamics parameters (LJ epsilon, atomic charge, LJ radius) are found to be significant for log P prediction, implying that they contain useful information that is not covered by atomic types alone.

Table 9:

The most important atomic attributes as predicted by ablation analysis. Atom types are groups of CGenFF atom types. See Table S1 in Supporting Information for more detail.

Rank	Atomic parameter	Average importance	STE
1	AC36 O2 (sp2 oxygen)	0.0716	0.0078
2	AC36 N3 (sp3 nitrogen)	0.0635	0.0054
3	AC36 N2R (sp2 nitrogen in ring)	0.0560	0.0049
4	LJ epsilon	0.0516	0.0048
5	AC36 H2 (polar hydrogen)	0.0499	0.0017
6	Atomic charge	0.0475	0.0029
7	AC36 C2 (sp2 carbon)	0.0448	0.0033
8	LJ radius	0.0416	0.0058
9	AC36 O3 (sp3 oxygen)	0.0392	0.0030
10	AC36 C2R (sp2 carbon in ring)	0.0373	0.0086

Distinguishing features of failed molecules

To investigate the common characteristics of failed molecules during the prediction of their log P value, we created molecular fingerprints, which have been used extensively in cheminformatics, QSAR/QSPR predictions, and drug design.²⁵ Here we employ ChemoPy³⁴ to create a set of constitutional fingerprints. To specify the failed molecules we define a failure cutoff value (here, 0.5) where if the difference between the actual and predicted log P values is larger than the cutoff, we consider the molecule as a failed prediction. We determine the failed molecules from ClassicalGSG models we described in Section 3. These models are trained on features constructed by CGenFF force fields, 2D structure and AC36 atom type classification method. The probability distribution of 30 constitutional fingerprints are calculated for all molecules in the OpenChem dataset and for failed molecules in each of the 5 GSGNN models. KullbackLeibler divergence (KL-divergence)⁶¹ values are determined by comparing probability distributions of all data with distributions of the failed molecules from each model. The KL-divergence values are averaged over five models and their standard error (STE) is shown in Table 10. We note that the PCX descriptors count the number of shortest paths of length X. The attributes with the highest KL-divergence values are: PC counts with lengths of 2,1,3 and 4; molecular weight (Weight); the number of carbon atoms (ncarb); and the number of heavy atoms (nhev). In other words, the distributions of failed molecules are enriched in particular values of these attributes.

Table 10:

The averaged KL-divergence between fingerprint distributions of all data versus failed molecules averaged over 5 GCGNN models.

Fingerprint	Average_KL	STE	Fingerprint	Average_KL	STE
PC2	0.048	0.005	nhet	0.028	0.003
PC1	0.047	0.006	noxy	0.026	0.003
PC3	0.046	0.007	nrot	0.026	0.004
Weight	0.045	0.004	nsulph	0.026	0.003
PC4	0.044	0.004	ndb	0.017	0.002
ncarb	0.043	0.005	ndonr	0.012	0.004
nhev	0.043	0.007	ncof	0.011	0.001
nta	0.043	0.007	AWeight	0.011	0.002
PC5	0.04	0.005	nnitro	0.01	0.001
naro	0.04	0.003	ncocl	0.009	0.002
PC6	0.039	0.005	nhal	0.008	0.001
nsb	0.038	0.004	nphos	0.007	0.003
naccr	0.036	0.002	ncobr	0.006	0
nring	0.035	0.004	ncoi	0.005	0.002
nhyd	0.031	0.003	ntb	0.001	0

The probability distributions of fingerprints with the highest KL-divergence values are shown in Figure 7. The distributions for the failed molecules largely follow the complete dataset distribution, but are enriched towards higher values, suggesting that the log P predictions are more likely to fail for larger molecules. Interestingly the distributions for attributes that count rare element types (e.g. number of Phosphorus (nphos), number of iodine atoms (ncoi) and number of bromine atoms (ncobr)) do not show large KL-divergence values, although this might have been expected given that they are poorly represented in the training set. The atom element types and their count in our dataset is shown in Figure S1.

Figure 7:

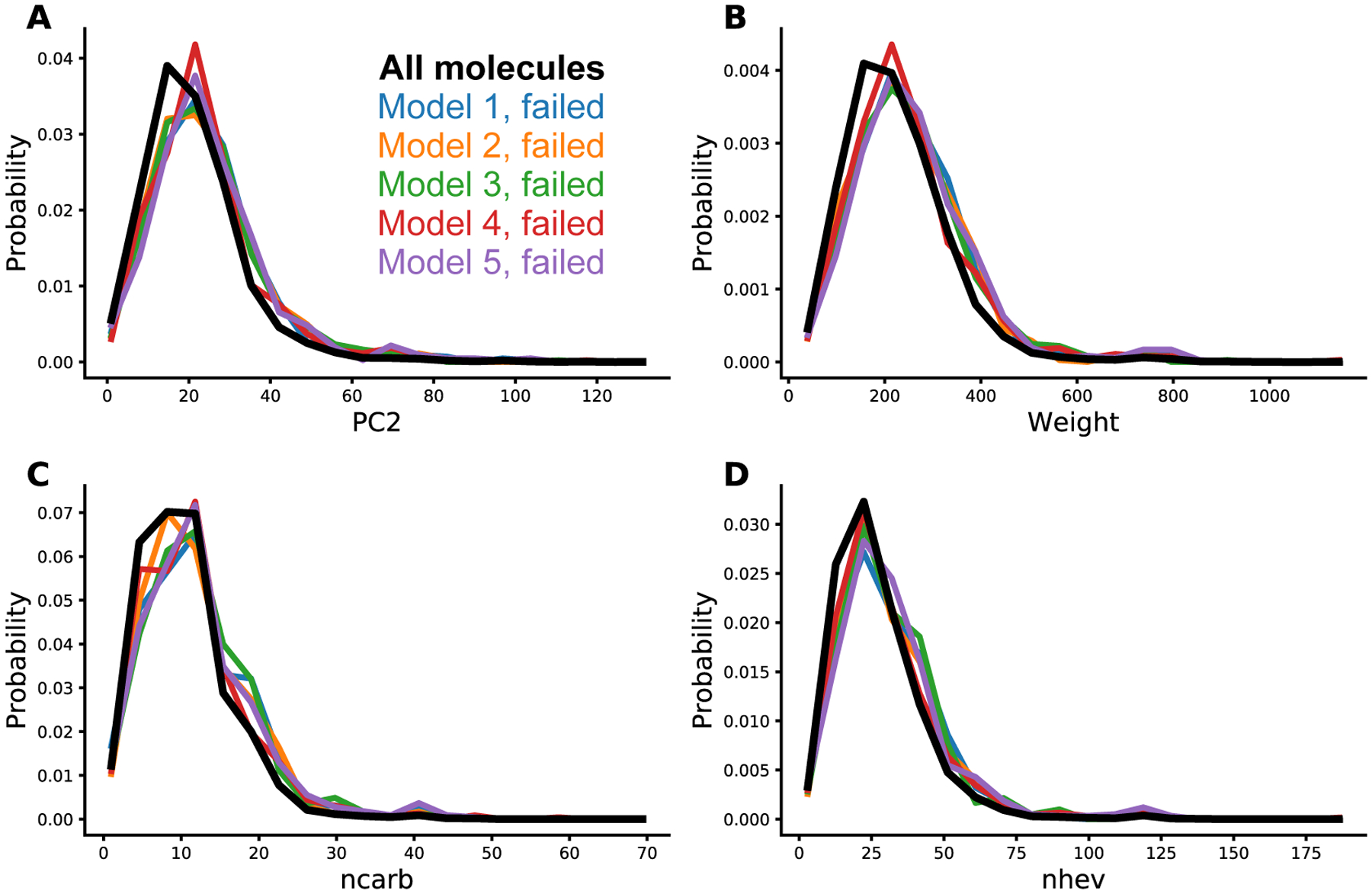
Probability distributions of molecular fingerprints. The histograms show the distribution of fingerprints of all data and failed molecules of 5 GCGNN models. The distribution of all data is shown in thick black line. A) The number of shortest paths of length 2, B) the atomic weight, C) the number of carbon atoms (ncarb) and D) the number of heavy atoms.

4. DISCUSSION AND CONCLUSIONS

In this paper, we introduced a method called ”ClassicalGSG” for predicting the partition coefficient. Our method uses atomic attributes that are usually utilized as parameters for classical MD simulations. These parameters include partial charges, Lennard-Jones well depth, Lennard-Jones radius and atomic type. The pipeline for generating these parameters includes: creating 3D structure from SMILES, creating PDB and Mol2 formatted files, and generating atomic parameters using either Antechamber (GAFF2) or CGenFF tools. We note that, in our implementation, the Antechamber tool is about 200 times slower than CGenFF, requiring a couple of days to process 10,000 molecules.

We employ the geometric scattering for graphs (GSG) method to transform the atomic attributes into molecular features that satisfy re-indexation symmetry. Our results indicate that GSG is powerful enough to capture the universal molecular features, as the average log P difference for all pairs of adjacent molecules in a t-SNE plot (〈Δlog P〉_N) is 0.81, which is a low value compared to the random pair log P difference (2.00). As these features are general to the molecule and not specific to log P, this suggests that they can be used in multi-task NNs to predict other molecular properties, such as solubility (log S), melting point, pKa, and intestinal permeability (e.g. Caco2).⁶²

Our results show that employing a 2D molecular structure in ClassicalGSG yields accurate log P predictions compared to 3D structures, and this confirms the same conclusion achieved previously.^63,64 This could be due to difficulties in generating appropriate 3D structures, or that a single 3D structure is insufficient to capture the high probability conformations of a given molecule. Additionally, our 3D adjacency matrix did not explicitly distinguish between bonded and non-bonded interactions, where the former are much more important to determine molecular properties.

The results reported here for four independent external test sets show that our log P ClassicalGSG method is generalizable to new molecules. However, we do not expect this model to perform well for molecules with new elements or functional groups that are not covered in the training set. Like other empirical methods, we expect the accuracy will improve as the availability of training data grows.