Abstract
Speed accuracy trade-off, the inverse relationship between movement speed and task accuracy, is a ubiquitous feature of skilled motor performance. Many previous studies have focused on the dominant arm, unimanual performance in both simple tasks, such as target reaching, and complex tasks, such as overarm throwing. However, while handedness is a prominent feature of human motor performance, the effect of limb dominance on speed-accuracy relationships is not well-understood. Based on previous research, we hypothesize that dominant arm skilled performance should depend on visual information and prior task experience, and that the non-dominant arm should show greater skill when no visual information nor prior task information is available. Forty right-handed young adults reached to 32 randomly presented targets across a virtual reality workspace with either the left or the right arm. Half of the participants received no visual feedback about hand position throughout each reach. Sensory information and task experience were lowest during the first cycle of exposure (32 reaches) in the no-vision condition, in which visual information about motion was not available. Under this condition, we found that the left arm group showed greater skill, measured in terms of position error normalized to speed, and by error variability. However, as task experience and sensory information increased, the right arm group showed substantial improvements in speed-accuracy relations, while the left arm group maintained, but did not improve, speed-accuracy relations throughout the task. These differences in performance between dominant and non-dominant arm groups during the separate stages of the task are consistent with complimentary models of lateralization, which propose different proficiencies of each hemisphere for different features of control. Our results are incompatible with global dominance models of handedness that propose dominant arm advantages under all performance conditions.
Keywords: Lateralization, Speed-accuracy tradeoff, Handedness, Reaching
Introduction
Speed accuracy trade-off, the inverse relationship between movement speed and task accuracy, is a ubiquitous feature of skilled motor performance in both human and non-human animals (Fitts 1954; Fitts and Peterson 1964; Yarrow et al. 2009; Heitz and Schall 2012; Heitz 2014). Depending on the demands of the task, we tend to move at a slower speed to gain greater accuracy or sacrifice accuracy to complete the task sooner. For example, when threading a needle, we tend to move very slowly to achieve the fine accuracy prescribed by the eye of the needle, while the main goal of hammering a nail is to achieve maximum momentum at adequate accuracy. As we become more skilled at each task, we can increase speed for the required accuracy. In fact, it has been suggested that motor skill acquisition is, in essence, the modification of this speed-accuracy relationship, in which we learn to perform a task with the same accuracy (i.e. hitting a nail) at a higher velocity, or we maintain velocity while improving accuracy (i.e. more often getting the thread through the eye of the needle) (Shmuelof et al. 2012).
Many previous studies of speed-accuracy trade-off in humans have focused on dominant arm unimanual performance in both simple tasks, such as target reaching (Plamondon and Alimi 1997), and complex tasks, such as overarm throwing (Sachlikidis and Salter 2007). However, a prominent feature of skilled motor performance is that the two arms exhibit different proficiencies that seem to reflect how we distribute components of a functional action to each arm. For example, when performing bimanual tasks, the non-dominant hand tends to stabilize the needle or the nail, while the dominant hand moves the thread or the hammer. This distribution of function is predicted by our bihemispheric model of motor lateralization, termed Dynamic Dominance. This model, based on empirical findings in typical adults and patients with unilateral brain damage (Bagesteiro and Sainburg 2002; Sainburg and Schaefer 2004; Schaefer et al. 2007, 2009; Haaland et al. 2009; Yadav and Sainburg 2014b), attributes predictive control mechanisms that can specify energetically efficient and spatially precise trajectories under consistent task conditions to the hemisphere contralateral to the dominant arm. Conversely, the non-dominant hemisphere appears specialized for achieving robust and stable positions under inconsistent and unpredictable environmental conditions, such as when the impending movement is not well-practiced or when unpredictable perturbations arise from environmental mechanics (Sainburg and Kalakanis 2000; Bagesteiro and Sainburg 2006; Wang and Sainburg 2007; Yadav and Sainburg 2014b). We have previously operationalized this model through computational simulations of these processes, combining them serially in different proportions to differentially simulate dominant and non-dominant arm movements (Yadav and Sainburg 2011,2014a,b). Our results showed that empirical movements of the dominant arm were best-fit by our model when predictive control mechanisms were employed throughout most of the movement. In this model, predictive control mechanisms were based on an optimization model that minimized mechanical work, spatial error, and speed. In contrast, the simulated non-dominant arm trajectories were best fit to empirical data when an impedance controller played a greater role in control (Yadav and Sainburg 2011, 2014a). While processes that predict impending limb dynamics should benefit substantially from experience, impedance control mechanisms might show less benefit from the experience. This is because control of trajectory through prediction of limb and task dynamics requires accurate estimates of limb and environmental conditions within the context of the task, and variations in these predictions can produce substantial variations in the resulting trajectories. On the other hand, an impedance controller that specifies steady state or transient stiffness and viscosity values should be robust to a large range of unexpected environmental and limb mechanical conditions.
In contrast to complementary dominance, the more prominent Global dominance models purport that the dominant hemisphere/hand is specialized for all features of motor planning and control, and thus predicts dominant arm superiority for all aspects of behavior (Liepmann 1908; Annett et al. 1979; Volkmann et al. 1998; Ziemann and Hallett 2001). Thus, the most striking prediction of our complimentary dominance model is that the non-dominant arm should demonstrate superior performance, or “dominance,” when task conditions favor non-dominant modes of control. The predictive nature of the dominant controller is dependent on accurate information about mechanical conditions, especially with regard to initial conditions, prior to movement. In addition, such control should be susceptible to inaccurate estimations or variations in mechanical conditions and/or perturbations that can arise from unfamiliar conditions. In contrast, an impedance controller should be robust to changes in sensory information and task experience.
We now test these models of lateralization within the context of motor skill, assessed through speed-accuracy trade-offs. While the global dominance hypothesis predicts the superior skill of the dominant arm under all conditions, our model predicts the better performance of the non-dominant arm when sensory information and task experience are lowest. Thus, we predict that the non-dominant arm should demonstrate a more advantageous speed-accuracy relationship when the controller is naive to the task and sensory information is limited. We also predict that the dominant arm should improve speed-accuracy relations with experience to a greater degree than the non-dominant arm, because estimates of limb and task dynamics should become more accurate for the dominant arm controller.
Materials and methods
Experimental setup
Forty young adults between the ages of 18 and 35 were recruited for this study (mean age 22.59 ± 0.69). All participants were right-handed, as determined by a questionnaire adapted by Hull (Hull 1936) that asks participants to self-report hand preference on a variety of daily tasks. The Hull inventory reflects an extended set of tasks, similar to those listed in the Edinburgh Inventory (Oldfield 1971). Potential participants were also screened to identify and exclude anyone with underlying neurological conditions that would affect their performance on the tasks conducted during the study. Informed consent was obtained for each participant, and all procedures were approved by the institutional review board of Penn State University.
Participants completed the experiment in a 2-D virtual-reality workspace, as outlined in Fig. 1. Each participant’s forearms were supported in the horizontal plane with an air sled, which reduced friction and limited fatigue over repeated trials. Above the arms, a mirror was placed to reflect images from an overhead LCD screen. The participant’s eye level was just above the height of the mirror, so they were unable to see their arms on the tabletop but able to view the visual display reflected onto the mirror.
Fig. 1.
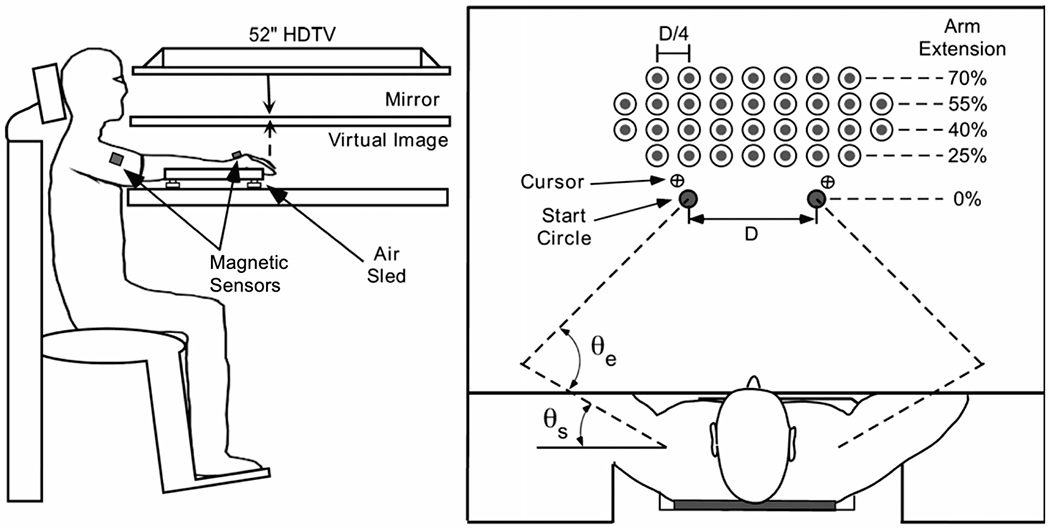
Experimental Setup (left); Workspace Setup (right), where target locations were normalized to each subject’s maximal reach. The start position for each trial, located at the start circle, was defined as the participant’s index fingertip location when εe = 75 degrees and εs = 25 degrees
Experimental task
Participants reached to targets 3.5 cm in diameter that would appear on the screen. The targets appeared one at a time in one of 32 different pre-set target locations so as to appear pseudorandom to the participant. The array of 32 targets is shown in Fig. 1 (top view). This array was scaled according to the reach extent of each individual. Target rows were set to 25%, 40%, 55% and 70% of reach, and target columns were set to 25% of the distance between left or right start positions (as represented by D in Fig. 1). These two start positions, represented by a 2 cm diameter circle for each arm, were set for each individual with respect to the elbow joint internal angle, θe = 75°, and shoulder joint external angle, θs = 25° (see Fig. 1, top view). Because the workspace extent was dependent on each participants’ arm length (reach extent), we measured arm length to test for group differences and subjected this measure to 1-way ANOVA. Our results indicated no significant differences between groups [F(1, 38) = 0.3333; p = 0.5672]. The experiment lasted approximately 15 min, with each participant completing 160 total reaches, thus reaching to each target location five times in pseudorandom order.
Prior to the start of the experiment, participants were randomly assigned to one of four groups (see Table 1), with a total of ten participants in each group. The group assignment designated the arm used and whether or not the group received cursor feedback (represented as a cursor on the screen) of the hand location throughout the duration of each trial. For groups 1 and 2, the reaches were performed with the left vs. right arm, respectively, and visual feedback was provided only prior to the start of each trial, disappearing when the participant started to move towards the target. Conversely, groups 3 and 4 also reached with the left vs. right arm, respectively, but received visual feedback on cursor location throughout the reach. The experiment was structured as a four-group design to prevent an effect of order and experience for visuomotor reaching tasks (Wang and Sainburg 2004; Birbaumer 2007). Research has shown that performance of a task with one arm transfers to affect performance in the opposite arm, and this transfer of learning across limbs is often asymmetrical depending on the order of dominant vs. non-dominant limb performance and workspace location (Sainburg and Wang 2002; Criscimagna-Hemminger et al. 2003; Wang and Sainburg 2006). All trials were self-paced. Each trial was initiated by an audiovisual go signal, after the cursor was returned to and remained in the start circle for 0.5 s. Participants were instructed to reach as quickly and accurately as possible. To encourage both a rapid and accurate reach for each trial, points were awarded for accuracy (10 points: within the target; 3 points: < 3.5 cm from target; 1 point: 3.5–7 cm from target) only when the participant reached a peak velocity threshold of 0.5 m/s. Following each reach, the participant received the knowledge of results in the form of a circle indicating final hand location.
Table 1.
Group characteristics
| No cursor feedback during reach | Cursor feedback during reach | |
|---|---|---|
| Task performed with left arm | Group 1 | Group 3 |
| Task performed with right arm | Group 2 | Group 4 |
Kinematics
Two 6-DOF magnetic sensors (Ascension TrakStar) were placed on the dorsal hand and upper arm of each participant, and bony landmarks were digitized relative to each sensor. The forearm and hand were supported by an air-sled, while the fingers were immobilized in a comfortable resting splint, to ensure rigid positioning relative to the hand sensor (see Fig. 1). Data were sampled at 116 Hz and smoothed via an 8 Hz low-pass Butterworth filter. We used custom programs designed in IgorPro (version 6.37; WaveMetrics) to process and analyze all kinematic data. Tangential velocity was calculated as the Pythagorean addition of the first time derivative of each 2-D component of finger displacement (X, Y). The beginning of each trial was defined as the first minimum of tangential velocity that was less than 5% of peak velocity, and movement offset was defined as the first minimum of tangential velocity that occurred after peak velocity and was lower than 5% of peak velocity. Two primary metrics were used in our statistical analysis: final position error and the maximum (peak) velocity of each trial. Final position error was calculated within each trial as the 2-D distance from the final cursor location to the center of the intended target at the point of calculated movement offset.
Statistical analysis
To assess changes in our outcome measures following the repeated presentation of each target location, we separated the 160 trials into five cycles of 32 trials. Within each cycle, the participant completed one reach to each target location in a pseudorandom order. Each participant completed five total cycles throughout the task. Our measures were subjected to the Shapiro–Wilk Test to assess for normality (Shapiro and Wilk 1965) and the Mauchly Test to assess for homogeneity of variance (Mauchly 1940). Any violations of normality were corrected using the Johnson transformation method (Johnson 1949), and any violations of sphericity were adjusted using Greenhouse–Geisser estimates for sphericity (Geisser and Greenhouse 1958). We then subjected these measures to omnibus analysis, using a 2 × 5 mixed factor ANOVA, with condition (visual feedback, no visual feedback) and arm (right, left) as between-subject factors, and cycle (1–5) as the within-subject factor. We then further subjected our metrics to two-way ANOVA (arm X cycle) within each feedback condition, to examine our a priori predictions of arm differences in performance under no visual feedback conditions following a repeated practice. Within each group (1–4 as outlined in Table 1), we utilized a simple linear regression model (error x peak velocity) to examine our a priori predictions of arm differences in speed-accuracy relationships.
When warranted, post-hoc analysis (Tukey HSD test) was used to compare the means of every treatment to the means of every other treatment; that is, it applies simultaneously to the set of all pairwise comparisons. This analysis thereby controls the family-wise error rate (Jackson Barnette and McLean 2005). The Tukey HSD method provided controls the overall error rate for all comparisons of interest by using a multiple comparison adjustment in calculating p-values and confidence limits (JMP 2016). We applied an alpha value of 0.05 for our analysis.
Results
In each of five consecutive cycles of targets, each group of right-handed participants performed reaches to 32 randomly presented targets across the workspace with either the left or the right arm. Two groups performed the task with the feedback of the cursor during motion, and two groups without visual feedback of the cursor. Because skilled performance reflects a relationship between speed and accuracy, we first describe accuracy, then speed of performance, and finally accuracy-speed relations.
Final position error and error variance
Figure 2a shows mean (± SE) values of final position error, across all five cycles of practice, separated by arm (black = left, gray = right) and feedback condition (dashed = vision, solid = no vision). The no visual feedback group performed the task more poorly, with mean error more than double that of the visual feedback group, regardless of cycle or arm used. Figure 2a also shows a reduction in error with practice, regardless of feedback condition or arm used. This reduction in error is most apparent in the right arm group of the no visual feedback condition, especially across cycles 1 and 2. These observations were supported by our statistical analyses: our 3-way mixed factor ANOVA (visual condition × arm × cycle) with Greenhouse–Geisser corrections (ε = 0.565) showed a significant interaction between condition and cycle [F(2.2603, 81.37) = 3.0151; p = 0.0484]. This reflects the greater slope of improvement across cycles for the no-vision group when compared to the vision group condition (Fig. 2a). This ANOVA also revealed a main effect of both cycle [F(2.2603, 81.37) = 21.4436; p = 0.0204] and feedback condition [F(1, 36) = 59.7533; p < 0.0001], neither of which was precluded by the interaction cited above. These main effects reflect the higher error for the no-vision condition across all cycles and both hands, and the downward trend between cycles for all groups. The follow-up two-way ANOVAs (arm x cycle) within each feedback group revealed a main effect of cycle for both conditions [Vision: F(4, 15) = 12.1833; p = 0.0001; No Vision: F(1.8631, 33.536) = 11.9310 (G-G corrected); p = 0.0002].
Fig. 2.
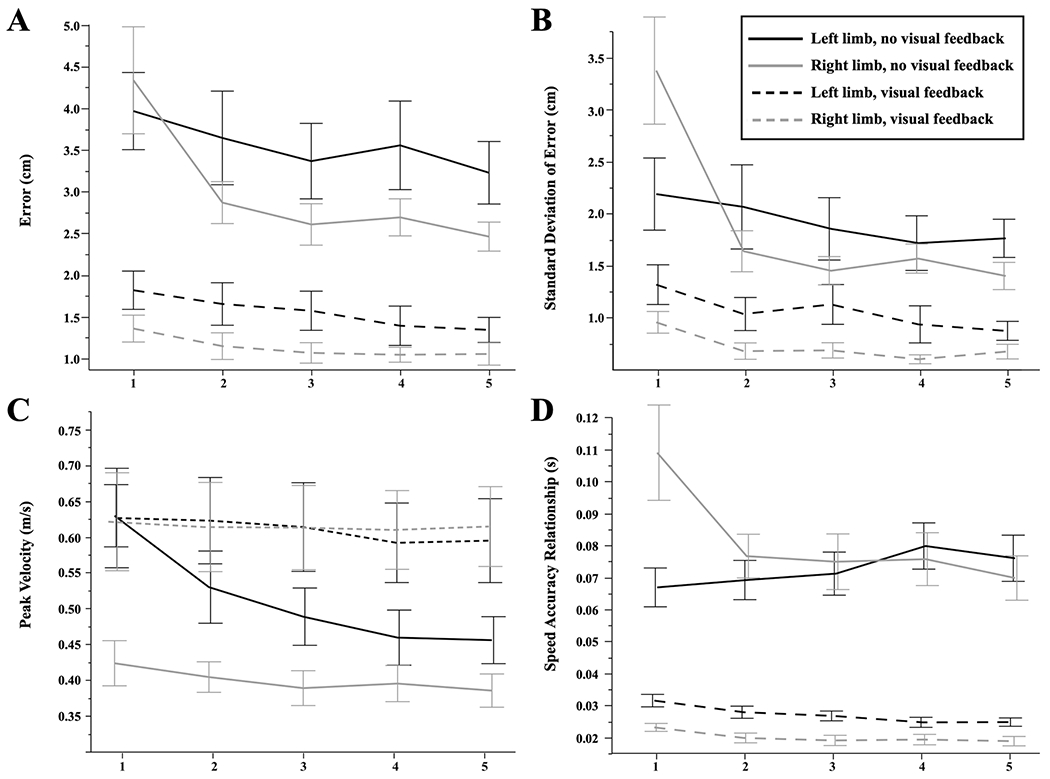
Performance across groups. Each cycle represents a reach to all 32 target locations in pseudorandom order. Error bars represent one standard error from the mean. a Final position error. b Standard deviation of error. c Peak tangential velocity. d Speed-accuracy relationships (error/speed)
We quantified error variability within a cycle of the task as the standard deviation of error within each cycle. As shown in Fig. 2b, the dominant arm group demonstrated a large reduction in variability of the right arm under the no-vision condition, most notably between cycle 1 and cycle 2. Conversely, the non-dominant arm group did not appear to decrease error variability as the task repetition increased. These error variability differences reflect differences in each arm group’s response to task experience and absence or presence of visual feedback. These observations were supported by our statistical analysis, as the Greenhouse–Geisser corrected (ε = 0.711) mixed-factor ANOVA (visual condition x arm x cycle) revealed a 3-way interaction between cycle, arm, and feedback condition [F(2.8421, 102.32) = 2.8306; p = 0.0449]. Separate ANOVA (arm x cycle) for each feedback condition revealed a main effect of cycle for the vision group [F(4, 15) = 6.1591; p = 0.0039], but no other effects. For the no-vision group, ANOVA revealed a significant arm x cycle interaction [F(2.182, 39.276) = 9.5685; p = 0.0003]. Post hoc analysis showed that this interaction was the result of a substantial reduction in variance between the first two cycles of performance, only for the right arm (Tukey HSD: p < 0.0001). These results emphasize the unique aspect of the first cycle of movement under the no vision condition for the right arm, indicating that this group experienced a large decrement in error variability following cycle 1.
Peak hand velocity
We measured speed as peak tangential velocity of the arm for each trial of movement. Figure 2c shows mean (± SE) values of peak velocity across all five cycles of practice, separated by arm (black = left, gray = right) and feedback condition (dashed = vision, solid = no vision). Overall, speed was consistent across cycles, with the exception of the no-vision-left arm group. This group showed a slight reduction in speed, most notably between the first and second cycles. Indeed, our Greenhouse–Geisser corrected (ε = 0.501) 3-way mixed factor ANOVA (feedback condition x arm x cycle) confirmed these observations, revealing a significant arm x cycle interaction [F(2.0022, 72.079) = 3.2845; p = 0.0431] and a feedback condition x cycle interaction [F(2.0022, 72.079) = 5.5624; p = 0.0057]. Separate two-way ANOVA (arm x cycle) performed for the visual feedback group showed no significant main effects or interactions. However, within the no visual feedback group, this ANOVA revealed a significant interaction between arm and cycle [F(1.7694, 31.849) = 3.5317; p = 0.0463]. This interaction can be seen in Fig. 2c as a steeper reduction in speed across cycles for the left arm. This ANOVA also showed a main effect of arm [F(1, 18) = 5.6490; p = 0.0288], reflecting the increased speed of the left arm across all cycles. Because this main effect crossed all cycles, it was not precluded by the interaction described above.
Speed accuracy relationship
To characterize speed-accuracy relations, we divided the final position error by peak velocity for each trial, thus providing a speed-normalized measure of each arm and cycle’s accuracy, which we term speed-accuracy relation. Figure 2d shows the mean (± SE) values for this measure of speed-accuracy relationship, across hands, cycles, and feedback conditions. The speed-accuracy relationship was initially worse for the right, dominant arm under the most information impoverished condition (cycle 1, no-vision). However, with practice, both arms converged to similar performance under the no-vision condition. Conversely, with visual feedback, the dominant arm showed better performance across all cycles. These observations were supported by our Greenhouse-Geiser corrected (ε = 0.564) mixed factor ANOVA (feedback condition x arm x cycle), which revealed a significant arm x cycle interaction [F(2.2571, 81.255) = 6.7099; p < 0.0013] and a feedback condition x arm x cycle interaction [F(2.2571, 81.255) = 7.2071; p < 0.0008], along with a main effect of feedback condition [F(1, 36) = 166.6106; p < 0.0001]. To follow-up these interactions, we conducted a separate two-way mixed factor ANOVA (arm × cycle) within each feedback condition. For the visual feedback condition, we found a main effect of both arm [F(1, 18) = 14.3816; p = 0.0013] and cycle [F(2.8594, 51.469) = 14.366; p < 0.0001], but no significant interaction (p = 0.767). These main effects reflect a consistent, though small, improvement across cycles for both arms and better performance (lower values) of the right arm across all cycles.
For the no-vision condition, this ANOVA revealed a significant arm x cycle interaction [F(2.0923, 37.661) = 7.8396; p = 0.0012; G-G corrected: (ε = 0.523]. This reflects the significantly worse performance (higher values) of the right (dominant) arm in the first cycle and the dramatic improvement in this arm’s performance by the second cycle. In contrast, the left-arm group’s speed-accuracy relation is initially more advantageous than that of the right arm group, as shown in Fig. 2d, but does not improve across practice. Post hoc analysis confirmed that the left arm showed a significantly more advantageous (lower) speed-accuracy relationship during the first (most novel) cycle of the task (Tukey HSD: right: 0.110 ± 0.008 vs. left: 0.067 ± 0.008; p = 0.048). However, the left arm did not show significant improvements as the cycles progressed, as post hoc analysis revealed no significant differences between both the first and second cycles (p ≅ 0.999) and first and fifth cycles (p = 0.8992). In contrast, the right arm showed significant improvements in speed-accuracy performance between the first and second cycles (p = 0.0020), and this difference was maintained through the fifth cycle (p < 0.0001).
Speed-accuracy correlations
To further characterize the speed-accuracy relationship for each group (right arm, left arm) and condition (visual feedback, no visual feedback), we examined the correlation between peak velocity and error, as shown in Fig. 3. Within the visual feedback condition, both arm groups demonstrated strong positive correlations (L: R2 = 0.92, R: R2 = 0.76) (L: p = < 0.001; R: p = 0.0011). However, the right arm group showed an apparent advantage in this relationship, as reflected by a lower slope. Thus, for a given increase of velocity, lower errors could be expected by the right arm group compared with the left arm group.
Fig. 3.
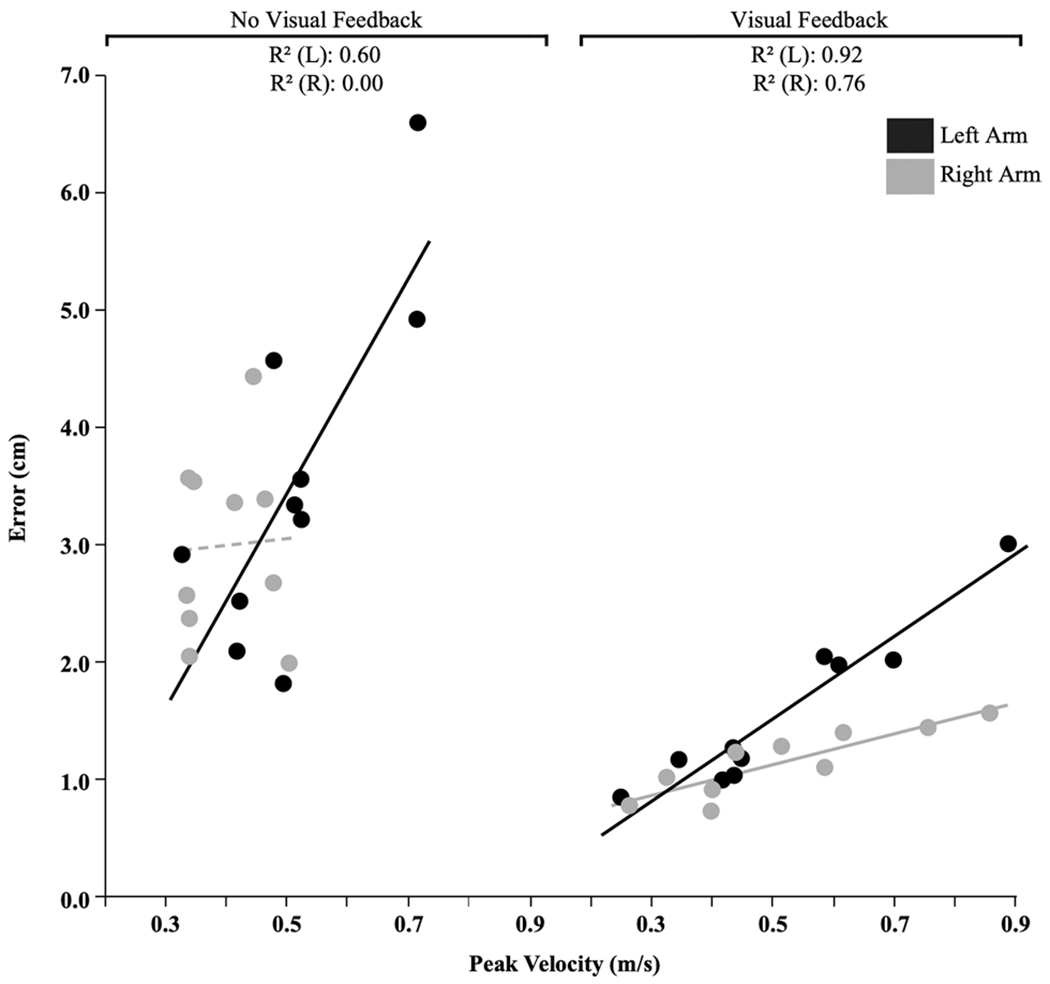
Relationship between speed and accuracy across all cycles. Each point represents participant averages collapsed across cycle and target. Note: the dashed line represents a statistically insignificant line of fit (p = 0.8913)
Within the no vision condition, the left arm group showed a moderate correlation (R2 = 0.60; p = 0.0087), in which larger errors correlated with larger velocities. However, the right arm group showed no significant relationship between error and speed but did show a restriction in the range of speed. This is also reflected by the higher velocities across all cycles for the left arm (see Fig. 2c), and the reported main effect of arm on velocity for the no visual feedback condition. Thus, without the benefit of visual feedback, the left arm group behaved similar to the performance with visual feedback. However, the right arm group’s range in speed was restricted, and error was not dependent on speed.
Discussion
The current study investigated speed-accuracy relationships, or skilled performance, in the context of hemispheric specializations in targeted reaching movement. We tested the prediction that the dominant hemisphere/limb system should demonstrate better speed-accuracy performance when task conditions provided the greatest information about limb and task states, while the non-dominant hemisphere/limb should show an advantage when sensory information is restricted and task experience is least. Four groups of participants performed a reaching task with either the right or left arm and either with or without visual feedback; the task was performed repetitively through five cycles of 32 targets, distributed throughout 70% of the reachable workspace. The feedback condition with the least sensory information and task experience was the first cycle of the task, performed without visual feedback. Remarkably, our findings revealed that for this condition, the non-dominant arm performed substantially better, as measured in terms of speed-normalized accuracy. With continued practice, the advantage of the non-dominant arm under the no-vision condition was eliminated. This occurred due to a practice-related improvement in dominant, but not non-dominant arm performance. In addition, under no-vision conditions, non-dominant arm group performance was characterized by a strong dependence of accuracy on speed, while dominant arm group performance was not. While previous studies have shown a greater reliance of the dominant arm on visual feedback for successful task performance (Roy et al. 1989; Apker et al. 2014), this study is the first, to our knowledge, to demonstrate an effect of both visual feedback conditions and task experience on interlimb differences in speed-accuracy relations.
Interlimb differences in control mechanisms
The differences in performance between dominant and non-dominant arm groups during the separate stages of the task may be the result of hemispheric specializations for different aspects of motor control (Bagesteiro and Sainburg 2002; Sainburg 2002; Schaefer et al. 2007; Yadav and Sainburg 2014a). In the first cycle of our reaching task, under no vision conditions, the non-dominant arm outperformed the dominant arm in terms of speed-accuracy relations. As task repetition increased, the dominant arm’s performance significantly improved, eventually matching the non-dominant arm. Without visual feedback, task information was limited prior to the first reach to each of the target locations. This lack of information appeared to negatively influence dominant but not non-dominant arm performance. Conversely, with visual feedback, both arm groups showed improvements in performance across repeated target presentations, even though the dominant arm outperformed the non-dominant throughout the task. These results are most consistent with a complimentary dominance model of lateralization, in which the non-dominant arm can ‘dominate’ the other arm when task experience and sensory information is limited.
These results appear to be consistent with our hypothesis of an optimal-like predictive controller for the dominant arm that is sensitive to prior state information, and an impedance controller for the non-dominant arm that is robust to variations in state estimates. Progressive improvement of dominant arm performance with practice may be due to experience-related improvements in estimates of limb conditions that provide advantages in predictive control mechanisms. In fact, only the dominant arm showed substantial improvement in speed-accuracy relation with practice. Conversely, the non-dominant arm showed a slight (but not statistically significant) increase in speed-accuracy relation that was associated with a gradual decrease in peak velocity, rather than an increase in accuracy. We expect that these differences were associated with experience-dependent improvements in predictive control for the dominant, but not for the non-dominant arm. This dominant arm advantage was likely associated with the accumulation of information about limb and task conditions, which allowed more accurate state estimates upon which to base future movements. These findings support the hypothesis that the dominant arm control algorithms may be more dependent on prior state information than those of the non-dominant arm.
We propose that non-dominant arm control relies more extensively on impedance control mechanisms that are less dependent on prior state information than optimal-control algorithms. Control of limb impedance is an essential component of the final deceleration and stopping phase of reaching movements, which has been shown to depend on reflex modulation mechanisms as well as muscle coactivation mechanisms (Damm and McIntyre 2008). Impedance control has been attributed to the control of both inertia, as well as forces associated with the deformation of non-contractile tissues, as required to reach a stable and more accurate final posture (Ghez et al. 2007; Scheidt and Ghez 2007; Damm and McIntyre 2008; Jayasinghe et al. 2020). Yadav and Sainburg (2011, 2014a) previously reported simulations that comprised a hybrid of an optimal feedforward controller that minimized energy and minimized both position and velocity errors, and an impedance controller that specified a final equilibrium position. While all movements were initially driven by the optimal controller, stopping the movement ultimately depended on a switch to the impedance controller. The time of this switch was left open in an optimization that fit the simulation to empirical data. The results indicated that, across trials and participants, empirically derived non-dominant arm reaching trajectories were best fit by the simulation when this switch point occurred prior to peak velocity, and dominant arm trajectories were the best fit when the switch occurred in the late deceleration phase of the movement. Thus, dominant arm trajectories relied on the feedforward optimal controller, while non-dominant trajectories were largely driven by the impedance controller. Predictions of this control scheme for the current study are that dominant arm accuracy should benefit most from task experience and prior state information, while non-dominant arm control should benefit less from such information. These predictions are consistent with our results.
It should be noted, however, that the idea that the non-dominant arm may be better adapted for stabilizing a steadystate position in the face of external loads has recently been challenged by Takagi et al. (2020). In this study, participants were asked to stabilize an object with both hands while sinusoidal perturbations were applied. The results demonstrated greater muscle co-activation in the dominant arm, contradicting the proposition that the non-dominant arm may be advantaged for general impedance control. It is plausible that previous studies characterizing non-dominant limb advantages in impeding unexpected perturbations during reaching movements (Sainburg 2002; Bagesteiro and Sainburg 2006; Duff and Sainburg 2007), stabilizing forces imposed by a shared object (spring) from voluntary movements of the other hand (Woytowicz et al. 2018), and achieving more accurate and stable final positions during reaching (Schabowsky et al. 2007; Wang and Sainburg 2007), may not recruit the same control processes as those in the Takagi et al. study, which required stabilizing an object against an imposed sinusoidal perturbation. In fact, a sinusoidal perturbation is predictable due to its inherent periodicity. Recent work has demonstrated a non-dominant arm advantage in reflex modulation during bimanual tasks, which might lead to less reliance on feedforward mechanisms to control impedance in the non-dominant arm and greater reliance on feedforward control of impedance in the dominant arm (Schaffer and Sainburg 2017).
Interlimb differences in proprioceptive processing
It is plausible that the differences in performance under no-vision conditions could also be attributed to the lateralization of proprioceptive acuity. While there is little evidence that proprioceptive acuity is different in the dominant and non-dominant arm, Goble and colleagues (Goble et al. 2006; Goble and Brown 2007, 2008, 2010) have demonstrated a non-dominant arm advantage in certain interlimb position matching paradigms, suggesting an advantage in some aspects of proprioceptive processing. It is possible that such differences might underlie the strategic control differences discussed above. However, Jayasinghe et al. (2020) recently reported interlimb differences in reaching movements in a patient with proprioceptive deafferentation. The patient and control participants made horizontal reaching movements to 3 different targets presented in a block of repeated trials with each arm, without visual feedback of the arm. Remarkably, the non-dominant arm of the patient showed very curved trajectories that ended by stabilizing the arm about an average position at the end of motion (Jayasinghe et al. 2020). In contrast, the dominant arm hand-paths were straighter than those of the non-dominant arm, yet did not stabilize at the end of motion, instead drifting far away from the target. The authors provided simulation results that indicated the non-dominant arm kinematics of the patient could be explained by a control strategy that depended less on feedforward mechanisms and was largely dependent on a poorly tuned impedance controller. Dominant arm kinematics were best explained by a control strategy that depended more on a poorly tuned feedforward controller and less on an extremely weak impedance controller. These findings indicated that the different control strategies associated with each arm are not entirely dependent on differences in proprioceptive feedback but appear to be intrinsic to the control algorithms associated with each arm.
Interlimb differences in patterns of error variability
The tendency to reduce error variability with practice is common across motor practice paradigms (Shmuelof et al. 2012; Wu et al. 2014; Dhawale et al. 2017; Krakauer et al. 2019). From one point of view, variance in early performance has been proposed to reflect poor ability to predict the parameters needed to accurately plan movement (Schmidt 2003), and thus variability may be seen as unwanted “noise,” with high variability impeding successful task performance (Schmidt et al 1979). From another point of view, variability early in performance can be associated with an adaptive strategy aimed at strategic exploration of state space as a mechanism for improving the accuracy of state information. Early performance variability has been shown to correlate with more stable and generalizable learning as task experience increases (Wu et al. 2014; Van Der Vliet et al. 2018; Krakauer et al. 2019). Consistent with this idea, Wu et al. (2014) demonstrated a relationship between task-related variability and motor performance for dominant arm movements, in which higher initial task-relevant variability corresponded with greater rates of learning. They proposed that the higher variability during naïve exposure to the task reflected the exploration of state-space, even though this exploration resulted in a temporary sacrifice in performance stability (Wu et al. 2014). It is possible to attribute the greater variability of the dominant arm early in practice to a dominant arm controller strategy involving exploration of task-space during initial exposure to allow the development of more accurate parameters upon which to base task-related motor plans. Thus, the lower speed-accuracy performance of the dominant arm during the least predictable portion of the task may, in fact, have been in service to the exploration of state-space, to develop a more accurate and generalizable feedforward control strategy. This interpretation is also consistent with the view that the dominant arm controller relies on feedforward control to a greater extent than the non-dominant arm controller. Whether or not the early variability and reduced speed-accuracy performance of the right arm in the first cycle of the task was strategic, our findings reveal substantial interlimb differences in performance early in task exposure that appear to reflect an advantage in performance of the non-dominant arm in this reduced information phase of the task.
Was non-dominant arm performance related to right-hemisphere specializations for visual-spatial processes?
It seems plausible that right-hemisphere specialization for visual-spatial functions might advantage the left non-dominant arm for spatial accuracy. Indeed, previous research with both neurotypical and lesioned populations have indicated the right hemisphere is specialized for aspects of visuospatial information processing (Fink et al. 1999; Boulinguez et al. 2003). However, in the current study, the non-dominant arm was not advantaged in spatial accuracy, but rather in speed-accuracy relations. In addition, under full visual feedback conditions, which should benefit visual-spatial advantages, the right dominant arm showed greater spatial accuracy across all cycles of performance. Therefore, it would be difficult to attribute the dominant arm advantage in speed-accuracy relations in the first cycle of the task to right-hemisphere related advantages in visuospatial processing.
Conclusion
Regardless of the neural asymmetries that might underlie non-dominant arm advantages during early exposure to this task, the results of this study support previous findings that conflict with global dominance models (Schabowsky et al. 2007; Przybyla et al. 2013; Yadav and Sainburg 2014b; Zabihhosseinian et al. 2020). Global dominance proposes that the dominant hemisphere and its contralateral arm should outperform the non-dominant on all aspects of movement, due to an overall superiority in control (Liepmann 1908). A more parsimonious explanation that takes into account current and previous studies revealing non-dominant arm advantages for performance under specific task conditions (Duff and Sainburg 2007) is that the dominant and non-dominant hemispheres are specialized for different aspects of control, and the non-dominant specialization confers advantages when task conditions lead to information deprived states (Duff and Sainburg 2007; Yadav and Sainburg 2014b).
Acknowledgments
Funding
The project described was supported by National Institutes of Health Award Number R01HD059783, along with the National Center for Advancing Translational Sciences, Grant TL1 TR002016 and Grant UL1 TR002014. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
Footnotes
Conflict of interest The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- Annett J, Annett M, Hudson PT, Turner A (1979) The control of movement in the preferred and non-preferred hands. Q J Exp Psychol 31:641–652. 10.1080/14640747908400755 [DOI] [PubMed] [Google Scholar]
- Apker GA, Dyson K, Frantz G, Buneo CA (2014) Efficiency of visual feedback integration differs between dominant and non-dominant arms during a reaching task. Exp Brain Res. 10.1007/s00221-014-4116-5 [DOI] [PubMed] [Google Scholar]
- Bagesteiro LB, Sainburg RL (2002) Handedness: dominant arm advantages in control of limb dynamics. J Neurophysiol. 10.1152/jn.00901.2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagesteiro LB, Sainburg RL (2006) Nondominant arm advantages in load compensation during rapid elbow joint movements. J Neurophysiol. 10.1152/jn.00189.2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birbaumer N (2007) Motor learning: passing a skill from one hand to the other. Curr Biol [DOI] [PubMed] [Google Scholar]
- Bortoli L, Robazza C, Durigan V, Carra C (1992) Effects o f contextual interference and age o n acquisition, retention, and transfer. Percept Mot Skills [DOI] [PubMed] [Google Scholar]
- Boulinguez P, Ferrois M, Graumer G (2003) Hemispheric asymmetry for trajectory perception. Cogn Brain Res. 10.1016/S0926-6410(02)00276-8 [DOI] [PubMed] [Google Scholar]
- Brady F (2004) Contextual interference: a meta-analytic study. Percept Mot Skills. 10.2466/pms.99.1.116-126 [DOI] [PubMed] [Google Scholar]
- Criscimagna-Hemminger SE, Donchin O, Gazzaniga MS, Shadmehr R (2003) Learned dynamics of reaching movements generalize from dominant to nondominant arm. J Neurophysiol. 10.1152/jn.00622.2002 [DOI] [PubMed] [Google Scholar]
- Damm L, McIntyre J (2008) Physiological basis of limb-impedance modulation during free and constrained movements. J Neurophysiol. 10.1152/jn.90471.2008 [DOI] [PubMed] [Google Scholar]
- Dhawale AK, Smith MA, Ölveczky BP (2017) The role of variability in motor learning. Annu Rev Neurosci. 10.1146/annurev-neuro-072116-031548 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duff SV, Sainburg RL (2007) Lateralization of motor adaptation reveals independence in control of trajectory and steadystate position. Exp Brain Res. 10.1007/s00221-006-0811-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fink GR, Marshall JC, Halligan PW, Frith CD, Driver J, Frackowiak RSJ, Dolan RJ (1999) The neural consequences of conflict between intention and the senses. Brain 122:497–512. 10.1093/brain/122.3.497 [DOI] [PubMed] [Google Scholar]
- Fitts PM (1954) The information capacity of the human motor system in controlling the amplitude of movement. J Exp Psychol. 10.1037/h0055392 [DOI] [PubMed] [Google Scholar]
- Fitts PM, Peterson JR (1964) Information capacity of discrete motor responses. J Exp Psychol. 10.1037/h0045689 [DOI] [PubMed] [Google Scholar]
- Geisser S, Greenhouse SW (1958) An extension of box’s results on the use of the F distribution in multivariate analysis. Ann Math Stat. 10.1214/aoms/1177706545 [DOI] [Google Scholar]
- Ghez C, Scheidt R, Heijink H (2007) Different learned coordinate frames for planning trajectories and final positions in reaching. J Neurophysiol. 10.1152/jn.00652.2007 [DOI] [PubMed] [Google Scholar]
- Goble DJ, Brown SH (2007) Task-dependent asymmetries in the utilization of proprioceptive feedback for goal-directed movement. Exp Brain Res. 10.1007/s00221-007-0890-7 [DOI] [PubMed] [Google Scholar]
- Goble DJ, Brown SH (2008) Upper limb asymmetries in the matching of proprioceptive versus visual targets. J Neurophysiol. 10.1152/jn.90259.2008 [DOI] [PubMed] [Google Scholar]
- Goble DJ, Brown SH (2010) Upper limb asymmetries in the perception of proprioceptively determined dynamic position sense. J Exp Psychol Hum Percept Perform. 10.1037/a0018392 [DOI] [PubMed] [Google Scholar]
- Goble DJ, Lewis CA, Brown SH (2006) Upper limb asymmetries in the utilization of proprioceptive feedback. Exp Brain Res. 10.1007/s00221-005-0280-y [DOI] [PubMed] [Google Scholar]
- Green S, Sherwood DE (2000) The benefits of random variable practice for accuracy and temporal error detection in a rapid aiming task. Res Q Exerc Sport. 10.1080/02701367.2000.10608922 [DOI] [PubMed] [Google Scholar]
- Haaland KY, Schaefer SY, Knight RT, Adair J, Magalhaes A, Sadek J, Sainburg RL (2009) Ipsilesional trajectory control is related to contralesional arm paralysis after left hemisphere damage. Exp Brain Res. 10.1007/s00221-009-1836-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitz RP (2014) The speed-accuracy tradeoff: history, physiology, methodology, and behavior. Front Neurosci 8:150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitz RP, Schall JD (2012) Neural Mechanisms of Speed-Accuracy Tradeoff. Neuron. 10.1016/j.neuron.2012.08.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hull CJ (1936) A study of laterality test items. J Exp Educ 4:287–290 [Google Scholar]
- Jackson Barnette J, McLean JE (2005) Type I error of four pairwise mean comparison procedures conducted as protected and unprotected tests. J Mod Appl Stat Methods. 10.22237/jmasm/1130803740 [DOI] [Google Scholar]
- Jayasinghe SAL, Sarlegna FR, Scheidt RA, Sainburg RL (2020) The neural foundations of handedness: Insights from a rare case of deafferentation. J Neurophysiol. 10.1152/jn.00150.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson NL (1949) Systems of frequency curves generated by methods of translation. Biometrika. 10.1093/biomet/36.1-2.149 [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Hadjiosif AM, Xu J, Wong AL, Haith AM (2019) Motor learning. Compr Physiol. 10.1002/cphy.c170043 [DOI] [PubMed] [Google Scholar]
- Liepmann H (1908) Die linke Hemisphäre und das Handeln. In: Drei Aufsätze aus dem Apraxiegebiet. Karger Publishers, pp 17–50 [Google Scholar]
- Magill RA, Hall KG (1990) A review of the contextual interference effect in motor skill acquisition. Hum Mov Sci. 10.1016/0167-9457(90)90005-X [DOI] [Google Scholar]
- Mauchly JW (1940) Significance Test for Sphericity of a Normal n-Variate Distribution. Ann Math Stat. 10.1214/aoms/1177731915 [DOI] [Google Scholar]
- Oldfield RC (1971) The assessment and analysis of handedness: The Edinburgh inventory. Neuropsychologia. 10.1016/0028-3932(71)90067-4 [DOI] [PubMed] [Google Scholar]
- Pauwels L, Swinnen SP, Beets IAM (2014) Contextual interference in complex bimanual skill learning leads to better skill persistence. PLoS ONE. 10.1371/journal.pone.0100906 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira EAH, Raja K, Gangavalli R (2011) Effect of training on interlimb transfer of dexterity skills in healthy adults. Am J Phys Med Rehabil. 10.1097/PHM.0b013e3181fc7f6f [DOI] [PubMed] [Google Scholar]
- Plamondon R, Alimi AM (1997) Speed/accuracy trade-offs in target-directed movements. Behav Brain Sci 20:279–303 [DOI] [PubMed] [Google Scholar]
- Przybyla A, Coelho CJ, Akpinar S, Kirazci S, Sainburg RL (2013) Sensorimotor performance asymmetries predict hand selection. Neuroscience 228:349–360 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy EA, Roy EA, Elliott D (1989) Manual Asymmetries in Aimed Movements. Q J Exp Psychol Sect A. 10.1080/14640748908402379 [DOI] [Google Scholar]
- Sachlikidis A, Salter C (2007) A biomechanical comparison of dominant and non-dominant arm throws for speed and accuracy. Sport Biomech 6:334–344 [DOI] [PubMed] [Google Scholar]
- Sainburg R (2002) Evidence for a dynamic-dominance hypothesis of handedness. Exp Brain Res. 10.1007/s00221-001-0913-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Kalakanis D (2000) Differences in control of limb dynamics during dominant and nondominant arm reaching. J Neurophysiol. 10.1152/jn.2000.83.5.2661 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Schaefer SY (2004) Interlimb differences in control of movement extent. J Neurophysiol. 10.1152/jn.00181.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Wang J (2002) Interlimb transfer of visuomotor rotations: Independence of direction and final position information. Exp Brain Res. 10.1007/s00221-002-1140-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schabowsky CN, Hidler JM, Lum PS (2007) Greater reliance on impedance control in the nondominant arm compared with the dominant arm when adapting to a novel dynamic environment. Exp Brain Res. 10.1007/s00221-007-1017-x [DOI] [PubMed] [Google Scholar]
- Schaefer SY, Haaland KY, Sainburg RL (2007) Ipsilesional motor deficits following stroke reflect hemispheric specializations for movement control. Brain. 10.1093/brain/awm145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaefer SY, Haaland KY, Sainburg RL (2009) Hemispheric specialization and functional impact of ipsilesional deficits in movement coordination and accuracy. Neuropsychologia. 10.1016/j.neuropsychologia.2009.06.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaffer JE, Sainburg RL (2017) Bimanual reflexes during shared bimanual tasks are asymmetric. In: Society for Neuroscience Annual Meeting [Google Scholar]
- Scheidt RA, Ghez C (2007) Separate adaptive mechanisms for controlling trajectory and final position in reaching. J Neurophysiol. 10.1152/jn.00121.2007 [DOI] [PubMed] [Google Scholar]
- Schmidt RA, Zelaznik H, Hawkins B, Frank JS, Quinn JT Jr (1979) Motor-output variability: a theory for the accuracy of rapid motor acts. Psychol Rev. 10.1037/0033-295X.86.5.415 [DOI] [PubMed] [Google Scholar]
- Shapiro SS, Wilk MB (1965) An analysis of variance test for normality (complete samples). Biometrika. 10.2307/2333709 [DOI] [Google Scholar]
- Shea JB, Morgan RL (1979) Contextual interference effects on the acquisition, retention, and transfer of a motor skill. J Exp Psychol Hum Learn Mem. 10.1037/0278-7393.5.2.179 [DOI] [Google Scholar]
- Shmuelof L, Krakauer JW, Mazzoni P (2012) How is a motor skill learned? Change and invariance at the levels of task success and trajectory control. J Neurophysiol 108:578–594. 10.1152/jn.00856.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takagi A, Maxwell S, Melendez-Calderon A, Burdet E (2020) The dominant limb preferentially stabilizes posture in a bimanual task with physical coupling. J Neurophysiol. 10.1152/jn.00047.2020 [DOI] [PubMed] [Google Scholar]
- Van Der Vliet R, Frens MA, De Vreede L, Jonker ZD, Ribbers GM, Selles RW, Van Der Geest JN, Donchin O (2018) Individual differences in motor noise and adaptation rate are optimally related. eNeuro. 10.1523/ENEUR0.0170-18.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volkmann J, Schnitzler A, Witte OW, Freund HJ (1998) Handedness and asymmetry of hand representation in human motor cortex. J Neurophysiol. 10.1152/jn.1998.79.4.2149 [DOI] [PubMed] [Google Scholar]
- Wang J, Sainburg RL (2004) Limitations in interlimb transfer of visuomotor rotations. Exp Brain Res. 10.1007/s00221-003-1691-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Sainburg RL (2006) The symmetry of interlimb transfer depends on workspace locations. Exp Brain Res. 10.1007/s00221-005-0230-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Sainburg RL (2007) The dominant and nondominant arms are specialized for stabilizing different features of task performance. Exp Brain Res. 10.1007/s00221-007-0936-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woytowicz EJ, Westlake KP, Whitall J, Sainburg RL (2018) Handedness results from complementary hemispheric dominance, not global hemispheric dominance: evidence from mechanically coupled bilateral movements. J Neurophysiol. 10.1152/jn.00878.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu HG, Miyamoto YR, Castro LNG, Ölveczky BP, Smith MA (2014) Temporal structure of motor variability is dynamically regulated and predicts motor learning ability. Nat Neurosci. 10.1038/nn.3616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yadav V, Sainburg RL (2011) Motor lateralization is characterized by a serial hybrid control scheme. Neuroscience. 10.1016/j.neuroscience.2011.08.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yadav V, Sainburg RL (2014a) Handedness can be explained by a serial hybrid control scheme. Neuroscience. 10.1016/j.neuroscience.2014.08.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yadav V, Sainburg RL (2014b) Limb dominance results from asymmetries in predictive and impedance control mechanisms. PLoS ONE. 10.1371/journal.pone.0093892 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarrow K, Brown P, Krakauer JW (2009) Inside the brain of an elite athlete: The neural processes that support high achievement in sports. Nat. Rev, Neurosci [DOI] [PubMed] [Google Scholar]
- Zabihhosseinian M, Gilley R, Andrew D, Murphy B, Yielder P (2020) Differential changes in early somatosensory evoked potentials between the dominant and non-dominant hand, following a novel motor tracing task. Brain Sci 10:290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziemann U, Hallett M (2001) Hemispheric asymmetry of ipsilateral motor cortex activation during unimanual motor tasks: Further evidence for motor dominance. Clin Neurophysiol. 10.1016/S1388-2457(00)00502-2 [DOI] [PubMed] [Google Scholar]


