Abstract
Elastography provides significant information on staging of fibrosis in patients with liver disease and may be of some value in assessing steatosis. However, there remain questions as to the role of steatosis and fibrosis as cofactors influencing the viscoelastic measurements of liver tissues, particularly shear wave speed (SWS) and shear wave attenuation (SWA). In this study, by employing the theory of composite elastic media as well as two independent experimental measurements on oil-in-gelatin phantoms and also finite element simulations, it is consistently shown that fat and fibrosis jointly influence the SWS and SWA measurements. At a constant level of fat, fibrosis stages can influence the SWA by factors of 2–4. Moreover, the rate of increase in SWA with increasing fat is strongly influenced by the stages of fibrosis; softer background cases (low fibrosis stages) have higher rate of SWA increase with fat than those with stiffer moduli (higher fibrosis stages). Meanwhile, SWS results are influenced by the presence of fat, however the degree of variability is more subtle. The results indicate the importance of jointly considering fat and fibrosis as contributors to SWS and SWA measurements in complex liver tissues and in the design and interpretation of clinical trials.
Keywords: liver elastography, steatosis, fibrosis, shear wave speed, shear wave attenuation, composite medium theory, finite element simulation
1. INTRODUCTION
Nonalcoholic fatty liver disease (NAFLD) spans a range of liver problems from simple steatosis, to early stages of fibrosis, to combination of steatosis and fibrosis, to fibrosis at advanced stages, and cirrhosis. Its prevalence is approximately 30% of the general populations in the United States and European countries which makes it one of the growing health concerns in the world (Ye et al., 2020). NAFLD develops initially (or is triggered) by an accumulation of lipid in the liver hepatocyte, greater than approximately 5%. Early diagnosis of NAFLD at the simple steatosis and early fibrosis stages could allow for treatment to reverse the disease process before it results in irreversible pathological damage to the liver (Ozturk et al., 2018). The gold standard for diagnosing these conditions is the liver biopsy, which is invasive and uncomfortable for patients and also relies on data from a small sample of the liver tissue which might not be representative of the entire liver (Angulo, 2002; Chalasani et al., 2018; Haga et al., 2015).
Ultrasound (US) elastography techniques are non-invasive and affordable alternatives to biopsy and have drawn considerable attention for the prognosis and monitoring of histological changes to the liver during treatment (Parker et al., 2010; Palmeri et al., 2011; Barry et al., 2012; Friedrich-Rust et al., 2012; Nightingale et al., 2015; Nenadic et al., 2016; Langdon et al., 2017; Barr, 2018; Parker et al., 2018a; Ormachea et al., 2019; Sharma et al., 2019; Gesnik et al., 2020). These studies aimed to characterize tissue properties and distinguish normal tissue from diseased tissue by correlating variation in measured biomechanical parameters with pathological changes.
Ideally, some ultrasound tissue characterization parameters could be derived which would produce a simple, monotonic change with specific pathology and which would be largely independent of other cofactors or conditions. For example, ideally the shear wave speed (SWS) of liver tissue would increase monotonically with increasing fibrosis in a simple, sensitive, and accurate fashion, not influenced by other factors. Unfortunately, the role of cofactors can be major, so various groups have attempted to mitigate or at least account for their roles (Ferraioli et al., 2018). For example, a clinical study of patients with varying degrees of steatosis and fibrosis was reported by Petta et al. (2017). In that study, the correlation of the liver stiffness measurement (LSM), and the controlled attenuation parameter (CAP), (a proprietary ultrasound attenuation measurement), was investigated where steatosis and fibrosis coexist. It was shown that for livers where CAP is high, the degree of fibrosis is overestimated by LSM, and this results in an increase in false positives in the diagnosis of liver fibrosis.
As more and more measurements related to US and elastography parameters become available on commercial scanners, the role of cofactors must be carefully considered (Mikolasevic et al., 2016; Parker et al., 2018a; Sharma et al., 2019). The roles of fibrosis and steato-fibrotic conditions on shear wave attenuation (SWA) measurements have not been extensively examined and previous studies have mainly focused on the acoustic attenuation coefficient which is associated with the decay in the longitudinal compressional waves (Lin et al., 1988). There was early disagreement in the results reported in the literature regarding the role of fibrosis on acoustic attenuation coefficients (Suzuki et al., 1992; Afschrift et al., 1987). Today, to the best of our knowledge, few studies have examined the role of fibrosis and steato-fibrosis on the shear wave attenuation where the results separate out the effect of the cofactors. Deffieux et al. (2015), in a study to investigate the effect of the viscosity on steatosis and fibrosis staging, reported no correlation between steatosis and viscosity.
Thus, two important clinical questions emerge in parallel: when we measure SWS in an attempt to gauge fibrosis, does the presence of fat (steatosis) confound or vary the results? Similarly, when we measure SWA in an attempt to gauge the accumulation of fat, do varying degrees of fibrosis confound or alter the result?
In a naïve view, SWS would simply increase with fibrosis, while SWA would simply increase with the amount of fat accumulating in a steatotic liver. However, in reality the two conditions are confounding cofactors which need to be understood jointly. We address this issue by assessing the cofactors’ roles within four independent methodologies:
From the theory of composite elastic media.
From experimental stress relaxation measurements on oil-in-gelatin phantoms.
From SWS and SWA measurements in oil-in-gelatin phantoms taken from a commercial scanner implementing push pulses.
From finite element (FE) simulations of shear waves in fatty livers.
In comparing these different methodologies, we utilize the theory of composite media as a common reference against which others are compared. Ultimately, these differing assessments lead to similar conclusions about the importance of fat and fibrosis as cofactors in liver elastography and are detailed in the following sections. The importance of these cofactors for stratifying clinical trials is a practical consequence of these findings.
2. THEORY
In the development of fibrosis, the shear modulus of liver typically increases. For a viscoelastic medium, the shear modulus is a complex parameter which is frequency-dependent and relates to the stiffness of the medium and the speed of wave propagation. When a shear wave propagates through a viscoelastic material, its two important propagation characteristics, SWS and SWA, depend on the complex shear modulus or the complex wave number of the underlying material as follows:
| (1) |
where , , and are the phase velocity, the real part of the wavenumber, and the attenuation, respectively, all depending on the frequency and the density of the material (Carstensen et al., 2008; Vappou et al., 2009; Carstensen and Parker, 2014; Kazemirad et al., 2016). Solving for and similar to the derivation of (Parker et al., 2018b; Zvietcovich et al., 2019), we have:
| (2) |
| (3) |
| (4) |
2.1. Composite theory
Steatotic liver tissue is characterized by microvesicular and macrovesicular accumulation of lipid vacuoles in the hepatocytes (Fromenty et al., 1997). Our approach is to model the simple steatotic liver as a composite medium with fat droplets considered as spherical inclusions distributed in a background material characteristic of the normal liver properties. In doing so, we can employ the theory proposed by Christensen (1969) and expanded by Lakes (1999) to model the fatty liver as a composite medium. This composite model was also incorporated more recently in a study of the rheological models that are capable of capturing the dominant viscoelastic behaviors associated with fat and inflammation in the liver (Parker et al., 2018a), along with the microchannel flow model (Parker, 2014). Those results did not consider the confounding effects of liver stiffening due to fibrosis, so further investigations are warranted.
Considering a normal liver with shear modulus , and fat inclusions with shear modulus distributed in the normal liver with a small volume fraction of , the simple steatotic liver will have a shear modulus of :
| (5) |
with the assumption of a nearly incompressible medium consistent with normal tissues having a Poisson’s ratio of and Christensen’s model (Christensen, 1969) of the inclusions as a general distribution of small spheres. This equation is valid for small volume fractions (and less than 0.5) and models a progressive departure from the properties of as increases from zero. To model the normal liver , we can employ the power law behavior using the Kelvin-Voigt fractional derivative (KVFD) model as follows:
| (6) |
where is the power law parameter and is a constant. Moreover, we can model the fat inclusions as a viscous oil fluid with the viscosity of as a simple dashpot element with the shear modulus of:
| (7) |
With the help of eqns (1) - (7) and our assumptions about fat being primarily a lossy term, we can now make some general statements about the interplay of factors. In practice, is in the range of 1 kPa for normal livers and dominates the (real modulus) term, whereas is from fat inclusions that we model as a purely viscous material which contributes to the imaginary part of the modulus. Let us assume that increasing amounts of fibrosis create a progressively higher storage modulus in eqn (2). In that case, in eqn (3) will increase monotonically and directly as both and increase. However, will decrease because of the subtraction term in eqn (4). Now if fat is added in increasing amounts, which makes the volume fraction in equation (5) increase, the imaginary component will increase according to eqn (7). In that case, in the “simple” range is small and dominates initially; then as fat is added, is increased through the increasing result of the subtraction term in eqn (4), and the material is actually softened by the addition of fat, resulting in a lower . As will be shown in the next sections, the accumulation of small amounts of fat in a fibrotic liver produces a slight decrease in SWS, this is easily disguised by other sources of variability. However increasing stiffness (fibrosis) creates a very strong drop in attenuation given a fixed amount of fat.
3. METHODS
To experimentally assess the role of fat and fibrosis as cofactors on the SWS and SWA measurements, two independent measures are employed to assess eight different viscoelastic phantoms. Separately, FE simulations are implemented to provide an independent test of the composite model. In this section, the details of experiments and the simulations are presented.
3.1. Phantom preparation
Eight different viscoelastic tissue-mimicking phantoms were made using a combination of gelatin powder, sodium chloride (NaCl), and agar in 900 mL of degassed water forming the base mixture, and castor oil used for the inclusion. The portion of each ingredient is listed in Table 1. Four phantoms have 18% castor oil and four others have 2% castor oil, based on four different gelatin percentages of 3%, 4%, 5% and 6%.
Table 1.
Portion of ingredients used for making viscoelastic phantoms.
| Ingredient | Amount | Manufacturer |
|---|---|---|
| Gelatin | 3% | 300 Bloom Pork Gelatin, Gelatin Innovations Inc., Schiller Park, IL, USA |
| 4% | ||
| 5% | ||
| 6% | ||
| Castor oil | 18% | Castor oil, Walter Price St. Cayce, SC, USA |
| 2% | ||
| NaCl | 0.9% | Sodium Chloride, BDH, West Chester, PA, USA |
| Agar | 0.15% | Difco Agar technical, Becton, Dickinson & Comp. Sparks, MD, USA |
| Surfactant | 40cc/l oil | Ultra-Ivory, Procter and Gamble Company, Cincinnati, OH, USA |
In order to make the oil-water solution stay more stable, first the base mixture and the castor oil were separately heated up to a temperature of approximately 65°C and then oil was added to the gelatin mixture slowly while stirring constantly using a magnetic stirrer. Surfactant was also added slowly to the oil-in-gelatin mixture to help keep the small oil droplets (already formed) suspended in the mixture without being aggregated in the whole process, making a uniform and stable oil-in-gelatin mixture. The solution was then cooled down to almost 30°C before it was poured into a cylindrical mold. The latter process was done slowly to avoid creating small bubbles in the mixture. The cylinder was sealed and placed on a low-speed rotator (model 33B, Lortone, Inc, Mukilteo, WA, USA) for almost 5 hours to rotate uniformly, letting the mixture solidify without oil drops aggregating. The phantoms were left at a temperature of 4°C overnight to solidify. The following day, the phantoms were allowed to reach room temperature before any ultrasound scanning or mechanical testing was done.
Figures 1(a) and (b) show a sample cut of a 4% pure gelatin phantom and a viscoelastic phantom with 4% gelatin and 18% castor oil, respectively, for comparison. In Figure 1(c), a magnified view of the viscoelastic phantom in 1(b) is presented where we observe a uniform homogeneous distribution of small drops of castor oil within the gelatin phantom. Most drops appear to have a diameter of less than 0.5 mm according to the magnified view.
Figure 1.

Comparative structure of the phantoms: (a) pure elastic phantom with 4% gelatin, (b) 18% castor-oil-in-gelatin phantom with 4% gelatin, (c) magnified view of the phantom structure shown in (b) with the scale of millimeters for reference. The scale bars are added to show the size of the cylindrical phantom cross-section and also the magnified region.
3.2. Ultrasound scanning
To obtain the mechanical properties of the viscoelastic phantoms and, therefore, the speed and attenuation of the shear waves propagating through the phantoms, a Samsung ultrasound scanner (model RS85, Samsung Medison, Seoul, South Korea) with a curved array transducer (model CAI-7A, Samsung Medison, Seoul, South Korea) was employed. It produced deformations that propagated as a shear wave in the phantom by applying radiation force excitation and then tracking the corresponding particle displacement. The center frequency of the transmit push beam is 2.5 MHz with an f-number of 2 or larger depending on depth, and a sampling frequency rate of 20 MHz. The SWS and SWA are calculated based on the theory presented in Parker et al. (2018c) where an analytical solution is derived to model a push pulse and propagating shear waves from a linear array transducer. This closed form solution is employed to estimate SWS and SWA from the displacement measurements. The shear wave produced by the push pulse has a peak frequency in the range of 100 – 150 Hz in phantoms (Parker et al., 2018b; Ormachea and Parker, 2020).
3.3. Stress relaxation test
Another widely used (Fung, 1981; Lakes, 1999) test on oil-in-gelatin phantoms is the stress relaxation test that we employed to evaluate the properties of the viscoelastic phantoms. This compression test was done on 3–4 small cylindrical cuts with an average diameter of 20 mm and average height of 24 mm out of each cylindrical phantom, as shown in Figure 2. This test was done on the same day as the ultrasound scanning to ensure that the properties of the phantoms did not change due to dehydration or aging, and so that the comparison of the two modalities was more consistent. Using a Q-Test/5 machine (MTS, Eden Prairie, MN, USA) with a 5N load cell, a 5% strain was applied on each sample with a compression rate of 0.5 mm/s, and the relaxation test was done for approximately 500 s. Then, the stress relaxation for each sample was fitted to the KVFD model (for , where hold time) as in eqn (8), similar to the work by Zhang et al. (2008). This fit produces three estimated coefficients , , and which are used in eqn (9). The complex Young modulus as a function of frequency is obtained from eqn (9) using the three fitted coefficients from the last step. Assuming that soft tissues and phantoms with high water content are nearly incompressible, the complex shear modulus is then calculated according to . Thus, in the time domain, the stress relaxation is obtained from:
| (8) |
and in the frequency domain the complex Young’s modulus obeys the following equation:
| (9) |
In these equations, is the power law parameter, is related to the viscous behavior of the material, and is an elastic modulus constant which is negligible for soft tissues and viscoelastic phantoms (Zhang et al., 2007).
Figure 2.

(a) A sample of a large cylindrical phantom (4% gelatin and 18% castor oil) with scale bar shown at the bottom. (b) Small cylindrical cuts for the stress relaxation test.
3.4. Finite element simulation
Shear wave propagations through homogeneous and inhomogeneous media were numerically simulated using Abaqus/CAE 2019 (Dassault Systems, Vélizy-Villacoublay Cedex, France). The simulation domain is a 3D block with the -direction as the propagation direction and the and as the lateral directions. For the shear wave excitation in the block, the x-y plane on the left side of the block shown in Figure 3(a) is subjected to a three-cycle 150 Hz toneburst transient displacement along the -direction. The displacement excitation function applied is symmetric with respect to both x and y axes. A 3D schematic of the block, its orientation, and the excitation plane are depicted in Figures 3(a) and (b).
Figure 3.
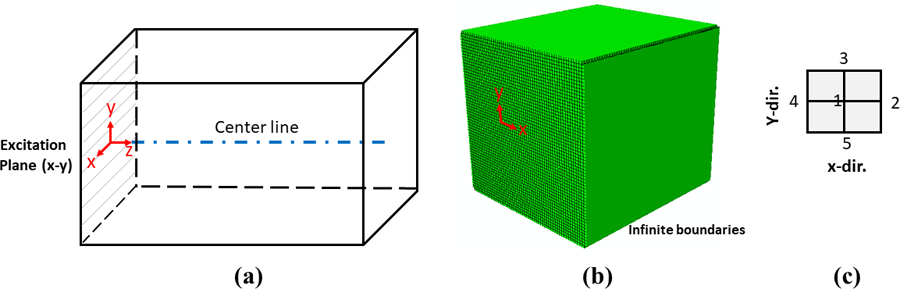
(a) Schematic of 3D block orientation, excitation plane, and the propagation centerline. The block dimensions are approximately 26.5 mm × 26.5 mm × 30.5 mm along the x, y, and z axes, respectively. (b) Computational meshes of the domain with the infinite boundaries in the FE simulation. (c) Definition of the four neighboring points around each center point on the z axis, less than one-fifth of a wavelength apart in each case.
The domain is meshed using 214,816 hybrid, quadrilateral linear elements (C3D8RH). The mesh size is approximately 0.45 mm which is refined to resolve the smallest wavelength in each simulation. The initial time increment is set for each simulation separately to resolve the smallest element size based on the maximum theoretical speed, so that the time step is less than the value suggested by the ratio of [min (mesh size)]/[max(propagation speed)]. The initial time step changes between 1.5E-5 to 8E-5 seconds depending on the simulations. The automatic time incrementation option in Abaqus/Standard is employed to adjust the subsequent time step increments assuring the convergence of the solution. The simulation models approximately 50 ms of wave propagation in the computational domain based on the dynamic-implicit method.
In order to avoid the reflection of the incident wave from the boundaries back into the domain and to avoid the unwanted interference, infinite boundaries are defined around the domain to minimize the reflection.
For the inhomogeneous simulation, the inclusion material is distributed randomly throughout the volume, implemented as single mesh elements within the background material of the 3D domain. The background material is modeled as an elastic material with a density of 998 kg/m3 and a Poisson’s ratio of 0.495. The viscous fat inclusions are implemented within the framework of the FE solid modeling options as predominantly viscous material by selecting a Zener model with small (10 Pa) and relatively high (10 kPa), and a viscosity of 1 Pa-s, based on the viscosity of castor oil at room temperature (Dutta et al., 1956).
The displacement at a number of points along the centerline of the propagation direction is calculated as well as four neighboring points around each -location. The displacement at each -location is then taken as the average of the displacement at that specific point and the surrounding four neighboring points; this minimizes any local fluctuations within the inhomogeneous media. The arrangement of these neighboring points is illustrated in Figure 3(c).
Finite element simulations are performed to extend the study to systematic variations of fat inclusion levels and also fibrosis stages where the effect of cofactors could be investigated in a more extensive (broader) range of conditions. In order to simulate graduated increase in steatosis condition in regular increments around our 18% phantom, four different inclusion percentages of 6%, 12%, 18%, and 24% were implemented in Abaqus. Moreover, to simulate the effect of fibrosis and the base material stiffness level on the SWS and SWA parameters, five different background materials were set up in Abaqus. The stiffness levels used for modeling fibrosis stages in the simulations are based on the METAVIR scoring system which is selected based on peak of the probable values of SWS (stiffnesses) for the fibrotic livers presented in the statement by the Society of Radiologists in Ultrasound (Barr et al., 2015). These five groups and their selected material SWS, which also represents the stiffness level, are reported in Table. 2.
Table 2.
Background material SWS for simulating different fibrosis stages.
| Fibrosis score (METAVIR) | SWS (m/s) |
|---|---|
| F0 | 0.9 |
| F1 | 1.1 |
| F2 | 1.4 |
| F3 | 1.75 |
| F4 | 2.2 |
Considering the effect of fat and fibrosis simultaneously, 20 inhomogeneous simulations in total were performed based on different fat inclusions and different background fibrosis (stiffness) stages. For each inhomogeneous simulation with inclusions, to compensate for the effect of geometric spreading on the amplitude decay, a corresponding homogeneous elastic simulation is also performed where the homogenous medium is matched to the same group velocity as the inhomogeneous case. This makes a total of 20 elastic simulations matching the 20 inhomogeneous simulations. Therefore, we can quantify the SWA as an exponential decay in peak amplitude, corrected for geometric spreading, for each combination of background stiffness and percentage of fat.
4. RESULTS
4.1. Phantom experiments
The stress relaxation curves for viscoelastic phantoms having 18% castor oil inclusions but at different background stiffnesses (gelatin percentages of 3%, 4%, 5%, and 6%) are shown in Figure 4. For each phantom, the test results on 3–4 samples are presented to show reproducibility. Under constant strain rate applied to all cases, the general trend in the stress relaxation curves is an increase in the stress level with increasing gelatin percentage when the castor oil inclusion amount is fixed. This trend is also observed in the value of the parameter in the KVFD model (eqn (9)): increases significantly with increasing gelatin percentage. The KVFD power law parameter oscillates in a small range around 0.045 for all cases, and is also negligible as expected, for viscoelastic material behavior. The details are reported in Table 3 as well as the means and standard deviations obtained from multiple samples tested.
Figure 4.
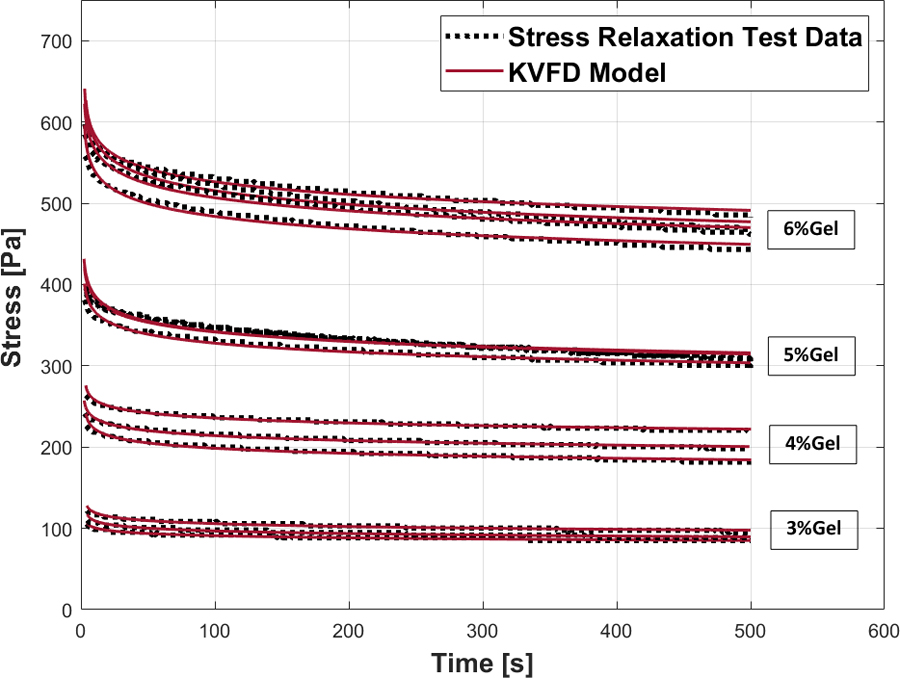
Stress relaxation test and the corresponding KVFD fitting curve for phantoms with 18% castor oil and different gelatin percentages: 3%, 4%, 5%, and 6%.
Table 3.
The averaged KVFD parameters for each viscoelastic phantom with the values of the standard deviations reported for the measurements of samples from the same batch. SD refers to the standard deviation.
| Gelatin % | SD | SD | SD | |||
|---|---|---|---|---|---|---|
| 3% gelatin | 2.19E-05 | 1.15E-05 | 0.046 | 0.0036 | 2487 | 134.9 |
| 4% gelatin | 2.11E-04 | 1.49E-04 | 0.045 | 0.003 | 5038 | 240.4 |
| 5% gelatin | 1.30E-04 | 1.07E-04 | 0.049 | 0.0017 | 8765 | 202.8 |
| 6% gelatin | 4.68E-05 | 7.2E-05 | 0.045 | 0.00167 | 12874 | 330.4 |
First, we utilized the two independent sets of results for SWS and SWA from both mechanical stress relaxation tests and ultrasound scans on the viscoelastic phantoms with 18% castor oil and compared the two experimental results with the composite theory predictions. In employing the composite model for the theoretical estimation of the shear modulus of each phantom with an 18% castor oil inclusion , the shear modulus of the background material is needed according to eqn (6). To approximate this for each phantom with 18% inclusions, a 2% inclusion phantom at the same background stiffness as that of the 18% phantom is used and its shear modulus is obtained to be used as . The reason for using the 2% results instead of pure gelatin (0% oil) is due to the observation that the addition of minimal castor oil drops with the surfactant and rotational processing may change the conformation of the gelatin background material itself. Therefore, the 2% castor oil is a sufficiently small amount of oil to represent the asymptotic approach of the composite properties to near zero inclusions.
In Figures 5 (a) and (b), the SWS and SWA are shown for different background stiffnesses (gelatin percentages) at 18% oil inclusion. The SWS and SWA are both calculated from two independent tests of: (i) ultrasound scan results used with the theory in Parker et al. (2018c), and (ii) the mechanical test results fit to the KVFD model at 150 Hz frequency. We find that results from both tests are consistent with the composite theory predictions for SWS as well as SWA when oil volume fraction is 0.18. The SWS increases with the increase in background stiffness and for the SWA, the general trend is decreasing SWA with increasing background stiffness, an observation supported by theory and phantom experimental results. The ultrasound scan results, KVFD estimates, and theory predictions are shown as box plots, blue bars and dashed line, respectively in Figures 5(a) and (b). The SWA measurements taken from the Samsung scanner, shown in the box plots of Figure 5(b), have a variability over 15% in these phantoms, plausibly due to some non-uniformity in the distribution of oil, and to errors in the displacement estimates. The variability in humans could be larger due to the effects of the overlying tissues, motion, and noise.
Figure 5.
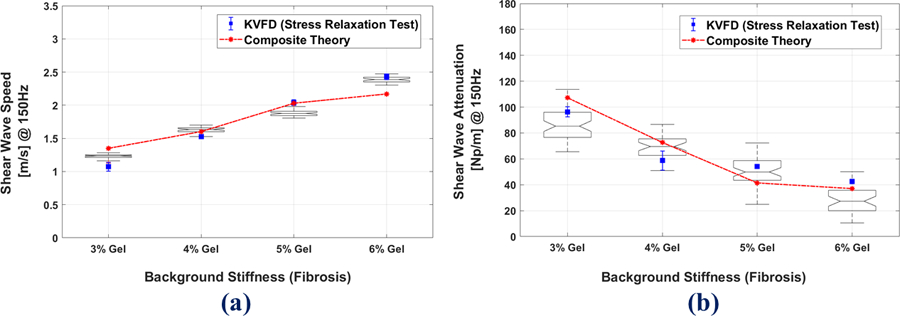
Comparison of (a) SWS (b) SWA, at 18 % oil and different fibrosis stages for the composite theory (red dashed lines) vs. the stress relaxation test (blue bars), and Samsung scan results shown as box plots. In the boxplots, the notched line represents the mean of the data.
A sample of B-scan and elastography images for the 4% and 6% gelatin phantoms both with the 18% castor oil inclusion are shown in Figures 6(a) and (b) with the average shear wave speed and attenuation coefficients.
Figure 6.
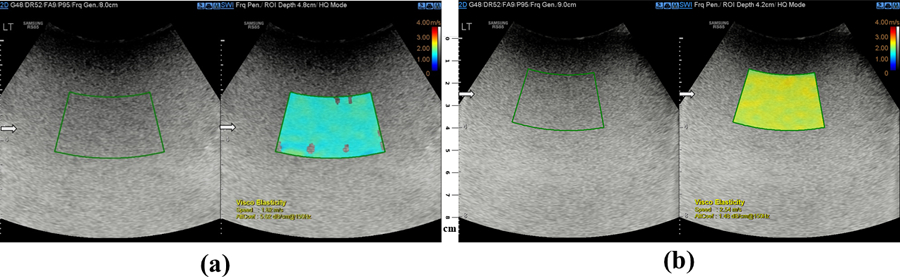
Sample of a B-scan (left side) and elastography images (right side) of a (a) 4% gelatin phantom and (b) 6% gelatin phantom, both having 18% of castor oil inclusions. The arrows indicate the focal region in the scan with the scale bar showing the depth of the scanned region.
4.2. Finite element simulation
Shear wave propagation results were evaluated from the FE simulations, and the SWS was obtained using the time-of-flight method. SWA was estimated from an exponential decay curve-fit after comparison against the geometric spreading in a corresponding elastic (non-attenuating) homogeneous medium of the same group velocity. The presence of inhomogeneous inclusions changes the wave front and also the displacement at nodal points.
Figures 7(a) and (b) show a snapshot in time of the propagating waveform of the homogeneous pure elastic and inhomogeneous 12% inclusions, respectively, both at F4 fibrosis (stiffness) stage. The presence of small inclusions in the background alters the wave to create small spatial fluctuations. Furthermore, looking at the displacement field as a function of time at fixed locations along the centerline in Figures 7(c) and (d), we see that the presence of the fat inclusions results in a decrease in the level of displacement in comparison to the homogeneous case. Moreover, the homogeneous pure elastic case itself presents amplitude decay along the propagation direction, which is associated with the geometric spreading of the wave.
Figure 7.
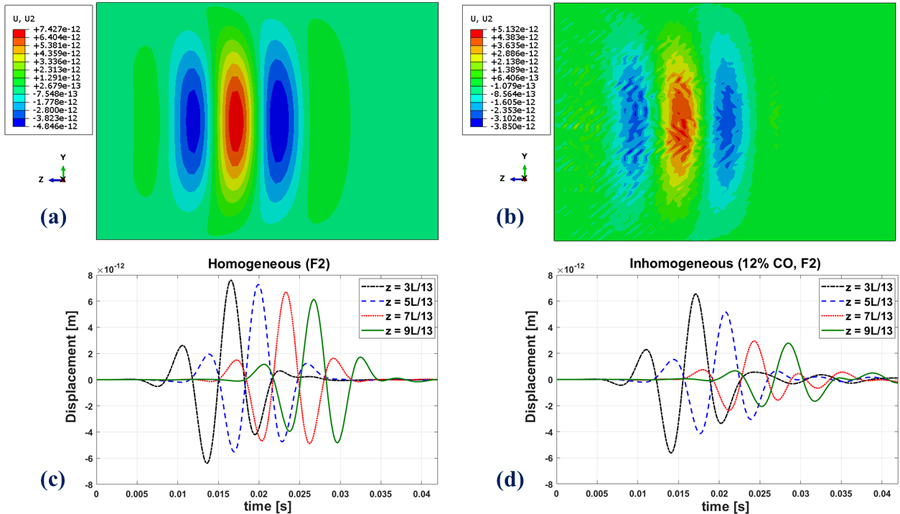
Top row: A snapshot in time of the propagating waveform in the FE simulation for (a) the homogeneous medium (b): the inhomogeneous medium. Displacement amplitudes will scale with source excitation in this linear model. Bottom row: Time evolution of shear waves at four different locations along a single line in the z-direction in the FE simulations in the (c) homogeneous and (d) inhomogeneous medium. All cases are at the fibrosis (stiffness) level of F4. The inhomogeneous medium has 12% inclusions.
Figures 8(a) and (b) illustrate the comparison of composite theory with the FE simulations for SWS, respectively. These figures depict the elevated SWS with the advance in fibrosis (background stiffness) stage and also the reduced SWS with the development of higher fat content. SWA comparison of composite theory with FE simulations are also presented in Figures 8(c) and (d), respectively. The two plots indicate the decreased level of SWA at higher fibrosis stages and also the increased SWA as a function of higher steatosis score. The plots of Figure 8 also indicate agreement between the theory and simulation for SWS and also the similar trend for SWA values.
Figure 8.
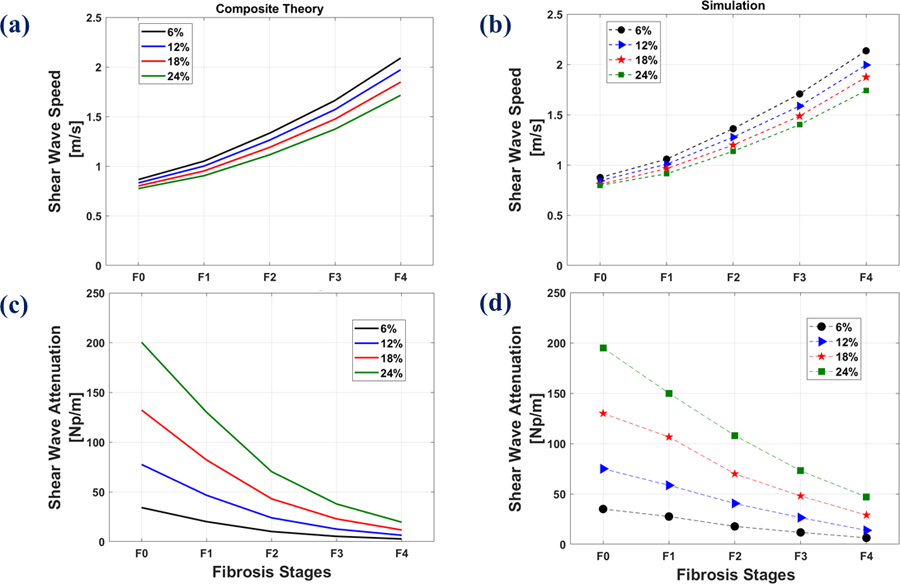
Composite theory vs. FE simulations at different fat percentages and different fibrosis stages at the frequency of 150 Hz. Top row: SWS of (a): composite theory, (b): FE simulation. Bottom row: SWA of (c): composite theory, (d): FE simulations.
5. DISCUSSION
5.1. General trends
Good agreement was observed between the trends of results for SWS and SWA from three different estimates derived from ultrasound shear wave scanning, stress relaxation tests, and the composite theory, all supporting the importance of considering the cofactors of fat and fibrosis. These trends are also observed in the results from FE simulations for the two parameters of SWS and SWA; this further underscores the significance of the two factors. Fat accumulation in low volume percentage is a weak cofactor influencing (decreasing) SWS, however this effect will be frequency-dependent and so could be confusing when comparing different studies’ results using different shear wave frequencies. However, at higher fat volume percentages, fat starts to decrease the SWS more significantly. On the other hand, baseline stiffness changes create a pronounced influence on SWA. This suggests the significance of considering these potential cofactors when interpreting the SWS and SWA measurements and correlating them with the histological conditions of tissues in diseases which have not yet been studied to the best of our knowledge.
In comparing the SWA of the composite theory and the FE simulations, although the trend is the same across different stiffness levels and different inclusion percentages, the SWA values from simulations are higher than that of theory. One of the important reasons behind that is the fact that the analytical solution in the composite theory is based on stress field theories in which the scattering phenomena are not considered. But in numerical simulations and also experiments, some degree of scattering of shear waves is present. The wave scattering occurs when the wave propagates in an inhomogeneous medium with an impedance mismatch between the medium and the small inhomogeneities (Wu and Aki, 1985). This introduces an additional component of loss to the forward propagating wave and therefore the estimated SWA coefficient would be higher in simulations that incorporate scattering phenomena.
5.2. Physics vs. statistics in clinical trials
In elastography clinical trials, a population may be studied under broad inclusion criteria incorporating different degrees of liver fibrosis and steatosis. Frequently, a linear correlation fit of the metrics against an independent diagnostic assay is attempted. To look at the cofactors’ roles (fibrosis and steatosis) on the SWA and SWS measurement, let us assume one patient is sampled for each of the 20 parameter pairs shown in the solid points of Figures 8(b) and (d) (five values of fibrosis, F0-F4; and four values of fat concentration for each fibrosis score). Because in clinical practice there are unavoidable errors in biopsy measurements of fat content and also shear wave propagation parameters, for more realistic accounting of variability (Parker et al., 2018b) we added a proportional 10% Gaussian noise to both the SWA and fat inclusion percentage measurements in Figure 8(d) and also to both the SWS and background stiffness in Figure 8 (b). For this distribution of parameters, some simple linear correlation plots of SWA vs. percent fat are presented in Figures 9(a) – (d) and the correlation plot of SWS vs. fibrosis stage (stiffness) is shown in Figure 9(e). The corresponding linear fitting parameters and the Spearman’s rank correlation coefficients as well as the p-values are reported in Table 4 for our simulation results. The correlation coefficient can change between −1, the strongest negative correlation, and 1, the strongest positive correlation, and small p-values (<0.001) indicate that the correlation is significantly different from the null hypothesis. For the SWA correlation with fat, the overall population of 20 cases are shown in Figure 9(a), and while a trend to increasing SWA with increasing fat is observed, the correlation is poor, and the variability of data is pronounced. The poor correlation would be even worse if a few more high fibrosis (F4) cases were included relative to the other samples within a study, and this could lead to a conclusion that fat has little effect on viscoelastic measures.
Figure 9.
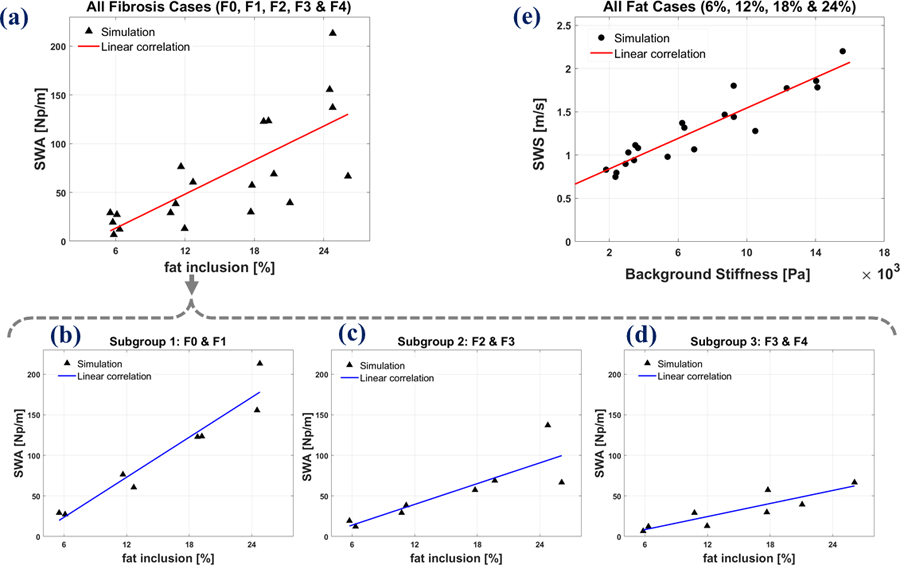
Correlation of SWA with fat inclusion percentage incorporating (a): all fibrosis cases, (b): F0 and F1 cases as subgroup 1, (c): F2 and F3 cases as subgroup (2) and (d): F3 and F4 cases as subgroup 3. (e): Correlation of SWS with fibrosis (background stiffness) at all fat inclusion cases. Data are based on 150 Hz simulation results shown in Figure 8, with a proportional distribution of random error included to represent clinical measurements.
Table 4.
Linear correlation details of the SWA with fat inclusion and the SWS with fibrosis level. The Spearman’s correlation coefficients r and the p-values are also reported.
| Cases | R2 (goodness of fit) | Correlation slope m (as in y=mx+b) | Spearman’s correlation | |
|---|---|---|---|---|
| r | p-value | |||
| All fibrosis cases (F0, F1, F2, F3, F4) | 0.555 | 5.82 (Np/m) / (% fat) | 0.75 | < 0.001 |
| subgroup 1 (F0, F1) | 0.924 | 8.21 (Np/m) / (% fat) | 0.96 | < 0.001 |
| subgroup 2 (F2, F3) | 0.723 | 4.26 (Np/m) / (% fat) | 0.85 | 0.0076 |
| subgroup 2 (F3, F4) | 0.785 | 2.68 (Np/m) / (% fat) | 0.89 | 0.0034 |
| All fat cases (6%, 12%, 18%, 24%) | 0.874 | 8.81 × 10−2 | 0.89 | < 0.001 |
However, when different subgroups of fibrosis stages are analyzed separately, the correlation plots are improved with enhanced R2 (a measure of correlation goodness of fit) and higher correlation coefficient r with small p-values given in Table 4. Moreover, this correlation is affected by the level of fibrosis stages: the lower fibrosis stages have higher correlation slopes of SWA with increasing fat as shown in Table 4. For instance, subgroup 1 as the combination of F0 and F1 groups has the highest correlation slope as well as R2 and correlation coefficients r (p-value < 0.001). This stratification by the degree of fibrosis improves the tighter interpretation of SWA measurements. Looking at the correlation plot of SWS vs. fibrosis stage for the overall population in Figure 9(e), we observe a trend of increasing SWS with increasing fibrosis. This plot has relatively less variation and spread of the SWS data due to the presence of different fat inclusion percentages.
Finally, there are additional factors that could confound the interpretation of SWS and SWA measurements in complex liver tissues, for example inflammation, lesions, and vascular pathologies. These represent other cofactors that need to be modeled as influences on viscoelastic properties for a better overall judgement of measurements. In our modeling, stiffness is increased as a material property of the background. A more fine-grain structural model of fibrosis has been developed by Wang et al. (Wang et al., 2017; Wang and Jiang, 2018, 2019). This approach could be combined with steatosis by the addition of small fat vacuoles but remains for future research.
Another important factor is the shear wave frequency. We have focused on shear waves near or at 150 Hz based on values recorded from push pulses (Parker et al., 2018b; Ormachea and Parker, 2020), however elastography using ultrasound, magnetic resonance (MR), and optical coherence tomography (OCT) can incorporate lower frequencies such as 50 Hz for large organs, or much higher frequencies of 1–2 kHz for small organs or structures. The linear dependence of viscous inclusions on frequency in eqn (7) is a strong driver of the effect of fat, and this remains as a key parameter that requires further verification against the composite theory.
Limitations of this study include the simple nature of the composite material model and the finite element simulation. The simulation applies a tone burst of shear displacement at the boundary, enabling a study of the wave propagation, however this is not an adequate model of the internal displacements caused by radiation force excitations utilized by some scanners. Furthermore, detailed comparisons of viscoelastic measures with quantitative liver histology and composition measures are required in future studies to validate and refine the quantitative predictions from the composite theory, the simulations, and the phantom experiments.
6. CONCLUSION
In this study, we find consistent results from composite theory, from two independent experimental measures, as well as FE simulations, all describing the role of steatosis and fibrosis as cofactors on SWS and SWA measurements. The results indicate that SWA and SWS are influenced by both the amount of fat and also the level of background stiffness. Considering the results from phantom experiments as well as the extension of the study using simulations, it is concluded that when the fat inclusion percentage is kept constant at levels within the range we studied (2% to 24% oil), the measured SWA will vary with the fibrosis stages by factors of 2–4. Furthermore, fibrosis stages have strong effects on the rate of change in SWA with respect to fat, i.e., cases with softer background show higher rate of change in comparison to the cases having stiffer background. On the other hand, the influence of fat on SWS is less dramatic and could easily be obscured in studies with significant measurement errors. The effect of accumulating fat is also a strong function of shear wave frequencies, so our examples must be understood to be representative of shear waves in the band around 150 Hz as produced by some systems’ push pulses. The joint influence of fat and fibrosis can be considered within viscoelastic models, or can be simply minimized in practice by designing clinical trials so as to stratify research subjects’ measurements into subgroups.
Acknowledgments
This work was supported by National Institutes of Health grant R21EB025290. We thank Samsung Medison Company Ltd. for the use of the scanner.
REFERENCES
- Afschrift M, Cuvelier C, Ringoir S and Barbier F 1987. Influence of pathological state on the acoustic attenuation coefficient slope of liver Ultrasound in medicine & biology 13 135–9 [DOI] [PubMed] [Google Scholar]
- Angulo P 2002. Nonalcoholic fatty liver disease New England Journal of Medicine 346 1221–31 [DOI] [PubMed] [Google Scholar]
- Barr RG 2018. Shear wave liver elastography Abdominal Radiology 43 800–7 [DOI] [PubMed] [Google Scholar]
- Barr RG, Ferraioli G, Palmeri ML, Goodman ZD, Garcia-Tsao G, Rubin J, Garra B, Myers RP, Wilson SR and Rubens D 2015. Elastography assessment of liver fibrosis: society of radiologists in ultrasound consensus conference statement Radiology 276 845–61 [DOI] [PubMed] [Google Scholar]
- Barry CT, Mills B, Hah Z, Mooney RA, Ryan CK, Rubens DJ and Parker KJ 2012. Shear wave dispersion measures liver steatosis Ultrasound in medicine & biology 38 175–82 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carstensen EL and Parker KJ 2014. Physical models of tissue in shear fields Ultrasound in medicine & biology 40 655–74 [DOI] [PubMed] [Google Scholar]
- Carstensen EL, Parker KJ and Lerner RM 2008. Elastography in the management of liver disease Ultrasound in medicine & biology 34 1535–46 [DOI] [PubMed] [Google Scholar]
- Chalasani N, Younossi Z, Lavine JE, Charlton M, Cusi K, Rinella M, Harrison SA, Brunt EM and Sanyal AJ 2018. The diagnosis and management of nonalcoholic fatty liver disease: Practice guidance from the American Association for the Study of Liver Diseases Hepatology 67 328–57 [DOI] [PubMed] [Google Scholar]
- Christensen R 1969. Viscoelastic properties of heterogeneous media Journal of the Mechanics and Physics of Solids 17 23–41 [Google Scholar]
- Deffieux T, Gennisson J-L, Bousquet L, Corouge M, Cosconea S, Amroun D, Tripon S, Terris B, Mallet V and Sogni P 2015. Investigating liver stiffness and viscosity for fibrosis, steatosis and activity staging using shear wave elastography Journal of hepatology 62 317–24 [DOI] [PubMed] [Google Scholar]
- Dutta AK, Ray BC and Rout HK 1956. Viscosity of liquids and ultrasonic studies Nature 177 1227–8 [Google Scholar]
- Ferraioli G, Wong VW, Castera L, Berzigotti A, Sporea I, Dietrich CF, Choi BI, Wilson SR, Kudo M and Barr RG 2018. Liver ultrasound elastography: an update to the WFUMB guidelines and recommendations Ultrasound Med Biol 44 2419–40 [DOI] [PubMed] [Google Scholar]
- Friedrich-Rust M, Romen D, Vermehren J, Kriener S, Sadet D, Herrmann E, Zeuzem S and Bojunga J 2012. Acoustic radiation force impulse-imaging and transient elastography for non-invasive assessment of liver fibrosis and steatosis in NAFLD European journal of radiology 81 e325–e31 [DOI] [PubMed] [Google Scholar]
- Fromenty B, Berson A and Pessayre D 1997. Microvesicular steatosis and steatohepatitis: role of mitochondrial dysfunction and lipid peroxidation J Hepatol 26 Suppl 1 13–22 [DOI] [PubMed] [Google Scholar]
- Fung YC 1981. Biomechanics : mechanical properties of living tissues (New York: Springer-Verlag; ) [Google Scholar]
- Gesnik M, Bhatt M, Cardinal M-HR, Destrempes F, Allard L, Nguyen BN, Alquier T, Giroux J-F, Tang A and Cloutier G 2020. In vivo Ultrafast Quantitative Ultrasound and Shear Wave Elastography Imaging on Farm-Raised Duck Livers during Force Feeding Ultrasound in Medicine & Biology [DOI] [PubMed]
- Haga Y, Kanda T, Sasaki R, Nakamura M, Nakamoto S and Yokosuka O 2015. Nonalcoholic fatty liver disease and hepatic cirrhosis: comparison with viral hepatitis-associated steatosis World journal of gastroenterology 21 12989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazemirad S, Bernard S, Hybois S, Tang A and Cloutier G 2016. Ultrasound shear wave viscoelastography: Model-independent quantification of the complex shear modulus IEEE transactions on ultrasonics, ferroelectrics, and frequency control 63 1399–408 [DOI] [PubMed] [Google Scholar]
- Lakes RS 1999. Viscoelastic solids (Boca Raton, FL: CRC Press LLC; ) [Google Scholar]
- Langdon JH, Elegbe E, Gonzalez RS, Osapoetra L, Ford T and McAleavey SA 2017. Measurement of Liver Stiffness Using Shear Wave Elastography in a Rat Model: Factors Impacting Stiffness Measurement with Multiple-and Single-Tracking-Location Techniques Ultrasound in medicine & biology 43 2629–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin T, Ophir J and Potter G 1988. Correlation of ultrasonic attenuation with pathologic fat and fibrosis in liver disease Ultrasound Med Biol 14 729–34 [DOI] [PubMed] [Google Scholar]
- Mikolasevic I, Orlic L, Franjic N, Hauser G, Stimac D and Milic S 2016. Transient elastography (FibroScan®) with controlled attenuation parameter in the assessment of liver steatosis and fibrosis in patients with nonalcoholic fatty liver disease-Where do we stand? World journal of gastroenterology 22 7236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nenadic IZ, Qiang B, Urban MW, Zhao H, Sanchez W, Greenleaf JF and Chen S 2016. Attenuation measuring ultrasound shearwave elastography and in vivo application in post-transplant liver patients Physics in Medicine & Biology 62 484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nightingale KR, Rouze NC, Rosenzweig SJ, Wang MH, Abdelmalek MF, Guy CD and Palmeri ML 2015. Derivation and analysis of viscoelastic properties in human liver: impact of frequency on fibrosis and steatosis staging IEEE transactions on ultrasonics, ferroelectrics, and frequency control 62 165–75 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ormachea J and Parker KJ 2020. Comprehensive viscoelastic characterization of tissues and the inter-relationship of shear wave (group and phase) velocity, attenuation and dispersion Ultrasound Med Biol 46 3448–59 [DOI] [PubMed] [Google Scholar]
- Ormachea J, Parker KJ and Barr RG 2019. An initial study of complete 2D shear wave dispersion images using a reverberant shear wave field Physics in Medicine & Biology 64 145009. [DOI] [PubMed] [Google Scholar]
- Ozturk A, Grajo JR, Gee MS, Benjamin A, Zubajlo RE, Thomenius KE, Anthony BW, Samir AE and Dhyani M 2018. Quantitative hepatic fat quantification in non-alcoholic fatty liver disease using ultrasound-based techniques: a review of literature and their diagnostic performance Ultrasound in medicine & biology 44 2461–75 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmeri ML, Wang MH, Rouze NC, Abdelmalek MF, Guy CD, Moser B, Diehl AM and Nightingale KR 2011. Noninvasive evaluation of hepatic fibrosis using acoustic radiation force-based shear stiffness in patients with nonalcoholic fatty liver disease Journal of hepatology 55 666–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker KJ 2014. A microchannel flow model for soft tissue elasticity Phys Med Biol 59 4443–57 [DOI] [PubMed] [Google Scholar]
- Parker KJ, Doyley MM and Rubens DJ 2010. Imaging the elastic properties of tissue: the 20 year perspective Physics in medicine & biology 56 R1. [DOI] [PubMed] [Google Scholar]
- Parker KJ, Ormachea J, Drage MG, Kim H and Hah Z 2018a. The biomechanics of simple steatosis and steatohepatitis Phys Med Biol 63 105013. [DOI] [PubMed] [Google Scholar]
- Parker KJ, Ormachea J and Hah Z 2018b. Group versus phase velocity of shear waves in soft tissues Ultrason Imaging 40 343–56 [DOI] [PubMed] [Google Scholar]
- Parker KJ, Ormachea J, Will S and Hah Z 2018c. Analysis of transient shear wave in lossy media Ultrasound in medicine & biology 44 1504–15 [DOI] [PubMed] [Google Scholar]
- Petta S, Wong VW-S, Cammà C, Hiriart J-B, Wong GL-H, Marra F, Vergniol J, Chan AW-H, Di Marco V, Merrouche W, Chan HL-Y, Barbara M, Le-Bail B, Arena U, Craxì A and de Ledinghen V 2017. Improved noninvasive prediction of liver fibrosis by liver stiffness measurement in patients with nonalcoholic fatty liver disease accounting for controlled attenuation parameter values Hepatology 65 1145–55 [DOI] [PubMed] [Google Scholar]
- Sharma AK, Reis J, Oppenheimer DC, Rubens DJ, Ormachea J, Hah Z and Parker KJ 2019. Attenuation of shear waves in normal and steatotic livers Ultrasound in medicine & biology 45 895–901 [DOI] [PubMed] [Google Scholar]
- Suzuki K, Hayashi N, Sasaki Y, Kono M, Kasahara A, Fusamoto H, Imai Y and Kamada T 1992. Dependence of ultrasonic attenuation of liver on pathologic fat and fibrosis: examination with experimental fatty liver and liver fibrosis models Ultrasound in medicine & biology 18 657–66 [DOI] [PubMed] [Google Scholar]
- Vappou J, Maleke C and Konofagou EE 2009. Quantitative viscoelastic parameters measured by harmonic motion imaging Physics in Medicine & Biology 54 3579. [DOI] [PubMed] [Google Scholar]
- Wang Y and Jiang J 2018. Influence of tissue microstructure on shear wave speed measurements in plane shear wave elastography: a computational study in lossless fibrotic liver media Ultrasonic Imaging 40 49–63 [DOI] [PubMed] [Google Scholar]
- Wang Y and Jiang J 2019. A two-dimensional (2D) systems biology-based discrete liver tissue model: A simulation study with implications for ultrasound elastography of liver fibrosis Computers in biology and medicine 104 227–34 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Wang M and Jiang J 2017. An analysis of intrinsic variations of low-frequency shear wave speed in a stochastic tissue model: the first application for staging liver fibrosis Phys Med Biol 62 1149–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu R and Aki K 1985. Elastic wave scattering by a random medium and the small‐scale inhomogeneities in the lithosphere Journal of Geophysical Research: Solid Earth 90 10261–73 [Google Scholar]
- Ye Q, Zou B, Yeo YH, Li J, Huang DQ, Wu Y, Yang H, Liu C, Kam LY, Tan XXE, Chien N, Trinh S, Henry L, Stave CD, Hosaka T, Cheung RC and Nguyen MH 2020. Global prevalence, incidence, and outcomes of non-obese or lean non-alcoholic fatty liver disease: a systematic review and meta-analysis Lancet Gastroenterol Hepatol 5 739–52 [DOI] [PubMed] [Google Scholar]
- Zhang M, Castaneda B, Wu Z, Nigwekar P, Joseph JV, Rubens DJ and Parker KJ 2007. Congruence of imaging estimators and mechanical measurements of viscoelastic properties of soft tissues Ultrasound Med Biol 33 1617–31 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang M, Nigwekar P, Castaneda B, Hoyt K, Joseph JV, di Sant’Agnese A, Messing EM, Strang JG, Rubens DJ and Parker KJ 2008. Quantitative characterization of viscoelastic properties of human prostate correlated with histology Ultrasound in medicine & biology 34 1033–42 [DOI] [PubMed] [Google Scholar]
- Zvietcovich F, Baddour N, Rolland JP and Parker KJ 2019. Shear wave propagation in viscoelastic media: validation of an approximate forward model Physics in Medicine & Biology 64 025008. [DOI] [PMC free article] [PubMed] [Google Scholar]


