IsRNA1: de novo prediction and blind screening of RNA 3D structures

Abstract

Modeling structures and functions of large RNAs especially with complicated topologies is highly challenging due to the inefficiency of large conformational sampling and the presence of complicated tertiary interactions. To address this problem, one highly promising approach is coarse-grained modeling. Here, following an iterative simulated reference state approach to decipher the correlations between different structural parameters, we developed a potent coarse-grained RNA model named IsRNA1 for RNA studies. Molecular dynamics simulations in the IsRNA1 can predict the native structures of small RNAs from sequence and fold medium-sized RNAs into near-native tertiary structures with the assistance of secondary structure constraints. A large-scale benchmark test on RNA 3D structure prediction shows that IsRNA1 gives improved performance for relatively large RNAs of complicated topologies, such as large stem-loop structures and structures containing long-range tertiary interactions. The advantages of IsRNA1 include the consideration of the correlations between the different structural variables, the appropriate characterization of canonical base-pairing and base-stacking interactions, and the better sampling for the backbone conformations. Moreover, a blind screening protocol was developed based on IsRNA1 to identify good structural models from a pool of candidates without prior knowledge of the native structures.

Graphical Abstract

1. INTRODUCTION

Ribonucleic acid (RNA) molecules play a wide variety of important roles in cells from carrying genetic information to regulating gene expression and enzymatic activity in biochemical reactions¹. Determining the three-dimensional (3D) structures of RNA molecules and their dynamic behaviors between distinct biologically active conformations is crucial for understanding RNA functions^2,3 and designing RNAs with new functionalities. However, compared with sequence determination^4,5, experimental determination of RNA 3D structures is severely limited by the size and flexibility of RNAs. This limitation has prompted the development of computational approaches, such as the folding simulation techniques to aid RNA 3D structure determination and study RNA dynamics between alternative states.^6–9

For structure prediction and folding simulations, coarse-grained (CG) modeling and simulation approaches are particularly attractive due to reduced degrees of freedom, less rugged free energy landscape, and more efficient conformational sampling^10,11. In recent decades, various CG models at different resolutions have been developed for RNA molecules to facilitate structure determination, probe folding stability, and estimate kinetics^11–24. For instance, the low-resolution model NAST¹² uses only one bead per nucleotide, and it can generate, cluster, and rank RNA 3D structures using RNA-specific statistical potentials that are supplemented by constraints on the secondary (2D) structure and tertiary contacts. The TIS¹³ model can predict folding thermodynamics of RNA in monovalent salt solutions by matching simulations with experimental melting data. Based on discrete Molecular Dynamics (MD) simulations, the three-bead CG model, iFoldRNA¹⁴, can provide good 3D structure prediction for structurally diverse RNAs, and its variations, iFoldRNAv2¹⁵ and iFoldNMR¹⁶, can employ hydroxyl radical probing data and sparse NMR constraints to guide the 3D folding of small to medium-sized RNA molecules, respectively. Using five beads for each nucleotide, the medium-resolution CG model RACER^17–19 can de novo fold short RNAs, and when supplemented by small-angle X-ray scattering (SAXS) structural information, it is able to characterize complex tertiary structures of large RNAs. A multilevel representation CG model, SimRNA²⁰, can predict structural and dynamical features of RNAs of up to 190 nucleotides (nts), especially when the 2D structure and/or additional long-range contact restraints are available. The latest version HiRE-RNAv3²¹ is a higher resolution model that uses six and seven beads per nucleotide for pyrimidines and purines, respectively, and can predict the structure, stability, and free energy surface for RNAs with sizes ranging from 12 to 76 nts and different levels of structural complexity.

In spite of the highly promising progress in CG modeling of RNA folding, several major challenges still remain^8,11. One prominent challenge is to design a more accurate CG force field to treat medium to large RNA molecules with complicated topologies, such as long-range kissing tertiary interactions. Recently, we developed the iterative simulated reference state method to build an accurate RNA CG force field²⁵ (IsRNA). Compared with the previous CG models, the parameterization of energy functions in IsRNA has the advantage of accounting for the local and nonlocal correlations between different structural degrees of freedoms and their interaction energies as well as effects from inherent chain connectivity and excluded volume. Furthermore, since contributions from both native-like and non-native conformations are considered in the simulated reference states, the IsRNA force field can account for both native and nonnative interactions in RNA folding. The simulated Boltzmann-like probability distributions based on the IsRNA force field agree with the statistical distributions from the experimental structures deposited in Protein Data Bank (PDB) for all the concerned structural variables such as bond length, bond angle, torsion angle, and pairwise distance²⁵. Recently, the IsRNA-based CG MD simulation has shown a number of successful applications to various problems. For example, by predicting a series of kinetically important intermediates and incorporating information from a nanopore experiment and a master equation analysis²⁶, IsRNA-based simulation successfully elucidated the folding pathway for an RNA pseudoknot. Furthermore, applications of IsRNA to problems such as Mg²⁺ ion effects in hepatitis C virus genomic RNA^27,28 and the relationship between nucleotide flexibility, RNA 3D structure energetics, and selective 2′-hydroxyl acylation analyzed by primer extension (SHAPE) reactivity²⁹ suggest that IsRNA-based CG MD simulations are able to provide a reliable 3D conformational ensemble for the study of various RNA folding properties. However, despite the successful applications of IsRNA to many simple RNA systems above, the ability of the IsRNA model to deal with complicated tertiary folding of RNAs remains to be systematically developed and explored.

In addition to the accuracy of the CG force field, another bottleneck for tertiary folding of large and topologically complex RNAs is inefficient sampling of the conformational space because of the huge number of degrees of freedom, even in the CG representation⁸. Since the folding of RNA molecules is thought to be hierarchical^30,31, the employment of 2D structure constraints in tertiary folding simulations of large RNAs can greatly improve the sampling efficiency and accuracy. Here, the 2D structure indicates the assignment of canonical base pairs in an RNA structure and can involve both non-cross-linked (in conventional RNA secondary structures) and cross-linked base pairs. In fact, for many RNAs, a significant portion of 2D structure information can be derived from multiple homologous sequence alignment methods (Rfam^32,33), free energy-based models (Mfold^34,35, RNAstructre^36,37, Vfold^38,39, DotKnot⁴⁰, CyloFold⁴¹, etc.), and data-driven approaches (the two-dimensional mutate-and-map strategy⁴² and SHAPE-directed 2D structure prediction^43–45).

Here, we present an improved IsRNA model called IsRNA1 by treating the base-pairing interactions as a synergistic sum of combined energy functions, rather than uncorrelated pairwise distance-dependent interactions in IsRNA. Moreover, the energy functions in the improved IsRNA1 model were reparametrized through a larger experimental PDB dataset (592 in IsRNA1 vs. 299 entries in IsRNA) to extract the observed probability distributions p_obs(x) and a more complete simulated dataset (121 in IsRNA1 vs. 40 cases in IsRNA) to construct the reference state distributions p_ref(x). Compared to the original IsRNA model, the improved IsRNA1 can provide a more accurate description for the canonical base-pairing and stacking interactions and guide more efficient and accurate sampling of the conformational space for tertiary folding of medium to large RNAs. Using MD simulations, we tested the ability of the IsRNA1 model to fold RNAs extensively. First, our test results indicate that the IsRNA model can perform de novo folding of small RNA molecules. Second, with the information of 2D structure as an input, an IsRNA-IsRNA1 pipeline can fold medium-sized RNAs into native-like 3D structures. Third, benchmark test on RNA 3D structure prediction indicates that, compared with the state-of-the-art CG models, the IsRNA1 model provides improved results for RNAs of relatively large size and complicated topologies. Finally, we developed an IsRNA1-based screening protocol to blindly identify good structures without prior knowledge of the native structure. And our test results with RNA-Puzzles suggest that the IsRNA1 energy function-based screening protocol can identify good models that have lower root-mean-square deviation (RMSD) relative to the native structure and higher Interaction Network Fidelity on Watson–Crick interactions (INF_WC).

2. MATERIAL AND METHODS

Coarse-grained RNA representation and the force field.

In agreement with the Vfold CG model^38,46, the IsRNA1 CG model uses two beads to represent the phosphate group (P) and ribose sugar ring (S) located at the P and C4’ atoms, respectively, to define the backbone. The model also uses three beads and two beads positioned at the center-of-mass of the constituent heavy-atom groups to define the purine and pyrimidine bases, respectively (See Fig. 1). More details about the CG beads used in the IsRNA1 model²⁵ can be found in Table S1 of the Supporting Information (SI). Similar to the previous study²⁵, the CG force field in IsRNA1 model can be written as

$$E_{total}={\sum }_{bonds}{E}_{bond}(b)+{\sum }_{\mathit{bond\; angles}}{E}_{angle}(\theta )+{\sum }_{\mathit{torsion\; angles}}{E}_{torsion}(\varphi )+{\sum }_{\mathit{base\; pairs}}{E}_{bp}(b,\theta ,\varphi )+{\sum }_{pairs}{E}_{pair}(r)+{\sum }_{\{j<i\}}{E}_{LJ}(r_{ij})$$ (1)

Figure 1.

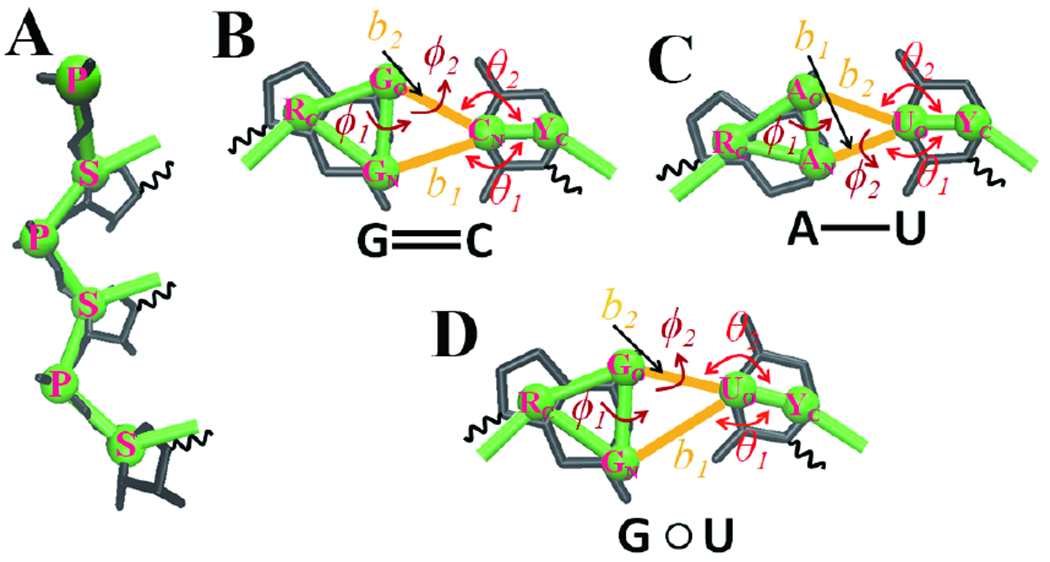
Schematic of the coarse-grained representation in IsRNA1 model and the structural variables used in the energy functions for canonical base-pairing interactions. (A) The backbone is defined by two beads P and S located at the P and C4’ atoms, respectively, and (B-D) the purine and pyrimidine bases are represented by three and two beads positioned at the center-of-mass of the grouped heavy atoms, respectively. Three canonical base-pairing interactions are accurately described by the combined covalent energy functions based on the selected reaction coordinates: (B) G-C base pair with ϕ₁ = ϕ(R_C − G_O − G_N− C_N) and ϕ₂ = ϕ(G_N − G_O − C_N − Y_c), (C) A-U base pair with ϕ₁ = ϕ(R_C − A_c − A_N − U_O) and ϕ₂ = ϕ(A_C − A_N − U_O − Y_C), and (D) G-U base pair with ϕ₁ = ϕ(R_C − G_O − G_N − U_O) and ϕ₂ = ϕ(G_N − G_O − U_O − Y_C).

Here the local covalent energy terms E_bond(b), E_angle(θ), and E_torsion(ϕ) represent the bond stretching, bond angle bending, and torsion angle energies, respectively. As shown below, the canonical base-pairing interaction E_bp(b,θ,ϕ) is described by a series of combined covalent energy functions. The non-local term E_pair(r) accounts for the remaining base-base, base-backbone, and backbone-backbone interactions. The last term E_LJ(r_ij) describes the excluded volume interaction between any two non-bonded beads i and j. Details of the energy functions are given in the SI Section I. Compared with the previous CG models^17–21, the current energy functions more fully capture the profiles of potential of mean forces for the structural variables and enable a broader and more accurate sampling of the conformational space²⁵.

Combined energy functions for base-pairing interactions.

In the original IsRNA model²⁵, a non-local pairwise base-base interaction is calculated as a function of the distance between two beads in the CG model. However, a base pair involves multiple interactions, whose strengths depend on multiple distances and angles together. Therefore, we introduced a multivariable function in the combined form for the canonical base-pairing energy:

$$E_{bp}(b,\theta ,\varphi )=E_{bond}(b_1)+E_{bond}(b_2)+E_{angle}({\theta }_1)+E_{angle}({\theta }_2)+E_{torsion}({\varphi }_1)+E_{torsion}({\varphi }_2)$$ (2)

As shown in the equation above, the two “bond” lengths, two “bond” angles, and the two torsion angles act collectively to determine the base-pairing interaction energy. Conversely, if a base pair is opened, all the related non-covalent energy functions are turned off. The definitions of the variables b₁, b₂, θ₁, θ₂, ϕ₁, and ϕ₂ for the G-C, A-U, and G-U canonical base-pairing interactions are given in Fig. 1 and SI Tables S3–S5. Because the simulated distributions based on the energy functions above can successfully reproduce the distributions derived from the PDB structure database for all the concerned structural parameters in a base pair, the combined energy functions given in Eq. (2) may have the potential to appropriately account for canonical (G-C, A-U, and G-U) base-pairing interactions. We call the IsRNA with the improved treatment for the base-pairing interactions (Eq. 2) as IsRNA1.

An iterative simulated reference state approach to parameterize energy functions.

Specifically, we used the probability distributions extracted from the experimental PDB dataset to parameterize the energy functions in IsRNA1 model. According to the inverse Boltzmann law, the statistical potential energy for a given structural variable x, such as the bond length b, bond angle θ, torsion angle ϕ, or pairwise distance r, can be calculated by

$$E(x)=-k_{\text{B}}T\ln [p_{obs}(x)/p_{ref}(x)]$$ (3)

where k_B is the Boltzmann constant, T is the temperature, p_obs(x) is the probability distribution for x observed from the experimental structures deposited in PDB database, and p_ref(x) is the probability distribution for the reference state. A challenge underlying the extraction of statistical potential energies through Eq. (3) is how to account for the correlation effect between different structural variables. This correlation effect stems from the inherent chain connectivity and many-body base-base interactions as well as the volume exclusion between different segments. (See SI Section II and Figures S1–S2 for some typical examples about the correlation effects.)

Since the total coarse-grained (CG) force field given in Eq. (1) is a linear combination of energy functions for different variables, we can add the energy terms one by one on-the-fly as guided by the iteratively simulated reference states, where in each step, the simulated distribution based on the existing variables is treated as the reference state distribution p_ref(x) for the next variable x to be added. In such a way, the correlation effect can be appropriately built into the reference state p_ref(x) through CG MD simulations and the probability distributions for the concerned structural variables approach the observed distributions from the PDB database. Because the energy function is built based on the distribution of the whole (simulated) conformational ensemble, including both the native and the nonnative states, it might be used to simulate the folding energy landscape of an RNA. However, as a caveat, we note that the derivation of the energy function relies on the selected dataset of (native) structures, thus whether the simulation can give the physical folding process remains a problem for further investigation.

The detailed parameterization procedure for the energy function through the iterative simulated reference state approach has been discussed in our previous work²⁵. For clarity, an illustrated flowchart of the parameterization procedure is given in Fig. 2 and described below.

Figure 2.

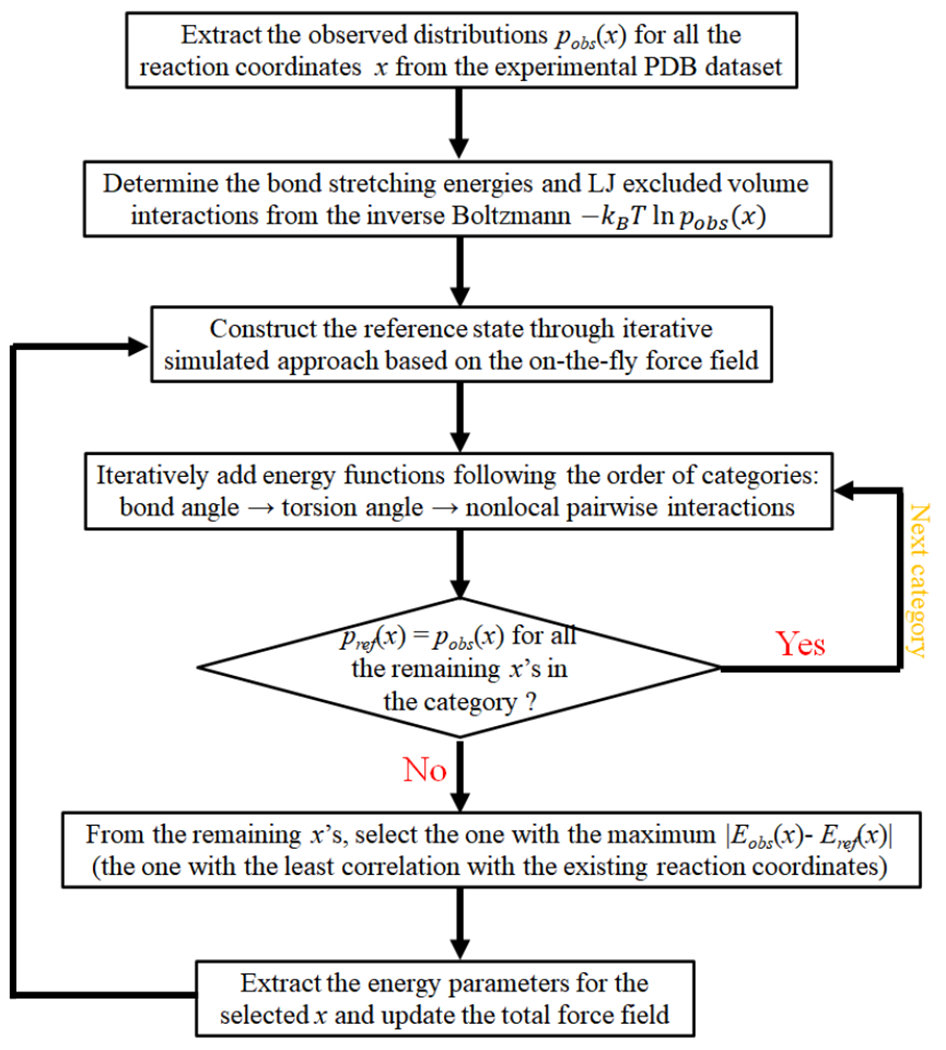
The flowchart of the parameterization procedure for energy functions in the IsRNA1 model.

1. To extract the observed probability distributions for the different structural variables, a large experimental PDB dataset contains 592 X-ray crystal and NMR structures with the redundant structures removed (relative to 299 entries in the original IsRNA) was constructed. The details about the extraction of probability distributions from the dataset are given in the SI Section III.

2. All the energy functions in the bond stretching category in IsRNA1 force field, including 6 types of the base-pairing interactions, were directly determined from the corresponding observed probability distributions ρ_obs(b) via E_bond(b) = −k_BTln ρ_obs(b). From the bond length data, we estimated the diameters σ for the excluded volume interactions E_LJ(r_ij) (see SI Eq. S5). The E_bond(b) and E_LJ(r_ij) parameters were used as the starting energy functions for the iteratively constructed force field.

3. In each of the following steps, we added an energy term E(x_i+1) (for variable x_i+1) to the existing energy function U_i = E(x₁)+E(x₂)+ …+E(x_i) determined from the previous steps (for variables x₁,x₂,…, x_i). MD simulations were performed based on the force field U_i to calculate the reference state distribution p_ref(x_i+1) for x_i+1. To construct a complete reference state, a large dataset (named simulated dataset) that contains 121 RNA molecules (relative to 40 RNAs in the original IsRNA) with size ranging from 12 to 120 nts was used in the simulations. This dataset covers a variety of structural topologies including stem-loop, junction, pseudoknot, triplex, and loop-related kissing tertiary interactions; See the SI Table S2 for the PDB IDs of the 121 RNAs. Starting from the native structures, the simulations collected in total 121,000 structure snapshots for the calculation of the distribution p_ref(xⁱ⁺¹) (See SI Section III for more details). Then the energy term E(x_i+1) was determined from Eq. (3). We note that no explicit artificial bias toward the native structures is introduced in the simulations. In fact, the reference state distribution p_ref(x_i+1) from the collected structure snapshots accounts for both the native and the non-native interactions. However, the derived energy function is dependent on the selected database for native structures, and it not clear whether the observed probability distribution p_obs(x) forms the physical Boltzmann distribution for the different variables. Therefore, it requires further investigation to determine whether the extracted energy function can accurately describe the physical free energy landscape for an RNA.

4. In the iterative procedure, we fitted energy terms following the order E_angle(θ) (bond angle bending energy) → E_torsion(ϕ) (torsion energy) → E_pair(r) (non-local pairwise interaction). The above energy terms were added to the CG force field one by one until the simulated conformational ensemble reproduced the target (observed) distributions for all the structural variables. To optimize the convergence speed, when adding the energies E(x) one by one, among all the structural variables within the same category, the one with the largest energy contribution was selected in each step and the corresponding energy function E(x) = −k_BTln[ρ_obs(x)/ρ_ref(x)] was added to the CG force field; See the SI Section IV for more details.

Overall, the proposed iteration procedure can identify correlations between the structural variables. For example, if the added energy E(x) is 0, the structural variable x is fully correlated to the existing structural variables (before x is added to the force field). In total, we found 18, 18, 26, and 41 weakly correlated (nearly independent) bond stretching lengths, bond angles, torsion angles, and pairwise interactions out of 18, 33, 31, and 55 observed ones, respectively. These weakly correlated variables were selected as the effective collective variables in the final IsRNA1 CG force field; See SI Table S3–S6 for the corresponding energy parameters.

Simulation protocol.

The CG MD simulations in the IsRNA/IsRNA1 model were performed through Langevin dynamics (NVT ensemble) in the modified open-source software, LAMMPS⁴⁷. LAMMPS runs efficiently on both single-processor and parallel computers by supporting the MPI message-passing library. The default time step for integration was set to Δt = 1fs. Apart from the conventional MD simulations at the desired temperature, we also employed two enhanced sampling techniques, simulated annealing MD and replica-exchange MD (REMD), to rapidly sample the 3D conformational space. In general, starting from the initial structures, a long time CG MD simulation was performed to relax or fold the RNA molecules with the IsRNA/IsRNA1 CG force field. Based on the simulated conformational ensemble from MD trajectories, we can compute the probability distributions, predict the most stable 3D structures, and calculate the average potential energies; see the SI Figure S3 for an illustrative flowchart for the 3D structure prediction.

The simulation details including simulation methods, simulation time, temperature, initial structure, structure snapshot collection, construction of the conformation ensemble, and total central processing unit (CPU) hours for each study are summarized in SI Table S7. For instance, to fold RNAs with medium size ranging from 22 to 78 nts into native-like 3D structures with 2D structure constraints, we developed an IsRNA-IsRNA1 pipeline. Specifically, REMD simulations starting from the coil structures were performed based on the IsRNA force field with 8 replicas and temperatures from 200 K to 375 K for 300 ns per replica. The constraints on base pairs in the IsRNA simulations were enforced using harmonic potentials E_rest(r) = k_r(r − r₀)² on the participating pairs of beads as shown in Fig. 1, such as pairs G_O-C_N and G_N-C_N for a G-C pair. To avoid unphysical artifacts caused by those restraints, the restraint spring coefficient k_r was gradually strengthened from 0.01 to 5 kcal/mol/Ų during the long simulation period to make the RNA fold into the proper conformation. After sufficient folding of RNA molecules in the first 200 ns, structure snapshots and their potential energies were collected from the last 100 ns in the interval of 100 ps for each replica and 8,000 structures were obtained in total. As a refinement step, the folded structure given by the IsRNA model served as the initial structure for an additional REMD simulation using the improved IsRNA1 CG force field. Specifically, the IsRNA1-based REMD simulation employed 11 replicas with temperatures from 150 K to 400 K for 100 ns simulation time per replica. The structure snapshots and potential energies were collected every 100 ps from the last 50-ns trajectory for each replica and 5,500 structures were obtained in total. The collected snapshots formed a conformational ensemble for the prediction of the final tertiary structure by the IsRNA1 model. The total CPU time for the folding of a 78-nt RNA molecule using the IsRNA-IsRNA1 pipeline is about 670 hours on a common desktop computer with Intel Core(TM) i7-5930K 3.5GHz CPU. Since the number of CG beads in IsRNA/IsRNA1 model is small (relative to all-atom model), only one CPU thread is required for each REMD replica and the multiple threads parallelization for each replica would not cause significant enhancement in the computational performance.

To further benchmark the performance of IsRNA1 model on 3D structure prediction on a large dataset and RNA-Puzzles challenges, with the sequence and the 2D structure as inputs, the template-based Vfold3D^39,48 and VfoldLA^49,50 algorithms were used to generate three 3D structures (if available) as the initial states of the CG MD simulations. For the complicated RNAs containing tertiary interactions (cross-linked base pairs), if Vfold3D/VfoldLA algorithms fail to generate the initial 3D structures, the cross-linked base pairs in the 2D structure will be ignored when building the initial 3D structures. To avoid unphysical 3D structures built with the VfoldLA algorithm, we ran 30-ns REMD simulations (10 replicas with temperature from 225 K to 450 K) with the aforementioned gradually strengthened harmonic restraints E_rest(r) to form and stabilize the cross-linked base pairs. Based on the initial 3D structures and the base-pairing constraints, we performed t-ns REMD simulations (10 replicas with temperature from 200 K to 425 K) to sample the 3D conformations, where t is 1.5 and 50 for junction and non-junction structures, respectively. After the first t/2-ns simulations for relaxation of the initial structures, the conformational snapshots and their potential energies from the last t/2-ns trajectories for all replicas were collected. As a result, from the three initial 3D structures, an ensemble of 15,000 conformations was generated for 3D structure prediction. The typical CPU time for the 3D structure prediction of a 101-nt RNA is about 330 hours (10 replicas in total) on a workstation with AMD Ryzen Threadripper 1950X 2.1 GHz CPU.

Inputs and outputs.

The typical inputs of IsRNA1 CG MD simulations include a starting 3D structure (PDB-formatted), a 2D structure in the dot-bracket format, and a configuration file that contains the basic parameters, such as simulation technique, simulation time, temperature, interval for collection of structure snapshots. The starting structure can be obtained from predictions given by IsRNA model or other computational approaches, such as Vfold3D⁴⁸, VfoldLA^49,50, etc., or even a coil structure. For the test cases, the 2D structures were extracted from the native 3D folds by the RNApdbee⁵¹ webserver or by the DSSR⁵² software. Cross-linked base-pairing interactions for pseudoknot and loop-kissing tertiary structures are directly supported in the dot-bracket format of the 2D structure. The IsRNA1 model can handle RNA molecules of one or multiple chains. Depending on the size and topology of the RNA, simulation parameters in the configuration file (such as the sampling technique, simulation time and temperature) can be easily changed from the default settings.

Additional constraints can also be fed into the IsRNA1 CG MD simulations. Two typical constraints are long-range contacts indicated by experiments and/or computational methods and 3D templates for structure motifs extracted from the homologous structures. Similar to the constraints for base pairs, long-range contacts constraints can be imposed using bond stretching energies between involved bead pairs with appropriate energy functions. In the LAMMPS library for bond stretching potentials, various types of energy functions with tunable parameters are available. Similarly, constraints on particular bond angles and torsional angles are also feasible. The constraints from structure templates can be accomplished by modeling each related template as a rigid body in the MD simulations. Other useful features of CG MD simulations include freezing groups of beads, adding flexible tethering or external force on specific nucleotides, and enabling a variety of sampling ensembles, such as canonical, isothermal-isobaric, and isenthalpic ensembles.

The primary outputs of IsRNA1 CG MD simulations are the folding trajectories, which are readable in VMD⁵³ to visualize the folding process. The potential energies for the different components listed in Eq. (1), such as E_bond, E_angle, E_torsion, E_bp, and E_pair, were recorded for each snapshot. For the purpose of 3D structure prediction, structures of top 10% lowest energy (E_total in Eq. 1) were selected from the conformational ensemble. Based on the pairwise RMSDs over all the CG beads, the selected low-energy structures in the conformational ensemble were clustered through an in-house program⁵⁴. In detail, any two structures with pairwise RMSD less than a threshold value were defined as a neighbor. Then the structure having the most neighbors was chosen as the 1st centroid structure. The first centroid structure and its neighbors were grouped into the 1st (largest) cluster and the 1st centroid structure was considered as the top 1 predicted 3D structure. Applying the same idea to the remaining conformations resulted in the 2nd, 3rd, … (smaller) clusters and the corresponding centroid structures. The cutoff RMSD threshold for the clusters is chosen such that the largest cluster contains about 65% of the candidate structures or the cutoff RMSD is equal to 0.1Å times the sequence length, depending on which RMSD cutoff is smaller. See SI Table S7 for more details in extracting the conformational ensemble for the present studies.

The four/five CG beads per nucleotide representation in IsRNA model permits a nearly one-to-one mapping between a CG conformation and the corresponding PDB all-atom model. To implement the all-atom reconstruction, a built-in single-nucleotide fragment matching algorithm was developed based on the PDB dataset. Finally, NAMD⁵⁵ with the CHARMM⁵⁶ force field was applied to perform energy minimizations to fix possible errors in local geometries (such as unphysical bond lengths) and to reduce the clash scores of the predicted all-atom structures. As the energy minimization mainly improves the local structural quality for the predicted models (such as clash score) and keeps the global features (such as the RMSD) nearly unchanged, other refinement methods, such as QRNAS⁵⁷ and RNAfitme⁵⁸, are also useful.

3. RESULTS

De novo folding of small RNA molecules into native structures.

Through simulated annealing MD simulations, starting from the coil structures, the original IsRNA model is able to de novo fold small RNAs into their native structures solely from the sequences. The simulation details are given in the “Materials and Methods” and in the SI Table S7. In total, there are 15 small RNA molecules collected from previous studies^{18, 21}. The lengths of the small RNAs range from 12 to 36 nts and their structural topologies are simple stem-loop structures, including duplexes, hairpins and bulge loops. The plots of RMSDs vs. potential energies during the folding process for some typical cases are given in the SI Fig. S4. As shown in Fig. 3, the original IsRNA model outperforms Ren’s model¹⁸ with average RMSDs of 2.49 Å (IsRNA) vs. 3.53 Å (Ren’s model) for 7 cases and the HiRE-RNA model²¹ with average RMSDs of 1.69 A (IsRNA) vs. 3.39 Å (HiRE-RNA) for 9 cases, respectively. However, when compared with the SimRNA^20,59 model with an average RMSD of 2.08 Å over all the 15 cases, the performance of the original IsRNA model (average RMSD of 2.29 Å) is slightly worse (see Fig. 3).

Figure 3.

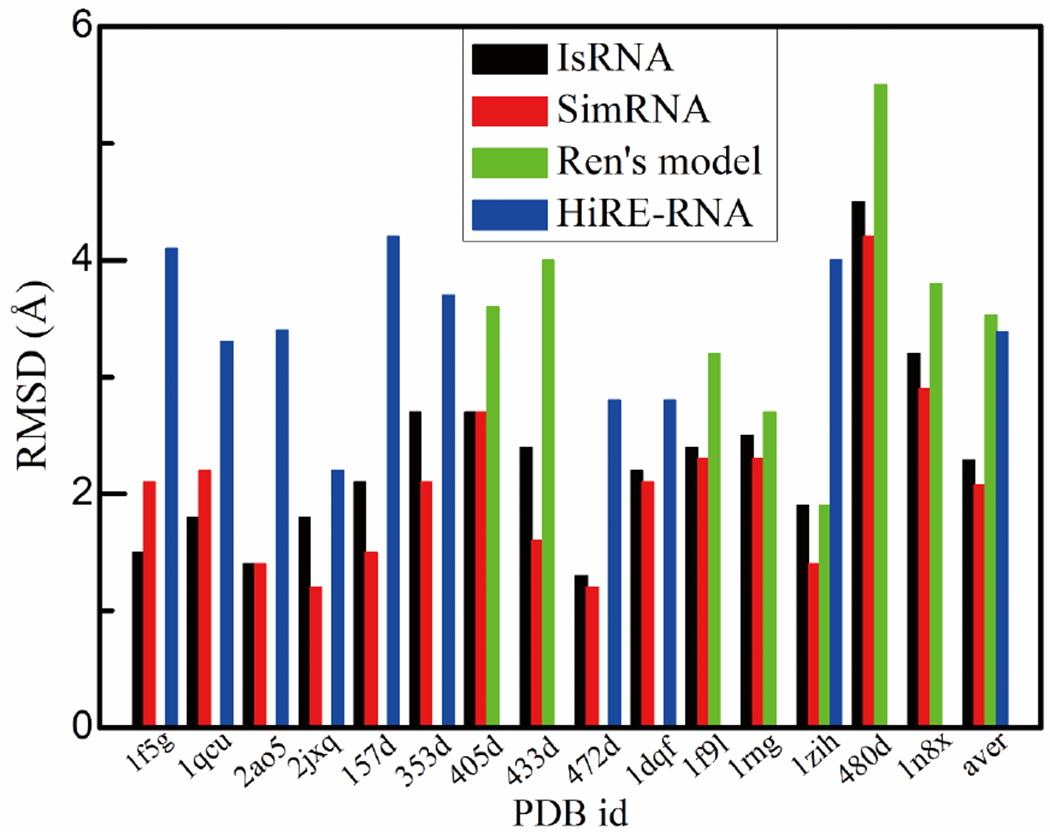
De novo folding of small RNA molecules with simple topology into native structures by the original IsRNA model. For comparison, the root-mean-square deviation (RMSD) data from the original works in Ren’s model and HiRE-RNA model are also given. For the SimRNA model, the top 1 prediction given by the SimRNAweb (https://genesilico.pl/SimRNAweb/) using the default parameters is chosen. The RMSDs are calculated over all the CG beads.

In detail, Ren’s model^17,18 uses a simple harmonic function to describe the local bond stretching and bond angle energies, a set of pairwise distance-dependent energy functions to represent the base-base interactions, and a simplified non-interacting ideal gas reference state to parameterize the force field. The HiRE-RNA²¹ model uses harmonic potentials for the local bond stretching and bond angle energies and describes the base-base interactions in a many-body fashion, but the reference state is not explicitly simulated during the parameterization. In contrast, the SimRNA²⁰ model depends on 3D statistical potentials for different base-base contacts to directly account for base-base interactions and uses the quasi-chemical approximation as the reference state. Therefore, the fact that IsRNA model outperforms the previous Ren’s model and HiRE-RNA model for all the cases in de novo folding of small RNAs suggests that a more rigorous reference state approach instead of the simple ideal gas reference state may be important for the construction of an accurate CG RNA force field. Moreover, accurate potential functions for the local covalent energy terms, such as those used in IsRNA1 model (see SI Section I), are also important. Furthermore, an accurate description of the base-base interactions (including base-pairing and base-stacking interactions) goes beyond pairwise distance-dependent interactions used by most previous models. For example, the SimRNA model employs direct base-base contact energies instead of simple pairwise energies along with sufficient sampling based on 80 replicas for each case. In conclusion, in addition to the rigorous reference state calculation (in IsRNA/IsRNA1), accurate descriptions of base-pairing and base-stacking interactions are also important for modeling RNA folding, and the current upgraded IsRNA1 considers the above key factors.

Tertiary structure folding of RNAs with 2D structure constraints.

As indicated by our previous work²⁶, for RNA molecules with relatively large size and complicated topology, folding simulations starting from an extended single strand without any 2D structure constraints will experience several intermediate and misfolded states and can be easily trapped into local minimums. Thus, when searching for native-like conformations, 2D structure constraints in tertiary structure folding of RNA molecules can substantially improve the sampling efficiency and accuracy. These improvements are more pronounced for large RNAs, where conformational sampling is a significant challenge for structure prediction. Starting from a coil state and using 2D structure constraints, an IsRNA-IsRNA1 CG MD simulation pipeline can predict near-native tertiary structures from the sequences (See “Materials and Methods” and SI Table S7 for details). Benchmark tests were performed for 65 RNAs (“dataset-65”) whose sequence lengths range from 22 to 78 nts, covering structural topologies such as stem-loops, pseudoknots, multi-way junctions, loop-related kissing tertiary structures, and other highly complex tertiary folds. As previous tests²⁰ suggest that the SimRNA model can provide comparable or better results than other similar methods such as iFoldRNA¹⁴ and FARNA/FARFAR^60,61, here we selected SimRNA^20,59 as the state-of-the-art CG model for comparison.

In the IsRNA-IsRNA1 pipeline, the IsRNA1-guided CG MD simulations (the second step in the pipeline) results in notable structure refinements with smaller RMSDs for 37 out of 65 test cases relative to the first IsRNA step. For 15 of the remaining 28 cases, comparable results with a slight RMSD difference ΔRMSD₀ = RMSD_IsRNA1 − RMSD_IsRNA ≤ 0.5 Å are observed. The complete detailed results are given in the SI Table S8. Overall, the average RMSD for the 65 test cases decreases from 6.38 ± 3.73 Å to 5.93 ± 3.21 Å after the IsRNA1-guided structure refinement, as shown in Fig. 4 and the SI Table S8. Compared with the SimRNA model, the IsRNA-IsRNA1 pipeline gives improved predictions for 26 cases (ΔRMSD = RMSD_simRNA − RMSD_IsRNA1 ≥ 0.5 Å) and comparable results with slight RMSD differences (|ΔRMSD| ≤ 0.5 Å) for 18 cases (see SI Table S8). For all 65 test cases, the average RMSD given by SimRNA is 6.40 ± 3.95 Å, which is close to the IsRNA-based result 6.38 ± 3.73 Å, but is larger than the IsRNA1-based result 5.93 ± 3.21 Å (see Fig. 4), suggesting that the original IsRNA performs comparable to SimRNA and IsRNA1 provides further improvement.

Figure 4.

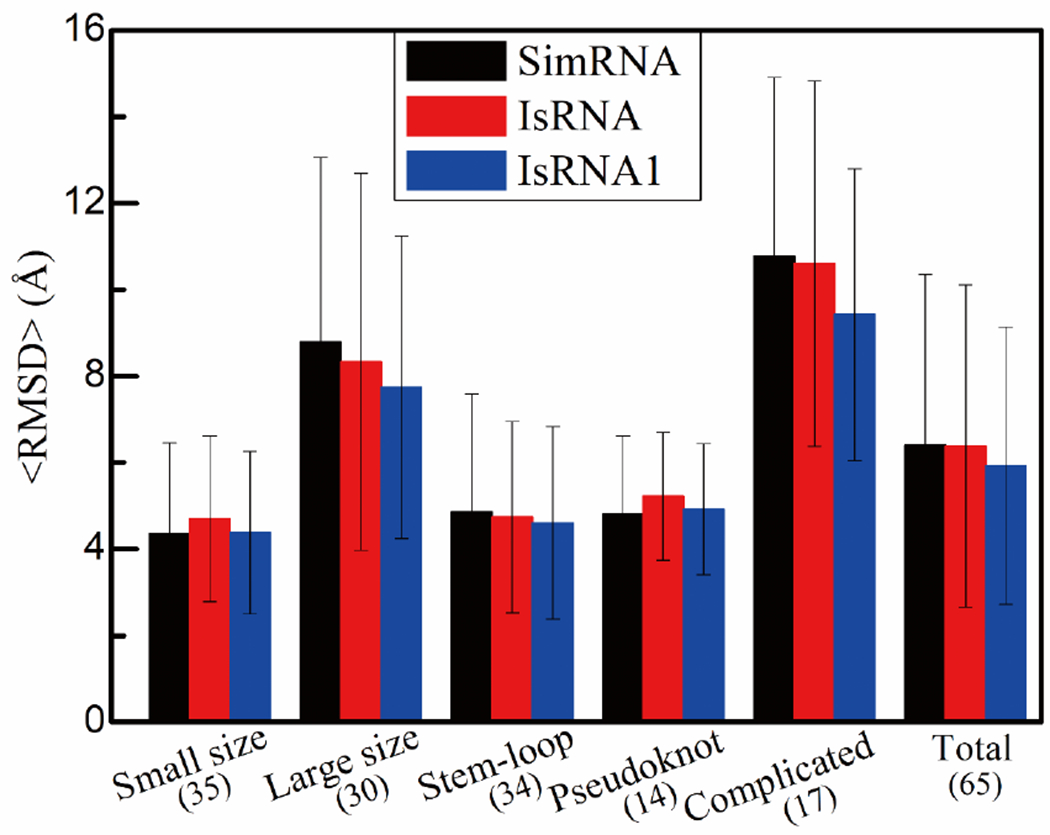
Tertiary structure folding of medium size RNAs (22~78 nts) with the assistance of 2D structures by the IsRNA-IsRNA1 pipeline (top 1 structure only). Performances on different RNA groups classified by the sequence length and 3D structural topologies are summarized in terms of average RMSDs. The numbers of cases involved in each group are given in parentheses, and the standard deviations serve as error bars. For SimRNA, the data are collected from the original paper, if available. Otherwise, the top prediction given by SimRNAweb (https://genesilico.pl/SimRNAweb/) using the default parameters is chosen. Calculations of RMSD are based on all-heavy atoms. Complete detailed data are given in the SI Table S8.

To uncover the underlying advantages and limitations of the IsRNA-IsRNA1 pipeline, we investigated the structure prediction results for different RNA groups classified by the sequence length or 3D structural topologies (see Fig. 4).

Specifically, according to the sequence length, 65 test RNAs were divided into two groups, one group including 35 small RNAs of size smaller than 40 nts, and the other group including 30 relatively large RNAs of size larger than 40 nts. For RNAs in the small-size group, because of the limited conformational space and relatively simple topology (such as stem-loop and H-type pseudoknot), tertiary structures predicted by a number of accurate CG models with the restraints of 2D structures can achieve near-atomic resolution, and de novo folding from the sequence is viable (such as the results shown in Fig. 3). Here, for 35 test RNA molecules in the small-size group, the average RMSDs given by SimRNA, IsRNA, and IsRNA1 are 4.35 ± 2.11 Å, 4.70 ± 1.91 Å, and 4.38 ± 1.88 Å, respectively (see Fig. 4), which indicates that IsRNA1 performs comparably relative to SimRNA for RNAs of relatively small size. For large RNAs, tertiary structure folding by CG simulations is generally hampered by inefficient conformational sampling (because of high flexibility of loop segments) and complicated intra- and inter-loop interaction networks. In such situations, an accurate force field becomes more important to guide conformational sampling and to simulate the interaction networks. For 30 test RNAs in the large-size group, the average RMSDs are 8.79 ± 4.27 Å, 8.33 ± 4.36 Å, and 7.74 ± 3.50 Å for SimRNA, IsRNA, and IsRNA1, respectively (see Fig. 4 and SI Table S8), which suggests that IsRNA1 may improve the performance in tertiary structure folding for relatively large RNAs.

In regard to the structural topology, the 65 test RNAs include 34 stem-loops, 14 pseudoknots, and 17 complicated structures of multi-way (3-way and 4-way) junctions and loop-kissing tertiary interactions. (i) For stem-loops containing only helices and hairpin/internal/bulge loops, many RNA 3D structure prediction programs can achieve a satisfactory accuracy, especially for the simple structures of small size (e.g., < 40 nts). As shown in Fig. 4, tertiary structure folding by SimRNA, IsRNA, and IsRNA1 give the average RMSDs of 4.86 ± 2.73 Å, 4.74 ± 2.21 Å, and 4.60 ± 2.23 Å for the 34 test stem-loop structures, respectively. (ii) For the H-type pseudoknot, due to the intercalated base-pairing interactions between two stems, an accurate tertiary structure folding simulation is quite challenging as the rich loop-helix non-canonical base-base/base-backbone interactions^62–64 and the potential environment effects, such as metal ions and ligand binding⁶⁵, can play important roles in folding. For 9 of 14 listed H-type pseudoknots, the IsRNA-IsRNA1 pipeline is able to predict 3D structures at near-atomic resolution with RMSDs to the native structures < 5 Å (see SI Table S8 for details). The average RMSDs for all the pseudoknots given by SimRNA, IsRNA, and IsRNA1 are 4.81 ± 1.80 Å, 5.22 ± 1.48 Å, and 4.92 ± 1.51 Å, respectively (see Fig. 4). (iii) Due to the large conformational degrees of freedom for loops, intricate loop-related interaction networks, and the effects from surrounding environment^8,66–70 (for instance, ions and ligand binding), computational modeling of complicated RNA systems containing multi-way junctions and/or long-range tertiary interactions (such as loop-loop kissing^71,72) is a bottleneck for structure prediction. Here, for 17 test RNAs of complicated structures with size from 41 to 76 nts, the IsRNA-IsRNA1 pipeline gives improved predictions (ΔRMSD > 0.5 Å) relative to SimRNA for 10 cases, and the average RMSD for the whole group decreases from 10.77 ± 4.13 Å by SimRNA to 9.42 ± 3.37 Å by IsRNA1 (see Fig. 4).

A large-scale benchmark for RNA 3D structure prediction.

To further test the performance on 3D structure prediction by IsRNA1 model for relatively large RNAs of complicated topologies, a large-scale benchmark test on a dataset of 130 relatively large RNA molecules (“dataset-130”) was performed and compared with other two CG models, namely iFoldRNA^14,15 and SimRNA^20,59 (see SI Table S9 for detailed results). In this benchmark dataset, the RNA size ranges from 40 to 161 nts, and there are 44 stem-loops, 43 multi-way (3-way, 4-way, and 5-way) junctions, and 43 structures of long-range tertiary interactions.

To enhance the sampling efficiency, here we combined IsRNA1 with the template/loop-based algorithms Vfold3D⁴⁸/VfoldLA⁴⁹ to predict 3D structures of large RNAs. Specifically, with the sequence and 2D structure as input, Vfold3D and VfoldLA programs were used to generate up to three 3D structures as the initial structures of the subsequent CG MD simulations in IsRNA1 model. For fairness, the native structure and its related entries were excluded from the template/loop database when generated the initial structures. Assuming the generated initial structures represent states near the native conformation, relatively short REMD simulations with 2D structure constraints were run in IsRNA1 model to predict the final 3D structures (see “Materials and Methods” and SI Table S7 for simulation details). For 12 of the 17 overlapped cases between “dataset-65” (for the IsRNA-IsRNA1 pipeline) and “dataset-130” (for the Vfold3D/Vfoldl_A-IsRNA1 pipeline), short (50 or 1.5 ns per replica) REMD simulations in the Vfold3D/VfoldLA-IsRNA1 pipeline provide comparable or slightly better 3D structure predictions (ΔRMSD < 0.5 Å) than the long (400 ns per replica) simulations in the IsRNA-IsRNA1 pipeline (see SI Tables S8 and S9). The results indicate that the combination of template/loop-based Vfold3DA/foldLA models and IsRNA1 MD simulations can indeed enhance sampling efficiency and quality for 3D structure prediction.

Apart from RMSD for global fold, two additional metrics were also used to assess the structural qualities of the predicted 3D structures. The first one is the Interaction Network Fidelity⁷³ for all the canonical and non-canonical base-pairing and base-stacking interactions, denoted as INF_all. In general, INF_all measures the accuracy of the interaction networks in the predicted structures. INF_all of 1.0 means the predicted structure perfectly reproduce the interaction networks in the native structure. The second metric is the clash score⁷⁴ to characterize the number of serious steric overlaps between all-atom contacts and a lower clash score represents a better structural quality. The three metrics were calculated using RNA-Puzzles toolkit⁷⁵ (for RMSD and INF_all) and RNAssess server⁷⁶ (for clash score).

Results of this large-scale benchmark test are summarized in Table 1. For the 130 RNAs, the average/median RMSDs for the predicted top 1 structure by IsRNA1, SimRNA, and iFoldRNA are 9.51/8.12 Å, 11.26/10.95 Å, and 11.87/11.37 Å, respectively, which further suggests the improved performance of the IsRNA1 model for large RNAs. The average/median INF_all of 0.75/0.75 by IsRNA1 is slightly better than that of 0.73/0.73 by SimRNA and that of 0.67/0.68 by iFoldRNA. And the average/median clash score of 4.0/2.7 by IsRNA1 is lower than that of 139.7/140.0 by SimRNA and that of 170.4/174.6 by iFoldRNA. Additionally, considering the top 3 predicted structures, the average RMSDs for the best model predicted by IsRNA1, SimRNA, and iFoldRNA are 8.34 Å, 9.73 Å, and 10.88 Å, respectively. And their average INF_all are 0.76 (IsRNA1), 0.72 (SimRNA), and 0.67 (iFoldRNA), respectively. The detailed results for RNAs containing stem-loops, multi-way junctions, and tertiary interactions are also given in Table 1 and illustrated below.

Table 1.

Benchmark test results for 3D structure prediction by IsRNA1, SimRNA, and iFoldRNA for 130 relatively large RNAs (40-161 nts) with native 2D structures as constraints. Average/median (in boldface) structural quality assessments in terms of RMSD, INF_all, and clash score are shown. The results are classified according to the structural topologies for the top-1 prediction and the best of the top-3 predictions (if available). The numbers of the test cases are given in parentheses. The prediction results for iFoldRNA and SimRNA were collected from iFoldRNAv2 webserver (https://dokhlab.med.psu.edu/ifoldrna/#/) and SimRNA program provided by authors (https://ftp.users.genesilico.pl/software/simrna/) using default parameters, respectively. RMSDs were calculated over all-heavy atoms. INF_all is the Interaction Network Fidelity for all the canonical and non-canonical base-pairing and base-stacking interactions.

Dataset and folding model	Top 1 prediction			Best of top 3 predictions
	RMSD (Å)	INFall	Clash Score	RMSD (Å)	INFall	Clash Score
Stem-loop
IsRNA1 (44)	5.79/5.08	0.80/0.82	2.0/1.4	5.15/4.57	0.81/0.82	1.8/1.3
SimRNA (44)	7.21/5.49	0.77/0.79	129.4/128.5	6.58/5.06	0.77/0.79	128.5/128.3
iFoldRNA (32)	7.90/5.57	0.70/0.73	153.2/143.1	7.29/5.17	0.71/0.73	151.4/143.1
Multi-way junction
IsRNA1 (43)	12.93/11.33	0.71/0.73	4.2/2.9	10.88/10.6	0.72/0.73	4.7/2.8
SimRNA (43)	14.91/13.36	0.69/0.69	143.3/144.4	12.42/11.48	0.69/0.70	143.7/144.4
iFoldRNA (34)	15.85/14.57	0.64/0.65	180.7/181.0	13.98/12.74	0.64/0.64	183.7/183.8
Tertiary interaction
IsRNA1 (43)	9.89/8.16	0.74/0.73	5.7/4.8	9.05/7.62	0.75/0.75	5.7/4.8
SimRNA (43)	11.75/10.91	0.73/0.73	146.5/150.7	10.28/8.94	0.71/0.72	147.9/144.9
iFoldRNA (29)	11.60/11.76	0.67/0.69	177.4/178.9	11.22/11.48	0.66/0.68	175.2/180.0
All
IsRNA1 (130)	9.51/8.12	0.75/0.75	4.0/2.7	8.34/7.13	0.76/0.76	4.07/2.45
SimRNA (130)	11.26/10.95	0.73/0.73	139.7/140.0	9.73/8.92	0.72/0.73	139.9/139.6
iFoldRNA (95)	11.87/11.37	0.67/0.68	170.4/174.6	10.88/10.46	0.67/0.68	170.2/173.1
Multiple chains
IsRNA1 (35)	8.72/7.93	0.78/0.79	3.4/2.3	7.78/6.24	0.79/0.79	3.5/2.4
SimRNA (35)	12.10/12.91	0.77/0.76	137.7/136.7	10.22/9.60	0.77/0.77	138.4/137.8

Stem-loop structures.

As the most frequently occurring RNA motif, the stem-loop structure has a simple topology. The challenge for 3D structure prediction of large stem-loop structures mainly comes from the presence of multiple large internal/bulge loops. For the 44 test stem-loop structures of relatively large size in the “dataset-130”, the average RMSD, INF_all, and clash score of the predicted top 1 structure by IsRNA1 are (5.79 Å, 0.80, 2.0), better than (7.21 Å, 0.77, 129.4) by SimRNA and (7.90 Å, 0.70, 153.2) by iFoldRNA. When the best of top 3 predictions is considered, the average structural qualities for IsRNA1 improves only slightly, with the average RMSD decreasing from 5.79 Å (top 1 prediction) to 5.15 Å (the best of top 3 predictions) (see Table 1), which indicates the top 1 prediction can represent the best structure in the sampled conformational ensemble for the majority of the stem-loop structures. In particular, for the 78-nt HIV-1 dimerization initiation site in the extended-duplex dimer⁷⁷ (PDB ID: 2d1a, see Fig. 5A) containing 4 internal loops and the 77-nt HCV IRES domain II⁷⁸ (PDB ID: 1p5p, see Fig. 5B) containing 6 bulge/internal/hairpin loops, IsRNA1 provides better predictions (best of top 3 predictions) with RMSDs of 4.12 Å (2d1a) and 6.89 Å (1p5p) compared to RMSDs of 10.71 Å (2d1a) and 11.17 Å (1p5p) by SimRNA and 18.57 Å (1p5p) by iFoldRNA (see SI Table S9). The result for 2d1a by iFoldRNA cannot be obtained because the iFoldRNA server does not deal with multiple chains. The RMSDs for those large stem-loop structures mainly come from the accumulative deviations caused by mis-configured loops containing complicated interaction networks.

Figure 5.

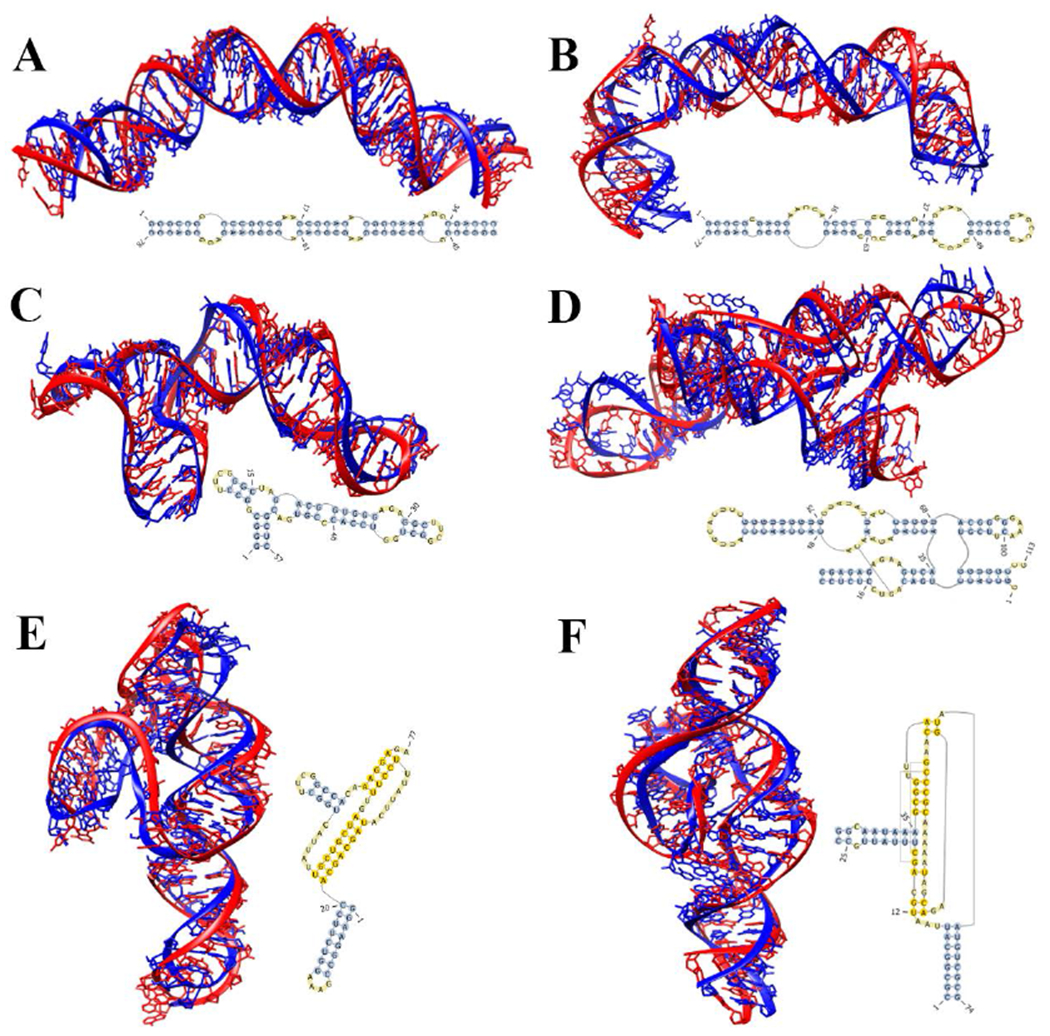
Predicted 3D structures by IsRNA1 model for several representative RNA molecules. (A) 78-nt HIV-1 dimerization initiation site in the extended-duplex dimer⁷⁷ (PDB ID: 2d1a), (B) 77-nt HCV IRES domain II⁷⁸ (PDB ID: 1p5p), (C) 57-nt rRNA fragment in the S15-rRNA complex⁷⁹ (PDB ID: 1dk1), (D) 21-nt RNA substrate and 92-nt RNA hairpin ribozyme complex⁸⁰ (PDB ID: 1m5o), (E) 77-nt PreQ1-ll riboswitch⁸³ (PDB ID: 5d5l), and (F) 74-nt twister ribozyme⁸⁴ (PDB ID: 4qjh). The predicted structures of lowest RMSD from the top 3 predictions given by IsRNA1 (in red) are superposed onto the native structures (in blue). Secondary structures used to impose constraints on IsRNA1 modeling are also. RMSDs over all heavy atoms are 4.12 Å, 6.89 Å, 5.37 Å, 5.99 Å, 6.54 Å, and 4.20 Å, respectively.

Multi-way junctions.

For 3D structure prediction of multi-way junctions, a major difficulty lies in the spatial arrangement of helices which can involve coaxial stacking interactions between helices. The underlying difficulty is the prediction of the non-canonical base-pairing interactions in multibranched loops. For 43 multi-way junctions tested here, as shown in Table 1, IsRNA1 performs better than SimRNA and iFoldRNA, as shown by the average RMSDs for the top 1 prediction given by these three models: 12.93 Å (IsRNA1), 14.91 Å (SimRNA), and 15.85 Å (iFoldRNA), respectively. Regarding the other two structural quality metrics, IsRNA1 also shows the highest average INF_all of 0.71 (compared to 0.69 for SimRNA and 0.64 for iFoldRNA) and the lowest average clash score of 4.2 (compared to 143.3 for SimRNA and 180.7 for iFoldRNA). When the top 3 predictions by IsRNA1 are considered, the average RMSD is improved from 12.93 Å (top 1 prediction) to 10.88 Å (the best of top 3 predictions), while the average INF_all and clash score are nearly unchanged (see Table 1). For SimRNA and iFoldRNA, the same tendencies are observed for the average structural qualities summarized in Table 1. Therefore, for all the CG models, consideration only the top 1 structure may miss the best structure, and multiple candidates, such as top 3 structures, are recommended for 3D structure prediction of RNA junctions. Particularly, for the 3-way junction rRNA fragment in the S15-rRNA complex⁷⁹ (PDB ID: 1dk1, 57 nts) shown in Fig. 5C, IsRNA1 performs better than SimRNA and iFoldRNA in terms of RMSDs of 5.37 Å (IsRNA1), 6.38 Å (SimRNA) and 6.46 Å (iFoldRNA), respectively. And for the 4-way junction RNA substrate and hairpin ribozyme complex⁸⁰ (PDB ID: 1m5o, 113 nts) shown in Fig. 5D, IsRNA1 performs better than SimRNA as shown by the RMSDs of 5.99 Å (IsRNA1) and 12.05 Å (SimRNA), respectively, while iFoldRNA cannot deal with this RNA of multiple chains. As it is shown, the configuration of junction loops, which is controlled by the interloop noncanonical base pairing interaction network, plays a key role in determining of the spatial arrangement of helices and dominates the predicted RMSD value.

Structures containing tertiary interactions.

Due to the lack of suitable templates in the database, 3D structure prediction for RNAs containing long-range tertiary interactions remains a challenge for many successful template-based approaches, including MC-sym⁸¹, Vfold3D⁴⁸, and 3dRNA⁸². Thus, the development of new template-free approaches, such as the present IsRNA1 model here, is much needed for understanding structures and functions of many important RNAs, such as riboswitches³. For 43 cases containing long-range tertiary interactions in the large-scale benchmark “dataset-130”, the average RMSD for (the top 1)/(the best within the top 3) structure predicted by IsRNA1 is 9.89/9.05 Å, which is smaller than the average RMSDs 11.75/10.28 Å and 11.60/11.22 Å predicted by SimRNA and iFoldRNA, respectively. Similarly, a moderate improvement in RMSD for the top 3 predictions from 9.89 Å to 9.05 Å by IsRNA1 demonstrates the necessity to consider multiple candidates for RNAs containing long-range tertiary interactions. Moreover, the average INF_all of 0.75 for the best of the top 3 predictions by IsRNA1 is higher than 0.71 by SimRNA and 0.66 by iFoldRNA, and the average clash score of 5.7 for the best of the top 3 predictions by IsRNA1 is lower than 147.9 by SimRNA and 175.2 by iFoldRNA. For example, for the 77-nt PreQ1-N riboswitch⁸³ (PDB ID: 5d5I, see Fig. 5E), the RMSD of the best of top 3 predictions by IsRNA1 is 6.54 Å, which is smaller than 16.48 Å by SimRNA and 14.08 Å by iFoldRNA. As another example, for the 74-nt twister ribozyme⁸⁴ (PDB ID: 4qjh, see Fig. 5F), IsRNA1 also shows improved predictions with an RMSD of 4.20 Å compared with 13.39 Å (by SimRNA). We note that iFoldRNA does not treat this multi-chain RNA. In determining of RNA 3D structure with tertiary interactions, the tertiary base pair constraints play a key role on global folding profile, while the interloop interaction networks (contain rich noncanonical base-pairing interactions) dominate the configuration of local segments. As shown in Fig. 5E and 5F, although the 3D structures predicted by IsRNA1 show similar global folds to the native structures, there are several misplaced segments associated with the interaction networks in the loops.

Compared with the initial 3D structures generated by Vfold3D/VfoldLA (see SI Table S10), the best model among the top 3 predictions by IsRNA1 generally improves with the average RMSD decreasing from 5.87 Å to 5.15 Å for stem-loop structures and from 10.68 Å to 9.05 Å for RNAs containing long-range tertiary interactions. These results suggest that the IsRNA1-bases simulation can indeed refine the template/loop-based models and the Vfold3D/VfoldLA template-based models improve folding efficiency. Furthermore, for the test multi-way junctions, the Vfold3D/VfoldLA-predicted models have an average RMSD of 9.27 Å (see SI Table S10) better than the final predictions (the best of top 3) by IsRNA1 with an average RMSD of 10.88 Å. The results suggest that for RNA junction structures, further optimization for the initial template-predicted and the IsRNA1 simulation-generated 3D structures would be useful.

Both IsRNA1 and SimRNA models can fold multi-strand. For 35 test cases containing multiple chains in the large-scale benchmark dataset, as summarized in Table 1, the IsRNA1 approach gives lower average RMSDs (8.72 Å vs. 12.10 Å for top 1 prediction), a slightly better average INF_all (0.78 vs. 0.77), and a smaller average clash score (3.4 vs. 137.7).

RNA 3D structure prediction for RNA-Puzzles.

As a collective and blind test for RNA 3D structure prediction, the “RNA-Puzzles” (http://www.rnapuzzles.org/) provides a primary platform for the assessment of leading-edge RNA structure prediction programs. Up to now, 21 challenges have been published^85–88 with RNA size ranging from 41 to 188 nts, covering most of the typical RNA structural topologies and motifs. To further explore the boundary of IsRNA1 for 3D structure prediction, we used the 2D structures extracted from the native folds as constraints and the Vfold3D/VfoldLA generated 3D structures (top 3 structures) as the initial states to run IsRNA1-guided MD simulations on the RNA-Puzzles challenge problems (see SI Table S7 for the simulation details). If available, highly scored (highly reliable) templates identified by Vfold3D⁴⁸ from known homologous structures (for challenges #4, #9, and #18) or given in advance as known information (for challenge #2) were also used as constraints in IsRNA1 structure modeling. For each challenge problem, we selected the top 5 predictions from the IsRNA1 simulation results.

As shown in Table 2, based on CG MD simulations only, for 12 of the 21 challenges, IsRNA1 provides better or comparable predictions (ΔRMSD < 0.5 Å) compared to the original Chen group results. And for 8 of them, predictions by IsRNA1 are better than or comparable to the best models predicted by all the groups. For example, for the Varkud satellite ribozyme⁸⁹ (puzzle #7, 185 nts, PDB ID: 4r4p) containing three 3-way junctions and the 5-hydroxytryptophan aptamer⁹⁰ (puzzle#9, 71 nts, PDB ID: 5kpy) containing tertiary interactions, IsRNA1 provides improved 3D structure predictions of RMSDs of 16.27 Å and 5.01 Å relative to 20.37 Å (23.48 Å) and 6.06 Å (6.06 Å) for the best model from all the groups (from the Chen group), respectively. To some extent, the overall performance of IsRNA1 (an average RMSD of 10.48 Å for the 21 challenges) compared to the best model from all the groups (an average RMSD of 6.59 Å for the 21 challenges) is expected, because template-based algorithms, template-free approaches, data-driven models, and even human efforts are involved in the submissions by all the groups and the performance of the different approaches varies for the different challenges^85–88.

Table 2.

The results for the IsRNA1-predicted RNA 3D structures for RNA-Puzzle challenges using sequences and the native 2D structures as input. The all heavy-atom RMSDs for the best candidates from the top 10% lowest energy structures (column “Best of top 10% structure”) and from the top 5 predictions by IsRNA1 (column “Best of top 5 predictions”) are shown for each challenge. For comparison, the best RMSDs for all the submissions (column “Best of all groups”) and for the Chen group submissions (column “Best of Chen group”) are also given. Predictions with RMSD less than or comparable to (ΔRMSD < 0.5 Å) the best of Chen group are marked in boldface, and those better than or comparable to the best of all the groups are printed in italics.

Puzzle (PDB id)	Length (nts)	Topology	Best of all groups	Best of Chen group	Best of top 10% structures	Best of top 5 predictions
1 (3mei)	46	stem-loop	3.41	4.33	2.33	3.12
2 (3p59)a	100	stem-loop	2.50	2.83	2.12	2.23
3 (3owz)	84	3-way junction	7.01	7.01	5.30	5.57
4 (3v7e)b	126	tertiary interaction	3.35	3.35	2.43	3.35
5 (4p8z)	188	tertiary interaction	8.97	25.61	24.54	27.23
6 (4gxy)	168	tertiary interaction	11.60	22.13	23.94	34.22
7 (4r4p)	185	3-way junction	20.37	23.48	14.68	16.27
8 (4l81)	96	tertiary interaction	4.80	11.29	12.43	14.25
9 (5kpy)c	71	tertiary interaction	6.06	6.06	4.32	5.01
10 tBox (4lck)	96	stem-loop	6.02	13.21	9.16	14.10
11 X-ray (5lys)	57	stem-loop	4.99	4.99	5.75	8.33
12 (4qlm)	125	tertiary interaction	10.06	16.06	12.15	14.99
13	71	tertiary interaction	5.55	6.55	4.67	7.61
14 Bound (5ddp)	61	3-way junction	5.12	7.64	6.28	6.97
14 Free (5ddo)	61	3-way junction	6.89	9.36	7.66	10.13
15 (5di4)	68	3-way junction	7.12	8.51	6.61	7.26
17 (5k7c)	62	tertiary interaction	7.16	9.45	10.67	11.78
18 (5tpy)d	71	tertiary interaction	3.21	3.74	2.72	3.87
19 (5t5a)	62	3-way junction	5.52	5.52	4.08	5.19
20 (5y85)	68	4-way junction	4.70	13.37	11.17	13.56
21 (5nz6)	41	pseudoknot	3.93	3.83	4.01	5.02
Average			6.59	9.92	8.43	10.48

^a: 3D coordinates of the nucleotides in the four inner strands were provided and kept rigid in the simulation.

^b: template extracted from 3IQP was used for nucleotides 1-48, 87-102, and 113-126.

^c: template extracted from 3DS7 was used for nucleotides 19-27 and 47-55.

^d: template extracted from 4PQV was used for nucleotides 1-24 and 42-50.

To explore the underlying reasons for the fair performance of IsRNA1 on 3D structure prediction of RNA-Puzzles challenges, we analyze the sampling (whether the near-native conformations are sampled) and scoring (whether the native/near-native structures are identified as top candidates) issues. Specially, the best candidate of the lowest RMSD in the top 10% low-energy structures, which were used for conformational clustering, was examined (see Table 2). For 11 (17) of the 21 challenges, IsRNA1 can sample better or comparable conformations (ΔRMSD < 0.5 Å) relative to the best model from all the groups (from the Chen group) in the top 10% low-energy structures. For the 10 challenges where IsRNA1 fail to sample conformations close to the best model from all the groups, there are five cases of quite large size and complicated topologies, including puzzle #5 with 188 nts, #6 with 168 nts, #8 with 96 nts, #10 with 96 nts, and #12 with 125 nts. For these large-size RNAs, the sampling issue is challenging even with the 2D structure as the input constraint for the simulations.

Blind screening of good predictions in RNA-Puzzles by IsRNA1 protocol.

As indicated by the blind test results in RNA-Puzzles^85–88, the performances of computational approaches in blind tests/challenges vary with RNAs. For instance, for the recent two challenges #20 and #21, the INF_wc values of the corresponding 68 and 41 submitted 3D models from all the participating teams vary in the range [0.0, 1.0] and [0.39, 0.91], respectively, and RMSDs vary in the range [4.7, 25.4] Å and [3.8, 18.1] Å, respectively. Thus, if the target native structure at atomic resolution is experimentally unavailable, a filtering protocol to identify good predictions from various candidate structures generated by different computational approaches would be highly valuable. To this end, a blind screening protocol based on IsRNA1 model was developed here to recognize good predictions of relatively lower RMSDs and higher INF_WC values from the structure pool without the knowledge of the native structures.

Using the 3D candidate structures as the initial structures and their own 2D structures as constraints, 5 duplicates (with different initial velocities) of short 0.5-ns conventional MD simulations were run in the IsRNA1 model for each 3D model (simulation details are given in SI Table S7). In such a way, not only the candidate structure but also its neighboring conformations having an RMSD of < 5 Å from the concerned structure were collected to calculate a conformational ensemble-averaged energy for blind assessment of a candidate structure. Compared with energy evaluation (scoring function) based on a single candidate structure, the conformational ensemble-averaged energy as a filtering protocol has two main advantages. First, it can eliminate the possible deviations/errors of local geometries and/or possible steric overlaps between atom contacts. Second, it can possibly capture the effect of loop flexibility.

The IsRNA1 blind screening protocol above was tested using the RNA-Puzzles challenges (details for challenges are summarized in SI Table S11). For instance, for the 41 submitted predictions in the recent challenge #21 shown in Fig. 6A, Pearson correlations between the conformational ensemble-averaged energy E and RMSD (R = 0.33) and between E and INF_WC (R = −0.30) are calculated. As the value of INF_WC is directly related to the 2D structure of the model, a higher INF_WC value means a better predicted 2D structure and a roughly lower folding free energy (a negative correlation coefficient between E and INF_WC). Therefore, the quality of a 3D model measured by INF_WC, an assessment of the 2D structure prediction, is expected to be directly coupled with the energy E. As shown in the bottom panel of Fig. 6B, the Pearson correlation coefficient R(E, INF_WC) of the submitted models in 10 typical RNA-Puzzles challenges ranges from −0.23 to −0.86, and the average correlation is −0.59. Complete results for all the challenges are given in the SI Table S11. The strong correlations R(E, INF_WC) indicate that, based on the IsRNA1 energies, good predictions of relatively higher INF_WC values or of more accurate 2D structures can be selected/filtered from the submitted candidate models.

Figure 6.

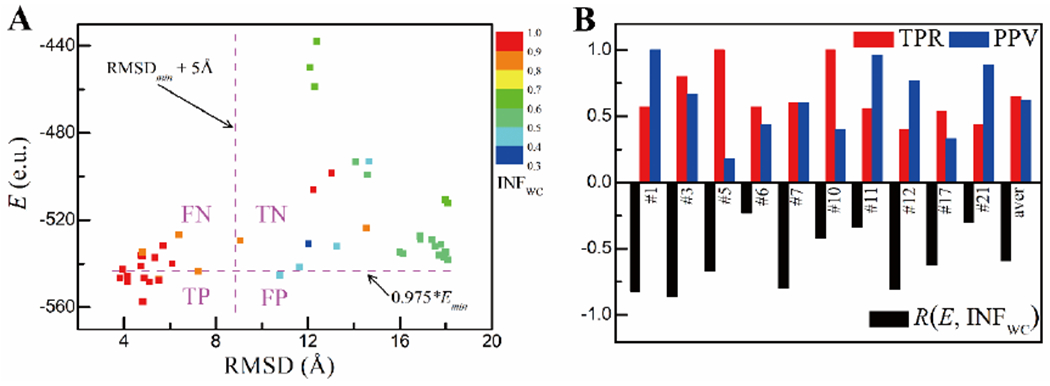
Blind screening of good predictions in RNA-Puzzles challenges by IsRNA1 protocol without knowledge of native structures in prior. (A) The plot of RMSDs to energies given by IsRNA1 (E, with e.u. as energy unit) for all the submitted models in challenge #21, along with the INF for canonical base-pairing interactions (INF_WC) displayed in a color map. The RMSD threshold (RMSD_min + 5 Å) used to classify relatively good predictions and the predefined energy value (0.975 * E_min) used to predict good models are shown in magenta dash lines, where RMSD_min is the lowest RMSD of all submitted structures relative to the native structure, and E_min is the lowest energy evaluated by IsRNA1 protocol from all the predictions. TP, TN, FP, and FN are the numbers of true positives, true negatives, false positives, and false negatives, respectively. (B) Performances of the IsRNA1 protocol in blind screening of the submitted models in a series of RNA-Puzzles challenges without prior knowledge of the native structures are characterized by the Pearson correlation coefficient R(E, INF_WC) between the evaluated energies and INF_WC values (bottom panel), and by sensitivity TPR=TP/(TP+FN) and precision PPV=TP/(TP+FP) (top panel).

Here, we consider our algorithm as a classification problem to filter good structures of lower RMSDs from a pool of candidate structures. Specifically, the candidate models are classified into good and poor classes based on the RMSDs relative to their native structures. The good class contains the best model of the lowest RMSD_min as well as other comparable models of RMSDs not greater than RMSD_min + 5 Å (see Fig. 6A), and the remaining models are considered as the poor class. In this way, on average about 35% of the candidate models are classified as good models for all the 19 RNA-Puzzles challenges. While the IsRNA1 protocol predicts the class of a model according to a predefined energy threshold 0.975 * E_min. The model of the lowest energy E_min and those of energies E_i ≤ 0.975 * E_min are predicted into the good class, and the remaining models are predicted into the poor class (see Fig. 6A). On average, about 34% of the candidate models are predicted as good structures according to the above energy-based classification (see SI Table S11 for details). The performance of the above IsRNA1-based screening protocol was quantified using sensitivity TPR and precision PPV (see the top panel in Fig. 6B). For example, for challenge #21 illustrated in Fig. 6A, 39% of the 46 models (of RMSDs 3.83~18.09Å) are classified as good models (with RMSDs from 3.83 to 7.24 Å), and 20% of the models are predicted as good models by our IsRNA1-based screening protocol. The sensitivity score TPR=0.44 means that 44% of true good models are selected by the filtering protocol and the precision PPV=0.89 means that 89% of the IsRNA1-predicted good models are true good ones. For the 10 RNA-Puzzles challenges shown in Fig. 6B, moderate (TPR=0.4) to high (TPR=1.0) sensitivity values are observed, while the precision also ranges from the moderate (PPV=0.33) to high (PPV=1.0) values except for challenge #5 (PPV= 0.18 and TPR= 1.0). And the average sensitivity and precision are TPR= 0.65 and PPV= 0.62, respectively. Overall, the results indicate that the IsRNA1-based blind screening protocol can identify good models of relatively lower RMSDs (good 3D structures) and relatively higher INF_WC values (good 2D structures) from a pool of candidate models without knowledge of the native structures.

4. DISCUSSION

Over the years, remarkable advances in the development of CG models for RNA structure prediction have been made^8,11, however, the challenges for large RNAs of complicated topologies remain. An accurate scoring function or force field for CG modeling of large RNAs of complicated topologies is required not only for the evaluation of the structural candidates, but also for guiding effective sampling. Here, based on MD simulation for conformational sampling and statistical potentials extracted from the known RNA structures as the force field, we developed an upgraded CG model, the IsRNA1 model, suitable for large and complicated RNA studies. The IsRNA1 model has several advantages.

1. Instead of simple harmonic potentials in conventional force fields functions for local structural variables (including bond stretching, bond angle, and torsion angle), a set of much more sophisticated energy functions are used to capture a broader conformational sampling for the backbone, which is particularly valuable for modeling of large and complicated RNAs.

2. The simulated reference state approach for the statistical potential in IsRNA1 allows the consideration of correlations between different energy terms as well as the inherent chain connectivity and the excluded volume effects.

3. Because the energy function is extracted from simulated conformational distributions (over the energy landscapes), the IsRNA1 energy function may account for both native and nonnative interactions.

4. Compared with the fixed ideal A-form helix in many template-based approaches^48,85,91, a set of combined energy functions in Eq. (2) can accurately describe canonical base-pairing and base-stacking interactions for the sampling of flexible helical conformations.

5. The MD simulations, including conventional, simulated annealing, and replica-exchange techniques, in IsRNA1 model is implemented in the open source software LAMM PS⁴⁷ (with modified source code), and a variety of restraints can be readily incorporated into the conformational sampling through the simulation platform.

Taken together, these advantages make the IsRNA1 a promising CG model to study the folding of RNAs of relatively large size and complicated structural topologies.

The IsRNA1 model was extensively tested on de novo folding of small RNAs, tertiary structure folding for relatively large RNAs given the 2D structures, 3D structure prediction for a large-scale benchmark dataset, and blind screening of 3D structural candidates. In detail, a blind screening protocol based on the IsRNA1 force field can identify good 3D structures of relatively lower RMSDs and higher INF_WC values from a pool of structural candidates predicted by different computational models. These results support the validity of the IsRNA1 force field as a potentially reliable scoring function. Based on the enhanced MD simulations to sufficiently sample the conformational space, the IsRNA/IsRNA1 model can de novo fold 15 small RNA molecules (≤ 36 nts) into the near-native structures with an average RMSD of 2.29 Å, and fold 65 medium-sized RNAs (22-78 nts) into the native-like 3D structures with an average RMSD of 5.93 Å given the native 2D structure constraints. Compared with previous CG models, though different models show different performances for the different RNA structures, IsRNA1 shows its promise to provide improved predictions (as indicated by the lower average RMSD in Fig. 4) for RNAs of relatively large size (>40 nts) and more complicated topology, such as long-range tertiary interactions, while maintaining similar overall performance to other models for other RNAs, including small stem-loop and H-type pseudoknot structures. These results confirm the importance of the use of rigorous reference states and accurate descriptions of base-pairing and base-stacking interactions in the development of CG force fields.

Using templated-based 3D structures (with 2D structures as input) as initial states for the simulations, the Vfold3D/VfoldLA-IsRNA1 pipeline can improve the sampling efficiency in the simulations toward the native structure and refine the predictions by Vfold3D/VfoldLA for relatively large RNAs. Based on 130 RNAs of relatively large size (40-161 nts) and different structural topologies, a large-scale benchmark test for RNA 3D structure predictions by the Vfold3D/VfoldLA-IsRNA1 pipeline further confirms the improved performance of the IsRNA1 model for large RNAs as compared with other existing CG models. Specifically, for large stem-loop structures, multi-way junction structures, and RNAs containing long-range tertiary interactions, IsRNA1 provides improved predictions with lower RMSDs, higher INFs, and much lower clash scores, while the intricate interaction networks in loops pose a challenge for further improvement of 3D structure prediction. Moreover, for the real-world challenges in RNA-Puzzles, IsRNA1 is able to sample improved or comparable results than the best predictions of all the submissions from the different approaches for 8 of 21 challenge problems solely based on CG MD simulations with 2D structures as constraints, and identify the near-native folds for 8 cases. In summary, with the continuous improvements in force field, sampling method, and model selection strategy, the current IsRNA1 model may provide a useful new approach for RNA structure prediction.

Limitations and future improvements of the IsRNA1 model.

Future improvements in IsRNA1 would focus on the further refinement of non-canonical base-base and base-backbone interactions, the design of more efficient conformational sampling techniques for large RNA molecules, and the consideration of the effects of in vivo environment.

First, unlike high-resolution CG models, such as SimRNA, the 2-bead CG representation for pyrimidine bases in the current IsRNA1 model cannot fully capture the various non-canonical base-pairing interactions in the cis-/trans-conformations. Thus, for many small stem-loop and H-type pseudoknot structures involving non-canonical interaction networks in the loops, the IsRNA1 model performs worse than SimRNA. To circumvent this limitation in the future, in the next generation of the IsRNA/IsRNA1 model, a more accurate CG representation is required to enable more accurate descriptions of various non-canonical base-pairing interactions. Moreover, in construction of an accurate force field for both canonical and non-canonical base-pairing interactions, we may consider the statistical frequency and physical strength simultaneously when parameterizing the energy functions, especially for the rare non-canonical interactions.

Second, due to the lack of atomic details and the simplification of the free energy landscape in the CG representation, simulations in CG model may lead to mispredicted configurations for junction loops and misplaced loop segments in complicated structures. A possible remedy for future improvement would be to resample the misfolded segments at the all-atom level with sufficient conformational sampling, such as the stepwise Monte Carlo method with a unique add-and-delete move set to predict non-canonical interactions⁹².

Third, for RNA puzzles of large size and complicated topology, CG MD simulations in the IsRNA1 model may suffer from insufficient conformational sampling even with 2D structure constraints. In such cases, integration of various experimental data⁹³, such as properly interpreted SHAPE reactivity²⁹, multidimensional chemical probing data⁹⁴, cryo-EM maps⁹⁵, into the IsRNA1 model is feasible and may significantly improve the sampling efficiency and accuracy for 3D structure prediction.

Finally, in the future development of the model, we would further calibrate the energy function using experimental thermodynamic data such as Turner parameters for RNA helices and simple loops. If successful, we can apply the model to explore the folding kinetics from extended coil state for large RNAs and study the folding thermodynamics from the nucleotide sequence.