The structural plasticity of nucleic acid duplexes revealed by WAXS and MD

The structural diversity of nucleic acid duplexes reflects the critical roles of sequence, ions, and waters.

Abstract

Double-stranded DNA (dsDNA) and RNA (dsRNA) helices display an unusual structural diversity. Some structural variations are linked to sequence and may serve as signaling units for protein-binding partners. Therefore, elucidating the mechanisms and factors that modulate these variations is of fundamental importance. While the structural diversity of dsDNA has been extensively studied, similar studies have not been performed for dsRNA. Because of the increasing awareness of RNA’s diverse biological roles, such studies are timely and increasingly important. We integrate solution x-ray scattering at wide angles (WAXS) with all-atom molecular dynamics simulations to explore the conformational ensemble of duplex topologies for different sequences and salt conditions. These tightly coordinated studies identify robust correlations between features in the WAXS profiles and duplex geometry and enable atomic-level insights into the structural diversity of DNA and RNA duplexes. Notably, dsRNA displays a marked sensitivity to the valence and identity of its associated cations.

INTRODUCTION

The tight coupling of structural changes to biological function, well recognized for proteins, is also important for DNA and RNA. For these molecules, double-stranded duplexes serve as fundamental building blocks of their architectures. DNA is composed of long double-stranded helices that undergo large-scale structural changes upon condensation or complexation with protein partners. RNA structures are more diverse, containing short double-stranded helices connected by linkers that impart flexibility. As a result, RNAs can fold to complex structures with the aid of cations and ligands (1–3).

The common perception that nucleic acid duplexes are homogeneous helices of only varying length is an appealing but incomplete view of the structural diversity of double-stranded DNA (dsDNA) or double-stranded RNA (dsRNA). This perspective misses subtle, yet critical structural variations. High-resolution crystal structures and solution studies provide considerable evidence for solvent- or partner-induced structural variations in double-stranded nucleic acids (dsNAs). For example, B-form–to–A-form transitions occur upon dehydration of dsDNA (4) or upon protein binding (5, 6). Sequence-dependent effects are also important and likely serve as a biological signal for binding site recognition (7, 8). Known correlations of structure with sequence include the minor groove widening of A tracts (9–13) or the appearance of curvature in G tracts (14, 15). The latter examples illustrate the importance of sequence-structure relationships in modifying local structure, crucial for understanding how dsNAs interact with other molecules in the cell.

Much insight into the dependence of duplex geometry on sequence has been derived from atomically detailed x-ray crystallographic studies (15). Care must be taken when interpreting these results as crystallization conditions may affect the duplex structure and cation hydration levels (16–18). Solution studies may more closely mimic cellular conditions in addition, offering the potential to reveal dynamic couplings between solvent distributions and nucleic acid structures. Numerous solution methods have already been successfully applied to characterize dsNAs. For example, the mobility of duplexes inferred by electrophoretic data serves as a practical method for differentiating the structural variations with limited resolution (13, 19–21). Single-molecule fluorescence resonance energy transfer measures structural variations in dsDNA structure (22). Nuclear magnetic resonance (NMR) spectroscopy with residual dipolar couplings is able to determine high-resolution nucleic acid structures. DNA’s global and local structural changes such as bending and kink formation have been determined using NMR (10, 13, 23). Given the differences in sample preparation, conflicting conclusions are sometimes reached between x-ray crystal structures and those derived from solution studies for dsDNA (24, 25). Similarly, x-ray crystallography and NMR spectroscopy reveal some systematic differences in dsRNA structures. The most notable is the substantially larger major groove widths (GWs) observed in NMR-derived structures (26).

The sequence-dependent variations in dsNA structures provide strong motivation to investigate the molecular origins of these effects. Different mechanisms are proposed to explain sequences that result in intrinsically bent DNAs (14, 27, 28). The wedge and junction models highlight the importance of distinct stacking preferences of A:T and G:C base pairs (bp) (29, 30), while electrostatic collapse models focus on the role of cation distribution (14, 28). All these models are compatible with each other (14), suggesting that both nucleic acid and solvent parameters must be considered for completeness. Computer simulations and theoretical studies have been used to decipher the physical principles of dsDNA bending (12, 31–34).

As a result of these studies, some correlations between sequence and structure have been established for dsDNA (14). Proving the generality of these rules requires more solution studies with diverse sequences and varied salt conditions. In dsRNA, on the other hand, the basic principles that dictate structural variations remain uncharted. The dynamic nature of RNA duplexes and their high sensitivity to the solvent add different levels of complexity to the problem. Solution studies of different sequences and salt conditions are required to establish and test correlations.

The main challenge in many experimental solution studies of these effects is the lack of sharp spatial resolution. Past studies on DNA show the importance of this type of information in deciphering the sequence variability of dsNA molecules, an area that needs further development (35). However, a promising line of study integrates experimental and computational approaches to study RNA conformations (36–43). Simulations provide atomic-level spatial resolution for macromolecular structure and dynamics while closely correlated experiments can be used to finely tune the simulation parameters (36, 38, 44) or guide the efficient exploration of conformational space sampled (37, 40, 43). For some experimental methods, strong signals from nucleic acid backbones can be used to bolster simulation results, effectively bypassing some of the resolution challenges imposed by the solution method.

Here, we use solution x-ray scattering at wide angles (wide-angle x-ray scattering or WAXS) to measure the structural ensemble of dsDNA and dsRNA duplexes with different sequences and in different solvent (salt) conditions. The ability of WAXS to access near-atomic resolution in varied salt conditions makes it an ideal tool to investigate the subtle differences between helix topologies. As a complement to WAXS, we used molecular dynamics (MD) simulations to create three-dimensional (3D) models of duplexes and to elucidate physical principles governing sequence-dependent changes in duplex geometry. This integration of WAXS and MD yields an ensemble of molecular conformations that are in excellent agreement over a broad range of sequence and solvent conditions. Furthermore, the agreement between computed and measured profiles was used as a criterion to assess the accuracy of the computational approach. The atomically detailed information that benefits from the synergy of these approaches allowed us to derive insights into the structure and dynamics of these duplexes. dsDNA synthesized with A and G tracts did not exhibit bending as was expected from crystallographic studies. The bending of dsRNA was observed in the presence of monovalent cations. Last, our analysis of cation distributions readily available to molecular simulations suggests a mechanism that explains the structural variations of dsDNA and dsRNA.

RESULTS

Our integrated approach, combining Sample-and-Select (SaS) MD with measurement by WAXS, provides structural properties of dsDNA and dsRNA duplexes. It is detailed in Materials and Methods and summarized in Fig. 1. Here, we describe the main findings based on this methodology.

Fig. 1. The computational approach used to resolve the structures of nucleic acid duplexes.

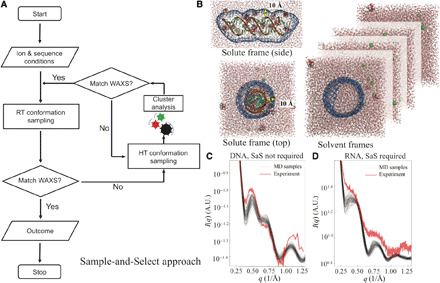
(A) SaS approach with enhanced sampling at higher temperature and selection based on agreement with experimental WAXS profiles. The feedback loop is triggered when the customized metric in Eq. 6 of all the sampled conformations is greater than 10.0. (B) Illustration of the molecular envelope constructed from a 3D probability density isosurface 10 Å from the RNA surface to encompass the solvent/ion shell. The same envelope was applied to solvent systems to compute the scattering amplitudes to be subtracted. (C) The WAXS profiles from experiment (red) and MD simulations with starting B-form conformation (black) of DNA duplex. Here, the sampling captures features of the experimental data. The selection feedback is not necessary. (D) Same as (C) for an RNA duplex. Here, none of the WAXS profiles from MD simulations (black) agree with experimental data (red). The SaS approach is required to enhance sampling to identify a plausible starting conformation.

Structural correlations

The correlation map reflects the relationship between profiles computed from simulated structures and the real space features of the duplexes. It represents a powerful approach for interpreting curves or variations in curves by correlating structures in the molecule with specific features in the scattering profile. Furthermore, comparison of a measured profile with simulation predictions can highlight areas of disagreement, providing essential feedback to the computation. The correlation map between all the RNA duplex structural parameters and intensity deviations from q = 0.1 to 1.25 Å⁻¹ is shown in Fig. 2A. The parameters with high correlation to scattering angles (∣ρ∣> 0.5) are highlighted in bold, while those with low correlation (∣ρ∣< 0.25) are in gray. We first identify the important structural parameters that define a helical geometry. Consistent with previous studies on shorter RNA duplexes (45), structural periodicities, such as twist, GWs, and helical radius, persist in the longer RNA duplex system, manifesting as WAXS features. The major GW has the highest correlation to curve features and provides key insight into variations in the experimental WAXS profiles. Note that there is almost zero correlation between the base-pair geometries because the solution x-ray scattering is mostly sensitive to the phosphate backbones and structural characteristics beyond d_min = 2π/q_max ≈ 5 Å. Second, from the correlation stripes, we can make structural inferences on a certain parameter. For example, at about q = 0.65 Å⁻¹, the helical radius exhibits positive correlation to the normalized deviations; i.e., the more negative the deviation, the smaller the helical radius. To illustrate the insight provided by this approach, Fig. 2B shows both the experimentally acquired scattering profile of RNA duplex in 400 mM KCl (red) along with 1000 profiles from the intermediate MD simulations in the SaS approach (gray). For these data (Fig. 2B), no single conformation accurately recapitulates the curve; however, from the correlation information in the left panel, it is clear that the helical radius of the real molecule in vitro must be larger than in any of the 1000 conformations. This inference is also supported by the same reasoning at different scattering angles. Note that Fig. 2B only serves as an illustration for qualitatively interpreting the structural patterns from the correlation map in Fig. 2A. Because no single structure agrees with the experimental data, more rounds of SaS are required. The maps of deviation-deviation correlation for RNA and DNA duplexes are shown in fig. S2, while the DNA structural-deviation correlation is shown in fig. S3.

Fig. 2. Mapping WAXS features to real space structural details.

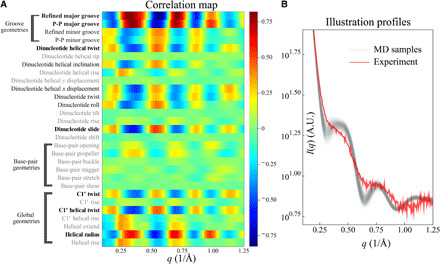
(A) The correlation map between RNA duplex geometries and normalized deviations between experiment and simulation (Eq. 11). The helical parameters with high correlations (∣ρ∣ > 0.5) are highlighted in boldface. (B) WAXS profiles of intermediate MD conformations and experimental data for interpreting the correlation map. Using the correlation map, we qualitatively interpret conformations that correspond to experimental data, despite the mismatch at this intermediate stage. For the profiles shown, the models clearly do not accurately recapitulate features at q values near 0.25 and 0.6 Å⁻¹, suggesting that the intermediate simulations do not capture the correct groove geometries and more rounds of SaS are required. See the main text for details. A.U., arbitrary units.

DNA conformations

We first applied our coupled MD-WAXS approach to study sequence-dependent variations in DNA duplexes. As described in Materials and Methods, simulations of DNA, beginning in the B-form, are performed in simulation boxes containing different salts, and results are compared against experimental data. Figure 3 shows the experimental solution x-ray scattering data for Mixed-sequence DNA (MixDNA) in 400 mM KCl (purple), 10 mM MgCl₂ (blue), and duplex DNA made from homopolymeric chain of dA₂₅ and its complementing sequence (ATDNA) in 100 mM NaCl (orange). This wide range of solution conditions was selected as a robust test of the ability of simulation to reproduce experimental data. It is immediately clear that the differences in the experimental profiles suggest distinct DNA duplex conformations in solution. The first sets of simulations were performed using the room temperature (RT) B-form conformations and the physical models mentioned in Materials and Methods. The computed scattering profiles closely resemble the measurements. In other words, traditional MD modeling for both DNA duplexes provides good agreement with experiment and does not require any feedback or enhanced sampling to reach it. The RT MD-sampled conformations are depicted as the gray spread in Fig. 3 (A to C). Within each MD-sampled ensemble, we identified the conformation $\widehat{k}$ that best agrees with experimental data using Eq. 6. Figure 3 (D to F) shows the computed x-ray scattering profiles of the single best-fitting conformation, as well as experimental data for MixDNA and ATDNA, respectively. The insets emphasize the sensitive wide-angle regime. On the basis of these results, we find that MixDNA resembles the canonical B-form duplex. In contrast, Fig. 3E shows that ATDNA adopts a different (non-B) helical conformation that exhibits unique features in the wide-angle regime. This non-B structure was accessed by the RT computations, beginning from the B-form. Structures of the best-fitting conformations of both DNA sequences are aligned and shown in Fig. 3J. The ATDNA adopts a narrower yet consistent (from 5′ to 3′ end) minor GW. This enhanced helical periodicity manifests as the peak at q = 0.75 Å⁻¹. On the other hand, the GWs for mixed-sequence DNA duplex vary with residue identity, which, in turn, creates or extinguishes wide-angle features in the experimental profile.

Fig. 3. Solution x-ray scattering profiles of DNA duplexes from experiment and simulation at different salt conditions.

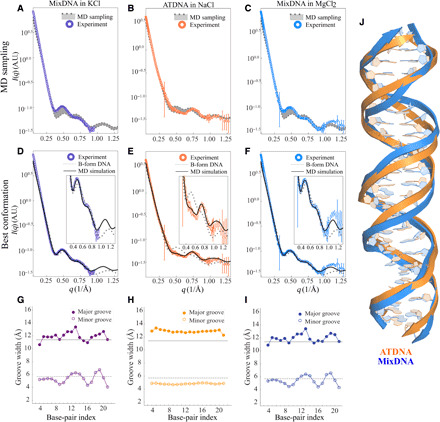
(A) MixDNA duplex in 400 mM KCl, (B) ATDNA in 100 mM NaCl, and (C) MixDNA in 10 mM MgCl₂. Conformations sampled from MD simulations (without SaS approach) are shown in the shaded area. (D) to (F) are the same comparison when the experimental profile is compared against the best-fitting conformation (black) and canonical B-form DNA duplex (gray dashed line), respectively. The insets highlight the differences between the profiles at the wide angle. The widths of the major and minor grooves for MixDNA in KCl, ATDNA in NaCl, and MixDNA in MgCl₂ are shown in (G) to (I), respectively. In these panels, the solid gray and dashed gray lines correspond to the canonical B-form major and minor GWs, respectively. The x axis gives the residue positions. (J) The comparison of dsDNA conformations obtained from the best-matching models highlights structural variations.

To extract more information from the structures shown in Fig. 3J, we use the correlation map approach to characterize the two topologies in more detail (Fig. 2). With this approach, it is straightforward to identify the structural feature(s) responsible for the differences in the WAXS profiles. On the basis of this analysis, we find that the GW most notably dictates the aforementioned changes. To confirm, we computed the GW for each residue pair from simulations (see Materials and Methods). Figure 3 (G to I) shows our results for each condition.

Profiles acquired in the presence of 10 mM MgCl₂ differ only slightly from those acquired in 400 mM KCl. This is further corroborated by the application of GW analysis of MixDNA in monovalent (Fig. 3G) and divalent salts (Fig. 3I). Under these conditions, the geometry appears to be confined in the (MD-derived) boundaries defined by the ideal B-form. The residue-level deviations from B-form DNA are likely linked to sequence differences that MixDNA have. Unlike MixDNA, ATDNA has a uniform groove structure (Fig. 3H) where ideal B-form geometry is no longer valid. Here, the minor groove is narrower and, as a result, the major groove is wider than in the B-form structure. We also investigate the solvent effect by extending the simulations of ATDNA to Mg²⁺ solution. Similar to the MixDNA, the WAXS curve and GW analysis show minor solvent-induced changes in ATDNA (figs. S4 and S5). Together, our analyses support the idea that dsDNA structure varies with sequence identity yet appears insensitive to changes in solvent (salt) conditions.

RNA conformations

Notable differences are detected in comparable studies of RNA duplexes. Unlike dsDNA, the WAXS profile of MixRNA shows notable variations with changing salt conditions (Fig. 4, A to C, and insets). In the presence of 400 mM K⁺, we observe a smearing of the first peak in the high q region of the WAXS profile (Fig. 4A). In the 100 mM NaCl solution, however, this peak flattens out. The conformations at 10 mM MgCl₂ distinguish themselves with a sharp peak at q ∼ 0.5.

Fig. 4. Solution x-ray scattering profiles of MixRNA duplexes from experiment and simulation at different salt conditions.

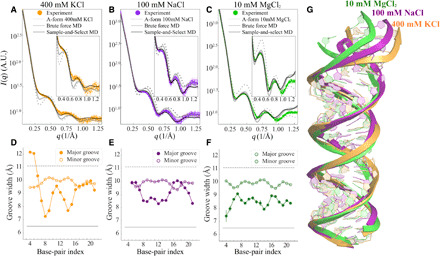
(A) The duplex in 400 mM KCl, (B) 100 mM NaCl, and (C) 10 mM MgCl₂, respectively. The dashed gray curve represents the computed profiles from canonical A-form RNA, while the solid gray curve represents the best agreement from MD sampled pool, where the starting conformation is A-form. The black curves show the agreement after SaS approach is used. Traces of major/minor GWs computed from best-fitted conformations for each salt condition, (D) 400 mM KCl, (E) 100 mM NaCl, and (F) 10 mM MgCl₂, respectively. The x axis gives the residue positions. The major GW exhibits residue specificity that affects overall RNA duplex conformation. This feature is detectable to WAXS because of its disruption of the structural periodicity in duplex topology. (G) The alignment of conformations in different salt conditions shows structural variations.

Computed WAXS profiles from an ideal A-form model helix deviate substantially from the observed signals in all salts, highlighting the importance of conformational flexibility in RNA systems (Fig. 4, A to C, and insets). MD simulations initiated from the A-form geometry have only limited success in capturing the experimentally observed WAXS signatures.

In an effort to improve the agreement between MD simulation and experimental data, we applied the SaS approach to investigate the salt-dependent RNA duplex conformations. This approach expands the conformational space accessible to simulations in a physically reasonable way. The experimental profiles for RNA duplex in 400 mM KCl, 100 mM NaCl, and 10 mM MgCl₂ are shown in Fig. 4 (A to C). The scattering profile of a canonical A-form RNA duplex is shown as a dashed line, and the inset of each panel emphasizes the wide-angle regime where fine structural details are mapped. The notable deviations seen in (A) to (C) highlight the conformational deviations from an assumed canonical A-form duplex (45). Moreover, the RT MD simulations starting with an A-form duplex conformation do not yield profiles that agree with any experimental data. The best scattering profile from the RT MD for each salt condition is shown as the solid gray line, identified using Eq. 6. We conclude that the RNA A-form conformation is not an ideal starting conformation. Because MD samples only limited conformations in the given time frame, we conclude that the real structure might vary from the A-form. Therefore, for the RNA studies, the SaS approach is necessary: The high-temperature simulation and feedback from experimental data are required to tackle the sampling issues by selecting a more plausible RNA duplex as the starting conformation. After selection, the MD simulations were run at RT, preserving the underlying physical models without introducing artifacts. The stability of the conformations is assessed by structural and thermodynamic measures (fig. S1 and Table 1). The sampled conformations from the final, post-SaS RT MD simulations are shown in fig. S6. The solid black line in Fig. 4 (A to C) is the best conformation in this final simulation and shows better agreement than without the SaS approach.

Table 1. Thermodynamic properties of MixRNA in monovalent ions (T = 300 K).

	ΔUAB (kJ/mol)*	$\mathbf{\Delta }{\mathit{S}}_{\mathbf{AB}}^{\mathbf{conf}}$ (J mol−1 K−1)*	ΔFAB (kJ/mol)*
KCl†	6.0	209.4	−56.8
NaCl†	12.0	315.0	−82.5
KCl‡	2.0	77.9	−21.4
NaCl‡	11.0	235.9	−59.8

*A, bend state; B, A-form state.

†AMBER14SB.

‡CUFIX.

The SaS approach enables good agreement and reveals the finer, measured structural variations. These features are only visible in the WAXS regime because of the length scales they represent. The correlation map approach (Fig. 2A) focuses our attention on the major and minor GWs; they are the important parameters. We find that different salts induce large changes in the grooves. Figure 4 (D and F) shows the RNA sequence (indicated by nucleotide number on the x axis), representative RNA duplex traces, and the major/minor GWs along the backbone. The horizontal lines indicate the GWs of a canonical A-form duplex. Most interesting is the salt dependence of the GW in 10 mM MgCl₂; although the widths vary from the A-form structure, they remain relatively stable along the backbone, e.g., without residue specificity, keeping the overall duplex straight. However, for monovalent salts, the duplex widens near the residues 7 to 9 (GGG) situated at the end. The end effect with the major groove opening induces a slight bend of the RNA duplex, disrupting the helical periodicity and smearing the duplex features in contrast to the MgCl₂ and A-form cases. This end effect is most pronounced at 400 mM KCl where the major GW widens abruptly near residues 18 to 20 (GGG) and renders an apparent bend in the duplex. The axial bending in the duplex is about 16^∘ and 22^∘ in NaCl and KCl, respectively, while the duplex remains straight in 10 mM MgCl₂. Figure 4G shows the alignment of the representative RNA conformations that best agree with the experimental data at the three salts explored. Last, note that there is still a subtle mismatch between the best MD conformation and the experimental data at 400 mM KCl, where the deviation defined in Eq. 11 near q = 0.65 Å⁻¹ is negative. According to the correlation map, the real conformation in 400 mM KCl exhibits a larger major GW and possibly higher bending.

Cation analysis

The origin of the above-described structural differences lies in the unique geometry of each distinct class of helices and likely in the distinct interactions of cations with these varied structures. To explore the molecular principles governing the relationships between the counterions and the structural response, we now turn to the cation distributions derived from the MD simulations. Once again, this analysis draws attention to the disparate behavior(s) of RNA and DNA. Figures 5 and 6 show our analysis of the cation distributions around the dsDNA structures. Figures 7 and 8 show the distributions around dsRNA for comparison.

Fig. 5. Cation distributions around DNA duplexes computed from simulations.

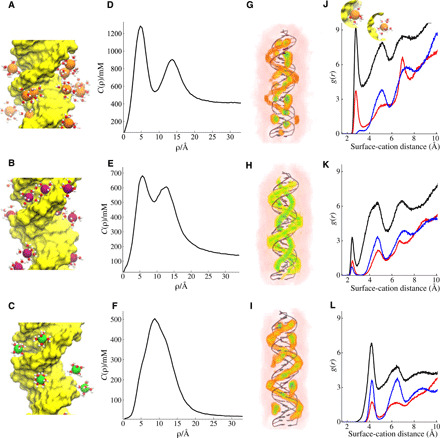
(A to C) A snapshot from each simulation setup where only the cations in the vicinity of the DNA with their first solvation shell water molecules are shown. (A) MixDNA in 400 mM KCl, (B) ATDNA in 120 mM NaCl, and (C) MixDNA in 10 mM MgCl₂. The average distribution of cations is monitored by cylindrical concentration profiles along the long axis of dsDNA. The solid line represents c(ρ) as a function of the distance from the central axis of the duplex. (D) KCl, (E) NaCl, and (F) MgCl₂. 3D ion density plots colored from white (low) to red to green (high) and shown in the same order as (G) KCl, (H) NaCl, and (I) MgCl₂, respectively. (J) Radial distribution function of K⁺ ions from the duplex surface. Different colors represent correlation of cations with different parts of the duplex; (black) with the whole duplex atoms, (red) with major groove, and (blue) with backbone phosphates. The inset in (J) depicts dehydrated (left, first peak) and hydrated (right, second peak) bound states. (K and L) Same as (J), but this time for Na⁺ and Mg²⁺, respectively.

Fig. 6. Analysis of the localization of cations to individual residues computed for dsDNA duplexes at different salt conditions.

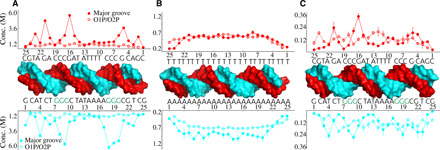
The binding is partitioned into two groups: binding to the major groove and binding to phosphate group oxygens, O1P and O2P (see Materials and Methods for details). (A) MixDNA in KCl, (B) ATDNA in NaCl, and (C) MixDNA in MgCl₂.

Fig. 7. Cation distributions around the MixRNA duplex computed from simulations.

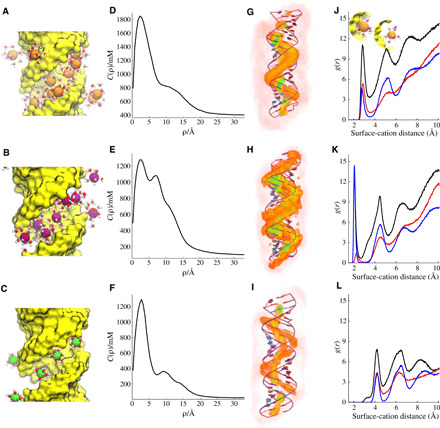
(A to C) A snapshot from each simulation setup where only the cations in the vicinity of the RNA are shown with their first solvation shell water molecules. (A) 400 mM KCl, (B) 100 mM NaCl, and (C) 10 mM MgCl₂. The average distribution of cations is monitored by cylindrical concentration profiles along the long axis of dsRNA. The solid line represents c(ρ) as a function of the distance from the central axis of the duplex with the same order. (D) KCl, (E) NaCl, and (F) MgCl₂. 3D ion density plots colored from white (low) to red to green (high) and shown in the same order as (G) KCl, (H) NaCl, and (I) MgCl₂, respectively. (J) Radial distribution function of K⁺ ions from the duplex surface. Different colors represent correlation of cations with different parts of the duplex: (black) with the whole duplex atoms, (red) with major groove, and (blue) with backbone phosphate. The inset in (J) depicts dehydrated (left, first peak) and hydrated (right, second peak) bound states. (K to L) Same as (J), but this time for Na⁺ and Mg²⁺, respectively.

Fig. 8. Analysis of the localization of cations to individual residues computed for MixRNA at different salt conditions.

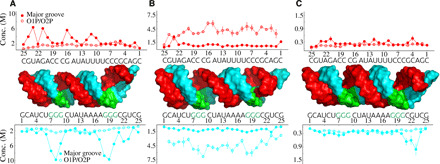
The binding is partitioned between two groups: major groove binding and binding to phosphate group oxygens. (A) KCl, (B) NaCl, and (C) MgCl₂.

We first focus on cation distributions around dsDNA. A snapshot from each simulation setup shows the relative size of cations, their first solvation shell water molecules, and their duplex topology (Fig. 5, A to C). Average cation distributions are computed from the simulations, and results are projected along the cylindrical axis (see Materials and Methods for details) (Fig. 5, D to F). We observe that cations localize at two binding sites around the dsDNA duplex. The first is to the major groove of dsDNA, marked by a peak in the concentration profile c(ρ) at 0 < ρ < 8 Å. The second peak of c(ρ) is located at 11 < ρ < 17 Å and reports the spatial correlation of cations juxtaposed between the phosphate groups of helical strands around the minor groove (Fig. 5D). We denote these two modes of binding as inner and outer layer binding. Figure 5 (G to I) shows these two layers in 3D density plots. The two-layer cation binding is a common feature of dsDNA (46–51). Depending on valence and cation size, we observe differences in their distribution. For monovalent cations, the two layers are distinct and well separated (Fig. 5, D and E). The larger K⁺ ions show a stronger inner shell binding. The smaller Na⁺ displays relatively weak major groove binding. The strong outer shell binding in Na⁺ coincides well with the narrow minor groove geometry in ATDNA (Fig. 3H). In the case of Mg²⁺ ions, the two peaks overlap in the c(ρ) for MixDNA. However, the two modes of binding remain distinguishable when the distribution is viewed in higher dimension (Fig. 5I). The existence of two well-separated layers is also evident in ATDNA in Mg²⁺ (fig. S7). The cations in the two layers further partition into hydrated and dehydrated cations. Figure 5 (J to L) shows their distribution obtained from radial distribution function. The inset in Fig. 5J demonstrates the two binding modes. Again, each cation shows distinct features. K⁺ ions are more prone to dehydration at the major groove, while Mg²⁺ cations stayed hydrated during simulation time despite their strong binding to the major groves. The cylindrical concentration profiles of DNA have been investigated extensively in a previous work (52). Despite the changes in the force field, salt conditions, and sequence, the two peaks observed in monovalent ions and one major peak observed for Mg²⁺ show good agreement with this study.

The derived concentration profiles provide an overview of how cations distribute around the helical structure. A deeper insight into the sequence-dependent differences can be gleaned by analyzing the cation-binding properties as a function of residue pairs. The residue-level local concentration analysis (see Materials and Methods) reveals how cations partition among the base pairs forming the duplex, information that helps to establish the relationship(s) between sequence and structural changes. Here, we show local concentration as a function of residue index for the three salt conditions (Fig. 6). K⁺ ions show a sequence-specific binding, with G tracts bearing a higher cation occupancy (Fig. 6A). This binding is mainly to the major groove and likely reflects the size of K⁺ ions that occupy the major groove. K⁺’s ability to exchange water facilitates stronger binding by promoting direct binding (53). Unlike the major grooves, K⁺ ions binding to the phosphate group are weak and nonspecific. Crystal structures reported discrete K⁺ ion binding to the major grooves (25, 54), supporting our simulation results. Na⁺ ions, on the other hand, show a more uniform binding pattern around the homopolymeric DNA sequence of ATDNA (Fig. 6B). Note that the sequence variability is limited in ATDNA. Here, Na⁺ ions bind more to the poly-A strand of the duplex. The partition of cations to the major groove and to the phosphates is almost equal. Last, we examined the distribution of Mg²⁺ ions. Mg²⁺ ions around MixDNA show relatively stronger binding patterns because of their higher valence (Fig. 6C). The major groove and phosphate binding are comparable in strength in Mg²⁺. The sequence specificity is not as evident as for K⁺ ions. Nevertheless, Mg²⁺ favorably binds to guanine (G) and adenine (A) nucleobases. Despite these differences, the WAXS profiles of the DNA duplexes are all very similar.

To understand the unique structural responsiveness of dsRNA, we extend our analysis to the cation distribution of MixRNA, where experimental data show strong salt dependence (Fig. 4). Figure 7 summarizes the distinct cation distribution of dsRNA. A snapshot from each simulation setup displays instantaneous ion positions around the dsRNA duplex (Fig. 7, A to C). As is evident from concentration profiles (Fig. 7, D to F) and from the 3D density plots (Fig. 7, G to I), the two-layer binding observed in dsDNA (Fig. 5, D to I) diminishes in dsRNA. The cations bind to dsRNA in two distinct ways: (i) strong condensation to deep major grooves and (ii) a weak diffusive binding to the phosphate backbone. As a result, c(ρ) shows only a single dominant peak around the major groove. The magnitude of the peak reflects the strength of attractive forces between positively charged cations and negatively charged RNA surface and reveals a stronger electrostatic potential for dsRNA than for dsDNA, supporting results of recent ion-counting experiments (42). The 3D ion density profiles visually highlight the ion-binding preferential locations (Fig. 7, G to I). A visual inspection highlights the difference between the two double strands (movie S1). Because of their size, K⁺ and hexahydrated Mg²⁺ ions are located at the center of the major grooves, whereas the smaller-sized Na⁺ ions explore alternative sites at the groove. The first site is on the phosphates facing inward to the major groove, and the second is in the central region of the major grooves (Fig. 7H). Similar to the dsDNA, the radial distribution function (Fig. 7, J to L) showed hydrated and dehydrated binding states. Distinct from dsDNA, Na⁺ ions show strong coordination with the backbone phosphates in dsRNA. In addition, cation binding is overall tighter in the case of dsRNA (Fig. 7, J to L).

The sequence-dependent counterion local concentrations show specificity with a general tendency toward higher affinity in the case of dsRNA (Fig. 8). K⁺/Mg²⁺ ions bind preferably to the major grooves, whereas Na⁺ ions have more affinity to the phosphates. Mg²⁺ ion binding is discrete but not specific (Fig. 8C). To describe the sequence-dependent cation-binding preferences, we compute the average number of cations that bind to each nucleobase. Figure 9 (A to C) compares the affinity of cations to each nucleobase. The two monovalent ions show higher affinity to guanine bases, while Mg²⁺ ions favor adenine. N7 and O6 are the binding sites for monovalent ions. The N6 atom that resides at the major groove of adenine is the binding site for Mg²⁺. Note that the binding sites of N7, O6, and N3 were reported earlier in previous simulation studies of dsDNA (52) and dsRNA (55). One notable observation revealed by the simulations is that the preferential binding is (sequence) context dependent. G tracts are favored by both K⁺ and Na⁺ ions (Fig. 8, A and B). As a result, the binding strength of monovalent ions to a G within a G tract is almost twice as high as that of an individual non–G tract guanine/G (Fig. 9D).

Fig. 9. Nucleobase-level bound cation analysis for MixRNA.

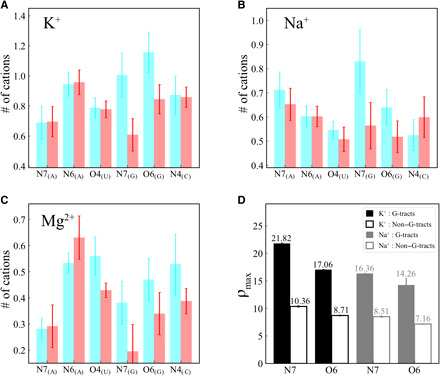
(A) RNA in KCl, (B) NaCl, and (C) MgCl₂. (D) The binding strength comparison of monovalent ions to G tracts (solid bars) and non–G tracts (empty bars). ρ_max represents the relative binding strength of cation obtained from the maximum of radial distribution function.

The sequence and context dependence of cation binding, especially observed in monovalent ions, gives rise to structural changes around the G tract regions. The high correlation between the total number of bound cations and major GW for dsRNA in monovalent ions (figs. S8 and S9) indicates the relationship between cation binding and structural changes observed in Fig. 4G. Our data suggest that it is the sequence-dictated cation binding that leads to the modulation of major groove binding. A larger GW is needed to accommodate more cations to locations where cations show high affinity. The localized widening of the major grooves results in bending the dsRNA in monovalents. On the other hand, Mg²⁺ ions are not selective enough to the sequences and, as a result, did not result in localized widening.

DISCUSSION

We effectively combine WAXS and molecular simulations to investigate the structures of dsDNA and dsRNA duplexes in different salt solutions. Explicit treatment of buffer, accurate representation of excluded volume, and molecular flexibility represent the state of the art in computing WAXS curves from simulation data. The perfect synergy of experiment, molecular simulation, and data science allows an accurate interpretation of each WAXS feature obtained from experiments as a physical attribute of the structure. The close connection with experiments enhances conformational sampling, specifically highlighting cases where critical adjustments to the structural pool are needed. Once agreement is achieved, atomic simulations provide a molecular view of the structure and nucleic acid interactions. The information gained clearly elucidates the structural differences between duplexes and further develops physical intuition into factors governing the duplex structure.

In dsDNA, WAXS profiles computed from simulations show excellent agreement with experiments. This agreement is achieved using brute force MD simulations, initiated from B-form geometries. However, for dsRNA, the simulations initiated from A-form geometries showed limited success in capturing the experimentally detected WAXS signatures. We demonstrate the disparate behavior of dsDNA and dsRNA using principal components analysis. Our findings are summarized in fig. S10. While the transition from the ideal B-form to the stable (experimental) state is diffusive for dsDNA, dsRNA must transition from a linear A-form structure to the bent state, which appears to be an activated process. High-temperature simulations accelerate the transitions between the two basins that represent these distinct states. Therefore, we attribute this effect to the insufficient sampling of the landscape. This consideration is especially important for RNA, whose energy landscape is known to be rugged. The typical time scale of simulation (∼400 ns) is found to be too short to navigate such a rugged landscape. Good agreement between experiments and simulations was achieved using the SaS approach. In the SaS approach, high temperature is used to enhance the sampling of the rugged energy landscape. Most critically, the experimental data assist in locating the regions of importance. This approach serves as a simple and practical strategy to study dsRNA conformations without perturbing the energy landscape or running long simulations. In addition, we note that a recent publication (56) describes the application of SaS to derive ensembles of RNA structures using NMR refinements. The microstates explored by this approach are assessed for thermodynamic and structural stability. Experimentally selected states showed lower free energies for each salt condition studied (Table 1), demonstrating the adequacy of the force fields used and the importance of sufficient conformational sampling in obtaining experimentally consistent observables.

The experimentally validated and atomically detailed structures resolved by our integrated approach uncover a notable finding. The dsDNA sequences studied here show structural resistance to changes in salt conditions. The largest variations in structure are found when comparing across sequences. Conversely, dsRNA show strong structural variation with changes in salt conditions. Using a correlation map approach that connects features in the curve with distinct properties of the structures, we identify the GWs as the most important parameter that influences the salient features in the WAXS profiles. The changes in the duplex topologies are parameterized using the GW descriptors extracted from MD simulation, providing an important metric for comparison. Figure S2 summarizes this approach, contrasting the unique behavior of dsDNA with its cousin dsRNA. The sensitivity of DNA to sequence and the response of RNA to solution conditions align perfectly well with their biological roles.

The structural differences between dsDNA and dsRNA are amplified by the unique relationship between duplex topology and cation distribution. Although structural differences can be visualized by a number of experiments (e.g., crystallography and NMR), access to the mobile cation distributions is uniquely enabled by simulation. Simulations report a two-layer cation binding for dsDNA, as reported in other theoretical works (51, 55, 57). They are known to facilitate DNA condensation in the presence of polyvalent cations (58–60) and divalent ions (49, 50). We find that their relative distribution balances the major and minor GWs, and we demonstrate that the two-layer cation distribution also serves to stabilize dsDNA upon solvent variations.

Despite the similarity between their sequences, dsRNAs show an uneven distribution of cations around the duplex relative to the (similar) dsDNAs. In dsRNAs, the outer shell of cation binding is not evident. The deeper and narrower major groove and the unique geometry of the phosphate oxygens that are facing inward to the major groove result in strong binding to the major groove. The asymmetrical distribution of cations at the helical surface leads to local structural changes of the dsRNA. We observe a strong correlation between cation binding and major groove widening. The major groove binding shows a sequence specificity that varies with cation size and valence. K⁺ ions bind mostly to G, while Mg²⁺ ions preferentially bind to A’s and G’s. Binding to the major groove can be amplified using tandem/repeating units. As a result, localized cations at such sites lead to spontaneous bending of dsRNAs.

Deriving an accurate description of the nucleic acid structure from WAXS is a daunting task. Our approach of coupling experiments and simulations provides immense opportunities in determining the structure of biologically important polynucleotides. Finding the molecular mechanism of cation localization and cation-induced changes in the molecular structure will help to resolve biological response. The insights gained from our study on repeating sequences have important implications. For example, tandem units serve as signaling regions for many biological functions (7, 8). Structural deformations around the repeating sequences are common (61–63). Our study illuminates these observations.

MATERIALS AND METHODS

Molecular modeling and simulation setup

Two DNA sequences were studied, a duplex containing the two homopolymeric chains, dA₂₅ paired with dT₂₅, denoted ATDNA, and a mixed sequence, GCA TCT GGGC TA TAA AAG GGC GTC G and its complement, denoted MixDNA. The latter sequence was also studied in dsRNA, replacing the thymine (T) residues with uracil (U) and denoted MixRNA. The former sequence in RNA, AURNA, favors triplex over duplex formation and will not be considered here.

Initial structural models of the 25-bp dsNA helices were constructed using nucleic acid builder (64). B-form geometry was assumed for the DNA helices, while RNA was treated as A-form. Once constructed, each duplex model was placed in a rectangular box aligning the long axis parallel to the z axis. To avoid possible end effects, the simulation box along the z axis was further extended by about 15 Å at both ends of the duplex, resulting in initial box sizes of 7.0 nm by 7.0 nm by 11.0 nm for a DNA duplex and 7.0 nm by 7.0 nm by 10.0 nm for an RNA duplex. Molecules were solvated and ions were added to match experimental conditions. Table S1 summarizes the simulation setup for each condition.

MD simulations and analyses were carried out using GROMACS 5.0.5 suite of programs (65). We used an optimized version of the AMBER force field (CUFIX) (66) to model inter-DNA interactions. We find this force field accurately describes DNA-DNA interactions (50). We used TIP3P (67) to model water. For RNA duplexes in monovalent salt, we used default AMBER14SB (68) with and without CUFIX corrections. For divalent salts, we only used CUFIX. For each simulation (salt concentration), the solvated system was first energy-minimized for 5000 steps to remove bad contacts that may arise because of random placement of water and ions. The equations of motion were integrated using the Leap-Frog method (69) with a time step of 2 fs. Long-range electrostatic interactions were computed using the particle mesh Ewald (70) summation method with a grid spacing of 0.12 nm and an interpolation of order 4. Periodic boundary conditions were applied in all directions during simulations. The nonbonded interactions were treated with a cutoff of 1.1 nm with dispersion corrections. For neighbor search, we used a cutoff radius of 1.1 nm and update the neighbor lists for every 10 steps. The covalent bond lengths were restrained by LINCS (71) algorithm.

We used an equilibration procedure (50) involving volume and solvent. First, we used isothermal-isobaric (NPT) simulations to determine the volume of the simulation box. During a 2-ns NPT equilibration period, the temperature was set to 300 K using the Berendsen thermostat, and pressure was kept constant at 1 bar using Parrinello-Rahman barostat (72). The volume of the system reached an equilibrium shortly. On the basis of the last frame of NPT simulation, a solvent equilibration procedure was followed. By restraining the duplex, we run for another 100 ns to equilibrate the distributions of cations and water. Harmonic restraints with a stiffness constant of 1000 kJ mol⁻¹ nm⁻² were applied to the heavy atoms of the duplex. Restrained simulations used in canonical ensemble (fixed NVT) allowed the equilibration of the solvent and cations around the macroion. Coordinates of the last step of the simulation are saved and used as the starting point of our unrestrained MD simulations. We used 300-ns-long unrestrained simulations and recorded data every 2 ps for further analysis.

Calculation of solution x-ray scattering profiles

To precisely compute the solution x-ray scattering profiles at both small and wide angles, the solvent/ion shell, excluded volume, and solvent degrees of freedom must be taken into account. Following the theory computing x-ray scattering intensity from the excess electron density (73, 74) of molecules in solution, the buffer-subtracted intensity is I(q) = I_A(q) − I_B(q), where I_A and I_B denote the scattering intensities of the sample solution and corresponding solvent background. The magnitude of the momentum transfer of incident x-ray photons, q, is defined as q = (4π/λ) sin θ, where λ and θ are the wavelength of the incident x-ray in angstroms and half of scattering angle, respectively. With A(q) and B(q) representing the complex scattering amplitudes from the sample solution and solvent background, we have

$$I(q)={⟨{\langle {\mid A(\mathit{q})\mid }^2\rangle }_{\mathrm{\omega }}-{\langle {\mid B(\mathit{q})\mid }^2\rangle }_{\mathrm{\omega }}⟩}_{\mathrm{\Omega }}$$ (1)

where 〈…〉_ω denotes the average over conformations and 〈…〉_Ω is the orientational average assuming the molecules rotate freely in the solution. In Eq. 1, 〈∣B(q)∣²〉_ω is computed using multiple MD frames of bulk solvent simulations as illustrated in Fig. 1B. We did not perform the solvent density correction (74) because the MD simulations were conducted at the exact same salt condition as in the experiments. Because our goal is to compute the small-angle x-ray scattering and WAXS profile for each MD-sampled conformation and select the conformations closest to those from experiment, we used fixed atomic coordinates for the sample as shown in Fig. 1B. With one set of atomic coordinates, the complex scattering amplitude for the sample solution is

$$A(\mathit{q})={\displaystyle \sum _{k=1}^{N_{\mathrm{A}}}}{f}_k(q)e^{-i\mathit{q}·{\mathit{r}}_{\mathit{k}}}$$ (2)

In Eq. 2, N_A is the total number of atoms in system A and f_k(q) is the atomic form factor of the kth atom located at coordinate r_k. Equation 2 also applies to the solvent system B. We computed f_k(q) for each atom using Cromer-Mann parameters (75) and correction of electron-withdrawing effects in the water molecules (76).

The solvent and ion shell around the molecule is modeled according to the force fields of the MD simulations, and it should be included in computing the profile. In practice, we designed a molecular envelope for systems A and B, beyond which the solvent is not affected by the molecule (bulk like). The electron densities are the sum of the electron densities from inside and outside the molecular envelope. The same envelope was applied to the solvent system, B. Given the absence of correlation between the inside and outside electron densities, the scattering intensity in Eq. 1 can be reduced to

$$I(q)={⟨{\langle {\mid A_i(\mathit{q})\mid }^2\rangle }_{\mathrm{\omega }}-{\langle {\mid B_i(\mathit{q})\mid }^2\rangle }_{\mathrm{\omega }}-2\text{Re}[{\langle B_i^{*}(\mathit{q})\rangle }_{\mathrm{\omega }}{\langle A_i(\mathit{q})-B_i(\mathit{q})\rangle }_{\mathrm{\omega }}]⟩}_{\mathrm{\Omega }}$$ (3)

where the subscript i denotes the scattering amplitude from atoms inside the envelope and Re represents the real part.

Previous studies (74, 77) applied an icospherical envelope from 5120 triangular faces with 8 Å separation to the molecular surface. In this work, this molecular envelope, encompassing both the solvent and the ion shell, is built using the probability density isosurface. We transformed the molecule into a 3D probability distribution and use one of the isosurfaces as the molecular envelope. Each conformation has the corresponding molecular envelope with the same separation, d, between the isosurface and molecular surface. The separation d dictates the probability density value of the isosurface. All N atoms (including explicit hydrogen atoms) of the molecule are modeled as a 3D Gaussian distribution with identity covariance matrix I located at the coordinates r_i, 𝒩(r∣r_i, I). The transformed molecule, ℳ(r), is then the linear combination of N identical Gaussian distributions

$$\mathcal{M}(\mathit{r})=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\mathcal{N}(\mathit{r}\mid {\mathit{r}}_{\mathbf{i}},\mathit{I})$$ (4)

Note that this transformation is essentially the Gaussian blurring of 3D Dirac delta functions. For a given separation d, we can find the value of probability density isosurface, t, and define the space inside the molecular envelope as ℐ ≔ {r∣ℳ(r) > t}. We chose isotropic Gaussian distributions such that t is mostly determined by the distance between the closest atom to the position r, i.e., min_i∣r_i−r∣. The scattering amplitude of sample solution within the envelope is then

$$A_{\mathrm{i}}(\mathit{q})={\displaystyle {\sum }_{k=1}^{N_{\mathrm{A}}}}{f}_k(q)e^{-i\mathit{q}·{\mathit{r}}_{\mathit{k}}}\mathbf{1}\{{\mathit{r}}_{\mathit{k}}\in \mathrm{ℐ}\}$$ (5)

where 1{…} is the indicator function. In this work, we set a fixed d = 10 Å to enclose the solvent and ion shells, shown as the blue mesh surface in Fig. 1B. We used 100 frames of solvent simulations for conformational average, 〈…〉_ω, and 1750 uniformly distributed points on a unit sphere (78) for the orientational average, 〈…〉_Ω. The solution x-ray scattering computation for 261 q points from q = 0 to 1.3 Å⁻¹ was implemented with Julia 1.6.0-DEV and deployed on Cornell RedCloud, a 28-core server node with Intel Xeon E5650 (2.7 GHz, Santa Clara, CA).

Generating conformational ensembles for WAXS computations

To compute WAXS profiles from simulation data, we extracted 100 snapshots from equal intervals along the MD trajectory. For buffer subtraction, a buffer solution containing the corresponding salt was prepared by adding ion pairs and water molecules in a periodic box with dimensions and concentrations matching those used in the duplex simulations. We run 20 ns of MD simulations in NVT ensemble to generate each bulk ensemble.

SaS approach

We start with a 100-ns-long high-temperature (HT) simulation, T = 340 K. HT simulations allow rapid exploration of conformational states in the neighborhood of the initial geometry that is otherwise not accessible by RT simulations. Later, we cluster the sampled conformations at HT using gromos (79) method. The clusters representing different regions of conformational space [with root mean square deviation (RMSD) cutoff > 0.18 nm] are then used to compute trial WAXS profiles. We select the cluster center structure that gives the best agreement with the experiment based on the following customized criterion without free parameters

$$\widehat{k}=\underset{k\in \{1,2\dots N\}}{\text{min}}\frac{1}{n-1}{\displaystyle \sum _{i=1}^{\mathrm{n}}}{\left\{\frac{{\text{log}}_{10}[I_k(q_i)]-{\text{log}}_{10}[I_{\text{exp}}(q_i)]}{\mathrm{\sigma }\prime (q_i)}\right\}}^2$$ (6)

Here, n is the number of q points, and N is the number of conformations. In Eq. 6, I_exp(q_i) and σ′(q_i) denote the experimental scattering intensity at q_i and the propagated error: σ′(q_i) = σ(q_i)/[I_exp(q_i) log 10], with σ(q_i) being the experimental error. This HT simulation was triggered when the customized metric in Eq. 6 of all the sampled conformations is greater than 10.0.

To generate an ensemble from the selected structures, we first perform a 20-ns solvent equilibration simulation at RT, followed by an unrestrained production run of 300 ns. Using the conformations sampled, we compute the average WAXS profile using the protocol described above.

We assess the structural stability of the initially started conformations by computing the time evolution of the RMSD. The lack of slope in RMSD (fig. S1) suggests that the conformations sampled are at a local minimum. The depth of the local energy minima are ranked on the basis of Helmholtz free energy. For that, we looked at the difference in ΔF between ensembles. Assuming the entropic contribution of the solvent degrees of freedom will be similar between the two microstates (A, B), the free energy difference is written as $\mathrm{\Delta }{F}_{\mathrm{AB}}\approx \mathrm{\Delta }{U}_{\mathrm{AB}}-T\mathrm{\Delta }{S}_{\mathrm{AB}}^{\text{conf}},$ where ΔU_AB is the internal energy difference that we computed directly from simulation. The conformational entropy of a state, S^conf, can be approximated from the principal components analysis of the duplex conformations using Schlitter’s formula (80). This way, the change in the conformational entropy, $\mathrm{\Delta }{S}_{\mathrm{AB}}^{\text{conf}}$, was directly obtained from the trajectory and used to compute ΔF_AB.

Computing major and minor GWs

Major and minor GWs were calculated from equilibrium simulations using the three-DNA program (81). The same 100 snapshots generated for WAXS computations were analyzed to extract these parameters. To avoid end effects, 3 bp from each terminus were excluded. The resultant outputs were averaged. We subtracted 5.8 Å from the values obtained to account for the apparent van der Waals radii of the phosphate groups. The error bars in all analyses were estimated by dividing the simulation data into three blocks of equal time intervals.

Cation density profiles

To visualize the structure of the cation cloud around the duplex, we computed cation (Mg²⁺, Na⁺, or K⁺) density profiles in Cartesian coordinates. For an arbitrary point in space r ≡ (x, y, z), the average cation number density ϕ(x, y, z) can be computed from the trajectory as

$$\mathbf{\varphi }(\mathbf{r})=⟨\frac{1}{V}{\sum }_i\mathrm{\delta }(\mathbf{r}-{\mathbf{r}}_i)⟩$$ (7)

where the sum goes over the cation index i in the simulation box of volume V. δ(x) is the Kronecker delta, and ⟨…⟩ represents the ensemble average.

Cylindrical concentration profiles

Serving as an ideal coordinate system for studies of helices, the concentration profile in a cylindrical coordinate c(ρ) is computed by a coordinate transformation ϕ(x, y, z) → ψ(ρ, θ, z), where ρ represents the distance from the helical center and N_A is Avogadro’s number.

$$\mathrm{c}(\mathrm{\rho })=\frac{1}{N_{\mathrm{A}}}{\iiint }_0^{\mathrm{\rho }}\mathrm{\rho }\prime \mathbf{\psi }(\mathrm{\rho }\prime ,\mathrm{\theta },z)d\mathrm{\rho }\prime d\mathrm{\theta }\mathit{dz}$$ (8)

The bulk concentration of cations was estimated from the asymptotic values of c(ρ).

Residue-level local concentration profiles

From the radial distribution functions (RDFs) of each residue, the local concentration (Conc.) was assessed by finding the highest point of the RDFs as

$$\mathrm{c}(X_i)=g_{\mathrm{Xi}}(r_{\text{max}})c_{\text{bulk}}$$ (9)

where g_Xi(r) is the radial distribution function of the subgroup of the residue i. The subgroups under study are X ≡ {(N7, N6) for A, (N7, O6) for G, O4 for (U, T), N4 for C, and (O1P, O2P) for Backbone}.

Bound cation and GW variation analysis

The number of bound cations to group X was computed from cumulative radial distribution function g_X(r) as

$${\mathrm{N}}_{\mathrm{X}}(\mathrm{R})=\frac{N_{\text{cation}}}{V}{\displaystyle {\int }_0^R}4\mathrm{\pi }{r}^2{g}_X(r)\mathit{dr}$$ (10)

Here, r is the distance between the cation and macroion surface and N_cation is the total number of cations in the simulation box. By picking R= 3 Å we count the inner sphere cations, while R = 6 Å gives the total number of cations bound (outer and inner sphere cations).

Structure-intensity correlation map

Distinct from SAXS data, where global parameters of the molecule can be obtained directly, the WAXS features at different scattering angles correlate with themselves (82) and reflect various structural periodicities within the molecular system. For RNA duplexes, previous studies have established a few critical helical parameters that can be estimated (45) and predicted by the integration of experimental WAXS data and MD simulations. Here, using the correlation map (83), (i) we investigate the important structural parameters that have high correlation to features in the WAXS profile, and (ii) we pinpoint the qualitative structural disagreements between experimental and computed profiles. The former supports our choices of structural parameters while the latter sheds light on fine molecular conformations despite the imperfect match between experimental data and MD simulations.

To derive the correlations, we computed the normalized deviation between logarithmic intensities of kth conformation and experiment, δ_k(q_i) at angle q_i, as the following

$${\mathrm{\delta }}_k(q_i)=\frac{{\text{log}}_{10}[I_k(q_i)]-{\text{log}}_{10}[I_{\text{exp}}(q_i)]}{\mathrm{\sigma }\prime (q_i)}$$ (11)

Note that Eq. 11 is similar to Eq. 6 but without the square. One thousand RNA duplex conformations were analyzed using the x3dna-dssr program (81) to obtain all the global and local parameters, including geometries of groove, base pair, and dinucleotide step. This method effectively identifies the structural features that are reflected at specific scattering angles, by correlating differences in predicted profiles with variations in those features.

Sample preparation

Two 25-bp dsDNA duplexes of sequences 5′-poly(dT)25 (ATDNA) and 5′-GCA TCT GGG CTA TAA AAG GGC GTC G (MixDNA) were purchased from Integrated DNA Technologies (Coralville, IA). The DNA strand and its complement for each DNA duplex were annealed at 95°C for 5 min and slowly cooled down to 22°C in 1 hour. Both DNA duplexes were purified and buffer-exchanged to a solution containing 1.0 mM MgCl₂, 10 mM sodium 3-(N-morpholino)propanesulfonic acid, and 20 μM ethylenediaminetetraacetic acid (pH 7). The final DNA concentrations were above 500 μM for further dilution at the beamline.

The sample preparation procedures of 25-bp dsRNA duplex of sequence 5′-GCA UCU GGG CUA UAA AAG GGC GUC G in 100 mM NaCl, 400 mM KCl, and 10 mM MgCl₂ were described in (45).

Solution x-ray scattering experiment

The solution x-ray scattering measurements for both ATDNA and MixDNA were conducted at 16-ID [Life Science X-ray Scattering (LiX)] beamline of National Synchrotron Light Source II (NSLS-II) (84) at Brookhaven National Laboratory. The DNA samples were diluted and measured at 80, 100, and 120 μM. Sixty microliters of solution sample, before and after buffer, was manually loaded to the sample holder and measured in the continuous-flow sample cell with five 1-s exposures at RT. On-site data screening on the pre- and post-buffer matching was enabled by the py4xs Python package. The scattering angle from q = 0.005 to q > 3.0 Å⁻¹ was recorded on a Pilatus 1M (small-angle) detector and two Pilatus3 300K (wide-angle) detectors (Dectris, Switzerland) in vacuum. The acquisition of solution x-ray scattering data for RNA in 100 mM NaCl, 400 mM KCl, and 10 mM MgCl₂ was described in an earlier work (45).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/17/eabf6106/DC1

View/request a protocol for this paper from Bio-protocol.