Graphical abstract
Keywords: Compartment modeling, SIRD model, Stratified analysis, Decision making, Epidemic, CoViD-19
Abstract
Background
Available national public data are often too incomplete and noisy to be used directly to interpret the evolution of epidemics over time, which is essential for making timely and appropriate decisions. The use of compartment models can be a worthwhile and attractive approach to address this problem.
The present study proposes a model compartmentalized by sex and age groups that allows for more complete information on the evolution of the CoViD-19 pandemic in Italy.
Material and methods
Italian public data on CoViD-19 were pre-treated with a 7-day moving average filter to reduce noise. A time-varying susceptible-infected-recovered-deceased (SIRD) model distributed by age and sex groups was then proposed.
Recovered and infected individuals distributed by groups were reconstructed through the SIRD model, which was also used to simulate and identify optimal scenarios of pandemic containment by vaccination. The simulation started from realistic initial conditions based on the SIRD model parameters, estimated from filtered and reconstructed Italian data, at different pandemic times and phases.
The following three objective functions, accounting for total infections, total deaths, and total quality-adjusted life years (QALYs) lost, were minimized by optimizing the percentages of vaccinated individuals in five different age groups.
Results
The developed SIRD model clearly highlighted those pandemic phases in which younger people, who had more contacts and lower mortality, infected older people, characterized by a significantly higher mortality, especially in males. Optimizing vaccination strategies yielded different results depending on the cost function used. As expected, to reduce total deaths, the suggested strategy was to vaccinate the older age groups, whatever the baseline scenario. In contrast, for QALYs lost and total infections, the optimal vaccine solutions strongly depended on the initial pandemic conditions: during phases of high virus diffusion, the model suggested to vaccinate mainly younger groups with a higher contact rate.
Conclusion
Because of the poor quality and insufficient availability of stratified public pandemic data, ad hoc information filtering and reconstruction procedures proved essential.
The time-varying SIRD model, stratified by age and sex groups, provided insights and additional information on the dynamics of CoViD-19 infection in Italy, also supporting decision making for containment strategies such as vaccination.
1. Introduction
Since December 2019, a virus named severe acute respiratory syndrome coronavirus 2, SARS-CoV-2, has rapidly affected Wuhan, China, and by March 2020 had already spread to nearly 200 countries [1], [2]. WHO declared a global pandemic on 11 March 2020 [3], in this way, CoViD-19 quickly became one of the major case studies in all scientific fields: the medical one first of all, the biostatistical and engineering one, and obviously the strategic-political one as a consequence.
CoViD-19 disease manifests itself with symptoms including fever, shortness of breath and altered sense of taste and smell, that could degenerate to a more severe state as pneumonia [4]. In general these symptoms and their severity have been observed to increase with age. In fact, mortality and lethality increased in age-dependent manner and were higher in the male sex [5].
Given the high contagiousness and spread, the efforts of the scientific community were soon directed toward improving etiological and therapeutic knowledge to diagnose and treat patients with CoViD-19. Understanding pandemic trends and the impact of protective measures has also been of considerable interest. Here, compartmentalized models and artificial intelligence have been the most widely used techniques [6], [7], [8].
Compartment models are the simplest models in the mathematical study of the dynamics of infectious diseases. They consider the average behavior of the system at the population level [9]. More specifically, it is assumed that the population is divided into compartments and that everyone in the same compartment has the same characteristics [10].
With this approach, analyzing and comparing the pandemic trend in different contexts is quite simple [11]. Many models, which include compartments of susceptible (S), infected (I), recovered (R), deceased (D) and exposed (E) individuals, such as the classic SIR, SIRD, SEIR models, but also more sophisticated compartmentalisations, have been implemented, depending on the type of information available [6], [12], [13], [14], [15].
This type of model can also be used to simulate pandemic containment strategies, such as lockdown schemes and/or vaccination plans. In particular, by stratifying the population into distinct groups, it is possible to understand on which population groups and to what extent to act, in order to achieve predefined targets, in line with political and/or health choices. To achieve these objectives, the optimal decision must be made, with respect to some criterion, from a set of available alternatives. From a mathematical point of view, this can be reached by minimizing an objective function that takes into account health, economic and/or social costs [16]. Such a function is called a cost or loss function.
Pandemic-trend models frequently use national public data. However, public data were affected by high variability and uncertainty. In particular, the number of new infected individuals depends on testing procedure, while the number of new deaths is affected by the delays in their communication. Moreover, the serological test and the nasal swab, both PCR and antigen, have a margin of error, therefore we do not have reliable estimates on the population that has been affected by the pandemic infection, especially at the beginning of the pandemic [17], [18], [19]. Finally, the actual infected population is underestimated due to the presence of many asymptomatic cases [20], [21], [22].
This study first describes a model-based approach to capture more complete information on the evolution of the pandemic by sex and age group. The model was designed on Italian public data, from which is possible to obtain stratified information on the age and sex of new infected and dead people. This information alone prevents us from exploiting the potential of compartment models that take into account gender and age group, due to the lack of information on the sex and age stratification of daily recovered individuals who therefore need to be estimated.
Based on the available and estimated Italian data, a susceptible-infected-recovered-deceased (SIRD) model with time-varying parameters, accounting for sex and age groups, is proposed to interpret the pandemic trend and to optimize mitigation plans such as vaccination.
2. Material and methods
2.1. Epidemic model
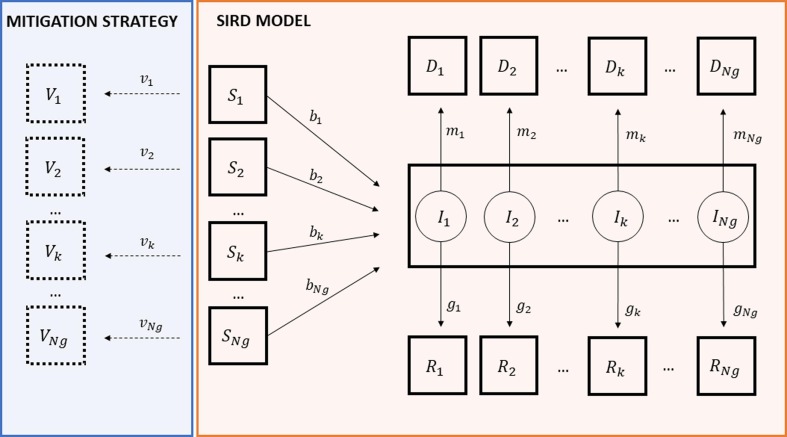
A time-varying epidemic model has been developed, structured by population groups. Because of the non-negligible proportion of infected individuals who die from the disease, the structure chosen for the model was of the SIRD type to account for the evidence that an infected person can either recover or die.
Given a generic partition of the entire population into Ng distinct groups, the group-distributed SIRD model, sketched in the right box of Fig. 1 , can be mathematically expressed as:
| (1) |
| (2) |
| (3) |
| (4) |
where
Fig. 1.
Orange box: SIRD distributed compartment model at each time point t; susceptible (, infected (, recovered (, deceased ( of kth group. Light blue box: vaccinated people of kth group (). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
, , and (k = 1,2,…,Ng) are the susceptible, infected, recovered and deceased individuals for the kth group, respectively;
, and are the time-varying model parameters thus defined: , represents the product between the average number of contacts per time unit, , of a subject belonging to group k, and the probability, , of the infection transmission by contact between a susceptible and an infected individual, while and , are the group-dependent recovery and death rate, respectively.
Note how equations (1) and (2) account for infectious contacts among groups through the total number of infected individuals, , interacting with susceptible individuals.
The box to the left of the SIRD model, in Fig. 1, represents the use of the model in an application for a mitigation strategy that can be implemented, for example, with a vaccination program, as will be detailed below. Clearly, in this case, equations 1–4 will have to be coherently rewritten to account for the added box that, for each group k, subtracts from eq.1 the quantity and introduces the following new differential equation:
| (5) |
where and represent the vaccinated individuals and the vaccination rate of group k, respectively.
To relate the group-distributed SIRD model back to the classical global population model, just apply the following equivalences:
| (6) |
where , and are the global population model parameters, and c(t) is the overall number of contacts. A similar equivalence applies to the vaccination compartment.
Based on equations 1–4 of the previous SIRD model, the group-dependent effective reproduction number, , can be expressed as:
| (7) |
From eq. (7) it is easy to observe that is a time-varying dimensionless ratio, representing the number of people (for each kth group) who become infected, per infected person at time t [23]. When > 1, the number of positive cases in that group will continue to increase, but when < 1, the infected cases in the group will tend to zero [24], [25].
2.2. Data collection
National public data from Italian Istituto Superiore di Sanità (ISS), which publishes an approximately weekly bulletin, and from the Protezione Civile (PrCi), which publishes daily data, were used to estimate the parameter of the SIRD model [26], [27]. The age, stratified in 10-year group, and sex of the new infected and dead individuals were extracted from the ISS bulletins. Additional information was extracted from the PrCi database which provides statistics regarding the total number of infected, dead and recovered individuals, as well as other useful data such as the number of nasal swabs and hospitalizations.
Analysis of this data requires special care, as the two data sources may not be perfectly synchronized. In addition, both sources are quite inaccurate, especially in the early period of the pandemic, due to lack of knowledge, low level of screening, and low accuracy of early swabs. Finally, PrCi daily data show high variability due to both delays in reporting deaths and test results and the difference between the number of tests performed on weekdays and holidays.
The time series analyzed in this study range from February 24, 2020, to January 23, 2021.
2.3. Data pre-processing
To obtain daily data grouped by gender and age, the PrCi daily data were distributed into groups according to the available ISS quasi-weekly distributions. Specifically, the distribution by sex and age groups, applied to each daily data, was that of the quasi-weekly bulletin including each specific day considered.
Then, PrCi data were filtered to reduce noise and excess variability, using a 7-day moving average filter. The first six days of pandemic were averaged over a shorter period, beginning with day 1. The number of points in the moving average window is a critical issue. A wider window would allow a greater noise filtering effect, but this may result in the loss of capturing significant rapid changes of the pandemic data. Moreover, one week roughly corresponds to the mean value of the incubation period of CoViD-19 [28]. Therefore, a 7-day windows can be taken as a fair smoothing compromise to account also for fluctuations in individually dependent incubation period.
2.4. Discrete-time data for the SIRD model
2.4.1. Publicly available Italian data
The pre-processed discrete data were used to implement the discrete time equations.
In particular, given the sampling time T = 1 day, useful available data at the discrete time j jT (j = 1,2, …, Nd; Nd = number of days) were:
-
•
number of infected individuals ;
-
•
number of group-distributed new infections ;
-
•
total of recovered individuals up to j, ;
-
•
total group-distributed deaths up to j, ;
where k ranges between 1 and the number, Ng, of groups considered, Ng = 20 (i.e. 10 age groups per gender).
Hence, the following associations allow the model equations 1–4 to be partly re-written in discrete time:
| (8) |
where and is the total population in kth group
| (9) |
| (10) |
To fully define the discrete-time group-distributed equations of the SIRD model, it is necessary to know the group distribution of the recovered individuals, , and infected individuals, .
2.4.2. Estimates of group-distributed recovered and infected individuals
The estimates of group-distributed recovered individuals were based on the assumption of equal removal (i.e. recovery plus death) rate for all groups, that is:
| (11) |
Eq. (11) allows to estimate recursively the unknown term , for each k group, once the initial value is known and must of course be nil, as:
| (12) |
Once was estimated, the number of infected individuals in the kth group was calculated as:
| (13) |
2.4.3. Parameter estimation
Model parameters, daily distributed across Ng groups, are estimated using a moving average approach, such as:
| (14) |
| (15) |
| (16) |
where: > 1 is an integer numbers of days, representing the moving average window length; are the mean values of I and the product , respectively, over the interval [j–q + 1, j]; , and are the sums of new infected, recovered and deceased individuals, respectively, detected in the kth group over the same interval.
2.5. Simulation of a vaccination program
The SIRD model was applied to show the impact of alternative vaccination plans by simulating various scenarios. Each of these scenarios considers a specific date chosen during the actual course of the pandemic as the starting point of the simulation; therefore, both the conditions and model parameter values set at the beginning of the simulation correspond to a real-world context. The expected length of time to complete the simulated vaccination plan was set at 60 days. At the end of this period, the model response was studied for an additional 60 days to observe the effect of the considered vaccination plan on the time course of the pandemic once the vaccination phase was completed. A total number of vaccine doses equal to 20% of the Italian population was taken. Vaccine administration was assumed to be evenly distributed over the 60-day period (constant mitigation rate), resulting in approximately 200,000 daily doses administered. This is just one of the countless possible simulations we have chosen to show the potential of the age-distributed SIRD model in a realistic situation, certainly not exhaustive.
Only 5 age groups (0–19 years, 20–39 years, 40–59 years, 60–79 years, >79 years) were considered because people within these groups showed a fairly uniform lethality. The influence of the sex was not considered. Simulations return the percentage of vaccines to be administer in each age group.
During the simulation, the parameters , and were estimated on a day-by-day basis using the moving average approach described above, where k ranges from 1 to 5.
Vaccination outcomes were assessed by considering three cost functions to be minimized: the number of individuals who have been infected, the number of deaths, and the number of quality-adjusted life years (QALYs) lost [29]. The QALY is a measure of the burden of disease often used in cost-utility analyses to guide decisions for the allocation of limited health resources. Since health is a function of length and quality of life, the QALY combines these attributes into a single numerical value. This value is obtained by multiplying the expected life years by a numerical coefficient between 0 and 1, which takes into account the weight of health-related quality of life. This coefficient, commonly referred to as the utility score, has been assigned different values for each age group, based on data from the literature [29], [30].
Exhaustive full-grid simulations were performed reproducing all possible combinations of vaccination percentages for each group at a 2% step and the minimum was detected for each cost function.
The Matlab software package, version R2019b, was used for the numerical implementation of the SIRD model.
3. Results
3.1. Data pre-processing
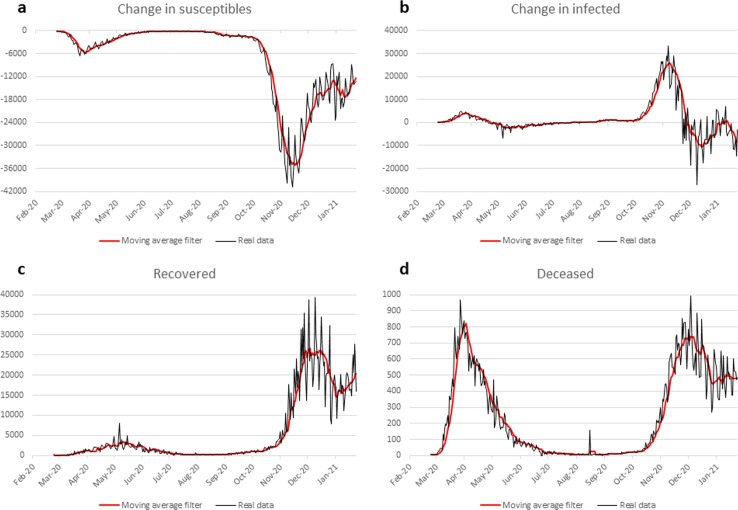
Fig. 2 shows that the PrCi data are highly noisy, especially in the compartment related to recovered individuals (frame c). Smoothing the data with a 7-point moving average filter (red line) provided significant noise reduction without causing excessive smoothing in the pandemic curves. Analyzing the trend of the pandemic curve we can observe two peaks of the epidemic, one in March and the other in November (see frame b). The peak observed in November is considerably higher than that observed in March and follows the summer period in which the pandemic had shown a significant slowdown. Also in frame d of Fig. 2, which shows the curve of the new deaths recorded day by day, two peaks are evident, but, in this case, their amplitude is similar. This could be due to the fact that in the first months of the pandemic the infected were poorly monitored, especially those with few or no symptoms, and this could have led to a significant underestimation of their actual numbers.
Fig. 2.
Daily time-behavior of change in susceptibles (a), change in infected (b), recovered (c), deceased (d). In black the Protezione Civile real data, in red the moving average filtered data. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
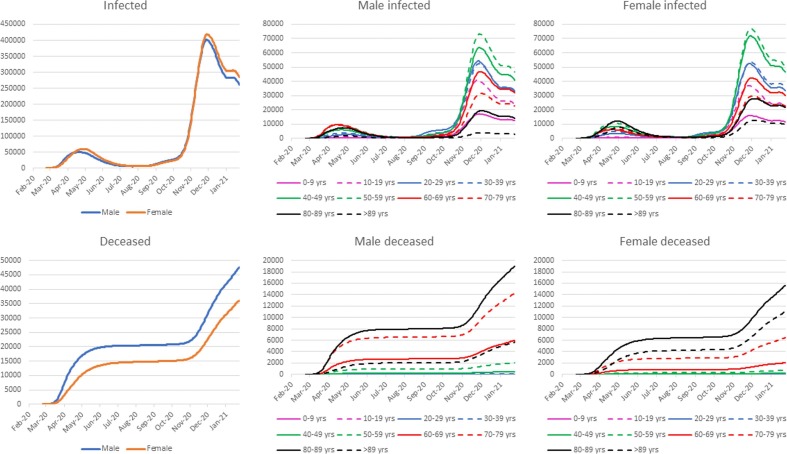
Fig. 3 shows the number of people in the compartments of infected and deceased individuals by sex and age. The number of infected individuals is similar in males and females, while the number of deceased is markedly different in the two groups. In fact, females presented about a quarter fewer death than males. During the second and highest peak of the pandemic, the groups with the greatest number of infected individuals were those aged 50–59 years and 40–49 years, for both males and females. In contrast, the greatest number of deaths occurred in the older groups and in particular in males and females aged 80–89 years. The age group with the largest differences between males and females is the >89 years. Since absolute frequencies are shown in Fig. 3, females have such a high number of deaths only because they are much more than men in this group (73% vs. 27%) [31].
Fig. 3.
Gender and gender-age grouped infected and deceased people.
3.2. Parameter estimates
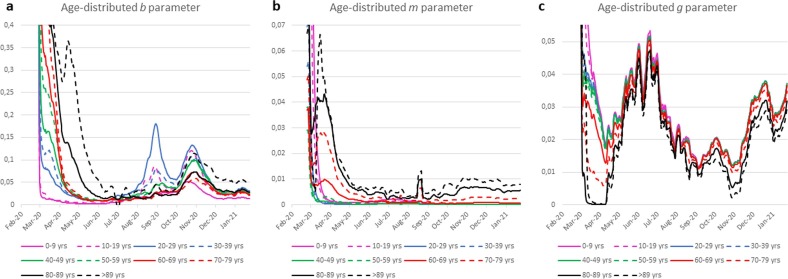
The analysis of the model estimates of the bk parameters grouped by age, shown in Fig. 4 a, allows us to focus on key points about the temporal evolution of the pandemic. First of all, it shows that at the beginning of the pandemic the oldest individuals had the highest values of , which would seem to indicate that they had more contact with infected individuals. This result is probably due to the fact that the elderly suffered from the worst symptoms and in that age group the few nasal swabs available were mainly used, neglecting the younger ones, mostly asymptomatic. During August and September, however, younger people (i.e., those younger than 40 years of age, but especially those aged 20–29 years) were those with the highest estimates, indicating that they had more contacts and, consequently, were the most infected. Later, during the November peak, the value also rose significantly in older persons. Young people probably contracted the virus during the summer due to a lack of attention to contacts, and then they transmitted it to the older relatives, especially coming back from vacations where the epidemic was stronger.
Fig. 4.
Moving average estimated age-grouped parameters during the pandemic.
Fig. 4b shows the time courses of the death rate estimates in the various age groups considered. It clearly indicates that, throughout the time period under review, the death rate was consistently higher in the older age groups. In particular, the maximum daily value of has always been observed in the age group between 80 and 89 years. On the contrary, the recovery rate assumes lower values in the older age groups and remains constantly the lowest in the age group with 90 years or more (see Fig. 4 c).
3.3. Vaccination program
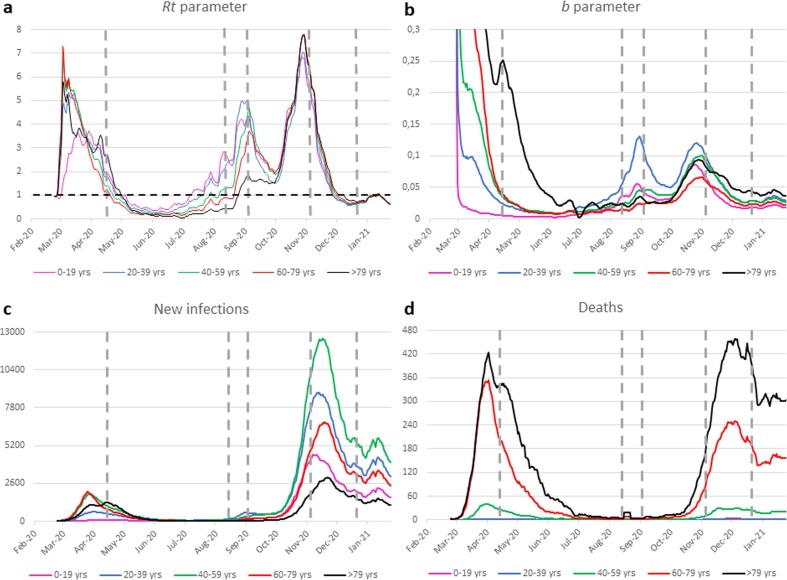
Five different starting scenarios were chosen to analyze the respective results obtained with the simulation model. Each of these initial scenarios corresponds to an actual condition recorded at a given time during the pandemic phase observed to date in Italy. Fig. 5 depicts the starting point chosen in each of the five simulations performed (vertical dashed gray lines) in relation to the actual trend of both Rt and b parameters (Fig. 5 a and b, respectively), the daily number of new infections detected (Fig. 5 c) and the daily number of deaths (Fig. 5 d). Table 1 details the initial conditions for each age group at each starting point. It also provides, for the various age groups, the vaccination percentages corresponding to the minima of the three chosen cost functions, identified through model simulation.
Fig. 5.
Daily time-behavior of the pandemic distributed across five age groups: Rt parameter (a); b parameter (b); new infections (c) deaths (d). Vertical gray dashed lines indicate the starting date of the vaccine simulations.
Table 1.
Initial conditions for each of the simulations performed and corresponding optimal percentages of vaccination in each age group. The dates in the first row represent the starting points of the simulations. The first two columns of each simulation report the starting conditions, i.e. the initial value of the Rt parameter and the total number, in thousands, of susceptible (S), infected (I), recovered (R) and deceased (D) individuals, respectively. The third column shows the simulation results, i.e., the percentage of people to be vaccinated within each age group to reach the minimum of each of the three cost functions considered (number of deaths, QALYs lost and number of infections).
| Age group | Apr 14th |
Aug 12th |
Sep 2nd |
Nov 4th |
Dec 20th |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rt | S,I,R,D (×103) | Dead, QALY, Infected | Rt | S,I,R,D (×103) | Dead, QALY, Infected | Rt | S,I,R,D (×103) | Dead, QALY, Infected | Rt | S,I,R,D (×103) | Dead, QALY, Infected | Rt | S,I,R,D (×103) | Dead, QALY, Infected | |
| 0–19 | 1.9 | 10,717.0 | 0% | 2.7 | 10,712.0 | 0% | 4.2 | 10,708.9 | 0% | 5.4 | 10,637.8 | 0% | 0.6 | 10,488.5 | 0% |
| 2.0 | 0% | 1.5 | 100% | 3.8 | 100% | 61.2 | 0% | 86.5 | 0% | ||||||
| 0.8 | 0% | 6.3 | 0% | 7.0 | 0% | 20.8 | 0% | 144.7 | 0% | ||||||
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |||||||||||
| 20–39 | 1.8 | 13,091.4 | 0% | 2.2 | 13,073.2 | 0% | 5.0 | 13,065.2 | 0% | 5.6 | 12,940.8 | 0% | 0.6 | 12,647.2 | 0% |
| 12.9 | 0% | 3.7 | 10% | 9.8 | 0% | 107.1 | 0% | 165.0 | 0% | ||||||
| 5.5 | 0% | 33.0 | 92% | 34.9 | 92% | 61.9 | 92% | 297.5 | 4% | ||||||
| 0.0 | 0.1 | 0.1 | 0.1 | 0.2 | |||||||||||
| 40–59 | 1.4 | 18,492.2 | 0% | 1.3 | 18,463.4 | 0% | 4.2 | 18,459.3 | 0% | 6.3 | 18,314.3 | 0% | 0.6 | 17,894.1 | 0% |
| 32.9 | 0% | 4.0 | 0% | 6.5 | 0% | 125.5 | 0% | 229.7 | 0% | ||||||
| 14.9 | 0% | 72.1 | 0% | 73.7 | 0% | 99.5 | 0% | 414.3 | 38% | ||||||
| 0.9 | 1.5 | 1.6 | 1.7 | 2.8 | |||||||||||
| 60–79 | 1.2 | 13,383.4 | 56% | 0.9 | 13,363.9 | 56% | 3.2 | 13,362.3 | 56% | 6.3 | 13,292.3 | 56% | 0.7 | 13,060.0 | 56% |
| 31.3 | 56% | 2.5 | 0% | 3.2 | 0% | 60.6 | 56% | 126.5 | 56% | ||||||
| 9.0 | 56% | 52.7 | 0% | 53.5 | 0% | 65.0 | 0% | 222.2 | 0% | ||||||
| 8.4 | 13.0 | 13.0 | 14.1 | 23.4 | |||||||||||
| >79 | 2.7 | 4,408.6 | 100% | 0.4 | 4,381.2 | 100% | 1.8 | 4,380.6 | 100% | 6.2 | 4,353.9 | 100% | 0.8 | 4,248.3 | 100% |
| 22.8 | 100% | 1.9 | 0% | 1.9 | 26% | 23.4 | 100% | 57.9 | 100% | ||||||
| 0.6 | 100% | 38.3 | 0% | 38.8 | 0% | 41.6 | 0% | 95.2 | 100% | ||||||
| 10.0 | 20.6 | 20.8 | 23.0 | 40.7 | |||||||||||
The first simulation starts on April 14, 2020, which represents the containment phase of the pandemic due to the lockdown imposed by the Italian government. At that date, the scenario was characterized by a mean Rt value of about 1.8, a number of about 100,000 infected individuals and a very high number of daily deaths in the most advanced age groups. With this starting scenario, the optimal vaccination plan is the same, whatever the chosen cost function. In particular, the minimum value of the cost function is always obtained by vaccinating 100% of people in the highest age group (i.e. those over 79 years old) and administering the remaining vaccine doses to people in the immediately preceding age group (i.e. aged between 70 and 79 years). If the chosen goal is to minimize the number of deaths or the number of QALYs lost, this strategy is likely due to the number of deaths recorded in mid-April in those age groups which is far greater than in other age groups (see Fig. 5 d). If, on the other hand, the chosen goal is to minimize the overall number of infections and, therefore, the daily number of new cases of infection, the strategy of vaccinating 100% of the oldest individuals is due to the very high value of b in this age group, which is about six times that observed in the 60–79 age group, i.e., the second highest at that date (see Fig. 5 b).
The second simulation starts from the scenario observed on August 12, 2020, which corresponds to a phase of the pandemic in which new cases of infection and deaths are few. At that date, however, individuals under 60 had a value of Rt greater than 1, while in the older age groups the Rt value was still below the critical threshold of 1 (see Fig. 5 a). In particular, the highest value of Rt, which is observed in the age range of the youngest, is equal to 3 times that observed in the age group ranging from 60 to 79 years and about 7 times that observed in people aged 80 or older. Moreover, at that date, the 20–39 age group had the highest value of parameter b, which was about twice as high as the second highest value found in the age group of the youngest (0–19 years). Older people showed significantly lower values of b (see Fig. 5 b). Despite the Rt and b values, the goal of minimizing the number of deaths is also achieved in this context by vaccinating 100% of persons in the highest age group (i.e., those over 79 years) and administering the remaining doses of vaccine to persons in the immediately preceding age group (i.e., those aged 70–79 years). On the other hand, the optimal strategy changes dramatically if the goal is to minimize the number of QALYs lost or the overall number of infections. To achieve either of these goals, available vaccine doses must be used to vaccinate the first two younger age groups. Specifically, if the goal chosen is to minimize the number of QALYs lost, the algorithm suggests vaccinating 100% of the first age group, i.e., the one with the highest Rt value, whereas if the goal is to minimize the overall number of infections, it is necessary to vaccinate almost all people aged 20–39 years, i.e., the age group with the highest b value.
The third simulation starts from the data collected on September 2, 2020. On this date, the estimated values of Rt and b in the 20–39 age group are the highest of all. It should be noted, however, that while the value of b in that age group is much higher than that observed in all other age groups, the value of Rt, while being the highest, is not dramatically greater than those observed in the two adjacent age groups, i.e., 0–19 years and 40–59 years (see Fig. 5 a and b). The largest number of new infections is also observed in the 20–39 year age group (see Fig. 5 c), while the greatest number of deaths, although still low, are found in individuals aged 80 and over (see Fig. 5 d). Again, the goal of minimizing the number of deaths is achieved by vaccinating 100% of people in the highest age group and administering the remaining doses of vaccine to people in the age group immediately before that. If, on the other hand, the chosen goal is to minimize the number of infections the suggested strategy requires vaccinating predominantly people belonging to the age group with the highest b value. Finally, minimizing lost QALYs requires vaccinating 100% of the individuals in the youngest age group and administering the remaining doses of vaccine to the oldest group of individuals. The choice to vaccinate all persons aged 0–19 years is probably due to the fact that this age group is the one to which the highest value of expected QALYs corresponds and has an Rt not far from the highest observed at that date. On the other hand, the strategy of using the remaining vaccines in the over-80-year-old group could be explained by the combination of a significantly high Rt value (almost twice as high as 1) and a drastically high lethality rate that characterizes this age group.
At the start date of the fourth simulation (November 4, 2020), the Rt value was dramatically high and very similar in all age groups (see Fig. 5 a). Consequently, at the time, the number of infected individuals and the number of daily deaths were growing rapidly (see Fig. 5 c and d). In this situation, where the Rt value is quite similar in the five age groups considered, the strategy suggested to minimize the number of deaths or that of QALY lost is the mass vaccination of over 80 s and the use of the remaining doses in individuals of the immediately preceding age group (i.e. between 60 and 79 years). Minimizing the number of infections, on the other hand, again requires vaccinating primarily those between the ages of 20 and 39 and does not include vaccinating the older population. In fact, even in early November, the highest value of parameter b was observed in the 20- to 39-year-old age group (see Fig. 5 b).
The results referring to the simulation starting from the scenario recorded on December 20, 2020, show that the optimization of the cost function that takes into account the number of deaths or the number of QALYs lost leads to a result identical to that obtained in the simulations performed starting from November 4, 2020: the suggested strategy is to vaccinate 100% of the over-80s and to use the remaining doses of vaccine for the 60–79 age group. Although starting from very different initial contexts, these simulations have in common the fact that Rt, while dramatically high on November 4 and significantly below 1 on December 20, assumes in the two scenarios rather similar values in the five age groups considered. This seems to indicate that when the value of Rt is uniform within the population, the choice to vaccinate the elderly pays off not only in terms of the number of deaths, but also in terms of QALYs lost. Different results are obtained if the cost function to be optimized takes into account the number of infections. Even in the initial December 20 scenario, however, the strategy chosen to minimize the number of infections confirms the priority of vaccinating age groups with a higher b value.
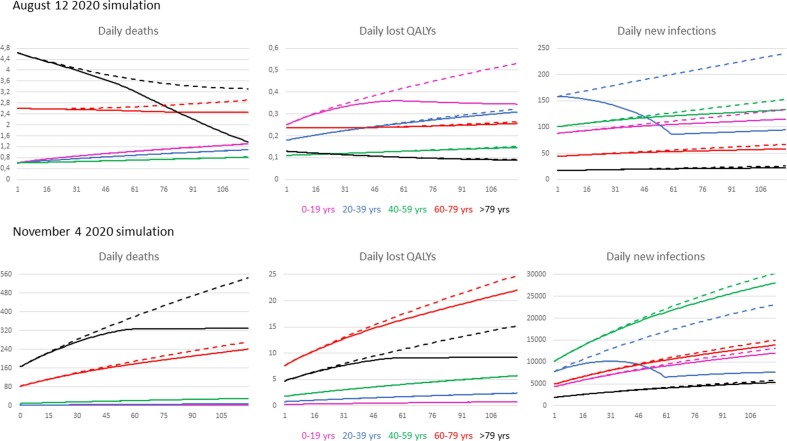
Fig. 6 provides quantitative information on the outcomes that can be obtained by applying the different vaccination plans suggested by the optimization of each cost function considered. In particular, for each cost function considered, the model outcome obtained by applying the optimal strategy is compared with the corresponding one obtained by assuming that no intervention, both behavioural and vaccinal, is carried out on the system to contain the pandemic. The comparison was made starting from the initial conditions recorded on a predetermined date and following the evolution of the pandemic predicted by the model in both hypothesized situations over the following 120 days. Two starting scenarios were examined corresponding to the dates of August 12 and November 4, 2020. In the figure, outcomes obtained in different age groups are marked with different colours. In particular, each solid line indicates the outcome obtained with the optimal strategy and the dashed one indicates what would have happened by letting the pandemic evolve without any containment intervention.
Fig. 6.
Vaccine simulation of the age-grouped SIRD model, starting from initial conditions identified from actual Italian CoViD data on August 12 and November 4. Dashed and solid lines represent simulation results without and with the best vaccination plan, respectively.
With the goal of minimizing the number of deaths, the strategy suggested by the simulation model, by reducing the number of daily deaths in the two older age groups, significantly reduces the total number of deaths at the end of the 120-day period. Starting from the most critical scenario recorded on November 4, Fig. 6 shows that, without any containment intervention, the number of daily deaths in the two oldest age groups would have increased linearly with a high slope, reaching at the end of the 120 days of observation a number of daily deaths in the oldest individuals equal to 560, i.e. more than 10 times greater than that obtained globally in the three youngest age groups. It is therefore obvious that in such a situation, the strategy to be followed to minimize deaths is to vaccinate the oldest. The result obtained with this strategy is a substantial containment of the number of daily deaths which, at the end of the 120 days of observation, are about 30% less than those that would have been observed in the absence of the vaccination plan. A similar behavior, although much less dramatic, is also obtained starting from the scenario recorded on August 12, 2020.
The decision to use the strategy based on the optimization of the cost function that takes into account the number of QALYs lost leads in both cases shown in Fig. 6 to choose a vaccination plan that gives priority to vaccinate those age groups to which, in the absence of any containment strategy, would correspond at the end of 120 days of observation the highest daily losses of QALYs. In particular, it is interesting to note that, starting from the scenario observed on August 12, the strategy suggested by the simulation model (see Table 1) indicates to vaccinate both the age group between 0 and 19 years and that between 20 and 39 years. In fact, the choice to totally vaccinate the first class might have been intuitive on August 12, because already at that date this group of people corresponded to the maximum of lost QALYs. In contrast, the choice to vaccinate the 20–39 age group was far from trivial, because with the data available on August 12, one could reasonably have chosen to vaccinate the 60–79 age group. This choice would have proved to be wrong in retrospect, because, in the absence of containment strategies, at the end of the 120-day observation period the number of daily QALYs lost in the 20–39 age group significantly exceeds that corresponding to the 60–79 age group. Undoubtedly, in the present case, vaccinating a small group of people aged 20–39 years did not lead to a meaningful outcome at the end of 120 days because the number of available vaccines was limited and only 10% of that age group could be vaccinated with the available doses. However, the simulation approach had undoubtedly identified the way forward, which would have led to a significant result if more vaccine doses were available.
Finally, in the two situations shown in Fig. 6, the goal of minimizing the number of infections is achieved using an identical strategy (see Table 1). In this case, while the strategy suggested by the model is clearly intuitive with respect to the choice made from the scenario observed on August 12, it is more difficult to explain the strategy suggested by the model from the November 4 scenario. However, in the latter case, the result obtained with the suggested strategy is really interesting, since at the end of the 120 days of observation the number of new daily infections decreased by about a quarter compared to what it would be in the absence of a containment strategy.
4. Discussion
Compartmental models, although based on stringent assumptions, have long been used to effectively explain the dynamics of epidemic phenomena and simulate their evolution, under a variety of different conditions [10].
Calafiore et al. also developed a time-varying SIRD model based on Italian public data, but the model does not account the differences between age and sex groups. Furthermore, while we propose the model for optimizing pandemic containment strategies, such as vaccination, starting from real conditions, Calafiore et al. focused on the consistency between the actual data and the predictions made [6].
The use of time-varying parameters allows the modeling of pandemic trends in which conditions change due to containment strategies such as lockdown, vaccination campaigns, changing characteristics of health care and infectious conditions, changes in recovery and mortality rates due to new therapies or increased infectivity resulting from genetic mutations, rule transgression, etc.
Having applied the model to vaccine strategy choices is an example aimed at concretely illustrating the utility of a SIRD model stratified by age groups. Age groups can also be traced to specific social and occupational activities, that are associated with increases or decreases in infections. For example, analyzing the age-group behavior of children and adolescents in open school conditions may allow to identify and quantify possible effects of increased infections and speculate on the appropriateness and effectiveness of targeted measures, such as school closures.
The choice of a SIRD-type model made it possible to reach a satisfactory compromise between the possibility of approximating Italian public data and the availability/quality of the latter in terms of disaggregation by sex and age groups. Given the general uncertainties about data collection, in terms of poor quality of available data, incompleteness, noise, temporal asynchrony, lack of precise and complete distributions by age group and sex, etc. [17], it seemed inadvisable to propose more complex models such as the SEIRD model, because the exposed individuals, E, are difficult to define with sufficient accuracy and far from easy to identify [12], [13]. On the other hand, simpler models, such as the SIR model, appeared limiting because differentiated data were available between healed and deceased, the latter also distributed by sex and age.
A major problem in the collection of daily data is their poor quality in terms of misses, delays in collection, and reporting [17], [18].
Our proposed model is not able to correct for data underreporting and under-ascertainment, which conversely other approaches address [32]. In general, techniques for the reconstruction of missing data are based on a priori assumptions that represent a weakness point. Our 7-days moving average window allows the influence of such biases on time-varying parameter estimates, which are more pronounced in the early stages of the pandemic, to be quickly forgotten. As time goes by, their impact tends to fade, thanks to more careful and effective testing procedures.
Daily fluctuations with an almost weekly periodicity, led us to pre-process the data with a 7-day moving average filter, as a suitable compromise between noise reduction and preservation of information regarding the correct dynamics of the phenomenon. Also another Italian institute (National Institute of Nuclear Physics), had already used the moving average technique to follow the pandemic trend in time and to reduce the variability, but using a period of 14 days [33].
As mentioned earlier, compartment epidemic models are based on stringent assumptions. The first concerns the fact that the system must be closed, with no contact with the outside world, which in the present case corresponds to contacts with neighboring nations or resulting from international transport. This hypothesis, during the CoViD-19 pandemic, is sufficiently respected as the States have closed the boundaries and reduced to a minimum the international contacts. In Italy, people have been often limited in the movements between different regions.
A second assumption underlying the compartmental models concerns the homogeneous distribution of individuals within compartments, which assumes that all individuals in the various compartments are equally likely to contact each other [9]. By dividing susceptible individuals into age and sex groups, we mitigated possible inhomogeneities in contact behavior by assigning different mean number of contacts, different recovery rate, and different mortality rate to the various classes.
The time-varying parameters of the SIRD model were estimated from the actual data using a simple moving average approach. A limitation of this approach is that it does not account for the uncertainty in the parameter estimates. Other more sophisticated techniques could be used to estimate time-varying parameters and to control noise, such as linear regression, Monte Carlo Markov Chains, recursive least squares techniques, etc. [6]. In addition, a sensitivity analysis would allow quantifying the effects of imprecise estimates on the simulation results, which, however, is beyond the scope of this paper. In fact, the parameter estimates, which we obtained from the real data, reproduce truthful initial conditions for the simulation, which fully satisfy the aims of the present study.
The model's assumption of an equal distribution of removal rates for each class function was necessary to estimate group-distributed recovered individuals, without which a model grouped by age and gender could not have been employed. Other hypotheses could have been made, regarding the different number of removed individuals in the different classes, possibly supported by specific literature data. To the best of our knowledge, no data have been published on the of sex- and age-distribution recovered individuals. This may be due to the less emphasis on recovered individuals and greater difficulty in accurately identifying them. Especially on this last point, there are discordant opinions regarding the recovered individuals who did not need hospital care. The period from the date of diagnosis to the date of discharge may give information about the recovery time; thus, the hypothesis could be improved. However, there is no uniformity on this aspect. Yan-ni Mi et al. estimated a cure time of 14.6 days (95% confidence interval 6.9–21.0); Manash et al. estimated a recovery rate of 25 days (95% confidence interval 16.1–33.9), however the sample was constituted by hospitalized subjected so they may be the ones with more severe symptoms [34], [35].
Another problem related to recovery time is the identification of disease onset because several days can pass between the time CoViD-19 was contracted, the onset of symptoms, and diagnosis. Having more information available, such as national or international data disaggregated by age group and sex, we could have estimated the parameters more accurately and avoided making reconstructive assumptions that, however, are not unrealistic.
The simulation of an optimized vaccination plan was proposed to concretely illustrate the usefulness of an age-distributed SIRD model. We decided to consider and show the results for three simple cost functions: the number of new infections, deaths and QALYs lost. Of course, other different cost functions could have been chosen. Other scenarios could have also been simulated, such as a different vaccination period/rate and a larger number of available doses.
The results obtained clearly showed that the optimal vaccination plan depends not only on the type of cost function chosen, but also on the initial conditions, such as the values of the model parameters, estimated from the real data at the beginning of the simulated vaccination program.
Although the identification of an optimal vaccine plan is only one example to assess the potential of the proposed modeling approach, the achieved results nevertheless provide some interesting information and confirmations. Thus, for example, if the goal is to minimize the number of deaths, the modeling approach indicates that regardless of the scenario taken as a starting point, the vaccination plan always requires vaccinating as many people as possible in the highest age groups. This is far from surprising, because it means that to minimize the number of deaths, it is always necessary to start vaccination from the age groups with the highest lethality rates. On the other hand, this is the vaccination strategy that has been chosen in many countries, such as Italy.
Less trivial is the fact that the choice to vaccinate the elderly also pays off in terms of lost QALYs when the Rt value is uniform within the population and, even more so, when it is higher in older age groups. Of course, the result changes if it is the young people who have the highest Rt values.
5. Conclusions
The approach proposed to decipher the course of the CoViD-19 pandemic in Italy, based on the time-varying SIRD compartment model, stratified by sex and age groups, allowed observing and quantifying group-dependent distributions of susceptible, infected, recovered, and deceased people, as well as rates of contact, recovery, and death.
Due to the poor quality and insufficient stratified availability of data collected by national and international authorities, ad hoc reconstruction and filtering procedures of existing data were developed.
An application for model simulation of optimal vaccination campaigns has shown interesting results, consistent with the specific features of the phenomenon. In particular, various scenarios represented starting from different phases of the pandemic and using different cost functions (amount of infected, lost QALY and deceased people), have provided outcomes highly dependent on initial and boundary conditions.
In conclusion, the proposed model seems to be a useful decision support tool, allowing predicting quantitatively the effects of ad hoc strategies to combat epidemics/pandemics, based on actions differentiated by population groups.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
CRediT authorship contribution statement
Alessandra Cartocci: Conceptualization, Writing - original draft, Writing - review & editing, Visualization, Data curation. Gabriele Cevenini: Conceptualization, Data curation, Methodology, Software, Writing - original draft, Writing - review & editing. Paolo Barbini: Conceptualization, Methodology, Writing - original draft, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The authors would like to thank the engineer Riccardo Gimignani for supporting this work by organizing the data.
References
- 1.Zhu N., Zhang D., Wang W., Li X., Yang B., Song J., Zhao X., Huang B., Shi W., Lu R., Niu P., Zhan F., Ma X., Wang D., Xu W., Wu G., Gao G.F., Tan W. China Novel Coronavirus Investigating and Research Team, A Novel Coronavirus from Patients with Pneumonia in China. N. Engl. J. Med. 2019;382(2020):727–733. doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wu F., Zhao S., Yu B., Chen Y.-M., Wang W., Song Z.-G., Hu Y., Tao Z.-W., Tian J.-H., Pei Y.-Y., Yuan M.-L., Zhang Y.-L., Dai F.-H., Liu Y., Wang Q.-M., Zheng J.-J., Xu L., Holmes E.C., Zhang Y.-Z. A new coronavirus associated with human respiratory disease in China. Nature. 2020;579:265–269. doi: 10.1038/s41586-020-2008-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cucinotta D., Vanelli M. WHO Declares COVID-19 a Pandemic. Acta Biomed. 2020;91:157–160. doi: 10.23750/abm.v91i1.9397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.T. Struyf, J.J. Deeks, J. Dinnes, Y. Takwoingi, C. Davenport, M.M. Leeflang, R. Spijker, L. Hooft, D. Emperador, S. Dittrich, J. Domen, S.R.A. Horn, A. Van den Bruel, Cochrane COVID-19 Diagnostic Test Accuracy Group, Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19 disease, Cochrane Database Syst. Rev. 7 (2020) CD013665. 10.1002/14651858.CD013665. [DOI] [PMC free article] [PubMed]
- 5.Jin J.-M., Bai P., He W., Wu F., Liu X.-F., Han D.-M., Liu S., Yang J.-K. Gender differences in patients with COVID-19: focus on severity and mortality. Front Public Health. 2020;8:152. doi: 10.3389/fpubh.2020.00152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Calafiore G.C., Novara C., Possieri C. A time-varying SIRD model for the COVID-19 contagion in Italy. Annu. Rev. Control. 2020;50:361–372. doi: 10.1016/j.arcontrol.2020.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ning W., Lei S., Yang J., Cao Y., Jiang P., Yang Q., Zhang J., Wang X., Chen F., Geng Z., Xiong L., Zhou H., Guo Y., Zeng Y., Shi H., Wang L., Xue Y., Wang Z. Open resource of clinical data from patients with pneumonia for the prediction of COVID-19 outcomes via deep learning. Nat. Biomed. Eng. 2020;4:1197–1207. doi: 10.1038/s41551-020-00633-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bonacini L., Gallo G., Patriarca F. Identifying policy challenges of COVID-19 in hardly reliable data and judging the success of lockdown measures. J. Popul. Econ. 2020:1–27. doi: 10.1007/s00148-020-00799-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tolles J., Luong T. Modeling Epidemics With Compartmental Models. JAMA. 2020;323:2515–2516. doi: 10.1001/jama.2020.8420. [DOI] [PubMed] [Google Scholar]
- 10.Chitnis N. Einführung in die mathematische epidemiologie: introduction to mathematical epidemiology: deterministic compartmental models. Autumn Semester. 2011 [Google Scholar]
- 11.J. Jia, J. Ding, S. Liu, G. Liao, J. Li, B. Duan, Modeling the control of COVID-19: Impact of policy interventions and meteorological factors. arXiv preprint arXiv:2003.02985 (2020).
- 12.G. Giordano, F. Banchini, R. Bruno, P. Colaneri, A. Di Filippo, A. Di Matteo, M. Colaneri, A SIDARTHE model of COVID-19 epidemic in Italy. arXiv preprint arXiv:2003.09861(2020). [DOI] [PMC free article] [PubMed]
- 13.López L., Rodó X. A modified model to predict the COVID-19 outbreak in Spain and Italy: simulating control scenarios and multi-scale epidemics. Results Phys. 2021;21 doi: 10.1016/j.rinp.2020.103746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.E. Loli Piccolomini, F. Zama, Preliminary analysis of COVID-19 spread in Italy with an adaptive SEIRD model. arXiv, arXiv-2003 (2020).
- 15.Balabdaoui F., Mohr D. Age-stratified model of the COVID-19 epidemic to analyze the impact of relaxing lockdown measures: nowcasting and forecasting for Switzerland. MedRxiv. 2020 [Google Scholar]
- 16.Jaberi-Douraki M., Moghadas S.M. Optimal control of vaccination dynamics during an influenza epidemic. Math. Biosci. Eng. 2014;11:1045–1063. doi: 10.3934/mbe.2014.11.1045. [DOI] [PubMed] [Google Scholar]
- 17.S. Richardson, D. Spiegelhalter, Coronavirus statistics: what can we trust and what should we ignore, The Guardian. https://www.theguardian.com/world/2020/apr/12/coronavirus-statistics-what-can-we-trust-and-what-should-we-ignore.
- 18.Sartor G., Del Riccio M., Dal Poz I., Bonanni P., Bonaccorsi G. COVID-19 in Italy: Considerations on official data. Inte J Infect Dis. 2020;98:188–190. doi: 10.1016/j.ijid.2020.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Böger B., Fachi M.M., Vilhena R.O., et al. Systematic review with meta-analysis of the accuracy of diagnostic tests for COVID-19. Am. J. Infect. Control. 2021;49:20–29. doi: 10.1016/j.ajic.2020.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mizumoto K., Kagaya K., Zarebski A., Chowell G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Euro Surveill. 2020;25 doi: 10.2807/1560-7917.ES.2020.25.10.2000180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen Y.C., Lu P.E., Chang C.S., Liu T.H. A time-dependent SIR model for COVID-19 with undetectable infected persons. IEEE Trans. Network Sci. Eng. 2020;7:3279–3294. doi: 10.1109/TNSE.2020.3024723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.COVID-19: What Proportion are Asymptomatic?. Centre for Evidence-Based Medicine, Oxford. https://www.cebm.net/covid-19/covid-19-what-proportion-are-asymptomatic/, 2020 (Accessed December, 2020).
- 23.Heesterbeek J.A.P., Roberts M.G. The type-reproduction number T in models for infectious disease control. Math. Biosci. 2007;206:3–10. doi: 10.1016/j.mbs.2004.10.013. [DOI] [PubMed] [Google Scholar]
- 24.Heesterbeek J.A.P. A brief history of R0 and a recipe for its calculation. Acta Biotheor. 2002;50:189–204. doi: 10.1023/a:1016599411804. [DOI] [PubMed] [Google Scholar]
- 25.Diekmann O., Heesterbeek J.A., Metz J.A. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- 26.CoViD-19 bulletin, Istituto superiore di Sanità. https://www.epicentro.iss.it/coronavirus/aggiornamenti, 2020 (Accessed January, 2021).
- 27.CoViD-19 data, Protezione Civile. https://github.com/pcm-dpc/COVID-19, 2020 (Accessed January, 2021).
- 28.McAloon C., Collins A., et al. Incubation period of COVID-19: a rapid systematic review and meta-analysis of observational research. BMJ Open. 2020;10(8) doi: 10.1136/bmjopen-2020-039652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Whitehead S.J., Ali S. Health outcomes in economic evaluation: the QALY and utilities. Br. Med. Bull. 2010;96:5–21. doi: 10.1093/bmb/ldq033. [DOI] [PubMed] [Google Scholar]
- 30.Italian life expectancy, ISTAT. http://dati.istat.it/Index.aspx?DataSetCode=DCIS_MORTALITA1, 2020. (Accessed December, 2020).
- 31.Age distributed Italian population, ISTAT. http://dati.istat.it/Index.aspx?QueryId=42869. (Accessed December, 2020).
- 32.Brookmeyer R., Yasui Y. Statistical analysis of passive surveillance disease registry data. Biometrics. 1995:831–842. doi: 10.2307/2532985. [DOI] [PubMed] [Google Scholar]
- 33.Istituto Nazionale di Fisica Nucleare. https://home.infn.it/it/, 2020 (Accessed December, 2020).
- 34.Mi Y.-N., Huang T.-T., Zhang J.-X., Qin Q., Gong Y.-X., Liu S.-Y., Xue H.-M., Ning C.-H., Cao L., Cao Y.-X. Estimating the instant case fatality rate of COVID-19 in China. Int. J. Infect. Dis. 2020;97:1–6. doi: 10.1016/j.ijid.2020.04.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Barman M.P., Rahman T., Bora K., Borgohain C. COVID-19 pandemic and its recovery time of patients in India: a pilot study. Diabetes Metab. Syndr. 2020;14:1205–1211. doi: 10.1016/j.dsx.2020.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]