Abstract
Near-infrared spectroscopy (NIRS) is a fast and powerful analytical tool in the food industry. As an advanced chemometrics tool, multi-way analysis shows great potential for solving a wide range of food problems and analyzing complex spectroscopic data. This paper describes the representative multi-way models which were used for analyzing NIRS data, as well as the advances, advantages and limitations of different multi-way models. The applications of multi-way analysis in NIRS for the food industry in terms of food process control, quality evaluation and fraud, identification and classification, prediction and quantification, and image analysis are also reviewed. It is evident from this report that multi-way analysis is presently an attractive tool for modeling complex NIRS data in the food industry while its full potential is far from reached. The combination of multi-way analysis with NIRS will be a promising practice for turning food data information into operational knowledge, conducting reliable food analyses and improving our understanding about food systems and food processes. To the best of our knowledge, this is the first paper that systematically reports the advances on models and applications of multi-way analysis in NIRS for the food industry.
Keywords: near-infrared spectroscopy, food industry, chemometrics, multi-way analysis, applications
1. Introduction
Near-infrared spectroscopy (NIRS) is a fast and powerful analytical tool. It has gained widespread acceptance in both the scientific community and industry. NIRS uses the near-infrared region of the spectrum, commonly defined from 780 nm to 2500 nm, where most absorption bands are molecular overtones or combination vibrations bands [1]. Compared with other spectroscopy methods, NIRS is deemed to be more attractive by virtue of its non-destructive nature, high speed of analysis, ease-of-use and low cost [2]. It is widely applied in various fields, such as environment [3,4], agriculture [5,6], food [7,8], pharmaceutical [9,10], clinical medicine [11,12], and remote sensing [13,14]. As one of the dominant vibrational spectroscopies in the food industry, NIRS is extensively used for food classification, component characterization, quality evaluation and process control, where its effectiveness for fingerprinting food materials and analyzing different critical parameters has been proven [15].
The rapid development of chemometrics during the past decades is progressing and advancing a lot of scientific areas which are highly overlapped with analytical science, including food science [16]. Combined with an instrumental analysis, the use of chemometrics tools leads to more advances in understanding food products and food systems [17]. However, some challenges arise in food science when entering a digital and instrument-heavy area. One of the biggest challenges is to effectively explore and model the complex and large data sets; NIRS data are one such data source. It is well known that NIRS suffers from the problems of nonlinear behavior, the scatter effect and broad overlapped bands, as well as the artifact effect, such as temperature disturbances, which easily lead to models with bad predictions and challenging interpretations. Previous studies have shown that rearranging data with nonlinear behavior into higher-order arrays can be a promising way to improve the predictions of the chemometrics model [18]. Dealing with this kind of high-order array requires high-order chemometrics tools which are complex but more promising for producing satisfying results. Meanwhile, the widely used two-way chemometrics tools for modeling NIRS related data, such as a principal component analysis (PCA) [19,20] and partial least square (PLS) [21,22], have different drawbacks in practice. For example, they have difficulty in predicting the new samples with a slightly different nature (e.g., due to unexpected temperature variations), and sometimes the interpretation of the models’ results can be very difficult because of the rotation freedom [20]. Moreover, the model performance can be easily affected if too much redundant information existed in the modeled spectra. Even though variable selection methods can be beneficial for improving models to some extent, the risk of overfitting cannot be ignored in this approach. Advanced chemometrics tools such as multi-way analysis methods could thus be considered by food technologists and researchers for the purpose of analyzing complex NIRS data and establishing valuable models with more flexibility, simple interpretations, and robust results [23].
In many scientific fields, a multi-way data analysis is popular and frequently appears under the name tensor analysis [24]. The multi-way analysis originated from the 1960s in social science [25,26]. Subsequently, many chemometricians contributed to the development of multi-way models and solved many issues in this area [27]. For example, Wold et al. [28] provided the initial idea of N-way partial least square regression (N-PLS) in the 1980s and illustrated it with chemical mixture data recorded from liquid chromatography and ultraviolet spectrometry. Bro [29] further developed the real N-PLS model for both three-way and higher order arrays, and illustrated the algorithms with an example from the sugar industry. The application of the multi-way analysis for solving food science problems is relatively new. It has, however, shown a great deal of success in analyzing complex food data and solving a wide range of food-related problems [30,31,32]. Owing to the so-called second order advantage [33], most of the multi-way analysis models have the ability to extract hidden information from complex data, finding the latent relationship between variables, while avoiding using a large number of different calibration sets [34]. For instance, the combination of multi-way analysis with spectroscopy can be used for the real-time reaction process monitoring of compounds of interest for a complex food system. It was reported that the combination of NIRS, multi-way chemometrics and process knowledge is taking place in process analytical technology (PAT) [23]; that is to say, multi-way analysis provides a useful tool for analyzing complex process data [35]. Moreover, other “higher-order advantages” of multi-way analyses, e.g., increasing sensitivity when the data dimension increases and the ability to solve high collinearity, are also beneficial for solving many practical problems [36].
In this paper, we focus on models and applications of multi-way analysis combined with NIRS for both food products and food process analyses. The contents of this paper are organized as follows. The second part explains the used notations and abbreviations. The third part describes the multi-way models which were used for analyzing NIRS data, as well as the advances, advantages and limitations of different models. The preprocessing techniques for multi-way analysis for analyzing NIRS data are briefly described in the fourth part. In the fifth part, the applications of multi-way analysis in NIRS for the food industry are reviewed in terms of food process control, quality evaluation and fraud, identification and classification, prediction and quantification, and image analysis. The available software and algorithms for multi-way analysis are introduced in the sixth part. The conclusions are formulated in the last part. To the best of our knowledge, this is the first paper that systematically reports the advances on models and applications of multi-way analysis in NIRS for the food industry.
2. Notation and Abbreviations
In order to avoid confusion, we will use the conventional and standard notations from the multi-way analysis community. Consistent with the notation used in Kiers [37], we use non-bold italic letters, boldface lower-case italic letters and boldface upper-case letters to denote the scalars, vectors and matrixes, respectively, e.g., is a matrix, is the ith column of matrix and is the number of components of the model. A three-way array is denoted by . Each dimension of the three-way array is called a mode. The element of the three-way array is denoted by where i, j and k mean the indexes belonging to each of three modes of . The symbol is used to represent the Kronecker product, while denotes the Hadamard product [38]. All the used abbreviations in this paper are shown in Table 1.
Table 1.
The meaning of used abbreviations in the paper.
| Abbreviations | Explanations | Abbreviations | Explanations |
|---|---|---|---|
| NIRS | Near-infrared spectroscopy | N-PLS-DA | N-way partial least square regression-discriminant analysis |
| N-PLS | N-way partial least square regression | ATLD | Alternating tri-linear decomposition |
| PARAFAC | Parallel factor analysis | M-PCA | Multiway principal component analysis |
| PARAFAC2 | Parallel factor analysis 2 | PAT | Process analytical technology |
| Tucker3 | A tensor decomposition method proposed by Tucker | MLR | Multiple linear regression |
| CP | The combination name of canonical decomposition and PARAFAC | COMDIM | Analysis of common dimensions and specific weights |
| SNV | Standard normal variate | MSC | Multiplicative scatter correction |
| PCA | Principal component analysis | PLS | Partial least square |
| DTLD | Direct trilinear decomposition | VIS/NIR | Visible-near-infrared spectroscopy |
| FT-NIR | Fourier transform near-infrared spectroscopy | FT-IR | Fourier-transform infrared spectroscopy |
3. Multi-Way Models
3.1. N-PLS
N-way partial least squares (N-PLS) is a regression algorithm combining tri-linear decomposition and the classical PLS. In fact, it is an extension of the two-way PLS model to the multi-way case. The real N-PLS model was proposed by Bro [29] in 1996, which can be expressed as:
| (1) |
where the matrix is the unfold version of three-way array (), and are the weights matrixes of the second and third modes, is the score matrix of the first mode, and is the residual matrix. Imagine contains the dependent variable, then , where and are the scores matrix and loading matrix of , and is the residual for . The aim of the N-PLS model is to find the weight matrixes and that maximize the covariance between and . It is necessary to point out that this initial N-PLS model was limited by some problematic issues such as the perfect fit problem, uniqueness issues and impossible validation assessments of the parameters [39]. In order to fix these problems, Bro et al. [39] later proposed a modified N-PLS model by introducing a core array in the model of , and the new version of N-PLS model is widely used in different software today. The modified N-PLS model can be written as:
| (2) |
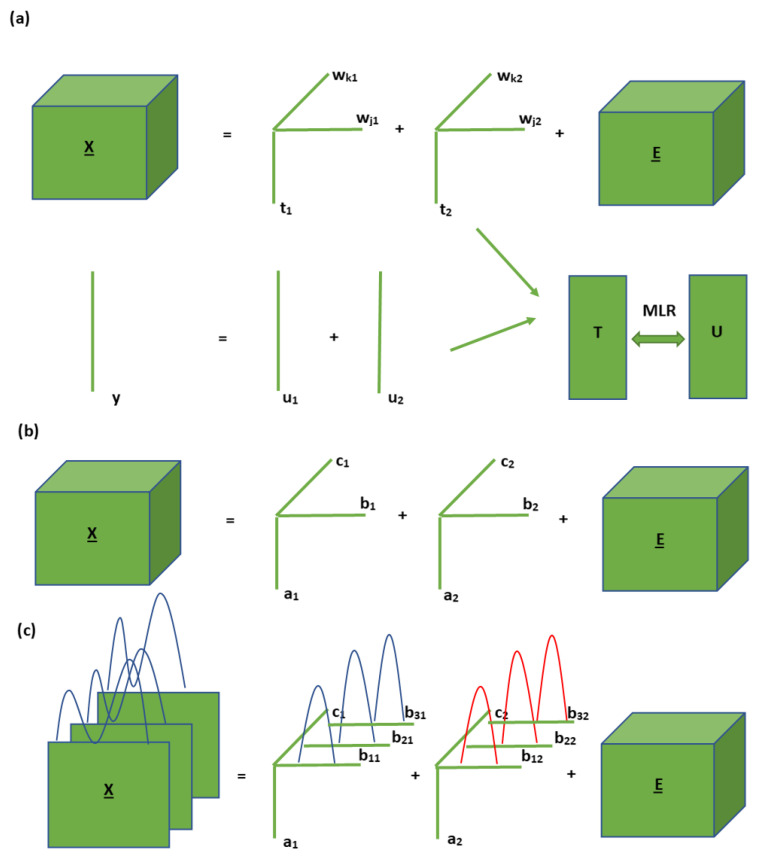
The difference with the old N-PLS model is the core array . It is the matricized core array of size , and it equals , where means the Moore–Penrose pseudo inverse. The new N-PLS model produces the same predictions as the original N-PLS model since only the way for modeling was optimized and nothing happened for the prediction part in the modified N-PLS model. More details about the calculation of the parameters can be found in Bro et al. [39]. The so-called N-way partial least square regression-discriminant analysis (N-PLS-DA) model is just the discriminant version of the N-PLS model. In N-PLS-DA, the dependent variable holds the class information, where each response variable is defined as a dummy variable with different values indicating a different category. A graphical representation of the reported multi-way models for three-way array with two components is shown in Figure 1.
Figure 1.
Graphical representation of the modeling process of: (a) N-way partial least square regression (N-PLS); (b) parallel factor analysis (PARAFAC) and (c) parallel factor analysis 2 (PARAFAC2) on three-way data with two components.
Compared with the two-way PLS model, the N-PLS model retains the multi-way information of the data, avoids the huge number of parameters caused by unfolding the multi-way array and the difficult model interpretation caused by the confounding of modes. It is capable of identifying multi-way data patterns and complex feature correlation. Apart from these advantages, N-PLS also has advantages in better modeling accuracy, robustness to noise, stabilized solution, increased predictability, etc. [40]. Some progress concerning the algorithm has been accomplished in recent years. Faber and Bro [41] investigated two methods for estimating the standard error of prediction in N-PLS models by calculating the estimates of all error variance and calculating an estimate of the standard deviation of the measurement error in the reference. In order to conduct variable selection for multi-way array with two spectral dimensions, Favilla et al. [42] extended the Variable Importance in Projection (VIP) method to the N-PLS model, which was illustrated to work well. Recently, Biancolillo et al. [43] proposed a sequential and orthogonalized N-PLS (SO-N-PLS) algorithm for analyzing multi-way data blocks by combining N-PLS and the so-called Sequential and Orthogonalized-PLS, and better model performances on small data sets and noisy data were achieved by this algorithm. Even though N-PLS is an attractive multi-way regression algorithm, it is important to point out that N-PLS models do not have second order advantages since they work under the same premises as ordinary PLS. This means that N-PLS cannot handle new interferences that were not in the calibration set. Furthermore, proper variable selection and preprocessing procedures are strongly recommended when using N-PLS for analyzing NIRS data in practice. Modeling the most interesting region by multi-way methods can always increase the knowledge of the studied system.
3.2. PARAFAC (Parallel Factor Analysis)
PARAFAC was first proposed by Harshman [44] in 1970. In the same year, Carroll and Chang [45] also proposed an identical model called Canonical Decomposition (CANDECOMP) in the context of multidimensional scaling. Since the name CANDECOMP is more common in other fields than in chemometrics, we will use name PARAFAC in this paper. PARAFAC can be regarded as an extension of PCA but with many other advantages for decomposing multi-way arrays [46]. Instead of containing a score vector and a loading vector in a component like in PCA, PARAFAC decomposes the data into a set of tri-linear components and each component is composed of three vectors representing the three modes, respectively. For a three-way array, the model for PARAFAC can be expressed as:
| (3) |
where is a matrix denoting the kth slab of three-way array , and the dimension of the three-way array is . Assuming is the number of components of the PARAFAC model, is a matrix for the first mode, is a matrix for the second mode, is a diagonal matrix in which the diagonal elements are the kth row of matrix and represent the profiles of components for the kth observation of the third mode, and is the residual matrix with the same dimension of . From a perspective of vectors, the PARAFAC model can be also expressed using the Kronecker product:
| (4) |
where , , denotes the fth column vector of loading matrixes , and respectively, and is the three-way residual array with the same dimension as .
One of the most attractive advantages of PARAFAC is the uniqueness of the solution [47], which means that the PARAFAC model cannot be rotated without a loss in fit. For PCA, it is well known that the inherent rotation freedom problem makes either external information or post-rotations necessary for the purpose of accurately identifying pure spectra. This is not the case in PARAFAC. If the data have a tri-linear structure and the noise in the data is appropriate, PARAFAC will always estimate the unique solutions (e.g., pure spectra) when using an appropriate number of components [46]. From a mathematical perspective, Kruskal [48] suggested the appropriate should fulfill the condition of in order to get the unique solution, where , and are the k-ranks of matrixes , and , respectively. Regarding more practical details about how to select the appropriate number of components for the PARAFAC model, we recommend to look into the paper written by Bro and Kiers [49]. Like many other multi-way models, PARAFAC is also less sensitive to the noise in the data and produces models with less complexity than two-way chemometrics methods; a detailed illustration regarding this can be found in Bro [46]. Furthermore, PARAFAC is also capable of analyzing multi-way data with large amounts of miss values. Tomasi and Bro [50] proposed that incorporating the ALS (alternating least squares) procedure with a single imputation or implementing the Levenberg–Marquadt procedure in the PARAFAC algorithm can deal with the data with a large number of missing values. Besides the aforementioned benefits, PARAFAC is also advantageous in its simple model structure, yielding more adequate and interpretable models, and dealing with a big and complex dataset [23,51].
Even though PARAFAC has gained extensive acceptance nowadays, there are still some issues hampering the use of PARAFAC in practice. For example, multi-way analysis and data arrangement experiences are needed; such knowledge can be challenging for people who are accustomed to using only two-way chemometrics tools. Apart from this, algorithm problems are maybe another major concern. For instance, slow convergence occurs especially when facing seriously collinear data. The two-factor degeneracy problem, which means two components become almost identical but with opposite signs, is also a practical concern. In order to improve the convergence speed of the conventional PARAFAC-ALS algorithm, a wide range of remedies have been developed, such as line search [52], enhanced line search [53], extrapolation with optimized step size and search direction [54] and compression [46]. Besides the ALS algorithm, some alternatives for calculating PARAFAC models have also been proposed, including the all-at-once algorithm [55], the hierarchical conjugate gradient algorithm [56], a random gradient algorithm [57,58], the fast damped Gauss–Newton algorithm [52], etc. These new alternatives were reported to have better convergence speed for many real cases. When fast convergence is required, these algorithms are valuable for exploration and test in the specific case. Regarding the two-factor degeneracy problem, it happens mostly from using too many components or because the established PARAFAC model is not appropriate for the data. Generally, the Tuckers congruence [59] and components plot can be used to detect the possible degeneracy problem. It was also reported that imposing some constraints on the PARAFAC model was beneficial for avoiding the degeneracy problem to some extent [60].
3.3. PARAFAC2 (Parallel Factor Analysis 2)
PARAFAC2 was also proposed by Harshman [61] in the 1970s. It is an important extension of the PARAFAC model because it allows the loading matrix in one mode to be shifted or have different lengths for different entities in one mode. Following Kiers et al. [62], the PARAFAC2 model can be written as:
| (5) |
where are defined in the same way as in the PARAFAC model. The difference is that the second mode matrix of PARAFAC is changed into in PARAFAC2, which means there is a specific and individual for each k of the—in this case—third mode. Thus, the strict tri-linearity assumption is actually relaxed in one mode in the PARAFAC2 model. Compared with the assumption of PARAFAC which is requiring to keep the same shape for each k, only the cross products of are constrained to be constant for each k in the third mode in PARAFAC2 [62]. This less strict constraint was illustrated to be a precondition for obtaining the uniqueness in PARAFAC2 by Ten Berge and Kiers [63]. The constant cross product property is obtained by making , where is an orthogonal matrix with dimension of thus and is a common matrix with dimension . Details about the mathematical proof can be found in the initial paper [62]. Hence, is concerned with the uniqueness for each observation in the varying mode (shift or different length) while is concerned with the observations [64]. Understanding the uniqueness and the model assumption of the PARAFAC2 model is of vital importance since it will directly affect whether it is applied in a proper way for real data.
Owing to the advantage of the less strict tri-linearity requirement, which is often more realistic in the real world, PARAFAC2 is widely applied for solving a wide range of complex data analysis problems, e.g., the problem of varying batch trajectories in food process analyses (different batches have different numbers of NIRS spectra) or analyzing complex NIRS image data. As an important multi-way analysis model, PARAFAC2 has all the advantages of the general PARAFAC model. One of the challenges of the PARAFAC2 algorithm is how to impose the non-negativity constraints on all three modes. For the conventional PARAFAC2-ALS algorithm, it is not possible to impose a non-negativity constraint on the shifted mode, thus only two modes can be constrained. Recently, Cohen and Bro [65] proposed a flexible PARAFAC2 algorithm and made it possible to impose non-negativity constraints on all the three modes by casting the PARAFAC2 model as a coupled matrix factorization model. For the applications where all the modes are required to be non-negative, this flexible PARAFAC2 algorithm will be of great value. Furthermore, a core based PARAFAC algorithm has also been proposed recently with a possibility of imposing non-negativity constraints [66]. However, strict non-negativity cannot be guaranteed in this algorithm since the transformation matrixes operate on orthogonal factor matrixes. Another practical concern is the local minima problem. The PARAFAC2 decomposition is inherently a non-convex optimization problem, and thus it is a NP-hard problem [67] with one of its aspects being the local minima. A useful remedy for avoiding the local minimum is to repeat the PARAFAC2 model calculation for several times, then choose the model with the best fit as the global minimum model. However, it is very ad hoc. More explorations from the algorithm perspectives will be important for avoiding such problems. The convergence speed is also an issue for the PARAFAC2 algorithm. A recent research of Tian et al. [68] reported the effects of different line search strategies for accelerating PARAFAC2-ALS convergence, and proposed an acceleration procedure called geometric search which was faster than the non-accelerated PARAFAC2-ALS algorithm. However, seeking the efficient alternatives of the ALS algorithm for estimating PARAFAC2 model is still needed for the future.
3.4. Other Multi-Way Models
There are many alternative multi-way analysis models available for analyzing multi-way dataset. For instance, Tucker3 is a multi-way model of the Tucker family, also called the three-mode principal components analysis [25,69,70]. Compared with the PARAFAC model, a super-diagonal core array exists in Tucker3 models. It basically compresses all three modes of the data so that the main information can be summarized by a few components for each mode. Therefore, the number of components in a Tucker3 model can be different for each mode. It is important to notice that the unique and best subspace can be found by the Tucker3 model, while the decomposed loadings are generally not unique due to the rotation freedom problem. Another promising multi-way model is alternating tri-linear decomposition (ATLD) [71]. It was used for decomposing three-way data but was shown to have faster convergence than the PARAFAC-ALS algorithm in the original paper [71]. It was also based on the ALS principle but with an improved iterative procedure using the Moore–Penrose generalized inverse with a singular value decomposition. Limited by the length of this paper, only simple descriptions about these models are introduced here. More details about many other different multi-way models can be found in the reference [23,72].
4. Preprocessing Techniques
Preprocessing plays an important role in chemometrics; however, it is more complicated when used for a multi-way array compared with two-way cases [60]. Some studies have been done in terms of centering and scaling for a multi-way array [46,72,73,74]. Basically, three ways of centering can be performed on a multi-way array, including single-centering, double-centering and triple-centering [46]. Single-centering can be done by unfolding the three-way array into a matrix, and then centering the matrix as in an ordinary two-way chemometrics method, such as PCA: for example, unfolding the array into matrix and centering it across the first mode. People can also center the data across one of other modes depending on the specific problem. Double-centering means two modes of the three modes are centered by first centering one mode; then, the outcomes of this centering are centered. In triple-centering, centering across all the three modes at a time will be performed. As stated by Bro et al. [60], single-centering is the only appropriate choice for performing centering on a multi-way array in order to fulfill the assumptions of multilinear models, e.g., the PARAFAC model. Regarding scaling, the assumptions of multilinear models also need to be considered. Since scaling column-wise (as in centering) will distort the underlying trilinear structure of the data [74], it is necessary to scale the whole slab within a specific mode instead of the columns. Several issues need to be taken into account when performing scaling on multi-way array. One of them is that scaling one mode will always affect the scale of other modes, which means that scaling within several modes can be more complicated. The amount of noise and unsystematic variation in the data may be increased after performing scaling on some types of multi-way data [74]; hence, centering across one mode or scaling within one mode is always the straightforward way to preprocess the multi-way array. More details about centering and scaling for a multi-way array can be found in the aforementioned references. For multi-way NIRS data, the conventional preprocessing techniques for NIR spectra can be used before rearranging the two-way NIR spectra into the multi-way array. Scatter correction and derivatives methods are the most widely used preprocessing techniques for NIR spectra. MSC [75], Inverse MSC [76], Extended MSC [77] and SNV [78] are commonly used for scatter correction, while first or second order Savitzky–Golay derivatives and Norris–Williams derivatives [79] are the widely used spectral derivative techniques. Moreover, the interval and combined versions of different preprocessing techniques are also frequently used in practice. For more details regarding parameters settings, the effects comparison and the methods selection for different preprocessing techniques for NIR spectra, we recommend the specific preprocessing references [80,81].
5. Applications of Multi-Way Analysis and NIRS in Food Industry
5.1. Process Analysis and Control
Food industrial processes and food productions often involve multi-way data. A number of reports have shown the great potential of multi-way analysis tools for analyzing high dimensional and complex food process data [82,83,84,85]. NIRS is widely applied in the process analysis, and a multi-way data analysis coupled with NIRS is gaining more and more acceptance in the food industry. Allosio-Ouarnier et al. [86] used PARAFAC to investigate the variation of barley during the malting process by analyzing the three-way array of wavelengths × batches × malting time. The batch difference and sample differences within a batch were both successfully observed. In order to confront the challenge of industrial complexity, Liu et al. [87] developed an industrial process analysis method by combining on-line NIRS and ATLD. The industrial process could be monitored by observing the variation of common property extracted from the ATLD model in different batches, and an application of tobacco production indicated that the multi-way analysis, such as ATLD, was more capable of extracting the intrinsic information hidden in the NIR spectra. This achieved a better performance in the process analysis compared with the conventional two-way analysis tools. Furthermore, Nielsen et al. [88] also applied an analysis of common dimensions and specific weights (COMDIM) [89] to analyze the NIRS data of wheat flours and argued that their proposal was a powerful tool for process control in the flour mill. The authors of this paper said that multi-way analysis was advantageous in simultaneously considering the variation in both the particle size and chemical data, while the two-way PCA analysis was insufficient. By doing so, different quality parameters could be optimized during the flour production. Temperature is a critical factor that cannot be ignored in NIRS in the process analysis. Peinado et al. [90] used PARAFAC-MLR to model the batch process of the in-line NIRS dataset of water and ethanol by considering temperature information as an additional parameter in the tensor. Even though the dataset has simultaneous changes in temperature and chemical composition, the physical–chemical changes happening in the evolving systems were extracted successfully by the PARAFAC model. The proposed tensor-based strategy was more attractive than PCA or PLS, and it was recommended to be implemented in various industrial applications. In the scientific literature, different multi-way analysis models have also been compared for food process analyses. Lillhonga and Geladi [91] monitored the fermentation of food waste mixture batches over time by combining multi-way analysis models and NIRS. They showed that PARAFAC and Tucker3 produce common time profiles for all the batches and that the half-lives can be estimated successfully, while PARAFAC2 yields an individual time profile for each batch with a little more noise and convergence problems. Vigni and Cocchi [92] studied the formulation effects on wheat flour during a leavening process by using PARAFAC and N-PLS. The mixtures’ differences regarding the leavening time were detected by the PARAFAC decomposition of the three-way NIRS dataset. The established N-PLS model on baked bread parameters successfully found the relationship among flour formulation, leavening time and the final product. The multi-way analysis was proven to be an effective tool for monitoring the industrial leavening process of wheat flours.
5.2. Fraud and Quality Evaluation
NIRS is widely used for the purpose of food quality evaluation and fraud detection [93,94,95]. Many studies have reported the effectiveness of the combination of NIRS and the multi-way analysis in dealing with such issues in the food industry. For example, the accurate information of adulterants in milk was generally difficult to be captured by two-way chemometric tools because of the weak and overlapped absorption bands of the adulterants [96]. Yang et al. [96] successfully used N-PLS to model the 2D NIR spectra data of melamine adulterated milk. By comparing with the PLS model results on 1D NIR spectra, the multi-way model was deemed to be more accurate and robust since its average relative error is only 22.9% while the average relative error of PLS model is 122.4%. Recently, some studies have reported the effectiveness of the multi-way analysis and NIRS in the oxidative stability evaluation of oil. Rosa et al. [97] reported that PARAFAC coupled with NIRS was powerful for evaluating the protective effect of plant-based substances and synthetic antioxidants against oxidation in soybean oil. The NIRS data were rearranged into a three-way array of samples by temperature by wavenumbers. They concluded that the proposed method was a simple and fast way to achieve the anti-oxidation evaluation for soybean oil. Furthermore, PARAFAC coupled with NIRS was also used for evaluating the degradation of thermal rice oil by Rosa et al. [98]. The oxidative stability of rice oils was evaluated in a fast way by combining the multi-way analysis and NIRS. Moreover, Favilla et al. [42] used NIRS and the N-PLS model to accurately model the critical properties of bread loaves. The flour performance of the leavening phase was then successfully and accurately predicted.
5.3. Identification and Classification
Identification and classification are important application fields of NIRS and chemometrics [99], and are also used for the consideration of the multi-way analysis. Cui et al. [100] compared the effects of M-PCA, ATLD and PARAFAC on both three-way and four-way temperature-dependent NIRS data. Their results showed that ATLD and PARAFAC were capable of capturing the spectral variation information for each component, while the loadings of M-PCA contained the mixed spectral information of all the components, even though it explained the variance of whole data. The authors concluded that the multi-way analysis model can determine the chemicals of aqueous solutions and it can be the best way for analyzing temperature-dependent NIR spectra. In order to find differences between the cultivars and localities, Geladi and Manley [101] used PARAFAC to analyze the three-way NIRS data of wheat flours and made a comparison with the two-way chemometric models. They showed that PARAFAC can detect the variation information of protein content and hardness values, which were associated with localities and cultivars separately, and merging the information of the cultivars and the localities in one-way and then building PCA or PLS models are not proper for their case. Allosio et al. [102] reported PARAFAC was useful for separating barley batches according to the malting process. Such classifications can be achieved by connecting the decomposed time mode profiles with wavelength mode information expressed as NIR spectral intensities. The authors state that PARAFAC had great potential in analyzing the time series NIR dataset. Recently, the multi-way analysis has been applied to the classification of milk. Yang et al. [103] combined N-PLS-DA and 2D NIR correlation spectra to illustrate the feasibility of classifying normal milk and tainted milk. They compared the effects of the N-PLS-DA model on 2D IR/IR, 2D NIR/NIR and 2D IR/NIR spectra using the correct classification rate (CCR). The results showed that N-PLS-DA models on 2D IR/NIR spectra can provide the best classification of milk with a CCR of 96.1%.
5.4. Prediction and Quantification
Multi-way analysis was also used for quantification and prediction purposes in the food industry [104]. In particular, the multi-way analysis coupled with NIRS has been successfully applied in many practical cases by virtue of better model predictive performance and the ability to simultaneously analyze chemical and physical variations [105,106]. Letíci et al. [107] used N-PLS models to predict the content of limonene and water in the spray-dried systems by analyzing the three-way NIRS data. The temperature variation can be modeled successfully and the prediction error of N-PLS model is only 0.2%, which was small compared with that of the two-way model. The conventional two-way NIRS calibration model faces many challenges because of its weak robustness when it is applied for analyzing the samples with a large amount of water [108]. To circumvent such a challenge, Peng et al. [108] developed a hybrid algorithm called wavelet packet transform orthogonal signal correction N-PLS (WPNOSC-N-PLS) by applying a wavelet packet transform and orthogonal signal correction into the N-PLS model. In combination with NIR, WPNOSC-N-PLS accurately determined the main components in the concentration of milk even in the presence of temperature variation interference. The authors argued that WPNOSC-N-PLS can provide better models with better precision and robustness, and it is attractive in solving a wide range of multidimensional problems. Recently, the multi-way analysis and NIRS has been applied to the component quantification in corn. Zhang et al. [109] reported the application of N-PLS on self-constructed three-dimensional NIR spectra which can capture accurate quantitative information of four components (moisture, oil, protein, and starch). Compared with the two-way PLS model, the proposed multi-way models achieved better predictive performance for the target compounds with a lower RMSEP (root mean square error of prediction). Benefiting from the multi-way advantage, N-PLS coupled with 3D NIR spectra was deemed to be a rapid and robust tool for the accurate quantification of food compounds.
5.5. Hyperspectral Image Analysis
Very little work has been done on a dedicated multi-way analysis for analyzing NIR image data even though multi-way methods have shown great potential for dealing with such types of structures. Folch-Fortuny et al. [110] used an N-PLS-DA model to detect the symptoms of Penicillium digitatum in citrus fruits by analyzing the multi-way features array of the NIR hyperspectral image. It was reported that almost 91% of citrus fruit infected by Penicillium digitatum can be successfully detected by the multi-way model at early stages of the harvest, which will be of great importance for automating fruit sorting systems so that infected citrus fruits can be expelled before affecting the normal fruits. Yang et al. [111] developed a combination system using a NIR hyperspectral image, wavelet transformation and N-PLS to predict the total viable count (TVC) of spiced beef during storage. The three-way array was organized as spiced beef samples by wavelength variables by the wavelet detail coefficient, then it was concluded that the three-way tri-linear data structures yield a more accurate model with better interpretations of TVC than the two-way data. The N-PLS model produced a better prediction and lower errors. Recently, PARAFAC2 was also applied for analyzing complex NIR image data and showed a satisfactory performance. For instance, Alexandrino et al. [112] monitored multiple solid-state transitions of lactose by analyzing the temperature series NIR hyperspectral image using PARAFAC and PARAFAC2 models. Their results showed that the PARAFAC model cannot work well in that case since the pixels data did not conform to the tri-linearity assumption strictly, while PARAFAC2 extracted the profile of the compounds successfully. This allowed one mode of the three-way data to be shifted. PARAFAC2 was recommended to be the best for analyzing the series hyperspectral image data. Obviously, the NIR hyperspectral image analysis is a promising technology for solving practical problems in the food industry. However, some inherent drawbacks, such as high dimensionality [113], huge amount of acquired data [114] and considerably time consumption of the analysis [115], cannot be ignored. How to build efficient models for analyzing such a large number of NIR image data is a challenge [116]. By virtue of the multi-way advantages in handling large datasets, the application of multi-way tools will be beneficial for dealing with such tasks. As stated by Koljonen et al. [117], the multi-way analysis is a potential field of future research for the hyperspectral NIR image analysis. The representative applications of the multi-way analysis coupled with NIRS for analyzing food related data in terms of process analysis and control, quality evaluation and fraud, identification and classification, quantification and prediction, and image analysis are summarized in Table 2.
Table 2.
Representative applications of multi-way analysis models coupled with near-infrared spectroscopy (NIRS) for analyzing food data.
| Applications | Analyte | Data Arrangement | Preprocessing | Variable Selection | Multi-Way Analysis Algorithm | Spectral Range (Wavenumber or Wavelength) | Analytical Technique | Reference |
|---|---|---|---|---|---|---|---|---|
| Process analysis and control | Malt | Wavelengths × batches × time | Centering | Manual | PARAFAC | 400–2500 nm | NIR | [86] |
| Tobacco | Samples × variables × batches | Continuous wavelet transform | Not specified | ATLD | 4000–12,000 cm−1 | NIR | [87] | |
| Wheat flour | Samples × wavelengths/laser particle size/chemical × number of data matrices | SNV | Not specified | COMDIM | 1100–2500 nm | NIR | [88] | |
| Food waste | Batches × time × wavelengths | Derivatives | Manual | PARAFAC, Tucker3 and PARAFAC2 | 905–1682 nm | NIR | [91] | |
| Water and ethanol mixture | Batches × wavelengths × temperature | Centering | Manual | PARAFAC | 580–1090 nm | NIR | [90] | |
| Wheat flour | Mixtures × wavelengths × leavening times | Savitsky–Golay and SNV | Not specified | PARAFAC and N-PLS | 1380–2250 nm | NIR | [92] | |
| Fraud and quality evaluation | Milk | Samples × wavelengths × wavelengths | Fourier transformation | Manual | N-PLS | 4000–10,000 cm−1 | FT-IR | [96] |
| Soybean oil | Samples × temperature × wavenumbers | Savitzky–Golay derivatives | Not specified | PARAFAC | 900–1680 nm | NIR | [97] | |
| Rice oil | Samples × temperature × spectra | Baseline correction and Savitzky–Golay derivatives | Not specified | PARAFAC | 900–1680 nm | NIR | [98] | |
| Bread | Leavening times × flour formulations × wavelengths | Savitsky–Golay derivatives and SNV | Variable importance in Projection | N-PLS | 1380–2250 nm | NIR | [42] | |
| Identification and classification | Ethanol | Temperature × wavelengths × samples | Continuous wavelet transform with a vanishing moment 2 | Not specified | PARAFAC and ATLD | 5500–12,000 cm−1 | NIR | [100] |
| Wheat flour | Locality × cultivar × wavelengths | Savitzy–Golay derivatives | Manual | PARAFAC | 4000–10,000 cm−1 | FT-NIR | [101] | |
| Milk | Samples × wavelengths × wavelengths | Mean-center | Manual | NPLS-DA | 4000–10,000 cm−1 | FT-IR | [103] | |
| Barley | Wavelengths × batches × time | Centering | Not specified | PARAFAC | 1100–2500 nm | NIR | [102] | |
| Prediction and quantification | Microcrystalline cellulose mixture | Concentration levels × wavelengths × compaction pressure levels | Centering, SNV, and Savitzky–Golay derivatives | Not specified | PARAFAC | 1097–2200 nm | NIR | [105] |
| Limonene and water | Samples × temperatures × wavelengths | Extended inverted signal correction, and direct orthogonalization | Interval-PLS | N-PLS | 1100–2498 nm | NIR | [107] | |
| Milk | Samples × temperatures × wavelengths | Discrete wavelet packet transform and 3D orthogonal signal correction | Not specified | WPNOSC N-PLS | 1100–2300 nm | FT-IR | [108] | |
| Corn | Spectral number × wavelengths × samples | Not specified | Not specified | N-PLS | 1100–2498 nm | NIR | [109] | |
| NIR image analysis | Citrus fruits | Fruit variety × features ×wavelengths | MSC and SNV | Permutation testing | NPLS-DA | 650–1080 nm | VIS/NIR hyperspectral imaging | [110] |
| Spiced beef | Spiced beef sample × wavelength variables × wavelet detail coefficient | Wavelet transform | Manual | N-PLS | 400–1000 nm | VIS/NIR hyperspectral imaging | [111] | |
| Lactose | Pixels × spectra × time/temperature | Logarithmization, SNV and Savitzky–Golay derivatives | Hypertools [118] | PARAFAC and PARAFAC2 | 1000–1700 nm | NIR hyperspectral imaging | [112] |
6. Software and Algorithms
During the past decades, a number of software packages have been developed for performing multi-way analysis. One of the original software is the N-way toolbox [119] for Matlab. Most of the multi-way analysis algorithms, such as PARAFAC, PARAFAC2, N-PLS, Tucker3 and DTLD, are available in this source. Users can easily impose a variety of constraints on these algorithms and run them with different initialization methods, such as SVD, random initialization and ATLD. Another software is CuBatch [35] which was originally built for the process analysis. It also contains many multi-way analysis algorithms including PARAFAC, Tucker models, etc. There are also some other open-source software implementations used for multi-way analyses from other communities. For instance, the Tensor toolbox developed by Kolda and Bader [120] is powerful for analyzing a wide types of tensor, including dense, sparse, and symmetric tensors. Phan et al. [121] also developed a tensor decomposition Matlab package called Tensorbox which contains various optimized algorithms for decomposing a tensor, such as the fast damped Gauss–Newton CP algorithm [122]. In addition to these free software, there is also a commercial software called PLS_Toolbox [123], widely used in the chemometrics community by virtue of its advantages in its easy-to-use, user-friendly interfaces and powerful visualization. All the aforementioned packages run under the Matlab environment. Recently, some multi-way analysis software packages running under the R environment have also been developed, such as ThreeWay [124] and multiway [125] packages developed by social science statisticians. Meanwhile, there are also some Python packages for multi-way analyses available, such as Tensorly [126] and TensorD [127]. The details of all the mentioned software are shown in Table 3, and simple introductions of different multi-way analysis algorithms can be found on the corresponding download websites.
Table 3.
Free and commercial multi-way analysis software.
| Software | Running Environment | Multi-Way Analysis Algorithms | Website for Installation |
|---|---|---|---|
| N-way toolbox | Matlab | PARAFAC, PARAFAC2, N-PLS, Tucker models, GRAM, DTLD, etc. | http://www.models.life.ku.dk/nwaytoolbox (7 April 2021) |
| CuBatch | Matlab | PARAFAC, PARAFAC2, N-PLS, Tucker models, etc. | http://www.models.life.ku.dk/cubatch (accessed on 7 April 2021) |
| Tensor toolbox | Matlab | PARAFAC, Tucker models, Poisson tensor factorization, Generalized CP tensor factorization, Symmetric CP tensor factorization, etc. | https://www.tensortoolbox.org/ (accessed on 7 April 2021) |
| Tensorbox | Matlab | PARAFAC, Tucker models, Generalized Kronecker tensor decomposition, Tensor deconvolution, Tensor train decomposition, etc. | https://github.com/phananhhuy/TensorBox (accessed on 7 April 2021) |
| PLS_Toolbox | Matlab | MPCA, PARAFAC, PARAFAC2, N-PLS, etc. | https://eigenvector.com/ (accessed on 7 April 2021) |
| ThreeWay | R | PARAFAC, Tucker models, etc. | https://cran.r-project.org/web/packages/ThreeWay/index.html (accessed on 7 April 2021) |
| multiway | R | PARAFAC, PARAFAC2, Tucker models, etc. | https://cran.r-project.org/web/packages/multiway/index.html (accessed on 7 April 2021) |
| Tensorly | Python | PARAFAC, Tucker models, Tensor train decomposition, etc. | http://tensorly.org/dev/index.html (accessed on 7 April 2021) |
| TensorD | Python | PARAFAC, Tucker models, Pairwise interaction tensor decomposition, etc. | https://github.com/Large-Scale-Tensor-Decomposition/tensorD (accessed on 7 April 2021) |
7. Conclusions
The application of multi-way analysis combined with NIR spectroscopy is still located at the initial stage for the food industry. So far, what we have seen about the synergy between rapid spectroscopic sensors and data analytic technologies, which has revolutionized the food industry, is only the beginning. Even though NIR spectroscopy can rapidly obtain thousands of data points in a short time, the potential of these big data sets has not been fully investigated. Deeper statistical and chemometric knowledge is desired by the food technologists, owing to the challenges of the high complexity of food processes and food products. As an advanced chemometric tool, multi-way analysis not only shows powerful advantages in food process analysis, quality evaluation, determination of chemical composition and structure, food image analysis, etc., but also makes the analysis process greener with the help of green and smart “mathematical separation” [36], fulfilling the requirement of a sustainable food industry. Therefore, the combination of multi-way analysis with NIR spectroscopy will be a promising practice for turning food data information into operational knowledge, conducting reliable food analyses, and improving our understanding about food systems and food processes. For the future of the research, making the multi-way algorithms more efficient and less prone to numerical problems, such as local minima and two factor degeneracy, are the main numerical challenges. How to analyze larger amounts of data coming from the food industry process and food products is also a practical issue. Parallel processor computing will be valuable for alleviating such issues. Moreover, extending preprocessing techniques used for two-way chemometric methods for multi-way cases and dealing with systematically missing data are also important issues.
Acknowledgments
We would like to acknowledge our appreciation to Rasmus Bro and Frans W.J. van den Berg of our chemometrics group in University of Copenhagen for their helpful comments in the course of this research.
Author Contributions
Conceptualization: H.Y. and M.K.; methodology, H.Y. and L.G.; formal analysis, H.Y. and M.K; investigation, H.Y. and L.G.; writing—original draft preparation, H.Y.; writing—review and editing, H.Y. and W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the PARADISe Project of Danish Dairy Research Foundation and the Program of China Scholarship Council (201807080012).
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Nicolai B.M., Beullens K., Bobelyn E., Peirs A., Saeys W., Theron K.I., Lammertyn J. Nondestructive measurement of fruit and vegetable quality by means of NIR spectroscopy: A review. Postharvest Biol. Technol. 2007;46:99–118. doi: 10.1016/j.postharvbio.2007.06.024. [DOI] [Google Scholar]
- 2.Huck-Pezzei V.A., Seitz I., Karer R., Schmutzler M., De Benedictis L., Wild B., Huck C.W. Alps food authentication, typicality and intrinsic quality by near infrared spectroscopy. Food Res. Int. 2014;62:984–990. doi: 10.1016/j.foodres.2014.05.021. [DOI] [Google Scholar]
- 3.Qiu Z., Zhao S., Feng X., He Y. Transfer learning method for plastic pollution evaluation in soil using NIR sensor. Sci. Total Environ. 2020;740:140118. doi: 10.1016/j.scitotenv.2020.140118. [DOI] [PubMed] [Google Scholar]
- 4.Naethe P., Delaney M., Julitta T. Changes of NOx in urban air detected with monitoring VIS-NIR field spectrometer during the coronavirus pandemic: A case study in Germany. Sci. Total Environ. 2020;748:141286. doi: 10.1016/j.scitotenv.2020.141286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rego G., Ferrero F., Valledor M., Campo J.C., Forcada S., Royo L.J., Soldado A. A portable IoT NIR spectroscopic system to analyze the quality of dairy farm forage. Comput. Electron. Agric. 2020;175:105578. doi: 10.1016/j.compag.2020.105578. [DOI] [Google Scholar]
- 6.Liu J., Han J., Xie J., Wang H., Tong W., Ba Y. Assessing heavy metal concentrations in earth-cumulic-orthic-anthrosols soils using Vis-NIR spectroscopy transform coupled with chemometrics. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2020;226:117639. doi: 10.1016/j.saa.2019.117639. [DOI] [PubMed] [Google Scholar]
- 7.Wold J.P., O’Farrell M., Tschudi J., Eskildsen C.E., Andersen P.V., Ottestad S. In-line and non-destructive monitoring of core temperature in sausages during industrial heat treatment by NIR interaction spectroscopy. J. Food Eng. 2020;277:109921. doi: 10.1016/j.jfoodeng.2020.109921. [DOI] [Google Scholar]
- 8.Rambo M.K.D., Ferreira M.M.C., MELO P.M.D., Santana Junior C.C., Bertuol D.A., Rambo M.C.D. Prediction of quality parameters of food residues using NIR spectroscopy and PLS models based on proximate analysis. Food Sci. Technol. 2020;40:444–450. doi: 10.1590/fst.02119. [DOI] [Google Scholar]
- 9.Desai P.M., Acharya S., Armstrong C., Wu E.L., Zaidi S.A. Underpinning mechanistic understanding of the segregation phenomena of pharmaceutical blends using a near-infrared (NIR) spectrometer embedded segregation tester. Eur. J. Pharm. Sci. 2020;154:105516. doi: 10.1016/j.ejps.2020.105516. [DOI] [PubMed] [Google Scholar]
- 10.Zhao J., Tian G., Qiu Y., Qu H. Rapid quantification of active pharmaceutical ingredient for sugar-free Yangwei granules in commercial production using FT-NIR spectroscopy based on machine learning techniques. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2021;245:118878. doi: 10.1016/j.saa.2020.118878. [DOI] [PubMed] [Google Scholar]
- 11.Chen J., Qi J., Chen C., Chen J., Liu L., Gao R., Zhang T., Song L., Ding D., Zhang P. Tocilizumab–Conjugated Polymer Nanoparticles for NIR-II Photoacoustic-Imaging-Guided Therapy of Rheumatoid Arthritis. Adv. Mater. 2020;32:2003399. doi: 10.1002/adma.202003399. [DOI] [PubMed] [Google Scholar]
- 12.Tiwari R., Shinde P.S., Sreedharan S., Dey A.K., Vallis K., Mhaske S.B., Pramanik S.K., Das A. Photoactivable Prodrug for Simultaneous Release of Mertansine, and CO along with a BODIPY Derivative as a Luminescent Marker in Mitochondria: A Proof of Concept for NIR Image-Guided Cancer Therapy. Chem. Sci. 2021;12:2667–2673. doi: 10.1039/D0SC06270G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Seifi M., Ahmadi A., Neyshabouri M.-R., Taghizadeh-Mehrjardi R., Bahrami H.-A. Remote and Vis-NIR spectra sensing potential for soil salinization estimation in the eastern coast of Urmia hyper saline lake, Iran. Remote Sens. Appl. Soc. Environ. 2020;20:100398. doi: 10.1016/j.rsase.2020.100398. [DOI] [Google Scholar]
- 14.Hill A.C., Laugier E.J., Casana J. Archaeological remote sensing using multi-temporal, drone-acquired thermal and Near Infrared (NIR) Imagery: A case study at the Enfield Shaker Village, New Hampshire. Remote Sens. 2020;12:690. doi: 10.3390/rs12040690. [DOI] [Google Scholar]
- 15.Grassi S., Alamprese C. Advances in NIR spectroscopy applied to process analytical technology in food industries. Curr. Opin. Food Sci. 2018;22:17–21. doi: 10.1016/j.cofs.2017.12.008. [DOI] [Google Scholar]
- 16.Marini F. Chemometrics in Food Chemistry. Newnes; Oxford, UK: 2013. [Google Scholar]
- 17.Truong V.K., Dupont M., Elbourne A., Gangadoo S., Pathirannahalage P.R., Cheeseman S., Chapman J., Cozzolino D. From academia to reality check: A theoretical framework on the use of chemometric in food sciences. Foods. 2019;8:164. doi: 10.3390/foods8050164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stordrange L., Rajalahti T., Libnau F.O. Multiway methods to explore and model NIR data from a batch process. Chemom. Intell. Lab. Syst. 2004;70:137–145. doi: 10.1016/j.chemolab.2003.10.010. [DOI] [Google Scholar]
- 19.Bro R., Smilde A.K. Principal component analysis. Anal. Methods. 2014;6:2812–2831. doi: 10.1039/C3AY41907J. [DOI] [Google Scholar]
- 20.Wold S., Esbensen K., Geladi P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987;2:37–52. doi: 10.1016/0169-7439(87)80084-9. [DOI] [Google Scholar]
- 21.Geladi P., Kowalski B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta. 1986;185:1–17. doi: 10.1016/0003-2670(86)80028-9. [DOI] [Google Scholar]
- 22.Wold S., Sjöström M., Eriksson L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001;58:109–130. doi: 10.1016/S0169-7439(01)00155-1. [DOI] [Google Scholar]
- 23.Smilde A., Bro R., Geladi P. Multi-Way Analysis: Applications in the Chemical Sciences. John Wiley & Sons; Hoboken, NJ, USA: 2005. [Google Scholar]
- 24.McConnell A.J. Applications of Tensor Analysis. Courier Corporation; Chelmsford, MA, USA: 2014. [Google Scholar]
- 25.Tucker L.R. Some mathematical notes on three-mode factor analysis. Psychometrika. 1966;31:279–311. doi: 10.1007/BF02289464. [DOI] [PubMed] [Google Scholar]
- 26.Tucker L.R. The extension of factor analysis to three-dimensional matrices. In: Gulliksen H., Frederiksen N., editors. Contributions to Mathematical Psychology. Holt, Rinehart and Winston; New York, NY, USA: 1964. pp. 110–127. [Google Scholar]
- 27.Bro R. Review on multiway analysis in chemistry—2000–2005. Crit. Rev. Anal. Chem. 2006;36:279–293. doi: 10.1080/10408340600969965. [DOI] [Google Scholar]
- 28.Wold S., Geladi P., Esbensen K., Öhman J. Multi-way principal components-and PLS-analysis. J. Chemom. 1987;1:41–56. doi: 10.1002/cem.1180010107. [DOI] [Google Scholar]
- 29.Bro R. Multiway calibration. multilinear pls. J. Chemom. 1996;10:47–61. doi: 10.1002/(SICI)1099-128X(199601)10:1<47::AID-CEM400>3.0.CO;2-C. [DOI] [Google Scholar]
- 30.Brasca R., Goicoechea H.C., Culzoni M.J. Food Safety and Preservation. Elsevier; Amsterdam, The Netherlands: 2018. Multiway Calibration Approaches for Quality Control of Food Samples; pp. 143–165. [Google Scholar]
- 31.Rinnan Å., Amigo J.M., Skov T. Multiway methods in food science. Math. Stat. Methods Food Sci. Technol. 2014:143–174. [Google Scholar]
- 32.Bro R. Multi-way Analysis in the Food Industry-Models, Algorithms, and Applications. [(accessed on 8 April 2021)]; Available online: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=265CD588FD4E914A42427F027A7F5D0D?doi=10.1.1.24.5344&rep=rep1&type=pdf.
- 33.Booksh K.S., Kowalski B.R. Theory of analytical chemistry. Anal. Chem. 1994;66:782A–791A. doi: 10.1021/ac00087a718. [DOI] [Google Scholar]
- 34.Escandar G.M., Olivieri A.C., Faber N.K.M., Goicoechea H.C., de la Peña A.M., Poppi R.J. Second-and third-order multivariate calibration: Data, algorithms and applications. Trac-Trends Anal. Chem. 2007;26:752–765. doi: 10.1016/j.trac.2007.04.006. [DOI] [Google Scholar]
- 35.Gourvénec S., Tomasi G., Durville C., Di Crescenzo E., Saby C., Massart D., Bro R., Oppenheim G. CuBatch, a MATLAB® interface for n-mode data analysis. Chemom. Intell. Lab. Syst. 2005;77:122–130. doi: 10.1016/j.chemolab.2004.01.027. [DOI] [Google Scholar]
- 36.Wu H.-L., Wang T., Yu R.-Q. Recent advances in chemical multi-way calibration with second-order or higher-order advantages: Multilinear models, algorithms, related issues and applications. Trac-Trends Anal. Chem. 2020;130:115954. doi: 10.1016/j.trac.2020.115954. [DOI] [Google Scholar]
- 37.Kiers H.A. Towards a standardized notation and terminology in multiway analysis. J. Chemom. 2000;14:105–122. doi: 10.1002/1099-128X(200005/06)14:3<105::AID-CEM582>3.0.CO;2-I. [DOI] [Google Scholar]
- 38.Liu S., Trenkler G. Hadamard, Khatri-Rao, Kronecker and other matrix products. Int. J. Inf. Syst. Sci. 2008;4:160–177. [Google Scholar]
- 39.Bro R., Smilde A.K., de Jong S. On the difference between low-rank and subspace approximation: Improved model for multi-linear PLS regression. Chemom. Intell. Lab. Syst. 2001;58:3–13. doi: 10.1016/S0169-7439(01)00134-4. [DOI] [Google Scholar]
- 40.Luo L., Bao S., Mao J., Tang D. Quality prediction and quality-relevant monitoring with multilinear PLS for batch processes. Chemom. Intell. Lab. Syst. 2016;150:9–22. doi: 10.1016/j.chemolab.2015.11.004. [DOI] [Google Scholar]
- 41.Faber N.K.M., Bro R. Standard error of prediction for multiway PLS: 1. Background and a simulation study. Chemom. Intell. Lab. Syst. 2002;61:133–149. doi: 10.1016/S0169-7439(01)00204-0. [DOI] [Google Scholar]
- 42.Favilla S., Durante C., Vigni M.L., Cocchi M. Assessing feature relevance in NPLS models by VIP. Chemom. Intell. Lab. Syst. 2013;129:76–86. doi: 10.1016/j.chemolab.2013.05.013. [DOI] [Google Scholar]
- 43.Biancolillo A., Næs T., Bro R., Måge I. Extension of SO-PLS to multi-way arrays: SO-N-PLS. Chemom. Intell. Lab. Syst. 2017;164:113–126. doi: 10.1016/j.chemolab.2017.03.002. [DOI] [Google Scholar]
- 44.Harshman R.A. Foundations of the PARAFAC Procedure: Models and Conditions for an “Explanatory” Multimodal Factor Analysis. [(accessed on 8 April 2021)]; Available online: https://www.psychology.uwo.ca/faculty/harshman/wpppfac0.pdf.
- 45.Carroll J.D., Chang J.-J. Analysis of individual differences in multidimensional scaling via an N-way generalization of “Eckart-Young” decomposition. Psychometrika. 1970;35:283–319. doi: 10.1007/BF02310791. [DOI] [Google Scholar]
- 46.Bro R. PARAFAC. Tutorial and applications. Chemom. Intell. Lab. Syst. 1997;38:149–171. doi: 10.1016/S0169-7439(97)00032-4. [DOI] [Google Scholar]
- 47.Ten Berge J.M., Sidiropoulos N.D. On uniqueness in CANDECOMP/PARAFAC. Psychometrika. 2002;67:399–409. doi: 10.1007/BF02294992. [DOI] [Google Scholar]
- 48.Kruskal J.B. Three-way arrays: Rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics. Linear Algebra Its Appl. 1977;18:95–138. doi: 10.1016/0024-3795(77)90069-6. [DOI] [Google Scholar]
- 49.Bro R., Kiers H.A. A new efficient method for determining the number of components in PARAFAC models. J. Chemom. 2003;17:274–286. doi: 10.1002/cem.801. [DOI] [Google Scholar]
- 50.Tomasi G., Bro R. PARAFAC and missing values. Chemom. Intell. Lab. Syst. 2005;75:163–180. doi: 10.1016/j.chemolab.2004.07.003. [DOI] [Google Scholar]
- 51.Salvatore E., Bevilacqua M., Bro R., Marini F., Cocchi M. Comprehensive Analytical Chemistry. Volumen 60. Elsevier; Amsterdam, The Netherlands: 2013. Classification Methods of Multiway Arrays as a Basic Tool for Food PDO Authentication; pp. 339–382. [Google Scholar]
- 52.Tomasi G., Bro R. A comparison of algorithms for fitting the PARAFAC model. Comput. Stat. Data Anal. 2006;50:1700–1734. doi: 10.1016/j.csda.2004.11.013. [DOI] [Google Scholar]
- 53.Rajih M., Comon P., Harshman R.A. Enhanced line search: A novel method to accelerate PARAFAC. Siam J. Matrix Anal. Appl. 2008;30:1128–1147. doi: 10.1137/06065577. [DOI] [Google Scholar]
- 54.Chen Y., Han D., Qi L. New ALS methods with extrapolating search directions and optimal step size for complex-valued tensor decompositions. IEEE Trans. Signal Process. 2011;59:5888–5898. doi: 10.1109/TSP.2011.2164911. [DOI] [Google Scholar]
- 55.Acar E., Dunlavy D.M., Kolda T.G. A scalable optimization approach for fitting canonical tensor decompositions. J. Chemom. 2011;25:67–86. doi: 10.1002/cem.1335. [DOI] [Google Scholar]
- 56.Liu L., Wang L., Xie J., Wang Y., Zhang Z. Signal parameter estimation through hierarchical conjugate gradient least squares applied to tensor decomposition. Etri J. 2020;42:922–931. doi: 10.4218/etrij.2019-0343. [DOI] [Google Scholar]
- 57.Erichson N.B., Manohar K., Brunton S.L., Kutz J.N. Randomized CP tensor decomposition. Mach. Learn. Sci. Technol. 2020;1:025012. doi: 10.1088/2632-2153/ab8240. [DOI] [Google Scholar]
- 58.Fu X., Ibrahim S., Wai H.-T., Gao C., Huang K. Block-randomized stochastic proximal gradient for low-rank tensor factorization. IEEE Trans. Signal Process. 2020;68:2170–2185. doi: 10.1109/TSP.2020.2982321. [DOI] [Google Scholar]
- 59.Lorenzo-Seva U., Ten Berge J.M. Tucker’s congruence coefficient as a meaningful index of factor similarity. Methodology. 2006;2:57–64. doi: 10.1027/1614-2241.2.2.57. [DOI] [Google Scholar]
- 60.Bro R., Workman J.J., Jr., Mobley P.R., Kowalski B.R. Review of chemometrics applied to spectroscopy: 1985-95, Part 3—Multi-way analysis. Appl. Spectrosc. Rev. 1997;32:237–261. doi: 10.1080/05704929708003315. [DOI] [Google Scholar]
- 61.Harshman R.A. PARAFAC2: Mathematical and technical notes; Proceedings of the UCLA Working Papers in Phonetics; Los Angeles, CA, USA. 1972. pp. 30–44. [Google Scholar]
- 62.Kiers H.A., Ten Berge J.M., Bro R. PARAFAC2—Part I. A direct fitting algorithm for the PARAFAC2 model. J. Chemom. 1999;13:275–294. doi: 10.1002/(SICI)1099-128X(199905/08)13:3/4<275::AID-CEM543>3.0.CO;2-B. [DOI] [Google Scholar]
- 63.Ten Berge J.M., Kiers H.A. Some uniqueness results for PARAFAC2. Psychometrika. 1996;61:123–132. doi: 10.1007/BF02296962. [DOI] [Google Scholar]
- 64.Bro R., Andersson C.A., Kiers H.A. PARAFAC2—Part II. Modeling chromatographic data with retention time shifts. J. Chemom. 1999;13:295–309. doi: 10.1002/(SICI)1099-128X(199905/08)13:3/4<295::AID-CEM547>3.0.CO;2-Y. [DOI] [Google Scholar]
- 65.Cohen J.E., Bro R. Nonnegative PARAFAC2: A flexible coupling approach; Proceedings of the International Conference on Latent Variable Analysis and Signal Separation; Guildford, UK. 2–5 July 2018; pp. 89–98. [Google Scholar]
- 66.Van Benthem M.H., Keller T.J., Gillispie G.D., DeJong S.A. Getting to the core of PARAFAC2, a nonnegative approach. Chemom. Intell. Lab. Syst. 2020;206:104127. doi: 10.1016/j.chemolab.2020.104127. [DOI] [Google Scholar]
- 67.Mehanna O., Huang K., Gopalakrishnan B., Konar A., Sidiropoulos N.D. Feasible point pursuit and successive approximation of non-convex QCQPs. IEEE Signal Process. Lett. 2014;22:804–808. doi: 10.1109/LSP.2014.2370033. [DOI] [Google Scholar]
- 68.Tian K., Wu L., Min S., Bro R. Geometric search: A new approach for fitting PARAFAC2 models on GC-MS data. Talanta. 2018;185:378–386. doi: 10.1016/j.talanta.2018.03.088. [DOI] [PubMed] [Google Scholar]
- 69.Kroonenberg P.M. Three-Mode Principal Component Analysis: Theory and Applications. Volume 2 DSWO Press; Leiden, The Netherlands: 1983. [Google Scholar]
- 70.Xu Y., Wu Z., Chanussot J., Wei Z. Hyperspectral computational imaging via collaborative tucker3 tensor decomposition. IEEE Trans. Circuits Syst. Video Technol. 2020;31:98–111. doi: 10.1109/TCSVT.2020.2975936. [DOI] [Google Scholar]
- 71.Wu H.L., Shibukawa M., Oguma K. An alternating trilinear decomposition algorithm with application to calibration of HPLC–DAD for simultaneous determination of overlapped chlorinated aromatic hydrocarbons. J. Chemom. 1998;12:1–26. doi: 10.1002/(SICI)1099-128X(199801/02)12:1<1::AID-CEM492>3.0.CO;2-4. [DOI] [Google Scholar]
- 72.Kroonenberg P.M. Applied Multiway Data Analysis. Volume 702 John Wiley & Sons; Hoboken, NJ, USA: 2008. [Google Scholar]
- 73.Bro R., Smilde A.K. Centering and scaling in component analysis. J. Chemom. 2003;17:16–33. doi: 10.1002/cem.773. [DOI] [Google Scholar]
- 74.Gurden S.P., Westerhuis J.A., Bro R., Smilde A.K. A comparison of multiway regression and scaling methods. Chemom. Intell. Lab. Syst. 2001;59:121–136. doi: 10.1016/S0169-7439(01)00168-X. [DOI] [Google Scholar]
- 75.Mishra P., Lohumi S. Improved prediction of protein content in wheat kernels with a fusion of scatter correction methods in NIR data modelling. Biosyst. Eng. 2021;203:93–97. doi: 10.1016/j.biosystemseng.2021.01.003. [DOI] [Google Scholar]
- 76.Hernández-Sánchez N., Gómez-del-Campo M. From NIR spectra to singular wavelengths for the estimation of the oil and water contents in olive fruits. Grasas Y Aceites. 2018;69:278. doi: 10.3989/gya.0457181. [DOI] [Google Scholar]
- 77.Andasuryani Y., Purwanto I., Budiastra K.S., Syamsu K. Non destructive and rapid analysis of catechin content in Gambir (Uncaria gambir Roxb.) using NIR spectroscopy. IJSER. 2013;4:383–389. [Google Scholar]
- 78.Basile T., Marsico A.D., Perniola R. NIR Analysis of Intact Grape Berries: Chemical and Physical Properties Prediction Using Multivariate Analysis. Foods. 2021;10:113. doi: 10.3390/foods10010113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Yan H., Tang G., Xiong Y., Min S. A new concept based on ensemble strategy and derivative for the quantitative analysis of infrared data. J. Chemom. 2021:e3323. [Google Scholar]
- 80.Jiao Y., Li Z., Chen X., Fei S. Preprocessing methods for near-infrared spectrum calibration. J. Chemom. 2020;34:e3306. doi: 10.1002/cem.3306. [DOI] [Google Scholar]
- 81.Rinnan Å., Van Den Berg F., Engelsen S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trac-Trends Anal. Chem. 2009;28:1201–1222. doi: 10.1016/j.trac.2009.07.007. [DOI] [Google Scholar]
- 82.Hu K., Yuan J. Multivariate statistical process control based on multiway locality preserving projections. J. Process Control. 2008;18:797–807. doi: 10.1016/j.jprocont.2007.11.002. [DOI] [Google Scholar]
- 83.Mori J., Yu J. Quality relevant nonlinear batch process performance monitoring using a kernel based multiway non-Gaussian latent subspace projection approach. J. Process Control. 2014;24:57–71. doi: 10.1016/j.jprocont.2013.10.017. [DOI] [Google Scholar]
- 84.Peres F.A.P., Peres T.N., Fogliatto F.S., Anzanello M.J. Fault detection in batch processes through variable selection integrated to multiway principal component analysis. J. Process Control. 2019;80:223–234. doi: 10.1016/j.jprocont.2019.06.002. [DOI] [Google Scholar]
- 85.Lele S.S., Chakraborty S. Multiway Statistical Methods for Food Engineering and Technology. Math. Stat. Appl. Food Eng. 2020 [Google Scholar]
- 86.Allosio-Ouarnier N., Boivin P., Courcoux P., Bertrand D. Near Infrared Spectroscopy, Proceedings of the 9th International Conference, Verona, Italy, June 1999. NIR Publications; Chichester, UK: Application of the parallel factor analysis to visible near infrared data for the control of the malting process; pp. 273–280. [Google Scholar]
- 87.Liu J., Ma X., Wen Y., Wang Y., Cai W., Shao X. Online near-infrared spectroscopy combined with alternating trilinear decomposition for process analysis of industrial production and quality assurance. Ind. Eng. Chem. Res. 2011;50:7677–7681. doi: 10.1021/ie200543v. [DOI] [Google Scholar]
- 88.Nielsen J.P., Bertrand D., Micklander E., Courcoux P., Munck L. Study of NIR spectra, particle size distributions and chemical parameters of wheat flours: A multi-way approach. J. Near Infrared Spectrosc. 2001;9:275–285. doi: 10.1255/jnirs.313. [DOI] [Google Scholar]
- 89.Qannari E.M., Wakeling I., Courcoux P., MacFie H.J. Defining the underlying sensory dimensions. Food Qual. Prefer. 2000;11:151–154. doi: 10.1016/S0950-3293(99)00069-5. [DOI] [Google Scholar]
- 90.Peinado A., Van Den Berg F., Blanco M., Bro R. Temperature-induced variation for NIR tensor-based calibration. Chemom. Intell. Lab. Syst. 2006;83:75–82. doi: 10.1016/j.chemolab.2006.01.006. [DOI] [Google Scholar]
- 91.Lillhonga T., Geladi P. Three-way analysis of a designed compost experiment using near-infrared spectroscopy and laboratory measurements. J. Chemom. 2011;25:193–200. doi: 10.1002/cem.1371. [DOI] [Google Scholar]
- 92.Vigni M.L., Cocchi M. Near infrared spectroscopy and multivariate analysis to evaluate wheat flour doughs leavening and bread properties. Anal. Chim. Acta. 2013;764:17–23. doi: 10.1016/j.aca.2012.12.018. [DOI] [PubMed] [Google Scholar]
- 93.Wilde A.S., Haughey S.A., Galvin-King P., Elliott C.T. The feasibility of applying NIR and FT-IR fingerprinting to detect adulteration in black pepper. Food Control. 2019;100:1–7. doi: 10.1016/j.foodcont.2018.12.039. [DOI] [Google Scholar]
- 94.Puertas G., Vázquez M. Fraud detection in hen housing system declared on the eggs’ label: An accuracy method based on UV-VIS-NIR spectroscopy and chemometrics. Food Chem. 2019;288:8–14. doi: 10.1016/j.foodchem.2019.02.106. [DOI] [PubMed] [Google Scholar]
- 95.López-Maestresalas A., Insausti K., Jarén C., Pérez-Roncal C., Urrutia O., Beriain M.J., Arazuri S. Detection of minced lamb and beef fraud using NIR spectroscopy. Food Control. 2019;98:465–473. doi: 10.1016/j.foodcont.2018.12.003. [DOI] [Google Scholar]
- 96.Yang R., Liu R., Xu K., Yang Y. Quantitative Analysis of Melamine by Multi-Way Partial Least Squares Model with Two-Dimensional Near-Infrared Correlation Spectroscopy; Proceedings of the Biomedical Vibrational Spectroscopy VI: Advances in Research and Industry; San Francisco, CA, USA. 1–2 February 2014. [Google Scholar]
- 97.Rosa L.N., Gonçalves T.R., Gomes S., Matsushita M., Gonçalves R.P., Março P.H., Valderrama P. N-Way NIR data treatment through PARAFAC in the evaluation of protective effect of antioxidants in soybean oil. Molecules. 2020;25:4366. doi: 10.3390/molecules25194366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Rosa L.N., Coqueiro A., Março P.H., Valderrama P. Thermal rice oil degradation evaluated by UV–Vis-NIR and PARAFAC. Food Chem. 2019;273:52–56. doi: 10.1016/j.foodchem.2018.03.065. [DOI] [PubMed] [Google Scholar]
- 99.Kharbach M., Yu H., Kamal R., Barra I., Marmouzi I., Cherrah Y., Alaoui K., Bouklouze A., Heyden Y.V. New insights into the Argan oil categories characterization: Chemical descriptors, FTIR fingerprints, and chemometric approaches. Talanta. 2021;225:122073. doi: 10.1016/j.talanta.2020.122073. [DOI] [PubMed] [Google Scholar]
- 100.Cui X., Zhang J., Cai W., Shao X. Chemometric algorithms for analyzing high dimensional temperature dependent near infrared spectra. Chemom. Intell. Lab. Syst. 2017;170:109–117. doi: 10.1016/j.chemolab.2017.08.010. [DOI] [Google Scholar]
- 101.Geladi P., Manley M. Three-way data analysis of a wheat growing experiment using near infrared spectral data. J. Chemom. 2008;22:247–251. doi: 10.1002/cem.1125. [DOI] [Google Scholar]
- 102.Allosio N., Boivin P., Bertrand D., Courcoux P. Characterisation of barley transformation into malt by three-way factor analysis of near infrared spectra. J. Near Infrared Spectrosc. 1997;5:157–166. doi: 10.1255/jnirs.109. [DOI] [Google Scholar]
- 103.Yang R., Liu R., Dong G., Xu K., Yang Y., Zhang W. Two-dimensional hetero-spectral mid-infrared and near-infrared correlation spectroscopy for discrimination adulterated milk. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2016;157:50–54. doi: 10.1016/j.saa.2015.12.017. [DOI] [PubMed] [Google Scholar]
- 104.Rinnan Å., Riu J., Bro R. Multi-way prediction in the presence of uncalibrated interferents. J. Chemom. 2007;21:76–86. doi: 10.1002/cem.1037. [DOI] [Google Scholar]
- 105.Alcalà M., Ropero J., Vázquez R., Romañach R.J. Deconvolution of chemical and physical information from intact tablets NIR spectra: Two-and three-way multivariate calibration strategies for drug quantitation. J. Pharm. Sci. 2009;98:2747–2758. doi: 10.1002/jps.21634. [DOI] [PubMed] [Google Scholar]
- 106.Hou X., Shi D., Li G., Yang S., Tian H., Feng X., Lin L. Non-destructive analysis for the in-flexible-containers liquid composition based on WTFE-NPLS method. Infrared Phys. Technol. 2019;99:277–283. doi: 10.1016/j.infrared.2019.05.005. [DOI] [Google Scholar]
- 107.Letíci A., Farhat I.A., Aeberhardt K., Bro R., Engelsen S.B. Modeling of temperature-induced near-infrared and low-field time-domain nuclear magnetic resonance spectral variation: Chemometric prediction of limonene and water content in spray-dried delivery systems. Appl. Spectrosc. 2009;63:141–152. doi: 10.1366/000370209787392094. [DOI] [PubMed] [Google Scholar]
- 108.Peng D., Dong K., Li X., Xu K. Multidimensional calibration of near infrared spectra for component concentration measurement in milk at different temperatures; Proceedings of the 2010 4th International Conference on Bioinformatics and Biomedical Engineering; Chengdu, China. 18–20 June 2010; pp. 1–4. [Google Scholar]
- 109.Zhang X.-Z., Ma A.-J., Feng N., Li B.Q. N-way partial least squares combined with new self-construction strategy—A promising approach of using near infrared spectral data for quantitative determination of multiple compounds. J. Near Infrared Spectrosc. 2020;28:113–121. doi: 10.1177/0967033519896037. [DOI] [Google Scholar]
- 110.Folch-Fortuny A., Prats-Montalbán J.M., Cubero S., Blasco J., Ferrer A. VIS/NIR hyperspectral imaging and N-way PLS-DA models for detection of decay lesions in citrus fruits. Chemom. Intell. Lab. Syst. 2016;156:241–248. doi: 10.1016/j.chemolab.2016.05.005. [DOI] [Google Scholar]
- 111.Yang D., Lu A., Ren D., Wang J. Detection of total viable count in spiced beef using hyperspectral imaging combined with wavelet transform and multiway partial least squares algorithm. J. Food Saf. 2018;38:e12390. doi: 10.1111/jfs.12390. [DOI] [Google Scholar]
- 112.Alexandrino G.L., Amigo J.M., Khorasani M.R., Rantanen J., Friderichsen A.V., Poppi R.J. Unveiling multiple solid-state transitions in pharmaceutical solid dosage forms using multi-series hyperspectral imaging and different curve resolution approaches. Chemom. Intell. Lab. Syst. 2017;161:136–146. doi: 10.1016/j.chemolab.2016.11.004. [DOI] [Google Scholar]
- 113.Wu L., He J., Liu G., Wang S., He X. Detection of common defects on jujube using Vis-NIR and NIR hyperspectral imaging. Postharvest Biol. Technol. 2016;112:134–142. doi: 10.1016/j.postharvbio.2015.09.003. [DOI] [Google Scholar]
- 114.Liu Y., Pu H., Sun D.-W. Hyperspectral imaging technique for evaluating food quality and safety during various processes: A review of recent applications. Trends Food Sci. Technol. 2017;69:25–35. doi: 10.1016/j.tifs.2017.08.013. [DOI] [Google Scholar]
- 115.Burger J., Gowen A. Data handling in hyperspectral image analysis. Chemom. Intell. Lab. Syst. 2011;108:13–22. doi: 10.1016/j.chemolab.2011.04.001. [DOI] [Google Scholar]
- 116.Feng L., Zhu S., Liu F., He Y., Bao Y., Zhang C. Hyperspectral imaging for seed quality and safety inspection: A review. Plant Methods. 2019;15:91. doi: 10.1186/s13007-019-0476-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Koljonen J., Nordling T.E., Alander J.T. A review of genetic algorithms in near infrared spectroscopy and chemometrics: Past and future. J. Near Infrared Spectrosc. 2008;16:189–197. doi: 10.1255/jnirs.778. [DOI] [Google Scholar]
- 118.Mobaraki N., Amigo J.M. HYPER-Tools. A graphical user-friendly interface for hyperspectral image analysis. Chemom. Intell. Lab. Syst. 2018;172:174–187. doi: 10.1016/j.chemolab.2017.11.003. [DOI] [Google Scholar]
- 119.Andersson C.A., Bro R. The N-way toolbox for MATLAB. Chemom. Intell. Lab. Syst. 2000;52:1–4. doi: 10.1016/S0169-7439(00)00071-X. [DOI] [Google Scholar]
- 120.Kolda T.G., Bader B.W. MATLAB Tensor Toolbox. Sandia National Laboratories; Albuquerque, NM, USA: 2006. [Google Scholar]
- 121.Phan A.-H., Tichavský P., Cichocki A. Tensorbox: A Matlab Package for Tensor Decomposition. LABSP RIKEN; Saitama, Japan: 2012. [Google Scholar]
- 122.Phan A.-H., Tichavsky P., Cichocki A. Low complexity damped Gauss--Newton algorithms for CANDECOMP/PARAFAC. Siam J. Matrix Anal. Appl. 2013;34:126–147. doi: 10.1137/100808034. [DOI] [Google Scholar]
- 123.Wise B.M., Gallagher N., Bro R., Shaver J., Windig W., Koch R.S. PLS Toolbox 4.0. Eigenvector Research; Wenatchee, WA, USA: 2007. [Google Scholar]
- 124.Giordani P., Kiers H.A., Del Ferraro M.A. Three-way component analysis using the R package ThreeWay. J. Stat. Softw. 2014;57:1–23. doi: 10.18637/jss.v057.i07. [DOI] [Google Scholar]
- 125.Helwig N.E. Multiway: Component Models for Multi-Way Data. R Package Version 1.0-5. [(accessed on 8 April 2021)]; Available online: https://CRAN.R-project.org/package=multiway.
- 126.Kossaifi J., Panagakis Y., Anandkumar A., Pantic M. Tensorly: Tensor learning in python. J Mach. Learn Res. 2019;20:1–6. [Google Scholar]
- 127.Hao L., Liang S., Ye J., Xu Z. TensorD: A tensor decomposition library in TensorFlow. Neurocomputing. 2018;318:196–200. doi: 10.1016/j.neucom.2018.08.055. [DOI] [Google Scholar]