How adding a single methylene to dihydrofolate reductase can change its conformational dynamics

Abstract

Studies of the effects of pressure on proteins from piezophilic (pressure-loving) microbes compared with homologous proteins from mesophilic microbes have been relatively rare. Interestingly, such studies of dihydrofolate reductase show that a single-site mutation from an aspartic acid to a glutamic acid can reverse the pressure-dependent monotonic decrease in activity to that in a monotonic pressure-dependent activation. This residue is near the active site but is not thought to directly participate in the catalytic mechanism. Here, the ways that addition of one carbon to the entire protein could lead to such a profound difference in pressure effects are explored using molecular dynamics simulations. The results indicate that the glutamate changes the coupling between a helix and the β-sheet due to the extra flexibility of the side chain, which further changes correlated motions of other regions of the protein.

I. INTRODUCTION

Elevated hydrostatic pressure environments are one of the largest parts of the biosphere.¹ Life has been found flourishing in the deepest part of the ocean, corresponding to a pressure of over ∼105 MPa (1.05 kbar). Microbial life has also been found in a range of temperatures from −20 to 122 °C.¹ Since both temperature and pressure affect the structure and function of proteins, microbial adaptations to both have been studied, although adaptation to temperature has generally been much more studied than adaptation to pressure. One issue is that there appears to be a balance of two opposing effects of high pressure on proteins: compression and unfolding.^2,3 Pressure-induced unfolding is thought to occur by infiltration of water into cavities,⁴ indicating that cavities might be disfavored in proteins from piezophiles (pressure-loving organism). However, proteins from piezophiles appear to have larger cavity volumes than those from mesophiles,^5,6 which may be an adaptation for compressibility since pressure causes cavity sizes to decrease.⁷

Many of the earliest experimental comparisons of a protein from a piezophile and a mesophile have focused on dihydrofolate reductase (DHFR)^6,8 because of its isolation from Moritella profunda (Mp) with optimal growth conditions of 220 bars at 6 °C⁹ in comparison to DHFR from Escherichia coli (Ec), a mesophile with optimal growth conditions of 37 °C and 1 bar. DHFR has been thoroughly studied by experimental and computational methods.^10,11 DHFR has been well-characterized structurally by crystallography, including steps along the enzymatic cycle of EcDHFR by complexes containing bound analogs of kinetic intermediates.¹² It has two subdomains that resemble rigid bodies connected by hinges [Figs. 1(a) and 1(b); see Fig. S1 of the supplementary material for the secondary structure assignment of the sequence]. The adenosine binding subdomain is composed of residues 38–106, which contains the CD loop; the β-strands B, C, D, and E; and α-helices C, E, and F. The loop subdomain is composed of residues 1–37 and 107–159, which contains the Met20, FG, and GH loops; the β-strands A, F, G, and H; and α-helix B. This study also indicates a prominent role for the Met20 loop, which adopts a closed conformation in the first half of the enzymatic cycle, an occluded conformation in the second half, and an open conformation that appears intermediate between the closed and occluded states. In addition, structural fluctuations on the nanosecond timescale have been noted for the Met20 and FG loops,¹³ with the movement of the Met20 loop appearing to depend on the freedom of the FG and GH loops to move.¹² Nuclear magnetic resonance (NMR) relaxation studies also indicate that picosecond/nanosecond and microsecond/millisecond backbone dynamics plays a role in loop flexibility and that long-range coupling occurs between distant regions of the protein.¹⁴ Computer simulation studies also indicate that mutations in DHFR cause long-range structural perturbations and that reduced activities in the mutants are associated with reduced correlation of motions between distant residues.¹⁵

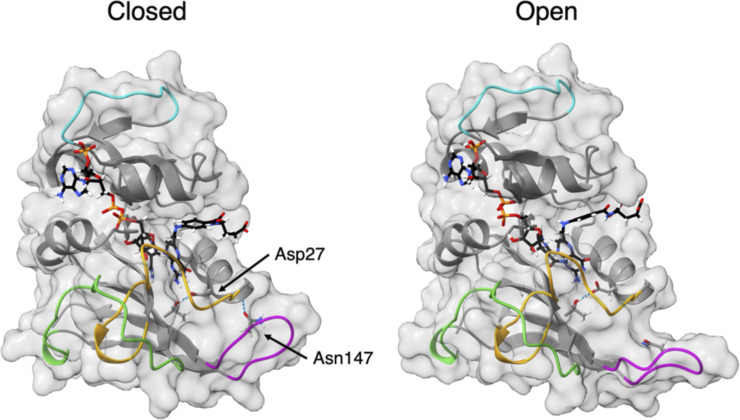
FIG. 1.

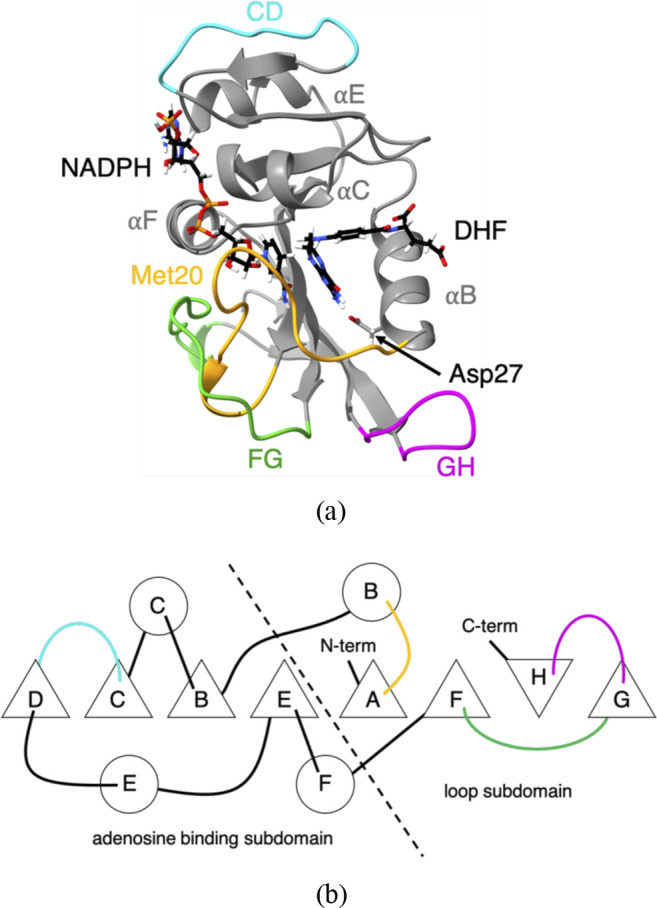
Structure of E. coli dihydrofolate reductase. (a) Ribbon representation of the structure of wild-type EcDHFR (PDB ID: 1RX2). Met20 (yellow), CD (blue), FG (green), and GH (pink) loops are highlighted. Cofactor (NADPH), ligand (DHF), and Asp27 are shown in the stick representation. (b) Schematic of ordering of the secondary structure and of contacts between secondary structure elements in EcDHFR. α-helices are given as circles, β-strands are given as triangles, and the loops are colored as in (a). Based on the figure by Sawaya and Kraut.¹²

Our initial simulation studies^16–18 also began with comparisons of simulations of MpDHFR with EcDHFR at all combinations of the growth temperatures and pressures of each. Our results indicated that the atomic fluctuations in MpDHFR were consistently higher at a given temperature and pressure than in EcDHFR but also that increased pressure tends to lead to larger atomic fluctuations. There appeared to be some sequence specific adaptations for activity at high pressure, namely, Glu27 in MpDHFR vs Asp27 in EcDHFR. Specifically, our simulations indicated that a strong, long lifetime (τ = ∼25 ns) Thr113 O_γ⋯Asp27 O_δ hydrogen bond between strand F and helix B in EcDHFR appeared to cause helix B to move in association with strand F. At a higher pressure, this Thr113 O_γ⋯Asp27 O_δ hydrogen bond led to weaker coupling of helix B with the GH loop, which, in turn, led to greater motion of the GH loop and decoupling of the GH loop from the Met20 loop. On the other hand, the Thr113 O_γ⋯Glu27 O_δ hydrogen bond in MpDHFR was weaker with a shorter lifetime (τ < 100 ps), presumably because of the greater flexibility of the Glu27 side chain. At increased pressure, this weaker coupling allowed helix B to remain correlated with the GH loop, reducing the pressure-sensitivity of the motions of the GH loop, further allowing the GH loop to remain coupled to the Met20 loop. In fact, the experimental studies showed that while EcDHFR is piezo-sensitive, a single-site mutant of Asp27 to Glu 27 (referred to here as EcDHFR^D27E) shows increasing activity with pressure, which resulted in a slightly opened substrate-binding cleft.¹⁹

However, many of the differences between MpDHFR and EcDHFR appeared to be adaptations for a difference in the growth temperature of the two organisms. Our conclusion was that while the initial increase in activity with pressure in MpDHFR was due to Glu27, the subsequent decrease above ∼500 bars was due to the adaptations for low temperature activity that made it less stable. Interestingly, other deep-sea and surface Moritella DHFR have Glu27, while DHFR from other deep-sea genera have Asp27.²⁰ Apparently, Glu27 can make DHFR more resistant against pressure; however, it is not mandatory for pressure resistance.

Here, the focus is on understanding how the single additional methylene in EcDHFR^D27E leads to an increase in activity with pressure, instead of decrease as observed in wild-type EcDHFR. The pressure effects on EcDHFR and EcDHFR^D27E both in complex with dihydrofolate (DHF) and NADPH are examined using molecular dynamics simulations at 4 °C and at 1 or 220 bars. While fluctuations increase at higher pressure in EcDHFR as in our previous work,^16–18 pressure appears to have opposite effects on fluctuations in EcDHFR^D27E, which are larger at 1 bar. While the smaller fluctuations for EcDHFR at 1 bar and EcDHFR^D27E at 220 bars are associated with a “closed” conformation of the GH loop, larger fluctuations are associated with a second “open” conformation. The different effects of pressure on the fluctuations of EcDHFR and EcDHFR^D27E, which differ by a single methylene group out of a total of 159 residues, are examined in light of changes in hydrogen bonding and correlated motion of the secondary structure. These effects are discussed in light of the balance of two opposing effects of pressure on proteins: compression and unfolding.

II. METHODS

A. Simulations

Coordinate manipulations and analyses were performed using molecular mechanics package CHARMM version 40b1.²¹ Molecular dynamics (MD) simulations were performed using molecular mechanics package OpenMM version 7.3.1²² compiled with CUDA version 9.2. The CHARMM36 all-atom non-polarizable potential energy parameter set was used to model the protein.^23,24 Water was modeled by TIP4P-Ew because of the importance of modeling changes in the properties of water under pressure.²⁵ A CHARMM General Force Field (CGenFF) was generated for DHF through ParamChem (v. 1.0.0)²⁶ with hydrogen bonding lists added manually. The force field developed by Pavelites et al.²⁷ was used to describe the reduced cofactor NADPH. Sequences were aligned using ClustalX v.2.1.²⁸ Ligand Reader and Modeler²⁹ in CHARMM-GUI was used to modify the pterin ring of folate from a planar system to the partially puckered ring of dihydrofolate (DHF), as well as to modify oxidized nicotinamide adenine dinucleotide phosphate (NADP⁺) to the reduced form (NADPH).

Coordinates for the proteins were generated with PDB Reader;³⁰ specifically, termini were capped with amino and carboxyl groups, and missing hydrogen coordinates were built. Starting coordinates for EcDHFR (PDB ID: 1RX2¹²) were obtained from the PDB. The Asp27Glu single-site mutation was built using GalaxyFill³¹ in PDB Reader. Crystal waters within 2.5 Å of any modeled residue were deleted. The DHFRs were solvated in a cubic simulation box of equilibrated TIP4P-Ew with a distance between faces of ∼70 Å. Solvent waters within 2.5 Å of any crystal water, ligand, or protein heavy atom were deleted. The smallest distance from a protein atom to a side of the box was ∼10 Å. The proteins were then neutralized in 0.15M KCl using the Monte Carlo placement method. For both proteins, there were 10 161 water molecules, 43 K⁺ and 27 Cl⁻.

The subsequent calculations were performed in OpenMM as described briefly here; in particular, changes from default settings are noted. The calculations were “mixed precision,” in which forces and integration are calculated in single and double precision, respectively. Nonbonded interactions had a cutoff of 12 Å, with the Lennard-Jones interactions switched off smoothly using the default OpenMM switching function beginning at 10 Å to the cutoff and no long-range corrections. The particle mesh Ewald (PME) summation algorithm,³² with an Ewald error tolerance of 1 × 10⁻⁵, was used for the electrostatics. Each system was minimized with 500 iterations of the L-BFGS algorithm.³³ During minimization, a harmonic restraint with a force constant of 100 kcal mol⁻¹ Å⁻² was applied to heavy atoms of the protein backbone to prevent large divergence from the starting coordinates. Initial stages of the simulations were performed using a leapfrog Verlet integrator with a time step of 0.001 ps and were maintained in the NPT ensemble using an Andersen thermostat³⁴ updated every 1000 steps and Monte Carlo (MC) barostat³⁵ updated every 25 steps. Each system was heated from an initial temperature of 0 K to the final temperature in 5 K intervals of 5 ps each, followed by the pressurization from 1 bar to the final pressure in 20 bars intervals of 20 ps each. A harmonic restraint with a force constant of 5 kcal mol⁻¹ Å⁻² was applied to the heavy atoms of the protein and ligands during heating and pressurization³⁶ and then gradually decreased from 5 to 0 kcal mol⁻¹ Å⁻² in 0.5 kcal mol⁻¹ Å⁻² intervals for a total of 20 ps. Next, the system was equilibrated for 5 ns in the NPT ensemble with all harmonic restraints removed. The final stages of the simulations were performed utilizing a velocity Verlet integrator with a time step of 0.001 ps maintained in the NVT ensemble using a Nosé–Hoover thermostat.^37–40 All simulations were run for an additional 100 ps, and the system volumes every 1 ps were compared to that of the average volume from the last 4 ns of the NPT equilibration run. For all simulations at 1 bar, the closest volume less than the average volume of the NPT equilibration run was used to start the NVT production run, while for all other conditions, the closest volume to the average of the NPT run was chosen. The system was equilibrated for another 5 ns followed by 50 ns of production run in the NVT ensemble.

B. Analysis

Average properties were calculated from coordinates written at 1 ps intervals except as noted. Standard deviations were calculated by block averaging over 5 ns blocks. The mean-squared fluctuations of the protein heavy atoms ⟨Δr_HA²⟩ were calculated within 5 ns blocks with respect to the average structure within each block and then averaged over all blocks. The mean-squared fluctuations ⟨Δr_CA²⟩ and cross-correlation (normalized covariance) matrices⁴¹ of C_α atoms were calculated from the entire 50 ns production run with respect to the average structure over the entire production run. While slight artifacts can arise for perpendicular or near-perpendicular displacement vectors in the vector cross-correlation matrices, these are not anticipated to be significant in the results reported here.⁴² Moreover, vector cross-correlation matrices allow anti-correlation and correlation to be identified. For the open and closed states, the part of the production run in that state the fluctuations were calculated for that part with respect to the average structure over that part. There was 20–30 ns for each state (for exact numbers, see Table S1 of the supplementary material).

Hydrogen bonds were defined as having a distance between the donor atom i and the acceptor atom j smaller than 2.40 Å and an angle of D–H⋯A larger than 130°. The time-averaged number of hydrogen bonds, N_HB, was calculated as the average number of hydrogen bonds at each time step. Hydrogen bonding events were calculated in CHARMM, while MATLAB was used to calculate the average occupancies and lifetimes for each hydrogen bond pair. Two hydrogen bonds simultaneously formed with the same protein atom were calculated as two separate events. For chemically equivalent hydrogen bonding donors or acceptors of the same residue, equivalent atoms (such as O_δ1/O_δ2 in Asp) were combined. The occupancy, n_ij, was defined as the fraction of the total simulation time in which i and j are hydrogen bonded. Bifurcated hydrogen bonds were treated as a single event so that the maximum occupancy would be one. The average hydrogen bond lifetime, ${\tau }_{ij}$, is the sum of the time, t_ij, that the donor atom i is in a hydrogen bond with any acceptor atom j, over the number of hydrogen bonding events, n_ij,

$${\tau }_{ij}=\frac{1}{n_{ij}}{\sum }_{i=1}^{n_{ij}}{t}_{ij}\left(n\right).$$ (1)

The average overall hydrogen bond lifetime between species α and β for a simulation, ${\tau }_{\alpha \beta }$, is

$${\tau }_{\alpha \beta }=\frac{1}{N}{\sum }_{i,j}{\tau }_{ij},$$ (2)

where ${\tau }_{ij}$ is the average hydrogen bond lifetime between any atom pair ij, respectively, and N is the total number of individual hydrogen bond pairs between the two species.

III. RESULTS

A. Structural changes with pressure

An overview of the differences in the simulations can be seen in the average properties of the proteins (Table I). Although the differences are not large, it appears that EcDHFR gets more flexible with increasing pressure since the mean-square fluctuations of the heavy atoms ⟨Δr_HA²⟩ increase, while the number of intra-protein hydrogen bonds N_HB decreases. Conversely, EcDHFR^D27E gets less flexible with increasing pressure since ⟨Δr_HA²⟩ decreases and N_HB increases. Thus, the addition of a single methylene group appears to cause opposite trends in flexibility with increasing pressure. In what follows, “Res”27 refers to Asp27 in EcDHFR and Glu27 in EcDHFR^D27E.

TABLE I.

Mean-square fluctuations of heavy atoms ⟨Δr_HA²⟩ and the average number of intraprotein hydrogen bonds N_HB at different pressures P.

Protein	P (bar)	⟨ΔrHA2⟩ (Å2)	NHB
EcDHFR	1	0.57 ± 0.07	105 ± 2
EcDHFR	220	0.60 ± 0.08	104 ± 4
EcDHFRD27E	1	0.60 ± 0.04	103 ± 3
EcDHFRD27E	220	0.50 ± 0.04	109 ± 1

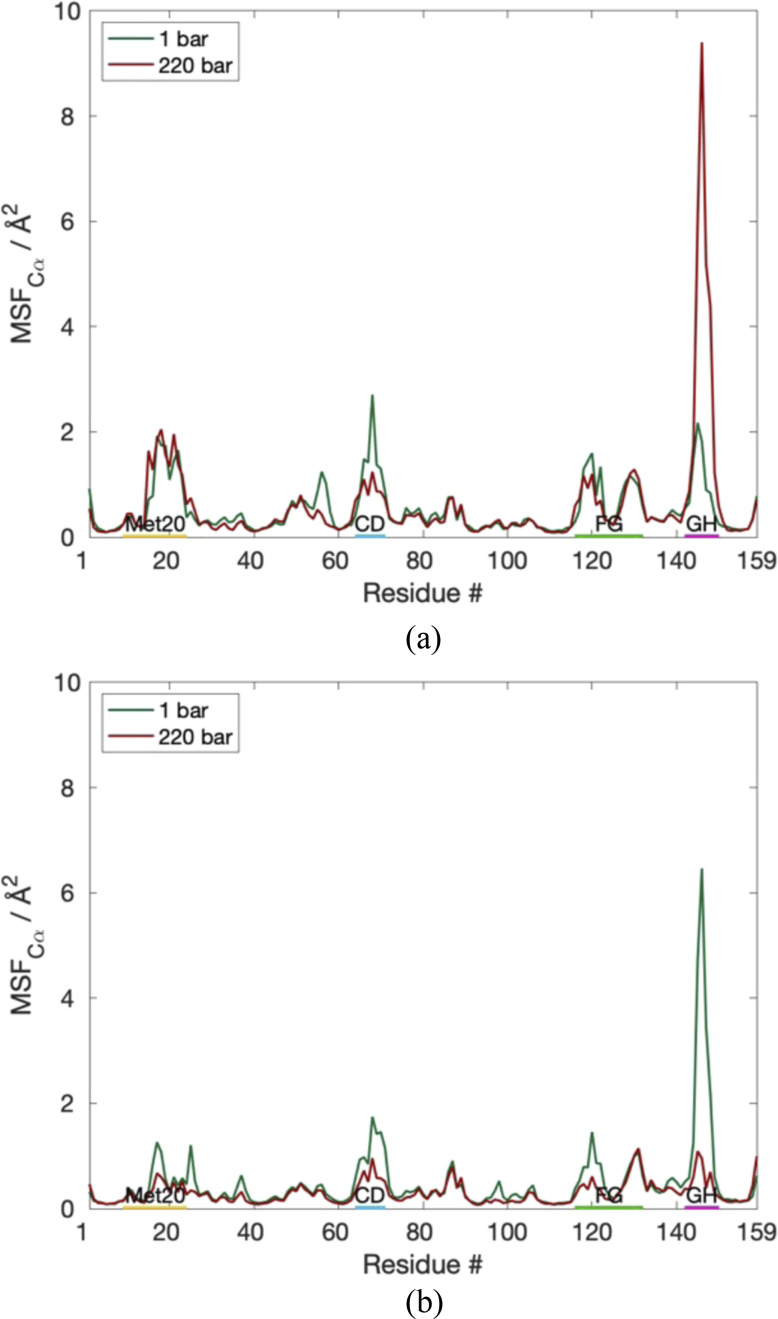
⟨Δr_Cα²⟩ per residue (Fig. 2) show that the differences in the fluctuations in both proteins can be attributed mainly to the GH loop. Interestingly, the GH loop becomes more flexible for EcDHFR at increasing pressure, while the GH loop becomes more stable for EcDHFR^D27E. Additionally, both EcDHFR and EcDHFR^D27E exhibit slight decreases in the fluctuations of the CD loop as a function of pressure.

FIG. 2.

Comparison of ⟨Δr_Cα²⟩ per residue for (a) EcDHFR^WT and (b) EcDHFR^D27E.

The simulations of EcDHFR at 220 bars and of EcDHFR^D27E at 1 bar show that the GH loop opens after 20–25 ns of the simulation, as illustrated for EcDHFR at 220 bars in (Fig. 3). Although the statistics for each state are poorer (approximately half; see the supplementary material), overall, ⟨Δr_HA²⟩ increase and N_HB decrease from the “closed” to “open” GH loop (Table II), so the “open” GH loop appears more flexible. In addition, the GH loop becomes more hydrated in the open state since the average number of hydrogen bonds between the GH loop and water (n_GH-w) increases (Table II). Thus, the reason for the increased flexibility for EcDHR at 220 bars and EcDHFR^D27E at 1 bar seems to be opening of the GH loop. EcDHFR remains in the “closed” state for nearly the entire production run at 1 bar, while EcDHFR^D27E stays in the “closed” state at 220 bars. In addition, n_GH-w is 32 ± 1 for the closed GH loop, similar to the closed GH loop in the other simulations, which opens later, indicating the similarity of the closed states.

FIG. 3.

Conformational states of the GH loop. Representative snapshots of EcDHFR at 220 bars with the (left) “closed” and (right) “open” GH loops.

TABLE II.

Mean-square fluctuations of heavy atoms ⟨Δr_HA²⟩, the average number of intraprotein hydrogen bonds N_HB, and the average number of waters hydrogen-bonded to the GH loops n_GH-w in different states of the GH loop.

Protein	P (bar)	Loop state	⟨ΔrHA2⟩ (Å2)	NHB	nGH-w
EcDHFR	220	Closed	0.55 ± 0.06	107 ± 1	32 ± 1
EcDHFR	220	Open	0.67 ± 0.05	99 ± 1	35 ± 1
EcDHFRD27E	1	Closed	0.57 ± 0.04	105 ± 2	32 ± 2
EcDHFRD27E	1	Open	0.62 ± 0.03	100 ± 1	38 ± 1

B. Changes in intraprotein hydrogen bonds with pressure

Examining the hydrogen bonds, it appears that pressure tends to increase the lifetime of high occupancy bonds but that the open GH loop decreases the occupancy of hydrogen bonds, resulting in the overall N_HB decrease (Table II). The occupancy n and lifetime τ of select hydrogen bonds, which appear to play critical roles in the different behaviors, are compared (Table III). In EcDHFR and EcDHFR^D27E at both pressures, there is a high occupancy, long lifetime hydrogen bond between Thr113 of strand F and Res27 of helix B, and the lifetime increases between 1 and 220 bars (Table III). Interestingly, since the lifetimes are shorter for EcDHFR^D27E, this results in similar lifetimes for EcDHFR at 1 bar and EcDHFR^D27E at 220 bars. This hydrogen bond has a remarkably high occupancy and long lifetime since the other hydrogen bonds in DHFR with full occupancy and nanosecond scale lifetimes are within elements of the secondary structure, i.e., the hydrogen bonds that determine helices and sheets. Another hydrogen bond of interest is between Ala26 of helix B and Asn147 of the GH loop, which is a short lifetime hydrogen bond with similar occupancies for EcDHFR at 1 bar and EcDHFR^D27E at 220 bars but lower occupancies at the other pressure.

TABLE III.

Occupancy n and lifetime τ of select hydrogen bonds. Res represents Asp for EcDHFR and Glu for EcDHFR^D27E.

		n (τ)
		EcDHFR	EcDHFR	EcDHFRD27E	EcDHFRD27E
Donor	Acceptor	(1 bar)	(220 bars)	(1 bar)	(220 bars)
Thr113 Oγ	Res27 Oδ/ε	1.0 (1.7 ns)	1.0 (6.2 ns)	1.0 (0.96 ns)	1.0 (1.2 ns)
Ala26 N	Asn147 Oδ	0.74 (6 ps)	0.47 (8 ps)	0.35 (5 ps)	0.75 (5 ps)

Examining the occupancies for the open and closed GH loops at the same pressure (Table IV), the Thr113⋯Res27 hydrogen bond remains highly occupied with long lifetimes in both states. On the other hand, breaking the Ala26⋯Asn147 hydrogen bond appears indicative of the GH loop opening.

TABLE IV.

Occupancy n and lifetime τ of select hydrogen bonds for different states of the GH loop. Res represents Asp for EcDHFR and Glu for EcDHFR^D27E.

		Occupancy (lifetime)
		EcDHFR	EcDHFR	EcDHFRD27E	EcDHFRD27E
Donor	Acceptor	(closed, 220 bars)	(open, 220 bars)	(closed, 1 bar)	(open, 1 bar)
Thr113 Oγ	Res27 Oδ/ε	1.0 (6.0 ns)	1.0 (5.0 ns)	1.0 (0.64 ns)	1.0 (1.8 ns)
Ala26 N	Asn147 Oδ	0.78 (8 ps)	0.0	0.71 (5 ps)	0.0

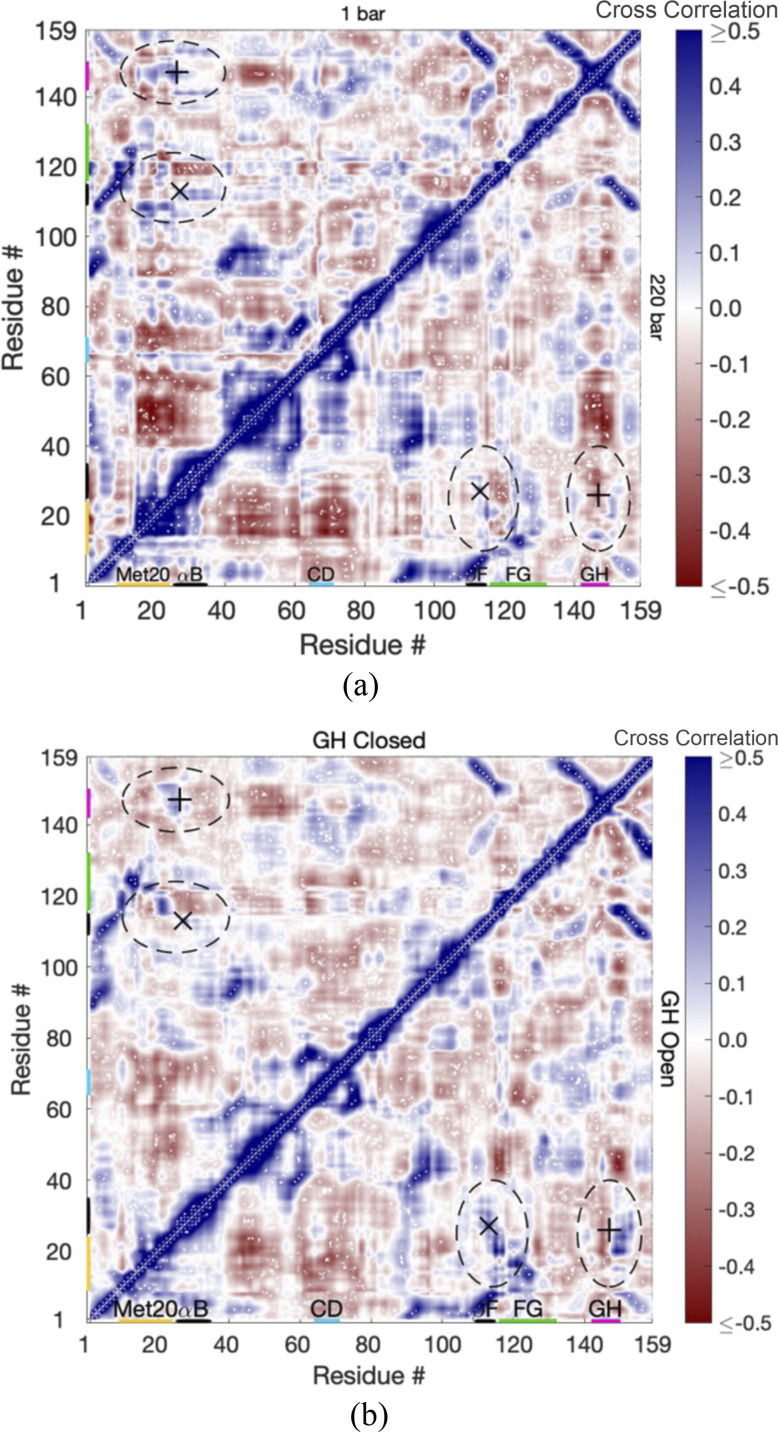
C. How Asp27 leads to opening GH loop in EcDHFR at 220 bars

Cross-correlation matrices of the C_α fluctuations of EcDHFR with the closed and open GH loops are examined first to see how the strong Thr113⋯Asp27 hydrogen bond leads to the opening of the GH loop. For reference, the matrix of interatomic distances between C_α is given in Fig. S2. Regions of the secondary structure are apparent in the interatomic distance matrix as regions of close separation, with helices appearing as thicker regions along the self-correlation diagonal, parallel strands of sheets appearing as diagonal regions parallel to but separated from the self-correlation diagonal, while antiparallel strands appearing as diagonal lines perpendicular to the self-correlation diagonal. Correlations are also high within these regions of the secondary structure as evident in cross-correlation matrices at 1 and 220 bars [Fig. 4(a)] because of the hydrogen bonds that hold them together.

FIG. 4.

The cross correlations in the fluctuations of C_α atoms per residue for EcDHFR (a) at 1 bar (upper-left) and 220 bars (lower-right) and (b) at 220 bars with the GH loop in the closed state (upper-left) and the open state (lower-right). The Thr113⋯Asp27 hydrogen bond is specified by “x,” and Ala26⋯Asn147 is specified by “+.” Regions discussed in the text are identified by dashed ovals.

However, examination of the correlations when the GH loop is closed vs when it is open at 220 bars [Fig. 4(b)] shows some key differences. While the correlations with the GH loop closed are similar to the correlations at 1 bar, the correlations with the GH loop open show that strong Thr113⋯Asp27 leads to an increase in the correlation of helix B with strand F. The interactions between helix B and the GH loop, such as the Ala26⋯Asn147 hydrogen bond, apparently weaken because helix B is coupled to F instead so that the GH loop becomes anticorrelated with helix B. In addition, while the Met20 loop appears somewhat correlated with the FG and GH loops at 1 bar, it becomes strongly correlated with the FG loop and anticorrelated with the GH loop when the GH loop is open.

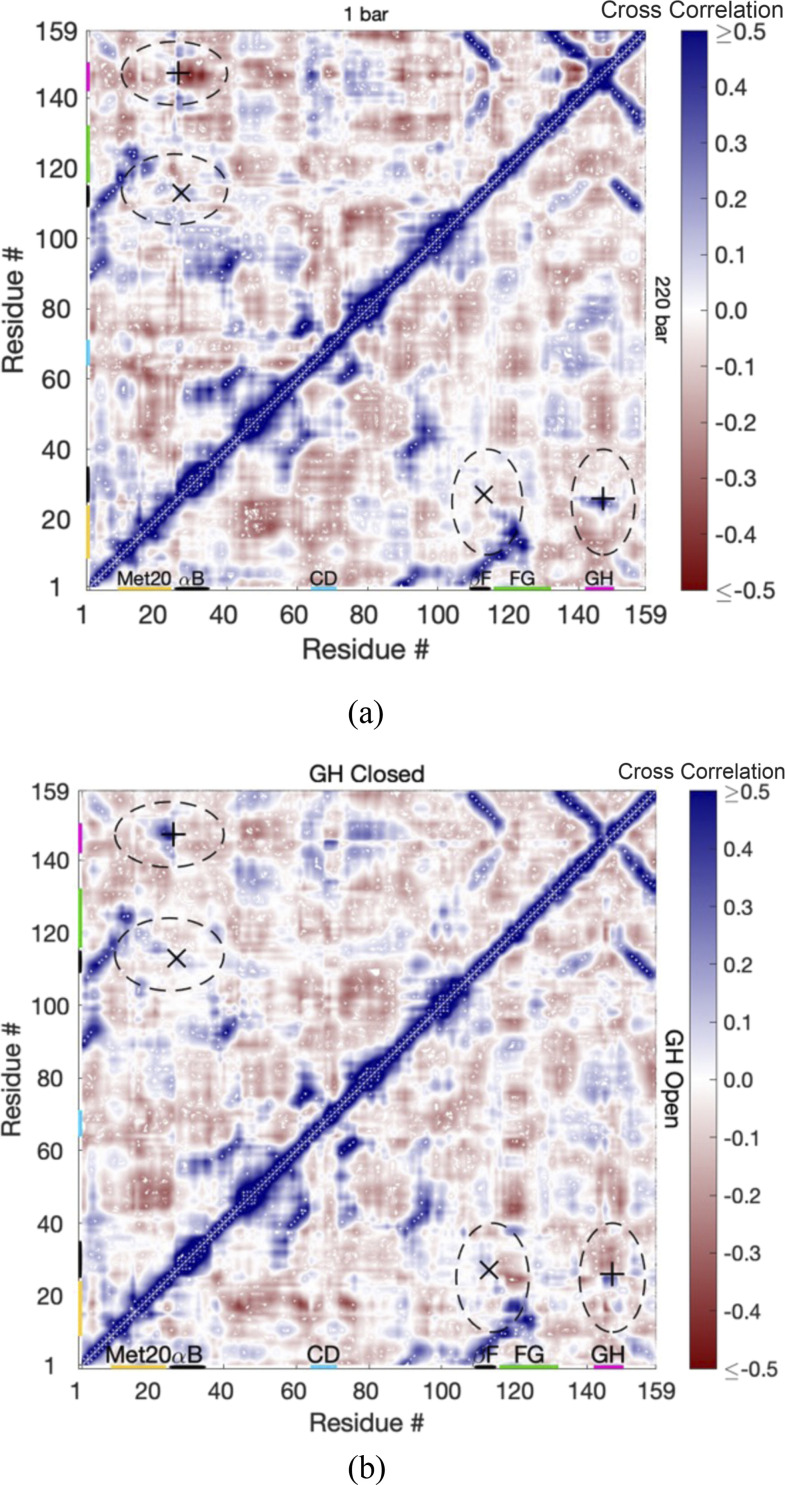
D. How Glu27 leads to opening GH loop in EcDHFR^D27E at 1 bar

Cross-correlation matrices of the C_α fluctuations between the closed and open states of EcDHFR^D27E are examined next to see how the relatively strong Thr113⋯Glu27 hydrogen bond (but weaker than Thr113⋯Asp27 in EcDHFR) leads to the opening of the GH loop at 1 bar. As in EcDHFR, correlations are also high within regions of the secondary structure as evident in cross-correlation matrices at 1 and 220 bars [Fig. 5(a)] because of the hydrogen bonds that hold them together. However, examination of the correlations when the GH loop is closed vs when it is open at 1 bar [Fig. 5(b)] shows some key differences from the behavior in EcDHFR. While the GH closed correlations are similar to the correlations at 1 bar, the GH open correlations show that the relatively strong Thr113⋯Glu27 does not lead to correlated motion of helix B with strand F. The extra single C–C bond apparently reduces the correlation by allowing more relative movement. Since helix B is less strongly coupled with strand F, some interactions between the GH loop and helix B are maintained such that the GH loop opening may not be as drastic as in EcDHFR at 1 bar.

FIG. 5.

The cross correlations in the fluctuations of C_α atoms per residue for EcDHFR^D27E (a) at 1 bar (upper-left) and 220 bars (lower-right) and (b) at 1 bar with the GH loop in the closed state (upper-left) and the open state (lower-right). The Thr113⋯Glu27 hydrogen bond is specified by “x,” and Ala26⋯Asn147 is specified by “+.” Regions discussed in the text are identified by dashed ovals.

IV. DISCUSSION

The simulations indicate that EcDHFR at 1 bar is relatively stable against GH loop opening, while at 220 bars, the GH loop becomes much more mobile, which is consistent with our previous simulations of EcDHFR.^16–18 The simulations indicate the reverse for EcDHFR^D27E, which at 1 bar shows the GH loop opening, while at 220 bars, it is relatively stable to GH loop opening. The latter results are consistent with other simulations for EcDHFR^D27E at those pressures with slightly different initial conditions (unpublished results). Given that structural fluctuations on the nanosecond timescale have been noted for the Met20 and FG loops, although not specifically for the GH loop,¹³ and movement of the Met20 loop appears to depend on the freedom of the FG and GH loops to move,¹² the nature, if not the specifics, of the correlated effects seen in the simulations appears reasonable. In particular, our focus is not on the specific loops that open at different pressures but on how the extra methylene group in EcDHFR^D27E gives rise to the opposite effects of the higher pressure on the GH loop compared to EcDHFR.

The major difference directly associated with the identity of residue 27 is the lifetime of the Thr113⋯Res27 hydrogen bond, which is a long lifetime regardless but is significantly longer for Thr113⋯Asp27 than for Thr113⋯Glu27. This hydrogen bond causes coupling of helix B with strand F of the β-sheet. However, the coupling is looser in EcDHFR^D27E apparently due to the extra methylene group in the side chain of glutamate, which makes the linkage between helix B and the β-sheet more flexible. The effects of pressure on the linkage between helix B and the β-sheet appear to be compressive so that the two become more tightly linked and more correlated. This increased correlation becomes excessive in EcDHFR so that the GH loop becomes detached from helix B, which also affects its correlation with the FG and Met20 loops. Since Met20 movement is apparently dependent on the flexibility of the FG and GH loops,¹² changes in the correlations of these loops from what is found at 1 bar could contribute to reduced activity in EcDHFR at higher pressures. Pressure is also correlated with solvation of the GH loop in EcDHFR, which has more water between helix B and the GH loop so that the GH loop is more solvated (i.e., see n_GH-w in Table II) in the open state at 220 bars. High-pressure crystallographic studies of EcDHFR also show a small cavity between helix B and the GH loop.⁷ In addition, the enhanced solvation of the GH loops suggests that the active site could also become more solvated than at 1 bar, although this must be examined further. On the other hand, the weaker coupling between helix B and the β-sheet in EcDHFR^D27E compared to that of EcDHFR may result in too little correlation at 1 bar. Experiments also indicate that EcDHFR^D27E has more open substrate-binding cleft.⁸ Here, pressure appears to be correlated with decreased solvation of the GH loop in EcDHFR^D27E since the closed state is favored at 220 bars, presumably because of the lack of compressive effect to counteract the too little correlation at 1 bar. If pressure increases correlation between helix B and the β-sheet, the increased correlation at 220 bars may make EcDHFR^D27E look more like EcDHFR at 1 bar; the cross-correlation matrices of EcDHFR^D27E at 220 bars [Fig. 5(a)] look similar to those of EcDHFR at 1 bar [Fig. 4(a)]. Thus, increasing pressure may enhance activity in EcDHFR^D27E by increasing these correlations.

V. CONCLUSIONS

Experimental studies have shown that while the activity of EcDHFR decreases with pressure, the activity of EcDHFR^D27E actually increases with pressure. Our simulations of EcDHFR and EcDHFR^D27E at 1 and 220 bars indicate that the added methylene in the Glu27 side chain of EcDHFR^D27E leads to a slightly more flexible linkage, namely, the Thr113⋯Res27 hydrogen bond between helix B and strand F of the β-sheet, compared to that of the Asp27 side chain of EcDHFR. The Thr113⋯Res27 hydrogen bond also affects correlations between helix B and the GH loop and between the FG, GH, and Met20 loops. The correlations appear optimal for EcDHFR at 1 bar such that when the pressure is increased to 220 bars, compression excessively increases the correlations between the loops. These correlations are thought to be important for proper functioning of the enzyme so that disruption of these correlations by pressure may lead to a decrease in activity. Conversely, correlations appear too low for EcDHFR^D27E at 1 bar so that compression caused by an increase in pressure to 220 bars results in increased correlations between the loops to mirror what is observed in EcDHFR at 1 bar.

SUPPLEMENTARY MATERIAL

See the supplementary material for the length of open and closed states in the simulations (Table S1) and plots of the secondary structure assignment of the sequence (Fig. S1) and the interatomic C_α distance matrix (Fig. S2).

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request.