Three machine learning algorithms and their utility in exploring risk factors associated with primary cesarean section in low-risk women: A Methods Paper

Abstract

Machine learning, a branch of artificial intelligence, is increasingly used in health research, including nursing and maternal outcomes research. Machine learning algorithms are complex and involve statistics and terminology that are not common in health research. The purpose of this methods paper is to describe three machine learning algorithms in detail and provide an example of their use in maternal outcomes research. The three algorithms, classification and regression trees, least absolute shrinkage and selection operator, and random forest, may be used to understand risk groups, select variables for a model, and rank variables’ contribution to an outcome, respectively. While machine learning has plenty to contribute to health research, it also has some drawbacks, and these are discussed as well. In order to provide an example of the different algorithms’ function, they were used on a completed cross-sectional study examining the association of oxytocin total dose exposure with primary cesarean section. The results of the algorithms are compared to what was done or found using more traditional methods.

Introduction

Childbirth is the leading reason for hospitalization in the United States (Martin et al., 2019). Birth outcomes for mother and baby are worse in the United States than in any other high-income country (Creanga et al., 2014). A great deal of effort focuses on identifying the reasons for this discrepancy and interventions to improve outcomes. Outcomes, however, are predicted by numerous variables, some known and some unknown, that interact with each other in complex ways that are not entirely understood. Standard statistical methods, such as logistic or linear regression, do not handle complexity well.

Artificial Intelligence is a branch of computer science that focuses on computers “thinking” like humans, i.e., being able to learn rules or problem solve. Machine learning (ML), a phrase coined by Arthur Samuel in 1959, is a branch of Artificial Intelligence wherein computers use algorithms to identify patterns in data. The computer (machine) is learning because it is not specifically programmed for a task. Instead, the computer uses an algorithm to complete the task it is given. ML algorithms are classified as supervised or unsupervised learning. Supervised learning involves specifying a target (e.g., an outcome of interest) and then allowing the algorithm to identify patterns leading to that outcome. In unsupervised learning, the algorithm looks for patterns in the data and groups information according to the patterns it identifies. If you had a single outcome and were trying to predict it from a set of variables, you would choose a supervised ML algorithm.

There are numerous ML algorithms that each do different things. Therefore, it is important to choose an ML algorithm that fits your research question. Some examples of ML algorithms include classification and regression trees (CART), least absolute shrinkage and selection operator (lasso), and random forest. The CART algorithm may be supervised or unsupervised, depending on the question, while lasso and random forest are both examples of supervised learning algorithms.

ML is increasingly used in health research to do everything from make predictions for precision medicine to choose variables for models. A quick search of PubMed shows that ML is being used in an array of disciplines – from emergency medicine, to cardiology, to nursing (Park et al., 2019). The use of ML in obstetric research is novel, with most papers published after 2017. Most papers use preexisting ML algorithms, such as CART, lasso, or random forest to answer questions about risk associations, prediction of outcomes, and clinical decision support via large datasets, such as electronic health records or other large, preexisting datasets. The papers using ML in obstetric research range from predicting gestational diabetes to identifying risk factors for severe neonatal morbidity in preterm birth and creating a decision-support aid for treating ectopic pregnancies (De Ramón Fernández et al., 2019; Hamilton et al., 2018; Qiu et al., 2017). While the use of ML in obstetric and nursing research is new, the field itself has existed for over half a century and is increasing in popularity and usage both in research and in clinical practice. The utility of ML for complex maternal outcomes research is only just beginning to receive attention, and no methods papers on the use of ML in obstetric research have been identified.

Cesarean section in low-risk women is an example of a complex phenomenon in maternal health that is both a focus of major quality improvement initiatives and a significant source of maternal morbidity. Caesarean section is complex due to patient-, provider- and system-level risk factors that interact with each other in ways that are not always well understood. We previously conducted a cross-sectional study examining the association of synthetic oxytocin dose with cesarean section in low risk women (ref). The purpose of this paper is to provide a detailed account of a secondary data analysis using three popular ML algorithms, CART, lasso, and random forest, to study cesarean section in low risk women and compare these algorithms to more traditional methods. Our goals were to: (a) try to understand the complexity of how variables interact with each other to increase or decrease the probability of the outcome of cesarean section via CART, (b) explore variable selection for regression models using lasso, and (c) rank the importance of the variables with regards to cesarean section using random forest. We were interested in exploring how these methods might further or challenge our findings from the cross-sectional study, which relied on more traditional methods of variable selection for models and standard statistical methods, such as logistic regression, for the analyses. Prior to delving into this account, however, we will provide a basic overview of all three algorithms.

Three Machine Learning Algorithms

CART

The CART algorithm may be used to predict the probability of a particular outcome, as well as to understand how different variables interact to increase or decrease the probability of an outcome. For that reason, CART is frequently used for building prediction models and understanding a patient’s risk for a given outcome. The CART algorithm creates a decision tree. The decision tree is called a classification tree if the outcome is binary and a regression tree if the outcome is continuous. The independent variables may be categorical or continuous. Regression models require simple, pre-specified interaction terms, whereas CART discerns associations between categories (categorical variable) or subregions (continuous variable) of different independent variables and the outcome without pre-specification.

In order to understand how the CART algorithm operates, suppose that having a cesarean section is the outcome of interest. The decision tree begins with the root, which includes the entire study sample. The algorithm then chooses a variable, out of all the variables that have been provided, that has the most similar probability of cesarean within a category of the variable and the most different probability of cesarean between the categories. The algorithm creates those two categories, also called “child nodes.” If the variable is continuous, CART will choose a cut-point where the homogeneity within the categories and the heterogeneity between categories, with regards to the outcome, is the greatest. If the variable is categorical, CART will group the original categories into two based on the above criteria. After a split, the variable is put back with the rest and the algorithm chooses again, based on the above criteria. The algorithm will continue to run until either there are no further splits possible or there are no more than 5 observations in a node.

For example, if CART determines that the variable BMI (in this instance, a categorical variable with three categories – normal, overweight, and obese) is the variable with the greatest homogeneity within and heterogeneity between two categories with regards to the outcome, BMI will be the first branch in the tree. The algorithm creates two categories, one category is women with overweight and obese BMIs, the other is women with normal BMIs. BMI is then put back in with the other variables and the algorithm repeats the process for each child node. Hence, the algorithm will next choose the variable that has the greatest homogeneity within and heterogeneity between its categories with regards to the outcome for women with an overweight or obese BMI and also for women with a normal BMI.

Since primary cesarean section is a complex, multi-factorial phenomenon, CART helps us understand how multiple variables can interact simultaneously to increase the risk of cesarean section for certain sub-groups of the population. For instance, CART might help us understand how race, age, BMI, and where a woman gives birth interact to increase or decrease her probability of having a cesarean section. For women with an obese or overweight BMI, the next most important variable might be oxytocin exposure. Meanwhile, for women with a normal BMI, the next most important variable, according to the algorithm, might be maternal age. From this, we might conclude that oxytocin exposure is more of a risk factor for cesarean section for women who are obese or overweight, than for women with a normal BMI. CART provides the area under the receiver operating characteristic curve (AUC) statistic and tests the model in an independent sample to demonstrate how well the model performs, as opposed to providing tests of significance (e.g., p-values).

Lasso

The lasso algorithm can be used for initial variable selection or as a way to review variables already selected by a different method. The lasso algorithm selects variables, determining prediction accuracy and the number of predictors as it does so. Variable selection in model development is a critical issue in research. Variables may be selected based on prior research, clinical expertise, or theoretical considerations. In traditional regression-based variable selection, researchers use statistical significance to decide which variables to keep or discard. These types of selection methods are sensitive to the presence of confounders and multicollinearity, yielding less accurate models. Due to the nature of the algorithm, as discussed below, the lasso algorithm is able to overcome some of the pitfalls of regression-based variable selection.

The lasso algorithm is a type of regression that uses shrinkage and can be used whether the outcome is continuous or binary. In traditional regression, coefficients are estimated to minimize the residual sum of squares (RSS) if the outcome is continuous and the deviance if outcome is binary. Lasso regression is similar to traditional regression, except that the coefficients are estimated by minimizing a slightly different quantity that not only considers the RSS or deviance, but also takes the total magnitude of the coefficient estimates into account. A parameter, often called a “tuning parameter,” is used to adjust the magnitudes of these coefficient estimates. We use “lasso parameter” in this paper to refer to the more technical “tuning parameter”.

When the lasso parameter is zero, the lasso regression is simply a fully adjusted traditional regression model (e.g. logistic/linear regression). As the lasso parameter increases, the magnitude of the coefficient estimates are forced to shrink (decrease), leading to some coefficient estimates shrinking to zero. As a result, variables with zero coefficient estimates are deselected. The larger the lasso parameter, the greater the number of independent variables deselected. When the lasso parameter is large enough, the regression is a null model without any independent variables. A computer program is able to select the “best” lasso parameter to achieve the lowest combination of RSS or deviance and magnitudes of coefficient estimates across all possible lasso parameters. The program returns the corresponding coefficient estimates for all variables, enabling researchers to pick the variables that have non-zero coefficient estimates for further analysis. In particular, the R package ‘glmnet,’ by default, uses a more sophisticated method called “10-folds cross validation” to choose the best lasso parameter. The lasso parameter can also be adjusted manually as needed, and the computer program is able to produce the set of coefficient estimates for any lasso parameter chosen by the user. Due to shrinkage, lasso estimates are biased and not appropriate for interpretation. Thus, although lasso could be used for prediction, we do not discuss this application here. Instead, we used lasso to identify important predictors, after which we used other statistical models, such as logistic regression, to obtain the unbiased parameter estimates. Lasso does not rank the importance of the variables with regards to the outcome of interest. In order to rank the importance of variables in relation to the outcome, a different algorithm is needed, such as a random forest.

Random Forest

The random forest algorithm is mainly used for prediction. It is able to rank variables in order of importance relative to a specified outcome of interest. As a result, random forest may be used for choosing which variables in a set may be most pertinent for inclusion in a model, or for trying to discern which factor should be the focus for intervention. In contrast, a researcher using traditional statistical methods might argue that a variable is most predictive of the outcome by using standardized regression coefficients or looking at how the R-squared statistic changes when a variable is added to the model.

The random forest algorithm builds and averages a collection of decision trees and produces a more accurate and stable prediction than traditional methods. Each tree uses a bootstrap sample (random sampling with replacement, which results in a subset of subjects with some subjects selected repeatedly) with the same number of subjects as the data, and a subset of independent variables for each split. Subjects not selected in the process of building the tree then obtain a prediction from the tree. As there are many trees, the outcome for each subject is then predicted many times by many trees. The final prediction is determined by averaging all predictions, and prediction accuracy can be obtained based on predictions of all subjects. The importance of each variable can also be obtained by comparing the prediction accuracy before and after removing the effect of the variable.

The researcher needs to specify the outcome variable and all independent variables and may need to adjust parameters manually since parameter values are defined by default. The number of trees is a parameter that could be adjusted manually. As each split uses only a subset of variables, trees are decorrelated. Thus, increasing the number of trees does not lead to overfitting, but rather improves prediction accuracy until the prediction accuracy is stable and no longer increases as the number of trees increases. By building and averaging a number of trees, however, the random forest algorithm improves prediction accuracy at the expense of interpretability. In this paper, we will not discuss how to use the random forest algorithm to predict the probability of cesarean section. Instead, we use random forest importance ranking for variable selection.

Methods

Parent Study

The parent study for this secondary analysis was a cross-sectional study on the association of total oxytocin exposure in labor with primary cesarean section among low-risk women using the Consortium on Safe Labor (CSL) data set (ref). The CSL is a publicly-available database initially developed to examine patterns in labor progression and the etiology of cesarean sections in the United States (Zhang et al., 2010). The data are housed at the Eunice Kennedy Shriver National Institute of Child Health and Human Development’s Data and Specimen Hub. Data for the CSL were collected from 12 sites (19 hospitals), representing the American Congress of Obstetricians and Gynecologists’ nine districts. Site investigators extracted data from the electronic medical records. Hospital and provider characteristics were collected from surveys of local investigators (Zhang et al., 2010). Data were transferred from the sites to the Data Coordinating Center where data were checked, cleaned, and recoded (Zhang et al., 2010). The database included 228,668 births between 2002–2008 with 9.5% of women contributing more than one birth. Patient information was de-identified before being sent to the Data Coordinating Center.

In the parent study, only first entries into the data set were kept. The inclusion criteria were: (a) gestational age greater than or equal to 37 weeks and less than 42 weeks, (b) parity of 0, (c) singleton fetus, (d) vertex presentation, and (e) oxytocin exposure during labor. Sample exclusion criteria for women included: (a) no exposure to oxytocin intrapartum, (b) incomplete oxytocin dose information (i.e., missing oxytocin dose or duration), and (c) admission for a pre-labor cesarean birth. In addition to total oxytocin dose, the adjusted model controlled for a number of variables based on the literature and clinical experience, including maternal race/ethnicity, maternal age, gestational age, BMI, diabetes (both chronic and gestational), hypertensive disorders (chronic and gestational hypertension, as well as preeclampsia and eclampsia), and hospital type (university teaching, community teaching, or community non-teaching). Women were clustered by provider to control for differences in provider practice.

We used ML algorithms in this paper to explore: (a) how the interaction of different risk factors increased or decreased the probability of cesarean section (CART), (b) which variables would be selected by lasso, and (c) the ranking of different lasso-selected variables relative to how much they contributed to predicting the outcome of interest (random forest). Table 1 compares similarities and differences between these ML methods and more traditional approaches.

Table 1:

Comparison of Machine Learning and Common Statistical Methods^*

Methodological Issue	Logistic Regression*	Classification tree	Lasso	Random Forest	Bivariate analysis	Backward/Forward/Stepwise regression
Purpose of the method	- Prediction - Estimate effect on outcome	- Prediction - Variable selection	- Prediction - Variable selection	- Prediction - Variable selection	- Determine the empirical association between two variables - Variable selection	- Variable selection
Is multicollinearity an issue?	Yes	No	No	No	No	Yes
Is confounding an issue for the purposes of the model? (except for confounded by unmeasured variables)	No, if confounders are identified and adjusted for.	- Confounding increases the difficulty of classification and may decrease true positive rates and accuracies of decision trees. - Trees are able to handle confounding variables.	No	No	Yes	Yes
Sample Size	- Adequate sample size is directly related to the complexity of the problem/model - Sufficient sample size, as determined by an a priori power analysis, is required if doing significance testing.	- No minimum sample size as determined by an a priori power analysis needed. - Larger dataset yields more reliable results.	Same as CART	Same as CART	Same as logistic regression	Sufficient sample size required as significance tests are used.
Missing Values	- Missing value results in listwise deletion of observation. - Other methods of handling missing data, such as multiple imputation, exist, but require specific assumptions about the nature of missing data and need to be handled separately.	- Algorithm deals with missing values by using another independent variable that is collinear to the variable missing data to provide data for the observation. - No specific assumptions about the nature of missing data required.	Missing values need to be handled separately.	Missing values need to be handled separately.	Missing values need to be handled separately.	Missing values need to be handled separately.
Outliers	Estimates are sensitive to outliers.	- Somewhat robust to outliers in prediction. - Outliers are detected by algorithm and isolated in separate child nodes.	Estimates are sensitive to outliers.	Somewhat robust to outliers in prediction.	Estimates are sensitive to outliers.	Estimates are sensitive to outliers.
Interactions	- Difficult to examine complex interactions between categories of multiple variables. - Interactions must be specified a priori.	- Algorithm shows relationships between different categories of different independent variables in the tree it creates.	- Not typically used with interactions.	- Like a “black box”, unable to interpret interaction.	No interaction is checked.	No interaction is checked.
Linearity	Independent variables assumed to be linearly associated with the log odds of the outcome variable	No assumption about linearity between independent and outcome variable(s)	Same as regression	No assumption on linearity	Same as regression	Same as regression
Results	- Association**: Odds ratios and 95% CI - Prediction: Odds ratios can be converted to probability by taking additional steps.	- Prediction: Probability of outcome for different subsets of the sample, subsets created by order of importance (e.g., probability of cesarean given birthing in a university hospital).	- Prediction: Gives probability of outcome as a prediction method. - Variable selection: Select variables that have non-zero estimates as a variable selection method.	- Prediction: Gives probability of outcome as a prediction method. - Variable selection: Rank the variables by importance	- Prediction: Odds ratios and 95% CI - Variable selection: focuses on P value.	- Variable selection: Focuses on P values to decide whether a variable should be selected.
Interpretability of result	Convenient	Convenient	Estimates are biased, not appropriate for interpretation.	Convenient in interpreting predicted probability, hard to explain why	Convenient	Inappropriate to use. Parameter estimates tend to be overestimated, P values and standard errors are biased toward 0

^*These comparisons are based on research questions involving a binary outcome, but are also applicable to outcomes that are continuous, such as linear regression, and all the methods here either handle (or have analogs for) continuous outcomes (e.g., regression trees, lasso).

^**Effects of predictors on outcome.

CART: Classification and Regression Tree; Lasso: Least Absolute Shrinkage and Selection Operator

CART

We used the CART algorithm to create a decision tree that would help us better understand how independent variables in our model interacted to increase or decrease the probability of cesarean section. We asked the algorithm to create a stratified random sample, randomly dividing the overall sample into three sub-samples that all had the same proportion of the outcome of primary cesarean section (18%). We entered the independent variables (listed above) from the adjusted model used in the cross-sectional study. Then we specified that the sample be divided into three subsamples. The first sub-sample (50%) was used for building the tree (training). The second sub-sample (25%) was used for validation, in order to prune the tree and minimize overfitting. The third sub-sample (25%) was used to test the tree on an independent sample. The CART algorithm provided three AUC curves, one for each sub-sample, allowing assessment of model accuracy. The model was considered to have acceptable accuracy if the AUC was greater than 0.7. JMP 14 (JMP, Version 14, n.d.) software was used to run CART.

Lasso

We used the lasso algorithm to identify the independent variables to be included in the adjusted regression model. While all of the available 779 variables in the CSL dataset could have been entered into lasso, 38 of those variables were selected and recoded. The 38 variables were selected if they were present or occurred before birth, and were therefore potential risk factors for cesarean section, and were missing less than 20% of observations. These variables are listed in Supplementary Table 1. As many of these variables might be collinear (e.g., height, weight, and BMI), including all of them in a traditional regression model would be inappropriate. The R package glmnet was used to run the lasso algorithm. The following steps were taken when using the glmnet package:

1. We obtained the best lasso parameter and examined the number of selected variables.

2. If we determined the number of selected variables was too high, and we wanted to reduce the number of predictors at the expense of least decreased prediction accuracy, we sought assistance from other methods (e.g., we fit the selected variables in a logistic regression and checked the significance (alpha level=0.05).

3. We repeated step 2 until the number of predictors suited the research, per the researchers’ determination (e.g. we stopped repeating step 2 when all lasso selected variables were statistically significant in the logistic regression). We were able to visualize the proportion of prediction accuracy that was sacrificed due to the reduction in the number of predictors and to decide if this trade-off was acceptable to the research. In our case, the decreased prediction accuracy was negligible.

Random Forest

We used the random forest algorithm to rank the importance of the independent variables chosen by the lasso algorithm for predicting cesarean section. The variables chosen by lasso were entered into the random forest algorithm. We specified that 5000 trees should be created. The random forest algorithm can use a number of different statistics to rank the importance of each variable in relation to the specified outcome. We instructed the algorithm to rank the variables based on mean decrease in accuracy, a measure of variable importance whose statistics are beyond the scope of this paper (Lu & Petkova, 2014). In brief, mean decrease in accuracy means that the more model accuracy decreases by excluding a variable, the more important that variable is for a model. The random forest algorithm ranked the importance of each variable in relation to the outcome of cesarean section using an array. The R package ‘randomForest’ was used for this analysis.

Results

CART

The classification tree that CART produced suggested that oxytocin exposure was important in increasing the risk for cesarean section among low-risk women, but not as important as maternal obesity or hospital type. The tree began with the parent node, in which women had an 18.4% probability of primary cesarean section. The first split occurred at hospital type. Women who delivered at university hospitals had a 26.2% probability of cesarean while women at community hospitals had a 12.4% probability (Figure 1). For women who delivered at university teaching hospitals in the sample, the next generation split was maternal BMI with obese women having a 33.8% probability of cesarean compared to normal and overweight women who had a 19% probability. For women who were obese and delivered at a university hospital, a third split occurred with oxytocin exposure greater than or equal to 11,400 mU having a 47.7% probability of cesarean, compared to 30.3% for those exposed to less than 11,400 mU of oxytocin (total oxytocin dose was a binary variable in the model). For normal and overweight women delivering at university hospitals, oxytocin exposure above 11,400-mU increased the risk of primary cesarean section for women over 20 years, but not for those younger than that. The classification tree’s AUC in the test sample was 0.7, indicating that the model accuracy is acceptable.

Figure 1.

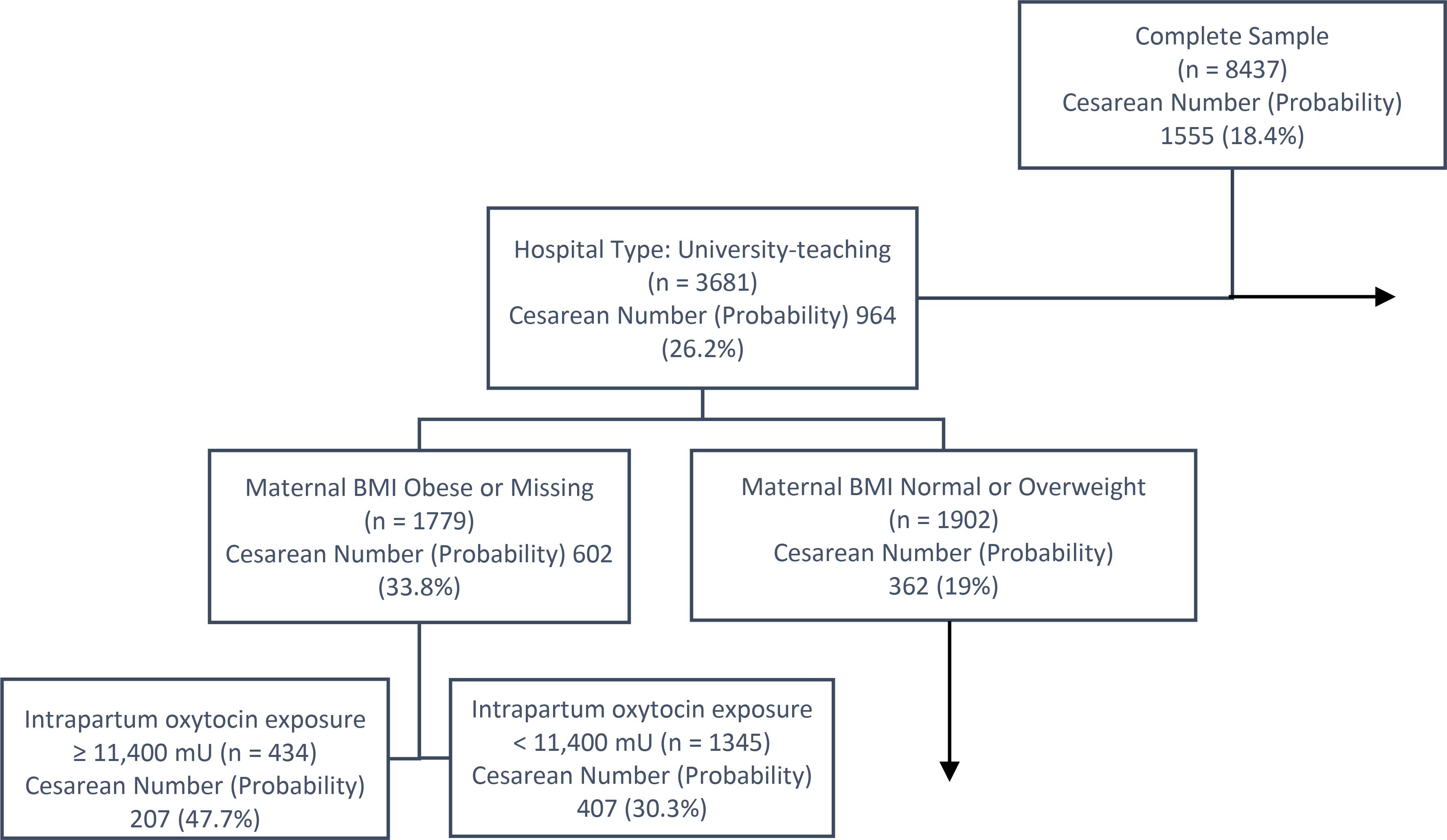
Portion of the Classification and Regression Tree classification tree (CART). The box at the top of the tree contains the complete sample. This is the root or parent node. Subsequent splits create subgroupings of the sample based on the probability of cesarean as an outcome. The first split is on hospital type, with university-teaching hospitals in one node and community teaching and non-teaching hospitals in the other. The horizontal arrow indicates a child node not included in this figure (i.e., community and non-teaching hospitals). Of the subgroup who gave birth in a university-teaching hospital, the next subgroup is based on maternal body mass index (BMI). The third subgroup was based on oxytocin exposure. The vertical arrow indicates that further child nodes were developed from this subgroup but were not included in the figure.

Lasso and Random Forest

Among the 38 variables initially entered into lasso, fifteen variables were returned and were also significantly associated with the outcome of cesarean section in the logistic model. The variables were total oxytocin dose, gestational age, maternal height, BMI on admission, spontaneous labor, diabetes, type of hospital, physician insurance, maternal race, maternal age, study site, eclampsia or preeclampsia, depression, physician gender, and smoking during pregnancy. Random forest ranked the importance of the 15 variables from lasso (Figure 2). The top five variables predicting cesarean section were total oxytocin dose, BMI, maternal age, maternal height, and eclampsia/pre-eclampsia.

Figure 2:

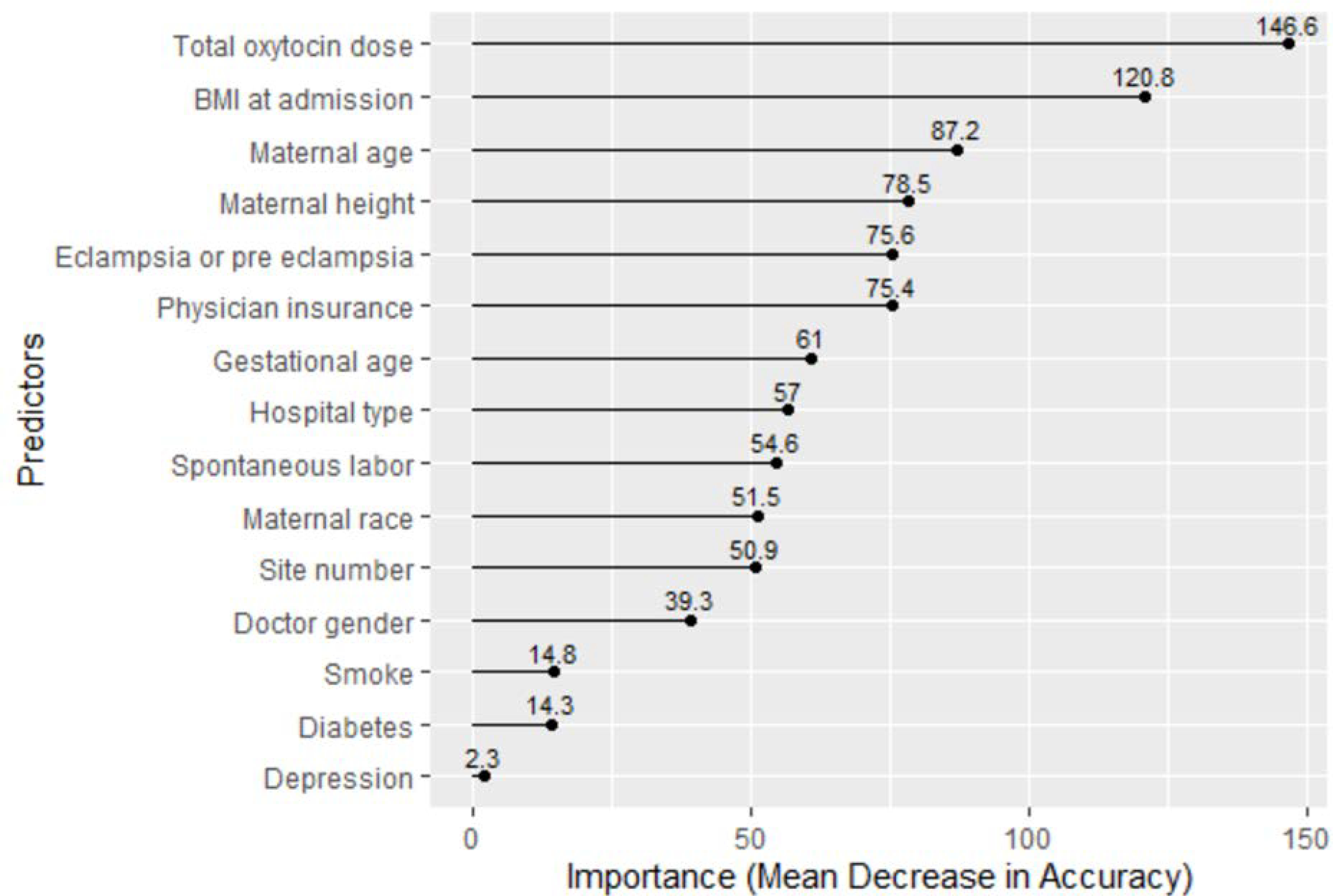
Random Forest’s Ranking of Risk Factors by Importance

Discussion

In this paper, we were interested in exploring how different ML algorithms could help us address our research question regarding the association of total dose oxytocin exposure with primary cesarean section in low-risk women. The different ML algorithms answered different kinds of questions. CART allowed us to understand how different independent variables interacted to increase or decrease the likelihood of cesarean section and also gave us a sense of which of the independent variables were the most important in predicting the outcome of cesarean section. Specifically, women with the greatest risk of cesarean section in this sample were those who delivered at a university hospital, were obese, and were exposed to more than 11,400-mU of oxytocin. Interestingly, the interaction of BMI and oxytocin was not statistically significant in the parent study regression model. The CART algorithm, however, was able to explore how the probability of having a cesarean section increased or decreased for women with normal, overweight, or obese BMIs giving birth in different locations who were then exposed to more or less oxytocin during labor (Figure 1), suggesting a more complex relationship between multiple variables. That the hospital where a woman delivers would be predictive of her likelihood of cesarean section is corroborated in the literature (Kozhimannil et al., 2013). Increased BMI is also strongly associated with an increased risk of cesarean delivery in the literature (Carlson et al., 2017; Kominiarek et al., 2015).

For CART, the risk adjustment variables were selected based on the literature and clinical expertise and were the same as those used in the adjusted regression models. We used the lasso algorithm to explore which of the 38 potential predictors available in the dataset would be selected for risk adjustment. We then used the random forest algorithm to rank which of the variables chosen by lasso were most predictive of cesarean section among low-risk women. Lasso selected 15 variables as more predictive of cesarean delivery. Many of these, such as gestational age, BMI, diabetes, type of hospital, maternal race and age, corresponded with the risk adjustment in the parent study (ref). Other variables found to be predictive, including maternal height, physician insurance, depression, physician gender and smoking in pregnancy, had not been included in the original risk adjustment. This finding stimulated discussion as to whether or not these variables would have been reasonable to include in the original risk adjustment. While the norm is to base variable selection for risk adjustment on the literature, validated algorithms, and clinical expertise, using lasso may offer suggestions for research teams to consider as variables. Physician insurance, for instance, was not a variable we had considered controlling for in the parent study but might be indicative of a physician practicing defensively and conducting more cesarean deliveries in order to avoid litigation. In the logistic regressions in the study, however, women were clustered by provider, thereby providing some control for this variable. Depression, also, was an interesting variable to consider as an adjusting covariate. One study did report increased odds of cesarean birth with antenatal depression (Khanghah et al., 2020), but this finding was contradicted by another, larger, study that found no significant association (Yoon Chang et al., 2014). There is no known association, however, between antepartum depression and an increased risk of intrapartum oxytocin exposure, thereby eliminating it from the pool of variables to be considered for risk adjustment. Still, lasso may have some utility as a means of quality assurance for model building, serving as a way to check the variables selected for risk adjustment. We would not, however, recommend allowing lasso to be the sole deciding factor in what variables are selected for risk adjustment.

The random forest algorithm ranked the importance of the variables selected by the lasso algorithm with regards to the outcome of cesarean section in the sample. Oxytocin exposure, BMI, maternal age and eclampsia/pre-eclampsia are all known risk factors for cesarean section. The random forest algorithm selected both maternal height and BMI as important variables predicting the outcome of cesarean section, but the algorithm does not specify directionality (e.g., whether taller or shorter maternal height is more predictive of cesarean). Recent research has found an association with short maternal height and an increased risk of cesarean, even when stratifying for BMI (Marshall et al., 2019; Mogren et al., 2018).

ML methods are just beginning to be used in obstetric research. Indeed, most of the papers we found were published after 2017. ML was used to predict obstetric conditions, such as gestational diabetes or pre-eclampsia, and obstetric outcomes, such length of stay and spontaneous preterm birth (Gao et al., 2017; Jhee et al., 2019; Qiu et al., 2017; A. Weber et al., 2018). One study used CART to identify risk factors for intrapartum cesarean section among nulliparous women (Kominiarek et al., 2015). Another study examined the utility of four different ML algorithms (multilayer perceptron, deep learning, support vector machine, and Naives Bayes) in building a decision support algorithm to help providers choose the best first treatment for an ectopic pregnancy (De Ramón Fernández et al., 2019). The researchers reported that the support vector machine and multilayer perceptron algorithms were the most helpful in supporting clinician decision making around ectopic pregnancy (De Ramón Fernández et al., 2019). Finally, one team of researchers used ML algorithms that they had developed to (a) identify other possible risk factors for severe maternal morbidity and (b) understand the pathway of how severe maternal morbidity develops (Gao et al., 2019b, 2019a). With the exception of this team, all of the other papers used previously created algorithms, such as random forest, lasso, CART, support vector machine, neural networks, or gradient boosting methods. The limitation most frequently mentioned in the papers was the quality of the data (A. Weber et al., 2018). Only one study reported finding no additional associations with the outcome of interest beyond what was already known (K. A. Weber et al., 2019).

In comparison to traditional regression models, the CART and random forest algorithms offer a number of potential advantages. Unlike regression models, which make assumptions about the distribution of the data, CART and random forest make no such assumptions and are able to manage non-linear distributions. While multicollinearity can cause output errors and may lead to the exclusion of independent variables from the model, this is not an issue with CART and random forest. In comparison to regression models, where outliers may have a significant impact on output, CART and random forest are able to partition outliers into separate nodes as needed. Missing data is a significant problem in research. In regression models, observations with missing values for variables in the model are dropped without the use of intentional work-arounds. CART automatically circumnavigates the issue of missing data with surrogate variables, that is, correlated variables that are not missing values for the particular case (Henrard et al., 2015).

We found that the decision tree output from the CART algorithm was relatively easy to interpret. Each node of the decision tree included the probability of the outcome for the women in that node (e.g., women in our sample who gave birth in a university hospital and were obese had a 34.5% probability of a cesarean section). CART also created AUC curves with the decision tree, thereby allowing us to evaluate whether or not the model was accurate. Model fit is roughly gauged in the output by the log likelihood chi-square and pseudo R-squared statistic, though there additional tests can be completed for model fit.

Our use of lasso and random forest was more straightforward in that we only used these algorithms to select and rank independent variables in relation to how important they were to the outcome of interest. We found that the lasso and random forest algorithms offered statistical confirmation of our choice of most of the variables in the parent model and provided some thought-provoking conversation about why other variables had not been included. Compared to more traditional model building, using the lasso algorithm was easier in the sense that we simply put variables into the algorithm and let it choose those with non-zero coefficient estimates. Variables for model building are typically selected via theory, research, and clinical expertise, and researchers provide rationale for their selections, which are easy to interpret. By contrast, the lasso and random forest algorithms use statistics that are far less common. Understanding which variables the lasso algorithm chose and the ranking of variables by the random forest algorithm may be easy, however, the statistical methods behind the choice or ranking is not.

While CART has much to recommend it, including not having a minimal required sample size for power calculation, regression models are still needed. CART is only as good as the variables provided to it; asking CART to choose important variables can lead to humorous results (K. A. Weber et al., 2019). While CART might optimize each split, the overall model may not be stable. For instance, a small change in the categories of a categorical variable may result in an entirely different tree. Figure 3 shows the decision tree CART created when given a BMI variable with four categories. In a similar manner, CART’s splitting of continuous variables may result in categories that are not clinically meaningful. With regards to the lasso and random forest algorithms, again, we would not discard – or even demote - the more standard way of choosing variables for regression models. Both algorithms share the limitation of providing statistical output that is not easy to interpret. Also, like CART, lasso and random forest are only as good as the input they are given. There are other important variables associated with the risk of primary cesarean section in low-risk women (e.g., hospital and provider characteristics), but since these variables were not available in our data set, the lasso algorithm was not able to select them from the pool of variables and the random forest algorithm was not able to rank them. In addition, as was discussed earlier, there is the possibility of a variable being selected by the algorithm that likely has no real-world bearing on the outcome of interest.

Figure 3.

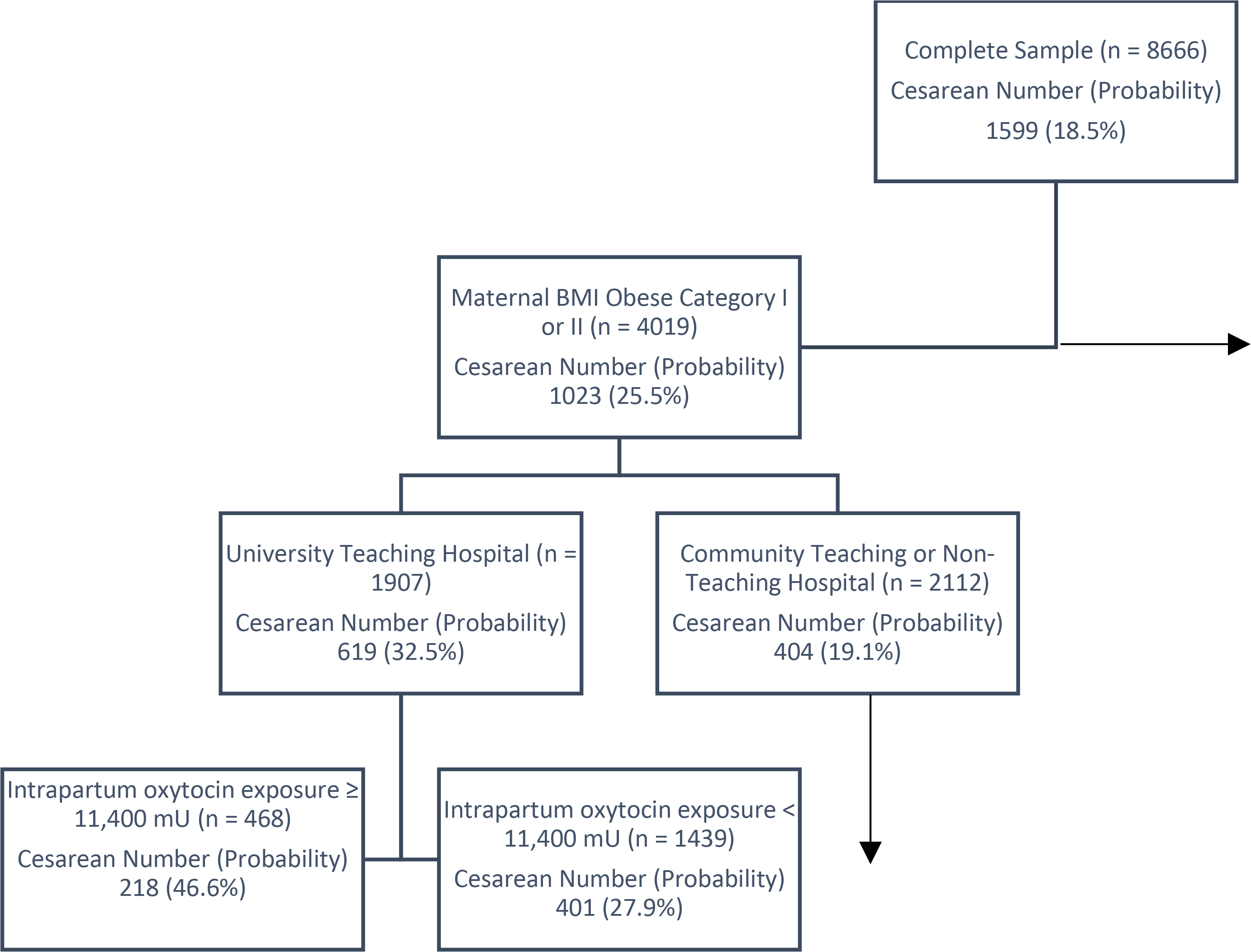
Portion of the Classification Tree with a Minor Change in the Categories of the BMI Variable. The box at the top of the tree contains the complete sample. This is the root or parent node. Subsequent splits create sub-groupings of the sample based on the probability of cesarean as an outcomes, as with Figure 1. The horizontal arrow indicates a child nodes not included in this figure (in this case, maternal body mass index (BMI) of overweight or normal weight). The vertical arrow indicates that further child nodes were developed from this sample sub-group but were not included in the figure. In each box, the “n” presents the total number of women in that group. Under “Cesarean Number (Probability)”, the number is the number of women in that group who had a cesarean and the probability of having a cesarean.

Compared to using traditional regression methods to select variables for a model, lasso focuses on both prediction accuracy and the number of predictors when returning the final set of selected predictors. Traditional regression methods, such as bivariate/backward/forward/stepwise regression methods, meanwhile, rely mostly on statistical significance, which is unable to guarantee the final prediction accuracy. In the bivariate method, a variable is selected when the p-value is smaller than a slightly broader alpha level set by the researcher, for example, 0.2. Without adjusting for potential confounders, however, this association may show a non-significant p-value when the true association is significant. As a result, the variable will, inappropriately, not be selected because of confounded bivariate association. Even after a variable is selected by the bivariate method, there are still additional steps to further reduce the model. In contrast, lasso selects variables as a whole and each variable is adjusted for all other variables available in the model, thus reducing confounding.

For backward/forward/stepwise regression methods, variables are selected by looking at p-values of the remaining variables in the model across all steps. Each step is closely related to the previous step, with a minor change of variables. Thus, a slightly different choice of one variable when p-values are similar in one step may result in big differences in the subsequent choices, especially when multicollinearity exists. Each p-value is also affected by sample size and random errors. A slightly different sample may result in major differences in variable selection. The lasso algorithm, by contrast, selects variables for one lasso parameter at a time, independent of other lasso parameters. Even though we fit lasso-selected variables in a logistic regression in our example, lasso and traditional regression share the same model structure (variables are linearly combined) implying that the relative effect of variables should be consistent for the two models.

The random forest algorithm is mainly used for prediction, and usually results in better prediction accuracy than (generalized) linear regressions because it averages a number of decision trees that could capture the non-linear relationship between the variables and outcome. Due to the limitations in interpretability, and as we were more interested in looking at individual risk factors, we only used random forest’s importance ranking function to visualize the importance of potential risk factors relative to the outcome. The random forest algorithm builds de-correlated trees through a de-correlating process by using only a subset of variables for each split. Thus, the importance of one variable may not always be concealed by a correlated variable as in CART. Consequently, a variable may have a higher importance ranking than others, even though this variable is not selected by a single decision tree. The de-correlating process, however, may not be able to completely decorrelate all trees, as there are still multiple variable candidates for each split. The fewer variable candidates there are for each split, the smaller the correlation between trees, and the importance of each variable would be less affected by other variables (but not totally unaffected). Thus, the importance ranking may be slightly different by using some different variables and specifying different number of variable candidates for each split (this is another parameter that could be adjusted in running a random forest model). Though the ranking is slightly sensitive to variables input and the sample, the importance will not diminish or drop/increase substantially as the calculation averages many trees, and thus is more stable in variable selection than CART. Unlike lasso, which clearly tells us which variable to choose and which to drop, random forest does not provide a cut point for importance. Instead, the variable selection is somewhat subjective and depends on the researcher. One may use the importance ranking generated by random forest to select variables. Researchers should be aware, however, that highly correlated variables may have similar rankings, though similar rankings do not imply correlation. This presents a problem if a researcher wants to use highly ranked variables in a regression, however, this may not be a problem in decision-making.

There are ethical issues involved with the use of ML algorithms (Chen & Decary, 2019). Our use of ML algorithms to identify patient risk groups, categorize patient risk, or guide our clinical decision-making may well out-strip our understanding of how the risk groups are being created or what biases are inherent in the algorithm due to the information it has been given. For instance, a study by Qiu, Li, Dong, Xin and Tan (2019) used ML to develop a model to predict the chance of live birth prior to the first in-vitro fertilization treatment. While the authors suggest that this model might be used to help counsel patients and help them manage their expectations, such models might also be used, in time, to limit patient choice or restrict access to certain therapies or resources. For the lasso algorithm, one ethical concern is that the answers lasso puts out are only as good as the data it receives. If the data entered into lasso are biased in some way, lasso’s results will also be biased. Two slightly different examples of this can be seen from our own work. First, there are risk factors for cesarean section in low-risk women, especially risk factors related to the hospital where a woman gives birth that were not available in the CSL data set. Second, of the available variables, we selected certain variables to enter into the lasso algorithm based on clinical understanding and research. As a result, there are risk factors for cesarean section in low-risk women that our rendering of lasso would not be able to identify. It is important, in using ML algorithms, to consider the quality of the data being used, and to consider what is being left out, and to address these factors in any conclusions drawn from the research. For the practicing clinician, an understanding of ML’s strengths and limitations may provide a more nuanced understanding of when and how to use algorithms based on ML, whether these are to predict a person’s risk of an outcome or to help guide clinical decision-making.

Some limitations of ML methods are more practical. These methods are more recent and, with not all researchers being familiar or comfortable with ML, it can be difficult to use these methods if a team has varying levels of comfort and facility with ML. The standard statistical software used by researchers may not support ML. Finally, for certain research questions, ML is more exploratory than theory-based, and this should be reflected in the way researchers use ML methods (Knafl et al., 2017). In the context of this paper, for instance, our uses of ML were exploratory, focusing on model building and prediction. For a research purpose to develop a decision-making support algorithm for a clinical condition, or to develop a predictive model to help patients understand their probability of developing a condition, ML may present an excellent means for answering that question.

The ML methods presented in this paper offer many opportunities for future research, beyond how they were used here. For instance, researchers might design a study examining the relationship between any of the variables selected by lasso, using the best lasso parameter, and the outcome, if this relationship is not fully understood. In another scenario, researchers studying the impact of an intervention on the outcome might use lasso-selected variables as possible confounders, if the intervention was delivered after the measurement of these variables. For the random forest algorithm, one could choose to rank all variables, not simply lasso-selected variables, and visualize the entire ranking and contribution of each variable in predicting the outcome of interest. In this example we only used the lasso-selected variables to discern which factors might be the focus of intervention. As always, the research question should determine the best method to use to answer that question. Finally, it should be noted that the way we used the three ML algorithms was based on the parent study and our interest in exploring ML methods. As a result we did not fully exploit the power and abilities of these methods.

Conclusion

ML may further research if used for appropriate research questions. There are numerous ML algorithms available to address a variety of research needs – from variable selection to risk prediction. ML methods are novel and innovative and may offer benefits over more traditional statistical methods that require parametric data or are sensitive to small numbers. Ultimately, however, ML is not a substitute for a research team’s expertise and needs to be applied and interpreted appropriately.