Abstract
Limited research work is available in the literature for the theoretical estimates of axial compressive strength of columns reinforced with fiber reinforced polymer (FRP) rebars. In the present work, an experimental database of 278 FRP-reinforced concrete (RC) compression members was established from the literature to recommend an empirical model that can accurately predict the axial strength (AS) of GFRP-RC specimens. An initial assessment of 13 different previously anticipated empirical models was executed to achieve a general form of the AS model. Finally, a new empirical equation for forecasting the AS of GFRP-RC short columns was proposed using the curve fitting and regression analysis technique. The performance of the proposed empirical model over the previous experimental database represented its higher accuracy as related to that of other models. For the further justification of the anticipated model, a numerical model of GFRP-RC columns was simulated using ABAQUS and a wide parametric study of 600 GFRP-RC samples was executed to generate a numerical database and investigate the influence of various parameters using numerical and empirical models. The comparison between theoretical and numerical predictions with R2 = 0.77 indicted that the anticipated empirical model is accurate enough to apprehend the AS of FRP-RC specimens.
Keywords: glass fiber reinforced polymer, axial capacity, finite element analysis, concrete columns, parametric study, coefficient of determination
1. Introduction
The high maintenance costs and limited-service life of conventional steel reinforcement in aggressive and corrosive environments have spurred the interest of modern research in advanced composite materials such as fiber-reinforced polymers (FRPs). The higher tensile strength, lower density, lighter weight, lower maintenance costs, higher resistance to corrosion, lower conductance to temperatures, and high resistance to chemical environments are the main advantages of FRPs [1,2,3,4,5]. These days, the construction industry is focusing on the replacement of corrosive steel reinforcement with the FRP rebars and confinements due to their superiorities over steel rebars to minimize the effects of corrosion in aggressive and corrosive environments [6,7,8,9]. Most of the concrete bridges in the United States and Canada employed the FRP reinforcement as a partial or total replacement of steel rebars [10]. Although, the use of FRPs in the construction industry has been increased still no design guidelines have been added in North American codes for such reinforcement. Furthermore, the use of FRP rebars as longitudinal compressive reinforcements has been prevented in Canadian codes [11,12] due to the limited research and advancement in this area. This may also be associated with the uncertain performance of FRP rebars in compression and limited experimental data.
During the last few decades, for providing the flexural and shear reinforcements, the employment of FRP rebars in reinforced concrete members is increasing [13,14]. Some investigations have been carried out to examine the performance of FRP rebars as longitudinal and transverse reinforcements in compressive and flexural members which depicted a better response of FRP rebars in these members [15,16,17,18,19,20,21]. As the axial compressive performance of FRP rebars is lower than that of steel rebars, therefore, some investigations have been carried out to determine the strength reduction coefficients for FRP rebars to secure the most optimum results under compressive loads [22,23,24,25]. But there is still a need for refining these coefficients using an experimental database consisting of various sample points. The previously suggested models for the axial strength of columns reinforced with FRP rebars have deficiencies such as they were suggested based on small data points, the axial contribution of FRP rebars was not included in the axial compressive performance and bending performance and the compressive and tensile properties of FRP rebars were assumed to be the same. The axial strength (AS) is significantly improved by improving the lateral confinement of the concrete core but the steel reinforcement performs better than FRP reinforcement in compressive members after increasing the lateral confinement of the core [26,27,28]. The predictions are underestimated by neglecting the axial influence of FRP bars in columns while the predictions portray a close agreement with the experimental outcomes by considering the influences of AS and axial stiffness of FRP rebars [17,29,30,31].
Mohamed et al. [32] examined the behavior of fourteen (14) sand-coated FRP-reinforced columns confined with FRP ties/spirals under axial compressive load. Using smaller ratios of transverse reinforcement (0.7%), damage of the specimens happened due to buckling of longitudinal rebars. Similarly, using moderate ratios of transverse FRP confinement (1.5% and 2.7%), the damage of specimens happened due to the damage of spirals and the crushing of the core. Afifi et al. [33] anticipated an equation for GFRP-confined concrete based on the criterion of Willam-Warnke. This model was adjusted utilizing the regression analysis method on the experimental testing outcomes for envisaging the ultimate AS and corresponding axial strain of GFRP-RC columns. Twelve (12) circular GFRP-RC columns (with 205 mm diameter and 800 mm height) were studied by Hadi et al. [34] under various loading circumstances. The testing results depicted that the bending moment capacity and AS of GFRP-RC compression members were less than their identical steel-RC columns. Additionally, ignoring the influence of GFRP bars in the loading strength of columns origins an extensive discrepancy between the testing measurements and analytical predictions. Karim et al. [35] proposed a model for forecasting the axial load-deflection performance of GFRP-RC columns confined with GFRP spirals. Moreover, the effect of spiral-pitch and external GFRP sheets was also investigated. There was observed a two-peak axial loading performance of GFRP-RC columns confined with sheets; the first peak represented the axial capacity of concrete cross-section and the second represented the axial capacity of FRP-confined concrete core.
As concerned with the finite element analysis (FEA) of FRP-reinforced compressive members, a large of studies could be found in the literature that investigates the structural performance of such members using FEA under various conditions [5,19,20,30,36,37,38,39,40,41]. From these studies, it was detected that the projected FEA models captured the structural behavior of FRP-reinforced concrete compressive members precisely. The finite element models (FEM) represent all the shortages of the empirical models. In comparison with the experimental work, finite element simulation saves time and cost by generating computational models that can correctly capture the complex damage behavior of composites [42]. As FEA consumes huge time during the simulations that can be minimized by making some assumptions but these assumptions should be in such a way that they should not affect the accuracy of the models and give close estimations with the experimental outcomes at the same time. One should keep a balance between the analysis time, complexity of the models, size of the elements, and different types of elements in the models. Thus, FEA having a strong background knowledge is a very important and effective tool for the analysis of the structural engineering problems related to composites [43].
Scope and Significance
It was observed from the literature review that there is a lack of studies on predicting the axial compressive strength of FRP-reinforced columns confined with FRP composites. Due to insufficient research data in this area, various international guidelines do not endorse the usage of such reinforcement in concrete columns. Therefore, detailed research is required in this area to provide some design guidelines for the structural performance of FRP-reinforced members under compressive loads. The main aims of the present investigation are: (a) To suggest a novel theoretical model for apprehending the axial compressive strength of FRP-reinforced concrete compressive elements based on various testing outcomes collected from the previous works; (b) to suggest a novel FEA model for accurately apprehending the compressive performance of such members with a minimum time; and (c) a detailed parametric investigation of GFRP-reinforced elements to observe the influence of various geometric and material variables of such members. To propose a novel theoretical model, an evaluation of the previous model over the constructed database has been performed to select the most suitable form. To perform FEM, a modified concrete damage plastic (CDP) model [30] is used for the simulations of the complex performance of concrete and the FRP bars are considered as a linear elastic material. The FEM has been proposed for the validation and comparison purposes of the newly anticipated theoretical model. The experimental results for the calibration and validation of FEA models have been taken from the literature [29]. Besides, widespread parametric training was accomplished using the anticipated FEM and empirical model to generate the results for the validation and comparison of the proposed models. A close agreement was observed between the predictions of the proposed empirical equation and FEM. The currently proposed empirical model has superiority over the previously suggested models for predicting the axial strength of GFRP-reinforced columns because it has been proposed over the large experimental dataset giving more accuracy and considering a large number of parameters of specimens. Furthermore, it is simpler and easier for practical applications. This research work is helpful for the analysis of GFRP-reinforced columns for the concrete construction industry.
2. Materials and Methods
Database for Empirical Modeling
Many experimental research investigations have been done in the literature to study the axial performance of GFRP-RC columns. In the present research, a database of 278 FRP-RC columns was created from different research papers. The longitudinal FRP rebars and steel ties, steel spirals, FRP ties, or FRP spirals were employed as the longitudinal and transverse reinforcements in all the specimens in the constructed database. In the database, ten (10) columns were transversely unconfined, seven (7) columns were transversely reinforced with CFRP spirals, one hundred and ten (110) columns were transversely reinforced with GFRP spirals, hundred (100) columns were transversely reinforced with GFRP ties, eighteen (18) columns were transversely reinforced with steel spirals, and thirty-three (33) columns were transversely reinforced with steel ties. Various parameters have been included in the development of the database such as transverse reinforcement ratio (), the elastic modulus of FRP bars (), concrete compressive strength (), longitudinal FRP reinforcement ratio (), the ultimate tensile strain of FRP bars (), the tensile strength of FRP bars (), breadth (), width (), and axial loading capacity () of specimens. Table 1 reports all the statistics of the parameters of the created database (provided in Appendix A).
Table 1.
Statistical details of different parameters of database.
| Parameter | B (mm) | H (mm) | (MPa) | D (mm) | Ag (mm2) | (%) | (%) | Af (mm2) | (%) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MIN | 150 | 150 | 20.0 | 150 | 17662 | 406 | 23.4 | 0.97 | 0.55 | 212.53 | 0.01 | 114 |
| MAX | 610 | 610 | 70.2 | 305 | 372100 | 1680 | 141 | 2.42 | 5.3 | 4051.60 | 5.3 | 15235 |
| Mean | 249 | 272 | 36.2 | 258 | 66289 | 1010 | 56.7 | 1.78 | 2.09 | 1214.58 | 1.38 | 1814 |
| *SD | 114 | 114 | 12.6 | 54 | 53039 | 339 | 25.1 | 0.39 | 1.06 | 764.62 | 1.06 | 1877 |
| **COV | 0.46 | 0.43 | 0.35 | 0.21 | 0.81 | 0.34 | 0.45 | 0.22 | 0.51 | 0.63 | 0.77 | 1.04 |
* Standard deviation, ** coefficient of variation.
3. Evaluation of Previous Models
Thirteen (13) existing models were assessed on the constructed database of GFRP-RC columns for selecting the most appropriate form of the newly proposed model. All the models that have been assessed for proposing the new general form of the model, are reported in Table 2. Three different statistical parameters (root mean squared error (RMSE), coefficient of determination (R2), and the mean absolute error (MAE)) were employed for the assessment of the models as reported by Equations (1)–(3). R2 is the most important parameter for examining the accuracy of a proposed theoretical model, therefore, the assessment of the models has been focused on using this parameter in the present research. The flow chart reported in Figure 1 presents the methodology of this investigation.
| (1) |
| (2) |
| (3) |
Table 2.
Axial strength (AS) models for assessment.
Figure 1.
Flow chart of the present work.
In these expressions, n reports the number of test points, reports the AS taken from experiments and reports the AS taken from the empirical models. Figure 2 depicts the evaluations of the previous models over the database. These evaluations portray that the best accuracy is given by the Afifi et al. [23] model with the maximum value of R2 i.e., R2 = 0.711. If R2 is close to one (1.0), it will report a good correlation of theoretical estimates with the experimental outcomes. A value close to zero will report a week performance of the theoretical model. Due to the highest performance of the Afifi et al. [23] model, the general shape of the developed model was kept similar to that in this model. This model considers the axial influence of FRP bars by assuming a reduction factor for the tensile strength of FRP rebars. Although including the fractal model concept during the modeling can give more accurate results [53] but the fractal model concept of FRP bars (curvy geometrical figure and initial geometric imperfection) in the present study has been neglected to make the proposed model simple for the practical applications and to avoid the complexity of the model. The general shape of the projected theoretical model is reported by Equation (4).
| (4) |
Figure 2.
Performance of previous models (a) ACI 318-08 (b) ACI 318-11 (c) CSA S806-02 (d) CSA S806-12 (e) AS 3600-18 (f) Afifi et al. [23] (g) Mohamed et al. [32] (h) Tobbi et al. [48] (i) Samani and Attard [46] (j) Hadhood et al. [52] (k) Khan et al. [47] (l) Mohamed et al. [32] (m) Pantelides et al. [49].
In this expression, and represent the reduction coefficients for the AS of FRP-reinforced compression members due to compressive influence of FRP rebars and confined core, is the area of FRP rebars, is the gross area of the column, is the tensile strength of FRP rebars. In the present investigation, the curve fitting method in MATLAB has been employed for securing the finest fit with the testing outcomes. The relationship for as recommended by Ref. [11] can be reported by Equation (5).
| (5) |
where β is another constant. Putting this value to Equation (6), the following relationship is obtained:
| (6) |
The obtained values from the curve fitting method in MATLAB for the constants and β were 0.0208 and 0.0029, correspondingly. Finally, the proposed model for the AS of FRP-reinforced members, after incorporating the values of the coefficients, has been reported by Equation (7).
| (7) |
where the reduction coefficient for AS of columns due to strength of concrete should be larger than 0.646 i.e., . Figure 3 depicts that the newly suggested model for the AS of columns reported higher accuracy than the previous models with R2 = 0.73.
Figure 3.
Performance of the suggested model.
Figure 4 reports the sample circulation of the previous testing and predicted AS of FRP-reinforced columns. In range 0–2000 kN, the experimental datapoints were counted to be 189 in the developed database. There were 194 datapoints of the predictions of the suggested model. In the range, 2001–6000 kN, the experimental and theoretical counts were 81 and 86, correspondingly. Similarly, in the range, 6001–10,000 kN, the experimental and theoretical counts were zero and 2, correspondingly. Similarly, in the range, 10,001–16,000 kN, the experimental and theoretical counts were 4 and 2, correspondingly. These comparisons show that the predicted values of the proposed model apprehended the AS of FRP-reinforced columns very well.
Figure 4.
Distribution of AS of fiber-reinforced polymers (FRP)-reinforced columns attained from various models.
Figure 5 reports the normal distribution of testing strengths to prophesied strengths of GFRP-reinforced compressive members from the created database for all models. The data of this figure has been obtained from the normalized predictions of various previous models over the developed database. The newly suggested model reported a deviation of only 5% for the average normalized strengths of the ratios of testing values to theoretical values. ACI-318-08 [44] reported a maximum deviation of 42%. Such errors may be ascribed to the cause that the model anticipated by ACI-318-08 [44] is for the steel rebars. This model has been used in this investigation for only a comparative purpose. Furthermore, the percent average eccentricities for the equations recommended by Afifi et al. [23], Khan et al. [47], CSA S806-12 [11] were 22%, 31%, and 5%, correspondingly.
Figure 5.
Normal distribution of testing to estimated strengths of GFRP-reinforced columns attained from various models.
4. Finite Element Modelling
This section presents the methodology of the FEA of GFRP-RC columns under various loading situations. A total of seven GFRP-RC specimens were defined using a finite element software ABAQUS whose experimental results were taken from the previous research of Elchalakani et al. [29]. The details of all specimen are provided in Table 3. A control model (G150-45) was selected for the calibration purpose of the GFRP-RC columns. During the calibration of the control specimen, various geometric and materials characteristics of the control specimen such as support conditions, the plastic performance of concrete, element sizes, and various element types were studied to gain the results that give the minimum error as compared with the experimental outcomes. The boundary conditions were applied to the control model such that the bottom end of the specimen was controlled in all directions and the top portion of the specimen could freely translate and rotate in all directions. The simulations of GFRP reinforcement and concrete material were done using three-dimensional 8-noded brick and three-dimensional 2-noded truss elements, correspondingly. The bond behavior between the reinforcement and concrete was simulated using the “embedded region” that joins the degrees of freedom (DOF) of the truss sections of FRP bars to the essential DOF of concrete three-dimensional stress elements. The load was applied to the top center of the specimen using the displacement control technique. The geometry and support conditions of the simulated specimens are presented in Figure 6.
Table 3.
Specimens for numerical simulations.
| Sample Label | Longitudinal Reinforcement | Transverse Reinforcement | Eccentricity (mm) | |
|---|---|---|---|---|
| GFRP Bars | Reinforcing Ratio (%) | |||
| G150-45 | 6-ɸ12.7 mm | 1.83 | 6.35 mm @ 150 mm c/c | 45 |
| G150-25 | 6-ɸ12.7 mm | 1.83 | 6.35 mm @ 150 mm c/c | 25 |
| G150-C | 6-ɸ12.7 mm | 1.83 | 6.35 mm @ 150 mm c/c | 0 |
| G75-35 | 6-ɸ12.7 mm | 1.83 | 6.35 mm @ 75 mm c/c | 35 |
| G75-25 | 6-ɸ12.7 mm | 1.83 | 6.35 mm @ 75 mm c/c | 25 |
| G75-C | 6-ɸ12.7 mm | 1.83 | 6.35 mm @ 75 mm c/c | 0 |
| G250-C | 6-ɸ12.7 mm | 1.83 | 6.35 mm @ 250 mm c/c | 0 |
Figure 6.
Finite element simulations of (a) geometry (b) interactions (c) support conditions (d) meshing of GFRP-RC specimens.
4.1. Simulation of Concrete Material
The behavior of concrete is complex due to the various constituents required for its manufacturing. The finite element simulation of this complex-natured material is a challenging task. In the present numerical work, the geometric performance of concrete was defined using three-dimensional brick elements with 8 nodes with reduced integration property (C3D8R). The average compressive strength of concrete material was 32 MPa at 28 days. The elastic behavior of concrete was defined using the equation given by ACI 318-11 [50] as presented by Equation (8).
| (8) |
The concrete damaged plastic (CDP) model available in ABAQUS was used for the definition of the plastic performance of concrete. This relationship considers the crushing of concrete under compressive loading and the cracking of concrete under tensile loading to accurately predict the plastic behavior of concrete [54,55]. The CDP model divides the plasticity behavior of concrete into three parts: plastic, compressive, and tensile behavior. The plastic performance of concrete material was calibrated for all the parameters of plasticity available in the CDP model of concrete i.e., stress ratio, dilation angle, shape factor, viscosity parameter, and eccentricity of concrete. For the definition of concrete performance under compressive loading, the stress–strain relationship provided by Eurocode 2 [56] was utilized as presented by Figure 7a. The linear elastic behavior of concrete was taken up to 40% of the ultimate strength of concrete [57]. The ultimate strain () and the strain at ultimate compressive strength of concrete () were calculated using Equation (9) and (10) as recommended by [58]. The compressive stresses () were calculated using the relationship given by Eurocode 2 [56] as presented by Equation (10).
| (9) |
| (10) |
| (11) |
where .
Figure 7.
(a) Stress–strain relationship for concrete structures. (b) Tension stiffening model for concrete.
The tensile behavior of concrete in the CDP model was defined using the modified tension stiffening model [59] as shown in Figure 7b. This model considers the behavior of concrete at post failure conditions of concrete such as tension stiffening, strain hardening, and softening and the interactions of FRP reinforcement with the concrete material. The tensile strength of concrete () was determined using the model proposed by Ref. [60].
| (12) |
4.2. Simulations of FRP Bars
The geometric definitions of reinforcing bars were accomplished using 3-D truss sections having two nodes with three DOF at each node (T3D2). The definition of elastic performance of FRP bars was carried out using two variables i.e., Poisson’s ratio and Young’s modulus that were taken as 0.25 [37] and 50 GPa, correspondingly [29]. FRP bars show sudden failure with rupture after yielding strength. Therefore, the plastic performance of GFRP bars was assumed as linear elastic up to failure without the application of any damaging criterion [38]. The tensile strengths of longitudinal and transverse GFRP bars were considered as 1200 MPa and 784 MPa, correspondingly [29]. Figure 8 represents the simulated behavior of GFRP longitudinal and transverse bars in ABAQUS.
Figure 8.
(a) Linear elastic performance of GFRP ties. (b) Linear elastic performance of GFRP longitudinal bars.
4.3. Calibration of FEM
One of the GFRP-RC columns (G150-45) was selected for calibration purposes. The numerical results of the load-deflection curve of the control model were compared with the experimental results from Ref. [29]. After calibrating the control model, it was used for the analysis of the other six specimens to further authenticate the accuracy of the anticipated finite element model. The control model was calibrated for different element types of GFRP and concrete material, mesh sizes, the eccentricity of concrete, shape factor, viscosity parameter, stress ratio, and dilation angle of concrete.
Various element types of concrete material and FRP reinforcement were evaluated to examine the effect of their variation on the load-deflection behavior of control finite element specimens. The 3-D stress elements available in the ABAQUS library for concrete material include hexahedral (C3D8R & C3D20R), tetrahedral (C3D4H & C3D10H), and triangular (C3D6H & C3D15H) elements that were studied during the calibration process. Similarly, the FRP reinforcing bars were studied for different truss (T3D2R & T3D3R) and beam (B31H & B32H) elements. It was observed that C3D8R and T3D2R gave the best results for concrete and reinforcement, correspondingly as presented in Figure 9 which displays the load-deflection response of the control column.
Figure 9.
Sensitivity of various element types on load-deflection behavior of control specimen (a) concrete elements (b) FRP bars elements.
The effect of increasing or decreasing the mesh size was also studied. The finite element models are always meshed size-dependent. This may be due to the phenomenon of strain localization that causes the unloading of some elements in the model. The studied mesh sizes were 15, 20, 25, 30, 40, and 50 mm. The best results were obtained while using a mesh size of 20 mm throughout the specimen. Figure 10a presents the load-deflection response of the control model by using different values of mesh size of the specimen.
Figure 10.
Sensitivity analysis of (a) mesh size (b) dilation angle (c) viscosity parameter (d) shape factor of concrete on the load-deflection curve of the control specimen.
The dilation angle of concrete, which represents the internal frictional angle, should range between 30° and 45° [61,62,63,64,65,66]. In the present investigation, the studied values of dilation angle were 30°, 33°, 35°, 38°, 40°, 43°, and 45°, correspondingly. The effect of variation of the dilation angle was not significant for the load-deflection response of the control specimen as reported in Figure 10b. However, the dilation angle of 35° gave a close agreement of numerical outcomes of the load-deflection curve with the experimental measurements.
The sensitivity of the viscosity parameter of concrete on the axial performance of the GFRP-RC column was also investigated. Various values of viscosity parameter used for the adjustment were 0.0068, 0.0058, 0.0048, 0.0038, 0.0028, and 0.0018. The effect of the viscosity parameter on the load-deflection response of the control model is presented in Figure 10c. There was an increase of 20.41% in the axial capacity of the specimen when the viscosity parameter was improved from 0.0018 to 0.0068. However, a close correlation with the experimental results was observed while using a viscosity parameter of 0.0058.
The effect of the shape factor for the yielding surface of the concrete on the load-deflection performance of the control model is presented in Figure 10d. With the increase or decrease of shape factor from 2/3, the ultimate load of the specimen decreases. Thus, the best approximation for the testing load-deflection behavior of the GFRP-RC control model was observed at a value of 2/3. Similarly, the effects of stress ratio and eccentricity of concrete were also examined. The results indicated that these two parameters have no significant effect on the axial performance of GFRP-RC specimens. Therefore, the default values i.e., 1.16 and 0.1 were used for these parameters, correspondingly.
5. Results and Discussion
The load-deflection curve of the control model represents that the percentage discrepancy between the numerical and experiments was 6.23% for the maximum loading capacity and 9.70% for the axial deflection at a maximum loading capacity of GFRP-RC specimen. However, the overall performance of the curve was closely captured by the proposed FEM. The minor discrepancies between the experimental and FEM results may be due to the differences between assumed boundary conditions in numerical simulations and experimental testing. Furthermore, the discrepancies may be associated with the geometric imperfections, differences in the strength of concrete and FRP material, the accuracy of laboratory instruments, manufacturing faults of specimens, and the assumptions made during the simulations.
After the validation of the control model, it was employed for the analysis of all other GFRP-RC columns from Ref. [29]. Table 4 represents the results obtained from the finite element simulations and their discrepancies from the experimental measurements. The average percentage discrepancy of finite element simulations from the experiments was 3.78% for loading capacity and 15.9% for the corresponding deflection at ultimate loading capacity.
Table 4.
Testing and numerical simulation results.
| Sample Label | Experimental Results | FEA Results from ABAQUS | % Difference in Peak Loads (KN) | % Difference in Vertical Def. at Peak Load (mm) | ||
|---|---|---|---|---|---|---|
| Peak Load (KN) | Vertical Deformation at Peak Load (mm) | Peak Load (KN) | Vertical Deformation at Peak Load (mm) | |||
| G150-45 | 584.21 | 5.67 | 547.81 | 5.12 | 6.23 | 9.70 |
| G150-25 | 880.28 | 4.86 | 883.94 | 5.36 | 0.41 | 10.28 |
| G150-C | 1366.76 | 6.87 | 1384.09 | 8.07 | 1.26 | 17.46 |
| G75-35 | 787.80 | 6.13 | 694.51 | 5.06 | 11.84 | 17.45 |
| G75-25 | 917.16 | 7.30 | 895.68 | 5.74 | 2.34 | 21.36 |
| G75-C | 1449.06 | 6.39 | 1486.26 | 7.28 | 2.56 | 13.92 |
| G250-C | 1401.8 | 5.79 | 1426.91 | 7.01 | 1.79 | 21.07 |
Load-Deflection Performance of FEM
The load-deflection curves of concentrically loaded GFRP-RC specimens are presented in Figure 11. The anticipated FEM predicted the axial behavior of concentric specimens with high accuracy in the elastic region of the load-deflection curve. However, the post-buckling behavior of specimens was not exactly traced. This may be due to the assumption of linear elastic performance of GFRP reinforcement up to failure in the simulations. In concentric columns, the GFRP bars are subjected to pure compression and the compressive performance of GFRP bars was taken as similar to the tensile behavior that may also be a reason for the discrepancy of results during the post-peak behavior. The FEM of the GFRP-RC specimen with 75 mm stirrup spacing tested under concentric loading (G75-C) portrayed the percentage faults of 2.56% and 13.92% for the maximum capacity and axial deflection at that capacity, correspondingly. The specimen G150-C showed percentage errors of 1.26% for axial capacity and 17.46% for the corresponding axial deflection. Similarly, the discrepancies for AS and axial deflections were 1.79% and 21.07%, correspondingly. The average differences between the simulations and experimental measurements of concentric GFRP-RCC specimens were 5.21% and 14.70% for peak loading capacity and axial deflection at that loading, correspondingly.
Figure 11.
Load-deflection performance of GFRP-RC concentric columns.
In the case of eccentric GFRP-RC columns, the proposed FEM predicted the axial performance of specimens with high accuracy. Figure 12 represents the finite element and experimental load-deflection curves of the eccentrically loaded GFRP-RC specimens. It can be observed that the FEM of the specimen G75-25 gave a percentage error of 2.34% and 21.36% for the axial ultimate load and equivalent axial deflection, correspondingly. The percent error for specimen G75-35 was 11.84% for axial load and 17.45% for the axial deflection of the columns. The column with 150 mm stirrups spacing tested with an eccentricity of 25 mm (G150-25) presented the discrepancies of 0.41% and 10.28% for axial capacity and corresponding deflection, correspondingly. Similarly, the control specimen G150-45 presented the errors of only 6.23% and 9.70% for load and deflection, correspondingly. All the eccentrically loaded specimens showed an average discrepancy of 5.21% for the peak load and an average discrepancy of 14.70% for the axial deflection at the peak load. This discussion represents that the anticipated FEM predicts the axial loads of concentric GFRP-RC columns and axial deflections of eccentric GFRP-RC columns with higher accuracy.
Figure 12.
Load-deflection performance of GFRP-RC eccentric columns (a) G75-25 (b) G75-35 (c) G150-25 (d) G150-45.
6. Parametric Investigation
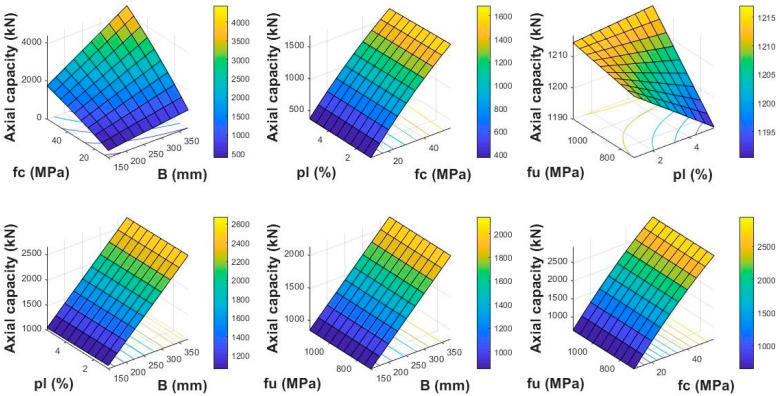
After validation, the anticipated FEM and empirical models were employed for the further analysis of 600 GFRP-reinforced rectangular columns under compressive loads. Four (4) different parameters of columns (a) longitudinal FRP reinforcement ratio (), (b) concrete compressive strength (), the tensile strength of GFRP rebars (), and width of column () was varied for different ranges to examine their effect on the axial capacity (strength) of the columns as reported in Table 5. The main aim of the parametric study was to construct a database of GFRP-RC columns with various geometrical and material parameters so that the predictions of proposed capacity models could be verified and compared by using these results.
Table 5.
Ranges of the parameters during the parametric investigation.
| Variable | Fixed Value | Studied Values |
|---|---|---|
| Concrete strength (MPa) | 30 | 10, 15, 20, 25, 30, 35, 40, 45, 50, 55 |
| Tensile strength (MPa) | 850 | 700, 750, 800, 850, 900, 950, 1000, 1050, 1100, 1150 |
| Side length of column (mm) | 200 | 150, 175, 200, 225, 250, 275, 300, 325, 350, 375 |
| Reinforcement ratio (%) | 1.94 | 0.97, 1.46, 1.94, 2.43, 2.92, 3.41, 3.89, 4.38, 4.86, 5.35 |
6.1. Using FEA Model
6.1.1. Influence of Width of Column (B)
Figure 13 reports the influence of the effect of “B” of the GFRP-reinforced column on their AS. The examined values of this parameter were 375, 350, 325, 300, 275, 250, 225, 200, 175, and 150 mm. The enhancement of “B” from 150 to 375 mm resulted in an increase of 1041% in the axial compressive strength of GFRP-reinforced members with the enhancement of from 10 to 55 MPa at of 1.94% and fu of 850 MPa as fixed. Similarly, the enhancement of “B” from 150 to 375 mm resulted in an upsurge of 151% in the AS with the enhancement of from 700 to 1150 MPa.
Figure 13.
Detailed parametric investigation using FEM.
6.1.2. Influence of Concrete Compressive Strength ()
Figure 13 reports the influence of on the axial compressive strength of columns. The upsurge of from 10 to 55 MPa resulted in an enhancement of 1041% in the AS with the increase of “B” from 150 to 375 mm. Similarly, the enhancement of with the increase of from 0.97% to 5.35% resulted in an improvement of 343% in the AS of columns. By enhancing from 10 to 55 MPa, the AS resulted in an improvement of 357% with the upsurge of from 700 to 1150 MPa. This portrays that the enhancement of tensile strength of FRP rebars and compressive strength of concrete results in a similar effect on the AS of FRP-reinforced concrete columns.
6.1.3. Influence of Longitudinal Reinforcement Ratio ()
The influence of reinforcement ratio was also reported in Figure 13. This parameter has been examined for the various values including 5.35%, 4.86%, 4.38%, 3.89%, 3.41%, 2.92%, 2.43%, 1.94%, 1.46%, and 0.97%. The enhancement of from 0.97% to 5.35% resulted in an improvement of 343% in the AS with an upsurge of from 10 to 55 MPa. Similarly, the enhancement of with the upsurge of fu from 700 to 1150 MPa resulted in an enhancement of only 0.6%. Furthermore, enhancing the “B” from 150 to 375 mm resulted in an improvement of 149% in the AS with the enhancement of from 0.97% to 5.35%.
6.1.4. Influence of Tensile Strength of FRP Rebars ()
The influence of changing the on the AS is reported in Figure 13. Different values of with an augmentation of 50 MPa was examined in the range of 700 to 1150 MPa. The enhancement of fu from 700 to 1150 MPa resulted in an improvement of only 0.6% in the axial compressive strength with the increase of from 0.97% to 5.35%. An improvement of 151% was observed by enhancing “B” from 150 to 375 mm. Similarly, the enhancement of from 700 to 1150 MPa resulted in an improvement of only 357% in the axial compressive strength with the upsurge of from 10 to 55 MPa. Finally, it was concluded that the influence of the area of column and strength of concrete was significant on its axial compressive strength as compared with the other parameters.
6.2. Using Empirical Model
6.2.1. Influence of Width of Column (B)
The same parameters were evaluated in the parametric investigation using the proposed empirical model as shown in Figure 14 that displays the influence of “” of GFRP-reinforced column on their AS. The examined values of this parameter were the same as in the numerical parameter study. The enhancement of “B” from 150 to 375 mm resulted in an increase of 1123% in the axial compressive strength of specimens with the enhancement of from 10 to 55 MPa at of 1.94% and fu of 850 MPa as fixed. Similarly, the enhancement of “” from 150 to 375 mm resulted in an upsurge of 214% in the AS with the enhancement of from 700 to 1150 MPa.
Figure 14.
Parametric investigation using an empirical model.
6.2.2. Influence of Concrete Compressive Strength ()
The effect of on the axial compressive strength of columns is reported in Figure 14. The upsurge of from 10 to 55 MPa resulted in an augmentation of 1123% in the AS with the increase of “” from 150 to 375 mm. Similarly, the enhancement of with the increase of from 0.97% to 5.35% resulted in an upgrading of 389% in the AS of columns. By enhancing from 10 MPa to 55 MPa, the AS resulted in an improvement of 469% with the upsurge of fu from 700 to 1150 MPa.
6.2.3. Influence of Longitudinal Reinforcement Ratio ()
Figure 14 also presents the influence of the FRP reinforcement ratio () on the axial capacity of specimens. This parameter has been examined for the various values as investigated in the numerical parametric study. The enhancement of from 0.97% to 5.35% resulted in an improvement of 389% in the AS with an upsurge of from 10 to 55 MPa. Similarly, the enhancement of with the upsurge of fu from 700 to 1150 MPa resulted in an enhancement of 125%. Furthermore, enhancing the “B” from 150 to 375 mm resulted in an improvement of 236% in the AS with the enhancement of from 0.97% to 5.35%.
6.2.4. Influence of Tensile Strength of FRP Rebars (fu)
The influence of changing the on the AS was reported in Figure 14. Different values of with an increase of 50 MPa were assessed in the range of 700–1150 MPa. The enhancement of from 700 to 1150 MPa resulted in an improvement of 125% in the axial compressive strength with the increase of from 0.97% to 5.35%. An improvement of 151% was observed by enhancing “B” from 150 to 375 mm. Similarly, the enhancement of from 700 to 1150 MPa resulted in an improvement of only 469% in the axial compressive strength with the upsurge of from 10 to 55 MPa. Therefore, it is concluded that during the parametric investigation, both the models (FEM and empirical models) have portrayed their predictions of the axial strength of GFRP-reinforced columns close to each other.
7. Validation and Comparison of Proposed Models
The purpose of the parametric study using the proposed FEM and empirical models in the present work was to generate a database of GFRP-reinforced compressive members to validate and compare the anticipated models for the axial compressive strength of GFRP-reinforced columns. The numerical and empirical database consisted of 600 results of AS of GFRP-reinforced concentric specimens. The theoretical predictions of these 600 GFRP-RC specimens calculated using the anticipated empirical model were compared with that of the numerical model. The comparative study of FEM and theoretical predictions are reported in Figure 15. It was noticed that the anticipated empirical axial capacity model performed well for the numerical parametric results with an R2 of 0.87. Thus, the anticipated empirical and FEM model is accurate enough to capture the AS of GFRP-reinforced concrete columns.
Figure 15.
Comparison of predictions of anticipated empirical and FEM.
8. Conclusions
In the present work, an experimental database of 278 FRP-RC compression members was established from the literature to recommend an empirical model that can accurately predict the AS of GFRP-RC specimens. An initial evaluation of 13 different previously anticipated empirical models was executed to achieve a general shape of the AS model. Finally, a new empirical equation for forecasting the AS of GFRP-reinforced short columns was proposed using the curve fitting and regression analysis technique. A validated FEM was suggested for GFRP-reinforced members and used along with an empirical model for a detailed parametric investigation. Following conclusions were extracted from this work.
A better performance has been reported by the newly developed empirical model for apprehending the axial compressive strength of FRP-reinforced concrete compressive members with R2 = 0.73 using a database of 278 experimental data points. This model depicted higher correctness as compared with all previous models for different statistical errors (RMSE and MAE). Furthermore, the new model has been proposed based on a large data of FRP-reinforced columns while the previously proposed models were proposed using small databases.
The axial contribution of FRP rebars has been involved in the model with a reduction factor of for the concrete strength and a reduction factor of 0.0208 for the AS of FRP rebars.
The suggested FEM also apprehended the structural performance of FRP-reinforced concrete members with a high accuracy depicting only the errors of 3.78% and 15.9% for AS and equivalent axial deflection, correspondingly.
The parametric investigation depicted that the AS of the concrete and cross-sectional area of the concrete column had a significant influence on the AS of such members. The enhancement of the cross-sectional area of the column by an increase of 1.5 times resulted in the AS up to 1041%. Correspondingly, the enhancement of concrete strength by 4.5 times resulted in an improvement of 357% in the AS of columns. The influence of reinforcement ratio of FRP rebars and tensile strength of FRP rebars reported no significant influence on the AS.
Six hundred (600) specimens were tested in ABAQUS and empirical model to perform the parametric investigation and to generate a theoretical database for the assessment purposed FEM with the estimates of the theoretical model. The comparison reported a close agreement among each other with R2 = 0.87. Thus, the anticipated theoretical and FEA models are precise enough to further analyze the FRP-reinforced concrete columns.
Appendix A
Table A1.
Constructed experimental database (GS = GFRP spirals, GH = GFRP hoops, SS = steel spirals, SH = steel hoops, N = no lateral reinforcement).
| Sr. No. | Research Study | Longitudinal Reinforcement | Transverse Reinforcement | Axial Strength | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (MPa) | (MPa) | (GPa) | (%) | Bars | (%) | Type | (%) | (kN) | ||
| 1 | Afifi et al. [23] | - | - | 300 | 20 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 1 | 2920 |
| 2 | Afifi et al. [23] | - | - | 300 | 20 | 934 | 55.4 | 1.56 | 4 No. 5 | 1.1 | GS | 1 | 2826 |
| 3 | Afifi et al. [23] | - | - | 300 | 20 | 934 | 55.4 | 1.56 | 12 No. 5 | 3.2 | GS | 1 | 2998 |
| 4 | Afifi et al. [23] | - | - | 300 | 20 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 0.45 | 2857 |
| 5 | Afifi et al. [23] | - | - | 300 | 20 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 1.87 | 3019 |
| 6 | Afifi et al. [23] | - | - | 300 | 20 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 2.07 | 2964 |
| 7 | Afifi et al. [23] | - | - | 300 | 20 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 0.69 | 2804 |
| 8 | Afifi et al. [23] | - | - | 300 | 20 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 1.03 | 2951 |
| 9 | Afifi et al. [23] | - | - | 300 | 20 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 1.03 | 2865 |
| 10 | Afifi et al. [33] | - | - | 301 | 21 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 1.5 | 2840 |
| 11 | Afifi et al. [33] | - | - | 302 | 22 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 1.5 | 2871 |
| 12 | Afifi et al. [33] | - | - | 303 | 23 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GS | 1.5 | 2935 |
| 13 | AlAjarmeh et al. [67] | - | - | 250 | 31.8 | 1237 | 60 | 2.1 | 6 No. 5 | 2.41 | GS | 1.49 | 1588 |
| 14 | AlAjarmeh et al. [67] | - | - | 250 | 31.8 | 1237 | 60 | 2.1 | 6 No. 5 | 2.47 | GS | 1.56 | 1408 |
| 15 | AlAjarmeh et al. [67] | - | - | 250 | 31.8 | 1237 | 60 | 2.1 | 6 No. 5 | 2.59 | GS | 1.69 | 1559 |
| 16 | AlAjarmeh et al. [67] | - | - | 250 | 31.8 | 1237 | 60 | 2.1 | 6 No. 5 | 2.78 | GS | 1.92 | 1411 |
| 17 | AlAjarmeh et al. [68] | - | - | 251 | 25 | 1281.5 | 61.3 | 2.1 | 6 No. 4 | 1.78 | GS | 1.57 | 1035.3 |
| 18 | AlAjarmeh et al. [68] | - | - | 252 | 25 | 1237.4 | 60.5 | 2.1 | 6 No. 5 | 2.79 | GS | 1.57 | 1109.2 |
| 19 | AlAjarmeh et al. [68] | - | - | 253 | 25 | 1270 | 60.5 | 2.1 | 6 No. 6 | 4 | GS | 1.57 | 1247.9 |
| 20 | AlAjarmeh et al. [68] | - | - | 254 | 25 | 1237.4 | 60.5 | 2.1 | 4 No. 5 | 1.86 | GS | 1.57 | 983.3 |
| 21 | AlAjarmeh et al. [68] | - | - | 255 | 25 | 1237.4 | 60.5 | 2.1 | 8 No. 5 | 3.72 | GS | 1.57 | 1406.1 |
| 22 | AlAjarmeh et al. [68] | - | - | 256 | 25 | 1281.5 | 61.3 | 2.1 | 9 No. 4 | 2.67 | GS | 1.57 | 1204.2 |
| 23 | Alsayed et al. [69] | 250 | 450 | - | 39 | 800 | 40 | 1.5 | 6 No. 5 | 1 | SH | 0.15 | 3285 |
| 24 | Alsayed et al. [69] | 250 | 450 | - | 39 | 800 | 40 | 1.5 | 6 No. 5 | 1 | SH | 0.15 | 3285 |
| 25 | Alsayed et al. [69] | 250 | 450 | - | 39 | 800 | 40 | 1.5 | 6 No. 5 | 1 | SH | 0.15 | 3285 |
| 26 | Alsayed et al. [69] | 250 | 450 | - | 38.5 | 800 | 40 | 1.5 | 6 No. 5 | 1 | GH | 0.18 | 3301 |
| 27 | Alsayed et al. [69] | 250 | 450 | - | 38.5 | 800 | 40 | 1.5 | 6 No. 5 | 1 | GH | 0.18 | 3301 |
| 28 | Alsayed et al. [69] | 250 | 450 | - | 38.5 | 800 | 40 | 1.5 | 6 No. 5 | 1 | GH | 0.18 | 3301 |
| 29 | De Luca et al. [70] | 610 | 610 | - | 43.7 | 608 | 44.2 | 1.38 | 8 No. 8 | 1 | GH | 0.63 | 15235 |
| 30 | De Luca et al. [70] | 610 | 610 | - | 40.6 | 712 | 44.4 | 1.6 | 8 No 8 | 1 | GH | 0.63 | 12949 |
| 31 | De Luca et al. [70] | 610 | 610 | - | 36.1 | 608 | 44.2 | 1.38 | 8 No. 8 | 1 | GH | 2.5 | 11926 |
| 32 | De Luca et al. [70] | 610 | 610 | - | 32.8 | 712 | 44.4 | 1.6 | 8 No 8 | 1 | GH | 2.5 | 10751 |
| 33 | Dong et al. [15] | - | - | 215 | 40 | 930 | 59 | 1.6 | 3 No. 3 | 0.55 | GS | 0.94 | 1018 |
| 34 | Dong et al. [15] | - | - | 215 | 40 | 930 | 59 | 1.6 | 4 No. 3 | 0.73 | GS | 0.94 | 1179 |
| 35 | Dong et al. [15] | - | - | 215 | 40 | 930 | 59 | 1.6 | 5 No. 3 | 0.92 | GS | 0.94 | 1288 |
| 36 | Dong et al. [15] | - | - | 215 | 40 | 930 | 59 | 1.6 | 6 No. 3 | 1.1 | GS | 0.94 | 1381 |
| 37 | Dong et al. [15] | - | - | 215 | 40 | 930 | 59 | 1.6 | 4 No. 3 | 0.73 | GS | 2.75 | 1459 |
| 38 | Dong et al. [15] | - | - | 215 | 40 | 930 | 59 | 1.6 | 4 No. 3 | 0.73 | GS | 2.75 | 1037 |
| 39 | Dong et al. [15] | - | - | 215 | 40 | 880 | 59 | 1.6 | 4 No. 3 | 0.73 | GS | 2.75 | 523 |
| 40 | Dong et al. [15] | - | - | 215 | 37 | 880 | 59 | 1.6 | 4 No. 3 | 0.73 | GS | 2.75 | 318 |
| 41 | Dong et al. [15] | - | - | 215 | 37 | 880 | 59 | 1.6 | 5 No. 3 | 0.73 | GS | 1.39 | 1290 |
| 42 | Dong et al. [15] | - | - | 215 | 37 | 880 | 59 | 1.6 | 6 No. 3 | 0.73 | GS | 1.39 | 944 |
| 43 | Dong et al. [15] | - | - | 215 | 37 | 880 | 59 | 1.6 | 7 No. 3 | 0.73 | GS | 1.39 | 527 |
| 44 | Dong et al. [15] | - | - | 215 | 37 | 880 | 59 | 1.6 | 8 No. 3 | 0.73 | GS | 1.39 | 296 |
| 45 | Elchalakani and Ma [26] | 160 | 260 | - | 32.8 | 1200 | 50 | 2.4 | 6 No. 4 | 1.8 | GH | 0.5 | 1367 |
| 46 | Elchalakani and Ma [26] | 160 | 260 | - | 32.8 | 1200 | 50 | 2.4 | 6 No. 4 | 1.8 | GH | 0.5 | 880 |
| 47 | Elchalakani and Ma [26] | 160 | 260 | - | 32.8 | 1200 | 50 | 2.4 | 6 No. 4 | 1.8 | GH | 0.5 | 584 |
| 48 | Elchalakani and Ma [26] | 160 | 260 | - | 32.8 | 1200 | 50 | 2.4 | 6 No. 4 | 1.8 | GH | 1 | 1449 |
| 49 | Elchalakani and Ma [26] | 160 | 260 | - | 32.8 | 1200 | 50 | 2.4 | 6 No. 4 | 1.8 | GH | 1 | 917 |
| 50 | Elchalakani and Ma [26] | 160 | 260 | - | 32.8 | 1200 | 50 | 2.4 | 6 No. 4 | 1.8 | GH | 1 | 788 |
| 51 | Elchalakani and Ma [26] | 160 | 260 | - | 32.8 | 1200 | 50 | 2.4 | 6 No. 4 | 1.8 | GH | 0.3 | 1402 |
| 52 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 0.3 | 1402 |
| 53 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 0.5 | 1367 |
| 54 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 1 | 1449 |
| 55 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 0.5 | 880 |
| 56 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 1 | 917 |
| 57 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 1 | 788 |
| 58 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 0.5 | 584 |
| 59 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 0.3 | 1041 |
| 60 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 0.5 | 1194 |
| 61 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 1 | 1357 |
| 62 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 0.5 | 657 |
| 63 | Elchalakani et al. [29] | 160 | 260 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 1 | 804 |
| 64 | Elchalakani et al. [29] | 160 | 160 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 0.5 | 353 |
| 65 | Elchalakani et al. [29] | 160 | 160 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 1 | 454 |
| 66 | Elchalakani et al. [29] | 160 | 160 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 0.5 | 234 |
| 67 | Elchalakani et al. [29] | 160 | 160 | - | 32.8 | 930 | 59 | 1.7 | 6 No. 4 | 1.8 | GH | 1 | 244 |
| 68 | Guerin et al. [71] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 6 No. 6 | 1 | GH | 0.66 | 4587 |
| 69 | Guerin et al. [71] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 6 No. 6 | 1 | GH | 0.66 | 3433 |
| 70 | Guerin et al. [71] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 6 No. 6 | 1 | GH | 0.66 | 1591 |
| 71 | Guerin et al. [71] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 6 No. 6 | 1 | GH | 0.66 | 645 |
| 72 | Guerin et al. [71] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 6 No. 6 | 1 | GH | 0.66 | 4616 |
| 73 | Guerin et al. [71] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 6 No. 6 | 1 | GH | 0.66 | 3405 |
| 74 | Guerin et al. [71] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 6 No. 6 | 1 | GH | 0.66 | 1576 |
| 75 | Guerin et al. [71] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 6 No. 6 | 1 | GH | 0.66 | 636 |
| 76 | Guerin et al. [72] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 8 No. 6 | 1.4 | GH | 0.84 | 5028 |
| 77 | Guerin et al. [72] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 8 No. 6 | 1.4 | GH | 0.84 | 3627 |
| 78 | Guerin et al. [72] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 8 No. 6 | 1.4 | GH | 0.84 | 2035 |
| 79 | Guerin et al. [72] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 8 No. 6 | 1.4 | GH | 0.84 | 914 |
| 80 | Guerin et al. [72] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 8 No. 8 | 2.5 | GH | 0.63 | 5294 |
| 81 | Guerin et al. [72] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 8 No. 8 | 2.5 | GH | 0.63 | 3790 |
| 82 | Guerin et al. [72] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 8 No. 8 | 2.5 | GH | 0.63 | 2110 |
| 83 | Guerin et al. [72] | 405 | 405 | - | 25.3 | 600 | 40 | 1.5 | 8 No. 8 | 2.5 | GH | 0.63 | 1008 |
| 84 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GH | 2.68 | 2564 |
| 85 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GH | 2.68 | 2060 |
| 86 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GH | 2.68 | 1511 |
| 87 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GH | 2.68 | 776 |
| 88 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GH | 2.68 | 366 |
| 89 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1 | 2608 |
| 90 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1 | 2134 |
| 91 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1 | 1513 |
| 92 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1 | 745 |
| 93 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1 | 654 |
| 94 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 12 No. 5 | 3.3 | GS | 1 | 2670 |
| 95 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 12 No. 5 | 3.3 | GS | 1 | 2123 |
| 96 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 12 No. 5 | 3.3 | GS | 1 | 1527 |
| 97 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 12 No. 5 | 3.3 | GS | 1 | 852 |
| 98 | Hadhood et al. [52] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 12 No. 5 | 3.3 | GS | 1 | 378 |
| 99 | Hadhood et al. [73] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1.8 | 2652 |
| 100 | Hadhood et al. [73] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1.8 | 2086 |
| 101 | Hadhood et al. [73] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1.8 | 1483 |
| 102 | Hadhood et al. [73] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1.8 | 747 |
| 103 | Hadhood et al. [73] | - | - | 305 | 35 | 1680 | 141 | 1.19 | 8 No. 5 | 2.2 | GS | 1.8 | 655 |
| 104 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 4709 |
| 105 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 3309 |
| 106 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 2380 |
| 107 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 1112 |
| 108 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 797 |
| 109 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GH | 1.1 | 4689 |
| 110 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GH | 1.1 | 3299 |
| 111 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GH | 1.1 | 2435 |
| 112 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GH | 1.1 | 1054 |
| 113 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GH | 1.1 | 838 |
| 114 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 12 No. 5 | 3.2 | GS | 1.1 | 4716 |
| 115 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 12 No. 5 | 3.2 | GS | 1.1 | 3380 |
| 116 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 12 No. 5 | 3.2 | GS | 1.1 | 2339 |
| 117 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 12 No. 5 | 3.2 | GS | 1.1 | 1135 |
| 118 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 12 No. 5 | 3.2 | GS | 1.1 | 713 |
| 119 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 5120 |
| 120 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 3671 |
| 121 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 2538 |
| 122 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 1392 |
| 123 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 611 |
| 124 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.7 | 4680 |
| 125 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.7 | 3341 |
| 126 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.7 | 2460 |
| 127 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.7 | 1061 |
| 128 | Hadhood et al. [73] | - | - | 305 | 70.2 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.7 | 682 |
| 129 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 2608 |
| 130 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 2134 |
| 131 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 1512 |
| 132 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 745 |
| 133 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 354 |
| 134 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 3090 |
| 135 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 2342 |
| 136 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 1746 |
| 137 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 995 |
| 138 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 529 |
| 139 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 2652 |
| 140 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 2086 |
| 141 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 1483 |
| 142 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 747 |
| 143 | Hadhood et al. [73] | - | - | 305 | 35 | 1289 | 54.9 | 2.3 | 8 No. 5 | 2.2 | GS | 1.1 | 355 |
| 144 | Hadi et al. [34] | - | - | 205 | 37 | 1200 | 50 | 2.4 | 6 No. 4 | 1.6 | GS | 2.1 | 1220 |
| 145 | Hadi et al. [34] | - | - | 205 | 37 | 1200 | 50 | 2.4 | 6 No. 4 | 1.6 | GS | 2.1 | 781 |
| 146 | Hadi et al. [34] | - | - | 205 | 37 | 1200 | 50 | 2.4 | 6 No. 4 | 1.6 | GS | 2.1 | 494 |
| 147 | Hadi et al. [34] | - | - | 205 | 37 | 1200 | 50 | 2.4 | 6 No. 4 | 1.6 | GS | 4.2 | 1309 |
| 148 | Hadi et al. [34] | - | - | 205 | 37 | 1200 | 50 | 2.4 | 6 No. 4 | 1.6 | GS | 4.2 | 767 |
| 149 | Hadi et al. [34] | - | - | 205 | 37 | 1200 | 50 | 2.4 | 6 No. 4 | 1.6 | GS | 4.2 | 479 |
| 150 | Hadi and Youssef [74] | 210 | 210 | - | 29.3 | 1641 | 67.9 | 2.41 | 4 No. 4 | 1 | GH | 2.74 | 1285 |
| 151 | Hadi and Youssef [74] | 210 | 210 | - | 29.3 | 1641 | 67.9 | 2.41 | 4 No. 4 | 1 | GH | 2.74 | 803 |
| 152 | Hadi and Youssef [74] | 210 | 210 | - | 29.3 | 1641 | 67.9 | 2.41 | 4 No. 4 | 1 | GH | 2.74 | 615 |
| 153 | Hassan et al. [75] | - | - | 150 | 40 | 800 | 30 | 0.97 | 6 No. 3 | 2.1 | SS | 1.7 | 426.59 |
| 154 | Hassan et al. [75] | - | - | 150 | 40 | 800 | 30 | 1.35 | 6 No. 3 | 2.1 | SS | 1.7 | 411.88 |
| 155 | Hassan et al. [75] | - | - | 150 | 40 | 800 | 30 | 1.57 | 6 No. 3 | 2.1 | SS | 1.7 | 387.36 |
| 156 | Hassan et al. [75] | - | - | 150 | 40 | 800 | 30 | 1.4 | 6 No. 3 | 2.1 | SS | 3.4 | 529.56 |
| 157 | Hassan et al. [75] | - | - | 150 | 40 | 800 | 30 | 1.7 | 6 No. 3 | 2.1 | SS | 3.4 | 490.33 |
| 158 | Hassan et al. [75] | - | - | 150 | 40 | 800 | 30 | 1.9 | 6 No. 3 | 2.1 | SS | 3.4 | 460.91 |
| 159 | Hassan et al. [75] | - | - | 150 | 40 | 800 | 30 | 1.28 | 6 No. 3 | 2.1 | GH | 1.7 | 490.33 |
| 160 | Hassan et al. [75] | - | - | 150 | 40 | 800 | 30 | 1.5 | 6 No. 3 | 2.1 | GH | 1.7 | 460.91 |
| 161 | Hassan et al. [75] | - | - | 150 | 40 | 800 | 30 | 1.7 | 6 No. 3 | 2.1 | GH | 1.7 | 430.4 |
| 162 | Karim et al. [35] | - | - | 205 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 1.91 | 1425 |
| 163 | Karim et al. [35] | - | - | 205 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 3.82 | 2041 |
| 164 | Karim et al. [52] | - | - | 206 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 1.91 | 1425 |
| 165 | Karim et al. [52] | - | - | 207 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 1.91 | 781 |
| 166 | Karim et al. [52] | - | - | 208 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 1.91 | 494 |
| 167 | Karim et al. [52] | - | - | 209 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 3.82 | 2041 |
| 168 | Karim et al. [52] | - | - | 210 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 3.82 | 767 |
| 169 | Karim et al. [52] | - | - | 211 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 3.82 | 479 |
| 170 | Karim et al. [52] | - | - | 212 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 1.91 | 3068 |
| 171 | Karim et al. [52] | - | - | 213 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 1.91 | 1450 |
| 172 | Karim et al. [52] | - | - | 214 | 37 | 1600 | 66 | 2.42 | 6 No. 4 | 4.72 | GS | 1.91 | 805 |
| 173 | Khan et al. [47] | - | - | 206 | 37 | 1395 | 56 | 1.5 | 6 No. 5 | 3.57 | GH | - | 2812 |
| 174 | Khan et al. [47] | - | - | 206 | 37 | 1395 | 56 | 1.5 | 6 No. 5 | 3.57 | GH | - | 1487 |
| 175 | Khan et al. [47] | - | - | 206 | 37 | 1395 | 56 | 1.5 | 6 No. 5 | 3.57 | GH | - | 910 |
| 176 | Khorramian & Sadeghian [27] | 150 | 150 | - | 37 | 629 | 38.7 | 1.62 | 6 No. 5 | 5.3 | N | - | 775 |
| 177 | Khorramian & Sadeghian [27] | 150 | 150 | - | 37 | 629 | 38.7 | 1.62 | 6 No. 5 | 5.3 | N | - | 775 |
| 178 | Khorramian & Sadeghian [27] | 150 | 150 | - | 37 | 629 | 38.7 | 1.62 | 6 No. 5 | 5.3 | N | - | 693 |
| 179 | Khorramian & Sadeghian [27] | 150 | 150 | - | 37 | 629 | 38.7 | 1.62 | 6 No. 5 | 5.3 | N | - | 693 |
| 180 | Khorramian & Sadeghian [27] | 150 | 150 | - | 37 | 629 | 38.7 | 1.62 | 6 No. 5 | 5.3 | N | - | 693 |
| 181 | Khorramian & Sadeghian [27] | 150 | 150 | - | 37 | 629 | 38.7 | 1.62 | 6 No. 5 | 5.3 | N | - | 578 |
| 182 | Khorramian & Sadeghian [27] | 150 | 150 | - | 37 | 629 | 38.7 | 1.62 | 6 No. 5 | 5.3 | N | - | 578 |
| 183 | Khorramian & Sadeghian [27] | 150 | 150 | - | 37 | 629 | 38.7 | 1.62 | 6 No. 5 | 5.3 | N | - | 354 |
| 184 | Khorramian & Sadeghian [27] | 150 | 150 | - | 37 | 629 | 38.7 | 1.62 | 6 No. 5 | 5.3 | N | - | 354 |
| 185 | Maranan et al. [76] | - | - | 250 | 34.42 | 1184 | 62.6 | 1.89 | 6 No. 5 | 2.43 | GH | 3.13 | 1772 |
| 186 | Maranan et al. [76] | - | - | 250 | 34.42 | 1184 | 62.6 | 1.89 | 6 No. 5 | 2.43 | GH | 3.13 | 1791 |
| 187 | Maranan et al. [76] | - | - | 250 | 34.42 | 1184 | 62.6 | 1.89 | 6 No. 5 | 2.43 | GH | 1.57 | 1981 |
| 188 | Maranan et al. [76] | - | - | 250 | 34.42 | 1184 | 62.6 | 1.89 | 6 No. 5 | 2.43 | GH | 0.78 | 1988 |
| 189 | Maranan et al. [76] | - | - | 250 | 34.42 | 1184 | 62.6 | 1.89 | 6 No. 5 | 2.43 | GS | 3.13 | 1838 |
| 190 | Maranan et al. [76] | - | - | 250 | 34.42 | 1184 | 62.6 | 1.89 | 6 No. 5 | 2.43 | GS | 1.57 | 2063 |
| 191 | Maranan et al. [76] | - | - | 250 | 34.42 | 1184 | 62.6 | 1.89 | 6 No. 5 | 2.43 | GH | 1.57 | 1624 |
| 192 | Maranan et al. [76] | - | - | 250 | 34.42 | 1184 | 62.6 | 1.89 | 6 No. 5 | 2.43 | GS | 1.57 | 1208 |
| 193 | Mohamed et al. [32] | - | - | 300 | 42.9 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GH | 2.23 | 2840 |
| 194 | Mohamed et al. [32] | - | - | 300 | 42.9 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GH | 2.68 | 2871 |
| 195 | Mohamed et al. [32] | - | - | 300 | 42.9 | 934 | 55.4 | 1.56 | 8 No. 5 | 2.2 | GH | 3.14 | 2935 |
| 196 | Pantelides et al. [49] | - | - | 254 | 36 | 740 | 43.3 | 1.71 | 4 No. 5 | 1.6 | GS | 0.75 | 1975 |
| 197 | Pantelides et al. [49] | - | - | 254 | 36 | 740 | 43.3 | 1.71 | 4 No. 5 | 1.6 | GS | 0.75 | 1788 |
| 198 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SS | 0.01 | 370 |
| 199 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SS | 0.01 | 370 |
| 200 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SS | 0.01 | 370 |
| 201 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SS | 0.02 | 365 |
| 202 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SS | 0.02 | 365 |
| 203 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SS | 0.02 | 365 |
| 204 | Prachasaree et al. [77] | - | - | 150 | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.9 | SS | 0.01 | 345 |
| 205 | Prachasaree et al. [77] | - | - | 150 | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.9 | SS | 0.01 | 345 |
| 206 | Prachasaree et al. [77] | - | - | 150 | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.9 | SS | 0.01 | 345 |
| 207 | Prachasaree et al. [77] | - | - | 150 | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.9 | SS | 0.02 | 315 |
| 208 | Prachasaree et al. [77] | - | - | 150 | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.9 | SS | 0.02 | 315 |
| 209 | Prachasaree et al. [77] | - | - | 150 | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.9 | SS | 0.02 | 315 |
| 210 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SH | 0.01 | 365 |
| 211 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SH | 0.01 | 365 |
| 212 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SH | 0.01 | 365 |
| 213 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SH | 0.02 | 370 |
| 214 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SH | 0.02 | 370 |
| 215 | Prachasaree et al. [77] | 150 | 150 | - | 20.8 | 735 | 50 | 1.5 | 4 No. 3 | 1.4 | SH | 0.02 | 370 |
| 216 | Sankholkar et al. [78] | - | - | 203 | 50 | 800 | 46.2 | 1.57 | 4 No. 5 | 2.5 | GS | 3.2 | 1353 |
| 217 | Sankholkar et al. [78] | - | - | 203 | 50 | 800 | 46.2 | 1.57 | 4 No. 5 | 2.5 | GS | 3.2 | 1285 |
| 218 | Sankholkar et al. [78] | - | - | 203 | 50 | 800 | 46.2 | 1.57 | 6 No. 5 | 3.7 | GS | 3.2 | 1623 |
| 219 | Sankholkar et al. [78] | - | - | 203 | 50 | 800 | 46.2 | 1.57 | 6 No. 5 | 3.7 | GS | 3.2 | 1570 |
| 220 | Sun et al. [79] | 150 | 150 | - | 23.51 | 1103 | 54.1 | 1.5 | 6 No. 3 | 1.04 | SH | 0.63 | 201 |
| 221 | Sun et al. [79] | 150 | 150 | - | 23.51 | 1103 | 54.1 | 1.5 | 6 No. 3 | 1.04 | SH | 0.63 | 174 |
| 222 | Sun et al. [79] | 150 | 150 | - | 23.51 | 1103 | 54.1 | 1.5 | 6 No. 3 | 1.04 | SH | 0.63 | 181 |
| 223 | Sun et al. [79] | 150 | 150 | - | 23.51 | 1103 | 54.1 | 1.5 | 6 No. 3 | 1.04 | SH | 0.63 | 291 |
| 224 | Sun et al. [79] | 150 | 150 | - | 23.51 | 1103 | 54.1 | 1.5 | 6 No. 3 | 1.04 | SH | 0.63 | 290 |
| 225 | Sun et al. [79] | 150 | 150 | - | 23.51 | 1103 | 54.1 | 1.5 | 6 No. 3 | 1.04 | SH | 0.63 | 347 |
| 226 | Sun et al. [79] | 150 | 150 | - | 23.51 | 1103 | 54.1 | 1.5 | 6 No. 3 | 1.04 | SH | 0.63 | 632 |
| 227 | Sun et al. [79] | 150 | 150 | - | 23.51 | 1103 | 54.1 | 1.5 | 6 No. 3 | 1.04 | SH | 0.63 | 677 |
| 228 | Sun et al. [79] | 150 | 150 | - | 23.51 | 1103 | 54.1 | 1.5 | 6 No. 3 | 1.04 | SH | 0.63 | 602 |
| 229 | Tikka et al. [80] | 150 | 150 | - | 25.7 | 630 | 40 | 1.5 | 4 No. 4 | 2.3 | CS | 0.33 | 401 |
| 230 | Tikka et al. [80] | 150 | 150 | - | 25.7 | 630 | 40 | 1.5 | 4 No. 4 | 2.3 | CS | 0.33 | 120 |
| 231 | Tikka et al. [80] | 150 | 150 | - | 25.7 | 630 | 40 | 1.5 | 6 No. 4 | 3.4 | CS | 0.33 | 215 |
| 232 | Tikka et al. [80] | 150 | 150 | - | 25.7 | 630 | 40 | 1.5 | 4 No. 4 | 2.3 | CS | 0.33 | 382 |
| 233 | Tikka et al. [80] | 150 | 150 | - | 25.7 | 630 | 40 | 1.5 | 4 No. 4 | 2.3 | CS | 0.33 | 129 |
| 234 | Tikka et al. [80] | 150 | 150 | - | 25.7 | 630 | 40 | 1.5 | 6 No. 4 | 3.4 | CS | 0.33 | 220 |
| 235 | Tikka et al. [80] | 150 | 150 | - | 25.7 | 630 | 40 | 1.5 | 6 No. 4 | 3.4 | CS | 0.33 | 116 |
| 236 | Tobbi et al. [22] | 350 | 350 | - | 32.6 | 728 | 47.6 | 1.53 | 8 No. 6 | 1.9 | GH | 2 | 3929 |
| 237 | Tobbi et al. [22] | 350 | 350 | - | 32.6 | 728 | 47.6 | 1.53 | 8 No. 6 | 1.9 | GH | 2 | 3991 |
| 238 | Tobbi et al. [22] | 350 | 350 | - | 32.6 | 728 | 47.6 | 1.53 | 9 No. 6 | 1.9 | GH | 1.7 | 4006 |
| 239 | Tobbi et al. [22] | 350 | 350 | - | 32.6 | 752 | 48.2 | 1.56 | 12 No. 5 | 1.9 | GH | 3.2 | 3938 |
| 240 | Tobbi et al. [22] | 350 | 350 | - | 32.6 | 751 | 48.2 | 1.56 | 12 No. 5 | 1.9 | GH | 4.8 | 4067 |
| 241 | Tobbi et al. [22] | 350 | 350 | - | 36.4 | 750 | 48.2 | 1.56 | 8 No. 6 | 1.9 | GH | 2.55 | 4297 |
| 242 | Tobbi et al. [22] | 350 | 350 | - | 36.4 | 749 | 48.2 | 1.56 | 12 No. 5 | 1.9 | GH | 3.41 | 4615 |
| 243 | Tobbi et al. [22] | 350 | 350 | - | 36.4 | 748 | 48.2 | 1.56 | 4 No. 4 + 4 No. 5 | 1 | GH | 2.55 | 4212 |
| 244 | Tobbi et al. [22] | 350 | 350 | - | 36.4 | 747 | 48.2 | 1.56 | 8 No. 4 | 0.8 | GH | 2.55 | 3900 |
| 245 | Tu et al. [81] | 200 | 200 | - | 32.1 | 660 | 44.25 | 1.52 | 4 No. 4 | 1.1 | GH | 5.3 | 970.9 |
| 246 | Tu et al. [81] | 200 | 200 | - | 32.1 | 660 | 44.25 | 1.52 | 4 No. 4 | 1.1 | GH | 3.1 | 951.6 |
| 247 | Tu et al. [81] | 200 | 200 | - | 32.1 | 660 | 44.25 | 1.52 | 4 No. 4 | 1.1 | GH | 2 | 937.7 |
| 248 | Tu et al. [81] | 200 | 200 | - | 32.1 | 735 | 46 | 1.6 | 4 No. 3 | 0.8 | GH | 3.1 | 936.8 |
| 249 | Tu et al. [81] | 200 | 200 | - | 32.1 | 660 | 44.25 | 1.52 | 4 No. 4 | 1.5 | GH | 3.1 | 981.7 |
| 250 | Tu et al. [81] | 200 | 200 | - | 32.1 | 660 | 44.25 | 1.52 | 4 No. 4 | 1.1 | GH | 5.2 | 954 |
| 251 | Tu et al. [81] | 200 | 200 | - | 32.1 | 660 | 44.25 | 1.52 | 4 No. 4 | 1.1 | GH | 3 | 943.2 |
| 252 | Tu et al. [81] | 200 | 200 | - | 32.1 | 660 | 44.25 | 1.52 | 4 No. 4 | 1.1 | GH | 1.9 | 927.7 |
| 253 | Xue et al. [82] | 300 | 300 | - | 39 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 3091 |
| 254 | Xue et al. [82] | 300 | 300 | - | 39 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 2855 |
| 255 | Xue et al. [82] | 300 | 300 | - | 39 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 2411 |
| 256 | Xue et al. [82] | 300 | 300 | - | 39 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 1900 |
| 257 | Xue et al. [82] | 300 | 300 | - | 39 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 647 |
| 258 | Xue et al. [82] | 300 | 300 | - | 39 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 806 |
| 259 | Xue et al. [82] | 300 | 300 | - | 39 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 1702 |
| 260 | Xue et al. [82] | 300 | 300 | - | 40.3 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 1678 |
| 261 | Xue et al. [82] | 300 | 300 | - | 40.3 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 1632 |
| 262 | Xue et al. [82] | 300 | 300 | - | 40.3 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 1500 |
| 263 | Xue et al. [82] | 300 | 300 | - | 40.3 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 1300 |
| 264 | Xue et al. [82] | 300 | 300 | - | 40.3 | 654 | 39 | 2.1 | 4 No. 5 | 0.9 | SH | 0.37 | 1564 |
| 265 | Xue et al. [82] | 300 | 300 | - | 40.3 | 729 | 44 | 2.1 | 8 No. 6 | 2.6 | SH | 0.37 | 1823 |
| 266 | Xue et al. [82] | 300 | 300 | - | 29.1 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 1025 |
| 267 | Xue et al. [82] | 300 | 300 | - | 55.2 | 654 | 39 | 2.1 | 6 No. 5 | 1.3 | SH | 0.37 | 2191 |
| 268 | Youssef and Hadi [83] | 210 | 210 | - | 29.3 | 405.9 | 23.4 | 1.8 | 4 No. 4 | 1.15 | GH | 2.24 | 1285 |
| 269 | Youssef and Hadi [83] | 210 | 210 | - | 29.3 | 405.9 | 23.4 | 1.8 | 4 No. 4 | 1.15 | GH | 2.24 | 803 |
| 270 | Youssef and Hadi [83] | 210 | 210 | - | 29.3 | 405.9 | 23.4 | 1.8 | 4 No. 4 | 1.15 | GH | 2.24 | 615 |
| 271 | Zhang and Deng [84] | 350 | 350 | - | 42.5 | 840 | 45 | 1.87 | 8 No. 5 | 1.39 | GH | 1.8 | 5670 |
| 272 | Zhang and Deng [84] | 350 | 350 | - | 42.5 | 840 | 45 | 1.87 | 8 No. 5 | 1.39 | GH | 1.8 | 4585 |
| 273 | Zhang and Deng [84] | 350 | 350 | - | 42.5 | 840 | 45 | 1.87 | 8 No. 5 | 1.39 | GH | 1.8 | 5361 |
| 274 | Zhang and Deng [84] | 350 | 350 | - | 42.5 | 840 | 45 | 1.87 | 8 No. 5 | 1.39 | GH | 2.7 | 5205 |
| 275 | Zhang and Deng [84] | 350 | 350 | - | 42.5 | 840 | 45 | 1.87 | 8 No. 5 | 1.39 | GH | 2.7 | 5357 |
| 276 | Zhang and Deng [84] | 350 | 350 | - | 42.5 | 840 | 45 | 1.87 | 8 No. 5 | 1.39 | GH | 2.7 | 4852 |
| 277 | Zhang and Deng [84] | 350 | 350 | - | 42.5 | 840 | 45 | 1.87 | 12 No. 5 | 2.09 | GH | 2.49 | 4500 |
| 278 | Zhang and Deng [84] | 350 | 350 | - | 42.5 | 840 | 45 | 1.87 | 12 No. 5 | 2.64 | GH | 2.49 | 4972 |
Author Contributions
Conceptualization, A.R., S.A.R.S., H.A., M.A. and S.R.; methodology, A.R., S.A.R.S.; software, A.R., S.A.R.S., H.A.; validation, M.A. and S.R.; formal analysis, A.R., M.A. and S.R.; investigation, A.R., S.A.R.S. and S.R.; resources, A.R., S.A.R.S. and S.R.; data curation, S.A.R.S., H.A., M.A. and S.R.; writing—original draft preparation, A.R., S.A.R.S.; writing—review and editing, H.A., M.A. and S.R.; visualization, H.A., M.A. and S.R.; supervision, S.A.R.S., H.A., M.A. and S.R.; project administration, S.A.R.S. and H.A.; funding acquisition, H.A., M.A. and S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received no external funding.
Data Availability Statement
Some or all data will be available upon request from the corresponding author.
Conflicts of Interest
The authors declare that there is no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.ElMesalami N., Abed F., El Refai A. Concrete Columns Reinforced with GFRP and BFRP Bars under Concentric and Eccentric Loads: Experimental Testing and Analytical Investigation. J. Compos. Constr. 2021;25:04021003. doi: 10.1061/(ASCE)CC.1943-5614.0001115. [DOI] [Google Scholar]
- 2.Aslam H.M.U., Khan Q.U.Z., Sami A., Raza A. Axial compressive behavior of damaged steel and GFRP bars reinforced concrete columns retrofitted with CFRP laminates. Compos. Struct. 2021;258:113206. doi: 10.1016/j.compstruct.2020.113206. [DOI] [Google Scholar]
- 3.Raza A., Rafique U., Haq F.U. Mechanical and durability behavior of recycled aggregate concrete made with different kinds of wastewater. J. Build. Eng. 2021;34:101950. doi: 10.1016/j.jobe.2020.101950. [DOI] [Google Scholar]
- 4.AlNajmi L., Abed F. Evaluation of FRP Bars under Compression and Their Performance in RC Columns. Materials. 2020;13:4541. doi: 10.3390/ma13204541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Raza A., Khan Q., Ahmad A. Numerical investigation of load-carrying capacity of GFRP-reinforced rec-tangular concrete members using CDP model in ABAQUS. Adv. Civ. Eng. 2019;2019:1745341. [Google Scholar]
- 6.ElMessalami N., Abed F., El Refai A. Response of concrete columns reinforced with longitudinal and transverse BFRP bars under concentric and eccentric loading. Compos. Struct. 2021;255:113057. doi: 10.1016/j.compstruct.2020.113057. [DOI] [Google Scholar]
- 7.Abed F., Mehaini Z., Oucif C., Abdul–Latif A., Baleh R. Quasi-static and dynamic response of GFRP and BFRP bars under compression. Compos. Part C Open Access. 2020;2:100034. doi: 10.1016/j.jcomc.2020.100034. [DOI] [Google Scholar]
- 8.ACI-440 . Guide for the Design and Construction of Structural Concrete Reinforced with Fiber Reinforced Poly-Mer (FRP) Bars. American Concrete Institute; Indianapolis, IN, USA: 2015. ACI 440.1 R-15. [Google Scholar]
- 9.ElMessalami N., El Refai A., Abed F. Fiber-reinforced polymers bars for compression reinforcement: A promising alternative to steel bars. Constr. Build. Mater. 2019;209:725–737. doi: 10.1016/j.conbuildmat.2019.03.105. [DOI] [Google Scholar]
- 10.ACI . Guide for the Design and Construction of Structural Concrete Reinforced with FRP Bars. American Concrete Institute; Indianapolis, IN, USA: 2006. [Google Scholar]
- 11.CSA . Design and Construction of Building Structures with Fibre-Reinforced Polymer. CAN/CSA; Toronto, ON, Canada: 2012. CAN/CSA S806-12. [Google Scholar]
- 12.Canadian Standards Association . Canadian Highway Bridge Design Code—(Section 16) CSA; Toronto, ON, Canada: 2006. CAN/CSA-S6-06. [Google Scholar]
- 13.Mohamed H.M., Benmokrane B. Reinforced Concrete Beams with and without FRP Web Reinforcement under Pure Torsion. J. Bridg. Eng. 2016;21:04015070. doi: 10.1061/(ASCE)BE.1943-5592.0000839. [DOI] [Google Scholar]
- 14.Mohamed H.M., Chaallal O., Benmokrane B. Torsional Moment Capacity and Failure Mode Mechanisms of Concrete Beams Reinforced with Carbon FRP Bars and Stirrups. J. Compos. Constr. 2015;19:04014049. doi: 10.1061/(ASCE)CC.1943-5614.0000515. [DOI] [Google Scholar]
- 15.Dong M., Elchalakani M., Karrech A., Pham T.M., Yang B. Glass fibre-reinforced polymer circular alkali-activated fly ash/slag concrete members under combined loading. Eng. Struct. 2019;199:109598. doi: 10.1016/j.engstruct.2019.109598. [DOI] [Google Scholar]
- 16.Elchalakani M., Dong M., Karrech A., Li G., Ali M.S.M., Yang B. Experimental Investigation of Rectangular Air-Cured Geopolymer Concrete Columns Reinforced with GFRP Bars and Stirrups. J. Compos. Constr. 2019;23:04019011. doi: 10.1061/(ASCE)CC.1943-5614.0000938. [DOI] [Google Scholar]
- 17.Elshamandy M.G., Farghaly A.S., Benmokrane B. Experimental behavior of glass fiber-reinforced poly-mer-reinforced concrete columns under lateral cyclic load. ACI Struct. J. 2018;115:337–349. doi: 10.14359/51700985. [DOI] [Google Scholar]
- 18.Raza A., Ali B., Masood B., Rehman A.U. Axial performance of GFRP composite bars and spirals in circular hollow concrete columns. Structures. 2021;29:600–613. doi: 10.1016/j.istruc.2020.11.043. [DOI] [Google Scholar]
- 19.Raza A., Rafique U. Efficiency of GFRP bars and hoops in recycled aggregate concrete columns: Experi-mental and numerical study. Compos. Struct. 2020;255:112986. doi: 10.1016/j.compstruct.2020.112986. [DOI] [Google Scholar]
- 20.Raza A., Khan Q., Ahmad A. Investigation of HFRC columns reinforced with GFRP bars and spirals un-der concentric and eccentric loadings. Eng. Struct. 2021;227:111461. doi: 10.1016/j.engstruct.2020.111461. [DOI] [Google Scholar]
- 21.Raza A., Ali B., Nawaz M.A., Ahmed I. Structural performance of FRP-RC compression members wrapped with FRP composites. Structures. 2020;27:1693–1709. doi: 10.1016/j.istruc.2020.07.071. [DOI] [Google Scholar]
- 22.Tobbi H., Farghaly A.S., Benmokrane B. Concrete Columns Reinforced Longitudinally and Transversally with Glass Fiber-Reinforced Polymer Bars. ACI Struct. J. 2012;109 doi: 10.14359/51683874. [DOI] [Google Scholar]
- 23.Afifi M.Z., Mohamed H.M., Benmokrane B. Axial Capacity of Circular Concrete Columns Reinforced with GFRP Bars and Spirals. J. Compos. Constr. 2014;18:04013017. doi: 10.1061/(ASCE)CC.1943-5614.0000438. [DOI] [Google Scholar]
- 24.Zadeh H.J., Nanni A. Design of RC Columns Using Glass FRP Reinforcement. J. Compos. Constr. 2013;17:294–304. doi: 10.1061/(ASCE)CC.1943-5614.0000354. [DOI] [Google Scholar]
- 25.Xue W., Hu X., Fang Z. 7th International Conference on Fiber Reinforced Polymer (FRP) Composites in Civil Engineering (CICE 2014) International Institute for FRP in Construction (IIFC); Kingston, ON, Canada: 2014. Experimental studies of GFRP reinforced concrete columns under static eccentric loading. [Google Scholar]
- 26.Elchalakani M., Ma G. Tests of glass fibre reinforced polymer rectangular concrete columns subjected to concentric and eccentric axial loading. Eng. Struct. 2017;151:93–104. doi: 10.1016/j.engstruct.2017.08.023. [DOI] [Google Scholar]
- 27.Khorramian K., Sadeghian P. Experimental and analytical behavior of short concrete columns reinforced with GFRP bars under eccentric loading. Eng. Struct. 2017;151:761–773. doi: 10.1016/j.engstruct.2017.08.064. [DOI] [Google Scholar]
- 28.Tabatabaei A., Eslami A., Mohamed H.M., Benmokrane B. Strength of compression lap-spliced GFRP bars in concrete columns with different splice lengths. Constr. Build. Mater. 2018;182:657–669. doi: 10.1016/j.conbuildmat.2018.06.154. [DOI] [Google Scholar]
- 29.Elchalakani M., Ma G., Aslani F., Duan W. Design of GFRP-reinforced rectangular concrete columns under eccentric axial loading. Mag. Concr. Res. 2017;69:865–877. doi: 10.1680/jmacr.16.00437. [DOI] [Google Scholar]
- 30.Raza A., ur Rehman A., Masood B., Hussain I. Finite element modelling and theoretical predictions of FRP-reinforced concrete columns con-fined with various FRP-tubes. Structures. 2020;26:626–638. doi: 10.1016/j.istruc.2020.04.033. [DOI] [Google Scholar]
- 31.Raza A., Khan Q.U.Z. Experimental and theoretical study of GFRP hoops and spirals in hybrid fiber reinforced concrete short columns. Mater. Struct. 2020;53:1–14. doi: 10.1617/s11527-020-01575-9. [DOI] [Google Scholar]
- 32.Mohamed H.M., Afifi M.Z., Benmokrane B. Performance Evaluation of Concrete Columns Reinforced Longitudinally with FRP Bars and Confined with FRP Hoops and Spirals under Axial Load. J. Bridg. Eng. 2014;19:04014020. doi: 10.1061/(ASCE)BE.1943-5592.0000590. [DOI] [Google Scholar]
- 33.Afifi M.Z., Mohamed H.M., Benmokrane B. Theoretical stress–strain model for circular concrete columns confined by GFRP spirals and hoops. Eng. Struct. 2015;102:202–213. doi: 10.1016/j.engstruct.2015.08.020. [DOI] [Google Scholar]
- 34.Hadi M.N.S., Karim H., Sheikh M.N. Experimental Investigations on Circular Concrete Columns Reinforced with GFRP Bars and Helices under Different Loading Conditions. J. Compos. Constr. 2016;20:04016009. doi: 10.1061/(ASCE)CC.1943-5614.0000670. [DOI] [Google Scholar]
- 35.Karim H., Sheikh M.N., Hadi M.N. Axial load-axial deformation behaviour of circular concrete columns reinforced with GFRP bars and helices. Constr. Build. Mater. 2016;112:1147–1157. doi: 10.1016/j.conbuildmat.2016.02.219. [DOI] [Google Scholar]
- 36.Abed F., Oucif C., Awera Y., Mhanna H.H., Alkhraisha H. FE modeling of concrete beams and columns reinforced with FRP composites. Def. Technol. 2021;17:1–14. doi: 10.1016/j.dt.2020.02.015. [DOI] [Google Scholar]
- 37.Elchalakani M., Karrech A., Dong M., Ali M.M., Yang B. Experiments and Finite Element Analysis of GFRP Reinforced Geopolymer Concrete Rectangular Columns Subjected to Concentric and Eccentric Axial Loading. Structures. 2018;14:273–289. doi: 10.1016/j.istruc.2018.04.001. [DOI] [Google Scholar]
- 38.Ibrahim A.M., Fahmy M.F., Wu Z. 3D finite element modeling of bond-controlled behavior of steel and basalt FRP-reinforced concrete square bridge columns under lateral loading. Compos. Struct. 2016;143:33–52. doi: 10.1016/j.compstruct.2016.01.014. [DOI] [Google Scholar]
- 39.Awera Y., Abed F. Axial Capacity of Circular Concrete Columns Reinforced with GFRP Bars and Spirals using FEA; Proceedings of the 2020 Advances in Science and Engineering Technology International Conferences (ASET); Dubai, United Arab Emirates. 4 February–9 April 2020; Piscataway, NJ, USA: Institute of Electrical and Electronics Engineers (IEEE); 2020. pp. 1–6. [Google Scholar]
- 40.Piscesa B., Attard M.M., Samani A.K. 3D Finite element modeling of circular reinforced concrete columns confined with FRP using a plasticity based formulation. Compos. Struct. 2018;194:478–493. doi: 10.1016/j.compstruct.2018.04.039. [DOI] [Google Scholar]
- 41.Hany N.F., Hantouche E.G., Harajli M.H. Finite element modeling of FRP-confined concrete using modified concrete damaged plasticity. Eng. Struct. 2016;125:1–14. doi: 10.1016/j.engstruct.2016.06.047. [DOI] [Google Scholar]
- 42.Shi Y., Swait T., Soutis C. Modelling damage evolution in composite laminates subjected to low velocity impact. Compos. Struct. 2012;94:2902–2913. doi: 10.1016/j.compstruct.2012.03.039. [DOI] [Google Scholar]
- 43.Matthews F.L., Davies G.A.O., Hitchings D., Soutis C. Finite Element Modelling of Composite Materials and Structures. Elsevier; Amsterdam, The Netherlands: 2000. [Google Scholar]
- 44.ACI . Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary. American Concrete Institute; Farmington Hills, MI, USA: 2008. p. 473. [Google Scholar]
- 45.Canadian Standards Association . Design and Construction of Building Components with Fibre-Reinforced Polymers. Canadian Standards Association; Mississauga, ON, Canada: 2002. p. 177. S806-02. [Google Scholar]
- 46.Samani A.K., Attard M.M. A stress–strain model for uniaxial and confined concrete under compression. Eng. Struct. 2012;41:335–349. doi: 10.1016/j.engstruct.2012.03.027. [DOI] [Google Scholar]
- 47.Khan Q.S., Sheikh M.N., Hadi M.N.S. Axial-Flexural Interactions of GFRP-CFFT Columns with and without Reinforcing GFRP Bars. J. Compos. Constr. 2017;21:04016109. doi: 10.1061/(ASCE)CC.1943-5614.0000771. [DOI] [Google Scholar]
- 48.Tobbi H., Farghaly A.S., Benmokrane B. Behavior of Concentrically Loaded Fiber-Reinforced Polymer Reinforced Concrete Columns with Varying Reinforcement Types and Ratios. ACI Struct. J. 2014;111 doi: 10.14359/51686630. [DOI] [Google Scholar]
- 49.Pantelides C.P., Gibbons M.E., Reaveley L.D. Axial Load Behavior of Concrete Columns Confined with GFRP Spirals. J. Compos. Constr. 2013;17:305–313. doi: 10.1061/(ASCE)CC.1943-5614.0000357. [DOI] [Google Scholar]
- 50.ACI . Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute; Farmington Hills, MI, USA: 2011. ACI 318-11. [Google Scholar]
- 51.Standards Australia . Australian Standard 3600: Concrete Structures. Standards Australia; Sydney, Australia: 2018. [Google Scholar]
- 52.Hadhood A., Mohamed H.M., Benmokrane B. Axial load–moment interaction diagram of circular con-crete columns reinforced with CFRP bars and spirals: Experimental and theoretical investigations. J. Compos. Constr. 2017;21:04016092. doi: 10.1061/(ASCE)CC.1943-5614.0000748. [DOI] [Google Scholar]
- 53.Xiao B., Huang Q., Chen H., Chen X., Long G. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals. 2021;29:2150017. doi: 10.1142/S0218348X21500171. [DOI] [Google Scholar]
- 54.Youssf O., El Gawady M.A., Mills J.E., Ma X. Finite element modelling and dilation of FRP-confined concrete columns. Eng. Struct. 2014;79:70–85. doi: 10.1016/j.engstruct.2014.07.045. [DOI] [Google Scholar]
- 55.Alfarah B., López-Almansa F., Oller S. New methodology for calculating damage variables evolution in Plastic Damage Model for RC structures. Eng. Struct. 2017;132:70–86. doi: 10.1016/j.engstruct.2016.11.022. [DOI] [Google Scholar]
- 56.British Standards Institution . Eurocode 2: Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings. British Standards Institution; Telford, UK: 2004. [Google Scholar]
- 57.Kmiecik P., Kamiński M. Modelling of reinforced concrete structures and composite structures with con-crete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011;11:623–636. doi: 10.1016/S1644-9665(12)60105-8. [DOI] [Google Scholar]
- 58.Majewski S. The Mechanics of Structural Concrete in Terms of Elasto-Plasticity. Publishing House of Silesian University of Technology; Gliwice, Poland: 2003. [Google Scholar]
- 59.Wahalathantri B., Thambiratnam D., Chan T., Fawzia S. A material model for flexural crack simulation in reinforced concrete elements using ABAQUS; Proceedings of the First International Conference on Engineering, Designing and Developing the Built Environment for Sustainable Wellbeing; Brisbane, Australia. 27–29 April 2011; pp. 260–264. [Google Scholar]
- 60.Genikomsou A.S., Polak M.A. Finite element analysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS. Eng. Struct. 2015;98:38–48. doi: 10.1016/j.engstruct.2015.04.016. [DOI] [Google Scholar]
- 61.Voyiadjis Z.G., Taqieddin Z.N. Elastic plastic and damage model for concrete materials: Part I-theoretical formulation. Int. J. Struct. Chang. Solids. 2009;1:31–59. [Google Scholar]
- 62.Ali L., Nawaz A., Bai Y., Raza A., Anwar M.K., Shah S.A.R., Raza S.S. Numerical Simulations of GFRP-Reinforced Columns Having Polypropylene and Polyvinyl Alcohol Fibers. Complexity. 2020;2020:1–14. doi: 10.1155/2020/8841795. [DOI] [Google Scholar]
- 63.Raza A., Ali B., Aslam H.M.U. Axial performance of hybrid fiber reinforced concrete columns having GFRP longitudinal bars and spirals. J. Build. Eng. 2020;35:102017. doi: 10.1016/j.jobe.2020.102017. [DOI] [Google Scholar]
- 64.Raza A., Ali B., Haq F.U. Compressive Strength of FRP-Reinforced and Confined Concrete Columns. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021:1–14. doi: 10.1007/s40996-020-00570-y. [DOI] [Google Scholar]
- 65.Raza A., Ali B., Rehman A.U. Structural Performance of Steel-Tube Concrete Columns Confined with CFRPs: Numerical and Theoretical Study. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020:1–18. doi: 10.1007/s40996-020-00492-9. [DOI] [Google Scholar]
- 66.Wu J.Y., Li J., Faria R. An energy release rate-based plastic-damage model for concrete. Int. J. Solids Struct. 2006;43:583–612. doi: 10.1016/j.ijsolstr.2005.05.038. [DOI] [Google Scholar]
- 67.Alajarmeh O., Manalo A., Benmokrane B., Karunasena W., Mendis P., Nguyen K. Compressive behavior of axially loaded circular hollow concrete columns reinforced with GFRP bars and spirals. Constr. Build. Mater. 2019;194:12–23. doi: 10.1016/j.conbuildmat.2018.11.016. [DOI] [Google Scholar]
- 68.Alajarmeh O.S., Manalo A.C., Benmokrane B., Karunasena W., Mendis P. Axial performance of hollow concrete columns reinforced with GFRP composite bars with different reinforcement ratios. Compos. Struct. 2019;213:153–164. doi: 10.1016/j.compstruct.2019.01.096. [DOI] [Google Scholar]
- 69.Alsayed S.H., Al-Salloum Y.A., Almusallam T.H., Amjad M.A. Concrete columns reinforced by glass fiber reinforced polymer rods. Spec. Publ. 1999;188:103–112. [Google Scholar]
- 70.Luca D.A., Matta F., Nanni A. Behavior of full-scale GFRP reinforced concrete columns under axial load. ACI Struct. J. 2010;107:589–596. [Google Scholar]
- 71.Guérin M., Mohamed H.M., Benmokrane B., Nanni A., Shield C.K. Eccentric Behavior of Full-Scale Reinforced Concrete Columns with Glass Fiber-Reinforced Polymer Bars and Ties. ACI Struct. J. 2018;115 doi: 10.14359/51701107. [DOI] [Google Scholar]
- 72.Guérin M., Mohamed H.M., Benmokrane B., Shield C.K., Nanni A. Effect of glass fiber-reinforced polymer reinforcement ratio on axial-flexural strength of re-inforced concrete columns. ACI Struct. J. 2018;115:1049-3. doi: 10.14359/51701279. [DOI] [Google Scholar]
- 73.Hadhood A., Mohamed H.M., Benmokrane B. Assessing Stress-Block Parameters in Designing Circular High-Strength Concrete Members Reinforced with FRP Bars. J. Struct. Eng. 2018;144:04018182. doi: 10.1061/(ASCE)ST.1943-541X.0002173. [DOI] [Google Scholar]
- 74.Hadi M.N.S., Youssef J. Experimental Investigation of GFRP-Reinforced and GFRP-Encased Square Concrete Specimens under Axial and Eccentric Load, and Four-Point Bending Test. J. Compos. Constr. 2016;20:04016020. doi: 10.1061/(ASCE)CC.1943-5614.0000675. [DOI] [Google Scholar]
- 75.Hassan A., Khairallah F., Mamdouh H., Kamal M. Structural behaviour of self-compacting concrete columns reinforced by steel and glass fi-bre-reinforced polymer rebars under eccentric loads. Eng. Struct. 2019;188:717–728. doi: 10.1016/j.engstruct.2019.03.067. [DOI] [Google Scholar]
- 76.Maranan G.B., Manalo A.C., Benmokrane B., Karunasena W., Mendis P. Behavior of concentrically loaded geopolymer-concrete circular columns reinforced longi-tudinally and transversely with GFRP bars. Eng. Struct. 2016;117:422–436. doi: 10.1016/j.engstruct.2016.03.036. [DOI] [Google Scholar]
- 77.Prachasaree W., Piriyakootorn S., Sangsrijun A., Limkatanyu S. Behavior and Performance of GFRP Reinforced Concrete Columns with Various Types of Stirrups. Int. J. Polym. Sci. 2015;2015:1–9. doi: 10.1155/2015/237231. [DOI] [Google Scholar]
- 78.Sankholkar P.P., Pantelides C.P., Hales T.A. Confinement Model for Concrete Columns Reinforced with GFRP Spirals. J. Compos. Constr. 2018;22:04018007. doi: 10.1061/(ASCE)CC.1943-5614.0000843. [DOI] [Google Scholar]
- 79.Sun L., Wei M., Zhang N. Experimental study on the behavior of GFRP reinforced concrete columns un-der eccentric axial load. Constr. Build. Mater. 2017;152:214–225. doi: 10.1016/j.conbuildmat.2017.06.159. [DOI] [Google Scholar]
- 80.Tikka T., Francis M., Teng B. Strength of concrete beam-columns reinforced with GFRP bars; Proceedings of the 2nd In-ternational Structures Specialty Conference; Winnipeg, MB, Manitoba. 9–12 June 2010. [Google Scholar]
- 81.Tu J., Gao K., He L., Li X. Experimental study on the axial compression performance of GFRP-reinforced concrete square columns. Adv. Struct. Eng. 2018;22:1554–1565. doi: 10.1177/1369433218817988. [DOI] [Google Scholar]
- 82.Xue W., Peng F., Fang Z. Behavior and design of slender rectangular concrete columns longitudinally reinforced with fiber-reinforced polymer bars. ACI Struct. J. 2018;115:311–322. doi: 10.14359/51701131. [DOI] [Google Scholar]
- 83.Youssef J., Hadi M.N. Axial load-bending moment diagrams of GFRP reinforced columns and GFRP encased square columns. Constr. Build. Mater. 2017;135:550–564. doi: 10.1016/j.conbuildmat.2016.12.125. [DOI] [Google Scholar]
- 84.Zhang X., Deng Z. Experimental study and theoretical analysis on axial compressive behavior of concrete columns reinforced with GFRP bars and PVA fibers. Constr. Build. Mater. 2018;172:519–532. doi: 10.1016/j.conbuildmat.2018.03.237. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Some or all data will be available upon request from the corresponding author.