Trend Analysis and Forecasting the Spread of COVID-19 Pandemic in Ethiopia Using Box–Jenkins Modeling Procedure

Abstract

Introduction

COVID-19, which causes severe acute respiratory syndrome, is spreading rapidly across the world, and the severity of this pandemic is rising in Ethiopia. The main objective of the study was to analyze the trend and forecast the spread of COVID-19 and to develop an appropriate statistical forecast model.

Methodology

Data on the daily spread between 13 March, 2020 and 31 August 2020 were collected for the development of the autoregressive integrated moving average (ARIMA) model. Stationarity testing, parameter testing and model diagnosis were performed. In addition, candidate models were obtained using autocorrelation function (ACF) and partial autocorrelation functions (PACF). Finally, the fitting, selection and prediction accuracy of the ARIMA models was evaluated using the RMSE and MAPE model selection criteria.

Results

A total of 51,910 confirmed COVID-19 cases were reported from 13 March to 31 August 2020. The total recovered and death rates as of 31 August 2020 were 37.2% and 1.57%, respectively, with a high level of increase after the mid of August, 2020. In this study, ARIMA (0, 1, 5) and ARIMA (2, 1, 3) were finally confirmed as the optimal model for confirmed and recovered COVID-19 cases, respectively, based on lowest RMSE, MAPE and BIC values. The ARIMA model was also used to identify the COVID-19 trend and showed an increasing pattern on a daily basis in the number of confirmed and recovered cases. In addition, the 60-day forecast showed a steep upward trend in confirmed cases and recovered cases of COVID-19 in Ethiopia.

Conclusion

Forecasts show that confirmed and recovered COVID-19 cases in Ethiopia will increase on a daily basis for the next 60 days. The findings can be used as a decision-making tool to implement health interventions and reduce the spread of COVID-19 infection.

Introduction

Corona Virus Disease 2019 (COVID-19) was reported in Hubei, China on 31 December 2019 and the WHO declared a global pandemic disease after one month. The infection was spreading at an alarming rate both domestically and internationally.¹ According to the WHO, more than 25 million confirmed cases of COVID-19 and 800,000 deaths have been reported globally as of 31 August 2020.² On March 13, 2020, the Ethiopian Federal Ministry of Health has confirmed a coronavirus disease (COVID-19) case in Addis Ababa, Ethiopia. Consequently, the government of Ethiopia suspended schools and public gatherings. The total confirmed cases increased to 51,910 and the reported death rate of 815 as of 31 August 2020.³

People infected with COVID-19 may have little or no symptoms and the symptoms ranged from mild symptoms to severe illnesses, and the incubation period of COVID-19 may last 2 weeks or longer. The disease may still be infectious during the latent period of infection and the virus can spread through respiratory droplets and close contact from person to person.⁴

In the fight against the pandemic, it is crucial to be able to identify the rate at which the epidemic spreads. Awareness at the level of spread at any given time has the ability to help governments plan and develop public health policies to deal with the consequences of the pandemic. The way to be aware of the magnitude of the spread, and thus the timing of its peak, is to be able to accurately predict the number of active cases at any given time.⁵

Epidemic mathematical models are best possible technique in analyzing the control and spread of infectious diseases. Time-series analysis is a tool to extrapolate forecasts, in which the mathematical model is established based on to the regularity and trend of the historical values observed over time and has been commonly used in predicting the spread of COVID-19. Modeling the disease and providing future forecasts of the possible number of cases per day may help the health care system to prepare for new patients. The statistical prediction models are therefore useful both in predicting and monitoring the global threat of pandemic. Therefore, it is extremely important to create models that are both computationally competent and practical in order to help policy makers and medical staff.^6,7

Auto Regressive Integrated Moving Average (ARIMA) models are the most commonly used methods.^8,9 The ARIMA model has been successfully applied in the field of medical research due to its simple structure, fast implementation and ability to explain the data set.¹⁰ The use of ARIMA to forecast time series is important with uncertainty as it assumes no knowledge of any underlying model or relationship as in some other methods. Generally, ARIMA depends on past series values as well as earlier forecast error terms. However, in relation to short-run forecasting, the ARIMA models are comparatively more robust and efficient than more complex structural models.^11,12

The ARIMA methodology is a statistical approach used to evaluate and create a forecasting model that best represents a time series by modeling the correlations in the data. Many of the advantages of the ARIMA model have been found in empirical research and support the ARIMA as an effective way in particularly short-term time series prediction. A major advantage of the ARIMA approach is that it makes no assumptions about the number of terms or the relative weights to be applied to the terms.^13,14

The advantage of the ARIMA model is its versatility to reflect with simplicity, numerous time series varieties, as well as the related Box–Jenkins methodology for optimum model construction operation.^8,15 In addition, ARIMA model gives weight to past values and error values to correct model prediction more reliable than other basic regression and exponential methods. Generally, ARIMA models frequently outshine more complex structural models in terms of short-term predictive capabilities.¹⁶

A number of studies were conducted to evaluate the global forecasts for COVID-19. A study in Iran showed that the ARIMA model predicts that Iran can easily show an increase in daily COVID-19 total confirmed cases and total deaths, while the daily total confirmed new cases, total new deaths. The study predicts that Iran will be able to control COVID-19 in the near future.¹⁷

A study conducted in Nigeria to develop an appropriate predictive model could be used as a decision-making tool for the health interventions and to minimize the spread of Covid-19 infection. Data on the daily spread were collected for the development of the autoregressive integrated moving average (ARIMA) model and the result showed a sharp increased trend of COVID-19 spread in Nigeria within the specified the time frame.¹⁸

A study conducted in Italy used the ARIMA model to forecast reported and recovered case of the COVID-19 outbreak. The projections for confirmed cases may exceed 182,757, and the recovered cases could be reported 81,635 at the end of May. The final findings suggest that there will be a decrease of about 35% in confirmed cases and an increase of 66% in recovered cases.¹⁹

To our knowledge, there is no study conducted on the trend analysis and forecasting of COVID-19 in Ethiopia. Thus, the main objective of the study was therefore to analyze trends in the spread of COVID-19 using ARIMA models and to find the best predictive model and apply it to the possible predictive occurrence of COVID-19 cases in Ethiopia. Therefore, this study will help policy makers and the public to adopt new strategies and strengthen existing preventive measures against the COVID-19 pandemic and can help predict the health infrastructure needs in the near future.

The contributions of this paper can be summarized as follows: The first contribution is to find the best empirical model that has been established for the prediction of newly reported and recovered cases of COVID-19, the precision of which helps governors in decision-making to handle the pandemic and health system strategies; Second contribution, we can highlight the trend of reported and recovered cases of COVID-19 in Ethiopia. In addition, this paper explores a sample forecasting approach 60 days ahead. This forecast result enables us to check the efficacy of the forecasting models in various situations, helping in the battle against COVID-19 in Ethiopia in future strategy.

The rest of the article is organized as follows:

Dataset Description includes a description of the dataset used for this study. The forecasting models used in this study are described in Auto-Regressive Integrated Moving Average (ARIMA) Models to Parameter Estimation and Model Validation for details of the procedures used in the research methodology. Results obtained, related discussions and conclusions on the performance forecasting models are given in Result, Discussion and Conclusion.

Materials and Methods

Dataset Description

Regular updates of officially confirmed cases of COVID-19 were collected from the official website of the Ethiopian Public Health Institute (EPHI). A total 172 observations of laboratory-confirmed, recovered and fatal cases of COVID-19 were included in the study from 13 March to 31 August 2020.³

Model Description

Auto-Regressive Integrated Moving Average (ARIMA) Models

The ARIMA model forecasting approach differs from other approaches because it does not consider specific trend in the historical data of the sequence to be predicted. It uses an interactive approach to identify a possible model from a general model class. The chosen model is then tested against historical data to see if the sequence is correctly represented.

Moving Average (MA) Process

This model uses past errors as a dependent variable.²⁰ Let 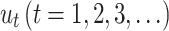be a white noise process, a sequence of random variables independently and identically distributed (ii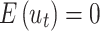d) and 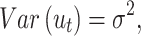then the 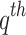order MA model is given as:

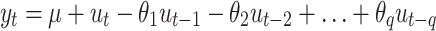(1)

This model is described in terms of past errors and thus, we estimate the coefficients 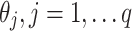. Therefore, only q errors will affect the existing 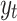level, but higher order errors do not affect 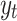. This indicates that it is a short memory model.

Auto-Regression (AR)

According to an autoregressive model of order p, an AR (p) can be expressed as;

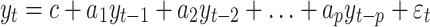(2)

The model is described in terms of past values and therefore we would like to estimate the coefficients 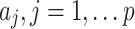, and use the model for forecasting. All previous values will have cumulative effects on the existing 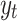level, which is a long-run memory model.²¹

Autoregressive Integrated Moving Average (ARIMA) Process

ARIMA modeling methods were used in this study based on a common method available for modeling and forecasting the time series data. ARIMA is the most common class of time series models which can be made “stationary” by differencing (if necessary), possibly in combination with non-linear transformations such as logging or deflating (if necessary)

ARIMA (p, d, q) is the general non-seasonal ARIMA model: where p is the number of autoregressive terms, d is the number of differences and q is the number of moving average terms. A white noise model is classified as ARIMA (0, 0, 0) since there is no AR part because 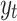does not depend on 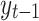, there is no differencing involved and also there is no MA part since 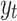does not rely on 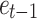. For instance, if 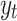is non-stationary, we take a first-difference of 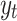so that 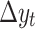becomes stationary. 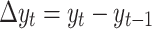(d = 1 implies one-time differencing)

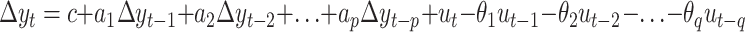(3)

is an ARIMA (p, 1, q) model. A random walk model is classified as ARIMA (0, 1, 0) because there is no AR and MA part involved and only one difference exists.²²

Model Identification

The data required should be stationary for the development of time series models. If non-stationary data are used in a model, the results can show a relationship that is misleading. Therefore, time series data must be checked for stationary before the model is defined.

Generally, a time series is stationary if it is described by constant mean and variance, and an autocovariance that does not depend on time. If any of these requirements are not fulfilled, the data shall be considered nonstationary. The autocorrelation function (ACF) will be used to define this problem, and if the ACF plot is positive and shows a very slow linear decay pattern, the data are non-stationary. The issue of non-stationarity can be resolved by appropriate data differencing if it is caused by mean or model transformation caused by variance. Partial autocorrelation (PACF) is characterized as a linear correlation between Y t and Y (t-k), which controls the possible effects of linear relationships between intermediate lag values. The next is to determine the initial values for seasonality and non-seasonality orders (P and q).²³

Parameter Estimation and Model Validation

After identifying the appropriate ARIMA order (p, d, q), we tried to find precise estimates of the model parameters using the least squares as described by Box and Jenkins. The parameters are obtained by the maximum probability for the time series, which is asymptotically accurate. For Gaussian distributions estimators are generally adequate, efficient and consistent and are asymptotically normal and efficient for non-Gaussian distributions. In this study, STATA v. 15 and SPSS version 25 softwares were used to develop the ARIMA model. The statistical significance level was set at 0.05. Models chosen in the last stage were validated using methods which include Root mean squared error (RMSE), mean absolute percentage error (MAPE) and normalize Bayesian information criteria (BIC).^23,24

Result

Study Data Characteristics

The overall data on the distribution of COVID-19 were collected and analyzed from 13 March 2020 to 31 August 2020. A total of 51,910 COVID-19 cases were observed from March 13, 2020 to 31 August 2020, and the incidence showed a rising trend day by day, with a high rate of increase after mid-August 2020. Total recovered and death rates as of 31 August 2020 were 37.2% and 1.57% of the totals, respectively, for the highest incidence and recovery ratio since the COVID-19 index in Ethiopia. The average total number of confirmed, recovered and reported cases per day from 13 March 2020 to 31 August 2020 was 301.8, 112.2 and 4.74, respectively (Table 1).

Table 1.

Descriptive Statistics of Confirmed, Recovered and Death Cases in Ethiopia

Descriptive Statistics
	N	Minimum	Maximum	Sum	Mean	Std. Deviation	Variance
New cases	172	0	1829	51,910	301.80	457.258	209,085.165
Recover	172	0	701	19,301	112.22	161.740	26,159.714
Dead	172	0	28	815	4.74	7.016	49.224

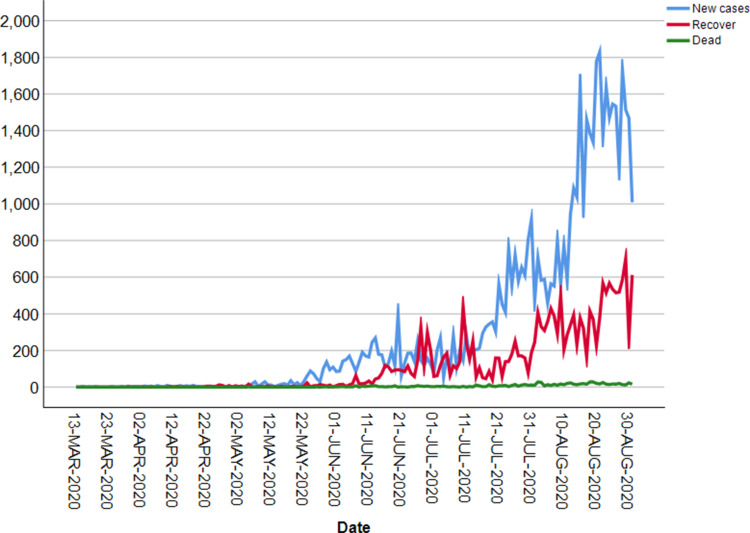
The descriptive analysis of the overall data showed that the new daily COVID-19 confirmed cases and recovered cases significantly increased after the 154th and 143th days, respectively, since the outbreak of the epidemic. It displayed a progressively upward trend, suggesting a possible un-stabilized epidemic and a steady upward trend. From 21 June to 21 July, the number confirmed and recovered cases was almost constant. However, the number of confirmed and recovered cases increased by almost double as of August 2020 compared to July 2020 reports. However, the number of deaths remained stable between 13 March to 30 August, 2020 with minor changes. In Ethiopia, the trend of COVID-19 has been increased progressively in the upward direction for six months starting from the first reported case on 13 March 2020 (Figure 1).

Figure 1.

COVID-19 outbreak trend over time.

Model Identifications

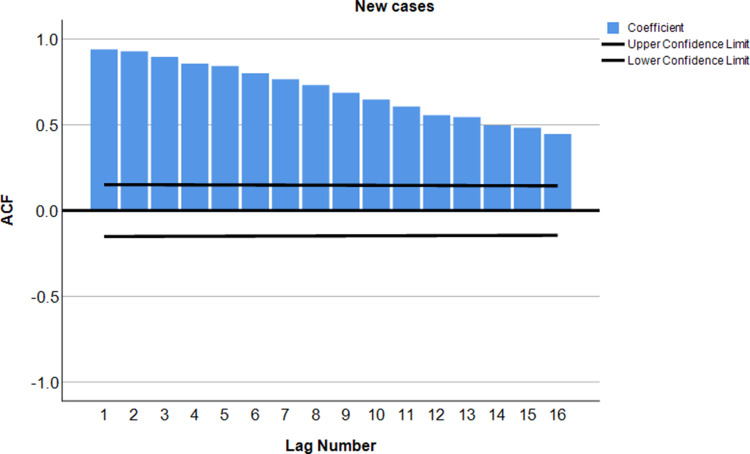
In the identification of the model, the ACF and PACF were applied in COVID-19 confirmed cases to check if the data were stationary. A very slow linear decay pattern can be corrected by first degree order of differentiation.

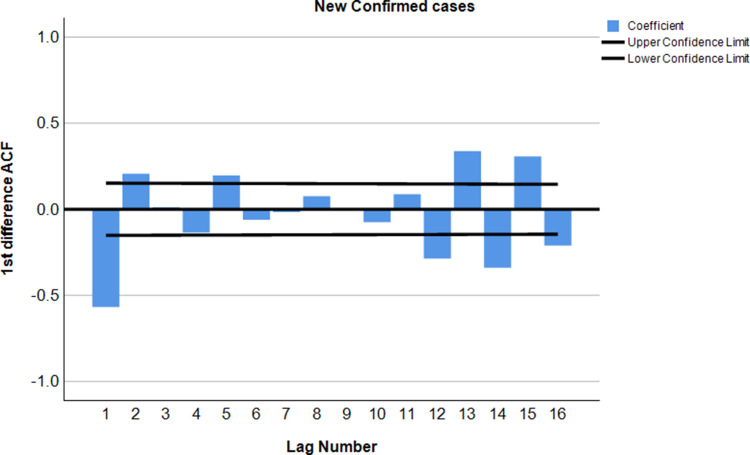
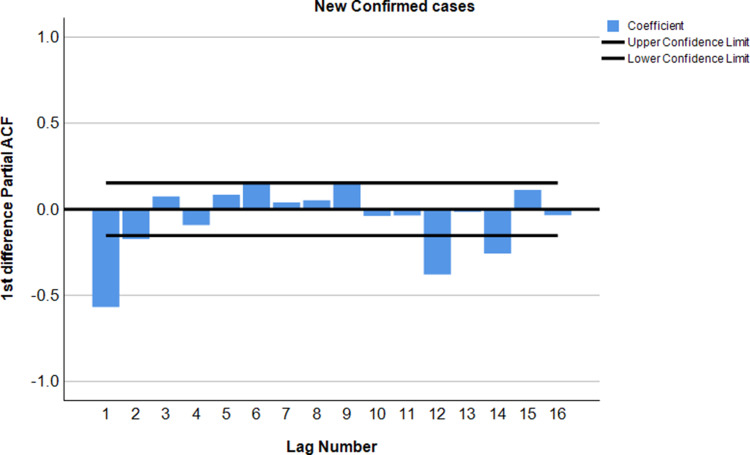
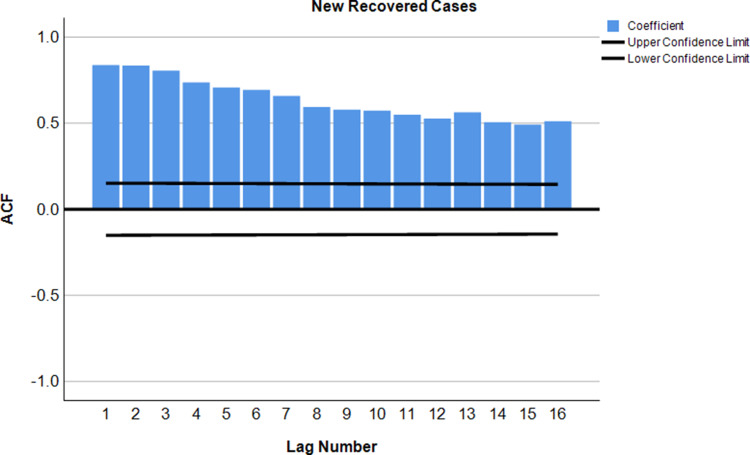
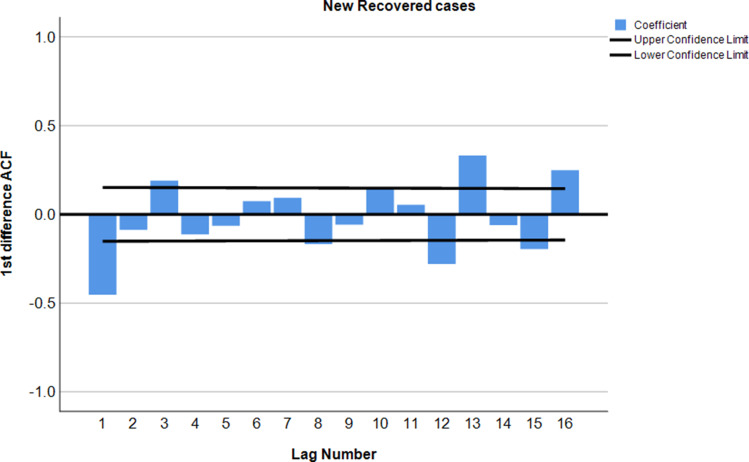
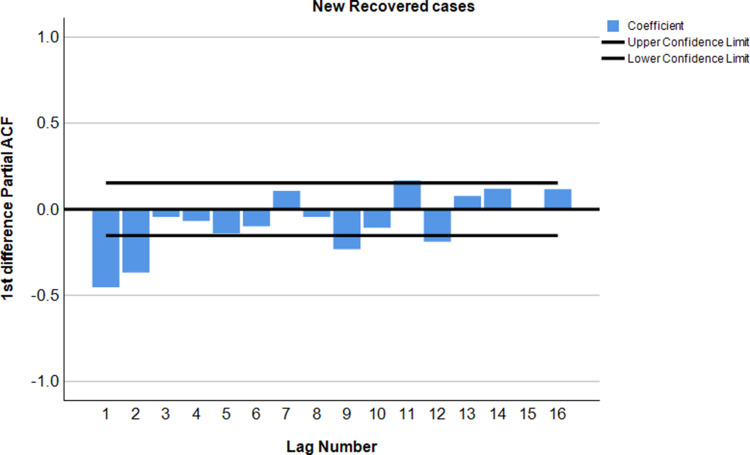
After applying autocorrelation, the moderately large negative spike at the second lag followed by correlations that bounce around between being positive and negative and all of which are either not statistically significant or just barely cross the threshold of statistical significance. The steady decline in the partial correlations towards zero. Finally, the first difference of COVID-19 confirmed cases was best characterized as the following a second- or third-order moving average process. This indicates that the first variation in COVID-19 recovered cases is better described as following the first–order moving average process (Figures 2–7).

Figure 2.

Autocorrelation plot of COVID-19 confirmed cases.

Figure 3.

ACF plot after 1st differencing of the COVID-19 confirmed cases data.

Figure 4.

PACF plot after 1st differencing of the COVID-19 confirmed cases data.

Figure 5.

Autocorrelation plot of COVID-19 recovered cases.

Figure 6.

ACF plot after 1st differencing of the COVID-19 recovered cases.

Figure 7.

PACF plot after 1st differencing of the COVID-19 recovered cases.

Stationarity Test

The stationary test was conducted using the Augmented Dickey–Fuller Test (ADF). In order to apply the ARIMA modeling technique effectively, the series must be stationary and free from any sort of trend. Thus, to confirm the status of the daily confirmed and recovered cases of COVID-19 in Ethiopia, the ADF test was used to validate the stationarity observed from the series transformation (ADF test: 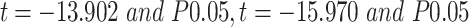for confirmed and recovered cases, respectively, indicating there is no unit root that means the series are stationary at first lag). However, the time series was not found to be stationary, which is the natural form of the data, and then we transformed into stationary by making the first difference (Table 2).

Table 2.

Stationarity Test of the Series with Augmented Dickey–Fuller Test for Confirmed and Recovered Cases

Augmented Dickey–Fuller Test for Confirmed Cases
Difference	Series Title		Dickey–Fuller Value	Lag Order	p-value	Remark
0	Daily COVID-19 confirmed cases		−0.306	1	0.9247	Not-stationary
1	Daily COVID-19 confirmed cases		−13.902	1	0.0000	Stationary
Augmented Dickey–Fuller Test for Recovered Cases
0	Daily COVID-19 Recovered cases	−1.383		1	0.5906	Not-stationary
1	Daily COVID-19 Recovered cases	−15.970		1	0.0000	Stationary

Candidate Model Identification

The order of the model was determined on the basis of ACF and PACF after a common difference. The following candidate models were developed based on the spikes seen in the ACF and PACF graphs. The candidate model with the lowest value of RMSE, MAPE and Normalize BIC was identified as the best model to match the daily spread of the COVID-19 in Ethiopia. The p and q parameters of the ARIMA models were predicted and the projected models were then compared to the RMSE, MAPE and BIC values. This suggests the estimation of ARIMA (0, 1, 5) and ARIMA (2, 1, 3) models for the forecasting of daily spread and the recovery cases of COVID-19 in Ethiopia, respectively.

The guess models below were compared to different ARIMA models using model selection criteria such as RMSE, MAPE and BIC, but the model suggested proved to be relatively robust compared to other competing models using SPSS V25 software. Considering the RMSE and BIC values, it is clear that the ARIMA (0, 1, 5) model has the lowest RMSE, MAPE and BIC values, making it the most effective modeling and forecasting of the spread of COVID-19 in Ethiopia. The same is true for the recovered cases, we were able to measure the aforementioned candidate models and also to use the above model selection criterion, finally we have detected that the daily recovered cases used ARIMA (2, 1, 3) as the best model with the lowest RMSE, MAPE and BIC values. The performance of the various ARIMA models with different orders of Autoregressive and Moving Average were checked and verified using statistics such as RMSE, MAPE and BIC. The results show that the proposed model performed well, both in-sample and out-of-sample (Table 3).

Table 3.

Model Fit for Confirmed and Recovered COVID-19 Cases in Ethiopia

Model Fit for COVID-19 Confirmed Cases
Fit Statistic	ARIMA (0, 1, 5)	ARIMA (1, 1, 2)	ARIMA (1, 1, 4)
RMSE	106.926	109.553	107.907
MAPE	130.722	131.369	139.204
Normalized BIC	9.501	9.513	9.543
Model Fit for COVID-19 Recovered Cases
Fit Statistic	ARIMA (3, 1, 3)	ARIMA (2, 1, 3)	ARIMA (2, 1, 4)
RMSE	64.916	64.856	64.956
MAPE	179.214	153.919	164.956
Normalized BIC	8.557	8.525	8.558

Abbreviations: RMSE, root mean square error; MAPE, mean absolute percentage error; BIC, Bayesian information criterion.

Model Coefficients Test

The best candidate models for confirmed and recovered cases were ARIMA (0, 1, 5) and ARIMA (2, 1, 3) respectively, based on the RMSE, MAPE and BIC criterion. The model was then estimated with its forecasting parameter for the daily confirmed and recovered series of COVID-19 in Ethiopia (Tables 4 and 5).

Table 4.

Parameter Estimation Using ARIMA (0, 1, 5) Model for Confirmed Cases of COVID-19 in Ethiopia

ARIMA Model Parameters for New Confirmed Cases
		Estimate	SE	t	Sig.
Constant		6.778	6.592	1.028	0.305
Difference		1
MA	Lag 1	0.880	0.081	10.859	0.000
	Lag 2	−0.343	0.106	−3.243	0.001
	Lag 3	0.058	0.109	0.533	0.595
	Lag 4	−0.161	0.107	−1.500	0.135
	Lag 5	−0.249	0.084	−2.965	0.003

Abbreviations: MA (Lag 1), moving average order 1; MA (Lag 2), moving average order 2; MA (Lag 3), moving average order 3; MA (Lag 4), moving average order 4; MA (Lag 5), moving average order 5; SE, standard error.

Table 5.

Parameter Estimation Using ARIMA (2, 1, 3) Model for Recovered Cases of COVID-19 in Ethiopia

ARIMA Model Parameters for New Recovered Cases
		Estimate	SE	t	Sig.
Constant		3.125	2.035	1.536	0.126
AR	Lag 1	−0.642	0.041	−15.638	0.000
	Lag 2	−0.985	0.039	−25.187	0.000
Difference		1
MA	Lag 1	0.021	0.086	0.244	0.808
	Lag 2	−0.627	0.059	−10.553	0.000
	Lag 3	0.537	0.080	6.678	0.000

Abbreviations: AR (Lag1), autoregressive order 1; AR (Lag2), autoregressive order 2; MA (Lag 1), moving average order 1; MA (Lag 2), moving average order 2; MA (Lag 3), moving average order 3; SE, standard error.

Examining the estimation results for confirmed cases, we see that the MA (1) coefficient is 0.88, the MA (2) coefficient is −0.343, and the MA (5) is −0.249 which are highly significant. The estimated standard errors are 0.081, 0.106 and 0.084, respectively.

The best suited models can be re-written based on the findings and evaluation of the different ARIMA model described as presented in Tables 4 and 5 respectively.

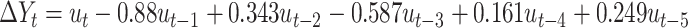(4)

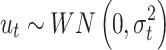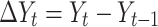Where; 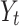represents the value of daily confirmed cases, 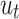: represents the error terms

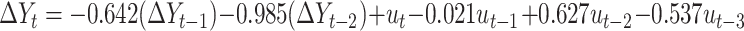(5)

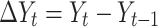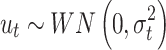Where; 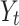represents the value of daily recovered cases, 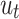: represents the error terms

Forecasting Using ARIMA Model

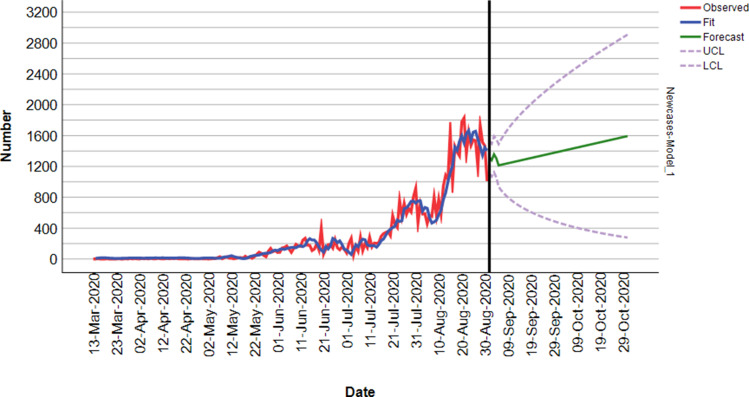
The daily spread data from 13 March to August 31, 2020, were predicted using the ARIMA (0,1,5) model and the daily recovered were predicted using the ARIMA (2,1,3) model based on the spread of COVID-19 in Ethiopia. The results indicated that the predicted values matched well with the actual values. The forecast date, point forecast and the upper and lower confidence limit values of the forecast for the next 2 months. The daily forecast was the point forecast with the 95% confidence limit of the upper and lower boundary values. The model’s forecasting power is very high as demonstrated by the slight gap between real and fitted values (Table 6).

Table 6.

Forecasting of Daily Total COVID-19 Confirmed Cases and Total Recovered Patients in Ethiopia for the Next 60 Days According to ARIMA Models with 95% CI

Date	Total Confirmed Cases Forecast Using ARIMA (0,1,5)	95% C.I for Total Confirmed Cases ARIMA (0,1,5)		Total Recovered Patients Forecast Using ARIMA (2,1,3)	95% C.I for TOTAL Recovered Patients ARIMA (2,1,3)
		Lb95	Ub95		Lb95	Ub95
01-Sep-2020	1318	1106	1529	579	451	707
02-Sep-2020	1282	1069	1494	475	340	610
03-Sep-2020	1357	1123	1591	534	389	679
04-Sep-2020	1306	1057	1555	607	450	764
05-Sep-2020	1214	938	1490	510	346	674
06-Sep-2020	1221	895	1546	509	338	679
07-Sep-2020	1227	859	1595	613	432	794
08-Sep-2020	1234	828	1640	555	367	744
09-Sep-2020	1241	800	1682	498	305	691
10-Sep-2020	1248	774	1721	600	398	802
11-Sep-2020	1254	751	1758	599	390	809
12-Sep-2020	1261	729	1793	508	294	722
13-Sep-2020	1268	709	1827	575	355	796
14-Sep-2020	1275	690	1860	630	402	859
15-Sep-2020	1282	672	1891	537	303	770
16-Sep-2020	1288	655	1922	551	313	789
17-Sep-2020	1295	639	1952	642	396	888
18-Sep-2020	1302	623	1981	578	327	828
19-Sep-2020	1309	609	2009	537	283	792
20-Sep-2020	1315	595	2036	635	373	896
21-Sep-2020	1322	581	2063	620	353	887
22-Sep-2020	1329	568	2090	542	271	812
23-Sep-2020	1336	556	2116	615	339	891
24-Sep-2020	1343	544	2141	653	371	936
25-Sep-2020	1349	532	2166	565	279	851
26-Sep-2020	1356	521	2191	592	302	882
27-Sep-2020	1363	510	2215	670	373	966
28-Sep-2020	1370	500	2239	602	301	902
29-Sep-2020	1376	490	2263	577	273	881
30-Sep-2020	1383	480	2286	668	359	978
01-Oct-2020	1390	471	2309	642	328	956
02-Oct-2020	1397	462	2332	577	260	894
03-Oct-2020	1404	453	2354	653	330	975
04-Oct-2020	1410	444	2376	676	349	1004
05-Oct-2020	1417	436	2398	595	265	925
06-Oct-2020	1424	428	2420	632	298	966
07-Oct-2020	1431	420	2442	697	357	1036
08-Oct-2020	1437	412	2463	627	284	970
09-Oct-2020	1444	404	2484	616	270	962
10-Oct-2020	1451	397	2505	700	349	1051
11-Oct-2020	1458	390	2526	665	310	1020
12-Oct-2020	1465	383	2546	613	255	971
13-Oct-2020	1471	376	2567	689	327	1051
14-Oct-2020	1478	369	2587	700	333	1066
15-Oct-2020	1485	363	2607	626	257	996
16-Oct-2020	1492	357	2627	671	298	1044
17-Oct-2020	1498	350	2646	723	345	1100
18-Oct-2020	1505	344	2666	654	273	1034
19-Oct-2020	1512	339	2685	655	272	1039
20-Oct-2020	1519	333	2705	730	342	1119
21-Oct-2020	1526	327	2724	689	297	1080
22-Oct-2020	1532	322	2743	650	255	1044
23-Oct-2020	1539	316	2762	724	326	1123
24-Oct-2020	1546	311	2781	723	321	1125
25-Oct-2020	1553	306	2799	659	254	1064
26-Oct-2020	1559	301	2818	709	301	1118
27-Oct-2020	1566	296	2836	748	336	1161
28-Oct-2020	1573	291	2855	682	267	1097
29-Oct-2020	1580	286	2873	694	276	1112
30-Oct-2020	1587	282	2891	760	338	1182
31-Oct-2020	1593	277	2909	714	289	1139

Abbreviations: CI, confidence interval; Lb, lower boundary; Ub, upper boundary.

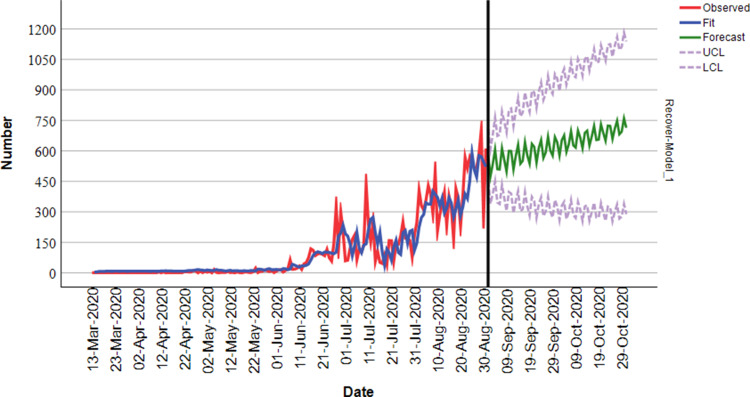
We can clearly conclude that the model selected can be used for modeling and forecasting the spread of COVID-19 in Ethiopia. Therefore, the forecasts showed that the spread of COVID-19 confirmed and recovered cases in Ethiopia would increase daily for the next sixty days (Figures 8 and 9).

Figure 8.

A 60 days forecast of total confirmed cases of COVID-19 according to ARIMA models with 95% confidence interval in Ethiopia.

Figure 9.

A 60-day forecast of total recovered cases of COVID-19 according to ARIMA models with 95% confidence interval in Ethiopia.

Discussion

The study presented current trends of COVID-19 outbreak from March 13, 2020 to 31 August, 2020 as visualized in the EPHI official website report. Since then, COVID-19 cases showed an uptrend. Total recovery and death rates as of 31 August, 2020 were 37.2% and 1.57%, respectively, which reflected the peak incidence and recovery ratio since the outbreak of COVID-19 in Ethiopia. And, the number of confirmed, recovered and death rates were increased significantly.

Based on the findings of the study, the spread of COVID-19 in Ethiopia was expected to move in an upward trend. Having developed an appropriate model, Ethiopia can apply this model to forecast the trend of COVID-19.

In Ethiopia, starting with the first reported case, the COVID-19 trend showed a progressive upward direction for six months, which was consistent with the Nigerian study.²⁵ However, the trend of confirmed COVID-19 cases in Ethiopia has shown that it is better than the US and European countries, though they had comparatively higher testing capacities. Having significant level of inadequate preventive practice measures in Ethiopia,^26,27 thus there is important to comprehend the trend of COVID-19 and to generalize the implications of the strategies used by the government to mitigate the spread of the disease.

The candidate models were obtained using the autocorrelation function (ACF) and the partial autocorrelation function (PACF). The models were designed based on the peaks found in the ACF and PACF charts. Both ARIMA (0, 1, 5) and ARIMA (2, 1, 3) were found to be the optimal model for confirmed and recovered COVID-19 cases, respectively, based on the lowest RMSE, MAPE and BIC values. This model was then used to study the trend of COVID-19 and the estimated increase in the number of confirmed and recovered cases. The finding of the study was consistent with the study conducted in Nigeria, which showed an upward trend in the spread of COVID-19 within the selected timeframe.¹⁸

The ARIMA model has been widely used in the infectious disease outbreak modelling. ARIMA, time series coupled with corrective gradual changes successfully predict a linear trend, but fails to forecast a series with turning points.²⁸ The current study used the complete periodic data to establish the ARIMA models and to forecast epidemic in the next 60 days. The ARIMA model fit well and is more suitable for short-term prediction. The ARIMA model was recently used to predict the dynamics of COVID19 disease with acceptable accuracy in a study conducted in Iran, Saudi Arabia, and a study conducted in the 15 most affected countries.^17,29,30 The optimal predictive ARIMA model was validated for confirmed and recovered COVID-19 cases based on lowest RMSE, MAPE and BIC value. It was estimated that the less out-of-sample forecast error and the lowest value are preferable, and which may contribute to the future forecast in Ethiopia.

In the current study, wide confidence intervals help to address any unforeseen changes in the forecast of dynamic COVID-19 cases. The prediction interval allows users to determine future uncertainty and to prepare different strategies for the range of possible outcomes. In addition, the wider prediction interval resulting from the non-stationary process was more practical in allowing for higher uncertainty and helps to illustrate the special significance of model identification, especially in evaluating whether or not the data is stationary.³¹

Furthermore, it is very important to discuss all the studies conducted on the basis of different techniques applied to COVID-19 prediction using statistical, mathematical/analytical and machine learning/data science models to control the spread of COVID-19 globally and for a specific country and to evaluate its impact, to create COVID–19 vulnerability index [1–16].

According to the model prediction, we need to be more aware of the tendency of COVID-19 spreading more than currently observed. In addition, based on the study findings, the trend towards the spread of COVID-19 in Ethiopia is expected to move upward. As a result, rapid control of infections in healthcare settings and in the community is mandatory in order to achieve success with COVID-19 prevention. It can also be used as a decision-making tool to allocate health interventions and mitigate the spread of Covid-19.

This tool can also be used to more reliably forecast short-term disease transmission indicators, to provide response control at all levels of the departments and to provide short-term emergency prevention programs for policy makers. Having established an appropriate model, Ethiopia can apply this model to predict the trend of COVID-19 in the country. ARIMA model forecasts are stable in all variables in the near future, which may be useful in prevention of the COVID-19 pandemic. The ARIMA model can provide rapid assistance in forecasting cases and developing a better preparedness plan in Iran.¹⁷

The ARIMA model is one of the most commonly used time series forecasting methods due to its simplicity and systematic structure and appropriate forecasting performance.³² Based on the findings of the study, it was predicted that the spread of COVID-19 in Ethiopia would move upward and the model could be used to predict the COVID-19 trend in the country.

ARIMA models were used to predict the progression of infectious diseases in order to identify the possible outcomes of an outbreak. However, artificial intelligence (AI) has the potential to help in all the stages of healthcare, from surveillance through to rapid diagnostic tests, and faster drug development. AI may also help to decide which patients should be prioritized for treatment and quickly learn which factors predict a higher risk of mortality, as well interventions and population-level controls, have led to reduced harm.^33,34 As the number of COVID-19 cases increased nationally in Ethiopia and different studies showed the majority of the community had poor practice on preventive measures,^26,27 there should be a need to focus on further measures to minimize the spread of COVID-19.

Conclusion

The current study showed that the spread of COVID-19 in Ethiopia is expected to move upward. Both ARIMA (0, 1, 5) and ARIMA (2, 1, 3) were found as the best model for confirmed and recovered COVID-19 cases, respectively, on the basis of the lowest RMSE, MAPE and normalized BIC values. Forecasts have shown that spread of COVID-19 confirmed and recovered cases in Ethiopia will progressively increase on a daily basis for the next 60 days. The study developed an appropriate statistical model which can be used as a decision-supporting method to implement health interventions and mitigate the spread of Covid-19 infection. While the accuracy of the proposed ARIMA models can be considered good, valid and satisfactory, and despite the fact that the projected values are classified as reliable forecasts. The study indicated that the ARIMA model was an easy-to-use modeling method for rapid forecasting the spread of COVID-19 in Ethiopia. In addition, we recommend to use other forecasting methods such as exponential smoothing and compare the results to our best selected ARIMA models as a baseline for new and recovered cases in Ethiopia. The limitation of the study was no risk factor was evaluated and analyzed, including demographic details of patients, their social network and travels due to the lack of individual-level data.

Funding Statement

The authors received no specific funding for this work.

Abbreviations

ACF, autocorrelation function; ANFIS, adaptive neuro-fuzzy inference system; ADF, augmented Dickey–Fuller test; ARIMA, autoregressive integrated moving average; BIC, Bayesian information criteria; PACF, partial autocorrelation function; CDC, communicable disease control; CI, confidence interval; CMC, composite Monte-Carlo; CUBIST, cubist regression; COVID-19, corona virus disease 2019; EPHI, Ethiopia Public Health Institute; MAPE, mean absolute percentage error; RF, random forest; RMSE, root mean squared error; SPSS, Statistical Package for Social Science; VMD, variational mode decomposition; WHO, World Health Organization.

Data Sharing Statement

All daily series of open-source data that support the findings of this study are also available from regular updates by the Ethiopian Public Health Institute: https://www.ephi.gov.et/[accessed on 10/01/2020].

Consent for Publication

All authors provided written informed consent to publish this study.

Author Contributions

Both authors made substantial contributions to conception and design, acquisition of data, or analysis and interpretation of data; took part in drafting the article or revising it critically for important intellectual content; agreed to submit to the current journal; gave final approval of the version to be published; and agreed to be accountable for all aspects of the work.

Disclosure

The authors reported no conflicts of interest for this work.