Abstract
Mechanics-based cardiac growth models can now predict changes in mass, chamber size, and wall thickness in response to perturbations such as pressure overload (PO), volume overload, and myocardial infarction with a single set of growth parameters. As these models move toward clinical applications, many of the most interesting applications involve predictions of whether or how a patient’s heart will reverse its growth after an intervention. In the case of PO, significant regression in wall thickness is observed both experimentally and clinically following relief of overload, for example following replacement of a stenotic aortic valve. Therefore, the objective of this work was to evaluate the ability of a published cardiac growth model that captures forward growth in multiple situations to predict growth reversal following relief of PO. Using a finite element model of a beating canine heart coupled to a circuit model of the circulation, we quantitatively matched hemodynamic data from a canine study of aortic banding followed by unbanding. Surprisingly, although the growth model correctly predicted the time course of PO-induced hypertrophy, it predicted only limited growth reversal given the measured unbanding hemodynamics, contradicting experimental and clinical observations. We were able to resolve this discrepancy only by incorporating an evolving homeostatic setpoint for the governing growth equations. Furthermore, our analysis suggests that many strain- and stress-based growth laws using the traditional volumetric growth framework will have similar difficulties capturing regression following the relief of PO unless growth setpoints are allowed to evolve.
Keywords: Growth, Reverse growth, Hypertrophy, Pressure overload, Finite element model
1. Introduction
Multiple published mechanics-based growth models can predict observed trends in cardiac hypertrophy due to hemodynamic overload, including myocyte and wall thickening following pressure overload (PO) or myocyte lengthening and chamber dilation in response to volume overload (VO) (Lin and Taber 1995; Taber 1998; Arts et al. 2005; Kroon et al. 2009; Göktepe et al. 2010; Rausch et al. 2011; Kerckhoffs et al. 2012a). A subset of these published models can even predict growth trends in response to multiple perturbations (such as PO, VO, and myocardial infarction) with a single set of growth parameters (Kerckhoffs et al. 2012a; Witzenburg and Holmes 2017, 2018). These successes raise the exciting possibility of using computational models to prospectively predict the time course of cardiac growth and remodeling in individual patients. However, most work to date has focused on predicting hypertrophy (‘forward’ remodeling), whereas many of the most interesting clinical applications revolve around whether or how a patient’s heart will reverse its growth after an intervention (Lee et al. 2015). For example, significant regression in wall thickness is observed both experimentally after aortic banding (Gao et al. 2005; Stansfield et al. 2007; Zhao et al. 2013) and clinically in aortic stenosis patients after aortic valve replacements (Monrad et al. 1988; Krayenbuehl et al. 1989; Villari et al. 1995; Matsumura et al. 2008; Hahn et al. 2013), where it is associated with better long-term survival (Beach et al. 2014; Hatani et al. 2016). Therefore, the objective of this work was to evaluate the ability of a published cardiac growth model that captures forward remodeling in multiple situations (Kerckhoffs et al. 2012a) to predict growth reversal following relief of pressure overload.
Previous modeling studies suggest that growth predictions in the heart are sensitive to the details of hemodynamic loading (Kerckhoffs et al. 2012b; Witzenburg and Holmes 2018). We therefore modified the cardiac growth model published by Kerckhoffs et al. (2012a) to quantitatively match data from a canine study in which detailed hemodynamics were reported before and after the creation of PO, at multiple time points as hypertrophy progressed, and then following the acute relief of PO (Sasayama et al. 1976). The growth model predicted limited growth reversal given measured post-release hemodynamics, contradicting experimental (Gao et al. 2005; Stansfield et al. 2007; Zhao et al. 2013) and clinical observations (Monrad et al. 1988; Krayenbuehl et al. 1989; Villari et al. 1995; Matsumura et al. 2008; Hahn et al. 2013). We were able to resolve this contradiction by incorporating an evolving growth setpoint into the governing growth equations. Furthermore, our results suggest that other strain-based growth laws would perform similarly given the measured hemodynamics. Overall, our simulations suggest that current formulations of phenomenological growth laws implemented within a volumetric growth framework will have difficulty matching both observed hemodynamics and observed growth regression following relief of PO unless growth setpoints are allowed to evolve.
2. Methods
2.1. Experimental data on aortic banding and release in canines
To fit the hemodynamic and growth parameters of the model employed here, we selected an experimental study conducted by Sasayama et al. (1976) in which pressure overload was induced via banding of the ascending aorta in 12 canines. We selected this study because detailed hemodynamic and growth data were reported prior to banding (baseline), immediately after banding (acutePO), following 9 and 18 days of hypertrophy, as well as immediately before and 1 day after relief of PO by release of the band. Reported hemodynamics included heart rate (HR), left ventricular (LV) end-diastolic pressure (EDP), maximum LV pressure (maxP), and percent short-axis shortening in the anterior–posterior cavity diameter (%short). Reported changes in LV dimensions included end-diastolic cavity diameter (EDD) and end-diastolic wall thickness (EDWth) measured via ultrasonic crystals placed within the LV. Since the experiment tracked the dogs for only 1 day after aortic band release, we relied on observations from other experiments (Gao et al. 2005; Stansfield et al. 2007; Zhao et al. 2013) and clinical studies (Monrad et al. 1988; Krayenbuehl et al. 1989; Villari et al. 1995; Matsumura et al. 2008; Hahn et al. 2013) to establish the expected speed and extent of growth reversal after release of PO. Such PO reversal studies consistently report significant regression of wall thickness, including a 25% decrease after 1 week in mice (Gao et al. 2005), 16% decrease after 1 week in rabbits (Zhao et al. 2013), and about a 20% decrease in EDWth over 2 years in patients (Hahn et al. 2013).
2.2. Finite element (FE) model of the canine heart
The canine biventricular finite element (FE) model employed in this study has been published previously (Kerckhoffs et al. 2012a). The nonlinear FE model consisted of 48 tricubic Hermite elements with realistic canine geometry and fiber distributions (Fig. 1a, b). The passive properties of the ventricle were defined using a transversely isotropic Fung-type material model:
| (1) |
| (2) |
| (3) |
| (4) |
W is the total passive strain energy density, a sum of transversely isotropic (Wpas) and slightly compressible (Wcomp) components; Eff, Ecc, and Err are the Lagrangian strain components in the fiber, crossfiber, and radial directions, respectively; and Ecr, Efc, and Efr are the associated shear strains. Here, J = det(F) is the determinant of the deformation gradient, F, and Cpas, bf, bt, bfr are the material parameters that describe the passive stiffness of the myocardium (Supplemental Methods).
Fig. 1.
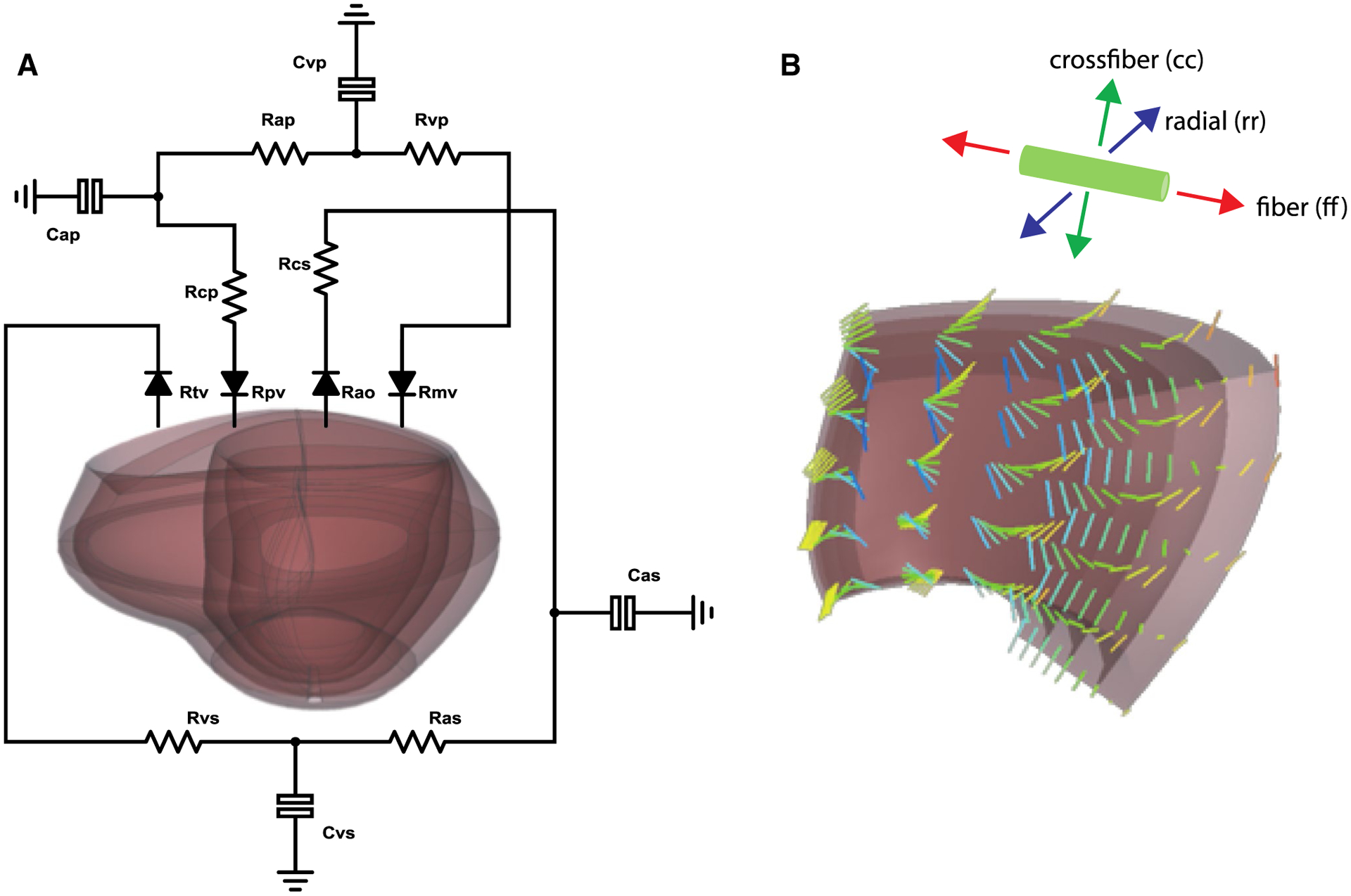
a Canine biventricular finite element model coupled to a lumped-parameter circulation model of systemic and pulmonary circulation. b Inset of the finite element mesh demonstrating the incorporated myofiber anatomy and the local coordinate system
To simulate myocyte contraction, we utilized a modified Hill-type active contraction model (Kerckhoffs et al. 2012a). The active tension (tact) was calculated as:
| (5) |
where Tmax is a constant that describes the maximum stress that the muscle can generate, C is a state variable that describes the contractility of the muscle as a function of time and fiber stretch, and Lse,norm is the length of the normalized series elastic element in the Hill-type model. Additional details and default parameter values of the active contraction model are available in the Supplemental Methods.
2.3. Lumped‑parameter circulation model
To account for hemodynamic loading, the ventricular chambers of the FE model were fully coupled to a previously published lumped-parameter circulation model (Santamore and Burkhoff 1991; Kerckhoffs et al. 2007) (Fig. 1a). To match the reported baseline hemodynamics, we simultaneously adjusted values for stressed blood volume (SBV), systemic resistance (Ras), and muscle contractility (Tmax) to match the reported EDP, maxP, and %short. To simulate the degree of acute constriction (acutePO) induced in the experiment, we simultaneously increased the aortic resistance (Rcs) and SBV to match the reported EDP and maxP and assumed ventricular material properties and all other circulation model parameters remained constant. Table 1 lists the resulting model parameters as well as the comparisons between model and reported hemodynamics. For baseline, acutePO, and for all growth steps, the coupled model ran multiple heartbeats to a hemodynamic steady state, defined as a < 1% difference in the stroke volume between the LV and right ventricle (RV). Additional circulation model parameters are listed in the Supplemental Methods. To test how well the available hemodynamic data constrained the choice of baseline and acutePO circulation parameters, we conducted a sensitivity analysis by increasing and decreasing individual circulatory parameters from the optimized baseline and acutePO values. Table 1 lists the most sensitive model outputs for each optimized circulation parameter and the minimum % change from the optimized value that leads to a z-score > 1. For example, EDP is most sensitive to SBV and a 5% change from the baseline SBV leads to a model baseline EDP outside the reported baseline EDP± one standard deviation (z-score > 1). All simulations were solved using Continuity 6.4b (http://continuity.ucsd.edu) on a Linux cluster using 8 cores. A time step of 1 ms was used for the heartbeat simulations.
Table 1.
Circulation model parameters and comparisons between model and reported hemodynamics for baseline and acutePO models
| baseline | acutePO (Δ% from Baseline) | %Change from optimized values for error > 1 SD | ||
|---|---|---|---|---|
| baseline | acutePO | |||
| Specified parameter | ||||
| HR (bpm) | 100 | 109 (+ 9%) | ||
| Fitted parameters | ||||
| SBV (ml) | 285 | 290 (+ 2%) | EDP: 5% | EDP: 3% |
| Ras (mmHg s/mL) | 1.9 | 1.9 | maxP: 7% | |
| Rcs (mmHg s/mL) | 0.2 | 1.09 (+ 145%) | maxP: 4% | |
| Tmax (kPa) | 84.0 | 84.0 | %short: 10% | |
| Matched hemodynamics | ||||
| Reported EDP (mmHg) | 11.1 ± 1.1 | 16.7 ± 0.9 | ||
| Model fit EDP (mmHg) | 11.2 | 16.7 | ||
| Reported maxP (mmHg) | 140 ± 6 | 220 ± 6 | ||
| Model fit maxP (mmHg) | 140 | 220 | ||
| Reported %short (%) | 30.0 ± 3.1 | 22.4 ± 2.2 | ||
| Model fit %short (%) | 32.0 | 20.3 | ||
Heart rate (HR) was specified based on reported values. Stressed blood volume (SBV), systemic resistance (Ras), aortic resistance (Rcs), muscle contractility (Tmax) were adjusted to match reported hemodynamic data. EDP: left ventricular end-diastolic pressure, maxP: left ventricular maximum pressure, %short: percent short-axis shortening in the anterior–posterior cavity diameter. HR and reported hemodynamics are from Sasayama et al. (1976). For each fitted parameter, the right-hand columns show the % change from the optimized value required to induce an error equal to 1 SD of the reported value (see text for more details)
2.4. Strain‑based growth law
After verifying that our final solutions minimized the errors between the model and measured hemodynamics, changes in local strains throughout the steady-state cardiac cycle relative to baseline were used to calculate the amount of ventricular growth for each element. Growth was implemented in both ventricles using a kinematic growth framework (Rodriguez et al. 1994), where the total deformation gradient (Ftot) maps the ungrown, unloaded heart to the grown, loaded heart. In this growth framework, Ftot is a product of the elastic (Fe) and growth (Fg) deformation gradients. We focused in this study on a modified form of a growth model published by Kerckhoffs et al. (2012a), which we have found to be the most successful among a library of published models in reproducing key aspects of forward growth due to PO, VO, and myocardial infarction with a single set of growth parameters (Witzenburg and Holmes 2017, 2018). In the Kerckhoffs growth law, myocyte lengthening is driven by the change in maximum fiber strain, which occurs during or near end-diastole. Myocyte thickening is driven by the change in the minimum of the first principal strain , which happens near end-systole. At growth step i, the growth stimuli are calculated as:
| (6) |
| (7) |
where is the first principal strain of the 2D myocyte cross-sectional strain tensor:
| (8) |
and are homeostatic growth setpoints defined as the maximum fiber strain and the minimum , respectively, during the baseline cardiac cycle. Thus, in a baseline, steady-state simulation, all growth stimuli are zero and there would be no growth.
The growth stretch, Fg, is a diagonal tensor with components in the fiber, crossfiber, and radial directions:
| (9) |
In the original formulation of the growth law, both Fg,cc and Fg,rr were driven by st, while Fg,ff was driven by sl. We found that modifying the growth law by setting Fg,cc = Fg,ff such that fiber and crossfiber growth are driven by sl and only Fg,rr is driven by st produced model predictions that were more consistent with the reported data (Sasayama et al. 1976); we note that this is consistent with prior work from our laboratory (Witzenburg and Holmes 2018) showing that this modification allows the Kerckhoffs law to better predict left ventricular growth and remodeling following pressure overload, volume overload, and myocardial infarction using a single set of growth parameters. Accordingly, the components of Fg at growth step i + 1 are calculated as:
| (10) |
| (11) |
These equations define sigmoidal growth curves in the fiber/crossfiber and radial directions, respectively (Kerckhoffs et al. 2012a; Witzenburg and Holmes 2017). Here, sl,50, st,50,positive, and st,50,negative define the width of a quiescent zone in which no growth occurs in response to relatively small changes in strain. When st,50,positive and st,50,negative are equal, the growth curves are symmetric such that equal, but opposite stimulus values lead to the same rates of positive and negative growth. Kff and krr are evolution growth functions (Kerckhoffs et al. 2012a) that reduce the growth rates to zero when Fg,ff reaches 1.35 Fg,rr reaches 1.28. fff,max, frr,max, ff and fr define the shape of the sigmoidal growth curves. Consistent with the original description of this growth law by Kerckhoffs et al. (Kerckhoffs et al. 2012a), we assumed that one growth step in the model is equivalent to 1.5 days of ventricular growth. Growth parameters are listed in the Supplemental Methods.
2.5. Forward growth simulations
We simulated three different cases of forward growth to explore how different modeling assumptions affect both forward growth due to PO and reversal following relief of the overload. For all cases, we ran the model for 18 forward growth days (12 forward growth steps) to match the time of aortic banding in the canine experiment. We also assumed that SBV and Ras could evolve in response to sustained PO and adjusted their values to match the reported time course of hemodynamics (EDP, maxP, and %short). To match the time course of reported LV end-diastolic wall thickness (EDWth), we adjusted the thickening growth parameter, st,50,positive.
2.5.1. Case 1 (standard): No changes in material properties, constant growth setpoints
In this first case, we assumed that growth adds material with identical material properties by keeping all material model parameters constant throughout forward and reverse growth. In addition, we assumed that the myocytes remember their original baseline state by holding the growth setpoints and constant throughout all simulations of forward and reverse growth.
2.5.2. Case 2 (fibrosis): Stiffen passive material properties, constant growth setpoints
Since fibrosis is commonly observed clinically in patients with aortic stenosis (Villari et al. 1995; Yarbrough et al. 2012; Treibel et al. 2018) as well as in animal experiments of aortic banding (Cutilletta et al. 1975; Gao et al. 2005; Zhao et al. 2013), in a second set of simulations we simulated fibrosis by linearly increasing the passive stiffness coefficients (bf, bt, bfr) by 20% over the course of forward growth. For these simulations, we assumed that the growth setpoints remained constant throughout forward and reverse growth as in Case 1.
2.5.3. Case 3 (evolving setpoint): No changes in material properties, evolving growth setpoints
Finally, to test the effect of allowing the myocardium to gradually adjust its homeostatic setpoints to the evolving mechanical state, we allowed the growth setpoints to change during growth. As a first implementation of this assumption, we used a 15-growth step weighted moving average of the previous elastic strains to specify the current setpoint. Consistent with the approximate 1-week half-life of assembled actin and myosin in cardiac sarcomeres (Kimata and Morkin 1971), we weighted strains from 8 growth steps prior to the current time most heavily, with strains from more recent and more distant times exerting less influence.
| (12) |
for the lengthening stimulus and
| (13) |
for the thickening stimulus, where superscripts indicate the growth steps prior to the current time i. We assumed that all hearts had been at steady state with strains matched to their setpoints for at least 22 days prior to the onset of PO. We tested two different formulations of the growth law for Case 3. First (Case 3a), we set st,50,positive = st,50,negative in (11), which assumes that the myocardium has equal capability for forward and reverse growth in the radial direction. We also tested a non-symmetric version of the growth equation (Case 3b), where we set st,50,positive > st,50,negative in (11), which assumes that rate of growth reversal induced by a given reduction in strain is larger than the rate of forward growth induced by the same magnitude increase in strain. As in Case 1, we kept all passive material parameters constant for these simulations.
2.6. PO release and reverse growth
After matching the forward hemodynamics and growth due to PO for all cases, we adjusted the circulation parameters, Rcs, SBV, and Tmax until the model matched the reported changes in maxP, EDP, and %short following acute unbanding (Sasayama et al. 1976). We ran simulations for 18 reverse growth days (12 reverse growth steps), keeping all circulation parameters constant.
3. Results
3.1. Model quantitatively matches hemodynamics and forward growth due to PO
We were able to quantitatively match the reported time course for both hemodynamics and growth over 18 days of PO in all cases (Figs. 2, 3). For Case 1 (no changes in material properties or setpoints), matching reported hemodynamics required reducing Ras by 45% and increasing SBV by 15% linearly over 12 forward growth steps (Table 2). The model matched the reported time course of remodeling, with little change in end-diastolic cavity diameter (EDD) and a 10% increase in end-diastolic wall thickness (EDWth). Inducing fibrosis (Case 2) affected the adjustments required to match experimental hemodynamics, requiring smaller changes in both arterial resistance and stressed blood volume (25% decrease in Ras, 10% increase in SBV), but did not alter predicted growth. Using identical growth parameters, the predicted time course of EDD and EDWth was nearly identical to Case 1. Incorporating an evolving growth setpoint (Case 3a,b) affected the growth parameters required to match the experimental data but had little impact on predicted hemodynamics, with the same changes to the circulation as in Case 1 (45% decrease in Ras, 15% increase in SBV) providing a good match to the measured hemodynamics. Matching EDWth required a reduction in the growth parameter, st,50,positive, to induce more wall thickening. With these adjustments, all predicted values were well within one standard deviation of the experimental mean (−1 < z-score < 1) for all cases (Fig. 4).
Fig. 2.
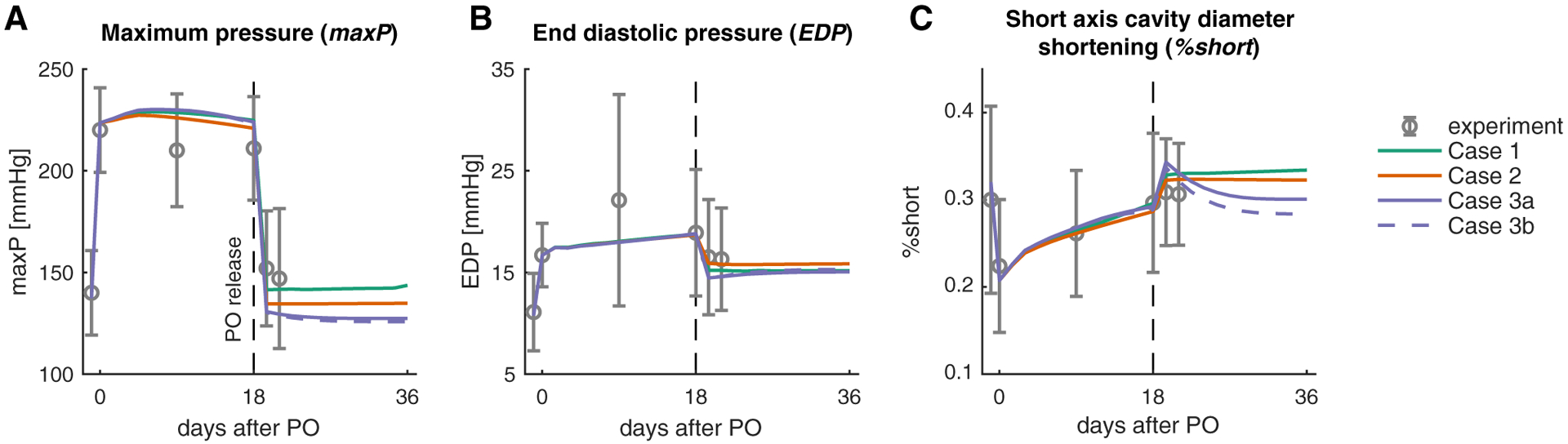
Model quantitatively matches the reported time course of hemodynamics for baseline (day −1.5), acutePO (day 0), forward growth (day 0–18), and at PO release (day 19.5). Figures show comparisons of the different simulated cases to data for a maximum LV pressure, b end-diastolic pressure, and c % shortening
Fig. 3.
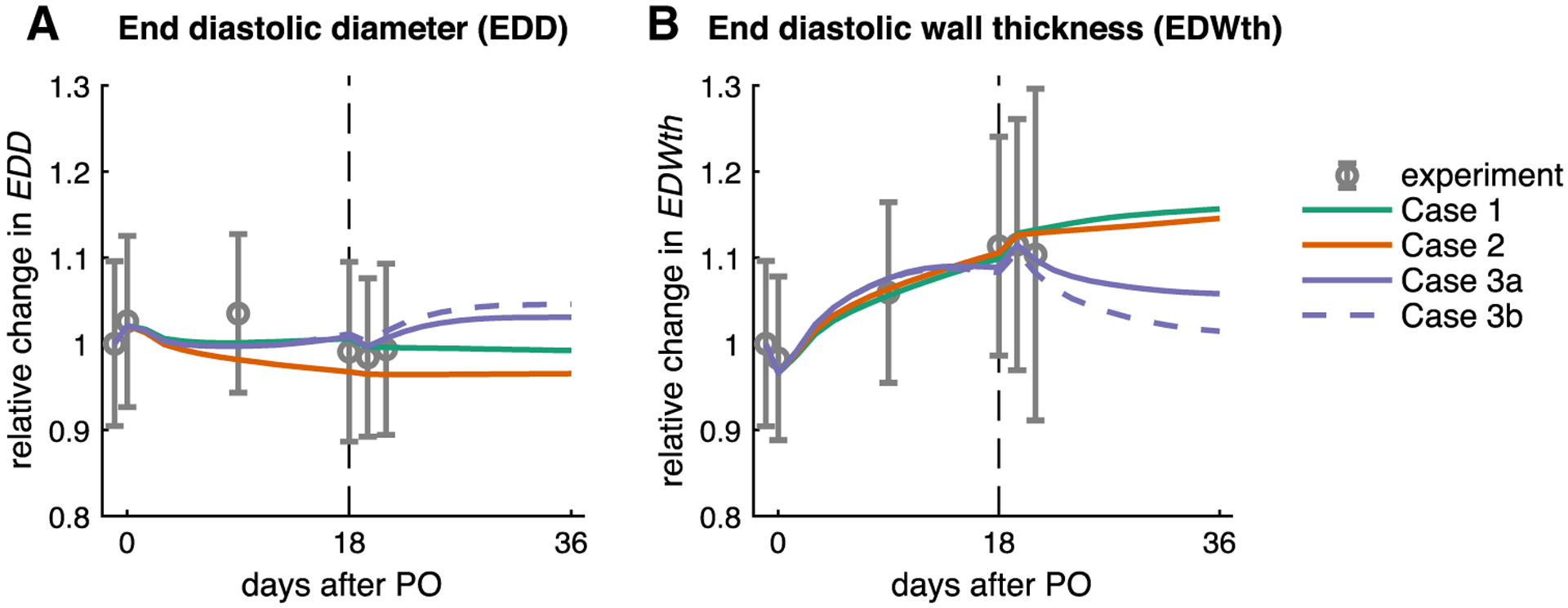
Model quantitatively matches the reported time course of remodeling for baseline (day −1.5), acutePO (day 0), and forward growth (day 0–18). Figures show comparisons of the four different simulated cases to data for a end-diastolic diameter (EDD) and b end-diastolic wall thickness (EDWth). Following PO release, only the simulations with an evolving setpoint (Cases 3a and 3b) predicted regression of wall thickening (see text)
Table 2.
Changes made in the circulation parameters during forward growth due to PO (% change from acutePO) and growth parameters set for each case
| Circulation changes | Growth parameter | |||
|---|---|---|---|---|
| Ras (mmHg s/ml) | SBV (ml) | st,50,positive | st,50,negative | |
| Case 1: Standard | 1.04 (−45%) | 334 (+ 15%) | 0.07 | 0.07 |
| Case 2: Fibrosis | 1.425 (−25%) | 319 (+ 10%) | 0.07 | 0.07 |
| Case 3a: Evolving setpoint (symmetric growth law) | 1.04 (−45%) | 334 (+ 15%) | 0.06 | 0.06 |
| Case 3b: Evolving setpoint (non-symmetric growth law) | 1.04 (−45%) | 334 (+ 15%) | 0.06 | 0.05 |
Fig. 4.
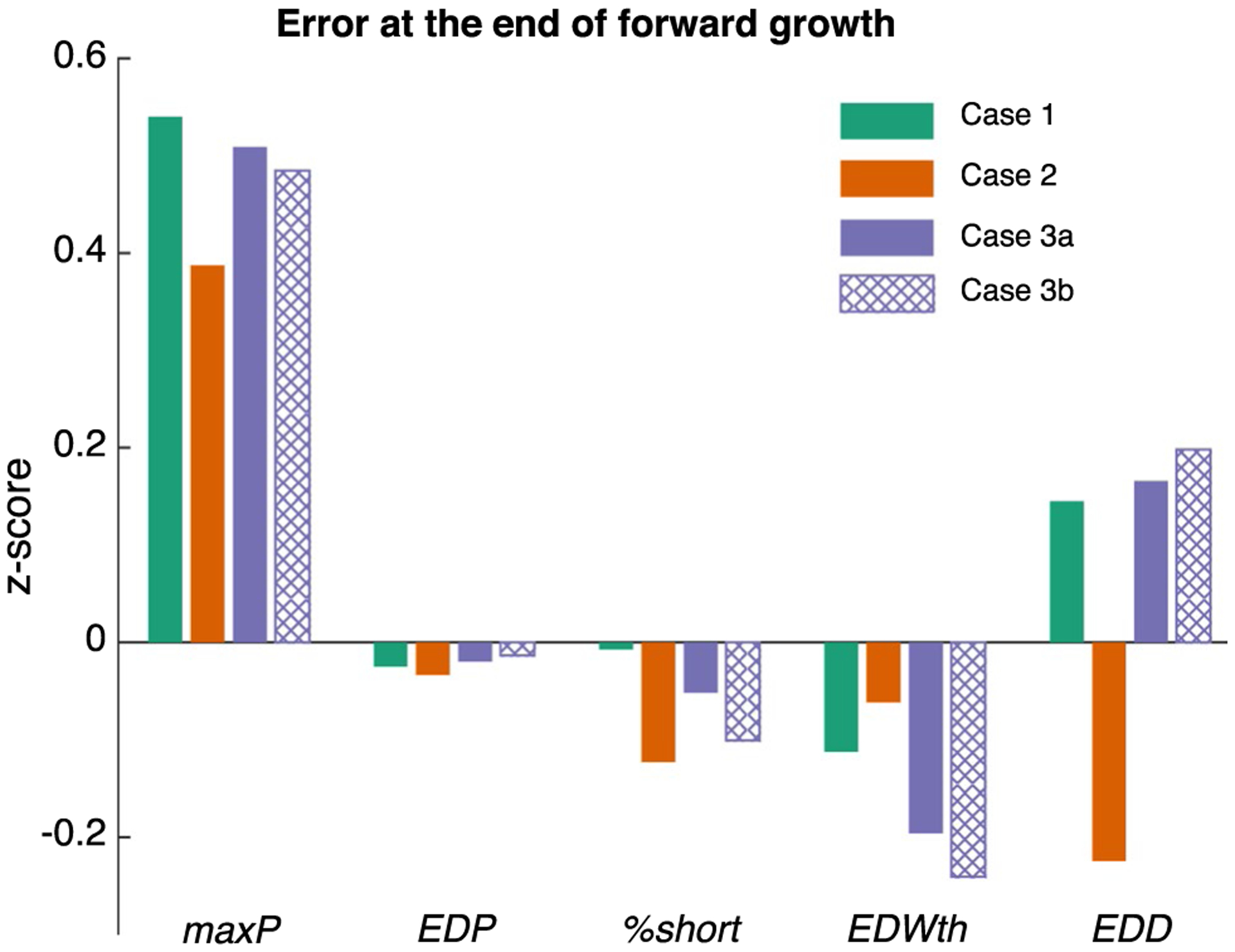
All cases of forward growth resulted in a similar quantitative match to experimental hemodynamics (maxP, EDP, and %short) and dimensions (EDWth and EDD) at the end of forward growth. Bar graphs show error as a fraction of the experimental standard deviation (z-score) at 18 days of forward growth. All predicted values were well within one standard deviation of the experimental mean (− 1 < z-score < 1) for all cases simulated
3.2. Evolving growth setpoints are necessary to predict growth reversal after relief of PO
After confirming quantitative agreement with Sasayama’s experimental data for forward growth and hemodynamics following aortic banding in dogs, we adjusted circulation model parameters to match the reported acute unbanding hemodynamics (Sasayama et al. 1976). The experimental data indicated that pressures returned to slightly above baseline values, accompanied by a small drop in EDP. Interestingly, %short had normalized to its baseline value over the course of the forward remodeling period and demonstrated very little additional change in response to unbanding (Fig. 2, day 19.5). Matching these data required a slight increase in SBV (+ 2% compared with end of forward growth), a 30% reduction in muscle contractility, Tmax, and reduction in the aortic resistance Rcs to a value higher than the pre-banding baseline [0.4 (ml/mmHg) compared with 0.2 (ml/mmHg)]. These changes to the coupled model restored the EDV and ESV of the grown ventricle to values very close to the pre-banding baseline for all cases (solid green PV loops in Fig. 5).
Fig. 5.
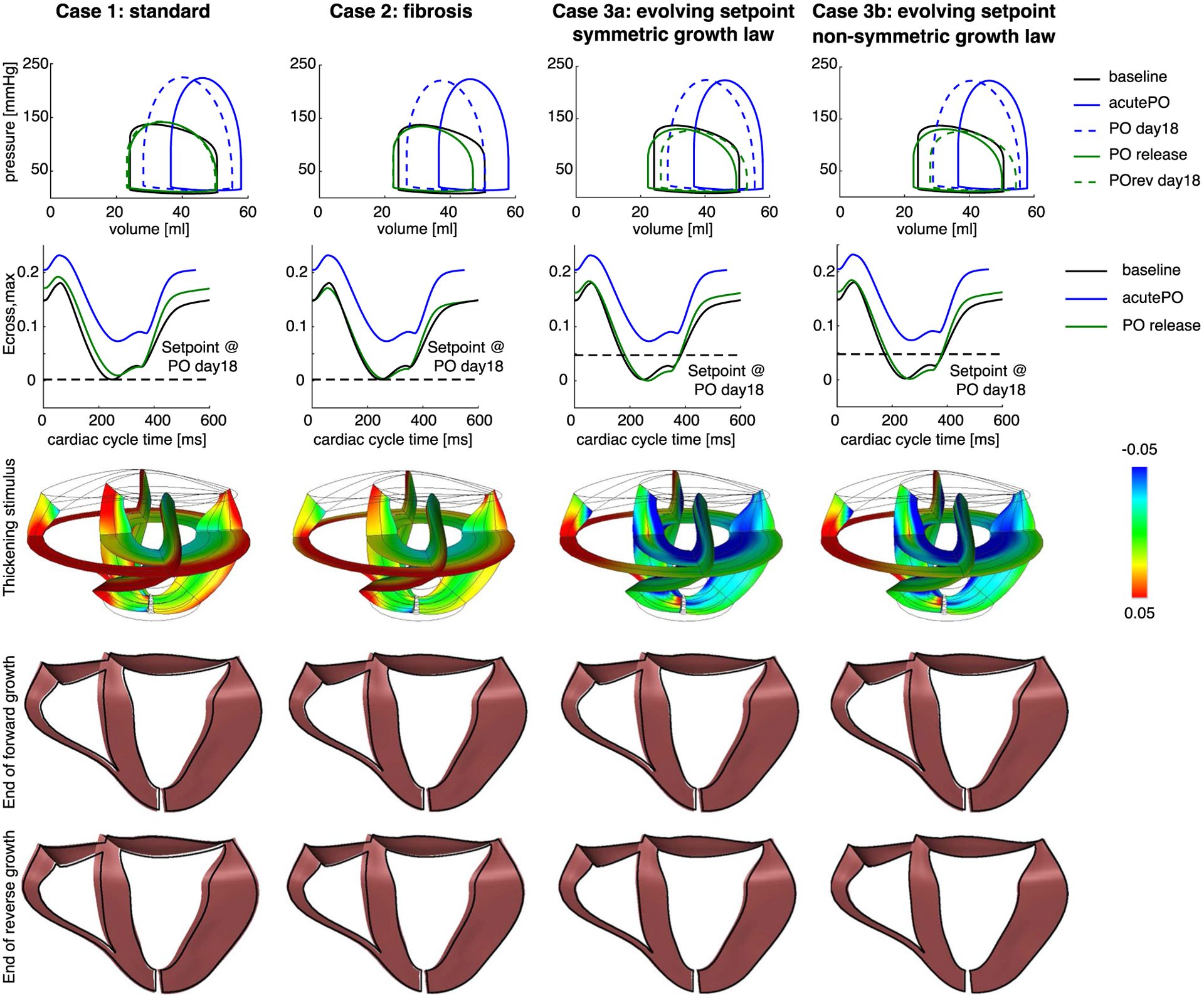
Matching PO release hemodynamics causes the elastic strains to return to baseline, triggering little-to-no regression in wall thickness. Each column represents one of the four cases simulated (see text). Top row: pressure–volume (PV) loops for baseline, acutePO, end of simulated forward growth, PO release, and end of simulated reverse growth. Second row: Ecross,max throughout the cardiac cycle for baseline, acutePO, and PO release for a midwall Gauss point on the lateral wall in the LV. Third row: contour plots of the thickening stimulus (st) immediately following PO release. Fourth row: unloaded grown geometry (colored in pink) at the end of forward growth (PO day 18) compared with the ungrown geometry (outline in black). All cases resulted in similar changes in the geometry. Bottom row: unloaded grown geometry (colored in pink) at the end of reverse growth (POrev day 18) compared with the ungrown geometry (outlined in black). Cases 1 and 2 did not lead to any changes in geometry compared with PO day 18, whereas Cases 3a and 3b resulted in a smaller heart compared to PO day 18
Surprisingly, the standard case (Case 1) showed no reversal of PO-induced wall thickening after PO release, as EDWth increased slightly (Figs. 3b, 5, column 1, rows 4–5). As with forward growth, simulating fibrosis (Case 2) did not affect growth predictions following simulated unbanding. When we allowed the growth setpoint to evolve (Case 3a), EDWth regressed slightly from 110 to 107% relative to the baseline EDWth (Figs. 3b, 5, column 3, rows 4–5). Only the combination of an evolving growth setpoint with a non-symmetric growth law (Case 3b) led to significant regression of EDWth from 110 to 101% relative to the baseline EDWth (Fig. 3b, column 4, rows 4–5). To understand why Cases 1, 2, and 3a displayed minimal reverse remodeling, we exam-ined the stimulus for radial growth, Ecross,max, throughout the cardiac cycle for a range of elements. The second row in Fig. 5 shows strain vs. cardiac cycle time curves for a representative midwall Gauss point. In all cases simulated, the elastic strains and therefore Ecross,max returned to baseline values when we matched the experimentally reported PO release hemodynamics. This restoration of the elastic strains resulted in a thickening stimulus near zero for the stand-ard and fibrosis cases, and a slightly negative thickening stimulus for the evolving setpoint simulations. Mapping the thickening stimulus across the entire model indicated values of the thickening stimulus that would cause no remodeling (green) or additional thickening (red) everywhere in the standard and fibrosis cases (Fig. 5, third row). By contrast, the evolving setpoint cases displayed values of the thickening stimulus immediately following unbanding that would induce thinning (blue) near the endocardium in the septal, anterior, and lateral walls but no change in thickness (green) elsewhere. By changing the growth curve to be more sensitive to negative thickening stimulus (Case 3b), the model was able to predict full regression of wall thickness.
3.3. Effect of forward growth duration and magnitude on reversal predictions
In order to test whether the lack of wall thickness regression observed in our simulations might be due to the relatively short duration and mild hypertrophy displayed during Sasayama’s experiments, we allowed the fibrosis simulation (Case 2) to continue for 54 days of forward growth under PO. Predicted wall thickening nearly doubled compared with the 18-day simulations (17% increase in EDWth) and appeared to be at or near a steady state (Fig. 6). We adjusted SBV, Ras, Rcs, and Tmax to generate a PV loop similar to our previous Case 2, PO release condition (Fig. 5, Case 2, solid green PV loop). Consistent with clinical reports in aortic stenosis patients post-aortic valve replacement (Hahn et al. 2013), these simulations showed an acute 5% decrease in end-systolic volume and 1% increase in end-diastolic volume due to relief of PO. However, we observed no predicted regression of EDWth over another 54 simulated days following PO release (Fig. 6). This result suggests that the absence of regression we observed following simulated PO release was not solely due to the limited duration or extent of the initial hypertrophy.
Fig. 6.
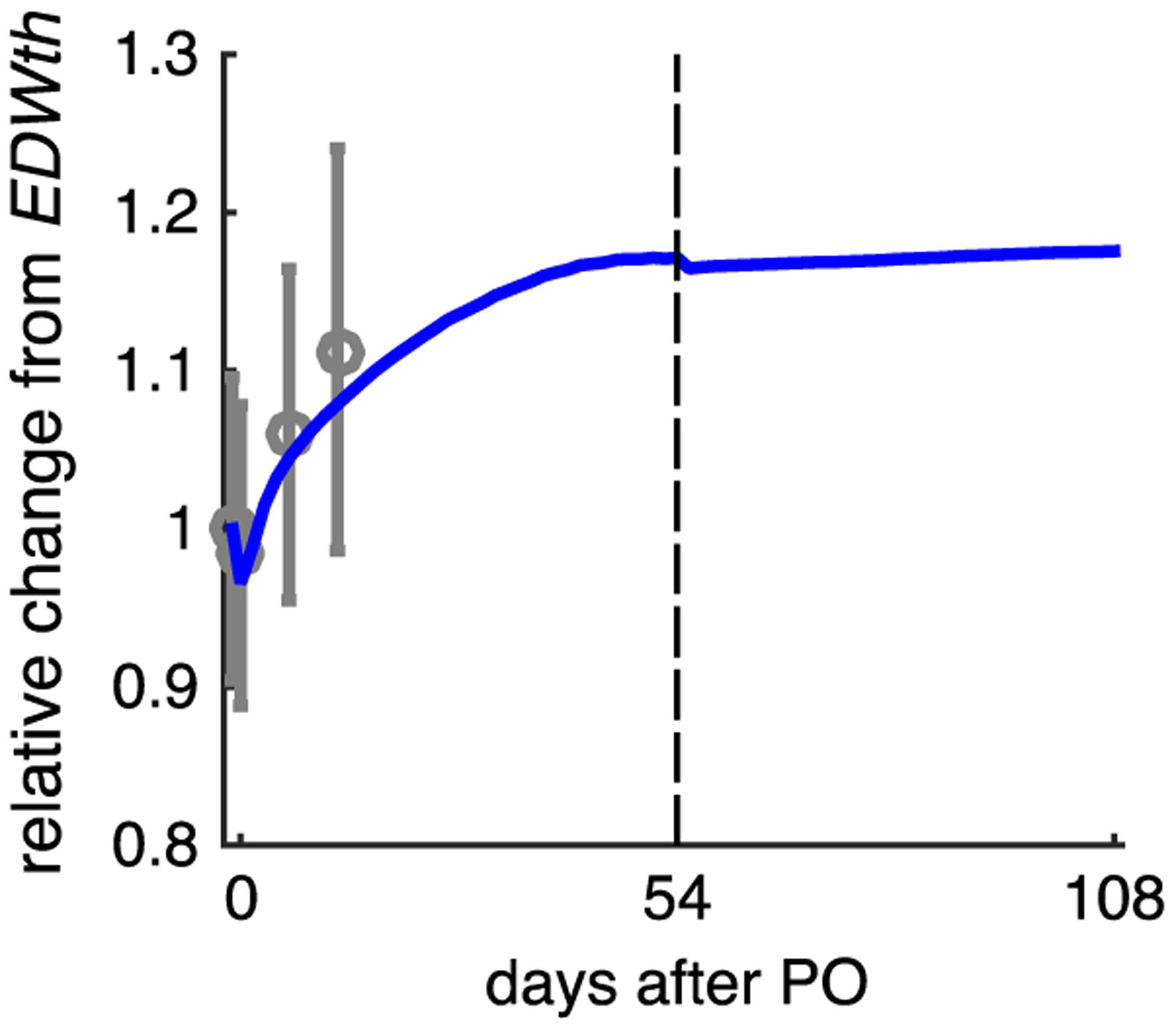
Increasing the duration and extent of forward growth due to PO does not significantly affect reverse growth predictions following simulated PO release. Solid line shows change in predicted EDWth for simulation Case 2 (fibrosis) over 54 days of forward growth followed by 54 days of continued simulation after PO release; symbols show data from Sasayama et al. (1976) during 18 days of forward growth following aortic constriction
4. Discussion
The objective of this study was to evaluate the ability of a specific cardiac growth model that has proven particularly successful at predicting the time course of forward growth due to multiple perturbations, to predict the reversal of hypertrophy following relief of hemodynamic overload. Using a FE model of a beating canine heart coupled to a lumped-parameter model of the circulation, we quantitatively matched the measured time course of hemodynamics and forward growth due to pressure overload in dogs induced by aortic banding under three different modeling assumptions. We then simulated relief of PO by unbanding and tracked the degree of predicted reversal of PO-induced hypertrophy. In general, we found that when we matched the actual hemodynamics associated with aortic unbanding in dogs, the standard and fibrosis cases were unable to reproduce the reversal of wall thickening that is known to occur following relief of pressure overload in animals and patients (Monrad et al. 1988; Krayenbuehl et al. 1989; Villari et al. 1995; Gao et al. 2005; Stansfield et al. 2007; Matsumura et al. 2008; Hahn et al. 2013; Zhao et al. 2013). We were able to remedy this discrepancy by incorporating an evolving growth setpoint and by re-parameterizing the portion of the growth law that governs wall thinning. Although this study focused on a slightly modified form of a specific strain-based growth law originally published by Kerckhoffs et al. (2012a), analysis of the underlying behavior of the model suggests that our results may have more general implications for many of the growth laws commonly employed in the cardiac modeling literature.
The canine study we simulated here reported that end-diastolic diameter (a surrogate for end-diastolic volume, EDV) was elevated due to higher diastolic pressures during overload but returned to baseline values following unloading. This observation tells us both that post-release EDV was similar to baseline EDV and that there was no appreciable dilation of the ventricle due to growth. Translated into the volumetric growth framework employed in this study, these observations imply that in the fiber and crossfiber directions, end-diastolic total stretch (Ftot,ff and Ftot,cc) returned to baseline following unbanding. Since very little growth occurred in the fiber or crossfiber directions during forward growth due to PO (Fg,ff = Fg,cc ~= 1), elastic stretches were also restored in the fiber/crossfiber directions. Furthermore, since myocardium is incompressible, radial strains following relief of PO would also be equal to their baseline values unless normally small shear strains change dramatically. Thus, no growth law that relies on stretches that occur at or near end-diastole would predict remodeling following unloading, unless the homeostatic setpoints controlling growth have changed. Furthermore, unless material properties change significantly due to PO-induced forward remodeling, a similar statement should apply to any stress-based growth law, since diastolic stresses depend directly on diastolic stretches. We note that this argument applies only to simulations of PO. In the case of VO, strain-based growth laws are able to predict reversal (Lee et al. 2015) when dilation during forward growth due to VO induces an increase in Fg,ff. In that situation, relieving VO and restoring cavity volumes causes Fe,ff to drop below baseline values and leads to regression of growth.
The growth law employed here relied on diastolic stretches to drive dilation, but systolic stretches to drive wall thickening; thus, in theory wall thickening induced by PO could have reversed despite the arguments outlined in the previous paragraph regarding diastolic stretches. Yet here we encountered the critical role of ventricular–vascular coupling and reflex regulation of hemodynamics in regulating cardiac growth. In Sasayama’s experiments, percent shortening (a surrogate for ejection fraction) returned to baseline values following unbanding, likely due at least in part to reflex regulation of arterial pressure. Thus, the same argument outlined above applies to end-systole: in the absence of growth in the fiber and crossfiber directions, the fact that observed systolic volumes, total stretches, and elastic stretches following unbanding were all equal to their baseline values means that a strain-based growth law will not predict regression unless the homeostatic strain levels change, and a stress-based growth law would only make a different prediction in the setting of dramatically altered material properties. Even when those homeostatic setpoints change, in the specific study simulated here we found that strain-growth relationships that correctly predicted wall thickening during banding did not automatically predict the expected degree of wall thinning following unbanding (Cases 1, 2, and 3a). In order to achieve regression of wall thickening consistent with the literature following relief of PO, we had to modify the stimulus-growth rate relation (Eq. 11) so that the curves relating increased strain to wall thickening and reduced strain to wall thinning were non-symmetric (Case 3b). More broadly, these results emphasize how critical hemodynamics are to the predictions of cardiac growth models (Kerckhoffs et al. 2012b; Holmes and Lumens 2018; Witzenburg and Holmes 2018). Even a model capable of predicting regression of hypertrophy in some settings may not accurately predict it when matched to measured hemodynamics.
While most published cardiac growth models use a volumetric growth formulation similar to the one employed here, other approaches to modeling biologic growth may be better poised to account for changes in both material properties and the growth setpoints (or reference stretches) that govern predicted growth. For example, constrained mixture approaches (Humphrey and Rajagopal 2002) assume that new constituents replace old constituents with new unloaded configurations, resulting in the evolution of the homeostatic setpoint.
One limitation in our reversal simulations is that we kept all circulation parameters constant following unbanding, since detailed hemodynamic data were not available. Given the high sensitivity of predicted growth to hemodynamic loading discussed above, it will be important in future studies to track not only geometric remodeling but also hemodynamic remodeling during regression of hypertrophy. Second, we prescribed a 20% increase in passive stiffness for our fibrosis simulations, but this is an arbitrary value and may not be indicative of what happens experimentally or clinically. The fibrosis simulations, however, predicted little growth reversal over a wide range of reversal conditions, so we do not believe our findings in those simulations depended strongly on the magnitude of the change in passive stiffness. We also confirmed that adding fibrosis to an evolving setpoint simulation (combining Cases 2 and 3a) did not substantially alter the predicted growth reversal. Therefore, we would still expect to see little to no reversal with more or less increase in passive stiffness.
In conclusion, computational models with the ability to predict reversal of heart growth after interventions such as a valve replacement could help answer important clinical questions. The modeling study presented here demonstrates that the current formulation of a state-of-the-art cardiac growth model with the ability to predict patterns of forward growth following multiple interventions incorrectly predicts little change in wall thickness following simulated PO release. Furthermore, the mechanisms underlying this behavior in the model suggest that phenomenological strain-and stress-based growth laws implemented in a volumetric growth framework will have difficulty capturing regression following relief of PO unless homeostatic setpoints are allowed to evolve.
Supplementary Material
Acknowledgements
This study was funded by the National Institutes of Health (U01 HL127654).
References
- Arts T, Delhaas T, Bovendeerd P et al. (2005) Adaptation to mechanical load determines shape and properties of heart and circulation: the CircAdapt model. Am J Physiol Heart Circ Physiol 288:H1943–H1954. 10.1152/ajpheart.00444.2004 [DOI] [PubMed] [Google Scholar]
- Beach JM, Mihaljevic T, Rajeswaran J et al. (2014) Ventricular hypertrophy and left atrial dilatation persist and are associated with reduced survival after valve replacement for aortic stenosis. J Thorac Cardiovasc Surg 147:362–369.e8. 10.1016/j.jtcvs.2012.12.016 [DOI] [PubMed] [Google Scholar]
- Cutilletta AF, Dowell RT, Rudnik M et al. (1975) Regression of myocardial hypertrophy. 1. Experimental model, changes in heart weight, nucleic-acids and collagen. J Mol Cell Cardiol 7:767–781. 10.1016/0022-2828(75)90042-5 [DOI] [PubMed] [Google Scholar]
- Gao X-M, Kiriazis H, Moore X-L et al. (2005) Regression of pressure overload-induced left ventricular hypertrophy in mice. Am J Physiol Heart Circ Physiol 288:H2702–H2707. 10.1152/ajpheart.00836.2004 [DOI] [PubMed] [Google Scholar]
- Göktepe S, Abilez OJ, Parker KK, Kuhl E (2010) A multiscale model for eccentric and concentric cardiac growth through sarcomero-genesis. J Theor Biol 265:433–442. 10.1016/j.jtbi.2010.04.023 [DOI] [PubMed] [Google Scholar]
- Hahn RT, Pibarot P, Stewart WJ et al. (2013) Comparison of transcatheter and surgical aortic valve replacement in severe aortic stenosis: a longitudinal study of echocardiography parameters in cohort a of the PARTNER trial (placement of aortic transcatheter valves). J Am Coll Cardiol 61:2514–2521. 10.1016/j.jacc.2013.02.087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatani T, Kitai T, Murai R et al. (2016) Associations of residual left ventricular and left atrial remodeling with clinical outcomes in patients after aortic valve replacement for severe aortic stenosis. J Cardiol 68:241–247. 10.1016/j.jjcc.2015.09.017 [DOI] [PubMed] [Google Scholar]
- Holmes JW, Lumens J (2018) Clinical applications of patient-specific models: the case for a simple approach. J Cardiovasc Transl Res 11:71–79. 10.1007/s12265-018-9787-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey JD, Rajagopal KR (2002) A constrained mixture model for growth and remodeling of soft tissues. Math Models Methods Appl Sci 12:407–430. 10.1142/S0218202502001714 [DOI] [Google Scholar]
- Kerckhoffs RCP, Neal ML, Gu Q et al. (2007) Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann Biomed Eng 35:1–18. 10.1007/s10439-006-9212-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerckhoffs RCP, Omens JH, McCulloch AD (2012a) A single strain-based growth law predicts concentric and eccentric cardiac growth during pressure and volume overload. Mech Res Commun 42:40–50. 10.1016/j.mechrescom.2011.11.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerckhoffs RCP, Omens JH, McCulloch AD (2012b) Mechanical dis-coordination increases continuously after the onset of left bundle branch block despite constant electrical dyssynchrony in a computational model of cardiac electromechanics and growth. Europace 14:v65–v72. 10.1093/europace/eus274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimata S, Morkin E (1971) Comparison of myosin synthesis in heart and red and white skeletal muscles. Am J Physiol 221:1706–1713. 10.1152/ajplegacy.1971.221.6.1706 [DOI] [PubMed] [Google Scholar]
- Krayenbuehl HP, Hess OM, Monrad ES et al. (1989) Left ventricular myocardial structure in aortic valve disease before, intermediate, and late after aortic valve replacement. Circulation 79:744–755. 10.1161/01.cir.79.4.744 [DOI] [PubMed] [Google Scholar]
- Kroon W, Delhaas T, Arts T, Bovendeerd P (2009) Computational modeling of volumetric soft tissue growth: application to the cardiac left ventricle. Biomech Model Mechanobiol 8:301–309. 10.1007/s10237-008-0136-z [DOI] [PubMed] [Google Scholar]
- Lee LC, Genet M, Acevedo-Bolton G et al. (2015) A computational model that predicts reverse growth in response to mechanical unloading. Biomech Model Mechanobiol 14:217–229. 10.1007/s10237-014-0598-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin IE, Taber LA (1995) A model for stress-induced growth in the developing heart. J Biomech Eng Trans ASME 117:343–349. 10.1115/1.2794190 [DOI] [PubMed] [Google Scholar]
- Matsumura Y, Gillinov AM, Toyono M et al. (2008) Usefulness of left ventricular shape to predict the early recovery of left ventricular function after isolated aortic valve replacement for aortic valve stenosis. Am J Cardiol 102:1530–1534. 10.1016/j.amjcard.2008.07.044 [DOI] [PubMed] [Google Scholar]
- Monrad ES, Hess OM, Murakami T et al. (1988) Time course of regression of left ventricular hypertrophy after aortic valve replacement. Circulation 77:1345–1355. 10.1161/01.cir.77.6.1345 [DOI] [PubMed] [Google Scholar]
- Rausch MK, Dam A, Göktepe S et al. (2011) Computational modeling of growth: systemic and pulmonary hypertension in the heart. Biomech Model Mechanobiol 10:799–811. 10.1007/s10237-010-0275-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez EK, Hoger A, McCulloch AD (1994) Stress-dependent finite growth in soft elastic tissues. J Biomech 27:455–467. 10.1016/0021-9290(94)90021-3 [DOI] [PubMed] [Google Scholar]
- Santamore WP, Burkhoff D (1991) Hemodynamic consequences of ventricular interaction as assessed by model analysis. Am J Physiol Heart Circ Physiol 260:H146–H157. 10.1152/ajpheart.1991.260.1.H146 [DOI] [PubMed] [Google Scholar]
- Sasayama S, Ross J, Franklin D et al. (1976) Adaptations of the left ventricle to chronic pressure overload. Circ Res 38:172–178. 10.1161/01.RES.38.3.172 [DOI] [PubMed] [Google Scholar]
- Stansfield WE, Rojas M, Corn D et al. (2007) Characterization of a model to independently study regression of ventricular hypertrophy. J Surg Res 142:387–393. 10.1016/j.jss.2007.01.037 [DOI] [PubMed] [Google Scholar]
- Taber LA (1998) Biomechanical growth laws for muscle tissue. J Theor Biol 193:201–213. 10.1006/jtbi.1997.0618 [DOI] [PubMed] [Google Scholar]
- Treibel TA, Kozor R, Schofield R et al. (2018) Reverse myocardial remodeling following valve replacement in patients with aortic stenosis. J Am Coll Cardiol 71:860–871. 10.1016/j.jacc.2017.12.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villari B, Vassalli G, Monrad ES et al. (1995) Normalization of diastolic dysfunction in aortic stenosis late after valve replacement. Circulation 91:2353–2358. 10.1161/01.cir.91.9.2353 [DOI] [PubMed] [Google Scholar]
- Witzenburg CM, Holmes JW (2017) A comparison of phenomenologic growth laws for myocardial hypertrophy. J Elast 129:257–281. 10.1007/s10659-017-9631-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witzenburg CM, Holmes JW (2018) Predicting the time course of ventricular dilation and thickening using a rapid compartmental model. J Cardiovasc Transl Res. 10.1007/s12265-018-9793-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarbrough WM, Mukherjee R, Ikonomidis JS et al. (2012) Myocardial remodeling with aortic stenosis and after aortic valve replacement: mechanisms and future prognostic implications. J Thorac Cardiovasc Surg 143:656–664. 10.1016/j.jtcvs.2011.04.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Z, Chen L, Xiao Y-B et al. (2013) A rabbit model to study regression of ventricular hypertrophy. Heart Lung Circ 22:373–382. 10.1016/j.hlc.2012.11.021 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


