Abstract
Background
Subtalar arthroereisis may cause sinus tarsi pain complications. In this study, we aimed to introduce a customised implant that facilitated treatment effect and less impingement. The biomechanical outcome between the intact and implant conditions was compared using finite element analysis.
Methods
A female patient with flatfoot (age: 36 years, height: 156 cm, body mass: 51 kg) was recruited as the model patient. The customised implant was designed from the extracted geometry. Boundary and loading conditions were assumed from the data of a normal participant. Four gait instants, including the ground reaction force first peak (25% stance), valley (45%), initial push-off (60%) and second peak (75%) were analyzed.
Results
The navicular height was elevated by 4.2% at 25% stance, whereas the strain of the spring, plantar cuneonavicular and plantar cuboideonavicular ligaments were reduced. The talonavicular joint force decreased and the calcaneocuboid joint increased by half and 67%, respectively, representing a lateralised load pathway. There was a stress concentration at the sulcus tali reaching 15.29 MPa
Conclusion
Subtalar arthroereisis using a customised implant may produce some positive treatment effects in terms of navicular height elevation, ligament strain relief and lateralised joint loading pathway. Although the concentrated stress at the sulcus tali did not exceed the threshold of bone breakdown, we could not rule out the potential of vascular disturbance owing to the remarkable elevation of stress. Future study may enlarge the contact area of the bone–implant interface by considering customisation based on the dynamic change of the sinus tarsi during walking gait.
The translational potential of this article
Geometry mismatch of prefabricated implants could be the reason for complications. With the advancement of 3D printing, customising implant becomes possible and may improve treatment outcome. This study implemented a theoretical model approach to explore its potential under a simulation of walking.
Keywords: Extra-osseous talotarsal stabilisation, Pes planus, Posterior tibial tendon dysfunction, Sinus tarsi implant, Talotarsal mechanism
Introduction
Flexible flatfoot deformity (pes planus) is a common medical condition among adults [1]. More than one-tenth of the population suffered from the problem [1]. Posterior tibialis tendon (PTT) dysfunction was believed to be the primary cause because strong association was found between the structural deformity and tendon dysfunction, whereas flatfoot deformity and PTT dysfunction were sometimes used interchangeably [2].
However, some studies opposed this view and suggested that the underlying etiology should be partial talotarsal joint (TTJ) dislocation, and PTT dysfunction could probably be a secondary problem [3]. Patients with flatfoot showed obliterated tarsal sinus axis and navicular displacement which cause hyperpronation [4]. This excessive TTJ motion could strain the adjacent soft tissue and subsequently impairs PTT [5].
Subtalar joint arthroereisis (SJA) has emerged that aims to fix flatfoot deformity by eliminating excessive joint motion through the insertion of a sinus tarsi implant [6]. Although some satisfactory clinical outcomes and joint realignment were reported [3], the patients did not demonstrate significant functional improvement [7]. The procedure also produced a high rate of sinus tarsi pain requiring implant removals [8].
The outcome of SJA was inconclusive [3,6,9]. This could be due to the difference in implant designs, despite that, all of them claimed to restrict excessive motion. The Maxwell–Brancheau implant (Kinetikos Medical Inc., Carlsbad, US) sits beneath the neck of talus and prevents the talus from touching the floor of sinus tarsi, while some implants are fixed on the calcaneus and alter the sinus tarsi axis [6]. For example, the STA-peg implant (Wright Medical Group, Memphis, US) and the Sgarlato implant (Futura Biomedical, Vista, US). A more recent concept brought up by Graham [9] suggested an extra-osseous talotarsal stabilisation procedure (EOTTS) that enforced the TTJ axis with a stent named HyProCure (GraMedica, Macomb, US). However, the contemporary concept had not abated the complication problem [3].
The biomechanics of SJA or EOTTS was evaluated in a few existing studies. Graham et al. [5,10,11] loaded cadaveric feet in a maximally pronated position and showed that EOTTS reduced one-third of the plantar fascia strain, half and 43% of the elongation of PTT and PTT nerve, respectively. Xu et al. [12] compared two kinds of EOTTS devices and found that both devices reduced the strain of the medial ligaments and shifted the medial load to the lateral column, which was similar to current findings. On the other hand, the studies conducted by Martinelli et al. [13] and Wong et al. [14] showed that SJA cannot restore the biomechanical environment to the normal state. However, we believed that the goal of SJA may not necessarily restore the biomechanics to normal state because the impaired soft tissue stabiliser cannot be fixed.
We believed that shape mismatch of the implant could be one of the reasons for the problem because the sinus tarsi tunnel is curved while enforcing a straight stent to the curved tunnel could lead to localised stress, pain or implant instability [9]. We believed that EOTTS could be improved by shape customisation, which is foreseeable with the nowadays 3D medical printing technology.
The objective of this study is to verify that a customised EOTTS implant can produce positive treatment outcome and may not lead to sinus tarsi complications from a biomechanical point of perspective. Finite element (FE) analysis provides a versatile platform to evaluate the biomechanics of the proof of concept in a controlled environment and has been used to evaluate the biomechanics of foot and ankle, including pathomechanism, trauma and surgical outcome [[15], [16], [17]].
Materials and methods
In this study, we have reconstructed a foot model from an adult patient with a flexible flatfoot postoperatively such that we assumed the TTJ axis was corrected normal. Then, we modeled a customised EOTTS stent based on the patient's sinus tarsi geometry. Two model conditions were involved. The patient-specific FE model with the customised implant (implant condition) would be compared with that without the customised implant (intact condition).
Patient recruitment
A female patient diagnosed with severe flexible flatfoot was recruited from the Shenzhen Pingle Orthopedic Hospital. She was aged 36, 156 cm tall and weighed 51 kg. Radiographic examination showed that she had severe navicular drop and arch collapse on both feet. Surgery was indicated and EOTTS was performed on the right foot. Ethical approval has been granted from the authority (Reference number: HSEARS2150121003). The patient was informed and agreed to contribute her clinical data for research purpose.
Model reconstruction—foot and ankle complex
Computer tomography scan (Emotion 16, Siemens Medical Solutions, Erlangen, Germany) was performed on the patient's right foot one-month postoperatively as determined by the orthopedic surgeon based on the patient condition. The resolution was 0.425 mm at 1-mm slice interval. The ankle joint was put at 90° with minimal support or compression on the plantar foot during the scan [18].
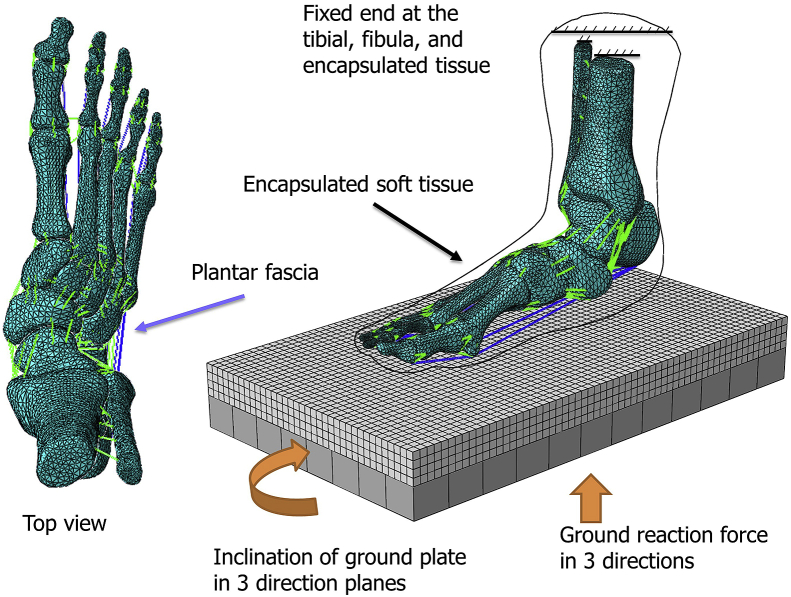
The geometry of the osseous structure and the encapsulated bulk tissue was segmented and reconstructed using commercially available software Mimics (Materialise, Leuven, Belgium) and Rapidform (INUS Technology Ltd., Seoul, Korea) (Figure 1). Ligaments, muscles/tendons, and plantar fascia were built using one-dimensional truss and connectors linking relevant insertion points on the reconstructed osseous geometry. The reconstructed geometry was confirmed with colleagues with expertise in anatomy [15]. The skin layer was defined by assigning a 2-mm membrane thickness over the encapsulated bulk tissue [19]. The geometry of the cartilage was disregarded but resembled by frictionless and nonlinear contact behavior between cartilaginous layer [20], whereas the coefficient of friction between the encapsulated bulk tissue and ground plate was 0.6 [21].
Figure 1.
Finite element model of the foot and ankle complex of a patient with flatfoot.
Model reconstruction—customised sinus tarsi implant
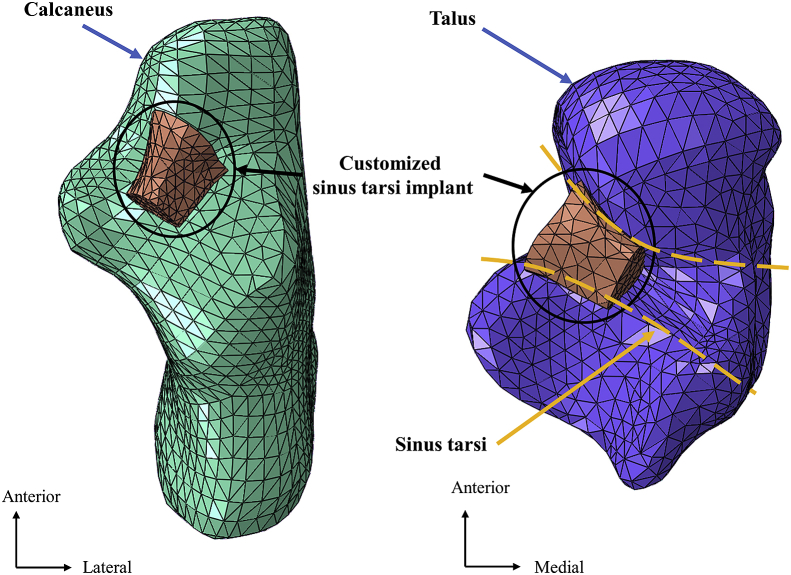
The customised sinus tarsi implant was modeled by the reconstructed geometry of the sinus tarsi using Rapidform (INUS Technology Ltd., Seoul, Korea) (Figure 2). The boundaries of the implant were filleted such that they would not impinge into the joint space. The interaction between the implant and the bone was assumed frictionless because the implant was placed and functioned by the talar impingement mechanism and was not fixed to the bone [22].
Figure 2.
Finite element model of the customised sinus tarsi implant in the talotarsal joint.
Mesh creation
The mesh of the reconstructed geometry was created using the FE software Abaqus (Simulia, Dassault Systèmes, France). Linear tetrahedral elements (C3D4) were assigned to the osseous structures, the encapsulated bulk tissue and the implant because tetrahedral elements were easier to be automatically generated and fitted better in irregular geometries, whilst linear elements were computationally less expensive than second-order elements [23]. Two-node linear three-dimensional elements (T3D2) were assigned to the ligaments. Three-node triangular membrane elements (M3D3) were assigned to the skin layer.
The global element size was 3 mm for the osseous structures and 5 mm for the encapsulated soft tissue and ground plate. The elements were refined locally to accommodate small part geometries, contact regions and abrupt geometrical changes. There were 80,789 elements created for the osseous structure; 265 elements for the ligaments and plantar fascia; 72,403 elements for the encapsulated soft tissue; 6688 elements for the skin layer; 850 elements for the implant and 8640 elements for the ground plate. Mesh convergence test was conducted on the outcome parameters with a reduction of element size of 10% under the simulation of ground reaction force second peak (GRF 2nd) which was the highest load-bearing instant. The deviations of the maximum tensile strain of the spring, plantar cuneonavicular and the plantar cuboideonavicular ligament were 2.7%, 0.0% and 6.9%, respectively. The deviations of the joint forces at the subtalar, talonavicular and calcaneocuboid joints were 4.1%, 5.5% and 9.3%, respectively. The deviations of the peak plantar pressure and the average von Mises stress of the concentrated stress region of the sinus tarsi were 4.5% and 7.9%, respectively. The mesh size was believed to give acceptable results if further refinement produced a deviation of less than 10% as recommended by the Abaqus documentation. Based on the mesh convergence test results, we viewed the size of the mesh in current simulation acceptable.
Material properties
The bones were assumed homogeneous and linearly elastic with the Young's modulus of 10 GPa and Poisson's ratio of 0.3 [24]. Encapsulated bulk tissue was assigned with hyperelastic material property with the second-order polynomial strain energy potential equation with the coefficients, C10 = 0.8556 Nmm−2, C01 = - 0.05841 Nmm−2, C20 = 0.03900 Nmm−2, C11 = - 0.02319 Nmm−2, C02 = 0.00851 Nmm−2, D1 = 3.65273 mm2N-1 [25]. The skin was assigned with hyperelastic material property with the first-order Ogden model with the coefficients, μ = 0.122 kPa and α = 18 [26]. The plantar fascia was modeled with slip-ring connectors that enabled windlass behavior at the metatarsophalangeal joint. The stiffness of the fascia ranged from 182.2 Nmm−1 to 232.5 Nmm−1 depending on the column [27].
The Young's modulus and cross-sectional area of the ligaments were assigned 264.8 MPa and 18.4 mm2, respectively [28,29]. The stiffness of some ligaments was reduced by half to resemble the pathology of flatfoot deformity and PTT insufficiency [30]. These ligaments included the spring (plantar calcaneonavicular) ligament, the long and short plantar (plantar calcaneocuboid) ligaments, the talocalcaneal interosseous ligament, the medial talocalcaneal ligament and the tibionavicular portion of the superficial deltoid ligaments [30,31].
Boundary and loading conditions
In the model assembly, the ends of the tibia and fibula were fixed. GRFs in three directions were applied on the ground plate that simultaneously rotated in accordance with the shank-ground angle extracted from our existing experimental data of a normal patient [32] (Figure 1). Muscle forces were estimated by the multiplication of percentage muscle activation from electromyographic study with the maximum muscle capacity [33,34]. Besides, the Achilles tendon force was obtained from another literature [35]. Tibialis posterior muscle was unloaded to mimic the pathology of PTT insufficiency.
Four instants in walking stance were extracted for analysis, including the occurrence of ground reaction force first peak (GRF 1st), the occurrence of ground reaction force valley (GRF valley), initial push-off and the occurrence of GRF 2nd. They corresponded approximately to 25%, 45%, 60% and 75% stance. The boundary and loading conditions in the four instants are summarised (Table 1).
Table 1.
Boundary and loading conditions of the FE analysis.
| Parameter | GRF 1st | GRF valley | Initial push-off | GRF 2nd |
|---|---|---|---|---|
| % stance | 25% | 45% | 60% | 75% |
| Shank-ground anglea: | ||||
| X: Tilt laterally | X: 1.3° | X: 1.7° | X: 1.7° | X: 3.1° |
| Y: Incline anteriorly | Y: 6.5° | Y: 12.4° | Y: 19.1° | Y: 27.8° |
| Z: Rotate internally | Z: 0.8° | Z: 0.2° | Z: - 1.8° | Z: - 6.6° |
| Ground Reaction Force (% Body weightb) | ||||
| X: (+) Anterior | X: - 11% | X: 1% | X: 4% | X: 10% |
| Y: (+) Medial | Y: 4% | Y: 2% | Y: 3% | Y: 4% |
| Z: Vertical | Z: 126% | Z: 86% | Z: 89% | Z: 106% |
| Achilles tendon force | 0 | 700 N | 1100 N | 1300 N |
| Peroneus brevis | 0 | 61 N | 92 N | 92 N |
| Peroneus longus | 0 | 65 N | 196 N | 0 |
| Flexor digitorum longus | 0 | 55 N | 82 N | 96 N |
| Flexor hallucis longus | 0 | 22 N | 240 N | 284 N |
| Tibialis anterior | 67 N | 0 | 0 | 0 |
Shank-ground angle refers to the rotation of the ground plate with respect to the transverse plane of the shank segment.
The body weight of the model patient is 51 kg. FE, finite element; GRF, ground reaction force.
Model output and analysis
The simulation was conducted with Abaqus 6.11 (Simulia, Dassault Systèmes, France) using the standard quasi-static solver. The intact flatfoot condition was compared with that with a customised sinus tarsi implant. The navicular height, plantar pressure distribution and the von Mises stress of the talus were analyzed. The navicular height was measured by the vertical distance between the navicular tuberosity and the line joining the calcaneal tuberosity and the base of the medial sesamoid. The node labels of the aforementioned landmarks were recorded to make sure that the measurements were consistent among different sets of simulation outcome. Besides, the joint force of the subtalar, talonavicular and calcaneocuboid joints, indicating the load transfer pathway of the rearfoot, were compared. Joint force was defined as the contact force at the joint. The tensile strain of the plantar ligaments of navicular was studied which denotes the stability of the medial longitudinal foot arch and implicates arch collapse. The peak plantar pressure and the average von Mises stress of the concentrated stress region at the sinus tarsi were extracted for evaluation.
Results
Navicular height
The implant consistently elevated the medial longitudinal arch during walking gait. The changes of navicular height from the intact to the implant condition were 28.03 mm–29.21 mm; 27.16 mm–27.43 mm; 26.82 mm–27.07 mm and 27.51 mm–27.71 mm, respectively at GRF 1st, GRF valley, initial push-off and GRF 2nd, respectively. The percentage changes were 4.2%, 1.0%, 0.9% and 0.7%, respectively.
Maximum tensile strain of ligaments
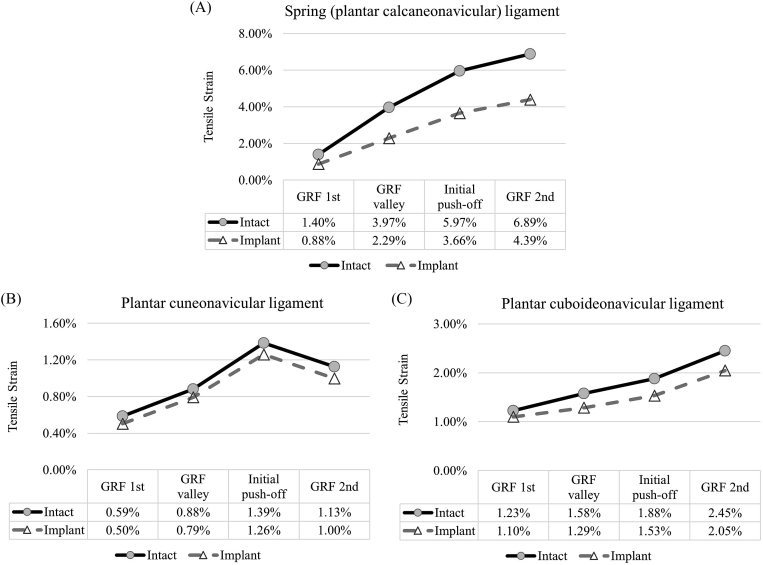
In all the gait instants, the implant conditions showed a lower strain value compared with the intact conditions (Figure 3). The implant produced a larger relief on the spring ligament with a 2.50% reduction of strain. The average reduction of maximum tensile strain over the gait instants were 1.75%, 0.11% and 0.29%, respectively for the spring, plantar cuneonavicular and the plantar cuboideonavicular ligament.
Figure 3.
The maximum tensile strain of the navicular ligaments between the intact and implant conditions during gait. (A) Spring (plantar calcaneonavicular) ligament; (B) plantar cuneonavicular ligament and (C) plantar cuboideonavicular ligament).
Rearfoot joint force
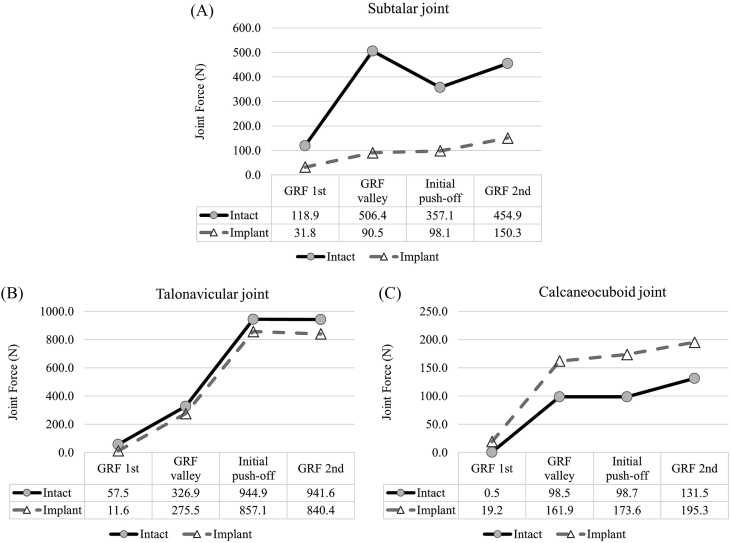
The rearfoot joint forces represented the load transfer pathway of the ankle and are summarised (Figure 4). The subtalar joint force was greatly reduced after the operation, from an average of 359.31 N–92.68 N over the gait instants. The calcaneocuboid joint force decreased while that of the talonavicular joint force increased, which indicated lateralisation of load transfer. The talonavicular joint load increased by 101.21 N at GRF 2nd. The calcaneocuboid joint load reduced by 74.88 N at initial push-off.
Figure 4.
Rearfoot joint forces between the intact and implant conditions during gait. (A) Subtalar joint force; (B) talonavicular joint force and (C) calcaneocuboid joint force.
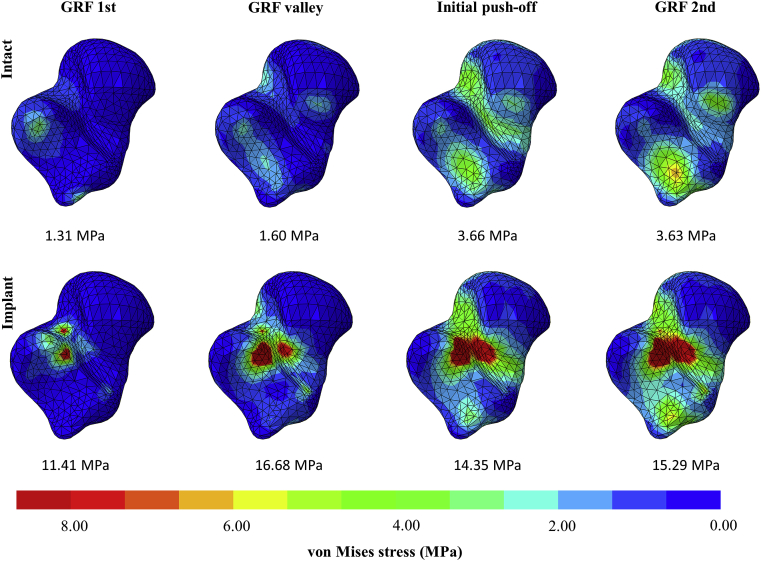
Von Mises stress of talus
The von Mises stress of the talus under the intact and implant conditions during the four gait instants were presented (Figure 5). The implant led to stress concentration at the sulcus tali and the sinus tarsi. The average stress of the concentrated stress region increased from 1.31 MPa to 11.41 MPa at GRF 1st and increased from 3.63 MPa to 15.29 MPa at GRF 2nd.
Figure 5.
Von Mises stress of the talus and the average von Mises stress values of the concentrated stress region at the sulcus tali and sinus tarsi between the intact and implant conditions during gait. (Inferior view).
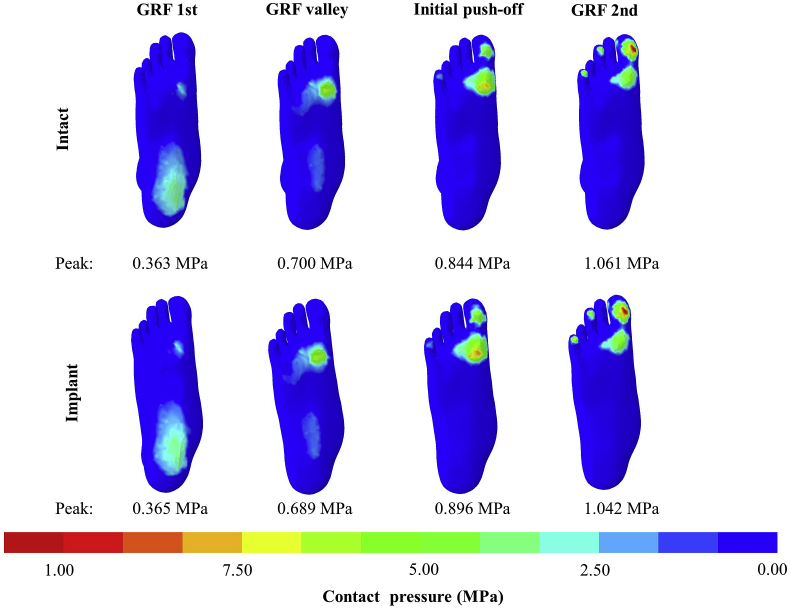
Plantar pressure distribution
There was no observable difference in the plantar pressure distribution between the intact and implant conditions (Figure 6). Under the implant condition, the peak pressures were 0.365 MPa, 0.689 MPa, 0.896 MPa and 1.042 MPa, respectively at GRF 1st, valley, initial push-off and GRF 2nd, which had a change less than 6.5% compared with the intact condition.
Figure 6.
Plantar pressure distribution between the intact and implant conditions during gait.
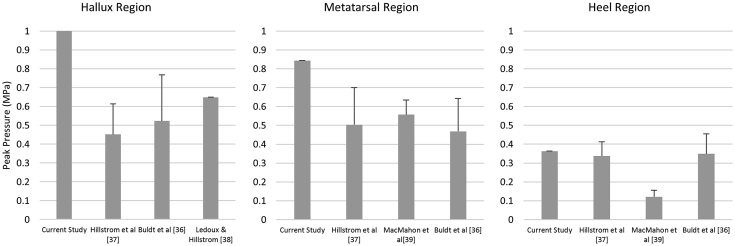
Validation (comparison with existing literature)
Although this study confined to a proof of concept, we attempted to validate the model by comparing our prediction to existing literature and justified the reasonableness of the outcome. The values of the peak plantar pressure among current and existing studies were listed and compared (Figure 7). The peak plantar pressures of this study (intact condition) were 1.061 MPa, 0.844 MPa and 0.363 MPa, respectively at the hallux, metatarsal and heel regions. Existing studies suggested that the peak plantar pressure were 0.452 MPa–0.649 MPa for the hallux region [[36], [37], [38]]; 0.468 MPa–0.557 MPa for the metatarsal region [36,37,39] and 0.121 MPa–0.349 MPa for the heel region [36,37,39]. The predicted values in this study were generally higher than existing literature but in the same order of magnitude.
Figure 7.
Comparison of peak plantar pressure of intact flatfoot in current and existing studies.
The discrepancy could be due to the inclusion of foot support in measurement, which included footwear, insole and the pressure sensor that redistributed the peak pressure. Morales-Orcajo et al. [23] also suggested that the outcome of FE prediction was generally higher than the measured value because of the difference in resolution. In consideration of the aforementioned factor, our findings were considered reasonable, being well within an order of magnitude [40,41].
Discussion
Our FE study supported that the customised SJA implant used for the ankle arthroereisis procedure produced positive treatment effect but may not fully eradicate the risk of sinus tarsi complications because of the alarming stress elevation. It shall also be noted that the conclusion of this simulation study was confined to a theoretical and patient-specific approach, and inherited some other limitations such that the implication and transformation of the findings shall be interpreted cautiously. In this study, we found that the navicular height was elevated after the customised SJA or EOTTS which could represent the alleviation of flatfoot condition. Despite the magnitude was minor, our model was reconstructed from a postoperative patient and the degree of the skeletal deformity was underestimated in the intact state, and thus the improvement by the implant might be underestimated as well. In addition, flatfoot or PTT deficiency involved arch instability ascribed by stretched ligaments [18]. Our study believed that the customised EOTTS alleviated deterioration, supported by the reduced strain of the plantar navicular ligaments in our prediction.
The alteration of internal joint loading may also help prevent the deterioration of flatfoot [18,32]. During walking, load transfer through the talonavicular joint could reach up to 95% of the body weight [42]. Instability of the medial column could divert load direction and exaggerate the arch-flattening effect, which was evidenced by the high and medialised plantar pressure at the midfoot [36]. Our study suggested that EOTTS using the customised implant reduced the medial load that may prevent collapse of the foot arch.
The customised sinus tarsi implant resulted in localised stress at the sulcus tali reaching 15.29 MPa at 75% stance, which was remarkable compared with the intact condition, despite the fact that it did not exceed the required strength (70 MPa) [43] However, it shall be noted that the sinus tarsi are covered with artery and large venous plexus. Additional stress may disturb venous outflow and could be the potential cause of sinus tarsi pain and syndrome [44]. We found no reports on the stress threshold on the vascular disturbance of the sinus tarsi or the sulcus tali.
In this study, we evaluated a proof of concept relating to the customisation of sinus tarsi implant through the FE approach. We believed that this is the first study of this kind using a reconstructed patient-specific flatfoot model, whereas previous research often focused on a flatfoot-related surrogate model from a normal foot [10,11,13]. Yet, the external validity of the study was limited by the single-patient design, predefined set of loading conditions and other assumptions, which was commonly faced by FE study [17]. Meanwhile, it remains difficult and impractical to reconstruct a number of sophisticated models with corresponding experiments to acquire the boundary and loading conditions, as well as validation [17,18]. To this end, the model participant was viewed as a typical patient with severe flexible flatfoot based on the clinical and radiographical observation of the orthopedic surgeon. However, it remains difficult to generalise the findings in this patient-specific approach because flatfoot was often compounded with different severities of different problems, such as different levels of rearfoot eversion, posterior tibial tendon dysfunction and hallux valgus [18,31]. A patient with flatfoot after SJA using EOTTS was recruited as the study model. The selection could facilitate a normal TTJ axis for the customised design. However, it should be noted that the neglection of skeletal deformity may underestimate some adverse biomechanical effect. We assumed the loading conditions of patients with flatfoot were similar to those of normal patients because there was no substantial evidence that the shank-to-ground angles and GRFs were significantly different among normal people and patients with flatfoot [18]. Future study should consider a full patient-specific profile, including kinematics, muscle force, plantar pressure and validation experiments.
Based on current findings, we expected that the implant design can be improved by the following symptoms: consideration of the dynamic change of the sinus tarsi; extension of implant along the medial canalis to allow larger contact area; reduction of implant stiffness, particularly the sulcus tali to reduce stress concentration. Future study should also evaluate the function of the sinus tarsi implant to resist excessive pronation. In addition, different implant designs shall be evaluated and compared to highlight the significance of implant customisation.
In conclusion, our study showed that subtalar arthroereisis using a customised sinus tarsi implant was positive to treatment and prevent progression, which was supported by the findings on elevated navicular height, strain relief on the plantar navicular ligament and lateralised rearfoot load transfer pathway. The concentrated stress in the sinus tarsi and sulcus tarsi may not lead to bone breakdown. However, the elevated stress could be alarming on vascular disturbance. The customised implant could be further improved by considering the dynamic change of the sinus tarsi and enlarged the contact area.
Conflict of Interest
The authors have no conflicts of interest to disclose in relation to this article.
Acknowledgements
This work was supported by National Key R&D Program of China granted by the Ministry of Science and Technology of China (grant number: 2018YFB1107000), General Research Fund granted by the Hong Kong Research Grant Council (grant numbers: PolyU152065/17E, PolyU152002/15E), Key Program and General Program granted by the National Natural Science Foundation of China (grant number: 11732015, 11972315).
Contributor Information
Duo Wai-Chi Wong, Email: duo.wong@polyu.edu.hk.
Yan Wang, Email: annie.wang@connect.polyu.hk.
Wenxin Niu, Email: niu@tongji.edu.cn.
Ming Zhang, Email: ming.zhang@polyu.edu.hk.
References
- 1.Aenumulapalli A., Kulkarni M.M., Gandotra A.R. Prevalence of flexible flat foot in adults: a cross-sectional study. J Clin Diagn Res: JCDR. 2017;11(6):AC17. doi: 10.7860/JCDR/2017/26566.10059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ross M.H., Smith M.D., Vicenzino B. Reported selection criteria for adult acquired flatfoot deformity and posterior tibial tendon dysfunction: are they one and the same? A systematic review. PloS One. 2017;12(12) doi: 10.1371/journal.pone.0187201. e0187201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Graham M.E., Jawrani N.T., Chikka A. Extraosseous talotarsal stabilization using HyProCure® in adults: a 5-year retrospective follow-up. J Foot Ankle Surg. 2012;51(1):23–29. doi: 10.1053/j.jfas.2011.10.011. [DOI] [PubMed] [Google Scholar]
- 4.Graham M.E., Jawrani N.T., Chikka A., Rogers R.J. Surgical treatment of hyperpronation using an extraosseous talotarsal stabilization device: radiographic outcomes in 70 adult patients. J Foot Ankle Surg. 2012;51(5):548–555. doi: 10.1053/j.jfas.2012.05.027. [DOI] [PubMed] [Google Scholar]
- 5.Graham M.E., Jawrani N.T., Goel V.K. Effect of extra-osseous talotarsal stabilization on posterior tibial nerve strain in hyperpronating feet: a cadaveric evaluation. J Foot Ankle Surg. 2011;50(6):672–675. doi: 10.1053/j.jfas.2011.07.004. [DOI] [PubMed] [Google Scholar]
- 6.Needleman R.L. Current topic review: subtalar arthroereisis for the correction of flexible flatfoot. Foot Ankle Int. 2005;26(4):336–346. doi: 10.1177/107110070502600411. [DOI] [PubMed] [Google Scholar]
- 7.Bresnahan P.J., Chariton J.T., Vedpathak A. Extraosseous talotarsal stabilization using HyProCure®: preliminary clinical outcomes of a prospective case series. J Foot Ankle Surg. 2013;52(2):195–202. doi: 10.1053/j.jfas.2012.11.013. [DOI] [PubMed] [Google Scholar]
- 8.Saxena A., Via A.G., Maffulli N., Chiu H. Subtalar arthroereisis implant removal in adults: a prospective study of 100 patients. J Foot Ankle Surg. 2016;55(3):500–503. doi: 10.1053/j.jfas.2015.12.005. [DOI] [PubMed] [Google Scholar]
- 9.Graham M.E. Macomb; Michigan, USA: 2013. HyProCure Extra-osseous talotarsal stabilization guide; p. 41.http://gramedica.com/flipBooks/eotts-guide/files/assets/basic-html/toc.html GraMedica, Available at: [Google Scholar]
- 10.Graham M.E., Jawrani N.T., Goel V.K. Effect of extra-osseous talotarsal stabilization on posterior tibial tendon strain in hyperpronating feet. J Foot Ankle Surg. 2011;50(6):676–681. doi: 10.1053/j.jfas.2011.06.015. [DOI] [PubMed] [Google Scholar]
- 11.Graham M.E., Jawrani N.T., Goel V.K. Evaluating plantar fascia strain in hyperpronating cadaveric feet following an extra-osseous talotarsal stabilization procedure. J Foot Ankle Surg. 2011;50(6):682–686. doi: 10.1053/j.jfas.2011.07.005. [DOI] [PubMed] [Google Scholar]
- 12.Xu J., Ma X., Wang D., Lu W., Zhu W., Ouyang K. Comparison of extraosseous talotarsal stabilization implants in a stage II adult-acquired flatfoot model: a finite element analysis. J Foot Ankle Surg. 2017;56(5):1058–1064. doi: 10.1053/j.jfas.2017.05.009. [DOI] [PubMed] [Google Scholar]
- 13.Martinelli N., Marinozzi A., Schulze M., Denaro V., Evers J., Bianchi A. Effect of subtalar arthroereisis on the tibiotalar contact characteristics in a cadaveric flatfoot model. J Biomech. 2012;45(9):1745–1748. doi: 10.1016/j.jbiomech.2011.11.009. [DOI] [PubMed] [Google Scholar]
- 14.Wong D.W.-C., Wang Y., Chen T.L.-W., Leung A.K.-L., Zhang M. Biomechanical consequences of subtalar joint arthroereisis in treating posterior tibial tendon dysfunction: a theoretical analysis using finite element analysis. Comput Methods Biomech Biomed Eng. 2017;20(14):1525–1532. doi: 10.1080/10255842.2017.1382484. [DOI] [PubMed] [Google Scholar]
- 15.Wong D.W.-C., Niu W., Wang Y., Zhang M. Finite element analysis of foot and ankle impact injury: risk evaluation of calcaneus and talus fracture. PloS One. 2016;11(4) doi: 10.1371/journal.pone.0154435. e0154435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wong D.W.-C., Wang Y., Zhang M., Leung A.K.-L. Functional restoration and risk of non-union of the first metatarsocuneiform arthrodesis for hallux valgus: a finite element approach. J Biomech. 2015;48(12):3142–3148. doi: 10.1016/j.jbiomech.2015.07.013. [DOI] [PubMed] [Google Scholar]
- 17.Wang Y., Wong D.W.-C., Zhang M. Computational models of the foot and ankle for pathomechanics and clinical applications: a review. Ann Biomed Eng. 2016;44(1):213–221. doi: 10.1007/s10439-015-1359-7. [DOI] [PubMed] [Google Scholar]
- 18.Wong D.W.-C., Wang Y., Leung A.K.-L., Yang M., Zhang M. Finite element simulation on posterior tibial tendinopathy: load transfer alteration and implications to the onset of pes planus. Clin BioMech. 2018;51:10–16. doi: 10.1016/j.clinbiomech.2017.11.001. [DOI] [PubMed] [Google Scholar]
- 19.Pailler-Mattei C., Bec S., Zahouani H. In vivo measurements of the elastic mechanical properties of human skin by indentation tests. Med Eng Phys. 2008;30(5):599–606. doi: 10.1016/j.medengphy.2007.06.011. [DOI] [PubMed] [Google Scholar]
- 20.Athanasiou K.A., Liu G., Lavery L., Lanctot D., Schenck R., Jr. Biomechanical topography of human articular cartilage in the first metatarsophalangeal joint. Clin Orthop Relat Res. 1998;348:269–281. [PubMed] [Google Scholar]
- 21.Zhang M., Mak A. In vivo friction properties of human skin. Prosthet Orthot Int. 1999;23(2):135–141. doi: 10.3109/03093649909071625. [DOI] [PubMed] [Google Scholar]
- 22.Graham M.E., Jawrani N.T. Extraosseous talotarsal stabilization devices: a new classification system. J Foot Ankle Surg. 2012;51(5):613–619. doi: 10.1053/j.jfas.2012.05.030. [DOI] [PubMed] [Google Scholar]
- 23.Morales-Orcajo E., Bayod J., de Las Casas E.B. Computational foot modeling: scope and applications. Arch Comput Methods Eng. 2016;23(3):389–416. [Google Scholar]
- 24.Chen W.-P., Ju C.-W., Tang F.-T. Effects of total contact insoles on the plantar stress redistribution: a finite element analysis. Clin BioMech. 2003;18(6):S17–S24. doi: 10.1016/s0268-0033(03)00080-9. [DOI] [PubMed] [Google Scholar]
- 25.Lemmon D., Shiang T., Hashmi A., Ulbrecht J.S., Cavanagh P.R. The effect of insoles in therapeutic footwear--a finite element approach. J Biomech. 1997;30(6):615–620. doi: 10.1016/s0021-9290(97)00006-7. [DOI] [PubMed] [Google Scholar]
- 26.Gu Y., Li J., Ren X., Lake M.J., Zeng Y. Heel skin stiffness effect on the hind foot biomechanics during heel strike. Skin Res Technol. 2010;16(3):291–296. doi: 10.1111/j.1600-0846.2010.00425.x. [DOI] [PubMed] [Google Scholar]
- 27.Kitaoka H.B., Luo Z.P., Growney E.S., Berglund L.J., An K.-N. Material properties of the plantar aponeurosis. Foot Ankle Int. 1994;15(10):557–560. doi: 10.1177/107110079401501007. [DOI] [PubMed] [Google Scholar]
- 28.Milz P., Mhz S., Steinborn M., Mittlmeier T., Putz R., Reiser M. Lateral ankle ligaments and tibiofibular syndesmosis: 13-MHz high-frequency sonography and MRI compared in 20 patients. Acta Orthop Scand. 1998;69(1):51–55. doi: 10.3109/17453679809002357. [DOI] [PubMed] [Google Scholar]
- 29.Siegler S., Block J., Schneck C.D. The mechanical characteristics of the collateral ligaments of the human ankle joint. Foot Ankle Int. 1988;8(5):234–242. doi: 10.1177/107110078800800502. [DOI] [PubMed] [Google Scholar]
- 30.Deland J.T., de Asla R.J., Sung I.-H., Ernberg L.A., Potter H.G. Posterior tibial tendon insufficiency: which ligaments are involved? Foot Ankle Int. 2005;26(6):427–435. doi: 10.1177/107110070502600601. [DOI] [PubMed] [Google Scholar]
- 31.Watanabe K., Kitaoka H.B., Fujii T., Crevoisier X., Berglund L.J., Zhao K.D. Posterior tibial tendon dysfunction and flatfoot: analysis with simulated walking. Gait Posture. 2013;37(2):264–268. doi: 10.1016/j.gaitpost.2012.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wong D.W.-C., Zhang M., Yu J., Leung A.K.-L. Biomechanics of first ray hypermobility: an investigation on joint force during walking using finite element analysis. Med Eng Phys. 2014;36(11):1388–1393. doi: 10.1016/j.medengphy.2014.03.004. [DOI] [PubMed] [Google Scholar]
- 33.Arnold E.M., Ward S.R., Lieber R.L., Delp S.L. A model of the lower limb for analysis of human movement. Ann Biomed Eng. 2010;38(2):269–279. doi: 10.1007/s10439-009-9852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Perry J., Burnfield J.M. Slack; 1993. Gait analysis: normal and pathological function; pp. 51–87. ISBN, 978-1-55642-192-1. [Google Scholar]
- 35.Fröberg Å., Komi P., Ishikawa M., Movin T., Arndt A. Force in the achilles tendon during walking with ankle foot orthosis. Am J Sports Med. 2009;37(6):1200–1207. doi: 10.1177/0363546508330126. [DOI] [PubMed] [Google Scholar]
- 36.Buldt A.K., Forghany S., Landorf K.B., Levinger P., Murley G.S., Menz H.B. Foot posture is associated with plantar pressure during gait: a comparison of normal, planus and cavus feet. Gait Posture. 2018;62:235–240. doi: 10.1016/j.gaitpost.2018.03.005. [DOI] [PubMed] [Google Scholar]
- 37.Hillstrom H.J., Song J., Kraszewski A.P., Hafer J.F., Mootanah R., Dufour A.B. Foot type biomechanics part 1: structure and function of the asymptomatic foot. Gait Posture. 2013;37(3):445–451. doi: 10.1016/j.gaitpost.2012.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ledoux W.R., Hillstrom H.J. The distributed plantar vertical force of neutrally aligned and pes planus feet. Gait Posture. 2002;15(1):1–9. doi: 10.1016/s0966-6362(01)00165-5. [DOI] [PubMed] [Google Scholar]
- 39.MacMahon A., Hillstrom H.J., Do H.T., Chan J.Y., Deland J.T., Ellis S.J. In vivo plantar pressures in adult-acquired flatfoot compared to control using an intraoperative pedobarographic device. HSS J®. 2017;13(2):136–145. doi: 10.1007/s11420-017-9542-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.DeVocht J.W., Goel V.K., Zeitler D.L., Lew D. Experimental validation of a finite element model of the temporomandibular joint. J Oral Maxillofac Surg. 2001;59(7):775–778. doi: 10.1053/joms.2001.24292. [DOI] [PubMed] [Google Scholar]
- 41.Verver M., Van Hoof J., Oomens C., Wismans J., Baaijens F. A finite element model of the human buttocks for prediction of seat pressure distributions. Comput Methods Biomech Biomed Eng. 2004;7(4):193–203. doi: 10.1080/10255840410001727832. [DOI] [PubMed] [Google Scholar]
- 42.Wang Y., Li Z., Wong D.W.-C., Cheng C.-K., Zhang M. Finite element analysis of biomechanical effects of total ankle arthroplasty on the foot. J Orthop Translat. 2018;12:55–65. doi: 10.1016/j.jot.2017.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yousefi A.-M. A review of calcium phosphate cements and acrylic bone cements as injectable materials for bone repair and implant fixation. J Appl Biomater Funct Mater. 2019;17(4) doi: 10.1177/2280800019872594. 2280800019872594. [DOI] [PubMed] [Google Scholar]
- 44.Schwarzenbach B., Dora C., Lang A., Kissling R. Blood vessels of the sinus tarsi and the sinus tarsi syndrome. Clin Anat. 1997;10(3):173–182. doi: 10.1002/(SICI)1098-2353(1997)10:3<173::AID-CA3>3.0.CO;2-V. [DOI] [PubMed] [Google Scholar]