Significance
Decline in winds over past decades were observed over high northern latitudes (>50°), yet its influence on the date of autumn leaf senescence (DFS) remains unknown. Using ground observations, flux measurements, and remote sensing imagery, here we show that decline in winds significantly extended DFS over high latitudes at a magnitude comparable with the temperature and precipitation effects. We found that decline in winds reduces evapotranspiration, causes fewer damaging effects, and also results in decreased cooling effect. Our results therefore are of great significance for carbon cycle modeling because an improved algorithm based on these findings projected overall widespread earlier DFS by the end of this century, contributing potentially to a positive feedback to climate.
Keywords: climate change, foliar senescence, high latitudes
Abstract
The high northern latitudes (>50°) experienced a pronounced surface stilling (i.e., decline in winds) with climate change. As a drying factor, the influences of changes in winds on the date of autumn foliar senescence (DFS) remain largely unknown and are potentially important as a mechanism explaining the interannual variability of autumn phenology. Using 183,448 phenological observations at 2,405 sites, long-term site-scale water vapor and carbon dioxide flux measurements, and 34 y of satellite greenness data, here we show that the decline in winds is significantly associated with extended DFS and could have a relative importance comparable with temperature and precipitation effects in contributing to the DFS trends. We further demonstrate that decline in winds reduces evapotranspiration, which results in less soil water losses and consequently more favorable growth conditions in late autumn. In addition, declining winds also lead to less leaf abscission damage which could delay leaf senescence and to a decreased cooling effect and therefore less frost damage. Our results are potentially useful for carbon flux modeling because an improved algorithm based on these findings projected overall widespread earlier DFS than currently expected by the end of this century, contributing potentially to a positive feedback to climate.
Understanding the responses of the date of autumn foliar senescence (DFS) to climate change has recently received increased focus for a better interpretation of carbon uptake, but accurately predicting DFS globally using models remains challenging (1). Nonurbanized lands in the high northern latitudes (>50°) are currently a large carbon sink but have experienced the greatest increase in air temperature (2–6). In those ecosystems, the annual net ecosystem productivity (NEP) has increased for years with an earlier start of spring leaf unfolding (7–11). A delay of DFS has been reported for middle to high latitudes from both eddy covariance (FLUXNET) measurements and remotely sensed observations of vegetation reflectance (8, 12–15). Such a trend of DFS was found to contribute to an overall increase of annual NEP for temperate forests (16, 17) but may potentially offset carbon uptake due to extended ecosystem respiration for higher latitude ecosystems (3).
Climate change over the last few decades has had substantial effects on vegetation phenology (18, 19). Global increases in autumn temperature could delay DFS (14, 20), yet there are also studies showing either earlier or relatively stable DFS, with a possible explanation from opposite changes in DFS in response to daytime and nighttime warming (21). Decreases in precipitation and associated drought may have more complicated influences on DFS, depending on the severity of drought and on regional characteristics of plant functional types (22). In addition to changes in temperature and precipitation, wind speed over the last three decades shows widespread decreasing trends in the northern hemisphere (23, 24) with possible impacts on plant growth, chemical composition, structure, and morphology (25–28). The drying effect of wind affects foliar gas and heat exchange and could increase water stress by reducing the thickness of foliar boundary layers (27), so the responses of DFS to wind may depend on water stress. We therefore ask 1) what are the physical and physiological impacts of declined winds on plant growth and 2) how these changes affect DFS accordingly at high northern latitudes where a pronounced decline in winds was observed. To this end, we used gridded meteorological data (temperature, precipitation, cloud cover, and wind speed) together with DFS data from three independent data sets: 1) 183,448 phenological observations at 2,405 ground sites since the 1980s, 2) 267 site-years of data from the FLUXNET eddy covariance network, across 18 long-term sites over 1994 to 2014 (SI Appendix, Fig. S1), and 3) latest Normalized Difference Vegetation Index data (NDVI, GIMMS3g.v1) for 1982 to 2015.
Results
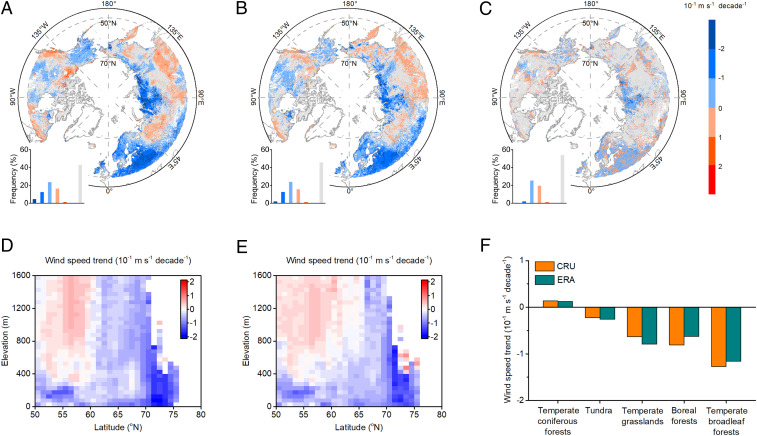
Climate forcing over the preseason, defined as the period during which a given climate variable is most correlated with ensuing leaf senescence, has a better predictive strength on DFS than forcing over autumn months (21), so we used these preseason variables (e.g., temperature, precipitation, etc.) in our analysis (Materials and Methods). Meteorological variables have been reported to be autocorrelated, so we used partial correlation to remove the effects of temperature, precipitation, and solar radiation for investigating the response of DFS to variations in wind speed, as similarly conducted in previous analyses (7). We found dominantly decreasing trends of wind speed for both climatic research unit (CRU) (69.6% versus 30.4%, Fig. 1A) and European Centre for Medium-Range Weather Forecasts (ECMWF) Re-Analysis (ERA) (70.1% versus 29.9%, Fig. 1B) climate datasets in the high latitudes, against increasing trends at lower latitudes at higher elevations (Fig. 1 D and E). The two datasets were highly consistent in terms of temporal trends (Fig. 1C). Wind trends over tundra and temperate coniferous forests were negligible comparing to (negative) trends over boreal forest, temperate broadleaf forests, and temperate grasslands (Fig. 1F).
Fig. 1.
Interannual trend of wind speed at high northern latitudes (>50°). A, B, and C represent temporal trend of wind speed from (A) CRU datasets and (B) ERA datasets and (C) the difference between CRU- and ERA-based wind speed trend, respectively. The gray color represents pixels with nonsignificant trends. (D and E) Variations of wind speed trend along elevation and latitude gradients for (D) CRU datasets and (E) ERA datasets, respectively. (F) Wind speed trend for different vegetation types for CRU and ERA datasets.
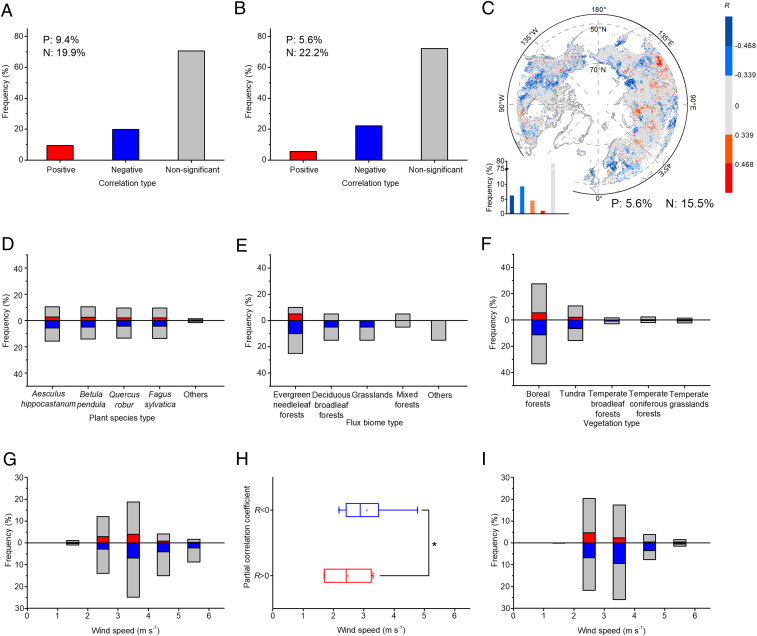
Analyses for site-level phenological observations found that wind speed was significantly correlated with DFS for 29.3% of the sites (Fig. 2A). In particular, more than two-thirds (67.9%) of the sites’ time series showed significant negative correlations (R < 0, P < 0.05). Grouping into species yielded similar results (Fig. 2D). Overall, wind speeds becoming lower (stilling) were correlated with a delayed DFS and vice versa. We also looked at the distributions of the correlation along mean wind speed gradients (Fig. 2G) and found a large fraction (82.4%) of significant positive correlations at wind speeds <4 m/s, which decreased to 17.6% for speeds >4 m/s.
Fig. 2.
Associations (partial correlations) between wind speed and the DFS north of 50°N. (A, D, and G) Fractions of ground phenological observation sites with partial correlations of distinct sign/significance for all the data, grouped per species, and grouped per mean wind speed categories. (B, E, and H) Same for eddy covariance observations. (C, F, and I) Same for satellite NDVI data. The gray pixels in C represent nonsignificant correlation. Significance was set at P < 0.05.
The analysis of flux measurements (267 time series at 18 sites) showed broadly similar results yet from few sites overall with five sites having significant (P < 0.05) partial correlation between wind speed and DFS, among which four having negative partial correlation values (Fig. 2B), three being forests and one nonforest (Fig. 2E). At the flux measurement sites, the DFS was defined as the local extrema in the rate of change of daily Gross Primary Productivity (GPP) in autumn. The median of wind speed for positively correlated sites was ∼2.3 m/s, 24.2% lower than that of negatively correlated sites (Fig. 2H).
The analysis of long-term NDVI data gives results generally consistent with site-level data, with 21.1% of the pixels having wind speeds significantly correlated with DFS, among which 73.4% pixels were negatively partially correlated (Fig. 2C). Site- and satellite-level observations showed good agreement for the fractions of data with significant association between wind speed and DFS (SI Appendix, Fig. S2). Classification of NDVI data into different plant functional types showed that boreal forests (3.9% of 60.8%) and tundra ecosystems (1.5% of 26.4%) had dominantly negative partial correlations (Fig. 2F). The most significantly positive correlations (88.7%) for satellite observations were found for low wind speeds <4 m/s, and only 11.3% of the correlations were positive when the wind speed reached above 4 m/s (Fig. 2I). We also found that pixels with positive correlations between DFS and winds were mainly located in regions experiencing a low level of climate warming but with sufficient precipitation increase (SI Appendix, Fig. S3).
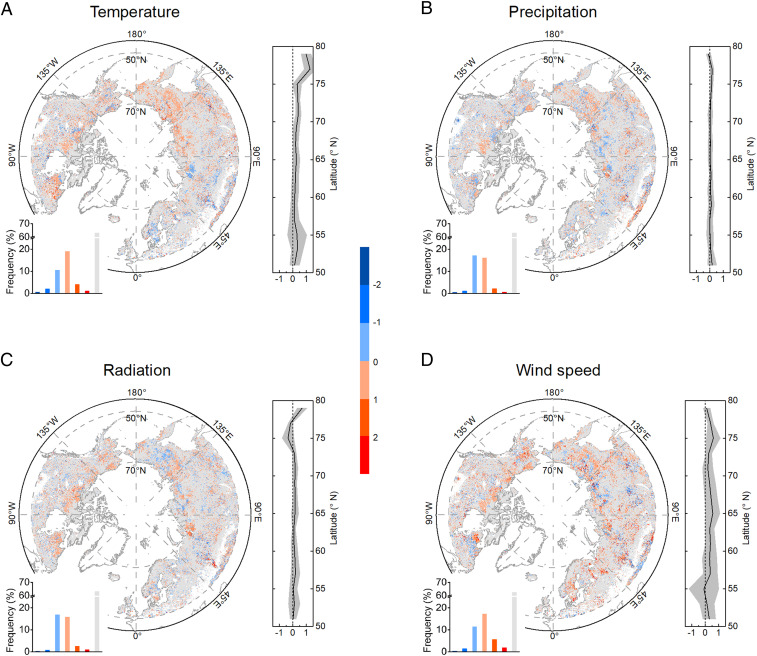
Multiple linear regressions were used to calculate the sensitivities of DFS to meteorological variables, and the Theil–Sen slope estimator was applied to calculate the temporal trend of DFS and meteorological variables. For pixels with a statistically significant F-value (P < 0.05) in the regression model, we calculated the contribution coefficients (Materials and Methods) of preseason temperature, precipitation, solar radiation, and wind speed to the interannual variations of DFS (Fig. 3). Overall, the regression model explains a significant amount of variance in the DFS for only 31% of pixels. Preseason wind can explain on average 33% of the variation of DFS, which is higher than temperature (24%), precipitation (9%), and solar radiation (14%).
Fig. 3.
Contribution coefficients of meteorological variables to interannual variations of DFS. (A–D) Degree to which (Materials and Methods) interannual variations of DFS can be explained by preseason temperature, precipitation, solar radiation, and wind speed, respectively. Left shows spatial distribution of contribution coefficients. Right shows contribution coefficients latitudinal distributions. The gray color represents nonsignificant correlation. Significance was set at P < 0.05.
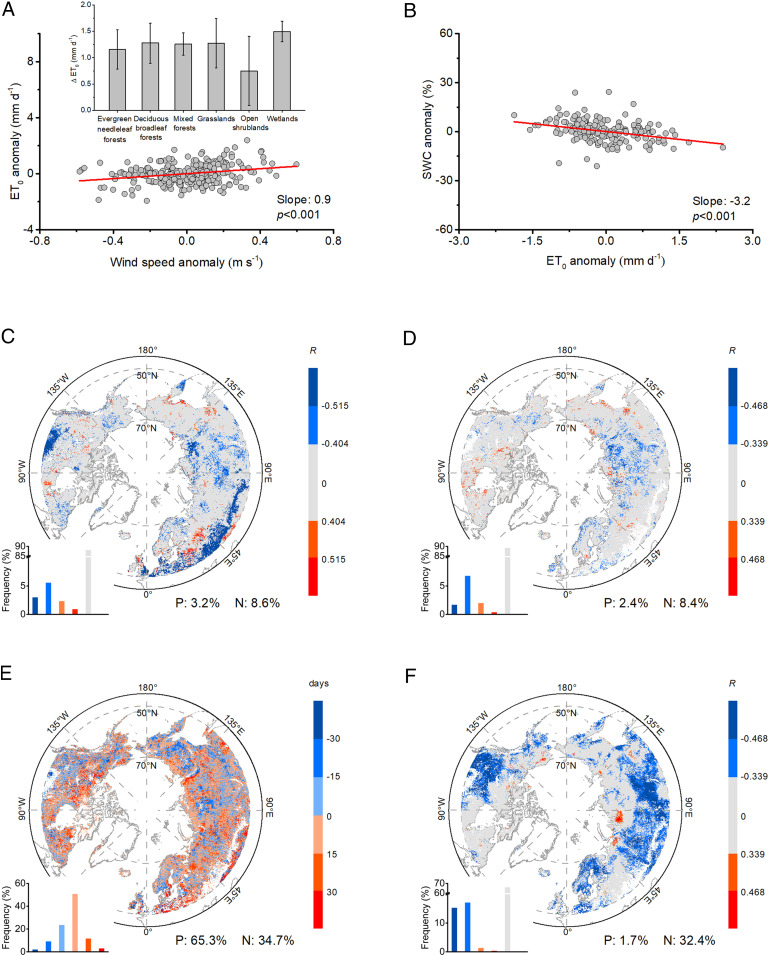
The decline in winds could have multiple beneficial effects sustaining a longer growth, including alleviated drying conditions and reduced risk from frost damage lengthening the senescence date of leaves (Fig. 4). Using flux measurements, we found a significantly positive correlation between wind speed anomaly and reference evapotranspiration (ET0) anomaly (P < 0.001), with an increase of ET0 by 1.2 ± 0.4 mm day−1 per unit increase (m · s−1) in wind (Fig. 4A). Combined with the negative relationship between ET0 and soil water content (SWC, Fig. 4B), we showed that stronger winds increase ET0 and further deplete soil water. Satellite observations further confirmed an alleviated drying effect under lower winds, given that more than two-thirds of the pixels with a significant correlation between wind speed and DFS showing a negative correlation between wind speed and Soil Moisture Saturation (SMS, Fig. 4C) and Volumetric Surface Soil Moisture (SMV, Fig. 4D), respectively. Similar patterns were also found between wind speed and three additional independent water stress indicators, including the Standardized Precipitation Evapotranspiration Index (SPEI), the Palmer Drought Severity Index (PDSI), and the Vegetation Optical Depth (VOD) (SI Appendix, Fig. S4). A later senescence of leaves under lower winds is supported by distributions of the difference between the DFS of the year with the lowest wind speed and the year with the highest wind speed for each pixel (Fig. 4E). We found that more than 65% of pixels showed positive values for this difference. An interesting result was that about 32.4% of the pixels showed that stronger winds could be significantly associated with a decrease in the dew point temperature (Tdew, Fig. 4F) and consequently increase vegetation exposure to frost damage. Therefore, the decline in winds would reduce the cooling effect, providing better leaf survival conditions for longer growth.
Fig. 4.
Relationships between wind speed and hydroclimatic variables affecting autumn DFS. (A) Relationship between wind speed anomaly and reference evapotranspiration (ET0, Materials and Methods) anomaly and the change in ET0 for a unit increase of wind speed in different wind speed categories. (B) Relationship between ET0 anomaly and soil water content (SWC, %) anomaly. C and D represent the partial correlation between wind speed and SMS (C) and SMV (D), respectively. (E) Difference of DFS between the year with the lowest wind speed and the highest wind speed. (F) Partial correlation between wind speed and Tdew. The gray color in C, D, and F represents nonsignificant correlation. Significance was set at P < 0.05.
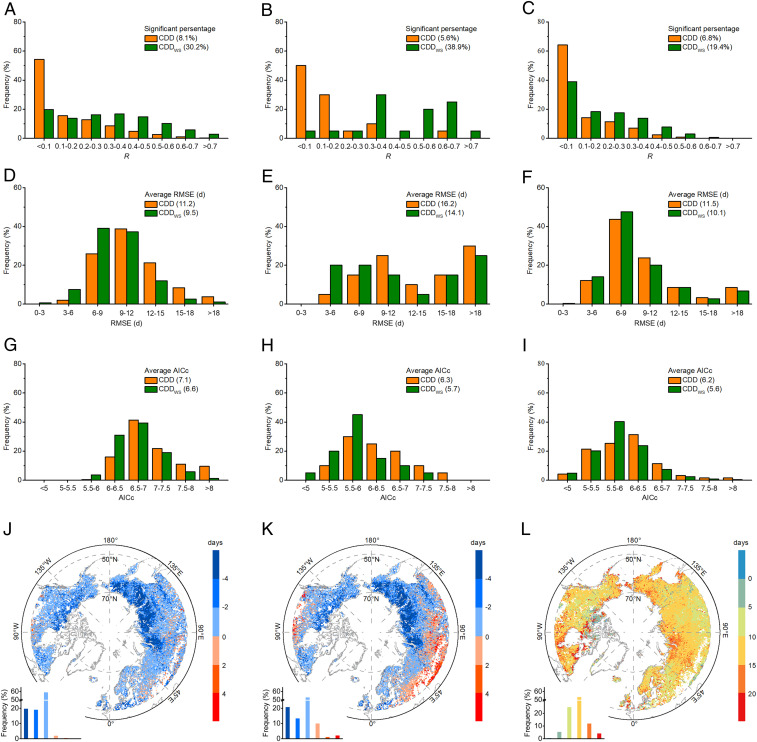
We built a model for predicting DFS by incorporating changes in wind speed into the traditional cooling degree day (CDD) model used in many ecosystem models (the model is called CDDWS, Materials and Methods). We compared the predictions of the CDD and CDDWS models using site-level and remotely sensed observations (Fig. 5 A–I). Using CDDWS for site-level observations was more accurate in terms of the percentage of significant pixels with observations, correlation coefficient (R), and the root mean square error (RMSE) between observed and modeled DFS, the corrected Akaike information criterion (AICc) (Fig. 5 A, D, and G). Only 8.1% of the modeled DFS time series were significantly correlated with observed values using the traditional CDD approach, and this percentage increased to 30.2% using the CDDWS approach. RMSE and AICc were reduced by ∼15% and ∼7%, respectively. Similar improvements were observed using the CDDWS model for explaining the observed DFS at the flux measurement sites, with seven sites having significant model–data correlations against only one for the CCD model and the CDDWS model having ∼13% and ∼10% lower of RMSE and AICc (Fig. 5 B, E, and H). Comparison with satellite data produced better results than ground observations as indicated by nearly three times more pixels having significant model–data correlations with the CDDWS model and ∼12% and ∼10% lower values of RMSE and AICc (Fig. 5 C, F, and I). More detailed results for species, flux site, and plant functional types are provided in SI Appendix, Figs. S5–S7. Give that the CDDWS model had a better predictive power for the variations of DFSs, we applied it to predict future DFS under two climate scenarios, the Representative Concentration Pathway (RCP) 4.5 and RCP 8.5 ones. With projected temperature and wind speed changes SI Appendix, Fig. S8), DFS was predicted to come earlier with the CDDWS model than with the CDD model under the RCP 4.5 scenario, across 96% of the pixels (Fig. 5J). The average difference of the predicted DFS between CDDWS and CDD was about 2.7 d. Interestingly, the DFS from the CDDWS model is projected to occur later at lower latitudes and earlier for most regions under the RCP 8.5 scenario (Fig. 5K). In addition, the DFS from the CDDWS model is projected to occur earlier under the RCP 8.5 scenario, by on average 11.8 d, compared with the RCP 4.5 scenario (Fig. 5L).
Fig. 5.
Comparison between the traditional CDD model for predicting DFS and the CDD model modified to include wind speed (CDDWS). (A, D, and G) Frequency of significant observations, RMSE (days), and the AICc using ground data, respectively. (B, E, and H) Frequency of significant observations, RMSE, and AICc using flux data, respectively. (C, F, and I) Frequency of significant observations, RMSE, and AICc for the NDVI3g data, respectively. (J and K) Differences between projected DFS using CDD and CDDWS under scenarios of RCP 4.5 (J) and RCP 8.5 (K), respectively. (L) Difference between projected DFS using CDDWS under the RCP 4.5 and the RCP 8.5. Significance was set at P < 0.05.
Discussion
Efforts have been made to explore the responses of DFS to changes in climate (29, 30). We here provided suggestive evidence that changes in wind speed over the last three decades could have contributed an overall negative effect on DFS at high latitudes where site-level and remotely sensed observations indicate that DFS has been extended (10, 14). Wind speed varied substantially due to changes in the roughness of terrestrial surfaces (e.g., land cover change) and increased levels of atmospheric aerosols (23, 24). The site-level and remotely sensed observations suggest that increased wind speed was associated with an earlier DFS and vice versa.
The alleviated drying effect from declined winds is the most probable explanation for the observed negative relationships between wind speed and DFS at about one-third of the locations/regions. Lower winds reduce ecosystem-level drought through decreased ET and thus enhanced water availability, as suggested from statistical analysis of flux measurements and remote sensing observations (Fig. 4 and SI Appendix, Fig. S4). Advanced DFS and leaf loss are also a mechanism for the adaption of drought because earlier DFS reduces the water demand and risks of xylem embolism and plant desiccation (31, 32). In addition, under water stress conditions, the increase in abscisic acid and the decline in cytokinins may induce senescence, causing a decline in photosynthesis and phloem loading (33). An earlier detachment of leaves under high winds is the result of physical damage from higher winds (e.g., by indirect abrasion due to soil or ice particles or direct damage leading to foliar tearing or branch loss). This process could aggravate the drying effect because the physical damage could lead to an unexpected faster loss of water that is associated with leaf folding and even wilting (25, 28, 34). The reduced risk from frost damage with declined winds may be particularly important for cold regions. Previous studies reported that windbreak or lower winds can increase plant environment temperature and thus extend growing season length for cold regions (35). Similarly, our results revealed that lower wind speed could decrease vegetation exposure to frost by rising Tdew in autumn, potentially further shifting to later leaf senescence (36).
Nearly one-third of satellite and ground site data with significant partial correlations between wind speeds and DFS has positive partial correlation values, suggesting that at those locations, a lower wind speed could lead to an earlier DFS. Ecological processes may be more important than physiological effects of water stress in explaining this response. Plants can resist to some types of wind damage as herbaceous plants can recover from wind damage, and woody plants may partially recover if sufficient supplies of water and nutrients are available (25). Plants, though, are also adapted to specific environments and develop several approaches of acclimation with attributes of reorientation and reconfiguration subject to wind variations (37). They can therefore survive if the winds are not too strong and can even grow better, because these species adaptations can lead to intrinsic differences in their timing of foliar senescence that are optimized to maximize carbon gain and minimize the loss of water (21). We suggest that the balance between the effects of climate warming and water supply on plant growth could explain these positive correlations. Precipitation has been reported to have a dominant positive role in extending DFS (13), especially in arid or semiarid regions. Our results also found that most positive wind–DFS correlations were distributed in regions with increasing precipitation (SI Appendix, Fig. S3 A and B), indicating that providing sufficient water supply could offset the drying effect of strong winds and delay DFS accordingly. In comparison, negative correlations dominated in regions with higher-rate temperature increases (SI Appendix, Fig. S3 A and C) because too much higher temperature would accelerate water loss from the surface of soil and canopy through ET processes even when precipitation is increasing, further triggering drought-induced DFS for environmental adaptation (38).
Conclusion
Future climate may be more variable, with larger changes in temperature and precipitation. Predicting how wind speeds will change with a changing climate remains challenging, but evidence suggests that wind speeds will be more extreme in several regions, even if the mean annual speed continues to decrease (39). The combination of extreme and chronic winds would have significant impacts on plant growth, and these consequences for regional and global carbon uptake may also be as important as that from variations in temperature and precipitation. While there are limitations on the gridded meteorological products over high latitudes, the overall findings of our analyses are reliable because the interannual variability of these variables was used instead of the absolute values. We found that DFS would be earlier than currently expected for most regions under two RCP scenarios and that this average gap would be even larger for a scenario with higher emissions of CO2. Given that the DFS has been tightly connected with annual carbon uptake, an earlier DFS projected would cause a positive feedback to the climate and consequently needs our attention and should be correctly represented in future ecosystem models.
Materials and Methods
Site-Level Phenological Data.
Two independent site-level phenological datasets were used in our study. The first phenological observations were obtained from the Pan European Phenology Project (PEP725), which has maintained long-term phenological records since 1868 for multiple growth stages and plant species. We used eight typical woody species with long-term records at all available sites (totally 2,405 sites and 183,448 records) from PEP725 at high northern latitudes (>50°) for 1982 to 2015 (40) (SI Appendix, Fig. S1 and Table S2). The region determination was based on the pronounced decline in winds (SI Appendix, Fig. E1). The foliar senescence date (DFS) was defined as the date when >50% of tree leaves changed color in autumn (green to red or yellow) (41). Records with fewer than 10 y of continuous time series were removed from the analysis due to their high uncertainty, which is required to statistically calculate the partial correlation coefficient between wind speed and DFS (42).
The second site-level phenological data were derived from flux-measured daily GPP, based on the eddy covariance technique. In this study, we used all available 18 flux sites with at least 10 y of continuous measurement at high northern latitudes (>50°, SI Appendix, Table S3), with totally 267 site-year records of GPP from FLUXNET (https://fluxnet.fluxdata.org/). All flux sites in our study were classified into different biome types by the International Geosphere–Biosphere Program classifications. Here, we applied the double logistic function to determine carbon flux DFS (43). We first smoothed the curve of daily GPP using Savitzky–Golay filter. Daily GPP time series were divided into two parts by the maximum GPP that often occurred in summer, then a piecewise logistic function was applied to fit each part:
| [1] |
where is the day of year (DOY), is the observed GPP or NDVI value at time, .a1 is the background GPP or NDVI, and a2 is the difference between the background and the amplitude of the late summer and autumn plateau both in GPP or NDVI units. a3 and a5 are the midpoints in DOYs of the transitions for green‐up and senescence/abscission, respectively. a4 and a6 are the transitions curvature parameters (normalized slope coefficients). a7 is the summer greendown parameter. DFS was then determined as the local extrema in the rate of change of the GPP or NDVI curve for the second part of the data.
Satellite-Derived DFS.
We used GIMMS3g NDVI data derived from the Advanced Very High Resolution Radiometer (41), with a spatial resolution of 1/12° and a 15-d interval to estimate DFS for 1982 to 2015 at high northern latitudes (>50°) (44, 45).
We eliminated the impact of agricultural ecosystems, in which DFS is affected by human activity, by using the MCD12Q1 MODIS Version 6 land cover product to exclude cropland (46). All analyses in this study were investigated for vegetation types using a global map of terrestrial ecoregions (47). We also removed areas with sparse vegetation by eliminating pixels with mean annual NDVI < 0.1. The NDVI time series were smoothed using a modified Savitzky–Golay filter to remove abnormal data and especially to remove the noise from the snow at high latitudes (48). We then used two methods to estimate NDVI3g-based DFS.
The first method was a midpoint threshold approach based on locally tuned NDVI and an annually defined threshold of the NDVI ratio (49). The NDVI ratio was calculated as:
| [2] |
where is the daily NDVI from the NDVI3g data and and are the annual maximum and minimum of the NDVI curve, respectively. DFS is defined as the day of the year when decreased to 0.5.
The second method was based on the double logistic function (Eq. 1) (50). In this study, we used average DFS from midpoint threshold approach and double logistic function as satellite-derived DFS.
Climatic Data.
For the analysis of site-level phenological and remotely sensed observations, we used two monthly 10 m wind speed products for 1982 to 2015. The first wind speed product is obtained from TerraClimate, a dataset of monthly climate for global terrestrial surfaces at a spatial resolution of 1/24°. The 10 m wind speed of TerraClimate is extracted from Climatic Research Unit Time Series (CRU-TS 4.00), which is interpolated by massive climatic stations (51). The second wind speed product is extracted from ERA5, the fifth generation European Centre for Medium-Range Weather Forecasts (ECMWF) Re-Analysis for the global climate and weather, monthly averaged reanalysis data at a spatial resolution of 0.25° (52). These two datasets showed similar spatial and temporal patterns (Fig. 1). We applied the average of wind speed from TerraClimate and ERA5 as final wind speed to reduce the uncertainty from using a single dataset in this study. The monthly temperature, precipitation, and cloud cover (a proxy of solar radiation) for 1982 to 2015 at resolutions of 0.5° were extracted from CRU-TS 4.00 (53). These climatic datasets were widely used to analyze the impact of meteorological variables on observational and satellite-derived phenology (7, 13, 21). Given the uncertainty of gridded climate factors (e.g., CRU products often provide underestimated predictions due to the limited distribution of weather stations) in high latitudes (SI Appendix, Figs. E2 and E3), cautions are needed when interpreting the partial correlations (Fig. 1) and temperature-based modeling results (Fig. 5 and SI Appendix, Figs. S5–S7). However, these limitations could be acceptable because our analyses mainly focused on the interannual variability of these data rather than on the absolute differences. For flux-based analysis, we used site measurements of ancillary physical variables (e.g., wind speed, air temperature, precipitation, and solar radiation). To determine the effect of wind speed on evapotranspiration (ET), we applied the FAO56 Penman–Monteith method to calculate the reference ET (ET0, mm · day−1), defined as the rate at which readily available soil water is vaporized from specified vegetated surfaces (54),
| [3] |
in which Rn is the net radiation at the vegetation surface (MJ m−2 · day−1), G is the soil heat flux density (MJ m−2 · day−1), T is the mean air temperature at 2 m height (°C), u2 is the wind speed at 2 m height, es is the vapor pressure of the air at saturation (kPa), ea is the actual vapor pressure (kPa), Δ is the slope of the vapor pressure curve (kPa · °C−1), and γ is the psychrometric constant (kPa ⋅ °C−1).
As to traditional CDD and CDD with wind speed (CDDWS), we used daily mean temperature acquired from the Physical Sciences Division of the National Oceanic and Atmospheric Administration Earth System Research Laboratory and daily mean wind speed from Global Land Data Assimilation System (GLDAS-1) (55) to model the past DFS (1982 to 2015). We predicted future DFS (2081 to 2100) using daily mean temperature and wind speed, simulated using the Community Climate System Model under the RCP 4.5 and RCP 8.5 scenarios of climate change.
Water Indicators.
We used six independent water indicators in total, including the SMS, SMV, Tdew, PDSI, SPEI, and VOD to account for the response of DFS to changes in wind speed at high latitudes. We provided a summary of the data used in this study (SI Appendix, Table S1).
Monthly SMS (%) for 1992 to 2015 and Monthly SMV (m3/m3) for 1982 to 2015 at a spatial resolution of 0.25° were derived from Copernicus Climate Change Service, providing estimates of soil moisture from numerous satellite sensors, including SSMI, AMSRE, AMSR2, and SMOS. Monthly Tdew (°C) for 1982 to 2015 at a spatial resolution of 0.1° were obtained from the ERA5-Land dataset, produced by replaying the land component of the ECMWF ERA5 climate reanalysis. Monthly PDSI for 1982 to 2015 were obtained from TerraClimate at a spatial resolution of 1/24°. The PDSI data set was generated by a modified Thornthwaite–Mather climatic water balance model and extractable soil water storage capacity data at a 0.5° grid (51). We acquired monthly SPEI for 1982 to 2015 at a spatial resolution of 0.5°, calculated using the difference between precipitation and potential ET from the SPEI base v. 2.5 at Consejo Superior de Investigaciones Científicas (56). The SPEI data set consisted of multiscalar monthly SPEI, so we selected 3-mo SPEI, given this time duration representing the accumulated climatic water balance with the highest correlation with DFS as the final water indicator (22). X-band (10.7 GHz) VOD was obtained from the land parameter data record (LPDR version 2) developed by the Numerical Terradynamic Simulation Group at the University of Montana (57). The daily VOD data were generated from the Advanced Microwave Scanning Radiometer for EOS (2002 to 2011) for both ascending and descending orbits at a spatial resolution of 0.25°. We selected the descending orbit retrievals and calculated average monthly VOD for 2002 to 2011.
Analyses.
We used partial correlation analysis to investigate the response of DFS to wind speed, controlling temperature, precipitation, and solar radiation. Temperature and precipitation strongly affect DFS, so directly using linear correlation between wind speed and DFS would bring uncertainties of factor-combined effect. Statistical significance at the 0.05 level was used in this study, with an R threshold of ±0.339 for an analysis of 34 y (1982 to 2015), ±0.404 for an analysis of 24 y (1992 to 2015), and ±0.632 for an analysis of 10 y (2002 to 2011). We applied the nearest neighbor method to resample satellite-derived DFS, water indicators, and climatic data into the same resolution, 1/12° for partial correlation analysis and 0.5° for DFS projection.
The relevant periods for the effect of wind speed on autumn foliar senescence differs among vegetation types, species, and locations. We determined the optimal length of the preseason based on wind speed (hereafter preseason) as the period (with steps of 1 mo until June) before the mean DFS for which the partial correlation coefficient between DFS and wind speed was highest during 1982 to 2015 for each pixel, controlling temperature, precipitation, and solar radiation (7, 21). We applied the same method to determine the wind speed–based preseason for flux sites and phenological sites. We used the Theil–Sen slope estimator, a nonparametric and median-based slope estimator, to analyze the temporal trends of DFS and preseason meteorological variables (i.e., average temperature and wind speed, accumulated precipitation, and solar radiation) at high latitudes for 1982 to 2015. The trends for each pixel were evaluated using the Mann–Kendall test, at a significance level of 0.05.
To quantitatively determine the impacts of different meteorological variables on interannual variations of DFS, we first used multiple linear regressions to estimate the sensitivity of DFS to meteorological variables (7) with DFS as the dependent variable and preseason average temperature and wind speed, accumulated precipitation, and solar radiation as independent variables (all variables nondetrended). Only significant pixels were analyzed for the further step (P < 0.05). We then calculated the contribution coefficients of different meteorological variables to interannual variations of DFS, respectively. For example, the contribution coefficient of preseason average temperature to interannual variations of DFS can be determined as
| [4] |
| [5] |
where , , , and represent the sensitivity of DFS to preseason average temperature (days · °C−1) and wind speed (days (m · s−1)−1), accumulated precipitation (days · mm−1), and solar radiation (days [w · m−2]−1), respectively. is the residual of multiple linear regression. is a contribution coefficient of preseason average temperature to interannual variations of DFS, and and represent the temporal trend of preseason average temperature (°C · year−1) and DFS (days · year−1) for 1982 to 2015, respectively. More than 99% of contribution coefficients were between −2 and 2. A higher absolute value of contribution coefficients represents a stronger impact of meteorological variables to interannual variations of DFS.
For the DFS model evaluation, we calculated the frequency of significant sites (pixels), the correlation coefficient (R), the RMSE, and the AICc for CDD and CDDWS, respectively. Given the sample size (time series for a site or pixel) is small, we used AICc to address potential overfitting of AIC. The AICc value of the model is the following:
| [6] |
| [7] |
| [8] |
where k is the number of parameters in the model, n is the sample size, is the log of maximized value of the likelihood function for the model, is the predicted DFS from the model in the ith year, and is the estimated DFS based on . The above analyses were performed on the Interactive Data Language (version 8.3).
DFS Modeled from CDDWS.
Our study indicated that DFS negatively responded to wind speed at high latitudes at both the site and satellite levels, so we developed a DFS model that incorporated wind speed into the traditional CDD model, based solely on the accumulated chilling degree (58).
The traditional CDD was determined as
| [9] |
| [10] |
where is the chilling degree on date , is the base temperature, set within 15 and 30 °C (with steps of 5 °C), is the daily mean temperature on date , is the accumulated chilling degree from to required for foliar senescence, and is the first day of accumulation, set to July 1. We determined as the yearly observation and derived DFS for each site and pixel. Finally, CDD-based DFS was defined as the date that first exceeded the multiyear average CDD threshold.
After incorporating wind speed into the traditional CDD model, our CDDWS model was defined as
| [11] |
| [12] |
where is a weighted factor ranging from −1 to 1 with a step of 1/ and is the ratio of , which is the daily mean wind speed in the day of year of , to , which is the mean wind speed during the preseason of the study period. The effect of wind speed on DFS is jointly controlled by , , and for each site or pixel. The traditional CDD model can estimate average DFS with certain accuracy; however, it fails to predict the temporal trend of DFS and leads to low R and high RMSE and AICc. We assume that for each site or pixel, using the average value of traditional CDDthreshold to conversely estimate DFS for each year would cause a delay for earlier DFS and an advance of later DFS, since DFS is generally positively related to CDDthreshold. Using CDDWS approach, for example, if k < 0, in the years with higher wind speed ( > 1), actual CDDthreshold would be lower than the average value of CDDthreshold, leading to overestimated DFSs and vice versa. Thus, wind speed is positively correlated with DFS. Similarly, if k > 0, in the years with lower wind speed (0 < < 1), actual CDDthreshold would be lower than the average value of CDDthreshold, leading to underestimated DFSs and vice versa. In this case, wind speed is negatively correlated with DFS. We found nearly two-thirds of pixels with positive k, confirming the dominance of a negative correlation between wind speed and DFS. Therefore, CDDWS incorporated the generally negative response of DFS to wind speed and improved the accuracy of estimating the interannual variation of DFS, with higher R and lower RMSE and AICc.
In this study, the most optimal parameters of the models were determined by comparing the RMSE between modeled and observed DFS. Tb and k with the lowest RMSE were regarded as the final parameters for each site or pixel. We also used the map of Tb, k and generated in the CDDWS for 1982 to 2015, as empirical input data, to predict projected DFS for 2,081 to 2,100.
Supplementary Material
Acknowledgments
This work was funded by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA19040103), the National Key R&D program of China (2018YFA0606101), the National Natural Science Foundation of China (41871255), and the Key Research Program of Frontier Sciences, CAS (QYZDB-SSW-DQC011). C.W. was also funded by the CAS Interdisciplinary Innovation Team (JCTD-2020-05). Y.H.F. was funded by the National Funds for Distinguished Young Scholars (Grant No. 42025101). J.P. and P.C. were funded by European Research Council Synergy Grant ERC-SyG-2013-610028 IMBALANCE-P. F.T was funded by the National Natural Science Foundation of China (42001299). R.L. was funded by the International Cooperation and Exchange Programs between National Natural Science Foundation of China and German Research Foundation (41761134082). We also appreciate flux site Principal Investigators in providing their valuable data for our analyses.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2015821118/-/DCSupplemental.
Data Availability
All study data are included in the article and SI Appendix. The specific links for data used in this study can be found in SI Appendix, Table S1.
References
- 1.Richardson A. D., et al., Terrestrial biosphere models need better representation of vegetation phenology: Results from the North American carbon program site synthesis. Glob. Change Biol. 18, 566–584 (2012). [Google Scholar]
- 2.White A., Cannell M. G. R., Friend A. D., The high-latitude terrestrial carbon sink: A model analysis. Glob. Change Biol. 6, 227–245 (2000). [Google Scholar]
- 3.Piao S., et al., Net carbon dioxide losses of northern ecosystems in response to autumn warming. Nature 451, 49–52 (2008). [DOI] [PubMed] [Google Scholar]
- 4.Lee X., et al., Observed increase in local cooling effect of deforestation at higher latitudes. Nature 479, 384–387 (2011). [DOI] [PubMed] [Google Scholar]
- 5.Schuur E. A. G., et al., Climate change and the permafrost carbon feedback. Nature 520, 171–179 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Qian H., Joseph R., Zeng N., Enhanced terrestrial carbon uptake in the northern high latitudes in the 21st century from the coupled carbon cycle climate model intercomparison project model projections. Glob. Change Biol. 16, 641–656 (2010). [Google Scholar]
- 7.Piao S., et al., Leaf onset in the northern hemisphere triggered by daytime temperature. Nat. Commun. 6, 6911 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Keenan T. F., et al., Net carbon uptake has increased through warming-induced changes in temperate forest phenology. Nat. Clim. Chang. 4, 598–604 (2014). [Google Scholar]
- 9.Vitasse Y., et al., Assessing the effects of climate change on the phenology of European temperate trees. Agric. For. Meteorol. 151, 969–980 (2011). [Google Scholar]
- 10.Richardson A. D., et al., Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 169, 156–173 (2013). [Google Scholar]
- 11.Tania S., et al., Air temperature triggers the recovery of evergreen boreal forest photosynthesis in spring. Glob. Change Biol. 9, 1410–1426 (2003). [Google Scholar]
- 12.Wu C., et al., Interannual variability of net ecosystem productivity in forests is explained by carbon flux phenology in autumn. Glob. Ecol. Biogeogr. 22, 994–1006 (2013). [Google Scholar]
- 13.Liu Q., et al., Delayed autumn phenology in the Northern Hemisphere is related to change in both climate and spring phenology. Glob. Change Biol. 22, 3702–3711 (2016). [DOI] [PubMed] [Google Scholar]
- 14.Zhu W., et al., Extension of the growing season due to delayed autumn over mid and high latitudes in North America during 1982–2006. Glob. Ecol. Biogeogr. 21, 260–271 (2012). [Google Scholar]
- 15.Baldocchi D., Breathing of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 56, 1–26 (2008). [Google Scholar]
- 16.Keenan T. F., Richardson A. D., The timing of autumn senescence is affected by the timing of spring phenology: Implications for predictive models. Glob. Change Biol. 21, 2634–2641 (2015). [DOI] [PubMed] [Google Scholar]
- 17.Myneni R. B., et al., Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 386, 698–702 (1997). [Google Scholar]
- 18.Buitenwerf R., Rose L., Higgins S. L., Three decades of multi-dimensional change in global leaf phenology. Nat. Clim. Chang. 5, 364–368 (2015). [Google Scholar]
- 19.Peñuelas J., Rutishauser T., Filella I., Ecology. Phenology feedbacks on climate change. Science 324, 887–888 (2009). [DOI] [PubMed] [Google Scholar]
- 20.Barichivich J., et al., Large-scale variations in the vegetation growing season and annual cycle of atmospheric CO2 at high northern latitudes from 1950 to 2011. Glob. Change Biol. 19, 3167–3183 (2013). [DOI] [PubMed] [Google Scholar]
- 21.Wu C., et al., Contrasting responses of autumn-foliar senescence to daytime and night-time warming. Nat. Clim. Chang. 8, 1092–1096 (2018). [Google Scholar]
- 22.Peng J., Wu C., Zhang X., Wang X., Gonsamo A., Satellite detection of cumulative and lagged effects of drought on autumn leaf senescence over the Northern Hemisphere. Glob. Change Biol. 25, 2174–2188 (2019). [DOI] [PubMed] [Google Scholar]
- 23.McVicar T. R., et al., Wind speed climatology and trends for Australia, 1975–2006: Capturing the stilling phenomenon and comparison with near-surface reanalysis output. Geophys. Res. Lett. 35, L20403 (2008). [Google Scholar]
- 24.Vautard R., Cattiaux J., Yiou P., Thépaut J. N., Ciais P., Northern Hemisphere atmospheric stilling partly attributed to an increase in surface roughness. Nat. Geosci. 3, 756–761 (2010). [Google Scholar]
- 25.Gardiner B., Berry P., Moulia B., Review: Wind impacts on plant growth, mechanics and damage. Plant Sci. 245, 94–118 (2016). [DOI] [PubMed] [Google Scholar]
- 26.De Langre E., Effects of wind on plants. Annu. Rev. Fluid Mech. 40, 141–168 (2008). [Google Scholar]
- 27.Mitchell S. J., Wind as a natural disturbance agent in forests: A synthesis. Forestry 86, 147–157 (2013). [Google Scholar]
- 28.Schelhaas M. J., Nabuurs G. J., Schuck A., Natural disturbances in the European forests in the 19th and 20th centuries. Glob. Change Biol. 9, 1620–1633 (2003). [Google Scholar]
- 29.Keyser A. R., Kimbal J. S., Nemani R. R., Running S. W., Simulating the effects of climate change on the carbon balance of North American high-latitude forests. Glob. Change Biol. 6, 185–195 (2000). [DOI] [PubMed] [Google Scholar]
- 30.Zhu Z., et al., Greening of the Earth and its drivers. Nat. Clim. Chang. 6, 791–795 (2016). [Google Scholar]
- 31.Estiarte M., Peñuelas J., Alteration of the phenology of leaf senescence and fall in winter deciduous species by climate change: Effects on nutrient proficiency. Glob. Change Biol. 21, 1005–1017 (2015). [DOI] [PubMed] [Google Scholar]
- 32.Lavrič M., Eler K., Ferlan M., Vodnik D., Gričar J., Chronological sequence of leaf phenology, xylem and phloem formation and sap flow of Quercus pubescens from abandoned karst grasslands Front. Front. Plant Sci. 8, 314 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pugnaire F. I., Chapin F. S. III, Environmental and physiological factors governing nutrient resorption efficiency in barley. Oecologia 90, 120–126 (1992). [DOI] [PubMed] [Google Scholar]
- 34.Buermann W., et al., Widespread seasonal compensation effects of spring warming on northern plant productivity. Nature 562, 110–114 (2018). [DOI] [PubMed] [Google Scholar]
- 35.Grace J., Plant response to wind. Agric. Ecosyst. Environ. 22, 71–88 (1988). [Google Scholar]
- 36.Liu Q., et al., Extension of the growing season increases vegetation exposure to frost. Nat. Commun. 9, 426 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Harder D. L., Speck O., Hurd C. L., Speck T., Reconfiguration as a prerequisite for survival in highly unstable flow-dominated habitats. J. Plant Growth Regul. 23, 98–107 (2004). [Google Scholar]
- 38.Fischer R. A., Turner N. C., Plant productivity in the arid and semiarid zones. Annu. Rev. Plant Physiol. 29, 277–317 (1978). [Google Scholar]
- 39.Armstrong A., Waldron S., Whitaker J., Ostle N. J., Wind farm and solar park effects on plant-soil carbon cycling: Uncertain impacts of changes in ground-level microclimate. Glob. Change Biol. 20, 1699–1706 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Templ B., et al., Pan European phenological database (PEP725): A single point of access for European data. Int. J. Biometeorol. 62, 1109–1113 (2018). [DOI] [PubMed] [Google Scholar]
- 41.Meier N., Rutishauser T., Pfister C., Wanner H., Luterbacher J., Grape harvest dates as a proxy for Swiss April to August temperature reconstructions back to AD 1480. Geophys. Res. Lett. 34, L20705 (2007). [Google Scholar]
- 42.Velicer W. F., Determining the number of components from the matrix of partial correlations. Psychometrika 41, 321–327 (1976). [Google Scholar]
- 43.Gonsamo A., Chen J. M., Price D. T., Kurz W. A., Wu C., Land surface phenology from optical satellite measurement and CO2 eddy covariance technique. J. Geophys. Res. BiogeoSci. 117, G03032 (2012). [Google Scholar]
- 44.Zhang X. Y., et al., Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 84, 471–475 (2003). [Google Scholar]
- 45.White M. A., et al., Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982–2006. Glob. Change Biol. 15, 2335–2359 (2009). [Google Scholar]
- 46.Friedl M. A., et al., MODIS collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 114, 168–182 (2010). [Google Scholar]
- 47.Olson D. M., et al., Terrestrial ecoregions of the world: A new map of life on Earth. Bioscience 51, 933–938 (2001). [Google Scholar]
- 48.Chen J., A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sens. Environ. 91, 332–344 (2004). [Google Scholar]
- 49.White M. A., Thornton P. E., Running S. W., A continental phenology model for monitoring vegetation responses to interannual climatic variability. Global Biogeochem. Cycles 11, 217–234 (1997). [Google Scholar]
- 50.Elmore A. J., Guinn S. M., Minsley B. J., Richardson A. D., Landscape controls on the timing of spring, autumn, and growing season length in mid-Atlantic forests. Glob. Change Biol. 18, 656–674 (2012). [Google Scholar]
- 51.Abatzoglou J. T., Dobrowski S. Z., Parks S. A., Hegewisch K. C., TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958-2015. Sci. Data 5, 170191 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hersbach H., Dee D., ERA5 reanalysis is in production. ECMWF Newsl. 147, 7 (2016). [Google Scholar]
- 53.Harris I., Jones P. D., Osborn T. J., Lister D. H., Updated high-resolution grids of monthly climatic observations - the CRU TS3.10 Dataset. Int. J. Climatol. 34, 623–642 (2014). [Google Scholar]
- 54.Allen R. G., Pereira L. S., Raes D., Smith M., Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56 (FAO, Rome, 1998), vol. 300, p. D05109. [Google Scholar]
- 55.Rodell M., et al., The global land data assimilation system. Bull. Am. Meteorol. Soc. 85, 381–394 (2004). [Google Scholar]
- 56.Vicenteserrano S. M., Beguería S., López-Moreno J. I., A multiscalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 23, 1696–1718 (2010). [Google Scholar]
- 57.Du J., et al., A global satellite environmental data record derived from AMSR-E and AMSR2 microwave earth observations. Earth Syst. Sci. Data 9, 791–808 (2017). [Google Scholar]
- 58.Delpierre N., et al., Modelling interannual and spatial variability of leaf senescence for three deciduous tree species in France. Agric. For. Meteorol. 149, 938–948 (2009). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and SI Appendix. The specific links for data used in this study can be found in SI Appendix, Table S1.