Performance of the Grade of Membership Model Under a Variety of Sample Sizes, Group Size Ratios, and Differential Group Response Probabilities for Dichotomous Indicators

Abstract

Social scientists are frequently interested in identifying latent subgroups within the population, based on a set of observed variables. One of the more common tools for this purpose is latent class analysis (LCA), which models a scenario involving k finite and mutually exclusive classes within the population. An alternative approach to this problem is presented by the grade of membership (GoM) model, in which individuals are assumed to have partial membership in multiple population subgroups. In this respect, it differs from the hard groupings associated with LCA. The current Monte Carlo simulation study extended on prior work on the GoM by investigating its ability to recover underlying subgroups in the population for a variety of sample sizes, latent group size ratios, and differing group response profiles. In addition, this study compared the performance of GoM with that of LCA. Results demonstrated that when the underlying process conforms to the GoM model form, the GoM approach yielded more accurate classification results than did LCA. In addition, it was found that the GoM modeling paradigm yielded accurate results for samples as small as 200, even when latent subgroups were very unequal in size. Implications for practice were discussed.

Researchers in the social sciences are frequently interested in identifying underlying groups within the population. Such mixtures within the population are taken to represent conceptually coherent subgroups of individuals who exhibit meaningful differences between one another on one or more measured variables, and in turn who cohere on these variables. These mixtures can differ in terms of the means of the measured variables, as well as with respect to parameters in linear models, generalized linear models, latent variable models, and growth models. Mixture modeling has been used in a variety of subject areas, including psychology (Klonsky & Olino, 2008; Lotzin et al., 2018; Magee et al., 2019), education (Gerick, 2018; Urick, 2016), sociology (Christens et al., 2015; Rid & Profeta, 2011), business (Crouch et al., 2016), and the health sciences (Lasry et al., 2018; Sadiq et al., 2018), among others.

There exist a variety of tools to identify underlying subgroups in a population. Common methods include k-means cluster analysis, model based clustering, and latent class analysis. Although they differ in terms of their statistical mechanisms, each of these approaches has the common goal of identifying unobserved mixtures in the population. Furthermore, all these methods presuppose that an individual belongs to a single population subgroup. In practice, individuals have associated probabilities of membership for each group and are assigned to the one for which they have the largest such value. The individual is then taken to be a member of that group only.

There is an alternative model for expressing latent groups that allows an individual to belong to multiple groups to varying degrees. For each member of a sample, this grade of membership (GoM) model has an associated degree of membership with each of the population subgroups, as is described in more detail below. As an example, a researcher might find that an individual is associated with latent group 1 for a 60% share, with latent group 2 for a 30% share, with latent group 3 with a 0% share, and with latent group 4 for a 10% share. The goal of this Monte Carlo simulation study was to expand on earlier research examining the performance of the GoM model under a variety of conditions and to compare its performance with another very commonly used tool for identifying underlying population subgroups, latent class analysis (LCA). Prior work has examined the performance of GoM modeling with very large samples (5,000), and with a limited array of relative sizes for these groups (e.g., Erosheva, 2003; Erosheva & Fienberg, 2005; Erosheva et al., 2007). The current work expands on these conditions, as well as on the relationship of the observed variables to group membership. In addition, prior published work has not compared the performance of LCA with that of GoM. Therefore the current study will expand on the literature in that regard as well. The remainder of the article is organized as follows. First, GoM models and LCA are described. Next, the goals of this study are described, and the study methodology is outlined. The results of the Monte Carlo simulation are then presented, followed by a discussion of these results, and in particular, implications for practice and directions for future work.

Latent Class Analysis

LCA is a model-based approach to identifying latent subgroups within the population, based on responses to set of observed variables (Lazarsfeld & Henry, 1968). Let $y=(y_1,y_2,\dots ,y_k)$ be a latent class membership vector such that $y_k=1$ for a member of class k, and 0 for all other classes. The probability density function of y is defined as follows:

$$f\left(y\right)=\{\begin{array}{ll}{\pi }_k,\hfill & \mathrm{if}{y}_k=1\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}.$$

The relationship between the probability of an individual being a member of a specific latent class, and the responses pattern I on the set of J observed variables can then be written as

$$pr\left(x=I|y\right)={\sum }_{k=1}^K{\pi }_k{\prod }_{j=1}^J{\lambda }_{kj{I}_j}$$ (1)

where ${\lambda }_{\mathrm{kj}{I}_j}=$ conditional probability of response pattern I for the J indicators when membership probability for class k = 1

This model posits that responses to the observed indicators are independent of one another, conditional on latent class membership; that is, local independence. Estimation of the model is typically carried out using maximum likelihood, with the parameters being the probability of response profile given latent class membership, and the probability of an individual being in a particular latent class.

Perhaps the primary decision that needs to be made by researchers using LCA is the number of classes to retain. In a typical exploratory LCA application, multiple models, featuring different numbers of classes, are fit to the data. The fit of these models are then compared with one another using statistics such as the Akaike information criterion (AIC), the Bayesian information criterion (BIC), or the bootstrap likelihood ratio test (McLachlan & Peel, 2000). The optimal model is that which yields relatively good fit, and that is substantively meaningful in terms of how individuals are grouped together (Bauer & Curran, 2004). Although it is used frequently in the context of mixture modeling, we should note that the regularity conditions underlying the BIC are violated in the context of mixture modeling (Drton & Plummer, 2017). Thus, researchers working in this context may want to consider investigating the adjusted BIC for use with singular model selection.

Grade of Membership Model

The GoM model represents a generalization of the latent class model where membership in multiple classes can take values larger than 0. Recall that for LCA, the membership probability for one class, $y_k$, was 1, and was 0 for all other classes. In contrast, GoM allows partial membership in multiple classes, which are known as extreme profiles. The vector of partial membership random variables is $g=(g_1,g_2,\dots ,g_k)$. Multiple value of $g$ can be nonzero, and $\sum g_k=1$. The GoM model is then written as

$$pr\left(x=I|g\right)={\prod }_{j=1}^J\left({\sum }_{k=1}^K{g}_k{\lambda }_{kj{I}_j}\right)$$

where ${\lambda }_{\mathrm{kj}{I}_j}=$ conditional probability of response I to the J indicators when membership probability for class k = 1 and $g_k=$ latent partial membership in class k, where $\sum _{k=1}^K{g}_k=1$.

The GoM model is simply a generalization of the LCA model with the constraint that one element of y = 1, and all others are 0 is been relaxed. The two model frameworks are equivalent when one element of g is 1 and the others are 0.

As an example of how the GoM model works, consider the case of four latent subgroups within the population. A given individual will have a portion of their membership assigned to each of these subgroups, and the sum of these portions (expressed as probability) will be 1. The larger an individual’s apportionment to a subgroup, the more strongly the individual is associated with that group. The vector of this mixed membership parameter corresponds to g, above. If the values of g are set such that each individual in the sample has a value of 1 for one subgroup, and 0 for the others, then the GoM model is equivalent to the LCA model.

GoMs can be estimated using a variational EM algorithm, which overcomes computational difficulties associated with using maximum likelihood estimation (Erosheva & Fienberg, 2005). We will not go into the details here about how this estimator works, but the interested reader is referred to Beal (2003) for a full discussion of this approach. It is important, however, to note a few points with regard to the use of the variational estimation approach. In particular, the use of priors is key to working with this method. For $g$ the most commonly used prior is

$$g~\mathrm{Dirichlet}\left(\alpha \right).$$

The hyperparameter $\alpha$ takes the form

$$\alpha =({\alpha }_0·{\xi }_{1,\dots ,}{\alpha }_0·{\xi }_K)$$

where

$${\alpha }_0>0$$

$$\xi =({\xi }_1,\dots ,{\xi }_K).$$

Each element of $\xi$ represents the expected proportion of observed variable values generated by the extreme profile for group k; that is, the relative importance of extreme profile k in determining the observed variable values. The parameter ${\alpha }_0$ represents the degree of concentration of the probability distribution around the expected value, with larger values of ${\alpha }_0$ indicate a greater degree of such concentration. In other words, larger values of ${\alpha }_0$ suggest that individuals are more closely associated with the extreme values of the population subgroups. Finally, the prior distribution for ${\lambda }_{\mathrm{jk}}$ is Dirichlet ($1_{n_j}$, or a uniform distribution over the simplex ${\mathrm{\Delta }}_{n_j-1}$), where $n_j$ is the number of individuals endorsing item j.

A number of strategies for determining the optimal number of extreme profiles to retain in the context of GoM models have been suggested, including the truncated sum of squared Pearson residuals (${\chi }_{\mathrm{tr}}^2$), Bayesian variants of the Akaike information criterion (AICM), the Bayesian Information Criterion (BICM), as well as the deviance information criterion (DIC). Simulation research has demonstrated that the ${\chi }_{\mathrm{tr}}^2$ statistic performed better than the various information indices in terms of correctly identifying the number of extreme profiles that should be retained (Erosheva, et al., 2007). The ${\chi }_{\mathrm{tr}}^2$ is calculated as the difference between the expected frequencies for response patterns of the observed indicators and the observed frequencies (Bishop et al., 1975).

Goals of the Current Study

The purpose of this study was to expand earlier work (e.g., Erosheva et al., 2007) by examining the performance of a variational EM algorithm estimator for the GoM using a simulation study design. This earlier work demonstrated that the GoM was able to accurately recover the latent structure underlying a set of observed dichotomous variables for a sample size of 5,000. However, it is unclear the extent to which these results are applicable to the smaller samples that are more typical of applied social science research. Thus, the current study sought to ascertain how well the GoM could recover the latent structure with samples of between 200 and 1,600 individuals, using dichotomous indicator variables. This study also expands on earlier work by including a wider array of conditions for the proportion of individuals associated with each of the extreme profiles, and the relationship between group membership and responses to the observed variables. The current study also examined estimation accuracy of the ${\alpha }_0$ parameter, as well as the number of classes selected by the procedure, as outcomes of interest. The latter has certainly been a feature of previous research but the latter has not been. Finally, in addition to the GoM model, LCA was also included in this study in order to determine how well it worked in terms of identifying the extreme response profiles when the underlying latent structure was generated based on both the GoM and LCA models. This latter question was of interest because many researchers are familiar with, and use LCA, and thus may apply it in some situations where the GoM model actually generated the data. Likewise, researchers may also employ the GoM model when the underlying structure actually conforms to the LCA framework. Thus, it is of interest to know how well (or poorly) both LCA and GoM work when the underlying data generating model is both similar to and different from the estimating model.

Based on the study design, which is described below, as well as prior research, several hypotheses were made regarding the performance of the GoM and LCA approaches. First, it was hypothesized that the GoM model would be more accurate than LCA at correctly identifying the number of extreme latent profiles when the underlying model was GoM, and LCA would be more accurate than GoM when the underlying model was LCA. Second, the rates of classification accuracy was expected to be higher for the model estimation algorithm that corresponded to the data generating process; that is, GoM should provide more accurate classification when the underlying model was GoM, and vice versa for the LCA estimation and data generating models. Third, estimation accuracy for the ${\alpha }_0$ parameter was expected to be higher for larger samples.

Method

In order to address the aforementioned study goals, a Monte Carlo simulation study was conducted, with 1,000 replications per combination of study conditions. The data were generated from either the GoM or LCA models under a variety of conditions. Specifically, one set of simulation results was generated using the rmixedMem function in the mixedMem library within the R software package, Version 3.6.2 (R Development Team, 2019) to generate GoM model data. Then both the GoM and LCA models were fit to the data. Separately, model were also generated from the LCA model using the poLCA.simdata function in the poLCA R library. Once again, both the GoM and LCA models were then applied to the data generated from the LCA model. For both data generating conditions, the observed indicators were generated to be dichotomous in nature. The purpose for using both data generating approaches was to ascertain the extent to which performance of each estimation model was affected by the underlying model form in terms of correctly identifying the latent structure present in the data. The following conditions were manipulated in this study.

Number of Observed Indicators

A total of 5, 10, or 20 dichotomous indicators were generated in this study. Prior simulation work examined 10 and 16 dichotomous items (Erosheva et al., 2007), and thus the current study builds on this earlier work by including a wider range of indicators.

Sample Size

Sample sizes for this study were set at 200, 400, 800, and 1,600. Previous simulation work examining the performance of GoM with dichotomous indicators included a total sample size of 5,000 individuals. Given that much research in the social sciences involves smaller samples than that, the current study sought to extend on prior work by examining the performance of the GoM model with samples that are somewhat more typical of much published research (e.g., Klonsky & Olino, 2008; Klug et al., 2019; van Lier et al., 2003; Zhou et al., 2018).

Number of Latent Extreme Profiles and Profile Ratios

Data were simulated to have two or four extreme latent profiles. For the two extreme profiles case, the ratios of the two groups’ sizes were 0.5/0.5, 0.75/0.25, and 0.9/0.1. In the case of four extreme profiles, the group size ratios were 0.25/0.25/0.25/0.25, 0.4, 0.2, 0.2, 0.2, 0.7/0.1, 0.1, 0.1, and 0.91/0.03/0.03/0.03. The value of ${\alpha }_0$ was set at 0.25, meaning that responses to the dichotomous items came primarily from a single profile for each individual. In other words, each member of the sample was primarily (though not totally) a member of a single profile.

Differences in Extreme Profiles’ Conditional Response Probabilities

Three different conditions were simulated with regard to differences in the conditional responses probabilities of the extreme profiles. The population differences in conditional response probabilities for the dichotomous indicators were 0.10, 0.20, or 0.3. For a given condition these differences held across all indicators.

Estimation Procedures

For each replication across all conditions, the GoM model was fit to the data using the mixedMemModel and mmVarFit functions in the mixedMem R library (Wang & Erosheva, 2015a, 2015b). Per the results of Erosheva et al. (2007), the ${\chi }_{\mathrm{tr}}^2$ test described above was used to ascertain the best fitting model for each simulation replication, as was the BICM. Results of this simulation demonstrated that ${\chi }_{\mathrm{tr}}^2$ was consistently more accurate than the BICM at identifying the correct number of extreme profiles to retain, which is in keeping with the prior work of Erosheva et al. (2007) Therefore, in the results described below, only those for the ${\chi }_{\mathrm{tr}}^2$ are presented. The mixedMem library uses the variational EM algorithm to estimate the GoM model parameters. This methodology, which is described in (Jaakkola & Jordan, 2000), provides inference on the approximate posterior distribution of $\lambda$ from Equation 1, and a pseudo-likelihood approach to estimate $\alpha$ and the group specific observed variable response parameters. The prior for $\theta$ was the dirichlet(0.5) distribution, and $\alpha$ was initialized with 0.2 for each class. A set of preliminary simulations was conducted using a variety of values for these hyperparameter and initialization factors, and the results were found to be largely insensitive to their choice. The selected values resulted in somewhat higher convergence rates, and thus were retained, in keeping with recommendations for practice (Wang & Erosheva, 2015a, 2015b). Several software default settings were used to fit the GoM, including a maximum of 500 total iterations, and a convergence criterion value of 0.000001. A total of five random restarts in the estimation algorithm were employed.

In addition to the GoM model, the LCA model was also estimated for the data using the poLCA function that is part of the poLCA library in R. Both AIC and BIC were used to determine the optimal number of latent classes to retain for each replication. For both GoM and LCA, models including from 1 to 6 latent groups were fit to the data. The appropriate statistics were then used to determine the optimal number of extreme profiles/latent classes to retain.

Outcomes of Interest

This study examined several outcomes of interest, including the mean number of extreme profiles/latent classes retained by each method, the overall accuracy rate of classifications for the correct number of profiles, and the sensitivity and specificity rates for each method, where the first extreme profile served as the target groups. The mean number of extreme profiles/latent classes recovered by each approach was selected as an outcome for this study because it reflects the ability of the methods to accurately identify the latent structure underlying the observed data, which is typically of primary interest to researchers using these techniques. Likewise, the classification accuracy metrics were included in the simulation study because they also provide information regarding how well each approach was able to classify individual cases into the correct underlying group. Researchers using these tools will want to know not only whether each method is able to ascertain the correct number of underlying groups but also which individuals belong in which of these groups. High levels of accuracy on both fronts (number of and membership in the latent classes) means that the methods were able to accurately uncover the underlying latent structure of the data.

Overall classification accuracy was calculated as the proportion of simulated individuals who were generated to be in the same category and who were also placed in the same category by the algorithm. Likewise, sensitivity was calculated as the proportion of simulated individuals in the target group who were correctly classified together in the target group. Finally, specificity was the proportion of individuals who were simulated not to belong to the target group who were in fact correctly classified as not belonging to the target group. In addition to the classification accuracy and number of recovered latent classes, for the GoM model, relative bias for the ${\alpha }_0$ parameter based on the posterior mean of the sample distribution for each replication. Relative bias was calculated as the ratio of the difference between the population value and the estimate, divided by the population value. Recall that ${\alpha }_0$ indicates the degree of extreme profile concentration inherent in the distribution of the observed indicators, and is thus of interest in understanding the ability of the GoM model to recover the underlying extreme profiles. Analysis of variance (ANOVA) was used to identify the main effects and interactions among the manipulated factors that were related to the outcomes of interest. In addition to statistical significance, the ${\eta }^2$ effect size was used to characterize the impact of manipulated study factors on each outcome. The overall Type I error rate across the ANOVAs was controlled through the use of the Bonferroni correction.

Results

Two Latent Classes

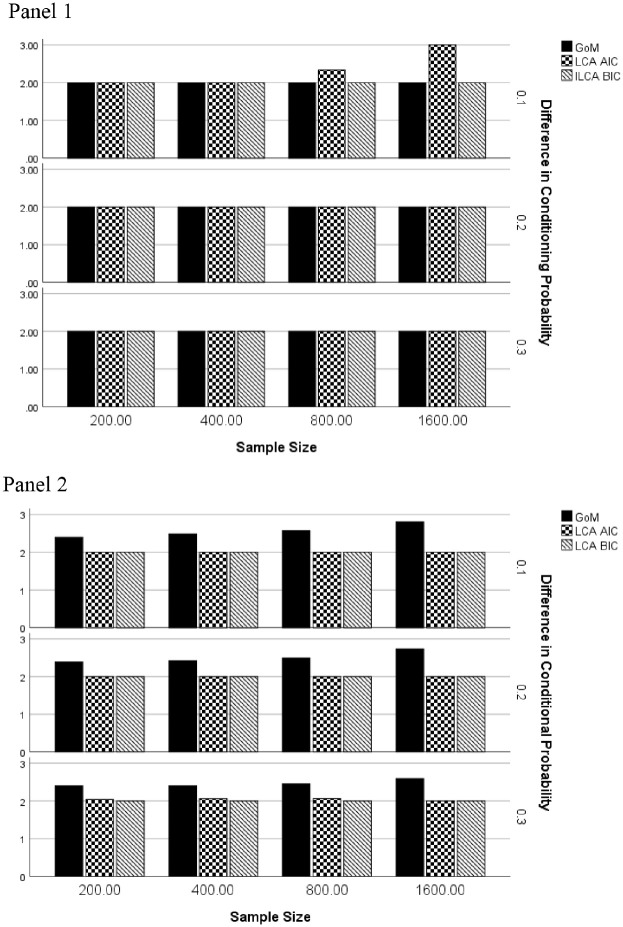
When two extreme latent classes were present in the population, ANOVA identified the interaction of data generating model by estimation method by sample size by the difference in conditional probability of item endorsement ($F_{7,12}=12.73,p<0.001,{\eta }^2=0.84$) to be significantly related to the number of extreme latent classes that were identified by each method. The mean number of extreme profiles identified by estimation method, sample size, difference in observed variable endorsement probability, and underlying model appear in Figure 1. For the GoM generating model (Panel 1), when the groups’ response probabilities on the indicators differed by 0.2 or 0.3 the GoM and both LCA based approaches accurately identified the number of extreme profiles (2) that simulated in the data. However, when the item endorsement probabilities differed by only 0.1, LCA using AIC tended to overestimate the number of profiles for samples of 800 and 1,600. The GoM model and LCA using BIC to identify the optimal number of profiles correctly identified 2 as being present. When the data generating model was LCA (Panel 2), both LCA based approaches accurately identified the number of latent classes, whereas GoM consistently overestimated the number of extreme profiles present.

Figure 1.

Mean number of extreme latent profiles by total sample size, difference in conditional item endorsement probability, and estimation method: Two extreme latent profiles. Panel 1: GoM generating model. Panel 2: LCA generating model.Note. GoM = grade of membership; LCA = latent class analysis.

ANOVA results indicated that the interaction of data generating model by estimation method by group size ratio by difference in conditional item endorsement probability was related to the overall classification accuracy ($F_{5,12}=6.89,p=0.01,{\eta }^2=0.731$), as was the interaction of method by sample size ($F_{4,12}=9.22,p<0.001,{\eta }^2=0.744$). GoM was consistently more accurate in terms of classifying individuals than was LCA (Table 1) when the data generating model was GoM. In addition, whereas sample size did not affect GoM accuracy, LCA was somewhat more accurate for larger samples. When the underlying model was LCA, the GoM model yielded slightly more accurate overall classification accuracy than did LCA for a sample size of 200. However, for the other sample sizes, LCA had somewhat higher accuracy rates with the difference in the two methods increasing concomitantly with larger samples.

Table 1.

Overall Classification Accuracy by Sample Size, Estimation Method, and Data Generating Model: Two Extreme Latent Profiles.

	GoM generating model		LCA generating model
Sample size	GoM	LCA	GoM	LCA
200	0.94	0.85	0.91	0.89
400	0.95	0.87	0.92	0.93
800	0.94	0.88	0.92	0.95
1,600	0.94	0.91	0.93	0.96

Note. GoM = grade of membership; LCA = latent class analysis.

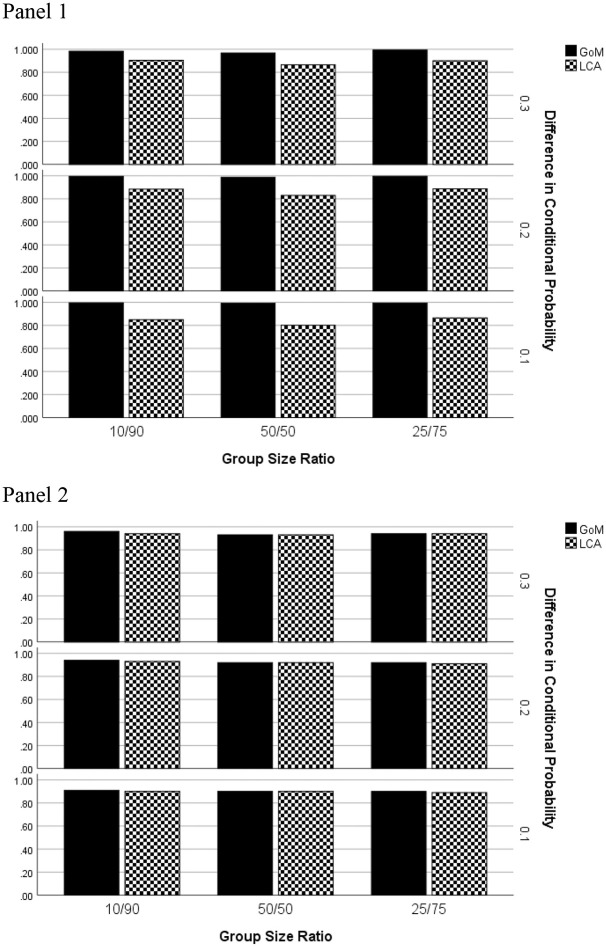
In terms of the group size ratio and differences in conditional probability of item endorsement when the data generating model was GoM (Figure 2, Panel 1), accuracy rates of GoM were largely consistent, whereas LCA yielded more accurate overall classification rates when the difference in the probability of item endorsement was larger, and when the groups were of unequal sizes. LCA yielded the least accurate classification results for the combination of a 50/50 group size ratio coupled with a difference in the conditional item probability of 0.1; that is, when the group differences in item response probability were least pronounced. When the data were generated by the LCA model (Panel 2), the two methods performed similarly across the group size ratio conditions.

Figure 2.

Overall classification accuracy by estimation method, group size ratio, and difference in group conditional probability of item endorsement: Two extreme latent profiles. Panel 1: GoM generating model. Panel 2: LCA generating model.Note. GoM = grade of membership; LCA = latent class analysis.

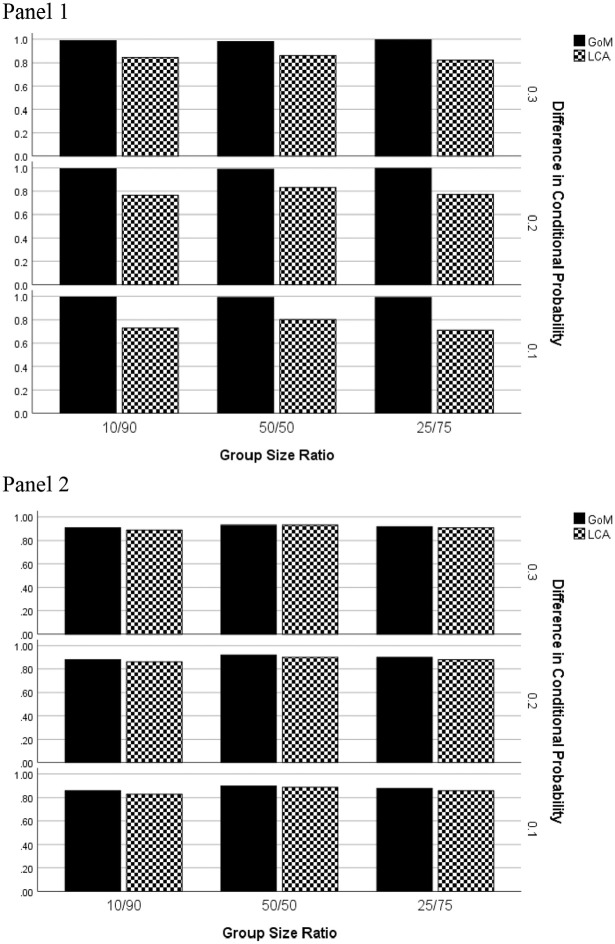
In terms of sensitivity, the interaction of data generating model by estimation method by group size ratio by difference in conditional item endorsement probability was found to be statistically significant ($F_{5,12}=5.11,p=0.01,{\eta }^2=0.613$). As with overall classification accuracy, when the data generating model was GoM, the GoM estimator yielded higher sensitivity rates than did LCA, and appeared to be largely impervious to the group size ratio or differences in conditional response probabilities among the groups (Figure 3, Panel 1). When the groups’ conditional item response probabilities differed by 0.1 or 0.2, LCA exhibited the highest sensitivity for cases where the groups were of the same size. However, when the group differences in conditional probability of item endorsement were at their largest (0.3), the group size ratio did not appear to affect LCA sensitivity. When the underlying model was LCA (Panel 2), the two estimation methods yielded very comparable sensitivity results across group size ratios, and differences in conditional item response probabilities.

Figure 3.

Sensitivity by estimation method, group size ratio, and difference in group conditional probability of item endorsement: Two extreme latent profiles. Panel 1: GoM generating model. Panel 2: LCA generating model.Note. GoM = grade of membership; LCA = latent class analysis.

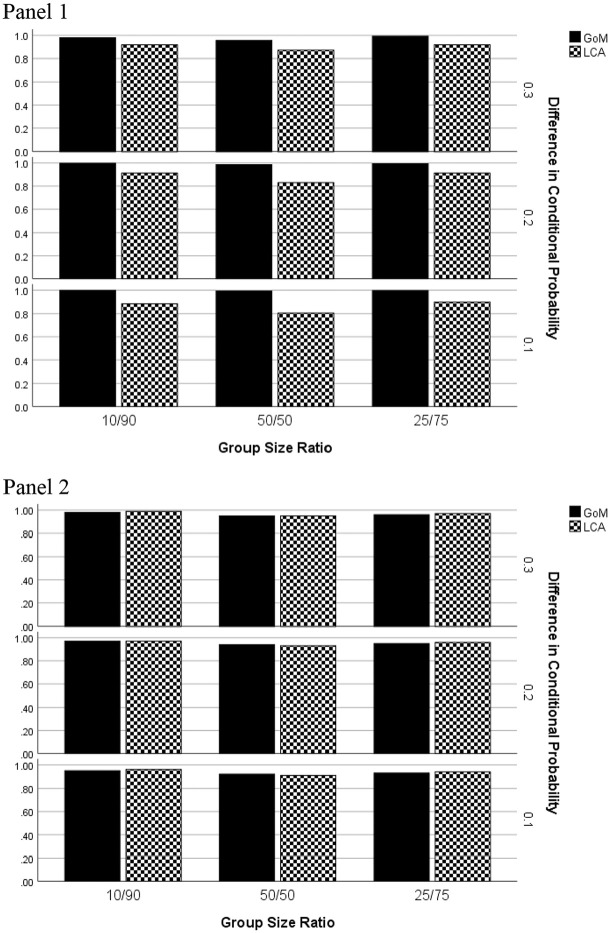
As was true of sensitivity, specificity rates were significantly associated with the interaction of data generating model by estimation method by group size ratio by the difference in conditional item endorsement probability ($F_{5,12}=16.91,p<0.001,{\eta }^2=0.674$). The pattern of results for specificity, with respect to sample size, group size ratio, and difference in conditional probability for both GoM and LCA generated data was very similar to that for sensitivity (Figure 4). The GoM model had consistently higher specificity rates than did LCA in the GoM data generating condition (Panel 1). On the other hand, when the data generating model was LCA, the two methods yielded very similar specificity results (Panel 2).

Figure 4.

Specificity by estimation method, group size ratio, and difference in group conditional probability of item endorsement: Two extreme latent profiles. Panel 1: GoM generating model. Panel 2: LCA generating model.Note. GoM = grade of membership; LCA = latent class analysis.

The final outcome to be investigated in this study was the relative bias in the ${\alpha }_0$ parameter estimate. The ANOVA results identified the main effects of sample size ($F_{1,12}=575.354,p<0.001,{\eta }^2=0.99$) and group size ratio ($F_{3,12}=82.214,p<0.001,{\eta }^2=0.95$) as significantly related to ${\alpha }_0$ bias. Estimation bias for ${\alpha }_0$decreased concomitantly with increases in sample size (Table 2). Furthermore, this decline in bias appears to have slowed for samples of 800 or more. With regard to the group size ratio, bias in ${\alpha }_0$ was lower when the group size ratio was 50/50, and increased concomitantly with larger differences in the group sizes.

Table 2.

Relative Estimation Bias of ${\alpha }_0$ by Sample Size and Group Size Ratio With Grade of Membership (GoM) Generating Model.

Study condition	Bias
Sample size
200	0.38
400	0.15
800	0.05
1,600	0.04
Group size ratio
50/50	0.07
25/75	0.14
10/90	0.25

Four Latent Classes

The ANOVA results revealed that the interactions of data generating model by estimation method by group size ratio ($F_{7,18}=9.33,p<0.001,{\eta }^2=0.592$), data generating model by method by difference in conditional item endorsement probability ($F_{5,18}=7.41,p<0.001,{\eta }^2=0.407$), and data generating model by estimation method by sample size ($F_{7,18}=4.99,p=0.019,{\eta }^2=0.333$) were all significantly related to the number of extreme latent groups that were identified by the various methods. Table 3 includes the mean number of extreme groups identified by method, sample size, group size ratio, and difference in conditional item endorsement probability for the GoM data generating model. The combination of LCA with AIC yielded more accurate results across all simulation conditions, when compared with the LCA BIC approach. In addition, GoM and LCA were both more accurate in terms of identifying the number of extreme latent groups for larger samples, more equal group sizes, and larger group differences in the conditional item response probabilities. Among the three approaches, GoM was generally the least affected by the conditions manipulated in this study when the underlying model was GoM, with smaller differences in its most and least accurate estimates of the number of extreme latent groups present in the data. When the underlying model was LCA, the GoM model tended to overestimate the number of latent classes across sample sizes, group size ratios, and differences in the conditional item response probabilities (Table 4). Conversely, both LCA based methods had the mean number of estimated classes within 0.1 of the actual value across study conditions.

Table 3.

Mean Number of Extreme Latent Profiles by Total Sample Size, Difference in Conditional Item Endorsement Probability, Group Size Ratio, and Estimation Method: Four Extreme Latent Profiles With GoM Generating Model.

Study condition	GoM	LCA AIC	LCA BIC
Sample size
200	3.3	2.8	2.1
400	3.4	3.5	2.4
800	3.5	3.7	2.6
1,600	3.7	3.8	3.1
Group size ratio
0.25/0.25/0.25/0.25	3.7	3.9	2.9
0.4, 0.2, 0.2, 0.2	3.5	3.7	2.8
0.7/0.1, 0.1, 0.1	3.4	3.2	2.4
0.91/0.03/0.03/0.03	3.3	2.6	2.2
Difference in conditional item response probability
0.3	3.6	3.6	3
0.2	3.4	3.5	2.5
0.1	3.4	3.3	2.2

Note. GoM = grade of membership; LCA = latent class analysis; AIC = Akaike information criterion; BIC = Bayesian information criterion.

Table 4.

Mean Number of Extreme Latent Profiles by Total Sample Size, Difference in Conditional Item Endorsement Probability, Group Size Ratio, and Estimation Method: Four Extreme Latent Profiles With LCA Generating Model.

Study condition	GoM	LCA AIC	LCA BIC
Sample size
200	4.2	3.9	3.9
400	4.2	3.9	3.9
800	4.3	4.1	4.0
1,600	4.4	4.0	4.0
Group size ratio
0.25/0.25/0.25/0.25	4.1	4.0	4.0
0.4, 0.2, 0.2, 0.2	4.2	4.1	4.0
0.7/0.1, 0.1, 0.1	4.3	4.0	3.9
0.91/0.03/0.03/0.03	4.4	4.1	4.0
Difference in conditional item response probability
0.3	4.3	4.0	4.0
0.2	4.2	4.1	4.0
0.1	4.1	3.9	3.9

Note. GoM = grade of membership; LCA = latent class analysis; AIC = Akaike information criterion; BIC = Bayesian information criterion.

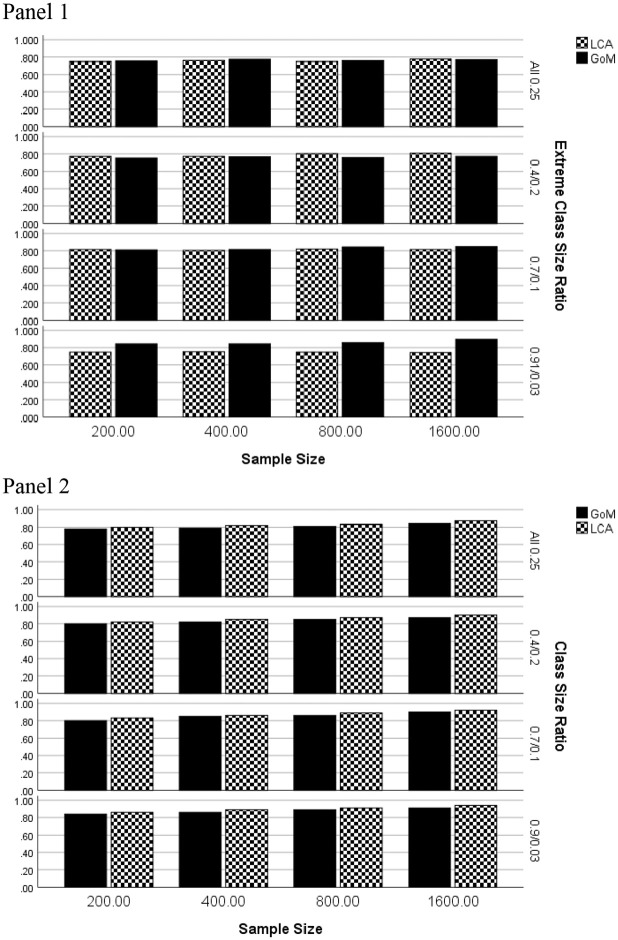
In terms of classification accuracy, ANOVA identified the interactions of data generating model by estimation method by group size ratio by difference in conditional probability ($F_{7,18}=7.14,p<0.001,{\eta }^2=0.688$) and data generating model by method by group size ratio by sample size ($F_{10,18}=6.31,p<0.001,{\eta }^2=0.743$) as being statistically significant. Overall accuracy rates for the GoM data generating model by method, sample size, and extreme class size ratio appear in Figure 5, Panel 1. When the ratios were equal, or 0.4/0.2/0.2/0.2, classification accuracy rates for the two methods were very similar for samples of 200 and 400, and were slightly higher for LCA for N = 800 and 1,600. However, when the group sizes were more unequal, GoM exhibited higher overall classification accuracy rates than did LCA. In contrast, when the data generating model was LCA (Panel 2), the two methods had very similar overall classification accuracy rates across conditions.

Figure 5.

Overall classification accuracy by estimation method, group size ratio, and sample size: Four extreme latent profiles. Panel 1: GoM generating model. Panel 2: LCA generating model.

Note. GoM = grade of membership; LCA = latent class analysis.

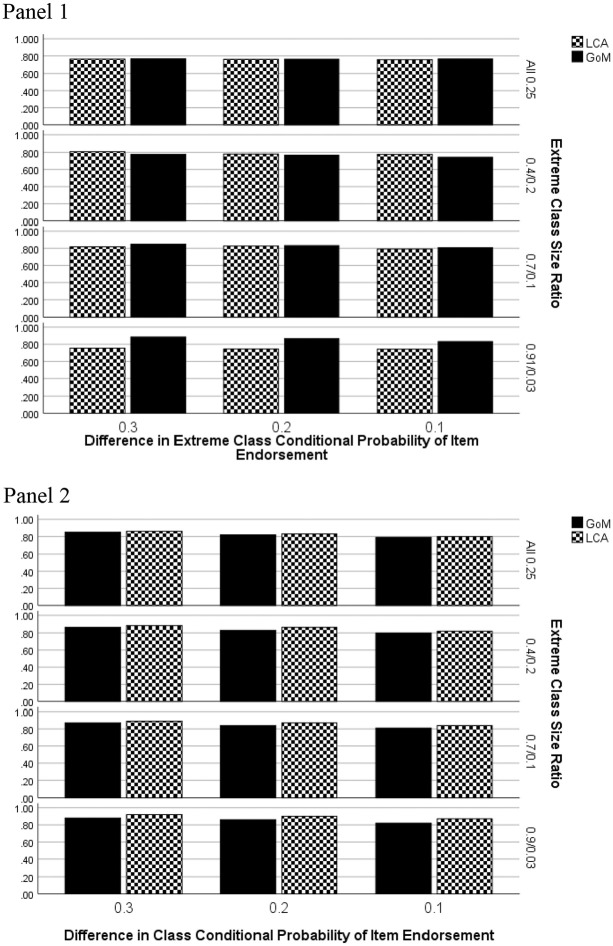
Figure 6 includes overall classification accuracy rates by data generating model, estimation method, difference in extreme class conditional probability of item endorsement, and class size ratio. These results are quite similar to those in Figure 5. In the GoM data generating case, the two methods performed similarly when the groups were of equal size or in the 0.4/0.2/0.2/0.2 condition. However, for the most unequal group sizes, GoM yielded more accurate overall classification rates. When the data were generated from the LCA model, the two methods yielded very similar classification accuracy rates across group size ratio and differences in conditional item response probabilities.

Figure 6.

Overall classification accuracy by estimation method, group size ratio, and difference in group conditional probability of item endorsement: Four extreme latent profiles. Panel 1: GoM generating model. Panel 2: LCA generating model.

Note. GoM = grade of membership; LCA = latent class analysis.

With regard to sensitivity for the first group, the ANOVA results indicated that the interactions of data generating model by estimation method by sample size ($F_{4,18}=9.93,p=0.001,{\eta }^2=0.580$), and data generating model by estimation method by group size ratio by difference in group probability of item endorsement ($F_{7,18}=4.96,p=0.029,{\eta }^2=0.512$) were statistically significant. Table 5 includes the sensitivity rates by data generating model, estimation method, and sample size for the four extreme profiles case. Across sample sizes, when the data were generated using the GoM model, the GoM estimator had higher sensitivity rates than did LCA. In addition, the impact of sample size was more marked for GoM, with higher sensitivity being associated with larger samples. In contrast, when the data were generated from the LCA model, the LCA estimator exhibited higher sensitivity rates than did the GoM approach, regardless of sample size.

Table 5.

Sensitivity by Sample Size and Estimation Method: Four Extreme Latent Profiles.

	GoM generating model		LCA generating data
Sample size	GoM	LCA	GoM	LCA
200	0.84	0.80	0.81	0.83
400	0.86	0.81	0.84	0.87
800	0.88	0.82	0.86	0.89
1,600	0.89	0.82	0.86	0.90

Note. GoM = grade of membership; LCA = latent class analysis.

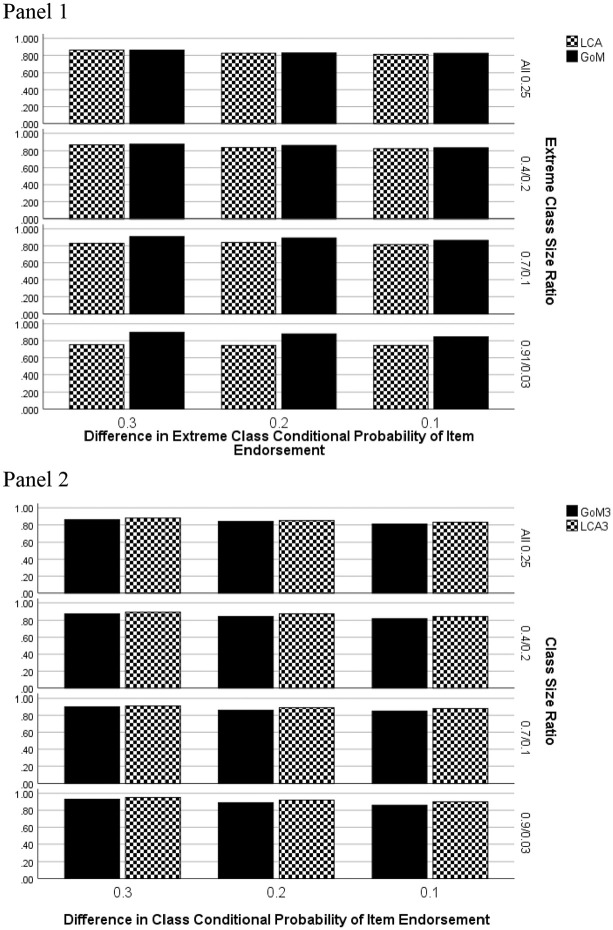
Sensitivity rates by data generating model, estimation method, group size ratio, and group difference in item endorsement probability appear in Figure 7. These results were very similar to those for overall accuracy for both data generating model. Namely, when the data generating model was GoM, the methods performed similarly for the All 0.25 and 0.4/0.2/0.2/0.2 conditions, and GoM had higher sensitivity rates for the two most unequal group size ratio conditions. When the underlying model was LCA, the sensitivity rates were slightly higher for LCA vis-à-vis GoM, across class size ratios, and differences in class conditional probabilities of item endorsement.

Figure 7.

Sensitivity by estimation method, group size ratio, and difference in group conditional probability of item endorsement: Four extreme latent profiles. Panel 1: GoM generating model. Panel 2: LCA generating model.

Note. GoM = grade of membership; LCA = latent class analysis.

Based on the ANOVA results, specificity rates were only statistically significantly affected by the interaction of data generating model by estimation method,and group size ratio ($F_{4,18}=4.83,p=0.007,{\eta }^2=0.41$). Given the results appearing in Table 6, when the data generating model was GoM, the largest difference in specificity among the estimation methods occurred for the most extreme difference in the class sizes, with GoM having a slightly higher specificity rate than LCA. When the underlying model was LCA, the LCA estimator consistently yielded higher specificity rates than was the case for GoM.

Table 6.

Specificity Rates by Extreme Class Size Ratio and Estimation Method: Four Extreme Latent Profiles.

	GoM generating model		LCA generating model
Class size ratio	GoM	LCA	GoM	LCA
0.25/0.25/0.25/0.25	0.84	0.84	0.83	0.86
0.4/0.2/0.2/0.2	0.84	0.83	0.82	0.85
0.7/0.1/0.1/0.1	0.83	0.83	0.82	0.84
0.91/0.03/0.03/0.03	0.84	0.81	0.81	0.82

Note. GoM = grade of membership; LCA = latent class analysis.

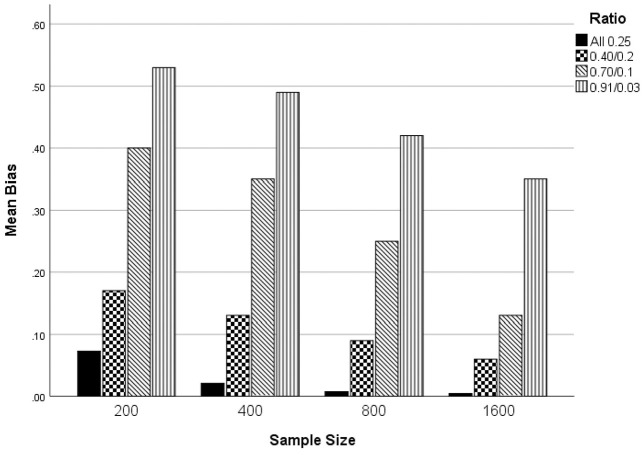
The relative bias in estimation of ${\alpha }_0$ was found to be statistically significantly related to the interaction of sample size and group size ratio ($F_{9,18}=5.675,p=0.001,{\eta }^2=0.74$). Relative estimation bias by sample size and extreme class size ratio appears in Figure 8. Regardless of the ratio, bias was smaller for larger samples. Likewise, regardless of the sample size, bias was lower for a more equal distribution of the extreme group sizes. This result mirrors that for the two-class case, as described above. The statistically significant interaction appears to be the result of the decline in the relative differences in bias among the ratio conditions as sample size increased. In other words, for larger sample sizes, the difference in relative bias was smaller across the group size ratio conditions. Taken together, these results suggest that GoM provides the most accurate estimate of ${\alpha }_0$ when it has maximum information available about each of the groups; that is, for relatively large and equally sized samples in each group.

Figure 8.

Estimation bias of ${\alpha }_0$ by sample size and group size ratio: Four extreme latent profiles.

Discussion

As stated above, the goal of this research was to investigate the performance of the GoM model under conditions that had not been heretofore examined, particularly with smaller samples, very unequal extreme latent class sizes, and an underlying LCA model. In addition, this study was also designed to compare the performance of the GoM model with that of perhaps the most popular latent group estimation approach, LCA. As was hypothesized, when the data were generated using the GoM model, GoM performed better than did LCA in terms of correctly classifying individuals into the appropriate latent classes. On the other hand, when the data were generated using the LCA model, the two approaches performed similarly for two latent classes but with LCA yielding somewhat more accurate results in the four subgroups case. One exception to this pattern of results, however, was that when two extreme classes were present in the population, LCA using BIC to identify the optimal model did perform as well as GoM in terms of identifying the number of classes to retain. Taken together, these results suggest that when the underlying model is based on GoM, the GoM approach will perform better that LCA, overall, though the results provided by LCA were also relatively close to that in the population. On the other hand, when the underlying model was LCA, and particularly with four latent classes present, then the LCA estimation approach generally yielded somewhat more accurate results than GoM, particularly when four classes were present. Again, this set of findings was hypothesized and thus does not come as a great surprise.

Of perhaps more interest than the direct comparison of LCA and GoM, was that the GoM model performed well and consistently across a variety of underlying population conditions, including even when the underlying model was LCA. Previous research had demonstrated that this model would accurately recover the number of extreme latent classes well for a sample size of 5,000, and when the classes were relatively equal in size. The current study extended this work by demonstrating that when the underlying data came from the GoM model, the GoM approach generally identified the correct number of underlying extreme latent classes for much smaller samples, and when the groups were of very different sizes. In addition, these results demonstrate that the estimator’s ability to do so was largely impervious to the number of extreme latent classes, sample size, group size ratio, or differences among the groups in the probability of endorsing the items in the set. In other words, researchers making use of the GoM model can have confidence in its ability to consistently recover the underlying latent structure for samples as small as 800 when the group size ratio was as unequal as 0.91/0.03/0.03/0.03 in the four latent classes case. Furthermore, when the underlying extreme groups are equal in size, the ability of the GoM model to accurately identify the number of underlying latent classes is high for samples as small 200 individuals. This latter result is most pronounced for the two extreme class case, but it also holds when four subgroups are present in the population.

When the underlying model was based on the LCA, GoM provided group classification results that were very comparable to those of LCA, when two subgroups were present in the population. However, GoM also had a tendency to overestimate the number of latent classes when the data were generated using LCA. Thus, researchers using the GoM should carefully consider the mixing parameter estimates, and if they seem to support the presence of extreme latent profiles rather than mixed profile membership for most individuals in the sample, then LCA may be preferable for characterizing the latent structure of the data. This latter recommendation is particularly trenchant when more latent subgroups are found to be present.

In terms of estimation bias for the ${\alpha }_0$ parameter, the results of this study demonstrated that larger samples and more equal group sizes are preferable. Specifically, in order for relative bias to be 0.05 or lower, samples need to be 400 or more, coupled with equal extreme latent class sizes. When the sample was 200, the relative bias was quite large for both the two and four group cases. This bias was exacerbated when the groups were also of different sizes, and generally smaller when two groups were present in the population, as opposed to four.

Implications for Practice

Given these results, several recommendations for practice can be made. First, if the researcher is reasonably confident that the underlying model is GoM (i.e., individuals in the population probably contain a mixture of the underlying subgroups) and there are only two extreme latent groups present in the data, then the GoM model estimator will perform well in terms of accurately identifying the number of groups, and placing individuals within these groups for samples as small as 200, even when the group size ratios are as extreme as 10/90. When extreme profiles are more likely, as with an underlying LCA model, then the GoM approach may tend to overestimate the number of classes present in the population.

A second recommendation is that when more extreme latent classes are believed to be present (e.g., four), then the researcher may need samples upward of 800, particularly if the subgroup sizes are unequal. However, if it is believed that the extreme latent classes are of approximately the same size, then samples of 400 may be large enough for researchers expecting to find approximately four such groups in the data.

Third, the determination of the underlying model appears to be more important when more latent classes are present in the data. The GoM model did not generally perform as well as LCA when the underlying model was LCA, and vice versa. Therefore, researchers should carefully consider both the theoretical likelihood of which model is more likely, as well as carefully examine the membership probability estimates. If it appears that most members of the sample belong to only a single group, then LCA will likely be the preferred approach for fitting the model.

A fourth implication for practice to come from this study is that performance of the GoM is largely unaffected by the degree to which the extreme latent classes differ in terms of their response probabilities on the dichotomous indicators, at least down to a difference of 0.1. Thus, its ability to accurately identify the number and individual memberships of these classes will generally be good, even for differences in the groups’ probabilities of item endorsement of 0.1. Finally, researchers who are interested in accurately estimating the ${\alpha }_0$ parameter, which expresses the degree to which individuals are concentrated in the extreme latent classes, will need to have samples of 800 or more, and relatively equal group sizes. Estimation accuracy for this parameter can be reasonably high for smaller samples, but only when the extreme classes are of the same size, which in practice may not be reasonable to expect.

Directions for Future Research

As with all research, the current study has limitations that need to be addressed in future work. Perhaps first and foremost, a wider array of extreme latent class size conditions is necessary, in conjunction with the smaller samples included in this study. Prior investigation into the performance of the GoM model (Erosheva et al., 2007) used as many as seven such classes in conjunction with a sample size of 5,000. Thus, future studies should examine more than four latent classes but with samples comparable to those included here. A second direction for future work in this area is to examine the performance of the GoM estimator with varying levels of extreme group concentration. In the current study, the data were simulated so that concentration in the extreme groups was relatively high. Future work should examine how well the GoM estimator works when the extreme group concentration is lower, and the sample sizes and group size ratios are similar to those included in this study. A third area for future research would be to examine how well the GoM estimator works when the indicator variables are not dichotomous in nature but rather polytomous or continuous. This research should also compare the performance of the two modeling paradigms in those cases.