Abstract
Background
National governments worldwide have implemented nonpharmaceutical interventions to control the COVID-19 pandemic and mitigate its effects.
Objective
The aim of this study was to investigate the prediction of future daily national confirmed COVID-19 infection growth—the percentage change in total cumulative cases—across 14 days for 114 countries using nonpharmaceutical intervention metrics and cultural dimension metrics, which are indicative of specific national sociocultural norms.
Methods
We combined the Oxford COVID-19 Government Response Tracker data set, Hofstede cultural dimensions, and daily reported COVID-19 infection case numbers to train and evaluate five non–time series machine learning models in predicting confirmed infection growth. We used three validation methods—in-distribution, out-of-distribution, and country-based cross-validation—for the evaluation, each of which was applicable to a different use case of the models.
Results
Our results demonstrate high R2 values between the labels and predictions for the in-distribution method (0.959) and moderate R2 values for the out-of-distribution and country-based cross-validation methods (0.513 and 0.574, respectively) using random forest and adaptive boosting (AdaBoost) regression. Although these models may be used to predict confirmed infection growth, the differing accuracies obtained from the three tasks suggest a strong influence of the use case.
Conclusions
This work provides new considerations in using machine learning techniques with nonpharmaceutical interventions and cultural dimensions as metrics to predict the national growth of confirmed COVID-19 infections.
Keywords: COVID-19, machine learning, nonpharmaceutical interventions, cultural dimensions, random forest, AdaBoost, forecast, informatics, epidemiology, artificial intelligence
Introduction
Background
In response to the COVID-19 pandemic, national governments have implemented nonpharmaceutical interventions (NPIs) to control and reduce the spread in their respective countries [1-5]. Indeed, early reports suggested the potential effectiveness of the implementation of NPIs to reduce the transmission of COVID-19 [2,4-8] and other infectious diseases [9-11]. Many epidemiological models that forecast future infection numbers have therefore suggested the role of NPIs in reducing infection rates [2,4,7,12], which can aid the implementation of national strategies and policy decision-making. Recent research incorporates publicly available data with machine learning for use cases such as reported infection case number forecasting [13-16]. Although these studies have used various features, such as existing infection statistics [13], weather [14], media and internet activity [15], and lockdown type [16], to predict infection case numbers, no study has yet examined the combination of NPIs and cultural dimensions in predicting infection growth. In this paper, we include the implementation of NPIs at the national level as features (ie, independent variables) in predicting the national growth of the number of confirmed infection cases. Based on recent studies that identify cultural dimensions as having influence in the effectiveness of NPIs [17-19], we also incorporate cultural dimensions as features. Prior work has focused on NPI variations in different regions of specific countries [2,5,6,20,21]. In contrast, our study involves 114 countries.
Various metrics may provide different perspectives and insights on the pandemic. In this study, we focus on one: confirmed infection growth (CIG), which we define as the 14-day growth in the cumulative number of reported infection cases. Other common metrics to measure the transmission rates of an infectious disease are the basic reproduction number, R0, which measures the expected number of direct secondary infections generated by a single primary infection when the entire population is susceptible [3,22] and the effective reproduction number, Rt [2], which accounts for immunity within a specified population. Although such metrics are typically used by epidemiologists as measures of the transmission of an infectious disease, these metrics are dependent on estimation model structures and assumptions; therefore, they are application-specific and can potentially be misapplied [22]. Furthermore, the public may be less familiar with such metrics as opposed to more practical and observable metrics, such as the absolute or relative change in cumulative reported cases.
Related Work
Mathematical modelling of the transmission of infectious disease is a common method to simulate infection trajectories. A common technique for epidemics is the susceptible-infected-recovered (SIR) model, which separates the population into three subpopulations (susceptible, infected, and recovered) and iteratively models the interaction and shift between these subpopulations, which change throughout the epidemic [23,24]. Variations of this model have since been introduced to reflect other dynamics expected of the spread of infectious diseases [25-27]. These variations of the SIR model have also been applied to the ongoing COVID-19 pandemic [28-31].
The recent increase in data availability through advances in the internet and other data sources has enabled the inclusion of other factors in epidemiology modelling [32,33]. Since the early months of the COVID-19 pandemic, Johns Hopkins University has managed the COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE), which aggregates daily statistics of reported infection and mortality numbers across multiple countries [34]. Data sets related to governmental policies and NPIs have also been released publicly on the web. Notable COVID-19–related data sets include the Oxford COVID-19 Government Response Tracker (OxCGRT) [1], Complexity Science Hub COVID-19 Control Strategies List [35], CoronaNet [36], county-level socioeconomic data for predictive modeling of epidemiological effects (US-specific) [37], and CAN-NPI (Canada-specific) [20]. Additional COVID-19 data sets relate to social media activity [38-41], scientific publications [42-44], population mobility [45-48], and medical images [49-52]. In this work, we focus on the use of NPIs in the forecast of COVID-19 infection growth. Specifically, we selected the CSSE data set for infection statistics and the OxCGRT for NPI features due to their global comprehensiveness. Although features can be extracted from additional COVID-19 data sets in our models, we limited the scope of this study to COVID-19 NPI features.
Recent research has also linked the effect of cultural dimensions in responses to the COVID-19 pandemic. Studies suggest that cultural dimensions may affect individual and collective behavior [53-57] and the effectiveness of NPIs [17-19], and that cultural dimensions should be considered when implementing NPIs [17]. Although these studies identify the importance of cultural dimensions in controlling the COVID-19 pandemic, to our knowledge, this work is the first to complement cultural dimensions with NPIs to forecast future COVID-19 infection growth. We recognize that various cultural dimension models exist, such as the six Hofstede cultural dimensions [58], Global Leadership and Organizational Effectiveness (GLOBE) [59], and the Cultural Value Scale (CVSCALE) [60], and that each model has their advocates and criticisms [61]. In this work, we selected the 2015 edition of the Hofstede model [62] due to the relevance of its cultural dimensions in the mentioned studies [17-19,55-57].
Machine learning has been used in applications to combat the COVID-19 pandemic, such as in patient monitoring and genome sequencing [63-66]. Recent studies have also used various statistical and machine learning techniques for short-term forecasting of infection rates for the COVID-19 pandemic [13,15,16,30,33] using reported transmission and mortality statistics, population geographical movement data, and media activity. Pinter et al [13] combined multilayer perceptron with fuzzy inference to predict reported infection and mortality numbers in Hungary with only case number features from May to August 2020. Although reported infection and mortality case numbers aligned with their predictions for May 2020, comparison of the predictions with actual reported numbers from June to August 2020 suggest inaccuracies. Liu et al [15] used internet and news activity predictors within a clustering machine learning model for reported COVID-19 case numbers within Chinese provinces. However, the predictors used within this work are heavily limited to Chinese populations (eg, Baidu search and mobility data, Chinese media sources), and they only predicted cases 2 days ahead. Malki et al [14] used weather, temperature, and humidity features as predictors for COVID-19 mortality rates in regressor machine learning models. Their results suggest that these predictors are relevant for COVID-19 mortality rate modelling. Similar to our work, Saba et al [16] implemented multiple machine learning models to forecast COVID-19 cases based on NPI implementation. However, their work differs in that it only includes lockdown type as an NPI feature (and does not consider cultural dimensions), the study is limited to 9 countries, and the reported case numbers are predicted instead of the change in case numbers. To our knowledge, no other studies have combined NPI and cultural dimension features to predict the growth of reported COVID-19 cases using machine learning. Furthermore, only this work forecasts COVID-19 growth as a measure of CIG (ie, 14-day growth in the cumulative number of reported cases at a national level) across 114 countries via three validation methods, each of which is applicable to a different use case of the model.
Description of the Study
Due to its direct inference from the number of reported cases, the CIG is a verifiable metric, and it may have a greater impact on the public perception of the magnitude of the COVID-19 pandemic than the actual transmission rate. In this work, CIG reflects the growth in the total number of reported cases within a country in 14 days relative to the total number of previously reported infections, including recoveries and mortalities. We selected 14 days as a suitable period for measuring the change in reported cases because of the expected incubation period of COVID-19. Researchers have found that 97.5% of reported patients with identifiable symptoms developed symptoms within 11.5 days, and 99% developed symptoms within 14 days [67]. We therefore propose the use of 14 days, or 2 weeks, as a suitable period to observe changes in reported case numbers occurring after the implementation of NPIs. A shorter period may lead to the misleading inclusion of reported infections that occurred prior to the implementation of an NPI. Results for a longer period may be misleading as well, given the higher likelihood of change in NPIs within this period that will not be accounted for during prediction. We propose that the CIG over 14 days is a suitable metric that enables inference of the effect of NPIs while being within a relevant period for short-term epidemiology forecasting. We emphasize that the reported number of infections may not necessarily be correlated with the actual transmission rate due to factors such as different testing criteria and varying accessibility in testing over time.
We deployed five machine learning models to predict the CIG for individual countries across 14 days. Explicitly, this value was the label (ie, dependent variable) we sought to predict. We used features (ie, independent variables) representing the implementation levels of NPIs and the cultural dimensions of each country. We obtained daily metrics for the implementation of NPIs at the national level from the OxCGRT data set [1]. Although different countries may implement similar NPIs, researchers have suggested that cross-cultural variations across populations lead to different perceptions and responses toward these NPIs [53,54,68]. We intended to capture any effects due to national cross-cultural differences by complementing the OxCGRT data set with national cultural norm values from the Hofstede cultural dimensions [58]. Our non–time series deep learning models predicted the expected future national CIG using both NPI implementation and cultural norm features. Although time series deep learning models (eg, recurrent neural networks or transformers) may also provide CIG predictions, these models generally require greater amounts of accurately labeled trajectory data and assume that past trajectory trends are readily available representatives of future trajectories. Instead, our non–time series models were trained on more granular data that did not necessarily need to be temporally concatenated into a trajectory. We also opted for less complex non–time series models due to indeterminacies in acquiring and verifying sufficient trajectory data, especially due to the lack of reliable data at the onset of the COVID-19 outbreak.
Our results suggest that non–time series machine learning models can predict future CIG according to multiple validation methods, depending on the user's application. Although we do not necessarily claim state-of-the-art performance for infection rate prediction given the rapidly growing amount of parallel work in this area, to the best of our knowledge, our work is the first to use machine learning techniques to predict the change in national cumulative numbers of reported COVID-19 infections by combining NPI implementation features with national cultural features.
Our implementation uses publicly available data retrieved from the internet and relies on the open-sourced Python libraries Pandas [69] and Scikit-Learn [70].
Methods
Data and Preprocessing
Candidate features at the national level were extracted from three data sets for input into our machine learning models: NPIs, cultural dimensions, and current confirmed COVID-19 case numbers.
OxCGRT provides daily level metrics of the NPIs implemented by countries [1]. This data set sorts NPIs into 17 categories, each with either an ordinal policy level metric ranging from 0 (not implemented) to 2, 3, or 4 (strictly enforced) or a continuous metric representing a monetary amount (eg, research funding). The value of each national NPI metric is assigned daily from data in publicly available sources by a team of Oxford University staff and students using the systematic format described in [1]. We limited our candidate features to the 13 ordinal policy categories and 4 computed indices, which represent the implementation of different policy types taken by governments, based on the implemented NPIs. This data set contains data starting from January 1, 2020.
To represent cultural differences across populations of different countries, the 2015 edition of the Hofstede cultural dimensions [62,71] was tagged to each country. Although these dimensions are rarely used in epidemiology studies, they have been used frequently in international marketing studies and cross-cultural research as indicators of the cultural values of national populations [61,72]. Multiple studies have also linked cultural dimensions to health care–related behavior, such as antibiotic usage and body mass index [73-76]. Because the 2015 edition of this data set groups certain geographically neighboring countries together (eg, Ivory Coast, Burkina Faso, Ghana, etc, into Africa West), we tagged all subgroup countries with the dimension values of their group. Although we recognize that this approach is far from ideal and will likely lead to some degree of inaccurate approximation in these subgroup countries, we performed this preprocessing step to include those countries in our study. The dimension values for each country were constant across all samples. Six cultural dimensions were presented for each country or region [71]:
Power distance index: the establishment of hierarchies in society and organizations and the extent to which lower hierarchical members accept inequality in power
Individualism versus collectivism: the degree to which individuals are not integrated into societal groups, such as individual or immediate family (individualistic) versus extended families (collectivistic)
Uncertainty avoidance: a society's tendency to avoid uncertainty and ambiguity through use of societal disapproval, behavioral rules, laws, etc
Masculinity versus femininity: Societal preference toward assertiveness, competitiveness, and division in gender roles (masculinity) compared to caring, sympathy, and similarity in gender roles (femininity)
Long-term versus short-term orientation: Societal values toward tradition, stability, and steadfastness (short-term) versus adaptability, perseverance, and pragmatism (long-term)
Indulgence versus restraint: The degree of freedom available to individuals for fulfilling personal desires by social norms, such as free gratification (indulgence) versus controlled gratification (restraint)
We extracted the daily number of confirmed cases, nt, for each country from the COVID-19 Data Repository by the CSSE at Johns Hopkins University [34]. We used a rolling average of the previous 5-day window to smooth fluctuations in nt, which may be caused by various factors, such as inaccurate case reporting, no release of confirmed case numbers (eg, on weekends and holidays), and sudden infection outbreaks. We refer to the smoothed daily number of confirmed cases for date t as 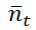 .
.
We computed the CIG for a specified date, τ, as:
 |
The CIG represents the expected number of new confirmed cases from date τ – 13 to date τ as a percentage of the total number of confirmed infection cases up to date τ – 14.
Our goal was to predict the CIG 14 days in advance (ie, CIGτ+14) given information from the current date τ for each country. Available candidate features included all ordinal policy metrics and the four computed indices from OxCGRT, the six cultural dimension values from the Hofstede model, the CIG of the current date CIGτ, and the smoothed cumulative number of confirmed cases 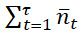 , for a total of 25 candidate features. Neither the date nor any other temporal features were included.
, for a total of 25 candidate features. Neither the date nor any other temporal features were included.
We trimmed samples with fewer than 10 cumulative confirmed infection cases and with the highest 2.5% and the lowest 2.5% of CIGτ+14 to remove outliers in the data. Because the lowest 2.5% of CIGτ+14 were all 0.0%, we removed the samples with CIGτ+14=0.0% by ascending date.
Our data range from April 1 to September 30, 2020, inclusively. We excluded all countries from our combined data set that had missing feature values. In total, our combined data set and our experiments applied to 114 countries: Algeria, Angola, Argentina, Australia, Austria, Bahrain, Bangladesh, Belgium, Benin, Botswana, Brazil, Bulgaria, Burkina Faso, Burundi, Cameroon, Canada, Central African Republic, Chad, Chile, China, Colombia, Comoros, Croatia, Czech Republic, Denmark, Djibouti, Egypt, El Salvador, Eritrea, Estonia, Ethiopia, Finland, France, Gabon, Gambia, Germany, Ghana, Greece, Guinea, Hong Kong, Hungary, India, Indonesia, Iran, Iraq, Ireland, Italy, Japan, Jordan, Kenya, Kuwait, Latvia, Lebanon, Lesotho, Liberia, Libya, Lithuania, Luxembourg, Madagascar, Malawi, Malaysia, Mali, Mauritania, Mauritius, Mexico, Morocco, Mozambique, Namibia, Netherlands, New Zealand, Niger, Nigeria, Norway, Oman, Pakistan, Palestine, Peru, Philippines, Poland, Portugal, Qatar, Romania, Russia, Rwanda, Saudi Arabia, Senegal, Serbia, Seychelles, Sierra Leone, Singapore, Slovenia, Somalia, South Sudan, Spain, Sudan, Sweden, Switzerland, Syria, Taiwan, Tanzania, Thailand, Togo, Trinidad and Tobago, Tunisia, Turkey, Uganda, United Arab Emirates, United States, Uruguay, Venezuela, Vietnam, Yemen, Zambia, and Zimbabwe.
The mean, standard deviation, and range of each candidate feature value for the above countries are shown in Table 1.
Table 1.
Statistical measurements of candidate feature values.
| Candidate features | Mean (SD) | Range | |
| Nonpharmaceutical interventions | |||
|
|
School closure | 2.23 (1.01) | 0.00 to 3.00 |
|
|
Workplace closure | 1.67 (0.92) | 0.00 to 3.00 |
|
|
Cancellation of public events | 1.64 (0.65 | 0.00 to 2.00 |
|
|
Restrictions on gatherings | 2.89 (1.27) | 0.00 to 4.00 |
|
|
Closure of public transport | 0.71 (0.77) | 0.00 to 2.00 |
|
|
Stay-at-home requirements | 1.17 (0.90) | 0.00 to 2.00 |
|
|
Restrictions on internal movement | 1.15 (0.88) | 0.00 to 2.00 |
|
|
International travel controls | 3.13 (1.00) | 0.00 to 4.00 |
|
|
Income support | 1.04 (0.79) | 0.00 to 2.00 |
|
|
Debt/contract relief | 1.23 (0.76) | 0.00 to 2.00 |
|
|
Public information campaigns | 1.97 (0.23) | 0.00 to 2.00 |
|
|
Testing policy | 1.84 (0.82) | 0.00 to 2.00 |
|
|
Contact tracing | 1.50 (0.64) | 0.00 to 2.00 |
|
|
Stringency Index | 63.02 (20.57) | 0.00 to 100.00 |
|
|
Government Response Index | 61.43 (15.03) | 0.00 to 95.54 |
|
|
Containment Health Index | 62.91 (16.50) | 0.00 to 98.96 |
|
|
Economic Support Index | 52.53 (28.93) | 0.00 to 100.00 |
| Current infection numbers | |||
|
|
Current cumulative number of confirmed cases: 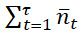
|
113,302.24 (505,170.50) | 4.00 to 7,155,220.00 |
|
|
CIG τ a | 0.85 (3.83) | –0.423 to 228.00 |
| Hofstede cultural dimensions | |||
|
|
Power distance | 66.74 (17.34) | 11.00 to 104.00 |
|
|
Individualism | 38.52 (18.71) | 12.00 to 91.00 |
|
|
Masculinity | 48.32 (14.06) | 5.00 to 95.00 |
|
|
Uncertainty avoidance | 64.17 (17.42) | 8.00 to 112.00 |
|
|
Long-term orientation | 35.36 (21.52) | 3.52 to 92.95 |
|
|
Indulgence | 46.88 (20.47) | 0.00 to 100.00 |
aCIGτ: confirmed infection growth on the current day.
The data preprocessing procedure is shown in Figure 1.
Figure 1.
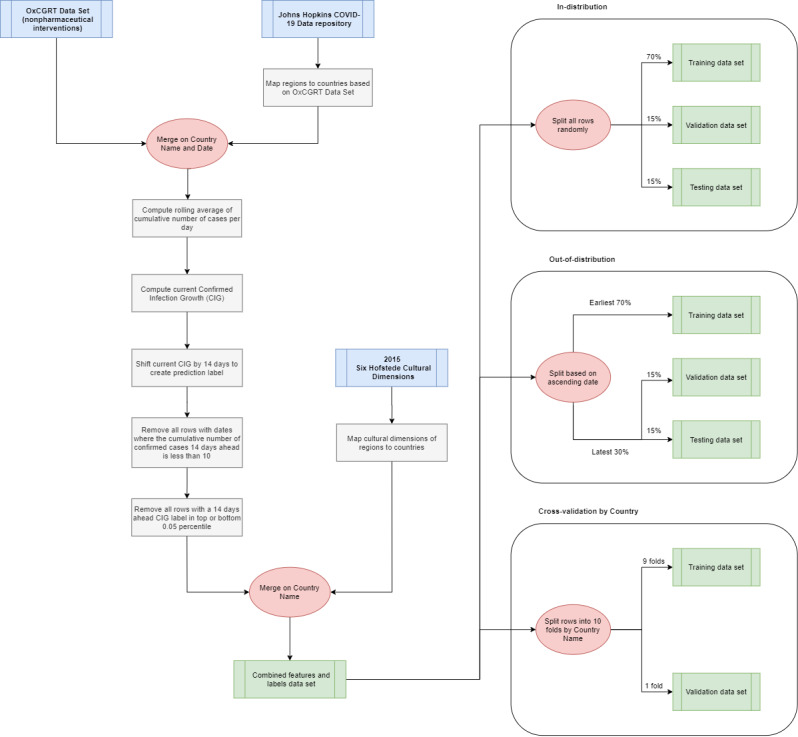
Data preprocessing pipeline from the OxCGRT data set, Johns Hopkins COVID-19 Data Repository, and six Hofstede cultural dimensions to the training, validation, and test data sets for each validation method. OxCGRT: Oxford COVID-19 Government Response Tracker.
Feature Selection and Processing
We selected features to input into our machine learning models from our candidate feature pool using mutual information [77]. Mutual information is a measure of the dependency between an individual feature (ie, the independent variable) and the label (ie, the dependent variable), and it captures both linear and nonlinear dependencies. However, mutual information does not capture multivariate dependencies or indicate collinearity between features. To include both linear and nonlinear dependencies, features are selected if they achieve substantially nonzero mutual information (ie, greater than 0.10). Feature selection was conducted prior to training with the training set in all validation methods. Similar feature filtering and selection techniques have been used in other machine learning applications [70,78]. The candidate features considered for input and their respective mutual information are listed in Table 2 for the in-distribution and out-of-distribution validation methods. Mutual information was also computed for each of the ten folds of the cross-validation method.
Table 2.
Mutual information of candidate features for the in-distribution and out-of-distribution validation methods. In the cross-validation method, the 10 folds have varying mutual information.
| Candidate feature | Mutual information | ||||
|
|
In-distribution | Out-of-distribution | |||
| Nonpharmaceutical interventions | |||||
|
|
School closurea,b | 0.184 | 0.205 | ||
|
|
Workplace closureb | 0.098 | 0.127 | ||
|
|
Cancellation of public eventsb | 0.089 | 0.127 | ||
|
|
Restrictions on gatheringsa,b | 0.107 | 0.112 | ||
|
|
Closure of public transportb | 0.094 | 0.124 | ||
|
|
Stay-at-home requirementsa,n | 0.139 | 0.163 | ||
|
|
Restrictions on internal movementa,b | 0.126 | 0.146 | ||
|
|
International travel controls | 0.099 | 0.099 | ||
|
|
Income supportb | 0.095 | 0.110 | ||
|
|
Debt/contract relief | 0.043 | 0.053 | ||
|
|
Public information campaigns | 0.020 | 0.023 | ||
|
|
Testing policy | 0.056 | 0.064 | ||
|
|
Contact tracing | 0.030 | 0.038 | ||
|
|
Stringency Indexa,b | 0.638 | 0.668 | ||
|
|
Government Response Indexa,b | 0.634 | 0.641 | ||
|
|
Containment Health Indexa,b | 0.621 | 0.655 | ||
|
|
Economic Support Indexa,b | 0.119 | 0.124 | ||
| Current infection numbers | |||||
|
|
Current cumulative number of confirmed cases: 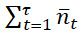 a,b a,b
|
0.517 | 0.557 | ||
|
|
CIG τ a,b,c | 0.866 | 0.798 | ||
| Hofstede cultural dimensions | |||||
|
|
Power distancea,b | 0.288 | 0.342 | ||
|
|
Individualisma,b | 0.309 | 0.355 | ||
|
|
Masculinitya,b | 0.310 | 0.372 | ||
|
|
Uncertainty avoidancea,b | 0.314 | 0.370 | ||
|
|
Long-term orientationa,b | 0.461 | 0.535 | ||
|
|
Indulgencea,b | 0.456 | 0.529 | ||
aSelected feature for the in-distribution method.
bSelected feature for the out-of-distribution method.
cCIGτ: confirmed infection growth on the current day.
All selected features were then normalized to the range [0,1] using standard min-max normalization.
Model Training and Validation
We trained the machine learning models by performing a grid search over the combinations of hyperparameters listed in Table 3 [70,79-82]. We optimized the models using the mean squared error (MSE) criterion and selected the model hyperparameters with the lowest mean absolute error (MAE) as the optimal configuration of the model. The MSE heavily penalizes large residual errors disproportionately, while the MAE provides an absolute mean of all residual errors [83]. The MAE of the training data acts as a measure of the goodness-of-fit of the model, while the MAE of the validation and testing data acts as a measure of the predictive performance [84].
Table 3.
Machine learning models and hyperparameter combinations used in the grid search.
| Model | Hyperparameters | |
| Ridge regression | ||
| α | 0.00, 0.25, 0.50, 0.75, 1.00, 1.25 | |
| Decision tree regression | ||
|
|
Depth | 5, 10, 15, 20, 25, 30 |
|
|
Minimum sample split | 2, 5, 10 |
|
|
Minimum sample leaves | 1, 2, 4, 8, 10 |
| Random forest regression | ||
|
|
Depth | 5, 10, 20, 25, 30 |
|
|
Estimators | 3, 5, 10, 15, 20, 30, 50, 75, 100, 125, 150 |
|
|
Minimum sample split | 2, 5, 10 |
|
|
Minimum sample leaves | 1, 2, 4, 8, 10 |
| AdaBoosta regression | ||
|
|
Weak learner | Decision tree (maximum depth: 2) |
|
|
Estimators | 3, 5, 10, 15, 20, 30, 50, 75, 100, 125, 150 |
|
|
Loss function | Linear |
|
|
Learning rate | 0.1, 0.5, 1.0 |
| Support vector regression | ||
|
|
ε | 0.00, 0.10, 0.20, 0.50 |
|
|
Kernel | Linear, radial, sigmoid |
aAdaBoost: adaptive boosting.
To validate in-distribution and out-of-distribution, we split our samples into 70-15-15 training-validation-test sets. For cross-validation [85,86], we split our samples into 10 folds (ie, 90-10). These three methods of validation each represent a different definition of performance for the machine learning models.
In-Distribution Validation
We randomly split the samples into training, validation, and test sets. Consequently, the models were trained from samples distributed across the entire date range available in our data. This is critical, as it is generally expected that model performance is best when training and test data are drawn from the same distribution. Because the COVID-19 infection numbers naturally constitute a time series, this method ensures that validation and test samples are indeed from the same distribution as the training samples. Because the samples are disassociated from their dates and all other known temporal features, the prediction of the validation and test samples using the training samples is unordered. This method may be applicable to use cases in which the date-to-predict is expected to be in a similar distribution as the training samples, such as predicting CIGτ+14 when data up to the current date τ are available.
Out-of-Distribution Validation
Although the in-distribution method can ensure that the training, validation, and test data are all sampled from the same distribution, it may not necessarily be the most practical method. Generally, the goal of long-term infection rate forecasting is to anticipate future infection rates, and it should not be represented as an in-distribution task, where we trained it with data from near or later than the date-to-predict. Therefore, we also validated the performance of our models by training on the earliest 70% of the samples. The validation and test sets were then randomly split between the remaining 30% of the samples. This setup ensures that all training samples occurred earlier than the validation and testing samples and that no temporal features (known or hidden) were leaked. However, due to the changing environment related to COVID-19 infections (eg, the introduction of new NPIs, seasonal changes, new research), the validation and testing distributions are likely different from that of the training set. This method may be applicable for use cases in which the date-to-predict is in the far future and not all data up to 14 days prior to the date-to-predict are available.
Country-Based Cross-Validation
As a compromise between the above two methods, we also used a cross-validation method in which we split the available countries into 10 folds. The aim was to evaluate validation samples from the same date range as the training samples, but not the same country trajectory. That is, only data from countries not in the validation set are included in the training set. Although the samples from the training and validation sets are therefore sampled from different distributions (ie, different countries), we anticipate that features from the Hofstede cultural dimensions [58] may assist in identifying similar characteristics between countries, thus reducing the disparity between the training and validation distributions. This method may be applicable in predicting the CIG of countries for which previous associated data is unavailable or unreliable.
Results
Feature Selection
For both the in-distribution and out-of-distribution training sets, we observed that most candidate features met our requirement of nonzero mutual information (≥0.10) (see Table 2).
In both training sets, the candidate features that did not meet the requirements were international travel control (0.099, 0.099), debt/contract relief (0.043, 0.053), public information campaigns (0.020, 0.023), testing policy (0.056, 0.064), and contact tracing (0.030, 0.038). Additional candidate features that did not meet the requirements for the in-distribution training set were workplace closure (0.098) and cancellation of public events (0.089). Overall, the in-distribution and out-of-distribution data sets contained 17 and 20 features, respectively.
CIGτ had the highest mutual information out of all features, suggesting similarities between the feature CIGτ and the label CIGτ+14. Further analysis showed a correlation of r=.309 between CIGτ and CIGτ+14. This may be due to similar trends in the CIG when the implementation of NPIs is consistent within a 14-day period. We also observed that all candidate features for the six Hofstede cultural dimensions had higher mutual information than all individual NPI candidate features, aside from the aggregated indices. This finding suggests a high statistical relationship between each cultural dimension feature and the label we sought to predict. Although the cultural dimension values may not fully represent the cultural differences of each country (see Limitations), there is sufficient information between each cultural dimension feature and the label for them to be relevant predictors of the label.
Comparison of Machine Learning Models
Out of all the available configurations (ie, hyperparameter combinations) of each model, we selected the model configurations with the lowest validation errors and computed the test errors. The parameters for these selected models are listed in Table 4. The mean training, validation, and test errors are included in Table 5, Table 6, and Table 7, respectively, for the in-distribution, out-of-distribution, and cross-validation methods. We also include the median percent error [87], which is the percentage difference of the prediction f(x(i)) and the label y(i) for each instance {x(i), y(i)}, computed as:
Table 4.
Hyperparameters of the optimal configuration (lowest validation mean absolute error) for each model for each validation method.
| Model | Validation method | |||
|
|
In-distribution | Out-of-distribution | Cross-validation | |
| Ridge regression | ||||
|
|
α | 0.00 | 0.25 | 0.00 |
| Decision tree regression | ||||
|
|
Depth | 25 | 10 | 5 |
|
|
Minimum sample split | 2 | 5 | 2 |
|
|
Minimum sample leaves | 1 | 1 | 4 |
| Random forest regression | ||||
|
|
Depth | 30 | 15 |
15 |
|
|
Estimators | 150 | 10 | 125 |
|
|
Minimum sample split | 2 | 2 | 2 |
|
|
Minimum sample leaves | 1 | 10 | 10 |
| AdaBoosta regression | ||||
|
|
Estimators | 5 | 5 | 3 |
|
|
Learning rate | 0.1 | 1.0 | 0.1 |
| Support vector regression | ||||
|
|
ε | 0.00 | 0.00 | 0.00 |
|
|
Kernel | Radial | Linear | Linear |
aAdaBoost: adaptive boosting.
Table 5.
Optimal MAE and median percent error values for the in-distribution validation method.
| Model | Train MAEa | Validation MAE | Test MAE | Validation percent error | Test percent error |
| Ridge regression | 0.270 | 0.269 | 0.259 | 1.58 | 0.60 |
| Decision tree regression | 0.001 | 0.041 | 0.039 | 1.00 | 0.00 |
| Random forest regressionb | 0.012 | 0.033 | 0.031 | 1.01 | 1.01 |
| AdaBoostc regression | 0.162 | 0.166 | 0.155 | 1.31 | 1.24 |
| Support vector regression | 0.170 | 0.172 | 0.165 | 1.00 | 1.01 |
aMAE: mean absolute error.
bThe model with the lowest test MAE.
cAdaBoost: adaptive boosting.
Table 6.
Optimal MAE and median percent error values for the out-of-distribution validation method.
|
|
Train MAEa | Validation MAE | Test MAE | Validation percent error | Test percent error |
| Ridge regression | 0.296 | 0.240 | 0.247 | 2.26 | 1.22 |
| Decision tree regression | 0.117 | 0.109 | 0.114 | 1.15 | 0.12 |
| Random forest regression | 0.098 | 0.098 | 0.105 | 1.45 | 0.44 |
| AdaBoostb regressionc | 0.207 | 0.081 | 0.089 | 1.40 | 0.39 |
| Support vector regression | 0.268 | 0.167 | 0.176 | 1.66 | 0.60 |
aMAE: mean absolute error.
bAdaBoost: adaptive boosting.
cThe model with the lowest test MAE.
Table 7.
Optimal MAE and median percent error values for the cross-validation method. Validation error is equivalent to test error for cross-validation.
| Model | Train MAEa | Validation MAE | Validation percent error |
| Ridge regression | 0.262 | 0.275 | 0.62 |
| Decision tree regression | 0.181 | 0.207 | 0.28 |
| Random forest regression | 0.073 | 0.175 | 0.40 |
| AdaBoostb regressionc | 0.164 | 0.167 | 0.27 |
| Support vector regression | 0.230 | 0.240 | 0.03 |
aMAE: mean absolute error.
bAdaBoost: adaptive boosting.
cThe model with the lowest test MAE.
 |
We observed that random forest regression had the lowest mean test error in the interpolation method (0.031) and adaptive boosting (AdaBoost) regression had the lowest mean test errors in the extrapolation and cross-validation methods (0.089 and 0.167, respectively) (see Table 5, Table 6, and Table 7). For all models aside from ridge regression, the in-distribution method had the lowest mean test errors and the lowest median percent error.
Analysis of Best-Performing Models
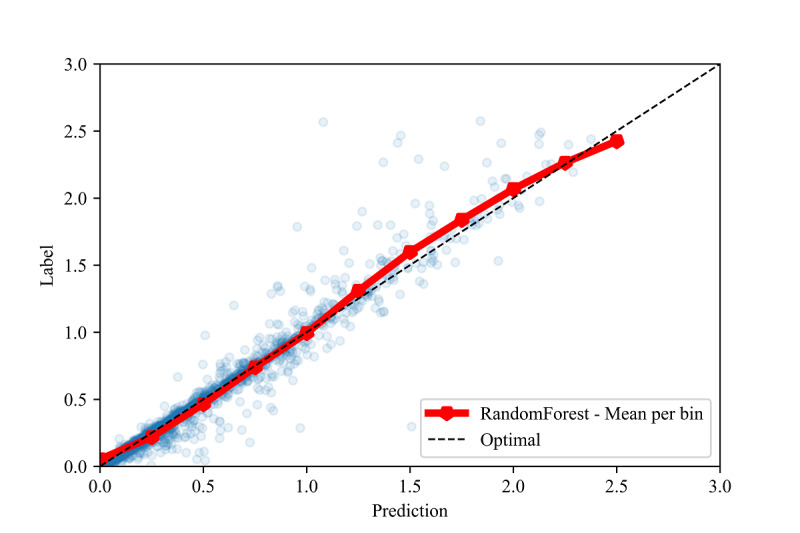
Intercepts near 0.0 and slopes near 1.0 are the linear calibration measures that indicate a perfect calibration relationship between the predictions and the labels [84]. For the optimal models in all the validation methods, we observed slopes close to 1.0 and intercepts close to 0.0 (see Table 8). Due to the large sample sizes, statistical significance testing indicated that several slopes and intercepts are significantly different from 1.0 and 0.0, respectively. However, the small mean differences (standardized to the standard deviation, ie, the z score) indicate that these differences have no practical significance. High correlations ( r>0.70) and moderate-to-high R2 values (R2>.50) [88,89] between the predictions and labels were observed in all three validation methods (see Figure 2, Figure 3, and Figure 4).
Table 8.
Linear calibration measures of the models with the lowest test mean absolute error for each validation method.
| Measure | Validation method | ||
|
|
In-distribution | Out-of-distribution | Cross-validation |
| Test sample size, n | 2847 | 2811 | 19,669 |
| Model | Random forest | AdaBoosta | AdaBoost |
| Correlation, r | 0.979 | 0.716 | 0.758 |
| Slope (SE) | 1.037 (0.004) | 0.986 (0.018) | 0.968 (0.006) |
| Slope standardized mean difference (z score) from 1 | 0.176 | –0.015 | –0.039 |
| Slope P value (mean of 1) | <.001 | .43 | <.001 |
| Intercept (SE) | –0.013 (0.002) | –0.011 (0.004) | 0.006 (0.003) |
| Intercept standardized mean difference (z score) from 0 | –0.119 | –0.044 | 0.014 |
| Intercept P value (mean of 0) | <.001 | .02 | .06 |
| R2 value | 0.959 | 0.513 | 0.574 |
aAdaBoost: adaptive boosting.
Figure 2.
Calibration plot between the labels and predictions for the interpolation validation method, with the mean of each prediction bin of size 0.25.
Figure 3.

Calibration plot between the labels and predictions for the extrapolation validation method, with the mean of each prediction bin of size 0.25.
Figure 4.
Calibration plot between the labels and predictions for the cross-validation method, with the mean of each prediction bin of size 0.25.
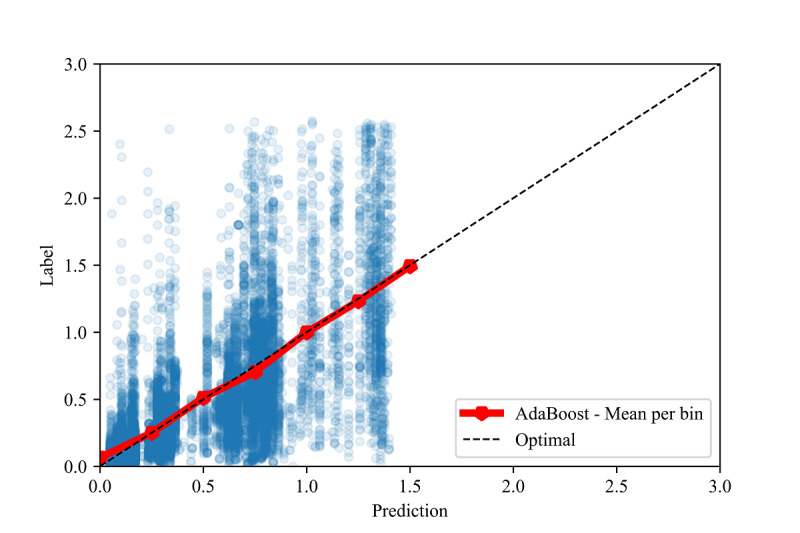
To assess the fine-grained model performance, we discretized both the true labels and model predictions into bins of size 0.5 for all three validation methods (see Figure 5, Figure 6, and Figure 7). Comparing the resulting empirical distributions, it can be seen that the resulting distributions are extremely similar in both the in-distribution and out-of-distribution methods. In the cross-validation method, the predictions skew slightly higher than the labels in the 0.0-1.0 range, showing a general tendency of the model to slightly overestimate the CIG within this range.
Figure 5.
Distributions of the test labels (ie, true confirmed infection growth) and model predictions (n=2847) for the in-distribution method.
Figure 6.
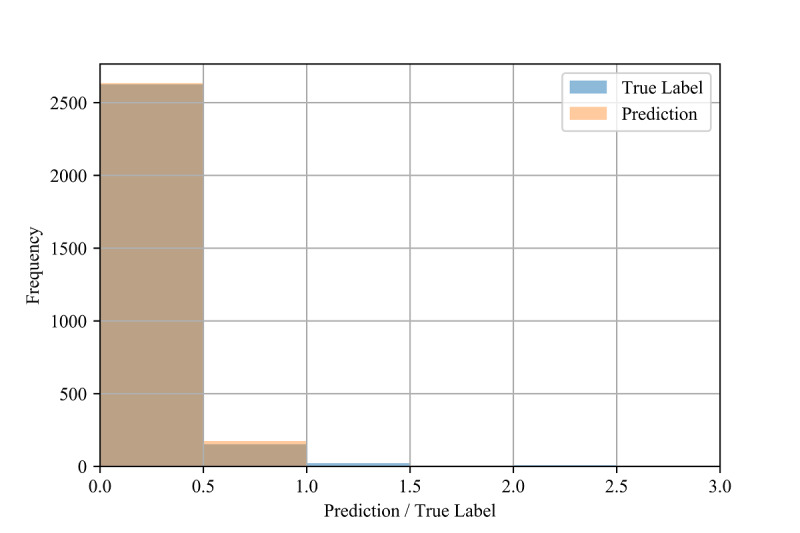
Distributions of the test labels (ie, true confirmed infection growth) and model predictions (n=2811) for the out-of-distribution method.
Figure 7.
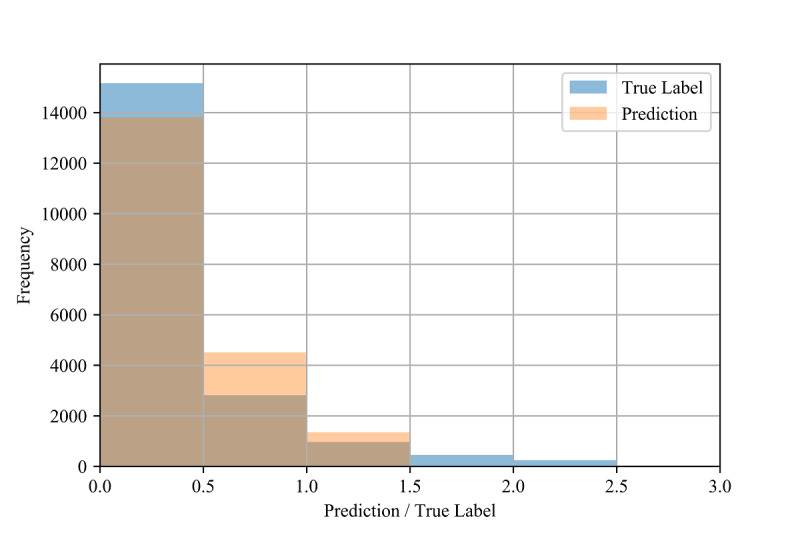
Distributions of the test labels (ie, true confirmed infection growth) and model predictions (n=19,669) for the cross-validation method.
Further analysis shows that the performance of the models varies with the values of the labels. In both the in-distribution and cross-validation methods, the test MAE is lowest for samples with labels of 0.0 (see Table 9 and Table 10), followed by the label range of 0.0-0.5. In the out-of-distribution method, the test MAE is lowest for samples with labels from 0.0-0.5 (see Table 11). For all validation methods, the mean MAE and median percent errors also increase with label bins greater than 1.0, showing a decrease in accuracy for a larger CIG.
Table 9.
Test errors and median percent errors of label bins of size 0.5 for the in-distribution validation method.
| Upper threshold | Count | Test mean nonabsolute error (SD) | Test mean absolute error (SD) | Test percent error |
| 0.0 | 20 | 0.000 (0.000) | 0.000 (0.000) | N/Aa |
| 0.5 | 2183 | 0.011 (0.052) | 0.017 (0.050) | 0.01 |
| 1.0 | 408 | 0.003 (0.076) | 0.047 (0.060) | 0.00 |
| 1.5 | 140 | –0.052 (0.139) | 0.094 (0.115) | –0.02 |
| 2.0 | 68 | –0.104 (0.205) | 0.158 (0.167) | –0.04 |
| 2.5 | 26 | –0.283 (0.309) | 0.297 (0.294) | –0.08 |
| 3.0 | 2 | –1.108 (0.470) | 1.108 (0.470) | –0.43 |
aN/A: not applicable.
Table 10.
Test errors and median percent errors of label bins of size 0.5 for the cross-validation method.
| Upper threshold | Count | Test mean nonabsolute error (SD) | Test mean absolute error (SD) | Test percent error |
| 0.0 | 114 | –0.059 (0.086) | 0.059 (0.086) | N/Aa |
| 0.5 | 15,056 | –0.073 (0.174) | 0.109 (0.153) | 0.493 |
| 1.0 | 2815 | –0.010 (0.282) | 0.217 (0.181) | –0.006 |
| 1.5 | 960 | 0.333 (0.337) | 0.393 (0.265) | –0.299 |
| 2.0 | 451 | 0.719 (0.370) | 0.719 (0.370) | –0.391 |
| 2.5 | 246 | 1.141 (0.321) | 1.141 (0.321) | –0.459 |
| 3.0 | 27 | 1.362 (0.266) | 1.225 (0.266) | –0.486 |
aN/A: not applicable.
Table 11.
Test errors and median percent errors of label bins of size 0.5 for the out-of-distribution validation method.
| Upper threshold | Count | Test mean nonabsolute error (SD) | Test mean absolute error (SD) | Test percent error |
| 0.0 | 19 | 0.076 (0.000) | 0.076 (0.000) | N/Aa |
| 0.5 | 2607 | 0.034 (0.096) | 0.071 (0.074) | 0.44 |
| 1.0 | 152 | –0.161 (0.228) | 0.225 (0.164) | –0.25 |
| 1.5 | 22 | –0.648 (0.222) | 0.648 (0.222) | –0.52 |
| 2.0 | 3 | –1.044 (0.147) | 1.044 (0.147) | –0.60 |
| 2.5 | 8 | –1.464 (0.116) | 1.464 (0.116) | –0.67 |
aN/A: not applicable.
Discussion
Principal Results
Our results suggest that traditional, non–time series machine learning models can predict future CIG to an appreciable degree of accuracy, as suggested by the moderate-to-high R2 values (R2>0.50) and strong linear calibration relationships (r>0.70) [88,89] between the labels and predictions in all the validation methods.
A comparison of our results for all the validation methods suggests differences in the predictive performance of the machine learning models across the varying use cases. The in-distribution method has the highest R2 value and the lowest test mean error and median percent error; this is to be expected, as the test samples were obtained from the same distribution as the training samples. Intuitively, although the samples in the in-distribution method are unordered (ie, no temporal features are included), the availability of samples across the entire temporal range in the training set enables the validation and test samples to interpolate between these training samples.
The out-of-distribution method achieved a higher test mean error and a lower R2 value than the in-distribution method. This is expected, as the evolving COVID-19 infection trajectories observed in most countries give distributions of training samples from earlier dates that may differ greatly from those of validation and test samples from later dates (ie, data shift), which machine learning models are often ill-equipped to handle [90].
Conversely, although the cross-validation method contained the training and validation sets within the same date range, the cross-validation method also separated countries across these sets (ie, the 10 folds) such that no country had samples in both the training and validation sets. This difference led to higher test mean errors and median percent errors than the other two methods and a similar R2 value to that of the out-of-distribution method, suggesting that including training samples from the same country as the validation samples is more important than ensuring temporal overlap. We speculate that this result occurs because the unique cultural dimensions per country may potentially act as categorical rather than continuous features for each country. In such cases, the cultural dimensions observed in the training set would be considered irrelevant to the cultural dimensions within the validation set.
The performance also varied depending on the value of the label (see Table 9, Table 10, and Table 11), which may be due to the imbalanced frequency of the training samples. That is, the rareness of samples with higher CIG compared to lower CIG in the training set may be the cause of their comparatively poor performance.
In Figure 3 and Figure 4, we also show constraints of the trained AdaBoost regression models. The discretization of the prediction values may be due to the low number of estimators used in the lowest mean test error configuration, as shown in Table 4. The low number of estimators in these configurations may also restrict the predictions to a maximum of 1.5 selected to the relatively low number of samples with labels greater than 1.5 (see Figure 6 and Figure 7). The label ranges with the most samples are selected over underrepresented ranges as candidates for prediction values in the discretized AdaBoost regression models. Although additional estimators in the AdaBoost regression models may result in less discrete prediction values, they may also cause over-fitting by increasing the complexity of the models.
Limitations
First, the scores in the OxCGRT and Hofstede cultural dimensions data sets are imprecise. NPI enforcement levels and definitions may vary even between countries with the same scores, while countries sharing similar cultural dimension scores may have unobserved differences in terms of cultural practices due to low representation of their cultures with only six dimensions. Although the Hofstede model is convenient for the goal of our work, it does not identify intracountry cultural differences. Furthermore, distinct countries may be grouped within specific geographical regions (eg, Africa West). We also acknowledge that there are trade-offs between different cultural models and different definitions of culture [61]. We encourage further exploration of appropriate cultural dimensions in addition to the Hofstede model, such as GLOBE [59] and CVSCALE [60]. Second, by predicting the CIG 14 days in advance of the current date, the models do not account for information regarding changes in NPIs between the current date and the date-to-predict. Third, the CIG is a measure of the change in the cumulative number of confirmed infections and may not necessarily be correlated with the change in the daily number of confirmed infections or the actual transmission rate of COVID-19. For example, differences in testing and reporting policies of different jurisdictions (eg, prioritizing high-risk patients, performing more tests per capita, and obfuscating test results) may lead to a misleading representation of the infection growth.
Conclusion
In this study, we trained five non–time series machine learning models to predict the CIG 14 days into the future using NPI features extracted from the OxCGRT data set [1] and cultural norm features extracted from the Hofstede cultural dimensions [58]. Together, these features enabled the prediction of near-future CIG in multiple machine learning models. Specifically, we observed that random forest regression and AdaBoost regression resulted in the most accurate predictions out of the five evaluated machine learning models.
We observed differences in the predictive performance of the machine learning models across the three validation methods; the highest accuracy was achieved with the in-distribution method and the lowest with the cross-validation method. These differences in performance suggest that the models have varying levels of accuracy depending on the use case. Specifically, predictions are expected to have higher accuracies when existing data from the same country in nearby dates are available (ie, in-distribution method). This enables applications such as predicting the CIG over the upcoming 14 days from the current date. The decrease in accuracy when data from nearby dates are unavailable (ie, the out-of-distribution method) suggests weaker performance in predicting the CIG over 14 days for relatively distanced future dates. We observed the greatest decrease in performance when data from the same country were unavailable (ie, the cross-validation method). However, with all validation methods, we observed appreciable calibration measures between the predictions and labels of the test set.
This study adds to the rapidly growing body of work related to predicting COVID-19 infection rates by introducing an approach that incorporates routinely available data on NPIs and cultural dimensions. Importantly, this study emphasizes the utility of NPIs and cultural dimensions for predicting country-level growth of confirmed infections of COVID-19, which to date have been limited in existing forecasting models. Our findings offer a new direction for the broader inclusion of these types of measures, which are also relevant for other infectious diseases, using non–time series machine learning models. Our experiments also provide insight into validation methods for different applications of the models. As the availability of this data increases and the nature of the data continues to evolve, we expect that models such as these will produce accurate and generalizable results that can be used to guide pandemic planning and other infectious disease control efforts.
Acknowledgments
FR is supported by a Canadian Institute for Advanced Research Chair in Artificial Intelligence.
Abbreviations
- CIG
confirmed infection growth
- CSSE
Center for Systems Science and Engineering
- CVSCALE
Cultural Value Scale
- GLOBE
Global Leadership and Organizational Effectiveness
- MAE
mean absolute error
- MSE
mean squared error
- NPI
nonpharmaceutical intervention
- OxCGRT
Oxford COVID-19 Government Response Tracker
- SIR
susceptible-infected-recovered
Footnotes
Conflicts of Interest: None declared.
References
- 1.Hale T, Petherick A, Phillips T, Webster S. Variation in government responses to COVID-19. Blavatnik School of Government Working Paper. 2020. [2021-04-16]. https://www.bsg.ox.ac.uk/sites/default/files/2020-12/BSG-WP-2020-032-v10.pdf.
- 2.Flaxman S, Mishra S, Gandy A, Unwin H, Coupland H, Mellan T. Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in European countries: technical description update. ArXiv. Preprint posted online on April 23, 2020 https://arxiv.org/abs/2004.11342. [Google Scholar]
- 3.Hens N, Vranck P, Molenberghs G. The COVID-19 epidemic, its mortality, and the role of non-pharmaceutical interventions. Eur Heart J Acute Cardiovasc Care. 2020 Apr;9(3):204–208. doi: 10.1177/2048872620924922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brauner J, Sharma M, Mindermann S, Stephenson A, Gavenčiak T, Johnston D, Salvatier J, Leech G, Besiroglu T, Altman G, Ge H, Mikulik V, Hartwick M, Teh YW, Chindelevitch C, Gal Y, Kulveit J. The effectiveness and perceived burden of nonpharmaceutical interventions against COVID-19 transmission: a modelling study with 41 countries. medRxiv. doi: 10.1101/2020.05.28.20116129. Preprint posted online on June 02, 2020. [DOI] [Google Scholar]
- 5.Pan A, Liu L, Wang C, Guo H, Hao X, Wang Q, Huang J, He N, Yu H, Lin X, Wei S, Wu T. Association of public health interventions with the epidemiology of the COVID-19 outbreak in Wuhan, China. JAMA. 2020 May 19;323(19):1915–1923. doi: 10.1001/jama.2020.6130. http://europepmc.org/abstract/MED/32275295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chang SL, Harding N, Zachreson C, Cliff OM, Prokopenko M. Modelling transmission and control of the COVID-19 pandemic in Australia. ArXiv. doi: 10.1038/s41467-020-19393-6. Preprint posted online on March 23, 2020 https://arxiv.org/abs/2003.10218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Davies N, Kucharski A, Eggo R, Gimma A, Edmunds W, Jombart T, O'Reilly K, Endo A, Hellewell J, Nightingale Es, Quilty Bj, Jarvis Ci, Russell Tw, Klepac P, Bosse Ni, Funk S, Abbott S, Medley Gf, Gibbs H, Pearson Cab, Flasche S, Jit M, Clifford S, Prem K, Diamond C, Emery J, Deol Ak, Procter Sr, van Zandvoort K, Sun Yf, Munday Jd, Rosello A, Auzenbergs M, Knight G, Houben Rmgj, Liu Y. Effects of non-pharmaceutical interventions on COVID-19 cases, deaths, and demand for hospital services in the UK: a modelling study. Lancet Public Health. 2020 Jul;5(7):e375–e385. doi: 10.1016/S2468-2667(20)30133-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cowling B, Ali S, Ng T, Tsang T, Li J, Fong M, Liao Q, Kwan My, Lee Sl, Chiu Ss, Wu Jt, Wu P, Leung Gm. Impact assessment of non-pharmaceutical interventions against coronavirus disease 2019 and influenza in Hong Kong: an observational study. Lancet Public Health. 2020 May;5(5):e279–e288. doi: 10.1016/s2468-2667(20)30090-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Aledort J, Lurie N, Wasserman J, Bozzette S. Non-pharmaceutical public health interventions for pandemic influenza: an evaluation of the evidence base. BMC Public Health. 2007 Aug 15;7(1):a. doi: 10.1186/1471-2458-7-208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Merler S, Ajelli M, Fumanelli L, Gomes M, Piontti Apy, Rossi L, Chao Dl, Longini Im, Halloran Me, Vespignani A. Spatiotemporal spread of the 2014 outbreak of Ebola virus disease in Liberia and the effectiveness of non-pharmaceutical interventions: a computational modelling analysis. Lancet Infect Dis. 2015 Feb;15(2):204–211. doi: 10.1016/s1473-3099(14)71074-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cowling BJ, Fung ROP, Cheng CKY, Fang VJ, Chan KH, Seto WH, Yung R, Chiu B, Lee P, Uyeki TM, Houck PM, Peiris JSM, Leung GM. Preliminary findings of a randomized trial of non-pharmaceutical interventions to prevent influenza transmission in households. PLoS One. 2008 May 07;3(5):e2101. doi: 10.1371/journal.pone.0002101. https://dx.plos.org/10.1371/journal.pone.0002101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ferguson N, Laydon D, Nedjati-Gilani G, Imai N, Ainslie K, Baguelin M. Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College London. 2020. Mar 16, [2021-04-16]. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-NPI-modelling-16-03-2020.pdf.
- 13.Pinter G, Felde I, Mosavi A, Ghamisi P, Gloaguen R. COVID-19 pandemic prediction for Hungary; a hybrid machine learning approach. Mathematics. 2020 Jun 02;8(6):890. doi: 10.3390/math8060890. [DOI] [Google Scholar]
- 14.Malki Z, Atlam E, Hassanien A, Dagnew G, Elhosseini M, Gad I. Association between weather data and COVID-19 pandemic predicting mortality rate: machine learning approaches. Chaos Solitons Fractals. 2020 Sep;138:110137. doi: 10.1016/j.chaos.2020.110137. http://europepmc.org/abstract/MED/32834583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liu D, Clemente L, Poirier C, Ding X, Chinazzi M, Davis Jt. A machine learning methodology for real-time forecasting of the 2019-2020 COVID-19 outbreak using Internet searches, news alerts, and estimates from mechanistic models. ArXiv. Preprint posted online on April 8, 2020 https://arxiv.org/abs/2004.04019. [Google Scholar]
- 16.Saba T, Abunadi I, Shahzad MN, Khan AR. Machine learning techniques to detect and forecast the daily total COVID-19 infected and deaths cases under different lockdown types. Microsc Res Tech. 2021 Feb 01; doi: 10.1002/jemt.23702. http://europepmc.org/abstract/MED/33522669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ibanez A, Sisodia G. The role of culture on 2020 SARS-CoV-2 country deaths: a pandemic management based on cultural dimensions. GeoJournal. 2020 Sep 30;:1–17. doi: 10.1007/s10708-020-10306-0. http://europepmc.org/abstract/MED/33020679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huynh TLD. Does culture matter social distancing under the COVID-19 pandemic? Saf Sci. 2020 Oct;130:104872. doi: 10.1016/j.ssci.2020.104872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang Y. Government policies, national culture and social distancing during the first wave of the COVID-19 pandemic: International evidence. Saf Sci. 2021 Mar;135:105138. doi: 10.1016/j.ssci.2020.105138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McCoy L, Smith J, Anchuri K, Berry I, Pineda J, Harish V, Lam AT, Yi SE, Hu S, COVID-19 Canada Open Data Working Group: Non-Pharmaceutical Interventions. Fine B. CAN-NPI: a curated open dataset of Canadian non-pharmaceutical interventions in response to the global COVID-19 pandemic. medRxiv. doi: 10.1101/2020.04.17.20068460. Preprint posted online on April 22, 2020. [DOI] [Google Scholar]
- 21.Lai S, Ruktanonchai N, Zhou L, Prosper O, Luo W, Floyd J, Wesolowski Amy, Santillana Mauricio, Zhang Chi, Du Xiangjun, Yu Hongjie, Tatem Andrew J. Effect of non-pharmaceutical interventions for containing the COVID-19 outbreak in China. medRxiv. doi: 10.1101/2020.03.03.20029843. doi: 10.1101/2020.03.03.20029843. Preprint posted online on March 06, 2020 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Delamater PL, Street EJ, Leslie TF, Yang YT, Jacobsen KH. Complexity of the basic reproduction number (R) Emerg Infect Dis. 2019 Jan;25(1):1–4. doi: 10.3201/eid2501.171901. doi: 10.3201/eid2501.171901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bjørnstad ON, Finkenstädt BF, Grenfell BT. Dynamics of measles epidemics: estimating scaling of transmission rates using a time series SIR model. Ecological Monographs. 2002 May;72(2):169–184. doi: 10.1890/0012-9615(2002)072[0169:domees]2.0.co;2. [DOI] [Google Scholar]
- 24.Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc Lond A. 1997 Aug 01;115(772):700–721. doi: 10.1098/rspa.1927.0118. [DOI] [Google Scholar]
- 25.Nåsell I. The quasi-stationary distribution of the closed endemic sis model. Adv Appl Probab. 2016 Jul 1;28(03):895–932. doi: 10.1017/s0001867800046541. [DOI] [Google Scholar]
- 26.Li MY, Muldowney JS. Global stability for the SEIR model in epidemiology. Math Biosci. 1995 Feb;125(2):155–164. doi: 10.1016/0025-5564(95)92756-5. [DOI] [PubMed] [Google Scholar]
- 27.Abrams D, Grant P. Testing the social identity relative deprivation (SIRD) model of social change: the political rise of Scottish nationalism. Br J Soc Psychol. 2012 Dec;51(4):674–89. doi: 10.1111/j.2044-8309.2011.02032.x. [DOI] [PubMed] [Google Scholar]
- 28.Chen Y, Lu P, Chang C, Liu T. A time-dependent SIR model for COVID-19 with undetectable infected persons. IEEE Trans Netw Sci Eng. 2020 Oct 1;7(4):3279–3294. doi: 10.1109/tnse.2020.3024723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Calafiore G, Novara C, Possieri C. A modified SIR model for the COVID-19 contagion in Italy. 59th IEEE Conference on Decision and Control (CDC); December 14-18, 2020; Jeju Island, South Korea. 2020. [DOI] [Google Scholar]
- 30.Yang Z, Zeng Z, Wang K, Wong S, Liang W, Zanin M, Liu P, Cao X, Gao Z, Mai Z, Liang J, Liu X, Li S, Li Y, Ye F, Guan W, Yang Y, Li F, Luo S, Xie Y, Liu B, Wang Z, Zhang S, Wang Y, Zhong N, He J. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J Thorac Dis. 2020 Mar;12(3):165–174. doi: 10.21037/jtd.2020.02.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fernández-Villaverde J, Jones C. Estimating and simulating a SIRD model of COVID-19 for many countries, states, and cities. NBER Working Paper Series. 2020. May, [2021-04-16]. https://www.nber.org/system/files/working_papers/w27128/w27128.pdf. [DOI] [PMC free article] [PubMed]
- 32.Shuja J, Alanazi E, Alasmary W, Alashaikh A. COVID-19 open source data sets: a comprehensive survey. Appl Intell. 2020 Sep 21;51(3):1296–1325. doi: 10.1007/s10489-020-01862-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mohamadou Y, Halidou A, Kapen PT. A review of mathematical modeling, artificial intelligence and datasets used in the study, prediction and management of COVID-19. Appl Intell. 2020 Jul 06;50(11):3913–3925. doi: 10.1007/s10489-020-01770-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dong E, Du H, Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis. 2020 May;20(5):533–534. doi: 10.1016/s1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Desvars-Larrive A, Dervic E, Haug N, Niederkrotenthaler T, Chen J, Di Natale Anna, Lasser Jana, Gliga Diana S, Roux Alexandra, Sorger Johannes, Chakraborty Abhijit, Ten Alexandr, Dervic Alija, Pacheco Andrea, Jurczak Ania, Cserjan David, Lederhilger Diana, Bulska Dominika, Berishaj Dorontinë, Tames Erwin Flores, Álvarez Francisco S, Takriti Huda, Korbel Jan, Reddish Jenny, Grzymała-Moszczyńska Joanna, Stangl Johannes, Hadziavdic Lamija, Stoeger Laura, Gooriah Leana, Geyrhofer Lukas, Ferreira Marcia R, Bartoszek Marta, Vierlinger Rainer, Holder Samantha, Haberfellner Simon, Ahne Verena, Reisch Viktoria, Servedio Vito D P, Chen Xiao, Pocasangre-Orellana Xochilt María, Garncarek Zuzanna, Garcia David, Thurner Stefan. A structured open dataset of government interventions in response to COVID-19. Sci Data. 2020 Aug 27;7(1):285. doi: 10.1038/s41597-020-00609-9. doi: 10.1038/s41597-020-00609-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cheng C, Barceló Joan, Hartnett AS, Kubinec R, Messerschmidt L. COVID-19 government response event dataset (CoronaNet v.1.0) Nat Hum Behav. 2020 Jul 23;4(7):756–768. doi: 10.1038/s41562-020-0909-7. [DOI] [PubMed] [Google Scholar]
- 37.Killeen B, Wu J, Shah K, Zapaishchykova A, Nikutta P, Tamhane A, Chakraborty S, Wei J, Gao T, Thies M, Unberath M. A county-level dataset for informing the United States' response to COVID-19. ArXiv. Preprint posted online on April 1, 2020 https://arxiv.org/abs/2004.00756?is=5e8d4f149b0f225dde35ccf1. [Google Scholar]
- 38.Zarei K, Farahbakhsh R, Crespi N, Tyson G. A first Instagram dataset on COVID-19. ArXiv. Preprint posted online on April 25, 2020 https://arxiv.org/abs/2004.12226. [Google Scholar]
- 39.Haouari F, Hasanain M, Suwaileh R, Elsayed T. arcCOV-19: The first Arabic COVID-19 Twitter dataset with propagation networks. ArXiv. Preprint posted online on April 13, 2020 https://arxiv.org/abs/2004.05861. [Google Scholar]
- 40.Qazi U, Imran M, Ofli F. GeoCoV19: a dataset of hundreds of millions of multilingual COVID-19 tweets with location information. SIGSPATIAL Spec. 2020 Jun 05;12(1):6–15. doi: 10.1145/3404820.3404823. [DOI] [Google Scholar]
- 41.Memon S, Carley K. Characterizing COVID-19 misinformation communities using a novel Twitter dataset. ArXiv. Preprint posted online on August 3, 2020 https://arxiv.org/abs/2008.00791. [Google Scholar]
- 42.Wang L, Lo K, Chandrasekhar Y, Reas R, Yang J, Eide D, Funk K, Katsis Y, Kinney R, Li Y, Liu Z, Merrill W, Mooney P, Murdick D, Rishi D, Sheehan J, Shen Z, Stilson B, Wade A, Wang K, Wang NXR, Wilhelm C, Xie B, Raymond D, Weld DS, Etzioni O, Kohlmeier S. CORD-19: the COVID-19 Open Research Dataset. ArXiv. Preprint posted online on April 22, 2020 https://arxiv.org/abs/2004.10706. [Google Scholar]
- 43.Chen Q, Allot A, Lu Z. LitCovid: an open database of COVID-19 literature. Nucleic Acids Res. 2021 Jan 08;49(D1):D1534–D1540. doi: 10.1093/nar/gkaa952. http://europepmc.org/abstract/MED/33166392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Guo X, Mirzaalian H, Sabir E, Jaiswal A, Abd-Almageed W. CORD19STS: COVID-19 semantic textual similarity dataset. ArXiv. Preprint posted online on July 5, 2020 https://arxiv.org/abs/2007.02461. [Google Scholar]
- 45.Pepe E, Bajardi P, Gauvin L, Privitera F, Lake B, Cattuto C, Tizzoni M. COVID-19 outbreak response, a dataset to assess mobility changes in Italy following national lockdown. Sci Data. 2020 Jul 08;7(1):230. doi: 10.1038/s41597-020-00575-2. doi: 10.1038/s41597-020-00575-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ribeiro-Dantas MDC, Alves G, Gomes RB, Bezerra LC, Lima L, Silva I. Dataset for country profile and mobility analysis in the assessment of the COVID-19 pandemic. Data in Brief. 2020 Aug;31:105698. doi: 10.1016/j.dib.2020.105698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Barbieri DM, Lou B, Passavanti M, Hui C, Lessa DA, Maharaj B, Banerjee A, Wang F, Chang K, Naik B, Yu L, Liu Z, Sikka G, Tucker A, Foroutan Mirhosseini A, Naseri S, Qiao Y, Gupta A, Abbas M, Fang K, Ghasemi N, Peprah P, Goswami S, Hessami A, Agarwal N, Lam L, Adomako S. A survey dataset to evaluate the changes in mobility and transportation due to COVID-19 travel restrictions in Australia, Brazil, China, Ghana, India, Iran, Italy, Norway, South Africa, United States. Data Brief. 2020 Dec;33:106459. doi: 10.1016/j.dib.2020.106459. https://linkinghub.elsevier.com/retrieve/pii/S2352-3409(20)31341-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kang Y, Gao S, Liang Y, Li M, Rao J, Kruse J. Multiscale dynamic human mobility flow dataset in the U.S. during the COVID-19 epidemic. Sci Data. 2020 Nov 12;7(1):390. doi: 10.1038/s41597-020-00734-5. doi: 10.1038/s41597-020-00734-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Afshar P, Heidarian S, Enshaei N, Naderkhani F, Rafiee M, Oikonomou A, Fard FB, Samimi K, Plataniotis KN, Mohammadi A. COVID-CT-MD: COVID-19 computed tomography (CT) scan dataset applicable in machine learning and deep learning. ArXiv. doi: 10.1038/s41597-021-00900-3. Preprint posted online on September 28, 2020 https://arxiv.org/abs/2009.14623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cohen J, Morrison P, Dao L, Roth K, Duong T, Ghassemi M. Covid-19 image data collection: prospective predictions are the future. ArXiv. Preprint posted online on June 22, 2020 https://arxiv.org/abs/2006.11988. [Google Scholar]
- 51.Yang X, He X, Zhao J, Zhang Y, Zhang S, Xie P. COVID-CT-Dataset: a CT image dataset about COVID-19. ArXiv. Preprint posted online on March 30, 2020 https://arxiv.org/abs/2003.13865. [Google Scholar]
- 52.Born J, Brändle G, Cossio M, Disdier M, Goulet J, Roulin J, Wiedemann N. POCOVID-Net: automatic detection of COVID-19 from a new lung ultrasound imaging dataset (POCUS) ArXiv. Preprint posted online on April 25, 2020 https://arxiv.org/abs/2004.12084. [Google Scholar]
- 53.Bavel Jay J Van, Baicker K, Boggio P, Capraro V, Cichocka A, Cikara M, Crockett Molly J, Crum Alia J, Douglas Karen M, Druckman James N, Drury John, Dube Oeindrila, Ellemers Naomi, Finkel Eli J, Fowler James H, Gelfand Michele, Han Shihui, Haslam S Alexander, Jetten Jolanda, Kitayama Shinobu, Mobbs Dean, Napper Lucy E, Packer Dominic J, Pennycook Gordon, Peters Ellen, Petty Richard E, Rand David G, Reicher Stephen D, Schnall Simone, Shariff Azim, Skitka Linda J, Smith Sandra Susan, Sunstein Cass R, Tabri Nassim, Tucker Joshua A, Linden Sander van der, Lange Paul van, Weeden Kim A, Wohl Michael J A, Zaki Jamil, Zion Sean R, Willer Robb. Using social and behavioural science to support COVID-19 pandemic response. Nat Hum Behav. 2020 May;4(5):460–471. doi: 10.1038/s41562-020-0884-z. [DOI] [PubMed] [Google Scholar]
- 54.Dryhurst S, Schneider CR, Kerr J, Freeman ALJ, Recchia G, van der Bles AM, Spiegelhalter D, van der Linden S. Risk perceptions of COVID-19 around the world. J Risk Res. 2020 May 05;23(7-8):994–1006. doi: 10.1080/13669877.2020.1758193. [DOI] [Google Scholar]
- 55.Guan Y, Deng H, Zhou X. Understanding the impact of the COVID-19 pandemic on career development: insights from cultural psychology. J Vocat Behav. 2020 Jun;119:103438. doi: 10.1016/j.jvb.2020.103438. http://europepmc.org/abstract/MED/32382162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Furlong Y, Finnie T. Culture counts: the diverse effects of culture and society on mental health amidst COVID-19 outbreak in Australia. Ir J Psychol Med. 2020 Sep;37(3):237–242. doi: 10.1017/ipm.2020.37. http://europepmc.org/abstract/MED/32406358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Ashraf B. Stock markets’ reaction to COVID-19: Cases or fatalities? Res Int Bus Finance. 2020 Dec;54:101249. doi: 10.1016/j.ribaf.2020.101249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hofstede G, Bond M. Hofstede's Culture Dimensions. J Cross Cult Psychol. 2016 Jul 27;15(4):417–433. doi: 10.1177/0022002184015004003. [DOI] [Google Scholar]
- 59.House R, Hanges P, Ruiz-Quintanilla S, Dorfman P, Javidan M, Dickson M. Advances in Global Leadership. Bingley, UK: Emerald Group Publishing Ltd; 1999. Cultural influences on leadership and organizations: Project Globe; p. 171. [Google Scholar]
- 60.Yoo B, Donthu N, Lenartowicz T. Measuring Hofstede's five dimensions of cultural values at the individual level: development and validation of CVSCALE. J Int Consum Mark. 2011:193. doi: 10.1080/08961530.2011.578059. [DOI] [Google Scholar]
- 61.Dahl S. Intercultural research: the current state of knowledge. SSRN Journal. 2004 Feb 02; doi: 10.2139/ssrn.658202. [DOI] [Google Scholar]
- 62.Hofstede G. Dimension data matrix. GeertHoftstede. 2015. [2021-04-16]. https://geerthofstede.com/research-and-vsm/dimension-data-matrix/
- 63.Alimadadi A, Aryal S, Manandhar I, Munroe PB, Joe B, Cheng X. Artificial intelligence and machine learning to fight COVID-19. Physiol Genomics. 2020 Apr 01;52(4):200–202. doi: 10.1152/physiolgenomics.00029.2020. http://europepmc.org/abstract/MED/32216577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Yan L, Zhang H, Xiao Y, Wang M, Sun C, Tang X, Jing L, Li S, Zhang M, Xiao Y, Cao H, Chen Y, Ren T, Jin J, Wang F, Xiao Y, Huang S, Tan X, Huang N, Jiao B, Zhang Y, Luo A, Cao Z, Xu H, Yuan Y. Prediction of criticality in patients with severe Covid-19 infection using three clinical features: a machine learning-based prognostic model with clinical data in Wuhan. medRxiv. doi: 10.1101/2020.02.27.20028027. Preprint posted online on March 03, 2020. [DOI] [Google Scholar]
- 65.Randhawa G, Soltysiak M, El Roz H, de Souza Cpe, Hill K, Kari L. Machine learning using intrinsic genomic signatures for rapid classification of novel pathogens: COVID-19 case study. PLoS ONE. 2020 Apr 24;15(4):e0232391. doi: 10.1371/journal.pone.0232391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Harmon SA, Sanford TH, Xu S, Turkbey EB, Roth H, Xu Z, Yang D, Myronenko A, Anderson V, Amalou A, Blain M, Kassin M, Long D, Varble N, Walker SM, Bagci U, Ierardi AM, Stellato E, Plensich GG, Franceschelli G, Girlando C, Irmici G, Labella D, Hammoud D, Malayeri A, Jones E, Summers RM, Choyke PL, Xu D, Flores M, Tamura K, Obinata H, Mori H, Patella F, Cariati M, Carrafiello G, An P, Wood BJ, Turkbey B. Artificial intelligence for the detection of COVID-19 pneumonia on chest CT using multinational datasets. Nat Commun. 2020 Aug 14;11(1):4080. doi: 10.1038/s41467-020-17971-2. doi: 10.1038/s41467-020-17971-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Lauer SA, Grantz KH, Bi Q, Jones FK, Zheng Q, Meredith HR, Azman AS, Reich NG, Lessler J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann Intern Med. 2020 May 05;172(9):577–582. doi: 10.7326/m20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Zhu N, Lu H, Chang L. Debate: facing uncertainty with(out) a sense of control - cultural influence on adolescents' response to the COVID-19 pandemic. Child Adolesc Ment Health. 2020 Sep;25(3):173–174. doi: 10.1111/camh.12408. http://europepmc.org/abstract/MED/32681578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.McKinney W. pandas: a foundational Python library for data analysis and statistics. SC11: Python for High Performance and Scientific Computing; November 18, 2011; Seattle, WA. 2011. https://www.dlr.de/sc/portaldata/15/resources/dokumente/pyhpc2011/submissions/pyhpc2011_submission_9.pdf. [Google Scholar]
- 70.Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O. Scikit-learn: machine learning in Python. J Mach Learn Res. 2011:2825. https://www.jmlr.org/papers/volume12/pedregosa11a/pedregosa11a.pdf. [Google Scholar]
- 71.Hofstede G. Dimensionalizing cultures: the Hofstede model in context. ORPC. 2011 Dec 01;2(1) doi: 10.9707/2307-0919.1014. [DOI] [Google Scholar]
- 72.Soares AM, Farhangmehr M, Shoham A. Hofstede's dimensions of culture in international marketing studies. J Bus Res. 2007 Mar;60(3):277–284. doi: 10.1016/j.jbusres.2006.10.018. [DOI] [Google Scholar]
- 73.Deschepper R, Grigoryan L, Lundborg CS, Hofstede G, Cohen J, Kelen GVD, Deliens L, Haaijer-Ruskamp FM. Are cultural dimensions relevant for explaining cross-national differences in antibiotic use in Europe? BMC Health Serv Res. 2008 Jun 06;8(1):123. doi: 10.1186/1472-6963-8-123. https://bmchealthservres.biomedcentral.com/articles/10.1186/1472-6963-8-123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Borg MA. National cultural dimensions as drivers of inappropriate ambulatory care consumption of antibiotics in Europe and their relevance to awareness campaigns. J Antimicrob Chemother. 2012 Mar 26;67(3):763–7. doi: 10.1093/jac/dkr541. [DOI] [PubMed] [Google Scholar]
- 75.Borg M. Lowbury Lecture 2013. Cultural determinants of infection control behaviour: understanding drivers and implementing effective change. J Hosp Infect. 2014 Mar;86(3):161–8. doi: 10.1016/j.jhin.2013.12.006. [DOI] [PubMed] [Google Scholar]
- 76.Masood M, Aggarwal A, Reidpath D. Effect of national culture on BMI: a multilevel analysis of 53 countries. BMC Public Health. 2019 Sep 03;19(1):1212. doi: 10.1186/s12889-019-7536-0. https://bmcpublichealth.biomedcentral.com/articles/10.1186/s12889-019-7536-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Ross BC. Mutual information between discrete and continuous data sets. PLoS One. 2014 Feb 19;9(2):e87357. doi: 10.1371/journal.pone.0087357. https://dx.plos.org/10.1371/journal.pone.0087357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Pirbazari A, Chakravorty A, Rong C. Evaluating feature selection methods for short-term load forecasting. 2019 IEEE International Conference on Big Data and Smart Computing (BigComp); February 27-March 2, 2019; Kyoto, Japan. 2019. pp. 1–8. [DOI] [Google Scholar]
- 79.Hoerl A, Kennard R. Ridge regression:biased estimation for nonorthogonal problems. Technometrics. 1970 Feb;12(1):55–67. doi: 10.1080/00401706.1970.10488634. [DOI] [Google Scholar]
- 80.Breiman L. Random forests. Mach Learn. 2001;45(1):32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- 81.Freund Y, Schapire RE. A decision-theoretic generalization of on-line learning and an application to boosting. J Comput Syst Sci. 1997 Aug;55(1):119–139. doi: 10.1006/jcss.1997.1504. [DOI] [Google Scholar]
- 82.Drucker H, Burges C, Kaufman L, Smola A, Vapnik V. Support vector regression machines. NIPS'96: Proceedings of the 9th International Conference on Neural Information Processing Systems; 9th International Conference on Neural Information Processing Systems; December 2-5, 1996; Denver, CO. 1996. Dec, pp. 155–161. [Google Scholar]
- 83.Willmott C, Matsuura K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim Res. 2005;30:79–82. doi: 10.3354/cr030079. [DOI] [Google Scholar]
- 84.Steyerberg E, Vickers A, Cook N, Gerds T, Gonen M, Obuchowski N, Pencina Michael J, Kattan Michael W. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology. 2010 Jan;21(1):128–38. doi: 10.1097/EDE.0b013e3181c30fb2. http://europepmc.org/abstract/MED/20010215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Schaffer C. Selecting a classification method by cross-validation. Mach Learn. 1993 Oct;13(1):135–143. doi: 10.1007/bf00993106. [DOI] [Google Scholar]
- 86.Browne MW. Cross-validation methods. J Math Psychol. 2000 Mar;44(1):108–132. doi: 10.1006/jmps.1999.1279. [DOI] [PubMed] [Google Scholar]
- 87.Ardabili S, Mosavi A, Ghamisi P, Ferdinand F, Varkonyi-Koczy A, Reuter U. COVID-19 outbreak prediction with machine learning. PsyArXiv. doi: 10.31234/osf.io/5dyfc. Preprint posted online on October 06, 2020. [DOI] [Google Scholar]
- 88.Mukaka M. Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Med J. 2012 Sep;24(3):69–71. http://europepmc.org/abstract/MED/23638278. [PMC free article] [PubMed] [Google Scholar]
- 89.Moore DS, Kirkland S. The Basic Practice of Statistics. New York, NY: WH Freeman; 2007. [Google Scholar]
- 90.Quionero-Candela J, Sugiyama M, Schwaighofer A, Lawrence N. Dataset Shift in Machine Learning. Cambridge, MA: The MIT Press; 2009. [Google Scholar]


