An Interpretable Machine Learning Survival Model for Predicting Long-term Kidney Outcomes in IgA Nephropathy

Abstract

IgA nephropathy (IgAN) is common worldwide and has heterogeneous phenotypes. Predicting long-term outcomes is important for clinical decision-making. As right-censored patients become common during the long-term follow-up, either excluding these patients from the cohort or labeling them as control will bias the risk estimation. Thus, we constructed a survival model using EXtreme Gradient Boosting for survival (XSBoost-Surv), to accurately predict the prognosis of IgAN patients by taking the time-to-event information into the modeling procedure. Shapley Additive exPlanations (SHAP) was employed to interpret the individual predicted result and the non-linear relationships between the predictors and outcome. Experiments on real-world data showed our model achieved superior discrimination performance over other conventional survival methods. By providing insights into the exact changes in risk induced by certain characteristics of the patients, this explainable and accurate survival model can help improve the clinical understanding of renal progression and benefit the therapies for the IgAN patients.

Introduction

Immunoglobulin A Nephropathy (IgAN), a condition that damages the glomeruli inside kidneys, is a leading cause of chronic kidney disease (CKD) and renal failure. Prevalence varies geographically, with higher incidence in Pacific Asian regions^1,2. IgAN usually progresses slowly over years, but the course of the disease varies from person to person. Some people leak blood in their urine without developing problems, some eventually achieve complete remission and others develop end-stage kidney failure. As shown in recent long-term follow-up studies, up to 30-40% of IgAN patients develop end-stage kidney disease (ESKD) within 10-25 years, which demonstrates the prognosis for IgAN is poor^2,3. Accurate long-term kidney prognosis prediction models are needed to support clinical decision making for precise treatment and management.

There have been some models established to predict the long-term prognosis of IgAN patients^3,4. During the long-term follow-up, more and more patients may leave the study, meaning their status are unknown before the end of the study. Therefore, most of the previous IgAN prognosis models employed statistical survival methods, such as cox regression⁵, to deal with these censored records. However, these models usually made too strict assumptions on the data distribution^3,5 and utilized small number of predictors, which resulted in inadequate performance. As the clinical presentations of IgAN patients are complicated, more complex models are needed to capture the relationships between variables and the target outcome. Machine learning models are more skilled in modeling the heterogeneous data and have achieved state-of-art results in many clinical tasks^6-8. However, common machine learning practices ignore the right-censoring issue in the time-to-event data. In other words, these censored patients are either removed from the study cohort or labeled as control samples, which results in biased estimation of the predicted risk.

In our paper, we employed a machine learning survival method to build the long-term prognosis model, aiming to simultaneously learn the complex patterns hidden in the time-to-event data and handle the right-censoring issue. Recently, the objective function of EXtreme Gradient Boosting (XGBoost)⁹ has been modified to support the survival analysis, which we utilized in our paper and named as XGBoost-Surv to distinguish from that for classification. Despite of the superior performance in prediction accuracy, the machine learning models are often hard to use in clinical practice⁷ due to the unexplainable result. We here utilized the Shapley Additive exPlanations (SHAP)¹⁰ to explain why a prediction is made by XGBoost-Surv. Results showed that XGBoost-Surv made significant improvements over other conventional survival methods. Moreover, the interpretations of the prediction results offered deeper insight into the changes in risk induced by certain characteristics and thus could benefit the early intervention of the modifiable factors.

This study is an extension of our previous work¹¹ by utilizing machine learning to build survival model instead of classification model and focus on offering explanations of the predicted result. We hope this work could make broad the application of machine learning in the clinical field.

Methods

2.1. Study population

Single-center data were retrieved consecutively from Nanjing Glomerulonephritis Registry between January 2006 and June 2009. Multicenter data were collected from 18 renal centers between January 1997 and June 2010. All follow-up data were updated to August 2017. This study followed the tenets of the Declaration of Helsinki, and was approved by the ethics committee of the Nanjing General Hospital (2010NLY-023), Nanjing, China. Written informed consent was obtained from all study participants.

The IgAN patients were recruited to our cohort according to the following criteria. Patients with biopsy-proven primary IgAN who were 18 years or older with a follow-up time exceeded 12 months, an estimated glomerular filtration rate (eGFR) ≥ 30 mL/min/1.73 m², proteinuria ≥0.5 g/d, and a biopsy specimen with 8 or more total glomeruli on periodic acid-Schiff (PAS) staining were eligible for inclusion. Patients who progressed to end-stage kidney disease (ESKD) and 50% reduction in the eGFR within the first 12 months of follow-up were also included. Patients with secondary causes of mesangial IgA deposits, such as IgA vasculitis and autoimmune disorders, or those with comorbid conditions, such as diabetes mellitus and Alport’s syndrome were excluded.

Based on the criteria described, 2,047 IgAN patients were included in the study cohort. Patient data from a single clinical center were used as the derivation cohort, while patient data from a multicenter cohort were used as the external validation cohort.

2.2. Variables and Target Outcome

The eGFR was estimated using the chronic kidney disease epidemiology collaboration (CKD-EPI) formula. ESKD was defined as eGFR<15 mL/min/1.73 m² for over 3 months, initiation of dialysis or transplantation. The mean arterial pressure (MAP) was defined as the diastolic pressure plus one-third of the pulse pressure. The time-averaged systolic, diastolic blood pressure, and MAP were calculated as previously reported⁴. Information about the type and duration of immunosuppressive treatment was recorded. Renin-angiotensin system blockade included any exposure to angiotensin-converting enzyme inhibitors, angiotensin receptor blockers, or both. The scoring sheet was based on the updated Oxford Classification for IgAN¹². The exact biopsy tissue sections to be scored were marked on the PAS slides. In addition, capillary necrosis, arteries score, and malignant vascular changes were scored in this study. A total of 36 variables were included for candidate predictors, including epidemiological characteristics, clinical manifestations, clinical characteristics, pathological findings and treatments (Table 1).

Table 1.

Variables in the data set

Category	Variable name
Epidemiological characteristics	Age at biopsy, Body Mass Index, Gender, Family history of kidney disease, Immunosuppression treatment prior to the biopsy, Renin-angiotensin system blockade prior to the biopsy
Clinical manifestations	Hypertension before biopsy, Macroscopic hematuria before biopsy
Clinical characteristics	Serum albumin (g/L), MAP (mm Hg), Serum creatinine (mg/dl),Estimated GFR (ml/min per 1.73m2), Urine protein (g/d), Serum cholesterol (mmol/L), Serum triglycerides (mmol/L), Serum uric acid (μmol/L), Microscopic hematuria (/microliter)
Pathological findings	M, E, S, T, C, N, Mean mesangial score, Endocapillary hypercellularity, Global sclerosis, Segmental sclerosis, Necrosis, Crescents, Tubular atrophy /Interstitial fibrosis, Arteriosclerosis interlobular arteries, Arteriolar hyalinosis
Treatments	Tonsillectomy, Immunosuppression treatment during follow-up time, Renin-angiotensin system blockade treatment during follow-up time, Statin treatment during follow-up time

In this study, we defined the target outcome as the combined event (50% reduction in the eGFR or ESKD) after biopsy.

2.3. Machine learning analysis

2.3.1. Model Construction and Evaluation

The survival model was constructed by XGBoost-Surv on the derivation set. XGBoost is a gradient boosting approach¹³ which ensembles a series of relatively weak base classifiers into a stronger one in the sequential manner. Compared to the original version of XGBoost for classification, the objective function of XGBoost-Surv was modified into Cox loss function⁵ to adapt to the time-to-event data. In the derivation set, we used 5-fold cross-validation to tune the hyper-parameters of the XGBoost-Surv, including the “max depth of trees”, the “minimum loss reduction” required to make a further partition on a leaf node, the “boosting learning rate” and the “number of estimators”. The “objective” was set to “survival:cox” and the “booster” was set to “gbtree”. Other parameters were fixed as default.

We compared the performance of XGBoost-Surv model with other conventional survival methods, including random survival forest (RSF)¹⁴, support vector machine for survival (SVM-Surv)^14,15 and the statistical method cox regression⁵ and cox with lasso penalty (lasso-cox)¹⁶. The hyper-parameters for lasso-cox, RSF and SVM-Surv were also optimized by 5-fold cross-validation on the derivation set.

2.3.1. Model Evaluation

We used the time-dependent concordance index (C^td-index)¹⁷ to quantify the concordance between the predicted and true survival time of a set of patients. This metric is commonly used to evaluate and compare predictive models with censored data¹⁸. The C^td-index evaluates whether predicted survival times are ranked in the same order as their true survival time. Because of censored data, the actual ordering of patient survival is not always available. For example, if patient i died at t_i and patient j is still alive at t_i and t_i > t_j, the actual order of this pair of patients’ survival is not available as patient j may or may not have died before t_i. This pair of patients is defined as a non-admissible pair, in opposition to admissible pairs, where the actual order of patient survival is available.

The C^td-index is defined as follows:

$$C^{td}-index=numberofconcordantpairs/numberofadmissiblepairs$$

where concordant pairs are the pairs of patients that are correctly classified and admissible pairs are the pairs of patients that can be ordered. For example, (i, j) is admissible if patients i and j are not censored, or if patient i dies at t = k and patient j is censored at t>k. On the contrary, if patient i died at t=k′ and patient j is censored at t < k′, (i, j) is not admissible.

2.3.2. Model Interpretation

Shapley Additive exPlanations (SHAP)¹⁰ was utilized to interpret the prediction result of our model. SHAP method transforms the original complex machine learning models to simple linear addition approximations around each data point. Formally, SHAP explains the output of a model as a sum of each contributing variable $y_{pred}^j={\displaystyle {\sum }_{i=1}^M{\text{Φ}}_{i,j}}$ where ${\text{Φ}}_{i,j}$ is the attribution of variable i to the predicted result $y_{pred}^j$ for sample j. ${\text{Φ}}_{i,j}$ greater than zero means the variable i at the current value increases the predicted risk for individual j while less than zero indicates the opposite.

In our study, we utilized these ${\text{Φ}}_{i,j}$ in the derivation cohort to interpret the predicted result of the XGBoost-Surv model in three levels: (1) The general variable importance in the model by calculating the mean magnitude of the attributions values of each variable $\left({\text{Φ}}_i={\displaystyle {\sum }_{j=1}^N{\text{Φ}}_{i,j}/N}\right)$. (2) The relationship between each variable and the combined renal event by investigating how the attributions varied with the variable values. To be mentioned, we modified the original main effect plot offered by SHAP by fitting more interpretable curves from the points using generalized additive model¹⁹. (3) Individualized risk explanation by the ${\text{Φ}}_{i,j}$ for each IgAN patient;

3. Results

3.1. Study cohorts

The derivation cohort was comprised of 1022 patients and the median follow-up was 7.9 years (interquartile range, 6.6-9.8). The 5- and 10-year renal survival rates were 96.8% and 92%, respectively. The external validation cohort recruited 1025 patients and the median follow-up was 7.8 years (interquartile range, 3.0-12.0). The 5- and 10-year renal survival rates were 83.8% and 76.4%, respectively.

Among the 36 variables, the overall rate of missing data was 0.75% in the derivation cohort and 1.18% in the external validation cohort. Missing values were imputed by mean or mode for continuous and categorical variable respectively.

3.2. Model Evaluatoin

We listed C^td-index of the applied methods in Table 2. The XGBoost-Surv model trained on the 36 variables had a C^td-index of 0.822 (95% CI: 0.784-0.860) on the external validation set. The XGBoost-Surv achieved overwhelmed performance over the cox regression (0.655, 95% CI: 0.601-0.708), lasso-cox (0.795, 95% CI: 0.757-0.833), RSF (0.773, 95% CI: 0.730-0.815) and SVM-Surv (0.781, 95% CI: 0.741-0.821) on the external validation set.

Table 2.

C^td-index (95% confidence interval) of different survival models

Method	Derivation set	External validation set
Cox Regression	0.860 (0.815-0.905)	0.655 (0.601-0.708)
Lasso-cox	0.831 (0.787-0.875)	0.795 (0.757-0.833)
RSF	0.854 (0.815-0.893)	0.773 (0.730-0.815)
SVM-Surv	0.866 (0.831-0.901)	0.781 (0.741-0.821)
XGBoost-Surv	0.872 (0.834-0.911)	0.822 (0.784-0.860)

3.3. Model Interpretation

3.3.1. General Variable Importance in the XGBoost-Surv model

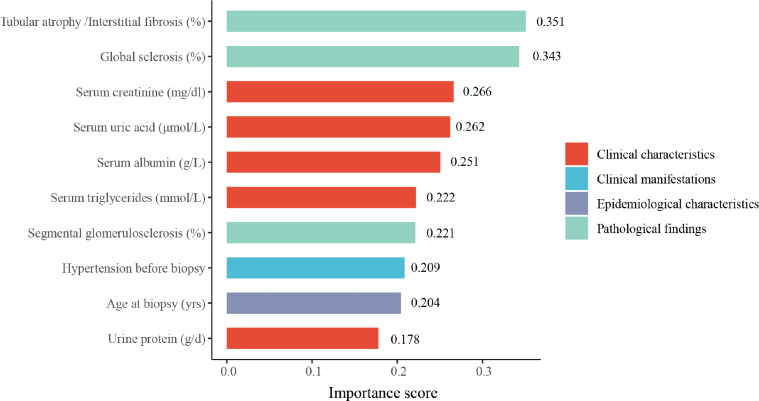
The general variable importance of the top ten variables obtained from SHAP as described in Methods were illustrated in Fig. 1. The Tubular atrophy/Interstitial fibrosis (%) and global sclerosis (%) were the strongest contributors to the model’s final decision. Among the top ten most important variables, five were clinical characteristics, three were pathological characteristics, one was the epidemiological information and one was the clinical manifestations.

Figure 1.

Top ten important variables in the XGBoost-Surv model.

3.3.2. Relationships between the variables and the predicted risk

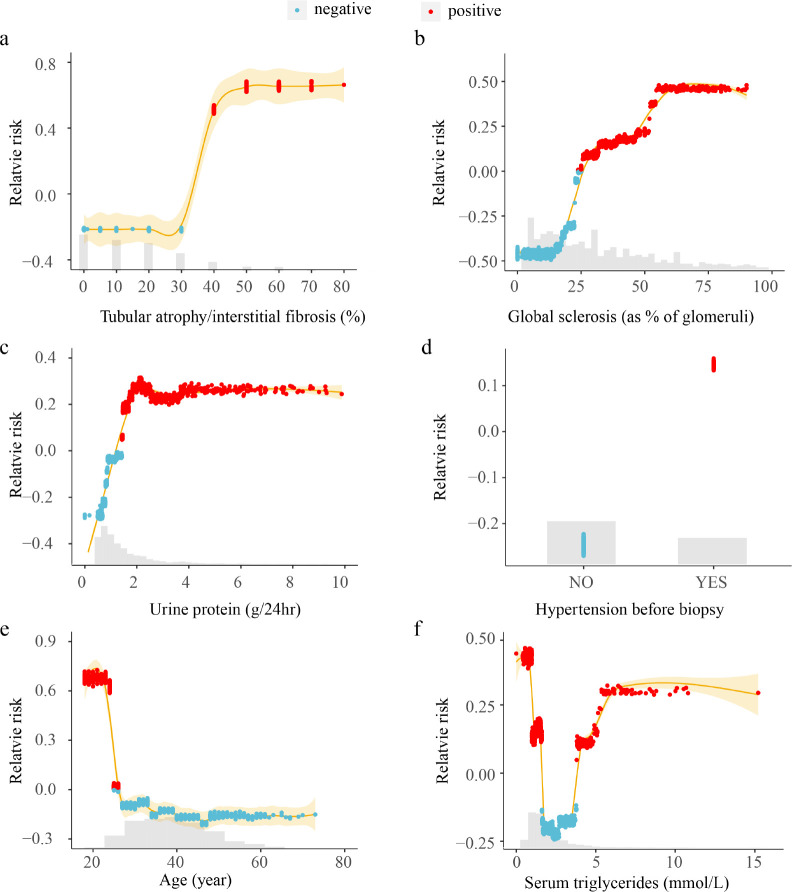
As described in the method, the effect of varying variable values indicates the relationship between the variable and the predicted risk. Fig. 2 demonstrated the results from some typical variables. Results showed that XGBoost-Surv did capture the non-linear relationships between the predictors and the combined renal event. The relationship of the tubular atrophy/interstitial fibrosis was two phased, segmented by the value between 30% and 40%. The tubular atrophy/interstitial fibro more than 40% increased the risk of IgAN progression while less than 30% would be beneficial for the progression. Similar pattern existed in the variable of age. It was interesting to discover that serum triglycerides displayed a U-shaped relationship with the combined renal event, which meant both too high or too low values would increase the predicted risk. The global sclerosis and urine protein linearly related to the predicted risk at lower values and then kept constant after reaching a certain threshold.

Figure 2.

Relationship between the variables and the predicted risk of the combined renal event. The horizontal axis represents the variable value and the vertical axis represents the variable attribution to the predicted result. Each data point corresponds to one prediction from a particular patient. Red means the variable at the current value increases the predicted value while blue decreases the predicted value. The yellow colored lines represent the smoothed fitted curve from the attribution values. The grey histograms on each plot show the distribution of values for that variable in the derivation set.

3.3.3. Individualized interpretation of the predicted risk

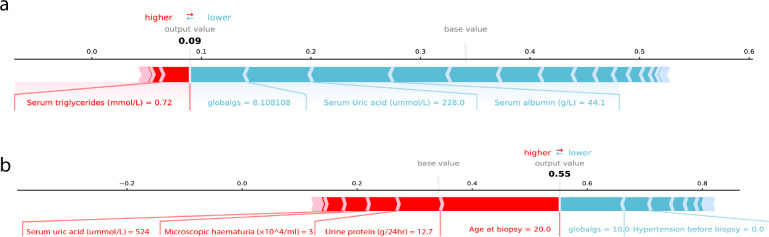
Fig. 3 demonstrated two examples of the individualized interpretation results from SHAP. The figure explained how the patients got his/her predicted risk of within 5-year combined renal event given the status of the 36 variables. For the IgAN patient in Fig. 3a, XGBoost-Surv predicted his/her risk as 0.09, mainly contributed by the variables listed in the horizontal line. The global sclerosis (% of glomeruli) 8.1%, Serum uric acid 228.0 μmol/L and serum albumin 44.1 g/L were the main factors that pushed the patient’s 5-year combined event risk to lower values from the baseline risk. The serum triglycerides 0.72 mmol/L was the main factor that pushed the predicted risk to higher values. For the patient in Fig. 3b, the predicted risk was 0.55, whose age of 20 years old, urine protein at 12.7 g/24hr were the top two contributors to the high predicted risk while the global sclerosis (% of glomeruli) 10% decreased the predicted risk.

Figure 3.

Explained combined event risk for two example individuals. The contributing variables are arranged in the horizontal line, sorted by the absolute value of their impact. Variables in the red arrow mean the impact values are positive while blue means negative. The length of the arrow bar represents the absolute value of the impact. The output value is the predicted within 5-year combined renal event risk. The base value means the predicted risk of the “average” IgAN patient, whose variable values equal to the mean values in the derivation cohort.

4. Discussion

Patients with IgAN have various clinical presentations and histological lesions leading to difference prognoses, and approximately 50% of these patients still have a risk of progression in five to ten years². Therefore, obtaining long-term accurate individualized risk estimates for decisions on further management are important²⁰. We proposed a survival model to predict the risk of combined renal event for IgAN patients by incorporating the machine learning method XGBoost-Surv and a model interpretation approach SHAP. The model we constructed achieved not only high accuracy but also good clinical interpretability. The observed efficacy suggests the ML models can be a powerful tool in predicting the prognosis for the IgAN patients.

During the long-term follow-up, patients may leave the study before the target event occur or the end of the study. As methods for classification task do not consider the time to event information, the common machine learning practice is to exclude the censored patients or label them as the control samples. However, the former means may result in insufficient data and the latter one decreases the event rate, both of which can bias the predicted risk. One rational solution is to utilize the survival analysis to handle the time-to-event data. Although the traditional statistical survival models such as cox regression⁵ can deal with the censored issue and are user-friendly, they often require strong assumptions in data, including the linear relationship, independence of observations and no multi-collinearity among variables²¹. For complex data, these oversimplified models may result in inadequate predictive accuracy and insufficient subsequent decision making.

Considering the above challenges, we employed the machine learning survival method XGBoost-Surv, to learn the complex relationships hidden in the time-to-event data. Specifically, XGBoost-Surv employs regression tree as its base classifier, which can handle numerical data that are highly skewed and multimodal. As observed, the XGBoost-Surv model achieved an overwhelmed C^td-index of 0.822 (95% CI: 0.784-0.860) than the cox regression model (0.655, 95% CI: 0.601-0.708) on the external validation set. The lasso-cox model (0.795, 95% CI: 0.757-0.833) behaved better than the cox mainly benefiting from its embedded feature selection mechanism. But it was still less accurate than XGBoost-Surv due to its strong assumption on the linearity. XGBoost-Surv also beat random survival forest on our data. Compared to random survival forest (0.773, 95% CI: 0.730-0.815), which is also an ensemble tree system, XGBoost-Surv is trained in an additive manner, which makes it focus on the residuals left by the previous training in each round. This mechanism helps XGBoost-Surv to gain more precise prediction under fine parameter tuning. We also applied SVM-Surv on our problem. As we know, SVM needs a kernel to project the data into a space where it can separate the data points when they are not linearly separable. However, it’s hard to find a kernel perfectly suitable to a data distribution. In contrast, XGBoost-Surv adapts to the data automatically and thus achieved better performance (0.822, 95% CI: 0.784-0.860) vs. (0.781, 95% CI: 0.741-0.821) on the IgAN data.

The complex mechanism of the machine learning approaches makes their results hard to interpret. Unlike the widely employed statistical approach cox regression, whose coefficients tell the effect of the predictive factors on the outcome, the un-transparency issue of the complex ML algorithm applied in medical tasks are seriously criticized and doubted in recent years^22-24. In this study, we showed that the machine learning algorithm could give better insight into the predicted risk by utilizing SHAP to demonstrate the complex relationship between predictors and outcome. Some of our findings showed consistency with the previous studies and some were novel and interesting discoveries. Prior studies have verified younger age as risk factor for aggressive IgAN, while advanced age is protective⁴, which is consistent with our results. Urine protein >1 g/d is a risk factor for IgAN that has long been widely recognized^4,25, which is very approximate with our turning point 1.25g/d. The risk factor hypertension found in the previous studies also agrees with our findings. In the IgAN Oxford classification²⁶, Tubular atrophy/ interstitial fibrosis plays important roles. Global sclerosis of the glomerulus has also been confirmed by many studies and has a significant influence on the prognosis of the kidney^27,28. This variable can predict long-term kidney prognosis more accurately when combined with tubular atrophy/interstitial fibrosis²⁹, which is also reflected in our result. Our study also explained why the model predicted the risk value for a specific individual. By providing the adverse and beneficial contributors, our proposed model allowed clinicians to plan appropriate interventions. For the patient in Fig. 3b, interventions should be made to lower the patient’s characteristic of urine protein. Deserved to be mentioned, the proposed model has been implemented in a risk prediction system for IgAN patients and used in real world application. Fig. 4 illustrated a screenshot of the system.

Figure 4.

Screenshot of the risk prediction system. (a) The interface for inputting patient characteristics. (b) Risk prediction result and the individualized contributing factors. (c) Interpretation of the risk prediction model.

Our study also demonstrated its limitations. Firstly, the cohort was not a prospective therapeutic trial, and the therapeutic interventions in patients were variable, although we did not identify treatment-related factors that significantly affect the prognosis. Secondly, the prediction model was established based on data obtained from the Chinese population, and the applicability of the results to other races and regions still needs to be verified. Thirdly, although XGBoost-Surv can capture the complex relationship between variable and the combined renal event, it is still limited by the proportional hazard assumption. In future work, deep learning for survival³⁰ which leverages from the assumption about the stochastic process can be tried.

Conclusion

In conclusion, the proposed XGBoost-Surv model in our study can be an effective tool to predict the long-term event of the IgAN patients, and offer explanations on how the patients’ characteristics and the clinical variables influence their prognosis. We hope the proposed model could benefit individualized treatment and management in IgAN patients and our work can contribute to make broad the applications of the machine learning techniques in clinical filed.

Acknowledgment

This work was funded by the China National Key R&D Program (Grant No. 2018YFC0910700).