A Bayesian Approach for Learning Gene Networks Underlying Disease Severity in COPD

Abstract

In this paper, we propose a Bayesian hierarchical approach to infer network structures across multiple sample groups where both shared and differential edges may exist across the groups. In our approach, we link graphs through a Markov random field prior. This prior on network similarity provides a measure of pairwise relatedness that borrows strength only between related groups. We incorporate the computational efficiency of continuous shrinkage priors, improving scalability for network estimation in cases of larger dimensionality. Our model is applied to patient groups with increasing levels of chronic obstructive pulmonary disease severity, with the goal of better understanding the break down of gene pathways as the disease progresses. Our approach is able to identify critical hub genes for four targeted pathways. Furthermore, it identifies gene connections that are disrupted with increased disease severity and that characterize the disease evolution. We also demonstrate the superior performance of our approach with respect to competing methods, using simulated data.

1. Introduction

1.1. General Motivation for Network Analysis in Genomics

Bayesian hierarchical models are becoming increasingly popular for inference with genomic data. These methods are powerful tools to understand the structure of complex diseases and to evaluate patterns of variable association, particularly for the analysis of studies with a small sample size. As complex diseases are multi-level illnesses defined by changes at the cellular level [17,32], we can apply network-based inference to genes and their products in order to better understand the underlying biological mechanisms and thereby develop more targeted treatments. In order to accomplish this goal, it is important to develop flexible and computationally efficient models which can adequately analyze the dependence structure of these highly dimensional datasets. A common approach to describe conditional dependence relationships of random variables is graphical models, which have been successfully applied to protein–protein interaction, co-expression, and gene regulatory networks [10,25,41,42].

1.2. Introduction to Statistical Methods for Networks Analysis

Bayesian approaches to network estimation have been found to be successful for both decomposable and unrestricted graphical models. These approaches have the critical advantage of quantifying the uncertainty associated to network estimation. For the decomposable setting, implementation of hyper-inverse Wishart priors enables the development of efficient stochastic search procedures to estimate network structure. [7] used this approach to determine explicitly the marginal likelihoods of the graph. This method was extended to Bayesian variable selection for both high-dimensional decomposable and nondecomposable undirected Gaussian graphical models [19]. [35] described a feature-inclusion stochastic search algorithm, which uses online estimates of edge-inclusion probabilities to guide Bayesian model determination for decomposable Gaussian graphical models. When compared to Markov Chain Monte Carlo, Metropolis-based searches, and lasso methods, their algorithm was found to be superior in both speed and stability.

In the context of biological networks, it is often inappropriate to restrict the model space to only decomposable graphs [26]. Efficient and flexible Bayesian methods for nondecomposable Gaussian graphical models were proposed using the G-Wishart prior by [2,11]. Rather than computing the normalizing constant of marginal likely-hoods analytically, as is the case for decomposable graphs, Markov Chain Monte Carlo methods are used to sample over the joint spaces of precision matrices and graphs in order to avoid posterior normalizing constant computation. Further improvement was proposed by [45] with the implementation of a new exchange algorithm requiring neither proposal tuning nor evaluation of normalizing constants for the G-Wishart distribution. Reduced computational complexity and greater flexibility in prior specification was described by [39] with graph theory results for local updates that facilitate fast exploration of the graph space.

In recent years, such evidence of successful single network structure estimation has led to extensions of the methods to inference for multiple graphical models. Approaches for multiple graphical models are particularly appropriate when the biological network evolves with respect to clinical features, such as disease stage. [16] extended the graphical lasso to multiple undirected graphs sharing the same variables with similar dependence structures. They propose a method which preserves common structure while allowing for differences through a hierarchical penalty targeting removal of common zeros in the precision matrices. [9] proposed the more general joint graphical lasso approach based on maximizing a penalized log likelihood. Their approach explores the properties of two penalty structures: the fused graphical lasso encouraging shared edge values and shared structure, and the group graphical lasso which supports shared structure but not shared edge values. [46] described a Bayesian approach assessing heterogeneous patterns of association between Gaussian directed graphs for related samples. Another Bayesian approach was proposed by [29] linking graph structure estimation with a Markov Random Field prior favoring an edge if the same edge is included in related sample group graphs. In their method, subgroups are not assumed related and shared structure is learned by defining a spike-and-slab prior on network relatedness parameters.

Computational burden is a major challenge for Bayesian graphical models, motivating the development of methods which are more efficient and have greater scalability. Successful developments in related problems have come from the use of continuous shrinkage priors. [13] used these priors in the form of a two-component normal mixture model in regression analysis. These priors have received even more attention as alternatives for regularizing regression coefficients, see [1,15,27]. When used in estimating covariance matrices through regularizing concentration elements, continuous shrinkage priors have been shown to result in fast and accurate estimation [21,43]. [44] developed a stochastic search structure learning algorithm for undirected graphical models. His method uses continuous shrinkage priors indexed by latent binary indicators, and allows for efficient block updates of the network parameters.

In this paper, we propose a new approach for multiple network analysis which builds on earlier methods [29] by improving scalability with a continuous shrinkage prior in the spirit of [44]. This results in a computationally more efficient approach that can be applied to larger networks. In particular, our work is motivated by the problem of analyzing network evolution of gene networks underlying the complex chronic obstructive pulmonary disease (COPD). Our paper is organized as follows: Section 2 provides a description of our motivating problem and the details of the dataset we apply our method to. Section 3 presents an introduction to Bayesian graphical models and introduces our proposed method, the prior models and the method for posterior inference—in addition to an outline of our Markov chain Monte Carlo method. Section 4 outlines our simulation studies, and section five describes the application of our method to four selected gene pathways involved in COPD. Section 6 concludes the paper.

2. The ECLIPSE COPD Cohort Study

Chronic obstructive pulmonary disease (COPD) is the 3rd leading cause of death in the US [37] and acute exacerbations of COPD (AECOPDs) are the 2nd leading cause of hospital stays [28,37]. Although 90 % of COPD patients are smokers, about 75 % of smokers do not develop COPD. There is a poor understanding of the risk factors that account for disease susceptibility or resistance to cigarette smoke (CS), as well as of the pathogenic mechanisms underlying the development of emphysema and airway inflammation.

Whole-blood gene expression data from 226 subjects were generated within the Evaluation of COPD Longitudinally to Identify Predictive Surrogate Endpoints (ECLIPSE) cohort using the Affymetrix Human Genome U133 Plus 2.0 Array and are available at NCBI GEO GSE22148 [12,36]. Raw data (CEL files) were log-transformed and normalized using the RMA method [18] in the affy R package. Probesets were filtered so that there were present calls in all samples for a final set of 12525 probesets.

Subjects were classified into four groups by severity of radiologic emphysema, a subtype of COPD; [0–5) percent emphysema (n = 61), [5–10) percent emphysema (n = 43), [10,20) percent emphysema (n = 46), and [20+] percent emphysema (n = 51). Twenty-five subjects had missing values for percent emphysema and were not used in subsequent analyses.

We examined four candidate pathways that were selected based on the analysis of genomic and metabolomic data from an independent study on the genetic epidemiology of COPD called COPDGene [31]. In the COPDGene cohort, gene expression data from peripheral blood mononuclear cells (PBMCs) were generated on 131 subjects using the same Affymetrix platform as the ECLIPSE data [3]. On those same subjects, plasma metabolite abundance was generated using liquid chromatography/mass spectrometry [4]. Differently expressed genes and differently abundant metabolites were identified for airflow obstruction (FEV1pp forced expiratory volume in 1 second percent predicted) correcting for age, sex, body mass index, and current smoking status. KEGG pathways [20] that showed enrichment of the significant genes and metabolites were prioritized and the top four candidate pathways were used to explore their role in emphysema for this work: glycerophospholipid metabolism (GPL), oxidative phosphorylation (OxPhos), regulation of autophagy (RegAuto), and Fc γ R-mediated phagocytosis (FcyR). For each of the pathways, there were 60 (GPL), 83 (OxPhos), 28 (RegAuto), and 104 (FcyR) probesets that were collapsed to 41 (GPL), 62 (OxPhos), 20 (RegAuto), and 57 (FcyR) unique genes by selecting the probeset with the strongest association with emphysema. These 4 pathways may play a role in the response to cigarette smoke exposure and are interesting candidates for more detailed exploration in emphysema.

3. Proposed Method

The goal of our work is to model and infer the network structure of multiple pathways relevant to COPD. For each pathway, we are interested in understanding how connections between genes break down between the four sample groups defined by the severity of emphysema. We achieve this via a Bayesian hierarchical model, described in 3.1 and 3.2, that allows to jointly estimate a separate network for each group while comparing networks across groups in order to determine pairwise relatedness.

For each given pathway, we observe four n_k × p data matrices X_k, where k = 1, …, K = 4 indexes the group, n_k is the sample size for group k, and p is the total number of genes in the pathway. Assuming samples are independent and identically distributed within each of the K groups, we can write the likelihood for subject i in group k as

$$X_{k,i}~N\left({\mu }_k,{\mathrm{\Omega }}_k^{-1}\right),i=1,\dots ,n,$$

where ${\mu }_k\in {ℝ}^P$ is the mean vector for group k and ${\mathrm{\Omega }}_k={\Sigma }_k^{-1}=\left({\omega }_{i,j,k}\right)$ is the precision matrix for group k, a symmetric positive definite matrix constrained to a set of restrictions ω_i,j,k = 0, as defined by a graph G_k which is an undirected graphical model representing the conditional dependence relationships existing between the p genes. Each G_k is a mathematical object consisting of two sets, vertices V = {1, …, p} and edges E ∈ V × V, so G = (V, E). In an undirected graph, an edge exists between vertices i and j if (i, j) ∈ E and (j, i) ∈ E. In the context of our application, each vertex in G_k corresponds to a gene. An edge is included in the network if the two corresponding genes are conditionally dependent, while the absence of an edge between two vertices means the two corresponding genes are conditionally independent given the remaining genes. For each group k, graph G_k can be thought of as a symmetric binary matrix where each off-diagonal element g_k,i,j denotes the inclusion of edge (i, j) in G_k.

3.1. Continuous Shrinkage Prior

In the context of Bayesian analysis of large networks, one of the main challenges is to define a prior distribution on Ω_k. The most common approach is to assign a G-Wishart prior, which is the Wishart distribution restricted to the space of precision matrices where zeros are specified by either a decomposable or nondecomposable graph [33]. While this provides a flexible formulation for modeling, both the prior and posterior normalizing constants are intractable, limiting the method in scalability and computation. We address these difficulties with a recent approach that overcomes these issues, and propose for each network a continuous shrinkage prior as defined by [44]. Let Ωk = (ω_{i, j,k}) _p×p be the p-dimensional concentration matrix for gene interactions for each group. Our prior is a product of p(p – 1)/2 two-component normal mixture densities, on the off-diagonal elements, and p exponential densities, on the diagonal elements, of the type

$$\begin{gathered} p\left({\mathrm{\Omega }}_k|G\right)={\left\{C(\theta )\right\}}^{-1}\prod _{i<j}\left\{(1-\pi )N\left({\omega }_{i,j}|0,v_0^2\right)+\pi N\left({\omega }_{i,j}|0,v_1^2\right)\right\} \\ \times \prod _i\text{Exp}\left({\omega }_{i,i}|\frac{\lambda }{2}\right)I_{{\mathrm{\Omega }}_k\in M^{+}}\propto \prod _{i<j}N\left({\omega }_{i,j}|0,v_{g_{i,j}}^2\right)\prod _i\text{Exp}\left({\omega }_{i,i}|\frac{\lambda }{2}\right), \end{gathered}$$

Where $v_{g_{i,j}}^2=v_1^2$ if edge (i, j) is a connection in the network, i.e., g_{i, j} = 1, and $v_{g_{i,j}}^2=v_0^2$ if g_{i, j} = 0 and the connection is not in the network. The two-component normal mixture model has been shown to be a successful prior in the context of variable selection, which in our case is equivalent to edge selection, and the choice of hyperparameters $v_0^2$ and $v_1^2$ has been closely studied by George and McCulloch (1993, 1997). The hyperparameter spaces for θ = {υ₀, υ₁, π, λ} are υ₀ > 0, υ₁ > 0, λ > 0, and π ∈ (0,1) and υ₀ and υ₁ can be set as either small or large, resulting in a spike-and-slab prior. If for example, υ₀ is chosen to be small, the event g_{i, j} = 0 indicates that the edge ω_i,j comes from the $N\left(0,v_0^2\right)$ or diffuse component of the mixture, and consequently ω_{i, j} is closer to zero and can be estimated as zero. In contrast, if υ₁ is chosen to be large, the event g_{i, j} = 1 means ω_{i, j} comes from the other component $N\left(0,v_1^2\right)$ and ω_{i, j} can then be thought of as substantially different from zero. C(θ) and the indicator function ensure that the density function integrated over the space M⁺ is one. We define this prior by introducing binary latent variables which can be viewed as edge-inclusion indicators $G\equiv {\left(g_{ij}\right)}_{i<j}\in \mathcal{G}\equiv {\{0,1\}}^{p(p-1)/2}$, creating a hierarchical model defined by

$$p\left({\mathrm{\Omega }}_k|G,\theta \right)={\left\{C\left(G,v_0,v_1,\lambda \right)\right\}}^{-1}\prod _{i<j}N\left({\omega }_{i,j}|0,v_{g_{i\text{,}j}}^2\right)\prod _i\mathrm{Exp}\left({\omega }_{i,i}\frac{\lambda }{2}\right).$$

and by the prior p(G|θ), that is outlined in Sect. 3.2. The constant C(G,υ₀, υ₁, λ) ∈ (0, 1) is a normalizing constant which ensures proper distributions. Further details on this constant can be found in [44].

3.2. Linking Graphs with a Markov Random Field Prior

To encourage selection of similar edges in related graphs, we define a Markov random field (MRF) prior on the graph structures. In Bayesian variable selection, MRF priors have been used to model dependencies between covariates in regression models [23,30,40]. Our prior follows a similar structure, but it is imposed on the indicators of edge inclusion contrary to indicators of variable inclusion. Each random variable in the set g_i,j = {g_{1,i, j}, …, g_{k,i, j}} is then binary and an indicator of edge inclusion within the model. Consequently, each g_{k,i, j} could be modeled by a Bernoulli prior. If all g_{k,i, j} were independent, a product of Bernoulli distributions could be used to model this binary vector. A MRF prior is introduced to capture and model the dependence structure between these binary random variables. A MRF distribution can be seen as a generalization of a set of independent Bernoulli distributions in a multivariate setting. For the binary vector of edge-inclusion indicators g_i,j = (g_{1,i, j}, …, g_{k,i, j})^T where 1 ≤ i < j ≤ p, we define a MRF prior distribution as

$$p\left(g_{ij}|v_{i,j},\mathrm{\Theta }\right)=C{\left(v_{i,j},\mathrm{\Theta }\right)}^{-1}\exp \left(v_{i,j}{1}^T{g}_{i,j}+g_{i,j}{}^T\mathrm{\Theta }{g}_{i,j}\right),$$

where v_{i, j} is a specific parameter for each set of edges g_i,j, Θ is a K × K symmetric matrix denoting pairwise relatedness for each sample group’s graph, and 1 is the unit vector of dimension K. The off-diagonal elements of Θ, θ_km, allow us to share information between sample groups k and m, when appropriate, as well as to obtain a measure of relative network similarity across groups. The normalizing constant is defined as

$$C\left(v_{i,j},\mathrm{\Theta }\right)=\sum _{g_{i\text{,}j}\in {\{0,1\}}^K}\exp \left(v_{i,j}{1}^T{g}_{i,j}+g_{i,j}{}^T\mathrm{\Theta }{g}_{i,j}\right).$$

As long as the number of sample groups K is reasonably small, the computation of the normalizing constant is straightforward. From the probability of the binary vector of edge-inclusion indicators, we can see that the prior probability of an edge (i, j) being absent from all K graphs is p(g_i,j = 0|v_{i, j}, Θ) = 1/C(v_{i, j}, Θ).

The joint prior on the graphs (G₁, …, G_K) is the product of the densities for each edge

$$p\left(G_1,\dots ,G_k|v,\mathrm{\Theta }\right)=\prod _{i<j}p\left(g_{ij}|v_{i,j},\mathrm{\Theta }\right),$$

where v = {v_{i, j}|1 ≤ i < j ≤ p}. The conditional probability of the inclusion of edge (i, j) in G_k, given the inclusion of that edge in all remaining graphs, is then

$$p\left(g_{k,i,j}|{\left\{g_{m,i,j}\right\}}_{m\ne k},v_{i,j},\mathrm{\Theta }\right)=\frac{\text{exp}\left(g_{k,i,j}\left(v_{i,j}+2{\sum }_{m\ne k}{\theta }_{k,m}{g}_{m,i,j}\right)\right)}{1+\text{exp}\left(v_{i,j}+2{\sum }_{m\ne k}{\theta }_{k,m}{g}_{m,i,j}\right)}.$$

We also define prior distributions on v and Θ to reduce false selection of edges to account for a lack of correction for multiple testing from a fixed prior probability of inclusion, as noted by [34] in the setting of variable selection. This approach also allows us to obtain posterior estimates of these parameters, reflecting more information learned from the data.

3.3. Prior on Network Similarity

We are interested in a measure of network similarity that characterizes the relatedness of the gene network between the disease subgroups, and allows us to study the disruption and conservation of gene pathways as COPD evolves.

We define Θ as a K × K symmetric super-graph with nonzero off-diagonal elements θ_k,m capturing similarity between group k and group m. Consequently, the magnitude of θ_k,m indicates pairwise similarity of the two graphs G_k and G_m. Then, we select our prior following [29] as a spike-and-slab prior on the off-diagonal entries θ_k,m. Because we want the “slab” portion defined on the positive domain to comply with positive values of θ_k,m for related networks, we desire a density in the positive domain that allows discrimination between zero and nonzero values. Since the Gamma(x|α, β) probability density function is equal to 0 at x = 0 and is nonzero for x > 0 and α > 1, it is an appropriate choice for the density of the slab portion of our mixture model prior. Our prior on the network relatedness parameters is then defined as

$$p\left({\theta }_{k,m}|{\gamma }_{k,m}\right)=\left(1-{\gamma }_{k,m}\right){\delta }_0+{\gamma }_{k,m}\frac{{\beta }^{\alpha }}{\mathrm{\Gamma }(\alpha )}{\theta }_{k,m}^{\alpha -1}{e}^{-\beta {\theta }_{k,m}},$$

with fixed hyperparameters α and β and latent indicator variable γ_k,m which indicates the event that graph k is related to graph m. We define an independent Bernoulli prior on the γ_k,ms, with hyperparameter w ∈ [0,1],

$$p\left({\gamma }_{k,m}|w\right)=w^{{\gamma }_{k,m}}{(1-w)}^{\left(1-{\gamma }_{k,m}\right)}.$$

This prior borrows strength between groups when appropriate without enforcing similarity if groups have different network structures. Our joint priors for the off-diagonal entries of the super-graph and for γ are then

$$p(\mathrm{\Theta }|\gamma )=\prod _{k<m}p\left({\theta }_{k,m}|{\gamma }_{k,m}\right),$$

$$p(\gamma )=\prod _{k<m}p\left({\gamma }_{k,m}|w\right).$$

3.4. Edge-Specific Prior

We can specify a prior for the edge-inclusion probability v_ij to encourage sparsity of the graphs G₁, …, G_k. This same prior can be used in order to incorporate prior knowledge of connections between genes. Negative values of v_{i, j} will reduce the prior probability of inclusion for edge (i, j) in all graphs G_k, and consequently a prior favoring smaller values of v will lead to a preference for model sparsity, which can be attractive in applications where it is beneficial to reduce the number of parameters and make results more interpretable. In contrast, larger values of v_{i, j} make edge (i, j) more likely to be selected according to whether or not it has been selected in other graphs. If we are given a known reference network, say G₀, we can use this network to define a prior which encourages higher selection probabilities for those edges in G₀. If θ_k,m = 0 for all m ≠ k, or if for nonzero θ_k,m no edges g_{m,i, j} are selected, the probability of inclusion of edge (i, j) in G_k can be written as

$$p\left(g_{k,i,j}|v_{i,j}\right)=\frac{e^{v_{i,j}}}{1+e^{v_{i,j}}}=q_{i,j}.$$

Then we can impose a prior on q_{i, j} which reflects the belief that graphs having similarities to the reference network G₀ = (V, E₀) are more likely than those with differing edges

$$q_{i,j}=\{\begin{array}{ll}\mathrm{Beta}(1+c,1)\hfill & \text{ if }(i,j)\in E_0\hfill \\ \mathrm{Beta}(1,1+c)\hfill & \text{ if }(i,j)\notin E_0,\hfill \end{array}$$

where c > 0. Then, because v_{i, j} = logit(q_{i, j}), we can apply a univariate transformation to the Beta(a, b) prior on q_{i, j} to write the prior on v_{i, j} as

$$p\left(v_{i,j}\right)=\frac{1}{B(a,b)}\frac{e^{a{v}_{i,j}}}{{\left(1+e^{v_{i,j}}\right)}^{a+b}}$$

If dealing with a case where there is no prior knowledge on the graph structure, one can choose a prior favoring lower values to encourage sparsity, such as q_{i, j} ~ Beta(1,4) for all edges (i, j). In the case where most edges are believed missing for all graphs but those edges present in one graph tend to be included in all other graphs, a prior favoring larger values for θ_k,m can be chosen with a prior favoring smaller values for v_{i, j}.

3.5. Posterior Inference

Defining Ψ as the set of all parameters and X as our observed data for all sample groups, our joint posterior is

$$\begin{gathered} p(\mathrm{\Psi }|X)\propto \prod _{k=1}^4\left[p\left(X_k|{\mu }_k,{\mathrm{\Omega }}_k\right)p\left({\mu }_k|{\mathrm{\Omega }}_k\right)p\left({\mathrm{\Omega }}_k|G_k\right)\right] \\ \prod _{i<j}\left[p\left(g_{i,j}|v_{i,j},\mathrm{\Theta }\right)\cdot p\left(v_{i,j}\right)\right]p(\mathrm{\Theta }|\gamma )p(\gamma ). \end{gathered}$$

This distribution is analytically intractable, so in order to obtain our posterior sample we construct a Markov Chain Monte Carlo (MCMC) sampler.

3.5.1. MCMC Sampling Scheme

Our MCMC scheme begins with a block Gibbs sampler in which we sample network-specific parameters Ω_k and G_k from full conditionals of their posterior distributions. Then, we sample the graph similarity parameters Θ and γ from their conditional posterior distributions using a Metropolis–Hastings method that is equivalent to a reversible jump and incorporates between-model and within-model moves.

The main advantages of our prior on the precision matrices and the latent graphs are that (1) simultaneous block updates of all p(p–1)/2 edge-inclusion indicators are enabled and (2) no Markov chain approximation of intractable normalizing constants is required. Our Gibbs sampler can be viewed as a p-coupled stochastic search variable selection algorithm in the spirit of [13]. The generic iteration t of our algorithm can be summarized as follows:

1. Update graph $G_k^{(t)}$ and precision matrix ${\mathrm{\Omega }}_k^{(t)}$ for each group k = 1, …, 4.

2. Update the network relatedness parameters ${\theta }_{k,m}^{(t)}$ and ${\gamma }_{k,m}^{(t)}$ for 1 ≤ k < m ≤ 4.

Details on Step a and Step b of our algorithm are provided in the Appendix.

3.5.2. Model Selection

There are two approaches for making inference on the graph structure. The first is to use a maximum a posteriori (MAP) estimate representing the mode of the posterior distribution for each sample group’s graph. However, since the space of possible graphs is so large and we may only visit a particular graph a few times during the MCMC, this approach is generally not preferred in the context of large networks. Here, to infer gene connections, we use a more practical approach and estimate the posterior marginal probability (MPP) of edge inclusion for edge g_{k,i, j} as the proportion of MCMC iterations after burn-in where edge (i, j) was included in graph G_k. Following [29], we then select those edges with marginal posterior probability of inclusion (MPP) > 0.5 for each of the four sample groups.

4. Simulation Studies

We use simulated data with related graph structures to assess the performances of the proposed approach. We also compare performances with alternate approaches. We consider two scenarios. The first scenario includes p = 25 nodes, the second scenario includes p = 50 nodes, to investigate how the method works for a larger scale problem. We begin by constructing four precision matrices Ω₁, Ω₂, Ω₃, and Ω₄, each corresponding, respectively, to graphs G₁, G₂, G₃, and G₄. For each graph, there are p × (p – 1)/2 possible edges to be predicted. Ω₁ is set to the p × p symmetric matrix with entries ω_i,i = 1 for i = 1, …, p, entries ω_i,i+1 = ω_i+1,i = 0.5 for i = 1, …, p – 1, and ω_i,i+2 = ω_i+2,i = 0.4 for i = 1, …, p – 2. For Ω₂, we randomly generated a matrix with 70 % of the edges in Ω₁. We constructed Ω₃ by randomly changing five zero entries of Ω₁ to be nonzero. Lastly, Ω₄ was generated as a symmetric matrix with entries ω_i,i = 1 for i = 1,… p, ω_i,i+1 = ω_i+1,i = 0.5 for i = 1, …, p – 1, and entries ω_1,p = ω_p,1 = 0.4. Graph structures for the four groups in the 25-node scenario are shown in Fig. 1. To ensure that each generated precision matrix was positive definite, we used a similar approach to that of [9] where each off-diagonal element is divided by the sum of the off-diagonal elements in its row, and then the matrix is averaged with its transpose. Consequently, Ω₂ and Ω₃ are symmetric and positive definite but with off-diagonal elements with values less than half of those for Ω₁ and Ω₄. As a result, the true value of connection strength is weaker which resulted in worse performance of any method for groups two and three. We generated the data matrices X_k of size n = 100, for k = 1, …, 4, from normal distributions $N\left(0,{\mathrm{\Omega }}_k^{-1}\right)$, characterized by Ω₁, …, Ω₁ as the true precision matrices. For the 25-node scenario, edge counts were 47, 43, 52, and 25 for group one to group four, respectively, and pairwise shared edges were

$$\text{Counts of shared edges }=\left(\begin{array}{cccc}\cdot & 43& 47& 24\\ & \cdot & 43& 22\\ & & \cdot & 24\\ & & & \cdot \end{array}\right)$$

For the 50-node scenario, edge counts were 97, 89, 102, and 50 for group one to group four, respectively, and pairwise shared edges were

$$\text{Counts of shared edges }=\left(\begin{array}{cccc}\cdot & 89& 97& 49\\ & \cdot & 89& 47\\ & & \cdot & 49\\ & & & \cdot \end{array}\right).$$

Fig. 1.

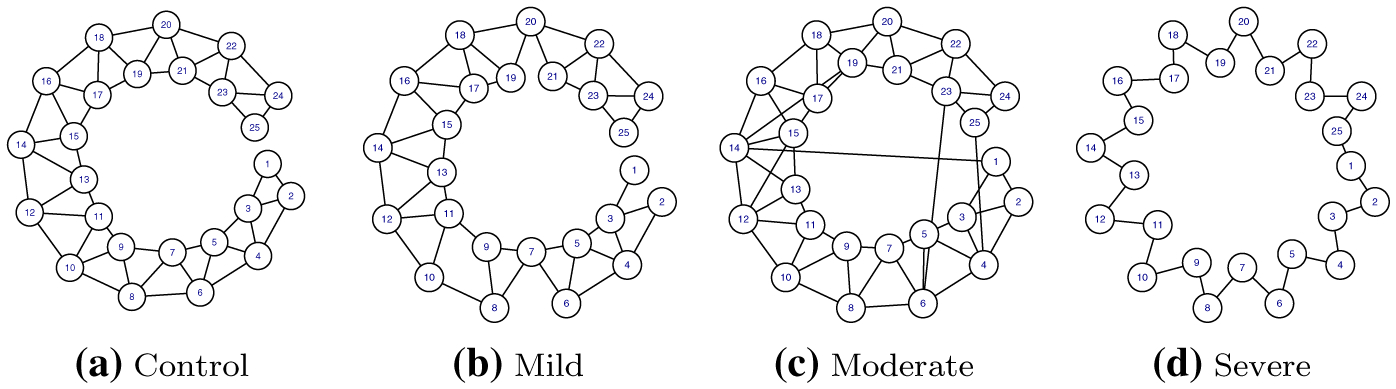
Simulation study: true graph networks for the 25-node setting

For prior specification, we used a Gamma(α, β) density with α = 1 and β = 9 for the slab portion of the mixture prior on θ_k,m which results in a prior with mean 0.111. The tail probability is 1 – P(θ_k,m ≤ 1) = 0.04, thereby avoiding assigning weight to larger values of θ_k,m and allowing for better discrimination between zero and nonzero values. To include the prior belief that the networks could be related, we set the hyperparameter w = 0.5 in the Bernoulli prior defining the network relatedness latent indicator γ_k,m. Parameters a and b were set to be a = 1 and b = 19 for all pairs (i, j) in the prior for v_{i, j}, resulting in a prior probability of edge inclusion around 5%. Hyperparameters υ₀ and υ₁ are set to be υ₀ = 0.02 and υ₁ = 1 according to published guidelines [44], ensuring the MCMC converges quickly and mixes well. The MCMC was run as described in Sect. 3 with 20,000 iterations of burn-in and 40,000 iterations as a basis for posterior inference. Marginal posterior probability of inclusion (MPP) for each edge g_{k,i, j} is estimated as the percentage of MCMC samples post burn-in which include edge (i, j) in graph k. In order to assess accuracy, we report results for 25 simulated data sets: the 25-node simulated scenario is presented in Table 1 and the 50-node case in Table 3. We report the true positive rate (TPR), the false positive rate (FPR), and the Matthews correlation coefficient (MCC) using a threshold of 0.5 for edge selection, and the area under the curve (AUC) (Table 2). The MCC is defined as follows:

$$\text{MCC}=\frac{\text{TP}\times \text{TN}-\text{FP}\times \text{FN}}{\sqrt{\left(\text{TP}+\text{FP}\right)\left(\text{TP}+\text{FN}\right)\left(\text{TN}+\text{FP}\right)\left(\text{TN}+\text{FN}\right)}},$$

where TP, TN, FP, and FN stand for the true positives, true negatives, false positives, and false negatives, respectively. MCC takes values between −1 (total disagreement) and +1 (perfect selection) and measures the quality of the edge selection for a given threshold. A value of 0 suggests that the network reconstruction approach is no better than tossing a coin. Results in Tables 1 and 3 suggest that the TPR is higher in groups one and four, accounting for the fact that the magnitudes of the nonzero entries of Ω₁ and Ω₄ are greater than those of Ω₂ and Ω₃. The perfect AUC values of 1.00 for group 1 and group 4 illustrate that the marginal posterior probabilities of edge inclusion successfully provide an accurate means for learning the graph structure. The overall expected false discovery rate, or FDR, for edge selection is 0.12 for both the 25- and 50-node scenarios (Table 4).

Table 1.

Simulation study: results of our method for the 25-node setting across 25 simulated datasets

	TPR (SE)	FPR (SE)	MCC (SE)	AUC (SE)
Group 1	1.000 (.0000)	0.0038 (.0045)	0.9883 (.0137)	1.0000 (.0000)
Group 2	0.4967 (.0966)	0.0168 (.0064)	0.5990 (.0798)	0.9272 (.0236)
Group 3	0.3838 (.0531)	0.0165 (.0558)	0.5133 (.0558)	0.8841 (.0259)
Group 4	1.000 (.0000)	0.0010 (.0017)	0.9941 (.0097)	1.0000 (.0000)

We report averaged true positive rate (TPR), false positive rate (FPR), Matthews correlation coefficient and area under curve (AUC), with associated standard error (SE)

Table 3.

Simulation study: results of our method for the 50-node setting across 25 simulated datasets

	TPR (SE)	FPR (SE)	MCC (SE)	AUC (SE)
Group 1	1.000 (.0000)	0.0029 (.0019)	0.9823 (.0115)	1.000 (.0000)
Group 2	0.5276 (.0416)	0.0091 (.0031)	0.6379 (.0418)	0.9297 (.0145)
Group 3	0.3843 (.0481)	0.0091 (.0036)	0.5268 (.0467)	0.8967 (.0229)
Group 4	1.000 (.0000)	0.0007 (.0007)	0.9915 (.0089)	1.000 (.0000)

We report averaged true positive rate (TPR), false positive rate (FPR), Matthews correlation coefficient, and area under curve (AUC), with associated standard error (SE)

Table 2.

Simulation study: results from competing methods for the 25-node setting across 25 simulated datasets

	TPR (SE)	FPR (SE)	MCC (SE)	AUC (SE)
Fused graphical lasso	0.96 (.0149)	0.4737 (.0433)	0.3386 (.0256)	0.8993 (.0065)
Group graphical lasso	0.9598 (.0152)	0.4749 (.0498)	0.3378 (.0282)	0.8489 (.0101)
Proposed method	0.5806 (.4264)	0.0006 (.0008)	0.6760 (.3354)	0.9528 (.0527)

We report averaged true positive rate (TPR), false positive rate (FPR), Matthews correlation coefficient (MCC), and area under curve (AUC) with standard errors (SE)

Table 4.

Results from competing methods for the 50-node setting across 25 simulated datasets

	TPR (SE)	FPR (SE)	MCC (SE)	AUC (SE)
Fused graphical lasso	0.9289 (.0154)	0.3301 (.0338)	0.3150 (.0181)	0.9462 (.0033)
Group graphical lasso	0.9285 (.0156)	0.3279 (.0339)	0.3163 (.0179)	0.8834 (.0071)
Proposed method	0.7280 (.2798)	0.0055 (.0045)	0.7846 (.2095)	0.9566 (.0471)

We report averaged true positive rate (TPR), false positive rate (FPR), Matthews correlation coefficient (MCC), and area under the curve (AUC), with standard errors (SE)

The average marginal posterior probability for elements of Θ is estimated as the percentages of MCMC samples with θ_k,m > 0 or γ_km = 1 for 1 ≤ k < m ≤ K. For the 25-node scenario, averaged MPPs for θ_k,m and their standard errors (SE) were

$$\mathrm{MPP}(\mathrm{\Theta })=\left(\begin{array}{cccc}\cdot & 0.9984(.0027)& 0.9917(.00155)& 0.9999(.0001)\\ & \cdot & 0.6496(.0646)& 0.5830(.0468)\\ & & \cdot & 0.5157(.0344)\\ & & & \cdot \end{array}\right).$$

For the 50-node scenario, averaged MPPs for θ_k,m and their standard errors (SE) were

$$\mathrm{MPP}(\mathrm{\Theta })=\left(\begin{array}{cccc}\cdot & 1.000(.0000)& 0.9983(.0031)& 1.000(.0000)\\ & \cdot & 0.6557(.0665)& 0.4613(.0488)\\ & & \cdot & 0.4618(.0656)\\ & & & \cdot \end{array}\right).$$

To emphasize scalability of our method, we expanded our simulation study to a 100 node scenario using the same data-generating mechanisms implemented in the smaller simulations. After running ten replicates of our method, averaged MPPs for θ_k,m and their standard errors (SE) were

$$\mathrm{MPP}(\mathrm{\Theta })=\left(\begin{array}{cccc}\cdot & 1.000(.0000)& 0.9999(.0002)& 1.000(.0000)\\ & \cdot & 0.6779(.0478)& 0.4674(.0698)\\ & & \cdot & 0.3785(.0547)\\ & & & \cdot \end{array}\right).$$

Increasing the network size had no impact on the overall expected false discovery rate for our method. While true positive rate decreases slightly, other measures of method performance seem to remain about the same. Further results for the 100-node scenario are shown in Table 5.

Table 5.

Simulation study: results of our method for the 100-node setting across 10 simulated datasets

	TPR (SE)	FPR (SE)	MCC (SE)	AUC (SE)
Group 1	1.000 (.0000)	0.0031 (.0008)	0.9630 (.0091)	1.000 (.0000)
Group 2	0.4553 (.0280)	0.0088 (.0013)	0.5344 (.0179)	0.9182 (.0117)
Group 3	0.4020 (.0357)	0.0082 (.0011)	0.5059 (.0302)	0.9131 (.0107)
Group 4	1.000 (.0000)	0.0007 (.0003)	0.9836 (.0068)	1.000 (.0000)

We report averaged true positive rate (TPR), false positive rate (FPR), Matthews correlation coefficient, and area under curve (AUC), with associated standard error (SE)

We compared the performances of our approach with two alternative multiple network methods. First, using the R package JGL [8], we applied the fused and joint graphical lasso methods of [9]. Accuracy of structure learning is given in Tables 2, 4, and 6 for the 25-, 50-, and 100-node scenarios, in terms of TPR, FPR, MCC, and AUC. For the lasso methods, AUC estimates were obtained by varying the sparsity parameter, while the similarity parameter was fixed. Results reported are the maximum for the sequence of similarity parameter values tested. Results indicate that the fused and group graphical lasso methods are quite good at the identification of true edges and seem to perform better for larger networks, but generally have high false positive rates. Our proposed method on the other hand has much lower sensitivity and achieves the best overall performance as measured by the AUC for the 25- and 50-node settings. For the 100-node setting, using the optimal penalty parameters for each replicate of the lasso methods resulted in an AUC slightly higher than that of our proposed method for fused lasso; however, false positive rates are significantly greater than that for our method.

Table 6.

Results from competing methods for the 100-node setting across 10 simulated datasets

	TPR (SE)	FPR (SE)	MCC (SE)	AUC (SE)
Fused graphical lasso	0.8658 (.0479)	0.2620 (.2632)	0.2775 (.0940)	0.9688 (.0016)
Group graphical lasso	0.8496 (.0095)	0.1739 (.0028)	0.3089 (.0042)	0.8982 (.0048)
Proposed method	0.7135 (.2929)	0.0053 (.0037)	0.7453 (.2334)	0.9578 (.0434)

We report averaged true positive rate (TPR), false positive rate (FPR), Matthews correlation coefficient (MCC) and area under the curve (AUC), with standard errors (SE)

5. Case Study on Disease Severity in COPD

This section illustrates the application of our method to infer the evolution of gene pathways in COPD subjects as emphysema increases in severity. We applied the proposed joint graphical model estimation method using hyperparameters α = 4 and β = 5 for the slab portion of the mixture prior on θ_k,m which results in a prior with mean 0.4. Because we had no prior reference network or knowledge of graph structure, for our edge-specific prior we chose q_{i, j} ~ Beta(1,9) for all edges (i, j). Other hyperparameters were set the same as in simulations. The MCMC sampler was run for 40,000 burn-in iterations followed by 80,000 iterations used for inference. For posterior inference, we selected those edges with marginal posterior probability of inclusion greater than 0.5. To verify convergence of our chains, we compared correlations of resulting MPP from two chains with different starting points. Pearson correlations were in the range of .9971–.9989, and Spearman correlations were in the range of .9705–.9967. The inferred network structures are shown in Figs. 2, 3, 4 and 5 for each of the four selected pathways, respectively. Network similarity across groups for each of the four pathways was estimated as

$$\mathrm{MPP}{(\mathrm{\Theta })}_{\mathit{\text{RegAuto}}}=\left(\begin{array}{cccc}\cdot & .76& .81& .83\\ & \cdot & .73& .84\\ & & \cdot & .77\\ & & & \cdot \end{array}\right),\mathrm{MPP}{(\mathrm{\Theta })}_{GPL}=\left(\begin{array}{cccc}\cdot & .96& .94& .95\\ & \cdot & .89& .91\\ & & \cdot & .96\\ & & & \cdot \end{array}\right)$$

$$\mathrm{MPP}{(\mathrm{\Theta })}_{\mathit{\text{OxPhos}}}=\left(\begin{array}{cccc}\cdot & 1.0& 1.0& 1.0\\ & \cdot & 1.0& 1.0\\ & & \cdot & 1.0\\ & & & \cdot \end{array}\right),\mathrm{MPP}{(\mathrm{\Theta })}_{\mathit{\text{FcyR}}}=\left(\begin{array}{cccc}\cdot & 1.0& 1.0& 1.0\\ & \cdot & 1.0& 1.0\\ & & \cdot & 1.0\\ & & & \cdot \end{array}\right)$$

For all final results, hub genes are defined as genes with at least four edges. Hub genes and edges were further examined for protein–protein interactions and disease-related gene annotation. protein–protein interactions were obtained from Biological General Repository for Interaction Datasets (BioGrids) v. 3.4.132 [5]. Disease annotation information was obtained from GeneCards [38] with the search term “lung” or “pulmonary” in the “Publications” search engine for GeneCards.

Fig. 2.

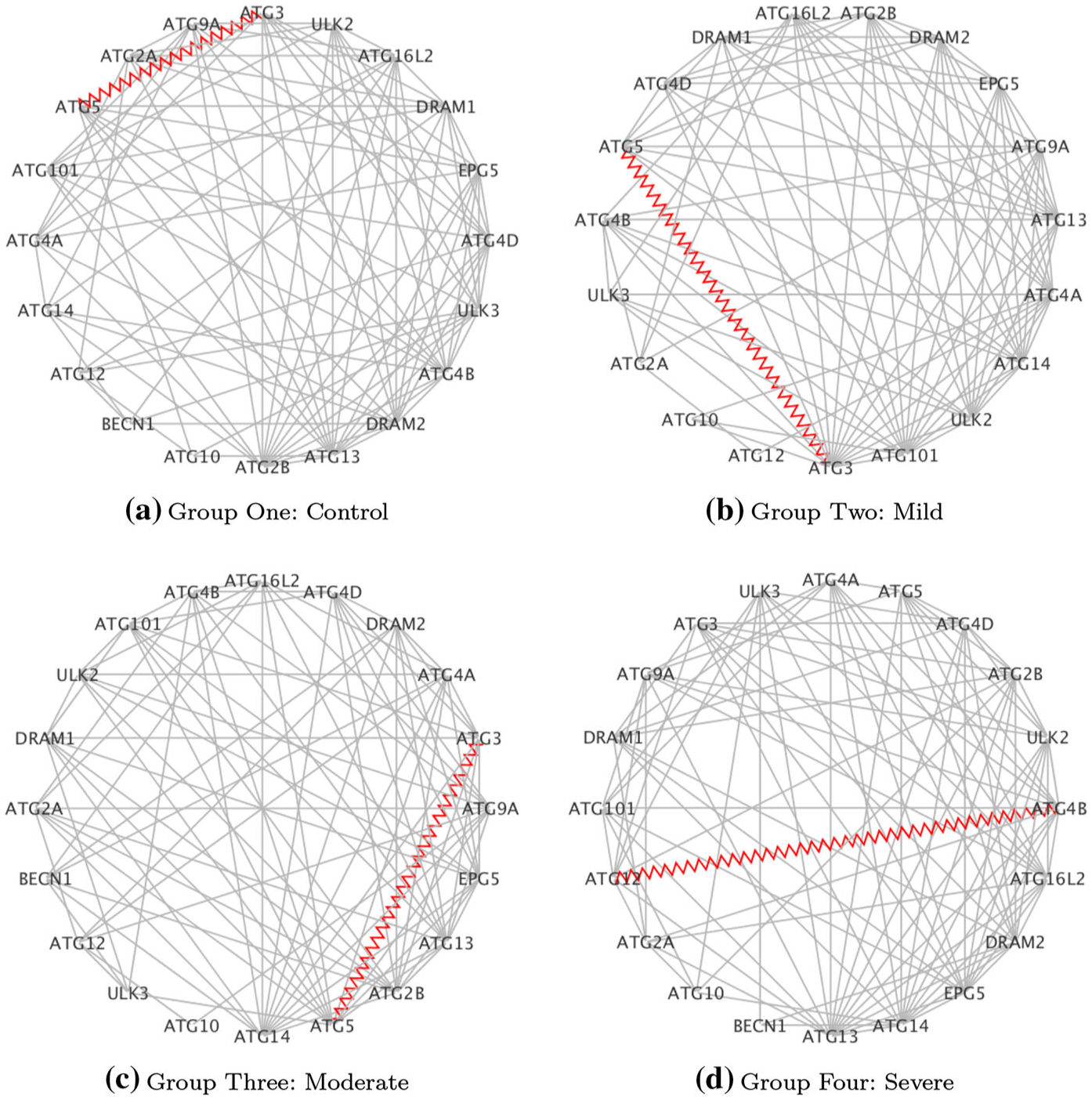
Case study on COPD: estimated networks for the Reg Auto pathway: red zig-zag edges denote known protein–protein interactions (PPI)

Fig. 3.

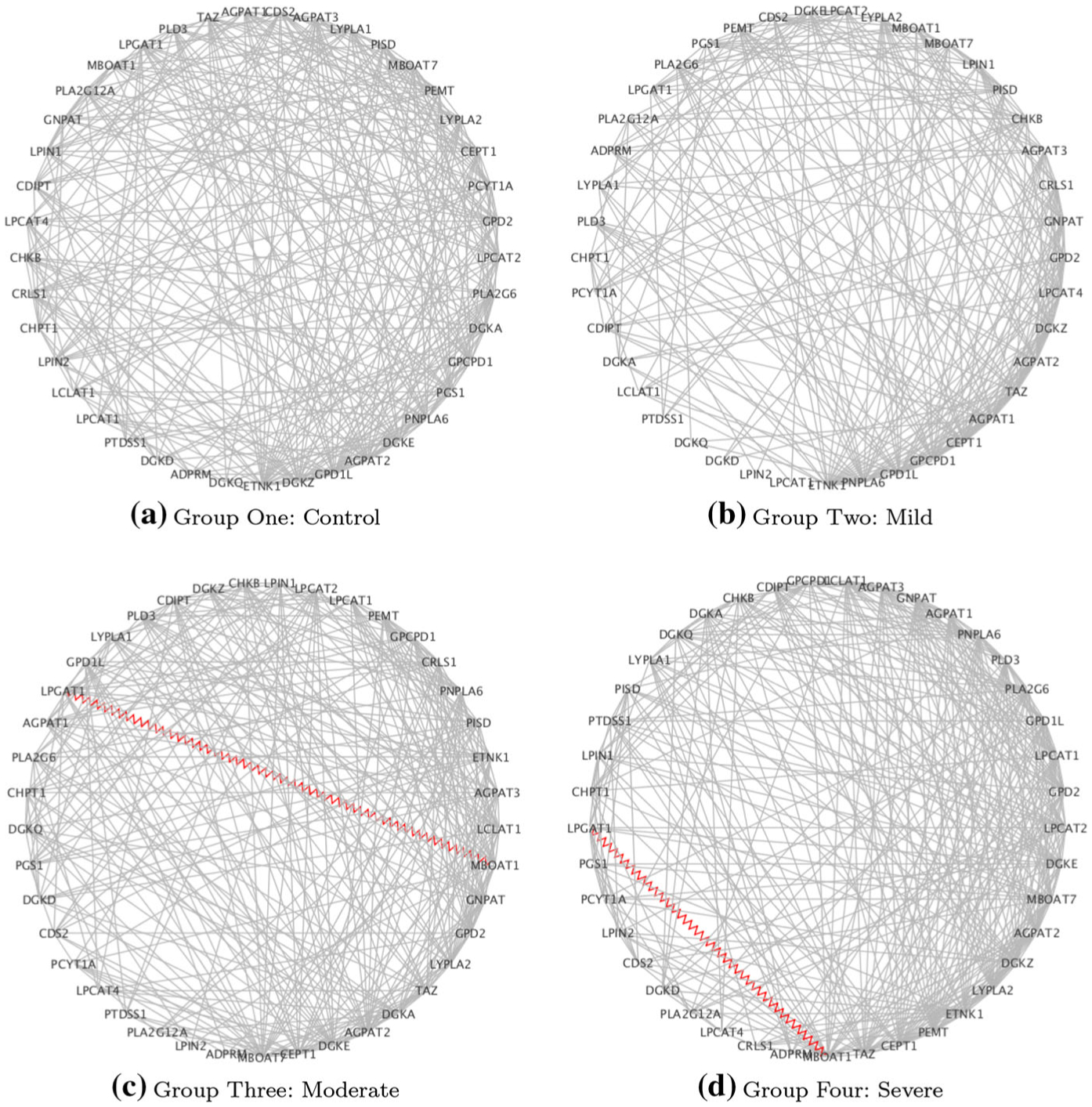
Case study on COPD: estimated networks for the GPL pathway: red zig-zag edges denote known protein–protein interactions (PPI).eps

Fig. 4.

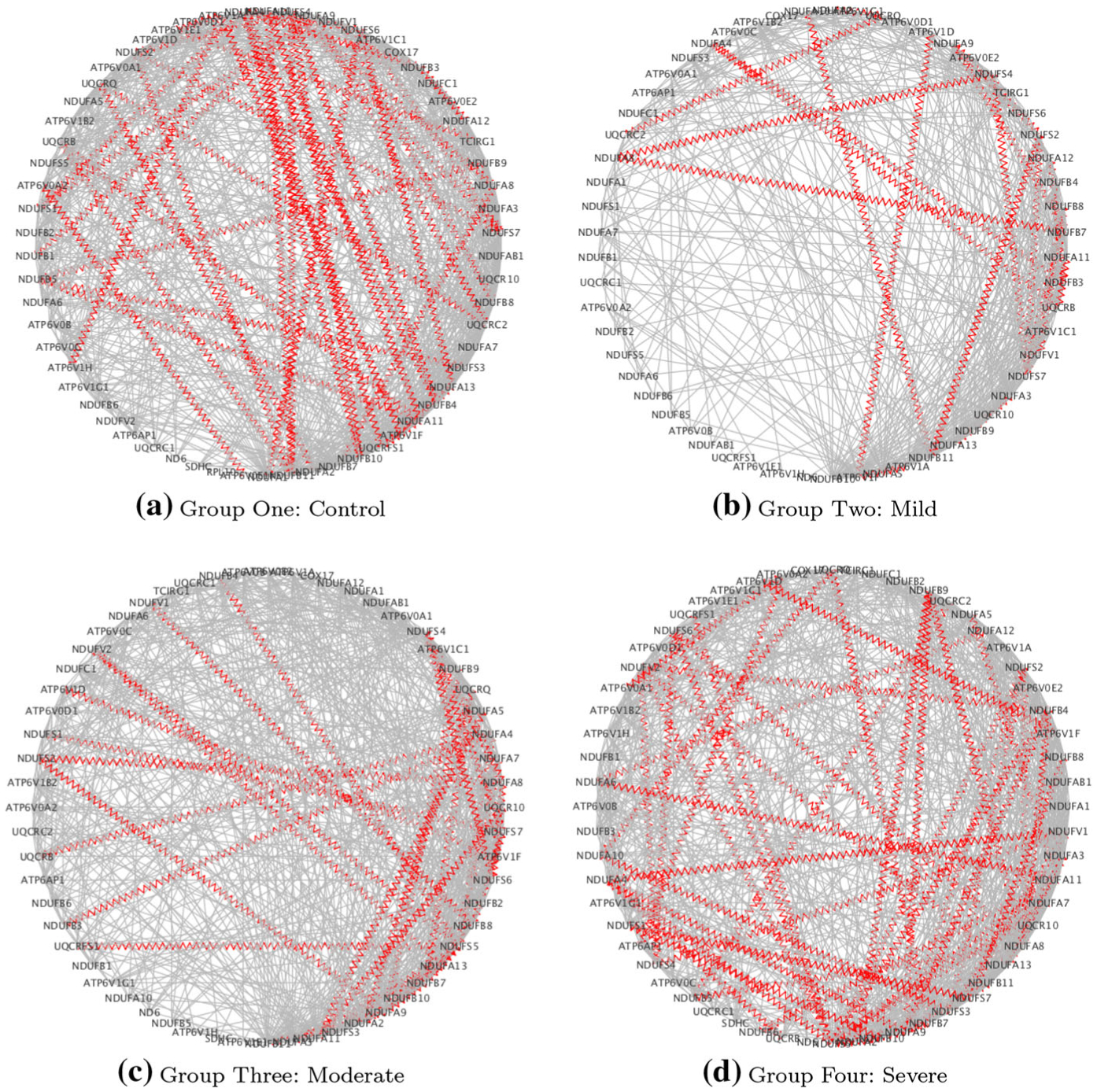
Case study on COPD: estimated networks for the OxPhos pathway: red zig-zag edges denote known protein–protein interactions (PPI)

Fig. 5.

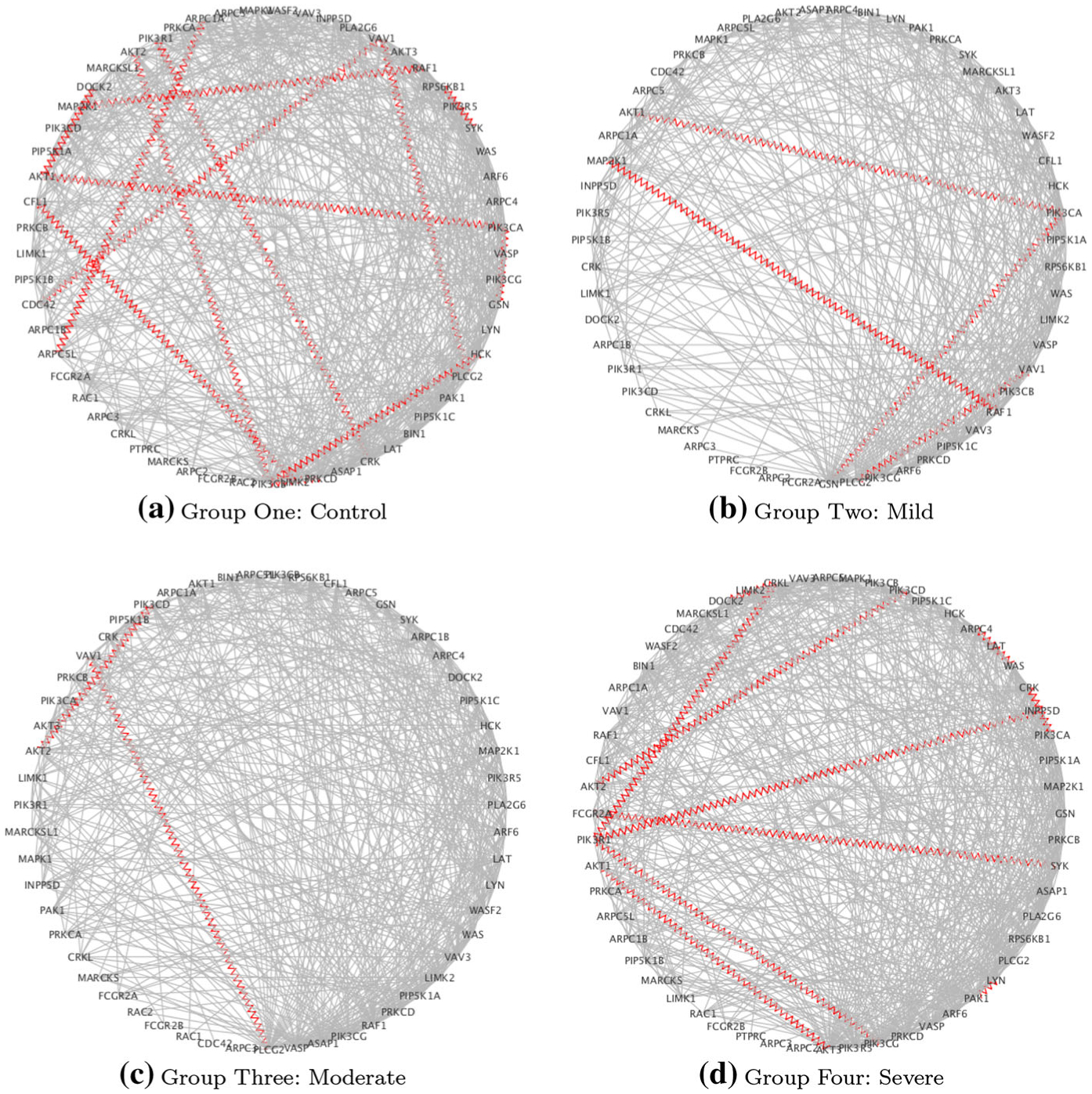
Case study on COPD: estimated networks for the FcyR pathway: red zig-zag edges denote known protein–protein interactions (PPI)

To further the comparison of our method with other methods, we also applied fused and joint graph lasso methods to the Reg Auto and GPL pathways from the ECLIPSE COPD dataset, using AIC to find optimal parameters. Overall, lasso methods seemed to have similar results to our proposed method with much denser networks due to higher false positive rates. This was expressed in particular by the Reg Auto pathway because every possible unique edge was selected by the lasso method. A detailed description of this comparison can be found in the Appendix.

5.1. Disrupted Interactions Due to Disease Severity

For each of the 4 pathways, we further examined all pairs of inferred gene interactions. Table 7 shows the total number of inferred pair interactions for each one of the 4 pathways, together with the number of those pairs that show evidence of disrupted interactions across disease severity. In the table, for each pathway, the four disease groups, ordered from least to most severe, are coded with 0’s and 1’s, with 1 indicating high MPP. For example, 1000 indicates that a pair has a MPP ≥0.50 in the least severe emphysema group (first group is indicated by 1) but not the others (last three groups are indicated by 0), while 0011 indicates that a pair has a MPP ≥0.50 in the two most severe groups (last two groups are indicated by 1), but not in the less severe disease cases (first two groups are indicated by 0).

Table 7.

Case study on COPD: numbers of total pairs of unique gene interactions and numbers of disease-disrupted pairs based on disease severity, for each one of the 4 selected pathways

	Total pairs	1000	1100	1110	0111	0011	0001	Total disrupted
GPL	539 (1)	58	26	28	21	40 (1)	59	232 (1)
FcyR	892 (50)	102 (8)	34 (3)	30 (1)	31	40 (1)	125 (9)	362 (22)
OxPhos	1072 (275)	127 (27)	37 (7)	25 (6)	23 (6)	62 (17)	120 (25)	394 (88)
RegAuto	153 (9)	13	2	11 (1)	8	4	11 (1)	49 (2)

There are four emphysema classes ordered by severity, with the first group being the no emphysema group and the last one the most severe emphysema group. For each pathway, the 4 groups are coded with 0’s and 1’s, with 1 indicating high MPP. For example, 1000 indicates that a pair has a MPP≥ 0.50 in the least severe emphysema group (first group is indicated by 1) but not the others (last three groups are indicated by 0), while 0011 indicates that a pair has a MPP≥ 0.50 in the two most severe groups (last two groups are indicated by 1), but not in the less severe disease cases (first two groups are indicated by 0). The number of pairs with known protein–protein interactions (PPI) is indicated in parentheses and listed further in Table 7

For all 4 pathways, we see larger numbers of disrupted pairs in the most extreme case, where the interactions are strongest either for the controls or the most severe emphysema. That is, we find that a pair has a high MPP (≥0.50) in the no emphysema subjects but low MPP (<0.50) in the mild-to-severe emphysema subjects; or vice versa, a high MPP in the more severe disease subjects but not in the less severe emphysema and control subjects. This observation highlights two interesting sets of interactions for further investigation; interactions that are disrupted even with mild levels of emphysema and interactions that only develop for the most severe emphysema cases.

Interestingly, some of the pairs identified in Table 7 are known to have protein–protein interactions (PPI). In Table 7, we report the numbers of such pairs in parentheses and list the actual pairs in Table 8. One notable edge that changes based on disease severity is the gene pair ATG5-ATG3 in the RegAuto pathway. The MPP of this interaction is higher for the less severe COPD group (0.52–0.59) but then decreases for the most severe COPD group (0.476), indicating a disrupted interaction associated with disease severity. ATG5 (autophagy-related gene 5) is also one of the top hub genes (discussed below) and is associated with the GO category of innate immune response.

Table 8.

Case study on COPD: subset of the disease-disrupted pairs in Table 7 with known protein–protein interactions

	Interaction in control (1000, 1100, 1110)	Interaction in disease (0111, 0011, 0001)
OxPhos	ATP6V0E1-ATP6V0A2,ATP6V1A-ATP6V0D1, ATP6V1A-ATP6V1E1, ATP6V1A-ATP6V1H, ATP6V1F-ATP6V1A, NDUFA1-NDUFS6, NDUFA10-NDUFA11, NDUFA10-NDUFB11, NDUFA4-NDUFB10, NDUFA4-NDUFB4, NDUFB1-NDUFA9, NDUFB3-NDUFA12, NDUFB3-NDUFA4,NDUFB5-NDUFA11, NDUFB5-NDUFB9, NDUFB7-NDUFA8, NDUFB8-NDUFV1, NDUFS1-NDUFA4, NDUFS1-NDUFA9, NDUFS2-NDUFB11, NDUFS2-NDUFS4, NDUFS2-NDUFS7, NDUFS3-NDUFB5, NDUFS4-NDUFA8, NDUFS4-NDUFB10, NDUFS4-NDUFB11, NDUFS4-NDUFB4, NDUFS4-NDUFS7, NDUFS6-NDUFA13, NDUFS6-NDUFA4, NDUFS6-NDUFS7, TCIRG1-ATP6V1E1, UQCRB-NDUFA11, UQCRB-NDUFB11, UQCRC2-NDUFA9, UQCRC2-UQCRQ, UQCRFS1-NDUFA11, UQCRFS1-NDUFA13, UQCRFS1-NDUFA4, UQCRQ-NDUFA2	ATP6AP1-ATP6V0A2, ATP6V0A1-ATP6V0A2, ATP6V1F-ATP6V1D,NDUFA2-NDUFB9, NDUFA3-NDUFA13, NDUFA5-NDUFA11, NDUFA6-NDUFA11,NDUFA6-NDUFA12, NDUFA8-NDUFB4, NDUFA8-NDUFB9, NDUFA9-NDUFA2, NDUFA9-NDUFA4, NDUFA9-NDUFB11, NDUFA9-NDUFB4, NDUFA9-NDUFB9, NDUFB5-NDUFA8, NDUFB6-NDUFA11, NDUFB7-NDUFA9, NDUFB8-NDUFS7, NDUFS1-NDUFB10, NDUFS1-NDUFS7, NDUFS2-NDUFA8, NDUFS2-NDUFA9, NDUFS3-NDUFA10, NDUFS3-NDUFS2, NDUFS3-NDUFV1, NDUFS5-NDUFA11, NDUFS5-NDUFA2, NDUFS5-NDUFA4, NDUFS5-NDUFA7, NDUFS5-NDUFB10, NDUFS5-NDUFB4, NDUFS5-NDUFB7, NDUFS5-NDUFS2, NDUFS5-NDUFS6, NDUFS5-NDUFV2, NDUFS5-UQCRFS1, NDUFS6-NDUFA8, NDUFS6-NDUFS4, NDUFV1-NDUFA4, NDUFV1-NDUFS4, NDUFV2-NDUFA13, NDUFV2-NDUFB4, NDUFV2-NDUFS4, UQCRB-NDUFA4, UQCRC2-NDUFB5, UQCRQ-NDUFA10, UQCRQ-NDUFB7
FcyR	ARPC1A-ARPC5L, CFL1-LIMK2, CRK-PIK3R1, GSN-PIK3CA, HCK-PIK3CB, PIK3CA-AKT1, PIK3CB-AKT2, PLCG2-VAV1, PRKCD-PIK3CB, RAF1-MAP2K1, RPS6KB1-SYK, VAV1-CDC42	AKT1-AKT3, ARPC4-WAS, CRK-PIK3CA, CRKL-DOCK2, CRKL-PIK3R1, FCGR2A-SYK, INPP5D-PIK3R1, LYN-PAK1, PIK3CD-AKT2, PIK3R5-PIK3CG
RegAuto	ATG5-ATG3	ATG4B-ATG12
GPL		LPGAT1-MBOAT1

5.2. Hub Genes

Hub genes are highly connected genes and, as such, are expected to play an important role in biology. Here, we explored all genes in our inferred networks with at least 2 edges appearing in any of the disease groups [22]. Table 9 indicates the hub genes for each of the 4 pathways, together with the numbers of disrupted pairs and the number of known PPIs involving hub genes. For RegAuto, two of the hub genes have also been discussed above (ATG5-ATG3). For this pathway, increased autophagy has been observed in lung tissue from COPD patients with increased activation of autophagic proteins including protein products of hub genes found in ATG5 and ATG4B [6]. Another gene of interest is PIK3CD in the FcyR pathway. Expression and signaling of this gene is increased in the lungs of patients with COPD and is associated with reduced glucocorticoid responsiveness. Some authors have suggested that selective inhibition of the protein product PI3Kdelta might restore glucocorticoid function in patients with COPD, therefore representing a potential therapeutic target [24].

Table 9.

Case study on COPD: summary of top hub genes. Disrupted pairs which are also known PPI are listed in Table 8

Pathway	Hub genes	Disrupted pairs with hub gene	PPI with hub gene	Disrupted pairs and PPI with hub gene
GPL	ADPRM, AGPAT1, AGPAT3, CDIPT, CDS2, CEPT1, CHKB, CHPT1, CRLS1, DGKA, DGKD, DGKZ, ETNK1, GNPAT, GPCPD1, GPD1L, GPD2, LCLAT1, LPCAT1,LPCAT2, LPGAT1, LPIN1, LPIN2, LYPLA1, LYPLA2, MBOAT7, PCYT1A, PEMT, PGS1, PISD, PLA2G6, PLD3, PNPLA6, PTDSS1	226	1	1
FcyR	AKT1, AKT3, ARF6, ARPC1A, ARPC1B, ARPC3, ARPC4, ARPC5, BIN1, CDC42, CFL1, CRK, CRKL, DOCK2, FCGR2A, GSN, HCK, INPP5D, LAT, LIMK1, LIMK2 LYN, MAP2K1, MAPK1, MARCKS, MARCKSL1, PIK3CA, PIK3CB, PIK3CD, PIK3R1, PIK3R5, PIP5K1A, PIP5K1B, PIP5K1C, PLA2G6,PLCG2, PRKCA, PRKCB, PRKCD, PTPRC, RAC1, RAF1, FPS6KB1,,SYK, VASP, VAV1, VAV3	354	50	22
OxPhos	ATP6AP1, ATP6V0A1, ATP6V0B, ATP6V0D1, ATP6V0E2, ATP6V1A, ATP6V1B2, ATP6V1C1, ATP6V1D, ATP6V1E1, ATP6V1F, ATP6V1G1, COX17, ND6, NDUFA1, NDUFA10, NDUFA13, NDUFA2, NDUFA3, NDUFA4, NDUFA5, NDUFA6, NDUFA7, NDUFA8, NDUFA9, NDUFAB1, NDUFB1, NDUFB11 NDUFB3, NDUFB4, NDUFB5, NDUFB6, NDUFB7, NDUFB8, NDUFC1, NDUFS1, NDUFS2, NDUFS3, NDUFS4, NDUFS5, NDUFS6, NDUFS7, NDUFV1, NDUFV2, SDHC, TCIRG1, UQCR10, UQCRB, UQCRC1, UQCRC2, UQCRFS1, UQCRQ	384	270	88
RegAuto	ATG101, ATG12, ATG13, ATG14, ATG3, ATG4A, ATG4B, ATG5, ATG9A, BECN1, DRAM1, DRAM2, ULK2	43	8	2

6. Conclusion

Motivated by the study of four critical pathways in COPD, we have proposed and implemented a novel approach to study how gene networks change with disease progression. We have introduced a novel Bayesian approach for multiple graphical models based on shrinkage and MRF priors. The combination of these two priors has allowed us to develop a computationally efficient algorithm and to perform a fully Bayesian analysis of the four targeted pathways. The proposed modeling approach allows to share information between sample groups, when appropriate, as well as to obtain a measure of relative network similarity across groups.

We have applied our approach to the ECLIPSE COPD dataset. Pathway enrichment of significant genes is often used in genomic research to identify candidate pathways but does not give additional information on how specific interactions within pathways are altered with disease severity. Using our Bayesian hierarchical approach, we were able to infer gene networks within 4 selected pathways. Our method has identified critical hub genes for all the four targeted pathways. Furthermore, several gene connections appeared to be disrupted with increased disease severity and constitute interesting candidates for further investigation, in an effort to characterize the disease evolution. Our analysis has clearly suggested that the autophagy-related gene ATG5 plays a critical role in COPD progression, highlighting critical interactions and highly connected genes that represent interesting targets for therapeutic targets. We also found several genes and gene interactions (ATG5, ATG3, and PIK3CD) that have already been associated with COPD. Further investigation of additional interactions such as UQCRC2-NDUFA1, which shows disruption based on disease severity, is the goal of future work. Using simulation studies, we have demonstrated the superior performance of our approach in comparison with competing methods.

Appendix

Details on our MCMC Algorithm

In this section, we provide a detailed description of Step a and Step b of our MCMC algorithm.

Step a. By partitioning Ω into $V=\left(v_{i,j}^2\right)$, a p × p symmetric matrix with zeroed diagonal entries and ${\left(v_{i,j}^2\right)}_{i<j}$ in the upper diagonal entries and setting S = X′X, we can focus on the last column and row to acquire

$$\mathrm{\Omega }=\left(\begin{array}{cc}{\mathrm{\Omega }}_{1,1}& {\omega }_{1,2}\\ {\omega }_{1,2}^{\prime }& {\omega }_{2,2}\end{array}\right),S=\left(\begin{array}{cc}{S}_{1,1}& s_{1,2}\\ s_{1,2}^{\prime }& s_{2,2}\end{array}\right),V=\left(\begin{array}{cc}{V}_{1,1}& v_{1,2}\\ v_{1,2}^{\prime }& 0\end{array}\right).$$

Changing variables from (ω_1,2, ω_2,2) to $\left(u={\omega }_{1,2},v={\omega }_{2,2}-{\omega }_{1,2}^{\prime }{\mathrm{\Omega }}^{-1}{\omega }_{1,2}\right)$, we have full conditionals

$$u|\cdot ~N\left(-C{s}_{1,2},C\right)\mathrm{ and }v|\cdot ~\mathrm{Gamma}\left(\frac{n}{2}+1,\frac{s_{2,2}+\lambda }{2}\right),$$

where $C={\left\{\left(s_{2,2}+\lambda \right){\mathrm{\Omega }}_{1,1}^{-1}+\mathrm{diag}\left(v_{1,2}^{-1}\right)\right\}}^{-1}$. Using this method, we can permute any column to attain the full conditional used to generate Ω|G, X. Our full conditional on G is then an independent Bernoulli of the form

$$P\left(g_{i,j}=1|\mathrm{\Omega },X\right)=\frac{N\left({\omega }_{i,j}|0,v_1^2\right)\pi }{N\left({\omega }_{i,j}|0,v_1^2\right)\pi +N\left({\omega }_{i,j}|0,v_0^2\right)(1-\pi )},$$

where the quantity $\frac{\pi }{1-\pi }$ is determined by the MRF prior on the graph structure such that

$$\frac{\pi }{1-\pi }=\frac{p\left(G_k^{\prime }|v_{i,j},\mathrm{\Theta },{\left\{G_m\right\}}_{m\ne k}\right)}{p\left(G_k|v_{i,j},\mathrm{\Theta },{\left\{G_m\right\}}_{m\ne k}\right)}=\text{exp}\{-v_{i,j}+2\sum _{m\ne k}{\theta }_{k,m}{g}_{m,i,j})\},$$

for proposed new graph $G_k^{\prime }$ which differs from the current graph G_k only in that edge (i, j) is excluded from $G_k^{\prime }$ and included in G_k.

Step b. In order to update θ_k,m and γ_k,m, we must consider the full conditional distribution. Considering only the terms of the joint prior for graphs G₁, …, G_k which include θ_k,m, we can see that

$$\begin{gathered} p\left(G_1,\dots ,G_4|v,\mathrm{\Theta }\right)=\prod _{i<j}C{\left(v_{i,j},\mathrm{\Theta }\right)}^{-1}\text{exp}\left(v_{i,j}{1}^T{g}_{i,j}+g_{i,j}{}^T\mathrm{\Theta }{g}_{i,j}\right) \\ \propto \prod _{i<j}C{\left(v_{i,j},\mathrm{\Theta }\right)}^{-1}\text{exp}\left(2{\theta }_{k,m}{g}_{k,i,j}{g}_{m,i,j}\right). \end{gathered}$$

The full conditional distribution of θ_k,m and γ_k,m can then be written as

$$\begin{gathered} p\left({\theta }_{k,m},{\gamma }_{k,m}|\cdot \right)=p\left(G_1,\dots ,G_k|v,\mathrm{\Theta }\right)p\left({\theta }_{k,m}|{\gamma }_{k,m}\right)p\left({\gamma }_{k,m}|w\right) \\ \alpha \left(\prod _{i<j}C{\left(v_{i,j},\mathrm{\Theta }\right)}^{-1}\text{exp}\left(2{\theta }_{k,m}{g}_{k,i,j}{g}_{m,i,j}\right)\right) \\ \times \left(\left(1-{\gamma }_{k,m}\right){\delta }_0+{\gamma }_{k,m}\frac{{\beta }^{\alpha }}{\mathrm{\Gamma }(\alpha )}{\theta }_{k,m}^{\alpha -1}{e}^{-\beta {\theta }_{k,m}}\right) \\ \times \left(w^{{\gamma }_{k,m}}{(1-w)}^{\left(1-{\gamma }_{k,m}\right)}\right). \end{gathered}$$

Because the normalizing constant from the joint prior on the graphs is analytically intractable, we use Metropolis–Hastings step to sample from θ_k,m and γ_k,m for each pair of (k,m),1 ≤ k < m ≤ 4 from the joint full conditional distribution. Each iteration has two steps based on the approach described by [14] to sample from mutually singular distribution mixtures. First, we perform a between-model move. If the current state is γ_k,m = 1, we propose ${\gamma }_{k,m}^{\star }=0$ and ${\theta }_{k,m}^{\star }=0$ resulting in the Metropolis–Hastings ratio

$$\begin{gathered} r=\frac{p\left({\theta }_{k,m}^{\star },{\gamma }_{k,m}^{\star }|\cdot \right)\times q\left({\theta }_{k,m}\right)}{p\left({\theta }_{k,m},{\gamma }_{k,m}|\cdot \right)}=\frac{\mathrm{\Gamma }(\alpha )}{\mathrm{\Gamma }\left({\alpha }^{\star }\right)}\frac{{\left({\beta }^{\star }\right)}^{{\alpha }^{\star }}}{{\beta }^{\alpha }}{\left({\theta }_{k,m}\right)}^{{\alpha }^{\star }-\alpha }{e}^{\left(\beta -{\beta }^{\star }\right){\theta }_{k,m}} \\ \times \prod _{i<j}\frac{C\left(v_{i,j},\mathrm{\Theta }\right)\text{exp}\left(-2{\theta }_{k,m}{g}_{k,i,j}{g}_{m,i,j}\right)}{C\left(v_{i,j},{\mathrm{\Theta }}^{\star }\right)}\frac{1-w}{w}, \end{gathered}$$

Where Θ^⋆ represents the network similarity matrix Θ with entry ${\theta }_{k,m}={\theta }_{k,m}^{\star }$. If moving instead from γ_k,m = 0 to ${\gamma }_{k,m}^{\star }=1$, the ratio is

$$\begin{gathered} r=\frac{p\left({\theta }_{k,m}^{\star },{\gamma }_{k,m}^{\star }|\cdot \right)}{p\left({\theta }_{k,m},{\gamma }_{k,m}|\cdot \right)\times q\left({\theta }_{k,m}\right)}=\frac{\mathrm{\Gamma }\left({\alpha }^{\star }\right)}{\mathrm{\Gamma }(\alpha )}\frac{{\beta }^{\alpha }}{{\left({\beta }^{\star }\right)}^{{\alpha }^{\star }}}\times {\left({\theta }_{k,m}\right)}^{\alpha -{\alpha }^{\star }}{e}^{\left({\beta }^{\star }-\beta \right){\theta }_{k,m}} \\ \times \prod _{i<j}\frac{C\left(v_{i,j},\mathrm{\Theta }\right)\text{exp}\left(-2{\theta }_{k,m}^{\star }{g}_{k,i,j}{g}_{m,i,j}\right)}{C\left(v_{i,j},{\mathrm{\Theta }}^{\star }\right)}\frac{w}{1-w}. \end{gathered}$$

Next, we perform the within-model move if the value of γ_k,m sampled from the between-model move is 1. Here, we propose a new value using the same proposal density as before, for θ_k,m. Our Metropolis–Hastings ratio is

$$\begin{gathered} r=\frac{p\left({\theta }_{k,m}^{\star },{\gamma }_{k,m}^{\star }|\cdot \right)\cdot q\left({\theta }_{k,m}\right)}{p\left({\theta }_{k,m},{\gamma }_{k,m}|\cdot \right)\cdot q\left({\theta }_{k,m}^{\star }\right)}={\left(\frac{{\theta }_{k,m}^{\star }}{{\theta }_{k,m}}\right)}^{\alpha -{\alpha }^{*}}\cdot e^{\left({\beta }^{\star }-\beta \right)\left({\theta }_{k,m}^{\star }-{\theta }_{k,m}\right)} \\ \times \prod _{i<j}\frac{C\left(v_{i,j},\mathrm{\Theta }\right)\text{exp}\left(2\left({\theta }_{k,m}^{\star }-{\theta }_{k,m}\right)g_{k,i,j}{g}_{m,i,j}\right)}{C\left(v_{i,j},{\mathrm{\Theta }}^{\star }\right)}. \end{gathered}$$

In our last step of the MCMC, we sample from the full conditional distribution of v_{i, j}. The terms of the joint prior on the graphs including v_{i, j} are

$$\begin{gathered} p\left(G_1,\dots ,G_k|v,\mathrm{\Theta }\right)=\prod _{i<j}C{\left(v_{i,j},\mathrm{\Theta }\right)}^{-1}\exp \left(v_{i,j}{1}^T{g}_{i,j}+g_{i,j}{}^T\mathrm{\Theta }{g}_{i,j}\right) \\ \propto C{\left(v_{i,j},\mathrm{\Theta }\right)}^{-1}\exp \left(v_{i,j}{1}^T{g}_{i,j}\right). \end{gathered}$$

Given the prior on v_{i, j}, we can attain the posterior full conditional given the data and all remaining parameters

$$\begin{gathered} p\left(v_{i,j}|\cdot \right)\propto \frac{\text{exp}\left(a{v}_{i,j}\right)}{{\left(1+e^{v_{i,j}}\right)}^{a+b}}C{\left(v_{i,j},\mathrm{\Theta }\right)}^{-1}\text{exp}\left(v_{i,j}{1}^T{g}_{i,j}\right) \\ =\frac{\text{exp}\left(v_{i,j}\left(a+1^T{g}_{i,j}\right)\right)}{C\left(v_{i,j},\mathrm{\Theta }\right)\cdot {\left(1+e^{v_{i,j}}\right)}^{a+b}}. \end{gathered}$$

We then propose a value q^⋆ from the density Beta(2,4) for each pair (i, j) where 1 ≤ i < j ≤ p and set v^⋆ = logit(q^⋆). We can write our proposal density in terms of v^⋆ as

$$q\left(v^{\star }\right)=\frac{1}{B\left(a^{\star },b^{\star }\right)}\frac{e^{a^{\star }{v}^{\star }}}{{\left(1+e^{{\nu }^{\star }}\right)}^{a^{\star }+b^{\star }}},$$

with Metropolis–Hastings ratio

$$\begin{gathered} r=\frac{p\left(v^{\star }|\cdot \right)}{p\left(v_{i,j}|\cdot \right)}\frac{q\left(v_{i,j}\right)}{q\left(v^{\star }\right)} \\ =\frac{\text{exp}\left(\left(v^{\star }-v_{i,j}\right)\cdot \left(a-a^{\star }+1^T{g}_{i,j}\right)\right)\cdot C\left(v_{i,j},\mathrm{\Theta }\right)\cdot {\left(1+e^{v_{i,j}}\right)}^{a+b-a^{\star }-b^{\star }}}{C\left(v^{\star },\mathrm{\Theta }\right)\times {\left(1+e^{v^{\star }}\right)}^{a+b-a^{\star }-b{I}^{\star }}}. \end{gathered}$$

Case Study: Comparison to the Fused and Joint Graphical Lasso

In this section, we compare the proposed Bayesian approach to the fused and joint graphical lasso in terms of the findings obtained from the analysis of the ECLIPSE dataset. Specifically, we focused on the Reg Auto and GPL pathways. For both the fused and joint graphical lasso, we selected the penalty parameters that minimized the AIC, as recommended by [9]. For the Reg Auto pathway, the fused graphical lasso penalty parameters were selected as λ₁ = 0.015 and λ₂ = 0.0001, and for the group lasso were selected as λ₁ = 0.015 and λ₂ = 0 (this value was selected after an extensive grid search with step size of .0000005). For the GPL pathway, penalty parameters were selected as λ₁ = 0.02 and λ₂ = 0.0005 for the fused lasso, and λ₁ = 0.02 and λ₂ = 0.0 for the group lasso. Results are summarized in the two tables below.

Reg auto: method edge count comparison

	Proposed method	Group fused lasso	Joint group lasso
Group 1 edge count	98	159	159
Group 2 edge count	95	155	155
Group 3 edge count	89	155	155
Group 4 edge count	98	146	146
Unique edge count	153	190	190

GPL: method edge count comparison

	Proposed method	Group fused lasso	Joint group lasso
Group 1 edge count	312	560	560
Group 2 edge count	255	553	553
Group 3 edge count	288	545	545
Group 4 edge count	314	536	536
Unique edge count	539	802	802

For the Reg Auto pathway, it can be seen that edge counts were equivalent for the fused lasso and the group lasso. Both lasso methods selected all the possible 190 edges; this illustrates the issue corresponding to high false positive rates for lasso methods and consequently hints at more difficult interpretation of results. Percentage overlap of unique edges for Reg Auto was computed as

$$\frac{\text{ Unique Edges in Proposed and Lasso Method }}{\text{ Unique Lasso Edge Count }},$$

and resulted in an overlap of 80 %. Lasso methods identified the same hub genes as the proposed Bayesian approach, plus ATG10 and ULK3.

Similar conclusions can be derived from the analysis of the GPL pathway. The same edges were selected by both the group and fused lasso for all disease groups; 802 out of 820 possible unique edges were selected. Of the 18 edges remaining which were not selected by the lasso methods, five were selected by our proposed method. This resulted in a percentage eoverlap of unique edges for GPL 67%. The lasso methods identified the same hub genes as our proposed method in addition to DGKE, DGKQ, and MBOAT1. Overall, the lasso methods have similar results to our proposed approach, but result in much more dense networks due to their higher false positive rates. The proposed Bayesian approach provides sparser solutions that can be more easily interpreted.