Skip to main content
PMC home page
PLOS Computational Biology logoLink to PLOS Computational Biology
. 2021 Apr 15;17(4):e1008798. doi: 10.1371/journal.pcbi.1008798

Accurate contact-based modelling of repeat proteins predicts the structure of new repeats protein families

Claudio Bassot 1,2, Arne Elofsson 1,2,*
Editor: Johannes Soeding3
PMCID: PMC8078820  PMID: 33857128

Abstract

Repeat proteins are abundant in eukaryotic proteomes. They are involved in many eukaryotic specific functions, including signalling. For many of these proteins, the structure is not known, as they are difficult to crystallise. Today, using direct coupling analysis and deep learning it is often possible to predict a protein’s structure. However, the unique sequence features present in repeat proteins have been a challenge to use direct coupling analysis for predicting contacts. Here, we show that deep learning-based methods (trRosetta, DeepMetaPsicov (DMP) and PconsC4) overcomes this problem and can predict intra- and inter-unit contacts in repeat proteins. In a benchmark dataset of 815 repeat proteins, about 90% can be correctly modelled. Further, among 48 PFAM families lacking a protein structure, we produce models of forty-one families with estimated high accuracy.

Author summary

Repeat proteins are widespread among organisms and particularly abundant in eukaryotic proteomes. Their primary sequence presents repetition in the amino acid sequences that origin structures with repeated folds/domains. Although the repeated units often can be recognised from the sequence alone, often structural information is missing. Here, we used contact prediction for predicting the structure of repeats protein directly from their primary sequences. We benchmark the methods on a dataset comprehensive of all the known repeated structures. We evaluate the contact predictions and the obtained models for different classes of repeat proteins. Further, we develop and benchmark a quality assessment (QA) method specific for repeat proteins. Finally, we used the prediction pipeline for all PFAM repeat families without resolved structures and found that forty-one of them could be modelled with high accuracy.

Introduction

Repeat proteins contain periodic units in the primary sequence that are likely the result of duplication events at the genetic level [1]. Repeat proteins emerge through replication slippage [2] and double-strand break repair [3]. This protein class is present in all genomes but is more frequent in eukaryotic organisms [4–6] where they are involved in a wide range of functions [7]. In particular, due to their extended structures, repeat proteins often behave as molecular scaffolds in protein signalling or for protein complexes as WD40 domain [8], or ankyrin repeats [9,10]. Repeat proteins are usually conserved among orthologs [4,11] while exhibiting a more accelerated evolution and divergence among paralogs [11].

A classification of repeat proteins was proposed by Kajava [12,13] based on the length of the repeat units and the tertiary structure of the repeat units. According to Kajava’s classification, there are five classes of repeat proteins. However, in this study, we ignore class I and II because there are no available structures for class I, and class II structures are folded in a coiled-coil structure possible to predict using other methods. Moreover, the extreme amino acid compositional bias of many of these proteins makes it difficult to identify the coevolving residues in these two classes.

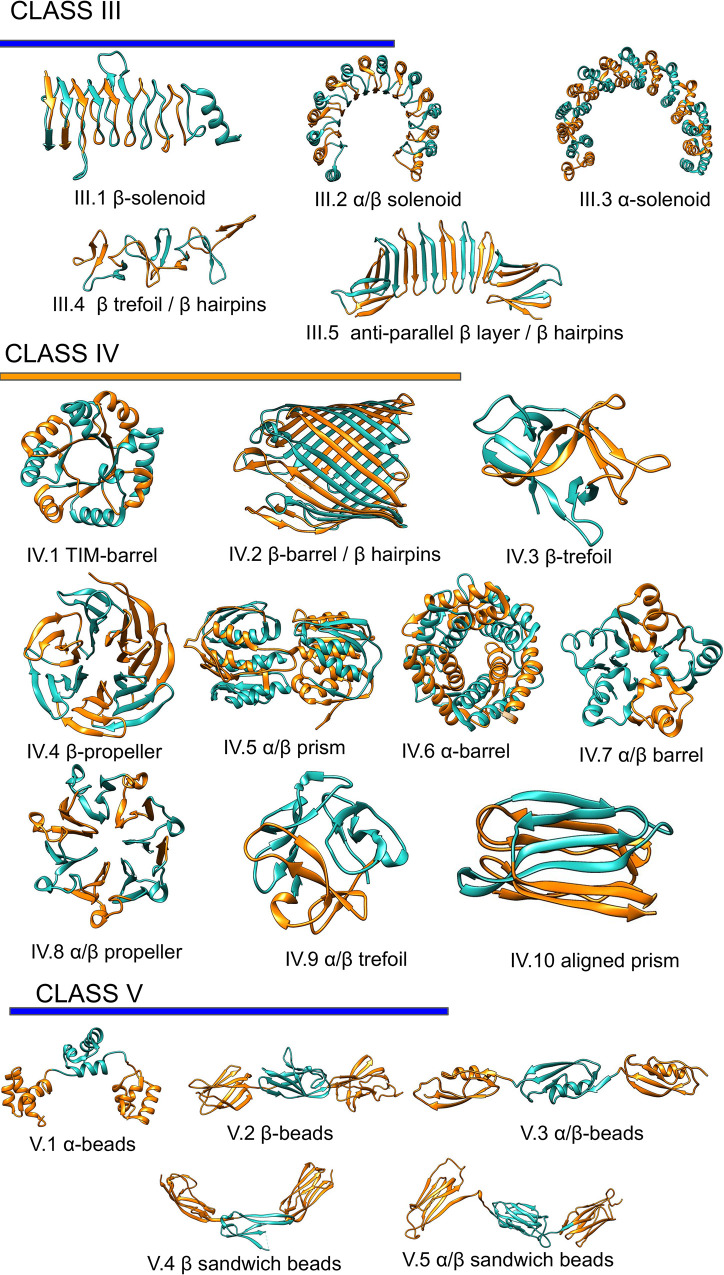
The dataset used in our study contains three classes of proteins divided into 20 subclasses by their secondary structure, according to RepeatsDB [14], Fig 1. The three types are; class III extended repeats (e.g. ɑ and β solenoids); class IV closed repeats structures (e.g. TIM and β barrels and β-propeller), and class V where the units appear as separate domains on a string. Further, class V the repeat units are longer than in the other classes.

Fig 1. Repeats proteins classification.

Fig 1

Open in a new tab

Representation of the repeats classes and subclasses as classified in repeatsDB 2.0 [14].

The solenoid structures (subclasses III.1, III.2 III.3) dominate Class III [13], and these proteins contain a wide range of repeated units (from 4 to 38), Fig 1. The length of the individual unit is also quite variable (from 10 to 50 residues) [14], with β-solenoids having significantly shorter repeats compared with α and α/β solenoid [13].

Members of class IV are constrained in variability by the closed fold. Indeed, despite ten subclasses of different units, the number of units varies between 3 and 16, and proteins with more than ten repeat units are rare. Even in this class, the length of the repeats units varies between 10 to 50 residues [13]. Finally, class V proteins are made up of the extended repeat units, often longer than 40 residues [14]. Each unit folds into proper domains, and they only have few inter-unit contacts.

Many repeat protein families lack a resolved structure. For these protein families, residue-residue contact prediction is the best method to obtain structural information [15]. Contact prediction methods use residue-residue co-evolution from multiple sequence alignment and identify the residues’ evolutionary constraints imposed by the tertiary protein structure [16]. Nevertheless, repeat proteins are a difficult target for contact prediction; the internal symmetry introduces artefacts in the contact map at a distance corresponding to the repeated units [17].

Here, we benchmark the deep-learning-based contacts prediction programs PconsC4 [18] trRosetta [19], DeepMetaPsicov [20] against the GaussDCA [21] on a comprehensive dataset generated from RepeatsDB [14]. The predicted contacts were then used as constraints to generate protein models. The model quality was evaluated, combining the quality assessment scores from Pcons [22] and QmeanDisCo [23] through a random forest regression. Based on the benchmark, we propose models for the protein structures of PFAM protein families missing resolved structures.

Results and discussion

General contact prediction analysis in repeat proteins

To assess the quality of the contacts predictions among repeat protein classes, we generate a dataset of proteins using the reviewed entries of RepeatsDB [14] and then clustered at 40% sequence identity. For each repeats region in the dataset, we also extracted a representative repeat unit and a pair of repeats, obtaining in this way three datasets: i) a single unit datasets; ii) a double unit datasets; iii) complete repeat region datasets.

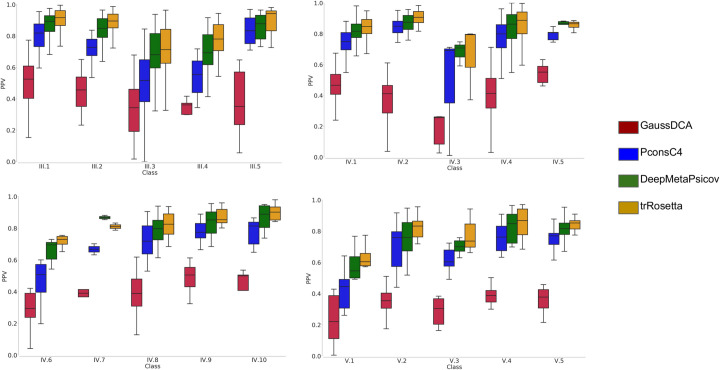
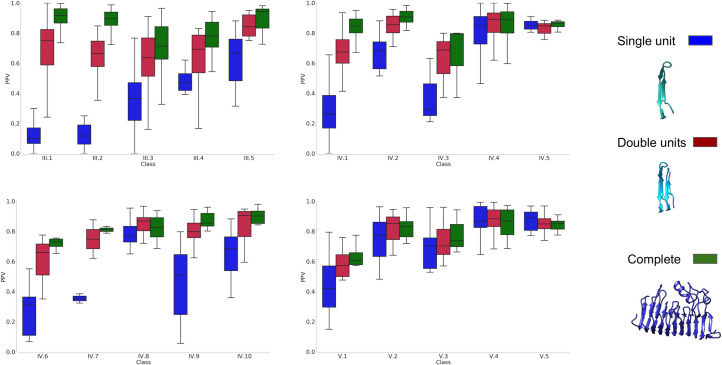
For all the three sets, multiple sequence alignments (MSA) and secondary structure predictions were generated. Subsequently using the MSA as input for trRosetta, PconsC4, DeepMetaPsicov, and GaussDCA contacts were predicted for each family. The performance of the contact predictions was then evaluated for each subclass separately. As expected, the most recent method, trRosetta outperforms an older deep learning method as PconsC4 and a simple DCA method as GaussDCA, but even ifcompared with the more recent, DeepMetaPsicov trRosetta shows a consistent improvement among all but two classes, Fig 2. In general for all the methods the predictions for the full-length regions give better results than when splitting the proteins into smaller units, Figs 3 and S1. In class V however, which is composed of entire domains, forming repeats of the “beads on a string” type, the splitting in units sometimes helps to reach better contact predictions for PconsC4, DeepMetaPsicov, and GaussDCA S1 Fig.

Fig 2. The precision of contact predictions.

Fig 2

Open in a new tab

Positive Predictive Value (PPV) for the GaussDCA (red), Pconsc4 (Blue), DeepMetaPsicov (green), and trRosetta (orange).

Fig 3. The precision of contact predictions of trRosetta for the three datasets.

Fig 3

Open in a new tab

Results are shown for the three datasets, in blue the single unit dataset, in red the double units dataset, and in green complete region dataset.

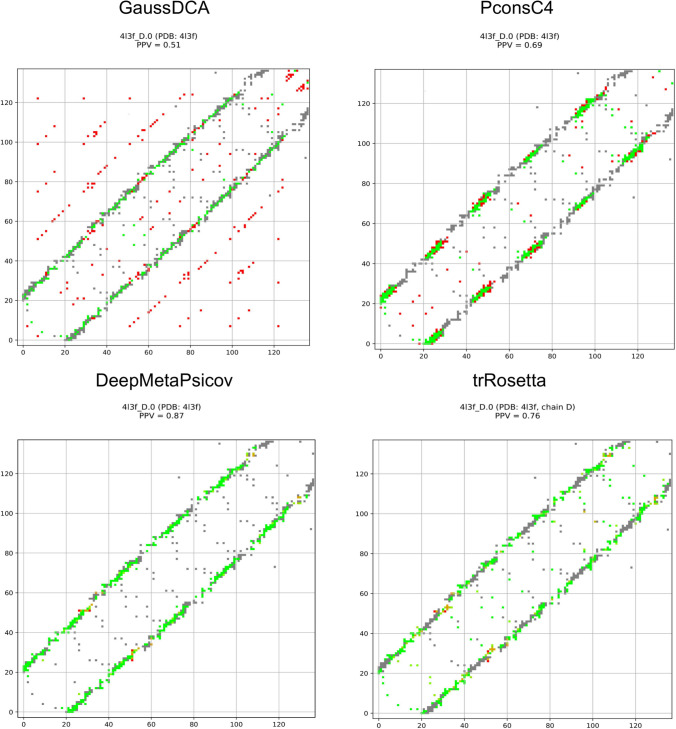
Here, it should be remembered that trRosetta, PconsC4 and DeepMetaPsicov, in addition to other information, use DCA predictions as an input and then learn to recognise specific patterns [18]. Therefore, artefacts present in the DCA predictions might propagate into these methods. In Fig 4, selected contact maps are shown as examples. The GaussDCA predictions contain periodic artefacts of wrong predictions (red dots) forming diagonal lines, occurring between equivalent positions in the repeat unit. PconsC4, DeepMetaPsicov, trRosetta appear efficient in removing the artefacts seen in GaussDCA. Here, it can be noted that there is only limited overlap between our repeat protein set and the training set of PconsC4 and DeepMetaPsicov, 25 out of 2856 and 29 out of 3456 proteins are identical respectively. Further, the accuracy for the shared proteins does not show a higher precision than the other proteins, S2 Fig. trRosetta instead has a much bigger training set of 15,051 proteins [19]. To our best knowledge, the IDs of the proteins are not available and in this case, we can not test the performance for the shared proteins. However, the high general consistency shown by trRosetta in our benchmark makes us confident that the results can be generalised, and that it is not strongly affected by a potential overlap with the training set.

Fig 4. GaussDCA, PconsC4, DeepMetaPsicov, and trRosetta contact maps.

Fig 4

Open in a new tab

Contact map for predictions obtained with GaussDCA, PconsC4, DeepMetaPsicov and trRosetta. In grey, the real contacts from the structure, in green, the corrected predicted contacts, and the falsely predicted contacts in red.

It is well known that the prediction quality is directly correlated with the number of sequences in the starting MSA for DCA methods [18]. Here, this trend is also observed, with trRosetta always showing the best performance Fig 5.

Fig 5. The relation between Precision and the effective number of sequences in the MSA.

Fig 5

Open in a new tab

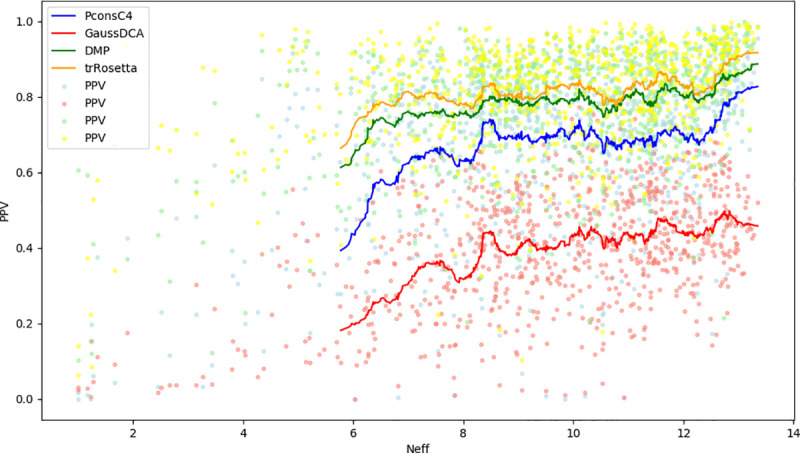
Positively Predicted Value for trRosetta in orange, GaussDCA in red, PconsC4 in Blue and DeepMetaPsicov in green on the Neff value (the effective number of sequences length weighted with the length of the protein). The single dots correspond to each protein in the datasets, and the line is the running average on (n = 50).

Differences among repeat classes in contacts prediction

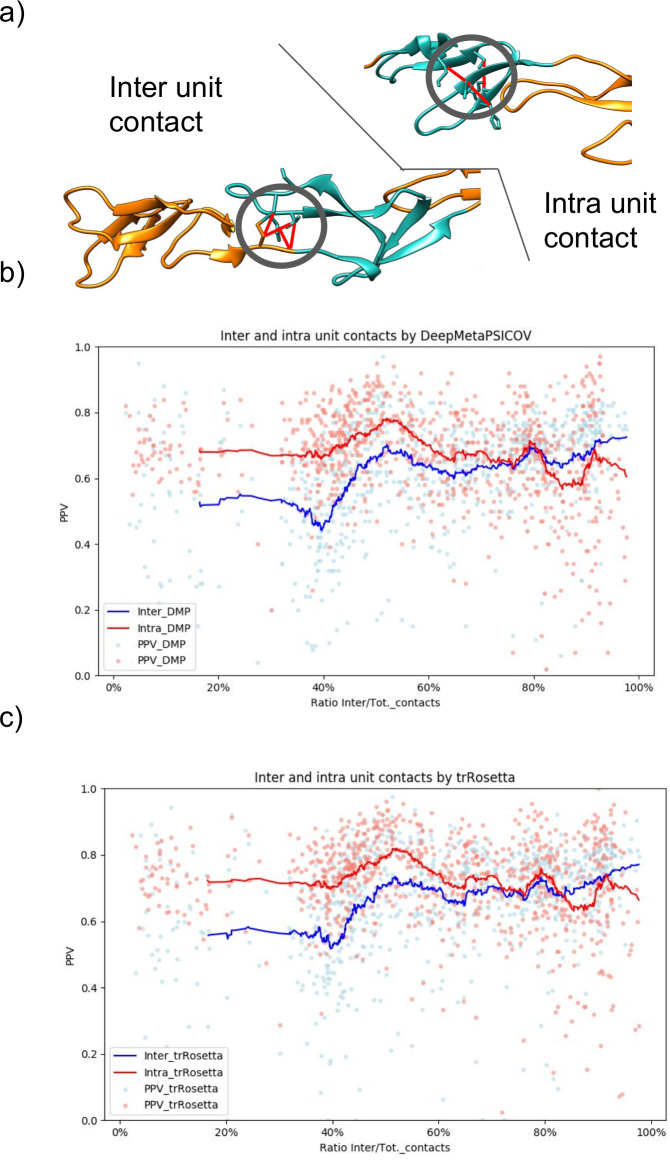
Fig 2 shows variations in the fraction of correctly predicted contacts among different protein repeat classes and subclasses in all the methods. To clarify the origin of these differences, we investigated, more in-depth, the source of the predicted contacts. One central aspect that affects the difficulty of prediction is the pattern of the contacts [24]. In general, contacts that are parts of larger interaction areas or close in the sequence are predicted more accurately. Therefore, we compared the intra-unit and inter-unit contacts predicted by DeepMetaPsicov and trRosetta, Fig 6. Here, we obtained the number of predicted intra and inter-unit contacts from the PDB structures and selected the same number of predicted intra- and inter-units contacts. The PPV was finally calculated using the number of correctly predicted contacts divided by the number of contacts.

Fig 6. Predicted contacts analysis.

Fig 6

Open in a new tab

a) Examples of inter- and intra- unit contacts. b) In red, the PPV for intra-units contacts in blue PPV for inter-units contacts predicted by DeepMetaPsicov. The lines are the respective running average of the PPV over the ratio of inter-unit contacts on the total of the protein contacts. c) In red, the PPV for intra-units contacts in blue PPV for inter-units contacts predicted by trRosetta. The lines are the respective running average of the PPV over the ratio of inter-unit contacts on the total of the protein contacts.

On average the intra-units contacts are predicted with higher accuracy than the inter-unit contacts in both DeepMetaPsicov and trRosetta, with trRosetta slightly over perform DeepMetaPsicov in both.

Protein model generation

For PconsC4 and DeepMetaPsicov, protein models were generated using CONFOLD [25] using the contact predictions from the respective method and combining it with secondary structure predictions from PSIPRED. For trRosetta instead, pyRosetta [26] was used for the protein model folding with the predicted distances and angles as input as described in Yang et al. [19]. Here, no secondary structure predictions were used.

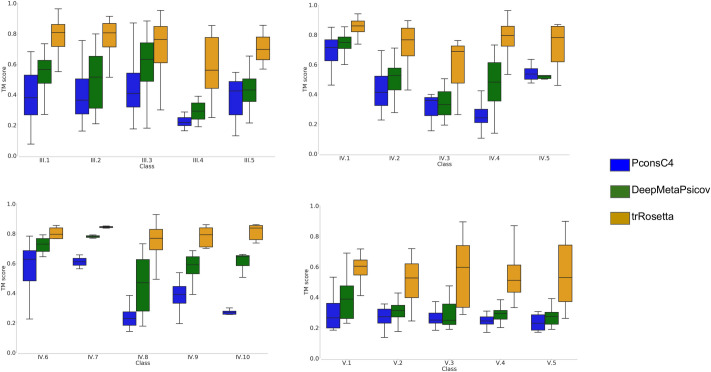
In Fig 7, we compare the TM-score between the models of the corresponding PDB protein structure. Here, the trRosetta pipeline outperforms the other two methods in all classes but has to be noted that the use of distances and angles instead of contacts is the main responsible for the difference in performance with DeepMetaPsicov that when compared on the contacts prediction precision show slightly inferior performance. In total with trRosetta 732 models out of 815 (89.8%) are predicted with at least a TM-score of 0.5.

Fig 7. Protein model quality.

Fig 7

Open in a new tab

TM-score for the subfamilies; Models from trRosetta in orange, PconsC4 in blue and DeepMetaPsicov in green.

Quality assessment of the models

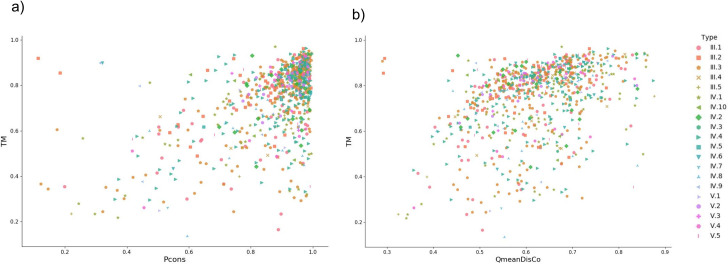
To evaluate the quality of the models obtained by trRosetta, we compare the TM-scores of the models with the quality assessment scores from Pcons [22] and QmeanDisCo [23]. Due to the general high quality of the models both the quality assessment methods fail to rank a significant number of models properly, Fig 8A and 8B.

Fig 8. TM-score versus QA methods.

Fig 8

Open in a new tab

a) TM-score versus Pcons-score for complete region models generated with trRosetta. b) TM-score versus QmeanDisCo score for full region models created from trRosetta contacts.

To improve the quality estimation, we developed a Random Forest Regression method using multiple inputs (Pcons, QmeanDisCo, protein length). Five-fold cross-validation was performed on the complete region dataset. The method obtained an average accuracy of 83.6%, and an average absolute error of 0.09 TM-score, see Fig 9A. The Random Forest Regression predicts the TM-score better than Pcons and QmeanDisCo alone, Fig 9B. We found that nine features were helpful for the prediction of the TM-score, S3 Fig. The most important features are the Pcons score, the local QmeanDisCo score, and protein length.

Fig 9.

Fig 9

Open in a new tab

a) Real TM-score versus Random Forest Predicted TM-score for complete region models generated with trRosetta. b) Pearson correlation coefficient between the TM-score and the QA methods.

Modelling of repeat protein families without known structures

We selected 48 PFAM repeat-families without resolved structure and fed them through the trRosetta structure prediction pipeline.

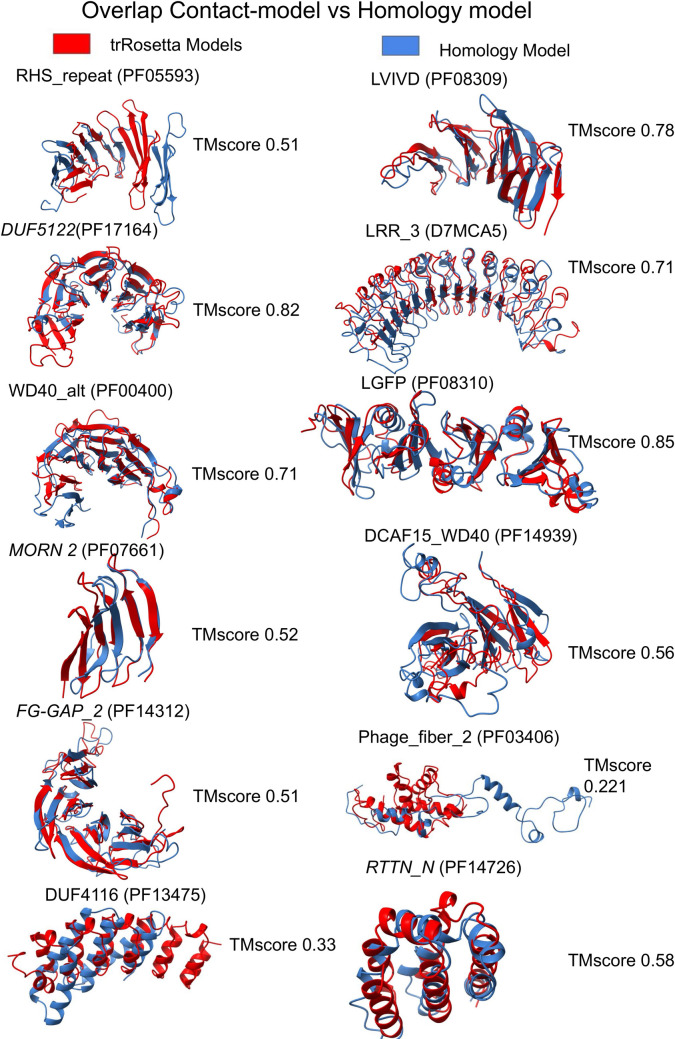
Among the models, 41 out of 48 (85%) are predicted with a TM-score higher than 0.5, Table 1. For twelve of these families, we could identify a template with a GMQE score [27] higher than 0.4 using Swissmodel [28]. In these cases, homology models were generated for comparison with the contact based models. We compared the similarity of the contact-based and homology-based models with the predicted TM-score for the contact-based model. For four families (LVIVD, LRR_3, WD40_alt, LGFP) the models obtained by homology agree with the predicted TM-score, the difference between the TM-scores is below 0.1, i.e. the estimated TM-score agrees with what would be estimated if the homology model was identical to an experimental structure. However, for the other six families, there is an overestimation of the quality (RHS_repeat, DCAF15_WD40, DUF4116, Phage_fiber_2, RTTN_N, MORN 2) and for other two an underestimation (DUF5122, FG-GAP_2), see Table 1.

Table 1. The models of the PFAM families with predicted TM-score.

In the columns: the family name, the PFAM ID, the Uniprot ID of the sequence used for the modelling, the predicted TM-score, the best template PDB ID, the Swismodel GMQE score, the identity between the target/template alignment, the TM-score between the contact-based model and the homology model.

PFAM family PFAM ID Representative protein Uniprot ID TM prediction Template PDB ID GMQE Identity TM-score between The contact model and Homology model
Nebulin PF00880 A0A094KVK3 0.483185 6b40_A 0.12 18.60% -
SWM_repeat PF13753 A0A0B0HSH2 0.45394 2ra1_A 0.21 20.72% -
Plasmod_MYXSPDY PF07981 A0A0L7M9B8 0.592519 - - - -
C_tripleX PF02363 A0A1A9WU23 0.440582 4xbm_A 0.28 29.08% -
RHS_repeat PF05593 A0A1G0MXS8 0.789065 6fay_A 0.7 28.10% 0.51
Plasmodium repeat MYXSPDY PF00839 A0A1I7SWM5 0.585336 0.02 9.09% -
LVIVD PF08309 A0A1V1NWB1 0.793165 4jsn_B 0.5 12.50% 0.78
DUF5122 PF17164 A0A1Z4C3E9 0.685674 2ymu_A 0.46 19.50% 0.82
Bacterial tandem repeat domain PF17660 A0A252E8A5 0.74885 4qp0_A 0.17 13.70% -
SprB PF13573 A0A257INW4 0.602068 2c26_A 0.31 16.36%
Lustrin_cystein PF14625 A0A2A2LSA2 0.521748 6nan_A 0.13 20.63% -
SPW PF03779 A0A2A3HD64 0.687938 - - - -
Chlorovi_GP_rpt PF06598 A7RAI0 0.627261 - - - -
CRAM_rpt PF07016 A7S4G3 0.667426 4aea9_A 0.39 17.65% -
Dicty_CTDC PF00526 D3BR65 0.566775 4u8u_N 0.17 19.23% -
RtxA PF07634 D3UXB8 0.744867 5vgz_A 0.03 20.51% -
YTV PF07639 D5SU36 0.591834 -
LRR_3 PF07725 D7MCA5 0.697779 2omx_A 0.59 18.97% 0.71
Ice_nucleation PF00818 F3GDU0 0.714233 - - - -
LSPR PF06049 G1RYA9 0.571161 - - - -
UCH-protein repeats PF13446 G1XIQ8 0.611722 2h5x_C 0.08 22.45% -
WD40_alt PF00400 G3VIY2 0.718139 5obm_A 0.59 22,78% 0.71
Lipoprotein_15 PF03640 I3BT02 0.449038 4yx7_A 0.02 16%
SSURE PF11966 J1S4N0 0.509385 - - - -
LGFP PF08310 L8TNF3 0.779499 6sx4_A 0.76 32.21% 0.85
zf-C2H2_3rep PF18868 O64827 0.588789 1z9v_A 0.04 12.12%
DCAF15_WD40 PF14939 Q29AL9 0.677563 6pai_B 0.67 29.69% 0.56
SVS_QK PF10578 Q6P6X2 0.605577 - - - -
DUF2963 PF11178 Q6YQH3 0.804535 5e9t_D 0.32 24.24%
Plasmo_rep PF12135 Q7RTC2 0.637834 4nee_C 0.07 23.08%
Curlin PF07012 Q8EIH3 0.669206 - - - -
MORN 2 PF07661 Q8RH85 0.71293 1h3i_A 0.68 27.87% 0.52
OGFr_III PF04680 Q9NZT2 0.679499 5xme_A 0.21 16.09%
HNH_repeat PF18780 R2SEH8 0.648563 2xsj_C 0.24 14.67%
ChW PF07538 R5P8A5 0.674395 - - - -
WG_beta_rep PF14903 R6YH89 0.681589 2ki4_A 0.06 7.41%
DUF4116 PF13475 R7MCC4 0.688163 5lu2_A 0.41 7.81% 0.33
PHINT_rpt PF14882 S6TLB9 0.460735 5lnk_Q 0.03 13.51%
Chlam_PMP PF02415 S7J9T7 0.674383 2m7o_A 0.13 25%
Xin PF08043 T0NQR8 0.680028 1ixv_A 0.1 8.33%
WXXGXW PF12779 U2FCE1 0.731013 - - - -
SBBP PF06739 U5QIU9 0.724106 6i3b_A 0.38 24.45%
Ish1 PF10281 U7Q0S5 0.433415 1jjr_A 0.1 15.73%
Phage_fiber_2 PF03406 V5CQL0 0.540125 5iv5_A 0.58 22.43% 0.21
FG-GAP_2 PF14312 W4LGN0 0.640251 5ffg_A 0.56 23.04% 0.82
CXCXC PF03128 W5N853 0.865153 1vgh_A 0.36 26.47%
RTTN_N PF14726 W5P499 0.6874 4plr_A 0.58 16.28% 0.58
WDCP PF15390 W5Q8K9 0.427924 5nnz_A 0.09 12.58%
Open in a new tab

Fig 10 shows the overlap between the contact and the homology models. Two trRosetta models differ significantly from the homology models: Phage_fiber_2 (PF03406) where the template as a partially disordered extended structure while the trRosetta model is packed and DUF4116 (PF13475) in which the trRosetta model is folded as an α-solenoid while the homology model in a longer helical bundle.

Fig 10. Comparison between the contact-based model and homology modelling.

Fig 10

Open in a new tab

The superposition between the contact-based model (red) and the homology model (blue) and respective TM-score.

Other 36 families do not have suitable templates, and, therefore, we cannot compare their trRosetta models with a homology-based model. However, the quality assessment shows high scores for the vast majority of the models.

Here we describe a few interesting models in more details, and all the models are available at https://figshare.com/articles/dataset/Repeats_Proteins_contact_prediction_based_modelling_datasets/9995618. We do encourage others to investigate the other models in details.

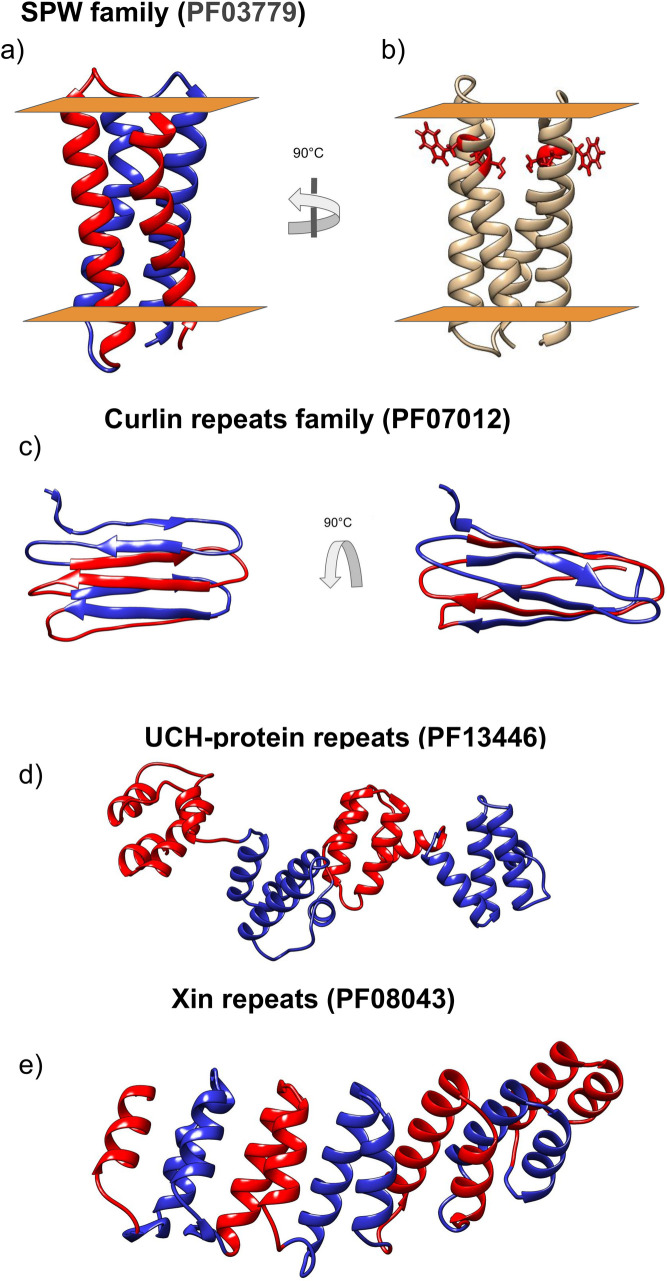
SPW family (PF03779)

According to the PFAM database [29], the SPW family is present in Bacteria and Archaea, and each protein consists of one or two repeat units. Some members also contain an additional domain, either a Vitamin K epoxide reductase (PF07884) or a NAD-dependent epimerase/dehydratase (PF01370). Each repeat unit is formed by two transmembrane alpha-helices and is characterised by an SPW motif [30]. According to our model, the repeated motif is buried in the membrane symmetrically located close to the extracellular side, Fig 11B. PFAM architectures show many proteins with only a single SPW motif however a more careful analysis of these sequences shows that in many cases they contain a second degenerate SPW unit with the proline residue conserved (S4 Fig).

Fig 11. Selected models.

Fig 11

Open in a new tab

The different protein units are coloured in red and blue. a) SPW, b) SPW in red the “SPW” motif c) Curlin d) UCH-protein are shown and e) Xin repeat.

The Tryptophan is on the outer side of the protein, facing the bilayer, while the proline is on the inner side of the protein, promoting the formation of a kink in the transmembrane helix [31]. The protein contains a ser-pro motif, rare among TM-proteins and most likely increases the bending effect of proline significantly due to their hydrogen bond pattern [32].

Curlin repeats family (PF07012)

Here, the trRosetta model has a higher predicted TM score (Table 1) and agrees better with information from the available literature [37]. Curlin is predicted to have a β-solenoid structure, see Fig 11C. DeBenedictis et al. presented ab-initio models for two members of the Curlin repeat family, CsgA and CsgB [37]. The structure of their best models is visually in agreement with our model (a direct comparison is difficult as the coordinates are not available for their models). Our model is also in agreement with the partial structure of the repeat units of CsgA published by Perov et al. [38]. This model contains two parallel β-sheets with individual units situated perpendicular to the fibril axis (corresponding PDB IDs are 6G8C, 6G8D, 6G8E).

UCH-protein (PF13446)

Our model (Fig 11D) suggests that this repeat region is a Class V.1 ɑ-beads, with four helical domains separated by a flexible linker.

UCH-protein repeats family is a repeat domain found in Ubiquitin carboxyl-terminal hydrolase. Despite UCH-proteins being widespread among eukaryotes, the repeated domain is present only in yeasts in a variable number of units. According to PFAM [29], the UCH-protein repeats could be involved in the formation of a complex of UCH with Rsp5 and Rup1.

Xin repeat (PF08043)

Xin repeats is a motif with a variable number of units, known for binding and stabilising F-actin [33]. In mouse and chicken is located in the adherens junction complex [33]. In humans Xin-repeat proteins are involved in the developmental and adaptive remodelling of the actin cytoskeleton [34] behaving as a scaffold protein showing multiple interacting partners: I) interact with the EVH1 domain of Mena/VASP/EVL [34]. II) Interact with the SH3 domain of Nebuline and Nebulette, despite the binding site is located in a disordered region [35] III) interact with Aciculin [36].

In our model Fig 11E, Xin-repeats result folded as an α-solenoid. This clarifies the fold of Xin-repeats proteins formed by an α-solenoid N-terminus and a long disordered C-terminal region.

Conclusion

Here, we performed a comprehensive coevolution analysis on repeat protein families, and we show that trRosetta contact-predictions method overcomes the traditional difficulties of previews Deep Learning and DCA methods for this class of proteins. We investigated the modelling of repeat units, and we developed a novel quality assessment method for repats proteins. Finally, we tested the pipeline on PFAM families without protein structures showing its usefulness in providing new structural information.

This paper summarises the extraordinary improvement of the structure prediction method in the past few years and shows that it is now possible to predict the structure of 85% of PFAM repeat families satisfactorily.

Materials and methods

Datasets generation

The repeat protein dataset was generated starting from the 3585 reviewed entries in RepeatsDB [14,39]. The proteins of class I and II were removed, and then the dataset was homology reduced using CD-HIT [40] at 40% identity resulting in 815 repeat regions. From this “complete region dataset” two other datasets were generated. First, a “single unit” dataset with one repeat unit from each family, and secondly a “double unit” dataset with two. In the two derived datasets, the representative units were selected, avoiding or at least minimising, the presence of insertions.

The non-resolved repeats protein family dataset was generated, collecting all the repeat proteins families with missing structural information present in PFAM [29] as of May 2019 and removing domains with a significant overlap with the disorder prediction. It results in 48 protein families. The representative sequence for each family of repeat was chosen for matching these criteria: 1) select the most common architecture; 2) Include when possible at least three repeat units.

Multiple sequence alignment (MSA)

The multiple sequence alignments (MSA) were carried out using HHblits [41] using an E-value cutoff of 0.001 against the Uniclust30_2017_04 database [42]. The number of effective sequences of the alignment, expressed as Neff-score, was calculated by HHblits and used for subsequent analysis. More detail about the Neff calculation can be found at https://github.com/soedinglab/hh-suite/wiki [41].

Contact prediction and models generation

For DeepMetaPsicov and PconsC4 the protein models were generated following the PconsFold2 protocol [43]. The secondary structure of the repeat regions was predicted by PSIpred [44]. Protein contacts were predicted using DeepMetaPsicov [45], or PconsC4 [18] and together with the secondary structure predictions used as input to Confold [25]. The modelling used the top scoring 1.5 L contacts (where L is the length of the modelled regions).

The Rosetta models were obtained running trRosetta locally [19] and use the predicted distances and angles as input for pyRosetta [26].

Contacts analysis

A protein contact was defined as two residues having a beta carbon distance equal to or lower than 8Å in the PDB structure and farther than five residues in the sequence. Using this definition, we assess the number of correctly predicted contacts the Positively Predicted Value (PPV) taking into account the top-scoring 1.5 L contacts.

Since trRosetta predicted distances instead of contacts between the residues we sum the probabilities for the distance bin equal or shorter than 8 Å as in Greener et al. [20] in order to compare them with the contacts predicted with the other methods.

In the intra/inter-unit contacts analysis, the predicted contacts of each protein were divided into i) intra-unit contacts, if between residues inside the same unit; ii) inter-units if the residues are in different repeat units. The units mapping was taken from the RepeatsDB database [14]. In this analysis, we calculate the number of intra- and inter-unit contacts in the PDB structure, and then we selected the same number of predicted intra- and inter-units contacts. The PPV was then calculated as the fraction of correct predictions.

Template search and homology modelling

The template search and the homology models were generated from the representative sequences using the default options from Swissmodel [28].

Protein models analysis

The model quality, expressed in TM-score, was assessed using a random forest regression model using the python module Sklearn. The random forest regression was optimized to include 240 estimators and a maximum depth of 60. The models from the trRosetta “complete region” benchmark set were used as a training set. The label of the training set was the TM-score of each model [46]. To ensure that the protein structure and the model were aligned correctly, the TMalign option -I was used, providing a local alignment of the two sequences.

For training, five cross-validation sets were generated. Several inputs were used for the random forest, described briefly below and in Table 1. The Confold and QmeanDisco inputs were obtained from analysing the first ranked model. Pcons was run using the option -d using all the models in the stage2 folder generated by Confold. Among the different sets of features tried, we select nine features that all improve the prediction of the random forest regression, see S3 Fig.

Supporting information

S1 Fig. The precision of contact predictions.

Positive Predictive Value (PPV) for the GaussDCA (red), Pconsc4 (Blue), and DeepMetaPsicov (green). For all three methods results are shown for the three datasets, in light colour the single unit dataset, in intermediate colour the double units dataset, and in the darker colour the complete region dataset.

(TIF)

Click here for additional data file. (214.3KB, tif)
S2 Fig. Performance expressed in PPV for the set of proteins contained in the training set of the contact predictions methods.

In light green, the Deep Meta Psicov (DMP) average precision for the proteins of the benchmark set not overlapping with the DMP training set, in dark green the DMP average precision for the proteins benchmark set present in the DMP training set, in light blue the PconsC4 average precision for the proteins of the benchmark set not overlapping with the PconsC4 training set, in dark blue the PconsC4 average precision for the proteins benchmark set present as well in the PconsC4 training set.

(TIF)

Click here for additional data file. (44.6KB, tif)
S3 Fig. Random Forest model features importance.

The features used in the random forest model are listed according to their relative importance.

(TIF)

Click here for additional data file. (154.7KB, tif)
S4 Fig. Amino Acid frequency of the single domain architecture sequences.

From the logo is possible to recognize two SPW domains, one of them degenerated (in particular the first Serine in the second motif) that is not recognized by PFAM.

(TIFF)

Click here for additional data file. (154.7KB, tiff)

Data Availability

All the protein models, contact prediction, and Multiple Sequence alignments are available at https://figshare.com/articles/dataset/Repeats_Proteins_contact_prediction_based_modelling_datasets/9995618.

Funding Statement

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 823886. AE is funded by grants from the Swedish Natural Science Research Council (Vetenskapsrådet) No VR-NT 2016-03798. SNIC provided computational resources under grant agreement No SNIC 2020/5-300. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

  • 1.Heringa J. Detection of internal repeats: how common are they? Curr Opin Struct Biol. 1998;8: 338–345. 10.1016/s0959-440x(98)80068-7 [DOI] [PubMed] [Google Scholar]
  • 2.Strand M, Prolla TA, Liskay RM, Petes TD. Destabilization of tracts of simple repetitive DNA in yeast by mutations affecting DNA mismatch repair. Nature. 1993;365: 274–276. 10.1038/365274a0 [DOI] [PubMed] [Google Scholar]
  • 3.Pâques F, Leung W-Y, Haber JE. Expansions and Contractions in a Tandem Repeat Induced by Double-Strand Break Repair. Molecular and Cellular Biology. 1998. pp. 2045–2054. 10.1128/mcb.18.4.2045 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Schaper E, Gascuel O, Anisimova M. Deep conservation of human protein tandem repeats within the eukaryotes. Mol Biol Evol. 2014;31: 1132–1148. 10.1093/molbev/msu062 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Marcotte E.M., Pellegrini M., Yeates T.O., Eisenberg D. A census of protein repeats. J Mol Biol. 1999;293: 151–160. 10.1006/jmbi.1999.3136 [DOI] [PubMed] [Google Scholar]
  • 6.Björklund AK, Ekman D, Elofsson A. Expansion of protein domain repeats. PLoS Comput Biol. 2006;2: e114. 10.1371/journal.pcbi.0020114 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Andrade MA, Perez-Iratxeta C, Ponting CP. Protein Repeats: Structures, Functions, and Evolution. Journal of Structural Biology. 2001. pp. 117–131. 10.1006/jsbi.2001.4392 [DOI] [PubMed] [Google Scholar]
  • 8.Stirnimann CU, Petsalaki E, Russell RB, Müller CW. WD40 proteins propel cellular networks. Trends Biochem Sci. 2010;35: 565–574. 10.1016/j.tibs.2010.04.003 [DOI] [PubMed] [Google Scholar]
  • 9.Li J, Mahajan A, Tsai M-D. Ankyrin repeat: a unique motif mediating protein-protein interactions. Biochemistry. 2006;45: 15168–15178. 10.1021/bi062188q [DOI] [PubMed] [Google Scholar]
  • 10.Mosavi LK, Cammett TJ, Desrosiers DC, Peng Z-Y. The ankyrin repeat as molecular architecture for protein recognition. Protein Sci. 2004;13: 1435–1448. 10.1110/ps.03554604 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Persi E, Wolf YI, Koonin EV. Positive and strongly relaxed purifying selection drive the evolution of repeats in proteins. Nat Commun. 2016;7: 13570. 10.1038/ncomms13570 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Kajava AV. Review: Proteins with Repeated Sequence—Structural Prediction and Modeling. Journal of Structural Biology. 2001. pp. 132–144. 10.1006/jsbi.2000.4328 [DOI] [PubMed] [Google Scholar]
  • 13.Kajava AV. Tandem repeats in proteins: From sequence to structure. Journal of Structural Biology. 2012. pp. 279–288. 10.1016/j.jsb.2011.08.009 [DOI] [PubMed] [Google Scholar]
  • 14.Paladin L, Hirsh L, Piovesan D, Andrade-Navarro MA, Kajava AV, Tosatto SCE. RepeatsDB 2.0: improved annotation, classification, search and visualization of repeat protein structures. Nucleic Acids Res. 2017;45: 3613. 10.1093/nar/gkw1268 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Abriata LA, Tamò GE, Monastyrskyy B, Kryshtafovych A, Dal Peraro M. Assessment of hard target modeling in CASP12 reveals an emerging role of alignment-based contact prediction methods. Proteins. 2018;86 Suppl 1: 97–112. 10.1002/prot.25423 [DOI] [PubMed] [Google Scholar]
  • 16.Pazos F, Helmer-Citterich M, Ausiello G, Valencia A. Correlated mutations contain information about protein-protein interaction. J Mol Biol. 1997;271: 511–523. 10.1006/jmbi.1997.1198 [DOI] [PubMed] [Google Scholar]
  • 17.Espada R, Parra RG, Mora T, Walczak AM, Ferreiro DU. Capturing coevolutionary signals inrepeat proteins. BMC Bioinformatics. 2015;16: 207. 10.1186/s12859-015-0648-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Michel M, Hurtado DM, Elofsson A. PconsC4: fast, accurate, and hassle-free contact predictions. Bioinformatics. 2018. 10.1093/bioinformatics/bty1036 [DOI] [PubMed] [Google Scholar]
  • 19.Yang J, Anishchenko I, Park H, Peng Z, Ovchinnikov S, Baker D. Improved protein structure prediction using predicted interresidue orientations. Proc Natl Acad Sci U S A. 2020;117: 1496–1503. 10.1073/pnas.1914677117 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Greener JG, Kandathil SM, Jones DT. Deep learning extends de novo protein modelling coverage of genomes using iteratively predicted structural constraints. Nat Commun. 2019;10: 3977. 10.1038/s41467-019-11994-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Baldassi C, Zamparo M, Feinauer C, Procaccini A, Zecchina R, Weigt M, et al. Fast and accurate multivariate Gaussian modeling of protein families: predicting residue contacts and protein-interaction partners. PLoS One. 2014;9: e92721. 10.1371/journal.pone.0092721 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Lundström J, Rychlewski L, Bujnicki J, Elofsson A. Pcons: a neural-network-based consensus predictor that improves fold recognition. Protein Sci. 2001;10: 2354–2362. 10.1110/ps.08501 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Studer G, Rempfer C, Waterhouse AM, Gumienny R, Haas J, Schwede T. QMEANDisCo-distance constraints applied on model quality estimation. Bioinformatics. 2020;36: 2647. 10.1093/bioinformatics/btaa058 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Skwark MJ, Raimondi D, Michel M, Elofsson A. Improved contact predictions using the recognition of protein like contact patterns. PLoS Comput Biol. 2014;10: e1003889. 10.1371/journal.pcbi.1003889 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Adhikari B, Bhattacharya D, Cao R, Cheng J. CONFOLD: Residue-residue contact-guided ab initio protein folding. Proteins. 2015;83: 1436–1449. 10.1002/prot.24829 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Chaudhury S, Lyskov S, Gray JJ. PyRosetta: a script-based interface for implementing molecular modeling algorithms using Rosetta. Bioinformatics. 2010;26: 689–691. 10.1093/bioinformatics/btq007 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Biasini M, Bienert S, Waterhouse A, Arnold K, Studer G, Schmidt T, et al. SWISS-MODEL: modelling protein tertiary and quaternary structure using evolutionary information. Nucleic Acids Res. 2014;42: W252–8. 10.1093/nar/gku340 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Waterhouse A, Bertoni M, Bienert S, Studer G, Tauriello G, Gumienny R, et al. SWISS-MODEL: homology modelling of protein structures and complexes. Nucleic Acids Res. 2018;46: W296–W303. 10.1093/nar/gky427 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.El-Gebali S, Mistry J, Bateman A, Eddy SR, Luciani A, Potter SC, et al. The Pfam protein families database in 2019. Nucleic Acids Res. 2019;47: D427–D432. 10.1093/nar/gky995 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Yeats C, Bentley S, Bateman A. New knowledge from old: in silico discovery of novel protein domains in Streptomyces coelicolor. BMC Microbiol. 2003;3: 3. 10.1186/1471-2180-3-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.von Heijne G. Proline kinks in transmembrane alpha-helices. J Mol Biol. 1991;218: 499–503. 10.1016/0022-2836(91)90695-3 [DOI] [PubMed] [Google Scholar]
  • 32.Deupi X, Olivella M, Govaerts C, Ballesteros JA, Campillo M, Pardo L. Ser and Thr Residues Modulate the Conformation of Pro-Kinked Transmembrane α-Helices. Biophysical Journal. 2004. pp. 105–115. 10.1016/S0006-3495(04)74088-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Sinn HW, Balsamo J, Lilien J, Lin JJ-C. Localization of the novel Xin protein to the adherens junction complex in cardiac and skeletal muscle during development. Dev Dyn. 2002;225: 1–13. 10.1002/dvdy.10131 [DOI] [PubMed] [Google Scholar]
  • 34.van der Ven PFM, Ehler E, Vakeel P, Eulitz S, Schenk JA, Milting H, et al. Unusual splicing events result in distinct Xin isoforms that associate differentially with filamin c and Mena/VASP. Exp Cell Res. 2006;312: 2154–2167. 10.1016/j.yexcr.2006.03.015 [DOI] [PubMed] [Google Scholar]
  • 35.Eulitz S, Sauer F, Pelissier M-C, Boisguerin P, Molt S, Schuld J, et al. Identification of Xin-repeat proteins as novel ligands of the SH3 domains of nebulin and nebulette and analysis of their interaction during myofibril formation and remodeling. Mol Biol Cell. 2013;24: 3215–3226. 10.1091/mbc.E13-04-0202 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Molt S, Bührdel JB, Yakovlev S, Schein P, Orfanos Z, Kirfel G, et al. Aciculin interacts with filamin C and Xin and is essential for myofibril assembly, remodeling and maintenance. J Cell Sci. 2014;127: 3578–3592. 10.1242/jcs.152157 [DOI] [PubMed] [Google Scholar]
  • 37.DeBenedictis EP, Ma D, Keten S. Structural predictions for curli amyloid fibril subunits CsgA and CsgB. RSC Adv. 2017;7: 48102–48112. [Google Scholar]
  • 38.Perov S, Lidor O, Salinas N, Golan N, Tayeb-Fligelman E, Deshmukh M, et al. Structural Insights into Curli CsgA Cross-β Fibril Architecture Inspired Repurposing of Anti-amyloid Compounds as Anti-biofilm Agents. 10.1101/493668 [DOI] [PMC free article] [PubMed]
  • 39.Hirsh L, Paladin L, Piovesan D, Tosatto SCE. RepeatsDB-lite: a web server for unit annotation of tandem repeat proteins. Nucleic Acids Res. 2018;46: W402–W407. 10.1093/nar/gky360 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Li W, Godzik A. Cd-hit: a fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics. 2006. pp. 1658–1659. 10.1093/bioinformatics/btl158 [DOI] [PubMed] [Google Scholar]
  • 41.Remmert M, Biegert A, Hauser A, Söding J. HHblits: lightning-fast iterative protein sequence searching by HMM-HMM alignment. Nature Methods. 2012. pp. 173–175. 10.1038/nmeth.1818 [DOI] [PubMed] [Google Scholar]
  • 42.Mirdita M, von den Driesch L, Galiez C, Martin MJ, Söding J, Steinegger M. Uniclust databases of clustered and deeply annotated protein sequences and alignments. Nucleic Acids Res. 2017;45: D170–D176. 10.1093/nar/gkw1081 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Bassot C, Menendez Hurtado D, Elofsson A. Using PconsC4 and PconsFold2 to Predict Protein Structure. Curr Protoc Bioinformatics. 2019; e75. 10.1002/cpbi.75 [DOI] [PubMed] [Google Scholar]
  • 44.McGuffin LJ, Bryson K, Jones DT. The PSIPRED protein structure prediction server. Bioinformatics. 2000. pp. 404–405. 10.1093/bioinformatics/16.4.404 [DOI] [PubMed] [Google Scholar]
  • 45.Kandathil SM, Greener JG, Jones DT. Prediction of interresidue contacts with DeepMetaPSICOV in CASP13. Proteins. 2019;87: 1092–1099. 10.1002/prot.25779 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Zhang Y, Skolnick J. TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res. 2005;33: 2302–2309. 10.1093/nar/gki524 [DOI] [PMC free article] [PubMed] [Google Scholar]
PLoS Comput Biol. doi: 10.1371/journal.pcbi.1008798.r002

Decision Letter 0

Nir Ben-Tal, Johannes Soeding

7 Oct 2020

Dear Arne,

Thank you very much for submitting your manuscript "Accurate contact-based modelling of repeat proteins predicts the structure of new repeats protein families." for consideration at PLOS Computational Biology.

As with all papers reviewed by the journal, your manuscript was reviewed by members of the editorial board and by several independent reviewers. In light of the reviews (below this email), we would like to invite the resubmission of a significantly-revised version that takes into account the reviewers' comments.

Two reviewers felt that the manuscript did not contain the amount of new methodological innovation expected of a PLoS Computational Biology article. Reviewer 2 suggested to include distances predicted by RaptorX-Contact to the evaluation. As such, the paper would earn its merits more as a benchmarking study, which seems to make sense, given that you have already included constraints from two different contact prediction methods. (If there are additional distance/contact predictors that can be included, it makes sense to include these too.) If you can add this analysis, we would be interested to receive a revision. We are sorry to not be able to be more positive at this point. 

We cannot make any decision about publication until we have seen the revised manuscript and your response to the reviewers' comments. Your revised manuscript is also likely to be sent to reviewers for further evaluation.

When you are ready to resubmit, please upload the following:

[1] A letter containing a detailed list of your responses to the review comments and a description of the changes you have made in the manuscript. Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.

[2] Two versions of the revised manuscript: one with either highlights or tracked changes denoting where the text has been changed; the other a clean version (uploaded as the manuscript file).

Important additional instructions are given below your reviewer comments.

Please prepare and submit your revised manuscript within 60 days. If you anticipate any delay, please let us know the expected resubmission date by replying to this email. Please note that revised manuscripts received after the 60-day due date may require evaluation and peer review similar to newly submitted manuscripts.

Thank you again for your submission. We hope that our editorial process has been constructive so far, and we welcome your feedback at any time. Please don't hesitate to contact us if you have any questions or comments.

Sincerely,

Johannes Soeding, Ph.D.

Guest Editor

PLOS Computational Biology

Nir Ben-Tal

Deputy Editor

PLOS Computational Biology

***********************

Reviewer's Responses to Questions

Comments to the Authors:

Please note here if the review is uploaded as an attachment.

Reviewer #1: The paper deals with an interesting and novel aspect of protein feature predictions. The authors took into considerations all the major criticisms raised by reviewers and edited the paper accordingly. The problem of redundancy is now correctly described.

Reviewer #2: The authors did some modifications of the manuscript by testing the contacts predicted by DeepMetaPSICOV and developing a random forest regression method to predict the quality of a 3D model. However, the authors did not test folding of distance (and orientation information used by trRosetta). It is unclear why the authors did not test the distance (and orientation) information predicted by RaptorX-Contact simply because it is a web server. In fact, it is much more convenient to use a web server than a standalone software package. A hassle-free strategy is to submit the test proteins to the RaptorX-Contact web server and then evaluate the contact/distance prediction and 3D models returned by the server. Overall, this manuscript represents a simple application of existing (but not very cutting-edge) techniques to an interesting problem. As a proof of concept, it may be sufficient, but it may not represent what we can do on the modeling of repeat proteins using existing techniques and tools.

Reviewer #3: I find that the paper does not features works of 'exceptional significance', but a specific evaluation of distinct methods to asses a specific technical question. The exceptional significance would be if the paper fully describe and asses novel structures for repeat proteins based on these findings, but I that this is lacking in the manuscript.

**********

Have all data underlying the figures and results presented in the manuscript been provided?

Large-scale datasets should be made available via a public repository as described in the PLOS Computational Biology data availability policy, and numerical data that underlies graphs or summary statistics should be provided in spreadsheet form as supporting information.

Reviewer #1: Yes

Reviewer #2: None

Reviewer #3: None

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: No

Figure Files:

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at figures@plos.org.

Data Requirements:

Please note that, as a condition of publication, PLOS' data policy requires that you make available all data used to draw the conclusions outlined in your manuscript. Data must be deposited in an appropriate repository, included within the body of the manuscript, or uploaded as supporting information. This includes all numerical values that were used to generate graphs, histograms etc.. For an example in PLOS Biology see here: http://www.plosbiology.org/article/info%3Adoi%2F10.1371%2Fjournal.pbio.1001908#s5.

Reproducibility:

To enhance the reproducibility of your results, PLOS recommends that you deposit laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. For instructions, please see http://journals.plos.org/compbiol/s/submission-guidelines#loc-materials-and-methods

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1008798.r004

Decision Letter 1

Nir Ben-Tal, Johannes Soeding

15 Feb 2021

Dear Arne,

We are pleased to inform you that your manuscript 'Accurate contact-based modelling of repeat proteins predicts the structure of new repeats protein families.' has been provisionally accepted for publication in PLOS Computational Biology.

Before your manuscript can be formally accepted you will need to complete some formatting changes, which you will receive in a follow up email. A member of our team will be in touch with a set of requests.

Please note that your manuscript will not be scheduled for publication until you have made the required changes, so a swift response is appreciated.

IMPORTANT: The editorial review process is now complete. PLOS will only permit corrections to spelling, formatting or significant scientific errors from this point onwards. Requests for major changes, or any which affect the scientific understanding of your work, will cause delays to the publication date of your manuscript.

Should you, your institution's press office or the journal office choose to press release your paper, you will automatically be opted out of early publication. We ask that you notify us now if you or your institution is planning to press release the article. All press must be co-ordinated with PLOS.

Thank you again for supporting Open Access publishing; we are looking forward to publishing your work in PLOS Computational Biology. 

Best regards,

Johannes Soeding, Ph.D.

Guest Editor

PLOS Computational Biology

Nir Ben-Tal

Deputy Editor

PLOS Computational Biology

***********************************************************

Reviewer's Responses to Questions

Comments to the Authors:

Please note here if the review is uploaded as an attachment.

Reviewer #2: The authors have applied trRosetta to their proteins and improved the results, and I think now the work is ready for publication.

By the way, in CASP14 Baker's trRosetta worked better than RaptorX mainly because the former used very large metagenome databases to generate MSAs while the latter does not, which is very important in CASP14 since it has quite a few test targets (from the same complex) that need metagenome data. Nevertheless the authors do not seem to use any metagenome data in this manuscript. The whole RaptorX package is also publicly available at https://github.com/j3xugit/RaptorX-3DModeling for local installation.

Reviewer #3: ok

**********

Have all data underlying the figures and results presented in the manuscript been provided?

Large-scale datasets should be made available via a public repository as described in the PLOS Computational Biology data availability policy, and numerical data that underlies graphs or summary statistics should be provided in spreadsheet form as supporting information.

Reviewer #2: None

Reviewer #3: Yes

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #2: No

Reviewer #3: No

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1008798.r005

Acceptance letter

Nir Ben-Tal, Johannes Soeding

31 Mar 2021

PCOMPBIOL-D-20-01386R1

Accurate contact-based modelling of repeat proteins predicts the structure of new repeats protein families.

Dear Dr Elofsson,

I am pleased to inform you that your manuscript has been formally accepted for publication in PLOS Computational Biology. Your manuscript is now with our production department and you will be notified of the publication date in due course.

The corresponding author will soon be receiving a typeset proof for review, to ensure errors have not been introduced during production. Please review the PDF proof of your manuscript carefully, as this is the last chance to correct any errors. Please note that major changes, or those which affect the scientific understanding of the work, will likely cause delays to the publication date of your manuscript.

Soon after your final files are uploaded, unless you have opted out, the early version of your manuscript will be published online. The date of the early version will be your article's publication date. The final article will be published to the same URL, and all versions of the paper will be accessible to readers.

Thank you again for supporting PLOS Computational Biology and open-access publishing. We are looking forward to publishing your work!

With kind regards,

Katalin Szabo

PLOS Computational Biology | Carlyle House, Carlyle Road, Cambridge CB4 3DN | United Kingdom ploscompbiol@plos.org | Phone +44 (0) 1223-442824 | ploscompbiol.org | @PLOSCompBiol

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Supplementary Materials

    S1 Fig. The precision of contact predictions.

    Positive Predictive Value (PPV) for the GaussDCA (red), Pconsc4 (Blue), and DeepMetaPsicov (green). For all three methods results are shown for the three datasets, in light colour the single unit dataset, in intermediate colour the double units dataset, and in the darker colour the complete region dataset.

    (TIF)

    Click here for additional data file. (214.3KB, tif)
    S2 Fig. Performance expressed in PPV for the set of proteins contained in the training set of the contact predictions methods.

    In light green, the Deep Meta Psicov (DMP) average precision for the proteins of the benchmark set not overlapping with the DMP training set, in dark green the DMP average precision for the proteins benchmark set present in the DMP training set, in light blue the PconsC4 average precision for the proteins of the benchmark set not overlapping with the PconsC4 training set, in dark blue the PconsC4 average precision for the proteins benchmark set present as well in the PconsC4 training set.

    (TIF)

    Click here for additional data file. (44.6KB, tif)
    S3 Fig. Random Forest model features importance.

    The features used in the random forest model are listed according to their relative importance.

    (TIF)

    Click here for additional data file. (154.7KB, tif)
    S4 Fig. Amino Acid frequency of the single domain architecture sequences.

    From the logo is possible to recognize two SPW domains, one of them degenerated (in particular the first Serine in the second motif) that is not recognized by PFAM.

    (TIFF)

    Click here for additional data file. (154.7KB, tiff)
    Attachment

    Submitted filename: Cover-Letter.docx

    Click here for additional data file. (13KB, docx)
    Attachment

    Submitted filename: Answer to the editor.docx

    Click here for additional data file. (7.8KB, docx)

    Data Availability Statement

    All the protein models, contact prediction, and Multiple Sequence alignments are available at https://figshare.com/articles/dataset/Repeats_Proteins_contact_prediction_based_modelling_datasets/9995618.

    Articles from PLoS Computational Biology are provided here courtesy of PLOS

    RESOURCES