A Comparison of Dyadic and Social Network Assessments of Peer Influence

Abstract

The present study compares two methods for assessing peer influence: the longitudinal Actor-Partner-Interdependence-Model (L-APIM) and the longitudinal Social Network Analysis Model (L-SNA). The data were drawn from 1,995 (49% girls; 51 % boys) 3^rd grade students (M_age=9.68 years). From this sample, L-APIM (n = 206 indistinguishable dyads; n = 187 distinguishable dyads) and L-SNA (n = 1,024 total network members) subsamples were created. Students completed peer nominations and objective assessments of mathematical reasoning in the spring of the 3^rd and 4^th grades. Patterns of statistical significance differed across analyses. Stable distinguishable and indistinguishable L-APIM dyadic analyses identified reciprocated friend influence such that friends with similar levels of mathematical reasoning influenced one another and friends with higher math reasoning influenced friends with lower math reasoning. L-SNA models with an influence parameter (i.e., average reciprocated alter) comparable to that assessed in L-APIM analyses failed to detect influence effects. Influence effects did emerge, however, with the addition of another, different social network influence parameter (i.e., average alter influence effect). The diverging results may be attributed to differences in the sensitivity of the analyses, their ability to account for structural confounds with selection and influence, the samples included in the analyses, and the relative strength of influence in reciprocated best as opposed to other friendships.

Peers influence many developmental outcomes. Peer influence is defined as the process whereby peer interactions -- with friends and with affiliates in the context of social networks -- shape subsequent individual behavior and adjustment (Laursen, 2018). Heightened similarity typically follows from peer influence, as participants change behaviors or attitudes to resemble one another. Capturing and measuring peer influence has been notoriously difficult, in part because of statistical challenges inherent in the analysis of nonindependent relationship data, and in part because influence occurs both within dyads and within groups. The present study is designed to contrast two approaches to the measurement of peer influence: longitudinal actor partner interdependence models (L-APIM), which use reciprocated liked-most (or friendship) nominations, and longitudinal social network analyses (L-SNA), which use liked-most nomination data from all members in a social network. To this end, we examine peer influence over mathematical reasoning in a sample of Finnish primary school students.

Understanding the Methodological Challenge

Conceptual and operational challenges confront those who would measure peer influence. Conceptually, concerns about where influence lies pose important challenges for those who would partition influence arising in relationships (e.g., friends) from influence arising in networks and groups (e.g., classrooms). Of course, the two are not independent; most friendships are nested in peer networks. Because children make friends and join groups on the basis of pre-existing similarities, resemblance alone is not a measure of influence. Instead, influence is usually measured in terms of behavioral change (Kandel, 1978).

Two designs dominate research that gauge influence in terms of behavioral change. The longitudinal Actor-Partner Interdependence Model (L-APIM) captures influence within dyads. L-APIM is a modification of a regression-based approach typically estimated in structural equation modeling (SEM) or a multilevel modeling (MLM) framework. The regression equation is represented as:

$$\mathrm{y}=\mathrm{\alpha }+\mathrm{\beta }\mathrm{X}+\mathrm{ϵ},$$

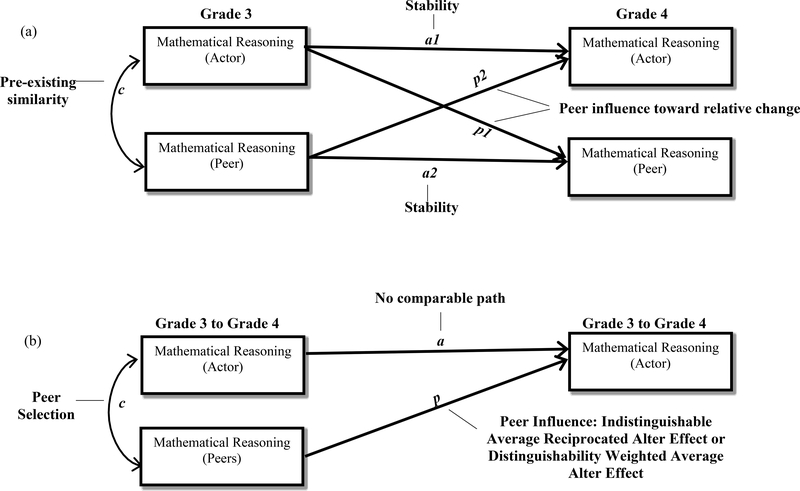
where y is the dependent variable, X is the independent variable, β is the slope of the line and α is the y -intercept). The original Actor-Partner Interdependence Model (APIM) (Kenny, Kashy, & Cook, 2006), separates variance shared by partners on the same variable from variance that uniquely describes concurrent within- and between partner associations between variables. Modifications for longitudinal data capture over time influence between partners. A longitudinal APIM is akin to a residual change model in that autoregressive effects serve as an index of stability (Popp, Laursen, Kerr, Stattin, & Burk, 2008). By accounting for the stability (see path a1 and a2 in Figure 1a) and for pre-existing similarities (see path c in Figure 1a), residual change can be predicted (see path p1 and p2 in Figure 1a). In the present study, longitudinal APIM analyses were used to determine the extent to which one reciprocated friend’s math achievement predicts changes in the other reciprocated friend’s math achievement, accounting for individual stability of math achievement and for initial similarity in reciprocated friend math achievement scores.

Figure 1.

Model specification of peer influence in (a) L-APIM for existing friendships only, statically modeled between Grade 3 and Grade 4; (b) L-SNA for pre-existing and new friendships, dynamically modeled across Grade 3 and Grade 4.

Note. Models are for illustrative purposes only. The SEM-style figure is for illustration only.

Two forms of longitudinal APIM analyses are possible. Distinguishable dyad L-APIM analyses start from the premise that partner influence is not equally distributed within a dyad, that influence systematically varies between reciprocated friends who differ on an attribute that is salient to members of the dyad. In these analyses, partners are categorized into roles to determine the unique influence of partner A (e.g., higher math achieving) on changes in the behavior of partner B (e.g., lower math achieving) and the unique influence of partner B on changes in the behavior of partner A. Indistinguishable dyad L-APIM analyses assume that partners do not differ in terms of their influence. In indistinguishable dyad analyses, partners are randomly assigned to roles (A or B) and influence is fixed to be equal across partners. L-APIM analyses typically involve reciprocated recognized relationships (i.e., both partners acknowledge the existence of the relationship) that are stable across assessment periods. Influence is measured across two time points; ideally, the first is near to the onset of the relationship when change is most likely to occur. The analyses remove pre-existing similarities from estimates of influence, but do not estimate similarity prior to the onset of the relationship. Instead, to measure selection similarity, it is possible to use intraclass correlations, measured before and after the relationship begins.

The Longitudinal Social Network Analysis (L-SNA) model is an agent-based model that uses a Markov Chain simulation process to assess peer influence (Steglich, Snijders, & Pearson, 2010). The evaluation function of an L-SNA model uses the formula:

$$f^{\mathrm{net}}(x)=\sum _k{\beta }_k^{\text{net}}{s}_{ik}^{\text{net}}(x),$$

where the first part of the equation represents the parameter and the second indicates user defined effects (see the SIENA Manual section 5.7 for additional details. The L-SNA model accounts for the influence of a peer’s behavior on a partner’s behavior, independent of (a) the linear trends of that same behavior in the peer group over time (a linear tendency effect) and (b) peer selection effects. Selection is measured by assessing the tendency for a relationship (defined as an outgoing like-most or friend nomination) to form across two time periods (e.g., no outgoing nomination from A to B in grade 3 followed by a nomination in grade 4). L-SNA models typically include all members of a defined social network (e.g., classroom or school) to capture change among members who did and did not identify one another as liked peers. The strength of individual influence across various members of the social network can be estimated with interaction terms in which the influence effect is crossed with an individual attribute (e.g., average alter influence on math achievement X relatively low/relatively high math achievement). To measure influence in reciprocated friendships, analyses must include an interaction term that specifies nominations that are returned (e.g., average alter influence on math achievement X reciprocity).

In the present study, we constructed L-SNA models in a manner designed to resemble L-APIM estimation strategies. Thus, L-SNA analyses include the average reciprocated alter parameter (akin to the use of indistinguishable dyads in L-APIM) to assess the overall impact of reciprocated peers in the social network. L-SNA analyses also include the average alter parameter weighted by distinguishable, reciprocated, and stable peer relationships status (akin to the use of distinguishable dyads in L-APIM). Distinguishable dyad weighting within L-SNA is not straightforward. We assessed the influence experienced by relatively higher achieving liked peers and relatively lower achieving liked peers using two 2-way interaction terms within a single L-SNA model. The first interaction effect coded for the influence of the relatively higher achieving liked peer (a code of 1) as compared to relatively lower achieving liked peer (a code of 0). The second interaction effect coded for the influence of the relatively lower achieving liked peer (a code of 1) as compared to relatively higher achieving liked peers (a code of 0). Each weighted covariate effect was crossed with the average alter influence effect to create an interaction term (e.g., average alter influence on math achievement X relatively low (or relatively high) dyadic math achievement). See Appendix 1 for the syntax.

We recognize that the two strategies do not yield equivalent output. L-APIM analyses (see Figure 1) address two kinds of influence: between-person (paths p1 and p2) and within-person (paths a1 and a2). In indistinguishable dyads analyses, influence effects are fixed to be equal across partners. In distinguishable dyad L-APIM analyses, it is possible to specify influence of each partner (e.g., higher achiever path and lower achiever path). L-SNA account for the complexities of who influences whom through dyadic weighting and/or the inclusion of interaction terms. L-SNA includes the complete social network of liked peer and their influence on individuals. Both distinguishable and indistinguishable L-APIM analyses are limited to one stable and reciprocated friendship; social contextual effects that are endogenous to a dynamic social network models are estimated with static (rather than dynamic) covariate effects, or alternative specifications of social influence.

The goal of the current paper is to illustrate similarities and differences between L-APIM and L-SNA in the measurement and estimates of peer influence. The participants are drawn from the same sample. We use different terms to refer to the subsamples and the relationships they assess. The term “reciprocated friends” refers to the stable dyads who nominated one another as top ranked, liked peers, the sample used in the L-APIM analyses. The term “liked peers” refers to outgoing liked peer nominations, the sample used in the L-SNA analyses. The conceptual comparisons of the analyses are illustrated in Figure 1a and Figure 1b. The L-APIM assessment of selection similarity consists of intraclass, within-dyad correlations. In theory, L-APIM assessments could include all dyadic relationships, reciprocated or not; in practice, scholars tend to narrow the sample so that each individual is only included once in the analyses, effectively limiting assessments to reciprocated best friendships (e.g., Hafen, Laursen, Burk, Kerr, & Stattin, 2011).

L-SNA assesses selection similarity through a modeling process that removes factors confounded with similarity in the formation of friendship. For example, there is a higher likelihood that friends of friends will later become friends because of structural features and positioning in the social network rather than similarity (e.g., Veenstra, Dijkstra, Steglich, & Van Zalk, 2013). It is possible to account for some of these confounds (e.g., transitivity, or the impact of friends of friends on behavior change) in L-SNA because analyses examine change in the formation of multiple dyads simultaneously. Focused only on dyads, L-APIM cannot address potential network confounds of selection similarity among dyads, triads, and other network members. Estimates of influence are also subject to potential confounds. For example, network level trends toward increasing or decreasing behavior (e.g., behavioral norms) may impact individual behavioral change over time. In other words, peer network characteristics may affect the influence process. It is possible to account for these confounds in L-SNA, because the analyses estimate influence continuously and simultaneously, such that variance attributed to network and behavioral confounds (e.g., transitivity effects, social network norms) is accounted for and, thus, does not inflate estimates of influence. Some of these confounds can be statically accounted for in L-APIM analyses by adding covariates to the model (e.g., average scores for all outgoing or reciprocated friends can remove variance associated with network level effects).

Failure to account for structural network effects may lead to inflated or biased estimates of peer selection and influence. Yet, little is known about whether efforts to remove confounds alter findings. Both analytic strategies have been used to identify selection similarity and peer influence on school related outcomes (DeLay, Laursen, Kiuru, Poikkeus, Aunoloa, & Nurmi, 2015/2016; Kiuru, DeLay, Laursen, Burk, Lerkkanen, Poikkeus, & Nurmi, 2017; Rambaran, Hopmeyer, Schwartz, Steglich, Badaly, & Veenstra, 2017; Shin & Ryan, 2014). Samples differed in these studies, however, and little effort was made to construct comparable analyses. As a consequence, it is not clear when and how findings from L-APIM and L-SNA models are similar and when they differ. Efforts to this end will improve our understanding and appropriate application of each analytic technique.

Two studies have compared results from L-SNA to alternative techniques in the assessment of influence. In the first, traditional regression-type techniques were compared to L-SNA analyses of peer influence. The results revealed few differences between strategies in sensitivity for detecting peer influence, suggesting that the inclusion of network process parameters do not render L-SNA more conservative than other strategies for estimating influence (Ragan, Osgood, Ramirez, Moody, & Gest, 2019). In the second, traditional multilevel model strategies were contrasted with L-SNA models. The results revealed a similar pattern of statistically significant results in the assessment of peer selection and influence (Kiuru, Burk, Laursen, Salmela-Aro, & Nurmi, 2010). Neither study specifically contrasted L-SNA strategies to L-APIM assessments of influence, which is the goal of the present study.

The Current Study

The current study is designed to provide a methodological comparison of L-APIM and the L-SNA strategies to measure selection similarity and peer influence, using the same variables and the same pool of participants. The samples included in the analyses necessarily differ because L-APIM analyses focus on reciprocated dyads, whereas L-SNA include all members of the social network. Unique to our study, the same outcome variable (i.e., mathematical reasoning) is used to assess behavioral similarity and change. A host of supplementary analyses will expand the L-APIM model so that it more closely resembles the L-SNA model. Nevertheless, the analytic strategies differ in their ability to account for potential confounding factors. To examine these differences, supplemental L-APIM analyses included the number of outgoing nominations, the number of reciprocated friendships, and the average mathematical reasoning of each member of the dyad as covariates, in parallel with L-SNA effects of outdegree, reciprocity, and inclusion of all social connections in a network. L-SNA structural covariates are considered as dynamic characteristics endogenous to the social network; in contrast, L-APIM covariates are calculated as single time point static effects. As a consequence, neither statistical tests nor effect size estimates provide a clear means for contrasting the results, but they do allow us to weigh their relative importance.

Method

Participants

Participants were drawn from the First Steps Study (Lerkkanen et al., 2016). The study was entitled “Lapset, vanhemmat ja opettajat yhteistyossa koulutien alussa eli ALKUPORTAAT” in Finnish and had received approval from the human subject ethical review committee at the University of Jyvaskyla (#15.06.2006). The sample was recruited from two municipalities in Central Finland, one in Western Finland, and one in Eastern Finland. The current study involves 1,995 (49% girls; 51 % boys) students in 3rd grade (ages 8–10 years) at the outset. Most participants came from biological two-parent families (83%), with the remainder divided between remarried (10%) and single mother (7%) families. About 50% of parents completed high school or vocational school, 46% of parents had an advanced degree, and the remainder did not complete high school.

Procedure

Parent consent and child assent were required for participation. Trained researchers administered identical surveys during regular school hours approximately one year apart, in the spring of grade 3 and in the spring of grade 4. To ensure reliable social network analyses of the class-based peer networks the participants in the L-SNA analyses were drawn from a pool of 1,024 students (51% of the total sample) who attended 49 classrooms with stable classroom composition, with at least 12 students, and with participation rates above 80% at both measurements (Kiuru et al., 2017), a figure consistent with recommendations for minimum participation in peer nomination studies (Cillessen, 2009). The average participation rates among the participating classrooms were the following: Grade 3: M = 83.73%, SD = 7.51%; and Grade 4: M = 80.43%, SD = 8.00%). Additional subsamples were created for indistinguishable dyad L-APIM analysis (n=412 individuals in 206 friend dyads) and for distinguishable dyad L-APIM analysis (n= 374 individuals in 187 friend dyads).

In almost all cases, children retained the same classmates from one year to the next. As is common in L-SNA, analyses were first conducted within classrooms, then classrooms were combined using a multi-group options in SIENA, and finally meta-analytic procedures were used to test for differences between samples (analyses are described in sections 11.1 and 11.2 of the SIENA Manual; Ripley et al., 2020). L-APIM analyses focused on dyadic rather than classroom level assessments.

Measures

Mathematical Reasoning.

At each time point, children completed the 30-item Arithmetic Reasoning Test (Räsänen, 2000). Mathematical reasoning was measured by number series induction tasks in which children were asked to continue a series of three numbers (e.g., 3, 5, 7) by selecting from 4 response alternatives a fourth number that best fit the series (e.g., 9). One point was given for each correct answer. Internal reliability was acceptable (α=.78 to .79).

Mathematical reasoning has been shown to predict performance in advanced mathematics, above and beyond the effect of computational skills (Lee, Ng, Bull, Pe, & Ho, 2011). Number-series or number-patterns are also widely used to assess mathematical or arithmetic reasoning (see Mullis et al., 2009), for example, as indicators of inductive reasoning in many intelligence tests, including the Stanford-Binet Intelligence Scales (for a review, see Liang, 2014). For L-APIM, the variable met the assumption of approximate normality as a function of visual assessment using graphical procedures as well as statistical checks for skew and kurtosis in the distribution of the variable. For L-SNA, the continuous 30-level mathematical reasoning variable was converted into a 12-level categorical ordinal variable by using .5 standard deviation breaks, consistent with suggestions that more intervals are preferable to fewer intervals (e.g., Niezink, 2018). The original variable and the 12-level categorical variable were highly correlated (r=.99, p<.001) at both time points.

Peer Nominations.

At both time points, participants were given a roster of all students in the classroom and asked to circle the names of three classmates with whom they “liked to spend time.” For purposes of L-SNA, classroom peer networks were combined into larger networks using multi-group options available in RSiena (see Ripley et al., 2020 for review of these modeling options). For purposes of L-APIM, reciprocated friends were defined as children who concurrently nominated each other as most-liked affiliates. Almost all children (80% in Grade 3; 85% in Grade 4) participated in at least one reciprocated friend dyad. Stable reciprocated friends nominated one another as most-liked affiliates at Grade 3 and at Grade 4. Of the 1,463 reciprocated friend dyads at Grade 3, 981 dyads (67%) remained reciprocated friends at Grade 4. Some participants (187 participants) had more than one stable friendship. For L-APIM analyses, each participant was limited to one stable reciprocated friendship. For children with more than one stable friend, preference was given to highest ranked pairs that maximized sample size. The final APIM sample consisted of 794 individuals in 397 stable same-sex friendships (410 boys; 384 girls). Each friend in each stable reciprocated friendship dyad was classified as either relatively higher achieving or relatively lower achieving on 3^rd grade mathematical reasoning. A total of 187 friend dyads had 3^rd grade mathematical reasoning scores that differed by 0.5 SD. Peer likeability was defined as the sum of liked-most peer nominations that a child received from classmates. Peer likeability was included as a covariate variable in L-APIM analyses.

Plan of Analysis

Two sets of analyses were conducted. First, dyadic analyses examined (a) selection similarity in future reciprocated friends, using within-dyad correlations, and (b) influence within stable reciprocated friends, using longitudinal Actor-Partner-Interdependence-Model (L-APIM) analyses. L-APIM analyses were conducted in Mplus 8.0 (Muthén, & Muthén, 1998–2018). Second, Longitudinal Social Network Analyses (L-SNA) examined selection and influence within the social network. L-SNA analyses were conducted in RSiena (Ripley, Snijders, Boda, Voros, & Preciado, 2020).

Although the L-APIM and L-SNA models were designed to be as comparable as possible, they were not identical; each employed different statistical programs with different assumptions requiring different samples. The within-dyad correlations and the L-APIM analyses involved unique dyads consisting of partners who reciprocally nominated one another at both time points. The L-SNA model involved social networks consisting of outgoing liked-most nominations. Thus, the L-SNA models included all participants in the social network whereas the dyadic analyses limited each participant to a single highest ranked reciprocated friendship dyad.

The parameters used to compare constructs were similar, but not identical. Behavioral stability was estimated using stability paths in L-APIM; there is no comparable endogenous effect in L-SNA models. Selection was estimated by within-dyad correlations between new reciprocated friends the year before the friendship began and by selection effects for liked peers in L-SNA. Peer influence was estimated by residual influence regression paths in L-APIM and by the average reciprocated alter and by the average alter X higher (or lower) achieving reciprocated and stable peer influence effect in L-SNA.

L-APIM analyses include regression diagnostic checks to assess the normality of the data, the linearity of the associations, and the normality of residual effects. In L-SNA, pre-existing behavioral similarities are assessed with Moran’s I, the amount of social network change is assessed with the Jaccard index, and the goodness of fit of the data to the network specification is assessed using the “sienaGOF” function. Thus, although both methods have strategies to test the suitability of the data for the model, preliminary data checks are not identical across methodologies.

Four sets of analyses were conducted. In the first set of analyses, participants were 206 stable reciprocated friendship dyads whose members did not differ in terms of mathematical reasoning—the indistinguishable L-APIM model. The second set of analyses involved all 1,024 participants in the sample. These analyses will assess social influence in the complete social network—the indistinguishable L-SNA model. The indistinguishable dyad L-SNA analyses were restricted to reciprocated relationships using the average reciprocated alter effect (avRecAlt). In the third set of analyses, participants were 187 stable reciprocated friendship dyads whose members differed by at least 0.5 SD on Grade 3 mathematical reasoning—the distinguishable L-APIM model. The fourth set of analyses involved again all 1,024 participants in the sample, restricted to reciprocated relationships using the average reciprocated alter effect (avRecAlt). We assessed the influence experienced by relatively higher achieving peers and relatively lower achieving peers using two 2-way interaction terms within a single L-SNA model. The first interaction effect compared the influence of the relatively higher achieving peer (a code of 1) to that of other peers (a code of 0). The second interaction effect compared the influence of the relatively lower achieving peer (a code of 1) to that of other peers (a code of 0). Each weighted covariate effect was then interacted with the average alter influence effect—the distinguishable L-SNA model. The weights used are based upon the distinguishable dyad weighting in L-APIM. More specifically, dyadic weighting was conducted at the first measurement point, at the same time when partners were categorized by ability for the distinguishable dyad L-APIM analyses. Further, once dyads were coded as relatively higher and relatively lower achieving within the network, we could limit analyses to these dyads by including a moderator for the influence from higher achievers on lower achievers and from lower achievers on higher achievers. This allowed us to use L-SNA to assess if there was a greater likelihood of influence from higher achievers on lower achievers or from lower achievers on higher achievers.

A series of t-tests determined that there were no greater than chance differences on any demographic or study variables (a) between those who did and those who did not participate in both waves of data collection, (b) between those with and those without stable reciprocated friends, and (c) between those who differed markedly from their friends and those who were highly similar.

L-APIM Model.

The top of Figure 1 illustrates the L-APIM measurement model. Behavioral stability, which describes intra-individual consistency of the dependent variables, is represented by two actor paths (a1 and a2), one for each member of the reciprocated friendship dyad. Initial (Grade 3) similarity is represented as the concurrent within-dyad correlation on mathematical reasoning (c). Influence, which describes the degree to which one reciprocated friend’s initial (Grade 3) score on mathematical reasoning predicts changes in the other reciprocated friend’s score from Grade 3 to Grade 4, is represented by two partner paths (p1 and p2).

L-APIMs were conducted in both indistinguishable and distinguishable dyad frameworks. Distinguishability in the L-APIM framework is an empirical construct that categorizes partners into distinct roles whose members differ (on a statistical test of distinguishability) in terms of means, variances, and covariances (Gonzalez & Griffin, 1999) on the dependent variable. In these analyses, partners are assumed to be exchangeable and their influence is assumed to be equivalent. Distinguishable dyad analyses partition effects between partners to determine who influences whom within the reciprocated friendship dyad, assessing the magnitude of influence as a function of researcher identified roles within the reciprocated friendship.

Supplemental L-APIM analyses.

Four sets of supplemental L-APIM analyses were conducted to approximate some of the parameters commonly included in L-SNA. First, we applied the COMPLEX function in Mplus, which corrects standard errors and model fit to account for the stratification and non-independence of classroom-level data (Muthén & Muthén, 1998–2018). In this way, the COMPLEX option within Mplus accounts for design effects when it is not possible to reliably estimate multilevel models due to limitations in sample size, as was the case for our dyadic level analyses. Second, we conducted latent change score analyses (e.g., McArdle, 2009; Henk & Castrol-Schilo, 2015) in Mplus. These analyses focus on interindividual differences in individuals’ change, and examine the extent to which one friend’s behavior predicts changes in the other friend’s behavior. In a latent change score model, a latent variable, delta, is estimated that represents the degree of change from Time 1 to Time 2. The result is a latent variable that provides an error-free estimate of the change score, with the mean of delta signifying the change from Time 1 to Time 2 and the variance of delta indicating the variability around that mean. Third, L-APIM analyses were restricted to dyads included in each of the L-SNA analyses. This reduced the indistinguishable dyad sample from 206 dyads to 65 dyads and the distinguishable dyad sample from 187 dyads to 84 dyads. Finally, separate analyses were conducted in which each partner’s score on a covariate—an alternative explanation for social influence—was added to the L-APIM model at grade 3. The covariate variables were: (1) the number of outgoing liking nominations; (2) the number of reciprocated friendships; and (3) the average mathematical reasoning of liked-most nominees.

L-SNA Model.

The bottom of Figure 1 depicts the L-SNA measurement model. Stability of the grand mean of the network is assessed with the linear tendency effect. The stability of the grand mean differs from individual level stability that is accounted for in L-APIM because one is a network level estimate and the other is an individual level estimate. Selection is assessed with the selection for similarity parameter, a longitudinal test of the selection process wherein similarities at Grade 3 predict relationship formation at Grade 4. Influence was assessed with the average reciprocated alter effect in the indistinguishable dyad analyses. The average reciprocated alter effect measures behavior change as a function of the reciprocated peer group’s behavioral profile [i.e., influence toward (a) increases in mathematical reasoning, (b) decreases in mathematical reasoning, or (c) stability in mathematical reasoning]. We focus here on the average reciprocated alter effect because this parameter provides an assessment of peer influence that is not restricted to increases in absolute levels of similarity, but rather on the degree to which individuals change in the direction of the behaviors of their reciprocated peers. Many other model specifications for influence are possible within L-SNA. For additional review of the possibilities of peer influence assessments using L-SNA see Ripley et al., 2020; Manual for SIENA. We selected this parameter because it most closely resembled the form of influence captured in L-APIM, a form of regression-based influence that also is not necessarily an increase in absolute levels of similarity between peers.

The assessment of distinguishable dyad analysis was more complex than the indistinguishable dyad analyses in L-SNA. For distinguishable dyad analyses we used interaction terms to weight the average alter influence effect. Specifically, two 2-way interaction terms were used within a single L-SNA model. The first interaction effect compared the influence of the relatively higher achieving peer (a code of 1) to that of other peers (a code of 0). The second interaction effect compared the influence of the relatively lower achieving peer (a code of 1) to that of other peers (a code of 0). Each weighted covariate effect was then interacted with the average alter influence effect. The dyads in the L-APIM were able to be distinguished into relatively higher and relatively lower achieving stable and reciprocated peer relationship dyads within the basic modeling framework.

Supplemental L-SNA analyses

Supplemental network analyses were conducted that included an additional measure of peer influence (i.e., average alter effect), an oft-used L-SNA parameter that accounts for the influence of all nominated peers (as opposed to influence from reciprocally nominated peers, which was assessed in the primary analyses). Three supplemental analyses were conducted. The first, the comparison model, differs from the model reported in the main analyses only in the addition of the average alter influence parameter. The second, the base model, differs from the model reported in the main analyses in that structural effects were limited to the RSIENA program defaults (i.e., outdegree, reciprocity, linear tendency, and quadratic shape). Practically speaking, the base model differed from the model reported in the main analyses in that the base model did not assess transitivity effects but did include the average alter influence parameter. The third, the best practices model, differs from the model reported in the main analyses in that it included theoretically recommended gender covariate effects (Ripley et al., 2020), as well as structural and behavioral covariates that emerged from sienaGOF analyses designed to identify effects that improve model fit (Snijders, Boda, Voros, & Preciado, 2020). Practically speaking, the best practices model differed from the model reported in the main analyses in that the best practices model included effects of gender on selection and influence, additional (empirically determined) structural effects, as well as the average alter influence parameter. The purpose of these additional models was twofold. First, to explore a different measure of influence, to determine if conventional network analyses (distinct from network influence effects that parallel those measured in dyadic analyses) reveal the presence of some form of peer influence. Second, to determine whether the inclusion of additional network covariates alters conclusions about peer influence.

Finally, we addressed the nested network data structure by first running analyses individually by classrooms (e.g., networks of peer affiliations were nested within classrooms) to determine that the patterns of results did not differ between classrooms. We then employed the multi-group options in L-SNA because some of our classrooms were too small for independent analysis (e.g., n=12 participants) and, thus, were combined using multi-group analyses. Finally, we assessed sample differences at the district level because we could not do so at the classroom level using the meta-analysis option described in sections 11.1 and 11.2 of the SIENA Manual (Ripley et al., 2020). Alternative model specifications and analyses of the L-SNA model can be found in the supplemental analyses (Tables S1, S2, S3). The programming scripts for the models used can be found in Appendix 1.

Results

Dyadic Analyses

Preliminary Analyses.

Descriptive assessments of the mathematical reasoning variable revealed that the variable met assumptions of approximate normality and linearity (i.e., there was no evidence of skew or kurtosis in the data). Data from the dyadic sample of reciprocated friends were not independent, a precondition for the L-APIM analysis: reciprocated friends resembled each other in mathematical reasoning during the 3^rd grade (intraclass r=.13, p<.05) and during the 4^th grade (intraclass r=.23, p<.01) grade. Pre-existing similarity within dyads were removed by partitioning out initial levels of similarity. Additional intraclass correlations were calculated on a sample of children who were not reciprocated friends in Grade 3 but who became reciprocated friends in Grade 4. Future friends were similar on mathematical reasoning the year before the reciprocated friendship began (e.g., Grade 3); intraclass correlations ranged from (r=.37 to .60, p <.05) among the dyads assessed.

A series of 2 (gender) X 2 (Grade: 3^rd or 4^th grade) repeated measures ANOVAs were conducted on the total sample total sample of children who participated in dyadic reciprocated friendships (n=794) to identify changes in mathematical reasoning. The main effect of Grade was significant. Mathematical reasoning increased from Grade 3 to Grade 4, F (1, 792) = 163.22, p < .001 (d = .45). There were no main effects or interactions involving gender.

Network Analyses

Preliminary Analyses.

The observed network autocorrelation statistics (Moran’s I; for formulae and interpretation, see Steglich, Snijders, & Pearson, 2010) did not indicate a strong degree of similarity in mathematical reasoning between network affiliates. Final estimates represent the average of the network effects after classroom (or network) effects were averaged. The social networks sample used for L-SNA analyses had no bias as a function of network descriptives. The average number of peer ties was between two and three. Approximately 40% of all nominations were reciprocated, and on average, about one third of the peer nominations involved cohesive relational structures of at least three individuals. The Jaccard index describes the relative stability of the network, with recommended values between .20 and .60 (Snijders, Van de Bunt, & Steglich, 2010). For the present data, the Jaccard index indicated that the peer networks did not change too rapidly or abruptly (Jaccard = .41). Approximately 40% of children increased, 34% decreased, and 26% remained stable in mathematical reasoning scores from Grade 3 to Grade 4.

Table 1 provides a summary of the L-SNA model, parameter estimates, standard error estimates, p-values, and convergence statistics. Convergence statistics were all less than 0.1 at the individual level and less than 0.25 for the overall maximum convergence of the models presented. The analysis presented in Table 1 are designed to replicate the L-APIM model and, as such, is an atypically simple L-SNA model.

Table 1:

Peer Selection and Influence Processes on the Basis of Mathematical Reasoning Among Indistinguishable and Distinguishable Dyads using L-SNA

	Est.	SE
Structural and Behavioural Covariates
Outdegree	−1.77**	0.04
Reciprocity	1.55**	0.06
Transitive triplets	0.34**	0.02
Linear tendency	0.04*	0.02
Quadratic shape	−0.07	0.01
Selection Effect
Selection for Mathematical Reasoning Similarity	0.43	0.29
Influence Effects
Indistinguishable Influence on Mathematical Reasoning (Average Reciprocated Alter)	0.03	0.02
Distinguishable Influence on Mathematical Reasoning from Lower on Higher Achiever (Weighted Interaction)	−0.04	0.13
Distinguishable Influence on Mathematical Reasoning from Higher on Lower Achiever (Weighted Interaction)	−0.07	0.11

Note. L-SNA models included the entire peer network (N=1,024). Peer influence within L-SNA was measured with the average reciprocated alter effect for indistinguishable dyad analyses and the average alter parameter weighted by stable and reciprocated higher and lower achieving peer relationships for distinguishable dyad analyses. Selection of same gender peers was also included for comparison and did not change the pattern of statistically significant results. Due to the model comparison nature of this paper, both interaction terms were estimated in the same model and we did not include additional effects suggested by Goodness of Fit (see Section 5.13 of the SIENA Manual) in this Table, although the contributions of these effects can be found in supplemental analyses (Tables S1 through S3). In the model presented, all individual effect convergence estimates were less than 0.1 in absolute value and the overall convergence estimate was below 0.25, indicating that excellent convergence was achieved as outlined in Section 6.3.2 of the SIENA Manual. Statistical significance of the mean parameter estimates is obtained by an approximate t-ratio of the estimate divided by its standard error (SE).

^*p < .05

^**p < .01

Indistinguishable Dyadic Analyses

L-APIM.

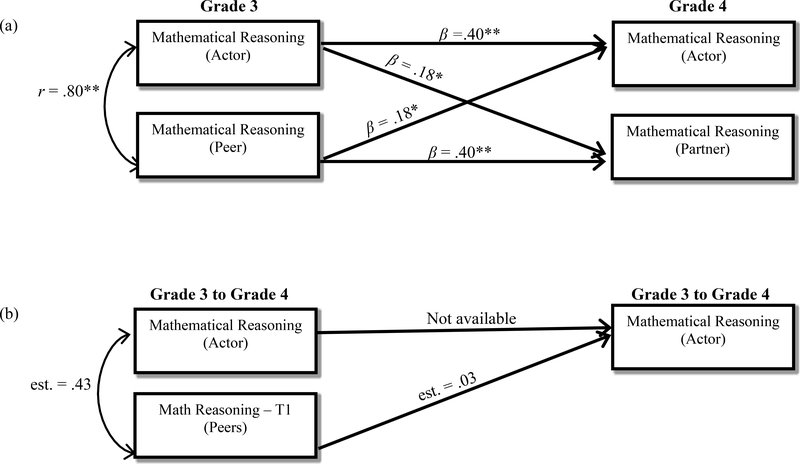
Figure 2 and Table 2 present results from the indistinguishable L-APIM analyses. Highest ranked reciprocated friends were similar on mathematical achievement (r =.80, p < .01). Individual mathematical reasoning scores were stable from grade 3 to grade 4 (β =.40, p < .01). Reciprocated friends influenced one another’s mathematical reasoning such that one partner’s score in the 3^rd grade predicted changes in the other partner’s score from the 3^rd to the 4^th grade (β =.18, p < .05).

Figure 2.

Estimates of peer influence on mathematical reasoning in (a) L-APIM and (b) L-SNA frameworks – indistinguishable dyads

Note. N=412 individuals in 206 dyads in indistinguishable dyad L-APIM. L-SNA included the entire peer network (N=1,024). Peer influence within L-SNA was measured with the average reciprocated alter parameter; models are for illustrative purposes only. Graphical notation was borrowed from SEM to create an illustration. **p < .01, *p < .05.

Table 2:

Peer Selection and Influence Processes on the Basis of Mathematical Reasoning Among Indistinguishable and Distinguishable Dyads using L-APIM

	Est.	SE
Stability Covariates
Stability of Mathematical Reasoning Indistinguishable Partner 1	0.40**	0.06
Stability of Mathematical Reasoning Indistinguishable Partner 2	0.40**	0.06
Stability of Mathematical Reasoning Distinguishable Higher Achieving Partner	0.67**	0.06
Stability of Mathematical Reasoning Distinguishable Lower Achieving Partner	0.41**	0.07
Selection Effects
Selection on Mathematical Reasoning Between Indistinguishable Partner 1 and Partner 2	0.80**	0.03
Selection on Mathematical Reasoning Between Distinguishable Higher Achieving and Lower Achieving Partner	0.56**	0.05
Influence Effects
Indistinguishable Influence on Mathematical Reasoning from Partner 1 to Partner 2	0.18*	0.06
Indistinguishable Influence on Mathematical Reasoning from Partner 2 to Partner 1	0.18*	0.06
Distinguishable Influence on Mathematical Reasoning from Lower Achieving on Higher Achieving Partner	−0.01	0.07
Distinguishable Influence on Mathematical Reasoning from Higher Achieving on Lower Achieving Partner	0.27**	0.07

Note. N=412 individuals in 206 dyads in indistinguishable dyad L-APIM. N=374 individuals in 187 dyads in distinguishable dyad L-APIM.

^**p < .01

^*p < .05.

Indistinguishable Network Analyses

L-SNA.

Figure 2 and Table 1 revealed no evidence of peer selection as a function of mathematical reasoning (est. = .43, p = .07). The effect of reciprocated peer influence on mathematical reasoning was not statistically significant (est. = .03, p = .07). Concerning network covariate parameters (see Table 3), there were statistically significant negative outdegree effects, suggesting that peer nominations are selective, and not made at random; statistically significant positive reciprocity effects, suggesting a tendency toward mutual peer liking; statistically significant transitivity effects, suggesting that peers who were liked by participants tended to also like one another; and statistically significant and positive linear tendency effect, suggesting that mathematical reasoning tends to increase rather than decrease among social network members. The quadratic shape effect was not significant.

Table 3:

Estimates for L-APIM and L-SNA Covariate Variables

Variables	Dyadic L-APIM Covariates - Indistinguishable	Network L-SNA Covariates - Indistinguishable	Dyadic L-APIM Covariates Distinguishable (High achiever /Low achiever)	Network L-SNA Covariates Distinguishable
	Outdegree (L-SNA) & Number of Outgoing Nominations (L-APIM)	−0.01	−1.77**	0.14 / 0.12	−1.77**
Reciprocity (L-SNA) & Number of Reciprocated Friendships (L-APIM)	0.13	1.55**	−0.17 / 0.49**	1.55**
Average Mathematical Reasoning of Reciprocated Nominations (L-APIM)	0.13	Endogenous to the L-SNA Model	0.02 / 0.04	Endogenous to the L-SNA Model
Transitive Triplets Effect (L-SNA)	Not an L-APIM option	0.34**	Not an L-APIM option	0.34**
Quadratic Shape Effect (L-SNA)	Not an L-APIM option	−0.07	Not an L-APIM option	−0.07
Linear Tendency Effect (L-SNA)	Not an L-APIM option	0.04*	Not an APIM option	0.04*

Note. L-SNA models included the entire peer network (N=1,024). Statistical significance of the mean parameter estimates is obtained by an approximate t-ratio of the estimate divided by its standard error (SE).

^*p < .05

^**p < .01

Summary of Indistinguishable Dyadic and Network Analyses.

The results of the indistinguishable dyadic and network analyses were not consistent in terms of the pattern of statistically significant estimates of selection and influence. Specifically, dyadic correlations revealed considerable similarity between reciprocated friends the year before the friendship began and APIM analyses revealed considerable similarity between reciprocated friends in the 3^rd grade. Selection effects were, however, not statistically significant in the L-SNA model. Furthermore, peer influence effects were significant in the L-APIM model but did not reach conventional levels of statistical significance in the L-SNA model.

Distinguishable Dyadic Analyses

L-APIM.

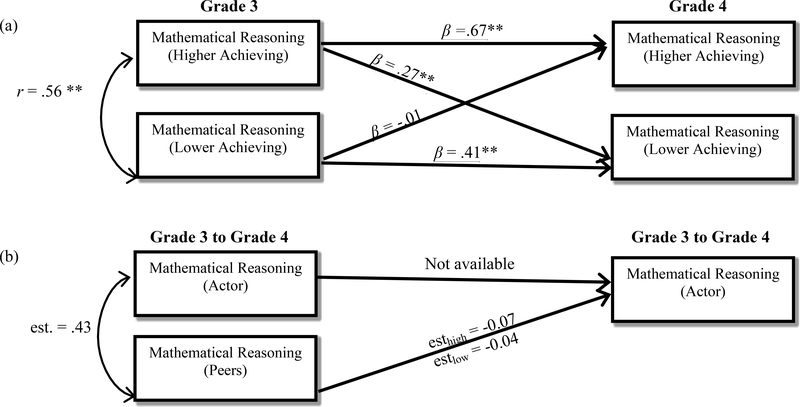
Figure 3 and Table 2 reveals considerable similarity between grade 3 reciprocated friends on mathematical achievement (r = .56, p < .001). Individual scores were stable from grade 3 to grade 4 for the higher achieving reciprocated friend (β =.67, p < .001) and the lower achieving reciprocated friend (β = .41, p < .001). The higher achieving friend influenced the mathematical reasoning of the lower achieving friend (β = .27, p < .01), such that higher levels of mathematic reasoning by the higher achieving friend in grade 3 predicted greater increases in the lower achieving friend’s mathematical achievement from grade 3 to grade 4. The lower achieving friend did not influence the mathematical achievement of the higher achieving friend (β = −.01, p = .10). Thus, lower achieving friends increased their mathematical reasoning to resemble higher achieving friends, whereas higher achieving friends did not change their mathematical reasoning to resemble lower achieving friends.

Figure 3.

Estimates of peer influence on mathematical reasoning in (a) L-APIM and (b) L-SNA frameworks – distinguishable dyads

Note. N=374 individuals in 187 dyads in distinguishable dyad L-APIM. L-SNA used dyadic weighting (higher achieving members of a dyad = 1, lower achieving members of a dyad = 0) with the entire sample (N=1,024). Peer influence within L-SNA was measured with the average alter parameter weighted by participation in a stable and reciprocated most-liked peer relationship. Graphical notation was borrowed from SEM to create an illustration. **p < .01, *p < .05. Models are for illustrative purposes only.

Distinguishable Network Analyses

L-SNA.

Figure 3 and Table 1 reveal limited evidence of peer selection as a function of mathematical reasoning (est. = .43, p = .07). When dyadic weighted covariates were included to account for relative levels of mathematical reasoning within reciprocated dyads, there were no statistically significant peer influence effects from the higher achieving peers to the lower achieving peers (est. = −.07, p = .25) or from the lower achieving peers to the higher achieving peers (est. = −.04, p = .37). Concerning network covariate parameters, there was a statistically significant negative outdegree effects, suggesting that liked peer nominations were selective, and not made at random; statistically significant positive reciprocity effects, suggesting a tendency toward mutual peer liking; statistically significant transitivity effects, suggesting that the liked peers of liked peers tend to form social bonds; and a statistically significant and positive linear tendency effect, suggesting that mathematical reasoning tends to increase rather than decrease among social network members. The quadratic shape effect was not significant.

Summary of Distinguishable Dyadic and Network Analyses.

The results of the distinguishable dyadic and network analyses were not consistent in terms of selection or influence. Specifically, dyadic correlations revealed considerable similarity between reciprocated friends the year before the reciprocated friendship began and L-APIM analyses showed considerable similarity between reciprocated friends in the 3^rd grade. Nevertheless, selection effects did not reach conventional levels of statistical significance in the L-SNA model. Further, L-APIM analyses revealed significant effects for influence, such that the higher achieving friend influenced the mathematical achievement of the lower achieving friend; there were no statistically significant influence effects in the L-SNA.

Supplemental L-APIM Analyses.

The same pattern of statistically significant results emerged when (a) L-APIM analyses were run with the COMPLEX function in Mplus to account for the nested structure of the data; (b) the L-APIM analyses were run as latent change models in order to focus on interindividual differences in individual’s change; and (c) the L-APIM analyses included grade 3 covariates to account for each child’s number of outgoing positive peer nominations, number of reciprocated friendships in the social network, and the average mathematical reasoning of all outgoing liked nominations (excluding the reciprocated friend included in APIM analyses).

L-APIM models were also restricted so that each individual was only represented once in the analyses. In the present case, we focused our analyses on the highest ranked reciprocated friendships. As a consequence, there was a loss of information for individuals in multiple stable reciprocated friendships. In contrast, L-SNA encompasses complete networks of peer relationships wherein reciprocity effects are added as covariate variables in the analyses. Nevertheless, L-SNA has strict requirements for within-network participation rates that may remove some highest rank friend dyads from the analyses if these friends are found within networks that do not reach the strict network-level participation rates required for L-SNA These differences in participation requirements resulted in slightly different samples, so we conducted additional L-APIM analyses with the same (albeit reduced) set of participants that were found in the L-SNA models. The same pattern of results emerged using this subsample.

Supplemental L-SNA analyses.

Three sets of supplemental L-SNA analyses were conducted. The first analyses (Table S1), the comparison model, was identical to the model reported in the main analyses, except for the addition of the average alter influence parameter. The average alter influence parameter was statistically significant, indicating the presence of influence from nominated peers. In all other respects, the same pattern of statistically significant effects emerged. The second analyses (Table S2), the base model, differed from the model reported in the main analyses in that it included the average alter influence parameter, but excluded transitivity effects (consistent with the default settings in RSIENA). The average alter influence parameter was statistically significant. In all other respects, the same pattern of statistically significant effects emerged. The third analyses (Table S3), the best practices model, differed from the model reported in the main analyses in several respects. First, the model included theoretically recommended effects of gender on selection and influence. Both were statistically significant, indicating that participants were more apt to nominate same-gender as opposed to other gender peers as friends and that those self-identified as boys were more apt to change their levels of mathematical reasoning than those self-identified as girls. Second, the model included several additional structural and behavioral covariate parameters that emerged from L-SNA sienaGOF analyses (designed to improve model fit): transitive reciprocated triplets, three cycles, transitive ties, outdegree popularity. Each was statistically significant. Finally, the model included the average alter influence parameter, which was statistically significant. Of note, there was also a statistically significant effect for selection for similarity, which was not found in any previous L-SNA analyses. This finding, similar to the dyadic intraclass correlations, indicated that children nominate friends who are similar on mathematical achievement.

Models were also extended to look at sample differences in the effects reported in L-SNA using the meta-analysis option in the L-SNA. There were no sample differences in selection and influence effects that emerged through the meta-analysis tests.

Discussion

The present study illustrates similarities and differences between dyadic and network assessment models of peer influence. Both models account for selection similarity and behavioral influence. L-APIM analyses revealed statistically significant effects for selection for similarity on mathematical reasoning that were, at best, marginal in L-SNA. Findings from the L-APIM and L-SNA models for peer influence diverged considerably. Indistinguishable dyad L-APIM analyses identified reciprocated friend influence and distinguishable dyad L-APIM analyses indicated that higher achieving reciprocated friends influenced their lower achieving partners but not the reverse. L-SNA analyses did not yield statistically significant findings for peer influence except when they were modified to account for the influence of all peer affiliates within the social network and included the recommended structural covariates observed in L-SNA literature.

Previous studies have contrasted L-SNA strategies to measure influence with multi-level modeling and regression alternatives (Ragan et al., 2019; Kiuru et al., 2010). In traditional linear ordinary least squares (OLS) regression techniques, static peer group scores can be used to predict individual change in a single linear equation. Multi-level models assess individual and peer group effects as separate, yet interacting, aspects of a statistical model. Results from prior studies indicate that network analyses are not more conservative in their estimates of influence, despite the inclusion of multiple parameters that gauge selection and network processes. Our study adds to this growing body of inquiry by contrasting L-SNA strategies with L-APIM, a specific form of a nested data analysis with a focus on peer dyads.

Gauging Selection Similarity

We open with a few words on similarity prior to relationship formation. As first demonstrated by Kandel (1978) and Cohen (1977), there is considerable behavioral similarity among future friends, prior to the establishment of their friendship. In this vein, we found significant and positive dyadic correlations on mathematical reasoning, both prior to the establishment of the friendship as well as during the further evolution of the friendship. Although similarity is known to predict friendship formation (Laursen, 2017), the L-SNA model demonstrated this only when using a best practices modeling approach. Therefore, one plausible explanation for the difference observed in the L-APIM and L-SNA comparison is that one must include parameters suggested for purposes of model fit when using L-SNA. Alternatively, a second potential explanation involves the distinction between top ranked reciprocated relationships and the much larger number of outgoing liked-most peer nominations. Children nominated many others as liked, but only a few of these qualify as new, best friendships. Those nominated as liked may be liked for many different reasons and may not be all that similar to one another; those who become friends are apt to be similar on many more characteristics; those who become top ranked friends are apt to be the most similar of all. Nevertheless, this difference may also be simply attributed to the fact that we were forced to limit the L-SNA sample a great deal, and potentially minimize the model’s computing power in the comparison models. Regardless of the reason for differences between analytic techniques, it is important to acknowledge that pre-existing similarities exist among future reciprocated friends that will inflate estimates of friend influence if not considered (Ennett & Bauman, 1994). Both L-APIM and L-SNA allow scholars to account for pre-existing behavioral similarities, minimizing the potential for biased (or inflated) estimates of peer influence within each assessment context (i.e., dyad vs. network). We hope future research will also aim to account for similarities that may be associated with similarities in mathematical reasoning. Both the L-APIM and the L-SNA offer unique ways of accounting for such effects.

Gauging Peer Influence

The two sets of analyses yielded somewhat different stories about peer influence over mathematical reasoning. Statistically significant peer influence effects emerged from both distinguishable and indistinguishable dyad L-APIM analyses. Similar effects did not emerge from comparable L-SNA but did emerge in expanded L-SNA. We consider five potential sources of difference: (1) samples; (2) the structural and relational covariates, or alternative specifications of social influence; (3) differences in how selection effects are partitioned from influence estimates; (4) differences in estimates of peer influence; and (5) differences in measurement sensitivity.

First, differences in patterns of results may be traced to differences between the samples included in each form of analysis. Distinguishable dyad L-APIM analyses included 187 friend pairs who reciprocally nominated one another as friends for two consecutive years. One friend’s mathematical achievement was notably above the others. Indistinguishable dyad analyses included 206 friend pairs who reciprocally nominated one another as reciprocated friends for two consecutive years. The mathematical achievement of these friends was fixed to be equal. The L-SNA included all potential friendship dyads in the social network. Thus, L-SNA models address the question of distinguishability, regardless of the strength of the relationship, whether participants reciprocate feelings about participation in the relationship, and whether members of the dyad differ in terms of their mathematical reasoning. The dyadic analyses addressed nominations that were top ranked and reciprocated. It is not a stretch to suggest that differences in results may arise because influence over mathematical reasoning is limited to a specific relationship context: stable reciprocated best friends.

Supplemental L-SNA identified peer influence with a measure that examines the effects of all who were nominated as friends (i.e., average alter effect). There was no evidence of peer influence in L-SNA that restricted effects to reciprocated friends. We leave it to others to determine if these variations truly reflect differences in sources of influence or if they instead reflect differences in the sensitivity of the influence parameters. It is also worth noting that L-SNA identified selection effects for mathematical reasoning that were consistent with those found in dyadic analyses only in the best practice model, a reminder that the inclusion of additional parameters does not necessarily make the network approach more conservative (see also Ragan et al, 2019) but may instead paradoxically increase the model’s ability to detect selection effects. In conclusion, L-APIM and L-SNA results more closely approximated one another in terms of findings for peer selection and indistinguishable influence when network models were not constrained to focus on dyadic influence.

Second, differences in patterns of results may be traced to differences in the degree to which analytic strategies are capable of endogenously removing variance from potentially confounding sources that might otherwise inflate estimates of influence. The L-SNA model includes several such factors. Although we conducted some supplemental L-APIM analyses to mimic these L-SNA variables, these were imperfect parallels insofar as they were static processes and did not parallel the dynamic and endogenous effects included in the L-SNA. It is possible that the different pattern of results arose because the L-SNA did a better job of removing confounds from influence estimates than the L-APIM analyses. The argument that L-SNA analyses are overly conservative, however, has not received support in other comparisons of influence assessments (Ragan et al., 2019).

Third, differences in patterns of results may be traced to differences in the way selection similarity is separated from peer influence estimates. The L-APIM partials out the impact of social selection on estimates of peer influence using bivariate correlations between dyad members to account for preexisting similarities at the outset. Thus, peer influence represents changes in mathematical reasoning over and above these initial similarities in mathematical reasoning. In contrast, the L-SNA estimate of selection determines if a peer relationship was not present at Grade 3 and is present at Grade 4 (a selection effect) as a kind of dynamic selection assessed alongside, or simultaneously with, peer influence effects. Put differently, different results may arise because the L-SNA and the L-APIM are removing different forms and amounts of antecedent similarity and doing so with differing degrees of caution.

Fourth, differences in patterns of results may be traced to differences in how peer influence is operationalized. Previous studies that compared two different network- or group-focused techniques (e.g., traditional multilevel analysis and L-SNA) yielded similar results and patterns of statistical significance (e.g., Kiuru et al., 2010). In contrast, the comparison of social network and dyadic assessments of peer influence conducted in the current study yield less similar results. Perhaps the operationalization of the influence in the dyad and in the network encompasses a meaningfully different measure of change in response to the behavior of a peer. Relatedly, influence may come in different forms. The L-APIM captures a general form of influence, whereas the L-SNA offers different strategies for conceptualizing influence (e.g., average similarity, total similarity, average alter, average reciprocated alter, total alter). It is important to understand that models and parameters operationalize influence differently, with profound implications for the interpretation of the results.

Fifth, differences in patterns of results may be traced to differences in measurement sensitivity. First, L-SNA typically uses a categorization approach of scaled variables that can give up measurement sensitivity. In addition, the type of influence measured in a distinguishable dyad L-APIM framework may not be easily measured in an L-SNA framework. Three- and four-way interactions of the sort required in L-SNA to identify influence from the higher achieving best friend to the lower achieving best friend produce incomplete network data and are notoriously difficult to interpret. Thus, for this reason, L-APIM analytic strategies may detect somewhat effects in a specific subsample of a social network that cannot be readily measured in the full network model. Effects specific to best friends may get lost in analyses designed to examine effects among liked peers. Conversely, scholars ought not attribute effects found within best friendships to the wider group of liked agemates.

Finally, although the current L-SNA findings failed to reach conventional levels of statistical significance, it is important to note that L-SNA models have the flexibility to consider multiple individual, dyadic, and subgroup characteristics that may be theoretically relevant within a complete L-SNA model. Additionally, it is important to consider the conceptual difference between the L-APIM and the L-SNA models. L-SNA is a generative model, that is, it is built around a probability model that directly reflects social influence such that one can simulate hypothetical data in which social influence occurs and compare such hypothetical data with the actual data. L-APIM is a method for testing social influence by looking at deviations from a null model without social influence.

Deciding on the Best Model to Use

In light of the findings of the current study, we offer a few suggestions for scholars interested in empirically assessing peer influence. As a starting point for analyzing peer influence data, we suggest that scholars consider two primary questions: (Question 1) What is the hypothesized source of influence? (Question 2) What is the hypothesized type of influence? Table 4 provides a series of suggestive steps that can be applied during the process of defining peer influence and in determining the best analytic approach to use to address these questions (for additional reading on the importance of definitions of peer influence see Kindermann & Skinner, 2019). We also suggest that scholars carefully consider recent work indicating that conventional statistical tools do not overestimate influence effects compared with network approaches (Ragan et al., 2019) and influence effects attained from cross-lagged models are unlikely to be false positives derived from unobserved variable biases (Thomas, McGloin, & Sullivan, 2019).

Table 4:

Comparing and contrasting L-APIM and L-SNA for their suitability in addressing questions of peer influence.

	APIM	SNA
Level of Relevant Social Context(s)	-Dyadic level only	-Dyadic level -Network level
Type of Influence	-Relative behavioral change	-Behavioral change -Behavioral contagion -Behavioral convergence
The influential partner	-A single source of influence (i.e., target partner) -Differential patterns of influence (i.e., compliment vs. contrast patterns)	-Multiple sources of dyadic influence -Different types of influence assessed simultaneously (e.g., increase, decrease, stability, change, convergence, contagion) -Additional network features accounted for (e.g., structural features of the network do not bias influence estimates)
Design	-Dyadic	-Complete Social Network
Analytic Frameworks	-OLS Regression -SEM -MLM	-SIENA
Data Structure	-Dyadic data structure -Requires unique and stable social relationship dyads	-Social network data structure -Requires complete and stable (~65% overall participation) social networks
Follow-up Strategies	-ANOVA / ANCOVA -Intraclass correlations	-Ego-Alter Influence tables -Number of increasers or decreasers in the network -Moran’s I -Set direction of influence (creation or endowment)
Implications	-Influence occurring within dyads that effects the relative position of an individual within the dyadic subsample	-Influence occurring within a network that effects the relative position of dyads within a network relative to all other social network members

Nevertheless, there remain important advantages in the flexibility and the contextual representation of L-SNA models. As an example, the L-APIM requires scholars to start by dividing the group into dyads. Left out of the analyses will be some stable and reciprocated relationships, excluded to avoid issues of double entry in the dyadic dataset. These complications of the L-APIM are further exacerbated by the phenomenon of transitivity, such that friends of friends may also be influential within the peer group. Transitivity effects cannot be captured within L-APIM. Thus, decisions on which methodological approach to use should be thoughtful and in service to unbiased influence estimates. Indeed, many forms of influence occur within complete social contexts rather than in isolated dyadic interactions.

Limitations and Future Directions

Our study is not the final word on differences between popular analytic techniques for the assessment of peer influence. Instead, our aim is to inspire a new line of inquiry into the potential merits and limitations of the L-APIM and L-SNA approach. In this spirit, we discuss several limitations that future research efforts should address. First, our illustration was based on one sample using one dependent variable. It would be inappropriate to draw sweeping conclusions about differences between the analytic strategies on the basis of this modest start. Second, although efforts were made to create comparable L-APIM and L-SNA models, the two differed in important ways that limit conclusions about differences in patterns of results. Unlike L-APIM, we could not limit the analyses to only the already established stable and reciprocated friends in L-SNA because this would lead to an incomplete network sample. Third, firm conclusions about the magnitude of effects derived from each analytic strategy are hindered by the fact that neither has a straightforward effect size estimate of influence that can be directly compared across the L-APIM and L-SNA framework. Fourth, differences may exist due to how the nested and nonindependence nature of peer relationships data is accounted for in the analysis. Specifically, the L-APIM controls for dyad level interdependence, whereas the L-SNA is broken down into group analyses wherein differences between groups (or networks) can be detected using the meta-analysis option. Fifth, we also note that discussions of power are often absent in L-APIM and L-SNA papers. We know very little about power analyses for L-SNA models, and almost nothing about ways of comparing the power estimates between L-APIM and L-SNA methodologies. Thus, it may be that the SIENA analyses conducted were underpowered, yet more research is needed in this area. Sixth, participation rates may bias outcomes if participation is related to target variables under study (e.g., students who have trouble forming friendships and students who have difficulty in school are less likely to participate). Participation rates can affect L-APIM and L-SNA analyses differently: L-APIM only include participants in reciprocated friendships; as such it requires data from both partners in a relationship. L-SNA include all participants in a network, but effects for reciprocity and transitivity are affected by participation rates when data from reciprocated and triadic relationships are missing. Finally, we suggest a necessary next step is to conduct simulation studies wherein scholars can manipulate sample sizes, levels of missing data, nominations protocols, as well as compare nesting procedures and the results and type I versus type II error rates of the various methods.

Conclusions

Our take-home message is simple: One analytic strategy for gauging peer influence is not superior to another. Scholars who argue something different do the field a disservice. We hold that the selection of an analytic tool should depend on the research question being asked. We have long since moved past the point where we seek to demonstrate the presence of peer influence. Scholars should tailor hypotheses as a function of relationship setting, and the type, timing, and form of influence to be assessed. Scholars should view these (and other) influence assessment tools as complementary, not competing, research strategies.

APPENDIX 1

Script for the analysis of the indistinguishable and the distinguishable L-APIM and for the indistinguishable and distinguishable L-SNA.

Appendix 1a.

Basic Script for the Indistinguishable Dyad L-APIM model within Mplus.

SCRIPT FOR THE MODEL:

A2 ON A1(a);
B2 ON B1(a);
B2 ON A1(p);
A2 ON B1(p);
A1(IV); B1(IV);
A2(DV); B2(DV);
[A1](I); [B1](I);
[A2](D); [B2](D);
A1 WITH B1;

Note. Partner 1 at Time 1 = A1; Partner 1 at Time 2 = A2; Partner 2 at Time 1 = B1; Partner 2 at Time 2 = B2.

Appendix 1b.

Basic Script for the Distinguishable Dyad L-APIM model within Mplus.

SCRIPT FOR THE MODEL:

A2 ON A1;
B2 ON B1;
B2 ON A1;
A2 ON B1;
A1 WITH B1;

Note. Higher Achieving Partner at Time 1 = A1; Higher Achieving Partner at Time 2 = A2; Lower Achieving Partner at Time 1 = B1; Lower Achieving Partner at Time 2 = B2.

Appendix 1c.

Basic Script for the Indistinguishable Dyad L-SNA model within SIENA

SCRIPT FOR THE MODEL:

mydata1 <- sienaDataCreate(likes, mathre)
myeff1 <- getEffects(mydata1)

myeff1<-includeEffects (myeff1, transTrip)
myeff1<-includeEffects (myeff1, simX, interaction1= "mathre")
myeff1<-includeEffects (myeff1, name = "mathre", avRecAlt, interaction1 = "likes")

Appendix 1d.

Basic Script for the Distinguishable Dyad L-SNA within SIENA

SCRIPT FOR THE MODELS:

mydata1 <- sienaDataCreate(likes, mathre, low, high)
myeff1 <- getEffects(mydata1)

myeff1<-includeEffects (myeff1, transTrip)
myeff1<-includeEffects (myeff1, simX, interaction1= "mathre")
myeff1<-includeEffects (myeff1, name = "mathre", avAlt, interaction1 = "likes")
myeff1<-includeEffects (myeff1, avAltAltX,name="mathre",interaction1 = "low",
interaction2="likes")
myeff1<-includeEffects (myeff1, avAltAltX,name="mathre",interaction1 = "high",
interaction2="likes")

Note. Mathematical Reasoning = mathre; Liked most peer relationships = likes; Lower Achieving Partner in Dyad = low; Higher Achieving Partner in Dyad = high.