Individualized learning potential in stressful times: How to leverage intensive longitudinal data to inform online learning

Abstract

Societal events – such as natural disasters, political shifts, or economic downturns – are time-varying and impact the learning potential of students in unique ways. These impacts are likely accentuated during the COVID-19 pandemic, which precipitated an abrupt and wholesale transition to online education. Unfortunately, the individual-level consequences of these events are difficult to determine because the extant literature focuses on single-occasion surveys that produce only group-level inferences. To better understand individual-level variability in stress and learning, intensive longitudinal data can be leveraged. The goal of this paper is to illustrate this by discussing three different techniques for the analysis of intensive longitudinal data: (1) regression analyses; (2) multilevel models; and (3) person-specific network models, (e.g., group iterative multiple model estimation; GIMME). For each technique, a brief background in the context of education research is provided, an illustrative analysis is presented using data from college students who completed a 75-day intensive longitudinal study of cognition, somatic symptoms, anxiety, and intellectual interests during the 2016 U.S. Presidential election – a period of heightened sociopolitical stress – and strengths and limitations are considered. The paper ends with recommendations for future research, especially for intensive longitudinal studies of online education during COVID-19.

1.0. Introduction

Online learning has proliferated in recent years with the percentage of students enrolled in at least one distance, remote, virtual, or web-based course rising from 8% in 2000 to 35.3% in 2017 (Allen & Seaman, 2017). Recently, the shift to online learning has been abrupt and – for many students across the globe – absolute during the coronavirus (COVID-19) pandemic, with an unprecedented number of elementary, secondary, and postsecondary schools conducting all of their learning virtually. Online learning has the potential to further educational opportunities for many students, offering access to a variety of courses regardless of time or location (Kebritchi et al., 2017), personalized course pacing and content differentiation across students (Sun & Chen, 2016), and cost-savings for both students and schools (Stone, 2017). The promise of online education, however, depends on the institution and individuals, including administrative support and infrastructure, the digital competency of academic staff, and student characteristics (Hofer et al., this issue).

There are many proximal (e.g., student skillset) and distal (e.g., macro-level stress) influences on students’ online learning experiences (see Sailer et al., this issue). Although under-studied, macro-level stressors – such as natural disasters, political shifts, or economic downturns – make unique contributions to students’ learning outcomes and educational experiences. For example, increases in community violence predict increases in learning difficulties and underachievement (Shields et al., 2008), and economic turmoil is associated with decreases in student test scores and academic self-efficacy as well as increases in absenteeism (Motti-Stefanidi & Asendorpf, 2017).

Despite accumulating evidence that macro-level stressors affect learning, it is still largely unknown whether their effects equally apply to all learners, or whether some learners are protected or at particular risk for poor outcomes. In other words, will an individual student flourish or struggle with online learning – and what forms of support will be most effective? This question is especially pressing in the COVID-19 era, as the large scale transition to online learning has made individual differences in learning – and societal inequities related to these differences – abundantly clear to parents and educators. For instance, there is evidence that school disruptions during COVID-19 are associated with learning losses, with larger losses for students from low-income households (Engzell et al., 2020). Individual differences in learning outcomes are widely studied, but outcome data are often aggregated across students, classrooms, or schools, with variability in outcomes conceptualized as noise. This variability, however, may actually contain valuable information about differences between individuals or even the learning of individual students (e.g., minority low-income students in a majority high-income school) that is obfuscated by averaging (Molenaar, 2004). Such individual effects can be revealed through intensive longitudinal data and analytic methods that capture daily biopsychosocial impacts on individual students’ learning potential.

1.1. The Necessity and Utility of Intensive Longitudinal Methods

The notion that data aggregation across students may not represent the learning of individual students is supported by ergodic theory (see the mathematical specification applied to psychological science in Molenaar, 2004). Briefly, studies of interindividual variation (or between-person studies of variation across people) assume that the psychological processes being investigated (e.g., learning) are homogeneous over time and across different individuals (Beltz et al., 2016; Molenaar & Beltz, 2020; Molenaar, 2015). This facilitates generalization beyond the sample to the population from which the sample was drawn. However, these assumptions are rarely tenable because many psychological processes evidence growth and individual differences – as such, these processes are non-ergodic, suggesting that between-person analytic techniques based on interindividual variation may produce spurious results that do not apply to any individual in a sample (e.g., Molenaar & Campbell, 2009). Studies of intraindividual variation (or within-person studies of variation in an individual across occasions) can instead be utilized to study non-ergodic psychological processes at the individual or person-specific level (Beltz et al., 2016; Molenaar & Beltz, 2020; Molenaar, 2015). Such person-specific analyses do not assume homogeneity and accurately capture heterogeneity across participants, but they require intensive longitudinal data (i.e., many repeated assessments of the same variables from the same individuals).

Intensive longitudinal methods are study designs in which participants’ experiences, thoughts, behaviors, or cognitions are repeatedly assessed as they unfold over time (Hamaker & Wichers, 2017; Schafer, 2006). Intensive longitudinal methods utilize sophisticated data collection techniques such as experience sampling (Barrett & Barrett, 2001; Bolger & Laurenceau, 2013; Moeller et al., 2020), ecological momentary assessments (Hufford, 2007; Shiffman et al., 2008), or 6- or 24-hour diaries or surveys (Fisher et al., 2018; Gunthert & Wenze, 2012); they employ a variety of assessment types (e.g., self-report, neuropsychological tests, or physiological monitoring) with frequent measurement occasions that reduce recall bias (Trull & Ebner-Priemer, 2014) and the cognitive aggregation of events (e.g., “How many of the following symptoms did you experience this month?”; Solhan et al., 2009). The proliferation of individual computing devices, such as smartphones, tablets, and laptops, particularly among youth, has increased the feasibility of using intensive longitudinal methods to assess online learning-related behaviors in context (compared to earlier “beeper” studies that required researcher-distributed devices; Raento et al., 2009).

There are a variety of techniques well-suited to the analysis of intensive longitudinal data. They all have the potential to provide insight into important research questions, but their unique features offer comparative advantages and disadvantages. In this paper, three analytic techniques with particular utility for the study online learning are considered. After providing brief definitions, their use in education research is reviewed. In subsequent sections of the paper, conceptual elaborations (with references to the mathematical elaborations) are given for each technique, in turn, including benefits and drawbacks for applications to intensive longitudinal data and the study of online learning.

Many approaches to intensive longitudinal data analysis involve averaging or summing data across assessments and individuals in an attempt to focus on interindividual variation and to make broad generalizations about between-person differences. For example, regression analyses have been used with intensive longitudinal tracking of online learning behaviors (e.g., self-regulation, procrastination, and study intervals) to reveal that aggregated measures of procrastination behaviors and fewer review sessions were associated with lower grade point averages (Li et al., 2018). There is no doubt that these regression techniques have provided valuable insights into education-linked outcomes, but there is growing awareness that students’ learning-related processes are rarely ergodic, challenging the practice of aggregating across assessments and generalizing broadly. Instead, learning-related processes may be dynamic, manifesting over time and in response to individuals’ unique environments (Cook et al., 2018; Hart, 2016).

Recently, multilevel modeling has emerged as the predominant statistical approach for the analysis of intensive longitudinal data because it can model interindividual variation between participants at the same time as intraindividual variation within participants (Bolger et al., 2003; Curran et al., 2004; Schafer, 2006). Although multilevel models are already widely-used in the education and learning literature, they are typically employed to analyze data from hierarchically-structured school-based samples in which lower-level observations (i.e., level one predictors) are nested within higher levels (i.e., level 2 predictors) as students are nested within classrooms or schools. When used with intensive longitudinal data, however, repeated measurements over time (at level one) are nested within students (at level two) to describe between-person patterns in within-person variation or change (i.e., from multiple assessments of the same individual).

Few (if any) intensive longitudinal studies have utilized multilevel models to study online learning specifically, but some have examined behavioral engagement and the cognitive processes underlying learning and achievement. For instance, multilevel models have been effectively utilized with intensive longitudinal data to reveal that within-person (but not between-person) patterns of behavioral engagement (i.e., momentary interest and activity choice) were the strongest predictors (in terms of effect size) of academic engagement, positive and negative affect, and learning perceptions over 20 measurement occasions (Beymer et al., 2020). Further, multilevel model analyses indicated that working memory performance measured across 100 days varied significantly from day-to-day as a function of other subjective experiences, such as affect and motivation (Brose et al., 2012). Thus, multilevel models can estimate between-person effects without aggregating across the within-person assessments that characterize intensive longitudinal data. However, they still may violate ergodic theory’s assumptions of homogeneity and stability in presuming that within-person processes (e.g., learning) operate similarly across individuals (Molenaar, 2015; Sterba & Bauer, 2010).

Person-specific techniques are underutilized for the analysis of intensive longitudinal data, but they may add significant, additional insight into the understanding of learning-related processes that are unique to individuals. These person-specific analysis techniques – such as intraindividual standard deviations (iSD; Nesselroade & Salthouse, 2004), dynamic factor analysis (Ram et al., 2013), and group iterative multiple model estimation (Gates & Molenaar, 2012) – utilize time series (such as intensive longitudinal) data from single participants as if each participant is a sample of one. They consider only intraindividual variation within a person across measurements, and they do not pool or average across people, providing person-specific results that accurately describe that person, but that do not necessarily describe any other person; such person-specificity is a necessity if the process being studied is non-ergodic (Beltz et al., 2016; Fisher & Boswell, 2016; Molenaar & Beltz, 2020).

GIMME has particular promise for the analysis of intensive longitudinal data because it not only is a person-specific technique that generates accurate behavioral networks for individual participants – but without averaging – it allows for those networks to contain some information that describes the full sample and generalizes to the population. It does this by including a so-called “group-level” relation in all person-specific models if there is indication that relation is statistically meaningful for the majority of the sample (usually 75%) using Lagrange multiplier equivalents tests in an iterative data-driven model search (Gates & Molenaar, 2012; Sörbom, 1989); thus, group-level relations in GIMME are included in the networks of all participants, but the direction and magnitude of those relations are person-specific because they are estimated in models that only consist of a single person’s data (N=1). In this way, GIMME is said to contain group-level relations that reflect homogeneity and facilitate generalization as well as individual-level relations (included and estimated uniquely for each person) that reflect heterogeneity. The relations also contain temporal information. They can be time-locked (i.e., contemporaneous or occurring at the same measurement occasion) or time-lagged (marking prediction from one measurement occasion to the next). There are several explications and tutorials on GIMME that describe its mathematics, model fitting, and development, which are supported by its performance accuracy in extensive simulations (Beltz & Gates, 2017; Gates & Molenaar, 2012; Lane et al., 2017).

GIMME has provided important person-specific insights into non-ergodic behavioral (Beltz et al., 2013; Kelly et al., 2020a), developmental (Beltz et al., 2013), and clinical processes (Dotterer et al., 2019; Ellison et al.; Wright et al., 2016). Excitingly, recent work suggests GIMME may have utility in education-related research, too: GIMME was utilized to assess person-specific associations between teacher feedback, student motivation, and mental health in a sample of 59 students across 30 measurement occasions, revealing that student motivation and teacher feedback were associated for some students at the individual-level (and not at the group-level), with considerable heterogeneity between individuals in the directionality, magnitude, and temporal nature of the relations (Thompson et al., 2020). These recently-reported findings suggest that the field is ripe to incorporate more intensive longitudinal methods and novel, personalized analytic techniques into the study of online learning, especially during stressful times that accentuate heterogeneity.

1.2. The Current Study

A focus on the individual is an essential, but relatively unexplored, component of online education. Many programs advertise personalized learning experiences for students with different learning styles and backgrounds (Yu et al., 2017) or claim to provide precision education services (Makhluf, 2020), but have educational programs based solely on evidence from traditional methods that do not measure or model heterogeneity within students across time. There is increasing evidence that cognitive learning potential (e.g., the capacity for learning) varies within individuals from day-to-day (Kelly & Beltz, 2020), so it is unlikely that current cross-sectional or short-term longitudinal research designs assessing the efficacy of online education are accurately capturing student experiences or outcomes, especially during the COVID-19 pandemic and similar societal events that may act as a “stress test” for educational systems which exacerbates individual differences (Sailer et al., this issue).

Despite their promise, intensive longitudinal methods and their accompanying analytic techniques may be unfamiliar to many researchers, leaving significant questions about online learning during COVID-19 unanswered or under-explored. Therefore, the aim of this paper is to expand educational researchers’ methodological tool set by: (a) describing three different techniques for the analysis of intensive longitudinal data; and (b) demonstrating how the ergodicity-related assumptions underlying each technique may impact inferences about psychological influences on online learning potential during stressful times. This will not only provide a deeper understanding of the theoretical, methodological, and statistical affordances of different approaches, but also help readers identify the best methods available to answer their specific research questions related to societal stress and learning.

The three analysis techniques for intensive longitudinal data reviewed are traditional regression approaches (that require aggregating across measurement occasions), multilevel modeling, and person-specific network modeling via GIMME. For each technique, a conceptual description is provided, a potential research question is listed, and a brief overview of data processing and analysis steps is shared, all while comparing and contrasting differences in model assumptions and interpretations as well as advantages and disadvantages. To concretize the comparisons, illustrative data from a subsample of college students whose completion of an online 75-day diary study overlapped with the 2016 U.S. presidential election and inauguration (i.e., election group; conceptualized as a macro-level stressor based on prior work; Hoyt et al., 2018; Stanton et al., 2010), as well as a control group of students whose daily data were collected a year later in 2017 were used. The illustrative data answer the overarching question: How do daily psychological processes contribute to daily learning potential during a period of heightened sociopolitical stress? Although participants in the study were not taking classes, an online test of working memory was used as an indicator of daily learning potential, and daily somatic symptoms, anxiety, and intellectual interests were hypothesized to be psychological influences on that potential. The paper closes with suggestions for future work that may illuminate how online learning in the COVID-19 era is impacting the education of individual youth.

2.0. Illustrative Data

Illustrative data come from a larger 75-day daily intensive longitudinal study on sex hormones, affect, and cognition in young adults. Participants selected for inclusion (N = 26; M_age = 19.32; 77% White) were matched across year (2016 election group vs. 2017 control group) on sex, age, and race/ethnicity and only included enrolled college students who completed 80% (or more) of the daily assessments, as less than 20% missing data in intensive longitudinal designs has been shown to have little impact on inferences (Rankin & Marsh, 1985). Data were collected between September 2016 and September 2018. During the study, each day at 5pm, participants received a unique link to a 20-minute Qualtrics survey that they were asked to complete online after 8pm or after that day’s activity on an electronic device (e.g., smartphone, tablet, or computer) with measures presented in the same order each day. Each diary included reports of daily experiences, standard psychological questionnaires, and the cognitive and personality measures that are the focus of this analysis. Additional details are available in other reports using this data set (Foster & Beltz, 2020; Kelly & Beltz, 2020; Kelly et al., 2020b; Weigard et al., 2019).

Working memory was conceptualized as an indicator of online learning potential and was assessed with a validated intensive longitudinal measure of delayed verbal recall (Kelly & Beltz, 2020). Participants were presented with five sets of word pairs (for 2 seconds each) and instructed to remember them. At the end of each survey, they were presented with the first word of the pair and asked to type the second word in a text box. Correct responses (including misspellings that did not generate new words) were awarded 1 point, and inaccurate plurals were award a half point; thus, daily scores ranged from zero to five. Somatic symptoms was assessed using three items from the Daily Inventory of Stressful Events (DISE; Almeida & Kessler, 1998), a measure designed for and widely used in intensive longitudinal data collection, in which participants indicated the extent to which they experienced body aches, cold or flu-like symptoms, or stomach pain (1 = “None of the time” to 5 = “All of the time”). Items were averaged to create a daily composite score. Anxiety (3 items related to daily experiences of worry, tension, or anxiety) and intellectual interests (3 items related to daily experiences of speculation, curiousness, and abstract reasoning) were assessed using valid and reliable rationally or analytically derived subscales from a daily version of the 60-item NEO-Personality Assessment (Costa & McCrae, 1985; Saucier, 1998). Participants indicated the extent to which they agreed with statements describing the way they felt that day on a 5-point Likert scale (1 = “Strongly disagree”; 5 = “Strongly agree”), and items from the subscales were averaged separately to create daily composites. Personality subscale composites are commonly used in intensive longitudinal research (Borkenau & Ostendorf, 1998; Hudson et al., 2020; Wendt et al., 2020). Descriptive statistics and zero-order correlations are presented in Table 1.

Table 1.

Descriptive Statistics and Variable Correlations for Illustrative Data by Group

	Mean (SD)	Correlations
		1	2	3
2016 Election Group (n=13)
1. Delayed verbal recall	3.62 (.97)	-
2. Somatic symptoms	1.47 (.40)	−.50†	-
3. Anxiety	2.69 (.55)	−.08	.25	-
4. Intellectual curiosity	2.99 (.47)	.35	.15	.39
2017 Control Group (n=13)
1. Delayed verbal recall	3.35 (.88)	-
2. Somatic symptoms	1.47 (.32)	.29	-
3. Anxiety	2.58 (.65)	−.10	.26	-
4. Intellectual curiosity	2.82 (.69)	−.36	−.16	.27

Notes:

^†p < 0.10

^*p < 0.05,

^**p < 0.01,

^***p < 0.001.

SD = standard deviation.

3.0. Analysis Techniques for Intensive Longitudinal Data

The illustrative data were analyzed using three different techniques that are often used with, or that have significant potential for use with, intensive longitudinal data: regression, multilevel models, and person-specific networks via GIMME. All analyses were conducted in R v1.2.5033 (Team, 2017); specific packages utilized for each analysis are listed below. Although detailed results are provided in Supplemental Materials, the focus here is on the affordances of each technique for inferences about the daily learning potential students ‘bring to the computer’. Thus, interpretations – conceptually, as depicted in figures, and in terms of variance explained (R²) – of the relation between verbal recall (i.e., daily learning potential) and three psychological predictors (i.e., somatic symptoms, anxiety, and intellectual interests) were considered in order to highlight the utility and limitations of each technique.

3.1. Regression Analyses

Traditional regression techniques are often used with intensive longitudinal data to answer education-related research questions. To make the data amenable to these techniques, assessments are usually aggregated across measurement occasions so that between-person inferences can be made based on interindividual variation. The mathematical bases and assumptions of regression analyses are widely known (see Tabachnick et al., 2007). Most relevant intensive longtudinal data collection, however, are that regression analyses assume that the sample is homogeneous, that predictors are independent and operate on outcomes in similar ways, and that unexplained variation is random (i.e., not containing meaningful information about individual differences); these assumptions are necessary corollaries of the ergodic theorem that facilitate the extrapolation of sample-level findings to a population (Tabachnick et al., 2007).

3.1.1. Regression Illustration

Data from the 75-day assessments of verbal recall, somatic symptoms, anxiety, and intellectual interests were analyzed using a regression to answer the question, “What is the generalizable contribution of daily psychological factors to learning potential for college students during 2016 election and for students one year later?” Specifically, data were aggregated by person across days to create separate, mean composites for verbal recall, somatic symptoms, anxiety, and intellectual interests. Then, in separate regression models, verbal recall was regressed onto group (0 = election, 1 = control), each grand mean centered predictor (Step 1), and their interaction (Step 2) using the lm function in R (https://cran.r-project.org/web/packages/tidypredict/vignettes/lm.html).

Inferential statistics from the regression analyses are provided in Supplemental Materials (Table S1), and scatterplots of the associations between verbal recall and each predictor by group are provided in Figure 1. Each data point represents the relation between verbal recall and a predictor variable for an individual, aggregated over 75 days. Trendlines represent group-level effects, which are the focus of the regression analyses (black: 2016 election group; gray: 2017 control group). The pattern of relations between verbal recall and each psychological predictor differed. For somatic symptoms, there was a negative association for the election group, but a positive association for the control group, suggesting increased physical symptoms predicted worse verbal recall during times of stress. For anxiety, there was no evident association for either group, suggesting it was not related to verbal recall. For intellectual interests, there was a positive association for the election group and a negative association for the control group, suggesting that high intellectual interest predicted increased verbal recall during times of stress.

Figure 1.

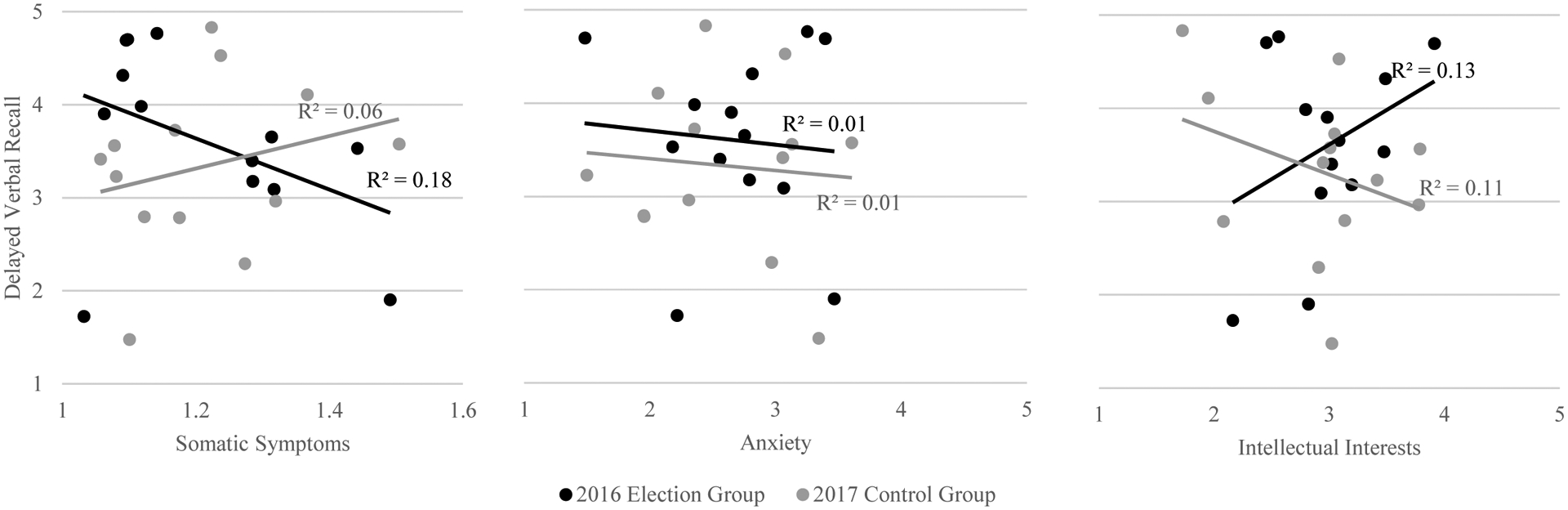
Scatterplots depicting results of a regression analyses used to analyze 75-day intensive longitudinal data (aggregated across individual students and days). Dots represent individuals’ paired scores between delayed verbal recall and a psychological predictor (i.e., somatic symptoms, anxiety, or intellectual interests), and lines represent the group-level trends between delayed verbal recall and the predictors. Black dots and lines reflect the 2016 election group, and gray dots and lines reflect the 2017 control group. R² reflects the proportion of variance in delayed verbal recall explained by each predictor for each group.

Although these results provide some preliminary evidence that the generalizable contribution of daily psychological factors to verbal recall may vary with macro-level stress, the R² – which represents the amount of variation in verbal recall captured by each predictor – and the comparison of individual points to the regression trendlines add significant nuance. For example, the R² indicates that the trendline for the somatic symptoms’ predictor captures a greater proportion of variance in verbal recall (R² = .18) for those in election group than for those in the control group (R² = .06). Further, the low R² for anxiety across both groups suggests that the trendlines are not capturing any meaningful information about the relationship between anxiety and verbal recall, and even though the R² is similar for both groups for intellectual interests, most individuals have scores around 3, so effects are driven by a few disparate values and by no means equally characterize all individuals. Regarding individual points, some students in the election and control groups have very similar sets of scores (e.g., those with lowest somatic symptoms and verbal recall scores, and many with mid-range intellectual interests and verbal recall scores), indicating that the average trendlines provide equally poor characterizations of some individuals in both groups. Thus, although these inferences provide some meaningful information about the generalizable contributions of psychological factors to learning potential during stressful times, they also misrepresent many individuals, and thus, call into question the accuracy of the generalizations.

3.1.2. Advantages and Limitations of Regression Analyses

There are several advantages of using regression techniques for the analysis of intensive longitudinal data. For instance, if influences on verbal recall are stable, then collapsing data across many assessments can minimize measurement error compared to single-occasion assessments, providing reliable estimates of learning-related processes (Tabachnick et al., 2007). Further, if assumptions about homogeneity – that individuals are similar to each other and that constructs act in similar ways within individuals over time – are true, then regression analyses that aggregate data can provide generalizable information about associations between variables (e.g., anxiety is not differentially related to verbal recall during times of heightened sociopolitical stress vs. calm). This is particularly useful for researchers and educators who aim to use empirical results in prevention and intervention efforts (e.g., interventions on teacher technology training have utilized regression analyses to determine that training benefits student achievement; Bond et al., 2018). Finally, regression analyses are flexible: Researchers can ask questions that utilize multiple data types (e.g., observational, self-report, and behavioral) with continuous, categorical, or ordinal data, model non-linear processes often evident in learning and education research (e.g., teacher effectiveness; Lazarev & Newman, 2013), or utilize sophisticated data collection methods, such as planned missing designs that reduce participant burden and increase study completion (Graham et al., 2006).

Although regression analyses may capture meaningful interindividual variation, growing evidence suggests that the assumptions inherent in the aggregation of data over time and between-person effects that generalize across people are unlikely to be tenable with respect to students’ learning potential in stressful times. First, regression analyses assume that predictors are independent even though learning-related processes are often correlated (e.g., students who experience anxiety tend to also report heightened stress; Salari et al., 2020). Second, analyses in education research often require making between-person inferences from clustered data (e.g., students within schools or time within students). When these data are analyzed without consideration of clustered effects, it can lead to high rates of Type I errors. Third, regression analyses are sensitive to outliers and other “noisy” data which may drive significant findings, as evidenced by several disparate scores in Figure 1 (Tabachnick et al., 2007). Although researchers have access to a variety of techniques (e.g., winsorizing or removing extreme values) to remove outliers, “noise” may actually be signal – reflecting important information about individuals (Molenaar, 2004). Finally, regression analyses assume that individuals are similar to each other and across time, however, Simpson’s paradox (Kievit et al., 2013) suggests that significant associations between individuals may be non-significant, or even reversed when subgroups or within-person processes are considered. This – along with evidence of non-ergodicity in verbal recall-associated learning processes – can be seen in Figure 1, as group-level trendlines do not characterize individuals equally well, particularly students with similar scores who are in different groups. Thus, analytic techniques that reflect individual variations over time and from group differences are necessary.

3.2. Multilevel Models

Multilevel models leverage the strengths of intensive longitudinal data by utilizing all data across time without aggregation to examine whether there are between-person differences or patterns in within-person variation (Bryk & Raudenbush, 1992). Multilevel models do this by accounting for the nested structure of the data (e.g., daily observations clustered within individual students) and adjusting for dependencies in the between-person estimates (i.e., fixed effects), while also calculating individual variation from those estimates (i.e., random effects). Their mathematical bases and assumptions are established (Bryk & Raudenbush, 1992; Ram & Grimm, 2016; Sterba & Bauer, 2010), but as their applications to intensive longtudinal data are uncommon in education, some relevant assumptions are worth stating: Namely that relationships between variables are linear (although multilevel models can be extended to examine non-linear relationships); that variance and covariance are homogenous across individuals; and that error terms are normally distributed (Schafer, 2006).

3.2.1. Multilevel Models Illustration

The illustrative data were analyzed using multilevel modeling to answer the question, “What are the between- and within-person contributions of daily psychological factors to 75-day learning potential for college students during the 2016 election and for students one year later?” Predictors in the model were day (centered at zero) and somatic symptoms, anxiety, and intellectual interests (grand mean centered, as is most common in multilevel modeling). A series of three models for each psychological predictor was estimated using restricted maximum likelihood (REML) in R (lmer4 package; https://cran.r-project.org/web/packages/lme4/index.html), which provides unbiased variances for small sample sizes (McNeish, 2017), using an unstructured error covariance. The models were compared using the Akaike Information Criteria (AIC), an indicator of relative fit in which lower values indicate better fit (Bryk & Raudenbush, 1992). First, correlated observations within students (i.e., from the 75 days) were considered in a random-intercept model in which students could deviate from the average verbal recall (i.e., fixed effect). Next, main effects (i.e., day, group, and the level-one psychological predictor) were added with random slopes, such that students could deviate from the average relations between psychological predictors (i.e., somatic symptoms, anxiety, and intellectual interest) and verbal recall. Finally, a moderation of psychological predictor by year was added. Primers and detailed tutorials on implementing multilevel models, particularly with intensive longitudinal data, are provided elsewhere (Bolger & Laurenceau, 2013; Foster & Beltz, 2018).

Multilevel model results are presented in Supplemental Materials (Table S2), and model-predicted relationships between verbal and each predictor and by group are provided in Figure 2. Each thin line represents an individual’s relation between verbal recall and each psychological predictor. Thick lines represent the fixed effects (i.e., between-person trends in interindividual variation for each psychological predictor) from which the random effects (i.e., individual deviations from the fixed effects based on within-person intraindividual variation; thin lines) are derived, as predicted using a linear mixed-effect model. R²s, representing the amount of variance in verbal recall explained by each predictor via the variation in random slopes as well as the variation of the random intercept, were calculated using the r2mlm package in R (https://cran.r-project.org/web/packages/r2mlm/index.html).

Figure 2.

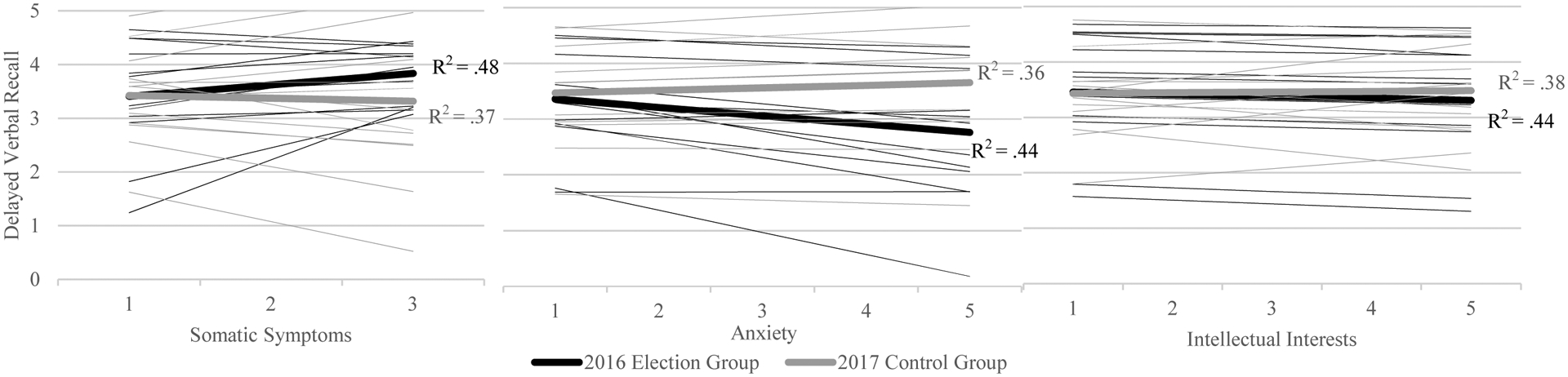
Line graphs depicting results of a multilevel model used to analyze 75-day intensive longitudinal data. Thick lines represent the fixed effects between delayed verbal recall and a psychological predictor variable (i.e., somatic symptoms, anxiety, or intellectual interests), and thin lines represent individual deviations from those group-level estimates. Black lines reflect the 2016 election group, and gray lines reflect the 2017 control group. R² reflects the proportion of variance in delayed verbal recall explained by each predictor for each group via the variation in fixed and random slopes as well as the variation of the random intercept (calculated using r2.MLM in R; https://cran.r-project.org/web/packages/r2mlm/index.html).

As with the regression analyses, the relations between verbal recall and each psychological predictor evidenced group differences (i.e., fixed effects), but the direction of the relations differed between the regression and multilevel models. In contrast to the regression findings, higher somatic symptoms was associated with better verbal recall for the election group (R² = .48), but not for the control group (R² = .37). While anxiety was not associated with verbal recall for either group in the regression analyses, the multilevel model results indicated that more anxiety was associated with worse verbal recall for the election group (R² = .44), but with better verbal recall for the control group (R² = .36); thus, high anxiety during stressful times was linked to reduced verbal recall. Changes in the group-level direction of effects from the regression to the multilevel model techniques are expected, given the significant heterogeneity across students and time in these relations; it is reasonable that changes in the modeling of within-person effects based on intraindividual variation might alter inferences. Unlike the regression findings, variation in intellectual interest was not associated with verbal recall for either group (election: R² = .44, control: R² = .38); this change in inferences is not surprising because most individual mean scores hovered around 3 for intellectual interests, suggesting that the significant results in the regression analyses may have been driven by atypical scores. Finally, the R² increased from the regression analyses to the multilevel models. Although this may be due in part to how R² is estimated in multilevel models, it is clear that the multilevel models explained greater variation in the data, owing to the inclusion of within-person effects. Overall, the multilevel model findings suggest that individual verbal recall performance can be predicted by psychological factors over many measurement occasions, and that interindividual differences may explain some (but not all) of the variation in that performance.

As in the regression results, the between-person results from the multilevel models provide some indication of a generalizable relation between verbal recall and psychological factors linked to learning potential during stressful times, but it is still unclear whether the within-person effects accurately reflect learning-related processes for each student. As, within-person effects are estimated in accordance with between-person effects in multilevel models, the two cannot always be disassociated (Curran & Bauer, 2011; Curran et al., 2004), and so, ergodicity-linked assumptions about homogeneity over time and people may be violated (Schafer, 2006). For instance, although the fixed effects indicate that higher somatic symptoms are associated with better verbal recall in the election group, several students’ associations are nearly flat and may be better characterized by the control group trendline (see Figure 2). The estimation of fixed and random effects in the same model can also constrain the functional form of the individual relations. This is also seen in Figure 2, as several students’ relations exceeded the verbal recall maximum score and were cut off by the upper bounds of the graph, suggesting that a quadratic or spline model may have been better characterizations for them. Thus, although certain individuals are well characterized by the between-person trends, many are not.

3.2.2. Advantages and Limitations of Multilevel Models

There are several advantages of using multilevel models to analyze intensive longitudinal data in education research. The primary one is that, unlike traditional regression techniques, multilevel models do not assume independent data; thus, they can actually take advantage of the multiple, nested measurement occasions to estimate both group-level effects and individual variations from those effects (Bryk & Raudenbush, 1992). Because multilevel models account for between-person differences across groups (i.e., fixed effects) and within-person variation from them (i.e., random effects) instead of leaving that variation unexplained or assuming it is random and can be aggregated, multilevel models have additional explanatory power to detect effects obfuscated by averaging. This is seen in the relation between anxiety and verbal recall in Figure 2, which was basically non-existent in the regression analyses but showed a negative trend for the election group in the multilevel models. Further, multilevel models are flexible with multiple extensions (Bock, 2014; Grimm & Ram, 2009; Klein & Kozlowski, 2000), centering options for the interpretation of different research questions (Hamaker & Grasman, 2015; Wang & Maxwell, 2015), and the ability to model individual-level trends over time (e.g., with empirical Bayes estimates; Strenio et al., 1983). For example, if interested in trajectories, researchers could include random intercepts and slopes for their time variable (e.g., day), which could indicate the extent to which individuals vary from their group at the beginning of the study and in their pattern of change over time, respectively (Grimm & Ram; Ram et al., 2013; Ram & Grimm, 2016).

Although multilevel models have many strengths, they also have some limitations when used with intensive longitudinal data. First, as in regression analyses, multilevel models are susceptible to outliers when calculating both between- and within-person effects; they can bias parameter estimates and inflate standard errors (Kloke et al., 2009; Wang et al., 2015). Second, the nested error structures of multilevel models can cause challenges for model convergence, especially if models have many random effects or potential bidirectional effects. Although some of these problems can be overcome using a structural equation modeling approach (see Hox & Stoel, 2014), challenges persist, and complex models are difficult to interpret, especially if samples are small. Relatedly, it can be difficult to disaggregate between- and within-person effects in multilevel models: One fundamental concern is that the relation between two variables may differ at the between-person level and the within-person level resulting in challenges with model parameterization and interpretability (Curran & Bauer, 2011; Curran et al., 2004). Third, multilevel models can still misspecify individual effects or trajectories. This is particularly relevant for non-ergodic learning processes that are often tracked in heterogenous populations over time; for example, evidence indicates that youth with IEPs follow different, sometimes non-linear, cognitive trajectories (Castellanos et al., 2002; Rucklidge & Tannock, 2002). If only a minority of a sample, these youth may not be well-represented by linear effects that characterize the majority of the sample.

3.3. Person-specific Network Models: GIMME

GIMME is a person-specific technique for the analysis of intensive longitudinal data ideal for the study of heterogeneous, non-ergodic learning-related processes (Gates & Molenaar, 2012). The mathematical specification of GIMME has been detailed in several articles and tutorials (e.g., Beltz & Gates, 2017; Gates & Molenaar, 2012). Conceptually, GIMME uses a group-level algorithm when fitting person-specific unified structural equation models (Gates & Molenaar, 2012), which integrates structural equation models (to examine contemporaneous or same-occasion relations) and vector autoregressive models (to examine time-lagged relations). Specifically, GIMME creates sparse person-specific networks of directed relations among a set of variables for each individual in a sample, but those networks contain both contemporaneous and lagged relations that are estimated for everyone in the sample (i.e., group-level) or uniquely for a person (i.e., individual-level); because the networks are person-specific, even so-called group-level relations are estimated separately within each participant’s intraindividual data and without averaging across participants. Although they are directed, the variable relations in GIMME networks do not imply causality, but instead reflect temporal covariation.

Many of these unique features of GIMME are afforded by the data-driven way it fits uSEMs to person-specific data. GIMME begins with a null (or empty) model for each person, and attempts to maximally explain variation among a set of variables using Lagrange Multiplier testing (i.e., modification indices; Sörbom, 1989) to determine whether estimating a relation (contemporaneous or lagged) between two variables would significantly improve a person’s model fit. If the same relation would improve model fit for a majority of the sample (75% based on simulations), then that group-level relation is estimated in the person-specific networks of everyone in the sample. This procedure iterates until there are no more relations that would improve the models of 75% of the group. Next, Lagrange Multiplier testing is used to determine if there are additional relations that could be added to each individual’s network that would significantly improve their (potentially) ill-fitting model. If so, the individual-level relation is estimated, and the procedure iterates until the person’s network fits the data well or until there are no more significant relations to add. A confirmatory model is then estimated for each person and evaluated with standard fit indices (Beltz & Gates, 2017; Gates & Molenaar, 2012; Lane et al., 2017).

3.3.1. GIMME Illustration

The illustrative data were analyzed using GIMME to answer the question, “What are the person-specific interrelations between daily psychological factors and learning potential for college students during the 2016 election and for students one year later?” Like similar time series approaches, GIMME assumes stationarity, so each person’s data were detrended by regressing each psychological variable and verbal recall onto day for each person and using the residuals in the subsequent analyses (Beltz & Gates, 2017). Separate GIMME networks were generated for the election group and the control group using the 75% criterion for group-level relations (as recommended by large scale simulations in Gates & Molenaar, 2012) using the gimme package in R (https://cran.r-project.org/web/packages/gimme/index.html). These group-level relations (reflecting homogeneity) were then evaluated, and the election and control groups were compared on network complexity (i.e., the number of relations in each network), which reflects the extent of integration among psychological factors underlining verbal recall.

Results showed that all person-specific GIMME networks fit the data well and contained both group- and individual-level relations; see Table S3 in Supplemental Materials. Group-level relations, summary individual-level relations, and exemplary person-specific networks are presented in Figure 3. Figures 3A–B depict summary networks with variable “nodes” depicted by circles, and with relations (or “edges”) between the variables depicted by directed arrows. The group-level relations (estimated for all when significant for 75% or more of a group) are represented by thick black lines, and the individual-level relations are represented by thin gray lines with their thickness corresponding to the proportion of students in the group who had that particular relation in their network. The contemporaneous (or same-day) relations are represented by solid lines, and the lagged (or next-day) relations are represented by dashed lines; thus, nodes that have dashed loops back to themselves have auto-regressive effects (e.g., yesterday’s anxiety predicts today’s anxiety).

Figure 3.

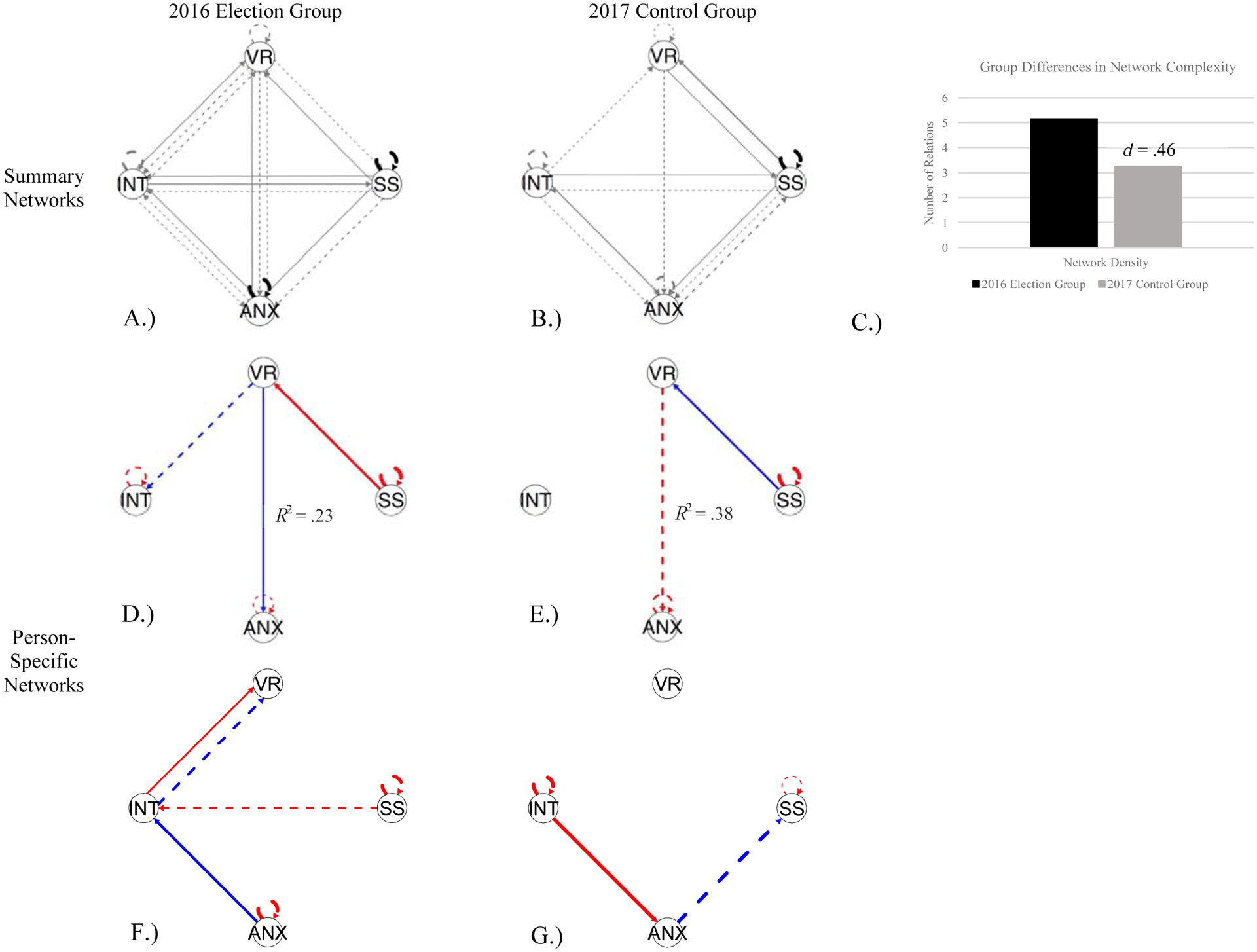
Networks depicting results of a person-specific model (i.e., GIMME) used to analyze 75-day intensive longitudinal data. Circles reflect nodes/variables, solid lines reflect same-day relations, dashed lines reflect lagged next-day relations, black lines reflect group-level relations in summary networks, gray lines reflect individual-level relations in summary networks (thickness is proportion of students with a given relation), blue lines reflect negative relations in person-specific networks, and red lines reflect positive relations in person-specific networks; for blue and red lines, thickness reflects relation magnitude. All networks fit the data well; see Supplemental Materials Table S3 for fit indices. A.) Summary network for students during a period of heightened sociopolitical stress (i.e., the 2016 election group) with two group-level autoregressive effects for somatic symptoms and anxiety. B.) Summary network for students in 2017 (i.e., the control group) with one group-level autoregressive effect for somatic symptoms. C.) Group differences in network complexity (i.e., the number of connections per network). D.) Example student-specific network from the election group with a negative, contemporaneous relation between verbal recall and anxiety (among others). E.) Example student-specific network from the control group with a positive, lagged relation between verbal recall and anxiety (among others). F.) Example student-specific network from the election group demonstrating denser relations with four edges and two autoregressive effects. G.) Example student-specific network from the control group demonstrating more sparse relations with two edges and two autoregressive effects. The R² reflects the strength of the relation between delayed verbal recall and anxiety for an individual student (calculated using a formula developed by Peterson & Brown, 2005). VR = delayed verbal recall; SS = somatic symptoms; ANX = anxiety; INT = intellectual interest.

Focusing on the group-level relations in Figures 3A–B, both the election and control group experienced persisting effects of somatic symptoms (i.e., autoregressive loop), and the election group additionally experienced a persisting effect of anxiety, providing some potentially generalizable evidence that macro-level stressors may systematically impact daily anxiety. Differences in network complexity (i.e., the number of connections in a network) are depicted in Figure 3C. Across individuals, the election group had greater network complexity than the control group (d = .46), which in this context, could reflect disruption of learning-related processes during stressful times and potential compensatory behavioral mechanisms.

Figures 3D and 3F represent exemplary student networks from the 2016 election group, whereas Figures 3E and 3G represent exemplary students from the 2017 control group. Negative relations between nodes are represented by blue lines, whereas positive relations between nodes are represented by red lines, with magnitude of the relations represented by line thickness. As in the summary models, solid lines reflect contemporaneous – or same day – relations while dashed lines reflect lagged – from one day to the next – relations. Although the person-specific networks demonstrate considerable heterogeneity, consistent with the summary maps and indices of network complexity, the 2016 student networks are denser than the 2017 student networks. For example, the 2016 student network in Figure 3D had a total of six relations (i.e., one positive, two negative, and three auto-regressive), whereas the 2017 student network in Figure 3E was sparser with four relations (i.e., one positive, one negative, and two autoregressive). Moreover, both of these student networks contained a relation between verbal recall and anxiety, but the magnitude and temporal nature of the relation differed. The relation between verbal recall and anxiety in the 2016 student network (Figure 3D) was negative and contemporaneous suggesting that there was daily correspondence between increased anxiety and decreased verbal recall. The relation between verbal recall and anxiety in the 2017 student network (Figure 3E) was positive and lagged, suggesting that today’s anxiety predicted tomorrow’s verbal recall. While the R² in regression and multilevel model models reflected the amount of variance captured by the model, in GIMME, the R² (calculated via Peterson & Brown, 2005) illustrates the magnitude of the relation between verbal recall and anxiety (2016 R² = .08 vs. 2017 R² = .13) for these specific students. Thus, the relation between verbal recall and anxiety is not only qualitatively different for these two individuals, but also quantitatively different.

Importantly, the student networks in Figures 3D and 3E, including their associations between verbal recall and anxiety, are not representative of all individuals within their respective group; if they were, the relations would have appeared at the group-level instead of at the individual-level in GIMME. For example, the 2016 student network in Figure 3F had four relations with intellectual interests and a feedback loop between intellectual interests and verbal recall (i.e., contemporaneous and lagged relations between intellectual interests and verbal recall), indicating a daily exchange between personality characteristics and learning potential. In contrast, the 2017 student network in Figure 3G only had two relations with anxiety and no relations with verbal recall, suggesting that learning potential was not integrally linked to somatic symptoms, anxiety, or intellectual interests for this learner. Thus, daily relations among psychological factors and learning potential are non-ergodic, as captured in the disparate person-specific networks of intraindividual variation estimated via GIMME.

3.3.2. Advantages and Limitations of GIMME

GIMME, which simulation studies indicate consistently and reliably detects true effects across heterogenous samples due to its unique way of identifying group-level relations in person-specific networks (Gates & Molenaar, 2012), has several noted advantages over regression and multilevel model techniques for analyzing intensive longitudinal data. GIMME avoids the major pitfalls of regression approaches by completely avoiding averages, and yet, estimating associations that represent homogeneity (i.e., group-level relations) and heterogeneity (i.e., individual-level relations. Unlike multilevel models, GIMME first estimates group-level relations (based on common patterns – not averages – across individuals) and then estimates individual-level relations in a student’s data, allowing participants to have unique patterns of associations that are not constrained by between-person effects. GIMME also uniquely considers the impact of time – using time series-based methods to estimate both contemporaneous and time-lagged relations, which has been shown to be important for accurate parameter estimation (Gates et al., 2010). Together, these advantages allow researchers to make generalizable group-level inferences about learning and behavior over time, while still accounting for heterogeneity evident in daily experiences and learning. This has particular utility for the study of online education. As online education courses become more personalized, GIMME can be utilized to meaningfully describe relations underlying successful learning that are applicable to all individuals (e.g., linked to teacher preparedness) as well as relations specific to certain individuals (e.g., family conflict). Networks could thus become a complementary component of precision education services and could be used to further understand why some students tend to fail or drop out of online education courses at greater rates than others.

Despite these advantages, GIMME has some limitations. GIMME requires intensive longitudinal data collection with over 60 measurement occasions that are equally-spaced (Lane et al., 2019); neither of these strict requirements is needed for regression or multilevel model analyses. This may prove difficult for educators and researchers seeking to use intensive longitudinal data to improve the efficacy of online learning outcomes during stressful times when data collection may be disrupted due to scheduling changes (Ting et al., 2020). GIMME also assumes stationarity, but that may not be realistic for learning-related behaviors, especially during periods of heightened macro-level stress, which is characterized by temporal variability. For example, the COVID-19 pandemic may have been more disruptive early in Spring 2020 when courses abruptly transitioned to virtual administration than in Fall 2020 when students and teachers were familiar with digital tools for online education. Thus, research questions aimed at understanding change over longer periods of time or processes linked to development may require a novel application of GIMME (e.g., using sliding windows; Beltz & Gates, 2017) or may be better served by multilevel models or other longitudinal modeling techniques (e.g., Ou et al., 2017), which have their own limitations. Finally, GIMME is not immune to data or model specification issues. Outliers can impact person-specific network estimation (although this somewhat attenuated at the group-level because GIMME does not use averages), and models can fail to converge, be misleading, or be challenging to interpret if they are overly complex, contain many bidirectional relations, or are based on data with missing or unequal measurement occasions.

4.0. Discussion

There is significant heterogeneity among students and in online learning experiences that are accentuated by stressful societal events, such as the 2016 U.S. Presidential election and the COVID-19 pandemic (Beltz & Gates, 2017; Bond et al., 2018; Brose et al., 2012; Hoyt et al., 2018). As indicated by ergodic theory, it is clear that this heterogeneity poses a unique challenge for understanding the learning potential of individual students, and for generalizing empirical research to optimize virtual education platforms. Fortunately, intensive longitudinal data – and the techniques used to analyze them –provide a unique opportunity to meet these challenges by revealing influences on the learning potential of individuals, with person-specific network techniques holding particular promise. The aim of this paper was to examine ways in which education researchers can leverage intensive longitudinal data to make inferences about daily factors that influence the learning potential students ‘bring to the computer’. Three analysis techniques (i.e., traditional regressions, multilevel models, and GIMME) were reviewed, and a 75-day empirical dataset from a period of heightened sociopolitical stress (i.e., college students during the 2016 U.S. Presidential election and students a year later in 2017) was used to illustrate the questions that could be answered with intensive longitudinal methods, as well as the strengths and limitations of each technique, with a focus on how the techniques model the data of individual students.

4.1. Summary

Each analysis technique provided different insights into the learning potential of individuals; this was expected because learning-related processes vary across students and time (i.e., they are non-ergodic process), and the analytic techniques handle this variability in disparate ways. Regressions were used to examine the generalizable contributions of psychological factors (i.e., somatic symptoms, anxiety, and intellectual interests) to learning potential (i.e., the capacity for learning as indexed by daily verbal recall). Data were aggregated across days, and although results indicated distinct influences of each psychological factor (and no links between anxiety and verbal recall), the regression trends did not reflect individual differences well.

Multilevel models were then used to adjust for the correlated nature of the data (i.e., measurement occasions nested within students), providing more accurate estimates of the between-person (i.e., fixed) effects as well as estimating within-person (i.e., random) effects that demonstrated how students deviated from their groups (i.e., the 2016 election versus 2017 control groups). Results showed a different pattern of relations between psychological factors and learning potential (e.g., anxiety predicted decreases in verbal recall for the election group only), but there was significant variation among students, whose individual trends were constrained by the average trend of their group.

Finally, GIMME was used to create person-specific networks for each student that contained group-level information without using averages. Although GIMME revealed some group-level autoregressions (e.g., anxiety predicted itself over time only for the 2016 election group), the person-specific networks highlighted the individualized interplay among learning-related behaviors, and the apparent misrepresentation of individual learners in regression analyses and multilevel models, which assume at least some degree of homogeneity across students in order to leverage the ergodic theorem to make generalizations.

Ultimately, the technique most appropriate for intensive longitudinal data analysis depends on the objectives of a particular study and the nature of the data available to achieve them. Regression techniques provide essential information about the population of learners and learning potential as a construct. With few or many assessments, aggregating data from students across time or classes can yield a measure of the “shared perception of the class environment” (Lüdtke et al., 2009) – at least when students are homogeneous. Multilevel models are particularly useful for educational research because they account for the correlated nature of most school-based data – that students are nested within classrooms within schools or that repeated measurements are nested within individuals (Bryk & Raudenbush, 1992). Multilevel models also provide substantial information about within-person learning-related processes as they unfold over time (from just a few to hundreds of assessments), although it can be difficult to parse between- and within-person effects (Curran & Bauer, 2011). GIMME and other person-specific modeling techniques (e.g., dynamic factor analysis; Epskamp & Fried, 2018) are well-suited for examining intraindividual variation in heterogeneous populations (e.g., students with IEPs). GIMME does not sacrifice generalizable inferences, though, because it creates person-specific networks of temporal covariation that contain both group- and individual-level information as long as there are sufficient number of assessments (Beltz & Gates, 2017).

Importantly, regression, multilevel model, and person-specific techniques can complement each other. In this paper, person-specific networks were utilized to accurately model the intensive longitudinal data, and then regression techniques were used to capture generalizable between-person differences in network features such as complexity. In future research, regression techniques could be utilized to, for example, broadly characterize homogenous learning domains and then person-specific analytic techniques could be utilized to develop individualized learning plans based on heterogenous student performance within those domains.

Although analytic techniques should always be matched to research questions, intensive longitudinal methods and person-specific analytic techniques such as GIMME hold significant, untapped potential in education research because online learning-related processes are likely non-ergodic, that is heterogeneous, especially during times of macro-level stress. As the illustrative dataset utilized data from the 2016 presidential election and not the COVID-19 pandemic, there are potentially different stressors (e.g., related to issues of access or resource management rather than stressors related to identity or distrust) that are ripe for future examination. Key areas for future person-specific research (among others considered in this special issue; see Sailer et al., this issue) include: investigating how online learning experiences may differ across developmental stages (e.g., how elementary school students’ daily experiences differentially impact their online learning outcomes compared to middle or high school students); examining the synchrony between teachers’ daily stress and the learning potential of each student in their class; understanding how psychological factors are dynamically related to different learning activities (e.g., code 10-second epochs of positive and negative affect in students as they collaborate on a virtual group project); and identifying the relations between behavioral trace data (e.g., log-data tracked in virtual learning platforms such as Canvas or Blackboard) and students’ daily motivation.

There are several mathematical extensions to GIMME (see Beltz & Gates, 2017; Gates et al., 2020; Weigard et al., 2020) that have particular utility for work in these educational areas. First, subgrouping can be used to cluster individuals into purely data-derived subgroups (Gates et al., 2017). This approach has proved insightful in understanding shared characteristics across temporal processes related to, for example, borderline personality disorder manifestations in day-to-day life (Woods et al., 2020); if conducted with the current dataset, subgroups might reflect individuals who have similar relations to (and from) verbal recall. In future research, GIMME’s data-driven subgrouping technique could be utilized to understand whether students who use digital learning platforms such as Blackboard or Canvas have similar learning networks. Second, GIMME for multiple solutions (GIMME-MS; Beltz et al., 2016) can be used to confirm the direction of relations in a network; if conducted in the current data set, these results might strengthen inferences about whether low verbal recall predicts or is predicted by high anxiety. GIMME-MS could be used to understand the directionally of teacher stress on the learning potential of individual students (e.g., does teacher stress affect student learning potential or does student learning potential affect teacher stress?). Third, GIMME can model exogeneous variables (i.e., variables outside of the behavioral network that can impact the network). In intensive longitudinal data collected during the current COVID-19 pandemic, GIMME could be used to examine relations between teacher instructions and student on-task behaviors – as modulated by student locations (i.e., whether students were learning online, physically in schools, or in a hybrid format). Finally, there are other GIMME extensions concerning latent variable modeling and bidirectional relations (see Gates, 2020; Molenaar & Lo, 2016) that provide exciting avenues for future research on online learning in stressful times.

In addition to basic research, intensive longitudinal methods and person-specific analytic techniques like GIMME hold promise for informing downstream interventions. Precision education services claim to tailor supports to the individual student, resulting in superior outcomes relative to standardized educational programs (Cook et al., 2018). Unfortunately, current methods utilized to assess these services struggle to identify which supports work for whom (and why they work). For example, although studies have been able to identify which interventions were most effective for subgroups of students (e.g., McMaster et al., 2012), subgroups were still heterogenous and individuals within them showed differential responses to treatments. Through the specification of person-specific networks, GIMME could potentially be used to understand the interrelated mechanisms underlying intervention effectiveness for unique students, and thus, inform individualized education models.

Conclusions

COVID-19 and the ensuing transition to online learning for many students around the world necessitates a long overdue examination of online learning efficacy for students with diverse experiences and skillsets. Intensive longitudinal methods present a promising approach for assessing these complicated, time-linked processes, but many novel techniques for the analysis of these data are underutilized. This paper reviewed three such techniques (regressions, multilevel models, and person-specific networks) relevant to online learning in the time of COVID-19 in order to guide education researchers by explicating the techniques’ suitability to different research questions as well as their strengths and weaknesses. After applying each technique to an empirical dataset with 75 measurement occasions during a period of heightened sociopolitical stress, it was clear that regressions and multilevel models provided generalized conclusions that relied (at least in part) on assumptions of homogeneity, and that person-specific techniques like GIMME held untapped promise for understanding how heterogenous students interact and learn. Thus, intensive longitudinal data coupled with person-specific analytic techniques may eventually inform individualized education models that can be used to enhance learning in the future of online education by assuming students are unique and dynamic over time.

Highlights:

• Stressful societal events impact the learning and education of individuals

• Intensive longitudinal methods can reveal individual-level effects

• Regression analyses facilitate generalization but obscure individual-level effects

• Multilevel models offer within-person insights limited by between-person effects

• Person-specific networks reveal processes unique to individuals