Network ecology in dynamic landscapes

Abstract

Network ecology is an emerging field that allows researchers to conceptualize and analyse ecological networks and their dynamics. Here, we focus on the dynamics of ecological networks in response to environmental changes. Specifically, we formalize how network topologies constrain the dynamics of ecological systems into a unifying framework in network ecology that we refer to as the ‘ecological network dynamics framework’. This framework stresses that the interplay between species interaction networks and the spatial layout of habitat patches is key to identifying which network properties (number and weights of nodes and links) and trade-offs among them are needed to maintain species interactions in dynamic landscapes. We conclude that to be functional, ecological networks should be scaled according to species dispersal abilities in response to landscape heterogeneity. Determining how such effective ecological networks change through space and time can help reveal their complex dynamics in a changing world.

1. Introduction

From the life sciences to mathematics, social sciences, computer science and physics, network theory has become a universal analytical tool to conceptualize, visualize and model the relationships (edges or links) among the discrete elements (nodes) of complex systems [1]. The appeal of network theory in all these disciplines stems from its intuitive representation of systems and its flexibility to model and study the strength of relationships (e.g. weighted links) among nodes (e.g. entities, points, species, populations, patches).

In ecology, network theory has been used successfully to investigate all aspects of species' life histories, relationships and flows: species interactions and food webs; dispersal and migration; metapopulation, metacommunity and metaecosystem dynamics; insect outbreaks and invasion; epidemics and disease spread. It is not surprising then that over the last few decades network ecology has emerged as an integrated discipline aimed to analyse, simplify and model ecological complexity to its essential components in order to understand the system's dynamics [2–10].

Here, we review how ecological networks can be analysed, compared and modelled using network theory. Specifically, we highlight the potential of multilayer networks to answer a broad range of questions about the dynamics of ecological entities and their relationships in a changing world. Then, we stress the importance of acknowledging how network topologies constrain the dynamics of ecological systems as a unifying framework in network ecology that we refer to as the ‘ecological network dynamics framework’. This framework emphasizes that the interplay between the inherent species interaction network topologies and the spatial layout of networks of habitat patches is essential for identifying which network properties (number and weights of nodes, links) and trade-offs among them are needed to maintain species interactions in dynamic landscapes. We end by stressing the need to estimate the direct and indirect interplay, as well as feedbacks, between species interaction networks and spatial networks of habitat patches while accounting for species dispersal ability throughout their life history from daily movement within home range, to dispersal and migration [11–13]. By doing so, ecologists will be able to model how functional ecological networks respond to the effects of landscape dynamics in a rapidly changing world.

2. Ecological networks

In species interaction networks (hereafter interaction networks), nodes are species and the links among them are interactions: trophic links in food webs [14], mutualistic relationships modelled by bi- and multipartite networks (pollination, seed-dispersal, gut microbiomes) [2,15,16] (figure 1a), antagonistic interactions (predation, herbivory, parasitism), among others.

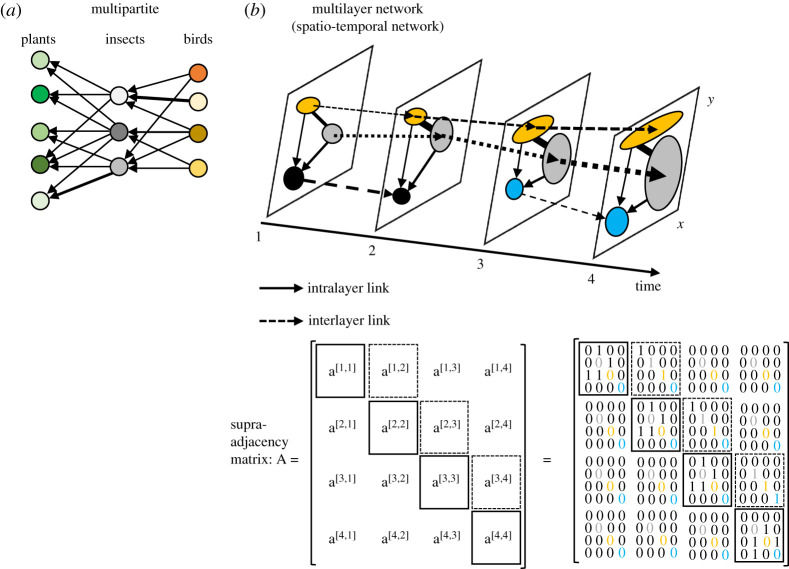
Figure 1.

Example of ecological networks: (a) species as nodes: multipartite network with interactions indicated by directed edges between sets (no edges within a set), and (b) patches as nodes: spatial-temporal network as multilayer network with corresponding supra-adjacency matrix. Each layer is a time; intralayer directed edges indicate dispersal; inter-layer edges indicate dependencies from one layer to another. (Online version in colour.)

Interaction networks can be represented and modelled as multilayer networks (figure 1) that are composed of several monolayer networks where each monolayer contains nodes connected via intralayer links, with interlayer links (often directed edges) connecting nodes from one monolayer to another [17–24] (figure 1b). Multilayer networks provide therefore a powerful framework to visualize and model how interaction networks vary through space and time as presented in the following sections.

3. Network dynamics and evolution

Ecological networks vary in space [25,26] and time [27] as a function of environmental conditions and gradients or other factors [5,6,16,28]. Furthermore, ecological networks are dynamic and thus can adapt and evolve due to evolutionary processes such as selection and coevolution [29]. In such dynamic networks, some or all network properties (degree of the nodes, transience of nodes and links, among others) change. For example, a network's dynamics can be:

• — Dynamics on the network: where nodes stay at the same location from one monolayer to another, but their weights or states change, and edges remain fixed although their weights may change. Such dynamics can be analysed using spatio-temporal networks where from time 1 to time 2 (see §4): (i) disease can spread [7], or (ii) dispersal paths between habitat patches can vary in capacity or use, according to patches' states and weights, altering the functional connectivity [30];
• — Dynamics of the network: where the number and states of nodes can change, and links can appear or disappear as well as change in weight [31]. Such dynamics can be analysed using spatio-temporal networks (see §4) where from time 1 to time 2: (i) species interactions rewire (i.e. changing links between nodes) [32], or (ii) available dispersal routes between habitat patches forming spatial networks, change through the loss or gain of edges, altering the structural connectivity. Furthermore, in dynamic landscapes the overall topology of spatial networks of habitat patches can change as nodes (habitat patches) are lost or gained, which in turn affect species’ interactions and their abilities to disperse [33].

These two types of network dynamics (on and of) can occur independently or in concert such that networks can evolve through time in numerous and complex ways.

Network dynamics can be modelled using various matrices (e.g. adjacency, Laplacian or Jacobian) that represent different network and ecological properties [1,34,35]. Then, the stability of networks' properties through time can be assessed by comparing the spectral properties of their topological matrices (e.g. changes in their eigenvalues).

Network dynamics can be modelled using probability matrices in state-and-transition models [36] where habitat patches in a dynamic landscape have different states (e.g. low/high habitat quality, pioneer/mature forest stands) and transitions governed by a first order Markov chain with constant probabilities. In this scheme, all patches follow the same sequence of states, although possibly at very different rates, determined by the probabilities of transitions.

The dynamics of spatial networks and transitions between states often depend, however, on conditions farther in the past than the state immediately preceding and on the states of spatial neighbours, farther away as well as near by (the spatial context). Hence, longer-term patch history, more distant neighbour effects, or non-stationarity (whether temporal or spatial) should be considered while modelling the dynamics of ecological networks. Furthermore, given that ecological systems are affected by multiple external processes, state transitions depend on multi-step history and on a spatial context beyond first-order neighbours, spatial networks require more flexible modelling approaches.

4. Spatio-temporal networks

We can test hypotheses about the underlying processes that affect the network topology and function by using spatio-temporal networks (i.e. multilayer networks with one spatial layer per time-period), and network properties at the node, link and network levels [3,10,33,37,38].

Spatio-temporal networks are a particular case of multilayer networks (figure 1b) where spatial and temporal links may appear and disappear. For example, spatio-temporal networks may have both spatial and temporal links that approximate the animals’ paths as they move through fragmented landscapes. For short-lived phenomena, such as lightning strikes, there are no within-individual links possible because no distinct individuals persist between time periods, but the links between events can be either purely spatial (joining contemporaneous strikes), purely temporal (joining time-instances of the same locations with strikes in successive time intervals), or a mixture of the two (creating spatio-temporal networks of aggregations).

Spatio-temporal networks can also be used to analyse the state-and-transition probabilities associated with ecological processes, species interactions, invasive species spread, insect outbreaks, or disease spread. For example, Grillet et al. [39] used spatio-temporal networks to develop a series of state transition indexes based on ‘incidence/non-incidence’ data allowing for the quantification of the different spatio-temporal patterns of malaria spread in Venezuela. de la Fuente [40] used the generalized connectivity model [41] to predict the spread of an invasive pest and from that analysis proposed a management strategy to limit the spread of the pest. Boulanger et al. [42] used spatial networks to assess the potential dispersal of a species through multiple generations.

The temporal dimension is a necessary feature of spatio-temporal networks for focusing on the importance of change. Here, nodes can represent individuals, species or habitat patches while the links between the nodes are their actions or dependencies (as directed links) from one time period to the next [27,43–46]. The study of dynamic ecological systems using time-series data [45,46] is critical to our understanding of the extent to which past ecological processes affect current and future processes, by carrying certain characteristics forward through a number of iterations or observation periods. The nodes may be short-lived (only one observation at a particular time) or they may be persistent (several observation periods or temporal steps), and organisms can also be sessile (e.g. trees) or mobile (e.g. mammals). When the nodes are sessile, the links may join instances of the same node at different times, giving time-only directed links. Temporal networks are, therefore, commonly used to study shifts in phenology [27,32,47] or the effects of landscape memory in ecological systems [48].

There are several ways in which systems can be modelled as spatio-temporal networks: temporal changes are added to spatial networks, or temporal networks are studied at several spatial locations where changes occur. Hence, changes can be at the node or link, for example:

• — Nodes change state (e.g. healthy to diseased)
• — Nodes change weight (e.g. population density increases)
• — Edges change position (e.g. two pollinators swap their two interactions between two different plants)
• — Edges change weight (e.g. water flow between lakes changes with season)
• — Both nodes and links change weights (e.g. lake depth and river flow both decline).

Because both nodes and links can vary, spatio-temporal networks can be modelled using one-step (e.g. supra-adjacency matrix in figure 1b) or k-steps of temporal memory, and spatial nearest neighbours or kth order of relative neighbours (e.g. nodes that are linked through another node and more than one edge) [49]. The determination of the spatial and temporal units to be used raises important issues to be considered while modelling and interpreting spatio-temporal networks. First, there is rarely true commensurability for the dimensions of time and space (how can a spatial distance in a network translate into a temporal network's ‘distance’ in time?). This lack of commensurability requires consideration of the dimensionality of the ecological system under study because spatial scaling and temporal scaling will both depend on the underlying processes that affect the network topology and function. Consequently, spatio-temporal analysis requires matching the time step with the processes and events that change either nodes or links, or both. The period of these time steps can be driven by external events such as disturbances and land use change, as well as by internal processes such as population dynamics, succession and dispersal, or by species' lagged responses to the synergies of external events and internal processes. For example, due to the dynamics of patches, there is often a connectivity window in time which allows species to reach habitat patches before they are lost or unavailable. Hence, to determine the importance of the temporal dimension in assessing connectivity, Martensen et al. [33] developed a spatio-temporal network algorithm that accounts for both an organism's dispersal ability and a given temporal connectivity window. Such temporal windows can be set to match a species' dispersal events or longevity. Then, the three spatio-temporal probability of connectivity metrics [33] can be calculated to determine the relative importance of the patch persistence, the availability of stepping-stone patches, or the ability to reach habitat patches directly in dynamic landscapes.

5. Network properties

To compare networks, network metrics and theoretical models can be used at the element-level (nodes, links) [38,50], subnetwork-level (motifs or graphlets), or network-level [1,35]. At the network level, network properties can be quantified using spectral graph properties [35] or network metrics (nestedness, modularity, connectance, partite class—bi-, multi-partite) to characterize relationships between two or more subsets of species [4,21,51]. Then, the observed distribution of the degree of the nodes can be compared with those of theoretical models such as random, scale-free, or small-world [3,10], or with exponential random graph models [52]. Furthermore, network structural properties can be tested against simulated networks based on null models or percolation network theory [1,4,31,37,52,53] that account for the number of nodes, the number of links, and the spatial configuration of the network. Process-based null models [53,54] that account for the dynamical effects of network topologies, can also be used for comparison, assessing how interaction networks differ based on various theoretical frameworks (e.g. random, niche and cascade models). Comparing observed network properties with those derived from known models is an important step in understanding the processes that affect the systems we study. In multilayer networks, not only do the intralayer network properties need to be tested against some null or restricted network structures (e.g. keeping the same connectance, keeping the same degree distribution) that account for the network's topologies and constraints, but so do the interlayer properties between nodes in different layers (e.g. nodes and links weighted, spatial modularity, time lags, trophic structure).

Ecological networks should not be compared using only one network property (e.g. node degree distribution or presence of cycles) because two networks can have the same degree distribution but differ in other characteristics such as diameter or the number of cycles. One should therefore always determine a priori which network properties are relevant to the hypotheses under study (e.g. path lengths, modularity, connectivity, node centrality). For example, with spatial networks, one could focus on comparing path length, path redundancy, and reachable area given an organism's dispersal range [50].

At the subnetwork level, characterization of interaction networks can be analysed by assessing the recurrence of basic small subnetworks, like those called ‘motifs' [55,56]. Milo et al. [55] proposed motifs based on weighted 3-node subnetworks corresponding to specific species interactions (e.g. competition, predation). Motifs have been used to compare changes in species interactions along environmental gradients [57] or the trophic position of species in food-webs [58]. The 3-node motifs are part of the family of graphlet approaches [3,10,59]. Graphlet analysis comprises both undirected and directed subnetworks, called graphlets, allowing to characterize positions of any node among the set of defined equivalent positions on these subnetworks.

At the element level, a node's attributes can be assessed (betweenness centrality, eigenvector centrality, etc. [3,10]) including the trophic levels of species (nodes) [14]. In some circumstances, the exact position of a node (e.g. species) in a subnetwork could provide insights on the dynamics of species interactions [58]. Motifs and directed graphlets can do this by determining the equivalent position of an individual node in a graphlet known as an orbit [3,10,59]. Electronic supplementary material, figure S1 illustrates the potential of directed graphlets [59] to identify changes in the frequency of orbits (e.g. species) through time as a trophic level is changed or removed. In this example, the frequencies of various lengths of antagonistic interactions are the most common (3-node and 4-node graphlets). Directed graphlets could therefore help analyse more complex interactions such as those found in bioinformatics and medicine with comparable ways to align networks [60] and in ecology for more complex trophic interactions (e.g. omnivory [61]).

6. Inferring interaction networks

Network theory often relies on the assumption that all the relevant nodes of the network under study are included [1]. However, this assumption is rarely met in ecological interaction networks as they are sampled targeting particular taxa or specific types of interactions (e.g. mutualistic interactions in plant–pollinator networks), missing the context of the rest of the community in which those interactions occur.

As most interaction networks are sampled only once, their variability through space or time cannot be determined [62]. Moreover, sampling tends to miss rare species/nodes and rare pairwise interactions/links. Such incomplete and possibly biased sampling of interaction networks has resulted in inaccurate estimates of network topologies [63,64]. More complete descriptions of species interactions via additional observations of time series of species abundances, are therefore needed to better infer interaction networks.

Often interaction networks are constructed by assuming that species co-occurring at a location have an interaction even if it is not observed. This approach has been criticized because presence/absence data may be a poor proxy for species interactions [65]. Novel approaches rely instead on species abundance data for determining species interactions [32]. The core assumption of these approaches is that if species have interactions, their abundances should be linked, after controlling for abiotic factors.

In a multilayer network, all the difficulties in assessing intralayer topology and interactions at a single time step prevail as well as those in assessing the interlayer edge weights or changes in node weights. So far, only a few empirical studies have tried to estimate both intralayer and interlayer ecological interactions (e.g. [22,24]). More empirical studies are needed to parameterize interlayer edges like the cumulative effects of permanent habitat patches, compared to those of ephemeral patches, on the dynamics of ecological networks.

7. Ecological network dynamics: a unifying framework

The topology of an interaction network constrains its species' ecological responses and that in turn changes the network topology and function [6,28]. Network properties can therefore be used to generate and test hypotheses about the underlying processes that shape interaction networks [10,47]. For example, Croft et al. [47] tested for social behaviours (e.g. grooming, aggressions; the links in the network) among individuals (the nodes) using restricted randomization procedures [10,53,54] to account for the non-independence of these behavioural interactions.

Similarly, spatial networks like dendritic stream networks can impose directionality and flow constraints on ecological systems that literally channel the potential dynamics of ecological processes and species interactions [32]. Benda et al. [66] formalized these network constraints as the ‘network dynamics hypothesis’ where a network of channels and their confluences can affect both the physical and riparian characteristics of dendritic networks as well as amplitude and stochasticity of disturbances in these stream networks. This network dynamics hypothesis specifies key predictions about the direct effects of dendritic topology, as well as the influence of the surrounding land (e.g. catchment size, elevation) on the number of run-offs, water volume, flow and quality. The effects of dendritic network constraints on species and community structure have been acknowledged in several empirical and modelling studies (e.g. [67–70], among others).

Similarly, the key properties of spatial networks of habitat patches (e.g. numbers and weights of nodes and links) are known to constrain properties and dynamics of species interaction networks [28]. For example, Gravel et al. [71] developed a conceptual model of the trophic interactions (e.g. predator–prey) in the context of island biogeography theory. Then, Guzman et al. [13] conceptualized how species dispersal abilities—that they termed ‘spatial use properties'—scale species interactions.

Here, we formalize all these previous concepts [28,71] and frameworks [13,66] as the ‘Ecological Network Dynamics Framework’ (hereafter ENDF; figure 2) that stresses the set of key network properties that constrain species interaction networks. ENDF conceives of the topology of the spatial network constraining the characteristics and dynamics of embedded interaction networks:

• 1. Topology of a spatial network and its changes constrain the characteristics and dynamics of the species interaction networks embedded within it.
• 2. Species traits and the strengths of their ecological interactions constrain how species respond to changes in the spatial network.
• 3. The interaction networks can directly or indirectly affect the structure and dynamics of the spatial network in which they occur.

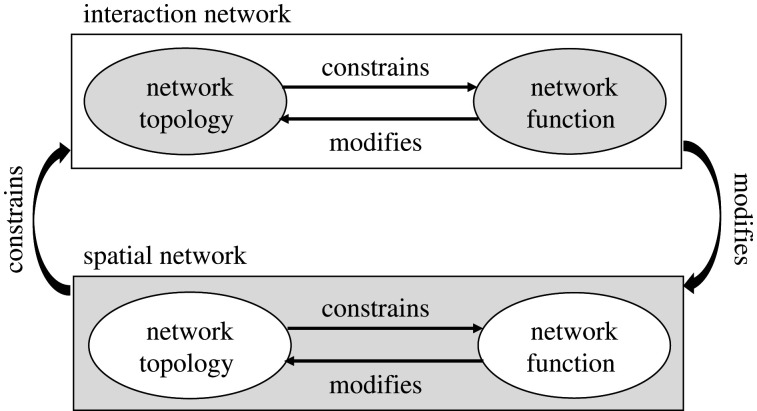
Figure 2.

Ecological network dynamics framework: a diagrammatic representation showing that the topology of spatial networks constrains the topology and functions of ecological networks which in turn can modify the topology and functions of the spatial network.

ENDF stresses the importance of the interplay between species interaction networks (e.g. trophic networks) and spatial networks (network of habitat patches), accounting explicitly for the topological, dynamic and directional constraints (e.g. temporal directionality, spatial layout constraints). Thus, a network's constraints resulting from species traits (e.g. dispersal ability, trophic level) and the strength of their interactions limit how species can respond to changes in the spatial network (number of patches, their size, quality, spatial layout; electronic supplementary material, figure S2).

ENDF can help elucidate the combinations of network properties that maintain a balance between positive effects (e.g. rescue effects through dispersal and gene flow) and negative effects (e.g. increased risk of species invasion, predation and disturbance spread) in dynamic landscapes. As such, a series of combinations of network properties (e.g. degree of the nodes or the transience of nodes and links) can offset the handicaps of nodes or of links (e.g. more nodes of lower quality or more links of lower strengths; electronic supplementary material, figure S2) to maintain species and their interactions [72,73]. Specifically, the ratio of nodes to links and feedback effects in these evolving systems need to be accounted for at the element- (node- and link-), subnetwork- and network-levels. For instance, changes to habitat patches (amount, quality; electronic supplementary material, figure S2) directly affect species richness and abundances, which in turn affects the number of interactions among species [72] and potentially rewiring the interactions, resulting in drastic effects on species assemblages such as spatial trophic cascade effects [74].

A series of specific research topics can be formulated for analysis at various network levels to investigate the potential effects of networks on ecological processes, for example:

• — At the network-level in interaction networks. The constraints of species interactions and trophic level topologies will determine species potential to rewire their interactions in changing environmental conditions such that membership of nodes that form modules change across a season.

Example of prediction:

• — Generalist species are likely to be able to rewire their food web topology in the event of environmental change.

• — At the network level in spatial networks. The interaction between the pace of landscape change and species traits (dispersal ability, dispersal rate, generation time) will determine the conditions (combinations of spatial network topologies) under which species will persist as well as their interactions.

Example of predictions:

• — Spatial networks of connected patches favour species dispersal but also the spread of predators, invasive species, diseases and disturbances.
• — Spatio-temporal dynamics of patches (changes in quality and quantity) that occur more rapidly than species' lifespans will impede species dispersal abilities, survival and local persistence.

• — At the link-level for species traits. The constraints of species traits (dispersal ability, reproduction strategy, longevity) will determine their response to dynamic network topologies (same number of nodes and links but with different weights; electronic supplementary material, figure S2).

Example of prediction:

• — Short-distance dispersers and species with slow dispersal rates will persist if they can reach spatio-temporal stepping stone patches.

These examples underscore the importance of determining how change in landscape heterogeneity disrupts interaction networks by accounting for constraints on species dispersal abilities and species interactions. In certain circumstances, the interaction networks can influence directly or indirectly the structure or topology of the spatial networks. For example, insects that are extirpated could prevent pollination events, which could be detrimental to other foundation species [75] thereby reducing or eliminating some of the vegetation patches that make up the spatial network. Yet, given climate change, foundation species may influence the topology of their spatial networks through their ability to disperse within their climatic envelope and colonize new and previously unreachable areas.

Then, when ecological systems that are apparently not constrained by network topologies do change, this would indicate that novel responses are due to the changes operating at levels beyond the networks themselves. Such knowledge is critical for understanding the response of ecological processes to a changing world.

8. Next steps

Network ecology enables ecologists to analyse and model complex spatial dynamics of species interactions across scales, trophic levels and ecosystem functions. Network analytical tools are powerful and well suited to study ecological lines of inquiry about species persistence in dynamic landscapes. Specifically, we stressed here the importance of the interplay between spatial network topology (weighted patches, weighted links, transient stepping stone patches) and species traits (dispersal ability, generation time, rewiring) as they are key to determine the trade-offs under which species will persist in functional ecological networks. Hence, ecological studies (experimentation in the field, in the laboratory, or analytically) can be designed to determine the trade-offs (electronic supplementary material, figure S2) among the synergistic effects of the dynamics of network topological and functional properties and the dynamic ecological processes that evolve on and in such networks. For example, the ENDF itself can be evaluated by tracing the dependencies in multilayer networks through time by coding constraints using the appropriate supra-adjacency matrix.

(a). Delineating functional spatial ecological networks

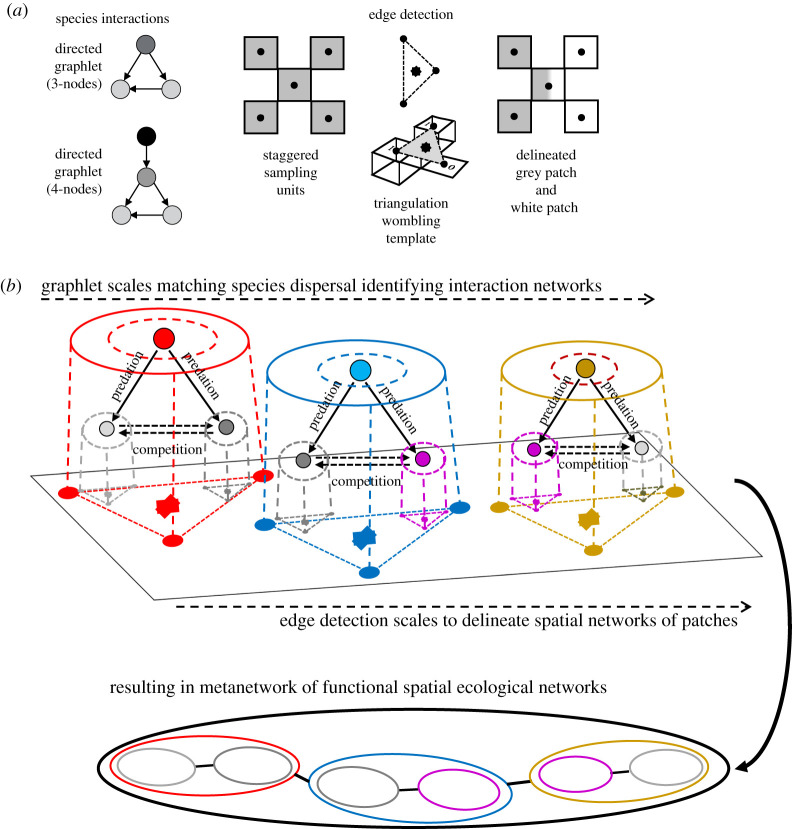
Natural and anthropogenic disturbances combine with climate change will limit the amount of habitat available for species persistence by decreasing patch size and quality and by making the landscape between the patches more inhospitable. Some species can compensate for these effects, up to a point, by the combination of their dispersal abilities or rates, longevity and interactions with other species. Then, given the various degree of landscape spatial heterogeneity, interaction networks and food webs can vary in their topologies. It is therefore important to delineate where habitat patches are, as well as where the properties of a food web stop in space. Here, we suggest delineating ‘functional spatial ecological networks’ in space-based species interaction modules and networks of habitat patches [13,76,77]. Several methods are available to identify interaction networks (species as nodes) [4] including graphlets (usually triads or quartets of nodes [3,4,54,55]). Types of species interactions can be calibrated by filters using graphlets as templates (figure 3a); these can be scaled according to species dispersal ranges (core versus extended home ranges, figure 3b), similarly to assessing the responses of high versus low matching scores as a function of scale and position in wavelet analysis [49].

Figure 3.

Example of how to delineate functional spatial ecological networks by scaling the spatial interaction networks (with species as nodes) that occur in spatial networks (with patches as nodes) using species dispersal abilities. (a) First, graphlet templates are used to characterize the species interaction networks (left panel) and then an edge detection algorithm is used to delineate spatial networks. Here, the triangulation-wombling algorithm detects boundaries by determining rates of change among triplets of samples indicated by dashed lines. Low rates of change among triplets indicate homogeneity (i.e. within-patch samples), whereas high rates of change suggest a boundary. (b) These two approaches are combined to compare and integrate scales for the two kinds of networks. Graphlet templates are scaled by species dispersal abilities of both predators (here three predators as indicated by three colours) and prey species (here three species as indicated by three colours). Predator's home range is scaled according to season and food availability. The core areas of the home ranges are indicated as dashed lines while extended home ranges are indicated by solid lines. Then, the edge detection (i.e. triangular template) is also scaled to delineate spatial habitat patches. Integrating the two types of templates (graphlets and spatial triangles) results in the delineation of functional spatial ecological networks at several scales. The functional spatial ecological networks detected correspond to the backbone of species interactions; these persist throughout the landscape although species identities may change (as indicated by colour coding of both predators and prey). These functional spatial ecological networks of possibly different interacting species form a metanetwork, as shown in the lower panel. (Online version in colour.)

In the same way, a spatial network of habitat patches can be delineated using an edge detection algorithm (figure 3a) [49] which is also scale-responsive, based on a scalable template using triplets of sampling locations (figure 3b). For a given scale and position, uniformity among the samples in the triplet indicates that it is within a patch at that scale and location; large differences among the values indicate an edge.

Combining interaction networks and spatial networks can help determine the conditions under which the interaction network's functions (or species traits) persist when species turnover or network rewiring occurs along spatial gradients (figure 3b). By using scalable templates based on species dispersal abilities, metanetworks of functional spatial ecological networks can be identified. Then, the stability and connectivity properties of those spatial ecological networks across space can be assessed. That can be done by examining changes in the eigenvalues of the Jacobian matrices for species interactions, or in the eigenvalues of the adjacency matrices for patch connectivity [1,78,79]. Alignment between interaction network modules, based on the redundancy of a set of graphlets among species interactions, and the patches in the spatial network can be used to determine the backbone of the functional spatial ecological network [80,81].

(b). Moving forward

The potential applications of networks in ecology, and especially multilayer networks, seem limitless in their ability to represent, model and test both spatial and temporal relationships and interactions among ecological units from individuals to communities. Yet, we need to be careful of including too many layers in a multilayer network because the strength of the network approach is the simplification of ecological complexity; too many layers may make it overly complicated and thus inhibit our attempts to understand the system. Of particular, interest may be the capacity of spatio-temporal networks to evaluate and analyse the speeds of ecological processes of change, and the longevity, reaction-time, and capacity of ‘ecological memory’ in the systems being studied. Hence, specific knowledge on changes in species time lag responses within spatial network topology should be acquired. Then, species rewiring and turnover should be assessed while accounting for the ratios of species generation times and landscape dynamics.

The next research agenda of the field of network ecology should therefore be to assess how local spatial effects (such as contingency or decay functions) compare with effects within the entire network (or its backbone) as well as with the legacy of temporal effects, which may be permanent, transient or fluctuating.

Data accessibility

Species interactions files are available from the Dryad Digital Repository: https://dx.doi.org/10.5061/dryad.m63xsj41b [82].

Authors' contributions

M.-J.F. 50%; M.R.T.D. 30%; C.B. 20%.

Competing interests

We declare we have no competing interests.

Funding

This research was funded by the NSERC Discovery grant no. 5134 and a Tier 1 Canada Research Chair to M.-J.F. C.B. was funded by an OGS. M.R.T.D.'s research was funded by UNBC.