Microstructural analysis of skeletal muscle force generation during aging

Abstract

Human aging results in a progressive decline in the active force generation capability of skeletal muscle. While many factors related to the changes of morphological and structural properties in muscle fibers and the extracellular matrix (ECM) have been considered as possible reasons for causing age-related force reduction, it is still not fully understood why the decrease in force generation under eccentric contraction (lengthening) is much less than that under concentric contraction (shortening). Biomechanically, it was observed that connective tissues (endomysium) stiffen as ages, and the volume ratio of connective tissues exhibits an age-related increase. However, limited skeletal muscle models take into account the microstructural characteristics as well as the volume fraction of tissue material. This study aims to provide a numerical investigation in which the muscle fibers and the ECM are explicitly represented to allow quantitative assessment of the age-related force reduction mechanism. To this end, a fiber-level honeycomb-like microstructure is constructed and modeled by a pixel-based Reproducing Kernel Particle Method (RKPM), which allows modeling of smooth transition in biomaterial properties across material interfaces. The numerical investigation reveals that the increased stiffness of the passive materials of muscle tissue reduces the force generation capability under concentric contraction while maintains the force generation capability under eccentric contraction. The proposed RKPM microscopic model provides effective means for the cellular-scale numerical investigation of skeletal muscle physiology.

1 |. INTRODUCTION

The performance and functioning of skeletal muscles deteriorate with age, causing a significant negative impact on people’s daily life. It is therefore important to understand the roles of different musculoskeletal factors (such as material properties, microstructures, and morphologies of muscle tissues) in affecting the force generation capacity. It is widely accepted that the force generation capability of skeletal muscle decreases with aging. The reasons behind the age-associated force reduction could be the loss of mass in contractile components, loss of motor units (neural-excitation), alterations in fiber types and passive material properties, changes in the specific fiber tension and contractile velocity, and fatty inclusions, and so forth.^1–3 It was also observed that the reduction of force exhibits significant differences between eccentric and concentric contraction,^4–7 where the loss of force generation under concentric contraction is usually greater than that under eccentric contraction, and sometimes even no age-related difference in force production during eccentric contraction is observed.^8,9 Nevertheless, limited quantitative studies have been conducted on the causal relationship between the previously mentioned determinants of age-related force loss and the fact that muscle tends to maintain force generation with aging under eccentric contraction.

Skeletal muscle consists of muscle fibers and an extracellular matrix (ECM), and thus, the overall mechanical properties of skeletal muscle tissue are determined by the individual properties of these two components and the interactions between them.¹⁰ At the cellular level, the muscle tissue is a honeycomb-like composite material with the connective tissue (CT) phase, that is, endomysium, and the muscle fiber phase.^11–13 In particular, CT is postulated to play an important role in myofascial force transmission of muscle, providing essential structural support to ensure muscle’s integrity, and protecting muscle cells from damages during muscle contraction.^13,14 In terms of ageing effects, two important biological observations about CT have been reported: (a) the stiffness of CT in skeletal muscle increases with aging,^15–18 and (b) the volume ratio or thickness of connective tissue (endomysium) increases with aging.^15,17 Thus, in this study, we investigate how these age-related microstructural variations could affect the biomechanical behaviors of skeletal muscle, especially the force generation capacity.

During the last few decades, computational modeling of skeletal muscles has advanced significantly, from the most simplified one-dimensional (1D) lumped-parameter model¹⁹ to the three-dimensional (3D) sophisticated muscle models represented by fiber-reinforced composite materials based on fiber-level constitutive models.^20–25 These macro-scale models enable a systematic study of the structural and functional properties of skeletal muscles. However, the simulation-based investigation into the effects of microstructural variations, such as microstructural composition and material properties on the skeletal muscle functionality, is less complete. A micromechanical model based on the concept of repeating unit cells extracted from histological cross-sections of rabbit muscles²⁶ was proposed to study the effects of microstructural geometry in both fiber and fascicle levels on the macroscopic along-fiber shear modulus of skeletal muscle. Virgilio et al²⁷ utilized an agent-based model to generate honeycomb-like micromechanical models of skeletal muscle and studied the influences of disease-associated alterations in muscle microstructure on muscle’s macroscopic along-fiber shear modulus. Recently, Spyrou et al proposed analytical and numerical homogenization models based on the honeycomb-like microstructure to bridge various length scales of skeletal muscle.^28,29

In this study, we proposed a micromechanical computational model based on the honeycomb-like structure for skeletal muscle to examine the effects of age-related changes in the material properties (muscle fiber and CT) and volume fraction on the force generation capability of skeletal muscle, with a focus on understanding the mechanism causing the force reduction difference between concentric and eccentric contraction. Furthermore, the proposed numerical model is constructed using the Reproducing Kernel Particle Method (RKPM),^30–32 which effectively models smooth transition of biomaterial properties across material interfaces and allows model discretization to be obtained directly using the pixel points from CT scans and avoids the complexity of constructing mesh-based models.^33,34

The rest of this article is organized as the followings. In Section 2, the construction of pixel-based meshfree models, material models and the loading conditions used in the simulations are introduced. Numerical validation of the meshfree computational framework is first presented in Section 3, followed by the discussion of numerical results of the force generation of contracted skeletal muscle microstructure in the same section. The conclusions are given in Section 4.

2 |. METHODS

2.1 |. Model construction from images

In this work, a honeycomb-like microstructure of skeletal muscle tissue is constructed based on a representative image of the cellular-scale cross-section of skeletal muscle tissue. A region-based level-set algorithm³⁵ is employed for image segmentation. In the honeycomb-like microstructure, two material phases are considered, that is, the CT (endomysium) phase and the muscle fiber phase. The two-dimensional (2D) segmented microstructure is then extruded along the out-of-plane direction (the z-direction) to generate the 3D model. Here, the pixel points used for image segmentation are then readily used as meshfree nodes for the discretization in the RKPM simulation model. The model construction processes are summarized in Figure 1 as follows. Figure 1A is extracted from,¹² which shows a representative unit cell of muscle fibers separated by the connective tissue, that is, the endomysium. Figure 1B shows the level-set segmented images and the associated pixel points. The 3D model is generated by extruding the 2D model as shown in Figure 1C, and the dimension of the honeycomb model is normalized to 1 × 1 × 1.

FIGURE 1.

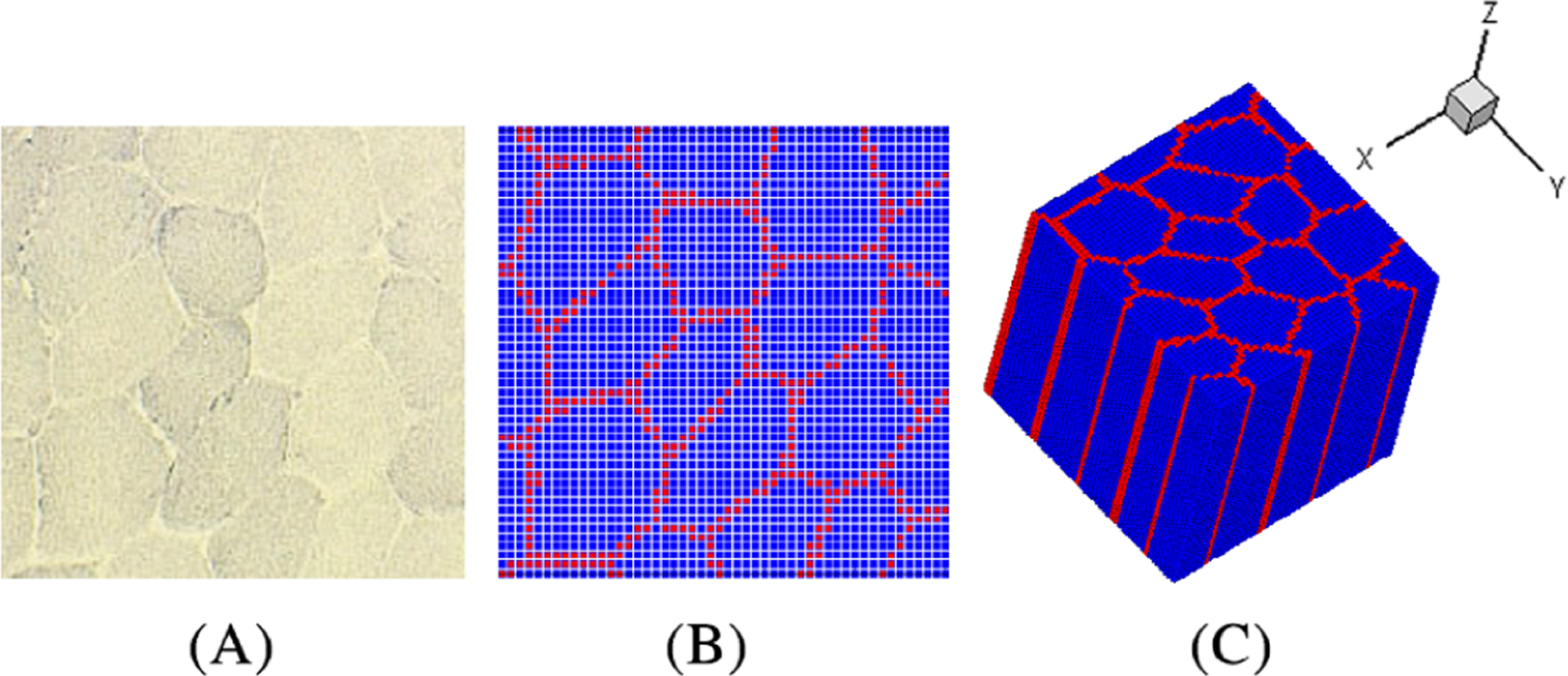
The procedure of constructing the 3D model from the 2D images of the cellular-scale cross-section of skeletal muscle tissue.¹² (A) the cross-sectional image of a representative unit cell of the muscle tissue, (B) level-set segmented cross-section, and (C) 3D model produced by extruding the 2D model along the z-direction. Blue points denote the muscle fiber phase and red points denote the connective tissue phase

In this work, an RKPM based approximation and discretization,^30,31 see Appendix A, together with the stabilized conforming nodal integration (SCNI)³² are employed to solve for the hyperelasticity boundary value problem. Note that biological material is commonly modeled as nearly incompressible hyperelasticity,³⁶ which usually requires special treatment to handle the incompressibility in structural analysis.³⁷ It has been shown that RKPM with SCNI provides proper numerical treatment of incompressibility, see details in.^31,32,38,39 Moreover, the arbitrarily high-order continuity of RKPM approximation allows the smooth transition of biomaterial properties across material interfaces to be effectively modeled.

2.2 |. Material models

In skeletal muscle, the contractile muscle fibers can generate positive stress even in the undeformed state, whereas CT is treated as passive material which deforms in response to the applied loads. Here, the CT material is modeled by a cubic polynomial hyperelastic model with the uniaxial tension-compressive behavior shown in Figure 2A where λ is the stretch ratio. Following,^19,21,40 the active stress-stretch curve of the skeletal muscle fiber and the combined active and passive response are shown in Figure 2B. The operation region of skeletal muscle defined as [0.9, 1.5] in this work,⁴¹ is shaded in Figure 2B, where λ < 1.0 and λ > 1.0 represents concentric and eccentric contractions, respectively.

FIGURE 2.

(A) The uniaxial stress-stretch relation of a cubic polynomial hyperelastic material model for connective tissue and (B) the normalized active and passive mechanical response of the muscle fiber model^19,21,40

The strain energy density function of the muscle fiber hyperelastic model is decomposed into the isotropic and the anisotropic parts,

$$W_{\text{fiber}}=W_{\text{iso}}\left({\overline{I}}_1,{\overline{I}}_2,J\right)+W_{\text{ani}}(\lambda ),$$ (1)

where λ is the along-fiber stretch ratio, ${\overline{I}}_1$, ${\overline{I}}_2$ are the reduced invariants of right Cauchy-Green strain tensor C^T = F^TF, defined as ${\overline{I}}_1=J^{-2/3}{I}_1$ and ${\overline{I}}_2=J^{-4/3}{I}_2$ with I₁ = tr(C) and $I_2=0.5\left[I_1^2-\text{tr}\left(C^2\right)\right]$, and J = det(F) is the relative change in volume. Here, F is the deformation gradient defined as $F=\frac{\partial x}{\partial X}$, where x and X are the material position vectors in the current and initial configuration, respectively. The isotropic part, associated with the contribution of membrane structures and biofluids contained in a muscle fiber,²⁸ is given by a quadratic polynomial type function,

$$W_{\text{iso}}={\sum }_{i+j=1}^2{C}_{ij}{\left({\overline{I}}_1-3\right)}^i{\left({\overline{I}}_2-3\right)}^j+\frac{K}{2}{(J-1)}^2,$$ (2)

where the material constants C_ij and the bulk modulus K are associated with the resistance against the deviatoric and volumetric deformations, respectively. The anisotropic strain energy density function W_ani is introduced to describe the behavior of the fiber’s contractile behavior,⁴⁰

$$\lambda \frac{\partial W_{\text{ani}}}{\partial \lambda }={\sigma }_{\text{max}}\frac{\lambda }{{\lambda }_0}\left(\alpha f_{\text{active}}+f_{\text{passive}}\right),$$ (3)

where σ_max is the fiber maximum isometric stress, λ₀ = 1.4 is chosen as the optimal stretch ratio at which muscle fiber generates maximum force,^21,40 as shown in Figure 2B, and α is the activation level ranging in [0, 1]. For instance, α = 0 indicates the muscle fiber is in a completely passive state, and α = 1 indicates a fully activated state. f_active and f_passive are the normalized active and passive parts of the muscle fiber force,^21,40 respectively, expressed as

$$f_{\text{active}}=\{\begin{array}{ll}9{\left({\lambda }^{*}-0.4\right)}^2\hfill & {\lambda }^{*}\le 0.6\hfill \\ 1-4{\left(1-{\lambda }^{*}\right)}^2\hfill & 0.6<{\lambda }^{*}\le 1.4\hfill \\ 9{\left({\lambda }^{*}-1.6\right)}^2\hfill & {\lambda }^{*}>1.4\hfill \end{array}$$ (4)

$$f_{\text{passive}}=\{\begin{array}{ll}0\hfill & {\lambda }^{*}\le 1\hfill \\ {\gamma }_1\left({\text{e}}^{{\gamma }_2\left({\lambda }^{*}-1\right)}-1\right)\hfill & 1<{\lambda }^{*}\le 1.4\hfill \\ \left({\gamma }_1{\gamma }_2{\text{e}}^{0.4{\gamma }_2}\right){\lambda }^{*}+{\gamma }_1\left(\left(1-1.4{\gamma }_2\right){\text{e}}^{0.4{\gamma }_2}-1\right)\hfill & {\lambda }^{*}>1.4\hfill \end{array}$$ (5)

where λ* is the normalized stretch as λ* = λ/λ₀. The diagram of f_active and f_passive are plotted in Figure 2B. It is noted that the passive part f_passive is mainly contributed by the protein inside the sarcomeres called titin,^42–44 and the adopted values of coefficients γ₁ and γ₂ associated with different age groups are discussed in the following section.

For the CT phase, a cubic polynomial hyperelastic material model is adopted,^45,46

$$W_{\text{CT}}={\sum }_{i=1}^3{C}_{i0}{\left({\overline{I}}_1-3\right)}^i+\frac{K}{2}{(J-1)}^2$$ (6)

The bulk modulus K used in Equations (2) and (6) are much bigger than the parameters C_ij so that the material is nearly incompressible. The nonlinear response introduced by the higher-order terms in the polynomial of the first reduced invariant is able to represent softer low-strain region and stiffer high-strain region.¹⁹

2.3 |. Material parameters

Titin, the muscle protein inside the sarcomeres, plays an important role in the passive stiffness of the muscle fiber.^42–44 It was reported that the titin-based passive stiffness of adult muscle is more than 50% greater than that of the young muscle.⁴⁷ To represent the age-related increase in titin’s stiffness at the cellular level, the titin related parameter (γ₁ in Equation (5)) associated with the passive fiber stiffness of Adult and Old muscle fibers is, respectively, set as one-and-a-half and two times of that of the Young muscle, as listed in Table 1^21,40

TABLE 1.

Material parameters of the normalized passive fiber force in Equation (5) with different titin stiffness^21,40

Age	Titin stiffness	γ1	γ2
Young	Soft	0.05	6.6
Adult	Medium stiff	0.075	6.6
Old	Stiff	0.1	6.6

As muscle fiber has little resistance under compression in the fiber direction, experimental data from skeletal muscle tissue under uniaxial compression along the fiber direction can be used to calibrate the material parameters of the CT material models.^28,48,49 Figure 3A summarizes the experimental data extracted from literature for the uniaxial compressive experiments in the muscle fiber direction, conducted on rat tibialis anterior muscle,^50,51 porcine, bovine, and ovine muscles,^52,53 and human forearm muscle.⁵⁴ The experimental data shows a large variation in stress-stretch relations. Previous studies reported that the stiffness of CT (endomysium) of old muscle is about twofold of that of the adult’s.^15–17 Wood et al found that the stiffness of ECM of old muscle increases by twelvefold, compared to that of the adult’s.¹⁸ Given the large variation in stress-stretch relations^50–54 and the observations on stiffness relations between muscles of different age groups,^15–18 three sets of CT materials with different material properties are defined corresponding to Young, Adult, and Old muscles in Table 2, where the CT stiffness of the Adult and Old muscles is set as four and eight times of that of the Young one, respectively. They are denoted as “Soft CT”, “Medium Stiff CT”, and “Stiff CT”, respectively, and their corresponding stress-stretch relations fitted using the CT model in Equation (6) are shown in Figure 3A. It is obvious that muscle units with stiffer materials yield larger stress at any given stretch ratio in both tensile and compressive deformations.

FIGURE 3.

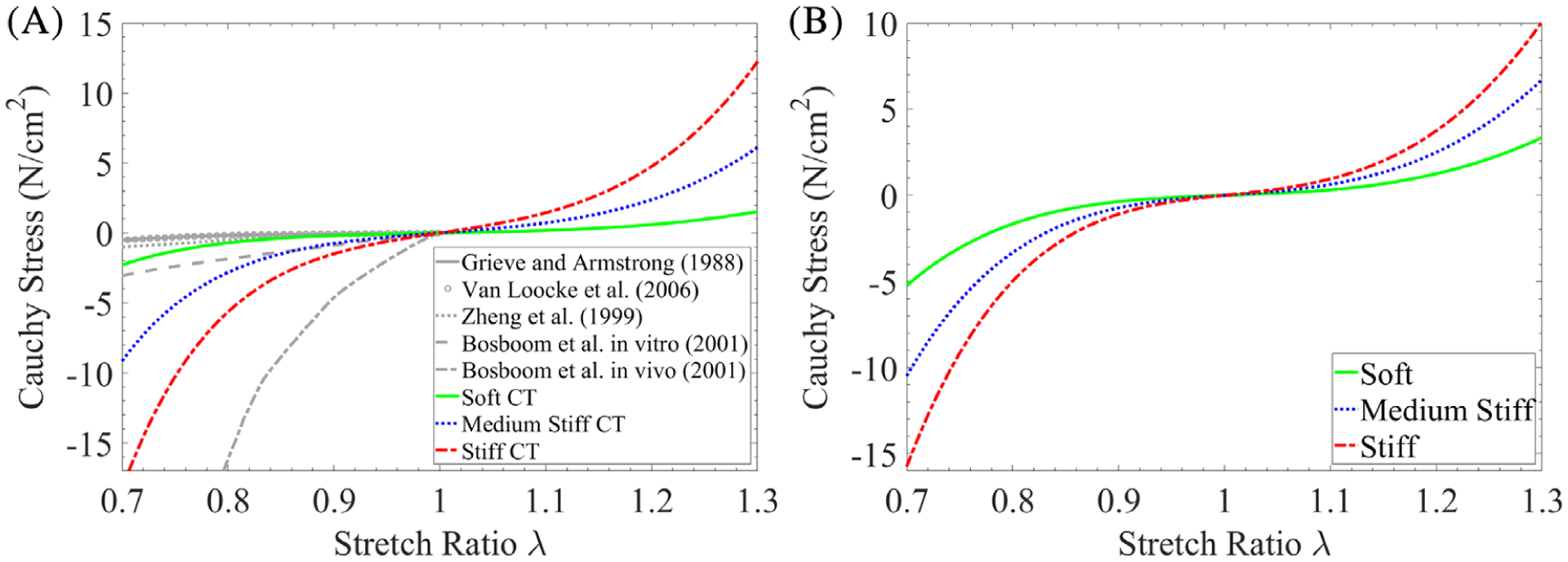
Stress-stretch relation of muscle materials under uniaxial deformation: (A) the comparison of compressive stress-stretch experimental data of muscle tissue and the response of the connective tissue (CT) material model fitted using Equation (6) with different stiffness; (B) the stress-stretch response of the isotropic part of the muscle fiber model in Equation (2) with different stiffness; The stretch ratio is along the direction in which the material is stretched or compressed

TABLE 2.

Material parameters of the connective tissue (CT) model in Equation (6) with different stiffness (unit: N/cm²)

Age	CT stiffness	C10	C20	C30	K
Young	Soft	0.36	1.63	0.95	5 × 103
Adult	Medium stiff	1.42	6.50	3.80	2 × 104
Old	Stiff	2.84	13.00	7.60	4 × 104

The isotropic material property of the Young muscle fiber is defined as twice that of the Young CT²⁸ and the isotropic material property of Adult and Old muscle fibers is set as two and three times that of the Young muscle fiber, respectively, as given in Table 3. Figure 3B shows the stress-stretch curves associated with the isotropic part of the adopted muscle fiber model in Equation (2) for Young, Adult and Old muscles, denoted by “Soft”, “Medium Stiff”, and “Stiff” according to their stiffness, respectively. The corresponding material parameters of the cubic hyperelastic model for CT (Equation (6)) and the quadratic hyperelastic model for the isotropic part of muscle fibers (Equation (2)) are listed in Tables 2 and 3, respectively.

TABLE 3.

Material parameters of the isotropic part of the muscle fiber model in Equation (2) with different stiffness (unit: N/cm²)

Age	Fiber’s isotropic stiffness	C10	C01	C20	C11	C02	K
Young	Soft	0.14	0.40	0.005	5.05	0.003	104
Adult	Medium stiff	0.28	0.80	0.010	10.10	0.006	2 × 104
Old	Stiff	0.42	1.20	0.015	15.15	0.009	3 × 104

As discussed above, the passive stiffness (PS) of the whole muscle tissue is contributed by passive components of fiber and CT. Overall, three sets of PS are defined corresponding to Young, Adult, and Old muscles for the following numerical studies. They are denoted as “Low PS”, “Medium PS”, and “High PS”, respectively, as listed in Table 4. For instance, “Low PS” indicates a combination of Soft titin-based passive fiber stiffness, Soft CT stiffness, and Soft fiber’s isotropic stiffness.

TABLE 4.

Summary of the employed passive stiffness of the muscle tissue components for Young, Adult, and Old muscles

Age	Passive stiffness	Titin stiffness	CT stiffness	Fiber’s isotropic stiffness
Young	Low	Soft	Soft	Soft
Adult	Medium	Medium stiff	Medium stiff	Medium stiff
Old	High	Stiff	Stiff	Stiff

2.4 |. Loading condition for force generation analysis

For simulation convenience, we adopt two loading stages although these two loading mechanisms co-exist in reality. In the first loading stage, the model is constrained at both ends (ie, the planes of z = 0 and z = 1 in Figure 4) and the muscle activation level is taken as 1, representing fully activated muscle fibers without deformation. In the second stage, a uniaxial compression (concentric contraction) or tension (eccentric contraction) is applied to the model so that the model shortens or lengthens to a certain stretch ratio λ of the original length. During this loading stage, boundary displacements are prescribed to control the overall stretch ratio, and the reaction force on the stretched surfaces is computed at different stretch ratios.

FIGURE 4.

The 2D diagram (lateral view) of the muscle model under uniaxial loading, where the striated areas represent the connective tissues, the blank areas represent the muscle fibers, the circles represent the roller boundary condition, and the arrows pointing downward on the top surface indicates concentric contraction (pointing upward for eccentric contraction)

The circles in Figure 4 represent the roller boundary condition, which allows the boundary surface to slide along the in-plane surface tangential directions (z or x) while the deformation is restrained in the out-of-plane direction. The loading method here is designed to mimic the loading procedures widely used in experiments,⁵⁵ where a small block of muscle tissue material is dissected and tested.

3 |. RESULTS AND DISCUSSION

3.1 |. Numerical validation

To validate the selected material parameters for the passive components of muscle tissue (fiber’s passive part and CT) during ageing process, as listed in Tables 1–4, a quasi-static numerical test is performed by applying uniaxial tensile loading to muscle tissue in the muscle fiber direction with different PS parameters (see Tables 1–4). Figure 5 shows the comparison of stress-stretch relations between the numerical results and the experimental data measured from rat tibialis anterior muscles^56,57 and rabbit extensor digitorum longus muscles.⁵⁸ The grey shaded area in the figure depicts the standard deviation of the experimental data by Calvo et al.⁵⁶ The experimental data shows a wide range of tensile response variations and the numerical results of the proposed muscle tissue models with three sets of passive stiffness parameters listed in Table 4 lie within the range of the experimental stress-stretch response. The agreement between numerical and experimental results validates the proper selection of the material parameters for different passive components during aging process, which will be used in the study of force generation mechanisms in Section 3.2.

FIGURE 5.

The comparison of experimental data and numerical results of muscle tissue under uniaxial tensile loading in the muscle fiber direction due to different muscle PS defined in Table 4, where the grey shaded area depicts the standard deviation of the experimental data.⁵⁶ “Thin CT” thickness is used for the numerical test (see Section 3.2.2 for more details)

3.2 |. Numerical investigation of force generation

The pixel-based cellular-scale micromechanical RKPM model described in Section 2.1 is used to study the causal relations between age-related microstructural variations in geometries and properties (including the passive stiffness of muscle, the thickness of CT, and the maximum isometric stress of muscle fibers) and macroscopic behaviors such as force generation capacity of skeletal muscles.

3.2.1 |. Effects of passive stiffness (PS)

The effect of PS on the force generation capacity of skeletal muscle under concentric and eccentric contraction is first investigated. Let us consider a muscle unit, as shown in Figure 7, where CT thickness of 18% volume ratio (refer to Section 3.2.2 for the study on CT thickness) and the fiber maximum isometric stress of 30 N/cm² are employed for simulations. The results of total force generation under concentric contraction by using different PS denoted in Table 4 is compared in Figure 6A. The results show that, at the same level of stretch, the muscle with higher PS generates smaller force under concentric contraction (λ < 1). Note that when λ = 1 the muscle is undeformed and the passive components (fiber’s passive part and CT) do not contribute to the muscle’s force generation; thus, it yields the same force generation given we maintain active muscle properties constant in this example. On the other hand, when the muscle units are under eccentric contraction (λ > 1), as shown in Figure 6B, the muscle with higher PS generates larger force, opposite to the case with concentric contraction. Mechanically, this opposite phenomenon can be explained by the superposition of the reaction force from passive components and active force from fibers. Note that higher PS yields greater reaction stress (tensile or compressive) under external loading (eccentric and concentric). Therefore, under eccentric contraction, muscle units generate a larger total force as the stress exerted by tensile action in fibers is further increased by a larger tensile stress in the passive components with larger higher PS. On the contrary, under concentric contraction, the stress from fiber tensile action is “compensated” by the compressive stress in passive components, and thus the muscle unit with higher PS yields less force. These effects can be visualized from stress distributions at the final configuration of simulation during concentric contraction (Figure 7). As can be seen, the fiber phase generates tensile stress (positive) and the CT phase shows compressive stress (negative) for all three cases, and thus the force from active tensile stress in fibers is offset by the force from passive compressive stress in the CTs. As a result, the muscle unit with stiffer CT (ie, higher PS) generates less force, as illustrated in Figure 6A. The opposite trend in force generation under eccentric contraction (Figure 6B) can be explained under a similar reasoning.

FIGURE 7.

The distribution of the Cauchy stress component σ_zz (the muscle fiber direction) at the final configuration under concentric contraction. Panels (A), (B) and (C) are the results of “Low PS”, “Medium PS”, and “High PS”, respectively

FIGURE 6.

The comparison of force generation for muscle tissue with three different passive stiffness (PS) (A) when the muscle tissue shortens and (B) when the muscle tissue lengthens. The force is the total reaction force calculated on the loading boundary. The “Thin” CT is used for the CT phase and σ_max = 30 N/cm² is used for the fiber phase

3.2.2 |. Effects of CT thickness

It was observed that the CT thickness of old muscles is about twofold to threefold of that of young muscles.^15,17 To examine the effect of this microstructural change in CT thickness, muscles with three different CT thicknesses are considered in Figure 8. Lieber et al reported that the fiber volume ratios are 38.5 ± 13.6% and 95.0 ± 8.8% for spastic muscle and healthy muscle, respectively.⁵⁹ Considering that aging muscle preserves fibers better than spastic muscle, we take the range of CT volume ratios as 10%–40%. As illustrated in Figure 8A–C, the CT volume ratios of “Thin CT”, “Medium Thick CT”, and “Thick CT” are 18%, 25%, and 36%, respectively. In the following simulations, the “High PS” and the fiber maximum isometric stress of 30 N/cm² are employed.

FIGURE 8.

Honeycomb-like models of skeletal muscle tissue with different volume ratios of connective tissue (CT), which are respectively denoted by “Thin CT”, “Medium Thick CT”, and “Thick CT”. The corresponding CT volume ratios are 18%, 25%, and 36%, respectively. The red nodes represent CT material and the blue nodes represent muscle fiber material

Figure 9 shows the influences of the CT thickness on the muscle’s force generation capacity during concentric and eccentric contraction. The muscle unit with a larger volume ratio of CT always generates smaller force under concentric contraction. During an eccentric contraction, however, the results show a more complex trend. There exists a critical stretch level (around λ = 1.6 in this case), and beyond that, the muscle tissue with thicker CT generates larger force. This is because the increase in the passive force due to thicker CT surpasses the decrease in the active force due to reduced volume ratio of muscle fibers beyond the critical stretch. Compared to the effects of passive stiffness, as shown in Figure 6, the influence of CT thickness on force generation is relatively less significant. Overall, the critical stretch is influenced by many factors, such as fiber contractile ability, muscle structural composition (volume ratio of components), and stiffness of muscle components.

FIGURE 9.

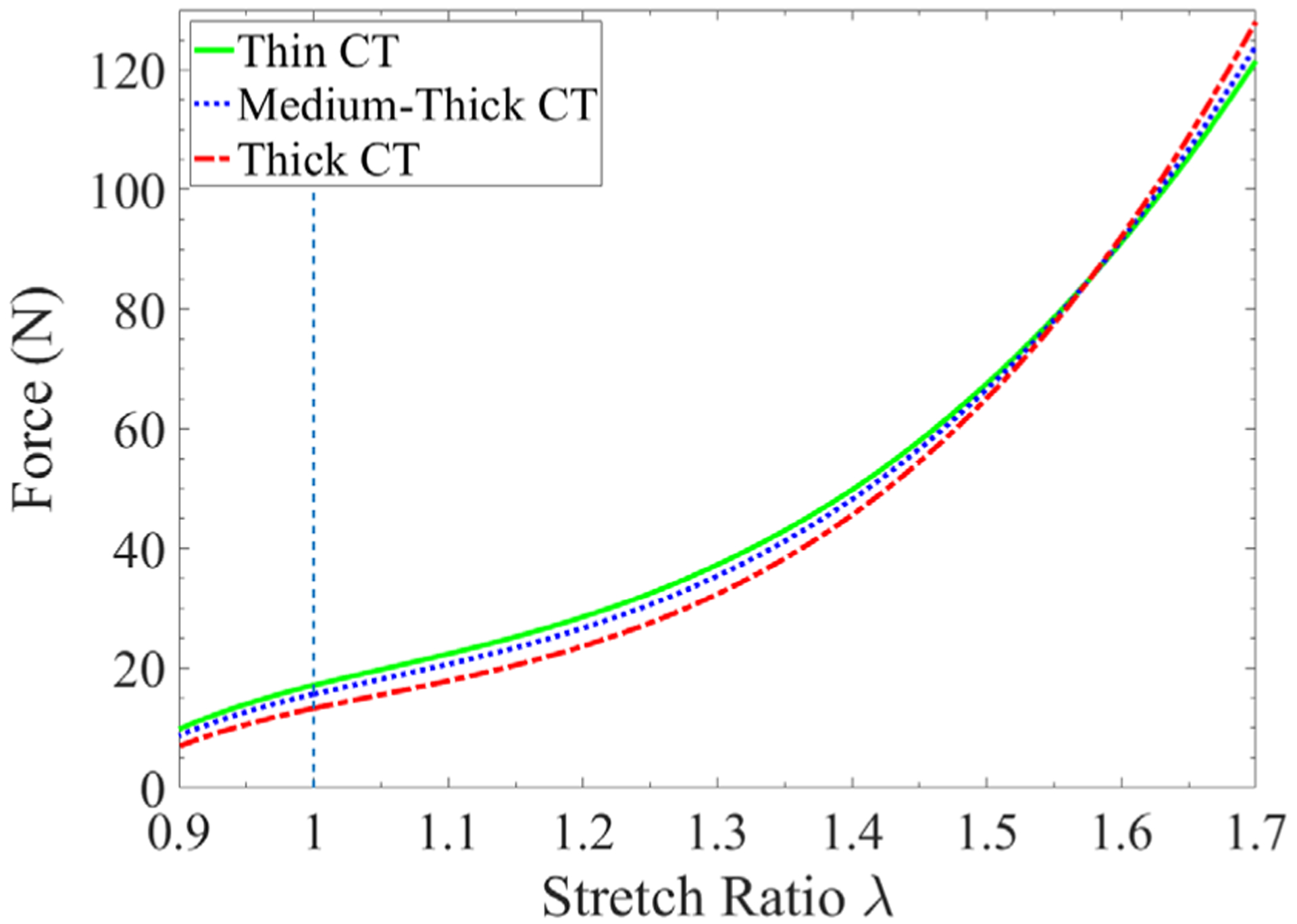
The comparison of force generation of muscle tissues with different connective tissue (CT) thickness. The muscle units with “High PS” and σ_max = 30 N/cm² are employed

The muscle fiber phase and the surrounding CT phase work together to generate force. As the muscle fibers and surrounding CT are strictly bonded at their interfaces,^60,61 the CT deforms synchronously when the activated muscle fibers shorten. Subsequently, the CT, as the passive material, shortens with compressive force to resist shortening deformations. As muscle fiber contracts, stiffer CT resists with larger compressive force during concentric contraction, leading to the reduced total force generated by the muscle tissue under concentric deformation. The trend is opposite for the eccentric contraction as both muscle fibers and CT exhibit tensile forces in this case and stiffer CT yields larger tensile force, leading to greater total force generation. Note that the stiffer CT can be due to larger hyperelastic constants or thicker CT thickness, and vice versa for the softer CT.

3.2.3 |. Effects of fiber maximum isometric stress

Apart from the microstructural changes in the passive components, the loss of muscle’s force generation capacity can result from other age-associated factors, such as the decreased force generation capacity of muscle fibers.⁶² It was reported that the specific force generated by muscle fiber decreases by around 30% with aging.⁶³ Furthermore, the range of values of the fiber maximum isometric stress commonly used in modeling skeletal muscle is from 22 N/cm² to 30 N/cm².⁶⁴ In this study, the fiber maximum isometric stress with values of 30 N/cm², 26 N/cm², and 22 N/cm² is adopted in the muscle fiber model (Equation (3)) to represent the Young, Adult, and Old cases, respectively. Here, the muscle passive stiffness and CT thickness employed in the simulations are the “Medium PS” and the “Medium Thick CT”, respectively. The numerical results displayed in Figure 10 show that the muscle tissues with higher fiber maximum isometric stress generate larger force during both concentric and eccentric contractions.

FIGURE 10.

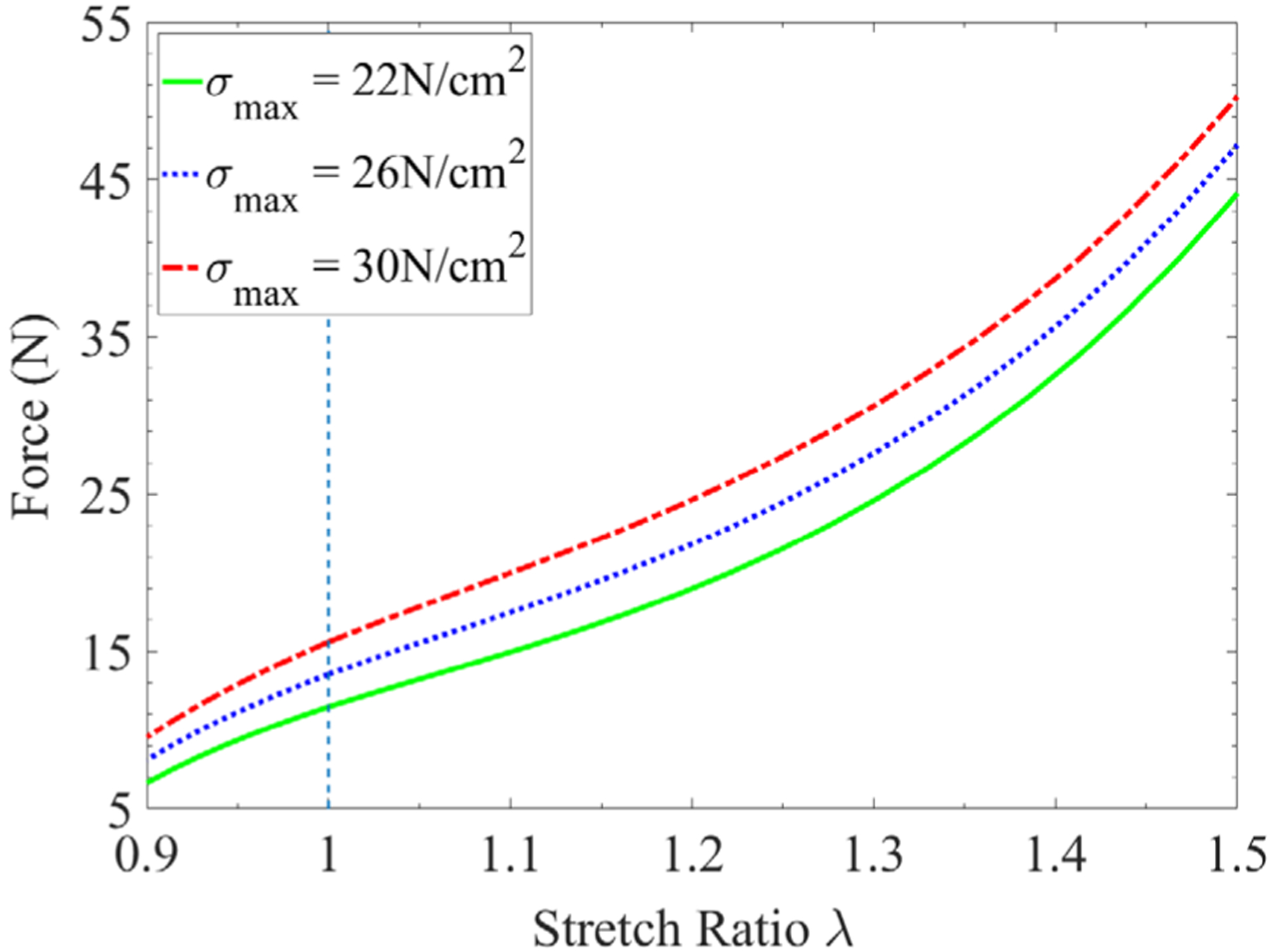
The comparison of force generation for muscle tissues with different fiber maximum isometric stresses. The “Medium PS” and “Medium Thick” CT are used

3.2.4 |. Effects of combined factors

The numerical studies above have shown the individual effects of muscle passive stiffness, CT thickness, and fiber maximum isometric stress, on the muscle’s force generation capacity. Finally, the combined effects of all these age-related microstructural changes are examined. To simulate the aging process, three age groups, that is, “Young”, “Adult”, and “Old”, are designed and their material properties are summarized in Table 5. The results shown in Figure 11 agree with the trend observed in experiments, that is, the skeletal muscle with aging tends to maintain force generation capability during eccentric contraction, and the decrease in force production is more for concentric contraction than isometric contraction.⁹ Figure 11 shows that with aging the reduction of force generation (from Young to Old) is about 60% (λ = 0.9) under concentric contraction, whereas it is about 3% (λ = 1.3) to 35% (λ = 1.1) under eccentric contraction.

TABLE 5.

Material properties for modeling the aging process, where the passive stiffness corresponds to Table 4 and the volume ratio of CT corresponds to Figure 8

Age	Young	Adult	Old
σmax (N/cm2)	30	26	22
Passive stiffness	Low	Medium	High
Volume ratio of CT	Thin	Medium-thick	Thick

FIGURE 11.

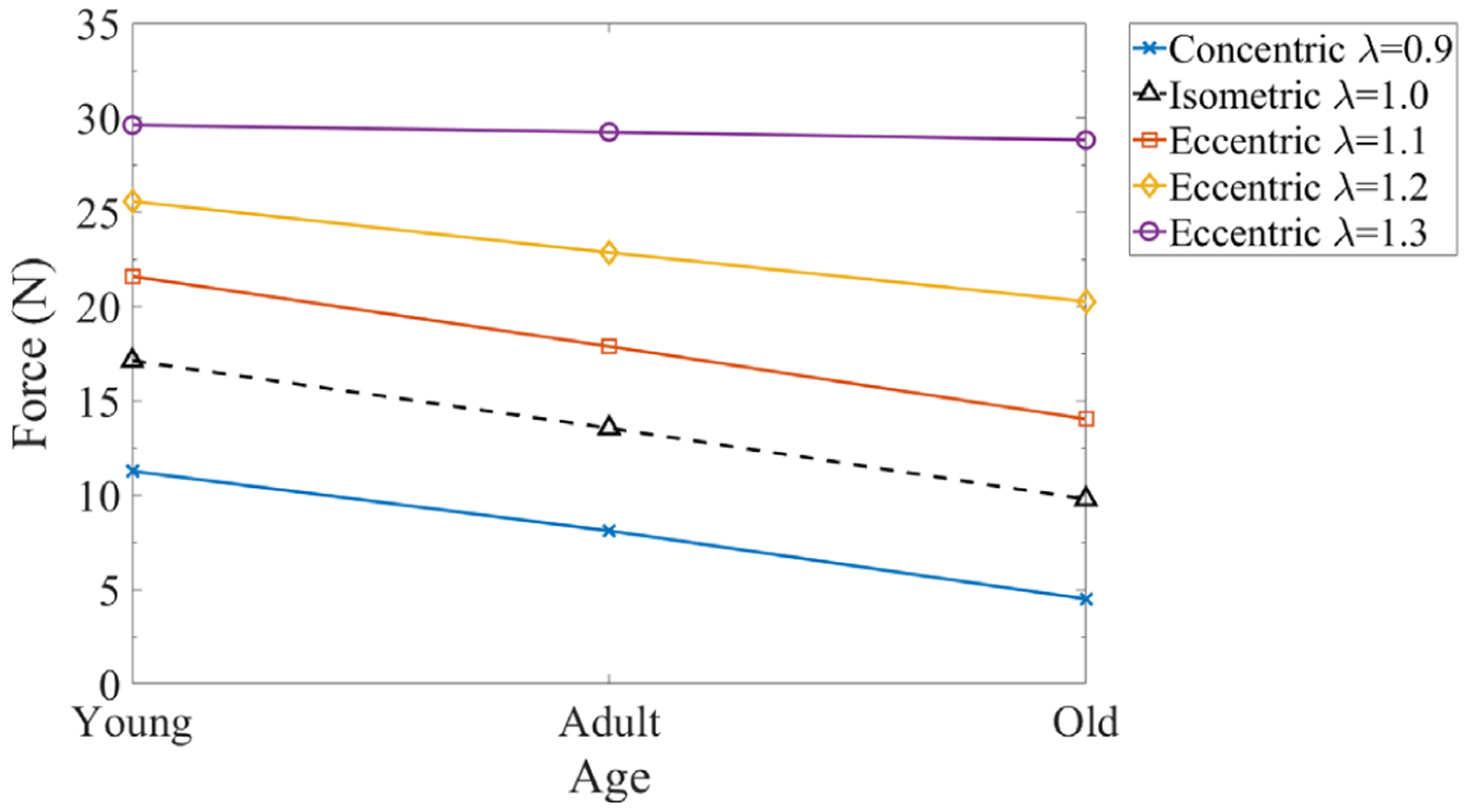
The aging effects of the combined factors on force generation capacity of muscle tissues

4 |. CONCLUSIONS

In this study, a cellular-scale honeycomb-like microstructural muscle model is developed to investigate the causal relations between age-related microstructural changes and the reduction in force generation capacity of skeletal muscle by using a pixel-based meshfree RKPM computational framework. By employing cellular-scale muscle units composed of muscle fibers and CT, the “intrinsic” force generation capability can be examined and the mechanisms of force generation can be explained.

The numerical experiments reveal that the muscle tissues with higher passive stiffness (stiffer CT phase) generate smaller force during concentric contraction because the CT in the compressive state offsets the total force generation. On the contrary, during an eccentric contraction, the muscle tissues with higher passive stiffness (stiffer CT and fiber’s passive part) tend to enhance force generation due to a greater tensile force contributed from the passive components. The volume ratio of CT is also demonstrated to have similar effects on force generation, but its enhancement effect on force generation occurs only when the stretch ratio is beyond a certain point, indicating a nonlinear influence from the variation of the microstructure geometry. Furthermore, it is shown that the reduction in the force capacity of muscle fibers (ie, the maximum isometric stress) reduces force generation under both concentric and eccentric contraction.

As the passive components, CT and fiber’s passive part, have a strong contribution to the passive stiffness of skeletal muscle, their age-related material stiffening usually results in an increase in the overall passive stiffness of skeletal muscle, which is considered as one of the major factors accounting for the fact that skeletal muscle tends to maintain force generation capacity during eccentric contraction and reduce generation capacity during concentric contraction. Finally, the combined effects of age-related changes in all three factors (muscle passive stiffness, endomysium thickness, and specific muscle fiber force) on muscle’s force generation capacity are demonstrated to agree with the experimental observation, that is, the age-associated reduction in skeletal muscle force generation is greater under concentric contraction than eccentric contraction.

The cellular-scale microstructural muscle models used in this study are constructed from histological cross-sectional images enabling us to create a realistic model of the in vivo structure. The numerical results offer a deep insight into the mechanism of how the skeletal muscle tissues work and how the connective tissue and muscle fiber phases coordinate and contribute to the overall active force generation. The computational method used in this study also demonstrates the effectiveness of the meshfree RKPM image-based models, where no geometry reconstruction and mesh generation of complex microstructures are involved in the construction of the simulation model.

With the RKPM pixel-based method, the proposed honeycomb-like microstructural muscle model can be easily extended to investigate the effects of age- or disease-associated alterations in microstructure on muscle’s macroscopic functional properties. It should be noted that the force generation of skeletal muscle is influenced by some other factors that have not been considered in this study. These include alterations in regional fiber properties and distribution, changes in velocity and history-dependent contractile properties of muscle fiber, loss of motor units, and so forth, and they demand a more comprehensive investigation in their influence on muscle force generation.^1,65 For instance, Seydewitz et al proposed a multi-scale constitutive model considering velocity and history effects by a dynamic function at the microscale model of fiber activation.⁶⁶ Moreover, the giant protein, titin, plays an important role in both passive and active force production and transmission of muscle, and its activation-dependent behavior links closely to the history-dependent behavior of muscle (residual force enhancement).^43,49 Previous studies have demonstrated that titin stiffness increases during muscle activation with varying titin isoforms during muscle development,^43,47 which is expected to be co-responsible for the differences in muscle’s force generation between concentric and eccentric contractions. In the future, more sophisticated multi-scale constitutive models for both active and passive components of muscle will be introduced, for example, a sub-cellular scale model to account for the effects of titin and an anisotropic model to consider the effects of collagen fibers of ECM. Apart from active and passive muscle properties, 3D muscle architecture also plays an important role in muscular contraction dynamics. Muscle morphology (eg, muscle dimension, pennation angle, muscle fascicle architecture, aponeurosis dimension, tendon-muscle fascicle length ratios, etc.) changes during aging and thus influences muscular functionalities (eg, force production and transmission).^67–69 However, to what extent the above-listed muscle structural changes during aging are related to mechanical properties and functionalities of muscle has not been understood thoroughly.^69,70 This requires more comprehensive investigation using 3D skeletal muscle models incorporated with the age-associated changes in muscle morphology.

Novelty Statement:

1. A cellular-scale honeycomb-like microstructural muscle model constructed from a histological cross-sectional image of muscle is employed to study the causal relations between age-associated microstructural changes and age-related force loss using Reproducing Kernel Particle Method (RKPM).

2. The employed RKPM offers an effective means for modeling biological materials based on pixel points in the medical images and allow modeling of smooth transition in the material properties across interfaces.

3. The proposed microstructure-informed muscle model enables quantitative evaluation on how cellular-scale compositions contribute to muscle functionality and explain differences in age-related force changes during concentric, isometric and eccentric contractions.

APPENDIX

In the meshfree reproducing kernel particle method (RKPM)^30,31 simulations, the skeletal muscle structure is discretized by a set of nodes, which is different from the mesh-based discretization used in the finite element method. This unique point-based discretization provides a natural way of constructing models using pixel points in MRI or CT scan images and avoids complexities involved in geometry reconstruction and mesh generation. Therefore, RKPM is preferred for the image-based numerical simulation

The reproducing kernel (RK) approximation functions are formulated to possess desired completeness and continuity, which are respectively determined by using proper basis function and kernel function so that certain degree of accuracy and continuity in the approximation are achieved. As shown in Figure 12A, let a domain Ω be discretized by a set of “NP” nodes and each node x_I be associated with an approximation function Ψ_I(x). For simulation, the displacement field is given by the RK approximation, denoted as u^h, is given by

$$u^h(x)={\sum }_{I=1}^{NP}{\Psi }_I(x)d_I,$$ (A1)

where d_I is the nodal coefficient associated with the I-th node. The RK approximation function Ψ_I is expressed as

$${\Psi }_I(x)=C\left(x;x-x_I\right){\varphi }_a\left(x-x_I\right)$$ (A2)

where ϕ_a(x − x_I) is a kernel function which defines a local support for the approximation function measured by support size “a” as well as its smoothness. For example, the cubic B-spline function is widely used as kernel function in RKPM, see Figure 12B,

$${\varphi }_a(z)=\{\begin{array}{c}\frac{2}{3}-4z^2+4z^3;\text{ for }0\le z<\frac{1}{2}\\ \frac{4}{3}-4z+4z^2-\frac{4}{3}{z}^3;\text{ for }\frac{1}{2}\le z<1\\ 0;\text{ for }z\ge 1\end{array}$$ (A3)

where z = ‖x − x_I‖/a. The term C(x; x − x_I) is a correction function constructed using a set of basis functions,

$$C\left(x;x-x_I\right)={\sum }_{i+j+k=0}^n{\left(x_1-x_{1I}\right)}^i{\left(x_2-x_{2I}\right)}^j{\left(x_3-x_{3I}\right)}^k{b}_{ijk}(x)=H^T\left(x-x_I\right)b(x)$$ (A4)

in which H(x − x_I) is a vector containing all the monomial basis functions, n is the order of the complete monomials, and b(x) is an unknown parameter vector determined by enforcing the n-th order reproducing conditions as below,

$${\sum }_{I=1}^{NP}{\Psi }_I(x)x_{1I}^i{x}_{2I}^j{x}_{3I}^k=x_1^i{x}_2^j{x}_3^k;|i+j+k|=0,1,\cdots ,n$$ (A5)

FIGURE 12.

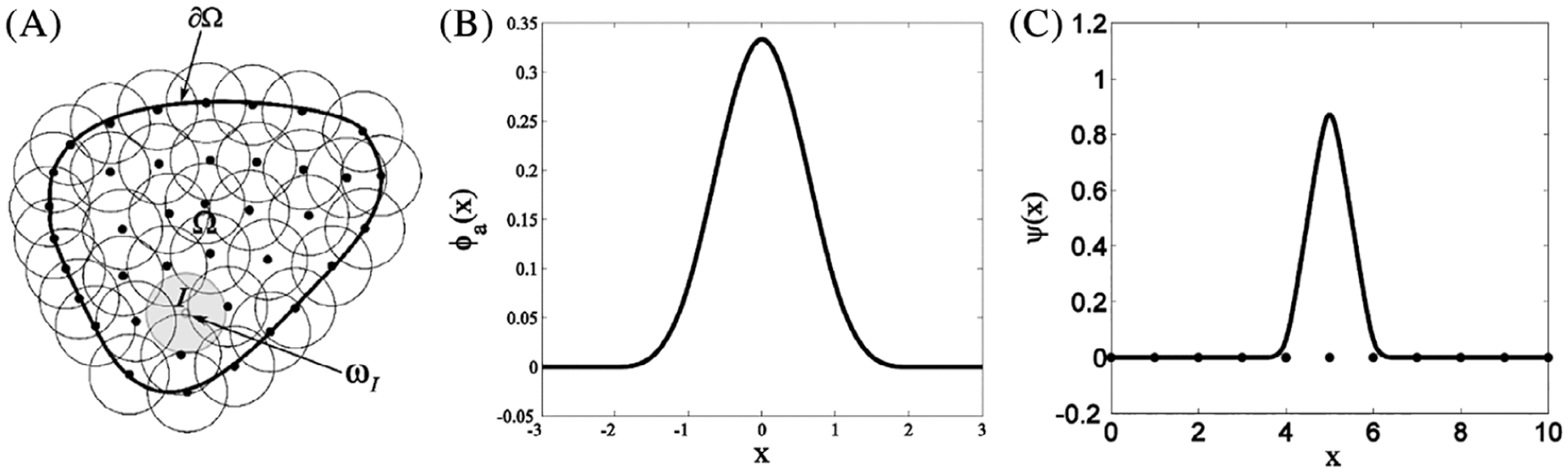
(A) Meshfree discretization of an object over the domain Ω; (B) A cubic B-spline function widely used as kernel function; (C) An example of RK approximation function centered at x = 5.0 and with support size α = 1.5 × (nodal spacing)

In this work, a linear basis is used such that H^T(x − x_I) = [1, (x₁ − x_1I), (x₂ − x_2I), (x₃ − x_3I)]. Introducing Equations (9) and (10) into Equation (11), the unknown vector can be obtained by b(x) = M⁻¹(x) H(0), where M(x) is the moment matrix given by,

$$M(x)={\sum }_{I=1}^{NP}H\left(x-x_I\right)H^T\left(x-x_I\right){\varphi }_a\left(x-x_I\right).$$ (A6)

Finally, the RK approximation function (see Figure 12c) is expressed as,

$${\Psi }_I(x)=H^T(0)M^{-1}(x)H\left(x-x_I\right){\varphi }_a\left(x-x_I\right)$$ (A7)

Note that the above RK approximation function does not possess the Kronecker delta property. Therefore, certain techniques are needed for RK approximation to have the kinematically admissible property and properly impose essential boundary conditions, such as transformation,^31,71,72 coupling with finite elements near essential boundary,^73,74 penalty method,⁷⁵ Nitsche’s method,^76–78 the modified variational principle,⁷⁹ or the Lagrange multiplier method.⁸⁰