Walking Humans Trade Off Different Task Goals To Regulate Lateral Stepping

Abstract

People walk in complex environments where they must adapt their steps to maintain balance and satisfy changing task goals. How people do this is not well understood. We recently developed computational models of lateral stepping, based on Goal Equivalent Manifolds that serve as motor regulation templates, to identify how people regulate walking movements from step-to-step. In normal walking, healthy adults strongly maintain step width, but also lateral position on their path. Here, we used this framework to pose empirically-testable hypotheses about how humans might adapt their lateral stepping dynamics when asked to prioritize different stepping goals. Participants walked on a treadmill in a virtual-reality environment under 4 conditions: normal walking, and while given direct feedback at each step to maintain constant step width, constant absolute lateral position, or constant heading (direction). Time series of lateral stepping variables were extracted, and variability and statistical persistence (reflecting step-to-step regulation) quantified. Participants exhibited less variability of the prescribed stepping variable compared to normal walking during each feedback condition. Stepping regulation results supported our models’ predictions: to maintain constant step width or position, people either maintained or increased regulation of the prescribed variable, but also decreased regulation of its complement. Thus, people regulated lateral foot placements in predictable and systematic ways determined by specific task goals. Humans regulate stepping movements to not only “just walk” (step without falling), but also to achieve specific goal-directed tasks within a specific environment. The framework and motor regulation templates presented here capture these important interactions.

INTRODUCTION

Our day-to-day environment is complex (Moussaïd et al., 2011; Orendurff et al., 2008). People readily modify their stepping to avoid obstacles and navigate complex terrain without falling or losing balance (Barton et al., 2017; Twardzik et al., 2019). Humans also modify foot placements to perform lateral maneuvers (Acasio et al., 2017) or negotiate destabilizing environments (Wu et al., 2017). This means they must be able to adapt how they regulate their stepping movements (Dingwell et al., 2010) to effectively adjust foot placement across these various contexts. This is particularly true for lateral stepping (Dingwell and Cusumano, 2019), as walkers are more unstable laterally (Bauby and Kuo, 2000; Dean et al., 2007; McAndrew et al., 2011). Following a loss of balance, appropriate lateral placement of the foot on the subsequent step can redirect the center of mass acceleration to recover balance and prevent falling (MacKinnon and Winter, 1993; Townsend, 1985). Even during unperturbed walking, appropriate step-to-step lateral foot placements are necessary to avoid loss of balance (Bruijn and van Dieën, 2018; Kuo, 1999). It is therefore important to better understand how humans regulate lateral foot placement from each step to the next as they walk.

We previously developed a computational framework that proposes goal functions to theoretically define a task and determine the sets of all possible stepping solutions as a Goal Equivalent Manifold (GEM) (Cusumano and Cesari, 2006; Cusumano and Dingwell, 2013; John et al., 2016). Simple mechanical models (e.g., inverted pendulum, mass-on-a-spring) can serve as biomechanical templates (Dickinson et al., 2000; Full and Koditschek, 1999; Holmes et al., 2006) that both describe fundamental aspects of locomotion dynamics (Gan et al., 2018; Geyer et al., 2006; Kuo, 1999; Srinivasan and Ruina, 2006) and also generate empirically testable hypotheses about high-level locomotor control strategies (Full and Koditschek, 1999). Directly analogous to these, our GEM-based models (Dingwell and Cusumano, 2015, 2019; Dingwell et al., 2010) serve as motor regulation templates that parsimoniously describe how people manipulate stepping movements from each step to the next. Our computational framework also poses concrete, experimentally testable a priori hypotheses about what step-to-step regulation strategies (e.g., “maintain speed”, “stay in the middle of the path”, etc.) people might adopt. As such, these motor regulation templates embody the two key features that define a “template” (Full and Koditschek, 1999; Holmes et al., 2006). They are also fully symbiotic with mechanical templates (Patil et al., 2020).

Our original GEM-based framework demonstrated how humans regulate sagittal plane stepping movements (Dingwell and Cusumano, 2015; Dingwell et al., 2010). That framework was validated and replicated by multiple independent studies (Decker et al., 2012; Roerdink et al., 2015; Roerdink et al., 2019; Terrier, 2016; Terrier and Dériaz, 2012) and our own work (Bohnsack-McLagan et al., 2016; Dingwell et al., 2018; Dingwell et al., 2017). We recently extended our GEM-based framework to identify goal functions for lateral stepping regulation (Dingwell and Cusumano, 2019). For normal walking, lateral stepping dynamics demonstrated strong control of step width, combined with weaker control of one’s absolute lateral position on their walking path (Dingwell and Cusumano, 2019). However, as contexts and/or goals change during real-world walking, we expect humans to adapt their stepping regulation. For example, when subjected to lateral perturbations, people more tightly regulated both step width and position (Dingwell et al., 2021; Kazanski et al., 2020). Given this framework, it is important to determine how different goals affect people’s lateral stepping strategies.

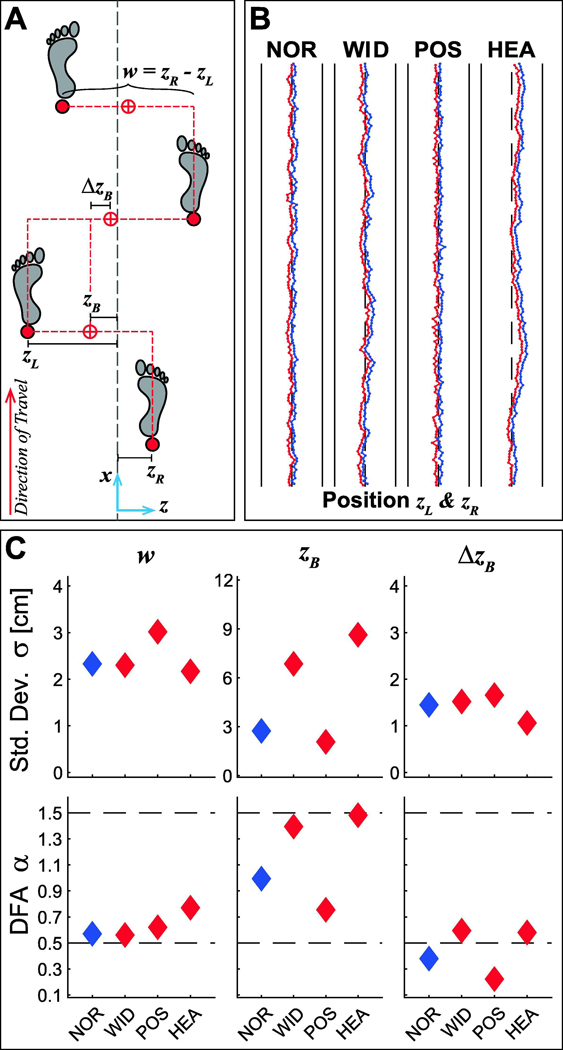
We used our lateral stepping framework (Dingwell and Cusumano, 2019) to derive testable hypotheses about how healthy young adults might adapt their lateral stepping dynamics when asked to prioritize specific task goals. Our framework defines how humans can adjust left and right lateral foot placements, {z_Ln, z_Rn}, at each step (n) to regulate step width (w_n), lateral position (z_Bn), and/or the first difference of position (Δz_Bn), taken as a proxy for lateral speed or heading (Fig. 1A; see Supplement for details). The step-to-step dynamics of normal walking were well-predicted by simulations that traded-off maintaining mostly step width for some lateral position (Dingwell and Cusumano, 2019).

Figure 1 – Lateral Stepping Variables and Models Simulations of Predicted Changes in Control.

A) Transverse plane schematic that demonstrates the primary lateral stepping variables that can be regulated from step-to-step, including: lateral positions of each foot (z_L and z_R), step width (w), absolute lateral body position (z_B: proxy for center-of-mass), and change in lateral position (Δz_B: proxy for lateral ‘heading’). B) Example time series data for a single representative trial simulated for parameter values based on the experimental data. The controller proportion was weighted at 85% step width / 15% position control. C) Hypothesized standard deviation (σ) and DFA scaling exponent (α) values for each variable (w, z_B, and Δz_B) across four conditions: normal walking (NOR) with controller proportions weighted at 85% step width / 15% position control; walking to regulate w (WID) with controller proportion weighted at 98% step width / 2% position control; walking to regulate z_B (POS) with controller proportions weighted at 65% step width / 35% position control; and walking to regulate Δz_B (HEA) with controller proportions weighted at 50% step width / 50% heading control. Each subplot shows the mean of 48 representative simulated trials from the model using the same parameter values as in (B).

Here, we hypothesized that to achieve specific stepping goals, humans would modify their lateral stepping regulation consistent with predictions of our framework. Specifically, we experimentally tested participants’ ability to maintain a constant value of each of the three lateral stepping variables {w, z_B,Δz_B}. Their goal was thus to minimize errors with respect to the experimental goal function:

$$F_q=q_n-q^{\ast }=0,$$ (1)

where q ∊ {w, z_B, Δz_B} and q* ≡ the desired goal value. We adapted our multi-objective control model to predict how, compared to normal walking (NOR), stepping dynamics might change when participants were asked to explicitly maintain constant w (WID), constant z_B (POS), or constant Δz_B (HEA) (Fig. 1B-C). Based on our framework and previous findings (Dingwell and Cusumano, 2019), we predicted that when asked to explicitly maintain either constant w or constant z_B, participants should shift the degree to which they traded off between each of these, and thus exhibit increased regulation of the prescribed variable, along with decreased regulation of the other (see Supplement). Conversely, heathy humans did not appear to regulate Δz_B (Dingwell and Cusumano, 2019). Our simulations, however, did identify multiple strategies to regulate combinations of w and Δz_B that people could have successfully adopted. Therefore, here we predicted that if people can regulate heading directly (but choose not to), then when explicitly asked to maintain constant Δz_B, participants might regulate heading and step width in such a way (Fig. 1B-C).

METHODS

Participants

Twenty-four young healthy adults (Table 1) participated. Participants were screened to ensure no medications, lower limb injuries, surgeries, musculoskeletal, cardiovascular, neurological, or visual conditions affected their gait. Prior to participating, each participant provided written informed consent, as approved by the Institutional Review Board of Pennsylvania State University.

Table 1 – Participant Characteristics.

All values except Sex are given as Mean ± Standard Deviation.

Characteristic:	Value:
Sex	12 M / 12 F
Age [yrs]	23 ± 3
Body Height [m]	1.74 ± 0.09
Body Mass [kg]	70.2 ± 12.3
Body Mass Index [kg/m2]	23.2 ± 3.0
Leg Length [m]	0.84 ± 0.06

Protocol

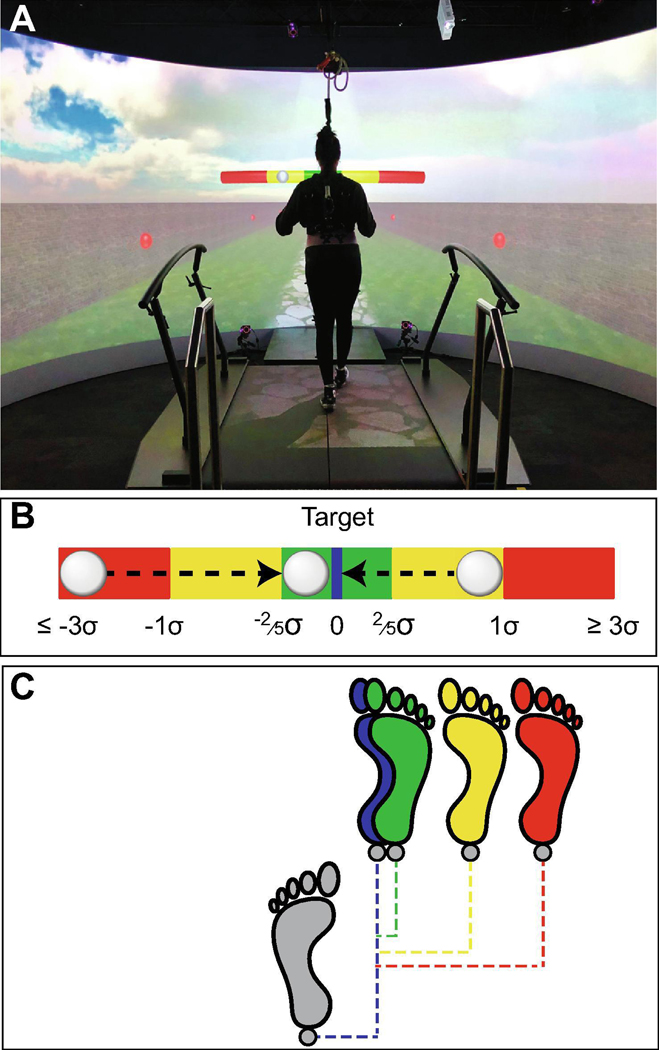
Participants walked on a 1.2 m wide treadmill in a “V-Gait” virtual reality (VR) system (Motekforce Link, Amsterdam, Netherlands; Fig. 2A) at a constant speed of 1.0 m/s for all trials. For all trials, the optic flow speed matched the treadmill belt speed. To prevent any potential injury, participants wore a safety harness.

Figure 2 – Experimental Setup.

A) Photo of a participant walking in the Motek “M-Gait” virtual reality environment. The Motek “M-Gait” integrates an instrumented treadmill, 220º semi-cylindrical screen, motion capture, and sound system. The VR scene used here included a cobblestone path lined on each side by brick walls with red spheres embedded to enhance optic flow. B) Schematic representation of “Bead-on-a-Wire” visual feedback. The position of the white dot (the “bead”) was updated at each step and represented the difference between the prescribed target value (q*) and the measured value (q_n) of the respective q ∊ {w, z_B, Δz_B}. This provided participants with direct visual feedback of their task performance in real-time. Participants were instructed to keep the bead on the target at the center of the wire (i.e., minimize error with respect to the goal) for the duration of the trial. Importantly, they were not instructed on how to do so. C) Illustration to demonstrate how, at any given current step (gray), the subsequent foot placement could move the bead either closer to the target (blue), or into the green, yellow, or red regions of the wire, contingent on how far away that step moves the target variable (q) from the desired location.

Participants first completed three 4-min walking trials to establish their baseline normal walking (“NOR”). Participants were instructed only to “walk and look straight ahead”. The first trial served as an acclimation period. The second and third trials were used to determine the participants’ average step width, and the variability of their lateral stepping variables, w, z_B, and Δz_B during normal walking.

Participants then completed three 4-min walking trials for each of three experimental conditions: walking to maintain, at each step, a prescribed step width (“WID”), absolute lateral body position (“POS”), or heading (“HEA”) from step-to-step. For WID, each participant’s own mean step width ($\overline{w}$) was calculated from their NOR data. The prescribed goal was to maintain this mean step width ($q^{\ast }\triangleq w^{\ast }=\overline{w}$). For POS, the prescribed goal was to stay at the lateral geometric center of the treadmill ($q^{\ast }\triangleq z_B^{\ast }=0$). For HEA, the prescribed goal was to “walk straight ahead” ($q^{\ast }\triangleq \text{Δ}{z}_B^{\ast }=0$). All three trials for each condition were presented consecutively. Order of presentation between conditions was counterbalanced across participants using a Latin Square design. To minimize fatigue, participants were allowed to rest (~1-min) after each trial.

For each condition, participants were told which variable they were to regulate and what their prescribed stepping goal was. Participants received direct “Bead-on-a-Wire” visual feedback of their performance (Fig. 2B). The bead’s position represented the difference between the measured and prescribed goal value (q_n – q^*) of each respective q ∊ {w, z_B, Δz_B} at each step (Fig. 2C). Each participant’s own average standard deviations of w, z_B, and Δz_B as calculated from the NOR condition defined the boundaries of the virtual penalty regions on the wire (Fig. 2B). For normally distributed data, ~31% of the data would fall within ±2/5^ths of one standard deviation (σ) and ~68% would fall within ±1σ. Thus, the green region extended from 0 to ±2/5σ and the yellow region extended from ±2/5σ to ±1σ. The red region indicated all foot placement errors beyond 1σ (Fig. 2B). Participants simultaneously received auditory feedback: a pleasant chime for steps in the green region, a flute sound for steps in the yellow region, and an annoying buzzer sound for steps in the red region. For each feedback condition, participants were instructed to keep the bead at the center of the wire (i.e., minimize error with respect to the goal), by maintaining the prescribed step width, position, or heading at each step.

Data Collection and Processing

Each participant wore 16 retroreflective markers on their lower body defining the Vicon Plug-in Gait lower body model (Oxford Metrics, Oxford, UK). Kinematic data were collected at 100 Hz from a 10-camera Vicon motion capture system (Oxford Metrics, Oxford, UK). These data were processed in real-time using D-Flow software (MotekForce Link, Amsterdam, Netherlands). Marker trajectories were filtered using a low-pass filter with a cut-off frequency of 15 Hz. Only the markers located on the feet were analyzed here. Heel strikes were determined using an established velocity-based detection algorithm (Zeni et al., 2008). For each step, left and right foot placements (z_L and z_R) were quantified as the lateral location of the heel marker at heel strike. These z_L and z_R were then used to calculate w, z_B, and Δz_B (Fig. 1A and Supplement; Dingwell and Cusumano, 2019). During the feedback conditions, the bead’s position on the wire (in terms of penalty region color) was recorded for each step. These data were exported from D-Flow and additional analyses were performed using MATLAB (The MathWorks, Inc., Natick, MA). Only the last 300 consecutive steps of each of the latter two trials for each condition were analyzed to maintain consistency across trials and participants.

Dependent Measures

To quantify each participant’s ability to maintain the bead’s position on the target at the center of the wire, we computed stepping errors relative to q* in each feedback trial. Target success rates were defined as the total number of steps that the bead position was in each of the green, yellow, or red regions, divided by the total number of steps × 100%.

To characterize the overall lateral stepping strategies participants used for each condition, several features of the primary lateral stepping variables (w, z_B, Δz_B) were quantified. First, means (μ) of each stepping time series were computed. Standard deviations (σ) of w, z_B, and Δz_B were calculated to quantify average magnitudes of variability. Scaling exponents (α) of w, z_B, and Δz_B time series were computed using Detrended Fluctuation Analysis (DFA) (Dingwell et al., 2010). DFA α quantifies the statistical persistence (the likelihood a deviation in one direction is followed by a deviation in the same direction), or anti-persistence (the likelihood that deviation is followed by a deviation in the opposite direction) in a time series. DFA α thus quantifies the degree to which participants corrected deviations of w, z_B, and Δz_B from each step to the next within a trial (Dingwell and Cusumano, 2010; 2019). Variables that are more tightly regulated exhibit more frequent corrections of step-to-step deviations, which typically yields α values close to 0.5.

For any single time series, it is always desirable to have longer time series, as this will yield more accurate estimates of the true DFA scaling exponents, α. However, DFA α can be just as accurately estimated from shorter time series by averaging estimates across multiple such time series, as was done here. In several studies, although the trial-to-trial variance of the calculated DFA α increased (approximately) exponentially as the length of the time series decreased, the estimated mean value (across trials) of DFA α was not biased and remained nearly constant (Delignières et al., 2006; Miramontes and Rohani, 2002; Pilgram and Kaplan, 1998). This has been demonstrated for time series as short as 64 data points (Delignières et al., 2006). Here, we likewise averaged DFA α estimates across multiple trials of 300 data points (steps) each from multiple participants to mitigate the effects of increased variance from conducting DFA analyses on shorter time series (Pierrynowski et al., 2005).

Statistical Analyses

All statistical analyses were performed using Minitab 18 (Minitab, Inc., State College, PA). Ninety-five percent confidence intervals were constructed to compare the mean percent of steps that landed within the green, yellow, and red regions of the wire during each feedback condition to those predicted for normal walking. Each dependent measure (μ, σ, α) was computed for each lateral stepping variable (w, z_B, Δz_B) from the latter two trials for each condition (NOR, WID, POS, HEA) for each participant. For each such measure, repeated measures mixed effects ANOVAs were conducted to test for significant differences between Conditions. Condition was a fixed factor, Subject was a random factor, and the two trials constituted the repeated measures. Standard deviations (σ) were first log-transformed so that all dependent variables satisfied the linearity and normality assumptions of the ANOVA model. Tukey’s post-hoc comparisons were then conducted to test pre-planned comparisons for differences between each feedback condition (WID, POS, HEA) and NOR.

RESULTS

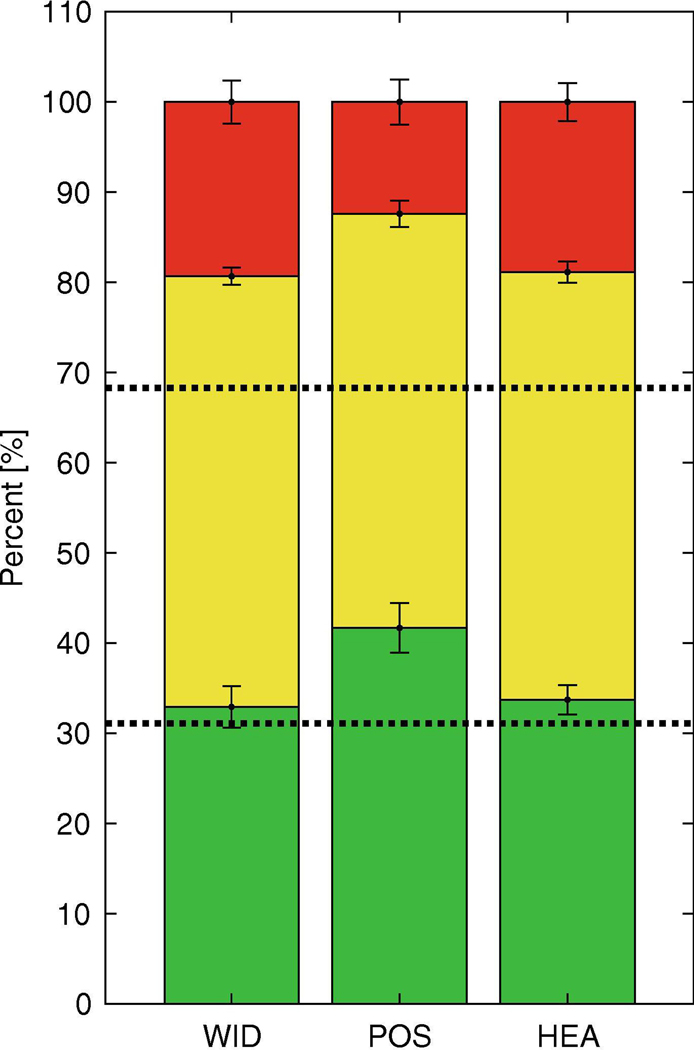
Participants took significantly more green steps than expected (> 31% within 2/5^thsσ) in the POS and HEA conditions, but not for WID (Fig. 3). For all three feedback conditions, participants took significantly more yellow steps than expected (> 68% within 1σ). Thus, participants maintained each prescribed lateral stepping variable to a greater extent than was otherwise expected during normal walking when given explicit task instructions to “stay on target” and given direct feedback.

Figure 3 – Target Success Rates.

Stacked bar chart showing the percent of steps that resulted with the bead in the green, yellow, and red regions of the wire, respectively, for each of the three experimental conditions: WID, POS, and HEA. Dashed lines at 31% and 68% represent the percent of steps that would be expected to result in the bead landing within 2/5^thσ and 1σ respectively during normal walking (NOR), if those data are normally distributed. The mean percent of steps less than 2/5^thσ, less than 1σ, and greater than 1σ from the target are depicted in green, yellow, and red bars respectively. Error bars are 95% Confidence Intervals for each mean. Error bars for green regions entirely above the 31% dashed line for POS and HEA indicate participants took significantly more green steps than expected for those conditions. Error bars for yellow regions entirely above the 68% dashed line for all 3 feedback conditions indicate participants took significantly more yellow steps than expected for all conditions.

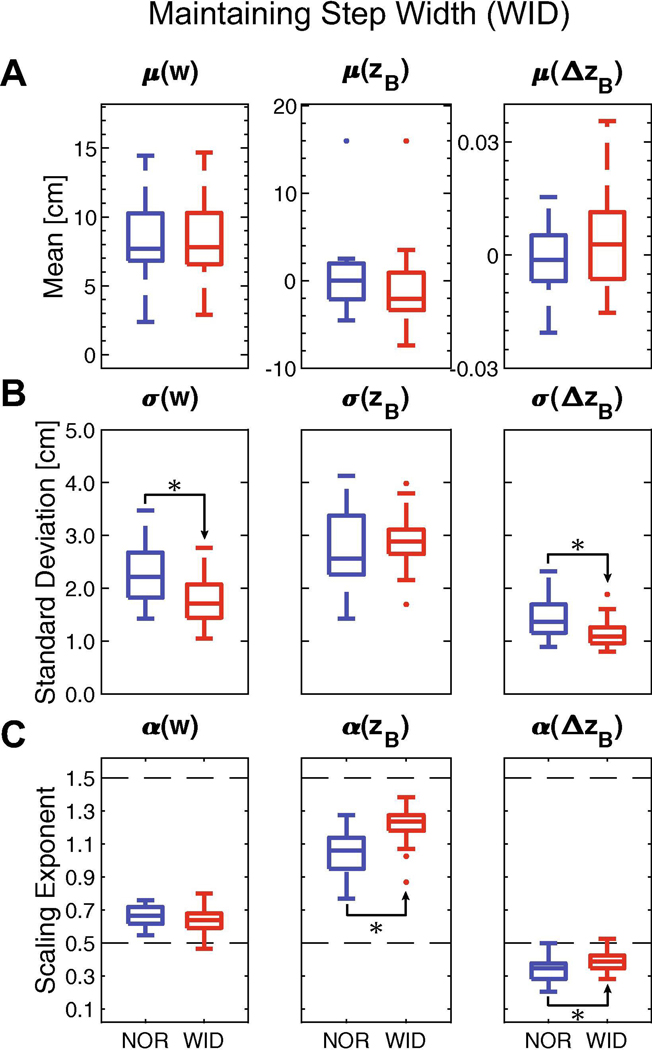
For the WID condition, participants maintained their mean step width (w: p = 0.993), lateral position (z_B: p = 0.137), and heading (Δz_B: p = 0.380) compared to NOR (Fig. 4A; Table 2). Standard deviation (Fig. 4B) of step width decreased significantly (w: p < 0.001), as did heading (Δz_B: p < 0.001), but variability of lateral position remained similar (z_B; p = 0.281). Participants did not exhibit significant changes in statistical persistence (Fig. 4C) of fluctuations in step width (w: p = 0.701), but did exhibit significant increases in persistence of fluctuations in lateral body position (z_B: p < 0.001) and heading (Δz_B: p < 0.001), consistent with heading being the first-difference of position (Dingwell and Cusumano, 2019).

Figure 4 – Maintaining Step Width (WID).

Participants were instructed to walk with a constant step width (w = mean from NOR condition) from step-to-step provided real-time performance feedback. A) Mean values of w, z_B, or Δz_B between NOR and WID conditions. B) Standard deviations (σ) of w, z_B, or Δz_B between NOR and WID conditions. C) DFA scaling exponents (α) for w, z_B, or Δz_B between NOR and WID conditions. The dashed line at 0.5 indicates a variable with strong statistical persistence. The dashed line at 1.5 indicates a variable with strong statistical anti-persistence. For (A)-(C), subplots demonstrate a summary boxplot showing the medial, 1^st and 3^rd quartiles, and whiskers extending to 1.5× interquartile range. Values beyond this range are shown as individual data points. Statistically significant differences are denoted with an asterisk. Results of statistical comparisons are provided in Table 2.

Table 2 – Primary Statistical Results.

Differences across Conditions (NOR, WID, POS, HEA) for dependent measures of the lateral stepping variables w, z_B, and Δz_B including mean, variability (σ), and DFA scaling exponent (α). Data are shown in Figures 4–6. ANOVA results (F-statistics and p-values) are provided for main effects of Condition. In cases where the Condition effect was significant, results of Tukey’s least significant difference pairwise comparisons are presented for differences of the 3 experimental conditions (WID, POS, HEA) compared to the NOR condition. Variability measures for w, z_B, and Δz_B were first log-transformed prior to statistical analyses to meet the normality and linearity assumptions of the ANOVA model. Significant differences (p < 0.05) are indicated in bold.

Data In	Dependent Measure	Condition Main Effects	Tukey’s (Condition Effects)
Figs. 4-6A:	Mean (w)	F(3,165) = 7.50 p < 0.001	WID: p = 0.993 POS: p = 0.007 HEA: p = 0.010
	Mean (zB)	F(3, 165) = 1.68 p = 0.173	WID: p = 0.137 POS: p = 0.894 HEA: p = 0.497
	Mean (ΔzB)	F(3, 165) = 1.28 p = 0.282	WID: p = 0.380 POS: p = 1.000 HEA: p = 1.000
Figs. 4-6B:	ln [σ (w)]	F(3, 165) = 49.46 p < 0.001	WID: p < 0.001 POS: p = 0.924 HEA: p < 0.001
	ln [σ (zB)]	F(3, 165) = 65.24 p < 0.001	WID: p = 0.281 POS: p < 0.001 HEA: p = 0.093
	ln [σ (ΔzB)]	F(3, 165) = 61.52 p < 0.001	WID: p < 0.001 POS: p = 0.755 HEA: p < 0.001
Figs. 4-6C:	α (w)	F(3, 165) = 5.5 p = 0.001	WID: p = 0.701 POS: p = 0.025 HEA: p = 0.972
	α (zB)	F(3, 165) = 203.57 p < 0.001	WID: p < 0.001 POS: p < 0.001 HEA: p < 0.001
	α (ΔzB)	F(3, 165) = 78.87 p < 0.001	WID: p < 0.001 POS: p < 0.001 HEA: p = 0.662

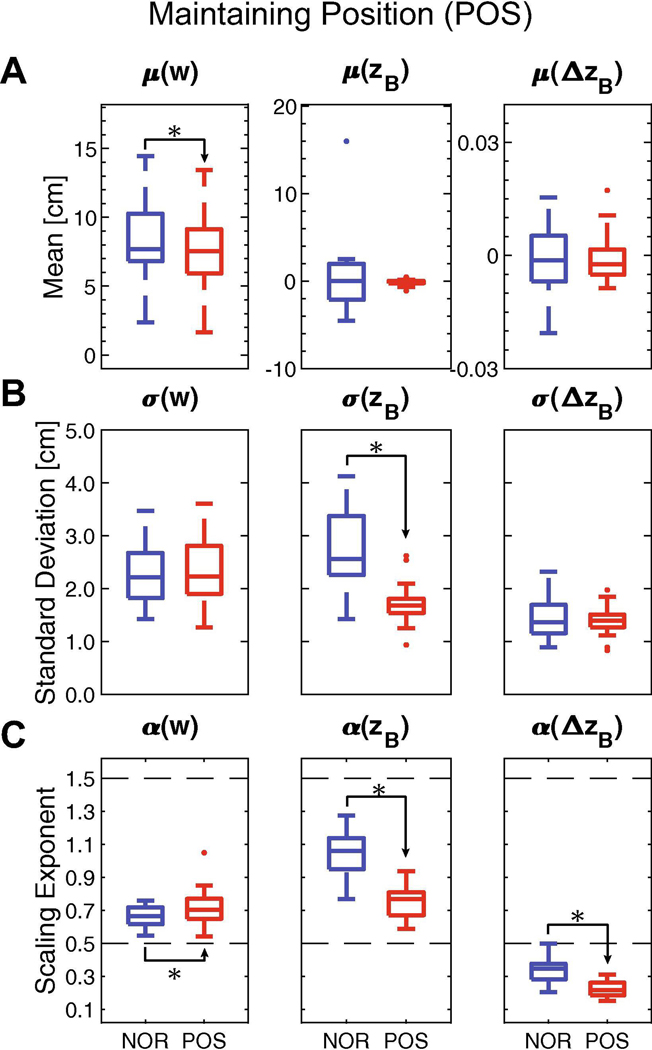
For the POS condition, participants maintained mean lateral body position (z_B: p = 0.849) and heading (Δz_B: p = 1.0), but took narrower steps (w: p = 0.007) compared to NOR (Fig. 5A; Table 2). Standard deviation (Fig. 5B) of lateral body position decreased significantly (z_B: p < 0.001), while variability of step width (w: p = 0.924) and heading (Δz_B: p = 0.755) remained unchanged. For all three lateral stepping variables, DFA scaling exponents (α) changed (Fig. 5C). Fluctuations in lateral body position exhibited decreased statistical persistence (z_B: p < 0.001), while fluctuations in step width exhibited increased persistence (w: p = 0.025). Fluctuations in heading exhibited greater anti-persistence, decreasing further below α < 0.5 (Δz_B; p < 0.001), again consistent with heading being the first-difference of position (Dingwell and Cusumano, 2019).

Figure 5 – Maintaining Lateral Position (POS).

Participants were instructed to walk with a constant lateral body position (z_B = 0) from step-to-step provided real-time performance feedback. A) Mean values of w, z_B, or Δz_B between NOR and POS conditions. B) Standard deviations (σ) of w, z_B, or Δz_B between NOR and POS conditions. C) DFA scaling exponents (α) for w, z_B, or Δz_B between NOR and POS conditions. The dashed line at 0.5 indicates a variable with strong statistical persistence. The dashed line at 1.5 indicates a variable with strong statistical anti-persistence. For (A)-(C), subplots demonstrate a summary boxplot showing the medial, 1^st and 3^rd quartiles, and whiskers extending to 1.5× interquartile range. Values beyond this range are shown as individual data points. Statistically significant differences are denoted with an asterisk. Results of statistical comparisons are provided in Table 2.

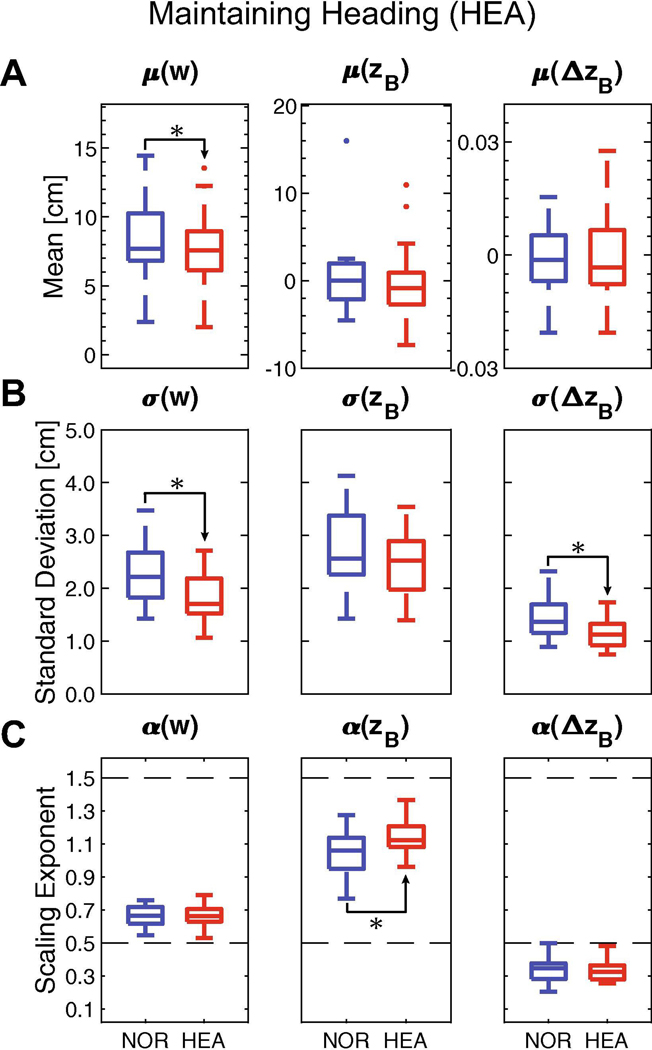
For the HEA condition, participants also maintained mean lateral position (z_B: p = 0.497) and heading (Δz_B: p = 1.0), but took somewhat narrower step widths (w: p = 0.010) compared to NOR (Fig. 6A; Table 2). Standard deviation (Fig. 6B) of heading decreased significantly (Δz_B: p < 0.001), as did step width (w: p < 0.001), but variability of lateral position remained similar (z_B: p = 0.093). Participants did not exhibit changes in statistical persistence (Fig. 6C) of fluctuations in step width (w: p = 0.972) or heading (Δz_B; p = 0.662). However, fluctuations in lateral position exhibited increased persistence further above α = 0.5 (z_B: p < 0.001) (Fig. 6C).

Figure 6 – Maintaining Heading (HEA).

Participants were instructed to walk with a constant heading (Δz_B = 0) from step-to-step provided real-time performance feedback. A) Mean values of w, z_B, or Δz_B between NOR and HEA conditions. B) Standard deviations (σ) of w, z_B, or Δz_B between NOR and HEA conditions. C) DFA scaling exponents (α) for w, z_B, or Δz_B between NOR and HEA conditions. The dashed line at 0.5 indicates a variable with strong statistical persistence. The dashed line at 1.5 indicates a variable with strong statistical anti-persistence. For (A)-(C), subplots demonstrate a summary boxplot showing the medial, 1^st and 3^rd quartiles, and whiskers extending to 1.5× interquartile range. Values beyond this range are shown as individual data points. Statistically significant differences are denoted with an asterisk. Results of statistical comparisons are provided in Table 2.

DISCUSSION

In the frontal plane, healthy young adults regulate lateral foot placement over consecutive steps primarily to maintain balance, but also to achieve task-relevant goals like staying on a given path or progressing in a particular direction. People walking in a complex world (Moussaïd et al., 2011; Orendurff et al., 2008) must continuously adapt their steps to satisfy new and/or changing task goals. Thus, it is important to quantify how humans regulate lateral foot placements across walking tasks and conditions. Here, we determined how participants modified their lateral stepping regulation when given goal-directed feedback and asked to prioritize specific task goals: maintain constant step width (w), lateral position (z_B), or heading (Δz_B).

We purposefully designed this experiment to give participants specified task goals that were easily achievable. Participants were then asked to maintain those values consistently from step-to-step. Across all feedback conditions (WID, POS, and HEA), mean values of the corresponding prescribed variables (w_n, z_Bn, and Δz_Bn, respectively) were not significantly different than baseline (NOR) values (Figs. 4–6A). Thus, participants completed all tasks with minimal changes to their average gait patterns. Most importantly, for each feedback condition, participants exhibited significantly decreased within-subject step-to-step variability of the corresponding prescribed variable (Figs. 4–6B). Thus, participants clearly reduced (on average) errors with respect to each prescribed goal: Eq (1).

However, variability measures offer no information regarding how deviations at each step are regulated (i.e., corrected) at the next step. DFA scaling exponents (α) can quantify this information (Dingwell and Cusumano, 2010; John et al., 2016). During normal (unrestrained and unperturbed) walking, healthy humans modulate z_Ln and z_Rn to trade off regulating predominantly w_n and to a lesser extent, z_Bn. (Dingwell and Cusumano, 2019; Kazanski et al., 2020). For both the WID and POS conditions, the opposing changes in DFA α for w and z_B compared to NOR supported our hypothesis that when provided goal-directed feedback, humans reweighted the proportions of w vs. z_B regulation to achieve each prescribed goal. Given WID feedback, participants decreased the variability of w by maintaining tight step-to-step corrections of w and correcting step-to-step deviations in z_B less (Fig. 4C). Given POS feedback, participants decreased the variability of z_B by correcting step-to-step deviations in z_B more and correcting step-to-step deviations in w less (Fig. 5C). That people, when given either WID or POS feedback, strongly regulated the prescribed variable (w for WID; z_B for POS) to reduce their step-to-step variability in that variable was not surprising. The important finding here was that for both feedback conditions, people decreased their step-to-step regulation of the complementary (but not prescribed) stepping variable (z_B for WID; w for POS). This complementary inverse coupling between w and z_B emerges from our GEM-based lateral stepping regulation templates (Dingwell and Cusumano, 2019), but is neither immediately intuitive, nor biomechanically or physiologically necessary. Nonetheless, the observed experimental results (Figs. 4–5) are in substantial agreement with our GEM-based model predictions (Fig. 1C).

Previously, stepping dynamics of both unperturbed (Dingwell and Cusumano, 2019) and laterally perturbed (Dingwell et al., 2021; Kazanski et al., 2020) walking were replicated by simulations that regulated only z_B and w. People did not regulate Δz_B, even though they could have (see Supplement). Here, when given HEA feedback, participants achieved the prescribed goal (Fig. 5A) and decreased Δz_B variability (Fig. 5B). They also exhibited more persistent fluctuations in lateral position (α(z_B); Fig. 5B), as our simulations predicted (Fig. 1C). However, they did not vary the degree to which they corrected fluctuations in either Δz_B itself or in w (Fig. 5C), which our simulations did predict (Fig. 1C). Importantly, as Δz_B is the first-difference of z_B, step-to-step fluctuations in these two quantities, and hence the DFA α’s of their respective time series, are not independent. Indeed, a position regulator that drives z_Bn to some constant z_B^* will automatically also drive Δz_B → 0, as our prior simulations demonstrate (Dingwell and Cusumano, 2019). Here, we tested whether people would regulate Δz_B directly when explicitly asked to do so. Participants did not do this, but instead reduced variability in Δz_B (Fig. 5B) by changing how they regulated z_B. Thus, humans appear to regulate w and z_B directly, even to control how they regulate Δz_B. This in fact further supports our prior GEM-based predictions that humans trade off regulating w and z_B (Dingwell and Cusumano, 2019).

As with our previous work (Dingwell and Cusumano, 2019), lateral stepping control simulations that directly manipulated Δz_B (Fig. 1C) took feasible steps, but again failed to replicate observed human stepping dynamics. However, this does not necessarily mean humans are not capable of adapting their Δz_B regulation. As there are infinite choices for each successive foot placement during walking, our experimental design did not require that participants adopt one specific strategy to minimize errors with respect to Eq. (1). This was reflected not only in our verbal instructions, but also in the nature of the visual feedback. We anticipated the goal-directed visual feedback (Fig. 2B) would translate across the WID, POS, and HEA conditions, but it is possible that heading errors were more difficult to correct during the HEA condition.

Our GEM-based framework enabled us to directly test empirically refutable hypotheses (Full and Koditschek, 1999) about how humans might choose to alter how they regulate lateral stepping when task goals were explicitly manipulated. Our empirical findings aligned well with our model simulations: human stepping dynamics were well predicted by relatively simple motor regulation templates (Dingwell and Cusumano, 2019; Patil et al., 2020). Humans readily adapted their lateral stepping regulation to meet each task presented (Figs. 4–6). But even as they did so, they consistently maintained tight regulation of step width across conditions, reflecting their need to maintain balance (Dean et al., 2007; McAndrew et al., 2011).

Importantly, they also made small but consistent corrections to deviations to their lateral position on the walking path. Correcting such deviations in absolute position relative to one’s surrounding environment is critical to achieving goal-directed walking (Matthis et al., 2017; Moussaïd et al., 2011). The biomechanics of how individuals walk thus depend not only on the entity doing the walking (here, humans), but also intrinsically on the environment in which the task is performed (Matthis et al., 2018; Twardzik et al., 2019) and also the goals of the walking task itself (Acasio et al., 2017; Moussaïd et al., 2011). Thus, humans regulate stepping movements to not only “just walk” (i.e., take steps without falling down), but also to achieve specific goal-directed walking tasks within a specific environment. The GEM-based framework and resulting motor regulation templates presented here captures these important interactions.