Fully Automated Segmentation of Head CT Neuroanatomy Using Deep Learning

Abstract

Purpose

To develop a deep learning model that segments intracranial structures on head CT scans.

Materials and Methods

In this retrospective study, a primary dataset containing 62 normal noncontrast head CT scans from 62 patients (mean age, 73 years; age range, 27–95 years) acquired between August and December 2018 was used for model development. Eleven intracranial structures were manually annotated on the axial oblique series. The dataset was split into 40 scans for training, 10 for validation, and 12 for testing. After initial training, eight model configurations were evaluated on the validation dataset and the highest performing model was evaluated on the test dataset. Interobserver variability was reported using multirater consensus labels obtained from the test dataset. To ensure that the model learned generalizable features, it was further evaluated on two secondary datasets containing 12 volumes with idiopathic normal pressure hydrocephalus (iNPH) and 30 normal volumes from a publicly available source. Statistical significance was determined using categorical linear regression with P < .05.

Results

Overall Dice coefficient on the primary test dataset was 0.84 ± 0.05 (standard deviation). Performance ranged from 0.96 ± 0.01 (brainstem and cerebrum) to 0.74 ± 0.06 (internal capsule). Dice coefficients were comparable to expert annotations and exceeded those of existing segmentation methods. The model remained robust on external CT scans and scans demonstrating ventricular enlargement. The use of within-network normalization and class weighting facilitated learning of underrepresented classes.

Conclusion

Automated segmentation of CT neuroanatomy is feasible with a high degree of accuracy. The model generalized to external CT scans as well as scans demonstrating iNPH.

Supplemental material is available for this article.

© RSNA, 2020

Summary

Deep learning can accurately segment neuroanatomy on CT scans; optimizations that improved segmentation performance for structures with varying size and slicewise prevalence were assessed, including the use of within-network normalization techniques and class weighting schemes.

Key Points

• ■ A fully automated deep learning model that simultaneously segments 11 intracranial structures at head CT was presented.

• ■ The effects of within-network normalization techniques, loss functions, and class weighting schemes on network training and performance were demonstrated.

• ■ The model generalized to external CT scans and scans demonstrating idiopathic normal pressure hydrocephalus; overall Dice coefficients were comparable to expert annotations and higher than those of existing segmentation methods.

Introduction

CT is a cornerstone of neuroimaging, and its use has increased steadily (1). Given the large volume of examinations, fully automated algorithms can potentially augment clinical workflow and improve diagnostic accuracy. Convolutional neural networks (CNNs) are the current standard in medical image analysis, and they can automate routine classification and segmentation tasks (2).

CNNs can accurately perform segmentation at US (3) and MRI (4). Several groups have also trained CNNs to delineate hemorrhage (5,6), tumors (7), whole brain (8), and cerebrospinal fluid (9) from head CT. Although algorithms that segment intracranial anatomy at MRI have been shown to facilitate structural analysis and disease characterization (4,10), there is currently no equivalent method for CT despite its higher utilization (1). Such an algorithm could be useful for a variety of reasons. First, knowledge of anatomy could enable downstream tools to localize pathologic features and predict neurologic outcome. For example, Takahashi et al (11) combined CNN and atlas-based approaches to identify acute ischemic stroke from noncontrast CT. Second, accurate segmentations can guide clinicians in treatment planning, such as radiation therapy and image-guided intervention using CT (12,13). Last, routine large-scale analysis of volumetric and morphologic information may lead to the discovery of new imaging biomarkers. Several studies have already demonstrated the clinical utility of volumetric information in head CT. For example, Diprose et al (14) found that cerebrospinal fluid volumes correlate with reduced functional independence after endovascular thrombectomy for ischemic stroke, and Anderson et al (15) found that lower ventricular volume is associated with clinical improvement following shunt insertion for idiopathic normal pressure hydrocephalus (iNPH). To improve the diagnosis of iNPH, Toma et al (16) further proposed the use of population-based image analytics to establish normal limits for intracranial compartment volumes. However, the adoption of these methods, as well as the development and assessment of new CT imaging features, have been hindered by the lack of an accurate and fully automated segmentation algorithm.

In this study, we trained and validated a U-Net (17) to simultaneously delineate multiple intracranial structures from noncontrast CT. As these structures ranged considerably in size and slicewise prevalence, we described strategies to mitigate challenges associated with multiclass segmentation and class imbalance. To ensure that our model learned generalizable features, we validated it on examinations demonstrating iNPH as well as on normal examinations from the Radiological Society of North America (RSNA) Intracranial Hemorrhage Detection Challenge. Finally, we compared its results with existing segmentation methods.

Materials and Methods

Data Acquisition

Primary dataset.—For this retrospective study, we obtained institutional review board approval with a waiver of informed consent and Health Insurance Portability and Accountability Act authorization. We retrieved a consecutive list of all noncontrast head CT scans performed between August and December 2018, and we excluded pediatric patients and patients with identifiable intracranial abnormalities (except brain parenchymal atrophy and leukoaraiosis). From this list, we randomly selected 62 unique examinations (mean patient age, 73 years; age range, 27–95 years; 35 women) and extracted their axial oblique series. There is no overlap of participants with previous studies.

Secondary test datasets.—We acquired two additional datasets to assess model generalizability. The first dataset contained 30 volumes from the RSNA Intracranial Hemorrhage Detection Challenge. All patients demonstrated varying degrees of brain parenchymal atrophy with no other intracranial abnormalities (no hemorrhage or chronic infarction). The second dataset contained 12 patients (mean age, 74 years; age range, 60–84 years; seven women) evaluated at our center for iNPH between August and December 2018. We intentionally selected only examinations that demonstrated severe ventriculomegaly. Six of these patients also had newly inserted ventricular shunts. We chose iNPH because ventricular enlargement distorts but does not efface normal anatomy. The presence of highly attenuating foreign objects further tested the model’s robustness. Table E1 (supplement) summarizes Digital Imaging and Communications in Medicine (DICOM) information for the primary and iNPH datasets. DICOM information was not published for the RSNA dataset.

Data Preparation

Primary dataset.—Patient volumes were split into 40 scans (1738 slices) for training, 10 (397 slices) for validation, and 12 (530 slices) for testing. Scans were segmented into 11 regions of interest (ROIs) by a team of radiography students trained by two radiologists (A.B., a neuroradiologist with 9 years of experience, and S.H., a general radiologist with 7 years of experience). They were subsequently corrected by a medical doctor (J.C.C.) and verified by A.B. Specifically, the 11 ROIs were as follows: brainstem and cerebrum (BC, as one class), caudate nucleus (CN), central sulcus (CS), cerebellum (CE), dural folds and venous sinuses (DV, as one class), insular cortex (CO), internal capsule (CA), lentiform nucleus (LN), septum pellucidum (SP), subarachnoid space (SS), and ventricular system (VS). The supratentorial structures were chosen because they represent regions typically supplied by the middle cerebral artery, the largest cerebral artery and the artery most commonly affected in ischemic stroke (18). Several structures are also components of the Alberta Stroke Programme Early CT Score (19). The transverse sinus was not segmented as it did not appear consistently in axial sections; it was included with either BC or CE. We used RIL-Contour to annotate the dataset (20).

Ground truth masks.—From the primary test dataset, we created a series of multiobserver consensus labels, which we refer to as ground truth masks. Specifically, from each volume we selected four to six slices to represent all 11 ROIs (59 total slices). One slice contained CE, one slice contained CS at its most visible level, and two to four contiguous slices contained CA, CN, CO, LN, and SP. The remaining classes were represented across multiple slices. All slices were independently annotated by A.B., S.H., and J.C.C. From each set of three observations, a ground truth mask was generated by majority voting. If all three observers disagreed, a voxel was deemed indeterminate and was excluded from performance metrics. Indeterminate voxels made up 1.1% of all annotated voxels. Our workflow is outlined in Figure 1.

Figure 1:

Model evaluation and test dataset workflow. AB = Arunnit Boonrod, MD; DICE = Dice coefficients; iNPH = idiopathic normal pressure hydrocephalus; JC = Jason Cai, MD; RSNA = Radiological Society of North America; SH = Safa Hoodeshenas, MD; VOL = differences in structure volume.

Secondary test datasets.—The iNPH dataset (12 volumes with 423 slices) was segmented in the same way as the primary dataset, while the RSNA dataset (30 volumes with 150 slices) was segmented in the same way as the ground truth masks, except that images were annotated by J.C. only. We could not identify the CS on two iNPH volumes owing to the severely distorted anatomy, and we excluded their Dice coefficients from subsequent statistical analyses.

Terminology.—We considered BC, CE, SS, and VS to be large classes, and on the primary dataset they represent 10.8%, 2.3%, 1.3%, and 0.6% of all voxels, respectively. The remaining structures were considered small classes. The small classes represented 0.01%–0.28% of all voxels; 85.5% of voxels were background.

Model Architecture

Our U-Net consisted of four downsampling steps, which transformed a two-dimensional 512 × 512 × 1 input image into a 32 × 32 × 1024 feature tensor, and four upsampling steps, which transformed this tensor into a 512 × 512 × 12 segmentation mask (where the third channel corresponds to the 11 ROIs plus background). The model contained 31 042 499 trainable parameters. After experimenting with various configurations, our final model differed from the U-Net developed by Ronneberger through the use of layer normalization (21) between every 3 × 3 convolution and rectified linear unit activation function. We used softmax with categorical cross-entropy loss for multiclass prediction. A schematic of our U-Net can be found in Figure E1 (supplement).

Model Training

Weights from all training sessions were randomly initialized using the method reported by He et al (22). We used the Adam optimizer (23) with an initial learning rate of 0.0001. Data augmentation included left-right flipping, anteroposterior flipping (to accommodate both “left, anterior, superior” and “left, posterior, superior” orientations), scaling (±8%), rotation (±7°), and translation (±20 voxels in x and y). We monitored validation loss and per-class soft Dice coefficients (24), which were the Dice coefficients of predicted softmax class probabilities before thresholding. We stopped training when the average soft Dice coefficient decreased by less than 0.001 over five consecutive epochs. Training was performed on Keras 2.2.4 (Google, Mountain View, Calif) using TensorFlow 1.12 (https://www.tensorflow.org/). We used an 11 GB NVIDIA GTX 1080Ti graphics processing unit (Nvidia, Santa Clara, Calif) with a batch size of three.

Experiments

We sequentially evaluated several models on the validation dataset to determine the optimal configuration (Table 1). We started by using the Ronneberger U-Net with Hounsfield units as input (model 1). Subsequently, we added layer normalization between every 3 × 3 convolution and rectified linear unit activation (model 2). With layer normalization in place, we compared three weighting schemes for categorical cross-entropy loss: balanced weighting (model 2) given by

,

where w_c is the weight of the cth class, n_c and n_i are the total number of voxels that belong to the cth and ith classes in the entire dataset, respectively (with 0 being background by convention), and k is the total number of structures in the dataset (11 in our case); attenuated weighting given by (model 3); and no class weighting (model 4). We implemented cube root because it reduced larger weights to a proportionately greater extent. We also compared Dice loss (model 5) with categorical cross-entropy loss (model 3). We did not use class weights with Dice loss because the Dice coefficient is invariant to the level of spatial representation. Last, we compared layer normalization (21), batch normalization (25) trained on batch sizes of three and 12 (models 6 and 7, respectively), and batch renormalization (model 8) (26). On the basis of validation dataset performance, we selected the most optimal model (model 3) and retrained it on data stratified by scan manufacturer (Appendix E1 [supplement]).

Table 1:

List of Model Configurations Evaluated on the Validation Dataset

Comparison with Existing Methodology

We compared our model to a publicly available tool (27) using the iNPH dataset. This algorithm registered head CT scans to the MNI152 space and performed segmentation using support vector machine and random forest classifiers. To match output labels, we merged CS with SS, SP with VS, and the remaining structures into “brain parenchyma.” Only a portion of each volume was used for inference (12 volumes with 217 slices) because the algorithm was designed to segment images containing the lateral ventricles. Registration failed for one of the 12 volumes because the vendor-specific DICOM coordinates were not properly aligned in the sagittal plane. We replaced this with another study acquired from the same patient using a different scanner at the next nearest date.

Statistical Analysis

We compared the model’s structure segmentation Dice coefficients and total volume metrics with the observers using ground truth masks as a reference to determine if the model’s segmentation differed from that of domain experts. We compared the model’s structure segmentation Dice coefficients on the primary and secondary test datasets to determine if the model’s segmentation differed across datasets. Statistical significance was determined using categorical linear regression with P < .05 in IBM SPSS statistics version 26 (IBM, Armonk, NY).

Model Availability

The trained model is available at https://jasonccai.github.io/HeadCTSegmentation/.

Results

Validation Dataset

Effect of within-network normalization.—The performance of the Ronneberger U-Net (model 1) varied between random initializations, from no learning to learning the large classes (eg, BC). Normalizing intermediate layer activations enabled the U-Net to predict all 11 structures. With batch normalization, validation performance fluctuated at the start of training (Fig 2). The fluctuation was alleviated in part by increasing the batch size from three to 12 (models 6 and 7, respectively) and circumvented by using batch renormalization (model 8) or layer normalization (model 3). Models that employ layer normalization, batch normalization, and batch renormalization delivered overall Dice coefficients of 0.80 ± 0.06 (standard deviation), 0.79 ± 0.06, and 0.80 ± 0.06, respectively (Table E2 [supplement]).

Figure 2a:

Training and validation performance of various model configurations. (a) Batch normalization (BN) demonstrated fluctuations in validation performance. (b) This was alleviated in part by increasing the batch size (BS) from three to 12. (c) Per-class Dice coefficients averaged over all examinations in the validation dataset. Error bars represent 1 standard deviation. Model 5 predicted only the brainstem and cerebrum, cerebellum, ventricular system, and subarachnoid space. RN = batch renormalization, LN = layer normalization.

Figure 2b:

Training and validation performance of various model configurations. (a) Batch normalization (BN) demonstrated fluctuations in validation performance. (b) This was alleviated in part by increasing the batch size (BS) from three to 12. (c) Per-class Dice coefficients averaged over all examinations in the validation dataset. Error bars represent 1 standard deviation. Model 5 predicted only the brainstem and cerebrum, cerebellum, ventricular system, and subarachnoid space. RN = batch renormalization, LN = layer normalization.

Figure 2c:

Training and validation performance of various model configurations. (a) Batch normalization (BN) demonstrated fluctuations in validation performance. (b) This was alleviated in part by increasing the batch size (BS) from three to 12. (c) Per-class Dice coefficients averaged over all examinations in the validation dataset. Error bars represent 1 standard deviation. Model 5 predicted only the brainstem and cerebrum, cerebellum, ventricular system, and subarachnoid space. RN = batch renormalization, LN = layer normalization.

Effect of loss functions.—Dice loss (model 5) has been reported to perform well on binary segmentation tasks (24). However, when we trained our model using Dice loss, it did not learn smaller classes such as CS, SP, and structures at the basal ganglia level. Instead, they were predicted as SS, VS, and BC, respectively. Figure 3 shows confusion matrices for Dice and cross-entropy loss on the validation dataset.

Figure 3a:

Confusion matrices for (a) model 3 (cross-entropy loss with attenuated weighting) and (b) model 5 (Dice loss) on the validation dataset. Numbers represent the percentage of voxels in each category.

Figure 3b:

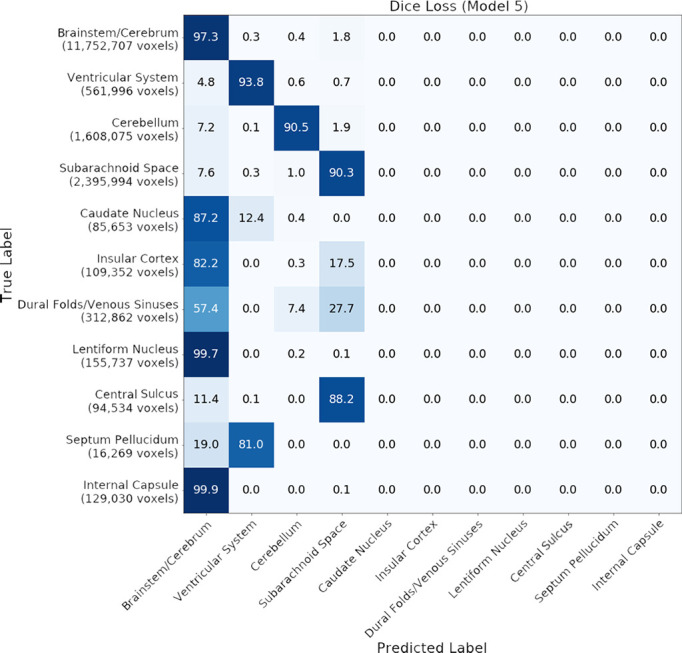
Confusion matrices for (a) model 3 (cross-entropy loss with attenuated weighting) and (b) model 5 (Dice loss) on the validation dataset. Numbers represent the percentage of voxels in each category.

Effect of class weighting.—When we used balanced class weights in model 2, the model reached an overall Dice coefficient of 0.78 ± 0.06 (Table E2 [supplement]). When we applied an element-wise cube root to these weights in model 3, the overall Dice coefficient improved slightly to 0.80 ± 0.06. Although differences fell within 1 standard deviation, model 3 delivered qualitatively better visual performance (Fig 4, C). Model 2 tended to overpredict all 11 ROIs; this manifested additionally as a thin layer of labeled voxels at the brain-cranium boundary (Fig 4, F), which was not present on manual segmentations (Fig 4, E). When trained without class weighting, model 4 eventually reached an overall Dice coefficient of 0.79 ± 0.06, which was comparable to the performance of model 3. However, model 4 took substantially longer to train. It also learned large classes at the expense of small classes and demonstrated fluctuations in validation performance at the start of training (Fig 4, A).

Figure 4:

A, Without class weights, the model quickly learned large classes (brainstem and cerebrum) at the expense of small classes (central sulcus and septum pellucidum). However, it eventually converged when given sufficient training time. The y-axis represents soft Dice coefficients, which are the Dice coefficients of predicted softmax class probabilities before thresholding. B, Manual segmentation, C, predictions from model trained with attenuated weighting (model 3), D, predictions from model trained with balanced weighting (model 2), E, enlarged section from B (yellow dotted lines), and, F, enlarged section from D (yellow dotted lines). The red arrowheads in F indicate a thin layer of labeled voxels over the brain-cranium boundary. This thin layer was not seen in the unweighted model. See the section on “Effect of Class Weighting” for details.

Primary Test Dataset

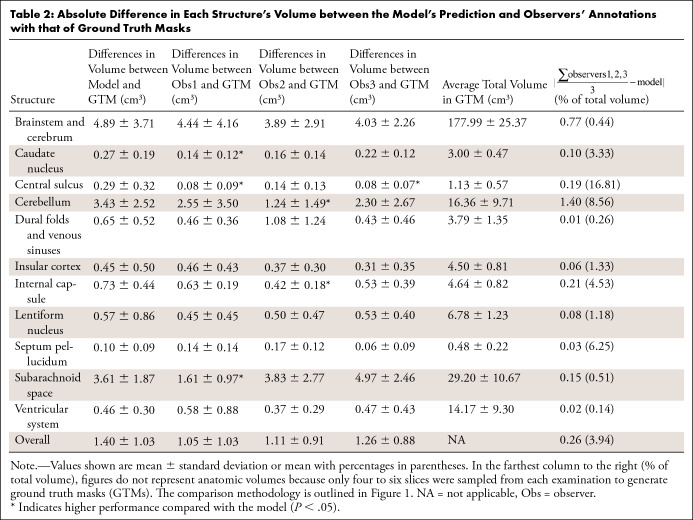
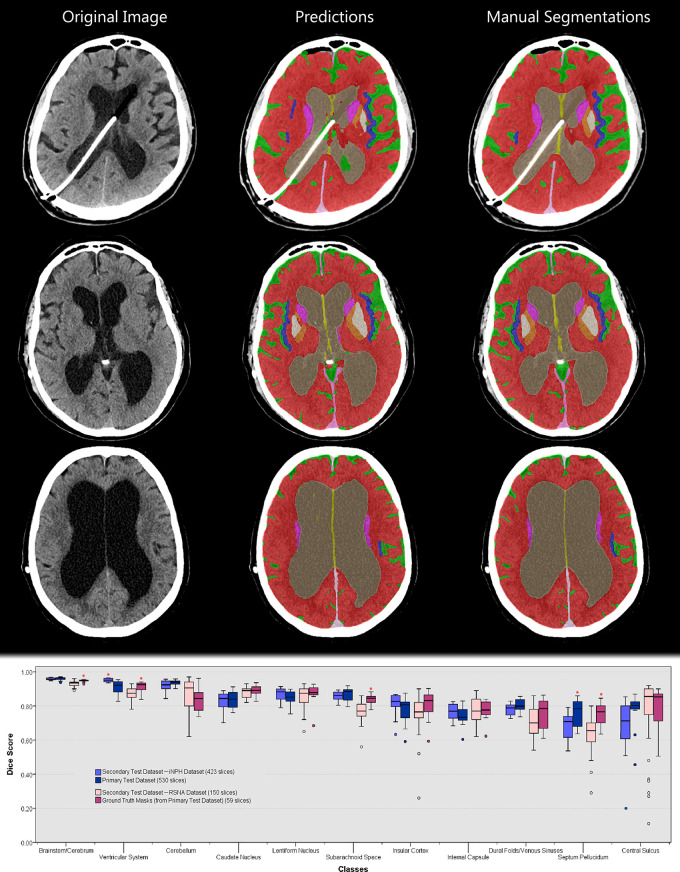
When structure volume was used to evaluate performance (Table 2), there was no difference between the model and all three observers in BC, CO, DV, LN, SP, and VS; the model was not different from two observers in CA, CE, CN, and SS, and from one observer in CS (P > .05). When using Dice coefficients to evaluate performance (Table 3), the model’s segmentation was not different from two of the three observers in CE, CO, DV, LN, SP, SS, and VS, and it was not different from one of the three observers in BC and CA (P > .05). The model did not perform as well as observers in CN and CS (P < .05). The average overall difference in segmentation performance was 4.0% for both measures. Samples of the observers’ annotations, ground truth masks, and model predictions are shown in Figure 5.

Table 2:

Absolute Difference in Each Structure’s Volume between the Model’s Prediction and Observers’ Annotations with that of Ground Truth Masks

Table 3:

Average Dice Coefficients of Each Structure with Reference to the Ground Truth Masks

Figure 5:

Sample image from the primary test dataset with corresponding model prediction, expert annotations, and ground truth mask. Images shown are, A, original image, B, observer 1 segmentation, C, observer 2 segmentation, D, observer 3 segmentation, E, ground truth mask generated by majority voting (unlabeled voxels indicate areas where all three observers disagree and are excluded from performance metrics), F, model prediction at basal ganglia level, G, model prediction at cerebellar level, and, H, model prediction at central sulcus level. I, Box and whisker plot of Dice coefficients using ground truth masks as reference (n = 59 slices). Asterisks indicate statistically significant results as compared with the model (P < .05). Dice coefficients are also presented in Table 3. The comparison methodology is outlined in Figure 1.

Secondary Test Datasets

There was no difference in the model’s performance between the RSNA dataset and ground truth masks in seven of 11 structures (P > .05); the model did not perform as well in BC, SP, SS, and VS (P < .05). There was no difference in the model’s performance between the iNPH dataset and the primary test dataset in 10 of 11 structures (P > .05). The model did not perform as well in segmenting the SP (P < .05). Table 4 and Figure 6 show performance on the secondary test dataset.

Table 4:

Performance between Primary and Secondary Test Datasets

Figure 6:

Top: Sample images from the idiopathic normal pressure hydrocephalus (iNPH) dataset. The model was not trained on iNPH scans. Coloring legend can be found in Figure 5. Bottom: Box and whisker plot comparing model performance between primary and secondary test datasets. Asterisks indicate statistically significant results (P < .05). Dice coefficients are also presented in Table 4. The comparison methodology is outlined in Figure 1.

We observed that the model was slightly better at segmenting the VS of patients with iNPH, although it was not trained on scans demonstrating ventricular enlargement. We also observed a positive correlation between structure size and Dice coefficients in general. This was examined in Appendix E2 (supplement).

Comparison with Existing Methodology

Our model produced the same overall Dice coefficients as a three-dimensional CNN that segmented the SS (9). It demonstrated higher Dice coefficients over a traditional approach (27) (P < .05) (Table E3 [supplement]).

Discussion

Several studies have shown that CT structural imaging features are predictive of neurologic disease and patient outcomes (14,15,29–31). However, the inability to rapidly and accurately segment neuroanatomy has impeded the routine clinical use of volumetric imaging features, as well as the discovery of new associations and normative population metrics for these features (16). To address this need, we developed a deep learning model that segmented 11 intracranial structures from noncontrast CT, and we tested the model on internal and external datasets. As these structures ranged considerably in size and slicewise prevalence, we explored the use of within-network normalization techniques, class weighting schemes, and loss functions to obtain the best configuration. These optimizations have general utility for future deep learning–based approaches to medical image segmentation.

The model’s performance was not different from observers for most structures, although the small number of samples tested may have reduced our ability to detect significant differences. However, the finding of an overall difference in Dice coefficient of 4% supports the concept that the model exhibited performance similar to that of humans. This difference was larger only for CE and CS, likely as a consequence of the two-dimensional design of the model. In particular, CS is identified by scrolling through the volume. Therefore, the inability of the model to identify features across the z-axis may have hindered its performance. Future work should include examining the possible incremental benefits of three-dimensional and multiplanar approaches to segmentation.

In our experiments, within-network normalization techniques facilitated multiclass learning. Batch normalization has been shown to improve performance by reducing internal covariate shift (25) and stabilizing intermediate activations (32). However, we observed that batch normalization produced significant fluctuations in validation metrics at the start of training. These random fluctuations may be attributed to its dependence on minibatch statistics. Batch normalization estimated the population mean and variance from moving averages calculated during training. With small minibatches (as in our case), such estimates likely became less accurate, resulting in poorer predictions. Increasing the minibatch size from three to 12 reduced but did not resolve this issue, suggesting that even larger minibatches may help. Because of its dependency on large, representative minibatches, batch normalization was less robust on our model.

Several alternatives have been proposed to address the limitations of batch normalization, including batch renormalization (26) and layer normalization (21). The overall Dice coefficients between these techniques were similar. We preferred layer normalization because it does not depend on minibatch size, does not introduce new hyperparameters, and does not contain parameters that must be learned during training.

Class imbalance degrades CNN performance, as models that learn from imbalanced datasets are biased to reflect the frequency of training samples (33). The soft Dice loss was proposed to reduce model bias for large structures (24). However, as shown on our dataset, the model failed to learn small structures when trained using soft Dice loss, suggesting that it did not entirely recapitulate properties of the Dice coefficient. Instead, we found that weighted categorical cross-entropy loss, which assigned higher misclassification penalties to infrequently represented classes, was better suited to imbalanced multiclass segmentation. This approach balanced gradient updates between classes, shortened overall training time, and promoted a more optimal convergence on our dataset.

A limitation of our work was that we trained our model on a small set of normal head CT scans. Although our model demonstrated good segmentation metrics on iNPH and external scans, it may not generalize equally well to other abnormal scans or imaging acquired using different protocols because the training dataset may not have fully captured the diversity of head CT scans. Transfer learning with fine-tuning is a well-established technique that enables deep learning models to be quickly optimized on new and previously unseen datasets. In making our model available to the artificial intelligence community, we hope that developers can use transfer learning to optimize it for their specific needs.

In conclusion, given the increasing amount of imaging data, algorithms that automatically extract quantitative information and spatial context from head CT can potentially assist in clinical decision making. In this study, we trained and validated a U-Net to simultaneously segment 11 intracranial structures on head CT. Our model correlated well with expert annotations, and it delivered equal or higher overall Dice coefficients as compared with existing automated segmentation methods. We showed that within-network normalization facilitated multiclass learning, and the choice of normalization technique affected the network’s overall robustness and stability. We also demonstrated the effects of loss functions and class weighting schemes on network performance. Our findings have general utility for future deep learning–based approaches to medical image segmentation. By adapting the U-Net for multiclass segmentation on head CT scans, we also set a framework for similar work in the future and further affirm the role of deep learning in supporting radiologists.