Well-Tempered MCMC simulations for population pharmacokinetic models

Abstract

A full Bayesian statistical treatment of complex pharmacokinetic or pharmacodynamic models, in particular in a population context, gives access to powerful inference, including on model structure. Markov Chain Monte Carlo (MCMC) samplers are typically used to estimate the joint posterior parameter distribution of interest. Among MCMC samplers, the simulated tempering algorithm (TMCMC) has a number of advantages : it can sample from sharp multi-modal posteriors; it provides insight into identifiability issues useful for model simplification; it can be used to compute accurate Bayes factors for model choice; the simulated Markov chains mix quickly and have assured convergence in certain conditions. The main challenge when implementing this approach is to find an adequate scale of auxiliary inverse temperatures (perks) and associated scaling constants. We solved that problem by adaptive stochastic optimization and describe our implementation of TMCMC sampling in the GNU MCSim software. Once a grid of perks is obtained, it is easy to perform posterior-tempered MCMC sampling or likelihood-tempered MCMC (thermodynamic integration, which bridges the joint prior and the posterior parameter distributions, with assured convergence of a single sampling chain). We compare TMCMC to other samplers and demonstrate its efficient sampling of multi-modal posteriors and calculation of Bayes factors in two stylized case-studies and two realistic population pharmacokinetic inference problems, one of them involving a large PBPK model.

1. Introduction

In modeling pharmacokinetics and pharmacodynamics, a Bayesian statistical framework gives access to a range of flexible inference options, including hierarchical non-conjugate models for population modeling (Damien et al. 1999; Gelman 2006) or seamless integration of prior and sequential knowledge. The incorporation of prior knowledge is particularly important in mechanistic modeling such as physiologically-based pharmacokinetic (PBPK) models (Gelman et al. 1996; Langdon et al. 2007; Tsamandouras et al. 2013; Zhang et al. 2011) or systems biology models (Bois 2009; Hamon et al. 2014). The development of powerful numerical Markov chain Monte Carlo (MCMC) algorithms (Girolami and Calderhead 2011; Robert and Casella 2011) has fueled the increasing use of Bayesian methods. However, those algorithms are still very computationally intensive and for complex models or large datasets can take hours or days to reach convergence on current computers (Hsieh et al. 2018). The problem is compounded by the fact that, in most cases, convergence should be assessed by running multiple simulated Markov chains (Gelman and Rubin 1992).

The tempered MCMC algorithm and its siblings, akin to simulated annealing (Geyer and Thompson 1995; Marinari and Parisi 1992), have the potential to dramatically improve this picture. In simulated tempering MCMC, the sampled posterior density (or just the data likelihood, in the so-called thermodynamic integration, TI, variant) is raised to a series of powers (inverse-temperatures, or perks) ranging from 0 to 1. At perk 0, the sampling density is uniform (or is equal to the prior in TI), and perk 1 corresponds to the target joint posterior distribution. The perk is treated as an auxiliary variable, sampled randomly along a discrete grid of values, so that the simulated Markov chain explores the whole parameter space over a series of powered posteriors.

This algorithm has good mixing properties and can deal with difficult or even multi-modal posteriors, as will be shown in this paper, because the set of powered distributions provides a smooth landscape that a Markov chain can efficiently explore. This translates into rapid convergence, and, if perk zero is reached, the chain renews and convergence is guaranteed with only a single chain being run (Geyer and Thompson 1995; Robert and Casella 2011). Reaching power zero also provides, at no extra computation cost, an estimate of the integrated data likelihood (the posterior normalization constant), which in turn can be used to compute Bayes factors enabling statistical testing of model structure (Calderhead and Girolami 2009; Friel and Wyse 2012; Geyer and Thompson 1995). To date, validation of this method has been confined to limited datasets and simple models, because setting adequate perk values in simulated tempering MCMC for complex or differential models has proved to be very difficult (Behrens et al. 2012).

We developed and implemented a new automatic perk grid setting algorithm which leads to a fully operational simulated tempering MCMC algorithm. We demonstrate its capabilities, in its TI variant, for the Bayesian calibration of population pharmacokinetic (PK) models of various complexity, using previously published PK models and data on theophylline and acetaminophen as test cases. We start by illustrating the advantages of TI with two simple inference problems, one of which has an analytical solution.

2. Materials and Methods

2.1. Simulated tempering MCMC Approach and Algorithms

Standard Metropolis-Hasting MCMC typically proceeds from one iteration to the next by sampling a proposed value, θ′, for a parameter of interest from a (typically) Normal kernel distribution G(∙) centered on the current value of the parameter, θ. The current value has a given probability density, P(θ), under the prior distribution and the proposed value has prior density P(θ′). The density of θ′ under the Normal kernel centered at θ will be noted G(θ′|θ) and the density of θ under the Normal kernel centered at θ′ will be noted G(θ|θ′). All model predictions that depend on parameter θ are recomputed and the likelihood of the data D, P(D|θ′), is evaluated numerically up to an unknown constant, P(D). The data likelihood given θ, P(D|θ), has been recorded previously. It can be shown (e.g., Roberts and Smith 1994) that if θ′ is accepted (and becomes the current value for the next step) with probability

$$r=\text{min}\left(\frac{P\left({\theta }^{\prime }\right)\cdot P\left(D\mid {\theta }^{\prime }\right)}{P(\theta )\cdot P(D\mid \theta )}\cdot \frac{G\left(\theta \mid {\theta }^{\prime }\right)}{G\left({\theta }^{\prime }\mid \theta \right)},1\right)$$ (1)

then the Markov chain converges in distribution to the posterior distribution of θ, P(θ)×P(D|θ). The unknown constant P(D) cancels out between the numerator and the denominator of Eq. 1. If the proposed value is not accepted, the value θ it kept (and becomes repeated in the simulated chain). When several parameters need to be sampled, it is sufficient to update them sequentially. In that case, the simulated chain converges to the joint posterior distribution of all parameters. The proposal kernel needs to be tuned so that jumps are large enough so that the simulated chain moves rapidly in the entire posterior distribution, but not too large, because too many samples would be rejected, leading to a non-moving chain (Roberts et al. 1997). The convergence of the simulated chain to the posterior distribution needs to be checked systematically, preferably by running several chains for long enough (Gelman and Rubin 1992). A sufficient number (typically thousands) of sampled parameter values or parameter vectors also need to be collected to form useful summaries, such as percentiles of their posterior distribution. Several algorithms, for example Hamiltonian MCMC (Girolami and Calderhead 2011), optimize the proposal mechanism and offer convergence in fewer iterations, albeit with a higher computation cost per iteration.

By contrast, in simulated tempering MCMC, a series of m perks λ values (inverse-temperatures, usually between 0 and 1) is defined and applied as a power either to the posterior distribution, in posterior-tempered MCMC, or to the data likelihood in the case of TI. The perk λ is an auxiliary parameter that is also randomly sampled, but from a discrete set of values, moving up or down one value at a time (Geyer and Thompson 1995). For a given perk λ, the acceptance probabilities r_pt and r_ti for posterior-tempered MCMC and TI are, respectively

$$r_{pt}=\text{min}\left({\left[\frac{P\left({\theta }^{\prime }\right)\cdot P\left(D\mid {\theta }^{\prime }\right)}{P(\theta )\cdot P(D\mid \theta )}\right]}^{\lambda }\cdot \frac{G\left(\theta \mid {\theta }^{\prime }\right)}{G\left({\theta }^{\prime }\mid \theta \right)},1\right)$$ (2)

for posterior-tempered MCMC, and

$$r_{ti}=\text{min}\left(\frac{P\left({\theta }^{\prime }\right)}{P(\theta )}\cdot {\left[\frac{P\left(D\mid {\theta }^{\prime }\right)}{P(D\mid \theta )}\right]}^{\lambda }\cdot \frac{G\left(\theta \mid {\theta }^{\prime }\right)}{G\left({\theta }^{\prime }\mid \theta \right)},1\right)$$ (3)

for TI. If λ equals 1, Eqs. 2 and 3 are identical to Eq. 1, and the θ samples are drawn from their posterior (target) distribution (the “cold” distribution in Geyer and Thompson’s paper). When λ equals zero, Eq. 2 implies sampling θ from a uniform distribution, while Eq. 3 samples θ from its prior distribution (the “hot” distribution of Geyer and Thompson; incidentally, Geyer and Thompson inverted by mistake the hot and cold distributions in their paper, page 910). Other values of λ (e.g., 0.1) correspond to intermediate distributions, which are generally not of interest but are used to increase mixing of the chain. The MCMC chain resets if the θ are independently sampled at perk zero. This automatically ensures that convergence is achieved, provided that the intermediate distributions are visited regularly. The Markov chain should still be simulated for long enough to gather a sufficient number of samples from the cold distribution to permit robust inference.

The values of λ must be set in such a way that the sampler often jumps from between them. The jump frequency depends strongly on a series of tuning parameters (called pseudo-priors, or π in the notation of Geyer and Thompson 1995). There is one pseudo-prior π_λ for each value of λ. A pseudo-prior is proportional to the normalization constant of the posterior distribution density raised to power λ. However, those pseudo-priors cannot be determined in advance. So, there are two adjustment problems to solve: adjusting the pseudo-priors for a set of perk values λ, and adjusting those perk values.

Geyer and Thompson consider those two problems separately and iterate between them. For adjusting the pseudo-priors, they suggest in particular to use stochastic Robbins-Munro process (Robbins and Monro 1951) (they propose two other methods, rather impractical: the first one implies that we already have good starting values for the pseudo-priors and hence cannot be used alone; the second one starts by using a Metropolis-coupled MCMC sampler, which increases dramatically the complexity of the approach). The Robbins-Munro they propose starts with any values for the pseudo-priors (e.g., 1.0 for all) and updates them as the chain progresses. At iteration k, the amount c₀/(m(k + n₀)) is added to log(π_λ) for each λ not equal to the current λ, and the amount c₀/(k + n₀) is subtracted from the current log(π_λ). The two positive constants c₀ and n₀ are chosen by the user. As defined above, m is the number of perks values in use.

For adjusting the set of perk values, Geyer and Thompson proposed to linearly interpolate the cumulated values of observed transition rates between a current set of perks, and set new perk values to obtain about 30% jump probabilities in the next round of adjustment. However, this simple algorithm gives no indication as to what to do if all transition rates are null at the start (in our hands, a frequent situation with realistic models) and tends to lead to too many perk values.

In our approach, we continuously optimize the pseudo-priors with the Robbins-Munro process suggested by Geyer and Thompson, setting c₀ and n₀ to 100. For setting the perk values, we noticed that when the relationship between well-tuned log-pseudo-priors and perk values is linear, jumps are easy and it is possible to reduce the number of perks. Therefore, we developed the following adaptive perk setting algorithm: Briefly, in the first batch of 100 MCMC simulations (sampling all model parameters θ to be inferred and perks λ), only two perks are used: 1.0 and 0.99. If the observed transition rate between the two perks is higher than 30%, a lower perk chosen from a preset table is added to the set, and the batch size is increased by 100. If the transition rate is below 30%, the lower perk is raised halfway toward 1.0. In both cases, a new batch is run. When more than three perks are in the grid, we check if some perks can be removed. If so, the batch size is lowered by 100. The algorithm similarly iterates until perk zero is reached or a preset number of MCMC iterations (currently 300,000) have been run. A pseudo-code listing of the algorithm is given as Supplementary Material, and the actual code is available at www.gnu.org/software/mcsim.

The above procedure minimizes the number of perks, optimizes their placement, and the jump frequencies between them, while computing the corresponding pseudo-priors. It is also possible for the user to bypass that initial phase and impose a set of predefined perks. Actual simulated tempering MCMC sampling is run subsequently with the set of perk values found, but the values of the pseudo-priors continue to be refined through the Robbins-Munro process. The occupancy numbers o_i (number of iterations spend at each perk λ_i are also recorded).

After running the sampler, estimating the probability of the data (integrated likelihood) given the model is straightforward: This probability is also the normalization constant of the target posterior density, which is inversely proportional to its pseudo-prior π₁ (Geyer and Thompson 1995):

$$P_1(D)=\alpha \frac{o_1}{{\pi }_1}$$ (4)

where o₁ is the occupancy number at perk 1 and α an unknown proportionality constant. An estimate of α can be obtained at perk 0, since we also have:

$$P_0(D)=\alpha \frac{o_0}{{\pi }_0}$$ (5)

However, at perk 0 the posterior distribution is equal to the prior and P₀(D) can be evaluated numerically (the prior is user-specified and needs to be evaluated at each step of the sampler; if a normalized prior is computed P₀(D) is equal to 1). Therefore,

$$P_1(D)=P_0(D)\frac{{\pi }_0{o}_1}{{\pi }_1{o}_0}$$ (6)

The normalized posterior parameter density can now be computed from the eventually unnormalized prior and likelihood:

$$P_1(\theta \mid D)=\frac{P_1(\theta )\cdot P_1(D\mid \theta )}{P_1(D)}$$ (7)

Comparing two models A and B amounts to calculating P₁(D) for each and forming the Bayes factor for A over B. If we denote by P₁(D | A) the integrated likelihood of model A and P₁(D | B) that for model B, the Bayes factor B_AB is simply P₁(D | A) over P₁(D | B). Values of B_AB higher than 1 indicated that model A should be favored (Calderhead and Girolami 2009).

2.2. Multi-modal posterior test case

Multi-modal posteriors are a challenge in MCMC sampling and can be found in pharmacometrics. A well-known example is the flip-flop phenomenon (Yáñez et al. 2011). The theophylline test case described below also exhibits this feature (see Results, section 3.3). The test case presented here is a simple Bayesian linear regression applied to an artificial dataset (see Figure 1). The data (x,y) are, in fact, a mixture of two linear components, for which we want to calibrate only one slope parameter a (data are given in Supplementary Material Table S1). There are clearly two solutions to this inference problem: a positive slope with one very small SD, σ₁, for the part of the data that is increasing with the independent variable x, the other SD, σ₂ (for the data decreasing with x), being other very large; or a negative slope, with σ₁ small and σ₂ large. The intercept was assumed to be known and equal to zero. The data likelihood was assumed to be Normal, with mean a∙x and SDs σ₁ or σ₂. Parameter a was assigned a uniform prior ranging from −10 to 10; σ₁ and σ₂ were assigned the same log-uniform prior ranging from 0.001 to 100.

Figure 1.

Artificial data (black dots) and posterior fits (lines) of the linear regression model at the different perks (inverse temperatures). The solution is clearly bimodal.

2.3. Inference about a Gaussian mean test case

This very simple model has a known solution and will be used to illustrate the derivation of the data probability (normalization constant). The mean, μ, of 100 data points (drawn from a standard Normal distribution, see Supplementary Material Table S2) was calibrated using the exact likelihood, with a Normal prior (0, 100) on μ. Given a prior mean on μ (μ₀) equal to 0, a prior precision λ₀ equal to 0.01, a true precision λ_true = 1, and n = 100 data points (whose mean was m = −0.0631515), the analytical posterior distribution is (Bernardo and Smith 1994):

$$\mu ~\mathit{\text{Normal}}\left(\frac{{\lambda }_0\cdot {\mu }_0+n{\lambda }_{\mathit{\text{true}}}\cdot m}{{\lambda }_0+n\cdot {\lambda }_{\mathit{\text{true}}}},\frac{1}{\sqrt{{\lambda }_0+n\cdot {\lambda }_{\mathit{\text{true}}}}}\right)$$ (8)

2.4. Theophylline population PK test case

To demonstrate population PK modeling with a compartmental model, we used plasma theophylline concentration data from the first six subjects (labeled 1 to 6) of a study by Trembath et al. (1980). Briefly, six healthy subjects aged 21–36 years were administered an immediate-release dose of 190 mg theophylline; plasma theophylline concentration was followed up to 12 hours after dosing. At another occasion the same subjects received five doses of a sustained release formulation containing 190 mg theophylline, twice a day; plasma concentration was measured up to 12 hours following the first and the fifth dose. In addition, subjects 4 and 6 received five doses of a sustained release formulation containing 380 mg of theophylline, twice a day, and plasma concentrations were measured up to 12 hours following fifth dose. The few measurements with null values were considered to be missing (all data are given in Supplementary Material Table S3).

We used a standard two-compartment distribution model with first-order input from the gut to the central compartment (see Figure 2). The quantity of drug released in the gut lumen was modeled by a first order infusion process. Elimination was from the central compartment. The model has six parameters: three first-order rate constants (k_r for release, k_a for absorption, and k_e for excretion), two transfer rate constants between the central and peripheral compartment (k_cp and k_pc), and the volume of distribution of the central compartment (V). The model can be turned into a one-compartment model by setting k_cp and k_pc to zero. Units are hours for time, liters for volumes and μmols for quantities. Immediate release was modeled as very brief (36 seconds) zero-order infusion into the gut lumen at dosing time. Sustained drug release was modeled as a similar infusion into the “drug dose” compartment, from which it is released in the gut lumen with first-order rate k_r. We considered two different population models, described next.

Figure 2.

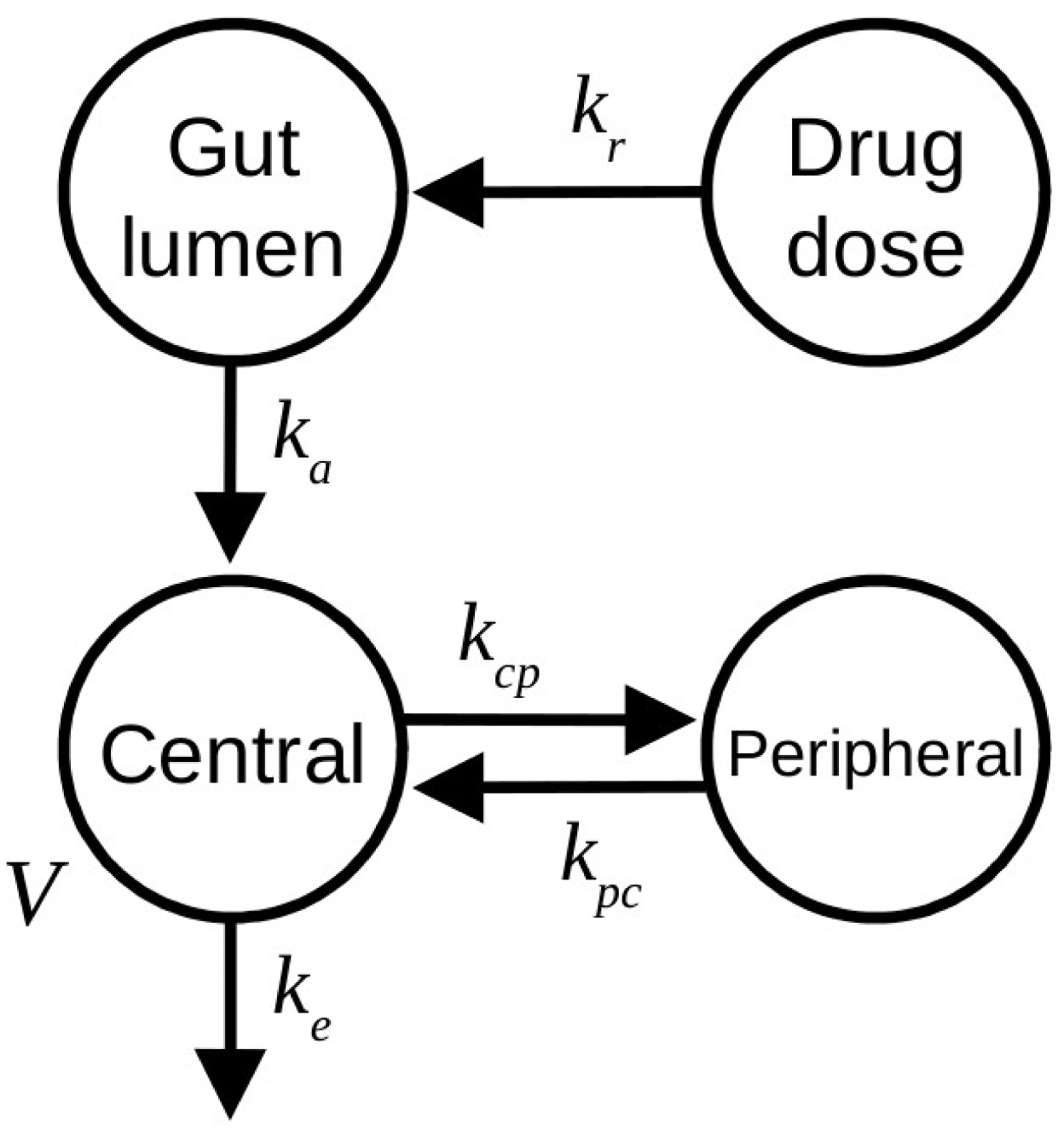
Two-compartment distribution model used for theophylline. Symbols are given in the text.

2.4.1. Inter-individual variability model

The inter-individual variability model has two levels: individuals and population. At the individual level, the likelihood of theophylline plasma concentration data (y_i,k) for subject i at occasion j_i and time k_i,j, was assumed to be log-normal:

$$\text{log}\left(y_{i,j,k}\right)~\mathit{\text{Normal}}\left(\text{log}\left(f\left(D_{i,j},{\theta }_i,t_{i,j,k}\right)\right),{\sigma }^2\right)$$ (9)

where f(∙) is the two-compartment model, function of theophylline dose D_i,j, of a vector θ_i of six parameters (k_r,i, k_a,i, k_e,i, k_cp,i, k_pc,i, V_i), and of time t_i,j,k; σ² is the experimental measurement variance (on the log scale).

The prior distribution of σ² was taken to be log-uniform, with bounds corresponding approximately to a relative error ranging from 10% to 70%:

$$\text{log}\left({\sigma }^2\right)~\mathit{\text{Uniform}}\left((\text{log}(0.01),\text{log}(0.5)\right)$$ (10)

At the individual level, parameters θ_i,l (l ranging from 1 to 6) for a given subject i were assumed to be log-normally distributed around population geometric means μ_l, with inter-individual variance δ²_l (on the log scale):

$$\text{log}\left({\theta }_{i,1}\right)~\mathit{\text{Normal}}\left({\text{log}}_{\left({\mu }_l\right)},{\delta }_l^2\right)$$ (11)

The prior distributions of the six population means were log-uniform and rather vague for the release rate constant k_r (with bounds corresponding to half-times of 1 hr and 20 hr) and the absorption rate constant k_a (with bounds corresponding to half-times of 6 min and 60 min). For the other parameters, log-normal distributions were used based on published information (Mitenko and Ogilvie 1973) and truncated at +/− 2 SDs:

$$\begin{gathered} \text{log}\left(k_r\right)~\mathit{\text{Uniform}}\left(-3.36,-0.367\right) \\ \text{log}\left(k_a\right)~\mathit{\text{Uniform}}\left(-0.367,1.94\right) \\ \text{log}\left(V\right)~\mathit{\text{Normal}}\left(\text{log}(20),\text{log}(2)\right)\left[\text{log}(5),\text{log}(80)\right] \\ \text{log}\left(k_e\right)~\mathit{\text{Normal}}\left(\text{log}(0.26),\text{log}(2)\right)\left[\text{log}(0.065),\text{log}(1.04)\right] \\ \text{log}\left(k_{cp}\right)~\mathit{\text{Normal}}\left(\text{log}(1),\text{log}(2)\right)\left[\text{log}(0.25),\text{log}(4)\right] \\ \text{log}\left(k_{pc}\right)~\mathit{\text{Normal}}(\text{log}(2.6),\text{log}(2))[\text{log}(0.65),\text{log}(10.4)] \end{gathered}$$ (12)

Informative prior distrutions for the six inter-individual variances δ²_l (in log space) were all set to:

$${\delta }_l^2~\mathit{\text{Inverse-Gamma}}\left(2.25,0.3125\right)$$ (13)

For simulations with the one-compartment model, k_cp, and k_pc were set at zero at all levels and the same priors as above were used for the other parameters.

2.4.2. Inter- and intra-individual variability model

This population model has three levels: occasions, individuals, and population. Each occasion corresponds to a dosing experiment (immediate release, sustained release, or repeated dosing at eventually two doses). At the occasion level, the likelihood of theophylline plasma concentration data (y_i,j,k) for subject i at occasion j_i and time k_i,j, was assumed to be log-normal:

$$\text{log}\left(y_{i,j,k}\right)~\mathit{\text{Normal}}\left(\text{log}\left(f\left(D_{i,j},{\mathit{\xi }}_{i,j},t_{i,j,k}\right)\right),{\sigma }^2\right)$$ (14)

where ξ_i,j is a vector of six parameters (k_r,i,j, k_a,i,j, k_e,i,j, k_cp,i,j, k_pc,i,j, V_i,j) specific to subject i and occasion j_i; the other symbols have the same meaning as in Eq. 9, and the prior distribution of σ² was as in Eq. 10.

At the occasion level, parameters ξ_i,j,l (l from 1 to 6) were assumed to be log-normally distributed around individual geometric means θ_i,l, with intra-individual variance φ²_l (on the log scale):

$$\text{log}\left({\xi }_{i,j,l}\right)~\mathit{\text{Normal}}\left(\text{log}\left({\theta }_{i,l}\right),{\phi }_l^2\right)$$ (15)

The prior distributions for the six intra-individual variances φ²_l (in log space) were all set to the informative prior

$${\phi }_k^2~\mathit{\text{Inverse-Gamma}}\left(2.25,0.3125\right)$$ (16)

At the individual level, parameters θ_i,l were assumed to be distributed as in Eq. 11. The prior distributions of the six population means and inter-individual variances were as in Eqs. 12 and 13, respectively.

Here also, for simulations with the one-compartment model, k_cp, and k_pc were set at zero at all levels and the same priors as above were used for the other parameters.

2.5. Acetaminophen population PBPK test case

Pharmacokinetic data from published clinical studies on acetaminophen and its metabolites, acetaminophen-sulfate and acetaminophen-glucuronide, were used for model calibration. The study references, their dose levels, number of subjects and mean body mass used are given in Supplementary Material Table S4. We focused on studies using single oral doses, ranging from 325 mg to about 1,400 mg (20 mg/kg). Within each study, the individual subjects’ data were averaged. The same data were used in Hsieh et al. (2018). The individual study data are given in Supplementary Material Tables S5 to S12.

For acetaminophen and its conjugated metabolites, we used a PBPK model described in Zurlinden and Reisfeld (2016, 2017). Model details such as structure, parameters, and state variables are detailed in those publications. Briefly, the model assumes physiological blood-flow limited transport. The body is subdivided into fat, muscle, liver, gastrointestinal tract (GI), and kidney compartments, the remaining tissues being lumped into either a rapidly- or a slowly-perfused compartment. Standard Michaelis-Menten kinetics were used to describe acetaminophen glucorinidation and sulfatation in the liver. The original PBPK model was able to predict the distribution of acetaminophen and its conjugates adequately. The model has 44 differential equations, 18 physiological parameters, and 50 chemical-specific parameters.

A subset of 21 chemical-specific PBPK model parameters has been previously calibrated in a hierarchical framework by Zurlinden and Reisfeld (2016, 2017). The hierarchy consisted of individual studies, with an overall average level above. The same framework was used by Hsieh et al. (2018) in their sensitivity analysis of the model. Hsieh et al. determined that only 15 of the original 21 parameters calibrated by Zurlinden and Reisfeld were really influential, and found another five other influential parameters worth calibrating. We calibrated here the 20 parameters of the updated list (see Supplementary Material Table S13).

At the individual study level, the likelihood of the plasma concentration data (y_i,j,k) for study i at time j_i, and for chemical species k (acetaminophen, acetaminophen-sulfate and acetaminophen-glucuronide) were assumed to be log-normal, as in Eq. 9. The prior distribution of each σ_k² was log-uniform, as in Eq. 10.

At the population level, parameters θ_i,l (l ranging from 1 to 20) for a given subject were assumed to be log-normally distributed around population geometric means μ_l, with variance δ²_l (on the log scale), as in Eq. 11 of the theophylline model. The prior distributions of the twenty population means are given in Supplementary Material Table S13. Those priors were derived from literature values and assumed to be uniform or truncated log-normal distributions (Zurlinden and Reisfeld 2016). We assumed that the parameters in the PBPK model were a priori independently distributed. This assumption is unlikely to hold completely. However, the most important and known dependencies between physiological parameters (e.g., on body mass) were modeled deterministically. For the other parameters, recent work suggests that they have a minimal impact on PBPK model predictions (Ring et al. 2017). The prior distributions for the twenty variances δ²_l were all set to the inverse-Gamma distribution given in Eq. 13 above.

2.6. Software and Hardware

GNU MCSim version 6.1.0 (www.gnu.org/software/mcsim) (Bois 2009) was used to run the models and perform MCMC sampling. R version 3.2.3 (www.R-project.org) (R Development Core Team 2013) was used for some processing calculations and graphics. The Stan software version 2.18.2 was used for Hamiltonian MCMC simulations for the linear regression model. All simulated tempering (TI) MCMC computations were performed on a 6-core 12-threads workstation equipped with Intel Xeon CPUs E5-1650 V2 clocked at 3.5 GHz. The GNU MCSim and Stan scripts used to perform the simulations are given in Supplementary Material Texts S1 to S10.

3. Results

3.1. Multi-modal posterior test case

First, a set of 12 values (0, 10⁻⁶, 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², 0.1, 0.2, 0.9, 0.95, 0.99, 1) of perk τ was found by optimization, requiring only a fraction of a second of computing time. Following that phase, one in 200 out of 10⁷ thermodynamic integration samples were recorded, yielding a sample of 50,000 parameter vectors (a, σ₁, σ₂). Total run time was 1.5 minutes on a laptop computer. Figure 3 displays the perks visited at each iteration. The jumps from one perk to another are very frequent and the sampler is mixing very well. About 4,200 parameter vectors were obtained at each perk value, with 3997 samples at perk 1, which was sufficient to draw reasonably precise inference.

Figure 3.

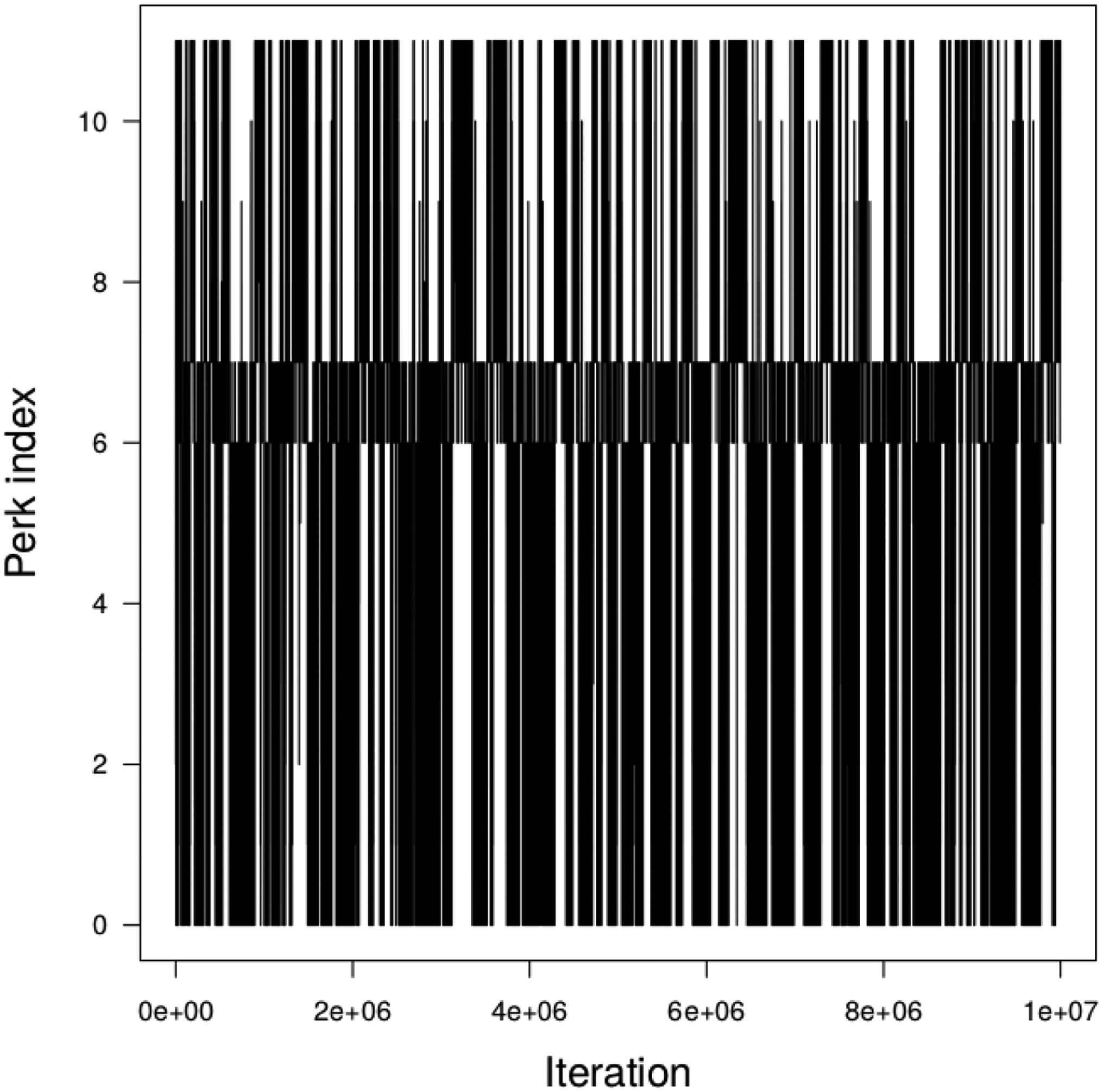
Perks values sampled as a function of the TI MCMC sampler iteration in the case of the linear regression model.

Figure 1 shows the model fit to the data at the different perks. For final fit checking and parameter inference, only the fit for the target posterior distribution (at τ = 1) should be used, but the fits for the other perks are shown here for illustration of the method. At low values of τ, the sampler explores intermediate solutions starting from a purely prior-based prediction at τ = 0. The bimodality of the solution is obvious at τ = 1. This is reflected in the relatively complex bimodality of the target posterior distribution of the estimated parameters.

Figure 4 shows the location of the 3997 parameter triplets (slope a, σ₁, σ₂) sampled from their joint target posterior distribution (τ = 1) in the parameter space. They form two thin needles, the approximate volume of which represents 6×10⁻⁸ percents of the volume of the prior parameter space. Sampling from such a posterior is literally akin to finding needles in a haystack, and jumping from one mode (needle) to the other requires a wide jump, not even in the same plane, but to another one. This is made possible by the progressive smoothing of the posterior as perks decrease. Supplementary Material Figures S1 to S3 show histograms of the posterior samples at each of the 12 perks used. The distribution of slope a goes from uniform (posterior = prior when τ = 0) to symmetric bimodal, while the distributions of σ₁ and σ₂ go from log-uniform to asymmetric bimodal. It would be extremely difficult to jump from the prior to the target posterior, but the intermediate perks offer landing patches easier to reach.

Figure 4.

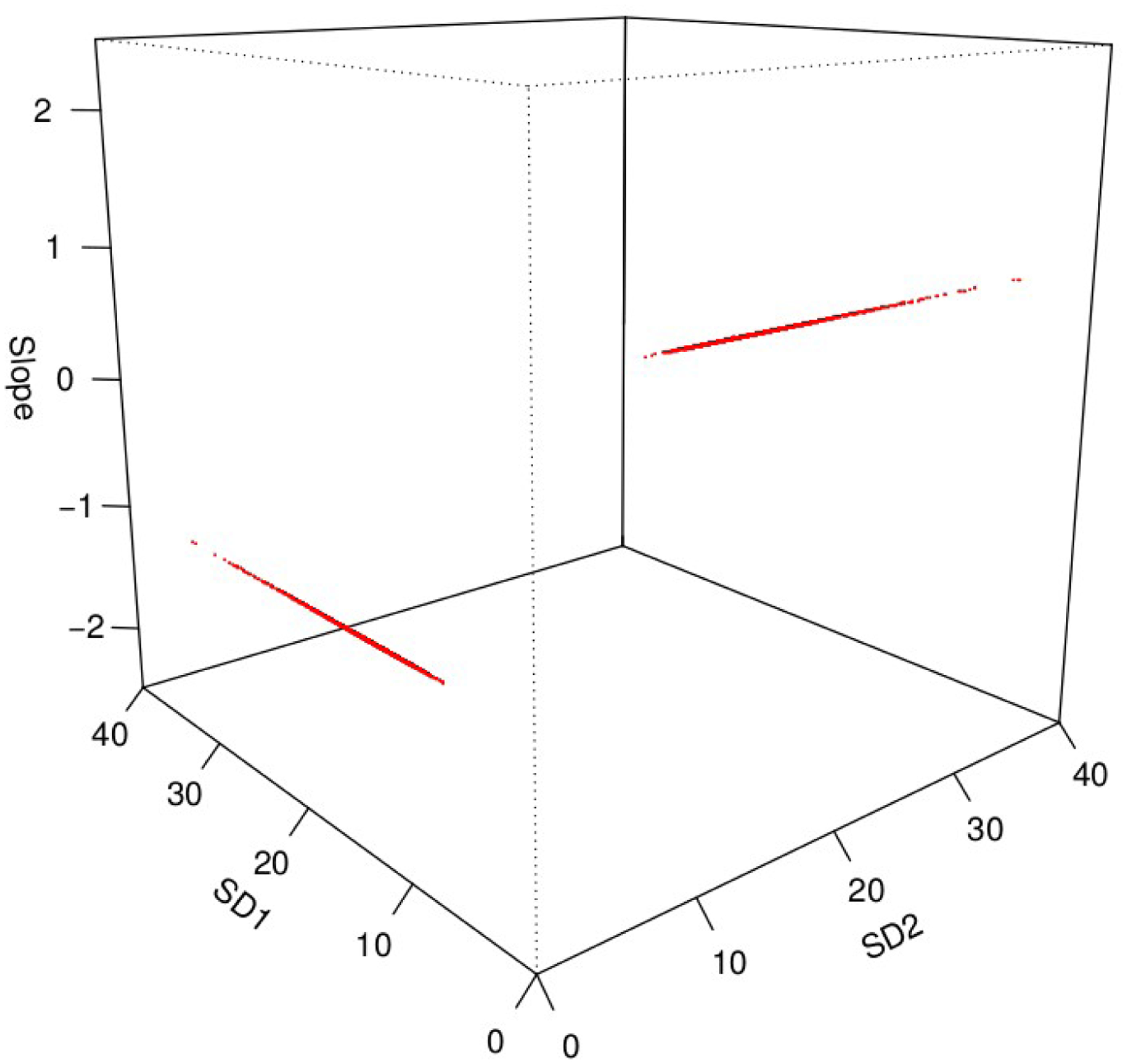
Three-dimensional plot of the positions of the 3997 parameter triplets (slope a, σ₁, σ₂) sampled from their joint target posterior distribution (perk = 1) in the parameter space of the linear regression model. They align along two thin needles and individual points are not discernable. Only a fraction (2.25%) of the prior parameter space is shown.

Figure 5 shows the marginal target posterior distribution of the sampled value of a (imagine the cube in Figure 4 being flattened by pressing the left sides against the right sides; arriving at a plane, and reorienting it, we get the image in Figure 5). The two peaks are widely separated (by about 2000 SDs), but still well sampled.

Figure 5.

Marginal target posterior distribution of the sampled values of slope a in the linear regression model. The two peaks are separated by a distance equal to about 600 times their width.

By comparison, neither standard Metropolis-Hasting MCMC nor the No-U-Turn sampler (a variant of standard Hamiltonian MCMC) was able to yield samples from the full posterior with only one simulated Markov chain. They remained stuck in one of the two modes for as long as we could run them (over a million iterations) (data not shown). Multiple chains started from uniformly sampled parameter values were able to retrieve the target multi-modal posterior, but many chains were required to obtain a reliable sample with a correct sampling frequency of the two modes.

3.2. Inference about a Gaussian mean test case

This problem has a known solution: the expected value of the posterior mean μ is −0.063 (close to the data average), and its posterior SD should be very close to 0.1 (Bernardo and Smith 1994). The probability density functions of the prior and exact posterior distributions of μ, shown on Supplementary Material Figure S4, were used to benchmark the results. Thermodynamic integration was performed with 500,000 iterations (one in five of them was recorded). Only one chain was needed, since perk zero was reached and convergence guaranteed. Figure 6 shows the evolution of the perks’ schedule, progressively adding or removing perks during the automatic adjustment phase. The eight perks proposed (0, 10⁻⁶, 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², 0.1, 1) were often visited by the sampler (Figure 7). Figure 8 displays a histogram of the TI sample of μ at perk 0 overlaid by the known prior density, and an overlay of the corresponding log-densities. As expected, they match closely, because sampling is correct and the log-densities of the sampled μ values under the prior were evaluated explicitly. TI allows us (Eq. 6) to evaluate the posterior’s normalization constant, which was equal to exp(−147). Using this value in Eq. 7, we normalized the log-posterior density recorded by GNU MCSim and found that it approximates very well the analytical solution (Figure 9). There was a 10% difference between the exact and estimated posterior densities of μ. Its best estimate was −0.0632 and its SD 0.101, as expected.

Figure 6.

Evolution of perks and associated pseudo-priors in the Gaussian inference problem at the various steps of the automatic perk scale adjustment. The scale was refined until perk zero was reached.

Figure 7.

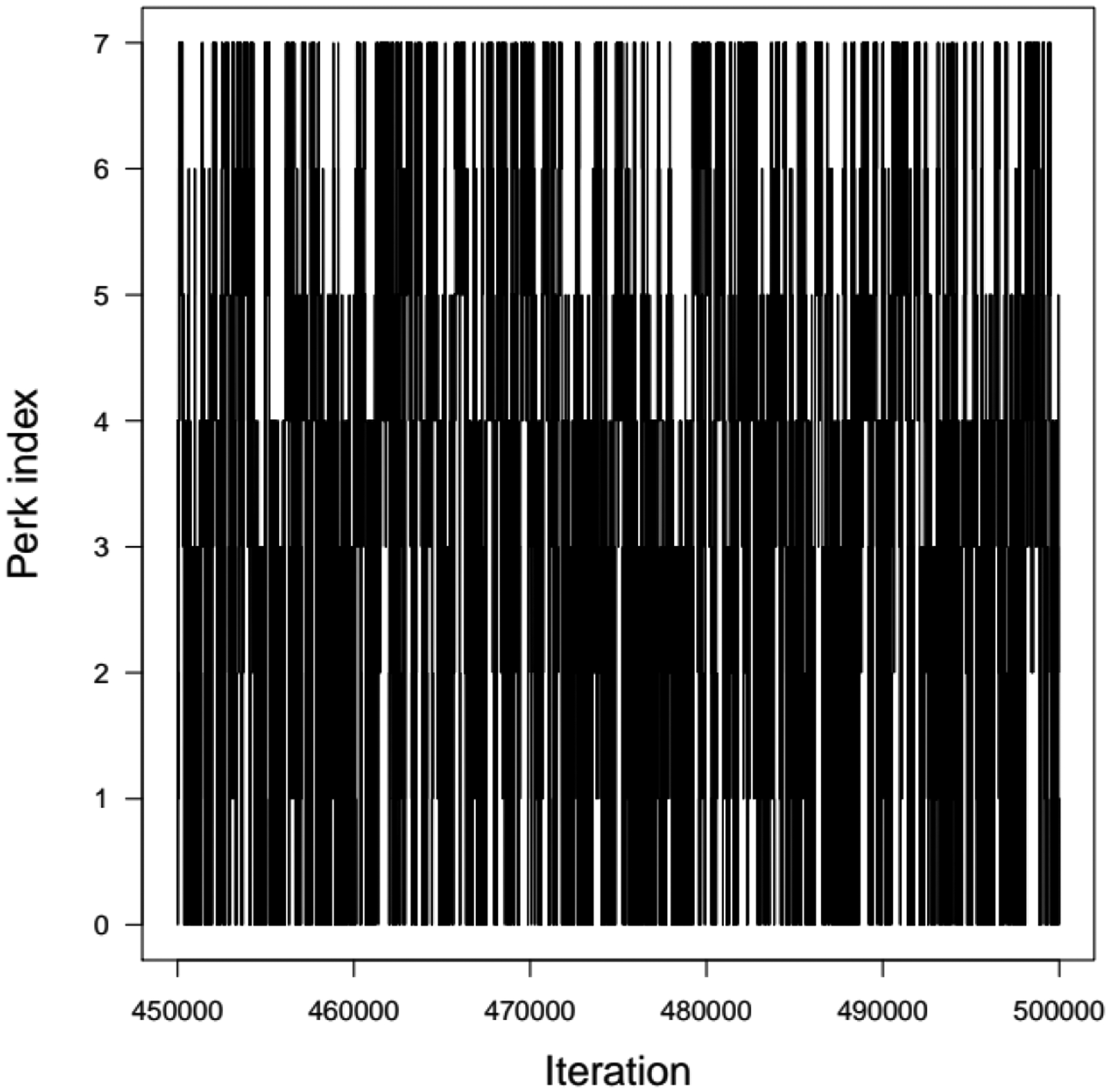
Perks values sampled as a function of the TI MCMC sampler iteration in the Gaussian inference problem.

Figure 8.

Top: Histogram of the TI MCMC sampled values of mean μ, at perk 0, in the Gaussian inference problem, overlaid by the known prior density (red line). Bottom: log-density of the same sample (crosses) and of the prior (red line).

Figure 9.

Top: Histogram of the TI MCMC sampled values of mean μ, at perk 1, in the Gaussian inference problem, overlaid by the known posterior density (red line). Bottom: log-density of the same sample, normalized by the integrated likelihood (crosses) and of the exact posterior (red line).

3.3. Theophylline population PK test case

For this relatively simple model, in the two-compartment case, a TI schedule of 18 perks, including perk zero, was found in 31 minutes. One TI MCMC chain of 20000 iterations took another 25 minutes to complete. The sampler jumps between perks were more difficult than in the two cases described above, with occupancy numbers ranging from 839 to 1443, the latter for τ = 1 (Figure 10)). Reference runs of 40,000 simulations were obtained with standard MCMC sampling. Each chain took 52 minutes to run (208 minutes of total computing time). The convergence of four chains was achieved after 20,000 simulations and one in ten of the last 20,000 iterations were kept.

Figure 10.

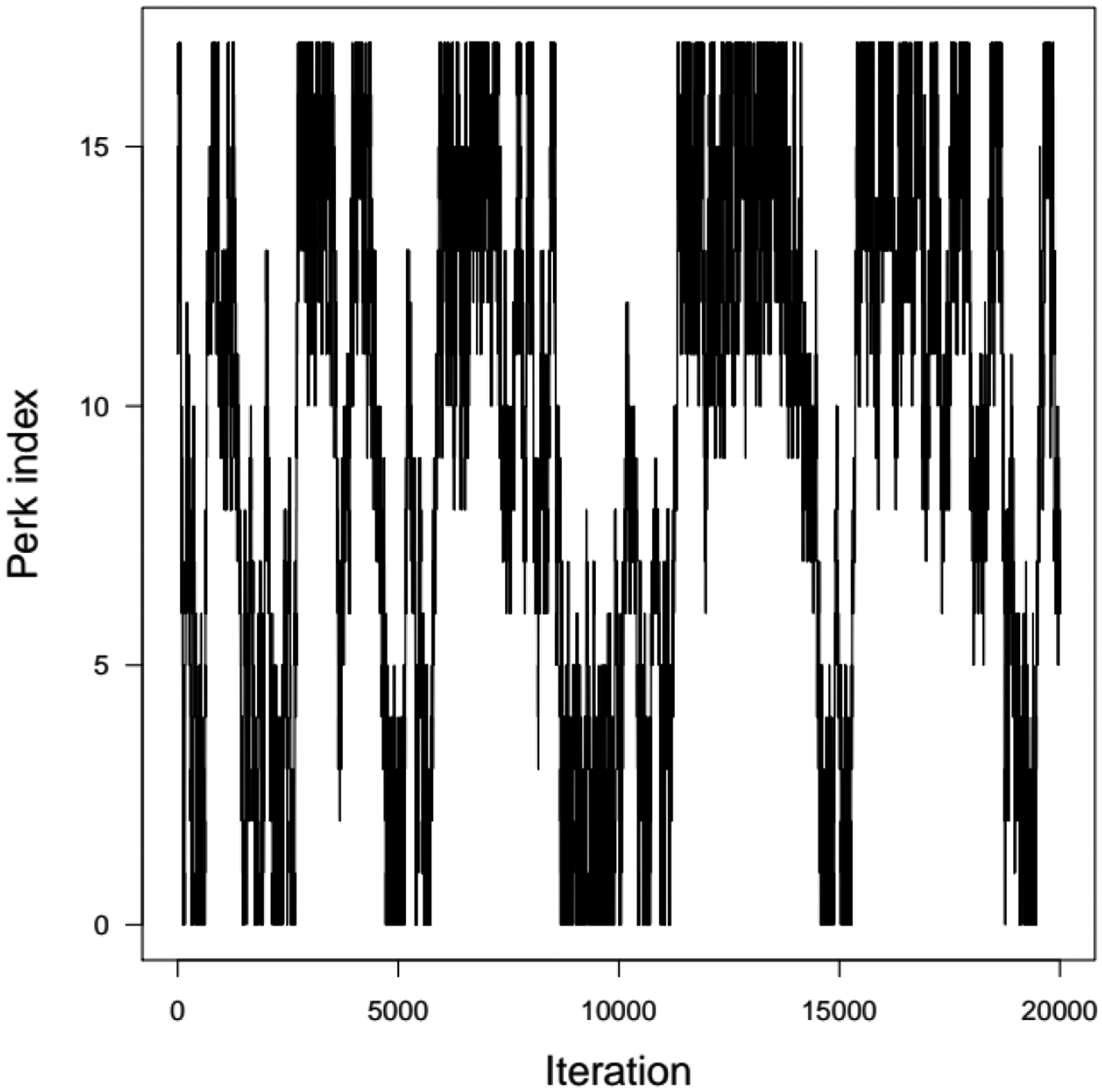
Perks values sampled as a function of the TI MCMC sampler iteration in the case of the theophylline two-compartment population PK model.

Figure 11 shows the TI posterior fits of the inter-individual variability model for each subject. The maximum posterior fit is shown, in addition to 20 random posterior fits, illustrating the (low) uncertainty in the predictions (σ² best estimate: 0.05, so about 22% CV for residuals). We obtained practically the same maximum posterior fit to the data compared to standard MCMC sampling (Figure 12), just twice as fast.

Figure 11.

Posterior fits of the two-compartment inter-individual variability population model to data on plasma theophylline concentration in six subjects (Trembath and Boobis 1980). Red line: maximum posterior predictions. Grey lines: 20 random posterior fits. Subjects (S1 to S6) are suffixed with the type of dosing: “i” means immediate release, “s” sustained release, “sr” sustained release repeated dosing, “srh” idem with a dose twice as high.

Figure 12.

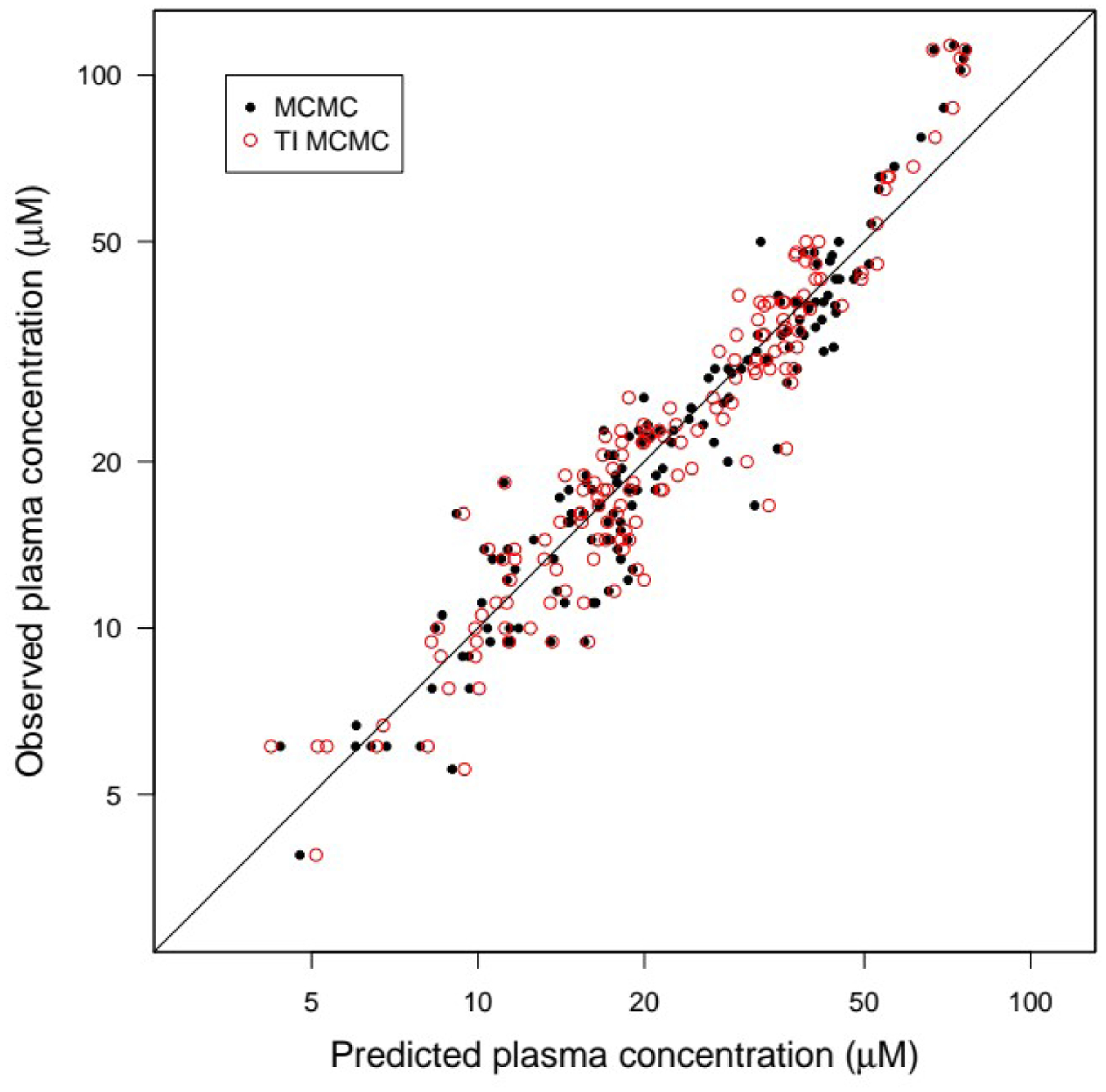
Observed data values vs. maximum posterior inter-individual variability model predictions for the theophylline data set, in the case of either standard or TI MCMC simulations, with the two-compartment inter-individual variability model.

Accounting for both inter- and intra-individual variability improved the fit, in particular for repeated dosing (Figure 13). The best estimate of σ² became 0.02, about a 14% CV. To formally test whether the improvement was significant, we computed the Bayes factor for the inter- and intra-variability model (inter+intra) over the inter-variability alone model (inter-only). According to TI, the integrated likelihood of the intra+inter model was exp(5.55), compared to exp(−15.2) for the inter-only model. The corresponding Bayes factor was, therefore, about 10⁹, leaving no doubt that the model including both inter- and intra-individual variability is more likely, and that that intra-individual variability is important.

Figure 13.

Posterior fits of the two-compartment inter- and intra-individual variability population model to data on plasma theophylline concentration in six subjects (Trembath and Boobis 1980). Red line: maximum posterior predictions. Grey lines: 20 random posterior fits. Subjects (S1 to S6) are suffixed with the type of dosing: “i” means immediate release, “s” sustained release, “sr” sustained release repeated dosing, “srh” idem with a dose twice as high.

The posterior parameter samples obtained by TI were generally similar (or slightly narrower) as compared to those obtained by standard Metropolis-Hastings sampling (Figures 14 and 15), with one major exception, apparent on Figure 16. The inter-individual variance for k_cp was higher and much more uncertain under TI. This result was due to a second mode identified by TI for that parameter, centered around 5.5 (Figure 17), amounting to a factor of 10 variation among individuals. The main mode is at 0.2, and was the only one found by standard MCMC simulations. The correlation between individual k_cp and k_pc values was not particularly high, but the possibility of vastly different values for k_cp pointed to an identifiability problem with the two-compartment model.

Figure 14.

Violin plots of theophylline posterior distributions of (A) population means μ, (B) inter-individual variances δ² and residual variance σ², for the two-compartment inter-individual variability model. For each parameter, the left sample (white) was obtained by TI MCMC simulations, and the right sample (gray) was obtained by standard MCMC simulations.

Figure 15.

Violin plots of theophylline individual parameters θ posterior distributions (subjects S1 to S6), for the two-compartment inter-individual variability model. For each subject, the parameters are respectively: k_r, k_a, V, k_e, k_cp, and k_pc. For each parameter, the left sample (white) was obtained by TI MCMC simulations, and the right sample (gray) was obtained by standard MCMC simulations.

Figure 16.

Standard MCMC vs. TI summaries (mean ± SD) of the posterior parameter distributions for the inter-individual variability model of theophylline pharmacokinetics. Colors code for population means (μ), population variances (Σ²), residual variance (σ²) and individual parameter values (θ_i). The non-matching parameter is Σ² for k_cp.

Figure 17.

Histograms of the posterior distribution of the inter-individual variance of k_cp, for the theophylline two-compartment inter-individual variability model. Panel A: parameter sample obtained by TI MCMC simulations; panel B: sample obtained by standard MCMC simulations.

This identifiability issue was confirmed by turning off the exchanges between the central and peripheral compartment and calibrating the resulting one-compartment model with the theophylline data. The data fits obtained are visually identical to those obtained with the two-compartment model (data not shown). According to TI, the integrated likelihood of the one-compartment inter- and intra-individual variability model (intra+inter-1cpt) was exp(8.73), and exp(−15) for the one-compartment inter-individual variability model (inter-only-1cpt). When comparing with the previous two-compartment results, when only inter-individual variability is included, the one-compartment model is only marginally better than the two-compartment model (exp(-15) versus exp(-15.2), or a Bayes factor of exp(0.2) = 1.2). On the other hand, when both inter- and intra-individual variability are included, the one-compartment model is substantially favored (exp(8.73) versus exp(5.55), or a Bayes factor of exp(3.18) = 24). Moreover, it is clear that including both sources of variability is better supported by the data. Summaries of the posterior parameter distributions for the one-compartment inter- and intra-individual variability model are shown in Figure 18.

Figure 18.

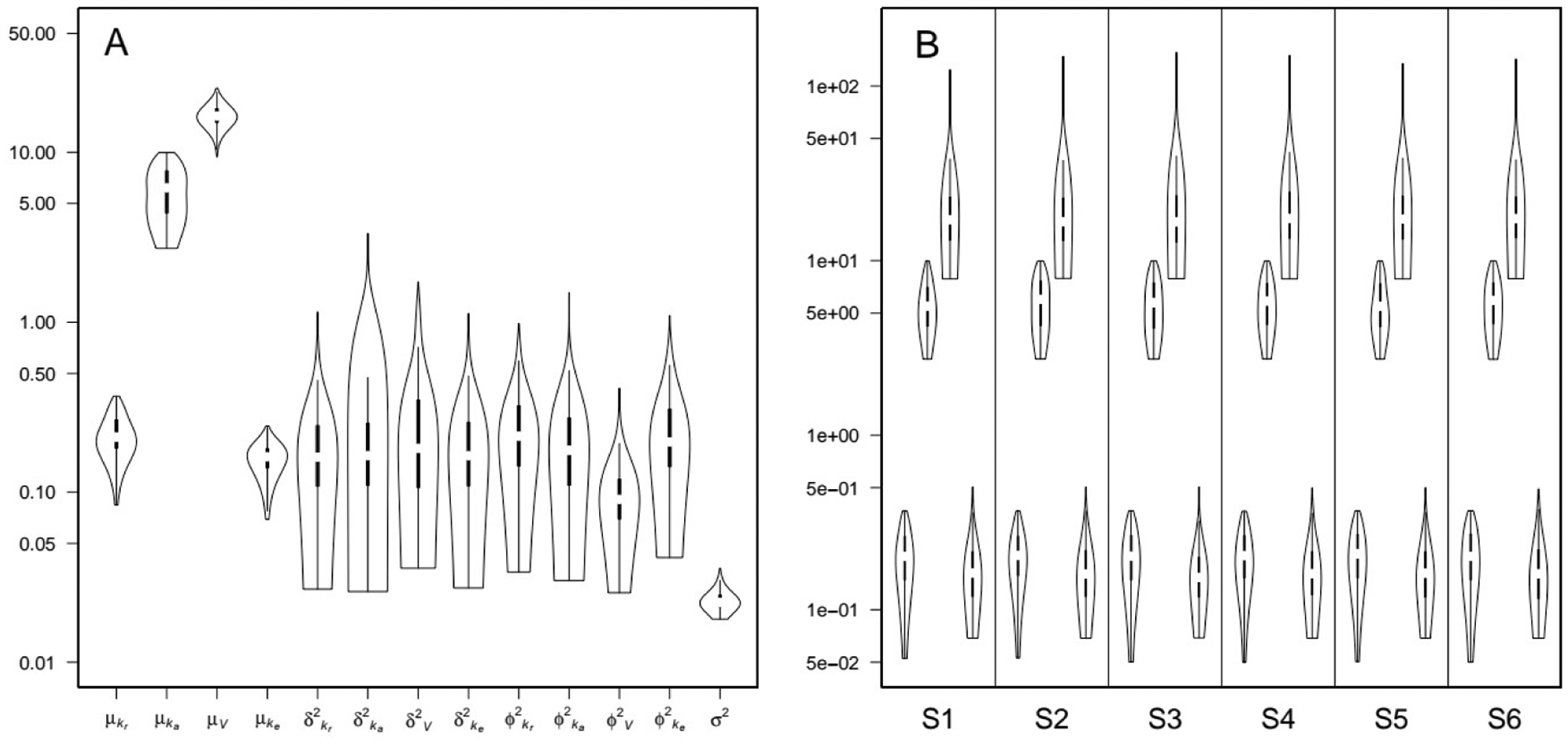
Violin plots of theophylline posterior distributions of the one-compartment model with inter- and intra-individual variability. Panel A: population means μ, inter-individual variances δ², intra-individual variances φ² and residual variance σ². Panel B: subjects’ means ξ. For each subject the parameters are respectively: k_r, k_a, V, and k_e. The parameter samples were obtained by TI MCMC simulations.

3.4. Acetaminophen population PBPK test case

The acetaminophen kinetic model is much more complex than the models tested above. For reference runs with standard MCMC sampling, 10 chains (of 300,000 simulations each) were needed to obtain convergence. The final sample contained 5000 parameter vectors (1 in 300 of the last 150,000 runs of 10 chains). Each chain took between 26 and 34 hours (average 33 hours) to run, amounting to 330 hours of total computing time.

With TI MCMC, finding an adequate TI schedule of 24 perks, including perk zero, required 67,000 iterations and 6 hours of computing time. An additional 100,000 iterations took 11 hours to complete. Individual perk visits ranged from 3059 to 4625, with 4124 at τ = 0 and 4286 at τ = 1 (see Supplementary Material Figure S5). Thus, a sample approximately equivalent to the reference one was obtained in 20 times less total computation time (twice less wall-clock time).

The maximum posterior fit obtained by TI MCMC was excellent, and equivalent to the one obtained with reference MCMC (Figure 19) (see also Hsieh et al. 2018, Figure 5). The posterior distributions are practically identical to those obtained by standard MCMC (Figures 20 and 21).

Figure 19.

Observed data values vs. maximum posterior model predictions for the acetaminophen data set, in the case of either standard or TI MCMC simulations.

Figure 20.

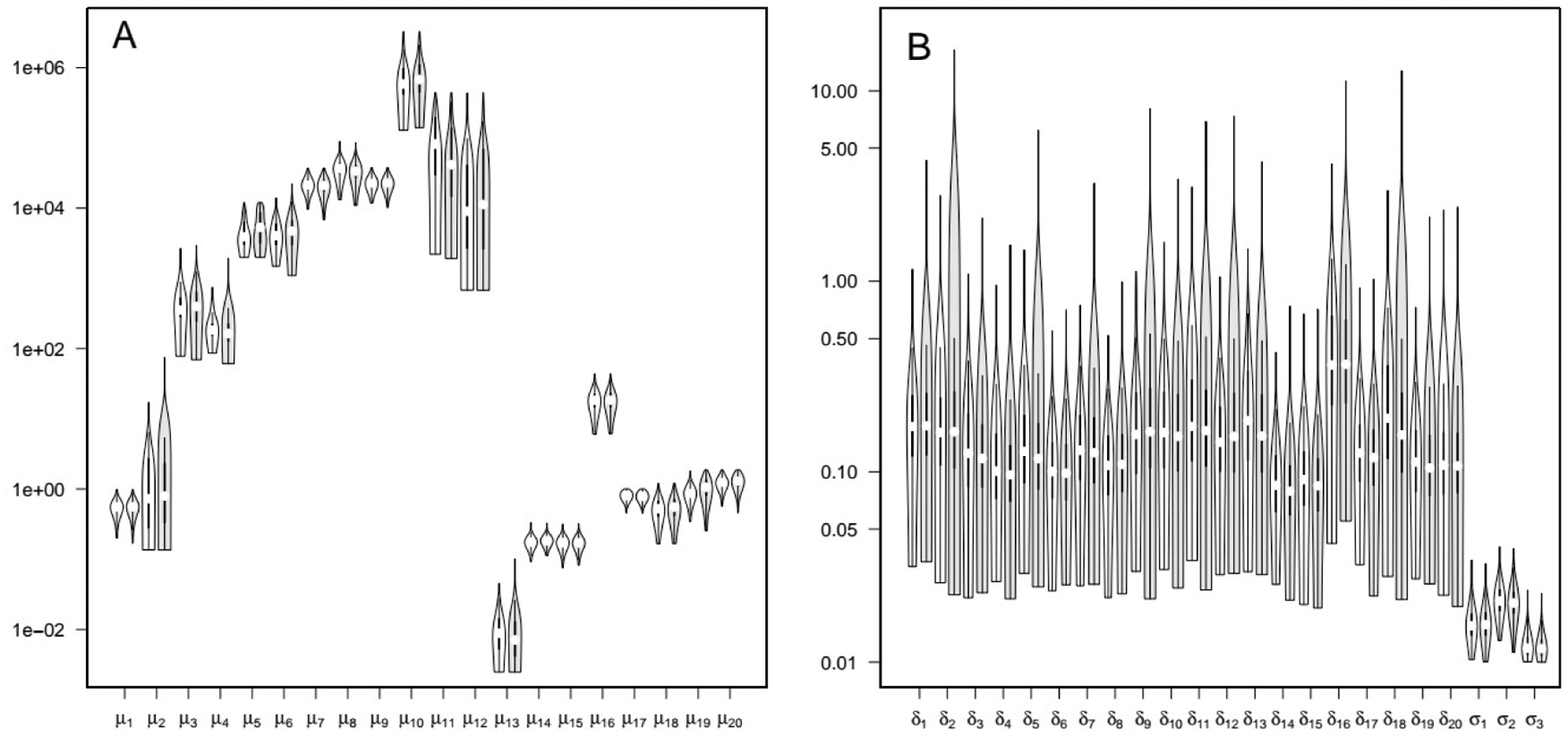
Violin plots of acetaminophen posterior parameter distributions. Panel A: population means μ. Panel B: inter-individual variances δ² and residual variances σ². For each parameter, the left sample (white) was obtained by TI MCMC simulations, and the right sample (gray) was obtained by standard MCMC simulations. Parameter indexing is specified in Supplementary Material Table S13.

Figure 21.

Violin plots of acetaminophen individual PBPK parameters θ posterior distributions (subjects S1 to S8). For each subject the parameters are in the same order as in Supplementary Material Table S13. For each parameter, the left sample (red) was obtained by TI MCMC simulations, and the right sample (gray) was obtained by standard MCMC simulations.

4. Discussion

We have implemented an algorithm to automatically set perk scales for simulated tempering MCMC. Finding appropriate scales (including perk zero) for complex models gives access to powerful Bayesian inference tools, applicable to a wide variety of complex models, including population PBPK models, for example. We had previously used simulated tempering MCMC in an in vitro PK context (Wilmes et al. 2015), but had to set the perk scale manually and did not reach perk zero (the lowest perk reached was 0.15). Still, that methodology allowed good mixing of the chains for an inference problem made difficult by missing and aggregated data. We demonstrated here efficient Bayesian parametric inference through TI in the case of complex multi-modal posteriors, and applications to model choice through Bayes factors. We focused on TI in our case-studies because going from the target posterior distribution to the prior is easier than going to a uniform distribution, and because it is efficient for inference, since the prior is known.

We have shown how tempered MCMC can help detect and characterize multi-modal posteriors. It would be a mistake to dismiss multi-modality as an artifact. It is very informative about the behavior of the model and the information content of the data. We often are blind to it because the algorithms we use get stuck in one mode, without any assurance that this is the optimum. The simplified, but still computationally difficult, multi-modal regression model we used in the first case-study was very efficiently solved. It is somewhat contrived and abstract, but realistic models’ calibration is fraught with multi-modal data likelihoods (for example in the case of cyclic behaviors, for which different periods can provide adequate solutions). Such problems are compounded by model imperfections, which make for no unique best fit, but for a range of less-than-optimal or even bad options. A concrete example of a multi-modal posterior arose in the theophylline case-study: TI identified a second mode in a variance parameter. That is a bit more subtle than the well-known flip-flop phenomenon. The presence of a high variability mode oriented us toward a reduction in model complexity. We do not dispute that theophylline distribution in the rat or human has an early fast distribution phase (Mitenko and Ogilvie 1973; Paalzow 1975); however, the oral dosing data of Trembath and Boobis (1980) do not allow a proper identification of transfers to a peripheral compartment, and the variability and imprecision of historical data did not allow us to set a very informative prior on those parameters. Yet, it is worth pointing that going from a complex model to a simpler one is a notably difficult problem. TI allowed us to perform what is, in essence, a powerful posterior sensitivity analysis (Gelman et al. 1996) for which detection of multi-modality was a prerequisite. Alternatives such as prior-based sensitivity analysis are definitely useful (Hsieh et al. 2018; Melillo et al. 2019), but they do not make full use of the data. Note also that the detection of the over-parameterization was partly enabled by the hierarchical structure of the population model with the intra-individual variance revealing the over-fitting.

The second case-study illustrated the application of TI to posterior density normalization. By itself, normalization is not very useful, since Bayesian inference can be made on the basis of the sampled parameter values, which do not require normalization of the posterior density to be obtained. However, the posterior normalization constant can be used to choose between competing models, through Bayes factors. Parsimony is favored and the models compared do not need to be nested as required by traditional methods such as the likelihood ratio test. We used Bayes factors to show that the theophylline dataset is much better described by a population model including both intra- and inter-individual variability than by a model with inter-individual variability only. In addition, for that dataset, a one-compartment model is preferable to a two-compartment model (for the sake of parsimony). However, as discussed above, other data may justify the use of a two-compartment model. The ability of TI variants to yield estimates of normalization constants justifies the interest it is currently receiving in the statistical literature (Behrens et al. 2012; Bhattacharya et al. 2019; Friel et al. 2014; Miasojedow et al. 2013; Zhou et al. 2016).

The two population PK case-studies also show that the same or better results are obtained with simulated tempering compared to those of standard Metropolis-Hasting MCMC sampling, but with a lower computational burden. In the case of acetaminophen, better sampling was achieved with 20 times fewer computations. However, for those two PK models, the mixing of the chain across perks was less efficient than with the smaller models.

This applies also to HMCMC, which shows good performance in algebraic models, or differential models of very low dimension. However, for PBPK models, HMCMC is handicapped by the expensive gradient sensitivities that need to be computed (Tsiros et al. 2019). Clearly, more research should be devoted to those issues.

It would be interesting to investigate methods for checking convergence and quality of tempered simulation chains, even when perk zero is not reached. In any case, enough parameter vectors should be obtained at the target perk value (perk 1 for standard inference, perks 0 and 1 if the value of the posterior normalizing constant is sought) to draw reasonably precise inference. This imposes an unavoidable lower limit on the number of simulations and computer time for complex models. However, it would be possible to parallelize the computation of multiple TI chains after perk schedule optimization. The algorithm could stop after having gathered a prescribed number of samples from the target distribution.

Though the methodology described here can be very effective, in some cases (not necessarily complex) the scale-setting algorithm fails to reach perk zero. In the worst cases, the pseudo-priors are not adjusted properly and the target temperature is rarely sampled. In our experience, that seems to be linked to sudden shifts in the location of the simulated Markov chain which render irrelevant the pseudo-prior estimates obtained so far. In such cases, manual tuning of the perk scale seems to be the only solution currently available, suggesting that further understanding of that phenomenon would be beneficial. Note also that we cannot claim that our algorithm yields the optimal perk schedule. It just provides good schedules. Obviously, the efficiency of the MCMC sampling is affected by the schedule obtained. A perk schedule can have too many, not enough, or badly spaced perks:

• With too many perks, jumping probability should be high but the chain needs a longer time to explore the various temperatures and reach the cold or hot distributions. Reaching the cold distribution (perk 1) is needed to obtain enough samples from the target posterior distribution; reaching the hottest distribution is needed for good mixing. Reaching perk zero is needed for guaranteed convergence or estimation of normalization constants. There will also be fewer samples in each tempered distribution. Exploration time should scale approximately with the square of the number of perks, and the sampling frequency of any perk should scale proportionally to that number, imposing a double penalty. In addition, Robbins-Munro pseudo-priors estimates will take a longer time to stabilize.

• With not enough or badly spaced perks, the probability of jumps between them can become extremely small and pseudo-priors may never stabilize in a reasonable time.

Overall, it is probably better to err on the side of too many perks. Note that the schedule can also be further optimized manually if needed.

Arguably, the use of complex models for population PK analyses is not common and many practitioners prefer minimal PK models for the sake of parsimony. Even in that case, the ability of TI to provide integration constants would be of interest, although a gain in speed would still be probably welcome. However, there are occurrences in which complex models are useful. For example, physiological and mechanistic models are preferable when extrapolating parameters obtained from animal data to humans, or for analyzing pregnancy data for dose-reconstruction in epidemiological studies (Brochot et al. 2019), multi-compartment gut transit models are useful for bioequivalence studies (Zhang et al. 2011), systems pharmacology or toxicology models are generating a lot of interest and benefit from parameter estimation (Hamon et al. 2014; Vyshemirsky and Girolami 2008). Such large models include many parameters, but also benefit from a lot of prior information, which requires a Bayesian framework to rigorously integrate evidence from new data (Gelman et al. 1996). The risk of over-fitting is real for such models, but sensitivity analysis has been shown to help solve the associated identifiability issues (Hsieh et al. 2018).

5. Conclusions

Statistical inference for complex models has progressed dramatically since the introduction of numerical Bayesian methods. However, high dimensional models and models specified by differential equations remain difficult to parameterize and test in terms of goodness of fit. A relatively large number of numerical methods have been proposed, but most of them were tested only on simplified models and remain inaccessible to practitioners owing to the lack of efficient, simple and flexible implementation. We have developed a simulated tempering MCMC algorithm that is efficient, amenable to automatic tuning, and available as free software. This has applications well beyond the realm of PK/PD modeling, but we expect that this approach will be especially useful in parameterizing and testing population PK/PD models and PBPK models, which are increasingly used in the context of population health and personalized medicine.

6 Nomenclature, abbreviations

CV

Coefficient of variation

MCMC

Markov chain Monte Carlo

PBPK

Physiologically-based pharmacokinetic

PK

Pharmacokinetic

SD

Standard deviation

TI

Thermodynamic integration