Optimal control problem and backward bifurcation on malaria transmission with vector bias

Abstract

This article aims to apply a mathematical model to investigate the spread of malaria by considering vector bias, saturated treatment, and an optimal control approach. A mathematical analysis of the equilibrium points and an investigation of the basic reproduction number show that if the basic reproduction number (${\mathcal{R}}_0)$ is less than one, the disease-free equilibrium is locally asymptotically stable. Furthermore, the center-manifold theory is applied to analyze the stability of the endemic equilibrium when ${\mathcal{R}}_0=1$. We find that our model performs a backward bifurcation phenomenon when the saturated treatment or vector bias parameter is larger than the threshold. Interestingly, we found that uncontrolled fumigation could increase the chance of the appearance of backward bifurcation. From the sensitivity analysis of ${\mathcal{R}}_0$, we find that the fumigation and vector bias are the most influential parameters for determining the magnitude of ${\mathcal{R}}_0$. Using the Pontryagin maximum principle, the optimal control problem is constructed by treating fumigation and medical treatment parameters as the time-dependent variable. Our numerical results on the optimal control simulation suggest that time-dependent fumigation and medical treatment could suppress the spread of malaria more efficiently at minimum cost.

Malaria; Vector bias; Fumigation; Saturated medical treatment; Backward bifurcation; Optimal control

1. Introduction

Malaria is a vector-borne disease that is transmitted to humans by the bite of a female Anopheles mosquito. There were an estimated 228 million cases worldwide in 2018, of which 405 000 ended with death [1]. Four main species of parasites cause malaria, P. falciparum, P. vivax, P. malariae, and P. ovale. It is malaria parasites infecting humans that attract female Anopheles mosquitoes to humans [2] because the parasite alters the human body odor, which attracts mosquitoes. Body odor is an unpleasant smell caused by chemicals, such as high heptanal, octanal, and nonanal aldehydes, resulting from the breakdown of sweat by the bacteria that live on the human skin. These chemicals are then detected by a mosquito antenna [3].

For ages, mathematical modeling has been used to understand how malaria is transmitted among humans. The mathematical model helps policymakers understand the disease, predict the future outcome of surveillance strategies, and much more. Mathematical modeling was first introduced by Ross [4] and extended by Macdonald [5]. Various other models have been introduced by many authors to describe malaria transmission considering the vector bias of Anopheles [6], [7], [8], [9]. Beretta et al. [10] described the effect of asymptomatic cases and Niger and Gumel [11] proposed a model to analyze the effect of reinfection, whereas Li et al. [12] investigated the effect of relapse on malaria transmission. Furthermore, several models have been introduced for malaria surveillance. Handari et al. [13] combined fumigation and bed-net usage in their model. Ghosh et al. [14] described the combined use of insecticide bed-nets, treatment, and indoor spraying for malaria eradication programs.

The application of the optimal control theory to find the best strategies for the eradication of disease transmission has been used by many authors [15], [16], [17], [18], [19], [20]. For an effective malaria eradication program using the optimal control approach, please see [21], [22], [23], [24] as another reference. These references used Pontryagin's maximum principle [25] to characterize their optimality system. The main purpose of the optimal control problem in disease transmission is to reduce the number of infected individuals (human and/or mosquito) at the lowest possible cost.

Here, a mathematical model is constructed to describe a malaria eradication strategy. Several important factors such as vector bias on malaria transmission are considered in the model to describe the preference of mosquitos to counter humans; saturated treatment to describe limitation on hospitalization resources; fumigation strategy to eradicate mosquitos; and an optimal control problem to describe a limited budget for the malaria eradication program. The model presented in this article has two equilibrium points: the malaria-free and malaria-endemic equilibrium points. We found that the malaria-free equilibrium is locally asymptotically stable when the basic reproduction number $({\mathcal{R}}_0)$ is less than unity.

In contrast, a malaria endemic equilibrium always exists when ${\mathcal{R}}_0$ is larger than unity. Our model may exhibit backward bifurcation on ${\mathcal{R}}_0=1$ depending on the saturated treatment and/or vector bias parameter. The larger these parameters, the greater the chance that our model exhibits a backward bifurcation. Furthermore, a sensitivity analysis was conducted to determine the most influential parameters for ascertaining the size of ${\mathcal{R}}_0$. Finally, a numerical simulation of the optimal control problem is carried out using the forward-backward iterative method to show the optimal intervention strategy for a malaria prevention program. Understanding the effect of vector bias in influencing the level of success of treatment and fumigation will significantly assist the optimal policy direction of related parties in the malaria control programs.

The remainder of this paper is organized as follows. We describe the construction of the model in Section 2. The existence and local stability of the equilibrium points, along with the basic reproduction number, is given in Section 3. Bifurcation analysis is described in Section 4. The characterization of the optimal control problem using the Pontryagin minimum principle (PMP) is described in Section 5. Some numerical experiments regarding the local sensitivity analysis of ${\mathcal{R}}_0$ and the optimal control simulations are described in Section 6. A discussion is provided in the last section of this article.

2. Model formulation

To develop the model for understanding the effect of vector bias, the human population is divided into two sub-populations: susceptible human $(S_h)$ and infected human $(I_h)$. As individuals who have recently recovered from malaria have no permanent immunity, we neglected the recovered population in our model. Consequently, individuals who recover from malaria infection can directly return to the susceptible population. In contrast, because of the short life span of mosquitoes, we also assume that the mosquito population can only divided into susceptible and infected mosquito sub-populations, denoted by $S_v$ and $I_v$, respectively.

The human population increased by a constant newborn parameter of ${\mathrm{\Lambda }}_h$ per unit time and was assumed to be susceptible. Infection occurs because of the direct contact between susceptible humans and infected mosquitoes with a successful transmission rate of ${\beta }_h$. In the case of malaria transmission, mosquitoes are more attracted to bite-infected humans [26]. This is because malaria infection changes the mixture of volatilities that infect human exhales. Hence, due to vector bias of the mosquito, the probability of the infected mosquito to bite a susceptible human is given by $\frac{S_h}{S_h+p{I}_h}$ where $p>1$ is the vector bias parameter. Note that when $p=1$, the vector bias is not considered in our model. Therefore, the number of meetings between susceptible and infected mosquitoes is given by $\frac{S_h{I}_v}{S_h+p{I}_h}$. Hence, the number of infections per unit time is given by ${\beta }_h\frac{S_h{I}_v}{S_h+p{I}_h}$. The infected susceptible humans were then transferred into an infected compartment. For more mathematical models that discuss the vector bias phenomena, please refer to our previous work in [27] or [6], [7], [8], [9] from other authors.

The infected human compartment then decreased because of the natural death rate ${\mu }_h$ per unit time and the recovery rate. Let us assume that only the $u_1$ proportion of $I_h$ undergoes medical treatment in the hospital, whereas the remaining $(1-u_1)$ only relies on the natural recovery rate by self-treatment at home with a rate of ${\delta }_0$. Hence, the recovery term for individuals who do not receive treatment in the hospital is given by ${\delta }_0(1-u_1)I_h$ per unit time. In contrast, instead of relying only on the natural recovery rate, individuals who undergo treatment in the hospital will receive an additional recovery rate with a maximum rate of ${\delta }_1$. The additional recovery rate in the hospital could only be at a maximum rate if the number of infected individuals was relatively small. More infected humans in the field will reduce the quality of treatment to increase the recovery rate. Therefore, the additional recovery rate depends on $I_h$. Let us call this $f({\delta }_1,I_h)$. This function should be a positive function that monotonically decreases with respect to the infected individual, and ${\lim }_{I_h\to \infty }f({\delta }_1,I_h)=0$. To achieve this aim, we define $f({\delta }_1,I_h):=\frac{{\delta }_1}{1+a{I}_h}$. Therefore, the number of infected individuals who recovered due to treatment in the hospital is given by ${\delta }_0+\frac{{\delta }_1}{1+a{I}_h}$. With this choice, we have ${\lim }_{I_h\to 0}{\delta }_0+\frac{{\delta }_1}{1+a{I}_h}={\delta }_0+{\delta }_1$, which describes the maximum recovery rate that can for the hospitalized individual when the number of infected individuals is relatively small. In contrast, ${\lim }_{I_h\to \infty }{\delta }_0+\frac{{\delta }_1}{1+a{I}_h}={\delta }_0$, which describes a situation in which the hospital can no longer maximize the recovery rate because of the large number of infected individuals.

The mosquito population was assumed to increase due to newborns with a per capita growth rate given by ${\mathrm{\Lambda }}_v$. As we assume that there is no vertical transmission of malaria among the mosquito population, we have all newborns entering the population via a susceptible mosquito population. Susceptible mosquito decreased due to infection because susceptible mosquitoes bite infected humans with the successful infection rate of ${\beta }_v$. The probability of susceptible mosquito counter infecting humans due to vector bias is given by $\frac{p{I}_h}{S_h+p{I}_h}$. Therefore, the number of susceptible mosquitoes infected by malaria per unit time is given by ${\beta }_v\frac{S_{v}p{I}_h}{S_h+p{I}_h}$. Furthermore, the mosquito population also decreased due to the natural death rate of ${\mu }_v$ and fumigation at a rate of $u_2$.

Based on the above description, the model to describe the transmission of malaria among human and mosquito population, considering vector bias, saturated medical treatment, and fumigation, can be expressed as:

$$\begin{array}{cc}\hfill \frac{d{S}_h}{dt}& ={\mathrm{\Lambda }}_h-\frac{{\beta }_h{S}_h}{p{I}_h+S_h}{I}_v-{\mu }_h{S}_h+(1-u_1){\delta }_0{I}_h+u_1({\delta }_0+\frac{{\delta }_1}{1+a{I}_h})I_h,\hfill \\ \hfill \frac{d{I}_h}{dt}& =\frac{{\beta }_h{S}_h}{p{I}_h+S_h}{I}_v-{\mu }_h{I}_h-(1-u_1){\delta }_0{I}_h-u_1({\delta }_0+\frac{{\delta }_1}{1+a{I}_h})I_h,\hfill \\ \hfill \frac{d{S}_v}{dt}& ={\mathrm{\Lambda }}_v-\frac{{\beta }_{v}p{I}_h}{p{I}_h+S_h}{S}_v-{\mu }_v{S}_v-u_2{S}_v,\hfill \\ \hfill \frac{d{I}_v}{dt}& =\frac{{\beta }_{v}p{I}_h}{p{I}_h+S_h}{S}_v-{\mu }_v{I}_v-u_2{I}_v,\hfill \end{array}\}$$ (1)

where all the parameters are positive, as described in Table 1. System (1), supplemented by non-negative initial conditions, can be expressed as:

$$S_h(t=0)=S_{h0},I_h(t=0)=I_{h0},S_v(t=0)=S_{v0},I_v(t=0)=I_{v0}.$$

Table 1.

Parameter description of system (1).

Parameters	Description	Unity
Λh	Human recruitment rate	$\frac{\text{human}}{\text{day}}$
Λv	Mosquitoes recruitment rate	$\frac{\text{mosquitoes}}{\text{day}}$
βv	Infection rate from mosquito to human	$\frac{\text{human}}{\text{mosquito}\times \text{day}}$
βv	Infection rate from human to mosquito	$\frac{1}{\text{day}}$
μh	Death rate of human	$\frac{1}{\text{day}}$
μv	Death rate of mosquitoes	$\frac{1}{\text{day}}$
p	Vector bias parameter	Nondimensional
δ0	Initial recovery rate	$\frac{1}{\text{day}}$
δ1	Additional recovery rate due to hospitalization	$\frac{1}{\text{day}}$
a	Saturation parameter for hospital capacity	$\frac{1}{\text{human}}$
u1	Proportion of infected humans who get hospitalized	nondimensional
u2	Fumigation rate	$\frac{1}{\text{day}}$

Model (1) is well-posed in a non-negative region ${\mathbb{R}}_{+}^4$ because all vector fields in the boundary are pointing inward. Therefore, using the above initial condition, the solution will always be non-negative for all times $t\ge 0$. Furthermore, it can be shown without any difficulties that the human population is bounded by ${\mathrm{\Lambda }}_h/{\mu }_h$, whereas the mosquito population is bounded by ${\mathrm{\Lambda }}_v/({\mu }_v+u_2)$.

3. Analysis of the model

3.1. The disease-free equilibrium and the basic reproduction number

System (1) has a disease-free equilibrium given by

$$E_0=(S_h,I_h,S_v,I_v)=(\frac{{\mathrm{\Lambda }}_h}{{\mu }_h},0,\frac{{\mathrm{\Lambda }}_v}{{\mu }_v+u_2},0).$$ (2)

Having the disease-free equilibrium in hand, we are now ready to calculate the basic reproduction number $({\mathcal{R}}_0)$. Modifying the original definition of the basic reproduction number in [28], the basic reproduction number in this study is defined as the expected number of newly infected malaria cases caused by an initial infection in a closed population during one infection period. To construct the basic reproduction number for system (1), we use the next-generation matrix approach [29]. The reader may see [30], [31], [32], [33], [34], [35], [36] for another example of the derivation of ${\mathcal{R}}_0$ using this method.

The transmission $(\mathcal{F})$ and transition $(\mathcal{V})$ matrix of system (1) evaluated in $E_0$ are given by

$$\mathcal{F}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill {\beta }_h\hfill \\ \hfill \frac{{\beta }_{v}p{\mathrm{\Lambda }}_v{\mu }_h}{{\mathrm{\Lambda }}_h({\mu }_v+u_2)}\hfill & \hfill 0\hfill \end{array}\right],\text{and}\mathcal{V}=\left[\begin{array}{cc}\hfill -(u_1{\delta }_1+{\delta }_0+{\mu }_h)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -({\mu }_v+u_2)\hfill \end{array}\right].$$

Hence, the next generation matrix of system (1) is given by

$$\mathcal{K}=-\mathcal{F}{\mathcal{V}}^{-1}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill \frac{{\beta }_h}{u_2+{\mu }_v}\hfill \\ \hfill \frac{p{\beta }_v{\mathrm{\Lambda }}_v{\mu }_h}{(u_2+{\mu }_v){\mathrm{\Lambda }}_h(u_1{\delta }_1+{\delta }_0+{\mu }_h)}\hfill & \hfill 0\hfill \end{array}\right].$$

Therefore, the corresponding basic reproduction number is

$${\mathcal{R}}_0=\rho (\mathcal{K})=\sqrt{\frac{p{\mathrm{\Lambda }}_v{\beta }_h{\beta }_v{\mu }_h}{{\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2({\delta }_1{u}_1+{\delta }_0+{\mu }_h)}}.$$ (3)

Using the above basic reproduction number for system (1), we state the local stability criteria for $E_0$ in the following theorem.

Theorem 1

The disease-free equilibrium $E_0$ of the malaria model in system (1) is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$.

Proof

Linearizing system (1) at $E_0$ yield

$$J(E_0)=\left[\begin{array}{cccc}\hfill -{\mu }_h\hfill & \hfill u_1{\delta }_1+{\delta }_0\hfill & \hfill 0\hfill & \hfill -{\beta }_h\hfill \\ \hfill 0\hfill & \hfill -(u_1{\delta }_1+{\delta }_0+{\mu }_h)\hfill & \hfill 0\hfill & \hfill {\beta }_h\hfill \\ \hfill 0\hfill & \hfill -\frac{{\beta }_{v}p{\mathrm{\Lambda }}_v{\mu }_h}{{\mathrm{\Lambda }}_h({\mu }_v+u_2)}\hfill & \hfill -({\mu }_v+u_2)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{{\beta }_{v}p{\mathrm{\Lambda }}_v{\mu }_h}{{\mathrm{\Lambda }}_h({\mu }_v+u_2)}\hfill & \hfill 0\hfill & \hfill -({\mu }_v+u_2)\hfill \end{array}\right].$$

The eigenvalues are ${\lambda }_1=-{\mu }_h<0$ and ${\lambda }_2=-{\mu }_v-u_2<0$, while ${\lambda }_3$ and ${\lambda }_4$ are taken from the root of the following quadratic equation:

$$a_2{\lambda }^2+a_1\lambda +a_0=0,$$

where $a_2={\mathrm{\Lambda }}_h({\mu }_v+u_2)>0$, $a_1={\mathrm{\Lambda }}_h({\mu }_v+u_2)(u_1{\delta }_1+{\delta }_0+{\mu }_h+{\mu }_v+u_2)>0$, and $a_0={\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2({\delta }_1{u}_1+{\delta }_0+{\mu }_h)(1-{\mathcal{R}}_0^2)$. If ${\mathcal{R}}_0<1$, then $a_0>0$. Thus, according to the Hurwitz stability criteria, the above polynomials have only roots with negative real parts. Consequently, the disease-free equilibrium $E_0$ is locally asymptotically stable if ${\mathcal{R}}_0<1$. In contrast, $E_0$ is unstable if ${\mathcal{R}}_0>1$.  □

From Theorem 1, it can be seen that a malaria-free equilibrium can be established in the community if the basic reproduction number can be reduced as small as possible, to a specific value of less than unity. Please note that ${\mathcal{R}}_0^2$ express as a multiplication between three component, i.e. (i) Number of new infected mosquito produced by infected human during human infection period, given by $\frac{p{\beta }_v}{{\delta }_0+{\delta }_1{u}_1+{\mu }_h}$, (ii) Number of new infected human produced by infected mosquito during mosquito infection period, given by $\frac{{\beta }_h}{{\mu }_v+u_2}$, and (iii) The ratio between mosquito and human population in $E_0$ which is given by $\frac{{\mathrm{\Lambda }}_v/({\mu }_v+u_2)}{{\mathrm{\Lambda }}_h/{\mu }_v}$. Reducing each of these components reduces ${\mathcal{R}}_0$. Different interventions should be considered for each component. For example, reducing ${\beta }_v$ in the first component could be done using a mosquito repellent [27], or any other genetic modification to reduce mosquito's capability to bite humans. Reducing the second component could be done by reducing the infection rate ${\beta }_h$ using a mosquito repellent or increasing the fumigation rate $u_2$. However, massive fumigation may confer resistance to mosquitoes for some chemical insecticides [37]. Furthermore, reducing ${\mathcal{R}}_0$ via the first component can be achieved by increasing the number of infected individuals treated in the hospital $(u_1)$ or increasing the quality of treatment in the hospital $({\delta }_1)$.

3.2. Endemic equilibrium

The endemic equilibrium point of system (1) is given by

$$E^{\mathrm{†}}=(S_h,I_h,S_v,I_v)=(S_h^{\mathrm{†}},I_h^{\mathrm{†}},S_v^{\mathrm{†}},I_v^{\mathrm{†}}),$$ (4)

where

$$S_h^{\mathrm{†}}=\frac{{\mathrm{\Lambda }}_h-{\mu }_h{I}_h^{\mathrm{†}}}{{\mu }_h},S_v^{\mathrm{†}}=\frac{{\mathrm{\Lambda }}_v}{u_2+{\mu }_v}-I_v^{\mathrm{†}},I_v^{\mathrm{†}}=\frac{p{I}_h^{\mathrm{†}}{\mathrm{\Lambda }}_v{\beta }_v{\mu }_h}{(u_2+{\mu }_v)((p{\mu }_h{I}_h^{\mathrm{†}}({\beta }_v+{\mu }_v+u_2))(u_2+{\mu }_v)({\mathrm{\Lambda }}_h-{\mu }_h{I}_h^{\mathrm{†}}))},$$

while $I_h^{\mathrm{†}}$ is taken from positive root of the following three degree polynomial

$$\mathcal{P}(I_h)=A_3{I}_h^3+A_2{I}_h^2+A_1{I}_h+A_0=0,$$ (5)

with

$$A_3=a{\mu }_h^2(p-1)({\mu }_v+u_2)({\mu }_h+{\delta }_0)((p-1)({\mu }_v+u_2)+p{\beta }_v)A_2=ap{\mathrm{\Lambda }}_v{\beta }_v{{\mu }_h}^2{\beta }_h+{\mu }_h(u_2+{\mu }_v)({\mu }_h(u_1{\delta }_1+{\delta }_0+{\mu }_h)(u_2+{\mu }_v+{\beta }_v)p^2+({\beta }_v+2{\mu }_v+2u_2)(a{\mathrm{\Lambda }}_h{\delta }_0+a{\mathrm{\Lambda }}_h{\mu }_h-{\delta }_1{\mu }_h{u}_1-{\delta }_0{\mu }_h-{{\mu }_h}^2)p-(u_2+{\mu }_v)(2a{\mathrm{\Lambda }}_h{\delta }_0+2a{\mathrm{\Lambda }}_h{\mu }_h-{\delta }_1{\mu }_h{u}_1-{\delta }_0{\mu }_h-{{\mu }_h}^2))A_1=-p{\mathrm{\Lambda }}_v{\beta }_v{\mu }_h(a{\mathrm{\Lambda }}_h-{\mu }_h){\beta }_h+{\mathrm{\Lambda }}_h(u_2+{\mu }_v)({\mu }_h(u_1{\delta }_1+{\delta }_0+{\mu }_h)({\beta }_v+2{\mu }_v+2u_2)p+(u_2+{\mu }_v)(a{\mathrm{\Lambda }}_h{\delta }_0+a{\mathrm{\Lambda }}_h{\mu }_h-2{\delta }_1{\mu }_h{u}_1-2{\delta }_0{\mu }_h-2{{\mu }_h}^2))A_0={\mathrm{\Lambda }}_h^2{({\mu }_v+u_2)}^2({\delta }_1{u}_1+{\delta }_0+{\mu }_h)(1-{\mathcal{R}}_0^2).$$

Theorem 2

System (1) always has an endemic equilibrium whenever ${\mathcal{R}}_0>1$.

Proof

The existence of the endemic equilibrium of the system (1) depends on the root of the polynomial (5). Because $A_3>0$, we have ${\lim }_{I_h\to \infty }\mathcal{P}(I_h)=\infty$, and ${\lim }_{I_h\to -\infty }\mathcal{P}(I_h)=-\infty$. If ${\mathcal{R}}_0=1$, then $\mathcal{P}(I_h)$ has $I_h=0$ as one of its roots, whereas the other two could be positive, negative, or even imaginary. Let us consider an extreme case in which we have no positive root of $\mathcal{P}(I_h)$ when ${\mathcal{R}}_0=1$. Then, when ${\mathcal{R}}_0>1$, we have $A_0<0$, which makes $\mathcal{P}(I_h)$ of ${\mathcal{R}}_0=1$ to shift downward parallel to the y-axis. Therefore, we had at least one new positive root. This completes the proof.  □

From the previous theorem, we can guarantee that there always exists at least one endemic equilibrium if ${\mathcal{R}}_0>1$. However, because $\mathcal{P}(I_h)$ is a cubic polynomial, we may have multiple endemic equilibria when ${\mathcal{R}}_0>1$ or ${\mathcal{R}}_0<1$. Hence, we analyze the maximum number of positive roots of the polynomial (5) using the Descartes rules of signs. The results are summarized in Table 2. It can be seen that whenever ${\mathcal{R}}_0<1$, then polynomial $\mathcal{P}(I_h)$ will either have zero or two positive roots. In contrast, when ${\mathcal{R}}_0>1$, we always have the possibility of having either one or three positive roots.

Table 2.

Number of possible positive real roots of polynomial (5).

Case	A3	A2	A1	A0	Condition of ${\mathcal{R}}_0$	Possible positive root
1	+	+	+	-	${\mathcal{R}}_0>1$	1
2	+	+	-	-	${\mathcal{R}}_0>1$	1
3	+	-	+	-	${\mathcal{R}}_0>1$	1 or 3
4	+	-	-	-	${\mathcal{R}}_0>1$	1
5	+	+	+	+	${\mathcal{R}}_0<1$	0
6	+	+	-	+	${\mathcal{R}}_0<1$	0 or 2
7	+	-	+	+	${\mathcal{R}}_0<1$	0 or 2
8	+	-	-	+	${\mathcal{R}}_0<1$	0 or 2

From Table 2, we can see that system (1) may have an endemic equilibrium point even though ${\mathcal{R}}_0<1$. Unfortunately, the results in Table 2 cannot provide a specific condition to guarantee the existence of the endemic equilibrium when ${\mathcal{R}}_0<1$. Therefore, we continue our analysis by determining a possible condition to guarantee the existence of an endemic equilibrium when ${\mathcal{R}}_0<1$, which is indicated by the sign of $\frac{\partial I}{\partial {\mathcal{R}}_0}$ to be negative when ${\mathcal{R}}_0=1$ and $I=0$. Furthermore, if it is fulfilled, then we will have two positive endemic equilibria when ${\mathcal{R}}_0<1$.

First, we make $A_i$ in $\mathcal{P}(I_h)$ for $i=0,1,2,3$ to make it a function depending on ${\mathcal{R}}_0$ by changing ${\beta }_h$ as

$${\beta }_h^{⁎}=\frac{{\mathcal{R}}_0^2{\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2({\delta }_1{u}_1+{\delta }_0+{\mu }_h)}{{\mu }_{h}p{\mathrm{\Lambda }}_v{\beta }_v}.$$

Substituting ${\beta }_h={\beta }_h^{⁎}$ into $A_3,A_2,A_1$, and $A_0$, and taking the partial derivative of $I_h$ with respect to ${\mathcal{R}}_0$ from $\mathcal{P}(I_h)$ and evaluating it in ${\mathcal{R}}_0=1,I_h=0$, give us:

$$\frac{\partial I_h}{\partial {\mathcal{R}}_0}{|}_{I_h=0,{\mathcal{R}}_0=1}=-\frac{\partial A_0/\partial {\mathcal{R}}_0}{A_1({\mathcal{R}}_0)}{|}_{I_h=0,{\mathcal{R}}_0=1},$$

where

$$\frac{\partial A_0}{\partial {\mathcal{R}}_0}{|}_{I_h=0,{\mathcal{R}}_0=1}=-2{\mathrm{\Lambda }}_h^2{({\mu }_v+u_2)}^2({\delta }_1{u}_1+{\delta }_0+{\mu }_h)$$

Because $\frac{\partial A_0}{\partial {\mathcal{R}}_0}<0$, $\frac{\partial I_h}{\partial {\mathcal{R}}_0}<0$ if and only if $A_1({\mathcal{R}}_0)<0$, or equivalently,

$$a>a^{⁎}=\frac{{\mu }_h({\delta }_1{u}_1+{\delta }_0+{\mu }_h)(p{\beta }_v+2p({\mu }_v+u_2)-{\mu }_v-u_2)}{({\mu }_v+u_2){\mathrm{\Lambda }}_h{\delta }_1{u}_1}.$$

This results state in the following theorem.

Theorem 3

System (1) has two endemic equilibriums in an interval when ${\mathcal{R}}_0<1$ if

$$a>a^{⁎}=\frac{{\mu }_h({\delta }_1{u}_1+{\delta }_0+{\mu }_h)(p{\beta }_v+2p({\mu }_v+u_2)-{\mu }_v-u_2)}{({\mu }_v+u_2){\mathrm{\Lambda }}_h{\delta }_1{u}_1}.$$ (6)

Based on Theorem 2, Theorem 3, we indicate the possibility of the existence of multiple endemic equilibrium points when ${\mathcal{R}}_0<1$; even the disease-free equilibrium is locally stable. This result means that society may misinterpret the endemicity of malaria in the population. When the endemicity of malaria is only indicated by the size of the basic reproduction number that should be less than one, the disease may die out but could persist (in a huge size of endemic level). Hence, it is essential to understand these phenomena in more detail. Further discussion about the local stability of this endemic equilibrium is provided in the following section.

4. Bifurcation analysis

In this section, we conduct a bifurcation analysis of our proposed malaria model in system (1) using the well-known Castillo-Song bifurcation theorem [38]. Many authors have used this approach to analyze the bifurcation phenomena in epidemiological models [39], [40], [41], [42], [43].

Theorem 4

If ${\mathcal{R}}_0<1$ and

$$a>a^{⁎}=\frac{{\mu }_h({\delta }_1{u}_1+{\delta }_0+{\mu }_h)(p{\beta }_v+2p({\mu }_v+u_2)-{\mu }_v-u_2)}{({\mu }_v+u_2){\mathrm{\Lambda }}_h{\delta }_1{u}_1},$$

then system (1) undergoes a backward bifurcation at ${\mathcal{R}}_0=1$. If $a<a^{⁎}$, then system (1) undergoes a forward bifurcation at ${\mathcal{R}}_0=1$.

Proof

Suppose, $x_1=S_h,x_2=I_h,x_3=S_v$ and $x_4=I_v$. The malaria model in the system (1) becomes

$$f_1=\frac{d{x}_1}{dt}={\mathrm{\Lambda }}_h-\frac{{\beta }_h{x}_1{x}_4}{p{x}_2+x_1}-{\mu }_h{x}_1+(1-u_1){\delta }_0{x}_2+u_1({\delta }_0+\frac{{\delta }_1}{1+a{x}_2})x_2,f_2=\frac{d{x}_2}{dt}=\frac{{\beta }_h{x}_1{x}_4}{p{x}_2+x_1}-{\mu }_h{x}_2-(1-u_1){\delta }_0{x}_2-u_1({\delta }_0+\frac{{\delta }_1}{1+a{x}_2})x_2,f_3=\frac{d{x}_3}{dt}={\mathrm{\Lambda }}_v-\frac{{\beta }_{v}p{x}_2{x}_3}{p{x}_2+x_1}-{\mu }_v{x}_3-u_2{x}_3,f_4=\frac{d{x}_4}{dt}=\frac{{\beta }_{v}p{x}_2{x}_3}{p{x}_2+x_1}-{\mu }_v{x}_4-u_2{x}_4.$$ (7)

We substitute ${\mathcal{R}}_0=1\leftrightarrow {\mathcal{R}}_0^2=1$ and let ${\beta }_h^{\mathrm{†}}=\frac{{\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2({\delta }_1{u}_1+{\delta }_0+{\mu }_h)}{{\mu }_{h}p{\mathrm{\Lambda }}_v{\beta }_v}$ as the bifurcation parameter. Then, the Jacobian matrix of system (7) at $E_0$ and ${\beta }_h={\beta }_h^{\mathrm{†}}$ is

$${\mathcal{J}}_0=\left(\begin{array}{cccc}\hfill -{\mu }_h\hfill & \hfill u_1{\delta }_1+{\delta }_0\hfill & \hfill 0\hfill & \hfill -\frac{{\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2({\delta }_1{u}_1+{\delta }_0+{\mu }_h)}{{\mu }_{h}p{\mathrm{\Lambda }}_v{\beta }_v}\hfill \\ \hfill 0\hfill & \hfill -(u_1{\delta }_1+{\delta }_0+{\mu }_h)\hfill & \hfill 0\hfill & \hfill \frac{{\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2({\delta }_1{u}_1+{\delta }_0+{\mu }_h)}{{\mu }_{h}p{\mathrm{\Lambda }}_v{\beta }_v}\hfill \\ \hfill 0\hfill & \hfill -\frac{{\beta }_{v}p{\mathrm{\Lambda }}_v{\mu }_h}{{\mathrm{\Lambda }}_h({\mu }_v+u_2)}\hfill & \hfill -({\mu }_v+u_2)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{{\beta }_{v}p{\mathrm{\Lambda }}_v{\mu }_h}{{\mathrm{\Lambda }}_h({\mu }_v+u_2)}\hfill & \hfill 0\hfill & \hfill -({\mu }_v+u_2)\hfill \end{array}\right).$$ (8)

The eigenvalues of ${\mathcal{J}}_0$ are ${\lambda }_1=0,{\lambda }_2=-{\mu }_h,{\lambda }_3=-({\mu }_v+u_2)$, and ${\lambda }_4=-({\delta }_1{u}_1+{\delta }_0+{\mu }_h+{\mu }_v+u_2)$. It can be seen that ${\mathcal{J}}_0$ has three negative eigenvalues and one zero eigenvalue. Now, we compute the left and right eigenvectors of ${\mathcal{J}}_0$ corresponding to ${\lambda }_1=0$. We consider the system ${\mathcal{J}}_0\mathbf{\text{w}}=0$ to compute the right eigenvector w. Assuming $\mathbf{\text{w}}={(w_1,w_2,w_3,w_4)}^T$ to be the right eigenvector, then a direct calculation yields

$$\mathbf{\text{w}}=[1,1,-\frac{{\mu }_{h}p{\mathrm{\Lambda }}_v{\beta }_v}{{\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2},\frac{{\mu }_{h}p{\mathrm{\Lambda }}_v{\beta }_v}{{\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2}].$$

Next, assuming $\mathbf{\text{v}}={(v_1,v_2,v_3,v_4)}^T$ to be the left eigenvector, then a direct calculation yields

$$\mathbf{\text{v}}=[0,1,0,\frac{{\mathrm{\Lambda }}_h({\mu }_v+u_2)({\delta }_1{u}_1+{\delta }_0+{\mu }_h)}{{\mu }_{h}p{\mathrm{\Lambda }}_v{\beta }_v}].$$

Because $v_1$ and $v_3$ are zero, we do not need the derivatives of $f_1$ and $f_3$. From the derivatives of $f_2$ and $f_4$, the second derivative with respect to each variable and ${\beta }_h^{\mathrm{†}}$, which are nonzero, is as follows:

$$\frac{{\partial }^2{f}_2}{\partial x_2^2}=2u_1{\delta }_{1}a,\frac{{\partial }^2{f}_2}{\partial x_2\partial x_4}=-\frac{{({\mu }_v+u_2)}^2({\delta }_1{u}_1+{\delta }_0+{\mu }_h)}{{\mathrm{\Lambda }}_v{\beta }_v},\frac{{\partial }^2{f}_4}{\partial x_1\partial x_2}=-\frac{{\beta }_{v}p{\mathrm{\Lambda }}_v{\mu }_h^2}{({\mu }_v+u_2){\mathrm{\Lambda }}_h^2},$$

$$\frac{{\partial }^2{f}_4}{\partial x_2^2}=-\frac{2{\beta }_v{p}^2{\mathrm{\Lambda }}_v{\mu }_h^2}{{\mathrm{\Lambda }}_h^2({\mu }_v+u_2)},\frac{{\partial }^2{f}_4}{\partial x_2\partial x_3}=\frac{{\beta }_{v}p{\mu }_h}{{\mathrm{\Lambda }}_h},\frac{{\partial }^2{f}_2}{\partial x_4\partial {\beta }_h^{\mathrm{†}}}=1.$$

To use the bifurcation theorem in [38], we have to compute $\mathcal{A}$ and $\mathcal{B}$, where

$$\mathcal{A}=\sum _{k,i,j=1}^n{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k}{\partial x_i\partial x_j}(0,0),\mathcal{B}=\sum _{k,i,j=1}^n{v}_k{w}_i\frac{{\partial }^2{f}_k}{\partial x_i\partial \varphi }(0,0).$$

It follows that

$$\mathcal{A}=\frac{1}{{\mathrm{\Lambda }}_h({\mu }_v+u_2)}\left(2\right(u_1{\delta }_{1}a{\mathrm{\Lambda }}_h({\mu }_v+u_2)-p{\beta }_v{\delta }_1{\mu }_h{u}_1-2p{\delta }_1{\mu }_h{u}_1({\mu }_v+u_2)-p{\beta }_v{\delta }_0{\mu }_h-p{\beta }_v{\mu }_h^2-2p{\delta }_0{\mu }_h({\mu }_v+u_2)-2p{\mu }_h^2({\mu }_v+u_2)+{\delta }_1{\mu }_h{u}_1({\mu }_v+u_2)+{\delta }_0{\mu }_h({\mu }_v+u_2)+{\mu }_h^2({\mu }_v+u_2)\left)\right),\mathcal{B}=\frac{v_2{w}_2{\mu }_{h}p{\mathrm{\Lambda }}_v{\beta }_v}{{\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2}.$$

Taking $v_2$ and $w_2$ to be positive, it is obvious that $\mathcal{B}>0$. Therefore, backward bifurcation occurs when $\mathcal{A}>0$, or equivalently, when

$$a>\frac{{\mu }_h({\delta }_1{u}_1+{\delta }_0+{\mu }_h)(p{\beta }_v+2p({\mu }_v+u_2)-{\mu }_v-u_2)}{({\mu }_v+u_2){\mathrm{\Lambda }}_h{\delta }_1{u}_1}=a^{⁎}.$$ (9)

Conversely, if $\mathcal{A}<0$ or $a<a^{⁎}$, forward bifurcation will occur. We see that the condition $a^{⁎}$ in equation (9) has the same condition as inequality (6).  □

The biological interpretation of Theorem 4 is that when the backward bifurcation phenomenon occurs, malaria may still exist in the community even when ${\mathcal{R}}_0<1$. This condition may lead to a misunderstanding of malaria eradication programs. Policymakers may think that they have succeeded in suppressing ${\mathcal{R}}_0$ to be less than unity and expect malaria will die out. Unfortunately, if backward bifurcation occurs, a large endemic equilibrium exists because hysteresis appears when ${\mathcal{R}}_0<1$. Our result in Theorem 4 indicates that policymakers need to increase the bed capacity or human resources for medical treatment in the hospital (reducing a) to avoid backward bifurcation.

Taking the derivative of $\mathcal{A}$ with respect to the vector bias parameter p, we obtain

$$\frac{\partial \mathcal{A}}{\partial p}=-2\frac{v_2{w_2}^2{\mu }_h({\delta }_1{u}_1+{\delta }_0+{\mu }_h)({\beta }_v+2{\mu }_v+2u_2)}{{\mathrm{\Lambda }}_h({\mu }_v+u_2)}<0.$$

Because $\frac{\partial \mathcal{A}}{\partial p}<0$, the higher number of mosquitos attracted to bite infected humans will increase the probability of the model to avoid backward bifurcation. The reason is that the new infection can be reduced as mosquitos prefer biting infected humans rather than susceptible humans.

Next, we analyzed the effect of the proportion of infected humans receiving medical treatment in the hospital. Taking the derivative of ${\mathcal{R}}_0$ with respect to $u_1$, we obtain

$$\frac{\partial \mathcal{A}}{\partial u_1}=2\frac{v_2{w_2}^2{\delta }_1(({\mu }_v+u_2)(a{\mathrm{\Lambda }}_h+{\mu }_h)-p{\mu }_h({\beta }_v+2{\mu }_v+2u_2))}{{\mathrm{\Lambda }}_h({\mu }_v+u_2)}<0$$

if

$$p>\frac{({\mu }_v+u_2)(a{\mathrm{\Lambda }}_h+{\mu }_h)}{{\mu }_h({\beta }_v+2({\mu }_v+u_2))}=p^{⁎}.$$

Again, it can be seen that the vector bias parameter plays an essential role in determining whether the medical intervention or hospitalization will be effective in avoiding backward bifurcation. It can be seen that hospitalization or medical intervention increases the probability of preventing backward bifurcation only when p is sufficiently small; to be precise, when $p>p^{⁎}$.

In contrast to $u_1$, increasing the fumigation rate $u_2$ will increase the probability of the occurrence of backward bifurcation because

$$\frac{\partial \mathcal{A}}{\partial u_2}=2\frac{v_2{w_2}^{2}p{\beta }_v{\mu }_h({\delta }_1{u}_1+{\delta }_0+{\mu }_h)}{{\mathrm{\Lambda }}_h{({\mu }_v+u_2)}^2}>0.$$

These policymakers need to pay attention to this result as fumigation is a common and favorable intervention when malaria cases start to increase in a community. Based on this result, we can conclude that a combination of fumigation needs to consider the treatment saturation parameter, which is related to the hospital's capability to handle an increase in the number of malaria cases. The chance that fumigation intervention will lead to backward bifurcation can be reduced if the treatment saturation parameter is sufficiently small; to be precise, when $a<a^{⁎}$.

Furthermore, if $a=0$, which means that there are no limitations on hospital capacity, the bifurcation coefficient $\mathcal{A}$ becomes

$${\mathcal{A}}^{⁎}=-2\frac{v_2{w_2}^2{\mu }_h({\delta }_1{u}_1+{\delta }_0+{\mu }_h)(({\mu }_v+u_2)(2p-1)+p{\beta }_v)}{{\mathrm{\Lambda }}_h({\mu }_v+u_2)}<0.$$

This condition means that without the saturated treatment, system (1) constantly undergoes a forward bifurcation when ${\mathcal{R}}_0=1$. This means that malaria will permanently be eliminated when ${\mathcal{R}}_0<1$, that is, if the bed capacity of the hospital very high. Furthermore, if the parameters change and result in ${\mathcal{R}}_0>1$ but close to one, a small endemic will occur.

5. Optimal control problem characterization

In this study, the optimal control model aims to minimize the number of infected humans $I_h$ and infected mosquitos $I_v$ while maintaining the intervention costs for hospitalization $u_1$ and fumigation $u_2$ as much as possible.

The first step is to re-model the malaria autonomous model in system (1) by changing $u_1$ and $u_2$ as time-dependent variables, $u_1(t)$ and $u_2(t)$, respectively. Hence, the new model is given by :

$$\begin{array}{cc}\hfill \frac{d{S}_h}{dt}& ={\mathrm{\Lambda }}_h-\frac{{\beta }_h{S}_h}{p{I}_h+S_h}{I}_v-{\mu }_h{S}_h+(1-u_1(t)){\delta }_0{I}_h+u_1(t)({\delta }_0+\frac{{\delta }_1}{1+a{I}_h})I_h,\hfill \\ \hfill \frac{d{I}_h}{dt}& =\frac{{\beta }_h{S}_h}{p{I}_h+S_h}{I}_v-{\mu }_h{I}_h-(1-u_1(t)){\delta }_0{I}_h-u_1(t)({\delta }_0+\frac{{\delta }_1}{1+a{I}_h})I_h,\hfill \\ \hfill \frac{d{S}_v}{dt}& ={\mathrm{\Lambda }}_v-\frac{{\beta }_{v}p{I}_h}{p{I}_h+S_h}{S}_v-{\mu }_v{S}_v-u_2(t)S_v,\hfill \\ \hfill \frac{d{I}_v}{dt}& =\frac{{\beta }_{v}p{I}_h}{p{I}_h+S_h}{S}_v-{\mu }_v{I}_v-u_2(t)I_v.\hfill \end{array}\}$$ (10)

Our objective functional that should be minimized described as follows:

$$\mathcal{J}(u_1,u_2)=\underset{0}{\overset{t_f}{\int }}[c_1{I}_h(t)+c_2{I}_v(t)+\frac{1}{2}{b}_1{u}_1^2(t)+\frac{1}{2}{b}_2{u}_2^2(t)]dt.$$ (11)

The first two components in $\mathcal{J}$ describe the cost related to the high number of infected humans and mosquitoes, such as media campaign costs and educational programs in the community about malaria. The last two components in $\mathcal{J}$ are related to the cost of hospitalization and fumigation intervention, respectively. Here, we assume that the relative costs are in a nonlinear form, and quadratic costs form in the controls. Note that coefficients $c_1,c_2,b_1$, and $b_2$ are the balancing parameters for the size and importance of the objective functionals. We seek to find the optimal controls $u_1^{⁎}$ and $u_2^{⁎}$ that satisfy

$$\mathcal{J}(u_1^{⁎},u_2^{⁎})=\underset{\mathrm{\Omega }}{\min }\mathcal{J}(u_1,u_2),$$ (12)

where $\mathrm{\Omega }=\{(u_1,u_2)\in L^1(0,t_f)|u_i^{\min }\le u_i\le u_i^{\max },i=1,2\}$. $u_i^{\min }$ and $u_i^{\max }$ are the acceptable domains for control values related to the policymaker's capability to implement the malaria intervention program.

The necessary conditions for the optimal control problem are obtained from Pontryagin's maximum principle [25]. First, we construct the related Hamiltonian of our problem in the form of:

$$\mathcal{H}=I_h(t)+I_v(t)+\frac{1}{2}{b}_1{u}_1^2(t)+\frac{1}{2}{b}_2{u}_2^2(t)+\sum _{i=1}^4{z}_i{g}_i,$$ (13)

where $z_i$ is the costate variable, and $g_i$ is the right-hand side of the malaria model (10) for the ith state variables. Using the Pontryagin maximum principle, we have the following theorem:

Theorem 5

There exists an optimal control $u_1^{⁎}$ and $u_2^{⁎}$, and the corresponding state variables $S_h^{⁎},I_h^{⁎},S_v^{⁎},I_v^{⁎}$ such that the cost function $\mathcal{J}(u_1,u_2)$ is minimized over Ω. Given these optimal solutions, there exist costate variables $z_1(t),z_2(t),z_3(t)$, and $z_4(t)$ that satisfy

$$\begin{array}{cc}\hfill \frac{d{z}_1}{dt}& =\frac{p{\beta }_h{I}_h{I}_v}{{(p{I}_h+S_h)}^2}(z_1-z_2)+{\mu }_h{z}_1+\frac{p{\beta }_v{S}_v{I}_h}{{(p{I}_h+S_h)}^2}(z_4-z_3),\hfill \\ \hfill \frac{d{z}_2}{dt}& =-c_1+\frac{p{\beta }_h{S}_h{I}_v}{{(p{I}_h+S_h)}^2}(z_2-z_1)+({\delta }_0+\frac{u_1{\delta }_1}{{(a{I}_h+1)}^2})(z_2-z_1)\hfill \\ \hfill & +{\mu }_h{z}_2+\frac{p{\beta }_v{S}_v{S}_h}{{(p{I}_h+S_h)}^2}(z_3-z_4),\hfill \\ \hfill \frac{d{z}_3}{dt}& =\frac{p{\beta }_v{I}_h}{p{I}_h+S_h}(z_3-z_4)+(u_2+{\mu }_v)z_3,\hfill \\ \hfill \frac{d{z}_4}{dt}& =-c_2+\frac{{\beta }_h{S}_h}{p{I}_h+S_h}(z_1-z_2)+(u_2+{\mu }_v)z_4,\hfill \end{array}\}$$ (14)

with the transversality conditions

$$z_i(t_f)=0,i=1,2,3,4.$$ (15)

Furthermore,

$$\begin{array}{cc}\hfill u_1^{⁎}& =\min \{\max \{u_1^{\min },\frac{1}{b_1}\left(\frac{{\delta }_1{I}_h}{1+a{I}_h}\right)(z_1-z_2)\},u_1^{\max }\},\hfill \\ \hfill u_2^{⁎}& =\min \{\max \{u_2^{\min },\frac{1}{b_2}(S_v{z}_3+I_v{z}_4)\},u_2^{\max }\}.\hfill \end{array}\}$$ (16)

Proof

We assume that the cost function (11) is a convex function of $u_1$ and $u_2$, and the state system (10) satisfies the Lipchitz properties with respect to the state variables because the state solutions are bounded by $L^{\infty }$.

By taking $-\frac{d\mathcal{H}}{d{S}_h}$, $-\frac{d\mathcal{H}}{d{I}_h}$, $-\frac{d\mathcal{H}}{d{S}_v}$, and $-\frac{d\mathcal{H}}{d{I}_v}$, $\frac{d{z}_1}{dt}$, $\frac{d{z}_2}{dt}$, $\frac{d{z}_3}{dt}$, and $\frac{d{z}_4}{dt}$, respectively, in system (14). Furthermore, the costate system is equipped with the transversal condition ${\lambda }_i(t_f)=0$ for $i=1,2,3,4$. To find the optimal solution for $u_1$ and $u_2$, we differentiate $\mathcal{H}$ with respect to each control variable:

$$\begin{array}{cc}\hfill \frac{d\mathcal{H}}{d{u}_1}& =b_1{u}_1-\frac{{\delta }_1{I}_h}{1+a{I}_h}(z_2-z_1)=0,\hfill \\ \hfill \frac{d\mathcal{H}}{d{u}_2}& =b_2{u}_2-S_v{z}_3-I_h{z}_4=0.\hfill \end{array}\}$$

Solving the above equation with respect to $u_1$ and $u_2$ gave us:

$$\begin{array}{cc}\hfill u_1^{⁎}& =\frac{1}{b_1}\left(\frac{{\delta }_1{I}_h}{1+a{I}_h}\right)(z_1-z_2),\hfill \\ \hfill u_2^{⁎}& =\frac{1}{b_2}(S_v{z}_3+I_v{z}_4).\hfill \end{array}\}$$

Using standard variation arguments with the lower and upper bounds for $u_i$, we obtain the optimal solution in (16).  □

The optimal control problem in this article for the malaria eradication program consists of the state system (malaria model (1)) with the initial conditions given, the costate system (14) with the terminal conditions, and the control characterizations (16).

6. Numerical experiments

6.1. Sensitivity analysis

As discussed in Sections 3 and 4, the basic reproduction number in (3) for the malaria model (1) in Section 2 has an important role in determining the qualitative behavior of malaria dynamics. Therefore, it is reasonable to analyze the sensitivity of ${\mathcal{R}}_0$ with respect to the changes in the parameters of the model. This information is crucial not only for data assimilation, but also for experimental design as a scientific back-up before the implementation of malaria eradication policy in a community. Sensitivity analysis is a common method for determining the robustness of model predictions with respect to the values of the parameters. Several benefits can be achieved from sensitivity analysis, such as determining the relation of parameter changes to the model and knowing the model's most influential parameter. Knowing the most influential parameters for ${\mathcal{R}}_0$ will help policymakers choose their best strategies to eliminate malaria from the community. Therefore, in this study, we use a sensitivity analysis to discover the most influential parameter on the threshold ${\mathcal{R}}_0$.

Definition 1

(See [45]). The normalized forward sensitivity index of ${\mathcal{R}}_0$ with respect to a given parameter θ is defined as:

$${\mathcal{E}}_{\theta }^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial \theta }\times \frac{\theta }{{\mathcal{R}}_0}.$$

The values of the sensitivity indices for each parameter's values in Table 3 are presented in Table 4. The simulation is performed for two different baselines of the parameter value, namely, when ${\mathcal{R}}_0>1$ and ${\mathcal{R}}_0<1$. The positive or negative sign of ${\mathcal{E}}_{\theta }^{{\mathcal{R}}_0}$ in Table 4 determines whether the parameters have a positive or negative influence on ${\mathcal{R}}_0$. Therefore, it can be seen that ${\mathcal{R}}_0$ increases when ${\beta }_h,{\beta }_v,{\mathrm{\Lambda }}_v,{\mu }_h$, and p increases. In contrast, increasing the value of ${\mathrm{\Lambda }}_h,{\mu }_v,u_1,u_2,{\delta }_0$, or ${\delta }_1$ will reduce ${\mathcal{R}}_0$. It can be seen that ${\mathcal{E}}_a^{{\mathcal{R}}_0}=0$, which means that the saturated treatment parameter does not influence the magnitude of ${\mathcal{R}}_0$. However, as already explained in Theorem 4, a determines the existence of backward bifurcation of the malaria model in (1) at ${\mathcal{R}}_0=1$. Furthermore, the value of ${\mathcal{E}}_{\theta }^{{\mathcal{R}}_0}$ for each parameter describes the extent to which ${\mathcal{R}}_0$ changes if θ changes by 1%. For example, because ${\mathcal{E}}_{u_2}^{{\mathcal{R}}_0}=1.3548$, if $u_2$ increases by 1%, ${\mathcal{R}}_0$ decreases by 1.3548% for ${\mathcal{R}}_0>1$ and 1.726% for ${\mathcal{R}}_0<1$. Therefore, the most potentially controllable parameter that can be modified to control the magnitude of ${\mathcal{R}}_0$ is $u_2$, followed by ${\beta }_h,{\beta }_v,u_1$, and ${\delta }_1$, whereas the other parameters cannot be manipulated. According to this sensitivity analysis of ${\mathcal{R}}_0$, it is reasonable to use fumigation and hospitalization as the control variables, which will be analyzed next.

Table 3.

List of parameters value for system (1).

Parameters	Value/range	References	Parameters	Value/range	References
βv	$\frac{49.35}{365}$	[7]	μv	$\frac{1}{21}$	[45]
Λh	$\frac{100000}{70\times 365}$	Assumption	u1	[0,1]	Varying
Λv	$\frac{10000}{21}$	Assumption	δ0	$\frac{1}{180}$	[7], [8]
p	4	[7]	δ1	$\frac{1}{180}$	Assumption
μh	$\frac{1}{70\times 365}$	[44]	u2	[0,1]	Varying

Table 4.

Elasticity indices of ${\mathcal{R}}_0$ respect to parameters in malaria model (1) using parameters value in Table (3).

Sens. to θ	${\mathcal{R}}_0>1$	${\mathcal{R}}_0<1$	Sens. to θ	${\mathcal{R}}_0>1$	${\mathcal{R}}_0<1$
${\mathcal{E}}_{{\mathcal{R}}_0}^{{\beta }_h}$	1	1	${\mathcal{E}}_{{\mathcal{R}}_0}^{u_1}$	-0.0903	-0.0903
${\mathcal{E}}_{{\mathcal{R}}_0}^{{\beta }_v}$	1	1	${\mathcal{E}}_{{\mathcal{R}}_0}^{u_2}$	-1.0244	-1.3548
${\mathcal{E}}_{{\mathcal{R}}_0}^{{\mathrm{\Lambda }}_h}$	-1	-1	${\mathcal{E}}_{{\mathcal{R}}_0}^{{\delta }_0}$	-0.9033	-0.9033
${\mathcal{E}}_{{\mathcal{R}}_0}^{{\mathrm{\Lambda }}_v}$	1	1	${\mathcal{E}}_{{\mathcal{R}}_0}^{{\delta }_1}$	-0.0903	-0.0903
${\mathcal{E}}_{{\mathcal{R}}_0}^{{\mu }_h}$	0.9936	0.9936	${\mathcal{E}}_{{\mathcal{R}}_0}^p$	1	1
${\mathcal{E}}_{{\mathcal{R}}_0}^{{\mu }_v}$	-0.9756	-0.6452	${\mathcal{E}}_{{\mathcal{R}}_0}^a$	0	0

Fig. 1 show how fumigation and medical treatment effect ${\mathcal{R}}_0$. The larger the medical treatment and fumigation intervention, lesser the value of ${\mathcal{R}}_0$.

Figure 1.

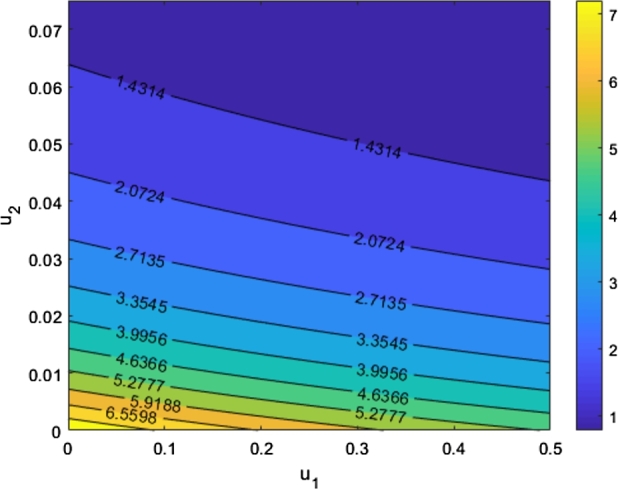
The graph shows the sensitivity of ${\mathcal{R}}_0$ to the changes of u₁ and u₂ while the other parameters remain fixed.

6.2. Backward and forward bifurcation

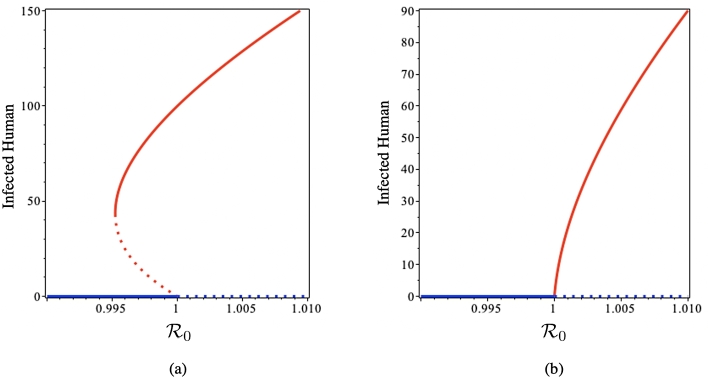
Fig. 2 illustrates the bifurcation diagram of system (1) using parameters value in Table 3. Using Theorem 4, we have $a^{⁎}=1/237$. Backward bifurcation occurs as illustrated in Fig. 2(a) using saturated parameter $a=1/143$. It can be seen that when ${\mathcal{R}}_0<0.995$, no endemic equilibrium point appears, while the disease-free equilibrium is stable. Hysteresis occurs in ${\mathcal{R}}_0=0.995$ when suddenly a new endemic equilibrium point appears, while the disease-free equilibrium still stable. When ${\mathcal{R}}_0$ starts getting larger than 0.995, two endemic equilibria exist; the smaller one is unstable, whereas the larger one is stable. In this interval, the disease-free equilibrium remains stable. Reaching ${\mathcal{R}}_0=1$, the large endemic equilibrium still exists and is stable, whereas the smaller one is extinct. At the same time, disease-free equilibrium became unstable. Fig. 2(b) show a forward bifurcation of system (1) when $a=1/250$. It can be seen that the disease-free equilibrium is stable when ${\mathcal{R}}_0<1$. Alteration of the disease-free equilibrium stability occurs at ${\mathcal{R}}_0=1$, while the endemic equilibrium starts to rise and grows concomitant with ${\mathcal{R}}_0$ getting larger.

Figure 2.

Backward (a) and forward (b) bifurcation diagram of system (1) using Theorem 4. Red and blue curves represent endemic and disease-free equilibria, respectively, whereas solid and dotted curves represent stable and unstable equilibria, respectively.

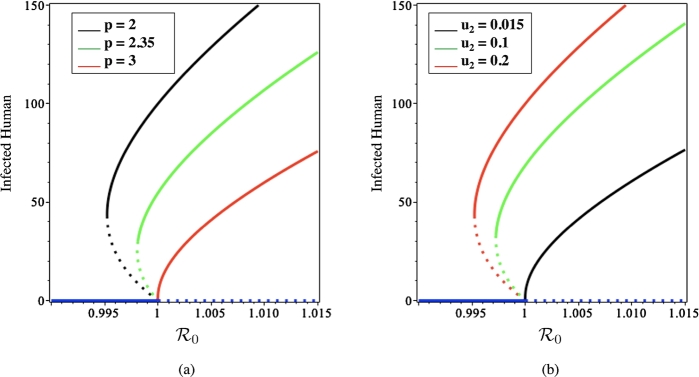
Next, we illustrate the discussion in Section 4 about the relation of $u_1,u_2$, and p on the existence of backward bifurcation of the system (1). Fig. 3 presents the effect of p and $u_1$ on the existence of backward bifurcation. It can be seen that when the vector bias increases, backward bifurcation is more likely to occur while increasing the fumigation rate, resulting in a greater likelihood of backward bifurcation.

Figure 3.

Bifurcation diagram of system (1) with using several values of p (a) and u₂ (b). The solid and dotted curves represent stable and unstable equilibrium, respectively.

6.3. Optimal control

6.3.1. Numerical method

We implement an iterative procedure to solve the boundary problem of our optimality system, which is described in Theorem 5. Let $x_i$ for $i=1,2,3,4$ denote $S_h,I_h,S_v$, and $I_v$ in system (10), respectively. The numerical computation method is given by the algorithm below [46]:

• (Step 1):

  Make an initial guess for $u_1$ and $u_2$ over $[0,t_f]$.

• (Step 2):

  While $\frac{\Vert x^{(k)}-x^{(k-1)}\Vert }{\Vert x^{(k)}\Vert }>\delta$, do step 3-5.

• (Step 3):

  Using the initial condition for state variable, solve state system (10) forward in time using a 4th-order Runge Kutta scheme.

• (Step 4):

  Using the transversality condition $\lambda (t_f)=0$ and the stored values for $u_i$ and $x_i$, solve the costate system (14) backward in time using a 4th-order Runge-Kutta scheme.

• (Step 5):

  Update $u_1$ and $u_2$ by entering new value for $x_i$ and $z_i$ into (16).

This algorithm can be explained as follows: First, we provide an initial guess for the control variables $u_1$ and $u_2$ for all $t\in [0,t_f]$, and then solve the state system (malaria model (10)) forward in time. Using the resulting values for the state and control variables, we calculate the costate variables by solving the costate system (14) for $t\in [0,t_f]$ backward in time using the transversality condition. Then, we update the control variables using optimality (16). This iterative process continues until it reaches the convergence criteria, which, in this case, the relative error between state variables is less than a specified value δ, that is, when $\frac{\Vert x^{(k)}-x^{(k-1)}\Vert }{\Vert x^{(k)}\Vert }<\delta$, where $\Vert \cdot \Vert$ is the $L^{\infty }$-norm.

To obtain meaningful optimal control profiles, a reasonable estimation of the weight parameters $c_1,c_2,b_1$, and $b_2$ is critical. In a balanced situation, we assume that:

$$c_1{I}_h\approxeq c_2{I}_v\approxeq b_1{u}_1^2\approxeq b_2{u}_2^2.$$

To conduct the simulation, we assume that the ratio between the human and mosquito populations is $10:1$. We assume that $N_h=100000$ and $N_v=10000$. Therefore, we have $\frac{c_1}{c_2}\approxeq \frac{I_v}{I_h}$. Taking $c_1$ as the baseline, we choose $c_1=1$. Furthermore, the medians of the maximum $I_h$ and $I_v$ are $50000$ and $5000$, respectively. Therefore, we have $c_2=10$. Furthermore, we assume that the control variables lie in the closed interval $[0,1]$. Using a similar approach, we find that $b_1$ and $b_2$ are $400000$.

6.3.2. Numerical examples

To conduct the numerical simulation for the optimal control problem in this section, we use the parameter values, as shown in Table 3 except for $u_1$ and $u_2$ that will be sought through simulation, the initial conditions used in the numerical experiment for the autonomous system in the previous section, and using the initial guess for $u_1=0.1$ and $u_2=0.01$ for $t\in [0,t_f]$.

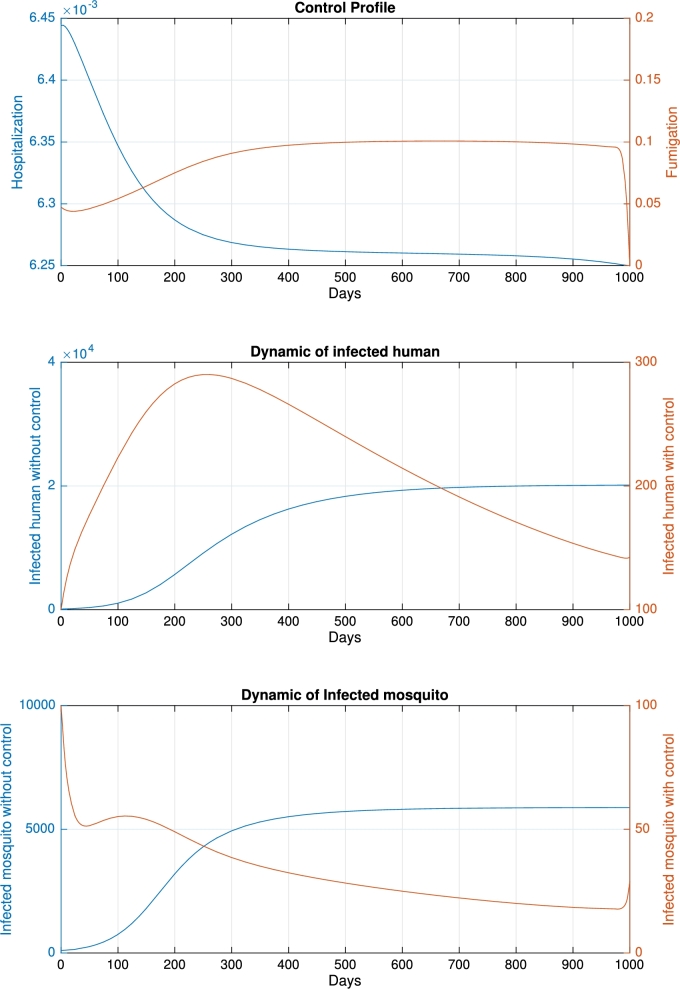
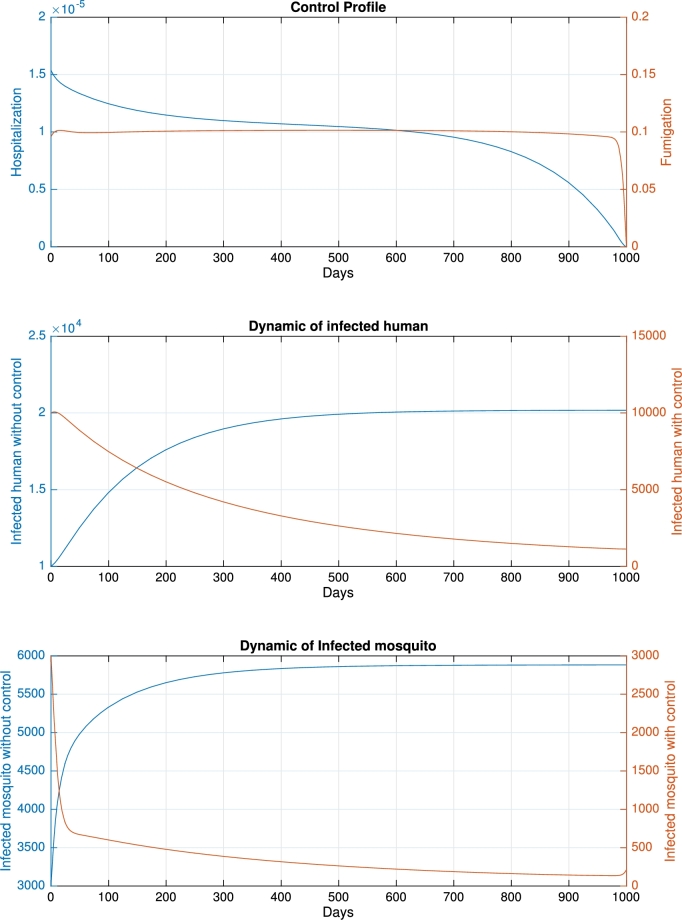
For the base-case when $(c_1,c_2,b_1,b_2)=(1,10,4\times {10}^5,4\times {10}^5)$ and the initial condition $(S_{h0},I_{h0},S_{v0},I_{v0})$$=(99000,1000,9900,100)$, we obtained the control profile shown in Fig. 4, with a cost function of $3.79\times {10}^3$. Without any intervention, the number of infected humans and mosquitoes increases over time and tends to reach an endemic equilibrium. To reduce the number of infected humans and mosquitoes, the profile of hospitalization monotonically decreased in response to decreasing trends in infected humans. In contrast, the profile of fumigation was almost constant due to a reduction in the number of mosquitoes. As a result, using the time-dependent control profile, the final number of infected humans and mosquitos is significantly reduced compared with a scenario when no control is implemented. The dynamics of infected humans increase at the beginning and then monotonically decrease after $t=240$. The dynamics of infected mosquitoes decrease rapidly at the beginning of the intervention period. In response to fumigation, the rate tends to reach zero. When the final time is close, the number of infected mosquitoes starts to rise again. In this scenario, $14054$ new infections in humans were avoided.

Figure 4.

Dynamic of control profile (top), infected human (middle), and infected mosquito (bottom) for the base-case.

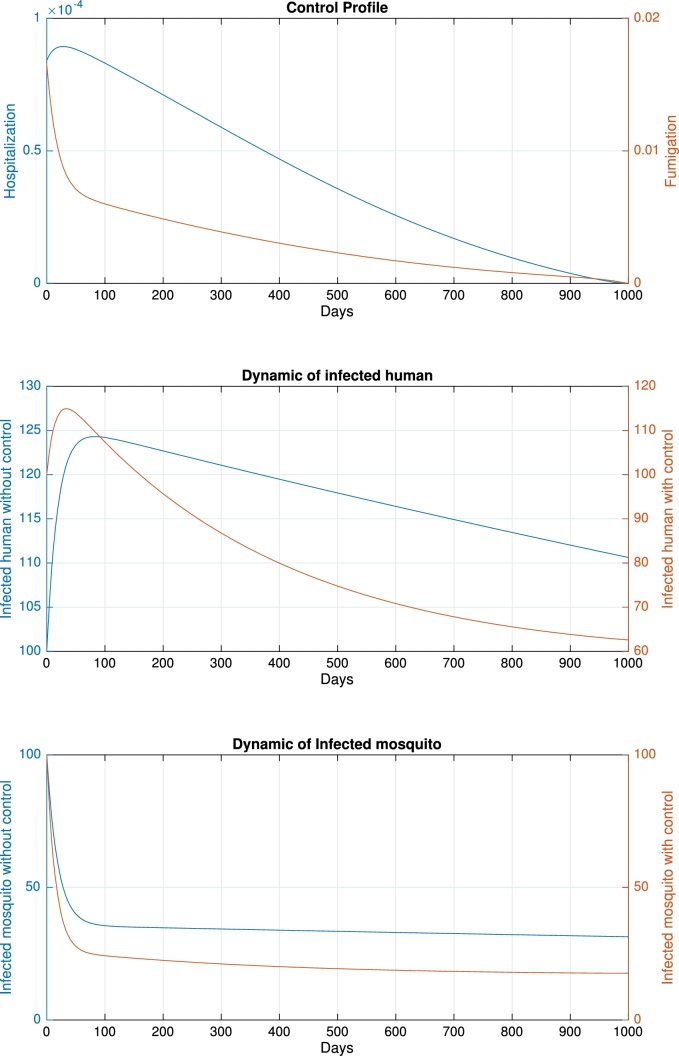
In the second scenario, we performed the simulation by changing the initial basic reproduction number when $t=0$. In the base case, we have ${\mathcal{R}}_0=7.84>1$, which indicates that the system will tend to the endemic equilibrium if no intervention is implemented. In the second case, we reduce ${\beta }_h,{\beta }_v$, and p to $7.05/365,24.675/365$, and 2, respectively. The other parameters remain the same as those in the base case. Consequently, we have ${\mathcal{R}}_0=0.98<1$, which indicates that the system will tend to be malaria-free even though no control is implemented. The numerical results for this scenario are shown in Fig. 5. In this scenario, the control profiles are almost monotonically decreasing for all simulation times following the dynamics of infected humans and mosquitoes. The maximum value of the control profile was also lower than that in the base case. Compared with the base case, which gives a functional cost of $3790$, in the second scenario, the cost function is only 298, which is less than 10% of the base case. Therefore, based on this simulation, we conclude that the cost of intervention is lower if the environment does not show the endemic's potential, which is indicated by the condition of the basic reproduction number that is less than unity.

Figure 5.

Dynamic of hospitalization, fumigation, infected human and infected mosquito when initial ${\mathcal{R}}_0$ when no control applied is less than unity.

In the third scenario, we performed an optimal control simulation for the endemic reduction scenario. In the base case, controls intend to prevent the endemic, which is indicated by the small number of infected humans and mosquitoes in the initial simulation time. In the third case, we change the initial condition to $(S_{h0},I_{h0},S_{v0},I_{v0})$$=(90000,10000,7000,3000)$ to describe a scenario when intervention is implemented “late” as the number of infected population is already high. The results of the endemic reduction scenario are shown in Fig. 6. It can be seen that the implementation of fumigation is almost constant at 0.1 for all simulation times. Because of the high cost of fumigation, the hospitalization rate is lower than in the base case. Because the infected population is already significant in the initial simulation time, and the high intensity of fumigation should be given for almost all simulation times, the cost function is substantial, which is $10935$, almost three times larger than that in the base case. From this simulation, we conclude that a control intervention should be provided at the early stage of infection in the community. Late intervention could end up at a high cost for the eradication of malaria in the community.

Figure 6.

Dynamics of hospitalization, fumigation, infected humans, and infected mosquitos for the endemic reduction scenario.

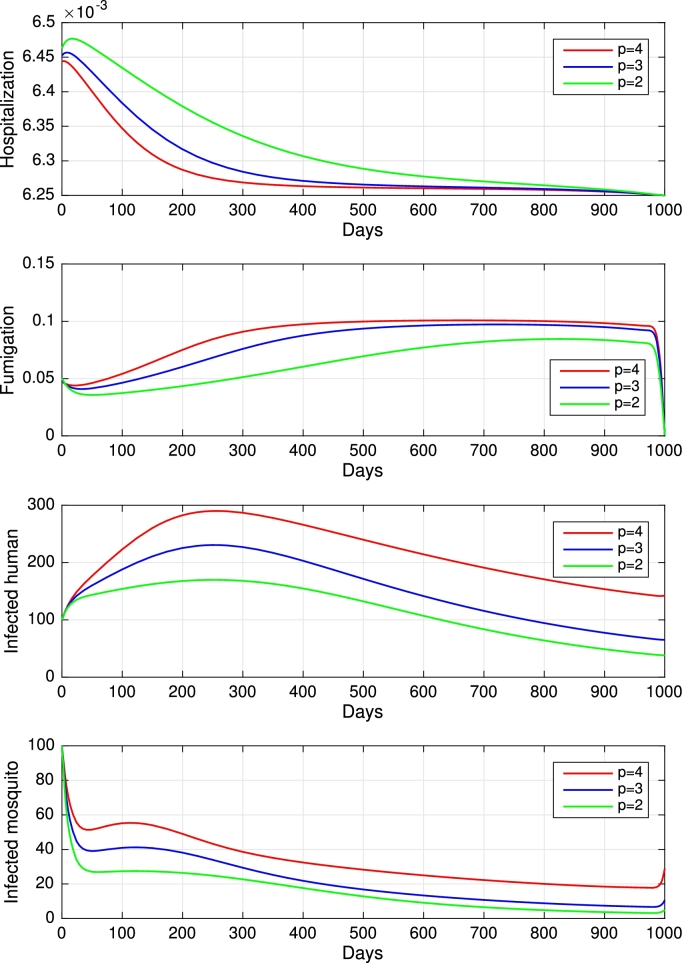
To study the effect of the vector bias on the control effort for malaria eradication, we computed the solutions of $u_1^{⁎}$ and $u_2^{⁎}$ for $p=4,3$, and 2, as shown in Fig. 7). Note that the basic reproduction number for each p is ${\mathcal{R}}_0(p=4)=7.84,{\mathcal{R}}_0(p=3)=5.88$, and ${\mathcal{R}}_0(p=2)=3.92$, which indicates that without intervention, malaria will persist in the population. The profile of the controls looks similar for each value of p. A larger p requires a higher rate of hospitalization and fumigation at all times t, which also gives a higher cost function value. For comparison, please see Table 5.

Figure 7.

Dynamics of hospitalization, fumigation, infected humans, and infected mosquitos for different values of p from top to the bottom, respectively.

Table 5.

Outcome of optimal control solution for different value of p.

Case	p = 4	p = 3	p = 2
${\mathcal{R}}_0$	7.84	5.88	3.92
Total Ih without control	14 200	13 660	11 100
Total Ih with control	216	155	116
Avoided new cases	14 200	13 444	10 984
Percentage of reduction	98.48%	98,42%	98,95%
$\mathcal{J}$	3 790	3 160	2 067

7. Discussion

According to the WHO [1], although the number of estimated malaria deaths saw a decline from 2017 to 2018, the number of new cases has been increasing during the same period. It is estimated that approximately 94% of all cases worldwide are in Africa. Therefore, malaria eradication represents an uphill task for the scientific community.

In this study, we proposed a mathematical model for malaria transmission, which accommodates important factors such as the effect of vector bias on fumigation and hospitalization success for the malaria eradication programs. We also consider the medical facility's limitation in treating infected individuals, such as the limitation of beds in the hospital or limitations with regard to the number of medical staff. Furthermore, the effect of the budget constraints for intervention is also discussed as an optimal control problem to find the optimal intervention for malaria eradication.

From the mathematical analysis, the existence and local stability of all equilibria points were rigorously analyzed, and their relation to the basic reproduction number was shown. We find that a stable disease-free equilibrium point always exists if the basic reproduction number is smaller than unity. Conversely, the malaria endemic equilibrium point always exists and is stable if the basic reproduction number is larger than unity. A backward bifurcation may occur if the hospital's bed capacity or the number of medical staff is sufficiently small. This backward bifurcation phenomenon allows for the existence of a large endemic equilibrium even when the basic reproduction number is smaller than unity. In biological terms, these results mean that the basic reproduction number, as one of the most used thresholds in many epidemiological models, can no longer describe the success of malaria eradication efforts. Furthermore, bistability phenomena occur under these circumstances. From the bifurcation threshold analysis, we find that increasing fumigation increases the probability of backward bifurcation. In biological terminology, our results indicate how fumigation may trigger a condition of the existence of malaria disease even though the basic reproduction number is already smaller than unity. Interestingly, a larger vector bias reduces the probability of the appearance of backward bifurcation. The existence of a backward bifurcation in the malaria transmission model is an interesting phenomenon because the disease can no longer be eradicated by relying only on the effort to reduce the basic reproduction number. Our analytical results show that an uncontrolled fumigation intervention could lead to a backward bifurcation phenomenon, which could be the reason why malaria is still endemic in many countries that focus more on fumigation than on other interventions [1].

Sensitivity analysis of the basic reproduction number implies that fumigation is the most influential parameter if the policymaker wants to reduce the basic reproduction number. Another significant intervention is the reduction in the infection parameter, for example, by the use of mosquito repellents or bed-nets. Our model simulations demonstrated that the total number of avoided new cases can be increased by using an adaptive control intervention based on the number of current infected humans and mosquitoes. We also observed that the cost of intervention increases if the vector bias parameter increases. All simulations conducted in the numerical experiments indicate that hospitalization should be provided in a high proportion at the beginning and should decrease as time passes. In contrast, the fumigation rate should be implemented slowly as the simulation time starts and remains constant until the end of the intervention.

Our model has some limitations. We have ignored several factors in malaria transmission, such as relapse, recrudescence, and reinfection. We also acknowledge that many of our parameters are based on the citations provided by other authors. Therefore, more data and reliable parameters will improve the results of this study.

Declarations

Author contribution statement

D. Aldila: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper. M. Angelina: Performed the experiments; Analyzed and interpreted the data.

Funding statement

This work was supported by Indonesian RistekBRIN with PDUPT research grant scheme (ID Number: NKB-159/UN2.RST/HKP.05.00/2021), 2021.

Data availability statement

No data was used for the research described in the article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.