SWIFT-Active Screener: Accelerated document screening through active learning and integrated recall estimation

Abstract

Background:

In the screening phase of systematic review, researchers use detailed inclusion/exclusion criteria to decide whether each article in a set of candidate articles is relevant to the research question under consideration. A typical review may require screening thousands or tens of thousands of articles in and can utilize hundreds of person-hours of labor.

Methods:

Here we introduce SWIFT-Active Screener, a web-based, collaborative systematic review software application, designed to reduce the overall screening burden required during this resource-intensive phase of the review process. To prioritize articles for review, SWIFT-Active Screener uses active learning, a type of machine learning that incorporates user feedback during screening. Meanwhile, a negative binomial model is employed to estimate the number of relevant articles remaining in the unscreened document list. Using a simulation involving 26 diverse systematic review datasets that were previously screened by reviewers, we evaluated both the document prioritization and recall estimation methods.

Results:

On average, 95% of the relevant articles were identified after screening only 40% of the total reference list. In the 5 document sets with 5,000 or more references, 95% recall was achieved after screening only 34% of the available references, on average. Furthermore, the recall estimator we have proposed provides a useful, conservative estimate of the percentage of relevant documents identified during the screening process.

Conclusion:

SWIFT-Active Screener can result in significant time savings compared to traditional screening and the savings are increased for larger project sizes. Moreover, the integration of explicit recall estimation during screening solves an important challenge faced by all machine learning systems for document screening: when to stop screening a prioritized reference list. The software is currently available in the form of a multi-user, collaborative, online web application.

1. Background

Systematic review is a formal, sequential process for identifying, assessing, and integrating the primary scientific literature with the aim of answering a specific, targeted question in pursuit of the current scientific consensus. This approach, already a cornerstone of evidence-based medicine, has recently gained significant popularity in several other disciplines including environmental health. It has been estimated that more than 4,000 systematic reviews are conducted and published annually (Bastian et al., 2010), and while the precise time commitment can vary depending on the subject matter and protocol, reviews often require a year or more to complete (Ganann et al., 2010, Borah et al., 2016). Due to the large investment of resources necessary to develop and maintain a systematic review, there has been considerable recent interest in methods and techniques for using machine learning and automation to make this process more efficient (Tsafnat et al., 2014). Significant progress has been made by our team and others in applying these techniques to various steps of systematic review including problem formulation (Howard et al., 2016), document screening (Wallace et al., 2012b; O’Mara-Eves et al., 2015), and risk-of-bias assessment (Marshall et al., 2015).

In the screening phase of systematic review, researchers use detailed inclusion/exclusion criteria to decide whether each article in a set of candidate articles is relevant to the research question under consideration. For each article examined, a researcher reads the title and abstract and evaluates its content with respect to prespecified inclusion criteria. A typical review may require screening thousands or tens of thousands of articles. For example, we have analyzed the screening times used to screen 391,613 abstracts for 749 distinct projects in Active Screener. The mean screening time per abstract was 35 s, with a standard deviation of 79 s. Under the assumption that it takes a skilled reviewer 30–90 s, on average, to screen a single abstract, dual-screening a set of 10,000 abstracts may require between 150 and 500 h of labor.

In recent years, considerable research has been conducted to assess the potential benefits of using machine learning to classify and/or prioritize documents during the screening phase of systematic review. For a review of some recent efforts see O’Mara-Eves et al. (2015). A common result of this research is that, in theory, it is possible to achieve significant time savings when screening a machine prioritized list instead of a randomly ordered list. Our own research, for example, has led to the creation of the SWIFT-Review software application which includes functionality that can be used to rank order documents using an appropriate training set (Howard et al., 2016). We have shown that by using SWIFT-Review, users can potentially reduce the total number of articles screened by 50% or more, provided that they are willing to trade a small reduction in recall for the reduced effort. However, there are a two practical limitations that limit the adoption of SWIFT-Review and similar machine learning tools for the purpose of reference screening during systematic review.

The first limitation shared by SWIFT-Review and other systems based on “traditional” machine learning is that they require a large training set for purposes of article prioritization. This can be problematic in many real-world settings. In contrast, the technique of active learning, in which the machine learning model is not trained only once, but repeatedly, in response to user feedback, eliminates the requirement for an initial training set (Settles, 2010). Variants of this active learning approach for document screening have been tested previously in several research scenarios (Wallace et al., 2010a, 2010b; Wallace and Small, 2011; Wallace et al., 2012a; Miwa et al., 2014; Mo et al., 2015; Rathbone et al., 2015). Probably the first example of such a system is “abstrakr” by Byron Wallace and colleagues (Wallace et al., 2012b). This system has had an important influence on our work; however, unfortunately, that system does not appear to be under active development or maintenance. Another popular document screening system, DistillerSR has recently added machine learning, but as far as we can tell (the methods are not published), it does not use active learning. EPPI-Reviewer, a software system for systematic review (Thomas et al., 2010), notes on its website that some form of machine-learning based document prioritization is available by request, but is not yet generally available. The Raayan software (Khabsa et al., 2016), also appears to use active learning to rank documents during screening, via a 5-star system, but they do not support integrated recall estimation. We are not aware of other active learning systems for document screening that are currently in widespread usage.

The second limitation shared by all of the above systems, including those using active learning, is that while they are able to produce an efficient ordering of the articles, it is usually not clear to the user how many articles need to be screened in order to create a comprehensive systematic review. For example, it might be possible to rank the documents such that 95% of the relevant documents occur within the top 25% of the ranked list. This could (ideally) result in a 70% reduction in the number of screened articles. The practical problem, however, is that unless one knows the true number of included articles in the entire list of candidates, it is impossible to calculate the level of recall achieved after screening the top 25% of the list. Thus, users can never be sure at exactly what point they should stop screening. Hence, to solve this “when to stop” problem, we need a method to accurately estimate the recall at each position in the ranked list. This estimate could then guide the decision of where to set the threshold to stop screening.

In general, solutions to this problem have fallen into three categories:

• Heuristic/classification approach. In this scenario, researchers solve the problem by using some non-probabilistic method or heuristic to decide where to set the threshold to stop screening. The most common approach is binary classification. Generally, the researchers design a classifier (e.g. support vector machine) that is intended to handle the problems of a) class imbalance and b) unequal cost of misclassifying positive and negative instances. Then they demonstrate that the classifier achieves a desirable level of recall on a small number of test data sets. A problem with this method is that it does not ensure a given level of recall on a new dataset nor does it attempt to assess the level of recall actually achieved on a new dataset. There is nothing built into the classifier that should make us expect any particular level of performance on future datasets. We are asked to simply trust that future performance will be similar to past performance. Publications discussing this approach include: Yu et al. (2008); Wallace et al. (2010c); Wallace et al. (2012a); and Wallace et al. (2012b).

• Sampling-based method. Other researchers have taken an approach that involves simple random sampling to assess the level of recall achieved. In other words, at some possible stopping point, the method chooses a finite number of additional documents for screening, sampled at random, in order to estimate the number of relevant documents remaining in the unscreened dataset. Although this method can provide some statistical assurances, it can also have a very high cost in terms of additional screening, especially when the inclusion rate is low. In addition, it doesn’t necessarily answer the question “when to stop” screening, but rather once one has stopped, “was it really ok to stop and did I miss anything?”; publications discussing this approach include Thomas and O’Mara (2011) and Shemilt et al. (2013).

• Ignore or side-step the problem. In by far the most common approach, researchers use a classifier to produce a ranked list and then report WSS or area under a receiver operating characteristic (ROC) curve to show that high recall can be achieved at the beginning of the list, that is, if you were to somehow know when to stop. In this case, the results demonstrate theoretically that document prioritization can be beneficial, but leave open a key question critical for practical usage. There are many examples of research from this category, including our own recent work (Cohen, 2006; Cohen et al., 2006; Martinez et al., 2008; Cohen et al., 2010; Matwin et al., 2010; Wallace et al., 2010a, 2010b; Cohen, 2011; Wallace and Small, 2011; Kim and Choi, 2012; Jonnalagadda and Petitti, 2013; Miwa et al., 2014; and Howard et al., 2016).

Here we introduce SWIFT-Active Screener, a web-based, collaborative systematic review software application which uses a variant of active learning called certainty-based sampling to efficiently prioritize articles for screening, eliminating the need for an initial seed. The software also incorporates a novel recall estimation method that is in a somewhat different category than previous systems, though it combines elements of the first two. It uses a robust statistical model and a retroactive sample to estimate the number of remaining relevant documents. Similar to the “heuristic” approaches described above, it also ascribes some of its justification from its observed performance on a large number of benchmark datasets. In this research, we describe these methods in detail and then investigate their performance using 26 diverse systematic review datasets that were previously screened by reviewers.

2. Methods

2.1. Datasets

We evaluated Active Screener’s active learning method for document prioritization as well as its novel recall estimation method using several systematic review datasets that were previously screened by reviewers (Table A.1). Twenty of these datasets are described in detail in Howard et al. (2016) and consist of lists of included and excluded titles and abstracts from several sources: the National Toxicology Program (NTP) Office of Health Assessment and Translation (OHAT), the Edinburgh CAMARADES group (Collaborative Approach to Meta-Analysis and Review of Animal Data from Experimental Studies), and datasets previously published in Cohen et al. (2006). As indicated in the “Label Type” column of Table A.1, 2 of these 20 datasets use as their label the “inclusion” status that resulted from title and abstract screening, while the others use final results obtained after full-text screening. In the case of full-text datasets, only the title and abstract (and not the reference full text) are used for training and evaluation. To supplement these datasets, we also added several additional new datasets obtained from various collaborators and early adopters of the Active Screener software. These include the “Mammalian” dataset from the Evidence-Based Toxicology Collaboration (EBTC) at the Johns Hopkins Bloomberg School of Public Health and 5 datasets, USDA1 - USDA5, from the United States Department of Agriculture. The study topics for these additional datasets have been obfuscated at the request of the associated organizations. All of these 6 new datasets (which unfortunately we cannot share at this time due to government restrictions) use title/abstract screening results as the label.

2.2. Log-linear model for document prioritization

The underlying machine learning model used by SWIFT-Active Screener is equivalent to the one previously described in Howard et al. (2016). Briefly, we use bag-of-words encoding for titles, abstracts and any available MeSH terms. All word counts are normalized using term frequency, inverse document frequency weightings (tf-idf). The resulting features and corresponding labels (“included” or “excluded”) for each abstract in the training set are then used to fit an L2-regularized log-linear model. Unlabeled documents are mapped to the same feature space and the model is used to score each unlabeled document according to its estimated probability of relevance.

2.3. Active learning

The paradigm of active learning (Settles, 2010; Wallace et al., 2010c) incorporates real-time feedback from human screeners, regularly rebuilding the underlying machine learning model and reprioritizing the documents as additional references are labeled by the screeners. There are several different approaches that can be used during each round of model-building to determine which documents will be screened next. For example, in some scenarios it might be advantageous to ask screeners to screen the most “ambiguous” documents first (uncertainty sampling) in order to obtain additional information about these problematic documents. In the context of systematic review, datasets are typically highly unbalanced with included items in the minority. In this scenario it has been shown that certainty sampling, which biases sampling towards the documents that are predicted to be most relevant, allows screeners to most efficiently identify the majority of the relevant documents (Miwa et al., 2014).

The active learning model used by Active Screener, which is an example of certainty-based screening, operates as follows. After creating an initial document ordering, either by randomizing the list or using an initial regularized log linear model created from a small initial training set (or “seed”), articles are presented to human screeners following that order. Screening proceeds in “batches” of a fixed size, n (here n = 30). After each set of n articles has been reviewed, the model is retrained using all previously screened articles, and the remaining articles are then re-sorted according to this revised model. In this way, the predictions for relevance are updated every 30 documents to incorporate feedback from users as screening continues.

2.4. Recall estimation

Here we describe a simple statistical method to estimate recall given a ranked list of references. We assume that a screener begins screening at the head of the list, sequentially providing a label to each item: “Included” or “Excluded.” We are interested in estimating when the screener has achieved a given level of recall (say, 95%) so that s/he can stop screening and realize the benefits of document ranking (while also retaining confidence that most of the relevant documents have been discovered).

The method works by examining the lengths of consecutive spans of excluded documents that occur between each relevant document during screening. The lengths of these spans provide a basis for estimating the local probability of document relevance. If documents were screened in random order, these span lengths would follow a geometric distribution with a rate (“success probability”) reflecting the underlying frequency of relevant (included) documents in the reference list. Similarly, if we consider the spans between a set of more than two consecutive included documents, then the total span length, a sum of independent geometric random variables, would follow the negative binomial distribution. Therefore, the observed span lengths of excluded documents can be used to estimate the underlying rate parameter for included documents. This rate can then, in turn, be used to estimate the number of relevant documents remaining in the unscreened document list. In practice, as the screener proceeds through the ranked list of references, the gaps between relevant documents will tend to increase in length, because, by design, the ranked lists are front-loaded with relevant documents. In other words, while the negative binomial distribution assumes that “successes” are independently and randomly distributed, in this setting, the success rate should be decreasing (rather than fixed or increasing). As a result, this method tends to result in a conservative estimate of recall. That is, the obtained true recall is often slightly higher than its estimated value.

This algorithm has one “tuning” parameter which we call “lookback,” denoted by δ. This parameter determines the number of spans considered when estimating the inclusion rate. We total up the span distance, D, (in number of documents) between the current screening position and the δ^th previously included document. If the inclusion rate for remaining documents is p, and supposing (hypothetically) that documents were sampled randomly for screening, then

$$D~\text{NegBin}(\delta ,p)$$

With this information, estimated recall is calculated based on $\widehat{p}$ as follows:

$$\mathit{\text{Estimated\hspace{0.17em}Recall}}=\frac{TP}{TP+\widehat{p}\times U}$$

where $\widehat{p}$ is an estimate of p based on the observed D, TP is the number of relevant documents identified so far by the screener, and U is the number of remaining unscreened documents.

2.5. Simulated screening framework

In order to evaluate the proposed methods with previously screened datasets, we must “simulate” the screening process “in silico.” We used the following framework to simulate user screening, subject to active learning. For scenarios in which no initial training seed is available, we begin by randomly shuffling the documents (i.e. titles and abstracts from one of the datasets described in Section 2.1) to achieve a random ordering; if the scenario does use a training seed, we instead build an initial log-linear model and use it to sort the remaining documents. We then proceed through a series of active learning “cycles,” each of length n = 30 documents, as follows. For cycle, c, the first cn labeled (“screened”) documents in the current ordered document list are used to train a new log-linear model that is then used to reorder the remaining unlabeled (“unscreened”) documents in the list. The cn documents at the head of the list are not reordered. This procedure continues until the entire set of documents has been processed. At the end of this exercise, we have simulated screening the entire set of documents using the same active learning procedure employed by SWIFT-Active Screener, but without human screeners. The final document list reflects the simulated screening order and this list, along with the manually assigned labels available in the dataset, can be used to compute various evaluation metrics of interest.

2.6. Evaluation metrics

Given an ordered list of labeled documents from a simulated screening experiment (Section 2.5), we can compute the following evaluation metrics.

2.6.1. Recall

Recall (or sensitivity) is the percentage of truly relevant documents discovered during screening. If all available documents are screened, recall should be 100%. However, if only a portion of the available documents is screened, then recall might be less than 100%. Recall is computed as

$$(\mathit{\text{True}})\mathit{\text{\hspace{0.17em}Recall}}=\frac{TP}{TP+FN}$$

where TP denotes true positives and FN denotes false negatives (contingent on the threshold at which screening stops).

In this manuscript we also make a distinction between “estimated recall,” which is a predicted recall computed according to the method described in Section 2.4, and “true recall” which can be computed using the equation above (but only if TP and FN are known, as is the case with a gold standard test dataset in which all documents have been screened). Given the final ordering of documents from the simulation, both estimate recall and true recall can be computed at each possible stopping threshold.

2.6.2. WSS

The “Work Saved over Sampling” (WSS) performance metric (Cohen et al., 2006) defines, for a desired level of recall, the percent reduction in effort achieved by a ranking method as compared to a random ordering of the documents. Specifically,

$$WSS@R=\frac{TN+FN}{N}-(1.0-R)$$

where TN denotes true negatives, N denotes the total size of the dataset, and R is the desired level of recall. The maximum possible WSS score of a perfectly ordered list (all included references at the beginning) approaches 1 as the percentage screened approaches 0, indicating a theoretical 100% reduction in screening burden. A WSS score of 0 or less indicates that random ordering would be just as effective or more effective than priority ranking.

The value TN + FN is equal to the total number of documents not screened. In this manuscript we make a distinction between “theoretical WSS,” which is computed using the values of TN and FN observed at the point where the true recall equals R and “obtained WSS,” which uses values of TN and FN observed at the point where the estimated recall equals R.

2.6.3. Percentage documents screened

This can be computed as

$$\mathit{\text{PercentageScreened}}=\frac{TP+FP}{N}$$

where FP denotes false positives.

2.6.4. Cost

“Cost” reflects the extra percentage of documents screened in order to obtain a given level of estimated recall.

$$\mathit{\text{Cost}}=\mathit{\text{PS\_Obtained}}-\mathit{\text{PS\_Theory}}$$

where

PS_Theory = Percentage documents screened to obtain the desired theoretical WSS@R

PS_ Obtained = Percentage documents screened to obtain the corresponding obtained WSS

2.7. Simulated score distributions

In Section 2.5, we described how we can use previously screened datasets to simulate the screening process “in silico.” Here, we describe how we can use these previously screened datasets to generate new hypothetical, simulated datasets with various desired properties. We can then use these datasets to further evaluate various features of the recall estimation method in a controlled manner. The following approach was used to generate hypothetical ranked document lists with specific desired properties. For four of the large datasets in Table A.1 (PFOA/PFOS and immunotoxicity; Bisphenol A (BPA) and obesity; Transgenerational inheritance of health effects; and neuropathic pain), we trained a regularized log linear model as previously described using a randomly selected seed containing 15 included and 15 excluded items (a modest seed size that is often reasonable in real reviews). This machine learning model was then used to rank the remaining documents. We then used kernel density estimation to characterize the distribution of the resulting ranking scores (i.e. inclusion probabilities according to the model) in each dataset, conditional on the Included/Excluded document label.

Given these results, we can now simulate randomized ranked lists of inclusion statuses arising from the same conditional score distributions, but with user-specified a) inclusion probability and b) total number of documents. We take this approach because it is expected that the overall inclusion rate and the total number of documents to screen may have an important impact on the success of our recall estimation method, and optimal choice for the lookback parameter, δ.

3. Results

3.1. Performance of active learning prioritization

Table A.2 shows the results of screening experiments simulated as described in Section 2.5 using the 26 available datasets. For these experiments, we used a seed size of 0 (to simulate screening with no prior training set) and a look back, δ, of 2 (which was shown to be a reasonable choice in preliminary work using simulated data). Metrics shown represent the average scores over 30 trials, after randomizing the initial ordering of the documents prior to each trial.

The datasets are sorted in the table as a decreasing function of the total number of documents available. The overall average WSS@95 obtained was 34%. As shown in Fig. A.2, the performance (obtained WSS@95) generally increases as a function of the total number of documents. For example, if we exclude the 9 datasets with fewer than 1,000 total documents, the average WSS@95 obtained increases to 41%; in document sets with 5,000 or more documents, the average WSS@95 obtained increases further to 61%. The overall WSS@95 across all datasets sets is 55%, if we weight each WSS score according to the total number of documents in the corresponding dataset.

Using the data in Table A.2, the overall theoretical WSS@95 is 51%. The difference between this percentage and the overall average WSS@ 95 obtained (34%) reflects the additional cost of estimating the recall, which generally requires screening additional documents to estimate the inclusion rate retroactively.

3.2. Performance of the recall estimate

Table A.2 also displays the true recall obtained for each simulation. In all cases, the target estimated recall was 95%. For the simulations in Table A.2, the median obtained recall was 99%, confirming our assertion that the estimated recall tends to be conservative, on average. For 23 out of 26 datasets, the obtained recall was greater than or equal to 95%. The lowest recall obtained in any of the simulations was for the dataset “atypical antipsychotics,” in which the true recall was 91.5%. As shown in Fig. A.3, a violin plot of the obtained true recall values, the performance on this dataset is an outlier.

3.2.1. Simulated score distributions

To investigate the effect of various variables on the performance of the recall estimation method, we next used the approach described in Section 2.7 to estimate the conditional score densities for four of the large datasets after ranking by machine learning. Fig. A.4 shows the score density estimates for each original dataset, along with score densities resulting from a corresponding simulated dataset. As expected, the simulated densities are similar in appearance to the original score densities.

In Fig. A.5, we illustrate the performance of the recall estimation algorithm using ranking scores simulated from the four original datasets. For each simulation, the inclusion rate parameter and length parameter were kept the same as actually observed in the original source dataset. For the PFOS/PFOA and BPA datasets we used δ = 2 and for the Transgenerational and Neurological Pain datasets we used δ = 5. The x-axis shows the total number of documents screened and the y-axis is recall. The red line shows the true recall rate as a function of the number of documents screened. The dotted horizontal green line is drawn at 95% recall, and the dotted vertical black line indicates the number of documents that must be screened to achieve this recall rate. The black circles show the estimate of recall, using the method described above, computed at each included item. As expected, the recall estimate is generally conservative, lying below the red line. However, this estimate improves as we travel down the ranked list and the local inclusion probability begins to stabilize. The red triangles represent the local inclusion rate (the number of included documents per bin / bin size, for bins of length 5% total documents screened.) In general, the inclusion rate is non-increasing (except for a small bump in the Neuropathic Pain dataset) and flattens out as more documents are screened. This indicates that our ranking algorithm (used to create the original score distributions) is placing the included items at the top of our list. Finally, the solid blue vertical line indicates the point at which the recall estimate hits 95%. The distance between the blue line and the dotted black line is the “cost” associated with this estimate (as compared to the ideal scenario where we could perfectly predict where to set the classification threshold).

Table A.3 shows the costs associated with setting the screening threshold based on the recall estimates in Fig. A.5. For example, if we had used this algorithm with δ = 5 to determine the point at which to stop screening the Transgenerational dataset in order to achieve an estimated 95% recall, then we would have incurred a cost of 3.3% WSS (0.349–0.316) compared to halting at the true 95% recall. At the stopping threshold, the obtained true recall would actually be 95.9%.

3.2.2. Effect of list length

In Table A.4, we show the cost resulting from several simulations using the BPA score distribution. For each simulation, the overall inclusion rate was set at p = 0.15 and the lookback, δ = 2. Using these parameters, we simulated ranked lists of various lengths. Resulting costs are averaged over 5 trials. As shown in the table, longer lists are associated with smaller costs. This is because, for a given local inclusion rate, there is a fixed number of documents that must be screened in order to achieve a good estimate of that rate. As the list length increases, this fixed number becomes smaller as a fraction of the total screening burden.

3.2.3. Effect of inclusion rate

Table A.5 shows the effect of the overall inclusion rate, p, on the cost. For each simulation, the list length was fixed at 10,000 documents and the lookback, δ = 2. Resulting costs are averaged over 5 trials. In general, the smaller the overall inclusion rate, the greater the cost. In order to estimate a small inclusion rate, it is necessary to screen more documents, which in turn increases the cost.

3.2.4. Effect of lookback δ

Table A.6 shows the effect of systematically varying the lookback, δ, on data simulated from the neuropathic pain dataset. For these experiments, list length was fixed at 30,000 and the inclusion rate, p, was set to 0.17. The resulting costs were averaged over 5 trials. The table shows that, in general, cost is an increasing function of δ. Note, that for δ = 1 and δ = 2, the cost was actually negative, indicating that the obtained true recall is actually below the targeted 95%. Hence, choosing δ values that are too small can lead to underestimating the recall.

Fig. A.6 illustrates the relationship between the variability of the recall estimate (and the corresponding cost) and the δ parameter. In Panel (a) δ = 1 and in Panel (b) δ = 100. Notice the dramatically decreased variability in the recall estimate for the higher value of δ. In general, increasing δ decreases the variability of the recall estimate. Hence, there is a trade-off between variability of cost and the expected value of cost. Ignoring variability, the optimal setting for δ, is, ideally, the smallest value such that the expected cost is non-negative. In general, larger δ may be ideal when p is larger. Conversely, when p is very low or the list is short, it may not be advisable to use a large δ.

3.3. Active screener application

The methods described in this manuscript have been operationalized in the form of SWIFT-Active Screener (Fig. A.1), a web-based, collaborative systematic review software application. Active Screener was designed to be easy-to-use, incorporating a simple, but powerful, graphical user interface with rich project status updates. The application uses the active learning methods described in this manuscript to save screeners time and effort by automatically prioritizing articles as they are reviewed, using user feedback to push the most relevant articles to the top of the list. Meanwhile, the recall estimation method estimates the number of relevant articles remaining in the unscreened document list. Together, the combination of the two methods allows users to screen relevant documents sooner and provides them with accurate feedback about their progress. Using this approach, the vast majority of relevant articles can often be discovered after reviewing only a fraction of the total number of articles. SWIFT-Active Screener is available at https://www.sciome.com/swift-activescreener/.

In addition to machine learning, Active Screener also includes all of the critical features needed to conduct the screening phase of a systematic review. For example, the application includes facilities for progress reporting and monitoring, reviewer conflict resolution, complex questionnaires, bulk upload of full text documents, and support for all the major bibliographic reference file types.

4. Discussion

SWIFT-Active Screener (or simply “Active Screener,” see Fig. A.1) is an improvement of our previous method for article prioritization which we have earlier shown to theoretically reduce by more than 50% the human effort required to screen articles for inclusion in a systematic review (Howard et al., 2016), and which we have made available in the form of a software application called SWIFT-Review (https://www.sciome.com/swift-review/). This software has enjoyed widespread usage, especially from users in the community of environmental health. However, this approach to literature prioritization suffers from several important limitations in the context of systematic review: (1) the software requires a large initial training set (or “seed”) to build the underlying statistical model; (2) the software does not have a facility for estimating the recall of included documents, so it is not always clear to users when they should stop screening a prioritized document list; and (3) the software is a single-user desktop application, which limits its applicability to large-scale, collaborative screening efforts. To address these limitations, SWIFT-Active Screener uses the combination of a new active learning-based document prioritization model along with a novel recall estimation model to help users to find relevant documents sooner and provide them with accurate feedback about their progress. This can potentially result in significant time and cost savings, especially for large projects.

Using a simulation involving 26 diverse systematic review datasets that were previously categorized manually by reviewers, we have evaluated both the document prioritization and recall estimation models of Active Screener. On average, 95% of the relevant articles were identified after screening only 40% of the total reference list. In the 5 document sets with 5,000 or more references, 95% recall was achieved after screening only 34% of the available references, on average. Note, however, that it is not currently possible to predict exactly how much screening can be saved when screening a specific dataset. Specific results are a function of the size of the dataset, the relative percentage of relevant/not relevant articles, and the inherent “difficulty” of the topic. Furthermore, the datasets we have evaluated represent a diverse mixture of reviews, some with some labels derived from title/abstract screening and some from full text screening. Here we report a range of performances with the smallest savings (10% WSS) observed in some of the smallest datasets and the largest savings (more than 60%) in the largest ones. Within this range there is substantial variability.

On the other hand, the consistent performance of the recall estimator suggests that it is a robust, conservative estimate of the percentage of relevant documents identified during the screening process. For example, when targeting 95% recall in simulated screening of these datasets, the median true recall obtained was 99%, with the majority of the obtained true recall values (23/26) above 95% (Fig. A.3). This finding has been corroborated with results recently observed on an additional set of 53 datasets together containing more than 61,000 screened references (data not shown).

There are a few limitations to the recall estimation method we have proposed, and we plan to address these in future work. For example, Section 3.2.4 discusses the effect of the choice for the lookback parameter δ. It is true that the optimal choice is a function of the dataset in question, but we do not currently have a good way to choose the optimal value a priori. In practice, we have found that using δ = 2 appears to be a reasonable choice, and the fact that our recall estimate is consistently conservative (Fig. A.3) seems to justify this choice. However, in future work, we do intend to explore this in more detail and to test if it is possible to somehow choose δ in a more data driven way for each new dataset. Similarly, although the estimates for recall are consistently conservative in our analysis, it would be useful if we could also provide a confidence interval around each estimate. So far, however, we have found that standard parametric confidence intervals tend to be too wide to be of practical usefulness and we are currently exploring Bayesian approaches as well as empirical approaches that leverage the results of the large number of datasets now available from users of our software. However, this work is ongoing; we plan to publish findings in subsequent manuscripts when completed.

Active Screener has been used successfully to reduce the effort required to screen articles for systematic reviews conducted at a variety of organizations including the National Institute of Environmental Health Science (NIEHS), the United States Environmental Protection Agency (EPA), the United States Department of Agriculture (USDA), The Endocrine Disruption Exchange (TEDX), and the Evidence-Based Toxicology Collaboration (EBTC). These early adopters have provided us with an abundance of useful data and user feedback, and we have identified several areas where we can continue to improve our methods and software. Several new features have been planned for the software, including better support for full-text screening, improved screening forms and improved user experience, and the software will be developed, improved and maintained for the foreseeable future.

5. Conclusions

SWIFT-Active Screener, which uses active learning and a novel method for recall estimation, can significantly reduce the overall effort required during document screening in the contexts of systematic review and evidence mapping. The software is currently available in the form of a multi-user, collaborative, online web application.

Abbreviations:

WSS

Work saved over sampling

WSS@95

Work Saved over random Sampling at 95% recall

MeSH

Medical Subject Headings

tf-idf

term frequency-inverse document frequency

PFOA/PFOS

Perfluorooctanoic Acid/Perfluorooctane Sulfonate

BPA

bisphenol A

SVM

Support Vector Machine

ROC

receiver operating characteristic

SBIR

Small Business Innovation Research

Appendix

See Figs. A1–A6 and Tables A1–A6.

Fig. A1.

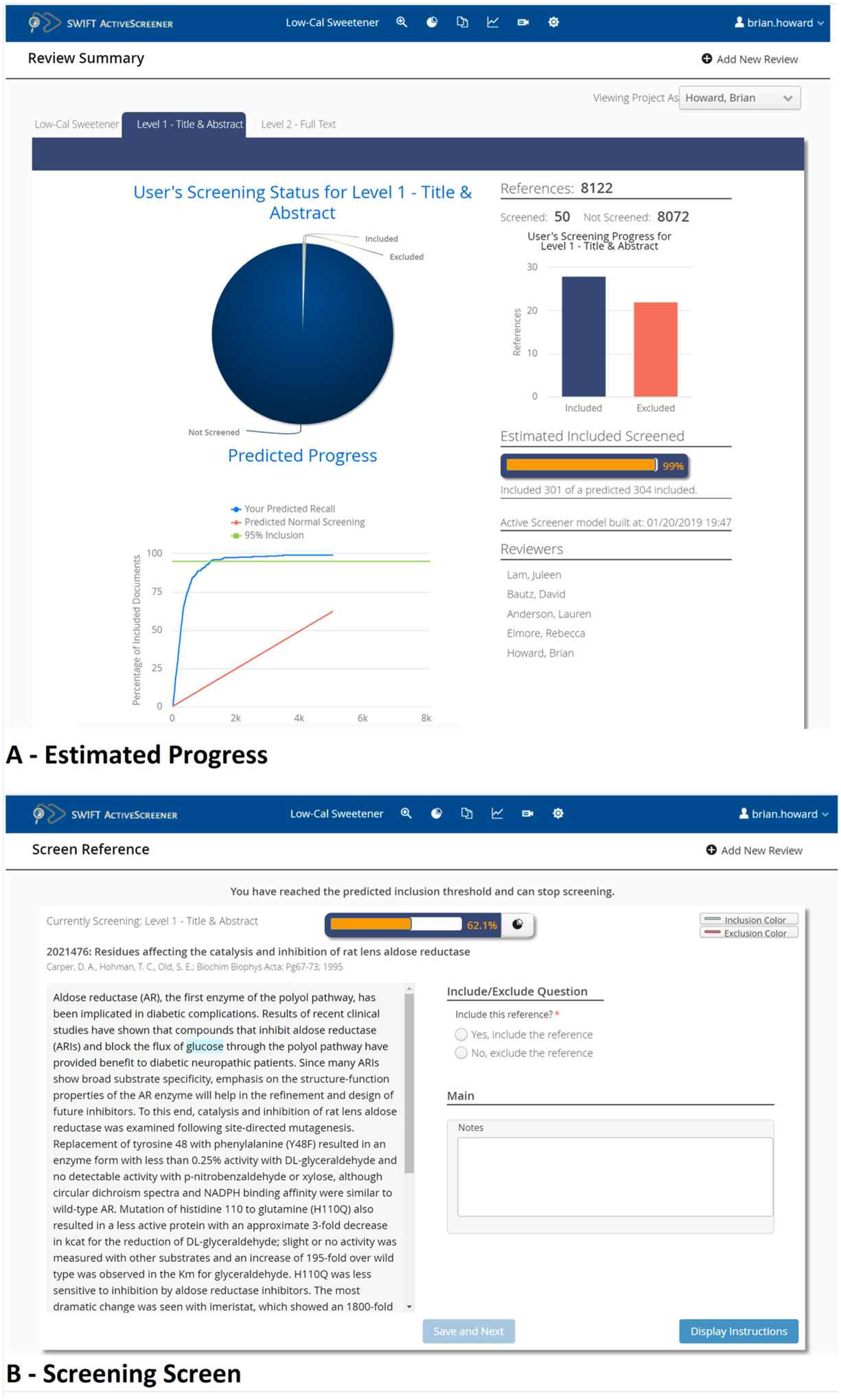
SWIFT-Active Screener user interface. The review summary screen (A) shows the progress so far on the review and includes the overall estimated recall along with number of included and excluded documents for each screener. The Screen References window (B) displays the current title and abstract to the screener for review.

Fig. A2.

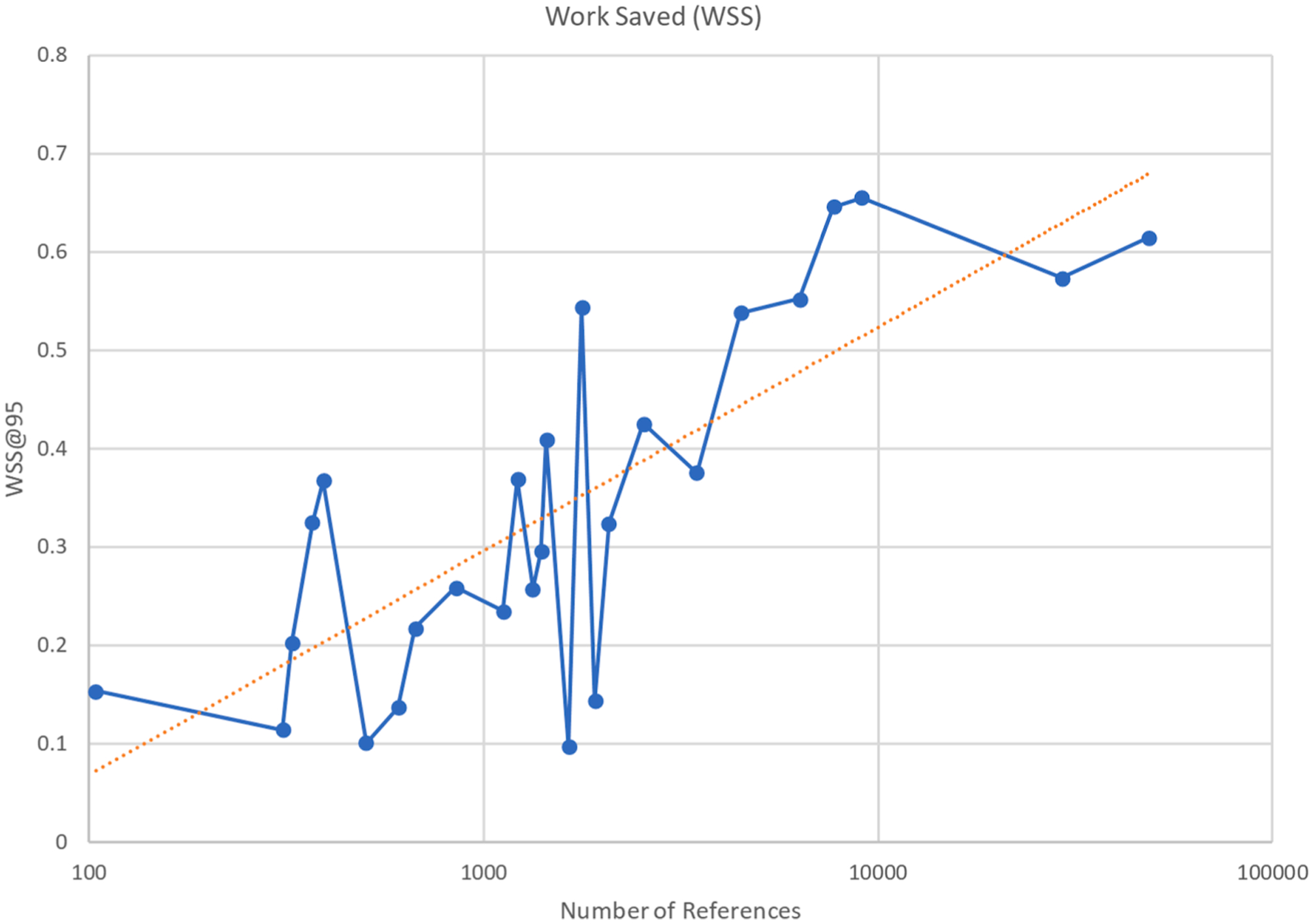
Performance (WSS) vs dataset size. The log-linear trendline (R² = 0.61) indicates that work saved over random sampling is an increasing function of the number of references in the project. However, the relationship is too weak on its own for accurate prediction of recall.

Fig. A3.

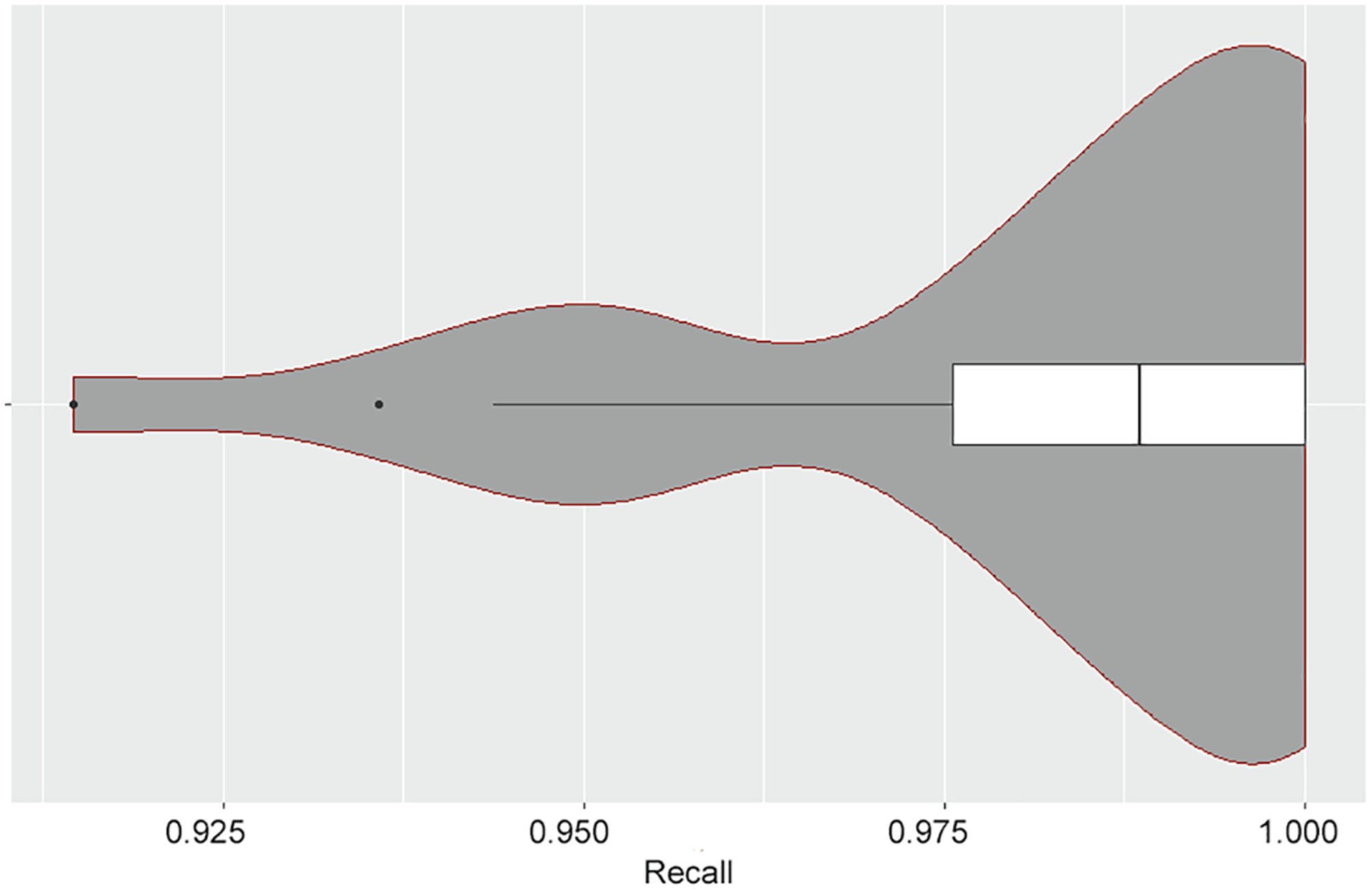
Violin plot of obtained true recall. The figure below shows the obtained recall for simulated screening of the 26 datasets, given estimated equal to 95%. The median obtained recall is 99%, indicating that the recall estimate tends to be conservative. In fact, the majority of the obtained true recall values (23/26) are above 95%. An outlier occurs at obtained recall equal to 91.5%.

Fig. A4.

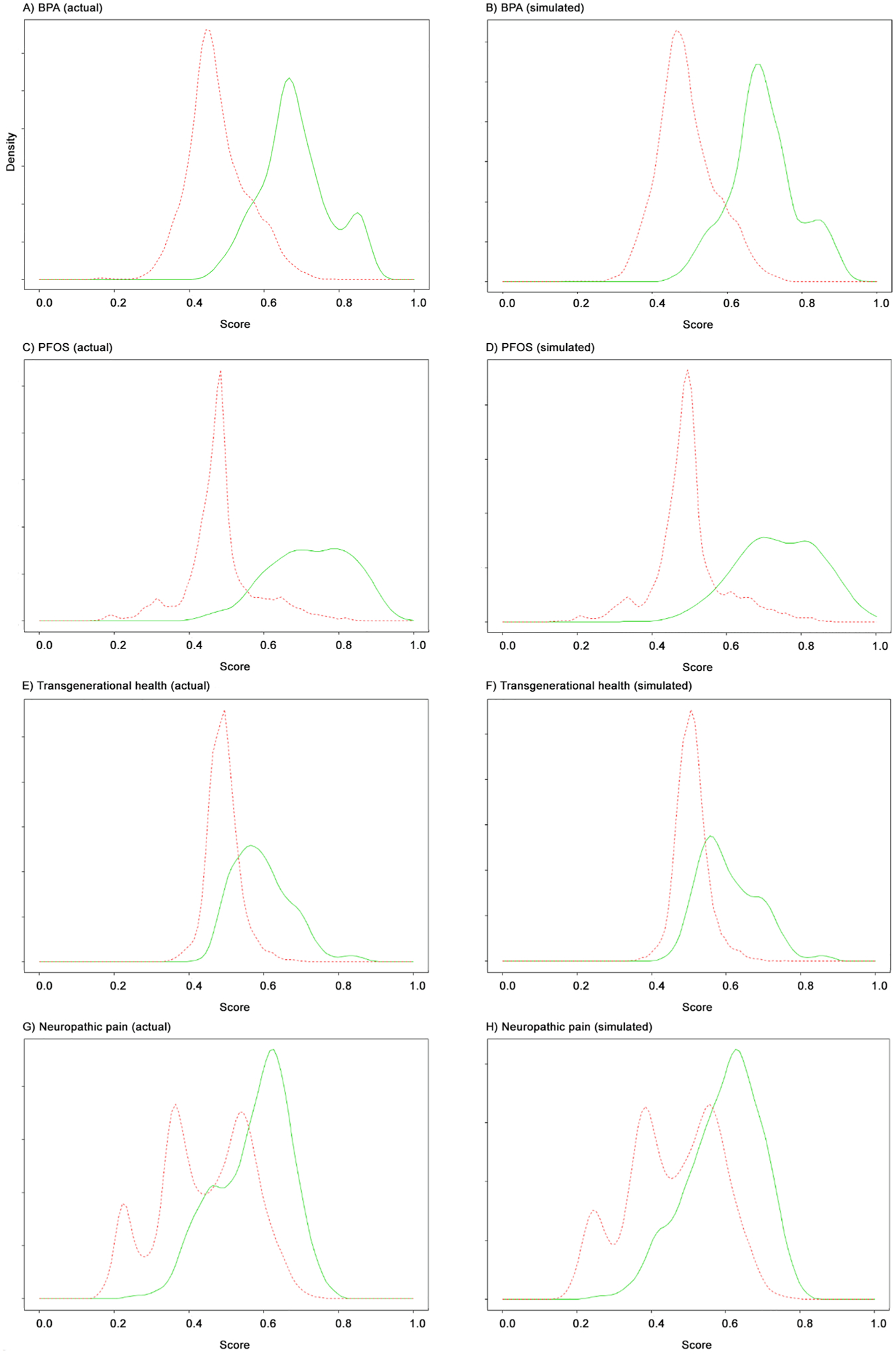
Actual and simulated score densities. Red line is for excluded documents; green is for included documents. All simulated data sets used overall inclusion rate of 0.05 and 10,000 total documents. Datasets shown are as follows: (a) BPA (actual); (b) BPA (simulated); (c) PFOS/PFOA (actual); (d) PFOS/PFOA (simulated); (e) Transgenerational health (actual); (f) Transgenerational health (simulated); (g) Neuropathic pain (actual); (h) Neuropathic pain (simulated). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. A5.

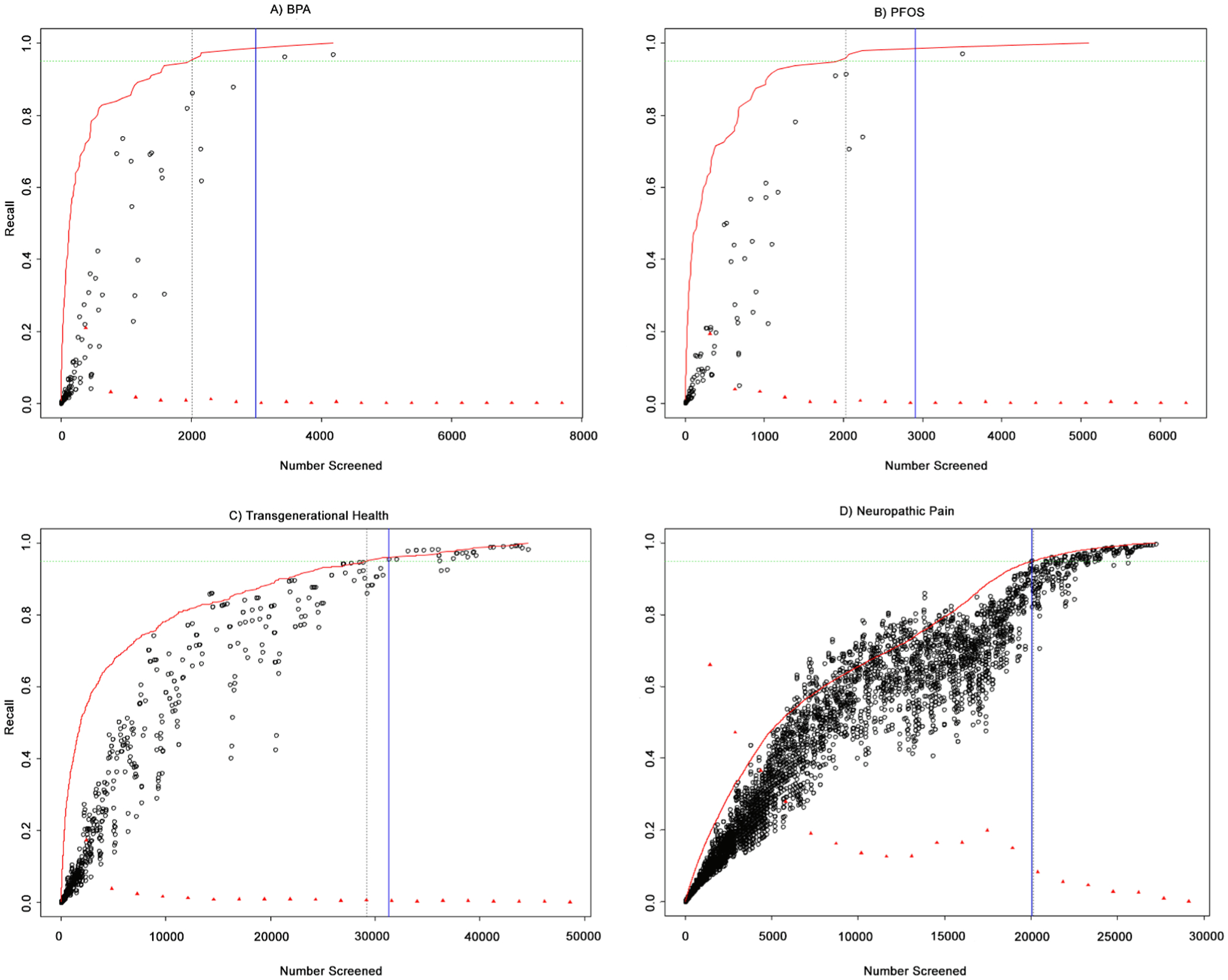
Estimated recall using simulated score densities. True recall versus estimated recall. Datasets shown are (a) BPA; (b) PFOS/PFOA; (c) Transgenerational; (d) Neuropathic pain.

Fig. A6.

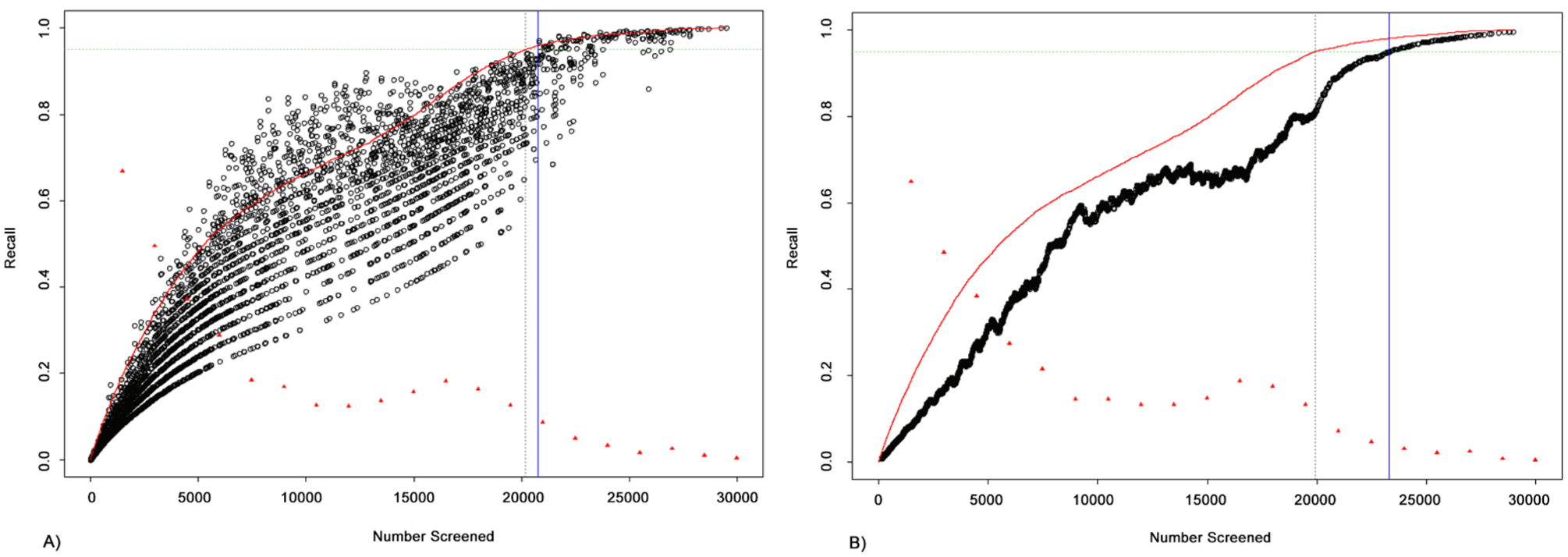
Effect of lookback, δ, on recall estimate variability. In panel (a) δ = 1 and in panel (b) δ = 100. The results illustrate that increasing lookback, δ, decreases variability in the recall estimate.

Table A1.

Summary of datasets used to assess performance of active learning and recall estimation methods.

Dataset	Source	Label Type	Records from Search	Included	Excluded
PFOA/PFOS and immunotoxicity	NIEHS	Full text	6331	95 (1.5%)	6236 (98.5%)
Bisphenol A (BPA) and obesity	NIEHS	Full text	7700	111 (1.4%)	7589 (98.6%)
Transgenerational inheritance of health effects	NIEHS	Tiab	48,638	765 (1.6%)	47,873 (98.4%)
Fluoride and neurotoxicity in animal models	NIEHS	Full text	4479	51 (1.1%)	4428 (98.9%)
Neuropathic pain	CAMARADES	Tiab	29,207	5011 (17.2%)	24,196 (82.8%)
Skeletal muscle relaxants	Cohen (2006)	Full Text	1643	9 (0.6%)	1634 (99.4%)
Opioids	Cohen (2006)	Full Text	1915	15 (0.8%)	1900 (99.2%)
Antihistamines	Cohen (2006)	Full Text	310	16 (5.2%)	294 (94.8%)
ADHD	Cohen (2006)	Full Text	851	20 (2.4%)	831 (97.6%)
Triptans	Cohen (2006)	Full text	671	24 (3.6%)	647 (96.4%)
Urinary Incontinence	Cohen (2006)	Full text	327	40 (12.2%)	287 (87.8%)
Ace Inhibitors	Cohen (2006)	Full text	2544	41 (1.6%)	2503 (98.4%)
Nonsteroidal anti-inflammatory	Cohen (2006)	Full text	393	41 (10.4%)	352 (89.6%)
Beta blockers	Cohen (2006)	Full text	2072	42 (2.0%)	2030 (98.0%)
Proton pump inhibitors	Cohen (2006)	Full text	1333	51 (3.8%)	1282 (96.2%)
Estrogens	Cohen (2006)	Full text	368	80 (21.7%)	288 (78.3%)
Statins	Cohen (2006)	Full text	3465	85 (2.5%)	3380 (97.5%)
Calcium-channel blockers	Cohen (2006)	Full text	1218	100 (8.2%)	1118 (91.8%)
Oral hypoglycemics	Cohen (2006)	Full text	503	136 (27.0%)	367 (73.0%)
Atypical antipsychotics	Cohen (2006)	Full text	1120	146 (13.0%)	974 (87.0%)
Mammalian	EBTC	Tiab	1442	263 (18.2%)	1179 (81.8%)
USDA 1	USDA	Tiab	1776	225 (12.7%)	1551 (87.3%)
USDA 2	USDA	Tiab	9103	382 (4.2%)	8721 (95.8%)
USDA 3	USDA	Tiab	608	9 (1.5%)	599 (98.5%)
USDA 4	USDA	Tiab	104	12 (11.5%)	92 (88.5%)
USDA 5	USDA	Tiab	1570	25 (1.6%)	1545 (98.4%)

Table A2.

Results of simulated screening experiments on 26 datasets using active learning and recall estimation with δ = 2. Mean and standard deviation over 30 trials with initially randomized order.

	Records from Search	% Screened	Cost	Theoretical WSS@95	Obtained WSS@95	Estimated Recall	Obtained True Recall
Transgenerational inheritance of health effects	48,638	0.371	0.128	0.742 (0.003)	0.613 (0.001)	0.950	0.986 (0.001)
Neuropathic pain	29,207	0.402	0.040	0.613 (0.001)	0.573 (0.022)	0.950	0.976 (0.014)
USDA 2	9,103	0.332	0.099	0.755 (0.004)	0.655 (0.010)	0.950	0.987 (0.001)
Bisphenol A (BPA) and obesity	7,700	0.354	0.161	0.807 (0.010)	0.646 (0.013)	0.950	1.000 (0.000)
PFOA/PFOS and immunotoxicity	6,331	0.448	0.280	0.833 (0.009)	0.552 (0.010)	0.950	1.000 (0.000)
Fluoride and neurotoxicity in animal models	4,479	0.443	0.324	0.862 (0.018)	0.538 (0.009)	0.950	0.981 (0.004)
Statins	3,465	0.576	0.024	0.399 (0.035)	0.375 (0.015)	0.950	0.951 (0.002)
Ace inhibitors	2,544	0.550	0.333	0.758 (0.023)	0.425 (0.013)	0.950	0.976 (0.000)
Beta blockers	2,072	0.629	0.262	0.586 (0.016)	0.324 (0.014)	0.950	0.953 (0.004)
Opioids	1,915	0.856	0.114	0.257 (0.028)	0.144 (0.038)	0.950	1.000 (0.000)
USDA 1	1,776	0.445	0.116	0.659 (0.007)	0.543 (0.009)	0.950	0.988 (0.004)
Skeletal muscle relaxants	1,643	0.902	0.191	0.289 (0.065)	0.098 (0.013)	0.950	1.000 (0.000)
USDA 5	1,570	0.704	0.328	0.624 (0.040)	0.296 (0.018)	0.950	1.000 (0.000)
Mammalian	1,442	0.580	0.121	0.529 (0.015)	0.408 (0.014)	0.950	0.988 (0.004)
Proton pump inhibitors	1,333	0.743	0.139	0.397 (0.018)	0.257 (0.009)	0.950	1.000 (0.000)
Calcium Channel Blockers	1,218	0.620	0.194	0.563 (0.021)	0.369 (0.024)	0.950	0.989 (0.005)
Atypical Antipsychotics	1,120	0.680	−0.070	0.165 (0.020)	0.235 (0.014)	0.950	0.915 (0.016)
ADHD	851	0.694	0.474	0.734 (0.046)	0.259 (0.017)	0.950	0.953 (0.013)
Triptans	671	0.782	0.240	0.458 (0.030)	0.218 (0.012)	0.950	1.000 (0.000)
USDA 3	608	0.863	0.094	0.231 (0.068)	0.137 (0.018)	0.950	1.000 (0.000)
Oral Hypoglycemics	503	0.835	−0.009	0.092 (0.018)	0.101 (0.019)	0.951	0.936 (0.039)
Nonsteroidal anti-inflammatory	393	0.632	0.254	0.621 (0.019)	0.368 (0.013)	0.950	1.000 (0.000)
Estrogens	368	0.664	0.129	0.454 (0.021)	0.325 (0.013)	0.951	0.989 (0.006)
Urinary Incontinence	327	0.798	0.199	0.401 (0.018)	0.202 (0.020)	0.951	1.000 (0.000)
Antihistamines	310	0.829	−0.042	0.072 (0.034)	0.115 (0.025)	0.951	0.944 (0.019)
USDA 4	104	0.846	0.325	0.479 (0.070)	0.154 (0.019)	0.952	1.000 (0.000)

Table A3.

Performance of recall estimation method on simulated score distributions.

Dataset	Lookback (δ)	Theoretical WSS@95	Obtained WSS@95	“Cost”	Actual Recall
PFOS/PFOA	2	0.637	0.520	0.117	0.979
BPA	2	0.693	0.594	0.099	0.982
Transgen	5	0.349	0.316	0.033	0.959
Neuropain	5	0.259	0.261	−0.002	0.948

Table A4.

Effect of list length on performance of recall estimation method. The dataset shown is BPA; the overall inclusion rate, p = 0.015; and the lookback, δ = 2. Cost is averaged over 5 trials.

List length	Cost
1,000	0.453
5,000	0.167
10,000	0.110
50,000	0.048
100,000	0.037

Table A5.

Effect of inclusion rate on performance of recall estimation method. The dataset shown is BPA; the list length = 10,000; and the lookback, δ = 2. Cost is averaged over 5 trials.

p	Cost
0.001	0.200
0.015	0.110
0.05	0.104
0.075	0.079
0.10	0.075
0.25	0.052

Table A6.

Effect of lookback, δ, on performance of recall estimation method. The dataset shown is neuropathic pain; the list length = 30,000; and p = 0.17. Cost is average over 5 trials.

δ	Cost
1	−0.063
2	−0.005
3	0.008
5	0.017
50	0.062
100	0.072