Did Lockdown Work? An Economist’s Cross-Country Comparison

Abstract

I explore the association between the severity of lockdown policies in the first half of 2020 and mortality rates. Using two indices from the Blavatnik Centre’s COVID-19 policy measures and comparing weekly mortality rates from 24 European countries in the first halves of 2017–2020, addressing policy endogeneity in two different ways, and taking timing into account, I find no clear association between lockdown policies and mortality development.

1. Introduction

The spread of a new corona virus, severe acute respiratory syndrome coronavirus 2 (Sars-CoV-2) that causes coronavirus disease 2019 (COVID-19), came as a genuine surprise to the world. Governments the world over decided to lock down their economies in order to suppress the virus, as early experience from Wuhan in China’s Hubei province brought them to believe that limiting social contacts would contain its spread, protect health care from reaching capacity limits, and limit its death toll. However, whether economic lockdowns work in the sense of suppressing the virus and preventing deaths remains an open question.

Epidemiologists have tried to answer it, indicating that thousands and perhaps millions have been saved. These first answers have nevertheless been exclusively based on forecasts derived from empirically untested models (cf., Flaxman et al. 2020). Conversely, Chaudhry et al. (2020), in an exploratory analysis of data on COVID-19-related deaths across 50 countries, find no association between the degree of lockdown and death rates. Similarly, in the only empirical assessment of its kind to date that takes the endogeneity of policy responses into account, Born et al. (2020) use a synthetic control method to suggest that Sweden’s decision not to lock down society did not contribute substantially to its death toll. They thus question the widely held political belief that lockdowns must have effectively suppressed the spread of the virus. A similar question is raised by, for example, Atkeson et al. (2020) and De Larochelambert et al. (2020), both of which find no difference in mortality development across different mitigation and lockdown strategies.

In this paper, I instead approach the question using a standard approach and standard econometric tools used in economics and political science instead of epidemiological modelling or single-case studies. I compare weekly general mortality rates in the first half of the year in 2017, 2018, 2019, and 2020 in 24 European countries that took very different policy measures against the virus at different points in time. Estimating the effects of these policy measures as captured by the Blavatnik Centre’s COVID-19 policy indices and taking the endogeneity of policy responses into account, the results suggest that stricter lockdown policies have not been associated with lower mortality.

2. Data and Empirical Strategy

The main data consist of weekly mortality numbers from 24 European countries covered by Eurostat (2020), which capture mortality for all causes. In subsequent tests, I use weekly all-cause mortality numbers in four age bands—0–39 years, 40–59 years, 60–79 years, and 80 years and older—from the same source. The reason for using weekly mortality data instead of official data on COVID-19-related deaths is the way these deaths are measured. While weekly mortality counts all actual deaths in the country, COVID-19-related deaths are counted as deaths where the deceased tested positive for the virus but where the death is not necessarily caused by the virus. Country-specific differences in reporting approach and reporting behaviour would therefore bias the results when using official measures of COVID-19-related deaths. As is standard in order to avoid outlier influence, I take the logarithm to these data (cf., Box and Cox 1964; Lütkepohl and Xu 2012).

As a measure of the severity of lockdown policies, I use two indices developed at Oxford University’s Blavatnik Centre by Hale et al. (2020). As documented in Petherick et al. (2020), the full government response index includes 13 elements: school closures, workplace closures, cancellation of public events, restrictions on gatherings, closing public transport, stay-at-home requirements, restrictions on internal movement, international travel controls, income support, debt and contract relief for households, public information campaigns, testing policies, and contact tracing. These components are all scored categorically, based on available public information from each country, between 0 and 4, such that 0 implies no interventions, 1 is mainly recommendations, and 2 to 4 are increasingly restrictive interventions. The Spanish restrictions on public gatherings are, for example, scored a maximum of 4 between 30 March and 1 June when the population was effectively banned from leaving the house for non-essential purposes. By 1 June, small gatherings were allowed, which resulted in a reduction of the rating to 3.

I use the containment and health index, which does not include the two economic elements of income support and debt relief that are irrelevant for virus spread. Alternatively, as a robustness test throughout, I use the stringency measure that in addition excludes the final three measures.¹ These indices are the main variables that I use to explore the association between mortality dynamics and policy responses to the new virus.

The specification in which I estimate this association includes three-way fixed effects capturing country-, year-, and week-specific differences, which implies that all effects are identified as week-specific changes in mortality relative to mortality rates in the same week in previous years, and relative to changes in other countries in the same year and week. As such, all approximately time-invariant factors in a four-year perspective such as geography, population density and demography, welfare state and health care type, the regular capacity of the health care system, institutional quality, and political institutions are therefore controlled for (cf., Cepaluni et al. 2020). This effectively reduces the risk of omitted variable bias. The specification is given in (i) where M_{t, I} is all-cause weekly mortality in week t in country i, α_i is a vector of country fixed effects, P_t–x,I is a policy index of country in period t–x (such that x is the lag), D_t is a vector of week fixed effects, A_t is a vector of annual fixed effects, and ε_t,i is an error term.

$${\mathrm{M}}_{t, i}={\alpha }_i+\beta { \mathrm{M}}_{t-1, i}+\gamma { \mathrm{P}}_{t-x, i}+{\delta }_w{\mathrm{D}}_t+{\delta }_y{\mathrm{A}}_t+{\epsilon }_{t, i}$$ (1)

A main problem with estimating effects of policy changes on the mortality rate is that effects are far from contemporaneous. The incubation period of Sars-CoV-2—the time from a person is exposed to the virus and until she develops symptoms in case that happens at all—is reported to vary between 2 and 14 days with a typical period around one week. If these symptoms develop further, she will typically be hospitalized after an additional seven days (Garg et al. 2020). Although there is relatively little knowledge of how rapidly COVID-19 results in deaths, Flaxman et al. (2020) implicitly assume a time lag of two to three weeks between infection and death, which appears to be the minimum typical time from infection to death. In the following, I therefore report the results using time lags of lockdown policies varying from one to four weeks.

The second identification problem is the potential endogeneity of the association, which derives from the nature of political reactions to the virus that could rely on the reported number of infections. If an increase in the reported infection rate leads government to introduce lockdown policies, and if a declining reported infection rate subsequently leads them to ease the lockdown, the estimated association between policy stringency and mortality is biased.

A first solution the identification problem relies on the timing of changes in lockdown policies and mortality rates. Although one might think that policy making reacts quickly to changing mortality during an emergency, exploring the determinants of changes in the stringency indices reveals that an increase in the contemporaneous mortality or an increase in the reported number of Sars-CoV-2 cases was not associated with stricter lockdown measures (see also Sebhatu et al. 2020). Lagging these indicators for the severity of the health crisis reveals that mortality changes become significant predictors of stricter measures when lagged three weeks. As such, it is highly unlikely that there is a substantial endogeneity problem in the following as mortality changes only affect policy changes with a three-week lag, and as policy changes cannot affect the mortality rate before another two to three weeks have passed. As such, any bias is likely to be small and practically negligible.

However, endogeneity or simultaneity bias may still be a problem if, for example, omitted time-variant political factors are important. Another standard way of alleviating the endogeneity bias is to find instrumental variables that provide identification of changes in policy stringency while not being associated with mortality dynamics. Although valid and sufficiently strong instrumental variables are often difficult to find in fixed effects settings, it is possible to identify variables that determine the policy indices and that may be plausibly exogenous. In the following, I use the logarithm to the number of days since the first Sars-CoV-2 case was identified in the country and its square, which I interact with the Benefit INEP (Index of Emergency Powers) measure developed by Bjørnskov and Voigt (2018), an index that essentially captures the degree to which the executive gains additional discretionary powers during a state of emergency.² The theoretical background for this instrumental approach is that, as indicated by previous research, policy responses to emergencies are often informed more by the promise of additional, unchecked power than the severity of the emergency. Bjørnskov and Voigt (2020) for example show that countries hit to the same extent by the Sars-CoV-2 virus were more likely to declare a state of emergency when their constitutional emergency provisions granted them more discretionary power. In other words, policy responses are likely to be stronger and more interventionist in countries in which the constitution effectively enables strong political responses. While the potential effect of constitutional provisions per se is captured by the country fixed effects, as constitutions do not change during the four years explored here, the interaction between the INEP and the time since the first case thus offers exogenous identification of the policy development, defined by the constitutional developments taking place years or decades before the virus could have been known.³

A final challenge is that the timing of the policies, and not just their severity, may affect mortality development. Pei et al. (2020) for example suggest that earlier intervention would have contained the spread of Sars-CoV-2 in the USA, while Maier and Brockmann (2020) make a similar argument for China. Differential effects depending on timing may be a challenge, as Aksoy et al. (2020) indicate that the speed with which the first non-pharmaceutical interventions were implemented varied substantially across countries. While the fixed effects approach prevents a direct assessment of whether early lockdowns were more effective, I approach this problem by separating countries in two groups according to two timing criteria: how quickly a country reached a level of lockdown after the first case was identified, and how quickly it happened after the first death was reported. I apply a cut-off of 40 on the index of containment and health and the policy stringency index, as this is the lowest index value that all countries in the sample reached at any point in time. I then interact these two dummy variables with the lockdown index, which provides a direct test of systematically heterogeneous effectiveness.

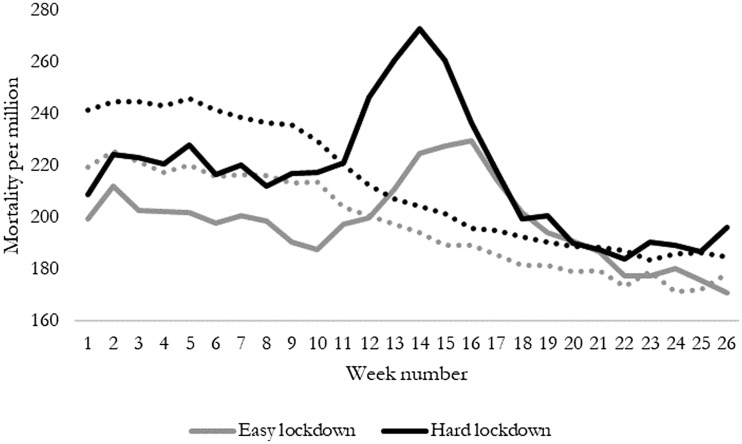
All data are summarized in the Appendix Table A1; all countries included are listed in Table A2 along with the number of days between the first registered case and registered death and the country reaching a value of 40 on the stringency index, as well as the mortality rate in the first half of 2020 relative to the three preceding years. However, before turning to the estimates, it may be worthwhile to provide a sense of the dynamics of mortality rates in 2020 and previous years. Figure 1 illustrates the development of weekly mortality (the full lines), relative to the average development in the same weeks in 2017–2019 (the dotted lines). The black line represents the average development in the 12 countries with an average containment and health index in 2020 above the median of all 24 countries, while the grey line represents the same development in countries with below-median indices. As such, the figure shows how mortality changed from week to week for the first half of the years.

Figure 1.

Mortality development in 2020, two groups

Notes: the grey lines depict weekly mortality in the first half of the year for countries that locked down less than the average, while black lines depict weekly mortality for countries that locked down harder than the average. The full lines depict mortality development in the first half of 2020, while the dotted lines depict average mortality development in the first halves of 2017, 2018, and 2019.

Exploring these data, a first interesting detail is that comparing 2020 to the previous years, it is clear that the average European country had negative excess mortality in the first 10 weeks of the year. On average, the 24 countries suffered 200 fewer deaths per million inhabitants (8.7%) in the first 10 weeks of 2020, compared with their averages in 2017–2019. From week 11 to 22, the 24 countries experienced an accumulated excess mortality of 248 deaths per million inhabitants (10.7%). However, as illustrated in Figure 1, the ‘hard lockdown’ group experienced 372 additional deaths per million, while the other group only experienced excess mortality of 123 deaths. This simple pattern may indicate that lockdowns have been directly counterproductive but may also indicate a severe endogeneity problem.

3. Main Results

Table 1 reports the results of estimating the effects of the containment and health index, while Table 2 employs the policy stringency index. In both tables, the goodness-of-fit statistics show that the simple specification does a good job explaining the actual development: year- and week-fixed effects along with a lagged dependent variable explain approximately 70% of the within-country variation. The results in both tables also clearly document the persistence and relatively slow development of mortality, as reflected in the lagged dependent variable.

Table 1.

Results, containment, and health

Lag length	One week	Two weeks	Three weeks	Four weeks
Lagged dependent	0.648** (0.071)	0.660** (0.072)	0.673** (0.073)	0.681** (0.071)
Containment and health index	0.072** (0.018)	0.047* (0.018)	0.022 (0.018)	0.004 (0.015)
Observations	2600	2600	2600	2600
R squared	0.996	0.996	0.996	0.997
F statistic	228.39	225.56	223.82	223.28
	Only data prior to turning point
Containment and health index	0.126** (0.032)	0.113** (0.035)	0.094* (0.036)	0.089* (0.041)
	Only data after turning point
Containment and health index	0.058 (0.077)	0.016 (0.069)	–0.028 (0.071)	–0.153* (0.069)
	Instrumental variables estimates
Containment and health index	–0.626 (0.325)	–0.601* (0.302)	–0.103* (0.049)	0.071 (0.031)

Notes: ** (**) denote significance at p < 0.001 (p < 0.05). The dependent variable is the logarithm to weekly all-cause mortality in the first half of 2017, 2018, 2019, and 2020. All estimates are obtained with an OLS estimator with country, year, and week fixed effects. Results denoted as ‘prior to turning point’ refer to effects in weeks prior to the week of 2020 with the highest mortality in a country; results denoted as ‘after turning point’ refer to effects in subsequent weeks.

Table 2.

Results, policy stringency

Lag length	One week	Two weeks	Three weeks	Four weeks
Lagged dependent	0.643** (0.071)	0.659** (0.073)	0.675** (0.074)	0.685** (0.072)
Policy stringency index	0.072** (0.019)	0.043* (0.018)	0.015 (0.028)	–0.006 (0.016)
Observations	2600	2600	2600	2600
R squared	0.996	0.996	0.886	0.996
F statistic	229.10	225.49	223.55	223.31
	Only data prior to turning point
Policy stringency index	0.119** (0.031)	0.099** (0.032)	0.068* (0.031)	0.050 (0.035)
	Only data after turning point
Policy stringency index	0.094 (0.072)	0.062 (0.069)	0.026 (0.077)	–0.094 (0.071)
	Instrumental variables estimates
Policy stringency index	0.472* (0.208)	–0.536* (0.238)	–0.122* (0.053)	0.002 (0.033)

Notes: ** (**) denote significance at p < 0.001 (p < 0.05). The dependent variable is the logarithm to weekly all-cause mortality in the first half of 2017, 2018, 2019, and 2020. All estimates are obtained with an OLS estimator with country, year, and week fixed effects. Results denoted as ‘prior to turning point’ refer to effects in weeks prior to the week of 2020 with the highest mortality in a country; results denoted as ‘after turning point’ refer to effects in subsequent weeks.

The main results in the tables show that the estimated effects of lockdown policies are all positive and significant when policy changes are lagged one or two weeks. However, when the lag length extends to three or fourth weeks, that is, the length that is reasonable from the perspective of the virology of Sars-CoV-2, the estimates become very small and insignificant.

The following panels in both tables separate the period in which the mortality rates increased and the subsequent decline. Although these estimates may arguably suffer from bias if lockdown policies significantly move the turning point of mortality development, which would be the case if the association is negative, they provide information about potentially asymmetric effects of the policies. However, the results clearly indicate that lockdown policies are positively associated with mortality development before the mortality rate peaks although the association again tends to break down with lag length. Conversely, there is no clear or significant relation between lockdown stringency and mortality after the virus has peaked. One result, the containment and health index lagged four weeks in the period after the turning point, is negative and significant but the corresponding estimate for the more precise policy stringency index is far from significance.

While the significant association with a one- or two-week lag prior to the turning point may indicate endogeneity—this particular lag structure could indicate that lockdowns follow increases in case numbers that eventually cause increasing mortality—two additional factors speak against this interpretation. First, the alternative approach of applying instrumental variables estimates as reported in the bottom panels is inconsistent with a substantial endogeneity problem.⁴ These results confirm the overall pattern by being negative and significant when lagged one or two weeks (the period when they cannot have worked) but turning positive and insignificant when lagged four weeks. They therefore do not indicate any substantial endogeneity bias that works against identifying an effect of lockdowns, but quite the opposite. Given the validity of the instruments, these estimates do not provide evidence suggesting that lockdown policies worked as intended. Second, the analysis of the timing of national lockdown decisions in Sebhatu et al. (2020) documents that these decisions were not clearly determined by case numbers or deaths. Additionally, the timing of the lockdowns occurred at the end of the regular virus season, which itself could yield the particular pattern observed in the lag structure.

4. Timing Heterogeneity

However, as indicated by Pei et al. (2020), not only the severity but also the particular timing of the lockdown policies may play a role in reducing the spread. In Tables 3 and 4, I allow for differential effects by interacting the policy indices with one of two dummy variables that capture policy timing relative to the first reported case and the first reported death in a country, respectively. The interaction terms thus indicate whether the effectiveness of lockdown policies is different in countries that implemented them relatively early. Taking into account how the implementation of lockdown policies was timed may arguably be necessary for two reasons. First, earlier implementation of restrictions may have saved lives by protecting the health care system from reaching capacity. Second, early implementation may also have avoided a subsequent situation where the government may perceive that the imposition of harder restrictions is necessary. As such, late implementation may have led countries to impose much tougher measures once the epidemic was seen to get out of control.

Table 3.

Results, timing of containment and health

Lag length	Three weeks	Four weeks	Three weeks	Four weeks
Lagged dependent	0.672** (0.073)	0.681** (0.071)	0.671** (0.073)	0.681** (0.072)
Containment and health index	0.024 (0.019)	0.004 (0.016)	0.026 (0.021)	0.004 (0.017)
Early timing (first case) * index	–0.003 (0.011)	–0.000 (0.009)
Early timing (first death) * index			–0.011 (0.012)	–0.002 (0.011)
Observations	2600	2600	2600	2600
R squared	0.996	0.996	0.996	0.997
F statistic	216.28	215.76	180.35	179.25

Notes: ** (**) denote significance at p<.001 (p<.05). The dependent variable is the logarithm to weekly all-cause mortality in the first half of 2017, 2018, 2019, and 2020. All estimates are obtained with an OLS estimator with country, year, and week fixed effects. Early timing refers to countries in which lockdown policies were implemented earlier than the average of the sample after the first COVID-related case or death was recorded in the country.

Table 4.

Results and timing of policy stringency

Lag length	Three weeks	Four weeks	Three weeks	Four weeks
Lagged dependent	0.675** (0.074)	0.685** (0.072)	0.674** (0.075)	0.685** (0.073)
Policy stringency index	0.016 (0.019)	–0.007 (0.016)	0.017 (0.021)	–0.007 (0.010)
Early timing (first case) * index	–0.003 (0.010)	–0.000 (0.008)
Early timing (first death) * index			–0.007 (0.012)	–0.005 (0.010)
Observations	2600	2600	2600	2600
R squared	0.996	0.997	0.996	0.997
F statistic	216.02	215.78	216.05	215.80

Notes: ** (**) denote significance at p < 0.001 (p < 0.05). The dependent variable is the logarithm to weekly all-cause mortality in the first half of 2017, 2018, 2019, and 2020. All estimates are obtained with an OLS estimator with country, year, and week fixed effects. Early timing refers to countries in which lockdown policies were implemented earlier than the average of the sample after the first COVID-related case or death was recorded in the country.

The results nevertheless reveal that the interactions are tiny and none of them are near significance at conventional levels.⁵ Although the two indices are not identical, the results do not support the claim that lockdowns are more effective when implemented early. In addition, exploring the data suggests that early lockdowns did not help governments avoid hard lockdowns, as there is no clear pattern between early timing and subsequent severity.

5. Age Differences

Most deaths in general, as well as most deaths related to Sars-CoV-2, occur among the relatively old. In the present sample, 89% of all deaths occurred among people older than 60 years and 53% occurred among people older than 80. A final issue to address is that it remains possible that the results outlined so far are affected by effect heterogeneity if lockdowns have different effects in different age groups.

However, the results in Table 5 do not substantially differ from those in previous tables. When the estimates are statistically significant, they are positive and as previous estimates, they tend to become smaller with longer lags.⁶ If anything, the results suggest that lockdowns may have led to significantly higher mortality among the population aged between 60 and 79 years. Across the tables, the overall findings thus indicate that neither differing the lag length, applying instrumental variables, separating countries based on the timing of their interventions, or estimating effects in specific age groups yield support for the effectiveness of such lockdowns.

Table 5.

Results, containment and health, age groups

Lag length	One week	Two weeks	Three weeks	Four weeks
	0–39 years
Lagged dependent	0.032 (0.029)	0.032 (0.029)	0.032 (0.029)	0.032 (0.030)
Containment and health index	–0.004 (0.043)	–0.044 (0.041)	–0.033 (0.045)	–0.026 (0.047)
Observations	2611	2611	2611	2611
R squared	0.489	0.487	0.489	0.493
F statistic	2.54	2.55	2.53	2.52
	40–59 years
Lagged dependent	0.156** (0.044)	0.157** (0.045)	0.158** (0.045)	0.159** (0.045)
Containment and health index	0.090** (0.029)	0.075* (0.033)	0.059 (0.032)	0.044 (0.032)
Observations	2595	2595	2595	2595
R squared	0.949	0.949	0.951	0.952
F statistic	8.26	8.14	8.02	7.92
	60–79 years
Lagged dependent	0.403** (0.101)	0.411** (0.104)	0.421** (0.106)	0.429** (0.107)
Containment and health index	0.111** (0.022)	0.087** (0.021)	0.059** (0.019)	0.034* (0.017)
Observations	2600	2600	2600	2600
R squared	0.988	0.988	0.989	0.989
F statistic	64.48	63.42	62.43	61.82
	80 years and over
Lagged dependent	0.621** (0.069)	0.632** (0.071)	0.645** (0.072)	0.653** (0.071)
Containment and health index	0.091** (0.019)	0.062** (0.019)	0.033 (0.019)	0.010 (0.017)
Observations	2600	2600	2600	2600
R squared	.994	0.994	0.994	0.994
F statistic	218.88	216.20	214.45	213.76

Notes: ** (**) denote significance at p < 0.001 (p < 0.05). The dependent variable is the logarithm to weekly all-cause mortality in the first half of 2017, 2018, 2019, and 2020 in each of the four age groups in the panel headlines. All estimates are obtained with an OLS estimator with country, year, and week fixed effects.

6. Conclusions

The lockdowns in most Western countries have thrown the world into the most severe recession since World War II and the most rapidly developing recession ever seen in mature market economies. They have also caused an erosion of fundamental rights and the separation of powers in large part of the world as both democratic and autocratic regimes have misused their emergency powers and ignored constitutional limits to policy making (Bjørnskov and Voigt 2020). It is therefore important to evaluate whether and to which extent the lockdowns have worked as officially intended: to suppress the spread of the Sars-CoV-2 virus and prevent deaths associated with it.

Comparing weekly mortality in 24 European countries, the findings in this paper suggest that more severe lockdown policies have not been associated with lower mortality. In other words, the lockdowns have not worked as intended. Further tests also show that early interventions offered no additional benefits or effectiveness and even indicate that the lockdowns of the spring of 2020 were associated with significantly more deaths in the particular age group between 60 and 79 years.

These general findings are consistent with the results of previous papers using a variety of simpler methods to test the effects of lockdowns. Contrary to persistent political claims, as indicated by recent research in Bendavid et al. (2021), the traditional approach of carefully disseminating public information about the epidemic and relying on voluntary measures may have represented the only policy significantly associated with fewer cases than no reaction at all, although almost all other countries went substantially further. Likewise, much has been made of the timing of lockdowns, but the present analysis does not indicate that early lockdowns were more effective. Examples also suggest that lockdown timing may not have been a significant determinant of mortality development: while Belgium and Portugal were among the countries that locked down soon after seeing the first COVID-related death, the former saw an 11% increase in mortality, compared with the preceding three years, while the latter only saw a 2% increase. Among countries that locked down later, the UK experienced an 18% higher mortality than the preceding years, while German mortality in the first half of 2020 was almost exactly average for the time of the year. As such, the data illustrate that strategic examples as are often used in popular media can be highly misleading, which necessitates a more comprehensive evaluation of lockdown efficacy.

The main problem at hand is therefore that the evidence presented here suggests that lockdowns have not significantly affected the development of mortality in Europe. They have nevertheless wreaked economic havoc in most societies and may lead to a substantial number of additional deaths for other reasons. A British government report from April for example assessed that a limited lockdown could cause 185,000 excess deaths over the next years, while UNICEF warns of an increase in child marriages, owing to the economic effects of Western lockdowns in developing countries (DHSC 2020; Philipose and Aika 2021). Evaluated as a whole, at a first glance, the lockdown policies of the Spring of 2020 therefore appear to be substantial long-run government failures.

Appendix

Table A1.

. Descriptive statistics

	Mean	Standard deviation	Observations
Log weekly mortality	7.405	1.454	2704
Log mortality, 0–39 years	3.549	1.296	2658
Log mortality, 40–59 years	4.920	1.445	2701
Log mortality, 60–79 years	6.358	1.439	2704
Log mortality, 80 years and over	6.771	1.489	2704
Policy stringency index	9.499	23.043	3078
Containment and health index	9.335	22.630	3078
Benefit INEP	0.497	0.211	3192

Table A2.

. Countries included

Country	Rel. mortality	Lockdown timing	Country	Rel. mortality	Lockdown timing
Austria	1.01	16/0	Latvia	0.92	11/–19
Belgium	1.11	39/3	Lithuania	0.965	–5/–7
Bulgaria	0.94	5/2	Luxembourg	0.86	12/–1
Czechia	0.87	10/–11	Netherlands	1.02	14/6
Denmark	0.97	12/1	Norway	0.97	15/0
Estonia	0.98	16/–11	Poland	0.84	8/0
Finland	0.99	43/–9	Portugal	1.02	10/-4
France	0.99	49/28	Slovakia	0.82	4/-8
Germany	0.98	42/0	Spain	1.19	39/26
Hungary	0.94	7/–4	Sweden	1.09	48/8
Iceland	0.99	17/–1	Switzerland	1.00	17/8
Italy	0.97	22/0	United Kingdom	1.19	51/17

Note: the second column numbers are mortality rates in the first half of 2020 relative to the average of 2017–2019; the numbers in the second columns are the number of days from the first registered Sars-Cov-2 case/death and the day the stringency index passed a value of 40.