Population Coding of Natural Electrosensory Stimuli by Midbrain Neurons

Abstract

Natural stimuli display spatiotemporal characteristics that typically vary over orders of magnitude, and their encoding by sensory neurons remains poorly understood. We investigated population coding of highly heterogeneous natural electrocommunication stimuli in Apteronotus leptorhynchus of either sex. Neuronal activities were positively correlated with one another in the absence of stimulation, and correlation magnitude decayed with increasing distance between recording sites. Under stimulation, we found that correlations between trial-averaged neuronal responses (i.e., signal correlations) were positive and higher in magnitude for neurons located close to another, but that correlations between the trial-to-trial variability (i.e., noise correlations) were independent of physical distance. Overall, signal and noise correlations were independent of stimulus waveform as well as of one another. To investigate how neuronal populations encoded natural electrocommunication stimuli, we considered a nonlinear decoder for which the activities were combined. Decoding performance was best for a timescale of 6 ms, indicating that midbrain neurons transmit information via precise spike timing. A simple summation of neuronal activities (equally weighted sum) revealed that noise correlations limited decoding performance by introducing redundancy. Using an evolution algorithm to optimize performance when considering instead unequally weighted sums of neuronal activities revealed much greater performance values, indicating that midbrain neuron populations transmit information that reliably enable discrimination between different stimulus waveforms. Interestingly, we found that different weight combinations gave rise to similar discriminability, suggesting robustness. Our results have important implications for understanding how natural stimuli are integrated by downstream brain areas to give rise to behavioral responses.

SIGNIFICANCE STATEMENT We show that midbrain electrosensory neurons display correlations between their activities and that these can significantly impact performance of decoders. While noise correlations limited discrimination performance by introducing redundancy, considering unequally weighted sums of neuronal activities gave rise to much improved performance and mitigated the deleterious effects of noise correlations. Further analysis revealed that increased discriminability was achieved by making trial-averaged responses more separable, as well as by reducing trial-to-trial variability by eliminating noise correlations. We further found that multiple combinations of weights could give rise to similar discrimination performances, which suggests that such combinatorial codes could be achieved in the brain. We conclude that the activities of midbrain neuronal populations can be used to reliably discriminate between highly heterogeneous stimulus waveforms.

Introduction

Understanding how neural populations process incoming sensory information remains a central problem in systems neuroscience. Indeed, population coding has been studied extensively both theoretically and experimentally (Georgopoulos et al., 1986; Abbott and Dayan, 1999; Averbeck et al., 2006; Ecker et al., 2010; Kohn et al., 2016; Mendels and Shamir, 2018). Of particular interest are the effects of correlations between the trial-to-trial variabilities of neural responses to repeated presentations of a given stimulus (i.e., “noise correlations”). On the one hand, noise correlations are thought to introduce redundancy between neural activities and thus should be eliminated or, at the very least, reduced in magnitude (Averbeck and Lee, 2006; Ecker et al., 2010). However, noise correlations can vary depending on stimulus attributes, which can introduce synergy to benefit coding (Moreno-Bote et al., 2014; Lin et al., 2015; Franke et al., 2016; Zylberberg et al., 2016). However, most studies of population coding to date have considered artificial stimuli because of their relative simplicity. As such, population coding of natural stimuli that are often complex because of their rich spatiotemporal structure (Attias and Schreiner, 1997; Simoncelli and Olshausen, 2001; Mante et al., 2005; Fotowat et al., 2013; Henninger et al., 2018) has been much less investigated to date (Mizrahi et al., 2014; Yoshida and Ohki, 2020). In particular, because single-neuron responses to natural stimuli cannot be predicted from their responses to artificial stimuli in general (Mizrahi et al., 2014), there is reason to believe that the strategies used by neural populations to encode natural stimuli will differ from those used to encode artificial stimuli.

Gymnotiform wave-type weakly electric fish generate an electric field around their body through an electric organ discharge (EOD) and can sense perturbations of this field through an array of electroreceptors distributed on their skin. Electroreceptors make synaptic contact onto pyramidal cells within the electrosensory lateral line lobe (ELL), which in turn project to downstream brain areas such as the torus semicircularis (TS; Bell and Maler, 2005). There are ∼50 different neuron types within TS described in the literature that contribute to electrosensory processing (Carr et al., 1981; Carr and Maler, 1985), which translates to large heterogeneities in responses to sensory input (Vonderschen and Chacron, 2011). Natural electrosensory stimuli comprise those caused by objects such as prey (Nelson and MacIver, 1999) as well as those caused by conspecifics (Zakon et al., 2002; for review, see Metzen, 2019). In the latter case, natural electrocommunication stimuli (i.e., “chirps”) consist of transient increases in EOD frequency that occur on top of the underlying sinusoidal background beat (Zupanc and Maler, 1993; Engler et al., 2000; Bastian et al., 2001; for review, see Zupanc, 2002; Kolodziejski et al., 2005). Chirp attributes (e.g., amplitude, duration) vary over a wide range for a given species (Zupanc and Maler, 1993; Zakon et al., 2002), which gives rise to a rich repertoire of different stimulus waveforms (for review, see Metzen, 2019). The coding of chip stimuli by electrosensory neurons has been the focus of previous studies (Benda et al., 2005, 2006; Marsat et al., 2009; Marsat and Maler, 2010; Vonderschen and Chacron, 2011; Walz et al., 2013, 2014; Metzen et al., 2016, 2020; Metzen and Chacron, 2017 for review, see Metzen, 2019). However, these have either considered single neurons or used nonsimultaneous recordings to study population coding, such that the effects of noise correlations were ignored.

Materials and Methods

Ethics statement.

All animal procedures were approved by the McGill University animal care committee (#5285) and were performed in accordance with the guidelines of the Canadian Council on Animal Care. All fish were immobilized by an intramuscular injection of 0.1–0.5 mg of tubocurarine before experiments.

Animals.

The wave-type weakly electric fish Apteronotus leptorhynchus (N = 3) of either sex was used exclusively in this study. Animals of either sex were purchased from tropical fish suppliers and were housed in groups (2–10) at controlled water temperatures (26–29°C) and conductivities (300–800 µS/cm) according to published guidelines (Hitschfeld et al., 2009).

Surgery.

Surgical procedures have been described in detail previously (Chacron et al., 2003; Toporikova and Chacron, 2009; Metzen et al., 2015). Briefly, 0.1–0.5 mg of tubocurarine (Sigma-Aldrich) was injected intramuscularly to immobilize the animals for electrophysiology experiments. The animals were then transferred to an experimental tank (30 × 30 × 10 cm) containing water from the animal's home tank and respired by a constant flow of oxygenated water through their mouth at a flow rate of 10 ml/min. Subsequently, the head of the animal was locally anesthetized with lidocaine ointment (5%; AstraZeneca), the skull was partly exposed, and a small window (∼5 mm²) was opened over the midbrain.

Stimulation.

The electric organ discharge of A. leptorhynchus is neurogenic, and therefore is not affected by the injection of curare. All stimuli consisted of amplitude modulations (AMs; or beats) of the EOD of the animal and were produced by triggering a function generator to emit one cycle of a sine wave for each zero crossing of the EOD, as done previously (Bastian et al., 2002). The frequency of the emitted sine wave was set slightly higher (30 Hz) than that of the EOD, which allowed the output of the function generator to be synchronized to the discharge of the animal. The emitted sine wave was subsequently multiplied with the desired AM waveform (MT3 Multiplier, Tucker-Davis Technologies), and the resulting signal was isolated from the ground (A395 Linear Stimulus Isolator, World Precision Instruments). The isolated signal was then delivered through a pair of chloridized silver wire electrodes placed 15 cm away from the animal on either side of the recording tank perpendicular to the rostrocaudal axis of the fish.

To elicit neuronal responses, we generated chirps with different attributes by systematically varying the chirp duration (8, 11, 14, 17, 20, 53, 141, 376, and 1000 ms), the amplitude (10, 35, 60, 85, and 110 Hz), and the phase (0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°) of the underlying beat cycle at which the chirp occurs (Fig. 1b). Importantly, when varying chirp duration or amplitude, we considered chirps occurring at either phase 90° or 270° of the beat cycle, on top of a sinusoidal beat with frequency f_beat = 4 Hz, as done previously (Vonderschen and Chacron, 2011; Metzen et al., 2016). As such, we used a total of 36 different chirp waveforms (18 for chirp duration, 10 for chirp amplitude, 8 for chirp phase). Parameter ranges were chosen to contain those observed in previous studies (Zupanc and Maler, 1993; Engler and Zupanc, 2001; Zupanc et al., 2006; Metzen et al., 2020), including durations that cover those of other electrocommunication signals such as long frequency rises (Kolodziejski et al., 2005) or long chirps (Henninger et al., 2018). It is important to note that the chirp amplitude is not equivalent to the actual spectral frequency content of the resulting AM stimulus, which is 50–100 Hz (Zupanc and Maler, 1993). We chose a 4 Hz beat because, as mentioned above, this was the frequency used in previous studies (Metzen et al., 2016, 2020). We note that the chirp stimuli considered here were consistently most frequently produced when the frequency difference between both animals was lowest for various conditions (Zupanc and Maler, 1993; Bastian et al., 2001; Engler and Zupanc, 2001; Hupé and Lewis, 2008). Previous studies have furthermore demonstrated a sex dimorphism in EOD frequency for A. leptorhynchus in that males have significantly higher EOD frequencies than females (Meyer et al., 1987; Zupanc et al., 2014). As such, same-sex encounters will on average lead to lower beat frequencies than opposite-sex encounters (Benda et al., 2006). To measure the stimulus intensity, a small dipole was placed close to the skin of the animal. Stimulus intensity was adjusted to produce changes in EOD amplitude that were ∼20% of the baseline level, as done previously (Metzen et al., 2016, 2020; Metzen and Chacron, 2017). Finally, each chirp stimulus waveform (i.e., a chirp with given duration, amplitude, or phase) was presented 60 times (i.e., 60 trials) with ∼1.5 s between subsequent presentations, followed by another waveform. We note that midbrain neurons do not display adaptation to repeated presentations of a given chirp stimulus (Vonderschen and Chacron, 2011; Metzen et al., 2016; see also Fig. 4).

Figure 1.

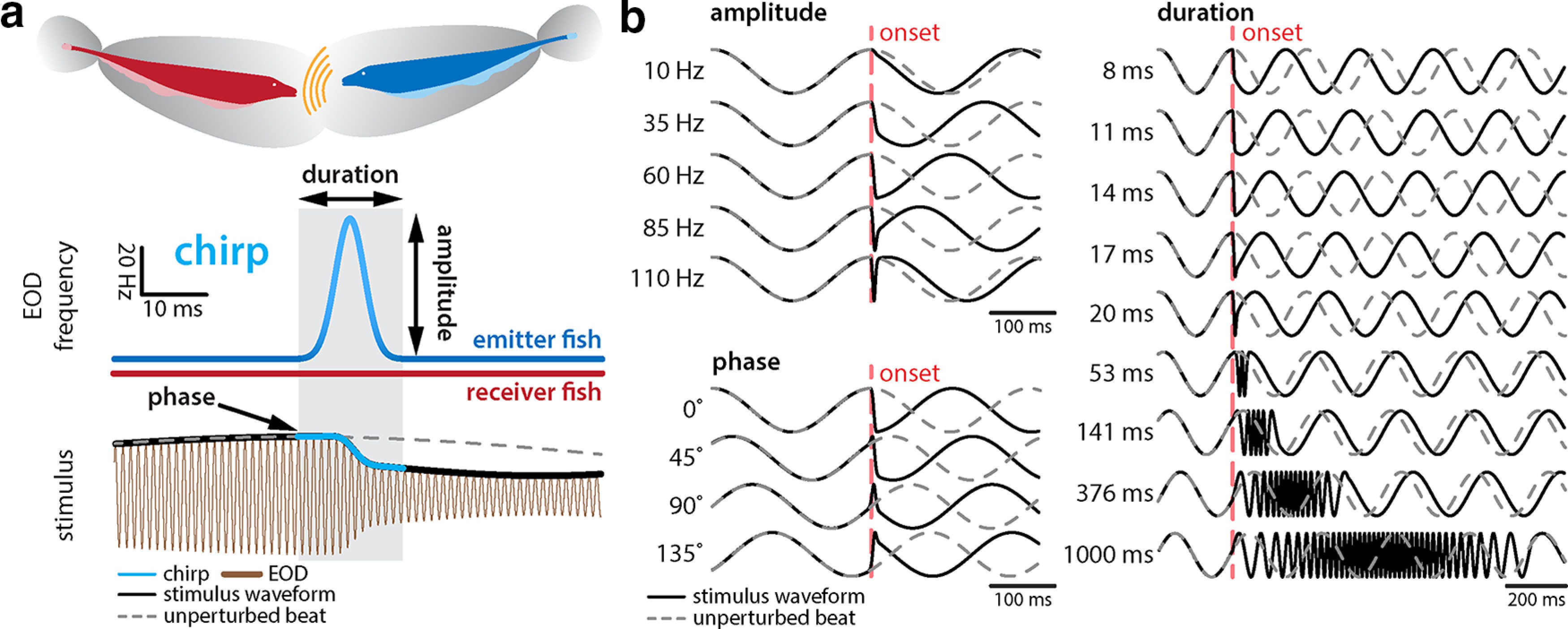
Chirp-induced AM waveforms are highly heterogeneous. a, During a chirp event, the EOD frequency (middle, blue trace) of the emitter fish (top, blue) is transiently increased by the maximum of amplitude for a brief duration (light blue, shaded box) while the EOD frequency (middle, red trace) of the receiver fish (top, red) remains constant. This can be characterized by the duration and amplitude of the frequency excursion. The chirp results in a phase advance of the beat (i.e., the beat will reach its maximum value earlier than if no chirp occurred; compare solid black with dashed gray). The chirp is shown in light blue. b, AM waveforms obtained by varying different parameters (black curves; left top, fixed chirp duration and phase, varying chirp amplitude; left bottom, fixed chirp duration and amplitude, varying chirp phase; right, fixed chirp phase and amplitude, varying chirp duration). Also shown are unperturbed beat waveforms (dashed gray). Note that different chirps give rise to different phase advances of the beat. The red dashed horizontal lines indicate chirp onset.

Figure 4.

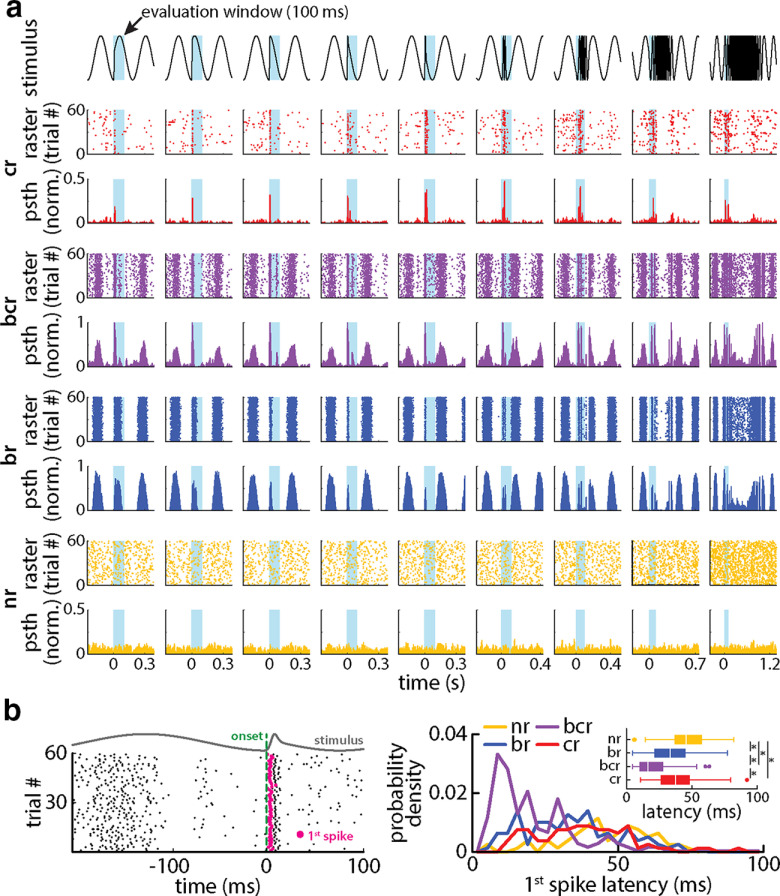
TS single neuronal responses to chirp stimuli are highly heterogeneous. a, Raster plots and time-dependent firing rate responses of four example midbrain neurons to different chirp waveforms (shaded box). The first neuron (red) strongly responded to the chirp waveform in a more or less invariant manner but not at all to the beat. The second (purple) responded to the chirp waveform but also phase locked to the beat. As such, the phase reset of the beat because of the chirp waveform also altered the response of this neuron. The third neuron (blue) responded to the beat but not to the chirp. The fourth neuron (yellow) did not respond to either the beat or the chirp. b, Left, Schematic of how response latencies were estimated for the first spike (magenta) occurring after a chirp onset (green dotted vertical line). Right, Probability distributions of the first spike latencies of the four neurons response classes (nr, yellow; br, blue; bcr, purple; cr, red). Inset, Boxplots showing the spike latencies obtained from the four response classes. The first spike latencies for bcr neurons are significantly lower than those of all other response classes (right inset; one-way ANOVA: df = 3, F = 52.66, p_bcr,nr = 2.35 * 10⁻²⁶, p_bcr,br = 3.75 * 10⁻¹¹, p_bcr,cr = 4.75 * 10⁻¹⁵, Bonferroni corrected).

Recordings.

Simultaneous extracellular recordings from TS neurons were made using Neuropixel probes (Imec). Recordings were digitized at 30 kHz using spikeGLX (Janelia Research Campus, Howard Hughes Medical Institute) and stored on a hard drive for further analysis. Spikes were sorted using Spike2 (Cambridge Electronic Design), because we did not observe any drifting of spiking activity across channels or record more than a maximum of three neurons on any single channel. In fact, most channels contained a single well isolated neuron (Fig. 2a, right). Overall, we recorded from a total of N = 158 neurons (40 for session 1, 28 chirp stimuli; 77 for session 2, 36 chirp stimuli; and 41 for session 3, 36 chirp stimuli). However, not all neurons were stable over the entire stimulus protocol such that only a subpopulation could be extracted that received a common set of stimuli (28 for session 1; 27 for session 2; 2 for session 3). The average baseline firing rate for our dataset was 14.0 ± 16.8 spikes (spk)/s, which is slightly higher than those obtained in previous studies (Vonderschen and Chacron, 2011; McGillivray et al., 2012; Metzen et al., 2016), which is in part because of the fact that we did not exclude neurons that did not respond to the stimuli presented. Overall, similar results were seen for all three recording sessions. Distances between neurons were computed as the distance between probe sites on which the action potentials of recorded neurons were highest. We note that the geometry of the recording channels on the Neuropixel probes could introduce “gaps” when calculating neuronal distances, as not all channels may contain sortable spikes. Based on the fact that the Neuropixel probe consists of 384 parallel recording channels (checkerboard, two columns) on a 10-mm-long shank with distances of 16 µm (column) and 20 µm (row; Jun et al., 2017), distances primarily reflect vertical distances along the probe shaft. The probe was angled at ∼15° with respect to vertical in order for the shaft to be approximately perpendicular to the layers of TS and advanced between 1500 and 2000 µm into TS with reference to the probe tip. As such, the reported distances primarily reflect distances across rather than within TS layers. Neurons were recorded at depths between 300 and 1900 µm from the brain surface. Of all neurons recorded from, ∼60% were located within the first 1000 µm and were thus mostly located within the first five layers of TS.

Figure 2.

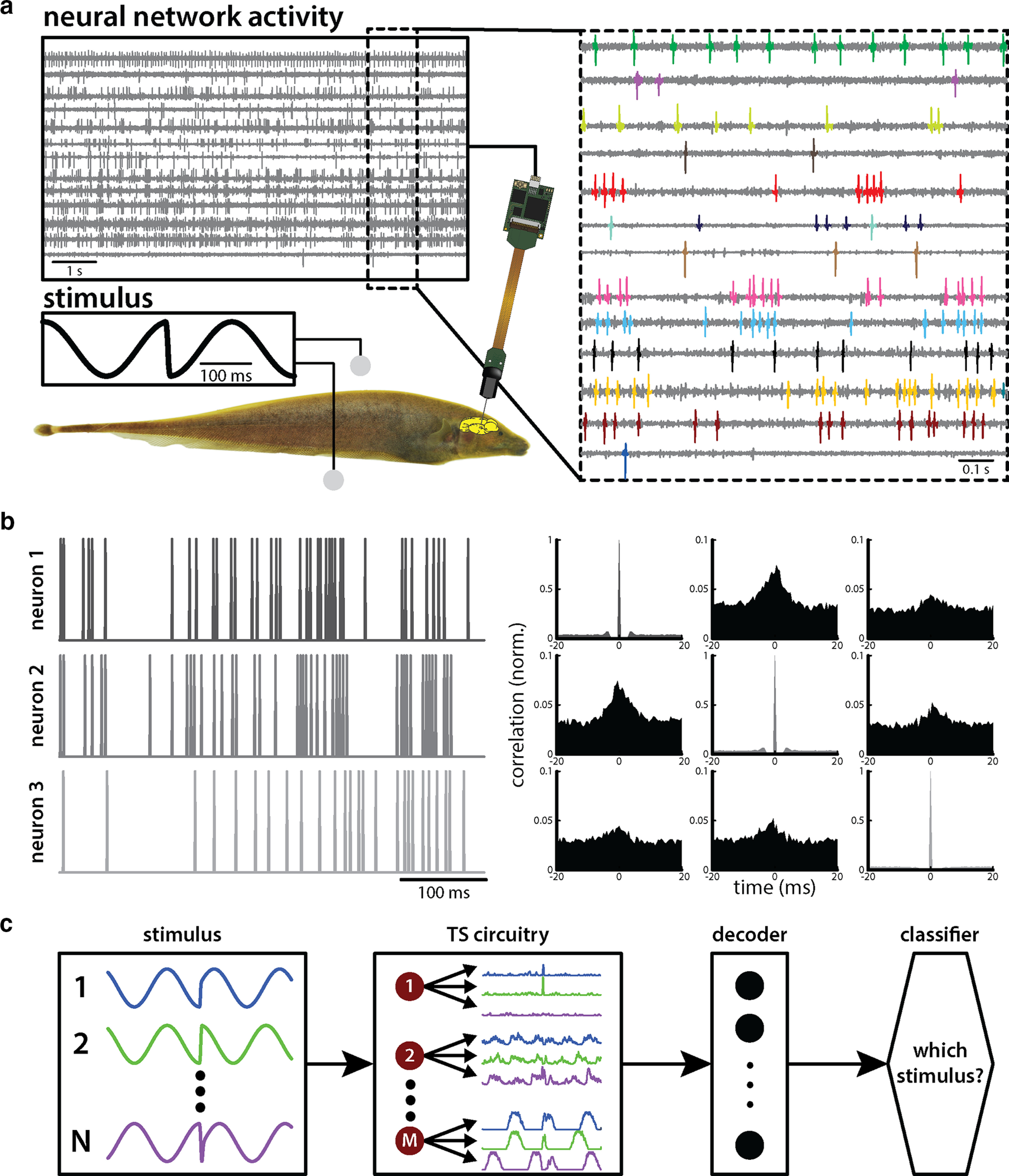
Methodologies used in this study. a, Schematic showing the experimental setup. A fish is placed in an otherwise empty tank and is stimulated (middle left) while neuronal activity (top left and right) is recorded. b, Left, Simultaneously recorded neurons display differential levels of baseline correlations as shown by the spike trains of three example neurons. Right, Autocorrelation and cross-correlation functions among these three different neurons. c, A set of electrocommunication stimuli with varying parameters (N, left) elicits differential responses in neurons within the midbrain torus semicircularis (TS, M, middle, left). These responses have to be decoded by downstream areas (middle, right) so as to optimally discriminate among the individual stimuli (right).

Data analysis.

Sorted and curated spike times for each neuron were converted into “binary” sequences sampled at 2 kHz. The content of a given bin was set to 2000 if a spike occurred within it and 0 otherwise. We note that, as the bin width was smaller than the refractory period of TS neurons, there can be at most one spike occurring during any given bin. The time-dependent firing rate of neuron i, $X_i\left(t\right)$, was obtained by filtering the binary sequence using a box-car filter with 6 ms. Latencies for single-neuron responses were estimated from the first spike after stimulus onset.

Determining neuron response type.

To quantify the response to the chirp, we used the chirp selectivity index (CSI) to determine whether a given neuron responded to the chirp as done previously (Vonderschen and Chacron, 2011), as follows:

$$\mathrm{C}\mathrm{S}\mathrm{I}=\frac{R_{\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{r}\mathrm{p}}-R_{\mathrm{b}\mathrm{e}\mathrm{a}\mathrm{t}}}{R_{\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{r}\mathrm{p}}+R_{\mathrm{b}\mathrm{e}\mathrm{a}\mathrm{t}}},$$ (1)

where R_chirp is the maximum firing rate obtained in a peristimulus time histogram (PSTH) during a time window of 100 ms starting with chirp onset, and R_beat is the maximum firing rate obtained during the ongoing beat in a time window of 2 s ending on chirp onset. The CSI ranges between −1 and 1, representing perfect selectivity for the beat at −1 and the chirp at 1. To measure the selectivity of a neuron to multiple chirp stimuli, the average CSI was used, as follows:

$${\mathrm{C}\mathrm{S}\mathrm{I}}_{\mathrm{a}\mathrm{v}\mathrm{g}}=\frac{1}{N}\sum _{i=1}^N{\mathrm{C}\mathrm{S}\mathrm{I}}_i,$$ (2)

where N is the number of chirp stimuli tested and CSI_i is the CSI to chirp stimulus i.

We also quantified neuronal gain to the 4 Hz background beat, which was measured as the ratio between the amplitude of the sinusoidal beat stimulus as extracted from the dipole recording by performing a Hilbert transform and low-pass filtering and the amplitude of the neuronal firing rate modulation.

CSI and gain were used to capture the response types of all neurons recorded. Because a negative CSI value only indicates the preference of a neuron response to the beat but not to the chirp, it is thus not able to correctly differentiate between nonresponding and beat-responding neurons. We thus used the gain to the beat to further distinguish between these two response types. As such, neurons that had an average CSI of ≥0.1 for all chirp stimuli presented where regarded as responding to the chirp, as done previously (Vonderschen and Chacron, 2011). Neurons with gain to the 4 Hz background beat ≥2 spk/s (mV/cm) where regarded as responding to the beat. Based on their response characteristics to the beat and the chirp, neurons were classified as follows: (1) beat responders [“br”; neurons that exclusively responded to the beat, but not to the chirp (i.e., CSI < 0.1 and gain ≥ 2 spk/s (mV/cm); 16 (57%) for session 1; 8 for session 2 (30%); 2 for session 3 (100%)]; (2) beat and chirp responders [“bcr”; neurons that responded to the beat as well as to the chirp (i.e., CSI ≥ 0.1 and gain ≥ 2 spk/s (mV/cm); 5 for session 1 (18%); 6 for session 2 (22%); 0 for session 3 (0%)]; (3) chirp responders [“cr”; neurons that responded exclusively to the chirp (i.e., CSI ≥ 0.1 and gain < 2 spk/s (mV/cm); 4 for session 1 (14%); 2 for session 2 (7%); 0 for session 3 (0%)]; and (4) nonresponders (“nr”; neurons that neither responded to the beat nor the chirp (i.e., CSI < 0.1 and gain < 2 spk/s (mV/cm); 3 for session 1 (11%); 11 for session 2 (41%); 0 for session 3 (0%)].

Computing signal and noise correlations.

We quantified correlations between neuron activities from all neurons (N = 158) recorded during all three recording sessions using spike count sequences that were obtained from each binary spike train (i.e., unfiltered) by counting the number of spikes occurring during successive and nonoverlapping 20 ms time windows that were always aligned with respect to the onset of the chirp stimulus during a 100 ms evaluation time window. This value was chosen because it comprises the neural response for most of the stimuli considered. In the case of larger durations, this time window comprises the initial portion of the response. We then computed the correlation coefficient between the two spike count sequences using Pearson's correlation coefficient between spike counts, as follows:

$$r_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left(n_1{n}_2\right)}{\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}\left(n_1\right)\mathrm{V}\mathrm{a}\mathrm{r}\left(n_2\right)}}.$$ (3)

To compute signal correlations, the 60 stimulus trials were first randomly permuted, and the spike count sequences were then recomputed (i.e., the timing of spikes within each trial is fixed). Signal correlations were then computed using Equation 3 on the shuffled spike counts and were averaged over 60 independent realizations of the shuffling procedure. Finally, noise correlations were computed as the correlation coefficient between the spike count residual sequences. The spike count sequences were first averaged over trials, and the mean spike count sequence (i.e., that because of the stimulus) was then subtracted from the spike counts for each trial to obtain the residual spike count sequences. As such, the residual spike count sequences represent the component of the neural response that cannot be explained by a given chirp stimulus waveform (i.e., “noise”) because, unlike the stimulus waveform itself, these are not constant across trials.

Ascertaining statistical significance for obtained correlation coefficient values.

The significance of correlations for each pair was determined in the following way. For each spike train, the sequence of interspike intervals (i.e., the times between consecutive action potentials) was obtained and then randomly shuffled using a permutation of the integers (i.e., the function “randperm” in MATLAB), and the spike times were then obtained by performing a cumulative sum (i.e., the function “cumsum” in MATLAB). Correlations were computed from the shuffled spike trains in otherwise the same manner as for the raw data as described above. The procedure was repeated 100 times to obtain the distributions of correlation coefficients. Correlation coefficients obtained from the raw (i.e., unshuffled) data were deemed to be significant if their probability of occurrence was <0.05 based on the distributions obtained from shuffled data. The mean shuffled signal and noise correlations for each possible pair for all distributions were not significantly different from zero (one-sample t test, n = 3572, p_signal > 0.05; p_noise > 0.05).

Classifier.

We used a classifier to quantify the performance of TS neuronal populations at stimulus discrimination. We combined TS neurons using either equally or unequally weighted sums for each chirp stimulus. For each individual chirp stimulus, the combined response (i.e., either an equally or unequally weighted sum of neural responses) to a random trial was taken as the template for a given chirp stimulus waveform. Next, each combined response was assigned as being generated by the stimulus that gave rise to a given template based on whether the distance between the combined response and the template was the minimum. We thus constructed a “confusion matrix” whose element (i,j) gives the probability that a response was assigned as being generated by stimulus j given that it was actually generated by stimulus i (Jamali et al., 2016, 2019). The diagonal elements of this matrix are the probabilities that a stimulus was correctly assigned, whereas nonzero off-diagonal elements indicate misclassification. For each confusion matrix obtained from the metric-space analysis, we computed the discrimination performance by averaging over the diagonal elements. The discrimination performance can thus vary between 0 (no discrimination) and 1 (perfect discrimination). Note that the chance level for discrimination performance was 0.0278 (i.e., 1 of 36) because we used a total of 36 different chirp stimuli. The distance between combined neuron activities was computed using the metric of van Rossum (2001). First, the combined neuronal activities were convolved with a decaying exponential kernel with time constant τ, as follows:

$$f\left(t\right)={\sum }_{i=1}^{M}H(t-t_i)e^{\frac{-(t-t_i)}{\tau }},$$ (4)

where t_i is the ith spike time, M is the total number of spikes, and H(t) is the Heaviside step function [H(10) = 0 if x < 0 and H(10) = 1 if x ≥ 0]. Next, the distance was then computed as the euclidian distance between convolved combined neuronal activities fR_j and fR_k, as follows:

$${D(f_{R_j},f_{R_k})}_{\tau }=\sqrt{\frac{1}{\tau }\int {\left[f_{R_j}-f_{R_k}\right]}^{2}dt}.$$ (5)

We varied τ between 1 and 100 ms to evaluate the effects of precise spike timing on classification. When the value of τ is small, the metric takes into account spike timing, whereas, when the value of τ is larger, the metric takes into account slower changes in firing rate. We also varied the chirp evaluation window between 20 and 1000 ms to evaluate the effects of the ongoing beat on discrimination performance (see Fig. 9). Performances reported in this article were averaged over templates, and error bars were generated over the total number of simulations for different τ and chirp evaluation windows (see Figs. 7e, 8c, middle, bottom, 9) or by bootstrapping for different population sizes (i.e., 100 random chosen neuron responses per population size k for n_k < n; see Figs. 7d, 8b, middle, bottom).

Figure 9.

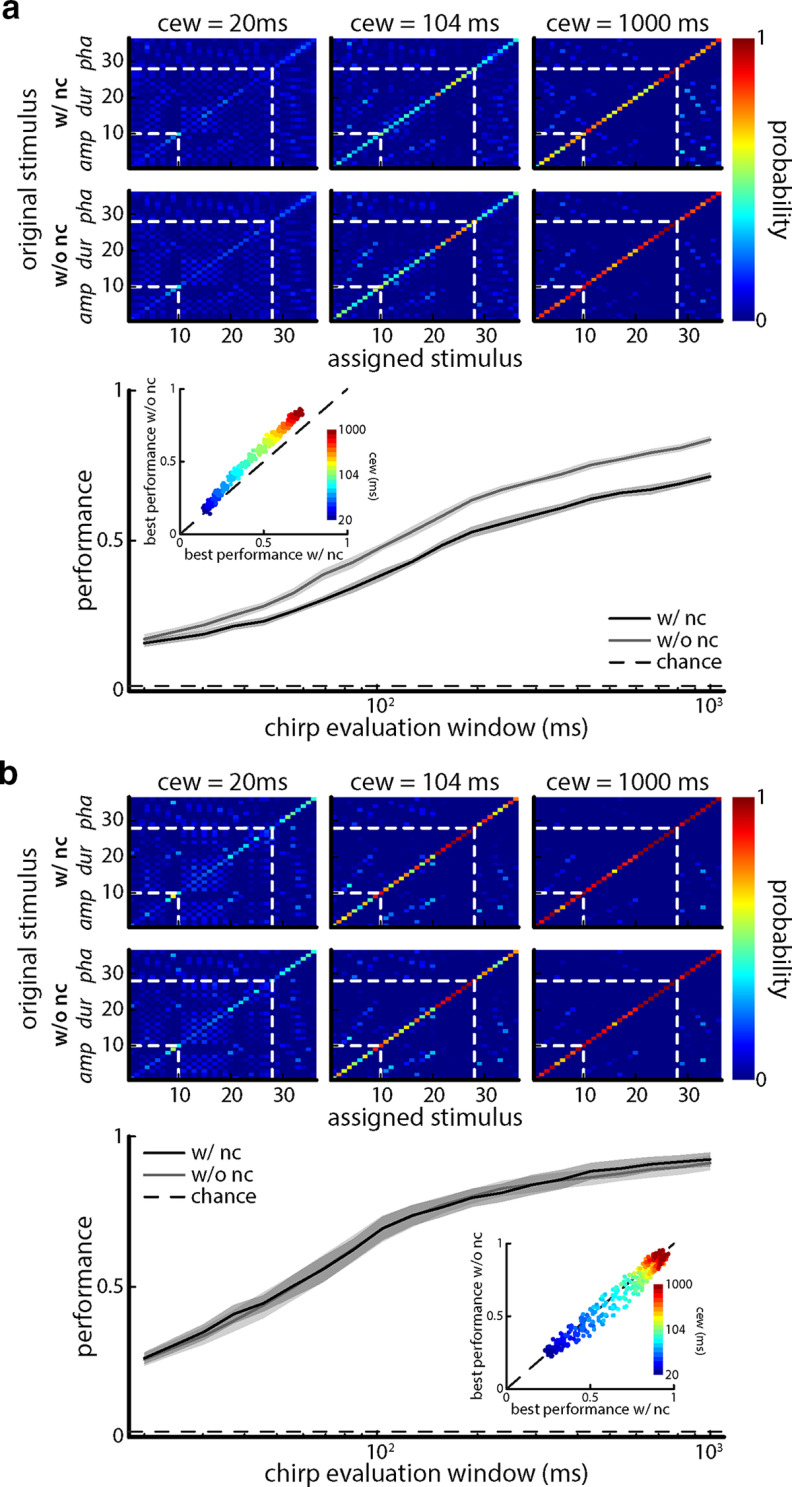
Performance increases for larger chirp evaluation windows. a, Top, Confusion matrices showing the conditional probability of assessing an equally weighted neuronal population response as being caused by stimulus i when it was actually caused by stimulus j computed from metric space analysis using the van Rossum measure with timescale τ = 6 ms, and a population size of 27 neurons for chirp evaluation window sizes of 20 ms (left), 104 ms (middle), and 1000 ms (right) with (top) and without (middle) noise correlations. The white dashed lines indicate borders between blocks of stimuli for which a given attribute (e.g., amplitude, duration, phase) was varied. Bottom, Discrimination performance as a function of chirp evaluation window with (black) and without (gray) noise correlation for the unequally weighted case. The dashed line indicates chance level (1 of 36 stimuli). Inset, Performance without noise correlations plotted against performance with noise correlations for the equally weighted case with color-coded chirp evaluation window size. b, Top, Same as a, but for the unequally weighted case with (top) and without (middle) noise correlations. Bottom, Discrimination performance as a function of chirp evaluation window with (black) and without (gray) noise correlations. The dashed line indicates chance level (1 of 36 stimuli). Inset, Performance without noise correlations plotted against performance with noise correlations for the unequally weighted case with color-coded chirp evaluation window size.

Figure 7.

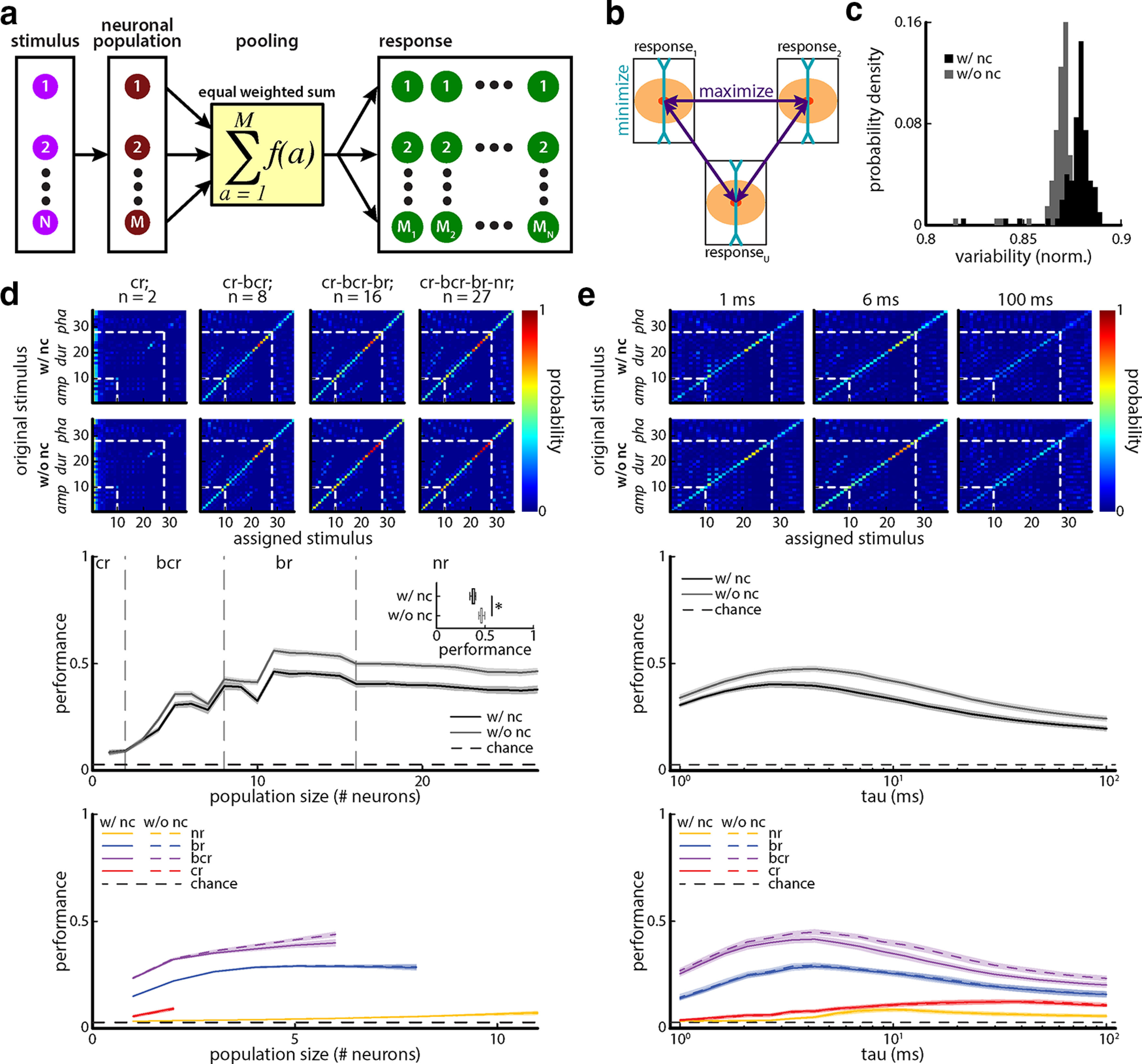
Noise correlations have detrimental effects on discrimination performance when taking the equally weighted sum of neuronal activities. a, Schematic showing how the population response to each stimulus (M₁ – M_N) was obtained by summing the responses (M) of each neuron to a given chirp stimulus for the equally weighted case. b, Theoretical assumption illustrating that the population response variability to individual stimuli should be minimized while the response distances should be maximized to optimally discriminate among individual stimuli. c, Variability probability densities with (black) and without (gray) noise correlations. The response variability to our 36 different chirp stimuli is significantly lower when noise correlations have been removed from our population by shuffling compared with the same population with noise correlations (one-way ANOVA: df = 3 F = 1.12 * 10⁴, p = 1.57 * 10⁻⁷, Bonferroni corrected). d, Top, Confusion matrices showing the conditional probability of assessing an equally weighted population response to be caused by stimulus i when it was actually caused by stimulus j computed from metric-space analysis using the van Rossum measure with timescale τ = 6 ms for population sizes of 2 (left), 8 (middle left), 16 (middle right), and 27 (right) neurons with (top) and without (bottom) noise correlations. The white dashed lines indicate borders between blocks of stimuli for which a given attribute (e.g., amplitude, duration, phase) was varied. Middle, Discrimination performance as a function of population size with (black) and without (gray) noise correlation for the equally weighted case. The dashed line indicates chance level (1 of 36 stimuli). Note that the jumps in performance occur when neurons with better discrimination performance are added. Inset, Performance with (black) and without (gray) noise correlations for population size of 27 were significantly different from one another (with noise correlations vs without noise correlations; one-way ANOVA: df = 3, F = 71.69, p = 2.38 * 10⁻¹³, Bonferroni corrected). Bottom, Discrimination performance as a function of population size with (solid) and without (dashed) noise correlation for the equally weighted case when neuronal populations consisting only of neurons of a given type (i.e., nr, br, bcr, and cr) are considered. e, Top, Same as c, but now for a population size of n = 27 neurons with (top) and without (bottom) noise correlations but for timescales of 1 ms (left), 6 ms (middle), and 100 ms (right). Middle, Discrimination performance of the equally weighted population as a function of timescale with (black) and without (gray) noise correlations. The dashed line indicates chance level (1 of 36 stimuli). Bottom, Discrimination performance as a function of timescale with (solid) and without (dashed) noise correlation for the equally weighted case when neuronal populations consisting only of neurons of a given type (i.e., nr, br, bcr, and cr) are considered.

Figure 8.

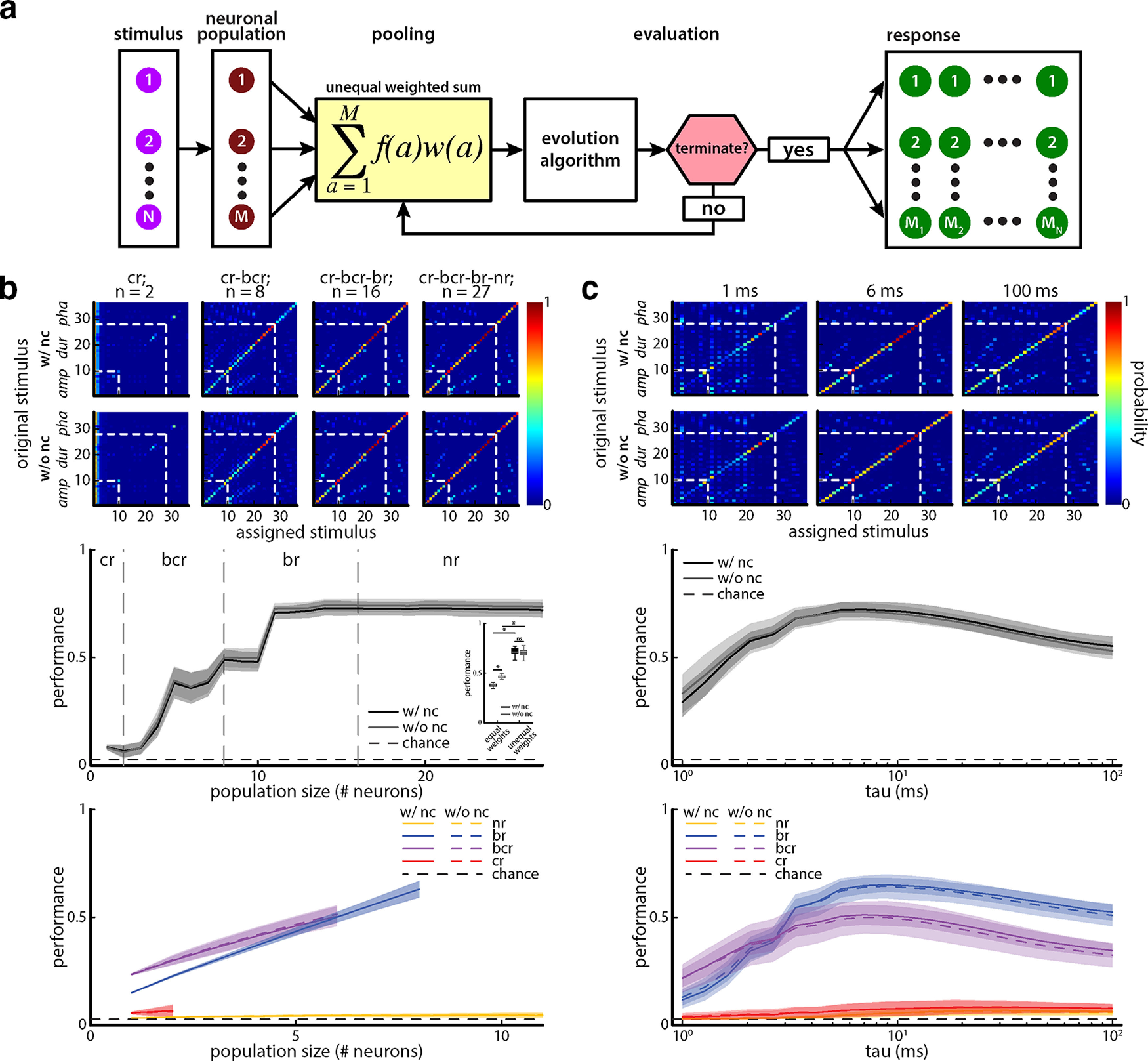
Taking an unequally weighted sum of neuronal activities greatly improves performance and mitigates the deleterious effects of noise correlations. a, Schematic illustrating how individual weights were obtained by an iterative EA. First, each neuronal response (M, left, dark red) to a given stimulus (left, pink) is weighted (middle, yellow) and its discrimination performance is compared with that of the previous iteration. If the discrimination performance is better, the respective weight value is kept; if not, a new weight value is generated by the EA (see Materials and Methods). This procedure is performed for each agent (middle). Finally, a population response to each stimulus (M₁ – M_N, right, green) is generated by summing the unequally weighted responses, and the discrimination performance of that population is assessed. b, Top, Confusion matrices showing the conditional probability of assessing an unequally weighted neuronal population response as being caused by stimulus i when it was actually caused by stimulus j computed from metric-space analysis using the van Rossum measure with timescale τ = 6 ms for population sizes of 2 (left), 8 (middle left), 16 (middle right), and 27 (right) neurons with (top) and without (bottom) noise correlations. The white dashed lines indicate borders between blocks of stimuli for which a given attribute (e.g., amplitude, duration, phase) was varied. Middle, Discrimination performance as a function of population size with (black) and without (gray) noise correlation for the unequally weighted case. The dashed line indicates chance level (1 of 36 stimuli). Inset, Performance with (black) and without (gray) noise correlations for population size of 27 were not significantly different from one another in the unequally weighted case (one-way ANOVA: df = 3, F = 721.3, p = 0.64, Bonferroni corrected). Also shown are values obtained for the equally weighted case for comparison. Bottom, Discrimination performance as a function of population size with (solid) and without (dashed) noise correlation for the unequally weighted case when neural populations consisting only of neurons of a given type (i.e., nr, br, bcr, and cr) are considered. c, Top, Same as c, but for the same population size (n = 27 neurons) with (top) and without (bottom) noise correlations and for timescales of 1 ms (left), 6 ms (middle), and 100 ms (right). Middle, Discrimination performance as a function of timescale with (black) and without (gray) noise correlations. The dashed line indicates chance level (1 of 36 stimuli). Bottom, Discrimination performance as a function of timescale with (solid) and without (dashed) noise correlation for the unequally weighted case when neural populations consisting only of neurons of a given type (i.e., nr, br, bcr, and cr) are considered.

Differential evolution algorithm.

To determine whether performing an unequally weighted sum of neuronal response gave rise to better classification than an equally weighted sum, we trained a differential evolution algorithm (EA) using the population responses on a randomly selected 60% of trials for each chirp stimulus as a training dataset. We then measured the classification accuracy of the trained classifier on the remaining 40% of trials (the test dataset). We chose recording session 2 for this analysis since it contained the greatest number of neurons recorded simultaneously that received all 36 stimuli (n = 27).

Specifically, each neuron was assigned a “weight,” which could vary between −2 and 2, and the goal was to choose a set of weights that maximizes the performance of the classification algorithm described above. The EA was described in detail in a previous study by our group (Aumentado-Armstrong et al., 2015). Specifically, a set of weight vectors (i.e., “agents”) is allowed to evolve by minimizing a fitness function F_fit over a series of iterations (i.e., “generations”). In keeping with the notation used in previous studies (Aumentado-Armstrong et al., 2015), we denote $X_k^r\left(i\right)$ as parameter i for agent r of generation k. First, the population of k individuals is randomly initialized with weight values that are uniformly distributed with zero mean and restrained between −2 and 2. For each individual at every generation, a new individual is constructed by two operations consisting of “differentiation” and “recombination.” In differentiation, the r^th new parameter vector $X_{k,\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{l}}^r$ is built by combining three other individuals $X_k^{r_1}$, $X_k^{r_2}$, and $X_k^{r_3}$, where r₁ ≠ r₂ ≠ r₃, as follows:

$$X_{k,\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{l}}^r=X_k^{r_1}+\left(X_k^{r_2}-X_k^{r_3}\right)F\forall r=1,...,N,$$ (6)

where the differential weight F = 0.5, and the three individuals are chosen based on a probability distribution that is preferentially weighted for more fit (i.e., lower fitness score) individuals, as follows:

$$p_k^{r_1}=\lambda \mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{{-F}_{fit}\left(X_k^{r_i}\right)}{\underset{\forall j}{\max }({1-F}_{fit}\left(X_k^j\right))}\right)\forall r_i=1,...,N,$$ (7)

where λ is a normalization constant such that the sum of probability values is equal to 1. Recombination is then performed as follows:

$$X_{\mathrm{m}\mathrm{u}\mathrm{t}}^r\left(i\right)=\left\{\begin{array}{c}{X}_{k,\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{l}}^r\left(i\right),ifu<CR\\ X_k^r\left(i\right),otherwise\end{array}\forall r=1,...,N;i=1,...,D\right.,$$ (8)

where u is a random variable generated from a uniform distribution U(0,1) and with crossover probability CR = 0.9. Selection is finally performed to produce the next generation via:

$$X_{k+1}^r=\left\{\begin{array}{c}{X}_{\mathrm{m}\mathrm{u}\mathrm{t}}^r,if{F}_{fit}\left(X_{\mathrm{m}\mathrm{u}\mathrm{t}}^r\right)<F_{fit}\left(X_k^r\right)\\ X_k^r,otherwise\end{array}\forall r=1,...,N\right..$$ (9)

In this study, the fitness function for a given individual was defined as follows:

$$F_{\mathrm{f}\mathrm{i}\mathrm{t}}\left(X_k^r\right)={1-DP}_{X_k^r},$$ (10)

where ${DP}_{X_k^r}$ is the discrimination performance estimated by computing the precision of events (i.e., spikes) of our neuronal population in response to our set of 36 chirp stimulus waveforms. The EA was terminated if the change in population discrimination performance for the previous 10 iterations was on average below a threshold value of 0.00001.

We repeated the EA 20 times over different initial conditions to test whether different sets of weights would give rise to similar discrimination performance values. Based on the above, it is clear that if a given weight vector gives rise to a given performance, then the set of weight vectors obtained by multiplying the initial one by any nonzero constant will also give rise to the same performance. Thus, there is degeneracy because there exists an infinite number of weight vectors that will give rise to the same performance. Such “trivial” degeneracies were eliminated by normalizing weight vectors by their SDs and, if necessary, further multiplied by −1 when testing whether different weight vectors gave rise to a given performance (see Fig. 11).

Figure 11.

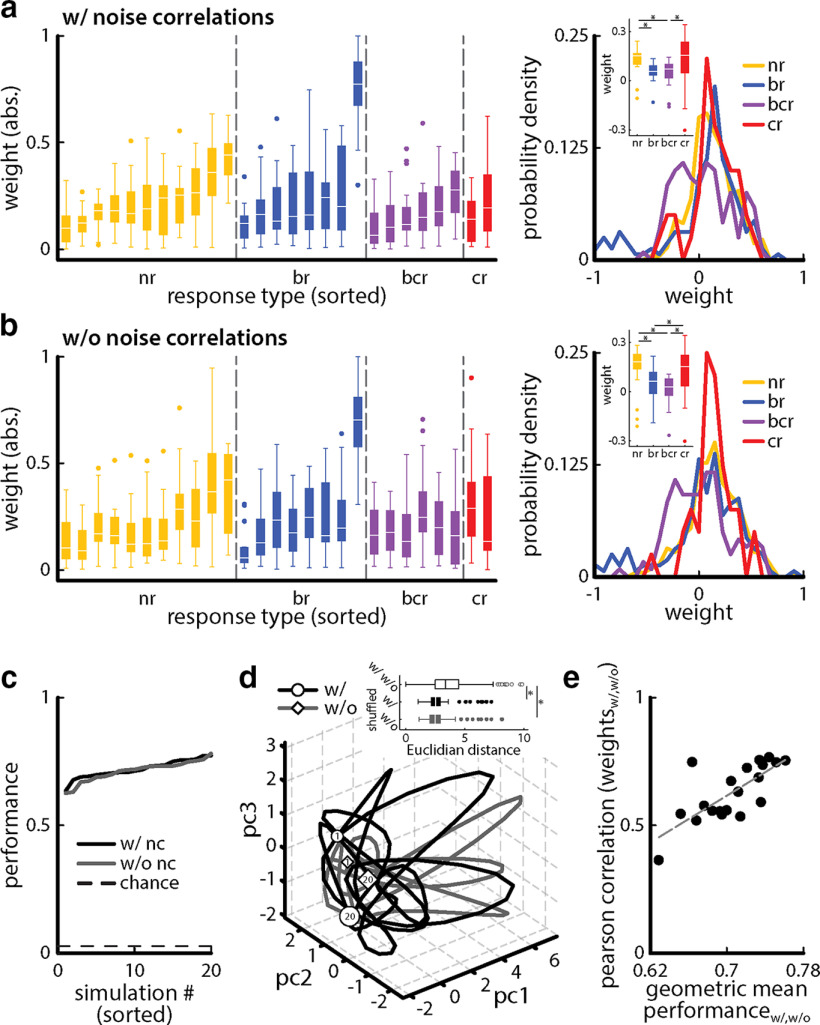
The weight matrices obtained for a neuronal population with (w/) and without (w/o) noise correlations are different. a, Left, Boxplot of the normalized absolute weights obtained by the EA and sorted for increasing performance for each response class (yellow, nr; blue, br; purple, bcr; red, cr) over 20 EA realizations (simulations) for a neuronal population (n = 27) with noise correlations. Right, Probability densities of weights obtained for each neuron type. Inset, Boxplots of weights for each neuron type. *Indicates statistical significance at the p = 0.05 level using a one-way ANOVA with Bonferroni correction. b, Same as a but for the same neuronal population (n = 27) without noise correlations. c, Discrimination performance for the unequally weighted neuronal population obtained after 20 EA simulations with (black) and without (gray) noise correlations sorted in ascending order. Note that both curves overlap. The dashed line indicates chance level (1 of 36 stimuli). d, Vector space of the first three principal components representing >60% of the observed variability computed from the unequally weighted neuronal populations with (black) and without (gray) noise correlations. The size of the circles (with noise correlations) and diamonds (without noise correlations) represent the magnitude of discrimination performance (small symbols, low discrimination values; big symbols, large discrimination values). The numbers within the symbols indicate the first (1) and last (20) sorted simulation number. Inset, The euclidian distance between the w/ and w/o trajectories in pc space is significantly higher than that between the shuffled w/ (one-way ANOVA; df = 2; F = 14.15; p = 1.26 * 10⁻⁵) and the shuffled w/o (one-way ANOVA: df = 2, F = 14.15, p = 2.74 * 10⁻⁵). e, Pearson correlation coefficient of sorted weight vectors with and without noise correlations as a function of the geometric mean of the sorted weight vectors with and without noise correlations. Note the positive relationship between the two quantities (Pearson correlation coefficient: 0.74, p = 2 * 10⁻⁴).

Principal component analysis.

Weight matrices obtained from the 20 EA simulations for a neuronal population with and without noise correlations were compared using principal component analysis (pca). Therefore, the sorted weight matrices were diagonalized using the singular value decomposition function in MATLAB. Trajectories were computed using the pca space of the first three principal components, explaining >60% of the variance of the 20 sorted EA simulations. It is important to note that we used the same decomposition (i.e., linear combination of weights) to visualize weight vectors obtained with and without noise correlations. Therefore, any difference between the principal components has to be because of existing differences between the weight vectors. We compared the difference of the principal components with and without noise correlations with the difference of either with or without noise correlations obtained by bootstrapping (15 bootstraps with each randomly taking 75% of the total weight vectors) using the euclidian distance, as follows:

$$d\left(p,q\right)=\sqrt{{\left(p_1-q_1\right)}^2+{\left(p_2-q_2\right)}^2+{\left(p_3-q_3\right)}^2,}$$ (11)

where (p,q) are the Cartesian coordinates of the trajectories with and without noise correlations in three dimensions.

Response trial-to-trial variability.

To quantify the response trial-to-trial variability of the summed (i.e., either equally or unequally weighted) population activity to a given chirp stimulus waveform with and without noise correlations (equally weighted and weighted), we used the distribution within the interquartile range in responses averaged over the 20 EA simulations, as follows:

$$\mathrm{v}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}=\frac{\sum _{i=1}^m\sum _{j=1}^n{D}_{{\mathrm{Q}}_2}^{{\mathrm{Q}}_3}\sigma \left(k_{m,n}\right)}{m},$$ (12)

where D is the distribution within the interquartile range (Q₂ = 0.25; Q₃ = 0.75), σ is the SD of the response (k; trial-to-trial variability) to each stimulus (m) and each EA simulation (n). All responses were normalized before computing the response variability.

Similarity index.

To quantify the similarity between individual responses (x₁,x₂) to the set of stimulus waveforms used, we computed the similarity index (SI), which is a distance metric to assess the similarity between a response to a given stimulus to the responses to all stimulus waveforms that was computed as follows (Aumentado-Armstrong et al., 2015; Metzen et al., 2016, 2020; Metzen and Chacron, 2017):

$$\mathrm{S}\mathrm{I}x,y=\frac{\sqrt{\mathrm{〈(}{x_1-\mathrm{〈}{x}_1\mathrm{〉}-x_2+\mathrm{〈}{x}_2\mathrm{〉)}}^2\mathrm{〉}}}{\max \left[\frac{\max \left(x_1\right)-\min \left(x_1\right)}{\sqrt{2}},\frac{\max \left(x_2\right)-\min \left(x_2\right)}{\sqrt{2}}\right]},$$ (13)

where <…> denotes an average over an evaluation window of 100 ms after chirp onset that is shown as a blue band in the figures. All responses were normalized before computing SI. The SI measure was used to assess how different the neural responses to a given stimulus waveform are to the responses to all other stimulus waveforms (see Fig. 10), which relates to the discriminability between neural responses to different stimulus waveforms.

Figure 10.

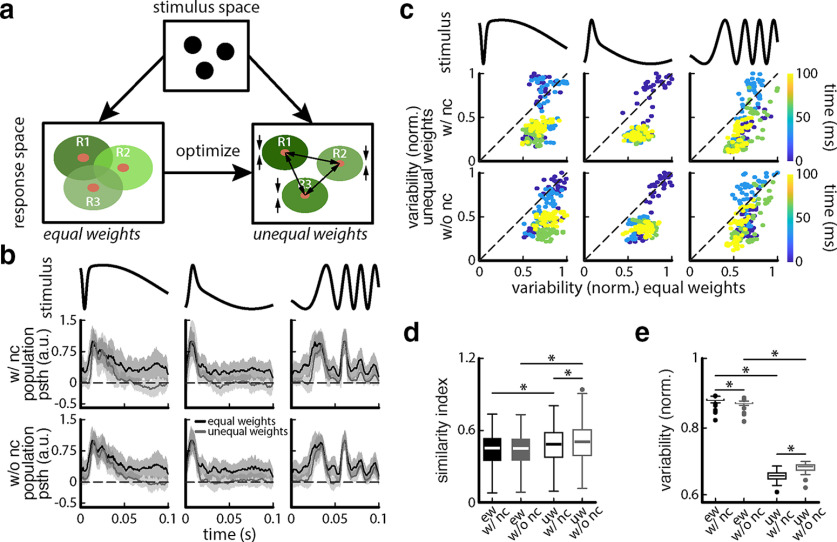
Increased performance is because of increased distance between trial-averaged responses as well as reduction in trial-to-trial variability. a, Schematic illustrating the response space of the equally weighted (bottom, left) and unequally weighted (bottom, right) neuronal population to a given stimulus space (top). The EA optimized the response space such as to minimize response variability while increasing their distances. b, Population PSTHs to three example chirp stimuli (top) with (middle) and without (bottom) noise correlations. Note that the PSTHs obtained in the unequally weighted (middle, with noise correlations, gray; bottom, without noise correlations, gray) and equally weighted (middle, with noise correlations, black; bottom, without noise correlations, black) cases both tended to follow the stimulus waveform. However, the former displayed greater variation compared with the latter and were thus more discriminable from one another. c, Variability of the unequally weighted population as a function of variability of the equally weighted population with (middle) and without (bottom) noise correlations for three different chirp stimuli (top). Datapoints are color coded according to their time of occurrence after stimulus onset. d, Boxplots showing the average SI of the population responses with and without noise correlations for the equally weighted (left) and unequally weighted (right) cases. SI significantly increased in both cases (with noise correlations, n = 630: equally weighted (solid black) vs unequally weighted (hollow black); one-way ANOVA: df = 3; F = 71.69; p = 3.19 * 10⁻⁴; without noise correlations, n = 630: equally weighted (solid gray) vs unequally weighted (hollow gray); one-way ANOVA: df = 3; F = 71.69; p = 4.55 * 10⁻³⁵, Bonferroni corrected). SI was also significantly higher for the unequally weighted population without noise correlations (n = 630; one-way ANOVA: df = 3; F = 71.69; p = 3.55 * 10⁻¹⁷, Bonferroni corrected). e, Boxplots showing the normalized average response variability of the population responses with and without noise correlations for the equally weighted (left) and unequally weighted (right) cases within the interquartile range (see Materials and Methods; n = 100 data points). Response variability across all chirp stimuli significantly decreased for equally weighted sums but actually increased for unequally weighted sums when removing noise correlations (equally weighted: with noise correlations (solid black) vs without noise correlations (solid gray), one-way ANOVA; df = 3; F = 1.12 * 10⁴; p = 1.57 * 10⁻⁷; unequally weighted: with (hollow black) vs without noise correlations (hollow gray, one-way ANOVA; df = 3; F = 1.12 * 10⁴; p = 6.56 * 10⁻³⁸, Bonferroni corrected). Note, that the response variability is significantly higher for with and without noise correlations in the equally weighted case (left) compared to the unequally weighted case (right) (with noise correlations: equally (left, solid black) vs unequally weighted (right, hollow black); one-way ANOVA; df = 3; F = 1.12 * 10⁴; p = 0.0001, Bonferroni corrected; without noise correlations: equally (left, solid gray) vs unequally weighted (right, hollow gray): one-way ANOVA; df = 3; F = 1.12 * 10⁴; p = 1.20 * 10⁻³¹¹, Bonferroni corrected). *Indicates statistical significance at the p = 0.05 level using a one-way ANOVA with Bonferroni correction.

Statistics.

Values are reported as the mean ± SD. Statistical tests were performed using a one-way ANOVA with Bonferroni correction, unless otherwise stated.

Results

Here we investigated for the first time how TS neuronal populations encode natural electrocommunication stimuli with highly heterogeneous attributes. Under natural conditions, chirps occur during social interactions in which the emitter fish sends the signal to the receiver fish (Fig. 1a, top). This signal consists of a transient increase in the EOD frequency of the emitter fish with a given time duration and amplitude (i.e., the amount by which the EOD frequency increases; Fig. 1a, middle). Interactions between the EOD frequencies of the two fish give rise to a background beat that consists of a sinusoidal AM of the EOD (Fig. 1a, bottom, dashed gray). When considering the stimulus sensed by the receiver fish, the chirp signal not only transiently perturbs the beat at a given phase (Fig. 1a, bottom, blue) but also causes a phase advance of the beat (Fig. 1a, bottom, compare solid black curves, dashed gray curves). As such, chirps with different attributes give rise to very different AM stimulus waveforms (Fig. 1b). We systematically varied multiple chirp attributes such as the amplitude (i.e., the amount by which the EOD frequency increases; Fig. 1b, top left), the beat phase at which the chirp occurs (Fig. 1b, bottom left), and the duration of the frequency increase (Fig. 1b, right). We recorded the simultaneous activities of TS neurons in response to chirp stimuli that were delivered via a pair of electrodes located on either side (Fig. 2a). The use of a high-density array allowed us to record the activities of up to 46 TS neurons simultaneously (Fig. 2a, right), and we found that TS neuronal activities were correlated in the absence of stimulation (Fig. 2b). We thus used chirps with different waveforms occurring on top of a sinusoidal waveform to understand how the activities of a neuronal population are integrated to distinguish between different stimuli (Fig. 2c).

Midbrain neuronal activities are correlated in the absence of stimulation

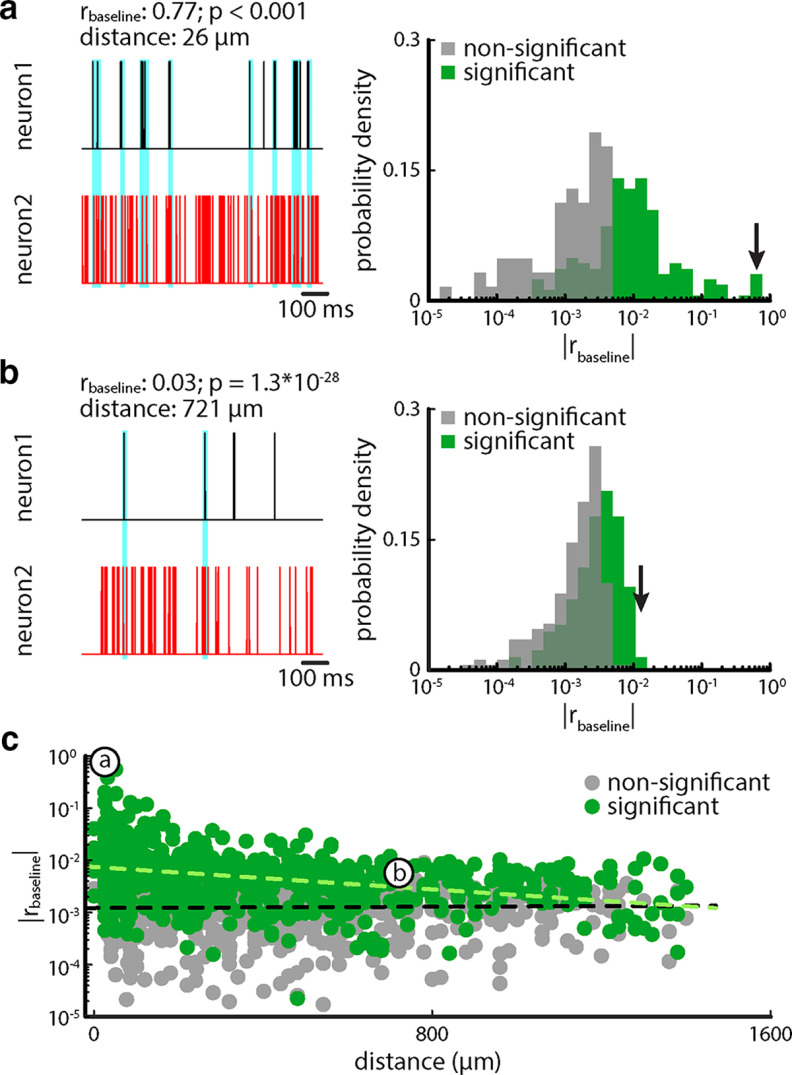
We first characterized correlations between the activities of midbrain neurons in the absence of stimulation since these are indicative of the presence of noise correlations during stimulation (Hofmann and Chacron, 2017). Overall, pairs of neurons that were recorded on probe sites that were located close to one another (Fig. 3a) tended to display higher baseline correlations in magnitude than pairs of neurons that were recorded on probe sites that were located farther apart (Fig. 3b). Indeed, baseline correlation magnitude decreased as a function of increasing physical distance when considering pairs with significant baseline correlations (Fig. 3c, green dots and light green dashed line; Pearson correlation coefficient: r = −0.18, p = 1.73 * 10⁻⁶). In contrast, for pairs with nonsignificant baseline correlations, its magnitude did not decrease significantly as a function of distance (Fig. 3c, gray dots and black dashed line; Pearson correlation coefficient: r = 0.002, p = 0.95). However, when considering all possible pairs (i.e., with significant and nonsignificant baseline correlation magnitudes), the decrease in baseline correlation magnitude remains significant (Pearson correlation coefficient: r = −0.14, p = 3.40 * 10⁻⁸). As mentioned above, the presence of baseline correlations is important as these can be seen as the limit toward which noise correlations tend as stimulus intensity goes to zero (Hofmann and Chacron, 2017). As such, we expected that TS neurons will display noise correlations under stimulation, which will impact population coding, as described above.

Figure 3.

Baseline correlations decrease with increasing distance. a, Left, Spiking activity for two example neurons (neuron 1, black; neuron 2, red) recorded on probe sites that were located close to one another (26 µm). This pair displayed a large baseline correlation coefficient, as evidenced from coincident spiking that occurred more often than expected by chance (cyan bars). Right, Histogram of baseline correlation magnitude for all pairs (n = 120) for which the distance was <100 µm. Shown are values significantly different from zero (green) and those that are not (gray). The black arrow indicates the value of correlation for the example shown in the left panel. b, Left, Spiking activity for two example neurons (neuron 1, black; neuron 2, red) recorded on probe sites that were located far from one another (721 µm). This pair displayed a baseline correlation coefficient near zero, as evidenced from coincident spiking that occurred as often as expected by chance (cyan bars). Right, Histogram of baseline correlation magnitude for all pairs (n = 295) for which the distance was ≥700 µm. Shown are values significantly different from zero (green) and those that are not (gray). The black arrow indicates the value of correlation for the example shown in the left panel. c, Baseline correlation magnitude decrease as a function of distance (Pearson correlation coefficient: r = −0.24, p = 1.02 * 10⁻²⁰). Shown are values significantly different from zero (green) and those that are not (gray). The labeled circles indicate the two examples shown in a and b. Throughout, correlations were computed for a timescale of 20 ms.

Midbrain neurons display signal and noise correlations under stimulation

The responses of single TS neurons in our dataset were highly heterogeneous and were similar to those described previously (Vonderschen and Chacron, 2011; Sproule et al., 2015). Overall, we found that neuronal responses to chirp stimuli were of four types, as shown in Figure 4a (see Materials and Methods for details on the classification). Some TS neurons responded exclusively to the chirp and not at all to the beat (Fig. 4a, red), and were termed cr; others instead responded to both the chirp and the beat (Fig. 4a, purple) and were termed bcr; and yet other neurons in a separate subset only responded to the beat (Fig. 4a, blue) and were termed br. Consistent with previous results (Vonderschen and Chacron, 2011; Sproule et al., 2015), some TS neurons did not respond to either the chirp or the beat (Fig. 4a, yellow) and were termed nr. Previous studies have shown that such neurons tend to respond to other behaviorally relevant stimuli such as moving objects or envelopes (Vonderschen and Chacron, 2011; Sproule et al., 2015). Response latencies of the first spike occurring after stimulus onset (Fig. 4b, left) were highly heterogeneous and ranged from a few milliseconds to 100 ms (Fig. 4b, right), with bcr neurons having the shortest latencies on average (Fig. 4b, right inset; nr: 46.19 ± 15.88 ms; br: 34.02 ± 16.67 ms; bcr: 19.84 ± 12.54 ms; cr: 38.12 ± 16.36 ms; one-way ANOVA: df = 3, F = 52.66; p_nr,br = 1.98 * 10⁻⁶; p_nr,bcr = 2.35 * 10⁻²⁶; p_nr,cr = 0.008; p_br,bcr = 3.75 * 10⁻¹¹; p_br,cr = 0.42; p_bcr,cr = 4.75 * 10⁻¹⁵; Bonferroni corrected).

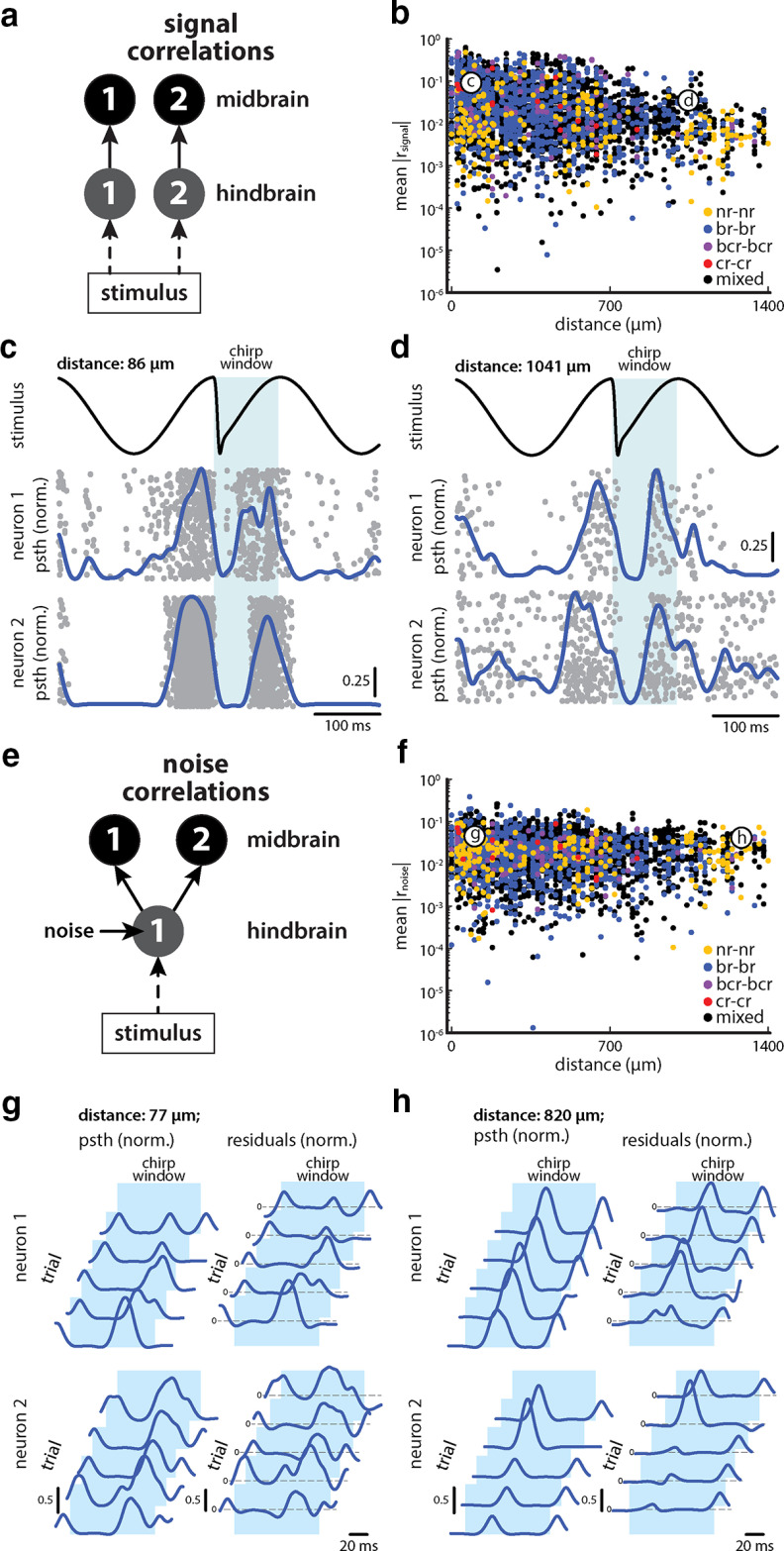
We next looked at the correlation structure of TS neurons under stimulation [i.e., the relationship between signal correlation coefficient (r_signal) and noise correlation coefficient (r_noise)]. As mentioned above, looking at the correlation structure is important because the sign relationship (i.e., whether they have the same sign or have opposite signs) between signal and noise correlations strongly influences whether correlations are beneficial or detrimental to information transmission (Averbeck et al., 2006). Specifically, if signal and noise correlations are either both positive or negative, then this will reduce information. In contrast, if signal correlations are positive and noise correlations negative or vice versa, they will increase information transmission.

In general, signal correlations are correlations that are induced by two neuron populations receiving a common signal (Fig. 5a). We found that signal correlations across our datasets ranged between −0.73 and 0.84, with mean magnitudes of 0.07 ± 0.09. Interestingly, r_signal magnitudes decreased with increasing physical distance for pairs consisting of all response classes except “bcr–bcr” and “cr–cr” pairs (Fig. 5b; Pearson correlation coefficient between r_signal and distance: bcr–bcr pairs: −0.16, p = 0.17; cr–cr pairs: −0.51, p = 0.07). A similar relationship was seen when only considering neuron pairs whose correlation values were significantly different from zero (Pearson correlation coefficient between r_signal and distance: bcr–bcr pairs: −0.17, p = 0.16; cr–cr pairs: −0.51, p = 0.070). In general, r_signal magnitude was high on average for neurons that were in close proximity (Fig. 5b,c; <100 µm, 0.09 ± 0.13) and low for pairs of neurons that were further apart (Fig. 5b,d; ≥700 µm, 0.04 ± 0.04). Indeed, neurons that were located close to one another tended to display more similar responses to chirp stimuli than neurons that were located farther apart (Fig. 5, compare c, d).

Figure 5.

Signal correlations decrease with physical distance while noise correlations are independent of physical distance. a, Schematic showing a hypothetical scenario in which a common stimulus is received by two afferent hindbrain neuron populations (gray circles). In this case, correlations between neuron populations “1” and “2” (black circles) will be exclusively because of the common stimulus and are referred to as signal correlations. b, Signal correlation magnitudes are on average higher in magnitude between pairs with small physical distance (≤100 µm) than in pairs with large physical distances (>700 µm). The colored dots indicate the relation of signal correlation magnitudes and physical distance of same response type pairings (nr–nr, yellow; br–br, blue; bcr–bcr, purple; cr–cr, red) as well as mixed pairings (black). The two labeled circles indicate the relation of signal correlation magnitudes and physical distance of the example pairs shown in c and d. Each datapoint corresponds to one pair for one stimulus waveform. c, An example pair of br TS neurons with small physical distance (83 µm) displays a signal correlation of 0.53 in response to a given chirp stimulus (top, black) because their PSTHs are similar to each other (middle, neuron 1; bottom, neuron 2). The gray dots show the spiking activity of both neurons to repeated presentations of the chirp stimulus (top, black). d, An example pair of br TS neurons with large physical distance (1005 µm) displays a signal correlation of 0.19 in response to a chirp stimulus (top, black) because their PSTHs are more dissimilar to each other (middle, neuron 1; bottom, neuron 2). The gray dots show the spiking activity of both neurons to repeated presentations of the same chirp stimulus (top, black). e, Schematic showing a hypothetical scenario in which a stimulus is received by one afferent neuron hindbrain population (gray circle) that also receives a noise input, which then projects to two TS neuronal populations “1” and “2” (black circles). In this case, correlations between neuronal populations “1” and “2” will not only be because of the stimulus (i.e., signal correlations), but will also be because of the noise received by the afferent neuronal population (i.e., noise correlations). f, Noise correlation magnitudes are on average independent of the physical distance between neurons. The colored dots indicate the relation of noise correlation magnitudes and physical distance of same response type pairings (nr–nr, yellow; br–br, blue; bcr–bcr, purple; cr–cr, red) as well as mixed pairings (black). The two labeled circles indicate the relation of noise correlation magnitudes and physical distance of the example pairs shown in g and h. Each datapoint corresponds to one pair for one stimulus waveform. g, An example pair of br TS neurons with small physical distance (77 µm) displays a noise correlation of 0.28 because their residuals covary within the chirp window of 100 ms (top right, neuron 1; bottom right, neuron 2) as shown for five representative trials to a given chirp stimulus. Also shown are the PSTHs for the same trials (top and bottom left). h, An example pair of br TS neurons with large physical distance (820 µm) displays a noise correlation of 0.25 because their residuals covary within the chirp window of 100 ms (top right, neuron 1; bottom right, neuron 2) as shown for five representative trials to the same chirp stimulus. Also shown are the PSTHs for the same trials (top and bottom left).

When looking at noise correlations, which arise when two neuronal populations receive common input from a neuronal population that displays trial-to-trial variability to repeated stimulus presentations (i.e., “noise”; Fig. 5e), we found that these ranged between −0.50 and 0.74 with mean magnitudes of 0.06 ± 0.05. The magnitudes of r_signal were significantly higher than those of r_noise (one-way ANOVA: df = 3, F = 7.74, p = 0.04, Bonferroni corrected). However, when only considering pairs that have correlation values significantly different from zero (see Materials and Methods), r_signal significantly decreases (0.05 ± 0.06; one-way ANOVA; df = 3, F = 27.74, p = 8.12 * 10⁻¹⁷, Bonferroni corrected), while r_noise significantly increases (0.07 ± 0.06; one-way ANOVA: df = 3, F = 27.74, p = 0.02, Bonferroni corrected) with r_signal and r_noise being significantly different from each other (one-way ANOVA: df = 3, F = 27.74, p = 5.55 * 10⁻¹⁴, Bonferroni corrected). Furthermore, we found no significant relationship between r_noise and physical distance for all but br–br pairs (Fig. 5f; Pearson correlation coefficient between r_noise and distance: “br–br” pairs: −0.15, p = 3.7 * 10⁻⁶). A similar relationship was seen when only considering neuron pairs that have correlation values significantly different from zero (Pearson correlation coefficient between r_signal and distance: br–br pairs: −0.16, p = 3.49 * 10⁻⁶). In general, r_noise magnitude was on average similar for pairs with small physical distances (Fig. 5f,g; <100 µm; 0.07 ± 0.06) and with large physical distances (Fig. 5f,h; ≥700 µm; 0.06 ± 0.05). This is most likely because of the presence of long-range connections both within and across TS layers (Carr et al., 1981; Carr and Maler, 1985, 1986). To better illustrate this result, we computed the residuals of neuronal responses to chirp stimuli, which are the components of neuronal responses that cannot be explained by the stimulus (see Materials and Methods). Indeed, residuals for neuron pairs that are close to one another (Fig. 5g) or farther away from one another (Fig. 5h) were similarly correlated.

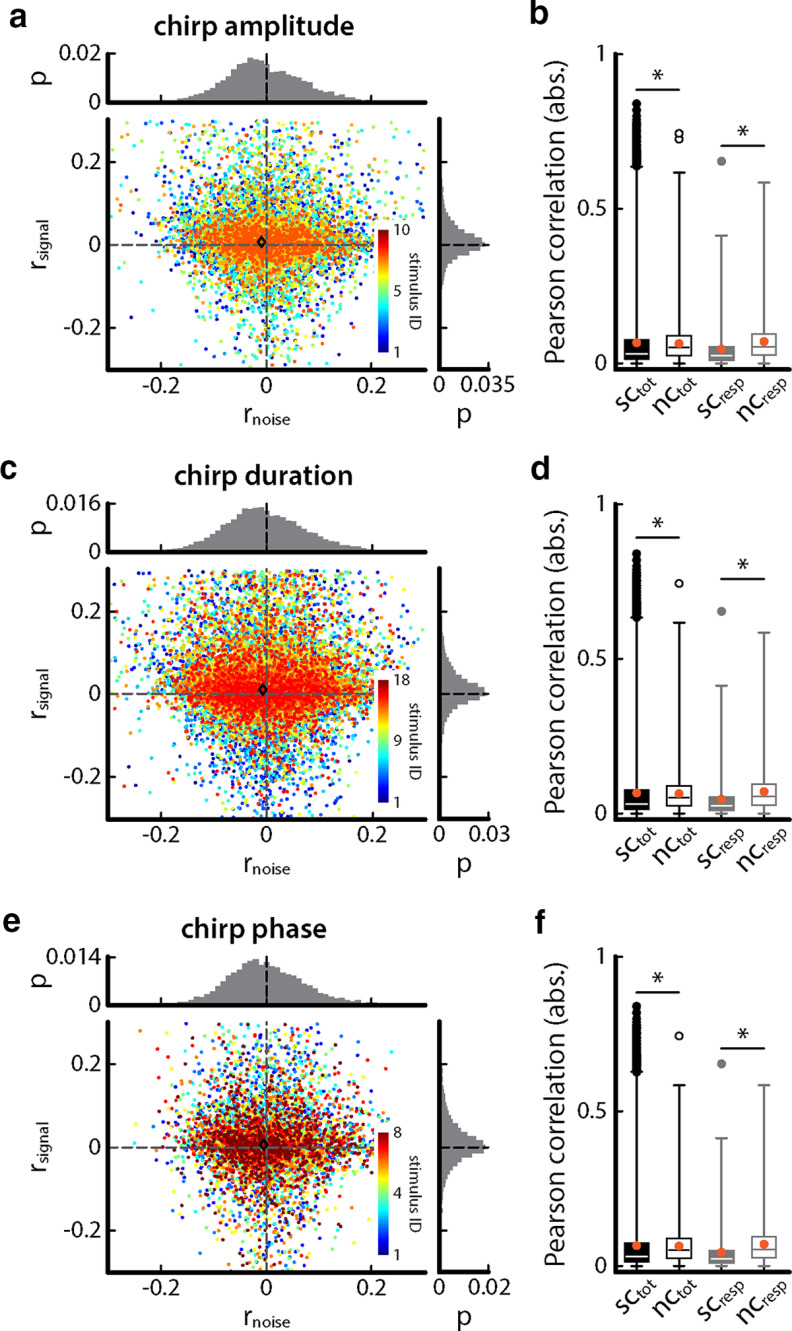
Overall, we found that signal and noise correlations were largely independent of chirp attributes. Indeed, signal and noise correlations were distributed in a similar manner for all chirp stimuli considered in the current study (r_signal: Kruskal–Wallis, p = 0.2784; r_noise: Kruskal–Wallis, p = 0.99). Figure 6a shows the relationship between signal and noise correlations when varying chirp amplitude. Overall, signal and noise correlations were independent of one another (Pearson correlation coefficient between r_signal and r_noise: −0.014; p = 0.15) with signal correlations (sc_tot) being significantly higher than noise correlations (nc_tot) on average for all possible pairs and significantly lower for neuron pairs that have correlation values significantly different from zero (sc_resp, nc_resp; see Materials and Methods; Fig. 6b; one-way ANOVA: df = 3, F = 32.16, p_tot = 9.93 * 10⁻⁵, p_resp = 9.68 * 10⁻¹⁴, Bonferroni corrected). Qualitatively similar results were obtained when varying chirp duration (Fig. 6c: Pearson correlation coefficient between r_signal and r_noise: −0.014; p = 0.06; Fig. 6d: one-way ANOVA: df = 3, F = 30.70, p_tot = 0.005, p_resp = 1.57 * 10⁻¹⁴, Bonferroni corrected) and chirp phase (Fig. 6e: Pearson correlation coefficient between r_signal and r_noise: −0.02; p = 0.14; Fig. 6f: one-way ANOVA: df = 3, F = 33.97, p_tot = 0.02, p_resp = 3.55 * 10⁻¹⁶, Bonferroni corrected).

Figure 6.

Noise and signal correlations are independent of the chirp and of one another. a, Signal correlations as a function of noise correlations obtained when varying chirp duration. The color code indicates the individual stimulus IDs. The summed probability distributions for signal (right, gray) and noise (top, gray) are also shown. The diamond shows the mean signal and noise correlations. b, Boxplot showing the magnitudes of signal (filled) and noise (hollow) correlation coefficients for all possible pairs (black) and for pairs that displayed correlation that have correlation values significantly different from zero. When considering all possible pairs, signal correlations were significantly higher than noise correlations but lower when considering pairs with correlation values significantly different from zero (one-way ANOVA: df = 3, F = 32.16, p_tot = 9.93 * 10⁻⁵, p_resp = 9.68 * 10⁻¹⁴, Bonferroni corrected). The orange dots indicate the mean values. c, Same as a but for chirp duration. d, Boxplot showing the magnitudes of signal (filled) and noise (hollow) correlation coefficients for all possible pairs (black) and for pairs that have correlation values significantly different from zero. Signal correlations were significantly lower than noise correlations when considering all pairs or just pairs for which correlation coefficients were significantly different from zero (one-way ANOVA: df = 3; F = 30.70, p_tot = 0.005, p_resp = 1.57 * 10⁻¹⁴, Bonferroni corrected). The orange dots indicate the mean values. e, Same as a but for chirp phase. f, Boxplot showing the magnitudes of signal (filled) and noise (hollow) correlation coefficients for all possible pairs (black) and for pairs that have correlation values significantly different from zero. In each case, signal correlations were significantly lower than noise correlations (one-way ANOVA: df = 3; F = 33.97, p_tot = 0.02, p_resp = 3.55 * 10⁻¹⁶, Bonferroni corrected). The orange dots indicate the mean values.

Decoding information from linear summation of midbrain neuronal activities

We next quantified the performance of TS neuronal populations at encoding chirps with different attributes and first considered that the activities of TS neurons are summed linearly (i.e., equally weighted; Fig. 7a). Combined responses to different stimuli were compared using a distance metric (see Materials and Methods). Next, to determine whether a given response was correctly predicted as having been elicited by a given stimulus, the discrimination performance was computed from the confusion matrix whose element ij gives the conditional probability that a response generated by stimulus i is classified as being generated by stimulus j. The diagonal elements thus represent correct assignments while off-diagonal elements instead represent incorrect assignments. Thus, if our classifier displayed 100% correct performance, then the diagonal of the confusion matrix would be unity with all off-diagonal elements zero. As such, we quantified the performance by taking the average value of the diagonal elements (see Materials and Methods). To maximize performance, we would expect that the sets of responses elicited by different chirp stimulus waveforms would be as distant from one another as possible, while making the size of each set (i.e., the trial-to-trial variability in the response) as small as possible (Fig. 7b).

To quantify the impact of noise correlations, we compared the performances of the equally weighted summed neuronal activities before and after randomly shuffling neuronal responses with respect to stimulus trials, which will eliminate noise correlations (see Materials and Methods). Indeed, we verified that the noise correlations computed after shuffling were not significantly different from zero (see Materials and Methods). Our results show that the variability in the equally weighted summed neuronal responses were significantly lower after shuffling (Fig. 7c: one-way ANOVA: df = 3, F = 1.12 * 10⁴, p = 1.57 * 10⁻⁷, Bonferroni corrected). This indicates that the variability in the responses can be better averaged away when noise correlations are not present (Zohary et al., 1994) and suggests that noise correlations have a detrimental effect with respect to discrimination performance overall. The top panel of Figure 7d compares the confusion matrices obtained for different population sizes before (top) and after (bottom) randomly shuffling to eliminate noise correlations. Neuronal populations were constructed in the following way: first, cr neurons were considered, then bcr neurons were added, then br neurons, and finally nr neurons were added. In general, adding more neurons gave rise to better performance as values on the main diagonal of the confusion matrices increased overall (Fig. 7d, top) as quantified by increased performance (Fig. 7d, middle). Noise correlations had a detrimental effect on performance (Fig. 7d, middle inset: one-way ANOVA, df = 3, F = 721.3, p = 2.38 * 10⁻¹³; Bonferroni corrected). Interestingly, the greatest improvement in performance was seen when bcr neurons and, to a lesser extent, “br” neurons were added to the population, while adding nonresponsive neurons actually decreased performance slightly (Fig. 7d, middle). This is further seen when comparing same-size populations of the different cell categories (Fig. 7d, bottom). As such, our results show that noise correlations, although overall small in magnitude, can have a significant effect on population coding by large neural populations, which is expected (Schneidman et al., 2006).

We also systematically varied the timescale used to compute the distance between spike trains (see Materials and Methods). Low values of timescale take precise spike timing into account while larger values take slower changes in firing rate (van Rossum, 2001; Jamali et al., 2016, 2019). Overall, maximum performance was observed for a timescale near 6 ms (Fig. 7e), indicating that information is contained in the precise spike timing of TS neurons. Overall, performances computed on the shuffled responses were significantly greater than those obtained before shuffling for all timescales tested (Fig. 7e, compare black curves, gray curves; t test, p < 3.86 * 10⁻⁸). Interestingly, when computing performance, almost no cell category displayed a significant difference in performance with and without noise correlations, although the performance magnitude greatly varied across the different cell categories (Fig. 7e, bottom).

Performing an unequally weighted sum of TS neuronal activities gives rise to improved performance and eliminates the detrimental effects of noise correlations

We next asked whether assigning individual weights to each neuron would give rise to increased discrimination performance. Weights were either positive or negative and could represent, for instance, the synaptic weights of connections to a downstream neuron. This question is particularly interesting here since signal and noise correlations were independent of one another. As such, theoretically, one should be able to combine neuronal activities so as to eliminate redundancy without compromising trial-averaged neuronal responses. Thus, we considered a decoder for which an unequally weighted sum of neuronal activities was performed (i.e., each neuron was assigned its own weight before summation; Fig. 8a). To find which combinations of weights (i.e., “weight vectors”) gave rise to the best performance, we used an EA (see Materials and Methods) that allowed weight vectors to “evolve” over “generations” (Fig. 8a; see Materials and Methods). Figure 8b shows confusion matrices obtained with (top) and without (second top) noise correlations averaged over different realizations of the EA. It is important to note that the EA simulations were performed independently on the raw and shuffled datasets and that the best weight vectors obtained with and without noise correlations differed from one another. Overall, performances obtained using unequally weighted sums were significantly improved over those obtained using equally weighted sums (compare Figs. 8b, 7d; Fig. 8b, middle inset: one-way ANOVA: df = 3, F = 721.3; with noise correlations equally weighted vs unequally weighted, p = 3.86 * 10⁻⁵⁰; without noise correlations equally vs unequally weighted, p = 1.20 * 10⁻³⁹; Bonferroni corrected). Adding more neurons improved performance overall but the greatest improvement was seen when bcr and br neurons were added to the pool (Fig. 8b, middle). Adding nr neurons did not give rise to any improvement in performance but did not degrade performance. Interestingly, similar performances were obtained with and without noise correlations (Fig. 8b, middle, compare black curves, gray curves; one-way ANOVA: df = 3, F = 721.3, p = 0.64, Bonferroni corrected), confirming our prediction that the deleterious effects of noise correlations seen when considering linear sums could indeed by mitigated. This is further seen when comparing same-size populations of the different cell categories (Fig. 8b, bottom). Varying the timescale in our distance metric gave rise to qualitatively similar results as those seen using linear sums as best performance was still observed for a timescale of 6 ms (Fig. 8c). We also looked at the effects of increasing chirp evaluation windows on performance (Fig. 9). We found that larger chirp evaluation windows also led to higher performances of our TS neuron population (Fig. 9). This is not surprising because for larger chirp evaluation windows, a larger portion of the response to the chirp-induced phase reset can be considered in the discrimination procedure.

The greater performances obtained using unequally weighted sums suggest that the decoder can effectively better separate responses to different chirp waveforms as well as minimize trial-to-trial variability, so as to improve discriminability (Fig. 10a). To test this prediction, we looked at the trial-averaged equally and unequally weighted summed activities in response to different chirp waveforms. We found that, indeed, the trial-averaged unequally weighted summed activities were more discriminable from each other than the trial-averaged equally weighted summed activities as they displayed greater variation (Fig. 10b, compare error bands). Furthermore, variability was in general greater early after stimulus onset compared with late after stimulus onset (Fig. 10c). Moreover, when computing trial-to-trial variability, we found greater values for equally weighted summed activities than for unequally weighted summed activities (Fig. 10b,c). These results are summarized in Figure 10, d and e. Specifically, the similarity index between the trial-averaged unequally weighted summed activities were significantly greater than those between the trial-averaged equally weighted summed activities (Fig. 10d; one-way ANOVA: df = 3; F = 71.69; with noise correlations equally weighted vs unequally weighted, p = 3.19 * 10⁻⁴; without noise correlations equally weighted vs unequally weighted, p = 4.55 * 10⁻³⁵; Bonferroni corrected). Moreover, trial-to-trial variability was significantly lower in the unequally weighted case with noise correlations (Fig. 10e: one-way ANOVA: df = 3; F = 1.12 * 10⁴; p = 0.0001; Bonjerroni corrected) and without noise correlations (Fig. 10e: one-way ANOVA: df = 3; F = 1.12 * 10⁴; p = 1.20 * 10⁻³¹¹; Bonferroni corrected). Interestingly, while the similarity index in the unequally weighted case was significantly higher for without than with noise correlations (Fig. 10d: one-way ANOVA: df = 3; F = 71.69; p = 3.55 * 10⁻¹⁷; Bonferroni corrected), the trial-to-trial variability was significantly higher after shuffling (Fig. 10e: one-way ANOVA: df = 3, F = 1.12 * 10⁴, p = 6.56 * 10⁻³⁸; Bonferroni corrected). This indicates that the EA identified solutions for each case (i.e., with and without noise correlations), which are different from one another, as a poorer similarity index is compensated for by a more beneficial trial-to-trial variability.

Different weight vectors can optimize performance

Finally, we investigated variability in the best weight vectors identified by our EA algorithm (i.e., those for which performance is best for a given simulation). For this analysis, we eliminated “trivial” degeneracies in the data, such as those introduced by multiplying a given weight vector by a nonzero constant, which does not alter performance (see Materials and Methods). Figure 11a (left) shows a boxplot of the absolute weights obtained for 20 different simulations for each neuron sorted for performance for each response class with noise correlations. The weights assigned to bcr and br neurons were on average significantly higher than the weights assigned to nr and cr neurons [Fig. 11a, right; one-way ANOVA: df = 3, F = 4.98, p_nr-br = 0.02, p_nr-bcr = 0.002, p_nr-cr = 0.72, p_br-bcr = 0.35, p_br-cr = 0.05, p_bcr-cr = 0.005; least significant difference (LSD) corrected]. Figure 11b (left) shows the same without noise correlations. The weights assigned to bcr and br neurons were on average significantly higher than the weights assigned to nr and cr neurons (Fig. 11b, right; one-way ANOVA: df = 3, F = 3.9, p_nr-br = 0.02, p_nr-bcr = 0.02, p_nr-cr = 0.97, p_br-bcr = 0.97, p_br-cr = 0.02, p_bcr-cr = 0.02, LSD corrected). Overall, weight vectors displayed clear similarity with one another. Notably, some neurons contributed more to discrimination performance than others (e.g., one br neurons was almost always assigned a weight near unity). We note that this single neuron displayed a discrimination performance of 0.63 ± 0.01. Not including this particular neuron and using the evolution algorithm to optimize the weights gave rise to a population performance of 0.55 ± 0.04 (with noise correlations) and 0.51 ± 0.05 (without noise correlations), respectively. Importantly, this did not affect the qualitative nature of our results, as the discrimination performance of the unequally weighted summed activities was still significantly higher than that of the equally weighted activities (with noise correlations: equal weights, 0.26 ± 0.01; unequal weights, 0.55 ± 0.04; without noise correlations: equal weights, 0.34 ± 0.02; unequal weights, 0.51 ± 0.05; one-way ANOVA: df = 3, F = 350.71, p_w/nc = 1.49 * 10⁻⁴⁰, p_{w/o nc} = 1.08 * 10⁻²⁶, Bonferroni corrected).

However, there were also some notable differences between the obtained weight vectors. For example, one cr neuron was assigned a greater range of weights (Fig. 11a, left). Qualitatively similar results were obtained without noise correlations (Fig. 11b, left). This suggests that there exist multiple weight vectors that give rise to the same level of performance. To test this hypothesis, we took advantage of the fact that similar a performance was obtained with and without noise correlations (Fig. 11c, compare black curves, gray curves). We thus used principal component analysis (see Materials and Methods) to decompose weight vectors into their first three components, which explain most of the variance. It is important to note that we used the same principal components for weight vectors obtained with and without noise correlations. As such, any difference seen has to be because of a difference that existed between both datasets. We then plotted “trajectories” (i.e., how the first three principal components change based on sorting according to increasing performance). We found that these differed from one another (Fig. 11d, inset; one-way ANOVA: df = 2, F = 14.15, p_{w/w/o, w/shuffled} = 1.26 * 10⁻⁵, p_{w/w/o, w/o shuffled} = 2.74 * 10⁻⁵, Bonferroni corrected), thereby suggesting that different weight vectors can indeed give rise to the same performance. The correlation coefficient between weight vectors increased with increasing performance (Fig. 11e), suggesting that the number of different combinations of weights that give rise to a given performance decreases when higher levels of performance are considered. The existence of nontrivial degeneracies is important as it makes finding one such solution easier, as discussed further below.

Discussion

Summary of results

We investigated how midbrain electrosensory neuronal populations encoded natural electrocommunication stimuli (i.e., chirps). These chirps consist of highly heterogeneous transient waveforms and furthermore give rise to different phase advances of the underlying background beat. To do so, we recorded the activities of multiple midbrain neurons simultaneously in response to chirps whose attributes were varied systematically. First, in the absence of stimulation, we found that the activities of midbrain neurons were correlated, and that such correlations decayed in magnitude with increasing physical distance, suggesting that midbrain neurons will display noise correlations under stimulation. Under stimulation, we found that neural responses, while highly heterogeneous, could be classified into four different groups. The cr neurons tended to respond only to the transient chirp with excitation and responded only weakly or not at all to the background beat, while br neurons tended to respond only to the background beat and weakly or not at all to the transient chirp. We found that br neurons responded to the different phase advances of the beat caused by the chirp and could thus discriminate between chirps. The bcr neurons responded to both beat and chirp, while nr neurons did not respond to either the beat or chirp. We next investigated the correlation structure displayed by midbrain neuronal populations in response to chirp stimuli. Overall, we found that signal correlations between midbrain neurons decreased with increasing physical distance for all response classes except bcr–bcr and cr–cr pairs when considering all possible pairs as well as when only considering pairs with correlation values significantly different from zero. As such, midbrain neurons located closer to one another tended to display more similar responses to a given chirp stimulus than midbrain neurons located farther apart. However, noise correlations were not dependent on physical distance for most response classes except br–br pairs when considering all possible pairs as well as when only considering pairs with correlation values significantly different from zero. Similar results have been found in previous modeling and experimental studies stating that neurons in close vicinity or of the same cluster tend to display larger noise correlations than neurons that are farther apart (for review, see Doiron et al., 2016). This is because closer neurons presumably share more common presynaptic neurons, as suggested by a modeling study (Kriener et al., 2009). Interestingly, both signal and noise correlations did not depend on the particular chirp stimulus presented and were furthermore independent of one another. This lack of dependence on stimulus waveform is unexpected since previous studies have shown that noise correlations generally depend on stimulus attributes (Snyder et al., 2014; Tan et al., 2014; Franke et al., 2016; Zylberberg et al., 2016). We next investigated the performance of a classifier at discriminating between different chirp waveforms using the combined activities of midbrain neurons. When activities were combined using an equally weighted sum, we found that discrimination performance was greatest when combining the activities of bcr neurons, followed by br neurons. Combining the activities of cr and nr neurons gave rise to poor performance overall. Noise correlations had a detrimental effect on performance both when varying population size as well as timescale. Next, we used an EA to find whether assigning each neuron a given weight before summation would improve performance. Our results show that considering unequally weighted sums of neuronal activities gave rise to significant improvement in performance, which was achieved by making trial averages to different chirp waveforms more discriminable from one another, as well as reducing trial-to-trial variability, which was achieved in part by strongly attenuating, if not eliminating, noise correlations. Overall, the greatest discrimination performance was achieved by br and bcr neurons, indicating that the algorithm favored different responses because of the different phase advances of the beat caused by chirp stimuli with different attributes, rather than the responses to the actual transient chirp stimulus waveform itself. Indeed, combining the activities of cr neurons in an equally or unequally weighted manner gave rise to poor discrimination performance that was barely above chance or that was obtained using only nr neurons. Interestingly, we found that there exist nontrivial degeneracies in weight vectors that give rise to a given performance. Specifically, while it is clear that multiplying all weights by the same nonzero constant will not affect discrimination performance, which is a trivial degeneracy. As such, our results show that there are different combinations of weights that are nontrivially related that give rise to similar discrimination performance. We thus conclude that heterogeneous midbrain neuronal populations transmit information to downstream brain areas that enable reliable discrimination of chirp stimulus waveforms if these activities are combined so as to include neurons that respond differentially to the different phase advances of the beat caused by different chirp stimuli, rather than to the chirp stimulus waveform itself. As such, our results have important implications for understanding how downstream brain areas decode information transmitted by heterogeneous neural populations about complex natural stimuli.

Heterogeneities in midbrain neuronal populations and implications for population coding

Our results are the first to investigate the effects of heterogeneities within TS neurons on population coding of natural electrocommunication stimuli. Specifically, they show that the neurons that respond most selectively to chirp stimuli (i.e., cr neurons) are actually among the least useful at being able to discriminate between different chirps, with performance barely above that of nonresponding neurons. Rather, it is the activities of neurons that respond to the beat and perturbations of the beat (i.e., the phase advance) by the chirp that make the greatest contribution toward discriminability. Similar to cr neurons, nr neurons also did not contribute to the discrimination performance. The existence of such nr neurons is, however, expected given that previous studies have shown that a significant subpopulation of TS neurons respond selectively to a given stimulus category. For example, some TS neurons respond selectively to moving objects, or envelopes, or chirps (Chacron et al., 2009; Chacron and Fortune, 2010; Khosravi-Hashemi et al., 2011; Vonderschen and Chacron, 2011; McGillivray et al., 2012; Sproule et al., 2015). In contrast, other TS neurons respond more broadly to different stimulus categories in a manner that is reminiscent of that displayed by ELL neurons (Vonderschen and Chacron, 2011; Sproule et al., 2015). The identified br and bcr neurons in the current study most likely correspond to “ELL-like” neurons, and our results show that it is these neurons that make the greatest contribution to discrimination performance. Importantly, neurons that respond selectively and nonselectively to sensory input were found throughout all layers of TS and can even coexist within the same layer (Sproule et al., 2015). As such, it is expected that heterogeneous neural responses similar to those reported here will be observed not only when recording across layers but also within a given layer. Further studies are needed to test this prediction.

We note that our results showing that cr neurons are the least useful to discriminate between different chirp waveforms in no way implies that these neurons do not have a function. Rather, because of their invariant responses to chirps, such neurons are most reliable at reporting the occurrence of a chirp rather than its detailed characteristics (i.e., feature detection; Vonderschen and Chacron, 2011; Aumentado-Armstrong et al., 2015; Metzen et al., 2016).

While the fact that we found that a few neurons contributed the most toward improving discrimination performance is similar to what has been seen in other systems when considering sparse coding of natural stimuli (Mizrahi et al., 2014; Yoshida and Ohki, 2020), there are important differences. This is because studies in other systems have shown that the best-performing neurons were most often those that best responded to the stimuli (Mizrahi et al., 2014; Yoshida and Ohki, 2020). In contrast, our results show that the neurons that are most useful toward discrimination are not those that best responded to the chirp stimuli.

Optimized decoding by weighted summed activities

Our results have shown that taking an unequally weighted sum of neuronal activities provided much better discriminability of chirp waveforms than an equally weighted sum. Such “combinatorial codes” can recover much more information about the stimulus and are thus advantageous (Seung and Sompolinsky, 1993; Sanger, 1996; Abbott and Dayan, 1999; Reich et al., 2001; Osborne et al., 2008; Liu et al., 2013; Pitkow et al., 2015). Because of this, together with the fact that TS neurons display large heterogeneities in their responses, it is not surprising that an unequally weighted sum performs better than an equally weighted sum. What was more surprising was how improved performance was achieved. Indeed, we found large overlap between the distribution of weights for all cell classes, indicating that the optimized weights for combinatorial code are obtained nontrivially.

On the one hand, combinatorial codes are physiologically realistic as the weights assigned to each neuron could, for example, represent the strength of synaptic connections to a downstream neuron. On the other hand, as one must then keep track of the identity of individual neurons, it is difficult to conceive how the brain would implement them. One possibility is that the weights should be proportional to the reliability of each individual neuron, which then does not require explicit knowledge of neuron identity and does not lead to information loss (Sharpee and Berkowitz, 2019). Our results suggest that another possibility is that, because there exist multiple solutions that give rise to a given performance (i.e., a degeneracy of solutions), it should theoretically be easier to find one such solution. Degeneracy is also expected to provide robustness to combinatorial codes, as seen for homeostasis (Turrigiano, 2011). This has, to our knowledge, not been explicitly demonstrated before.

Another important issue pertains to how a sensory system would actually learn the weights that allow for the best discrimination between different waveforms. It is likely that such learning would occur during development as the animal is exposed to various stimuli during interactions with conspecifics and heterospecifics. Studies performed in songbirds have shown that specific learning rules can optimize information transmission (Jeanne et al., 2013), and we hypothesize that similar learning rules would lead to decoding that maximizes performance. It is likely that learning requires the forebrain, which has recently been the focus of much investigation (Giassi et al., 2012a,b,c; Trinh et al., 2016; Wallach et al., 2018; Fotowat et al., 2019).

Independence of signal and noise correlations in TS neurons

Our results show that signal and noise correlations were independent of one another in midbrain electrosensory neurons. It is important to note that the correlation structure observed in TS strongly differs from that seen for ELL neurons for which there is a positive relationship between signal and noise correlations (Hofmann and Chacron, 2018), which resembles that seen in other systems (Averbeck and Lee, 2006; Liu et al., 2013). Since correlation structures in both ELL and TS neurons were obtained for stimuli that had similar contrasts, the observed differences between the correlation structures in TS and ELL are unlikely to be because of the fact that all the stimuli used in this study had similar contrasts. Rather, it should be noted that the correlation structures seen for ELL neurons and in other systems were obtained for artificial stimuli. As such, it is conceivable that the independence of signal and noise correlations seen for midbrain neurons in response to natural electrocommunication stimuli is a signature of optimized coding at the population level based on an adaptation to natural stimulus statistics. In particular, we hypothesize that such a correlation structure enables a combinatorial code for which any detrimental effects of noise correlations can be eliminated by suitably choosing weights without compromising signal quality. Further studies are needed to test these predictions.

We further hypothesize that the independence of noise correlations on recording distance is because of horizontal (i.e., within layer) and vertical (i.e., across layers) connections within TS (Carr et al., 1981; Carr and Maler, 1985) that are activated under stimulation. This is because such long-range connections would have a “normalizing” effect rather than making noise correlations occur because of local connections between neurons. Alternatively, such correlations could also be because of descending projections from the forebrain (Giassi et al., 2012a,b,c). It is well known that noise correlations are strongly dependent on inputs received by neural populations, such as the relative balance between excitation and inhibition (Doiron et al., 2016). Further studies are needed to understand the origins of noise correlations within the TS.

Discrimination of chirp waveforms: implications for behavior

Our results provide an answer to the ongoing debate as to whether different chirp stimulus waveforms can be discriminated from another by ELL neurons. Indeed, on the one hand, it has been argued that, based on the responses of ELL neurons, chirps could not be discriminated from one another (Marsat et al., 2009; Allen and Marsat, 2018). However, this analysis relied on simple summation of neuronal activities and was furthermore based on nonsimultaneous recordings that were later combined, which ignores the effects of noise correlations. We hypothesize instead that considering an unequally weighted sum of ELL neuron activities will reveal much better discrimination performance. This is because the data-processing inequality states that information can only be retained or lost, but never recovered (Cover and Thomas, 1991); our results imply that the activities of ELL neuronal populations, which provide afferent input to TS neurons, can be used to reliably discriminate between different chirp stimulus waveforms. Further, we hypothesize that ELL pyramidal neurons will display noise correlations under chirp stimulation. This is because noise correlations were seen in response to other stimuli (Chacron and Bastian, 2008) and the fact that ELL pyramidal cells display correlations between their activities in the absence of stimulation (Hofmann and Chacron, 2017).

It is important to note here that, while our results demonstrate that midbrain neuronal populations transmit information that can reliably be used by downstream brain areas to discriminate between different stimulus waveforms, they do not demonstrate that the organism actually takes advantage of this. This is because information is only useful to an organism if it is actually decoded. Previous studies have demonstrated that weakly electric fish display echo responses to chirp stimuli (Hupé and Lewis, 2008; Gama Salgado and Zupanc, 2011). These consist of a fish “responding” to the chirp of the other fish with a chirp of its own, which consists of modulations of its own EOD. Previous studies have shown that weakly electric fish displayed similar echo responses when chirp attributes such as beat phase as well as amplitude and duration were varied (Metzen et al., 2016, 2020). While this suggests that the activities of invariant TS neurons are decoded downstream, these results do not demonstrate that weakly electric fish cannot distinguish between different chirp stimulus waveforms. Importantly, other behavioral assays, such as habituation with a given chirp waveform and a test with a different chirp waveform (Allen and Marsat, 2018) or a two-alternative forced-choice task (Graff et al., 2004), show that weakly electric fish can distinguish between different stimuli but have not been used to specifically test whether animals can distinguish between chirp stimulus waveforms with different attributes (e.g., amplitude). Further studies investigating how the activities of TS neurons are decoded in downstream brain areas as well as using different behavioral assays are thus needed to test whether weakly electric fish can indeed discriminate between different chirp waveforms.

Implications for other systems

Our results provide several new insights that we expect will be applicable to other systems. This is because of known anatomic and physiological similarities between the electrosensory system and sensory modalities in mammals (e.g., vision, audition, vestibular; Clarke et al., 2015). Indeed, as mentioned above, our results show that it is not necessarily the neurons that respond most selectively to a given sensory input that are best at discriminating between different stimulus waveforms. This has important implications for object–background segregation (Olveczky et al., 2003), which must be performed by all modalities to some extent.

While it is now widely agreed that the effects of correlations on information transmission ultimately depend on how neuronal activities are integrated by downstream brain areas (Cohen and Kohn, 2011; Kohn et al., 2016). To this end, studies have used various decoders to predict the effects of correlations. In particular, linear decoders have mostly been used because one can find the best solution analytically (Seung and Sompolinsky, 1993; Zohary et al., 1994; Sanger, 1996; Abbott and Dayan, 1999; Liu et al., 2013; Pitkow et al., 2015). It is, however, important to note that nonlinear decoders can, in theory, extract much more information than linear decoders (Shamir and Sompolinsky, 2004). This is in part because nonlinear decoders can take into account information that is carried by precise spike timing. Temporal codes have been observed across systems and species (Bair and Koch, 1996; Borst and Theunissen, 1999; Johansson and Birznieks, 2004; Uzzell and Chichilnisky, 2004; Butts et al., 2007; Mackevicius et al., 2012; Harvey et al., 2013; Zuo et al., 2015; Jamali et al., 2016, 2019). In particular, our results showing that some TS neurons perform much better at stimulus discrimination than others resemble recent results obtained in the visual cortex where it was shown that a few neurons performed best at image reconstruction (Yoshida and Ohki, 2020). We further note that evolution algorithms have been used extensively in neural networks. Indeed, such algorithms have been used to optimize the architecture of artificial neural networks toward optimizing performance (Angeline et al., 1994; Ding et al., 2013). Our methodology of using an evolution algorithm to find the weights that optimize discrimination performance can thus be used in other systems where it is believed that spike timing carries important information.