Abstract
The building of an effective wastewater-based epidemiological model that can translate SARS-CoV-2 concentrations in wastewater to the prevalence of virus shedders within a community is a significant challenge for wastewater surveillance. The objectives of this study were to investigate the association between SARS-CoV-2 wastewater concentrations and the COVID-19 cases at the community-level and to assess how SARS-CoV-2 wastewater concentrations should be integrated into a wastewater-based epidemiological statistical model that can provide reliable forecasts for the number of COVID-19 infections and the evolution over time as well. Weekly variations on the SARS-CoV-2 wastewater concentrations and COVID-19 cases from April 29, 2020 through February 17, 2021 were obtained in Borough of Indiana, PA. Vector autoregression (VAR) model with different data forms were fitted on this data from April 29, 2020 through January 27, 2021, and the performance in three weeks ahead forecasting (February 3, 10, and 17) were compared with measures of Mean Absolute Error (MAE) and Mean Absolute Percentage Error (MAPE). A stationary block bootstrapping VAR method was also presented to reduce the variability in the forecasting values. Our results demonstrate that VAR(1) estimated with the logged data has the best interpretation of the data, but a VAR(1) estimated with the original data has a stronger forecasting ability. The forecast accuracy, measured by MAPE, for 1 week, 2 weeks, and 3 weeks in the future can be as low as 11.85%, 8.97% and 21.57%. The forecasting performance of the model on a short time span is unfortunately not very impressive. Also, a single increase in the SARS-CoV-2 concentration can impact the COVID-19 cases in an inverted-U shape pattern with the maximum impact occur in the third week after. The flexibility of this approach and easy-to-follow explanations are suitable for many different locations where the wastewater surveillance system has been implemented.
Keywords: COVID-19, SARS-CoV-2, Community wastewater surveillance, Forecasting
Graphical abstract
1. Introduction
As the COVID-19 pandemic continues, clinical diagnostic testing for COVID-19 on individual levels does not by itself provide a holistic indicator of community health risk. One significant concern with COVID-19 is that most cases in the U.S. are often asymptomatic and presymptomatic, allowing infected individuals to spread the virus without knowing that they are carriers (Moghadas et al., 2020). Moreover, a considerable percent of patients recovered from COVID-19 could still carry and shed virus (Landi et al., 2021). This implies that to monitor the current state and spread of the epidemic, other surveillance tests should be used in conjunction with the clinical testing data. Among the common surveillance strategies, wastewater-based epidemiology (WBE) to monitor for the SARS-CoV-2 virus in wastewater has demonstrated to be an effective technology for public health surveillance (U.S. CDC). As more and more municipalities, laboratories, and universities have taken the efforts to implement systematic wastewater surveillance in the U.S., crucial areas were also identified requiring additional research to further strengthen this approach and take full advantage of its potential for public health actions (Kitajima et al., 2020; Shakil et al., 2020).
Of those challenges, how the data generated from wastewater surveillance should be analyzed (Graham et al., 2021) and be used to build a feasible and reliable wastewater-based epidemiological model that can translate SARS-CoV-2 concentrations in wastewater to the prevalence of virus shedders within a community is an urgent need. Currently, descriptive and graphical analyses, correlation analysis (Duvallet et al., 2021), and linear regression analysis (U.S. CDC; Vallejo et al., 2020) are the major tools in the public health interpretation and of wastewater surveillance data. The descriptive analysis and visualizations provide a summary of the sample studied, but the findings are limited to empirical descriptions and interpretations of the epidemic phenomena (Duvallet et al., 2021). In addition, the Spearman's rank correlation test and the regression analysis have limitations, i.e. they are primarily designed for independent data with linear correlations. The wastewater-based epidemiology data being analyzed are in the context of time series data, i.e., dependent data, and may not be linearly correlated either. Thus, the use of those methods may produce misleading inferences.
The fact that the majority of the current studies applied only basic and simple statistical analysis is because the time span of the available wastewater surveillance data is insufficient for robust time series analysis. With the data that constructed in this work, it can be seen that multivariate time series models are applicable to address the non-linearity, endogeneity, and especially the lagging issues (Peccia et al., 2020) that exist in wastewater-based epidemiology data. Therefore, the present work seeks to use vector autoregression (VAR) combined with bootstrapping inferences to build a wastewater-based epidemiological statistical model for clarifying the structure of wastewater surveillance data as well as for forecasting the COVID-19 evolution over time at the community-level. The flexibility of this approach and easy-to-follow explanations are suitable for many different locations where the wastewater surveillance system has been implemented.
2. Methods
2.1. Study populations
Our major data come from the Borough of Indiana Wastewater Treatment Plant (WWTP), which is located within Center Township, Pennsylvania. This plant services a population of approximately 30,000 people, which includes the Borough of Indiana, Indiana University of Pennsylvania (IUP), and the Township of White as shown in Fig. 1 . The Wastewater treatment plant is an activated sludge, secondary treatment facility with a hydraulic design capacity of 8.2 MGD, and an organic capacity of 10,000 pounds per day. The service area is almost entirely comprised of residential units and contains the only hospital within the County.
Fig. 1.
15,701 and 15,705 (white area in the center) Zip Code Postal Districts. Please note, 7.55% of 15,701 Zip District is not sewered.
To validate our data analysis, modeling, and forecasting, data from the Green Bay Metropolitan Sewerage District (MSD) that located in Wisconsin and Salt Lake City Water Reclamation Facility (WRF) that is in Utah are investigated. The Green Bay MSD currently serves an estimated of 189,000 people, while the Salt Lake City WRF serves 209,645 people.
2.2. Wastewater sampling in Indiana WWTP
Since April 2020, Indiana Borough has been partnering with Biobot Analytics, Inc., an MIT-based startup that analyzes wastewater samples for SARS-CoV-2, the virus responsible for COVID-19. Weekly flow proportional samples were collected beginning on April 8th, 2020 and continue today. Each sample is collected over a 24-h period every Thursday at approximately 7:00 AM from a refrigerated Isco sampler located at the headworks of the facility. The sample is then poured into three 50 ml plastic sample containers and shipped overnight to Biobot's analytical lab in Cambridge, Massachusetts. An insulated envelope and ice pack are used to maintain the sample's temperature at or below 4 degrees C. The sample's metadata is collected via online form, which contains the location, date, time, and flow rate on the sampling day, as well as sample type, and the amount of any precipitation events.
2.3. Lab analysis and data processing
Lab analysis and data processing for SARS-CoV-2 RNA are done by Biobot Analytics, Inc. (Cambridge, MA). Their protocol for detecting SARS-CoV-2 in sewage have been adapted from the CDC protocol, which includes steps to filter, concentrate, and test for the virus genetic material using the Polymerase Chain Reaction (PCR) procedure according to Wu et al. (2021). PCR amplifies the signal so it can be detected and is the same type of analysis that is used to test for infection in humans. Quantification of the SARS-CoV-2 virus genetic material present in the water samples are given by the raw viral copies per liter of sewage and normalized concentrations. The normalized concentrations, denoted as viral copies, are used in this study.
Local COVID-19 case data were obtained from the within the Borough of Indiana by zip code. Cases were reported by the previous date of sample collection, i.e. every Wednesday. Weekly confirmed cases were calculated by subtracting the cumulative confirmed cases between Wednesdays. Finally, wastewater data and epidemiology data were combined to make the time series, see Table 1 , for modeling and forecasting (Data used in this work as well as the updated data are presented in an online web App, which can be viewed at https://ytcao.shinyapps.io/wwapp2/).
Table 1.
Part of the wastewater-based epidemiology data from Indiana Borough WWTP.
| Time | Ave daily flow (MGD) | Influent BOD (MG/L) | COVID-19 viral copies (X1000) | Weekly clinical change (15701 and 15705) |
|---|---|---|---|---|
| 4/29/2020 | 6.09 | 59 | 0.1 | 21 |
| 5/6/2020 | 8.55 | 114 | 0 | 1 |
| 5/13/2020 | 3.7 | 137 | 0 | 1 |
| ⁝ | ⁝ | ⁝ | ⁝ | ⁝ |
| 2/3/2021 | 3.47 | 169 | 180.80 | 17 |
| 2/10/2021 | 3.26 | 207 | 397.27 | 37 |
| 2/17/2021 | 5.23 | 83.0 | 159.75 | 31 |
Note: There are two missing values in this data set, which occurred on November 4, 2020 and January 6, 2021.
Data from Green Bay MSD and Salt lake City (WRF) are available from https://www.dhs.wisconsin.gov/covid-19/wastewater.htm and https://deq.utah.gov/water-quality/sars-cov-2-sewage-monitoring, respectively.
2.4. Statistical analysis
In the conducted study, based on the characteristic of each time series with some correlation structure between each other, Vector Autoregression (VAR) method is applied. VAR, at its core, is basically an extension of univariate autoregressive (AR) model. Since the seminal work of (Sims, 1980), different kinds of VAR models have increased their presence and importance within the field of economics and econometric analysis. It has been found that these kinds of simple models, with a small number of variables and parameters, can seriously compete in terms of their forecasting capabilities with the large macroeconomic models that have hundreds of variables and parameters (Alvarez-De-Toledo et al., 2008).
Prior to VAR model was completely formed eventually, a model selection procedure should be taken place by evaluating its lag value p. In the conducted study, in order to assess the optimal lag of the COVID-19 case forecast model, it required applying Aikake's Information Criterion (AIC) calculation for some k independent variables where the AIC value is generally defined using the following mathematical equation.
| (1) |
where with . In which y i is the observed value at the ith-time, k is the number of parameters in the model, y r is the mean of the process, and n is number of observations. In this case, it can be stated that a better lag value p is achieved at a smaller AIC value.
After accomplishing to determine the (p) lag value with AIC, the VAR model as a combination of the weekly change in COVID-19 cases (WC) and SARS-CoV-2 viral copies (VC) on the log scale can be written in the form of a matrix equation as follows:
| (2) |
or, more compactly,
| (3) |
In which y WC, t is the COVID-19 cases at time t; y VC, t is the SASR-CoV-2 viral copies at time t. Meanwhile, c is a constant indicating the intercept; ϵ t′s are the error terms and ϵ t~N(0, Σ); and p is the lag length. In this case, the model parameter a's can be estimated by using Ordinary Least Square (OLS) method, i.e. by minimizing the value of squared error (minimizing ϵ 2 values).
Since all variables in a VAR model depend on each other, individual coefficient estimates only provide limited information on the reaction of the system to one shock. To get a better picture of the model's dynamic behavior, impulse responses (IR) are used. The departure point of every impulse response function for a linear VAR model is its moving average (MA) representation, which is also the forecast error impulse response (FEIR) function. Mathematically, the FEIR Φi for the ith period after the shock is obtained by
| (4) |
with Φi = I k and Aj = 0 for j > p where k is the number of endogenous variables and p is the lag order of the VAR model.
Once the best model was obtained and able to be used for forecasting, the forecast accuracy level of the model can also be evaluated by Mean Absolute Error (MAE) and/or Mean Absolute Percentage Error (MAPE), which are given by the following mathematical equations, respectively
| (5) |
| (6) |
where is the forecast value at the h-step ahead, y T+h is the actual value at the h-step ahead, and H is length of time requires forecast.
If one fits a VAR model but the model cannot be able to fully capture the structure and/or behavior exits in the series in a satisfactory way and thus leads to poor forecast, then bootstrapped time series can be applied to improve the forecast accuracy. Bootstrap aggregating (bagging) prediction models is a general method for fitting multiple versions of a prediction model and then combining (or ensembling) them into an aggregated prediction (Breiman, 1996). Bagging is a straight-forward algorithm in which b bootstrap copies of the original training data are created, the regression or classification algorithm is applied to each bootstrap sample and, in the regression context, new predictions are made by averaging the predictions together from the individual optimal algorithms. There are several bootstrapping methods appeared in the literature, the stationary block bootstrap scheme as outlined in (Politis and Romano, 1994) was applied to investigate the performance of bagging VAR on our data in this study. A non-parametric stationary block bootstrapping algorithm is developed and demonstrated in Table 2 . All the visualizations and statistical analysis were performed in R 4.0.3 (R Development Core Team). A web App is also developed to go along with this paper and can be viewed at https://ytcao.shinyapps.io/wwapp2/.
Table 2.
The non-parametric stationary block bootstrapping algorithm with a VAR model.
| Step 0 | Estimate a VAR model of order p using the original data and obtain the point forecast(s). |
| Step 1 | Draw random samples with the stationary resampling procedure from the original data with the same size, estimate the VAR model of order p and obtain the point forecast(s). |
| Step 2 | Repeat step 1 for b times. |
| Step 3 | Combine the b + 1 forecast(s). |
| Step 4 | Calculate the point forecast(s) using mean if the bootstrap distribution is symmetric and median if the bootstrap distribution is skewed. Construct the 95% CI by taking the 2.5th percentile and 97.5th percentile together. |
3. Results
3.1. Variables exploration and transformation
In the Indiana Borough (IB) data, influent wastewater characteristics such as average daily flow in MGD and biochemical oxygen demand (BOD) were also obtained. However, no correlation was detected between the two and SARS-CoV-2 concentrations or COVID-19 cases. This finding was also confirmed in (Vallejo et al., 2020). Therefore, influent wastewater characteristics will not be analyzed in what follows. Descriptive statistics of SARS-CoV-2 concentrations and COVID-19 cases for the three studied catchment areas are summarized in Table 3 . Fig. 2 (top panel) illustrates the distributions of the weekly COVID-19 cases and SARS-CoV-2 Concentrations in the IB data. It can be seen that the distribution of SARS-CoV-2 Concentrations is right skewed, after logarithm transformation the distribution becomes less skewed but more regular. That is why most of the data analysis on wastewater data suggest to log transform this variable (U.S. CDC). Distribution of the weekly COVID-19 cases is more like uniform but with some spikes as expected. These spikes can make the data analysis more challenge and the forecasting less reliable. A logarithm transformation can make this variable a slightly more stable. Same conclusion can be drawn for the Salt Lake (SL) City and Green Bay (GB) data as all the mean values are greater than the median values in these data (Table 3).
Table 3.
Summary statistics of SARS-CoV-2 Concentrations and COVID-19 Cases for the three studied locations in the U.S.
| SARS-CoV-2 concentrations |
COVID-19 Cases |
|||
|---|---|---|---|---|
| Mean (sd) | Median (IQR) | Mean (sd) | Median (IQR) | |
| Indiana Borough | 318.37 (463.98) | 137.9 (458.72) | 45.5 (50) | 25.5 (61.25) |
| Salt Lake City | 116.8 (163.98) | 69 (141.8) | 231.68 (157.43) | 185.6 (238.55) |
| Green Bay | 14.043 (8.15) | 11.717 (11.636) | 55.71 (21.45) | 54.12 (37.97) |
Notes: (1) For Indiana Borough data: the timespan is 4/29/2020 through 1/27/2021 (n = 38, due to 2 missing values); the unit for SARS-CoV-2 Concentrations is thousand genome copies per liter of sewage; the unit for COVID-19 cases is the weekly confirmed cases. (2) For Salt Lake City data: the timespan is 5/7/2020 through 1/19/2021 (n = 38); the unit for SARS-CoV-2 Concentrations is million gene copies per liter of sewage; the unit for COVID-19 cases is the weekly confirmed cases per 100,000 people. (3) For Green Bay data: the timespan is 8/31/2020 through 1/13/2021 (n = 20); the unit for SARS-CoV-2 Concentrations is million gene copies per person; the unit for COVID-19 cases is the 7-day rolling average per 100, 000 people.
Fig. 2.
Distributions of the COVID-19 cases, logged COVID-19 cases, SARS-CoV-2 concentrations, and logged SARS-CoV-2 concentrations in Indiana Borough data.
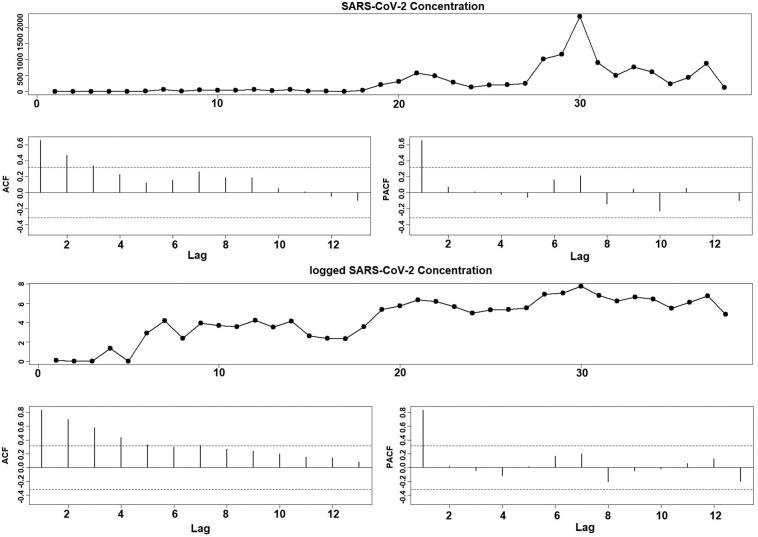
Fig. 3, Fig. A1, Fig. A2 show the time series plot of the SARS-CoV-2 concentrations in the three studied catchment areas along with their autocorrelation characteristics. It can be observed that both the SARS-CoV-2 concentration and logged SARS-CoV-2 concentration exhibit an AR(1) process property (ACF plot shows an exponential decay and PACF shows a cutoff after lag 1) in IB and SL City with the exception that the (logged) SARS-CoV-2 concentration in GB shows a random walk property. This may be due to the short time span of this data set. Fig. 4, Fig. A3, Fig. A4 show the dependence pattern in the change of COVID-19 cases in the three areas. Again, they all demonstrate an AR(1) property regardless of the form and time span of the variables, i.e., whether it is the weekly change cases, the logged weekly change cases, the 7-day rolling average cases, or the logged 7-day rolling average cases. Phillips-Perron Unit Root Test shows that the logged change in COVID-19 cases from IB is a stationary process (p < 0.01), but all the other logged variables are non-stationary. The most common feature that can be found from these figures is that the logged variables are more stable, i.e., showing less variability and spikes than that in their raw variables. Fig. 5, Fig. A5, Fig. A6 demonstrate the correlation between the weekly change in COVID-19 cases and SARS-CoV-2 concentrations in both the original form and the logged form. It is clear that an increase in SARS-CoV-2 concentration has been consistently associated with an increased number of COVID-19 infections. Furthermore, the logarithm transformation on both variables can significantly stabilize their relationship, mainly because they are both non-negative variables and are skewed to the right.
Fig. 3.
Time series plot of SARS-CoV-2 and logged SARS-CoV-2 concentration and their ACF and PACF plots for Indiana Borough data.
Fig. 4.
Time series plot of COVID-19 cases and logged COVID-19 cases concentration and their ACF and PACF plots for Indiana Borough data.
Fig. 5.
The correlation between weekly change in COVID-19 cases and SARS-CoV-2 concentration; and logged weekly change in COVID-19 cases and logged SARS-CoV-2 concentration in IB data.
Taken together, the findings in Fig. 3, Fig. 4, Fig. 5 provide a consistent of evidence that a VAR system can be used to model the association exits in the data on either the raw level or the logged level for interpretation and forecasting as well.
3.2. Model building and forecasting
To build a reliable VAR system, performance of multiple models on fitting the data (measured with AIC) and forecasting future values (measured with MAE and MAPE) were investigated in this section. Specifically, for each of the IB, SL, and GB data, a VAR(1) model was fitted with both the original data and the logged data, i.e. VAR(1) log-log. The results are summarized in Table 4 .
Table 4.
Comparison of the model fitting and forecasting performance of a VAR(1) model in the original form and log-log form on the three data sets.
| IB data |
SL data |
GB data |
||||
|---|---|---|---|---|---|---|
| Measures | VAR(1) | VAR(1) log-log |
VAR(1) | VAR(1) log-log |
VAR(1) | VAR(1) log-log |
| AIC | 869.42 | 190.54 | 878.31 | 125.5 | 273.3 | 21.63 |
| Actual.1 | 17 | 17 | 277.6 | 277.6 | 32.35 | 32.35 |
| Forecast.1 95% CI |
27 (−27, 80) |
25 (4, 33) |
310.5 (178.7, 442.4) |
349.3 (202.4, 595.9) |
42.6 (22.4, 62.8) |
47 (30.9, 71.5) |
| Actual.2 | 37 | 37 | 264.3 | 264.3 | 27.66 | 27.66 |
| Forecast.2 95% CI |
30 (−41, 100) |
26 (2, 214) |
280.4 (100.6, 460.1) |
340.4 (162.4, 706.3) |
49.22 (20.7, 77.8) |
51.4 (30, 87.4) |
| Actual.3 | 31 | 31 | 180 | 180 | 17.76 | 17.76 |
| Forecast.3 95% CI |
32 (−49, 113) |
27 (2, 286) |
264.2 (52.2, 476.2) |
333.6 (139.8, 796.3) |
51 (19.1, 82.8) |
53.5 (29.7, 95.6) |
| MAE.1 | 10 | 8 | 32.9 | 71.7 | 10.25 | 14.65 |
| MAPE.1 | 58.8% | 47.06% | 11.85% | 25.83% | 31.65% | 45.29% |
| MAE.2 | 8.5 | 9.5 | 24.5 | 73.9 | 15.9 | 19.19 |
| MAPE.2 | 38.85% | 38.4% | 8.97% | 27.31% | 54.8% | 65.56% |
| MAE.3 | 6 | 5.67 | 44.4 | 100.47 | 21.68 | 24.71 |
| MAPE.3 | 27% | 29.9% | 21.57% | 69.97% | 98.87% | 110.8% |
Notes: (1) VAR(1) means the model was estimated with the original data, while VAR(1) log-log means the model was estimated using the logged data. (2) Actual.1, Actual.2, and Actual.3 denote the actual values in the first, second, and third week after the model fitting data. For IB, these three weeks are 2/3/2021, 2/10/2021, and 2/17/2021; for SL these three weeks are 1/25/2021, 2/1/2021, and 2/8/2021; for GB these three weeks are 1/20/2021, 1/27/2021, and 2/3/2021. (3) Forecast.1, Forecast.2, and Forecast.3 are the model forecast values for the first, second, and third week ahead. (4) MAE.1, MAE.2, and MAE.3 are the MAE measures for the forecasting accuracy for 1 week, 2 weeks and 3 weeks in the future, while MAPE.1, MAPE.2, and MAPE.3 are the MAPE measures for the forecasting accuracy for 1 week, 2 weeks and 3 weeks in the future.
The overall conclusion that can be drawn from this comparison is that the log-log VAR(1) model fits the data better as a smaller AIC value is achieved in each of the three cases, but the VAR(1) model estimated with the original data has a much stronger prediction power. The best forecasting performance of VAR(1) comes from the SL data, as can be seen that the MAPE for 1 week forecast is 11.85% and that for 2 weeks is only 8.97%, both are close to the 10% range. According to Shumway and Stoffer (2017), MAPE close to 10% indicating a good forecasting performance. The worst forecasting performance comes from the GB data, even though the MAPE for the first week is 31.65%, which can be considered reasonable. The low performance on the GB data is mainly due to the short time span as the length is only 20 weeks. The forecasting ability for the VAR(1) and log-log VAR(1) are very close to each other based on the IB data. The log-log VAR(1) models forecasts slightly better for the first week, but the VAR(1) model forecasts better for both week 2 and week 3 in the future. Thus, it can be concluded that the VAR(1) outperforms the log-log VAR(1) in fitting the data, but not in forecasting future COVID-19 cases. Moreover, one can see that the 95% confidence intervals generated from the VAR(1) model for the IB data includes negative values, which is because there are some zero (0) cases in the data. This problem can be overcome by using the Bootstrap methods.
The main purpose of impulse response analysis is to describe the evolution of a VAR model's variables in reaction to a shock in one or more variables. This feature allows to trace the transmission of a single shock within an otherwise noisy system of equations and, thus, makes them very useful tools in understanding the dynamic relations. As the goal is to forecast the COVID-19 cases from the SARS-CoV-2 concentration in wastewater, Fig. 6 shows how a single shock in SARS-CoV-2 concentration impact the COVID-19 cases in the future based on the log-log VAR(1) model for IB data. It can be observed that an increase in the SARS-CoV-2 concentration in the current week implies a steadily increase in the COVID-19 cases in the following three weeks and with the maximum impact occur in the third week. Then the impact will go down and eventually disappear after 6 weeks in the future.
Fig. 6.
The orthogonal impulse response of logged weekly change in COVID-19 cases from the logged change in SARS-CoV-2 concentration with 95% bootstrap CI (b = 500).
3.3. Bootstrapping with VAR
To overcome the possible negative values in the statistical inference as well as to better quantify the uncertainty for using a single model for forecasting, bootstrapping results based upon the IB data were provided in this section. Displayed in Fig. 7 are the non-parametric bootstrapping distributions (b = 1000) for the first week, second week, and third week forecast respectively. Since all the distributions are skew to the right, median value of the distribution is used to obtain a robust point forecast (as marked by the dots in Fig. 7). Therefore, the point forecasts for week 1, week 2, and week 3 in the future are 31, 35, and 37, respectively. Taking together the 2.5th percentile and 97.5th percentile of the bootstrap results, one can construct the 95% prediction interval, which, in this case, are (6, 152), (10, 142), and (11,132), respectively. Again, the forecasts for week 2 and 3 are reasonable and are much better than that for week 1. In terms of the accuracy measures, MAE.1 = 14 (MAPE.1 = 82.35%), MAE.2 = 8 (MAPE.2 = 43.88%), and MAE.3 = 7.3 (MAPE.3 = 35.7%) were calculated.
Fig. 7.
The Bootstrap distributions for the first week, second week and third week forecasts. Results are from 1000 non-parametric stationary block bootstraps. The black dot denotes the median value in the distribution.
4. Discussion
Since the start of the ongoing COVID-19 pandemic, scientists have found that detecting SARS-CoV-2 RNA, the virus that causes the COVID-19 infection in sewage, can serve as an important indicator of COVID-19 spread within the community. Despite many successful “proof of concept” efforts that have been done so far; it is important to elevate the potential benefits of wastewater surveillance to the next level - delivering the results to better inform public health efforts, including using this information to better understand the spread of the epidemic in order to mitigate the risk of virus transmission. There are, however, two major obstacles (see NIH https://grants.nih.gov/grants/guide/rfa-files/RFA-OD-20-015.html) in this process: (1) how to enhance and standardize the methods to reduce the cost, time, and inaccuracies in detecting the SARS-CoV-2 concentration in wastewater, and (2) how to analyze the data collected and deliver the results to the public. The present work contributes to the existing literature on COVID-19 and wastewater surveillance by using the environmental and clinical data to build models that aim to understand the spread of the epidemic and mitigate the risk of virus transmission within a community.
Although the results demonstrate effectiveness and usability of the methodology presented in this work, several limitations should also be noted. There are two limitations to our model. First, the forecasting reliability of the model depends heavily on the length of time series. As it can be seen from the GB data (the sample size for modeling is only 21), the forecasting error can be as high as 100%. Thus, care must be taken when the length of the data is short in practice. Second, the basic VAR model can only be used to model regular (i.e., daily, weekly, monthly, etc.) data, but not the irregular data. However, it was noticed that in some areas wastewater was monitored multiple times and/or irregularly in each week (such as in some areas in Utah, SARS-CoV-2 concentration were measured irregularly every Sundays, Mondays, Wednesdays, or sometimes even on Thursdays). If this is the case, to benefit from as much as of the data collected, Mixed-Frequency VAR (Schorfheide and Song, 2015) or Bayesian Mixed Frequency VARs (Eraker et al., 2015) are recommended.
Another limitation to this work needs to be addressed is the accuracy of the data used. Two types of inaccuracy worth to be emphasized. The first one is that there is a discrepancy between the wastewater sample collection time and the COVID-19 cases report time. For example, in the IB data, wastewater sample were collected every Thursday at approximately 7:00 AM, but the COVID-19 cases used were reported on later Wednesday. The second discrepancy is between the wastewater catchment area (where the wastewater sample collected) and the corresponding ZIP code area (where the COVID-19 cases reported). Take the IB data as an example again, where the wastewater catchment area includes two ZIP code areas (15,701 and 15,705), but these two areas together just cover 92.45% of the population in the wastewater sewer shed. Therefore, more fitting and forecasting accuracy can be gained if the reliability of data collection procedure can be improved.
5. Conclusions
It has been widely recognized that there is a strong association between the SARS-CoV-2 concentration in the wastewater and the population-level of COVID-19 cases within a community, thus the former can be used to forecast the latter without even clinical testing data. Benefiting from the relatively abundant time series data available, this study has presented that a multivariate time series model, VAR, can be used to forecast the COVID-19 cases at a community level using SARS-CoV-2 concentration in the wastewater. Several important conclusions can be drawn from our data and analysis. First, if the goal is to understand the dynamic relationship between the COVID-19 cases and SARS-CoV-2 concentration in wastewater (Fig. 6), then the VAR(1) model should be estimated using the logged data. But, if the primary goal to is forecast the future trend and infection counts in the future, the model should be estimated with the original raw data. This conclusion is quite contrary to the current analysis recommendations (U.S. CDC). Second, for short time series, the forecast for the first week is more reliable than that for two or more weeks ahead; but when the time series is relative long, the forecasts for two to three weeks can be reliable. Finally, bootstrapping method can be used to further improve the quality of model estimation and forecasting.
CRediT authorship contribution statement
• Yongtao Cao: Conceptualization, Methodology, Data management and analysis, Software, and paper writing.
• Roland Francis: Sample collection, Data retrieve, and editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We thank Frederick Adkins, Hilliary Creely, Michelle Fryling, Timothy Moerland, Khatmeh Osseiran-Hanna, Deanne Snavely (Indiana University of Pennsylvania) and Michael Foote (Indiana Borough, PA) for study coordination, field research efforts, and analytic support. We also wish to express gratitude to the reviewers and editor-in-chief who reviewed this work and allowed us the opportunity to improve the paper.
Editor: Damia Barcelo
Appendix A.
Fig. A1.
Fig. A2.
Fig. A3.
Fig. A4.
Fig. A5.
Fig. A6.
References
- Alvarez-De-Toledo P., Marquez A.C., Nunez F., Usabiaga C. Introducing VAR and SVAR predictions in system dynamics models. Int. J. Simul. Process. Model. 2008;4(1):7–17. [Google Scholar]
- Breiman L. Bagging predictors. Springer Mach. Learn. 1996;24(2):123–140. doi: 10.1007/BF00058655. [DOI] [Google Scholar]
- Duvallet, Claire, Kyle McElroy, Noriko Endo, Max Imakaev, Róisín Floyd-O'Sullivan, Morgan M Powell, Samuel Mendola, Francis Cruz, Tamar Melman, Eric Alm, Timothy Erickson, MD Newsha Ghaeli, Peter Chai, Mariana Matus. 2021. Nationwide Trends in COVID-19 Cases and SARS-CoV-2 Wastewater Concentrations in the United States. preprints. [DOI] [PMC free article] [PubMed]
- Eraker, Bjørn, Ching Wai (Jeremy) Chiu, Andrew T. Foerster, Tae Bong Kim, Hernán D. Seoane, 2015. Bayesian mixed frequency VARs, J. Finan. Econ., Volume 13, Issue 3, Pages 698–721, doi: 10.1093/jjfinec/nbu027. [DOI]
- Graham K.E., Loeb S.K., Wolfe M.K., Catoe D., Sinnott-Armstrong N., Kim S., Yamahara K.M., Sassoubre L.M., Mendoza Grijalva L.M., Roldan-Hernandez L., Langenfeld K., Wigginton K.R., Boehm A.B. SARS-CoV-2 RNA in wastewater settled solids is associated with COVID-19 cases in a large urban sewershed. Environ. Sci. Technol. 2021;55(1):488–498. doi: 10.1021/acs.est.0c06191. [DOI] [PubMed] [Google Scholar]
- Kitajima, M., Ahmed, W., Bibby, K., Carducci, A., Gerba, C.P., Hamilton, K.A., Haramoto, E. and Rose, J.B., 2020. SARS-CoV-2 in wastewater: state of the knowledge and research needs. Sci. Total Environ., p.139076, doi: 10.1016/j.scitotenv.2020.139076. [DOI] [PMC free article] [PubMed]
- Landi F., Carfì A., Benvenuto F., Brandi V., Ciciarello F., Monaco M.R.L., Martone A.M., Napolitano C., Pagano F., Paglionico A., Petricca L. Predictive factors for a new positive nasopharyngeal swab among patients recovered from covid-19. Am. J. Prev. Med. 2021;60(1):13–19. doi: 10.1016/j.amepre.2020.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moghadas S.M., Fitzpatrick M.C., Sah P., Pandey A., Shoukat A., Singer B.H., Galvani A.P. The implications of silent transmission for the control of COVID-19 outbreaks. Proc. Natl. Acad. Sci. 2020;117(30):17513–17515. doi: 10.1073/pnas.2008373117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peccia J., Zulli A., Brackney D.E., Grubaugh N.D., Kaplan E.H., Casanovas-Massana A., Ko A.I., Malik A.A., Wang D., Wang M., Weinberger D.M. SARS-CoV-2 RNA concentrations in primary municipal sewage sludge as a leading indicator of COVID-19 outbreak dynamics. MedRxiv. 2020 doi: 10.1101/2020.05.19.20105999. [DOI] [Google Scholar]
- Politis D.N., Romano J.P. The stationary bootstrap. J. Am. Stat. Assoc. 1994;89(428):1303–1313. doi: 10.1080/01621459.1994.10476870. [DOI] [Google Scholar]
- Schorfheide F., Song D. Real-time forecasting with a mixed-frequency VAR. J. Bus. Econ. Stat. 2015;33(3):366–380. doi: 10.1080/07350015.2014.954707. [DOI] [Google Scholar]
- Shakil M.H., Munim Z.H., Tasnia M., Sarowar S. COVID-19 and the environment: a critical review and research agenda. Sci. Total Environ. 2020;745:141022. doi: 10.1016/j.scitotenv.2020.141022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shumway R.H., Stoffer D.S. 4th edition. Springer International Publishing; 2017. Time Series Analysis and Its Applications. [Google Scholar]
- Sims C.A. Macroeconomics and reality. Econometrica J. Econ. Soc. 1980:1–48. doi: 10.2307/1912017. [DOI] [Google Scholar]
- U.S. Centers for Disease Control and Prevention National Wastewater Surveillance System (NWSS) https://www.cdc.gov/coronavirus/2019-ncov/cases-updates/wastewater-surveillance.html
- Vallejo J.A., Rumbo-Feal S., Conde-Pérez K., López-Oriona Á., Tarrío J., Reif R., Ladra S., Rodiño-Janeiro B.K., Nasser M., Cid Á., Veiga M.C. Highly predictive regression model of active cases of COVID-19 in a population by screening wastewater viral load. MedRxiv. 2020 doi: 10.1101/2020.07.02.20144865. [DOI] [Google Scholar]
- Wu F., Xiao A., Zhang J., Moniz K., Endo N., Armas F., Bushman M., Chai P.R., Duvallet C., Erickson T.B., Foppe K., Ghaeli N., Gu X., Hanage W.P., Huang K.H., Lee W.L., Matus M., McElroy K.A., Rhode S.F., Wuertz S., Thompson J., Alm E.J. Wastewater surveillance of SARS-CoV-2 across 40 U.S. states. medRxiv [Preprint] 2021.03.10.21253235. 2021 doi: 10.1101/2021.03.10.21253235. PMID: 33758888; PMCID: PMC7987047. [DOI] [PMC free article] [PubMed] [Google Scholar]